Department of Computer Science, POSTECH, Pohang , Korea. (x 0 (t); y 0 (t)) 6= (0; 0) and N(t) is well dened on the
|
|
|
- Jayson Stokes
- 6 years ago
- Views:
Transcription
1 Comparing Oset Curve Approximation Methos Gershon er +, In-Kwon, an Myung-Soo Kim + Department of Computer Science, Technion, IIT, Haifa 32000, Israel Department of Computer Science, POSTECH, Pohang , Korea Oset curves have iverse engineering applications, which have consequently motivate extensive research concerning various oset techniques. Oset research in the early 980s focuse on approximation techniques to solve immeiate application problems in practice. This tren continue until 988, when chek [, 2] applie non-linear optimization techniques to the oset approximation problem. Since then, it has become quite icult to improve the state-of-the-art of oset approximation. Oset research in the 990s has been more theoretical. The founational work of Farouki an Ne [3] clarie the funamental iculty of exact oset computation. Farouki an Sakkalis [4] suggeste the Pythagorean Hoograph curves which allow simple rational representation of their exact oset curves. Although many useful plane curves such as conics o not belong to this class, the Pythagorean Hoograph curves may have much potential in practice, especially when they are use for oset approximation. In a recent paper [5] on oset curve approximation, the authors suggeste a new approach base on approximating the oset circle, instea of approximating the oset curve itself. To emonstrate the eectiveness of this approach, we have mae extensive comparisons with previous methos. To our surprise, the simple metho of ler an Hanson [6] outperforms all the other methos for osetting (piecewise) quaratic curves, even though its performance is not as goo for high egree curves. The experimental results have reveale other interesting facts, too. If these etails ha been reporte several years ago, we believe, oset approximation research might have evelope somewhat ierently. This paper is intene to ll in an important gap in the literature. Qualitative as well as quantitative comparisons are conucte employing a whole variety of contemporary oset approximation methos for freeform curves in the plane. The eciency of the oset approximation is measure in terms of the number of control points generate while the approximations are mae within a prescribe tolerance. Oset of Planar Curves Given a regular parametric curve, C(t) (x(t); y(t)), in the plane, its oset curve C (t) by a constant raius, is ene by: C (t) C(t) + N(t); () where N(t) is the unit normal vector of C(t): N(t) (y0 (t);?x 0 (t)) px 0 (t) 2 + y 0 (t) 2 : (2) The regularity conition of C(t) guarantees that (x 0 (t); y 0 (t)) 6 (0; 0) an N(t) is well ene on the curve C(t). Equation (2) has a square root term in the enominator. Therefore, even if the given curve C(t) is a polynomial curve, its oset is not a polynomial or rational curve, in general. This funamental eciency has motivate the evelopment of various polynomial an rational approximation techniques of C (t). While the oset to a polynomial or rational parametric curve must be approximate, it is somewhat counter-intuitive that a close cousin of the oset, the evolute, is inee always representable as a rational curve (see Siebar on Evolute). Most oset approximation techniques are base on an iterative process of tting an approximation curve, measuring the accuracy, an subiviing the problem into smaller problems if the approximation error is larger than the tolerance. This ivie an conquer approach exploits the subivision property of the base curve C(t). Henceforth, we assume C(t) is represente by a Bezier or NURBS curve. Traitionally, the oset approximation error has been measure only at nite sample points along C(t), computing i kc(t i )?C a(t i)k?. er an Cohen [7] propose a symbolic metho which computes the global error between square istances: (t) kc(t)? C a (t)k 2? 2 : (3) The error function (t) is obtaine by symbolically computing the ierence an inner prouct of Bezier or NURBS curves (see Siebar on Symbolic Computation an Reference [8]). Therefore, it can be represente as a Bezier or NURBS scalar function. As a scalar el, the largest coecient of (t) globally bouns the maximal possible error ue to the convex hull property of Bezier or NURBS formulation. In this article, we exploit the error functional (t) of Equation (3) to measure all the oset approximation errors. This provies not only a global boun for each metho, but also an equal basis for the comparison of ierent methos.
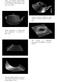
2 Evolute The evolute of C(t) is ene as: E(t) C(t) + N(t) (t) ; where (t) is the curvature of C(t) (x(t); y(t)): (t) x0 (t)y 00 (t)? x 00 (t)y 0 (t) (x 0 (t) 2 + y 0 (t) 2 ) 32 : That is, E(t) is a variable raius oset with oset raius (t) (t). Figure shows two examples of evolute curves. Quite surprisingly, E(t) is a rational curve, provie C(t) is a rational or polynomial curve: E(t) C(t) + N(t) (t) C(t) + C(t) + (y 0 (t);?x 0 (t)) (x 0 (t) 2 +y 0 (t) 2 ) 2 x 0 (t)y 00 (t)?x 00 (t)y 0 (t) (x 0 (t) 2 +y 0 (t) 2 ) 32 x 0 (t) 2 + y 0 (t) 2 x 0 (t)y 00 (t)? x 00 (t)y 0 (t) (y0 (t);?x 0 (t)): (a) C(t) 20 E(t) (b) E(t) C(t) In contrast to the oset computation in Equation (), there is no square root term in the representation of E(t). In Figure, the curves an their evolutes are both represente as B-spline curves. Figure : In (a), a B-spline curve, C(t), in light curve, is shown along with its evolute, E(t), in bol curve. In (b), the evolute E(t) for a cubic polynomial approximation of a circle, C(t), is shown. E(t) is scale up by a factor of 20. Qualitative Comparisons Control Polygon Base Methos Let C(t) be a B-spline curve with k control points of orer n an ene over a knot sequence ft i g ; 0 i < n + k. The i-th noe parameter value i of C(t) is ene as: i P i+n? ji+ t j ; (7) n? for 0 i < k. Hence, a noe parameter value is an average of n? consecutive knots in. Each control point, P i, of C(t), is associate with one noe, i. C( i ) is typically close to P i ; however, it is not the closest point of C(t) to P i, in general. b [9] translate each control point, P i, by N( i ), whereas ler an Hanson [6] translate each ege of the control polygon into the ege normal irection by a istance. Unfortunately, b [9] always uner-estimates the oset; i.e., (t) 0, for all t. (For the proof an relate issues, see Siebar on Uner an Over-Estimation.) ler an Hanson [6] o not uner-estimate the oset curve. In aition to computing the exact linear an circular oset curves, their metho outperforms all the other methos for the case of osetting (piecewise) quaratic curves. However, for osetting high egree curves, this simple metho has a similar performance to that of b [9]. uillart [0] solve the uner-estimating problem. The istance between P i an C( i ), an the curvature ( i ) of C(t) at i are taken into account. Numerical approximation is also taken to compute the closest point of C(t) to the control point P i, while using C( i ) as an initial solution. With all these enhancements, uillart [0] was able to oset the linear an circular segments exactly. er an Cohen [] took a ierent approach that exactly computes the osets of linear an circular elements. Using the values of (t) (in Equation (3)) at t 0 ; : : : ; n, the error in the neighborhoo of each control point, P i, is estimate an use to ajust the translational istance applie to P i. This perturbation base approach is an iterative metho that converges to the exact circular oset segment. For general curves, when the result of b [9] is use as an initial solution, the perturbation process typically reuces the oset approximation error of [9] by an orer of magnitue. In principle, this metho can be applie to any oset approximation metho that prouces piecewise polynomial curves. Most traitional techniques subivie C(t) at the mile of the parametric omain; however, a better caniate is the parameter of the location with the maximum error. Since (t) represents the exact 2
3 Symbolic Computation In this article, we have employe (t) (in Equation (3)) an m(t) (in Equation ()) to estimate the oset approximation error. Furthermore, we also nee to compute the composition of U(s(t)) (in Equation (0)). The symbolic computation of these equations involves the ierence, prouct, an sum of (piecewise) scalar polynomial or rational curves. Let C (t) P m i0 PiBi; (t) an C2(t) P n j0 PjBj;(t) be two (piecewise) polynomial regular parametric curves, in the Bezier or NURBS representations. The computation of C (t) C 2(t) can be accomplishe by elevating both C (t) an C 2(t) to a common function space. The orer of the common function space is equal to the maximal orer of C (t) an C 2(t). If either C (t) or C 2(t) is a B-spline curve, the common function space is ene by consiering both knot vectors an an preserving the lowest egree of continuity at each knot. Once the common function space is etermine, both C (t) an C 2(t) are elevate to this space via egree raising an renement. (See [8] for more etails as well as the extension to rationals.) The computation of C (t)c 2(t) is somewhat more involve. Here, we consier only the case of Bezier polynomial curves. (See [8] for the more general cases of piecewise polynomials an rationals.) The i-th Bernstein Bezier basis function of egree k is ene by: B k i (t) k i t i (? t) k?i : (4) The prouct of two Bernstein Bezier basis functions is: Bi k (t)bj(t) l k t i (? t) k?i l t j (? t) l?j i j k l t i+j (? t) k+l?i?j i j Therefore, we have: C (t)c 2(t)? k i? k+l i+j? l j mx i0 mx Bi+j k+l (t): (5) i0 j0 mx P ib m i (t) i0 j0 m+n X k0 j0 P jb n j (t) P ip jb m i (t)b n j (t)? m? n i j P ip j? m+n i+j B m+n i+j (t) Q kb m+n k (t); (6) ( m+n i+j ) where Q k accumulates all the combinatorial terms ( m i )( n P ip j j), for k i + j. Hence, C(t)C2(t) is represente as a Bezier polynomial curve of egree m + n. square error function, one can n the parameter location of the maximal error an subivie C(t) there. Alternatively, instea of subiviing C(t), one can insert new knots into C(t) at the parameter locations with error larger than the allowe tolerance. er an Cohen [7] took this renement approach. Interpolation Methos ss [2] use a cubic Hermite curve to approximate the oset curve. The cubic Hermite curve is etermine by interpolating the position an velocity of the exact oset curve at both enpoints. The numerical approximation proceure of ss [2] is quite unstable when the oset curve becomes almost at. Therefore, instea of using the original algorithm [2], we compute the rst erivative of the oset curve base on the following simple close form equation (see also [3]): C 0 (t) ( + (t))c 0 (t); (8) where (t) is the curvature of C(t). chek [] suggeste a least squares solution for the etermination of C 0 (t) at the curve enpoints. That is, at each enpoint of C (t), the irection of C 0 (t) is maintaine to be parallel to C0 (t); however, instea of using Equation (8), their lengths are etermine so that the cubic Hermite curve best ts C (t) in the least squares sense. For computational eciency, only nite samples of C (t) are use in the optimization. chek an Wissel [2] use a general non-linear optimization technique to approximate a high egree spline curve with low egree spline curves. They applie the same technique to approximate an exact oset curve with low egree spline curves. The least squares base methos [, 2] are expecte to perform better than other methos. However, there still remains a question about whether the least squares solution is optimal when searching for the smallest number of (say cubic) curve segments to approximate an exact oset curve. The answer is negative, in general. In the special case of osetting quaratic curves, the simple metho of ler an Hanson [6] performs much better than the least squares methos [, 2]. It is important to question how this unexpecte result coul be obtaine. The answer might be quite useful in improving the accuracy of oset approximation. The least squares solution optimizes the integrate summation of the least squares errors in the approximation. Therefore, even if a small portion of the approximation curve has a large error, as long as the rest of the curve tightly approximates the exact curve, the overall least squares error can be very small. That is, the least squares solution provies an optimal solution with respect to an L 2 norm. When this L 2 optimal solution is further evaluate with respect to the L norm (of Equation (3)), the optimal- 3
4 Uner an Over-Estimation The oset approximation of b [9] is formally ene as follows: C a (t) i0 i0 (P i + N( i)) B i(t) P ib i(t) + C(t) + V (t): i0 N( i)b i(t) where kn( i)k P, for i 0; : : : ; n. The vector el n curve V (t) N(i)Bi(t) has all its control points i0 N( i) on the unit circle S. By the convex hull property, we have kv (t)k an D(t) (b) kc(t)? C a (t)k kv (t)k kv (t)k : C(t) (a) C a (t) If N( i) 6 N( j), for some 0 i; j n, we have min kv (t)k <, an this results in an error in the oset approximation. Hence, this metho always unerestimates the exact oset. Figure 2(a) shows a quartic Bezier curve C(t) an its oset approximation C a (t). In Figure 2(b), the ierence vector el D(t) C(t)? C a (t) is completely containe in a isk of raius. All the control points of D(t) are on the circumference of the isk. Uner-estimation of osets may lea to unesirable results. For example, in NC machining, the unerestimation leas to gouging. Assume the unerestimation of the oset is boune from below by: min min(kv (t)k): When we translate control point P i in the irection of N( i), by a istance min, the resulting curve completely over-estimates the exact oset (see Figure 3): kc(t)? C a (t)k V (t) min kv (t)k V (t) : One can reuce the relative error in the oset approximation by alternating the uner an over-estimations. This can be one by ajusting the oset istance at each control point appropriately. Figure 4 shows an example of this approach. We use the same quartic Bezier curve as in Figures 2 an 3. The quartic Bezier oset approximation curve interpolates the exact oset at ve iscrete locations, corresponing to the noe values, i 4 ; 0 i 4. Figure 2: In (a), an oset approximation C a (t) compute by translating the control points of the original curve C(t) (ashe lines) by an amount equal to the oset istance will always uner-estimate the real oset. In (b), D(t) C(t)? C a (t) is foun to be fully containe in a circle of the oset raius size,. (b) D(t) C a (t) C a (t) C(t) D(t) C(t) (b) (a) Figure 3: In (a), an oset approximation C a (t) of a quartic Bezier curve C(t) (ashe lines) is compute by forcing C a (t) to over-estimate the error. D(t) (t) is shown in (b). Compare with Figure 2. C(t)?C a (a) Figure 4: In (a), an oset approximation C a (t) of a quartic Bezier curve C(t) (ashe lines) is compute by enforcing C a (t) to interpolate at ve locations on the exact oset curve compute at the noe values on C a(t). D(t) C(t)? Ca (t) is shown in (b). Compare with Figures 2 an 3. 4
5 ity is no longer guarantee. This is an important observation which suggests possible improvements over the nearly optimal solutions [, 2]. Pham [3] suggeste a simple B-spline interpolation metho to approximate the oset curve. Finite sample points are generate on the exact oset curve, an they are interpolate by a piecewise cubic B-spline curve. It is also interesting to note that this simple metho also performs pretty well. In many examples, its performance is only slightly worse than an sometimes even better than the local least squares methos [, 2]. Circle Approximation Methos Assume the base curve C(t), t 0 t t, is a polynomial curve with no inection point, an a unit circular arc U(s), s 0 s s, is parameterize so that: C 0 (t 0 ) k U 0 (s 0 ) an C 0 (t ) k U 0 (s ): If one can compute a reparameterization s(t) so that: C 0 (t) k U 0 (s(t)); the oset curve is then computable as: C (t) C(t) + U(s(t)): (9) The oset curve is not a polynomial or rational curve; therefore, we have to approximate U(s) an/or s(t) by a polynomial or rational. et al. [5] approximate the unit circle U(s) with piecewise quaratic polynomial curve segments Q j (s), j 0; : : : ; n. The Hoograph curve Q 0 j (s) is piecewise linear; therefore, the parallel constraint: C 0 (t) k Q 0 (s(t)) provies the reparameterization of s(t) as a rational polynomial of egree?, where is the egree of C(t). For a polynomial curve C(t) of egree, the resulting oset approximation (compute as in Equation (9)) is a rational curve of egree 3? 2. (For a rational curve C(t) of egree, the oset approximation curve is of egree 5? 4.) For a quaratic polynomial curve C(t), this technique also provies a simple metho to represent the exact oset curve C (t) as a rational curve of egree six. Assume that the exact circle, Q(s), 0 s, is represente by a rational quaratic curve. Then, the parallel constraint: C 0 (t(s)) k Q 0 (s) provies the reparameterization of t(s) as a rational polynomial of egree two. Therefore, the exact oset curve C (t) is a rational curve of egree six. Even with the high egree of six, the exact oset capability suggests this metho as the metho of choice for osetting (piecewise) quaratic polynomial curves, especially for high precision oset approximation. However, this exact oset capability oes not exten to rational quaratic curves. (There are some rational quaratic curves which have no exact rational parametrization of their oset curves.) One can attempt to globally approximate s(t) by maximizing the constraint energy: max s(t) Z t t 0 hc 0 (t); U 0 (s(t))i kc 0 (t)k ku 0 t: (0) (s(t))k This approach was taken in et al. [4], in which the composition of U(s(t)) (U s)(t) is carrie out symbolically [8] (see also Siebar on Symbolic Computation). The oset approximation in [5] epens on the metho use for the piecewise quaratic approximation to the circle. The error in the oset approximation stems only from the quaratic polynomial approximation of the circular arc, scale by the oset raius. et al. [5] use ve ierent circle approximation methos. Two of the ve methos generate G -continuous circle approximations with quaratic Bezier curve segments. In the rst metho, the unit circle U(s) is totally containe in the close convex region boune by the quaratic curve segments. The corresponing oset curve approximation completely over-estimates the exact oset curve. In the secon metho, the quaratic curve segments pass through both the interior an exterior of the unit circle U(s). Therefore, the oset approximation curve both over an uner-estimates the exact oset curve, while the approximation error is reuce by half from the over-estimating rst metho. We use this secon metho, referre to as in the next section, for comparison with other methos. In contrast, et al. [4] approximate the reparametrization s(t), while representing the circle U(s) exactly by a rational quaratic curve. In this metho, the error stems only from the inaccurate reparameterization function s(t), which results in a mismatch in the parallel constraint of C 0 (t) k U 0 (s(t)). To the authors' knowlege, this is the only oset approximation metho for which the use of (t) is completely ineective in the global error boun. The term (t) is always equal to zero. et al. [4] measure the angular eviation of U(s(t)) from the exact oset irection N(t) by using the following error function: m (t) hc(t)? Ca (t); C0 (t)i 2 2 kc 0 (t)k 2 : () The error is equal to zero if orthogonality is preserve. Otherwise, it is equal to cos 2, where is the angle between U(s(t)) an C 0 (t). Quantitative Comparisons We consier how eciently each metho approximates the oset curve, given a prescribe tolerance. Several examples of Bezier an B-spline curves are given, both in polynomial an rational forms. All 5
6 the methos (compare in this article) are implemente using the IRIT [5] soli moeling system that has been evelope at the Technion, Israel, with some of the oset approximation methos implemente at POSTECH, Korea. Methos uner Comparison We quantitatively compare the following methos: : The simple metho of b [9] in which the control points are translate by the oset istance. This metho always creates unerestimate osets. (See Siebar on Uner an Over-Estimation.) : An aaptive oset renement approach that was suggeste in er an Cohen [7]. Instea of subiviing the base curve, whenever the error is too large, the oset curve is rene to yiel a better approximation (by using more control points). The error analysis of (t) is exploite to n better caniate locations for re- nement. This metho also uner-estimates the oset curves. : The enhancement suggeste by uillart [0] that allows the exact oset representation of linear as well as circular segments. : The metho of ler an Hanson [6] in which the eges of the control polygon, rather than the control points, are translate. ss: The metho of ss [2] that ts a cubic Bezier curve to each oset curve segment to interpolate the bounary points an velocities of the exact oset curve. Pham: The metho of Pham [3] that interpolates a sequence of nite sample points on the exact oset curve by a non-uniform piecewise cubic B-spline curve. (The original metho of Pham [3] uses a uniform B-spline curve; however, we have moie the metho.) Whenever the oset approximation error is larger than the prescribe tolerance, more sample oset points are use for a better t. : The global least squares approximation that ts a uniform piecewise cubic B-spline curve to the oset curve. Whenever the oset approximation error is larger than the prescribe tolerance, more control points are use for a better t. : The least squares metho of chek [, 2] that ts a cubic Bezier curve to each oset curve segment. Whenever the error is larger than the tolerance, the base curve is subivie into two subsegments an the oset approximation is repeate recursively. : The approach suggeste by et al. [5] that approximates the curve of the convolution between C(t) an the oset circle U(s) of raius. Traitionally, the oset approximation error has been measure only at nite sample points of C(t) an C a (t). As previously mentione, we aopt the symbolic approach of error estimation [7]. Therefore, we can provie an L global upper boun on the oset approximation error for each of the methos uner comparison. The global error boun is erive by symbolically computing the error function (t) (in Equation (3)). Because of the convex hull property of the Bezier or NURBS representation of the scalar function (t), we can easily etermine its upper boun as the maximum coecient of the Bezier or NURBS basis functions. Comparison Results an Remarks Figures 5{6 show the results of osetting (piecewise) quaratic curves. We compare the number of control points with respect to the accuracy of oset approximation. In these examples, the metho of ler an Hanson [6] outperforms all the other methos even if the base curve has sharp corners with high curvature (Figure 6). This surprising result has never been reporte in the literature. In fact, we have assume that the least squares methos provie near optimal solutions to the oset approximation problem. However, the superior performance of ler an Hanson [6] tells us that this is not true, in general. At this moment, we have no clear explanation of the unerlying geometric properties of this unusual phenomenon. Nevertheless, it is not icult to point out at least two possible sources of the nonoptimality in the current least squares methos: As iscusse above, the least squares methos provie the optimal solutions in an L 2 norm, which may be quite ierent from the optimal solutions in an L norm. The least squares optimization proceure solves an over-constraine problem, the solution of which epens on the istribution of nite sample points on the oset curve. In some egenerate cases, the least squares solution may have large variation epening on the istribution of ata points. Further investigations are require to eliminate these limitations, an this may avance the state-of-theart of oset curve approximation. Figures 7, 9, an 0 show other examples of osetting (piecewise) cubic B-spline curves. Throughout the conucte tests, we have observe the following consistent results: The uner-estimating oset approximation metho,, is oing quite poorly. The aaptive oset renement approach,, is better than, especially when high precision is esire. In the case of osetting (piecewise) quaratic curve segments, the simple metho of ler an Hanson [6] outperforms all the other methos, especially when high precision is require. 6
7 Offset Error 0? ? ? ? ? ? ? 0?2 0?3 0?4 0? ? ? ? ? ? ? Offset Error 0? 0?2 0?3 0?4 Figure 5: An oset approximation (light curve) for a quaratic polynomial B-spline curve with eight control points. 0? In the case of osetting (piecewise) cubic curve segments, the least squares methos, an, perform much better than all the other methos, especially when high precision is require. In many examples, the local cubic B-spline interpolation metho, Pham, has similar { an sometimes even better { performance to. However, its performance eteriorates when the base curve has a raius of curvature similar to the oset raius. The only geometrical metho that approaches the eciency of the least squares methos is followe not so closely by. For the case of osetting (piecewise) cubic curves, the global least squares metho,, outperforms all the other methos, while it is closely followe by the local least squares metho,, an also by the local cubic B-spline interpolation metho, Pham. Many practical situations require the prouction of local optimal solutions base only on the local ata Figure 6: An oset approximation (light curve) for a quaratic polynomial with sharp corners. that is available. For example, for ata storage saving, we can store only the subivision locations of the curve, instea of all the control points that are generate. We then use the local methos to generate the control points (on the y) by consiering only local ata. In this case, an Pham are the methos of choice. As iscusse in the above observation, the performance of Pham is closely relate to the raius of curvature of the base curve. When the raius of curvature is similar to the oset raius, the sample oset points are clustere together. The B-spline interpolation of these clustere points generates unulation, which is the main source of large approximation error. In this case, it is better to use a smaller number of ata points for the interpolation. Figures {2 exemplify this phenomenon by comparing the relative performances of ierent oset approximation methos. Given a xe base curve, by increasing the oset raius graually, we can observe that Pham's 7
8 0? ? ? ? ? ? ? ? ? ? ? ? Offset Error 0? 0?2 0?3 0?4 0? Figure 7: An oset approximation (light curve) for a polynomial cubic Bezier curve. Offset Error 0? 0?2 0?3 0?4 0? Figure 8: An oset approximation (light curve) for a rational quaratic B-spline circle with nine control points. metho has the worst relative performance near the oset istance which starts to evelop cusps in the oset curve. For a better visualization of the relative performance, only four methos are shown in the graphs of Figures {2. There is another source of unulation we have to consier in Pham's metho. That is, the mismatch in spees between the two curves, i.e., the base curve an the oset curve, also cause eterioration in the quality of the oset approximation. For the implementation of Pham, we use a non-uniform cubic B- spline curve, in which the ata points of the oset inherit the knot values of the base curve points. When the oset ata points are clustere, their knot values are much sparser compare with the oset curve length. This unnatural assignment of knot values generates unulation. Therefore, for a better oset approximation, it is also important to rearrange the knot values of the oset ata points. The superior performance (in the quaratic case) of the simple metho,, suggests the possibility of improvement over the current least squares methos. This improvement may be achieve by resolving the limitations of least squares methos as is- cusse above. The limitation resulting from the L 2 norm seems more serious. To resolve this problem, we nee to evelop an ecient algorithm to compute an optimize the L norm of the oset approximation error; that is, the maximum of the error function (t) (in Equation (3)): max t nkc(t)? C a (t)k2? 2 o ; (2) or a more precise geometric istance measure base on the following Hausor metric: n o max max min kc(s)? C a t s (t)k 2? 2 ; (3) max s min t n kc(s)? C a (t)k2? 2 o where s is assume to be a local perturbation of the parameter t. Note that the metho of b [9] essentially moels the L norm of Equation (2) in terms of the maximum an minimum magnitues of the istance curve, D(t) C(t)? C a (t), in Figures 2{4. Let's consier a variant of b [9] which uses the least 8
9 0? ? ? ? ? ? Offset Error 0? 0?2 0?3 0?4 0?5 0? ? ? ? ? ? Offset Error 0? 0?2 0? Figure 9: An oset approximation (light curve) for a cubic polynomial B-spline curve with 3 control points. 0?4 0? squares technique to optimize the oset istance at each control point so that the istance curve D(t) is a best t to the oset circle of raius. This metho measures the oset error in the L sense of Equation (2). (Note that the approximation of D(t) to an oset circle still has the limitation of L 2 norm.) Although we have not provie all the etails of in this article, the metho of et al. [5] actually measures the oset approximation error uner the L norm of Equation (3), which is more precise than the L norm of Equation (2). We expect that future oset approximation techniques (while incorporating these L norms into their optimization proceures) may provie more accurate results than the current least squares methos. Conclusion We have compare several contemporary oset approximation techniques for freeform curves in the plane. In general, the least squares methos perform very well. However, for the case of osetting quaratic curves, the simple metho of ler an Hanson [6] is the metho of choice. Therefore, the least squares methos nee further improvement to prouce near-optimal solutions in all cases. Some of the current methos [5, 7, 9] have geometric repre- Figure 0: An oset approximation (light curve) for a cubic polynomial perioic B-spline curve with four control points. sentations of the oset approximation error (in certain L norms), whereas none of the current least squares methos have such geometric interpretation of their respective error bouns. We also pointe out two limitations of the current least squares methos: (i) the L 2 norm employe in these methos an (ii) the epenency on the nite sample points use in the optimization. The B-spline interpolation metho also nees further investigation to eliminate the curve unulation resulting from the curve spee mismatch between the base curve an the oset curve. In this respect, there are still many ways to improve the current state-of-the-art of oset curve approximation. We hope that the experimental results reporte in this article an the relate remarks will serve as useful guielines for future research. References [] chek, J., (988), \Spline Approximation of Oset Curves," Computer Aie Geometric Design, Vol. 5, pp. 33{40. 9
10 Offset Distance Offset Distance Figure 2: Pham's metho has the worst performance for the oset istances aroun 0.4. Base curve is a cubic B-spline curve. Tolerance of 0.00 is use for oset approximation error Figure : Pham's metho has the worst relative performance for the oset istances between 0.4 an 0.6. Base curve is a cubic B-spline curve. Tolerance of is use for oset approximation error. [2] chek, J., an Wissel, N., (988), \Optimal Approximate Conversion of Spline Curves an Spline Approximation of Oset Curves," Computer-Aie Design, Vol. 20, No. 8, pp. 475{483. [3] Farouki, R., an Ne, C., (990), \Analytic Properties of Plane Oset Curves" & \Algebraic Properties of Plane Oset Curves," Computer Aie Geometric Design, Vol. 7, pp. 83{99 & pp. 0{27. [4] Farouki, R., an Sakkalis, T., (990), \Pythagorean Hoograph," IBM J. Res. Develop., 34, pp [5], I.-K., Kim, M.-S., an er, G., (995), \Planar Curve Oset Base on Circle Approximation," to appear in Computer-Aie Design. [6] ler, W., an Hanson, E., (984), \Osets of Two Dimensional Proles," IEEE Computer Graphics & Application, Vol. 4, pp. 36{46. [7] er, G., an Cohen, E., (99), \Error Boune Variable Distance Oset Operator for Free Form Curves an Surfaces," International Journal of Computational Geometry an Applications, Vol., No., pp. 67{78. [8] er, G., (992). \Free Form Surface Analysis using a Hybri of Symbolic an Numeric Computation," Ph.D. thesis, University of Utah, Computer Science Department. [9] b, B., (984), Design of Sculpture Surfaces Using The B-spline Representation, Ph.D. thesis, University of Utah, Computer Science Department. [0] uillart, S., (987), \Computing Oset of B-spline Curves," Computer-Aie Design, Vol. 9, No. 6, pp. 305{309. 0
11 [] er, G., an Cohen, E., (992), \Oset Approximation Improvement by Control Points Perturbation." Mathematical Methos in Computer Aie Geometric Design II, Tom Lyche an Larry L. Schumaker, Acaemic Press, pp [2] ss, R., (983), \An Oset Spline Approximation for Plane Cubic Splines," Computer- Aie Design, Vol. 5, No. 4, pp. 297{299. [3] Pham, B., (988), \Oset Approximation of Uniform B-splines," Computer-Aie Design, Vol. 20, No. 8, pp. 47{474. [4], I.-K., Kim, M.-S., an er, G., (995), \Planar Curve Oset by Curve Tangent Matching," Technical Report, CS-CG-TR , Dept. of Computer Science, POSTECH, November, 995. [5] IRIT soli moeller (995), IRIT 5.0 User's Manual, Technion.
B-Splines and NURBS Week 5, Lecture 9
 CS 430/585 Computer Graphics I B-Splines an NURBS Week 5, Lecture 9 Davi Breen, William Regli an Maxim Peysakhov Geometric an Intelligent Computing Laboratory Department of Computer Science Drexel University
CS 430/585 Computer Graphics I B-Splines an NURBS Week 5, Lecture 9 Davi Breen, William Regli an Maxim Peysakhov Geometric an Intelligent Computing Laboratory Department of Computer Science Drexel University
Transient analysis of wave propagation in 3D soil by using the scaled boundary finite element method
 Southern Cross University epublications@scu 23r Australasian Conference on the Mechanics of Structures an Materials 214 Transient analysis of wave propagation in 3D soil by using the scale bounary finite
Southern Cross University epublications@scu 23r Australasian Conference on the Mechanics of Structures an Materials 214 Transient analysis of wave propagation in 3D soil by using the scale bounary finite
Polynomial/Rational Approximation of Minkowski Sum Boundary Curves 1
 GRAPHICAL MODELS AND IMAGE PROCESSING Vol. 60, No. 2, March, pp. 136 165, 1998 ARTICLE NO. IP970464 Polynomial/Rational Approximation of Minkowski Sum Boundary Curves 1 In-Kwon Lee and Myung-Soo Kim Department
GRAPHICAL MODELS AND IMAGE PROCESSING Vol. 60, No. 2, March, pp. 136 165, 1998 ARTICLE NO. IP970464 Polynomial/Rational Approximation of Minkowski Sum Boundary Curves 1 In-Kwon Lee and Myung-Soo Kim Department
Approximation with Active B-spline Curves and Surfaces
 Approximation with Active B-spline Curves an Surfaces Helmut Pottmann, Stefan Leopolseer, Michael Hofer Institute of Geometry Vienna University of Technology Wiener Hauptstr. 8 10, Vienna, Austria pottmann,leopolseer,hofer
Approximation with Active B-spline Curves an Surfaces Helmut Pottmann, Stefan Leopolseer, Michael Hofer Institute of Geometry Vienna University of Technology Wiener Hauptstr. 8 10, Vienna, Austria pottmann,leopolseer,hofer
2D Spline Curves. CS 4620 Lecture 13
 2D Spline Curves CS 4620 Lecture 13 2008 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes [Boeing] that is, without discontinuities So far we can make things with corners
2D Spline Curves CS 4620 Lecture 13 2008 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes [Boeing] that is, without discontinuities So far we can make things with corners
Trimming Local and Global Self-intersections in Offset Curves/Surfaces using Distance Maps
 Trimming Local and Global Self-intersections in Offset Curves/Surfaces using Distance Maps Joon-Kyung Seong a Gershon Elber b, Myung-Soo Kim a,c a School of Computer Science and Engineering, Seoul National
Trimming Local and Global Self-intersections in Offset Curves/Surfaces using Distance Maps Joon-Kyung Seong a Gershon Elber b, Myung-Soo Kim a,c a School of Computer Science and Engineering, Seoul National
Learning Polynomial Functions. by Feature Construction
 I Proceeings of the Eighth International Workshop on Machine Learning Chicago, Illinois, June 27-29 1991 Learning Polynomial Functions by Feature Construction Richar S. Sutton GTE Laboratories Incorporate
I Proceeings of the Eighth International Workshop on Machine Learning Chicago, Illinois, June 27-29 1991 Learning Polynomial Functions by Feature Construction Richar S. Sutton GTE Laboratories Incorporate
Need for Parametric Equations
 Curves and Surfaces Curves and Surfaces Need for Parametric Equations Affine Combinations Bernstein Polynomials Bezier Curves and Surfaces Continuity when joining curves B Spline Curves and Surfaces Need
Curves and Surfaces Curves and Surfaces Need for Parametric Equations Affine Combinations Bernstein Polynomials Bezier Curves and Surfaces Continuity when joining curves B Spline Curves and Surfaces Need
Kinematic Analysis of a Family of 3R Manipulators
 Kinematic Analysis of a Family of R Manipulators Maher Baili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S. 6597 1, rue e la Noë, BP 92101,
Kinematic Analysis of a Family of R Manipulators Maher Baili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S. 6597 1, rue e la Noë, BP 92101,
6 Gradient Descent. 6.1 Functions
 6 Graient Descent In this topic we will iscuss optimizing over general functions f. Typically the function is efine f : R! R; that is its omain is multi-imensional (in this case -imensional) an output
6 Graient Descent In this topic we will iscuss optimizing over general functions f. Typically the function is efine f : R! R; that is its omain is multi-imensional (in this case -imensional) an output
Parametric curves. Brian Curless CSE 457 Spring 2016
 Parametric curves Brian Curless CSE 457 Spring 2016 1 Reading Required: Angel 10.1-10.3, 10.5.2, 10.6-10.7, 10.9 Optional Bartels, Beatty, and Barsky. An Introduction to Splines for use in Computer Graphics
Parametric curves Brian Curless CSE 457 Spring 2016 1 Reading Required: Angel 10.1-10.3, 10.5.2, 10.6-10.7, 10.9 Optional Bartels, Beatty, and Barsky. An Introduction to Splines for use in Computer Graphics
Research Article Inviscid Uniform Shear Flow past a Smooth Concave Body
 International Engineering Mathematics Volume 04, Article ID 46593, 7 pages http://x.oi.org/0.55/04/46593 Research Article Invisci Uniform Shear Flow past a Smooth Concave Boy Abullah Mura Department of
International Engineering Mathematics Volume 04, Article ID 46593, 7 pages http://x.oi.org/0.55/04/46593 Research Article Invisci Uniform Shear Flow past a Smooth Concave Boy Abullah Mura Department of
Rational Bezier Curves
 Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
2D Spline Curves. CS 4620 Lecture 18
 2D Spline Curves CS 4620 Lecture 18 2014 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes that is, without discontinuities So far we can make things with corners (lines,
2D Spline Curves CS 4620 Lecture 18 2014 Steve Marschner 1 Motivation: smoothness In many applications we need smooth shapes that is, without discontinuities So far we can make things with corners (lines,
Polynomial Decomposition and Its Applications
 Polynomial Decomposition and Its Applications Joon-Kyung Seong School of Computer Science and Engineering Seoul National University, Seoul 151-742, South Korea E-mail: swallow@3map.snu.ac.kr and Gershon
Polynomial Decomposition and Its Applications Joon-Kyung Seong School of Computer Science and Engineering Seoul National University, Seoul 151-742, South Korea E-mail: swallow@3map.snu.ac.kr and Gershon
Indexing the Edges A simple and yet efficient approach to high-dimensional indexing
 Inexing the Eges A simple an yet efficient approach to high-imensional inexing Beng Chin Ooi Kian-Lee Tan Cui Yu Stephane Bressan Department of Computer Science National University of Singapore 3 Science
Inexing the Eges A simple an yet efficient approach to high-imensional inexing Beng Chin Ooi Kian-Lee Tan Cui Yu Stephane Bressan Department of Computer Science National University of Singapore 3 Science
Lecture 25: Bezier Subdivision. And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10
 Lecture 25: Bezier Subdivision And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10 1. Divide and Conquer If we are going to build useful
Lecture 25: Bezier Subdivision And he took unto him all these, and divided them in the midst, and laid each piece one against another: Genesis 15:10 1. Divide and Conquer If we are going to build useful
Yet Another Parallel Hypothesis Search for Inverse Entailment Hiroyuki Nishiyama and Hayato Ohwada Faculty of Sci. and Tech. Tokyo University of Scien
 Yet Another Parallel Hypothesis Search for Inverse Entailment Hiroyuki Nishiyama an Hayato Ohwaa Faculty of Sci. an Tech. Tokyo University of Science, 2641 Yamazaki, Noa-shi, CHIBA, 278-8510, Japan hiroyuki@rs.noa.tus.ac.jp,
Yet Another Parallel Hypothesis Search for Inverse Entailment Hiroyuki Nishiyama an Hayato Ohwaa Faculty of Sci. an Tech. Tokyo University of Science, 2641 Yamazaki, Noa-shi, CHIBA, 278-8510, Japan hiroyuki@rs.noa.tus.ac.jp,
A Classification of 3R Orthogonal Manipulators by the Topology of their Workspace
 A Classification of R Orthogonal Manipulators by the Topology of their Workspace Maher aili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S.
A Classification of R Orthogonal Manipulators by the Topology of their Workspace Maher aili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S.
COMPUTER AIDED GEOMETRIC DESIGN. Thomas W. Sederberg
 COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
COMPUTER AIDED GEOMETRIC DESIGN Thomas W. Sederberg January 31, 2011 ii T. W. Sederberg iii Preface This semester is the 24 th time I have taught a course at Brigham Young University titled, Computer Aided
Figure 1: Schematic of an SEM [source: ]
![Figure 1: Schematic of an SEM [source: ] Figure 1: Schematic of an SEM [source: ]](/thumbs/85/92721477.jpg) EECI Course: -9 May 1 by R. Sanfelice Hybri Control Systems Eelco van Horssen E.P.v.Horssen@tue.nl Project: Scanning Electron Microscopy Introuction In Scanning Electron Microscopy (SEM) a (bunle) beam
EECI Course: -9 May 1 by R. Sanfelice Hybri Control Systems Eelco van Horssen E.P.v.Horssen@tue.nl Project: Scanning Electron Microscopy Introuction In Scanning Electron Microscopy (SEM) a (bunle) beam
Holy Halved Heaquarters Riddler
 Holy Halve Heaquarters Riler Anonymous Philosopher June 206 Laser Larry threatens to imminently zap Riler Heaquarters (which is of regular pentagonal shape with no courtyar or other funny business) with
Holy Halve Heaquarters Riler Anonymous Philosopher June 206 Laser Larry threatens to imminently zap Riler Heaquarters (which is of regular pentagonal shape with no courtyar or other funny business) with
Shift-map Image Registration
 Shift-map Image Registration Svärm, Linus; Stranmark, Petter Unpublishe: 2010-01-01 Link to publication Citation for publishe version (APA): Svärm, L., & Stranmark, P. (2010). Shift-map Image Registration.
Shift-map Image Registration Svärm, Linus; Stranmark, Petter Unpublishe: 2010-01-01 Link to publication Citation for publishe version (APA): Svärm, L., & Stranmark, P. (2010). Shift-map Image Registration.
B-spline Curves. Smoother than other curve forms
 Curves and Surfaces B-spline Curves These curves are approximating rather than interpolating curves. The curves come close to, but may not actually pass through, the control points. Usually used as multiple,
Curves and Surfaces B-spline Curves These curves are approximating rather than interpolating curves. The curves come close to, but may not actually pass through, the control points. Usually used as multiple,
Bends, Jogs, And Wiggles for Railroad Tracks and Vehicle Guide Ways
 Ben, Jogs, An Wiggles for Railroa Tracks an Vehicle Guie Ways Louis T. Klauer Jr., PhD, PE. Work Soft 833 Galer Dr. Newtown Square, PA 19073 lklauer@wsof.com Preprint, June 4, 00 Copyright 00 by Louis
Ben, Jogs, An Wiggles for Railroa Tracks an Vehicle Guie Ways Louis T. Klauer Jr., PhD, PE. Work Soft 833 Galer Dr. Newtown Square, PA 19073 lklauer@wsof.com Preprint, June 4, 00 Copyright 00 by Louis
P. Fua and Y. G. Leclerc. SRI International. 333 Ravenswood Avenue, Menlo Park, CA
 Moel Driven Ege Detection P. Fua an Y. G. Leclerc SI International 333 avenswoo Avenue, Menlo Park, CA 9425 (fua@ai.sri.com leclerc@ai.sri.com) Machine Vision an Applications, 3, 199 Abstract Stanar ege
Moel Driven Ege Detection P. Fua an Y. G. Leclerc SI International 333 avenswoo Avenue, Menlo Park, CA 9425 (fua@ai.sri.com leclerc@ai.sri.com) Machine Vision an Applications, 3, 199 Abstract Stanar ege
Generalized Filleting and Blending Operations toward Functional and Decorative Applications
 Generalized Filleting and Blending Operations toward Functional and Decorative Applications Gershon Elber Computer Science Department Technion Haifa 3000, Israel Email: gershon@cs.technion.ac.il Abstract
Generalized Filleting and Blending Operations toward Functional and Decorative Applications Gershon Elber Computer Science Department Technion Haifa 3000, Israel Email: gershon@cs.technion.ac.il Abstract
Linear First-Order PDEs
 MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 9 Lecture 2 Linear First-Orer PDEs The most general first-orer linear PDE has the form a(x, y)z x + b(x, y)z y + c(x, y)z = (x, y), (1) where a, b,
MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 9 Lecture 2 Linear First-Orer PDEs The most general first-orer linear PDE has the form a(x, y)z x + b(x, y)z y + c(x, y)z = (x, y), (1) where a, b,
Characterizing Decoding Robustness under Parametric Channel Uncertainty
 Characterizing Decoing Robustness uner Parametric Channel Uncertainty Jay D. Wierer, Wahee U. Bajwa, Nigel Boston, an Robert D. Nowak Abstract This paper characterizes the robustness of ecoing uner parametric
Characterizing Decoing Robustness uner Parametric Channel Uncertainty Jay D. Wierer, Wahee U. Bajwa, Nigel Boston, an Robert D. Nowak Abstract This paper characterizes the robustness of ecoing uner parametric
More Accurate Representation of Conics by NURBS. One of the argument usually given to explain the popularity of NURBS is the fact that they
 More Accurate Representation of Conics by NURBS Carole Blanc Christophe Schlick LaBRI 1, 51 cours de la liberation, 405 Talence (FRANCE) [blancjschlick]@labri.u-bordeaux.fr 1 Introduction One of the argument
More Accurate Representation of Conics by NURBS Carole Blanc Christophe Schlick LaBRI 1, 51 cours de la liberation, 405 Talence (FRANCE) [blancjschlick]@labri.u-bordeaux.fr 1 Introduction One of the argument
Spline curves. in polar and Cartesian coordinates. Giulio Casciola and Serena Morigi. Department of Mathematics, University of Bologna, Italy
 Spline curves in polar and Cartesian coordinates Giulio Casciola and Serena Morigi Department of Mathematics, University of Bologna, Italy Abstract. A new class of spline curves in polar coordinates has
Spline curves in polar and Cartesian coordinates Giulio Casciola and Serena Morigi Department of Mathematics, University of Bologna, Italy Abstract. A new class of spline curves in polar coordinates has
Metamorphosis of Planar Parametric Curves via Curvature Interpolation
 Metamorphosis of Planar Parametric Curves via Curvature Interpolation Tatiana Surazhsky and Gershon Elber Technion, Israel Institute of Technology, Haifa 32000, Israel. Abstract This work considers the
Metamorphosis of Planar Parametric Curves via Curvature Interpolation Tatiana Surazhsky and Gershon Elber Technion, Israel Institute of Technology, Haifa 32000, Israel. Abstract This work considers the
Online Appendix to: Generalizing Database Forensics
 Online Appenix to: Generalizing Database Forensics KYRIACOS E. PAVLOU an RICHARD T. SNODGRASS, University of Arizona This appenix presents a step-by-step iscussion of the forensic analysis protocol that
Online Appenix to: Generalizing Database Forensics KYRIACOS E. PAVLOU an RICHARD T. SNODGRASS, University of Arizona This appenix presents a step-by-step iscussion of the forensic analysis protocol that
Computer Graphics Curves and Surfaces. Matthias Teschner
 Computer Graphics Curves and Surfaces Matthias Teschner Outline Introduction Polynomial curves Bézier curves Matrix notation Curve subdivision Differential curve properties Piecewise polynomial curves
Computer Graphics Curves and Surfaces Matthias Teschner Outline Introduction Polynomial curves Bézier curves Matrix notation Curve subdivision Differential curve properties Piecewise polynomial curves
MA 323 Geometric Modelling Course Notes: Day 14 Properties of Bezier Curves
 MA 323 Geometric Modelling Course Notes: Day 14 Properties of Bezier Curves David L. Finn In this section, we discuss the geometric properties of Bezier curves. These properties are either implied directly
MA 323 Geometric Modelling Course Notes: Day 14 Properties of Bezier Curves David L. Finn In this section, we discuss the geometric properties of Bezier curves. These properties are either implied directly
Flank Millable Surface Design with Conical and Barrel Tools
 461 Computer-Aided Design and Applications 2008 CAD Solutions, LLC http://www.cadanda.com Flank Millable Surface Design with Conical and Barrel Tools Chenggang Li 1, Sanjeev Bedi 2 and Stephen Mann 3 1
461 Computer-Aided Design and Applications 2008 CAD Solutions, LLC http://www.cadanda.com Flank Millable Surface Design with Conical and Barrel Tools Chenggang Li 1, Sanjeev Bedi 2 and Stephen Mann 3 1
CHAPTER 6 Parametric Spline Curves
 CHAPTER 6 Parametric Spline Curves When we introduced splines in Chapter 1 we focused on spline curves, or more precisely, vector valued spline functions. In Chapters 2 and 4 we then established the basic
CHAPTER 6 Parametric Spline Curves When we introduced splines in Chapter 1 we focused on spline curves, or more precisely, vector valued spline functions. In Chapters 2 and 4 we then established the basic
CONSTRUCTION AND ANALYSIS OF INVERSIONS IN S 2 AND H 2. Arunima Ray. Final Paper, MATH 399. Spring 2008 ABSTRACT
 CONSTUCTION AN ANALYSIS OF INVESIONS IN S AN H Arunima ay Final Paper, MATH 399 Spring 008 ASTACT The construction use to otain inversions in two-imensional Eucliean space was moifie an applie to otain
CONSTUCTION AN ANALYSIS OF INVESIONS IN S AN H Arunima ay Final Paper, MATH 399 Spring 008 ASTACT The construction use to otain inversions in two-imensional Eucliean space was moifie an applie to otain
Animated Surface Pasting
 Animate Surface Pasting Clara Tsang an Stephen Mann Computing Science Department University of Waterloo 200 University Ave W. Waterloo, Ontario Canaa N2L 3G1 e-mail: clftsang@cgl.uwaterloo.ca, smann@cgl.uwaterloo.ca
Animate Surface Pasting Clara Tsang an Stephen Mann Computing Science Department University of Waterloo 200 University Ave W. Waterloo, Ontario Canaa N2L 3G1 e-mail: clftsang@cgl.uwaterloo.ca, smann@cgl.uwaterloo.ca
Investigation into a new incremental forming process using an adjustable punch set for the manufacture of a doubly curved sheet metal
 991 Investigation into a new incremental forming process using an ajustable punch set for the manufacture of a oubly curve sheet metal S J Yoon an D Y Yang* Department of Mechanical Engineering, Korea
991 Investigation into a new incremental forming process using an ajustable punch set for the manufacture of a oubly curve sheet metal S J Yoon an D Y Yang* Department of Mechanical Engineering, Korea
The speed-controlled interpolator for machining parametric curves
 COMPUTER-AIDED DESIGN Computer-Aie Design 31 (1999) 349 357 www.elsevier.com/locate/ca The spee-controlle interpolator for machining parametric curves S.-S. Yeh, P.-L. Hsu* Department of Electrical an
COMPUTER-AIDED DESIGN Computer-Aie Design 31 (1999) 349 357 www.elsevier.com/locate/ca The spee-controlle interpolator for machining parametric curves S.-S. Yeh, P.-L. Hsu* Department of Electrical an
Parametric curves. Reading. Curves before computers. Mathematical curve representation. CSE 457 Winter Required:
 Reading Required: Angel 10.1-10.3, 10.5.2, 10.6-10.7, 10.9 Parametric curves CSE 457 Winter 2014 Optional Bartels, Beatty, and Barsky. An Introduction to Splines for use in Computer Graphics and Geometric
Reading Required: Angel 10.1-10.3, 10.5.2, 10.6-10.7, 10.9 Parametric curves CSE 457 Winter 2014 Optional Bartels, Beatty, and Barsky. An Introduction to Splines for use in Computer Graphics and Geometric
Representing Curves Part II. Foley & Van Dam, Chapter 11
 Representing Curves Part II Foley & Van Dam, Chapter 11 Representing Curves Polynomial Splines Bezier Curves Cardinal Splines Uniform, non rational B-Splines Drawing Curves Applications of Bezier splines
Representing Curves Part II Foley & Van Dam, Chapter 11 Representing Curves Polynomial Splines Bezier Curves Cardinal Splines Uniform, non rational B-Splines Drawing Curves Applications of Bezier splines
The Convex Hull of Rational Plane Curves
 Graphical Models 63, 151 162 (2001) doi:10.1006/gmod.2001.0546, available online at http://www.idealibrary.com on The Convex Hull of Rational Plane Curves Gershon Elber Department of Computer Science,
Graphical Models 63, 151 162 (2001) doi:10.1006/gmod.2001.0546, available online at http://www.idealibrary.com on The Convex Hull of Rational Plane Curves Gershon Elber Department of Computer Science,
Design considerations
 Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
BISECTOR CURVES OF PLANAR RATIONAL CURVES IN LORENTZIAN PLANE
 INTERNATIONAL JOURNAL OF GEOMETRY Vol. (03), No., 47-53 BISECTOR CURVES OF PLANAR RATIONAL CURVES IN LORENTZIAN PLANE MUSTAFA DEDE, YASIN UNLUTURK AND CUMALI EKICI Abstract. In this paper, the bisector
INTERNATIONAL JOURNAL OF GEOMETRY Vol. (03), No., 47-53 BISECTOR CURVES OF PLANAR RATIONAL CURVES IN LORENTZIAN PLANE MUSTAFA DEDE, YASIN UNLUTURK AND CUMALI EKICI Abstract. In this paper, the bisector
Regularized Laplacian Zero Crossings as Optimal Edge Integrators
 Regularize aplacian Zero rossings as Optimal Ege Integrators R. KIMME A.M. BRUKSTEIN Department of omputer Science Technion Israel Institute of Technology Technion ity, Haifa 32, Israel Abstract We view
Regularize aplacian Zero rossings as Optimal Ege Integrators R. KIMME A.M. BRUKSTEIN Department of omputer Science Technion Israel Institute of Technology Technion ity, Haifa 32, Israel Abstract We view
Generalized Edge Coloring for Channel Assignment in Wireless Networks
 TR-IIS-05-021 Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu, Pangfeng Liu, Da-Wei Wang, Jan-Jan Wu December 2005 Technical Report No. TR-IIS-05-021 http://www.iis.sinica.eu.tw/lib/techreport/tr2005/tr05.html
TR-IIS-05-021 Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu, Pangfeng Liu, Da-Wei Wang, Jan-Jan Wu December 2005 Technical Report No. TR-IIS-05-021 http://www.iis.sinica.eu.tw/lib/techreport/tr2005/tr05.html
Curve Representation ME761A Instructor in Charge Prof. J. Ramkumar Department of Mechanical Engineering, IIT Kanpur
 Curve Representation ME761A Instructor in Charge Prof. J. Ramkumar Department of Mechanical Engineering, IIT Kanpur Email: jrkumar@iitk.ac.in Curve representation 1. Wireframe models There are three types
Curve Representation ME761A Instructor in Charge Prof. J. Ramkumar Department of Mechanical Engineering, IIT Kanpur Email: jrkumar@iitk.ac.in Curve representation 1. Wireframe models There are three types
Considering bounds for approximation of 2 M to 3 N
 Consiering bouns for approximation of to (version. Abstract: Estimating bouns of best approximations of to is iscusse. In the first part I evelop a powerseries, which shoul give practicable limits for
Consiering bouns for approximation of to (version. Abstract: Estimating bouns of best approximations of to is iscusse. In the first part I evelop a powerseries, which shoul give practicable limits for
Classifying Facial Expression with Radial Basis Function Networks, using Gradient Descent and K-means
 Classifying Facial Expression with Raial Basis Function Networks, using Graient Descent an K-means Neil Allrin Department of Computer Science University of California, San Diego La Jolla, CA 9237 nallrin@cs.ucs.eu
Classifying Facial Expression with Raial Basis Function Networks, using Graient Descent an K-means Neil Allrin Department of Computer Science University of California, San Diego La Jolla, CA 9237 nallrin@cs.ucs.eu
Approximation of 3D-Parametric Functions by Bicubic B-spline Functions
 International Journal of Mathematical Modelling & Computations Vol. 02, No. 03, 2012, 211-220 Approximation of 3D-Parametric Functions by Bicubic B-spline Functions M. Amirfakhrian a, a Department of Mathematics,
International Journal of Mathematical Modelling & Computations Vol. 02, No. 03, 2012, 211-220 Approximation of 3D-Parametric Functions by Bicubic B-spline Functions M. Amirfakhrian a, a Department of Mathematics,
Dgp _ lecture 2. Curves
 Dgp _ lecture 2 Curves Questions? This lecture will be asking questions about curves, their Relationship to surfaces, and how they are used and controlled. Topics of discussion will be: Free form Curves
Dgp _ lecture 2 Curves Questions? This lecture will be asking questions about curves, their Relationship to surfaces, and how they are used and controlled. Topics of discussion will be: Free form Curves
Knot Insertion and Reparametrization of Interval B-spline Curves
 International Journal of Video&Image Processing and Network Security IJVIPNS-IJENS Vol:14 No:05 1 Knot Insertion and Reparametrization of Interval B-spline Curves O. Ismail, Senior Member, IEEE Abstract
International Journal of Video&Image Processing and Network Security IJVIPNS-IJENS Vol:14 No:05 1 Knot Insertion and Reparametrization of Interval B-spline Curves O. Ismail, Senior Member, IEEE Abstract
CS 475 / CS Computer Graphics. Modelling Curves 3 - B-Splines
 CS 475 / CS 675 - Computer Graphics Modelling Curves 3 - Bézier Splines n P t = i=0 No local control. B i J n,i t with 0 t 1 J n,i t = n i t i 1 t n i Degree restricted by the control polygon. http://www.cs.mtu.edu/~shene/courses/cs3621/notes/spline/bezier/bezier-move-ct-pt.html
CS 475 / CS 675 - Computer Graphics Modelling Curves 3 - Bézier Splines n P t = i=0 No local control. B i J n,i t with 0 t 1 J n,i t = n i t i 1 t n i Degree restricted by the control polygon. http://www.cs.mtu.edu/~shene/courses/cs3621/notes/spline/bezier/bezier-move-ct-pt.html
Particle Swarm Optimization Based on Smoothing Approach for Solving a Class of Bi-Level Multiobjective Programming Problem
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 17, No 3 Sofia 017 Print ISSN: 1311-970; Online ISSN: 1314-4081 DOI: 10.1515/cait-017-0030 Particle Swarm Optimization Base
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 17, No 3 Sofia 017 Print ISSN: 1311-970; Online ISSN: 1314-4081 DOI: 10.1515/cait-017-0030 Particle Swarm Optimization Base
Inuence of Cross-Interferences on Blocked Loops: to know the precise gain brought by blocking. It is even dicult to determine for which problem
 Inuence of Cross-Interferences on Blocke Loops A Case Stuy with Matrix-Vector Multiply CHRISTINE FRICKER INRIA, France an OLIVIER TEMAM an WILLIAM JALBY University of Versailles, France State-of-the art
Inuence of Cross-Interferences on Blocke Loops A Case Stuy with Matrix-Vector Multiply CHRISTINE FRICKER INRIA, France an OLIVIER TEMAM an WILLIAM JALBY University of Versailles, France State-of-the art
form property surface and its zero set (bottom). This surface isthe same as in plate 2. Plate 13 Teapot curvature estimation using
 (top). The surface second fundamental form property surface and its zero set (bottom). This surface isthe same as in plate. Plate 13 Teapot curvature estimation using curvature property surface computation.
(top). The surface second fundamental form property surface and its zero set (bottom). This surface isthe same as in plate. Plate 13 Teapot curvature estimation using curvature property surface computation.
Sung-Eui Yoon ( 윤성의 )
 CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
Curves and Surfaces 1
 Curves and Surfaces 1 Representation of Curves & Surfaces Polygon Meshes Parametric Cubic Curves Parametric Bi-Cubic Surfaces Quadric Surfaces Specialized Modeling Techniques 2 The Teapot 3 Representing
Curves and Surfaces 1 Representation of Curves & Surfaces Polygon Meshes Parametric Cubic Curves Parametric Bi-Cubic Surfaces Quadric Surfaces Specialized Modeling Techniques 2 The Teapot 3 Representing
Technion - Computer Science Department - Technical Report CIS
 Linearizing the Area and Volume Constraints Gershon Elber Computer Science Department Technion Haifa 32000, srael Email: gershon@cs.technion.ac.il Abstract Positional, tangential, and orthogonality constraints
Linearizing the Area and Volume Constraints Gershon Elber Computer Science Department Technion Haifa 32000, srael Email: gershon@cs.technion.ac.il Abstract Positional, tangential, and orthogonality constraints
d 3 d 4 d d d d d d d d d d d 1 d d d d d d
 Proceeings of the IASTED International Conference Software Engineering an Applications (SEA') October 6-, 1, Scottsale, Arizona, USA AN OBJECT-ORIENTED APPROACH FOR MANAGING A NETWORK OF DATABASES Shu-Ching
Proceeings of the IASTED International Conference Software Engineering an Applications (SEA') October 6-, 1, Scottsale, Arizona, USA AN OBJECT-ORIENTED APPROACH FOR MANAGING A NETWORK OF DATABASES Shu-Ching
Fast Fractal Image Compression using PSO Based Optimization Techniques
 Fast Fractal Compression using PSO Base Optimization Techniques A.Krishnamoorthy Visiting faculty Department Of ECE University College of Engineering panruti rishpci89@gmail.com S.Buvaneswari Visiting
Fast Fractal Compression using PSO Base Optimization Techniques A.Krishnamoorthy Visiting faculty Department Of ECE University College of Engineering panruti rishpci89@gmail.com S.Buvaneswari Visiting
A Versatile Model-Based Visibility Measure for Geometric Primitives
 A Versatile Moel-Base Visibility Measure for Geometric Primitives Marc M. Ellenrieer 1,LarsKrüger 1, Dirk Stößel 2, an Marc Hanheie 2 1 DaimlerChrysler AG, Research & Technology, 89013 Ulm, Germany 2 Faculty
A Versatile Moel-Base Visibility Measure for Geometric Primitives Marc M. Ellenrieer 1,LarsKrüger 1, Dirk Stößel 2, an Marc Hanheie 2 1 DaimlerChrysler AG, Research & Technology, 89013 Ulm, Germany 2 Faculty
Bézier Splines. B-Splines. B-Splines. CS 475 / CS 675 Computer Graphics. Lecture 14 : Modelling Curves 3 B-Splines. n i t i 1 t n i. J n,i.
 Bézier Splines CS 475 / CS 675 Computer Graphics Lecture 14 : Modelling Curves 3 n P t = B i J n,i t with 0 t 1 J n, i t = i=0 n i t i 1 t n i No local control. Degree restricted by the control polygon.
Bézier Splines CS 475 / CS 675 Computer Graphics Lecture 14 : Modelling Curves 3 n P t = B i J n,i t with 0 t 1 J n, i t = i=0 n i t i 1 t n i No local control. Degree restricted by the control polygon.
Non-homogeneous Generalization in Privacy Preserving Data Publishing
 Non-homogeneous Generalization in Privacy Preserving Data Publishing W. K. Wong, Nios Mamoulis an Davi W. Cheung Department of Computer Science, The University of Hong Kong Pofulam Roa, Hong Kong {wwong2,nios,cheung}@cs.hu.h
Non-homogeneous Generalization in Privacy Preserving Data Publishing W. K. Wong, Nios Mamoulis an Davi W. Cheung Department of Computer Science, The University of Hong Kong Pofulam Roa, Hong Kong {wwong2,nios,cheung}@cs.hu.h
Bezier Curves, B-Splines, NURBS
 Bezier Curves, B-Splines, NURBS Example Application: Font Design and Display Curved objects are everywhere There is always need for: mathematical fidelity high precision artistic freedom and flexibility
Bezier Curves, B-Splines, NURBS Example Application: Font Design and Display Curved objects are everywhere There is always need for: mathematical fidelity high precision artistic freedom and flexibility
Here are a couple of warnings to my students who may be here to get a copy of what happened on a day that you missed.
 Preface Here are my online notes for my Calculus I course that I teach here at Lamar University. Despite the fact that these are my class notes, they shoul be accessible to anyone wanting to learn Calculus
Preface Here are my online notes for my Calculus I course that I teach here at Lamar University. Despite the fact that these are my class notes, they shoul be accessible to anyone wanting to learn Calculus
Keyword: Quadratic Bézier Curve, Bisection Algorithm, Biarc, Biarc Method, Hausdorff Distances, Tolerance Band.
 Department of Computer Science Approximation Methods for Quadratic Bézier Curve, by Circular Arcs within a Tolerance Band Seminar aus Informatik Univ.-Prof. Dr. Wolfgang Pree Seyed Amir Hossein Siahposhha
Department of Computer Science Approximation Methods for Quadratic Bézier Curve, by Circular Arcs within a Tolerance Band Seminar aus Informatik Univ.-Prof. Dr. Wolfgang Pree Seyed Amir Hossein Siahposhha
BIJECTIONS FOR PLANAR MAPS WITH BOUNDARIES
 BIJECTIONS FOR PLANAR MAPS WITH BOUNDARIES OLIVIER BERNARDI AND ÉRIC FUSY Abstract. We present bijections for planar maps with bounaries. In particular, we obtain bijections for triangulations an quarangulations
BIJECTIONS FOR PLANAR MAPS WITH BOUNDARIES OLIVIER BERNARDI AND ÉRIC FUSY Abstract. We present bijections for planar maps with bounaries. In particular, we obtain bijections for triangulations an quarangulations
Skyline Community Search in Multi-valued Networks
 Syline Community Search in Multi-value Networs Rong-Hua Li Beijing Institute of Technology Beijing, China lironghuascut@gmail.com Jeffrey Xu Yu Chinese University of Hong Kong Hong Kong, China yu@se.cuh.eu.h
Syline Community Search in Multi-value Networs Rong-Hua Li Beijing Institute of Technology Beijing, China lironghuascut@gmail.com Jeffrey Xu Yu Chinese University of Hong Kong Hong Kong, China yu@se.cuh.eu.h
(Refer Slide Time: 00:02:24 min)
 CAD / CAM Prof. Dr. P. V. Madhusudhan Rao Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture No. # 9 Parametric Surfaces II So these days, we are discussing the subject
CAD / CAM Prof. Dr. P. V. Madhusudhan Rao Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture No. # 9 Parametric Surfaces II So these days, we are discussing the subject
Estimating Velocity Fields on a Freeway from Low Resolution Video
 Estimating Velocity Fiels on a Freeway from Low Resolution Vieo Young Cho Department of Statistics University of California, Berkeley Berkeley, CA 94720-3860 Email: young@stat.berkeley.eu John Rice Department
Estimating Velocity Fiels on a Freeway from Low Resolution Vieo Young Cho Department of Statistics University of California, Berkeley Berkeley, CA 94720-3860 Email: young@stat.berkeley.eu John Rice Department
p y = 0 x c Figure : Stereographic projection. r p p y = 0 c p Figure : Central projection. Furthermore, we will discuss representations of entire sph
 Circle and Sphere as rational splines Claudia Bangert and Hartmut Prautzsch Universitat Karlsruhe, Fakultat fur Informatik D-8 Karlsruhe, Germany corresponding author, e-mail: prau@ira.uka.de Abstract
Circle and Sphere as rational splines Claudia Bangert and Hartmut Prautzsch Universitat Karlsruhe, Fakultat fur Informatik D-8 Karlsruhe, Germany corresponding author, e-mail: prau@ira.uka.de Abstract
Intro to Curves Week 1, Lecture 2
 CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University Outline Math review Introduction to 2D curves
CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University Outline Math review Introduction to 2D curves
CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2
 CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 Outline Math review Introduction to 2D curves
CS 536 Computer Graphics Intro to Curves Week 1, Lecture 2 David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 Outline Math review Introduction to 2D curves
Computational Geometry
 Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture 1: Introduction and convex hulls Geometry: points, lines,... Geometric objects Geometric relations Combinatorial complexity Computational geometry Plane (two-dimensional), R 2 Space (three-dimensional),
Lecture IV Bézier Curves
 Lecture IV Bézier Curves Why Curves? Why Curves? Why Curves? Why Curves? Why Curves? Linear (flat) Curved Easier More pieces Looks ugly Complicated Fewer pieces Looks smooth What is a curve? Intuitively:
Lecture IV Bézier Curves Why Curves? Why Curves? Why Curves? Why Curves? Why Curves? Linear (flat) Curved Easier More pieces Looks ugly Complicated Fewer pieces Looks smooth What is a curve? Intuitively:
MA 323 Geometric Modelling Course Notes: Day 21 Three Dimensional Bezier Curves, Projections and Rational Bezier Curves
 MA 323 Geometric Modelling Course Notes: Day 21 Three Dimensional Bezier Curves, Projections and Rational Bezier Curves David L. Finn Over the next few days, we will be looking at extensions of Bezier
MA 323 Geometric Modelling Course Notes: Day 21 Three Dimensional Bezier Curves, Projections and Rational Bezier Curves David L. Finn Over the next few days, we will be looking at extensions of Bezier
Curves. Computer Graphics CSE 167 Lecture 11
 Curves Computer Graphics CSE 167 Lecture 11 CSE 167: Computer graphics Polynomial Curves Polynomial functions Bézier Curves Drawing Bézier curves Piecewise Bézier curves Based on slides courtesy of Jurgen
Curves Computer Graphics CSE 167 Lecture 11 CSE 167: Computer graphics Polynomial Curves Polynomial functions Bézier Curves Drawing Bézier curves Piecewise Bézier curves Based on slides courtesy of Jurgen
Almost Disjunct Codes in Large Scale Multihop Wireless Network Media Access Control
 Almost Disjunct Coes in Large Scale Multihop Wireless Network Meia Access Control D. Charles Engelhart Anan Sivasubramaniam Penn. State University University Park PA 682 engelhar,anan @cse.psu.eu Abstract
Almost Disjunct Coes in Large Scale Multihop Wireless Network Meia Access Control D. Charles Engelhart Anan Sivasubramaniam Penn. State University University Park PA 682 engelhar,anan @cse.psu.eu Abstract
Dual Arm Robot Research Report
 Dual Arm Robot Research Report Analytical Inverse Kinematics Solution for Moularize Dual-Arm Robot With offset at shouler an wrist Motivation an Abstract Generally, an inustrial manipulator such as PUMA
Dual Arm Robot Research Report Analytical Inverse Kinematics Solution for Moularize Dual-Arm Robot With offset at shouler an wrist Motivation an Abstract Generally, an inustrial manipulator such as PUMA
TO DUY ANH SHIP CALCULATION
 TO DUY ANH SHIP CALCULATION Ship Calculattion (1)-Space Cuvers 3D-curves play an important role in the engineering, design and manufature in Shipbuilding. Prior of the development of mathematical and computer
TO DUY ANH SHIP CALCULATION Ship Calculattion (1)-Space Cuvers 3D-curves play an important role in the engineering, design and manufature in Shipbuilding. Prior of the development of mathematical and computer
Generalized Edge Coloring for Channel Assignment in Wireless Networks
 Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu Institute of Information Science Acaemia Sinica Taipei, Taiwan Da-wei Wang Jan-Jan Wu Institute of Information Science
Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu Institute of Information Science Acaemia Sinica Taipei, Taiwan Da-wei Wang Jan-Jan Wu Institute of Information Science
Shift-map Image Registration
 Shift-map Image Registration Linus Svärm Petter Stranmark Centre for Mathematical Sciences, Lun University {linus,petter}@maths.lth.se Abstract Shift-map image processing is a new framework base on energy
Shift-map Image Registration Linus Svärm Petter Stranmark Centre for Mathematical Sciences, Lun University {linus,petter}@maths.lth.se Abstract Shift-map image processing is a new framework base on energy
Parameterization. Michael S. Floater. November 10, 2011
 Parameterization Michael S. Floater November 10, 2011 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to generate from point
Parameterization Michael S. Floater November 10, 2011 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to generate from point
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.eu 6.854J / 18.415J Avance Algorithms Fall 2008 For inormation about citing these materials or our Terms o Use, visit: http://ocw.mit.eu/terms. 18.415/6.854 Avance Algorithms
MIT OpenCourseWare http://ocw.mit.eu 6.854J / 18.415J Avance Algorithms Fall 2008 For inormation about citing these materials or our Terms o Use, visit: http://ocw.mit.eu/terms. 18.415/6.854 Avance Algorithms
Circular Arc Approximation by Quartic H-Bézier Curve
 Circular Arc Approximation by Quartic H-Bézier Curve Maria Hussain Department of Mathematics Lahore College for Women University, Pakistan maria.hussain@lcwu.edu.pk W. E. Ong School of Mathematical Sciences
Circular Arc Approximation by Quartic H-Bézier Curve Maria Hussain Department of Mathematics Lahore College for Women University, Pakistan maria.hussain@lcwu.edu.pk W. E. Ong School of Mathematical Sciences
CSE 167: Introduction to Computer Graphics Lecture #13: Curves. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017
 CSE 167: Introduction to Computer Graphics Lecture #13: Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Project 4 due Monday Nov 27 at 2pm Next Tuesday:
CSE 167: Introduction to Computer Graphics Lecture #13: Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2017 Announcements Project 4 due Monday Nov 27 at 2pm Next Tuesday:
Analysis of half-space range search using the k-d search skip list. Here we analyse the expected time for half-space
 Analysis of half-space range search using the k- search skip list Mario A. Lopez Brafor G. Nickerson y 1 Abstract We analyse the average cost of half-space range reporting for the k- search skip list.
Analysis of half-space range search using the k- search skip list Mario A. Lopez Brafor G. Nickerson y 1 Abstract We analyse the average cost of half-space range reporting for the k- search skip list.
Advanced method of NC programming for 5-axis machining
 Available online at www.scienceirect.com Proceia CIRP (0 ) 0 07 5 th CIRP Conference on High Performance Cutting 0 Avance metho of NC programming for 5-axis machining Sergej N. Grigoriev a, A.A. Kutin
Available online at www.scienceirect.com Proceia CIRP (0 ) 0 07 5 th CIRP Conference on High Performance Cutting 0 Avance metho of NC programming for 5-axis machining Sergej N. Grigoriev a, A.A. Kutin
CSE 167: Introduction to Computer Graphics Lecture #11: Bezier Curves. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016
 CSE 167: Introduction to Computer Graphics Lecture #11: Bezier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Project 3 due tomorrow Midterm 2 next
CSE 167: Introduction to Computer Graphics Lecture #11: Bezier Curves Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2016 Announcements Project 3 due tomorrow Midterm 2 next
MORA: a Movement-Based Routing Algorithm for Vehicle Ad Hoc Networks
 : a Movement-Base Routing Algorithm for Vehicle A Hoc Networks Fabrizio Granelli, Senior Member, Giulia Boato, Member, an Dzmitry Kliazovich, Stuent Member Abstract Recent interest in car-to-car communications
: a Movement-Base Routing Algorithm for Vehicle A Hoc Networks Fabrizio Granelli, Senior Member, Giulia Boato, Member, an Dzmitry Kliazovich, Stuent Member Abstract Recent interest in car-to-car communications
NURBS: Non-Uniform Rational B-Splines AUI Course Denbigh Starkey
 NURBS: Non-Uniform Rational B-Splines AUI Course Denbigh Starkey 1. Background 2 2. Definitions 3 3. Using NURBS to define a circle 4 4. Homogeneous coordinates & control points at infinity 9 5. Constructing
NURBS: Non-Uniform Rational B-Splines AUI Course Denbigh Starkey 1. Background 2 2. Definitions 3 3. Using NURBS to define a circle 4 4. Homogeneous coordinates & control points at infinity 9 5. Constructing
COMPUTER AIDED ENGINEERING DESIGN (BFF2612)
 COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
CS130 : Computer Graphics Curves (cont.) Tamar Shinar Computer Science & Engineering UC Riverside
 CS130 : Computer Graphics Curves (cont.) Tamar Shinar Computer Science & Engineering UC Riverside Blending Functions Blending functions are more convenient basis than monomial basis canonical form (monomial
CS130 : Computer Graphics Curves (cont.) Tamar Shinar Computer Science & Engineering UC Riverside Blending Functions Blending functions are more convenient basis than monomial basis canonical form (monomial
An Adaptive Routing Algorithm for Communication Networks using Back Pressure Technique
 International OPEN ACCESS Journal Of Moern Engineering Research (IJMER) An Aaptive Routing Algorithm for Communication Networks using Back Pressure Technique Khasimpeera Mohamme 1, K. Kalpana 2 1 M. Tech
International OPEN ACCESS Journal Of Moern Engineering Research (IJMER) An Aaptive Routing Algorithm for Communication Networks using Back Pressure Technique Khasimpeera Mohamme 1, K. Kalpana 2 1 M. Tech
State Indexed Policy Search by Dynamic Programming. Abstract. 1. Introduction. 2. System parameterization. Charles DuHadway
 State Inexe Policy Search by Dynamic Programming Charles DuHaway Yi Gu 5435537 503372 December 4, 2007 Abstract We consier the reinforcement learning problem of simultaneous trajectory-following an obstacle
State Inexe Policy Search by Dynamic Programming Charles DuHaway Yi Gu 5435537 503372 December 4, 2007 Abstract We consier the reinforcement learning problem of simultaneous trajectory-following an obstacle
Efficient Degree Elevation and Knot Insertion for B-spline Curves using Derivatives
 Efficient Degree Elevation and Knot Insertion for B-spline Curves using Derivatives Qi-Xing Huang a Shi-Min Hu a,1 Ralph R Martin b a Department of Computer Science and Technology, Tsinghua University,
Efficient Degree Elevation and Knot Insertion for B-spline Curves using Derivatives Qi-Xing Huang a Shi-Min Hu a,1 Ralph R Martin b a Department of Computer Science and Technology, Tsinghua University,
Iterative Computation of Moment Forms for Subdivision Surfaces
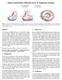 Iterative Computation of Moment Forms for Subivision Surfaces Jan P. Hakenberg ETH Zürich Ulrich Reif TU Darmstat Figure : Solis boune by Catmull-Clark an Loop subivision surfaces with centrois inicate
Iterative Computation of Moment Forms for Subivision Surfaces Jan P. Hakenberg ETH Zürich Ulrich Reif TU Darmstat Figure : Solis boune by Catmull-Clark an Loop subivision surfaces with centrois inicate
