Kidney Paired Donation: Optimal and Equitable Matchings in Bipartite Graphs
|
|
|
- Ashlyn Douglas
- 5 years ago
- Views:
Transcription
1 Rose-Hulman Undergraduate Mathematics Journal Volume 17 Issue 1 Article 11 Kidney Paired Donation: Optimal and Equitable Matchings in Bipartite Graphs Robert John Montgomery St. Lawrence University Follow this and additional works at: Recommended Citation Montgomery, Robert John (2016) "Kidney Paired Donation: Optimal and Equitable Matchings in Bipartite Graphs," Rose-Hulman Undergraduate Mathematics Journal: Vol. 17 : Iss. 1, Article 11. Available at:
2 ROSE- H ULMAN UNDERGRADUATE MATHEMATICS JOURNAL KIDNEY PAIRED DONATION: OPTIMAL AND EQUITABLE MATCHINGS IN BIPARTITE GRAPHS Robert John Montgomery a VOLUME 17, NO. 1, SPRING 2016 Sponsored by Rose-Hulman Institute of Technology Mathematics Department Terre Haute, IN mathjournal@rose-hulman.edu a St. Lawrence University
3 ROSE-HULMAN UNDERGRADUATE MATHEMATICS JOURNAL VOLUME 17, NO. 1, SPRING 2016 KIDNEY PAIRED DONATION: OPTIMAL AND EQUITABLE MATCHINGS IN BIPARTITE GRAPHS Robert John Montgomery Abstract. If a donor is not a good match for a kidney transplant recipient, the donor/recipient pair can be combined with other pairs to find a sequence of pairings that is more effective. The group of donor/recipient pairs, with information on the potential effectiveness of each match, forms a weighted bipartite graph. The Hungarian Algorithm allows us to find an optimal matching for such a graph, but the optimal outcome for the group might not be the most equitable for the individual patients involved. We examine several modifications to the Hungarian method which consider a balance between the optimal score for the group and the most uniformly equitable score for the individuals. Acknowledgements: I am especially grateful to my faculty sponsor, Patti Frazer Lock, who inspired my initial interest in Graph Theory, and has fed my curiosity ever since. She has had a profound impact on me as a mathematician and most importantly as a person. I would also like to thank my freshman year roommate Spencer Timerman for all the work he did programming the algorithms we developed. Finally, I would like to thank my summer internship sponsor, Dr. Segev of the Transplant Center at Johns Hopkins Hospital.
4 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE Introduction Kidney transplantation is widely accepted as the preferred treatment for the majority of patients with end stage renal disease [11]. Patients who experience kidney failure can survive on dialysis for extended periods of time; however, dialysis is both time intensive and expensive. Not only do patients grow physically weaker during their time on dialysis, but the treatments cost insurance providers, often Medicare, $51,000 annually per patient [7]. In addition, dialysis is not a viable long-term survival option for patients with kidney failure [5]. With the high success rate of kidney transplants, more patients are being encouraged to explore and pursue kidney transplantation as a treatment for end stage renal disease. Although the number of patients added to the deceased donor waiting list continues to increase, the rate at which organs become available remains relatively constant. There are currently over 99,000 patients on the deceased donor kidney waiting list in the United States. These kidney patients represent just over 80% of the total population of patients on the organ waiting list. Each year doctors perform roughly 14,000 kidney transplants, yet the number of patients on the waiting list continues to rise, leaving an annual gap of roughly 4,000 between the number of patients added to the list and transplants performed [9]. Thus, the world of transplantation is faced with a limited supply and increasing demand problem for a very unique commodity. As a result, alternative avenues need to be explored and utilized in order to more closely meet the need for organ donors. Often the best option for patients on the deceased donor waiting list is to explore live donor kidney transplantation. Patients who receive live donor kidneys have a significantly shorter wait time for transplantation than deceased donor kidney recipients [1]. In addition, live donor kidneys, on average, have five years greater functional life expectancy than deceased donor kidneys [3]. Live donor kidneys are often easier to match because a high percentage of the willing donors are family members of the patient, and thus have a higher probability of being a suitable match. As live donors are considered the best option for patients in need of kidney transplants, it becomes important to identify potential willing live donors for these patients. Proponents of organ donation continue to support many initiatives to increase the number of willing live donors. As initiatives attempt to increase the willingness of individuals to donate, it is important not to overlook a population of already willing donors who are turned away because they are not suitable matches for their intended recipients. Around 35% of people who volunteer to donate a kidney are not utilized because the individuals are not matches for their intended recipients [11]. The incompatibilities between potential pairs often stem from differences in blood type, but can also result from a number of other factors leading to high potential for organ rejection. This group of volunteers represents a population of people who are willing and ready to donate but, up until recent years, have not otherwise been utilized. In an attempt to employ this pool of
5 PAGE 160 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 donors, doctors have developed certain antirejection therapies, which allow for transplants to cross existing incompatible barriers. These techniques are only used in a limited number of transplant centers, as they carry risk in the administration, and the implementation requires certain expertise not widely mastered. At centers where the therapies are utilized, the process offers an alternative for hard to match patients, who would otherwise not be able to find a match. However, this may not be the best route for the general population of patients. Instead, if the patients and their non-matching willing donors are pooled together, the organs can be redistributed through a series of matches, which allow all the recipients in the group to receive a kidney. This type of matching, often referred to as kidney paired donation, relies on the willingness of potential donors to give kidneys as long as their intended recipients receive acceptable kidneys in return. Figure 1. A two-way kidney paired donation exchange An example of kidney paired donation is shown in Figure 1. This is a two-way exchange with two donors and two recipients, and represents the smallest number of patients possible to carry out an effective exchange under the kidney paired donation model. On the left side of Figure 1, donor 1 volunteers to donate to recipient 1, and the dotted line from the donor to the recipient represents intent to donate. Below donor 1 and recipient 1, an identical line connects donor 2 and recipient 2. Two pairs are formed between this group of four people, thus it can be said that a matching exists. However, both donors are not compatible matches for their intended recipients, due to some factor (in this basic example, blood type is used). Yet, donor 1 is an adequate match for recipient 2 and donor 2 is an adequate match for recipient 1. Therefore, as shown on the right image of Figure 1, if the donors agree to an arranged switch and each give a kidney to the intended recipient of the other donor, then both recipients are able to receive kidneys that match their blood types. This reassignment strategy can be applied to groups with larger numbers of patients, and it is in these cases with complex potential matches that opportunity exists for graph theory to play a significant role.
6 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 161 Using this type of exchange as our basis, we move to section 2, where we cover important graph theory concepts needed build our allocation strategies. Topics covered in section 2 include: bipartite graphs, perfect matchings, and minimum weight matching. In section 3, we introduce the Hungarian Algorithm for finding the minimum weight matching in a weighted bipartite graph, which serves as the basis for the allocation strategies we develop. Section 4 explores the ethical implications of using mathematical models to allocate kidneys. In this same section we propose Monty s Dilemma which focuses on the differences between predicted outcomes for patients within the context of a favorable group result, and the need to balance equity across patients within the group while still optimizing the resource. In section 5, we incorporate measures of spread to the analysis of matchings; in doing so, we introduce two original algorithmic alternatives to the Hungarian Algorithm. In section 6, we explain the methodology for comparing the results from 1,000 random trials using the three test algorithms. The results are analyzed in section 7, which support the proposition that the minimum weight matching algorithm does not always produce the best matching for a group of donors and recipients. We conclude with section 8, which places our result in the greater context of limited resource allocation. 2 Graph Theory Formulation Graph Theory provides us with a highly effective way to examine organ distribution and other forms of resource allocation. In a given graph, each vertex will represent an individual patient (donor or recipient), with each edge representing a potential for transplantation between a donor and a recipient. Figure 2 shows a graph with four donor-recipient pairs. The edges reveal which donors are potential matches for which recipients. Figure 2. Potential matches in a four-way kidney paired donation exchange
7 PAGE 162 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 The graphs used to represent the relationships between donors and recipients are bipartite graphs, since the vertices can be divided into two distinct vertex sets where no two vertices in the same set are adjacent to one another. Transplantation relies on a natural bipartition of donors and recipients, as the donors can only donate to recipients and the recipients can only receive organs from donors. From our graph of potential matches, we want to find a subgraph in which every vertex in the group of donors is paired with exactly one vertex in the group of recipients. Such a subgraph is called a perfect matching. Figure 3 shows two possible perfect matchings for the graph of all potential matches in Figure 2. Figure 3. Two possible matchings from the graph in Figure 2 As can be seen in both examples from Figure 3, every vertex is paired with another in the opposite set of vertices, ie. donors are uniquely connected to recipients. In this way, we are given potential pairings that satisfy the compatibilities established in Figure 2. As many of these graphs produce several perfect matchings, it becomes important to establish a system to differentiate the various possible perfect matchings for each graph. In doing so, we can ultimately choose the best matching. Doctors use a number of factors to discern the goodness of fit for a donor and recipient pair. The compatibilities between these patients fall upon a spectrum. A more favorable match indicates a higher probability for a patient s body to accept the organ. Factors that contribute to the favorability of a match include: blood type, HLA type, antigens, age, previous sensitization, and can even include considerations such as the ability and willingness of a patient to travel to other transplant centers for the procedure. In our model, these various classifications can be used in specialized scoring systems which rate the desirability of matches between potential donors and recipients. These scores can be added to the edges of the graphs to produce weighted bipartite graphs. The ways in which these pairings are scored can vary, and a decision must be made whether to use lower scores to represent more favorable matches, or higher scores to represent
8 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 163 more favorable matches. For this examination we chose to use a 20-point scale where a smaller score represents a more favorable match. Figure 4 shows a donor-recipient graph with weights added to the edges. Figure 4. Graph from Figure 2 with weights added Figure 5 shows two different matchings from the graph in Figure 4: one with the sum of the edge weights equal to 30 and one with the sum of the edge weights equal to 25. Since lower weights predict more favorable outcomes, we prefer perfect matchings with lower total weights, so the matching on the right, with a total score of 25, is preferable. A minimum weight matching is a matching for which the sum of the total weight of the edges in the matching is as small as possible. Fortunately, there exist several algorithms for finding a minimum weight perfect matching within a graph. Figure 5. Two potential matchings with weights from the graph in Figure 4
9 PAGE 164 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 3 Optimal Matchings and the Hungarian Algorithm Several algorithms exist to find a minimum weight perfect matching within a graph. The various algorithms are often specific to certain types of graphs, and the Hungarian Algorithm is a relatively simple algorithm which can find the maximum or minimum weight matching in a weighted bipartite graph. The details for the Hungarian Algorithm can be found in Kocay and Kreher [6], and are omitted here. We apply the algorithm to the randomly generated weighted bipartite graph with 8 donors and 8 recipients in Figure 6. The weights corresponding to the edges in Figure 6 are shown in Table 1 below. Figure 6. Randomly generated 8x8 weighted bipartite graph of donor and recipient pairings The capital letters on the left of Table 1 represent the donors, while the lowercase letters at the top of the columns represent the recipients. a b c d e f g h A B C D E F G H Table 1. Matrix representation of weighted bipartite graph in Figure 6
10 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 165 In order to run the algorithm we must have a complete bipartite graph, so all the spaces in the matrix must be assigned scores. We fill in all the empty spaces with dummy values. In this case we use 20, because it is the highest possible score in our scoring system and represents no match between the patients. The result of adding the dummy values is shown in Table 2. a b c d e f g h A B C D E F G H Table 2. Matrix representation of weighted bipartite graph with dummy values We are now able to run the Hungarian Algorithm on this matrix. (The Step-by-step process of running the Hungarian Algorithm on this matrix is given in Montgomery [10]). The minimum weight perfect matching for this set of donor/recipient pairs is given in matrix form in Table 3 (with optimal weights shown in red text) and in graphical form in Figure 7. a b c d e f g h A B C D E F G H Table 3. Matrix representation of the optimal matching from Table 1
11 PAGE 166 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 Figure 7. Graphical representation of the optimal matching from Table 1 The matrix in Table 3 and the graph in Figure 7 represent the optimal matching of the randomly generated graph in Figure 6. Each of the edges in the matching represents a pairing between a donor and a recipient, and thus all of the recipients are assigned a live donor. It is widely accepted that the above graph is the best possible matching for the weighted bipartite graph because it gives the perfect matching with the lowest total score (in this case 53). However, we feel that the current system overlooks certain favorable matchings and we ask to expand the definition of best matching to incorporate more than just the lowest possible overall score of the edges in the graph. 4 Ethical Considerations Algorithms such as the Hungarian Algorithm are used in situations where the overall score of the group is the principal concern. The solution given by the Hungarian Algorithm is at first an obvious option for assigning matchings of donors and recipients for transplantation. Yet the consideration of individual patients in the kidney paired donation process adds an additional layer to the decision of determining the best matching for a given graph. Consider the matching given by the Hungarian Algorithm in Figure 7. We know that this is the lowest possible score for the entire group, but it includes a 17, which is not an attractive score. Especially when this score
12 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 167 of 17 is considered in the context of the group where two recipients receive pairings with a value of 3, the person who receives the score of 17 will likely not be satisfied with the matching. The group of patients as a whole must be taken into account, as doctors look to maximize utility with the organs available for transplantation. Thus, the important consideration should be finding the matching which gives the best result for the group as a whole. However, in this situation, each individual has a strong interest in his or her score. As such, the recipients are intent on receiving the best possible match for themselves. The donors who agree to participate in the exchange also have a vested interest in the scores of their intended recipients. This is the rationale behind the dilemma that serves as the centerpiece of this examination. Monty s Dilemma: A Minimum Weight Bipartite Matching Algorithm can give the best overall matching for the group of vertices, but does not always give the most equitable matching across individual vertices. In the context of paired kidney donation, it is important that equal opportunity be taken into consideration for all members of the exchange. If a donor s intended recipient is given a pairing which is significantly less favorable than the other recipients in the matching, it is possible that the donor and recipient will not agree to be a part of the process. Perfect equity is not feasible in most situations, but attempting to give all pairs a relatively equal score will likely increase the satisfaction of the individuals who would otherwise receive less favorable scores at the expense of a better score for the group as a whole. Thus, with Monty s Dilemma in mind, we consider several alterations to the Hungarian Algorithm that attempt to include equity between individual scores. 5 Considering Equity: Modifying the Hungarian Algorithm In the context of this examination, when assessing the goodness of fit for the various possible matchings, three metrics are taken into account: total score, variance, and range. The reason for including the total score is explained earlier, as it shows the best results for the group as a whole. The variance and range of the scores in a given matching are the values by which we have chosen to measure how close the scores are to one another. Although they each measure slightly different aspects of the spread of scores, together they provide a more complete picture of the differences between the values. Thus, total score is our measure of utility whereas range and variance are used to measure equity. Figure 7 shows the minimum weight perfect matching, given by the Hungarian Algorithm, for the example in Section 3. Underneath the graph in Figure 7, we see that the total
13 PAGE 168 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 score of this matching is 53, the range is 14 (with a high of 17 and a low of 3), and the variance of the eight weights in this matching is 19. In addition to the preexisting Hungarian Algorithm, we propose two new algorithms, which account for these three measurements (range, variance, and total score) to varying degrees. For consistency, we test these algorithms on the same eight by eight matrix shown in both Figure 6 and Table 1. Each of the proposed algorithms begins with an adjustment made to the matrix set of edge weights to account for different priorities in outcomes, and then relies on the Hungarian Algorithm as the principal means for reducing the graph to a perfect matching. We have termed this process of adjusting the weights prior to running the algorithm front-end manipulation Minimum Difference From The Mean Algorithm The Hungarian Algorithm is known to give the optimal solution for the group in terms of minimal total score. We developed the Minimum Difference from The Mean Algorithm to give us a quantitative measure of the other extreme: the most equitable solution for the individuals. We do this by finding the matching with the smallest total variation (subject to integer round off). This algorithm focuses specifically on selecting a matching with edges whose weights are closest to the mean weight of all edges in the original graph. The algorithm ignores total score and instead attempts to reduce both the range and the variance. Minimum Difference from The Mean Algorithm 1. Arrange weights in matrix with donors on left and recipients on top and fill in empty spaces with dummy values; compute the mean of all scores. 2. Subtract the mean from each score in the matrix and take the absolute value. 3. Round all the scores to the nearest integer. 4. Apply Hungarian Algorithm. We illustrate the algorithm using the graph in Figure 6, with its matrix representation (with dummy values added) in Table 2. The mean of all the scores is 13.8, so we subtract 13.8 from all the scores in the matrix and take the absolute value to produce the matrix in Table 4. As the algorithm only works with integer values, we round each score in Table 4 to the nearest integer, producing the matrix in Table 5.
14 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 169 a b c d e f g h A B C D E F G H Table 4. The matrix of absolute values of differences between the scores and the mean a b c d e f g h A B C D E F G H Table 5. Matrix with scores rounded to nearest integer Table 5 represents the last step in the front-end manipulation portion of the Minimum Difference from The Mean Algorithm. Next we apply the Hungarian Algorithm to the matrix, and produce the matching shown in Table 6 and Figure 8. a b c d e f g h A B C D E F G H Table 6. Minimum Difference from The Mean Algorithm results in matrix form
15 PAGE 170 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 Figure 8. Minimum Difference from The Mean Algorithm results in graph form We see in the outcome given at the bottom of the graph in Figure 8 that the total score for this matching is 105, the range is 10, and the variance is As expected, the weights of edges from this matching are closer together than when the Hungarian Algorithm was used, resulting in both a reduced range and variance. However, the individual scores are much higher and this leads to a significantly higher total score for the matching. In using the Minimum Difference from The Mean Algorithm, the cost of bringing the values closer together has a disproportionally adverse impact on the overall score of the group of patients. This is not a tradeoff we are willing to make and we can do better. 5.2 Standard Deviation Cutoff Algorithm We now have an algorithm to give the minimum total score and an algorithm to give minimum variation. Our goal is to find an algorithm that prioritizes lower scores, since low is clearly better, while also giving some consideration to equity. After experimenting with multiple ideas, we developed the Standard Deviation Cutoff Algorithm. Like the Minimum Difference from The Mean Algorithm, the Standard Deviation Cutoff Algorithm attempts to reduce the range and variance. However, this algorithm gives preference to the smaller scores over the larger scores and in doing so places a greater emphasis on finding a matching which balances equity and total score. The algorithm begins by finding the interval
16 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 171 created by extending one standard deviation above and one standard deviation below the mean of all the scores. Scores that fall within this interval remain unchanged, but all scores that fall outside of this interval are doubled. This method essentially eliminates values that are greater than one standard deviation above the mean because the doubling has a much greater effect on larger values. It brings the remaining values closer together, as doubling smaller values has less of an effect, and the values that were one standard deviation below the mean are still in consideration under the subsequent steps of the algorithm. Standard Deviation Cutoff Algorithm 1. Arrange weights in matrix with donors on left and recipients on top and fill in empty spaces with dummy values (highest score). 2. Calculate the mean and standard deviation of all scores; compute the interval that is one standard deviation above and below the mean. 3. Double all values that fall more than one standard deviation away from the mean, leaving the other values unchanged. 4. Apply Hungarian Algorithm. We apply this algorithm to the same graph shown in Figure 6 with its matrix representation (with dummy values added) in Table 2. The mean of the scores in the matrix is and the standard deviation of the scores is This gives an interval from 7.34 to for values that fall within one standard deviation of the mean. Since the upper bound of one standard deviation from the mean is greater than 20, all the values greater than 7.34 will remain unchanged. However, in other graphs that were considered, the upper bound of one standard deviation from the mean was less than 20, and thus these larger values were doubled as well. The scores that fall more than one standard deviation from the mean are bolded and colored red in Table 7. Doubling the relevant scores produces the matrix in Table 8. a b c d e f g h A B C D E F G H Table 7. All values more than one standard deviation from the mean are bolded and red
17 PAGE 172 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 a b c d e f g h A B C D E F G H Table 8. The matrix with selected scores doubled Applying the Hungarian Algorithm to this matrix produces the matching shown in Table 9 and Figure 9. a b c d e f g h A B C D E F G H Table 9. Standard Deviation Cutoff Algorithm results in matrix form
18 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 173 Figure 9. Standard Deviation Cutoff Algorithm results in graph form In this matching, we see that the total score is 56 with a range of 10 and a variance of 11. The values are once again closer together than in the Hungarian Method and thus have a smaller range and variance. In the previous algorithm, the reduction in range and variance came at a high cost to the total score. This result is remarkable in that the total score only increased by 3 points, while reducing the range by 4 points and the variance by 8 points. We also see that the worst pairing in this matching is 12, significantly better than the worst pairing of 17 using the original Hungarian Method. This initial case shows that the Hungarian Algorithm does not always provide the best matching in the context of kidney paired donation, and suggests the need for a larger scale comparison between the algorithms. 6 Trial Parameters To test the effectiveness of each of the three algorithms (Hungarian, Minimum Difference from The Mean, and Standard Deviation Cutoff) we generated a large sample of random graphs. We decided to use bipartite graphs with sixteen vertices divided evenly between the two sets of vertices as this size reflects that of several kidney paired donation operations which have already been performed. Additionally, graphs of this size lend themselves to a greater number of potential matchings and a greater ability to differentiate between the effectiveness of the
19 PAGE 174 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 algorithms. To simulate real populations of donor and recipient pairs, the edges connecting the donors with their intended recipients were given the score of 20, which is equivalent to no match as these patients would likely not participate in these swaps if they were already a match with their partner. A quarter of the remaining scores were also randomly assigned the value of 20 to reflect the national incompatibility rates of patients. The remaining 42 edges in the graph were randomly assigned scores between 1 and 20. We randomly generated 1,000 graphs following this format. We then ran all graphs through the three algorithms: Hungarian, Minimum Difference from The Mean, and Standard Deviation Cutoff. With these results, we produced charts comparing the total score, range, and variance, between the algorithms. In several instances, a given algorithm produced more than one matching that had the same total score but different sets of edges comprising the matching. An example of this is shown in Figure 10 below which shows the weights of the eight selected edges as well as the total score, range, and variance for each case. Since two different matchings give the minimum total score, we must select which one to use and we term this approach to selection postoperative choice. Postoperative choice comes into play when there are multiple matching subgraphs which share the lowest possible score. In Figure 10, the choice would normally be trivial as both produce the same result for the group as a whole. However, in this case where we are focused on the importance of the individual vertices, and are attempting to introduce equity when possible, the selection holds real significance. When postoperative choice is an option, we choose the matching with the smallest variance as this demonstrates greater equity. For the matchings in Figure 10 we select the second option, producing a result with a significantly lower range and variance. [ 9,3,10,10, 2, 2,11, 9] Total Score: 56 Range: 9 Variance: 13.5 [ 8, 6,10, 6, 5,8, 6, 7] Total Score: 56 Range: 5 Variance: 2.25 Figure 10. Two matchings with equal total score; candidates for postoperative choice 7 Results To test the algorithms, we ran 1,000 randomly generated samples. The three metrics we considered were range, variance, and total score for the matchings given by each of our three algorithms. The output for one of these samples is shown in Appendix A. The output from the first 100 randomly generated graphs can be found in the comprehensive version of this report [10]. For each sample, we needed to determine at what point the reduction in range and variance
20 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 175 did or did not warrant the increase in total overall score. In doing so, we subjectively selected which algorithm gave the more favorable result for each sample. In the cases we examined, there were few results in which we couldn t determine an outright best option for the group as a whole. We define the best matching as the matching which balances both equity and optimization. If the cost of introducing equity is too high for the overall score, then we default to the optimal score given by the Hungarian Algorithm. However, if we can improve the equity by using the Standard Deviation Cutoff Algorithm without increasing the overall score by too much, then we select this second algorithm. Despite the heavy reliance on computers to provide the outputs from the algorithms, the selection of the best matchings is ultimately made at the discretion of the person charged with interpreting the data. We believe that using an equation to determine the best fit would be too restrictive in certain cases, and feel that this case-by-case analysis and determination is in keeping with the needs and practices of the medical world. In our simulations, the Hungarian Algorithm provided the best combination of optimization and equity most often. Of the 1,000 randomly generated graphs, 10 could not produce a perfect matching, so these were not considered, giving us a total of 990 trials. The results are shown below in Table 10. The Hungarian Algorithm gave the best result 565 times, which accounts for 57.1% of the trials. There were 320 graphs for which the Hungarian Algorithm gave the same result as the Standard Deviation Cutoff Algorithm, accounting for 32.3% of the trials. These graphs were placed in the Tie category, which indicates that either algorithm could have been used to give the best result. Finally, the Standard Deviation Cutoff Algorithm gave a better result in 105 graphs, which represent 10.6% of trials. Counts Percentages Hungarian % Tie % Standard Deviation Cutoff % Total 990 Table 10. Results for the three algorithms applied to 990 randomly generated graphs To illustrate how we selected which of the algorithms produced the best result, we show an assortment of eight trials in Table 11. Of these eight trials, the result from the Hungarian Algorithm was selected in five, the result from the Standard Deviation Cutoff Algorithm was selected in two, and one produced a tie. In Table 11, the selected method (or methods in the case of a tie) is shown in red text.
21 PAGE 176 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 Random Graph Score Range Variance Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Optimal Min Difference StDev Cutoff Table 11. Detailed results from 8 of the graphs produced in our sample of 990 Although the Hungarian Algorithm gave the best matching in the majority of cases, the Standard Deviation Cutoff Algorithm gave a more favorable matching in over 10% of the cases. The possibilities of deriving a matching using this and other methods are overlooked by limiting the matchings to only those produced by a minimum weight algorithm. Therefore, this examination recommends that when deciding which matching should be used for a group of patients, the results of both the Hungarian and Standard Deviation Cutoff Algorithms should be considered.
22 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE Conclusion In the process of arriving at the Minimum Difference from The Mean and Standard Deviation Cutoff algorithms, we formulated several other algorithms to focus on the same variables (range, variance, and total score) in different ways. One such version used the idea that a recipient shouldn t compare his or her scores in the matchings with those of the other recipients, but instead with the possible scores available to him or her in the original graph. In this algorithm, we tried to adjust the values in the matrices by changing each column depending on what values were available to each recipient. In doing so, the hope was that we would establish a multidimensional form of equity that took into consideration the potential for each recipient. We found the minimum value of each column and subtracted these values plus 1 from each respective column. However, the manipulations we made prior to running the Hungarian Algorithm had no effect, and we produced identical results to running the Hungarian Algorithm alone. Although the execution did not pan out, there may still be effective ways to capture this comparison. This algorithm represented one of several we developed which did not produce significant results; however, we encourage further examination of these ideas. Additionally, as the medical field progresses, we will understand more about the viability of different matches. We might find that there is a breaking point such that, for example, donor-recipient pairs with a score greater than 12 have a much lower chance of success than those with a score less than 12. This might argue for modifying the Standard Deviation Cutoff Algorithm to double all scores greater than 12. We need to continue to develop dynamic algorithms that have the capability to evolve and incorporate new information. We have focused on the problem of allocating live donor kidneys to patients in need of a kidney transplant, but we believe this idea of balancing equity and optimality in matchings has applications in a wide variety of other fields. There exist many situations, both within and outside of medicine, that require the allocation of limited special resources, and they range from financial aid disbursement to providing relief services following a natural disaster. Cases such as these often carry strong ethical implications and the option of constructing a matching that is close to optimal while being more uniformly equitable can be desirable. We hope that this examination has served as the introduction to a much larger discussion of incorporating equity into kidney paired donation and other forms of unique resource allocation modeling.
23 PAGE 178 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 References [1] Benefits of Living Donation. Comprehensive Transplant Center. Johns Hopkins Medicine, n.d. Web. 2 May [2] Bondy, J.A., and U.S.R. Murty. Graph Theory with Applications. New York: American Elsevier Publishing Co., Print. [3] Garonzik-Wang, Jacqueline, Robert A. Montgomery, Lauren Kucirka, Jonathan Berger, Daniel Warren, and Dorry Segev. Incompatible Live-Donor Kidney Transplantation in the United States: Results of a National Survey. Clinical Journal of the American Society of Nephrology 6.8 (2011): Web. 2 May [4] Gibbons, Alan. Algorithmic Graph Theory. Cambridge: Cambridge University Press, Print. [5] Eggers, P.W. Mortality rates among dialysis patients in Medicare s End-Stage Renal Disease Program. American Journal of Kidney Disease 15.5 (1990): Web. 6 Apr [6] Kocay, William, and Donald L. Kreher. Graphs, Alographs, and Optimization. Boca Raton: Chapman & Hall/CRC, Print. [7] Lee, Helen, Braden Manns, Ken Taub, William Ghali, Staffon Dean, David Johnson, and Cam Donaldson. Cost analysis of ongoing care of patients with end-stage renal disease: The impact of dialysis modality and dialysis access. American Journal of Kidney Disease 40.3 (2002): Web. 7 May [8] Lovasz, Laszlo, and Michael D. Plummer. Matching Theory. Providence: AMS Chelsea Publishing, Print. [9] Organ Donation and Transplant Statistics. National Kidney Foundation, Jan Web. 2 May [10] Montgomery, R.J., Kidney Paired Donation: Optimal and Equitable Matchings in Bipartite Graphs, Honors Thesis, St. Lawrence University, [11] Segev, Dorry, Sommer Gentry, Daniel Warren, Brigitte Reeb, and Robert A. Montgomery. Kidney Paired Donation and Optimizing the Use of Live Donor Organs. JAMA (2005): Web. 5 Dec
24 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 179 Appendix A: Annotated Computer Output [ x8 randomly generated matrix ] Hungarian: [(0, 6), (1, 7), (2, 0), (3, 5), (4, 2), (5, 4), (6, 3), (7, 1)] edges selected by algorithm [8, 3, 6, 4, 9, 2, 1, 12] values selected by algorithm [(45, 0, 11, )] [(total score, total score-optimal score, range, variance)] [(0, 6), (1, 7), (2, 3), (3, 5), (4, 2), (5, 4), (6, 0), (7, 1)] [8, 3, 6, 4, 9, 2, 1, 12] [(45, 0, 11, )] Min Diff: [(0, 4), (1, 6), (2, 5), (3, 0), (4, 1), (5, 7), (6, 2), (7, 3)] [18, 13, 11, 11, 13, 12, 11, 13] [(102, 57, 7, )] Std Dev Cutoff: [(0, 6), (1, 5), (2, 1), (3, 7), (4, 2), (5, 4), (6, 0), (7, 3)] [8, 8, 8, 1, 9, 2, 1, 13] [(50, 5, 12, )]
1 Introduction RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 159
 RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 159 1 Introduction Kidney transplantation is widely accepted as the preferred treatment for the majority of patients with end stage renal disease [11]. Patients
RHIT UNDERGRAD. MATH. J., VOL. 17, NO. 1 PAGE 159 1 Introduction Kidney transplantation is widely accepted as the preferred treatment for the majority of patients with end stage renal disease [11]. Patients
A Study of the Shortest Perimeter Polyhedron
 Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue Article 3 A Study of the Shortest Perimeter Polyhedron Kaitlyn Burk Lee University, kburk000@leeu.edu Adam Carty Lee University Austin Wheeler
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue Article 3 A Study of the Shortest Perimeter Polyhedron Kaitlyn Burk Lee University, kburk000@leeu.edu Adam Carty Lee University Austin Wheeler
arxiv: v3 [cs.gt] 22 Oct 2017
![arxiv: v3 [cs.gt] 22 Oct 2017 arxiv: v3 [cs.gt] 22 Oct 2017](/thumbs/81/84345664.jpg) Maximum Matchings in Graphs for Allocating Kidney Paired Donation arxiv:1710.00953v3 [cs.gt] 22 Oct 2017 Sommer Gentry Mathematics Department, United States Naval Academy, Annapolis MD 21402, gentry@usna.edu
Maximum Matchings in Graphs for Allocating Kidney Paired Donation arxiv:1710.00953v3 [cs.gt] 22 Oct 2017 Sommer Gentry Mathematics Department, United States Naval Academy, Annapolis MD 21402, gentry@usna.edu
Squaring The Circle In The Hyperbolic Disk
 Rose-Hulman Undergraduate Mathematics Journal Volume 15 Issue 1 Article 2 Squaring The Circle In The Hyperbolic Disk Noah Davis Aquinas College, nkd001@aquinas.edu Follow this and additional works at:
Rose-Hulman Undergraduate Mathematics Journal Volume 15 Issue 1 Article 2 Squaring The Circle In The Hyperbolic Disk Noah Davis Aquinas College, nkd001@aquinas.edu Follow this and additional works at:
HARNESSING CERTAINTY TO SPEED TASK-ALLOCATION ALGORITHMS FOR MULTI-ROBOT SYSTEMS
 HARNESSING CERTAINTY TO SPEED TASK-ALLOCATION ALGORITHMS FOR MULTI-ROBOT SYSTEMS An Undergraduate Research Scholars Thesis by DENISE IRVIN Submitted to the Undergraduate Research Scholars program at Texas
HARNESSING CERTAINTY TO SPEED TASK-ALLOCATION ALGORITHMS FOR MULTI-ROBOT SYSTEMS An Undergraduate Research Scholars Thesis by DENISE IRVIN Submitted to the Undergraduate Research Scholars program at Texas
Constructing Mobius Transformations with Spheres
 Rose-Hulman Undergraduate Mathematics Journal Volume 13 Issue 2 Article 8 Constructing Mobius Transformations with pheres Rob iliciano Princeton University, rsilicia@princeton.edu Follow this and additional
Rose-Hulman Undergraduate Mathematics Journal Volume 13 Issue 2 Article 8 Constructing Mobius Transformations with pheres Rob iliciano Princeton University, rsilicia@princeton.edu Follow this and additional
Modeling Plant Succession with Markov Matrices
 Modeling Plant Succession with Markov Matrices 1 Modeling Plant Succession with Markov Matrices Concluding Paper Undergraduate Biology and Math Training Program New Jersey Institute of Technology Catherine
Modeling Plant Succession with Markov Matrices 1 Modeling Plant Succession with Markov Matrices Concluding Paper Undergraduate Biology and Math Training Program New Jersey Institute of Technology Catherine
The Edge Slide Graph of the 3-cube
 Rose-Hulman Undergraduate Mathematics Journal Volume 12 Issue 2 Article 6 The Edge Slide Graph of the 3-cube Lyndal Henden Massey University, Palmerston North, New Zealand, lyndal_henden@hotmail.com Follow
Rose-Hulman Undergraduate Mathematics Journal Volume 12 Issue 2 Article 6 The Edge Slide Graph of the 3-cube Lyndal Henden Massey University, Palmerston North, New Zealand, lyndal_henden@hotmail.com Follow
Klein Links and Braids
 Rose- Hulman Undergraduate Mathematics Journal Klein Links and Braids David Freund a Sarah Smith-Polderman b Volume 14, No. 1, Spring 2013 Sponsored by Rose-Hulman Institute of Technology Department of
Rose- Hulman Undergraduate Mathematics Journal Klein Links and Braids David Freund a Sarah Smith-Polderman b Volume 14, No. 1, Spring 2013 Sponsored by Rose-Hulman Institute of Technology Department of
Extremal Graph Theory: Turán s Theorem
 Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Heuristic Approaches for Multi-Criteria Optimisation in Kidney Exchange Programs
 21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 Nov to 4 Dec 2015 www.mssanz.org.au/modsim2015 Heuristic Approaches for Multi-Criteria Optimisation in Kidney Exchange
21st International Congress on Modelling and Simulation, Gold Coast, Australia, 29 Nov to 4 Dec 2015 www.mssanz.org.au/modsim2015 Heuristic Approaches for Multi-Criteria Optimisation in Kidney Exchange
Distributions of random variables
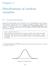 Chapter 3 Distributions of random variables 31 Normal distribution Among all the distributions we see in practice, one is overwhelmingly the most common The symmetric, unimodal, bell curve is ubiquitous
Chapter 3 Distributions of random variables 31 Normal distribution Among all the distributions we see in practice, one is overwhelmingly the most common The symmetric, unimodal, bell curve is ubiquitous
September 11, Unit 2 Day 1 Notes Measures of Central Tendency.notebook
 Measures of Central Tendency: Mean, Median, Mode and Midrange A Measure of Central Tendency is a value that represents a typical or central entry of a data set. Four most commonly used measures of central
Measures of Central Tendency: Mean, Median, Mode and Midrange A Measure of Central Tendency is a value that represents a typical or central entry of a data set. Four most commonly used measures of central
Directed Graphs of Commutative Rings
 Rose-Hulman Undergraduate Mathematics Journal Volume 14 Issue 2 Article 11 Directed Graphs of Commutative Rings Seth Hausken University of St. Thomas, hauskenseth@gmail.com Jared Skinner University of
Rose-Hulman Undergraduate Mathematics Journal Volume 14 Issue 2 Article 11 Directed Graphs of Commutative Rings Seth Hausken University of St. Thomas, hauskenseth@gmail.com Jared Skinner University of
Particle Swarm Optimization applied to Pattern Recognition
 Particle Swarm Optimization applied to Pattern Recognition by Abel Mengistu Advisor: Dr. Raheel Ahmad CS Senior Research 2011 Manchester College May, 2011-1 - Table of Contents Introduction... - 3 - Objectives...
Particle Swarm Optimization applied to Pattern Recognition by Abel Mengistu Advisor: Dr. Raheel Ahmad CS Senior Research 2011 Manchester College May, 2011-1 - Table of Contents Introduction... - 3 - Objectives...
Downloaded from
 UNIT 2 WHAT IS STATISTICS? Researchers deal with a large amount of data and have to draw dependable conclusions on the basis of data collected for the purpose. Statistics help the researchers in making
UNIT 2 WHAT IS STATISTICS? Researchers deal with a large amount of data and have to draw dependable conclusions on the basis of data collected for the purpose. Statistics help the researchers in making
MAT 142 College Mathematics. Module ST. Statistics. Terri Miller revised July 14, 2015
 MAT 142 College Mathematics Statistics Module ST Terri Miller revised July 14, 2015 2 Statistics Data Organization and Visualization Basic Terms. A population is the set of all objects under study, a sample
MAT 142 College Mathematics Statistics Module ST Terri Miller revised July 14, 2015 2 Statistics Data Organization and Visualization Basic Terms. A population is the set of all objects under study, a sample
of Nebraska - Lincoln
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership -007 The Polygon Game Kyla Hall Follow this and additional
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership -007 The Polygon Game Kyla Hall Follow this and additional
Tangent circles in the hyperbolic disk
 Rose-Hulman Undergraduate Mathematics Journal Volume 14 Issue 1 Article 2 Tangent circles in the hyperbolic disk Megan Ternes Aquinas College, meganternes@yahoo.com Follow this and additional works at:
Rose-Hulman Undergraduate Mathematics Journal Volume 14 Issue 1 Article 2 Tangent circles in the hyperbolic disk Megan Ternes Aquinas College, meganternes@yahoo.com Follow this and additional works at:
ANNUAL REPORT OF HAIL STUDIES NEIL G, TOWERY AND RAND I OLSON. Report of Research Conducted. 15 May May For. The Country Companies
 ISWS CR 182 Loan c.l ANNUAL REPORT OF HAIL STUDIES BY NEIL G, TOWERY AND RAND I OLSON Report of Research Conducted 15 May 1976-14 May 1977 For The Country Companies May 1977 ANNUAL REPORT OF HAIL STUDIES
ISWS CR 182 Loan c.l ANNUAL REPORT OF HAIL STUDIES BY NEIL G, TOWERY AND RAND I OLSON Report of Research Conducted 15 May 1976-14 May 1977 For The Country Companies May 1977 ANNUAL REPORT OF HAIL STUDIES
A genetic algorithm for kidney transplantation matching
 A genetic algorithm for kidney transplantation matching S. Goezinne Research Paper Business Analytics Supervisors: R. Bekker and K. Glorie March 2016 VU Amsterdam Faculty of Exact Sciences De Boelelaan
A genetic algorithm for kidney transplantation matching S. Goezinne Research Paper Business Analytics Supervisors: R. Bekker and K. Glorie March 2016 VU Amsterdam Faculty of Exact Sciences De Boelelaan
Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded
 Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded Cemil Dibek Tınaz Ekim Pinar Heggernes Abstract We determine the maximum number of edges that a claw-free
Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded Cemil Dibek Tınaz Ekim Pinar Heggernes Abstract We determine the maximum number of edges that a claw-free
1 The Arthur-Merlin Story
 Comp 260: Advanced Algorithms Tufts University, Spring 2011 Prof. Lenore Cowen Scribe: Andrew Winslow Lecture 1: Perfect and Stable Marriages 1 The Arthur-Merlin Story In the land ruled by the legendary
Comp 260: Advanced Algorithms Tufts University, Spring 2011 Prof. Lenore Cowen Scribe: Andrew Winslow Lecture 1: Perfect and Stable Marriages 1 The Arthur-Merlin Story In the land ruled by the legendary
Distributions of Continuous Data
 C H A P T ER Distributions of Continuous Data New cars and trucks sold in the United States average about 28 highway miles per gallon (mpg) in 2010, up from about 24 mpg in 2004. Some of the improvement
C H A P T ER Distributions of Continuous Data New cars and trucks sold in the United States average about 28 highway miles per gallon (mpg) in 2010, up from about 24 mpg in 2004. Some of the improvement
Complementary Graph Coloring
 International Journal of Computer (IJC) ISSN 2307-4523 (Print & Online) Global Society of Scientific Research and Researchers http://ijcjournal.org/ Complementary Graph Coloring Mohamed Al-Ibrahim a*,
International Journal of Computer (IJC) ISSN 2307-4523 (Print & Online) Global Society of Scientific Research and Researchers http://ijcjournal.org/ Complementary Graph Coloring Mohamed Al-Ibrahim a*,
An Edge-Swap Heuristic for Finding Dense Spanning Trees
 Theory and Applications of Graphs Volume 3 Issue 1 Article 1 2016 An Edge-Swap Heuristic for Finding Dense Spanning Trees Mustafa Ozen Bogazici University, mustafa.ozen@boun.edu.tr Hua Wang Georgia Southern
Theory and Applications of Graphs Volume 3 Issue 1 Article 1 2016 An Edge-Swap Heuristic for Finding Dense Spanning Trees Mustafa Ozen Bogazici University, mustafa.ozen@boun.edu.tr Hua Wang Georgia Southern
Chapter 3 Analyzing Normal Quantitative Data
 Chapter 3 Analyzing Normal Quantitative Data Introduction: In chapters 1 and 2, we focused on analyzing categorical data and exploring relationships between categorical data sets. We will now be doing
Chapter 3 Analyzing Normal Quantitative Data Introduction: In chapters 1 and 2, we focused on analyzing categorical data and exploring relationships between categorical data sets. We will now be doing
H. W. Kuhn. Bryn Mawr College
 VARIANTS OF THE HUNGARIAN METHOD FOR ASSIGNMENT PROBLEMS' H. W. Kuhn Bryn Mawr College The author presents a geometrical modelwhich illuminates variants of the Hungarian method for the solution of the
VARIANTS OF THE HUNGARIAN METHOD FOR ASSIGNMENT PROBLEMS' H. W. Kuhn Bryn Mawr College The author presents a geometrical modelwhich illuminates variants of the Hungarian method for the solution of the
Incorporating Known Pathways into Gene Clustering Algorithms for Genetic Expression Data
 Incorporating Known Pathways into Gene Clustering Algorithms for Genetic Expression Data Ryan Atallah, John Ryan, David Aeschlimann December 14, 2013 Abstract In this project, we study the problem of classifying
Incorporating Known Pathways into Gene Clustering Algorithms for Genetic Expression Data Ryan Atallah, John Ryan, David Aeschlimann December 14, 2013 Abstract In this project, we study the problem of classifying
CPSC 536N: Randomized Algorithms Term 2. Lecture 5
 CPSC 536N: Randomized Algorithms 2011-12 Term 2 Prof. Nick Harvey Lecture 5 University of British Columbia In this lecture we continue to discuss applications of randomized algorithms in computer networking.
CPSC 536N: Randomized Algorithms 2011-12 Term 2 Prof. Nick Harvey Lecture 5 University of British Columbia In this lecture we continue to discuss applications of randomized algorithms in computer networking.
Sources for this lecture. 3. Matching in bipartite and general graphs. Symmetric difference
 S-72.2420 / T-79.5203 Matching in bipartite and general graphs 1 3. Matching in bipartite and general graphs Let G be a graph. A matching M in G is a set of nonloop edges with no shared endpoints. Let
S-72.2420 / T-79.5203 Matching in bipartite and general graphs 1 3. Matching in bipartite and general graphs Let G be a graph. A matching M in G is a set of nonloop edges with no shared endpoints. Let
HEURISTIC OPTIMIZATION USING COMPUTER SIMULATION: A STUDY OF STAFFING LEVELS IN A PHARMACEUTICAL MANUFACTURING LABORATORY
 Proceedings of the 1998 Winter Simulation Conference D.J. Medeiros, E.F. Watson, J.S. Carson and M.S. Manivannan, eds. HEURISTIC OPTIMIZATION USING COMPUTER SIMULATION: A STUDY OF STAFFING LEVELS IN A
Proceedings of the 1998 Winter Simulation Conference D.J. Medeiros, E.F. Watson, J.S. Carson and M.S. Manivannan, eds. HEURISTIC OPTIMIZATION USING COMPUTER SIMULATION: A STUDY OF STAFFING LEVELS IN A
Data Analysis and Solver Plugins for KSpread USER S MANUAL. Tomasz Maliszewski
 Data Analysis and Solver Plugins for KSpread USER S MANUAL Tomasz Maliszewski tmaliszewski@wp.pl Table of Content CHAPTER 1: INTRODUCTION... 3 1.1. ABOUT DATA ANALYSIS PLUGIN... 3 1.3. ABOUT SOLVER PLUGIN...
Data Analysis and Solver Plugins for KSpread USER S MANUAL Tomasz Maliszewski tmaliszewski@wp.pl Table of Content CHAPTER 1: INTRODUCTION... 3 1.1. ABOUT DATA ANALYSIS PLUGIN... 3 1.3. ABOUT SOLVER PLUGIN...
The Oberwolfach Problem in Graph Theory
 The Oberwolfach Problem in Graph Theory Andrea Zentz Andrea Zentz graduated Magna Cum Laude from Ball State in May with a major in Mathematics Education. She plans to work as a teacher while eventually
The Oberwolfach Problem in Graph Theory Andrea Zentz Andrea Zentz graduated Magna Cum Laude from Ball State in May with a major in Mathematics Education. She plans to work as a teacher while eventually
Prepare a stem-and-leaf graph for the following data. In your final display, you should arrange the leaves for each stem in increasing order.
 Chapter 2 2.1 Descriptive Statistics A stem-and-leaf graph, also called a stemplot, allows for a nice overview of quantitative data without losing information on individual observations. It can be a good
Chapter 2 2.1 Descriptive Statistics A stem-and-leaf graph, also called a stemplot, allows for a nice overview of quantitative data without losing information on individual observations. It can be a good
An Initial Seed Selection Algorithm for K-means Clustering of Georeferenced Data to Improve
 An Initial Seed Selection Algorithm for K-means Clustering of Georeferenced Data to Improve Replicability of Cluster Assignments for Mapping Application Fouad Khan Central European University-Environmental
An Initial Seed Selection Algorithm for K-means Clustering of Georeferenced Data to Improve Replicability of Cluster Assignments for Mapping Application Fouad Khan Central European University-Environmental
Math 120 Introduction to Statistics Mr. Toner s Lecture Notes 3.1 Measures of Central Tendency
 Math 1 Introduction to Statistics Mr. Toner s Lecture Notes 3.1 Measures of Central Tendency lowest value + highest value midrange The word average: is very ambiguous and can actually refer to the mean,
Math 1 Introduction to Statistics Mr. Toner s Lecture Notes 3.1 Measures of Central Tendency lowest value + highest value midrange The word average: is very ambiguous and can actually refer to the mean,
CS 224W Final Report Group 37
 1 Introduction CS 224W Final Report Group 37 Aaron B. Adcock Milinda Lakkam Justin Meyer Much of the current research is being done on social networks, where the cost of an edge is almost nothing; the
1 Introduction CS 224W Final Report Group 37 Aaron B. Adcock Milinda Lakkam Justin Meyer Much of the current research is being done on social networks, where the cost of an edge is almost nothing; the
Data can be in the form of numbers, words, measurements, observations or even just descriptions of things.
 + What is Data? Data is a collection of facts. Data can be in the form of numbers, words, measurements, observations or even just descriptions of things. In most cases, data needs to be interpreted and
+ What is Data? Data is a collection of facts. Data can be in the form of numbers, words, measurements, observations or even just descriptions of things. In most cases, data needs to be interpreted and
Squaring the Circle in Elliptic Geometry
 Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 2 Article 1 Squaring the Circle in Elliptic Geometry Noah Davis Aquinas College Kyle Jansens Aquinas College, kyle.jansens@aquinas.edu Follow
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 2 Article 1 Squaring the Circle in Elliptic Geometry Noah Davis Aquinas College Kyle Jansens Aquinas College, kyle.jansens@aquinas.edu Follow
Mail Findings. Australia Post Consumer Survey. Research into consumer preferences of transactional communications
 Australia Post Consumer Survey Mail Findings August 2013 Australia Post Consumer Survey Mail Findings Research into consumer preferences of transactional communications Methodology The Australia Post Consumer
Australia Post Consumer Survey Mail Findings August 2013 Australia Post Consumer Survey Mail Findings Research into consumer preferences of transactional communications Methodology The Australia Post Consumer
Raw Data is data before it has been arranged in a useful manner or analyzed using statistical techniques.
 Section 2.1 - Introduction Graphs are commonly used to organize, summarize, and analyze collections of data. Using a graph to visually present a data set makes it easy to comprehend and to describe the
Section 2.1 - Introduction Graphs are commonly used to organize, summarize, and analyze collections of data. Using a graph to visually present a data set makes it easy to comprehend and to describe the
New Trials on Test Data Generation: Analysis of Test Data Space and Design of Improved Algorithm
 New Trials on Test Data Generation: Analysis of Test Data Space and Design of Improved Algorithm So-Yeong Jeon 1 and Yong-Hyuk Kim 2,* 1 Department of Computer Science, Korea Advanced Institute of Science
New Trials on Test Data Generation: Analysis of Test Data Space and Design of Improved Algorithm So-Yeong Jeon 1 and Yong-Hyuk Kim 2,* 1 Department of Computer Science, Korea Advanced Institute of Science
MAT 110 WORKSHOP. Updated Fall 2018
 MAT 110 WORKSHOP Updated Fall 2018 UNIT 3: STATISTICS Introduction Choosing a Sample Simple Random Sample: a set of individuals from the population chosen in a way that every individual has an equal chance
MAT 110 WORKSHOP Updated Fall 2018 UNIT 3: STATISTICS Introduction Choosing a Sample Simple Random Sample: a set of individuals from the population chosen in a way that every individual has an equal chance
A Fuzzy Logic Approach to Assembly Line Balancing
 Mathware & Soft Computing 12 (2005), 57-74 A Fuzzy Logic Approach to Assembly Line Balancing D.J. Fonseca 1, C.L. Guest 1, M. Elam 1, and C.L. Karr 2 1 Department of Industrial Engineering 2 Department
Mathware & Soft Computing 12 (2005), 57-74 A Fuzzy Logic Approach to Assembly Line Balancing D.J. Fonseca 1, C.L. Guest 1, M. Elam 1, and C.L. Karr 2 1 Department of Industrial Engineering 2 Department
WELCOME! Lecture 3 Thommy Perlinger
 Quantitative Methods II WELCOME! Lecture 3 Thommy Perlinger Program Lecture 3 Cleaning and transforming data Graphical examination of the data Missing Values Graphical examination of the data It is important
Quantitative Methods II WELCOME! Lecture 3 Thommy Perlinger Program Lecture 3 Cleaning and transforming data Graphical examination of the data Missing Values Graphical examination of the data It is important
Challenges of Analyzing Parametric CFD Results. White Paper Published: January
 Challenges of Analyzing Parametric CFD Results White Paper Published: January 2011 www.tecplot.com Contents Introduction... 3 Parametric CFD Analysis: A Methodology Poised for Growth... 4 Challenges of
Challenges of Analyzing Parametric CFD Results White Paper Published: January 2011 www.tecplot.com Contents Introduction... 3 Parametric CFD Analysis: A Methodology Poised for Growth... 4 Challenges of
Towards Systematic Usability Verification
 Towards Systematic Usability Verification Max Möllers RWTH Aachen University 52056 Aachen, Germany max@cs.rwth-aachen.de Jonathan Diehl RWTH Aachen University 52056 Aachen, Germany diehl@cs.rwth-aachen.de
Towards Systematic Usability Verification Max Möllers RWTH Aachen University 52056 Aachen, Germany max@cs.rwth-aachen.de Jonathan Diehl RWTH Aachen University 52056 Aachen, Germany diehl@cs.rwth-aachen.de
CONSECUTIVE INTEGERS AND THE COLLATZ CONJECTURE. Marcus Elia Department of Mathematics, SUNY Geneseo, Geneseo, NY
 CONSECUTIVE INTEGERS AND THE COLLATZ CONJECTURE Marcus Elia Department of Mathematics, SUNY Geneseo, Geneseo, NY mse1@geneseo.edu Amanda Tucker Department of Mathematics, University of Rochester, Rochester,
CONSECUTIVE INTEGERS AND THE COLLATZ CONJECTURE Marcus Elia Department of Mathematics, SUNY Geneseo, Geneseo, NY mse1@geneseo.edu Amanda Tucker Department of Mathematics, University of Rochester, Rochester,
Robustness of Centrality Measures for Small-World Networks Containing Systematic Error
 Robustness of Centrality Measures for Small-World Networks Containing Systematic Error Amanda Lannie Analytical Systems Branch, Air Force Research Laboratory, NY, USA Abstract Social network analysis is
Robustness of Centrality Measures for Small-World Networks Containing Systematic Error Amanda Lannie Analytical Systems Branch, Air Force Research Laboratory, NY, USA Abstract Social network analysis is
Allstate Insurance Claims Severity: A Machine Learning Approach
 Allstate Insurance Claims Severity: A Machine Learning Approach Rajeeva Gaur SUNet ID: rajeevag Jeff Pickelman SUNet ID: pattern Hongyi Wang SUNet ID: hongyiw I. INTRODUCTION The insurance industry has
Allstate Insurance Claims Severity: A Machine Learning Approach Rajeeva Gaur SUNet ID: rajeevag Jeff Pickelman SUNet ID: pattern Hongyi Wang SUNet ID: hongyiw I. INTRODUCTION The insurance industry has
ANNUAL PROGRAM REPORT. Multiple and Single Subject Credential Programs. Credential programs are not subject to 5 year reviews
 ACADEMIC SENATE Committee on Academic Planning and Review ANNUAL PROGRAM REPORT College Department Program CEAS Teacher Education Multiple and Single Subject Credential Programs Reporting for Academic
ACADEMIC SENATE Committee on Academic Planning and Review ANNUAL PROGRAM REPORT College Department Program CEAS Teacher Education Multiple and Single Subject Credential Programs Reporting for Academic
Rectangular Matrix Multiplication Revisited
 JOURNAL OF COMPLEXITY, 13, 42 49 (1997) ARTICLE NO. CM970438 Rectangular Matrix Multiplication Revisited Don Coppersmith IBM Research, T. J. Watson Research Center, Yorktown Heights, New York 10598 Received
JOURNAL OF COMPLEXITY, 13, 42 49 (1997) ARTICLE NO. CM970438 Rectangular Matrix Multiplication Revisited Don Coppersmith IBM Research, T. J. Watson Research Center, Yorktown Heights, New York 10598 Received
STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I. 4 th Nine Weeks,
 STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I 4 th Nine Weeks, 2016-2017 1 OVERVIEW Algebra I Content Review Notes are designed by the High School Mathematics Steering Committee as a resource for
STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I 4 th Nine Weeks, 2016-2017 1 OVERVIEW Algebra I Content Review Notes are designed by the High School Mathematics Steering Committee as a resource for
GUIDELINES FOR MASTER OF SCIENCE INTERNSHIP THESIS
 GUIDELINES FOR MASTER OF SCIENCE INTERNSHIP THESIS Dear Participant of the MScIS Program, If you have chosen to follow an internship, one of the requirements is to write a Thesis. This document gives you
GUIDELINES FOR MASTER OF SCIENCE INTERNSHIP THESIS Dear Participant of the MScIS Program, If you have chosen to follow an internship, one of the requirements is to write a Thesis. This document gives you
Univariate Statistics Summary
 Further Maths Univariate Statistics Summary Types of Data Data can be classified as categorical or numerical. Categorical data are observations or records that are arranged according to category. For example:
Further Maths Univariate Statistics Summary Types of Data Data can be classified as categorical or numerical. Categorical data are observations or records that are arranged according to category. For example:
8/3/2017. Contour Assessment for Quality Assurance and Data Mining. Objective. Outline. Tom Purdie, PhD, MCCPM
 Contour Assessment for Quality Assurance and Data Mining Tom Purdie, PhD, MCCPM Objective Understand the state-of-the-art in contour assessment for quality assurance including data mining-based techniques
Contour Assessment for Quality Assurance and Data Mining Tom Purdie, PhD, MCCPM Objective Understand the state-of-the-art in contour assessment for quality assurance including data mining-based techniques
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
The Four Color Theorem: A Possible New Approach
 Governors State University OPUS Open Portal to University Scholarship All Student Theses Student Theses Fall 2016 The Four Color Theorem: A Possible New Approach Matthew Brady Governors State University
Governors State University OPUS Open Portal to University Scholarship All Student Theses Student Theses Fall 2016 The Four Color Theorem: A Possible New Approach Matthew Brady Governors State University
The Structure and Properties of Clique Graphs of Regular Graphs
 The University of Southern Mississippi The Aquila Digital Community Master's Theses 1-014 The Structure and Properties of Clique Graphs of Regular Graphs Jan Burmeister University of Southern Mississippi
The University of Southern Mississippi The Aquila Digital Community Master's Theses 1-014 The Structure and Properties of Clique Graphs of Regular Graphs Jan Burmeister University of Southern Mississippi
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching
 Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Graceful Graphs and Graceful Labelings: Two Mathematical Programming Formulations and Some Other New Results
 Graceful Graphs and Graceful Labelings: Two Mathematical Programming Formulations and Some Other New Results Timothy A. Redl Department of Computational and Applied Mathematics, Rice University, Houston,
Graceful Graphs and Graceful Labelings: Two Mathematical Programming Formulations and Some Other New Results Timothy A. Redl Department of Computational and Applied Mathematics, Rice University, Houston,
Testing Isomorphism of Strongly Regular Graphs
 Spectral Graph Theory Lecture 9 Testing Isomorphism of Strongly Regular Graphs Daniel A. Spielman September 26, 2018 9.1 Introduction In the last lecture we saw how to test isomorphism of graphs in which
Spectral Graph Theory Lecture 9 Testing Isomorphism of Strongly Regular Graphs Daniel A. Spielman September 26, 2018 9.1 Introduction In the last lecture we saw how to test isomorphism of graphs in which
Predicting Messaging Response Time in a Long Distance Relationship
 Predicting Messaging Response Time in a Long Distance Relationship Meng-Chen Shieh m3shieh@ucsd.edu I. Introduction The key to any successful relationship is communication, especially during times when
Predicting Messaging Response Time in a Long Distance Relationship Meng-Chen Shieh m3shieh@ucsd.edu I. Introduction The key to any successful relationship is communication, especially during times when
A NOTE ON THE NUMBER OF DOMINATING SETS OF A GRAPH
 A NOTE ON THE NUMBER OF DOMINATING SETS OF A GRAPH STEPHAN WAGNER Abstract. In a recent article by Bród and Skupień, sharp upper and lower bounds for the number of dominating sets in a tree were determined.
A NOTE ON THE NUMBER OF DOMINATING SETS OF A GRAPH STEPHAN WAGNER Abstract. In a recent article by Bród and Skupień, sharp upper and lower bounds for the number of dominating sets in a tree were determined.
Tree-Based Minimization of TCAM Entries for Packet Classification
 Tree-Based Minimization of TCAM Entries for Packet Classification YanSunandMinSikKim School of Electrical Engineering and Computer Science Washington State University Pullman, Washington 99164-2752, U.S.A.
Tree-Based Minimization of TCAM Entries for Packet Classification YanSunandMinSikKim School of Electrical Engineering and Computer Science Washington State University Pullman, Washington 99164-2752, U.S.A.
Managing Returned Mail to Drive Non-Profit Donations
 Moving business forward July 2008 Managing Returned Mail to Drive Non-Profit Donations Non-profit organizations of all kinds have always faced the dual challenges of fundraising and building their memberships.
Moving business forward July 2008 Managing Returned Mail to Drive Non-Profit Donations Non-profit organizations of all kinds have always faced the dual challenges of fundraising and building their memberships.
The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs
 The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs G. Ayorkor Mills-Tettey Anthony Stentz M. Bernardine Dias CMU-RI-TR-07-7 July 007 Robotics Institute Carnegie Mellon University
The Dynamic Hungarian Algorithm for the Assignment Problem with Changing Costs G. Ayorkor Mills-Tettey Anthony Stentz M. Bernardine Dias CMU-RI-TR-07-7 July 007 Robotics Institute Carnegie Mellon University
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems. Problems, Hints, and Solutions
 Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
CHAPTER 2: SAMPLING AND DATA
 CHAPTER 2: SAMPLING AND DATA This presentation is based on material and graphs from Open Stax and is copyrighted by Open Stax and Georgia Highlands College. OUTLINE 2.1 Stem-and-Leaf Graphs (Stemplots),
CHAPTER 2: SAMPLING AND DATA This presentation is based on material and graphs from Open Stax and is copyrighted by Open Stax and Georgia Highlands College. OUTLINE 2.1 Stem-and-Leaf Graphs (Stemplots),
Fundamentals of Operations Research. Prof. G. Srinivasan. Department of Management Studies. Indian Institute of Technology, Madras. Lecture No.
 Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture No. # 13 Transportation Problem, Methods for Initial Basic Feasible
Fundamentals of Operations Research Prof. G. Srinivasan Department of Management Studies Indian Institute of Technology, Madras Lecture No. # 13 Transportation Problem, Methods for Initial Basic Feasible
Star Decompositions of the Complete Split Graph
 University of Dayton ecommons Honors Theses University Honors Program 4-016 Star Decompositions of the Complete Split Graph Adam C. Volk Follow this and additional works at: https://ecommons.udayton.edu/uhp_theses
University of Dayton ecommons Honors Theses University Honors Program 4-016 Star Decompositions of the Complete Split Graph Adam C. Volk Follow this and additional works at: https://ecommons.udayton.edu/uhp_theses
Characteristics of Students in the Cisco Networking Academy: Attributes, Abilities, and Aspirations
 Cisco Networking Academy Evaluation Project White Paper WP 05-02 October 2005 Characteristics of Students in the Cisco Networking Academy: Attributes, Abilities, and Aspirations Alan Dennis Semiral Oncu
Cisco Networking Academy Evaluation Project White Paper WP 05-02 October 2005 Characteristics of Students in the Cisco Networking Academy: Attributes, Abilities, and Aspirations Alan Dennis Semiral Oncu
Enumerating Perfect Matchings in a Ring of Diamonds
 Enumerating Perfect Matchings in a Ring of Diamonds Shiena P. Tejada and Rhudaina Z. Mohammad College of Science of Mathematics Western Mindanao State University Abstract This paper presents an algorithm
Enumerating Perfect Matchings in a Ring of Diamonds Shiena P. Tejada and Rhudaina Z. Mohammad College of Science of Mathematics Western Mindanao State University Abstract This paper presents an algorithm
CS 229: Machine Learning Final Report Identifying Driving Behavior from Data
 CS 9: Machine Learning Final Report Identifying Driving Behavior from Data Robert F. Karol Project Suggester: Danny Goodman from MetroMile December 3th 3 Problem Description For my project, I am looking
CS 9: Machine Learning Final Report Identifying Driving Behavior from Data Robert F. Karol Project Suggester: Danny Goodman from MetroMile December 3th 3 Problem Description For my project, I am looking
Math 302 Introduction to Proofs via Number Theory. Robert Jewett (with small modifications by B. Ćurgus)
 Math 30 Introduction to Proofs via Number Theory Robert Jewett (with small modifications by B. Ćurgus) March 30, 009 Contents 1 The Integers 3 1.1 Axioms of Z...................................... 3 1.
Math 30 Introduction to Proofs via Number Theory Robert Jewett (with small modifications by B. Ćurgus) March 30, 009 Contents 1 The Integers 3 1.1 Axioms of Z...................................... 3 1.
Combining PGMs and Discriminative Models for Upper Body Pose Detection
 Combining PGMs and Discriminative Models for Upper Body Pose Detection Gedas Bertasius May 30, 2014 1 Introduction In this project, I utilized probabilistic graphical models together with discriminative
Combining PGMs and Discriminative Models for Upper Body Pose Detection Gedas Bertasius May 30, 2014 1 Introduction In this project, I utilized probabilistic graphical models together with discriminative
BACKUP TO THE FUTURE A SPICEWORKS SURVEY
 BACKUP TO THE FUTURE A SPICEWORKS SURVEY 02 BACKUP TO THE FUTURE A SPICEWORKS SURVEY METHODOLOGY This research study was conducted by Spiceworks, the professional network for the IT industry, from a survey
BACKUP TO THE FUTURE A SPICEWORKS SURVEY 02 BACKUP TO THE FUTURE A SPICEWORKS SURVEY METHODOLOGY This research study was conducted by Spiceworks, the professional network for the IT industry, from a survey
Notes for Lecture 24
 U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
U.C. Berkeley CS170: Intro to CS Theory Handout N24 Professor Luca Trevisan December 4, 2001 Notes for Lecture 24 1 Some NP-complete Numerical Problems 1.1 Subset Sum The Subset Sum problem is defined
STANDARDS OF LEARNING CONTENT REVIEW NOTES. ALGEBRA I Part II. 3 rd Nine Weeks,
 STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I Part II 3 rd Nine Weeks, 2016-2017 1 OVERVIEW Algebra I Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
STANDARDS OF LEARNING CONTENT REVIEW NOTES ALGEBRA I Part II 3 rd Nine Weeks, 2016-2017 1 OVERVIEW Algebra I Content Review Notes are designed by the High School Mathematics Steering Committee as a resource
Comparing Implementations of Optimal Binary Search Trees
 Introduction Comparing Implementations of Optimal Binary Search Trees Corianna Jacoby and Alex King Tufts University May 2017 In this paper we sought to put together a practical comparison of the optimality
Introduction Comparing Implementations of Optimal Binary Search Trees Corianna Jacoby and Alex King Tufts University May 2017 In this paper we sought to put together a practical comparison of the optimality
Hand Therapy Certification and the CHT Examination
 Hand Therapy Certification and the CHT Examination Mission The mission of the Hand Therapy Certification Commission, Inc. is to support a high level of competence in hand therapy practice and to advance
Hand Therapy Certification and the CHT Examination Mission The mission of the Hand Therapy Certification Commission, Inc. is to support a high level of competence in hand therapy practice and to advance
Welfare Navigation Using Genetic Algorithm
 Welfare Navigation Using Genetic Algorithm David Erukhimovich and Yoel Zeldes Hebrew University of Jerusalem AI course final project Abstract Using standard navigation algorithms and applications (such
Welfare Navigation Using Genetic Algorithm David Erukhimovich and Yoel Zeldes Hebrew University of Jerusalem AI course final project Abstract Using standard navigation algorithms and applications (such
At the end of the chapter, you will learn to: Present data in textual form. Construct different types of table and graphs
 DATA PRESENTATION At the end of the chapter, you will learn to: Present data in textual form Construct different types of table and graphs Identify the characteristics of a good table and graph Identify
DATA PRESENTATION At the end of the chapter, you will learn to: Present data in textual form Construct different types of table and graphs Identify the characteristics of a good table and graph Identify
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Using Genetic Algorithms to Solve the Box Stacking Problem
 Using Genetic Algorithms to Solve the Box Stacking Problem Jenniffer Estrada, Kris Lee, Ryan Edgar October 7th, 2010 Abstract The box stacking or strip stacking problem is exceedingly difficult to solve
Using Genetic Algorithms to Solve the Box Stacking Problem Jenniffer Estrada, Kris Lee, Ryan Edgar October 7th, 2010 Abstract The box stacking or strip stacking problem is exceedingly difficult to solve
The State of the American Traveler TM
 The State of the American Traveler TM MOBILE EDITION Fall 2018 Volume 30 The Mobile Edition THIS FALL EDITION of The State of the American Traveler TM continues our ongoing exploration of travelers use
The State of the American Traveler TM MOBILE EDITION Fall 2018 Volume 30 The Mobile Edition THIS FALL EDITION of The State of the American Traveler TM continues our ongoing exploration of travelers use
Some Strong Connectivity Concepts in Weighted Graphs
 Annals of Pure and Applied Mathematics Vol. 16, No. 1, 2018, 37-46 ISSN: 2279-087X (P), 2279-0888(online) Published on 1 January 2018 www.researchmathsci.org DOI: http://dx.doi.org/10.22457/apam.v16n1a5
Annals of Pure and Applied Mathematics Vol. 16, No. 1, 2018, 37-46 ISSN: 2279-087X (P), 2279-0888(online) Published on 1 January 2018 www.researchmathsci.org DOI: http://dx.doi.org/10.22457/apam.v16n1a5
Data Set Specification Post Survey Tables
 Data Set Specification Post Survey Tables ANZDATA selection of metadata items. Created: 1 July 2016 Page 1 of 19 Australia and New Zealand Dialysis and Transplant Registry 2016 We have made all reasonable
Data Set Specification Post Survey Tables ANZDATA selection of metadata items. Created: 1 July 2016 Page 1 of 19 Australia and New Zealand Dialysis and Transplant Registry 2016 We have made all reasonable
Activity 1 Creating a simple gradebook
 Activity 1 Creating a simple gradebook 1 Launch Excel to start a new spreadsheet a. Click on the Excel icon to start a new workbook, either from the start menu, Office Toolbar, or an Excel icon on the
Activity 1 Creating a simple gradebook 1 Launch Excel to start a new spreadsheet a. Click on the Excel icon to start a new workbook, either from the start menu, Office Toolbar, or an Excel icon on the
Basic Statistical Terms and Definitions
 I. Basics Basic Statistical Terms and Definitions Statistics is a collection of methods for planning experiments, and obtaining data. The data is then organized and summarized so that professionals can
I. Basics Basic Statistical Terms and Definitions Statistics is a collection of methods for planning experiments, and obtaining data. The data is then organized and summarized so that professionals can
y (B) x (B) x (B)
 Copyright Cambridge University Press 00. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/05498 You can buy this book for 0 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/
Copyright Cambridge University Press 00. On-screen viewing permitted. Printing not permitted. http://www.cambridge.org/05498 You can buy this book for 0 pounds or $50. See http://www.inference.phy.cam.ac.uk/mackay/itila/
MASS Modified Assignment Algorithm in Facilities Layout Planning
 International Journal of Tomography & Statistics (IJTS), June-July 2005, Vol. 3, No. JJ05, 19-29 ISSN 0972-9976; Copyright 2005 IJTS, ISDER MASS Modified Assignment Algorithm in Facilities Layout Planning
International Journal of Tomography & Statistics (IJTS), June-July 2005, Vol. 3, No. JJ05, 19-29 ISSN 0972-9976; Copyright 2005 IJTS, ISDER MASS Modified Assignment Algorithm in Facilities Layout Planning
A TIGHT BOUND ON THE LENGTH OF ODD CYCLES IN THE INCOMPATIBILITY GRAPH OF A NON-C1P MATRIX
 A TIGHT BOUND ON THE LENGTH OF ODD CYCLES IN THE INCOMPATIBILITY GRAPH OF A NON-C1P MATRIX MEHRNOUSH MALEKESMAEILI, CEDRIC CHAUVE, AND TAMON STEPHEN Abstract. A binary matrix has the consecutive ones property
A TIGHT BOUND ON THE LENGTH OF ODD CYCLES IN THE INCOMPATIBILITY GRAPH OF A NON-C1P MATRIX MEHRNOUSH MALEKESMAEILI, CEDRIC CHAUVE, AND TAMON STEPHEN Abstract. A binary matrix has the consecutive ones property
THE STATE OF IT TRANSFORMATION FOR RETAIL
 THE STATE OF IT TRANSFORMATION FOR RETAIL An Analysis by Dell EMC and VMware Dell EMC and VMware are helping IT groups at retail organizations transform to business-focused service providers. The State
THE STATE OF IT TRANSFORMATION FOR RETAIL An Analysis by Dell EMC and VMware Dell EMC and VMware are helping IT groups at retail organizations transform to business-focused service providers. The State
CS 229 Final Project - Using machine learning to enhance a collaborative filtering recommendation system for Yelp
 CS 229 Final Project - Using machine learning to enhance a collaborative filtering recommendation system for Yelp Chris Guthrie Abstract In this paper I present my investigation of machine learning as
CS 229 Final Project - Using machine learning to enhance a collaborative filtering recommendation system for Yelp Chris Guthrie Abstract In this paper I present my investigation of machine learning as
An Algorithmic Approach to Graph Theory Neetu Rawat
 An Algorithmic Approach to Graph Theory Neetu Rawat nrwt12345@gmail.com, Assistant Professor, Chameli Devi Group of Institutions, Indore. India. Abstract This paper compares two different minimum spanning
An Algorithmic Approach to Graph Theory Neetu Rawat nrwt12345@gmail.com, Assistant Professor, Chameli Devi Group of Institutions, Indore. India. Abstract This paper compares two different minimum spanning
Vocabulary. 5-number summary Rule. Area principle. Bar chart. Boxplot. Categorical data condition. Categorical variable.
 5-number summary 68-95-99.7 Rule Area principle Bar chart Bimodal Boxplot Case Categorical data Categorical variable Center Changing center and spread Conditional distribution Context Contingency table
5-number summary 68-95-99.7 Rule Area principle Bar chart Bimodal Boxplot Case Categorical data Categorical variable Center Changing center and spread Conditional distribution Context Contingency table
Drexel University Electrical and Computer Engineering Department. ECEC 672 EDA for VLSI II. Statistical Static Timing Analysis Project
 Drexel University Electrical and Computer Engineering Department ECEC 672 EDA for VLSI II Statistical Static Timing Analysis Project Andrew Sauber, Julian Kemmerer Implementation Outline Our implementation
Drexel University Electrical and Computer Engineering Department ECEC 672 EDA for VLSI II Statistical Static Timing Analysis Project Andrew Sauber, Julian Kemmerer Implementation Outline Our implementation
Alumni Survey Hawken School February 2007
 Alumni Survey Hawken School February 2007 For each question, please select the most appropriate number, indicating your response. We encourage you to expand on your answers in the comment section. If there
Alumni Survey Hawken School February 2007 For each question, please select the most appropriate number, indicating your response. We encourage you to expand on your answers in the comment section. If there
