Data Structures and Algorithms. Werner Nutt
|
|
|
- Domenic Atkins
- 6 years ago
- Views:
Transcription
1 Data Structures and Algorithms Werner Nutt Part 6 Academic Year
2 Acknowledgements & Copyright Notice These slides are built on top of slides developed by Michael Boehlen. Moreover, some material (text, figures, examples) displayed in these slides is courtesy of Kurt Ranalter. Some examples displayed in these slides are taken from [Cormen, Leiserson, Rivest and Stein, ``Introduction to Algorithms'', MIT Press], and their copyright is detained by the authors. All the other material is copyrighted by Roberto Sebastiani. Every commercial use of this material is strictly forbidden by the copyright laws without the authorization of the authors. No copy of these slides can be displayed in public or be publicly distributed without containing this copyright notice. 2
3 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 3
4 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 4
5 Dictionaries A dictionary D is a dynamic data structure with operations: Search(D, k) returns a pointer x to an element such that x.key = k (null otherwise) Insert(D, x) adds the element pointed to by x to D Delete(D, x) removes the element pointed to by x from D An element has a key and data part. 5
6 Ordered Dictionaries In addition to dictionary functionality, we may want to support operations: Min(D) Max(D) and Predecessor(D, k) Successor(D, k) These operations require keys that are comparable (ordered domain). 6
7 A List-Based Implementation Unordered list search, min, max, predecessor, successor: O(n) insertion, deletion: O(1) Ordered list search, insertion: O(n) min, max, predecessor, successor, deletion: O(1) 7
8 Refresher: Binary Search Narrow down the search range in stages findelement(22) 8
9 Run Time of Binary Search The range of candidate items to be searched is halved after comparing the key with the middle element. Binary search runs in O(log n) time. What about insertion and deletion? search: O(log n) insert, delete: O(n) min, max, predecessor, successor: O(1) The idea of a binary search can be extended to dynamic data structures binary trees. 9
10 Binary Trees (Java) class node { int int key; node left; node right; node parent; } node root; root
11 Binary Trees (C) struct node { int int key; struct node* left; struct node* right; struct node* parent; } struct node* root; root
12 Binary Search Trees A binary search tree (BST) is a binary tree T with the following properties: each internal node stores an item (k,e) of a dictionary keys stored at nodes in the left subtree of v are less than or equal to k keys stored at nodes in the right subtree of v are greater than or equal to k Example BSTs for 2, 3, 5, 5, 7,
13 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 13
14 Tree Walks Keys in a BST can be printed using "tree walks" Keys of each node printed between keys in the left and right subtree inorder tree traversal InorderTreeWalk(x) 01 if x NIL then 02 InorderTreeWalk(x.left) 03 print x.key 04 InorderTreeWalk(x.right) 14
15 Tree Walks/2 InorderTreeWalk is a divide-and-conquer algorithm. It prints all elements in monotonically increasing order. Running time Θ(n). 15
16 Tree Walks/2 4 Inorder tree walk can be thought of as a projection of the BST nodes onto a one dimensional interval
17 Tree Walks/3 Other forms of tree walk: A preorder tree walk processes each node before processing its children. A postorder tree walk processes each node after processing its children. 17
18 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 18
19 Searching a BST To find an element with key k in a tree T compare k with T.key if k < T.key, search for k in T.left otherwise, search for k in T.right 19
20 Pseudocode for BST Search 5 Recursive version: divide-and-conquer Search(T,k) 01 if T = NIL then return NIL 02 if k = T.key then return T 03 if k < T.key 04 then return Search(T.left,k) 05 else return Search(T.right,k) Iterative version Search(T,k) 01 x := T 02 while x NIL and k x.key do 03 if k < x.key 04 then x := x.left 05 else x := x.right 06 return x 20
21 Search Examples Search(T, 11)
22 Search Examples/2 2 Search(T, 6)
23 Analysis of Search Running time on tree of height h is O(h) After the insertion of n keys, the worstcase running time of searching is O(n)
24 BST Minimum (Maximum) Find the minimum key in a tree rooted at x. TreeMinimum(x) 01 while x.left NIL do 02 x := x.left 03 return x Maximum: same, x.right instead of x.left Running time O(h), i.e., it is proportional to the height of the tree. 24
25 Successor Given x, find the node with the smallest key greater than x.key. We can distinguish two cases, depending on the right subtree of x Case 1: The right subtree of x is non-empty (succ(x) inserted after x) successor is the leftmost node in the right subtree. this can be done by returning TreeMinimum(x.right) x 7 10 succ(x) 8 25
26 Successor/2 Case 2: the right subtree of x is empty (succ(x), if any, was inserted before x). The successor (if any) is the lowest ancestor of x whose left subtree contains x. Note: it x had a right child, then it would be smaller than succ(x) 5 succ(x) x
27 Successor Pseudocode TreeSuccessor(x) 01 if x.right NIL 02 then return TreeMinimum(x.right) 03 y := x.parent 04 while y NIL and x = y.right 05 x := y 06 y := y.parent 03 return y For a tree of height h, the running time is O(h). Note: no comparison among keys needed! 27
28 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 28
29 BST Insertion The basic idea derives from searching: construct an element p whose left and right children are NULL and insert it into T find location in T where p belongs to (as if searching for p.key), add p there The running time on a tree of height h is O(h). 29
30 BST Insertion: Pseudocode Notice: trailing pointer technique TreeInsert(n, root) front:=root; rear:=nil; while front NIL NIL do do rear:=front; if if n.key < front.key then front:=front.left else front:=front.right if if rear = NIL NIL then n.parent:=nil; return n; n; elsif n.key < rear.key then rear.left:=n; else rear.right:=n; n.parent:=rear; return root; 30
31 BST Insertion Code (java) Have a one step delayed pointer. node insert(node p, p, node r) r) { //insert p in in r node y = NULL; node x = r; r; while (x (x!=!= NULL) { y := := x; x; if if (x.key < p.key) x = x.right; else x = x.left; } if if (y (y == == NULL) {r {r = p; p; p.parent=null;}// r is is empty else if if (y.key < p.key) y.right = p; p; else y.left = p; p; p.parent =y; =y; return r; r; } 31
32 BST Insertion Code (C) Have a one step delayed pointer. struct node* insert(struct node* p, p, struct node* r) r) { struct node* y = NULL; struct node* x = r; r; while (x (x!=!= NULL) { y := := x; x; if if (x->key < p->key) x = x->right; else x = x->left; } if if (y (y == == NULL) {r {r = p;p->partent=null} else if if (y->key < p->key) y->right = p; p; else y->left = p; p; p->parent = u; u; return r; r; } 32
33 BST Insertion Example Insert
34 BST Insertion: Worst Case In what kind of sequence should the insertions be made to produce a BST of height n? A B C D 34
35 BST Sorting Use TreeInsert and InorderTreeWalk to sort a list of n elements, A TreeSort(A) 01 T := NIL 02 for i := 1 to n 03 TreeInsert(T, BinTree(A[i])) 04 InorderTreeWalk(T) 35
36 BST Sorting/2 Sort the following numbers Build a binary search tree Call InorderTreeWalk
37 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 37
38 Deletion Delete node x from a tree T We can distinguish three cases x has no child x has one child x has two children 38
39 Deletion Case 1 If x has no children: simply remove x D A F B x D A F 39
40 Deletion Case 2 If x has exactly one child, make parent of x point to that child and delete x. D x A F B D B F 40
41 Deletion Case 3 If x has two children: find the largest child y in the left subtree of x (i.e. y is predecessor(x)) Recursively remove y (note that y has at most one child), and replace x with y. Specular version with successor(x) (CLRS) A A B y x D B F F 41
42 Deletion Pseudocode Delete(T,x) if if x.left = nil nil or or x.right = nil nil then drop := := x else drop := := Succ(x) if if drop.left nil nil then keep := := drop.left else keep := := drop.right if if keep nil nil then keep.parent := := drop.parent if if drop.parent = nil nil then T.root := := keep else if if drop = drop.parent.left then drop.parent.left := := keep else drop.parent.right := := keep if if drop x then x.key := := drop.key % x.info := := drop.info with parent Version with pointer 42
43 BST Deletion Code (java) Version without parent field Note again the trailing pointer technique node delete(node root, node x) x) { front = root; rear = NULL; while (front!=!= x) x) { rear := := front; if if (x.key < front.key) front := := front.left; else front := := front.right; } // // rear points to to a parent of of x (if (if any) 43
44 BST Deletion Code (java)/2 x has less than 2 children Fix pointer of parent of x if if (x.right == == NULL) { if if (rear == == NULL) root = x.left; else if if (rear.left == == x) x) rear.left = x.left; else rear.right = x.left;} else if if (x.left == == NULL) { if if (rear == == NULL) root = x.right; else if if (rear.left == == x) x) rear.left = x.right; else rear.right = x.right; else { 44
45 BST Deletion Code (java)/3 x has 2 children succ = x.right; srear = succ; while (succ.left!=!= NULL) { srear:=succ; succ:=succ.left; } if if (rear == == NULL) root = succ; else if if (rear.left == == x) x) rear.left = succ; else rear.right = succ; succ.left = x.left; if if (srear!=!= succ) { srear.left = succ.right; succ.right = x.right; } return root 45
46 BST Deletion Code (C) Version without parent field struct node* delete(struct node* root, struct node* x) x) { u = root; v = NULL; while (u (u!=!= x) x) { v := := u; u; if if (x->key < u->key) u := := u->left; else u := := u->right; } // // v points to to a parent of of x (if (if any) 46
47 BST Deletion Code (C)/2 x has less than 2 children Fix pointer of parent of x if if (u->right == == NULL) { if if (v (v == == NULL) root = u->left; else if if (v->left == == u) u) v->left = u->left; else v->right = u->left; else if if (u->left == == NULL) { if if (v (v == == NULL) root = u->right; else if if (v->left == == u) u) v->left = u->right; else v->right = u->right; else { 47
48 BST Deletion Code (C)/3 x has 2 children p = x->left; q = p; p; while (p->right!=!= NULL) { q:=p; p:=p->right; } if if (v (v == == NULL) root = p; p; else if if (v->left == == u) u) v->left = p; p; else v->right = p; p; p->right = u->right; if if (q (q!=!= p) p) { q->right = p->left; p->left = u->left; } return root 48
49 Balanced Binary Search Trees Problem: execution time for tree operations is Θ(h), which in worst case is Θ(n). Solution: balanced search trees guarantee small height h = O(log n)
50 Suggested exercises Implement a binary search tree with the following functionalities: init, max, min, successor, predecessor, search (iterative & recursive), insert, delete (both swap with succ and pred), print, print in reverse order TreeSort 50
51 Suggested exercises/2 Using paper & pencil: draw the trees after each of the following operations, starting from an empty tree: 1. Insert 9,5,3,7,2,4,6,8,13,11,15,10,12,16,14 2.Delete 16, 15, 5, 7, 9 (both with succ and pred strategies) simulate the following operations after 1: Find the max and minimum Find the successor of 9, 8, 6 51
52 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 52
53 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 53
54 Red/Black Trees A red-black tree is a binary search tree with the following properties: 1. Nodes (or incoming edges) are colored red or black 2. NULL leaves are black 3. The root is black 4. No two consecutive red nodes on any root-leaf path. 5. Same number of black nodes on any root-leaf path (called black height of the tree). 54
55 Java's TreeMap 55
56 RB-Tree Properties Some measures n # of internal nodes h height bh black height 2bh 1 n bh h/2 2h/2 n +1 h 2 log(n +1) BALANCED! 56
57 RB-Tree Properties/2 Operations on a binary-search tree (search, insert, delete,...) can be accomplished in O(h) time. The RB-tree is a binary search tree, whose height is bounded by 2 log(n +1), thus the operations run in O(log n). Provided that we can maintain red-black tree properties spending no more than O(h) time on each insertion or deletion. 57
58 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 58
59 Rotation B A A B γ α α β β γ right rotation of B left rotation of A 59
60 Right Rotation RightRotate(B) 01 A := B.left 02 B.left := A.right 03 B.left.parent := B 04 if (B = B.parent.left) B.parent.left := A 05 if (B = B.parent.right) B.parent.right := A 06 A.parent := B.parent 07 A.right := B 08 B.parent := A B A γ α α β β γ 60
61 The Effect of a Rotation Maintains inorder key ordering a, b, c γ we can state the invariant a<= A <= b <= B <= c After right rotation Depth(α) decreases by 1 Depth(β) stays the same Depth(γ) increases by 1 Left rotation: symmetric Rotation takes O(1) time 61
62 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 62
63 Insertion in the RB-Trees RBInsert(T,n) 01 Insert n into T using the binary search tree insertion procedure 02 n.left := NIL 03 n.right := NIL 04 n.color := red 05 RBInsertFixup(n) n p n p 63
64 Fixing Up a Node: Intuition Case 0: parent is black => ok Case 1: both parent and uncle are red => change colour of parent/uncle to black => change colour of grandparent to red => fix up the grandparent Exception: grandparent is root => then keep it black Case 2: parent is red and uncle is black, and node and parent are in a straight line => rotate at grandparent Case 3: parent is red and uncle is black, and node and parent are not in a straight line => rotate at parent (leads to Case 2) 64
65 Insertion Let n = the new node p = n.parent g = p.parent In the following assume: p = g.left n p g 65
66 Insertion: Case 0 p.color = black No properties of the tree are violated we are done. p g n 66
67 Insertion: Case 1 6 Case 1 n s uncle u is red Action p.color := black u.color := black g.color := red n := g Note: the tree rooted at g is balanced enough (black depth of all descendants remains unchanged). n p g u n p g u 67
68 Insertion: Case 2 Case 2 n s uncle u is black and n is a left child Action p.color := black g.color := red RightRotate(g) Note: the tree rooted at g is balanced enough (black depth of all descendents remains unchanged). n p g u n p g u 68
69 Insertion: Case 3 Case 3 n s uncle u is black and n is a right child Action Note LeftRotate(p) n := p p n g u n p g u The result is a case 2. 69
70 Insertion: Mirror cases All three cases are handled analogously if p is a right child. Exchange left and right in all three cases. 70
71 Insertion: Case 2 and 3 Case 2m mirrored n s uncle u is black and n is a right child Action p.color := black g.color := red LeftRotate(g) Case 3m n s uncle u is black and n is a left child Action RightRotate(p) n := p 71
72 Insertion Summary If two red nodes are adjacent, we do either a restructuring (with one or two rotations) and stop (cases 2 and 3), or recursively propagate red upwards (case 1) A restructuring takes constant time and is performed at most once. It reorganizes an offbalanced section of the tree Propagations may continue up the tree and are executed O(log n) times (height of the tree) The running time of an insertion is O(log n). 72
73 An Insertion Example Inserting "REDSOX" into an empty tree E D R O S Now, let us insert "CUBS" X 73
74 Insert C (case 0) E E D R D R O S C O S X X 74
75 Insert U (case 3, mirror) E E D R D R C O S C O S X X U 75
76 Insert U/2 E E D R D R C O S C O U X S X U 76
77 Insert B (case 2) E E D R D R C O U C O U S X B S X 77
78 Insert B/2 E E D R C R C O U B D O U B S X S X 78
79 Insert S (case 1) E E C R C R B D O U B D O U S X S X S 79
80 Insert S/2 (case 2 mirror) E R C R E U B D O U C O S X S X B D S S 80
81 Data Structures and Binary Search Trees Tree traversals Searching Insertion Deletion Red-Black Trees Properties Rotations Insertion Deletion Algorithms Week 6 81
82 Deletion We first apply binary search tree deletion. We can easily delete a node that has at least one nil child If the key to be deleted is stored at a node u with two children, we replace its content with the content of the largest node v of the left subtree and delete v instead. 7 u 5 u v
83 Deletion Algorithm 1. Remove u 2. If u.color = red, we are done. Else, assume that v (replacement of u) gets additional black color: If v.color = red then v.color := black and we are done! Else v s color is double black. u v v u v v 83
84 Deletion Algorithm/2 How to eliminate double black edges? The intuitive idea is to perform a color compensation Find a red edge nearby, and change the pair (red, double black) into (black, black) Two cases: restructuring and recoloring Restructuring resolves the problem locally, while recoloring may propagate it upward. Hereafter we assume v is a left child (swap right and left otherwise) 84
85 Deletion Case 1 Case 1 v s sibling s is black and both children of s are black Action s.color := red v = p Note v We reduce the black depth of both subtrees of p by 1. Parent p becomes more black. p s v p s 85
86 Deletion: Case 1 If parent p becomes double black, continue upward. p p v s v s 86
87 Deletion: Case 2 Case 2 v s sibling s is black and s s right child is red. Action s.color = p.color p.color = black s.right.color = black LeftRotate(p) v p s r v p s r Idea: Compensate the extra black ring of v by the red of r Note: Terminates after restructuring. 87
88 Deletion: Case 3 Case 3 v s sibling s is black, s s left child is red, and s s right child is black. Idea: Reduce to case 2 Action s.left.color = black s.color = red RightRotation(s) s = p.right Note: This is now case 2 v p l s v p l s 88
89 Deletion: Case 4 Case 4 v s sibling s is red Idea: give v a black sibling Action s.color = black p.color = red LeftRotation(p) s = p.right Note v p s v p s This is now a case 1, 2, or 3 89
90 Delete
91 Delete 9/2 Case 2 (sibling is black with black children) recoloring
92 Delete
93 Delete 7: restructuring
94 How long does it take? Deletion in a RB-tree takes O(log n) Maximum three rotations and O(log n) recolorings 94
95 Suggested exercises Add left-rotate and right-rotate to the implementation of binary trees Implement a red-black search tree with the following functionalities: (...), insert, delete 95
96 Suggested exercises/2 Using paper & pencil: draw the RB-trees after each of the following operations, starting from an empty tree: 1. Insert 1,2,3,4,5,6,7,8,9,10,11,12 2.Delete 12,11,10,9,8,7,6,5,4,3,2,1 Try insertions and deletions at random 96
97 Other Balanced Trees 11 Red-Black trees are related to trees (non-binary) AVL-trees have simpler algorithms, but may perform a lot of rotations Red-Black 97
98 Next Week Hashing 98
Data Structures and Algorithms. Chapter 6. Binary Search Trees
 1 Data Structures and Algorithms Chapter 6 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 6 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
ECE250: Algorithms and Data Structures Binary Search Trees (Part A)
 ECE250: Algorithms and Data Structures Binary Search Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
ECE250: Algorithms and Data Structures Binary Search Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
CSE2331/5331. Topic 6: Binary Search Tree. Data structure Operations CSE 2331/5331
 CSE2331/5331 Topic 6: Binary Search Tree Data structure Operations Set Operations Maximum Extract-Max Insert Increase-key We can use priority queue (implemented by heap) Search Delete Successor Predecessor
CSE2331/5331 Topic 6: Binary Search Tree Data structure Operations Set Operations Maximum Extract-Max Insert Increase-key We can use priority queue (implemented by heap) Search Delete Successor Predecessor
Binary search trees (BST) Binary search trees (BST)
 Tree A tree is a structure that represents a parent-child relation on a set of object. An element of a tree is called a node or vertex. The root of a tree is the unique node that does not have a parent
Tree A tree is a structure that represents a parent-child relation on a set of object. An element of a tree is called a node or vertex. The root of a tree is the unique node that does not have a parent
Announcements. Problem Set 2 is out today! Due Tuesday (Oct 13) More challenging so start early!
 CSC263 Week 3 Announcements Problem Set 2 is out today! Due Tuesday (Oct 13) More challenging so start early! NOT This week ADT: Dictionary Data structure: Binary search tree (BST) Balanced BST - AVL tree
CSC263 Week 3 Announcements Problem Set 2 is out today! Due Tuesday (Oct 13) More challenging so start early! NOT This week ADT: Dictionary Data structure: Binary search tree (BST) Balanced BST - AVL tree
CSE 502 Class 16. Jeremy Buhler Steve Cole. March A while back, we introduced the idea of collections to put hash tables in context.
 CSE 502 Class 16 Jeremy Buhler Steve Cole March 17 2015 Onwards to trees! 1 Collection Types Revisited A while back, we introduced the idea of collections to put hash tables in context. abstract data types
CSE 502 Class 16 Jeremy Buhler Steve Cole March 17 2015 Onwards to trees! 1 Collection Types Revisited A while back, we introduced the idea of collections to put hash tables in context. abstract data types
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Binary Search Trees. Antonio Carzaniga. Faculty of Informatics University of Lugano. October 21, Antonio Carzaniga 1
 Binary Search Trees Antonio Carzaniga Faculty of Informatics University of Lugano October 21, 2010 2006 Antonio Carzaniga 1 Binary search trees Outline Randomized binary search trees 2006 Antonio Carzaniga
Binary Search Trees Antonio Carzaniga Faculty of Informatics University of Lugano October 21, 2010 2006 Antonio Carzaniga 1 Binary search trees Outline Randomized binary search trees 2006 Antonio Carzaniga
CS 380 ALGORITHM DESIGN AND ANALYSIS
 CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
Binary search trees. Binary search trees are data structures based on binary trees that support operations on dynamic sets.
 COMP3600/6466 Algorithms 2018 Lecture 12 1 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees are data structures based on binary trees that support operations on dynamic
COMP3600/6466 Algorithms 2018 Lecture 12 1 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees are data structures based on binary trees that support operations on dynamic
CMPS 2200 Fall 2017 Red-black trees Carola Wenk
 CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
Binary Tree. Preview. Binary Tree. Binary Tree. Binary Search Tree 10/2/2017. Binary Tree
 0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Algorithms. 演算法 Data Structures (focus on Trees)
 演算法 Data Structures (focus on Trees) Professor Chien-Mo James Li 李建模 Graduate Institute of Electronics Engineering National Taiwan University 1 Dynamic Set Dynamic set is a set of elements that can grow
演算法 Data Structures (focus on Trees) Professor Chien-Mo James Li 李建模 Graduate Institute of Electronics Engineering National Taiwan University 1 Dynamic Set Dynamic set is a set of elements that can grow
Different binary search trees can represent the same set of values (Fig.2). Vladimir Shelomovskii, Unitech, Papua New Guinea. Binary search tree.
 1 Vladimir Shelomovskii, Unitech, Papua New Guinea, CS411 Binary search tree We can represent a binary search tree by a linked data structure in which each node is an object. Each node contains (Fig.1):
1 Vladimir Shelomovskii, Unitech, Papua New Guinea, CS411 Binary search tree We can represent a binary search tree by a linked data structure in which each node is an object. Each node contains (Fig.1):
Data Structures and Algorithms. Roberto Sebastiani
 Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 0 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 0 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
Binary Search Trees. July 13th, Computer Information Systems. c 2009 Vaidė Narváez
 Binary Search Trees Vaidė Narváez Computer Information Systems July 13th, 2010 Introduction Dynamic set operations: Search, Minimum, Maximum Predecessor, Successor Insert, Delete Time proportional to the
Binary Search Trees Vaidė Narváez Computer Information Systems July 13th, 2010 Introduction Dynamic set operations: Search, Minimum, Maximum Predecessor, Successor Insert, Delete Time proportional to the
ץע A. B C D E F G H E, B ( -.) - F I J K ) ( A :. : ע.)..., H, G E (. י : י.)... C,A,, F B ( 2
 נת ני ני, 1 עץ E A B C D F G H I J K. E B, ( -.)F- )A( : ע :..)...H,G,E (. י י:.)...C,A,F,B ( 2 עץ E A B C D F G H I J K v : -,w w.v- w-.v :v ע. v- B- 3 ע E A B C D F G H I J K ע - v,1 B ( v-.)? A 4 E
נת ני ני, 1 עץ E A B C D F G H I J K. E B, ( -.)F- )A( : ע :..)...H,G,E (. י י:.)...C,A,F,B ( 2 עץ E A B C D F G H I J K v : -,w w.v- w-.v :v ע. v- B- 3 ע E A B C D F G H I J K ע - v,1 B ( v-.)? A 4 E
Binary search trees 3. Binary search trees. Binary search trees 2. Reading: Cormen et al, Sections 12.1 to 12.3
 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees 3 Binary search trees are data structures based on binary trees that support operations on dynamic sets. Each element
Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees 3 Binary search trees are data structures based on binary trees that support operations on dynamic sets. Each element
CS 3343 Fall 2007 Red-black trees Carola Wenk
 CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
Balanced Binary Search Trees
 Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
CMPS 2200 Fall 2015 Red-black trees Carola Wenk
 CMPS 2200 Fall 2015 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/9/15 CMPS 2200 Intro. to Algorithms 1 ADT Dictionary / Dynamic Set Abstract data type
CMPS 2200 Fall 2015 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/9/15 CMPS 2200 Intro. to Algorithms 1 ADT Dictionary / Dynamic Set Abstract data type
Design and Analysis of Algorithms Lecture- 9: Binary Search Trees
 Design and Analysis of Algorithms Lecture- 9: Binary Search Trees Dr. Chung- Wen Albert Tsao 1 Binary Search Trees Data structures that can support dynamic set operations. Search, Minimum, Maximum, Predecessor,
Design and Analysis of Algorithms Lecture- 9: Binary Search Trees Dr. Chung- Wen Albert Tsao 1 Binary Search Trees Data structures that can support dynamic set operations. Search, Minimum, Maximum, Predecessor,
Week 8. BinaryTrees. 1 Binary trees. 2 The notion of binary search tree. 3 Tree traversal. 4 Queries in binary search trees. 5 Insertion.
 Week 8 Binarys 1 2 of 3 4 of 5 6 7 General remarks We consider, another important data structure. We learn how to use them, by making efficient queries. And we learn how to build them. Reading from CLRS
Week 8 Binarys 1 2 of 3 4 of 5 6 7 General remarks We consider, another important data structure. We learn how to use them, by making efficient queries. And we learn how to build them. Reading from CLRS
Week 8. BinaryTrees. 1 Binary trees. 2 The notion of binary search tree. 3 Tree traversal. 4 Queries in binary search trees. 5 Insertion.
 Week 8 Binarys 1 2 3 4 5 6 7 General remarks We consider, another important data structure. We learn how to use them, by making efficient queries. And we learn how to build them. Reading from CLRS for
Week 8 Binarys 1 2 3 4 5 6 7 General remarks We consider, another important data structure. We learn how to use them, by making efficient queries. And we learn how to build them. Reading from CLRS for
Balanced search trees
 Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Data Structures and Algorithms. Roberto Sebastiani
 Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 07 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 07 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Data Structures and Algorithms
 Data Structures and Algorithms Searching Red-Black and Other Dynamically BalancedTrees PLSD210 Searching - Re-visited Binary tree O(log n) if it stays balanced Simple binary tree good for static collections
Data Structures and Algorithms Searching Red-Black and Other Dynamically BalancedTrees PLSD210 Searching - Re-visited Binary tree O(log n) if it stays balanced Simple binary tree good for static collections
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
A set of nodes (or vertices) with a single starting point
 Binary Search Trees Understand tree terminology Understand and implement tree traversals Define the binary search tree property Implement binary search trees Implement the TreeSort algorithm 2 A set of
Binary Search Trees Understand tree terminology Understand and implement tree traversals Define the binary search tree property Implement binary search trees Implement the TreeSort algorithm 2 A set of
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
2-3 Tree. Outline B-TREE. catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS
 Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
Data Structures and Algorithms CMPSC 465
 Data Structures and Algorithms CMPSC 465 LECTURE 24 Balanced Search Trees Red-Black Trees Adam Smith 4/18/12 A. Smith; based on slides by C. Leiserson and E. Demaine L1.1 Balanced search trees Balanced
Data Structures and Algorithms CMPSC 465 LECTURE 24 Balanced Search Trees Red-Black Trees Adam Smith 4/18/12 A. Smith; based on slides by C. Leiserson and E. Demaine L1.1 Balanced search trees Balanced
Binary Trees. Recursive definition. Is this a binary tree?
 Binary Search Trees Binary Trees Recursive definition 1. An empty tree is a binary tree 2. A node with two child subtrees is a binary tree 3. Only what you get from 1 by a finite number of applications
Binary Search Trees Binary Trees Recursive definition 1. An empty tree is a binary tree 2. A node with two child subtrees is a binary tree 3. Only what you get from 1 by a finite number of applications
Chapter 3. Graphs CLRS Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 3 Graphs CLRS 12-13 Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 57 CLRS 12 Binary Search Trees Binary Search Trees The search tree data structure supports
Chapter 3 Graphs CLRS 12-13 Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 57 CLRS 12 Binary Search Trees Binary Search Trees The search tree data structure supports
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Algorithms, Spring 2014, CSE, OSU Lecture 5: Red-black trees
 6331 - Algorithms, Spring 2014, CSE, OSU Lecture 5: Red-black trees Instructor: Anastasios Sidiropoulos January 17, 2014 Red-black trees For every node x: x.color : red or black x.k : key x.p : pointer
6331 - Algorithms, Spring 2014, CSE, OSU Lecture 5: Red-black trees Instructor: Anastasios Sidiropoulos January 17, 2014 Red-black trees For every node x: x.color : red or black x.k : key x.p : pointer
18. Binary Search Trees
 Trees. Binary Search Trees [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Trees are Generalized lists: nodes can have more than one successor Special graphs: graphs consist of nodes and edges.
Trees. Binary Search Trees [Ottman/Widmayer, Kap..1, Cormen et al, Kap. 12.1-12.] Trees are Generalized lists: nodes can have more than one successor Special graphs: graphs consist of nodes and edges.
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms
 Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
Binary Trees
 Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
CS102 Binary Search Trees
 CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Red-Black Trees (2) Antonio Carzaniga. April 23, Faculty of Informatics Università della Svizzera italiana Antonio Carzaniga
 Red-Black Trees (2) Antonio Carzaniga Faculty of Informatics Università della Svizzera italiana April 23, 2013 Recap on Red-Black Trees 2006 Antonio Carzaniga Recap on Red-Black Trees 12 5 18 2 9 15 19
Red-Black Trees (2) Antonio Carzaniga Faculty of Informatics Università della Svizzera italiana April 23, 2013 Recap on Red-Black Trees 2006 Antonio Carzaniga Recap on Red-Black Trees 12 5 18 2 9 15 19
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Red-Black Trees. Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood
 Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
ADVANCED DATA STRUCTURES
 ADVANCED DATA STRUCTURES Lecture 1 Introduction. Binary search trees. Efficiency issues Mircea Marin mircea.marin@e-uvt.ro Organizatorial items Lecturer and Teaching Assistant: Mircea Marin email: mircea.marin@e-uvt.ro
ADVANCED DATA STRUCTURES Lecture 1 Introduction. Binary search trees. Efficiency issues Mircea Marin mircea.marin@e-uvt.ro Organizatorial items Lecturer and Teaching Assistant: Mircea Marin email: mircea.marin@e-uvt.ro
Binary Search Trees. Nearest Neighbor Binary Search Trees Insertion Predecessor and Successor Deletion Algorithms on Trees.
 Binary Search Trees Nearest Neighbor Binary Search Trees Insertion Predecessor and Successor Deletion Algorithms on Trees Philip Bille Binary Search Trees Nearest Neighbor Binary Search Trees Insertion
Binary Search Trees Nearest Neighbor Binary Search Trees Insertion Predecessor and Successor Deletion Algorithms on Trees Philip Bille Binary Search Trees Nearest Neighbor Binary Search Trees Insertion
Chapter 13. Michelle Bodnar, Andrew Lohr. April 12, 2016
 Chapter 13 Michelle Bodnar, Andrew Lohr April 1, 016 Exercise 13.1-1 8 4 1 6 10 14 1 3 5 7 9 11 13 15 We shorten IL to so that it can be more easily displayed in the document. The following has black height.
Chapter 13 Michelle Bodnar, Andrew Lohr April 1, 016 Exercise 13.1-1 8 4 1 6 10 14 1 3 5 7 9 11 13 15 We shorten IL to so that it can be more easily displayed in the document. The following has black height.
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Binary Search Trees. Binary Search Trees. Nearest Neighbor. Nearest Neighbor
 Philip Bille Nearest Neighbor Nearest neighbor. Maintain dynamic set S supporting the following operations. Each element has key x.key and satellite data x.data. PREDECESSOR(k): return element with largest
Philip Bille Nearest Neighbor Nearest neighbor. Maintain dynamic set S supporting the following operations. Each element has key x.key and satellite data x.data. PREDECESSOR(k): return element with largest
Data Structures and Algorithms. Chapter 7. Hashing
 1 Data Structures and Algorithms Chapter 7 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
1 Data Structures and Algorithms Chapter 7 Werner Nutt 2 Acknowledgments The course follows the book Introduction to Algorithms, by Cormen, Leiserson, Rivest and Stein, MIT Press [CLRST]. Many examples
Search Trees: BSTs and B-Trees
 3//13 Search Trees: BSTs and B-Trees Administrative David Kauchak cs302 Spring 13 Proof by contradiction Number guessing game I m thinking of a number between 1 and n You are trying to guess the answer
3//13 Search Trees: BSTs and B-Trees Administrative David Kauchak cs302 Spring 13 Proof by contradiction Number guessing game I m thinking of a number between 1 and n You are trying to guess the answer
Principles of Computer Science
 Principles of Computer Science Binary Trees 08/11/2013 CSCI 2010 - Binary Trees - F.Z. Qureshi 1 Today s Topics Extending LinkedList with Fast Search Sorted Binary Trees Tree Concepts Traversals of a Binary
Principles of Computer Science Binary Trees 08/11/2013 CSCI 2010 - Binary Trees - F.Z. Qureshi 1 Today s Topics Extending LinkedList with Fast Search Sorted Binary Trees Tree Concepts Traversals of a Binary
Algorithms and Data Structures (INF1) Lecture 8/15 Hua Lu
 Algorithms and Data Structures (INF1) Lecture 8/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Trees Basics Rooted trees Binary trees Binary tree ADT Tree traversal
Algorithms and Data Structures (INF1) Lecture 8/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Trees Basics Rooted trees Binary trees Binary tree ADT Tree traversal
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Lecture 3: B-Trees. October Lecture 3: B-Trees
 October 2017 Remarks Search trees The dynamic set operations search, minimum, maximum, successor, predecessor, insert and del can be performed efficiently (in O(log n) time) if the search tree is balanced.
October 2017 Remarks Search trees The dynamic set operations search, minimum, maximum, successor, predecessor, insert and del can be performed efficiently (in O(log n) time) if the search tree is balanced.
Binary Search Tree. Sorting and Searching in a Dynamic Set. S.V. N. (vishy) Vishwanathan. University of California, Santa Cruz
 Binary Search Tree Sorting and Searching in a Dynamic Set S.V. N. (vishy) Vishwanathan University of California, Santa Cruz vishy@ucsc.edu February 29, 2016 S.V. N. Vishwanathan (UCSC) CMPS101 1 / 23 Outline
Binary Search Tree Sorting and Searching in a Dynamic Set S.V. N. (vishy) Vishwanathan University of California, Santa Cruz vishy@ucsc.edu February 29, 2016 S.V. N. Vishwanathan (UCSC) CMPS101 1 / 23 Outline
CSCI Trees. Mark Redekopp David Kempe
 CSCI 104 2-3 Trees Mark Redekopp David Kempe Trees & Maps/Sets C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed This allows
CSCI 104 2-3 Trees Mark Redekopp David Kempe Trees & Maps/Sets C++ STL "maps" and "sets" use binary search trees internally to store their keys (and values) that can grow or contract as needed This allows
A red-black tree is a balanced binary search tree with the following properties:
 Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Balanced Trees Part One
 Balanced Trees Part One Balanced Trees Balanced search trees are among the most useful and versatile data structures. Many programming languages ship with a balanced tree library. C++: std::map / std::set
Balanced Trees Part One Balanced Trees Balanced search trees are among the most useful and versatile data structures. Many programming languages ship with a balanced tree library. C++: std::map / std::set
Data Structures Week #6. Special Trees
 Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 2 AVL Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 3 Motivation for
Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 2 AVL Trees 21.Aralık.2010 Borahan Tümer, Ph.D. 3 Motivation for
8. Binary Search Tree
 8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Jana Kosecka. Red-Black Trees Graph Algorithms. Many slides here are based on E. Demaine, D. Luebke slides
 Jana Kosecka Red-Black Trees Graph Algorithms Many slides here are based on E. Demaine, D. Luebke slides Binary Search Trees (BSTs) are an important data structure for dynamic sets In addition to satellite
Jana Kosecka Red-Black Trees Graph Algorithms Many slides here are based on E. Demaine, D. Luebke slides Binary Search Trees (BSTs) are an important data structure for dynamic sets In addition to satellite
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Module 4: Dictionaries and Balanced Search Trees
 Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Practical session No. 6. AVL Tree
 Practical session No. 6 AVL Trees Height- Balance Property AVL Tree AVL Interface AVL Height For every internal node v of a tree T, the height of the children nodes of v differ by at most 1. Any binary
Practical session No. 6 AVL Trees Height- Balance Property AVL Tree AVL Interface AVL Height For every internal node v of a tree T, the height of the children nodes of v differ by at most 1. Any binary
Algorithms, Spring 2014, CSE, OSU Lecture 4: Binary search trees
 6331 - Algorithms, Spring 2014, CSE, OSU Lecture 4: Binary search trees Instructor: Anastasios Sidiropoulos January 15, 2014 Binary search trees For every node x: x.k : key x.p : pointer to the parent
6331 - Algorithms, Spring 2014, CSE, OSU Lecture 4: Binary search trees Instructor: Anastasios Sidiropoulos January 15, 2014 Binary search trees For every node x: x.k : key x.p : pointer to the parent
Multi-way Search Trees! M-Way Search! M-Way Search Trees Representation!
 Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Algorithms. Red-Black Trees
 Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Questions from the material presented in this lecture
 Advanced Data Structures Questions from the material presented in this lecture January 8, 2015 This material illustrates the kind of exercises and questions you may get at the final colloqium. L1. Introduction.
Advanced Data Structures Questions from the material presented in this lecture January 8, 2015 This material illustrates the kind of exercises and questions you may get at the final colloqium. L1. Introduction.
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
Quiz 1 Solutions. (a) f(n) = n g(n) = log n Circle all that apply: f = O(g) f = Θ(g) f = Ω(g)
 Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Solutions Problem 1. Quiz 1 Solutions Asymptotic orders
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Solutions Problem 1. Quiz 1 Solutions Asymptotic orders
Sorted Arrays. Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min
 Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
CS 361, Lecture 21. Outline. Things you can do. Things I will do. Evaluation Results
 HW Difficulty CS 361, Lecture 21 Jared Saia University of New Mexico The HW in this class is inherently difficult, this is a difficult class. You need to be able to solve problems as hard as the problems
HW Difficulty CS 361, Lecture 21 Jared Saia University of New Mexico The HW in this class is inherently difficult, this is a difficult class. You need to be able to solve problems as hard as the problems
Friday Four Square! 4:15PM, Outside Gates
 Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Define the red- black tree properties Describe and implement rotations Implement red- black tree insertion
 Red black trees Define the red- black tree properties Describe and implement rotations Implement red- black tree insertion We will skip red- black tree deletion October 2004 John Edgar 2 Items can be inserted
Red black trees Define the red- black tree properties Describe and implement rotations Implement red- black tree insertion We will skip red- black tree deletion October 2004 John Edgar 2 Items can be inserted
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
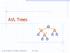 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Trees. Chapter 6. strings. 3 Both position and Enumerator are similar in concept to C++ iterators, although the details are quite different.
 Chapter 6 Trees In a hash table, the items are not stored in any particular order in the table. This is fine for implementing Sets and Maps, since for those abstract data types, the only thing that matters
Chapter 6 Trees In a hash table, the items are not stored in any particular order in the table. This is fine for implementing Sets and Maps, since for those abstract data types, the only thing that matters
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
