T Seminar on Theoretical Computer Science Spring 2007 Distributed Computation. Constructing a spanning tree Toni Kylmälä
|
|
|
- Neil Lyons
- 6 years ago
- Views:
Transcription
1 T Seminar on Theoretical Computer Science Spring 2007 Distributed Computation Constructing a spanning tree Toni Kylmälä toni.kylmala@tkk.fi 1
2 Spanning tree To construct a spanning tree we must get every node in the graph G to choose a subset of its neighbours to be in the acyclic graph T that spans the entire graph G. which we then call the spanning tree. Constraints We first look at a Unique Initiator case and limit ourselves to a fully connected network of bidirectional links where no failures occur. Denote RI. 2
3 Shout Shout is a simple spanning tree construction protocol in which entities ask their neighbours whether they are neighbours in the spanning tree as well. 1. An entity will answer yes the first time it is asked. 2. Otherwise it will answer no. The initiator s will always reply no. 3. Each entity terminates indepently when it has received a reply from all its neighbours. Summarising this kind of protocol is a flood with an acnowledgement for every information message. This type of structure will be called Flood + Reply. 3
4 PROTOCOL Shout Status: S = {INITIATOR, IDLE, ACTIVE, DONE} S INIT = {INITIATOR, IDLE} S T ERM = {DONE} Restrictions: R;UI; INITIATOR Spontaneuosly root := true Tree-neighbours := /0 s(q)ton(x) counter := 0 becomeact IV E IDLE Receiving (Q) root := false parent := ser Tree neighbours := {ser} s(yes)to{ser} counter := 1 ifcounter = N(x) then becomedone else s(q)ton(x) {Ser} becomeact IV E if ACT IV E Receiving (Q) s(no)to{ser} Receiving (Yes) Tree neighbours := Tree neighbours S {ser} counter := counter + 1 if counter= N(x) then become DONE if Receiving (No) counter := counter + 1 if counter= N(x) then become DONE if 4
5 Proof of correctness Because of the correctness of flooding every entity will receive Q. And by construction reply either yes or no to each Q. Since every entity only replies yes the first time it receives Q there can be no cycles. And because every x s is connected to s through a path of parents where on every link a yes was sent the tree spans the entire graph G. Important Shout s in local termination. No entity is aware of global termination. This is fairly common in distributed computing. However Shout can easily be modified to allow global termination knowledge. 5
6 Costs The message costs of Flood + Reply, and thus of Shout, are simple to analyze. Flood + Reply consists of executing Flooding(Q) with a reply for every Q: M[Flood + Reply]=2M[Flooding]. T[Flood + Reply]=T[Flooding] + 1. Thus: M[Shout]=4m - 2n + 2 T[Shout]=r(s )+1 d + 1 6
7 Theorem Proof M(SPT/RI) m. Similarly to the broadcast problem. If fewer than m messages are sent then there can be an entity that neither receives Q nor ss replies. Theorem T(SPT/RI) d. These imply that Shout is both time and message optimal. Property The message complexity of spanning tree construction under RI is O(m). Property The ideal time complexity of spanning tree construction under RI is O(d). 7
8 Hacking Do we have to s no messages? We would only s no to entities that s us Q after we have received Q for the first time. By this time we have already sent those same entities Q. Thus we s Q and no to exactly the same entities. No messages can therefore be left out. The resulting Shout+ has message complexity: T[Shout+]=r(s )+1 d + 1 M[Shout+]=2m Note that time complexity does not change. 8
9 Other SPT constructions with Single Initiator SPT construction by traversal. A depth first traversal actually constructs a spanning tree (df-tree) of G. We obtain the tree by removing back-edges. Simple changes in local bookkeeping will allow entities to correctly determine tree neighbours. Thus costs are unchanged: M[df-SPT]=4m - 2n + f + 1. T[df-SPT]=2n - 2. We can now better analyze the variable f. It is exactly the number of leaves in the df-tree. SPT construction by broadcasting. With simple modifications flooding and df-traversal can be used to construct a spanning tree if a unique initiator is present. This is part of an interesting phenomenon: under RI. The execution of any broadcast protocol constructs a spanning tree. Any broadcast execution will result in all entities receiving the information. Every entity will call the entity it first received it from a parent. Every x s has one parent while s has none. 9
10 Theorem The parent relationship x y defines a spanning tree rooted in the initiator s. Relation between broadcast, traversal, spanning tree and global protocols As found previously in section every traversal protocol performs broadcast. Thus under RI any traversal protocol constructs a spanning tree. Bcast SPT(UI). (2.20) Actually we can make a much stronger statement. Call a problem global if every entity must participate in its solution. Clearly all three above are global. Now every single-initiator protocol that solves a global problem P solves also Bcast; thus from equation 2.20 under RI The execution of any solution to any global problem P constructs a spanning tree. Consider the constructed tree Using the spanning tree we can perform broadcast and traversal with optimal O(n) messages instead of O(m) messages which could be as bad O(n 2 ) 10
11 Important Trees constructed with different methods are different. In fact because of unpredictable communication delays every possible spanning tree can be constructed with shout. This has implications for time costs. Broadcast time will be d(t) instead of d(g). But d(t) can be much greater. In a fully connected graph n-1 as opposed to 1. Thus we want to construct a tree that has minimal d(t), a broadcast tree. For this we need to find the center c of the graph for the initiator node and use a breadth-first algorithm BFT(c, G). Center is the node x with minimum radius. r G (x) = Max{d G (x,y) : y v}. The radius of G is the minimum radius of all nodes x. r(g) = Min{r G (x) : x V}. Relationship between radius and diameter of G in every graph G r(g) d(g) 2r(G). Unfortunately center finding and Breadth-First SPT construction are not simple problems to solve as will be seen in later chapters. 11
12 Theorem BFT(c, G) is a broadcast tree of G. Application: better traversal Use Shout+ to construct a spanning tree T and perform traversal of T using DF_Traversal. M[SmartTraversal]=2(m + n - 1) T[SmartTraversal]= 2n + d - 1 SmartTraversal is simple as well as time and message optimal. 12
13 Spanning tree with multiple initiators Unfortunately a single initiator is a strong assumption as well as difficult and expensive to guarantee. In Shout if we have more than one initiator the result is a spanning tree forest since initiators have no parents and all other entities have only one parent. Removing the single initiator restriction brings out the true nature of the problem. Theorem The SPT problem is deterministically unsolvable under R. Impossibility result This means that there is no deterministic protocol that always correctly terminates within finite time. 13
14 Proof Consider a simple three entity system where all three are connected. In the ning all are in an identical state. If a solution A exists it must work here as well. Consider a synchronous schedule (i.e. an execution where communication delays are unitary) and let all three start the execution of A simultaneously. Since the states are identical they will all execute the same steps and in possibly new identical states. However for there to be a spanning tree one of the tree edges must be removed. Thus the entities will have to in distinct states with different values. But since the states are always identical no solution A exists. SPT with Initial Distinct values Despite this very negative result we can solve the problem with additional constraints. ID:s are an often used solution. These can be used to distinguish between initiators. A simple solution is to have many overlapping spanning trees. This however requires much local bookkeeping. The costs dep solely on the number k of initiators. In the case of Shout+ there will be 2mk messages which could be as bad as O(n 3 ). 14
15 Selective construction A better solution is to allow only one of these to complete and kill all the others. This can be done by letting the minimum (or maximum) valued initiators SPT be completed. Thus every time an entity receives Q with a lower initiator than the one it currently has it discards all previously collected information and joins the new tree. This reduces local bookkeeping and ensures that all entities have a single shared spanning tree. Important An entity might have terminated when it must start again when it receives Q with lower initiator. Thus we must have some way to ensure effective local termination. This is accomplished by having the initiator become aware that the tree is finished and all other trees have been killed and notifying all other entities using the newly constructed spanning tree. This protocol is called MultiShout. Theorem Protocol MultiShout constructs a spanning tree rooted in the initiator with the smallest initial value. 15
16 Costs of MultiShout It s clearly better than the first one although the worst case can be as bad as O(n 3 ). Consider an n-node graph with a fully connected subgraph with n - k nodes. The k nodes are initiators all with a single connection to the subgraph whose messages arrive in the subgraph in valued order so that when the subgraph has completed the construction a message Q arrives from the next k with a smaller ID. This is possible because we have unpredictable message delays. Thus the SPT will be constructed k times. with n - k nodes in each iteration. O((n - k) 2 ) messages in the subgraph. Thus a total of O(k(n - k) 2 ) messages will be used. If k is a linear fraction of n (e.g. k=n/2), then the cost will be O(n 3 ). This does not imply that the selective construction is not efficient. Merely that the solution here is not. This will be further examined in leader election. 16
17 PROTOCOL MultiShout Status: S = {IDLE, ACTIVE, DONE} S INIT = {IDLE} S T ERM = {DONE} Restrictions: R;ID; IDLE Spontaneously root := true root_id := v(x) Tree-neighbours := /0 s(q, root_id)ton(x) counter := 0 check_counter := 0 becomeact IV E Receiving(Q, id) CONST RUCT 17
18 ACTIVE Receiving(Q,id) if root_id = id then counter := counter + 1 if counter= N(x) then done := true CHECK if else if root_id > id then CONSTRUCT if Receiving(Yes, id) if root_id = id then Tree-neighbours := Tree-neighbours S {ser} counter := counter + 1 if counter= N(x) then done := true CHECK if if Receiving(Check, id) if root_id = id then check_counter := check_counter + 1 if (done check_counter= Children ) then TERM if if Receiving(Terminate) s(terminate) to Children become DONE 18 Procedure CONSTRUCT root := false root_id := id Tree-neighbours := {ser} parent := ser s (Yes,root_id) to {ser} counter := 1 check_counter = 0 if counter = N(x) then done := true CHECK else s(q,root_id) to N(x) - {ser} if become ACTIVE Procedure CHECK Children := Tree-neighbours - {parent} if Children = /0 then s (Check,root_id) to parent if Procedure TERM if root then s(terminate) to Tree-neighbours become DONE else s(check,root_id) to parent if
Broadcast: Befo re 1
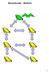 Broadcast: Before 1 After 2 Spanning Tree ffl assume fixed spanning tree ffl asynchronous model 3 Processor State parent terminated children 4 Broadcast: Step One parent terminated children 5 Broadcast:Step
Broadcast: Before 1 After 2 Spanning Tree ffl assume fixed spanning tree ffl asynchronous model 3 Processor State parent terminated children 4 Broadcast: Step One parent terminated children 5 Broadcast:Step
GIAN Course on Distributed Network Algorithms. Spanning Tree Constructions
 GIAN Course on Distributed Network Algorithms Spanning Tree Constructions Stefan Schmid @ T-Labs, 2011 Spanning Trees Attactive infrastructure : sparse subgraph ( loop-free backbone ) connecting all nodes.
GIAN Course on Distributed Network Algorithms Spanning Tree Constructions Stefan Schmid @ T-Labs, 2011 Spanning Trees Attactive infrastructure : sparse subgraph ( loop-free backbone ) connecting all nodes.
GIAN Course on Distributed Network Algorithms. Spanning Tree Constructions
 GIAN Course on Distributed Network Algorithms Spanning Tree Constructions Stefan Schmid @ T-Labs, 2011 Spanning Trees Attactive infrastructure : sparse subgraph ( loop-free backbone ) connecting all nodes.
GIAN Course on Distributed Network Algorithms Spanning Tree Constructions Stefan Schmid @ T-Labs, 2011 Spanning Trees Attactive infrastructure : sparse subgraph ( loop-free backbone ) connecting all nodes.
21. Distributed Algorithms
 21. Distributed Algorithms We dene a distributed system as a collection of individual computing devices that can communicate with each other [2]. This denition is very broad, it includes anything, from
21. Distributed Algorithms We dene a distributed system as a collection of individual computing devices that can communicate with each other [2]. This denition is very broad, it includes anything, from
A distributed algorithm for minimum weight spanning trees
 A distributed algorithm for minimum weight spanning trees R. G. Gallager, P. A. Humblet and P. M. Spira Prepared by: Guy Flysher and Amir Rubinshtein Preface In this document we will review Gallager,
A distributed algorithm for minimum weight spanning trees R. G. Gallager, P. A. Humblet and P. M. Spira Prepared by: Guy Flysher and Amir Rubinshtein Preface In this document we will review Gallager,
GraphTheory Models & Complexity BFS Trees DFS Trees Min Spanning Trees. Tree Constructions. Martin Biely
 Tree Constructions Martin Biely Embedded Computing Systems Group Vienna University of Technology European Union November 29, 2006 Biely Tree Constructions 1 Outline 1 A quick Repetition on Graphs 2 Models
Tree Constructions Martin Biely Embedded Computing Systems Group Vienna University of Technology European Union November 29, 2006 Biely Tree Constructions 1 Outline 1 A quick Repetition on Graphs 2 Models
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
CSE 373 MAY 10 TH SPANNING TREES AND UNION FIND
 CSE 373 MAY 0 TH SPANNING TREES AND UNION FIND COURSE LOGISTICS HW4 due tonight, if you want feedback by the weekend COURSE LOGISTICS HW4 due tonight, if you want feedback by the weekend HW5 out tomorrow
CSE 373 MAY 0 TH SPANNING TREES AND UNION FIND COURSE LOGISTICS HW4 due tonight, if you want feedback by the weekend COURSE LOGISTICS HW4 due tonight, if you want feedback by the weekend HW5 out tomorrow
Leader Election in Rings
 Leader Election Arvind Krishnamurthy Fall 2003 Leader Election in Rings Under different models: Synchronous vs. asynchronous Anonymous vs. non-anonymous (knowledge of unique id) Knowledge of n (non-uniform)
Leader Election Arvind Krishnamurthy Fall 2003 Leader Election in Rings Under different models: Synchronous vs. asynchronous Anonymous vs. non-anonymous (knowledge of unique id) Knowledge of n (non-uniform)
2. True or false: even though BFS and DFS have the same space complexity, they do not always have the same worst case asymptotic time complexity.
 1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
A generalization of Mader s theorem
 A generalization of Mader s theorem Ajit A. Diwan Department of Computer Science and Engineering Indian Institute of Technology, Bombay Mumbai, 4000076, India. email: aad@cse.iitb.ac.in 18 June 2007 Abstract
A generalization of Mader s theorem Ajit A. Diwan Department of Computer Science and Engineering Indian Institute of Technology, Bombay Mumbai, 4000076, India. email: aad@cse.iitb.ac.in 18 June 2007 Abstract
Clock Synchronization. Synchronization. Clock Synchronization Algorithms. Physical Clock Synchronization. Tanenbaum Chapter 6 plus additional papers
 Clock Synchronization Synchronization Tanenbaum Chapter 6 plus additional papers Fig 6-1. In a distributed system, each machine has its own clock. When this is the case, an event that occurred after another
Clock Synchronization Synchronization Tanenbaum Chapter 6 plus additional papers Fig 6-1. In a distributed system, each machine has its own clock. When this is the case, an event that occurred after another
A synchronizer generates sequences of clock pulses at each node of the network satisfying the condition given by the following definition.
 Chapter 8 Synchronizers So far, we have mainly studied synchronous algorithms because generally, asynchronous algorithms are often more di cult to obtain and it is substantially harder to reason about
Chapter 8 Synchronizers So far, we have mainly studied synchronous algorithms because generally, asynchronous algorithms are often more di cult to obtain and it is substantially harder to reason about
Parallel and Sequential Data Structures and Algorithms Lecture (Spring 2012) Lecture 16 Treaps; Augmented BSTs
 Lecture 16 Treaps; Augmented BSTs Parallel and Sequential Data Structures and Algorithms, 15-210 (Spring 2012) Lectured by Margaret Reid-Miller 8 March 2012 Today: - More on Treaps - Ordered Sets and Tables
Lecture 16 Treaps; Augmented BSTs Parallel and Sequential Data Structures and Algorithms, 15-210 (Spring 2012) Lectured by Margaret Reid-Miller 8 March 2012 Today: - More on Treaps - Ordered Sets and Tables
THE FIRST APPROXIMATED DISTRIBUTED ALGORITHM FOR THE MINIMUM DEGREE SPANNING TREE PROBLEM ON GENERAL GRAPHS. and
 International Journal of Foundations of Computer Science c World Scientific Publishing Company THE FIRST APPROXIMATED DISTRIBUTED ALGORITHM FOR THE MINIMUM DEGREE SPANNING TREE PROBLEM ON GENERAL GRAPHS
International Journal of Foundations of Computer Science c World Scientific Publishing Company THE FIRST APPROXIMATED DISTRIBUTED ALGORITHM FOR THE MINIMUM DEGREE SPANNING TREE PROBLEM ON GENERAL GRAPHS
Part IV. Common Reduction Targets
 Part IV Common Reduction Targets 413 Chapter 13 Depth-First Search As we have seen in earlier chapters, many problems can be characterized as graph problems. Graph problems often require the searching
Part IV Common Reduction Targets 413 Chapter 13 Depth-First Search As we have seen in earlier chapters, many problems can be characterized as graph problems. Graph problems often require the searching
Design and Analysis of Distributed Algorithms. Chapter 1: DISTRIBUTED COMPUTING ENVIRONMENTS
 Design and Analysis of Distributed Algorithms Chapter 1: DISTRIBUTED COMPUTING ENVIRONMENTS c 2005, Nicola Santoro. Contents 1 Entities 1 2 Communication 3 3 Axioms and Restrictions 4 3.1 Axioms.......................................
Design and Analysis of Distributed Algorithms Chapter 1: DISTRIBUTED COMPUTING ENVIRONMENTS c 2005, Nicola Santoro. Contents 1 Entities 1 2 Communication 3 3 Axioms and Restrictions 4 3.1 Axioms.......................................
CMSC th Lecture: Graph Theory: Trees.
 CMSC 27100 26th Lecture: Graph Theory: Trees. Lecturer: Janos Simon December 2, 2018 1 Trees Definition 1. A tree is an acyclic connected graph. Trees have many nice properties. Theorem 2. The following
CMSC 27100 26th Lecture: Graph Theory: Trees. Lecturer: Janos Simon December 2, 2018 1 Trees Definition 1. A tree is an acyclic connected graph. Trees have many nice properties. Theorem 2. The following
INDIAN STATISTICAL INSTITUTE
 INDIAN STATISTICAL INSTITUTE Mid Semestral Examination M. Tech (CS) - I Year, 2016-2017 (Semester - II) Design and Analysis of Algorithms Date : 21.02.2017 Maximum Marks : 60 Duration : 3.0 Hours Note:
INDIAN STATISTICAL INSTITUTE Mid Semestral Examination M. Tech (CS) - I Year, 2016-2017 (Semester - II) Design and Analysis of Algorithms Date : 21.02.2017 Maximum Marks : 60 Duration : 3.0 Hours Note:
Info 2950, Lecture 16
 Info 2950, Lecture 16 28 Mar 2017 Prob Set 5: due Fri night 31 Mar Breadth first search (BFS) and Depth First Search (DFS) Must have an ordering on the vertices of the graph. In most examples here, the
Info 2950, Lecture 16 28 Mar 2017 Prob Set 5: due Fri night 31 Mar Breadth first search (BFS) and Depth First Search (DFS) Must have an ordering on the vertices of the graph. In most examples here, the
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
4 Basics of Trees. Petr Hliněný, FI MU Brno 1 FI: MA010: Trees and Forests
 4 Basics of Trees Trees, actually acyclic connected simple graphs, are among the simplest graph classes. Despite their simplicity, they still have rich structure and many useful application, such as in
4 Basics of Trees Trees, actually acyclic connected simple graphs, are among the simplest graph classes. Despite their simplicity, they still have rich structure and many useful application, such as in
Distributed Algorithms 6.046J, Spring, Nancy Lynch
 Distributed Algorithms 6.046J, Spring, 205 Nancy Lynch What are Distributed Algorithms? Algorithms that run on networked processors, or on multiprocessors that share memory. They solve many kinds of problems:
Distributed Algorithms 6.046J, Spring, 205 Nancy Lynch What are Distributed Algorithms? Algorithms that run on networked processors, or on multiprocessors that share memory. They solve many kinds of problems:
CSc Leader Election
 CSc72010 Leader Election Reading Skim 3.5 Read 3.6, General synchronous networks Read 4.1 Leader election algorithms Lelann/Chang/Roberts: O(n) time complexity O(n 2 ) message complexity Hirschberg/Sinclair
CSc72010 Leader Election Reading Skim 3.5 Read 3.6, General synchronous networks Read 4.1 Leader election algorithms Lelann/Chang/Roberts: O(n) time complexity O(n 2 ) message complexity Hirschberg/Sinclair
Chapter 3 Trees. Theorem A graph T is a tree if, and only if, every two distinct vertices of T are joined by a unique path.
 Chapter 3 Trees Section 3. Fundamental Properties of Trees Suppose your city is planning to construct a rapid rail system. They want to construct the most economical system possible that will meet the
Chapter 3 Trees Section 3. Fundamental Properties of Trees Suppose your city is planning to construct a rapid rail system. They want to construct the most economical system possible that will meet the
Clearly there is a close relation between the radius R and the diameter D of a graph, such as R D 2R.
 Chapter 2 Tree Algorithms In this chapter we learn a few basic algorithms on trees, and how to construct trees in the first place so that we can run these (and other) algorithms. The good news is that
Chapter 2 Tree Algorithms In this chapter we learn a few basic algorithms on trees, and how to construct trees in the first place so that we can run these (and other) algorithms. The good news is that
Graph Algorithms Using Depth First Search
 Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Graph Algorithms Using Depth First Search Analysis of Algorithms Week 8, Lecture 1 Prepared by John Reif, Ph.D. Distinguished Professor of Computer Science Duke University Graph Algorithms Using Depth
Models of distributed computing: port numbering and local algorithms
 Models of distributed computing: port numbering and local algorithms Jukka Suomela Adaptive Computing Group Helsinki Institute for Information Technology HIIT University of Helsinki FMT seminar, 26 February
Models of distributed computing: port numbering and local algorithms Jukka Suomela Adaptive Computing Group Helsinki Institute for Information Technology HIIT University of Helsinki FMT seminar, 26 February
Reference Sheet for CO142.2 Discrete Mathematics II
 Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Flow Graph Theory. Depth-First Ordering Efficiency of Iterative Algorithms Reducible Flow Graphs
 Flow Graph Theory Depth-First Ordering Efficiency of Iterative Algorithms Reducible Flow Graphs 1 Roadmap Proper ordering of nodes of a flow graph speeds up the iterative algorithms: depth-first ordering.
Flow Graph Theory Depth-First Ordering Efficiency of Iterative Algorithms Reducible Flow Graphs 1 Roadmap Proper ordering of nodes of a flow graph speeds up the iterative algorithms: depth-first ordering.
Partitioning Complete Multipartite Graphs by Monochromatic Trees
 Partitioning Complete Multipartite Graphs by Monochromatic Trees Atsushi Kaneko, M.Kano 1 and Kazuhiro Suzuki 1 1 Department of Computer and Information Sciences Ibaraki University, Hitachi 316-8511 Japan
Partitioning Complete Multipartite Graphs by Monochromatic Trees Atsushi Kaneko, M.Kano 1 and Kazuhiro Suzuki 1 1 Department of Computer and Information Sciences Ibaraki University, Hitachi 316-8511 Japan
1 Digraphs. Definition 1
 1 Digraphs Definition 1 Adigraphordirected graphgisatriplecomprisedofavertex set V(G), edge set E(G), and a function assigning each edge an ordered pair of vertices (tail, head); these vertices together
1 Digraphs Definition 1 Adigraphordirected graphgisatriplecomprisedofavertex set V(G), edge set E(G), and a function assigning each edge an ordered pair of vertices (tail, head); these vertices together
The Postal Network: A Versatile Interconnection Topology
 The Postal Network: A Versatile Interconnection Topology Jie Wu Yuanyuan Yang Dept. of Computer Sci. and Eng. Dept. of Computer Science Florida Atlantic University University of Vermont Boca Raton, FL
The Postal Network: A Versatile Interconnection Topology Jie Wu Yuanyuan Yang Dept. of Computer Sci. and Eng. Dept. of Computer Science Florida Atlantic University University of Vermont Boca Raton, FL
Trees Rooted Trees Spanning trees and Shortest Paths. 12. Graphs and Trees 2. Aaron Tan November 2017
 12. Graphs and Trees 2 Aaron Tan 6 10 November 2017 1 10.5 Trees 2 Definition Definition Definition: Tree A graph is said to be circuit-free if, and only if, it has no circuits. A graph is called a tree
12. Graphs and Trees 2 Aaron Tan 6 10 November 2017 1 10.5 Trees 2 Definition Definition Definition: Tree A graph is said to be circuit-free if, and only if, it has no circuits. A graph is called a tree
Chapter 4. Relations & Graphs. 4.1 Relations. Exercises For each of the relations specified below:
 Chapter 4 Relations & Graphs 4.1 Relations Definition: Let A and B be sets. A relation from A to B is a subset of A B. When we have a relation from A to A we often call it a relation on A. When we have
Chapter 4 Relations & Graphs 4.1 Relations Definition: Let A and B be sets. A relation from A to B is a subset of A B. When we have a relation from A to A we often call it a relation on A. When we have
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems. Problems, Hints, and Solutions
 Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Chapter 9 Graph Algorithms
 Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
Chapter 9 Graph Algorithms 2 Introduction graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 3 Definitions an undirected graph G = (V, E)
11/22/2016. Chapter 9 Graph Algorithms. Introduction. Definitions. Definitions. Definitions. Definitions
 Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
Introduction Chapter 9 Graph Algorithms graph theory useful in practice represent many real-life problems can be slow if not careful with data structures 2 Definitions an undirected graph G = (V, E) is
MAL 376: Graph Algorithms I Semester Lecture 1: July 24
 MAL 376: Graph Algorithms I Semester 2014-2015 Lecture 1: July 24 Course Coordinator: Prof. B. S. Panda Scribes: Raghuvansh, Himanshu, Mohit, Abhishek Disclaimer: These notes have not been subjected to
MAL 376: Graph Algorithms I Semester 2014-2015 Lecture 1: July 24 Course Coordinator: Prof. B. S. Panda Scribes: Raghuvansh, Himanshu, Mohit, Abhishek Disclaimer: These notes have not been subjected to
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS
 Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
Department of Computer Science University of Babylon LECTURE NOTES OF ALGORITHMS: DESIGN TECHNIQUES AND ANALYSIS By Faculty of Science for Women( SCIW), University of Babylon, Iraq Samaher@uobabylon.edu.iq
CSE 21 Mathematics for Algorithm and System Analysis
 CSE 21 Mathematics for Algorithm and System Analysis Unit 4: Basic Concepts in Graph Theory Section 3: Trees 1 Review : Decision Tree (DT-Section 1) Root of the decision tree on the left: 1 Leaves of the
CSE 21 Mathematics for Algorithm and System Analysis Unit 4: Basic Concepts in Graph Theory Section 3: Trees 1 Review : Decision Tree (DT-Section 1) Root of the decision tree on the left: 1 Leaves of the
Seminar on Algorithms and Data Structures: Multiple-Edge-Fault-Tolerant Approximate Shortest-Path Trees [1]
![Seminar on Algorithms and Data Structures: Multiple-Edge-Fault-Tolerant Approximate Shortest-Path Trees [1] Seminar on Algorithms and Data Structures: Multiple-Edge-Fault-Tolerant Approximate Shortest-Path Trees [1]](/thumbs/89/97828842.jpg) Seminar on Algorithms and Data Structures: Multiple-Edge-Fault-Tolerant Approximate Shortest-Path Trees [1] Philipp Rimle April 14, 2018 1 Introduction Given a graph with positively real-weighted undirected
Seminar on Algorithms and Data Structures: Multiple-Edge-Fault-Tolerant Approximate Shortest-Path Trees [1] Philipp Rimle April 14, 2018 1 Introduction Given a graph with positively real-weighted undirected
Trees. Arash Rafiey. 20 October, 2015
 20 October, 2015 Definition Let G = (V, E) be a loop-free undirected graph. G is called a tree if G is connected and contains no cycle. Definition Let G = (V, E) be a loop-free undirected graph. G is called
20 October, 2015 Definition Let G = (V, E) be a loop-free undirected graph. G is called a tree if G is connected and contains no cycle. Definition Let G = (V, E) be a loop-free undirected graph. G is called
An algorithm for Performance Analysis of Single-Source Acyclic graphs
 An algorithm for Performance Analysis of Single-Source Acyclic graphs Gabriele Mencagli September 26, 2011 In this document we face with the problem of exploiting the performance analysis of acyclic graphs
An algorithm for Performance Analysis of Single-Source Acyclic graphs Gabriele Mencagli September 26, 2011 In this document we face with the problem of exploiting the performance analysis of acyclic graphs
A Note on Scheduling Parallel Unit Jobs on Hypercubes
 A Note on Scheduling Parallel Unit Jobs on Hypercubes Ondřej Zajíček Abstract We study the problem of scheduling independent unit-time parallel jobs on hypercubes. A parallel job has to be scheduled between
A Note on Scheduling Parallel Unit Jobs on Hypercubes Ondřej Zajíček Abstract We study the problem of scheduling independent unit-time parallel jobs on hypercubes. A parallel job has to be scheduled between
Verifying Safety Property of Lustre Programs: Temporal Induction
 22c181: Formal Methods in Software Engineering The University of Iowa Spring 2008 Verifying Safety Property of Lustre Programs: Temporal Induction Copyright 2008 Cesare Tinelli. These notes are copyrighted
22c181: Formal Methods in Software Engineering The University of Iowa Spring 2008 Verifying Safety Property of Lustre Programs: Temporal Induction Copyright 2008 Cesare Tinelli. These notes are copyrighted
1. Graph and Representation
 Chapter Graphs Tree Root Direction: parent-child relationships No cycles Graph Vertices + Edges No tree restrictions Examples World Wide Web Maps. Graph and Representation A graph G: a pair (V, E) vertices
Chapter Graphs Tree Root Direction: parent-child relationships No cycles Graph Vertices + Edges No tree restrictions Examples World Wide Web Maps. Graph and Representation A graph G: a pair (V, E) vertices
2 The Fractional Chromatic Gap
 C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
C 1 11 2 The Fractional Chromatic Gap As previously noted, for any finite graph. This result follows from the strong duality of linear programs. Since there is no such duality result for infinite linear
COMP3121/3821/9101/ s1 Assignment 1
 Sample solutions to assignment 1 1. (a) Describe an O(n log n) algorithm (in the sense of the worst case performance) that, given an array S of n integers and another integer x, determines whether or not
Sample solutions to assignment 1 1. (a) Describe an O(n log n) algorithm (in the sense of the worst case performance) that, given an array S of n integers and another integer x, determines whether or not
Definition: A graph G = (V, E) is called a tree if G is connected and acyclic. The following theorem captures many important facts about trees.
 Tree 1. Trees and their Properties. Spanning trees 3. Minimum Spanning Trees 4. Applications of Minimum Spanning Trees 5. Minimum Spanning Tree Algorithms 1.1 Properties of Trees: Definition: A graph G
Tree 1. Trees and their Properties. Spanning trees 3. Minimum Spanning Trees 4. Applications of Minimum Spanning Trees 5. Minimum Spanning Tree Algorithms 1.1 Properties of Trees: Definition: A graph G
Graph Connectivity G G G
 Graph Connectivity 1 Introduction We have seen that trees are minimally connected graphs, i.e., deleting any edge of the tree gives us a disconnected graph. What makes trees so susceptible to edge deletions?
Graph Connectivity 1 Introduction We have seen that trees are minimally connected graphs, i.e., deleting any edge of the tree gives us a disconnected graph. What makes trees so susceptible to edge deletions?
Greedy Algorithms 1. For large values of d, brute force search is not feasible because there are 2 d
 Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
Lecture 4 Feb 21, 2007
 6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 4 Feb 21, 2007 Scribe: Mashhood Ishaque 1 Overview In the last lecture we worked in a BST model. We discussed Wilber lower bounds
6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 4 Feb 21, 2007 Scribe: Mashhood Ishaque 1 Overview In the last lecture we worked in a BST model. We discussed Wilber lower bounds
11.9 Connectivity Connected Components. mcs 2015/5/18 1:43 page 419 #427
 mcs 2015/5/18 1:43 page 419 #427 11.9 Connectivity Definition 11.9.1. Two vertices are connected in a graph when there is a path that begins at one and ends at the other. By convention, every vertex is
mcs 2015/5/18 1:43 page 419 #427 11.9 Connectivity Definition 11.9.1. Two vertices are connected in a graph when there is a path that begins at one and ends at the other. By convention, every vertex is
Solutions to relevant spring 2000 exam problems
 Problem 2, exam Here s Prim s algorithm, modified slightly to use C syntax. MSTPrim (G, w, r): Q = V[G]; for (each u Q) { key[u] = ; key[r] = 0; π[r] = 0; while (Q not empty) { u = ExtractMin (Q); for
Problem 2, exam Here s Prim s algorithm, modified slightly to use C syntax. MSTPrim (G, w, r): Q = V[G]; for (each u Q) { key[u] = ; key[r] = 0; π[r] = 0; while (Q not empty) { u = ExtractMin (Q); for
Approximation Algorithms
 Approximation Algorithms Given an NP-hard problem, what should be done? Theory says you're unlikely to find a poly-time algorithm. Must sacrifice one of three desired features. Solve problem to optimality.
Approximation Algorithms Given an NP-hard problem, what should be done? Theory says you're unlikely to find a poly-time algorithm. Must sacrifice one of three desired features. Solve problem to optimality.
Λέων-Χαράλαμπος Σταματάρης
 Λέων-Χαράλαμπος Σταματάρης INTRODUCTION Two classical problems of information dissemination in computer networks: The broadcasting problem: Distributing a particular message from a distinguished source
Λέων-Χαράλαμπος Σταματάρης INTRODUCTION Two classical problems of information dissemination in computer networks: The broadcasting problem: Distributing a particular message from a distinguished source
CS2 Algorithms and Data Structures Note 10. Depth-First Search and Topological Sorting
 CS2 Algorithms and Data Structures Note 10 Depth-First Search and Topological Sorting In this lecture, we will analyse the running time of DFS and discuss a few applications. 10.1 A recursive implementation
CS2 Algorithms and Data Structures Note 10 Depth-First Search and Topological Sorting In this lecture, we will analyse the running time of DFS and discuss a few applications. 10.1 A recursive implementation
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Verteilte Systeme/Distributed Systems Ch. 5: Various distributed algorithms
 Verteilte Systeme/Distributed Systems Ch. 5: Various distributed algorithms Holger Karl Computer Networks Group Universität Paderborn Goal of this chapter Apart from issues in distributed time and resulting
Verteilte Systeme/Distributed Systems Ch. 5: Various distributed algorithms Holger Karl Computer Networks Group Universität Paderborn Goal of this chapter Apart from issues in distributed time and resulting
CSE 100: GRAPH ALGORITHMS
 CSE 100: GRAPH ALGORITHMS Dijkstra s Algorithm: Questions Initialize the graph: Give all vertices a dist of INFINITY, set all done flags to false Start at s; give s dist = 0 and set prev field to -1 Enqueue
CSE 100: GRAPH ALGORITHMS Dijkstra s Algorithm: Questions Initialize the graph: Give all vertices a dist of INFINITY, set all done flags to false Start at s; give s dist = 0 and set prev field to -1 Enqueue
Solutions to Midterm 2 - Monday, July 11th, 2009
 Solutions to Midterm - Monday, July 11th, 009 CPSC30, Summer009. Instructor: Dr. Lior Malka. (liorma@cs.ubc.ca) 1. Dynamic programming. Let A be a set of n integers A 1,..., A n such that 1 A i n for each
Solutions to Midterm - Monday, July 11th, 009 CPSC30, Summer009. Instructor: Dr. Lior Malka. (liorma@cs.ubc.ca) 1. Dynamic programming. Let A be a set of n integers A 1,..., A n such that 1 A i n for each
On vertex types of graphs
 On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
Depth-First Search Depth-first search (DFS) is another way to traverse the graph.
 Depth-First Search Depth-first search (DFS) is another way to traverse the graph. Motivating example: In a video game, you are searching for a path from a point in a maze to the exit. The maze can be modeled
Depth-First Search Depth-first search (DFS) is another way to traverse the graph. Motivating example: In a video game, you are searching for a path from a point in a maze to the exit. The maze can be modeled
Joint Entity Resolution
 Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Module 11. Directed Graphs. Contents
 Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Problem Set 3. MATH 776, Fall 2009, Mohr. November 30, 2009
 Problem Set 3 MATH 776, Fall 009, Mohr November 30, 009 1 Problem Proposition 1.1. Adding a new edge to a maximal planar graph of order at least 6 always produces both a T K 5 and a T K 3,3 subgraph. Proof.
Problem Set 3 MATH 776, Fall 009, Mohr November 30, 009 1 Problem Proposition 1.1. Adding a new edge to a maximal planar graph of order at least 6 always produces both a T K 5 and a T K 3,3 subgraph. Proof.
Algorithms for Finding Dominators in Directed Graphs
 Department of Computer Science Aarhus University Master s Thesis Algorithms for Finding Dominators in Directed Graphs Author: Henrik Knakkegaard Christensen 20082178 Supervisor: Gerth Støling Brodal January
Department of Computer Science Aarhus University Master s Thesis Algorithms for Finding Dominators in Directed Graphs Author: Henrik Knakkegaard Christensen 20082178 Supervisor: Gerth Støling Brodal January
Distributed Algorithms 6.046J, Spring, 2015 Part 2. Nancy Lynch
 Distributed Algorithms 6.046J, Spring, 2015 Part 2 Nancy Lynch 1 This Week Synchronous distributed algorithms: Leader Election Maximal Independent Set Breadth-First Spanning Trees Shortest Paths Trees
Distributed Algorithms 6.046J, Spring, 2015 Part 2 Nancy Lynch 1 This Week Synchronous distributed algorithms: Leader Election Maximal Independent Set Breadth-First Spanning Trees Shortest Paths Trees
CIS 121 Data Structures and Algorithms Minimum Spanning Trees
 CIS 121 Data Structures and Algorithms Minimum Spanning Trees March 19, 2019 Introduction and Background Consider a very natural problem: we are given a set of locations V = {v 1, v 2,..., v n }. We want
CIS 121 Data Structures and Algorithms Minimum Spanning Trees March 19, 2019 Introduction and Background Consider a very natural problem: we are given a set of locations V = {v 1, v 2,..., v n }. We want
Lecture 19. Broadcast routing
 Lecture 9 Broadcast routing Slide Broadcast Routing Route a packet from a source to all nodes in the network Possible solutions: Flooding: Each node sends packet on all outgoing links Discard packets received
Lecture 9 Broadcast routing Slide Broadcast Routing Route a packet from a source to all nodes in the network Possible solutions: Flooding: Each node sends packet on all outgoing links Discard packets received
Advanced routing topics. Tuomas Launiainen
 Advanced routing topics Tuomas Launiainen Suboptimal routing Routing trees Measurement of routing trees Adaptive routing Problems Fault-tolerant tables Point-of-failure rerouting Point-of-failure shortest
Advanced routing topics Tuomas Launiainen Suboptimal routing Routing trees Measurement of routing trees Adaptive routing Problems Fault-tolerant tables Point-of-failure rerouting Point-of-failure shortest
CSC 172 Data Structures and Algorithms. Lecture 24 Fall 2017
 CSC 172 Data Structures and Algorithms Lecture 24 Fall 2017 ANALYSIS OF DIJKSTRA S ALGORITHM CSC 172, Fall 2017 Implementation and analysis The initialization requires Q( V ) memory and run time We iterate
CSC 172 Data Structures and Algorithms Lecture 24 Fall 2017 ANALYSIS OF DIJKSTRA S ALGORITHM CSC 172, Fall 2017 Implementation and analysis The initialization requires Q( V ) memory and run time We iterate
Distributed minimum spanning tree problem
 Distributed minimum spanning tree problem Juho-Kustaa Kangas 24th November 2012 Abstract Given a connected weighted undirected graph, the minimum spanning tree problem asks for a spanning subtree with
Distributed minimum spanning tree problem Juho-Kustaa Kangas 24th November 2012 Abstract Given a connected weighted undirected graph, the minimum spanning tree problem asks for a spanning subtree with
Number Theory and Graph Theory
 1 Number Theory and Graph Theory Chapter 6 Basic concepts and definitions of graph theory By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: satya8118@gmail.com
1 Number Theory and Graph Theory Chapter 6 Basic concepts and definitions of graph theory By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: satya8118@gmail.com
Fundamental Algorithms
 Fundamental Algorithms Chapter 8: Graphs Jan Křetínský Winter 2017/18 Chapter 8: Graphs, Winter 2017/18 1 Graphs Definition (Graph) A graph G = (V, E) consists of a set V of vertices (nodes) and a set
Fundamental Algorithms Chapter 8: Graphs Jan Křetínský Winter 2017/18 Chapter 8: Graphs, Winter 2017/18 1 Graphs Definition (Graph) A graph G = (V, E) consists of a set V of vertices (nodes) and a set
A graph is a set of objects (called vertices or nodes) and edges between pairs of nodes.
 Section 1.4: raphs and Trees graph is a set of objects (called vertices or nodes) and edges between pairs of nodes. Eq Co Ve Br S Pe Bo Pa U Ch Vertices = {Ve,, S,, Br, Co, Eq, Pe, Bo,Pa, Ch,, U} Edges
Section 1.4: raphs and Trees graph is a set of objects (called vertices or nodes) and edges between pairs of nodes. Eq Co Ve Br S Pe Bo Pa U Ch Vertices = {Ve,, S,, Br, Co, Eq, Pe, Bo,Pa, Ch,, U} Edges
Depth First Search A B C D E F G A B C 5 D E F 3 2 G 2 3
 Depth First Search A B C D E F G A 4 3 2 B 4 5 4 3 C 5 D 3 4 2 E 2 2 3 F 3 2 G 2 3 Minimum (Weight) Spanning Trees Let G be a graph with weights on the edges. We define the weight of any subgraph of G
Depth First Search A B C D E F G A 4 3 2 B 4 5 4 3 C 5 D 3 4 2 E 2 2 3 F 3 2 G 2 3 Minimum (Weight) Spanning Trees Let G be a graph with weights on the edges. We define the weight of any subgraph of G
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
CS 6783 (Applied Algorithms) Lecture 5
 CS 6783 (Applied Algorithms) Lecture 5 Antonina Kolokolova January 19, 2012 1 Minimum Spanning Trees An undirected graph G is a pair (V, E); V is a set (of vertices or nodes); E is a set of (undirected)
CS 6783 (Applied Algorithms) Lecture 5 Antonina Kolokolova January 19, 2012 1 Minimum Spanning Trees An undirected graph G is a pair (V, E); V is a set (of vertices or nodes); E is a set of (undirected)
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CS 341: Algorithms. Douglas R. Stinson. David R. Cheriton School of Computer Science University of Waterloo. February 26, 2019
 CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
Elementary Graph Algorithms. Ref: Chapter 22 of the text by Cormen et al. Representing a graph:
 Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. Representing a graph: Graph G(V, E): V set of nodes (vertices); E set of edges. Notation: n = V and m = E. (Vertices are numbered
Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. Representing a graph: Graph G(V, E): V set of nodes (vertices); E set of edges. Notation: n = V and m = E. (Vertices are numbered
Efficient load balancing and QoS-based location aware service discovery protocol for vehicular ad hoc networks
 RESEARCH Open Access Efficient load balancing and QoS-based location aware service discovery protocol for vehicular ad hoc networks Kaouther Abrougui 1,2*, Azzedine Boukerche 1,2 and Hussam Ramadan 3 Abstract
RESEARCH Open Access Efficient load balancing and QoS-based location aware service discovery protocol for vehicular ad hoc networks Kaouther Abrougui 1,2*, Azzedine Boukerche 1,2 and Hussam Ramadan 3 Abstract
CS525 Winter 2012 \ Class Assignment #2 Preparation
 1 CS525 Winter 2012 \ Class Assignment #2 Preparation Ariel Stolerman 2.26) Let be a CFG in Chomsky Normal Form. Following is a proof that for any ( ) of length exactly steps are required for any derivation
1 CS525 Winter 2012 \ Class Assignment #2 Preparation Ariel Stolerman 2.26) Let be a CFG in Chomsky Normal Form. Following is a proof that for any ( ) of length exactly steps are required for any derivation
Problem Set 2 Solutions
 Design and Analysis of Algorithms February, 01 Massachusetts Institute of Technology 6.046J/18.410J Profs. Dana Moshkovitz and Bruce Tidor Handout 8 Problem Set Solutions This problem set is due at 9:00pm
Design and Analysis of Algorithms February, 01 Massachusetts Institute of Technology 6.046J/18.410J Profs. Dana Moshkovitz and Bruce Tidor Handout 8 Problem Set Solutions This problem set is due at 9:00pm
MAT 7003 : Mathematical Foundations. (for Software Engineering) J Paul Gibson, A207.
 MAT 7003 : Mathematical Foundations (for Software Engineering) J Paul Gibson, A207 paul.gibson@it-sudparis.eu http://www-public.it-sudparis.eu/~gibson/teaching/mat7003/ Graphs and Trees http://www-public.it-sudparis.eu/~gibson/teaching/mat7003/l2-graphsandtrees.pdf
MAT 7003 : Mathematical Foundations (for Software Engineering) J Paul Gibson, A207 paul.gibson@it-sudparis.eu http://www-public.it-sudparis.eu/~gibson/teaching/mat7003/ Graphs and Trees http://www-public.it-sudparis.eu/~gibson/teaching/mat7003/l2-graphsandtrees.pdf
CS 580: Algorithm Design and Analysis. Jeremiah Blocki Purdue University Spring 2018
 CS 580: Algorithm Design and Analysis Jeremiah Blocki Purdue University Spring 2018 Chapter 11 Approximation Algorithms Slides by Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved.
CS 580: Algorithm Design and Analysis Jeremiah Blocki Purdue University Spring 2018 Chapter 11 Approximation Algorithms Slides by Kevin Wayne. Copyright @ 2005 Pearson-Addison Wesley. All rights reserved.
Trees Algorhyme by Radia Perlman
 Algorhyme by Radia Perlman I think that I shall never see A graph more lovely than a tree. A tree whose crucial property Is loop-free connectivity. A tree which must be sure to span. So packets can reach
Algorhyme by Radia Perlman I think that I shall never see A graph more lovely than a tree. A tree whose crucial property Is loop-free connectivity. A tree which must be sure to span. So packets can reach
Computing optimal total vertex covers for trees
 Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Graphs and Network Flows ISE 411. Lecture 7. Dr. Ted Ralphs
 Graphs and Network Flows ISE 411 Lecture 7 Dr. Ted Ralphs ISE 411 Lecture 7 1 References for Today s Lecture Required reading Chapter 20 References AMO Chapter 13 CLRS Chapter 23 ISE 411 Lecture 7 2 Minimum
Graphs and Network Flows ISE 411 Lecture 7 Dr. Ted Ralphs ISE 411 Lecture 7 1 References for Today s Lecture Required reading Chapter 20 References AMO Chapter 13 CLRS Chapter 23 ISE 411 Lecture 7 2 Minimum
Undirected Graphs. DSA - lecture 6 - T.U.Cluj-Napoca - M. Joldos 1
 Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Undirected Graphs Terminology. Free Trees. Representations. Minimum Spanning Trees (algorithms: Prim, Kruskal). Graph Traversals (dfs, bfs). Articulation points & Biconnected Components. Graph Matching
Polygon Triangulation
 Polygon Triangulation Definition Simple Polygons 1. A polygon is the region of a plane bounded by a finite collection of line segments forming a simple closed curve. 2. Simple closed curve means a certain
Polygon Triangulation Definition Simple Polygons 1. A polygon is the region of a plane bounded by a finite collection of line segments forming a simple closed curve. 2. Simple closed curve means a certain
Randomized Graph Algorithms
 Randomized Graph Algorithms Vasileios-Orestis Papadigenopoulos School of Electrical and Computer Engineering - NTUA papadigenopoulos orestis@yahoocom July 22, 2014 Vasileios-Orestis Papadigenopoulos (NTUA)
Randomized Graph Algorithms Vasileios-Orestis Papadigenopoulos School of Electrical and Computer Engineering - NTUA papadigenopoulos orestis@yahoocom July 22, 2014 Vasileios-Orestis Papadigenopoulos (NTUA)
CSI 604 Elementary Graph Algorithms
 CSI 604 Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. (Second edition) 1 / 25 Graphs: Basic Definitions Undirected Graph G(V, E): V is set of nodes (or vertices) and E is the
CSI 604 Elementary Graph Algorithms Ref: Chapter 22 of the text by Cormen et al. (Second edition) 1 / 25 Graphs: Basic Definitions Undirected Graph G(V, E): V is set of nodes (or vertices) and E is the
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret
 Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Routing. Information Networks p.1/35
 Routing Routing is done by the network layer protocol to guide packets through the communication subnet to their destinations The time when routing decisions are made depends on whether we are using virtual
Routing Routing is done by the network layer protocol to guide packets through the communication subnet to their destinations The time when routing decisions are made depends on whether we are using virtual
CS6702 GRAPH THEORY AND APPLICATIONS 2 MARKS QUESTIONS AND ANSWERS
 CS6702 GRAPH THEORY AND APPLICATIONS 2 MARKS QUESTIONS AND ANSWERS 1 UNIT I INTRODUCTION CS6702 GRAPH THEORY AND APPLICATIONS 2 MARKS QUESTIONS AND ANSWERS 1. Define Graph. A graph G = (V, E) consists
CS6702 GRAPH THEORY AND APPLICATIONS 2 MARKS QUESTIONS AND ANSWERS 1 UNIT I INTRODUCTION CS6702 GRAPH THEORY AND APPLICATIONS 2 MARKS QUESTIONS AND ANSWERS 1. Define Graph. A graph G = (V, E) consists
Introduction to Optimization
 Introduction to Optimization Greedy Algorithms October 28, 2016 École Centrale Paris, Châtenay-Malabry, France Dimo Brockhoff Inria Saclay Ile-de-France 2 Course Overview Date Fri, 7.10.2016 Fri, 28.10.2016
Introduction to Optimization Greedy Algorithms October 28, 2016 École Centrale Paris, Châtenay-Malabry, France Dimo Brockhoff Inria Saclay Ile-de-France 2 Course Overview Date Fri, 7.10.2016 Fri, 28.10.2016
