Math 308, Section 101 Solutions to Study Questions for Final Exam (Thursday, December 16, 2004)
|
|
|
- Laura Patrick
- 5 years ago
- Views:
Transcription
1 NEUTRAL GEOMETRY Math 308, Section 0 Solutions to Study Questions for Final Exam (Thursday, December 6, 00) I. Given a triangle AEF, let M be the midpoint of the segment EF. Choose a point D on the ray AM such that AD = AM. Prove that DF E AEF. Note that since M is between A and D, we have AM + MD = AD = AM, and so AM = MD. We also know that F M = ME since M is the midpoint of EF. Finally, the vertical angles AM F and DM E are certainly congruent. Therefore, by SAS, AMF DME; in particular, AF = DE. A similar argument shows that AME DMF and hence AE = DF. Finally, EF = F E trivially. We now know enough to conclude from SSS that DF E AEF. Define the defect of a triangle ABC, written δ( ABC), to be δ( ABC) = 80 A B C. Notice that by the Saccheri-Legendre Theorem, the defect of a triangle is always a nonnegative number of degrees. II. Suppose that D, E, and F are points on the sides BC, AC, and AB of ABC, respectively. Prove that δ( ABC) = δ( AEF ) + δ( BDF ) + δ( CDE) + δ( DEF ). The right-hand side is δ( AEF ) + δ( BDF ) + δ( CDE) + δ( DEF ) = (80 AEF AF E F AE) + (80 BDF BF D DBF ) + (80 CDE CED DCE) + (80 DEF EF D F DE) = 70 F AE DBF DCE ( AEF + DEF + CED) ( CDE + F DE + BDF ) ( BF D + EF D + AF E) = 70 F AE DBF DCE = 80 BAC CBA BCA = δ( ABC). All we used was that angles that together form a straight line add up to 80. III. Legendre gave the following incorrect argument when he was trying to prove that the Parallel Postulate follows from the neutral geometry axioms. Find the mistake in the following proof that the sum of the angles of every triangle must equal 80 (a fact which would indeed imply the Parallel Postulate, if proven correctly). First we claim that for any triangle AEF, there exists a triangle ABC whose defect is at least twice as big, that is, δ( ABC) δ( AEF ). To see this, let M be the midpoint of the segment EF, and choose a point D on the ray AM such that AD = AM ; we know that DF E AEF. In particular, δ( DF E) = δ( AEF ). Now draw any line through D that intersects the rays AF and AE; call the points of intersection B and C, respectively. We then have δ( ABC) = δ( AEF ) + δ( BDF ) + δ( CDE) + δ( DEF ) δ( AEF ) δ( DEF ) = δ( AEF ).
2 Now suppose, for the sake of contradiction, that a triangle AEF existed with an angle sum less than 80, so that δ( AEF ) > 0. We can find a sequence of triangles whose defects are at least δ( AEF ), δ( AEF ), 8δ( AEF ), and so on. Eventually, the numbers k δ( AEF ) are bigger than 80, which is absurd, since the largest possible defect of a triangle is 80. Therefore no triangle with positive defect exists, that is, every triangle has angle sum exactly 80. (Remember, this proof is incorrect what is the mistake?) The sole problem with the proof is the following statement: Now draw any line through D that intersects the rays AF and AE. In hyperbolic geometry (and hence in neutral geometry), it is quite possible for a point D to lie inside an angle EAF, yet no line exists that intersects both rays AF and AE. It just goes to show how misleading our Euclidean geometry intuition can be when studying hyperbolic geometry. (At least we have an advantage over Legendre: we know that hyperbolic geometry actually exists!) EUCLIDEAN GEOMETRY IV. (Baragar, p. 39, #7.) Let P be a point inside a circle centered at O. Let T be a point where the perpendicular to P O intersects the circle. Let P be the point where the tangent to the circle at T intersects OP. Show that P is the image of P under inversion in the circle. It would be clearer to say Let T be a point where the perpendicular to P O at P intersects the circle. The outline of the solution is as follows: prove that the right triangles OP T and T P P are similar, using the fact that OT P + P T P = 90. Conclude that P O / OT = T O / OP, which is the equality needed to show that P is the image of P under inversion in the circle (since P is already on the ray OP where that image needs to be). V. In ABC, trisect each side. That is, choose points A and A between B and C such that BA = A A = A C ; choose points B and B between C and A such that CB = B B = B A ; and choose points C and C between A and B such that AC = C C = C B. Let P be the intersection of the segments C A and A B. Prove that C P B A P A. Note that AC / AB = /3 = AB / AC, since we have trisected the various sides. It follows that AC B ABC and that the segments C B and BC are parallel. Therefore the opposite interior angles C B P and A A P are congruent, as are B C P and A A P. We also have that C B / BC = /3, again by the similarity of AC B and ABC. But we also have A A / BC = /3, and so C B = A A. Therefore by ASA, C P B A P A. [Remark: P is actually the centroid of ABC!] VI. Let P and Q be two points on a circle and A a point outside the circle, and let the rays AP and AQ intersect the circle again in the points P and Q, respectively. Suppose that P is the midpoint of the segment AP and that Q is the midpoint of the segment AQ. Prove that P QP = QP Q. First we prove: if W, X, Y, Z are points on a circle centered at O, and W X = Y Z, then the angular measures of the arcs W X and Y Z are the same. To see this, note that OW X OY Z by the SSS theorem, since OW = OY and OX = OZ because they are all radii of the same circle, and we are given W X = Y Z. In particular, the central angles W OX and Y OZ are congruent, which means that the angular measures of the arcs W X and Y Z are the same.
3 Now, using the power of the point theorem, we know that AP AP = AQ AQ. But AP = P P and AP = P P since P is the midpoint of the segment AP, and similarly AQ = QQ and AQ = QQ ; therefore we conclude that P P P P = QQ QQ, which implies that P P = QQ. From the fact proved in the previous paragraph, we see that the angular measures of the arcs P P and QQ are the same. But by the Star Trek Lemma, P QP is half the measure of the arc P P, while QP Q is half the measure of the arc QQ ; therefore P QP = QP Q as desired. VII. Given a triangle ABC, let D be a point on BC, E a point on AC, and F a point on AB. Suppose that AE = 3, AF =, BD = 6, BF = 8, and CD = 9. (a) What are the possible values of CE? (b) If the lines AD, BE, and CF all intersect in a single point, what is the value of CE? (a) We have AB = AF + F B = and BC = BD + DC =, and also AC = AE + CE = 3+ CE. By the triangle inequality, we must have 3+ CE = AC AB + BC = + = 7, or in other words CE. We must also have = BC BA + AC = +(3+ CE ) = + CE, which in this case only gives us the obvious inequality CE 0. The triangle inequality AB AC + BC is equally unhelpful in this case (we obtain CE 6). Therefore the only restriction is that 0 CE ; and if we want to restrict to non-degenerate triangles (those in which the three vertices don t all lie on a line), then we need 0 < CE < with strict inequality. (b) By Ceva s theorem, AF BD CE F B DC EA =, or in other words, CE = F B DC EA / AF BD = 8 9 3/( 6) = 9. VIII. (Baragar, p. 0, #.3) Find formulas for F, V, and E in terms of m and n for a Platonic solid with m n-gons at each vertex. Since each face has n edges and each edge adjoins two faces, we have E = nf. Since each face has n vertices and each vertex belongs to m faces, we also have mv = nf. Using this, the Euler formula becomes = F + nf/m nf/, which implies that F = m/(m + n mn). The first two equations then show that E = mn/(m+n mn) and V = n/(m+n mn). (Notice that if mn m + n, then the denominator is either zero or negative, and hence no such Platonic solid exists.) IX. Name all (three-dimensional) regular polyhedra, sometimes called Platonic solids. Which ones are dual to each other? Explain. The answer is in Chapter of the textbook. It is important to understand how to form the dual to a convex polyhedron and why this makes the cube and the octahedron, for example, each other s duals. X. How many edges, vertices, triangular faces, and pentagonal faces are there on the snub dodecahedron, which is represented by (3,3,3,3,)? What about its dual? The textbook (Baragar, page 09) tells us that there are F = pentagonal faces on the snub dodecahedron, and also gives us the equations V = F = 3F 3 / and E = (3F 3 +F )/. 3
4 We quickly find V = 60, F 3 = 80, and E = 0, so the snub dodecahedron has 60 vertices, 0 edges, and 80 triangular faces for a total of 9 faces. The dual of a convex polyhedron is formed by having one vertex for every face of the original polyhedron, and one face for every vertex. In this case, the dual polyhedron will have 9 vertices and 60 faces (and 0 edges again, since the equation V E + F = still holds). Since each vertex of the original polyhedron is adjacent to five other vertices, this means that each face of the dual polyhedron is adjacent to five other faces; in other words, each face of the dual polyhedron is a pentagon. We can also say that 80 of the dual polyhedron s vertices belong to 3 pentagons, while the other vertices belong to pentagons. (Hence the dual polyhedron is not semiregular. But it s still nice.) HYPERBOLIC GEOMETRY XI. For this question, draw means draw, with reasonable accuracy, a picture using the Poincaré half-plane model of the hyperbolic plane. For this question, do not allow any of your hyperbolic lines to look like vertical Euclidean lines. (a) Draw three lines L, M, and N such that L and M are parallel to each other, L and N are ultraparallel to each other, and M and N intersect each other. (Be sure to label the lines correctly.) (b) Draw a quadrilateral ABCD such that each of its four angles is less than 30. (Be sure that all four vertices really are points in the hyperbolic plane.) (c) Draw a line L through a point P, and draw the image of L under the isometry (of the hyperbolic plane) that is a rotation around P through a 0 angle. Mark the 0 angle in your drawing, and label the line L to distinguish it from its image line. 0 L N M A B C D L P XII. Suppose that in the Poincaré half-plane, the line AB is an arc of a semicircle with one endpoint at the real number x. Prove that the horizontal translation z z x followed by inversion in the unit circle is an isometry of the Poincaré half-plane that sends the line AB to a vertical line. After the horizontal translation, the line AB is a Euclidean semicircle with one endpoint at the origin and the other at some real number w, say. The image of the whole circle under inversion in the unit circle is either a circle or a line. On the other hand, the image of the whole circle under inversion in the unit circle only intersects the real axis once, namely at the point /w. Furthermore, it is perpendicular to the x-axis there, since the original circle was perpendicular to the x-axis at w; in particular, the image cannot be a circle that it tangent to the x-axis. Since any circle that is not tangent to a line must intersect that line in 0 or points, the image cannot be a circle at all; that is, the image must be a straight line. And since the original circle was perpendicular to the x-axis, the resulting line must also be perpendicular to the x-axis, that is, it is a vertical line. (One can also solve this problem simply by noting that a semicircle with one endpoint at the origin has the equation
5 (x r) + y = r for some real number r, and computing the image of any point under inversion in the unit circle and noticing that the real part of the answer is the constant /r.) XIII. Find the distance between i and 7 + 8i in the Poincaré half-plane. First we find the Euclidean semicircle that makes up the hyperbolic line between the two points i and 7 + 8i; that circle turns out to be centered at 8 and have radius 7, so that its endpoints are 9 and. Then we can translate horizontally by 9, sending the two points to 9 + i and + 8i, and then invert in the unit circle, sending them to + i and i, respectively. The distance between the two points is thus ln ( / ) = ln. Or, we can simply calculate directly that the cross ratio (i, 7 + 8i; 9, ) equals, which gives the distance as ln(i, 7 + 8i; 9, ) = ln as well. XIV. Using the definitions of the hyperbolic trigonometry functions, prove that cosh x sinh x =. Since cosh x = (e x + e x )/ and sinh x = (e x e x )/, we have ( e cosh x sinh x + e x ) ( e x e x ) x = = (ex ) + e x e x + (e x ) = ex + + e x ex + e x (ex ) e x e x + (e x ) = + XV. Let ABC be a right triangle with right angle C. Suppose that CB = ln and CA = ln 3. Verify, using the Hyperbolic Pythagorean Theorem cosh c = cosh a cosh b, that AB = ln(7 + ). We calculate: cosh a = cosh(ln ) = eln + e ln = + / = 6/ = 3 cosh b = cosh(ln 3) = eln 3 ln 3 + e 3 + /3 = = 70/3 = 8 3, and therefore cosh a cosh b = (3/)(8/3) = 7; thus we need to check that cosh c = 7 as well. Now cosh c = cosh(ln(7 + )) ) + e ln(7+ ) = eln(7+ We calculate that 7 + = 7 (7 + )(7 ) Therefore cosh c = (7 + ) + /(7 + ) as asserted. =. = (7 + ) + /(7 + ). 7 = 7 ( 7 = ) 89 = 7. = (7 + ) + (7 ) = 3 = 7,
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES. V : Introduction to non Euclidean geometry
 FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
FIGURES FOR SOLUTIONS TO SELECTED EXERCISES V : Introduction to non Euclidean geometry V.1 : Facts from spherical geometry V.1.1. The objective is to show that the minor arc m does not contain a pair of
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
8 Standard Euclidean Triangle Geometry
 8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
1 Appendix to notes 2, on Hyperbolic geometry:
 1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
Transformations and Isometries
 Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
1 Solution of Homework
 Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
Math 3181 Dr. Franz Rothe February 2, 2012 All3181\4080_spr12h1.tex Name: Use the back pages for extra space due date: February 10 1 Solution of Homework Figure 1: A neutral construction of the tangents
7th Bay Area Mathematical Olympiad
 7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
University of South Carolina Math 222: Math for Elementary Educators II Instructor: Austin Mohr Section 002 Fall Midterm Exam Solutions
 University of South Carolina Math 222: Math for Elementary Educators II Instructor: Austin Mohr Section 002 Fall 2010 Midterm Exam Solutions Please write your solutions (including work) on the blank paper,
University of South Carolina Math 222: Math for Elementary Educators II Instructor: Austin Mohr Section 002 Fall 2010 Midterm Exam Solutions Please write your solutions (including work) on the blank paper,
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 8 Table of Contents Title Author Regular Triangles Cameron Hertzler Regular Pentagon Cameron Hertzler Hemispheres and Right Angles Cameron Hertzler
Transactions in Euclidean Geometry Volume 207F Issue # 8 Table of Contents Title Author Regular Triangles Cameron Hertzler Regular Pentagon Cameron Hertzler Hemispheres and Right Angles Cameron Hertzler
Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points.
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 6 Table of Contents Title Author Not All Kites are Parallelograms Steven Flesch Constructing a Kite Micah Otterbein Exterior Angles of Pentagons Kaelyn
Transactions in Euclidean Geometry Volume 207F Issue # 6 Table of Contents Title Author Not All Kites are Parallelograms Steven Flesch Constructing a Kite Micah Otterbein Exterior Angles of Pentagons Kaelyn
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
Transactions in Euclidean Geometry Volume 207F Issue # 4 Table of Contents Title Author Square Construction Katherine Bertacini, Rachelle Feldmann, & Kaelyn Koontz Squares and Rectangles Rachelle Feldmann
EXTREME POINTS AND AFFINE EQUIVALENCE
 EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
 Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
The statement implies that any three intersection points of two distinct planes lie on a line.
 Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
 Tools of Geometry 1. X + 9 = 24 2. 25 X = 15 3. X + 3 = -2X -10 4. 3X + 4Y = 2 Place in slope intercept form. 5. Y = ½ X 2 What is the slope? What is the Y- Intercept? Inductive Reasoning is reasoning
Tools of Geometry 1. X + 9 = 24 2. 25 X = 15 3. X + 3 = -2X -10 4. 3X + 4Y = 2 Place in slope intercept form. 5. Y = ½ X 2 What is the slope? What is the Y- Intercept? Inductive Reasoning is reasoning
TOURNAMENT OF THE TOWNS, Glossary
 TOURNAMENT OF THE TOWNS, 2003 2004 Glossary Absolute value The size of a number with its + or sign removed. The absolute value of 3.2 is 3.2, the absolute value of +4.6 is 4.6. We write this: 3.2 = 3.2
TOURNAMENT OF THE TOWNS, 2003 2004 Glossary Absolute value The size of a number with its + or sign removed. The absolute value of 3.2 is 3.2, the absolute value of +4.6 is 4.6. We write this: 3.2 = 3.2
Chapter 2 Similarity and Congruence
 Chapter 2 Similarity and Congruence Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definition ABC =
Chapter 2 Similarity and Congruence Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definitions Definition AB = CD if and only if AB = CD Remember, mab = AB. Definition ABC =
Geometry Vocabulary Word Wall Cards
 Geometry Vocabulary Word Wall Cards Mathematics vocabulary word wall cards provide a display of mathematics content words and associated visual cues to assist in vocabulary development. The cards should
Geometry Vocabulary Word Wall Cards Mathematics vocabulary word wall cards provide a display of mathematics content words and associated visual cues to assist in vocabulary development. The cards should
Math-2 Lesson 8-6 Unit 5 review -midpoint, -distance, -angles, -Parallel lines, -triangle congruence -triangle similarity -properties of
 Math- Lesson 8-6 Unit 5 review -midpoint, -distance, -angles, -Parallel lines, -triangle congruence -triangle similarity -properties of parallelograms -properties of Isosceles triangles The distance between
Math- Lesson 8-6 Unit 5 review -midpoint, -distance, -angles, -Parallel lines, -triangle congruence -triangle similarity -properties of parallelograms -properties of Isosceles triangles The distance between
Chapter 10 Similarity
 Chapter 10 Similarity Def: The ratio of the number a to the number b is the number. A proportion is an equality between ratios. a, b, c, and d are called the first, second, third, and fourth terms. The
Chapter 10 Similarity Def: The ratio of the number a to the number b is the number. A proportion is an equality between ratios. a, b, c, and d are called the first, second, third, and fourth terms. The
We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance.
 Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
1. CONVEX POLYGONS. Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D.
 1. CONVEX POLYGONS Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D. Convex 6 gon Another convex 6 gon Not convex Question. Why is the third
1. CONVEX POLYGONS Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D. Convex 6 gon Another convex 6 gon Not convex Question. Why is the third
Proving Theorems about Lines and Angles
 Proving Theorems about Lines and Angles Angle Vocabulary Complementary- two angles whose sum is 90 degrees. Supplementary- two angles whose sum is 180 degrees. Congruent angles- two or more angles with
Proving Theorems about Lines and Angles Angle Vocabulary Complementary- two angles whose sum is 90 degrees. Supplementary- two angles whose sum is 180 degrees. Congruent angles- two or more angles with
Geometry Semester 1 Final Exam Study Guide FCS, Mr. Garcia
 Name Date Period This is your semester 1 exam review study guide. It is designed for you to do a portion each day until the day of the exam. You may use the following formula to calculate your semester
Name Date Period This is your semester 1 exam review study guide. It is designed for you to do a portion each day until the day of the exam. You may use the following formula to calculate your semester
An Approach to Geometry (stolen in part from Moise and Downs: Geometry)
 An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
Geometry Practice. 1. Angles located next to one another sharing a common side are called angles.
 Geometry Practice Name 1. Angles located next to one another sharing a common side are called angles. 2. Planes that meet to form right angles are called planes. 3. Lines that cross are called lines. 4.
Geometry Practice Name 1. Angles located next to one another sharing a common side are called angles. 2. Planes that meet to form right angles are called planes. 3. Lines that cross are called lines. 4.
Postulates, Theorems, and Corollaries. Chapter 1
 Chapter 1 Post. 1-1-1 Through any two points there is exactly one line. Post. 1-1-2 Through any three noncollinear points there is exactly one plane containing them. Post. 1-1-3 If two points lie in a
Chapter 1 Post. 1-1-1 Through any two points there is exactly one line. Post. 1-1-2 Through any three noncollinear points there is exactly one plane containing them. Post. 1-1-3 If two points lie in a
Preparing High School Geometry Teachers to Teach the Common Core
 Preparing High School Geometry Teachers to Teach the Common Core NCTM Regional Meeting Atlantic City, NJ October 22, 2014 Timothy Craine, Central Connecticut State University crainet@ccsu.edu Edward DePeau,
Preparing High School Geometry Teachers to Teach the Common Core NCTM Regional Meeting Atlantic City, NJ October 22, 2014 Timothy Craine, Central Connecticut State University crainet@ccsu.edu Edward DePeau,
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 2 Table of Contents Title Author Construction of a Rhombus Micah Otterbein Kite Construction Emily Carstens Constructing Kites Grant Kilburg Star
Transactions in Euclidean Geometry Volume 207F Issue # 2 Table of Contents Title Author Construction of a Rhombus Micah Otterbein Kite Construction Emily Carstens Constructing Kites Grant Kilburg Star
a) 1/3 area of triangle ABC b) 3.6 c) 3 d) e) Euclid s fifth postulate is equivalent to: Given a line and a point not on that line
 1. Given is a right triangle with AD a perpendicular from the right angle to the hypotenuse, find the length of AD given AB = 6, BC = 10 and AC = 8. B D A C a) 7.5 b) 6.5 c) 4.8 d) e) 2. Using the figure
1. Given is a right triangle with AD a perpendicular from the right angle to the hypotenuse, find the length of AD given AB = 6, BC = 10 and AC = 8. B D A C a) 7.5 b) 6.5 c) 4.8 d) e) 2. Using the figure
Life is what you make it. Mr. H s dad
 Life is what you make it. Mr. H s dad You can classify triangles by if their sides are congruent. Scalene Triangle This triangle has no congruent sides. Isosceles Triangle This triangle has at least 2
Life is what you make it. Mr. H s dad You can classify triangles by if their sides are congruent. Scalene Triangle This triangle has no congruent sides. Isosceles Triangle This triangle has at least 2
euclidean geometry given a line and a point P which is not on, how many lines pass through P and are parallel to?
 euclidean geometry my goal with all of these lessons is to provide an introduction to both euclidean non-euclidean geometry. the two geometries share many features, but they also have very fundamental
euclidean geometry my goal with all of these lessons is to provide an introduction to both euclidean non-euclidean geometry. the two geometries share many features, but they also have very fundamental
Modeling with Geometry
 Modeling with Geometry 6.3 Parallelograms https://mathbitsnotebook.com/geometry/quadrilaterals/qdparallelograms.html Properties of Parallelograms Sides A parallelogram is a quadrilateral with both pairs
Modeling with Geometry 6.3 Parallelograms https://mathbitsnotebook.com/geometry/quadrilaterals/qdparallelograms.html Properties of Parallelograms Sides A parallelogram is a quadrilateral with both pairs
Circular inversions = hyperbolic isometries
 Circular inversions = hyperbolic isometries Recall how all isometries of the Euclidean plane are products of at most three line reflections. In the (Beltrami-Poincaré model of the) hyperbolic plane, we
Circular inversions = hyperbolic isometries Recall how all isometries of the Euclidean plane are products of at most three line reflections. In the (Beltrami-Poincaré model of the) hyperbolic plane, we
University of Sioux Falls. MATH 303 Foundations of Geometry
 University of Sioux Falls MATH 303 Foundations of Geometry Concepts addressed: Geometry Texts Cited: Hvidsten, Michael, Exploring Geometry, New York: McGraw-Hill, 2004. Kay, David, College Geometry: A
University of Sioux Falls MATH 303 Foundations of Geometry Concepts addressed: Geometry Texts Cited: Hvidsten, Michael, Exploring Geometry, New York: McGraw-Hill, 2004. Kay, David, College Geometry: A
Select the best answer. Bubble the corresponding choice on your scantron. Team 13. Geometry
 Team Geometry . What is the sum of the interior angles of an equilateral triangle? a. 60 b. 90 c. 80 d. 60. The sine of angle A is. What is the cosine of angle A? 6 4 6 a. b. c.. A parallelogram has all
Team Geometry . What is the sum of the interior angles of an equilateral triangle? a. 60 b. 90 c. 80 d. 60. The sine of angle A is. What is the cosine of angle A? 6 4 6 a. b. c.. A parallelogram has all
EUCLID S GEOMETRY. Raymond Hoobler. January 27, 2008
 EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
And Now From a New Angle Special Angles and Postulates LEARNING GOALS
 And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
Mth 97 Fall 2013 Chapter 4
 4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
4.1 Reasoning and Proof in Geometry Direct reasoning or reasoning is used to draw a conclusion from a series of statements. Conditional statements, if p, then q, play a central role in deductive reasoning.
CCGPS UNIT 5 Semester 2 COORDINATE ALGEBRA Page 1 of 38. Transformations in the Coordinate Plane
 CCGPS UNIT 5 Semester 2 COORDINATE ALGEBRA Page 1 of 38 Transformations in the Coordinate Plane Name: Date: MCC9-12.G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line,
CCGPS UNIT 5 Semester 2 COORDINATE ALGEBRA Page 1 of 38 Transformations in the Coordinate Plane Name: Date: MCC9-12.G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line,
Suggested List of Mathematical Language. Geometry
 Suggested List of Mathematical Language Geometry Problem Solving A additive property of equality algorithm apply constraints construct discover explore generalization inductive reasoning parameters reason
Suggested List of Mathematical Language Geometry Problem Solving A additive property of equality algorithm apply constraints construct discover explore generalization inductive reasoning parameters reason
Geometry Curriculum Map
 Geometry Curriculum Map Unit 1 st Quarter Content/Vocabulary Assessment AZ Standards Addressed Essentials of Geometry 1. What are points, lines, and planes? 1. Identify Points, Lines, and Planes 1. Observation
Geometry Curriculum Map Unit 1 st Quarter Content/Vocabulary Assessment AZ Standards Addressed Essentials of Geometry 1. What are points, lines, and planes? 1. Identify Points, Lines, and Planes 1. Observation
Geometry Midterm Review 2019
 Geometry Midterm Review 2019 Name To prepare for the midterm: Look over past work, including HW, Quizzes, tests, etc Do this packet Unit 0 Pre Requisite Skills I Can: Solve equations including equations
Geometry Midterm Review 2019 Name To prepare for the midterm: Look over past work, including HW, Quizzes, tests, etc Do this packet Unit 0 Pre Requisite Skills I Can: Solve equations including equations
Solutions to the Test. Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written?
 Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Segment Addition Postulate: If B is BETWEEN A and C, then AB + BC = AC. If AB + BC = AC, then B is BETWEEN A and C.
 Ruler Postulate: The points on a line can be matched one to one with the REAL numbers. The REAL number that corresponds to a point is the COORDINATE of the point. The DISTANCE between points A and B, written
Ruler Postulate: The points on a line can be matched one to one with the REAL numbers. The REAL number that corresponds to a point is the COORDINATE of the point. The DISTANCE between points A and B, written
3 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
High School Mathematics Geometry Vocabulary Word Wall Cards
 High School Mathematics Geometry Vocabulary Word Wall Cards Table of Contents Reasoning, Lines, and Transformations Basics of Geometry 1 Basics of Geometry 2 Geometry Notation Logic Notation Set Notation
High School Mathematics Geometry Vocabulary Word Wall Cards Table of Contents Reasoning, Lines, and Transformations Basics of Geometry 1 Basics of Geometry 2 Geometry Notation Logic Notation Set Notation
Geometry: Semester 1 Midterm
 Class: Date: Geometry: Semester 1 Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. The first two steps for constructing MNO that is congruent to
Class: Date: Geometry: Semester 1 Midterm Multiple Choice Identify the choice that best completes the statement or answers the question. 1. The first two steps for constructing MNO that is congruent to
There are two ways to name a line. What are the two ways?
 Geometry: 1-1 Points, Lines and Planes What are the Undefined Terms? The Undefined Terms are: What is a Point? How is a point named? Example: What is a Line? A line is named two ways. What are the two
Geometry: 1-1 Points, Lines and Planes What are the Undefined Terms? The Undefined Terms are: What is a Point? How is a point named? Example: What is a Line? A line is named two ways. What are the two
5200/7200 Fall 2007 Concurrence theorems for triangles
 5200/7200 Fall 2007 Concurrence theorems for triangles There are two basic concurrence theorems for triangles that hold in neutral geometry, that of medians and of angle bisectors, but it seems hard to
5200/7200 Fall 2007 Concurrence theorems for triangles There are two basic concurrence theorems for triangles that hold in neutral geometry, that of medians and of angle bisectors, but it seems hard to
Chapter 5. Relationships Within Triangles
 Chapter 5 Relationships Within Triangles 5.1 Midsegment Theorem and Coordinate Proof Objective: Use properties of midsegments. Essential Question: How do you find the midsegment of a triangle? Midsegment
Chapter 5 Relationships Within Triangles 5.1 Midsegment Theorem and Coordinate Proof Objective: Use properties of midsegments. Essential Question: How do you find the midsegment of a triangle? Midsegment
Spherical Geometry MATH430
 Spherical Geometry MATH430 Fall 014 In these notes we summarize some results about the geometry of the sphere that complement should the textbook. Most notions we had on the plane (points, lines, angles,
Spherical Geometry MATH430 Fall 014 In these notes we summarize some results about the geometry of the sphere that complement should the textbook. Most notions we had on the plane (points, lines, angles,
CHAPTER TWO. . Therefore the oblong number n(n + 1) is double the triangular number T n. , and the summands are the triangular numbers T n 1 and T n.
 CHAPTER TWO 1. Since AB BC; since the two angles at B are equal; and since the angles at A and C are both right angles, it follows by the angle-side-angle theorem that EBC is congruent to SBA and therefore
CHAPTER TWO 1. Since AB BC; since the two angles at B are equal; and since the angles at A and C are both right angles, it follows by the angle-side-angle theorem that EBC is congruent to SBA and therefore
Geometry Final Exam - Study Guide
 Geometry Final Exam - Study Guide 1. Solve for x. True or False? (questions 2-5) 2. All rectangles are rhombuses. 3. If a quadrilateral is a kite, then it is a parallelogram. 4. If two parallel lines are
Geometry Final Exam - Study Guide 1. Solve for x. True or False? (questions 2-5) 2. All rectangles are rhombuses. 3. If a quadrilateral is a kite, then it is a parallelogram. 4. If two parallel lines are
15. K is the midpoint of segment JL, JL = 4x - 2, and JK = 7. Find x, the length of KL, and JL. 8. two lines that do not intersect
 Name: Period Date Pre-AP Geometry Fall Semester Exam REVIEW *Chapter 1.1 Points Lines Planes Use the figure to name each of the following: 1. three non-collinear points 2. one line in three different ways
Name: Period Date Pre-AP Geometry Fall Semester Exam REVIEW *Chapter 1.1 Points Lines Planes Use the figure to name each of the following: 1. three non-collinear points 2. one line in three different ways
9 Circles CHAPTER. Chapter Outline. Chapter 9. Circles
 www.ck12.org Chapter 9. Circles CHAPTER 9 Circles Chapter Outline 9.1 PARTS OF CIRCLES & TANGENT LINES 9.2 PROPERTIES OF ARCS 9.3 PROPERTIES OF CHORDS 9.4 INSCRIBED ANGLES 9.5 ANGLES OF CHORDS, SECANTS,
www.ck12.org Chapter 9. Circles CHAPTER 9 Circles Chapter Outline 9.1 PARTS OF CIRCLES & TANGENT LINES 9.2 PROPERTIES OF ARCS 9.3 PROPERTIES OF CHORDS 9.4 INSCRIBED ANGLES 9.5 ANGLES OF CHORDS, SECANTS,
GEOMETRY PRACTICE TEST END OF COURSE version A (MIXED) 2. Which construction represents the center of a circle that is inscribed in a triangle?
 GEOMETRY PRACTICE TEST END OF COURSE version A (MIXED) 1. The angles of a triangle are in the ratio 1:3:5. What is the measure, in degrees, of the largest angle? A. 20 B. 30 C. 60 D. 100 3. ABC and XYZ
GEOMETRY PRACTICE TEST END OF COURSE version A (MIXED) 1. The angles of a triangle are in the ratio 1:3:5. What is the measure, in degrees, of the largest angle? A. 20 B. 30 C. 60 D. 100 3. ABC and XYZ
PROVE THEOREMS INVOLVING SIMILARITY
 PROVE THEOREMS INVOLVING SIMILARITY KEY IDEAS 1. When proving that two triangles are similar, it is sufficient to show that two pairs of corresponding angles of the triangles are congruent. This is called
PROVE THEOREMS INVOLVING SIMILARITY KEY IDEAS 1. When proving that two triangles are similar, it is sufficient to show that two pairs of corresponding angles of the triangles are congruent. This is called
WAYNESBORO AREA SCHOOL DISTRICT CURRICULUM ACCELERATED GEOMETRY (June 2014)
 UNIT: Chapter 1 Essentials of Geometry UNIT : How do we describe and measure geometric figures? Identify Points, Lines, and Planes (1.1) How do you name geometric figures? Undefined Terms Point Line Plane
UNIT: Chapter 1 Essentials of Geometry UNIT : How do we describe and measure geometric figures? Identify Points, Lines, and Planes (1.1) How do you name geometric figures? Undefined Terms Point Line Plane
Unit 2: Triangles and Polygons
 Unit 2: Triangles and Polygons Background for Standard G.CO.9: Prove theorems about lines and angles. Objective: By the end of class, I should Using the diagram below, answer the following questions. Line
Unit 2: Triangles and Polygons Background for Standard G.CO.9: Prove theorems about lines and angles. Objective: By the end of class, I should Using the diagram below, answer the following questions. Line
Geometry - Chapter 1 - Corrective #1
 Class: Date: Geometry - Chapter 1 - Corrective #1 Short Answer 1. Sketch a figure that shows two coplanar lines that do not intersect, but one of the lines is the intersection of two planes. 2. Name two
Class: Date: Geometry - Chapter 1 - Corrective #1 Short Answer 1. Sketch a figure that shows two coplanar lines that do not intersect, but one of the lines is the intersection of two planes. 2. Name two
Unit 4 Syllabus: Properties of Triangles & Quadrilaterals
 ` Date Period Unit 4 Syllabus: Properties of Triangles & Quadrilaterals Day Topic 1 Midsegments of Triangle and Bisectors in Triangles 2 Concurrent Lines, Medians and Altitudes, and Inequalities in Triangles
` Date Period Unit 4 Syllabus: Properties of Triangles & Quadrilaterals Day Topic 1 Midsegments of Triangle and Bisectors in Triangles 2 Concurrent Lines, Medians and Altitudes, and Inequalities in Triangles
Geometry Curriculum Guide Lunenburg County Public Schools June 2014
 Marking Period: 1 Days: 4 Reporting Category/Strand: Reasoning, Lines, and Transformations SOL G.1 The student will construct and judge the validity of a logical argument consisting of a set of premises
Marking Period: 1 Days: 4 Reporting Category/Strand: Reasoning, Lines, and Transformations SOL G.1 The student will construct and judge the validity of a logical argument consisting of a set of premises
CHAPTER 2 REVIEW COORDINATE GEOMETRY MATH Warm-Up: See Solved Homework questions. 2.2 Cartesian coordinate system
 CHAPTER 2 REVIEW COORDINATE GEOMETRY MATH6 2.1 Warm-Up: See Solved Homework questions 2.2 Cartesian coordinate system Coordinate axes: Two perpendicular lines that intersect at the origin O on each line.
CHAPTER 2 REVIEW COORDINATE GEOMETRY MATH6 2.1 Warm-Up: See Solved Homework questions 2.2 Cartesian coordinate system Coordinate axes: Two perpendicular lines that intersect at the origin O on each line.
Chapter 4 Triangles: Congruency & Similarity
 1 Chapter 4 Triangles: Congruency & Similarity Concepts & Skills Quilting is a great American pastime especially in the heartland of the United States. Quilts can be simple in nature or as in the photo
1 Chapter 4 Triangles: Congruency & Similarity Concepts & Skills Quilting is a great American pastime especially in the heartland of the United States. Quilts can be simple in nature or as in the photo
PRACTICE TEST ANSWER KEY & SCORING GUIDELINES GEOMETRY
 Ohio s State Tests PRACTICE TEST ANSWER KEY & SCORING GUIDELINES GEOMETRY Table of Contents Questions 1 30: Content Summary and Answer Key... iii Question 1: Question and Scoring Guidelines... 1 Question
Ohio s State Tests PRACTICE TEST ANSWER KEY & SCORING GUIDELINES GEOMETRY Table of Contents Questions 1 30: Content Summary and Answer Key... iii Question 1: Question and Scoring Guidelines... 1 Question
11 The Regular Pentagon
 11 The Regular Pentagon 11.1 The Euclidean construction with the Golden Ratio The figure on page 561 shows an easy Euclidean construction of a regular pentagon. The justification of the construction begins
11 The Regular Pentagon 11.1 The Euclidean construction with the Golden Ratio The figure on page 561 shows an easy Euclidean construction of a regular pentagon. The justification of the construction begins
Section 1-1 Points, Lines, and Planes
 Section 1-1 Points, Lines, and Planes I CAN. Identify and model points, lines, and planes. Identify collinear and coplanar points and intersecting lines and planes in space. Undefined Term- Words, usually
Section 1-1 Points, Lines, and Planes I CAN. Identify and model points, lines, and planes. Identify collinear and coplanar points and intersecting lines and planes in space. Undefined Term- Words, usually
Problem 2.1. Complete the following proof of Euclid III.20, referring to the figure on page 1.
 Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Chapter 2 QUIZ. Section 2.1 The Parallel Postulate and Special Angles
 Chapter 2 QUIZ Section 2.1 The Parallel Postulate and Special Angles (1.) How many lines can be drawn through point P that are parallel to line? (2.) Lines and m are cut by transversal t. Which angle corresponds
Chapter 2 QUIZ Section 2.1 The Parallel Postulate and Special Angles (1.) How many lines can be drawn through point P that are parallel to line? (2.) Lines and m are cut by transversal t. Which angle corresponds
Name: Period: Date: Geometry Midyear Exam Review. 3. Solve for x. 4. Which of the following represent a line that intersects the line 2y + 3 = 5x?
 Name: Period: Date: Geometry Midyear Exam Review 1. Triangle ABC has vertices A(-2, 2), B(0, 6), and C(7, 5). a) If BD is an altitude, find its length. b) XY is the midsegment parallel to AC. Find the
Name: Period: Date: Geometry Midyear Exam Review 1. Triangle ABC has vertices A(-2, 2), B(0, 6), and C(7, 5). a) If BD is an altitude, find its length. b) XY is the midsegment parallel to AC. Find the
7) Are HD and HA the same line?
 Review for Exam 2 Math 123 SHORT ANSWER. You must show all work to receive full credit. Refer to the figure to classify the statement as true or false. 7) Are HD and HA the same line? Yes 8) What is the
Review for Exam 2 Math 123 SHORT ANSWER. You must show all work to receive full credit. Refer to the figure to classify the statement as true or false. 7) Are HD and HA the same line? Yes 8) What is the
Geometry Ch 4 Practice Exam
 Name: Class: Date: Geometry Ch 4 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If BCDE is congruent to OPQR, then BC is congruent to?.
Name: Class: Date: Geometry Ch 4 Practice Exam Multiple Choice Identify the choice that best completes the statement or answers the question. 1. If BCDE is congruent to OPQR, then BC is congruent to?.
MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined
 MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined terms used to create definitions. Definitions are used
MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined terms used to create definitions. Definitions are used
BENCHMARK Name Points, Lines, Segments, and Rays. Name Date. A. Line Segments BENCHMARK 1
 A. Line Segments (pp. 1 5) In geometry, the words point, line and plane are undefined terms. They do not have formal definitions but there is agreement about what they mean. Terms that can be described
A. Line Segments (pp. 1 5) In geometry, the words point, line and plane are undefined terms. They do not have formal definitions but there is agreement about what they mean. Terms that can be described
m 6 + m 3 = 180⁰ m 1 m 4 m 2 m 5 = 180⁰ m 6 m 2 1. In the figure below, p q. Which of the statements is NOT true?
 1. In the figure below, p q. Which of the statements is NOT true? m 1 m 4 m 6 m 2 m 6 + m 3 = 180⁰ m 2 m 5 = 180⁰ 2. Look at parallelogram ABCD below. How could you prove that ABCD is a rhombus? Show that
1. In the figure below, p q. Which of the statements is NOT true? m 1 m 4 m 6 m 2 m 6 + m 3 = 180⁰ m 2 m 5 = 180⁰ 2. Look at parallelogram ABCD below. How could you prove that ABCD is a rhombus? Show that
Videos, Constructions, Definitions, Postulates, Theorems, and Properties
 Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
Accelerated Geometry: Course Level: 10th or 11th grade (students who have not had Geomtery I) Course Code: MA?? Course Length: ( Pre-requisite
 Accelerated Geometry: Course Level: 10 th or 11 th grade (students who have not had Geomtery I) Course Code: MA?? Course Length: (1 semester) Pre-requisite: Algebra I (MA113/123) Description: This accelerated
Accelerated Geometry: Course Level: 10 th or 11 th grade (students who have not had Geomtery I) Course Code: MA?? Course Length: (1 semester) Pre-requisite: Algebra I (MA113/123) Description: This accelerated
Chapter 1. acute angle (A), (G) An angle whose measure is greater than 0 and less than 90.
 hapter 1 acute angle (), (G) n angle whose measure is greater than 0 and less than 90. adjacent angles (), (G), (2T) Two coplanar angles that share a common vertex and a common side but have no common
hapter 1 acute angle (), (G) n angle whose measure is greater than 0 and less than 90. adjacent angles (), (G), (2T) Two coplanar angles that share a common vertex and a common side but have no common
Geometry 1-1. Non-collinear Points not on the same line. Need at least 3 points to be non-collinear since two points are always collinear
 Name Geometry 1-1 Undefined terms terms which cannot be defined only described. Point, line, plane Point a location in space Line a series of points that extends indefinitely in opposite directions. It
Name Geometry 1-1 Undefined terms terms which cannot be defined only described. Point, line, plane Point a location in space Line a series of points that extends indefinitely in opposite directions. It
Chapter 4 UNIT - 1 AXIOMS, POSTULATES AND THEOREMS I. Choose the correct answers: 1. In the figure a pair of alternate angles are
 STD-VIII ST. CLARET SCHOOL Subject : MATHEMATICS Chapter 4 UNIT - 1 AXIOMS, POSTULATES AND THEOREMS I. Choose the correct answers: 1. In the figure a pair of alternate angles are a) and b) and c) and d)
STD-VIII ST. CLARET SCHOOL Subject : MATHEMATICS Chapter 4 UNIT - 1 AXIOMS, POSTULATES AND THEOREMS I. Choose the correct answers: 1. In the figure a pair of alternate angles are a) and b) and c) and d)
 1 www.gradestack.com/ssc Dear readers, ADVANCE MATHS - GEOMETRY DIGEST Geometry is a very important topic in numerical ability section of SSC Exams. You can expect 14-15 questions from Geometry in SSC
1 www.gradestack.com/ssc Dear readers, ADVANCE MATHS - GEOMETRY DIGEST Geometry is a very important topic in numerical ability section of SSC Exams. You can expect 14-15 questions from Geometry in SSC
Section Congruence Through Constructions
 Section 10.1 - Congruence Through Constructions Definitions: Similar ( ) objects have the same shape but not necessarily the same size. Congruent ( =) objects have the same size as well as the same shape.
Section 10.1 - Congruence Through Constructions Definitions: Similar ( ) objects have the same shape but not necessarily the same size. Congruent ( =) objects have the same size as well as the same shape.
Geometry Advanced Fall Semester Exam Review Packet -- CHAPTER 1
 Name: Class: Date: Geometry Advanced Fall Semester Exam Review Packet -- CHAPTER Multiple Choice. Identify the choice that best completes the statement or answers the question.. Which statement(s) may
Name: Class: Date: Geometry Advanced Fall Semester Exam Review Packet -- CHAPTER Multiple Choice. Identify the choice that best completes the statement or answers the question.. Which statement(s) may
TOPIC 2 Building Blocks of Geometry. Good Luck To
 Good Luck To Period Date PART I DIRECTIONS: Use the Terms (page 2), Definitions (page 3), and Diagrams (page 4) to complete the table Term (capital letters) 1. Chord 2. Definition (roman numerals) Pictures
Good Luck To Period Date PART I DIRECTIONS: Use the Terms (page 2), Definitions (page 3), and Diagrams (page 4) to complete the table Term (capital letters) 1. Chord 2. Definition (roman numerals) Pictures
Geometry. Instructional Activities:
 GEOMETRY Instructional Activities: Geometry Assessment: A. Direct Instruction A. Quizzes B. Cooperative Learning B. Skill Reviews C. Technology Integration C. Test Prep Questions D. Study Guides D. Chapter
GEOMETRY Instructional Activities: Geometry Assessment: A. Direct Instruction A. Quizzes B. Cooperative Learning B. Skill Reviews C. Technology Integration C. Test Prep Questions D. Study Guides D. Chapter
Mathematics For Class IX Lines and Angles
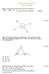 Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Problem 3.1 (Building up geometry). For an axiomatically built-up geometry, six groups of axioms needed:
 Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Use the figure to name each of the following:
 Name: Period Date Pre-AP Geometry Fall 2016 Semester Exam REVIEW *Chapter 1.1 Points Lines Planes Use the figure to name each of the following: 1) three non-collinear points 2) one line in three different
Name: Period Date Pre-AP Geometry Fall 2016 Semester Exam REVIEW *Chapter 1.1 Points Lines Planes Use the figure to name each of the following: 1) three non-collinear points 2) one line in three different
Lesson 9: Coordinate Proof - Quadrilaterals Learning Targets
 Lesson 9: Coordinate Proof - Quadrilaterals Learning Targets Using coordinates, I can find the intersection of the medians of a triangle that meet at a point that is two-thirds of the way along each median
Lesson 9: Coordinate Proof - Quadrilaterals Learning Targets Using coordinates, I can find the intersection of the medians of a triangle that meet at a point that is two-thirds of the way along each median
Test for the unit is 8/21 Name:
 Angles, Triangles, Transformations and Proofs Packet 1 Notes and some practice are included Homework will be assigned on a daily basis Topics Covered: Vocabulary Angle relationships Parallel Lines & Transversals
Angles, Triangles, Transformations and Proofs Packet 1 Notes and some practice are included Homework will be assigned on a daily basis Topics Covered: Vocabulary Angle relationships Parallel Lines & Transversals
Geometry/Trigonometry Summer Assignment
 Student Name: 2017 Geometry/Trigonometry Summer Assignment Complete the following assignment in the attached packet. This is due the first day of school. Bring in a copy of your answers including ALL WORK
Student Name: 2017 Geometry/Trigonometry Summer Assignment Complete the following assignment in the attached packet. This is due the first day of school. Bring in a copy of your answers including ALL WORK
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions
 Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
5. THE ISOPERIMETRIC PROBLEM
 Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Mathematics As A Liberal Art
 Math 105 Fall 2015 BY: 2015 Ron Buckmire Mathematics As A Liberal Art Class 26: Friday November 13 Fowler 302 MWF 10:40am- 11:35am http://sites.oxy.edu/ron/math/105/15/ Euclid, Geometry and the Platonic
Math 105 Fall 2015 BY: 2015 Ron Buckmire Mathematics As A Liberal Art Class 26: Friday November 13 Fowler 302 MWF 10:40am- 11:35am http://sites.oxy.edu/ron/math/105/15/ Euclid, Geometry and the Platonic
Similar Polygons. These rectangles are not similar. In the investigation, you will explore what makes polygons similar.
 CONDENSED LESSON 11.1 Similar Polygons In this lesson, you Learn what it means for two figures to be similar Use the definition of similarity to find missing measures in similar polygons Explore dilations
CONDENSED LESSON 11.1 Similar Polygons In this lesson, you Learn what it means for two figures to be similar Use the definition of similarity to find missing measures in similar polygons Explore dilations
Chapter 7 Coordinate Geometry
 Chapter 7 Coordinate Geometry 1 Mark Questions 1. Where do these following points lie (0, 3), (0, 8), (0, 6), (0, 4) A. Given points (0, 3), (0, 8), (0, 6), (0, 4) The x coordinates of each point is zero.
Chapter 7 Coordinate Geometry 1 Mark Questions 1. Where do these following points lie (0, 3), (0, 8), (0, 6), (0, 4) A. Given points (0, 3), (0, 8), (0, 6), (0, 4) The x coordinates of each point is zero.
