Master of Science Thesis
|
|
|
- Marion Neal
- 5 years ago
- Views:
Transcription
1 Master of Science Thesis Experimental design for cryo-transmission electron microscopy single particle reconstruction: a simulation study on the effect of the defocus and electron dose August 6, 2010
2
3 Experimental design for cryo-transmission electron microscopy single particle reconstruction: a simulation study on the effect of the defocus and electron dose Master of Science Thesis For obtaining the degree of Master of Science in Applied Physics at Delft University of Technology August 6, 2010 Supervisors: Dr. ir. A.J. den Dekker Dr. ir. S.W. van der Hoeven Prof. dr. ir. P.M.J. Van den Hof Dr. B. Carragher Dr. C.S. Potter Faculty of Applied Physics Delft University of Technology
4 The work in this thesis has been done in collaboration with AMI-group, The Scripps Research Center. Copyright c Delft Center for Systems and Control All rights reserved.
5 Abstract With single particle analysis using cryo-specimen preparation and a transmission electron microscope (TEM) to record the images, the 3D distribution of the potential of a biological molecule can be reconstructed. In this thesis, instead of 3D, only 2D reconstructions of the molecule s projected potential were considered to keep the reconstruction scheme simple. The goal of this project was to study the quality of the reconstructions as a function of defocus for different electron doses, when taking into account registration errors. For this purpose we carried out a simulation study with a 2D projection of the potential of the GroEL chaperone from the Protein Data Bank. We assumed the weak phase object approximation is satisfied, only the partial spatial coherence envelope function had to be taken into account and that the influence of the phase contrast transfer function (PCTF) on the reconstruction can be fully corrected for. We derived that the effect of registration errors can be described by an envelope function, similar to that for partial coherence. The width of the registration error envelope function depends on the signal to noise ratio (SNR) of the particle images and thus on the electron dose and defocus. The resolution is strongly dependent on the magnitude of the registration errors. We found that the higher the electron dose, the lower the defocus that leads to a maximal resolution of the reconstruction. We conclude from the results of the simulation study performed in this thesis that the resolution according to the Fourier Ring Correlation (FRC) and Spectral Signal to Noise Ratio (SSNR) is identical to the information limit when the PCTF is fully corrected for and the threshold levels are chosen appropriately. We thus interpret the resolution according to the FRC for this threshold as the maximum spatial frequency for which the signal power is twice the noise variance. Further, the mean squared error (MSE) and resolution are equivalent if the reconstruction is fully corrected for the PCTF. This is a very important conclusion; the defocus for which the MSE is maximal corresponds to a minimal resolution of the reconstruction. It should be realized that the defocus for which the MSE and resolution have their optimal value as a function of defocus depends on the potential of the molecule. As a result all
6 conclusions drawn from the simulation study performed in this thesis are thus specific to the GroEL chaperone projected potential. This is amongst others, a consequence of the dependence of the SNR on object-characteristics.
7 ii Abstract
8 Table of Contents Abstract 3 1 Introduction Project Goal Outline Image formation Introduction Overview of the image formation Linear system theory Transfer function of the TEM Detected image Phase contrast microscopy Transmission function of a phase object Dependence of the object s phase shift on the projected object potential Weak phase object approximation Envelope function of the TEM Wave aberration function of the TEM Concluding remarks Detected images Introduction Electron dose Image discretization Discretized intensity distribution in the Fourier Domain D Fast Fourier transform Discretized projected potential
9 iv Table of Contents Discretized intensity distribution Expected electron count at the CCD camera Particle images Normalization Parameters Noise Gaussian additive noise Gaussian additive noise in the Fourier domain Noise variance of sample average Registration error Concluding remarks Image reconstruction Introduction Cross-correlating two images Aligned particle images Normalization of the aligned particle images The 2D average Introducing an alternative notation for the 2D average D Convolution of images Using the 2D convolution to describe registration errors D Average Fourier transform of the reconstructed image Image padding Registration error matrix D Average Correcting for the PCTF Concluding remarks Measures describing the quality of a reconstruction Introduction The signal to noise ratio SNR of sample average Full Width at Half Maximum Mean squared error Bias Variance Sample variance Fourier Ring Correlation Radial average Definition of the FRC
10 Table of Contents v Approximate expressions for the FRC Example of an FRC-curve Expressing the resolution based on the FRC-curve Spectral Signal to Noise Ratio Definition of the SSNR Approximate expression for the sample variance of a reconstruction Approximate expressions for the SSNR Example of an SSNR-curve Expressing the resolution based on the SSNR-curve Information limit Comparing the FRC, SSNR and the information limit The FRC and the information limit The SSNR and the FRC Concluding remarks Results from simulations Introduction Signal to noise ratio Dependence of the SNR on the defocus Signal to noise ratio as a function of the window size Registration error The registration error matrix in real space The registration error matrix in Fourier space Comparing the width of the real-space and Fourier transformed registration error matrix Mean squared error Bias Variance Sample variance in Fourier domain Resolution Approximations to the FRC and SSNR The resolution limitation due to the registration errors and the envelope function respectively The resolution limitation due to both the registration errors and the envelope function Comparing the MSE to the resolution Concluding remarks Conclusions and future work Framework and assumptions made Conclusions Future work
11 vi Table of Contents Acronyms 98 Operators 99 Nomenclature 100 Bibliography 105
12 Chapter 1 Introduction This MSc thesis is the final part of the two-year program of the Master Applied Physics at the Delft University of Technology. The first months were devoted to writing a literature report [27], to get more acquainted with recent scientific publications related to the topic of thesis. The project is a collaboration between the Delft Center for Systems and Control (DCSC) and the Automated Molecular Imaging (AMI)-group of The Scripps Research Institute (TSRI). The author spent three months of the project time at the AMI-group in California, USA and the remainder in Delft. The AMI-group developed the Appion software package [24] that can be used for single-particle applications and has expertise in the single-particle analysis field and working with the transmission electron microscope (TEM). At the Delft Center for Systems and Control research is focussed, amongst other topics, on model-based quantitative electron microscopy. The current project is aimed at evaluating how certain parameters can best be chosen specific to single particle analysis. Below, the project goals will be discussed more specifically. First, some of the concepts involved will be introduced in more detail. With the increasing computational power, more and more techniques have been developed that make a three-dimensional (3D) reconstruction of the molecule s potential possible. With single particle analysis using cryo-specimen preparation and a TEM to record the images, the 3D distribution of the potential of a biological molecule can be reconstructed. In Figure 1-1, several layers of a virus, the rota-virus, are depicted. The principles of single particle reconstruction and cryogenic specimen preparation are outlined below. As compared to twodimensional (2D) images that are the projection of the 3D potential, the ease of interpretation is greatly increased by viewing a 3D representation. For example, when imaging the subsequent stages of a binding reaction, the shape changes of the molecule are easier to see from a 3D structure than from 2D images. Knowledge of such a reaction may facilitate the development of drugs. With an electron microscope highly magnified images can be made. High-energy electrons are used to illuminate the specimen and are detected with a CCD camera [17]. The signal to noise ratio of the images depends on the total number of electrons that is used for the recording. The more electrons are detected, the stronger the signal to noise ratio at the
13 2 Introduction Figure 1-1: The 3D structure of the Rota-virus. It was formed using cryo-electron microscopy and single particle analysis. From [2]. detector. However, at the same time, the biological molecules are damaged by the interaction with the electrons. Thus, to minimise radiation damage, low exposure is required, which means the images have a low signal to noise ratio. If radiation damage would not form a constraint on the imaging, a single molecule could be imaged from all directions. For each direction, the image represents the projected potential of the molecule and when combining this set of images using, for example, weighted back projection the 3D potential distribution can be computed. For radiation sensitive molecules, single particle analysis can be used to reconstruct the 3D potential distribution. The principle of single particle analysis is as follows: A specimen containing many identical molecules is imaged once with a TEM. The images of each of the molecules are selected from the composite recorded image. Large numbers (tens of thousands) of particles are picked in this way. The orientation of the particles is determined from the images and once the projection direction is known for each of the particles, the images are processed to form a reconstruction of the 3D structure. Thus, instead of imaging a single particle from many directions, many identical particles are imaged from a single direction. Assuming the particles have a random orientation within the specimen and are truly identical, effectively the particle structure is imaged from many directions. The advantage of this scheme is that the number of electrons per unit area for each of the molecules is minimal, since the dose is spread over many particles. For imaging with an electron microscope, a vacuum has to be established. This puts constraints on the specimen preparation, since the evaporation of any water from the specimen interferes with the vacuum requirement. Therefore, conventionally, the specimen is dehydrated before it is inserted into the microscope. A disadvantage of this technique is that it
14 3 Figure 1-2: Steps involved in a 2D reconstruction procedure. Particle images are selected from an image containing many particles. These are registered and finally averaged to form a reconstruction that has a lower noise variance and thus a lower signal to noise ratio. can cause biological molecules to collapse. An alternative to dehydration is cryogenic specimen preparation. This is a specimen preparation technique where the specimen is hydrated by a substance referred to as vitreous ice. Vitreous ice forms when an aqueous specimen is frozen very quickly to low, liquid nitrogen temperatures and is an unordered crystal. Vitreous ice has properties similar to liquids and preserves the structure of the specimen well [8]. The aim is to form reconstructions that contain high resolution information. The highest frequency component in the reconstruction is related to the smallest detail in the image. Physically, the smallest detail corresponds to the atoms (having a size of circa 0.1nm) and therefore an upper limit for the spatial frequency is circa 10nm 1 [5]. The resolution of detected images is often worse than this ultimate limit for several reasons. For example, the magnetic lenses in the microscope have non-ideal properties, the illumination may be partially coherent and there is a spread in energy with which electrons leave the source. These resolution limitations can be theoretically described by envelope functions. Currently, the best achievable resolution of 2D images recorded with a transmission electron microscope approaches that of the size of an atom, with resolutions 5nm 1-10nm 1 [11]. The best resolution of 3D maps obtained with cryo-tem single particle analysis, however, only approaches 2nm 1 [24]. An important question that people in the biological imaging field would like to be answered is: What limits the achievement of better resolution in cryo-tem maps? And also: How should the settings of the microscope be chosen to lead to the highest resolution information in the reconstruction [24]? The research described in this thesis is a first step towards a full-scale treatment of these questions an focuses on the influence of the defocus and the electron dose on the resolution. To simplify the analysis, only 2D, instead of 3D reconstructions are considered. However, since a 3D reconstruction is formed from many 2D images in single-particle analysis, it is reasonable to assume that optimum settings for a 2D reconstruction will extrapolate to an optimal 3D reconstruction. In Figure 1-2 the 2D reconstruction process is depicted schematically. Many particles with the same orientation are detected. It is assumed that the particles are identical and that the noise contribution is random. In addition, the location of the particles within the total image is not known. First, the particles are selected in the boxing step, resulting in boxes
15 4 Introduction each containing the noise-disturbed projected potential of a molecule. As is illustrated in Figure 1-2, the selected particles may not be located at the center of their box. The next step is the registration of the particle images and this should lead to particle images that are better aligned relative to each other. In the final step, the aligned particle images are averaged to form a 2D reconstruction that has a lower noise variance and thus a higher signal to noise ratio than the original images. Depending on the signal to noise ratio of the particle images, there may be a residual alignment error after the registration step. Even though the particles are assumed to be identical, averaging over misaligned particle images will introduce a blur. We take into account alignment errors as one of the factors that degrades the quality of a reconstruction in this project. There are several measures that are used to quantify the quality of a reconstruction. Firstly, in the single particle analysis field the Fourier Ring Correlation (FRC) and the Spectral Signal to Noise Ratio (SSNR) are commonly used to express the resolution of a reconstruction [8]. Further, in the high-resolution transmission electron microscopy field, the information limit [6] is used to express the resolution of images. Finally, the quality of the reconstructions can be quantified by the mean squared error (MSE). This measure takes account of both bias and variance aspects of the reconstruction. In this project we consider all above mentioned measures. Both for the information limit and the MSE it is essential to have a ground truth. Therefore, no recorded images are used, but particle images are simulated in Matlab [16]. The protein that is considered is the prokaryotic molecular chaperone GroEL, that promotes the protein folding in bacteria [29]. The 3D potential of this molecule is projected and Poisson noise is added that has a variance dependent on the electron dose. The reconstruction and the quality of this reconstruction are also computed using Matlab. 1-1 Project Goal The goal of this project is to study what influence the defocus and electron dose setting have on the quality of the reconstruction. Ultimately, we would like to discover what is the best defocus and electron dose setting for a certain object. Specifically, we would like to answer the following questions. How does the SNR vary as a function of defocus? Are the registration errors directly related to the SNR of a set of images? How does the resolution according to the Fourier Ring Correlation (FRC) relate to that according to the Spectral Signal to Noise Ratio (SSNR) and the information limit? How do the registration errors influence the defocus for which the resolution is highest? Is there a direct relationship between the resolution and the MSE? In other words, does a low resolution imply that the MSE is high? Are optimal settings generic in the sense that they are independent of the object being studied?
16 1-2 Outline 5 Can a rule of thumb be formulated as to how to choose the optimal defocus based on the electron dose setting? Finding the optimal defocus setting for single-particle applications is very interesting. In the high-resolution transmission electron microscopy an example of an optimal setting is Scherzer defocus. With Scherzer defocus, the phase shift as a consequence of the out-of focus imaging partly compensates for the spherical aberration to result in a large pass-band of low spatialfreqencies [28]. However, when using low electron doses (not to damage the specimen) there is too little contrast in the images to correctly register images for Scherzer defocus in case of a single particle reconstruction. In this project we focus on finding an optimal setting for defocus when using low electron doses and taking registration errors into account. 1-2 Outline This thesis is structured as follows. In chapter 2, the image formation in the electron microscope is outlined. Approximations valid for imaging biological molecules are given. At the end of this chapter, an expression for the distribution of electrons in the plane of the detector is formulated. The image formation is described in terms of continuous variables. However, when a CCD camera is used to detect the images, a discrete formulation is more appropriate. Therefore it is essential to relate the number of electrons that are detected at each pixel of the detector to the distribution that was stated in chapter 2. In chapter 3, the approximations required to go from the continuous description to a discrete description are outlined. Additionally, the properties of noise in the images are considered. After these chapters, all theory required to create a hypothetical data set of particle images has been discussed. In chapter 4, it is outlined how a reconstruction can be formed from the particle images. An expression for the 2D reconstruction taking into account registration errors is formulated. This is done both in the real and the spatial frequency domain. In chapter 5, we introduce measures that can be used to quantify the quality of the reconstructions. First we consider the definitions of the signal to noise ratio that are used in literature. As a result of low signal to noise ratios there may be alignments errors and measures that express the severity of the registration errors are described subsequently. After this, the definition of the mean squared error is stated as a measure to quantify the resemblance between a reconstruction and the object. Three resolution measures are considered, the Fourier Ring Correlation (FRC), Spectral Signal to Noise Ratio (SSNR) and the information limit. For the FRC and SSNR approximate expressions are derived. In chapter 6, we test the validity of the approximations in a simulation study for a 2D projection of the potential of the GroEL chaperone and discuss the characteristics of each of the quality of the reconstructions measures as a function of defocus. In chapter 7, we formulate the most important findings regarding the project goals outlined in the preceding section and outline recommendations for future work.
17 6 Introduction
18 Chapter 2 Image formation 2-1 Introduction With the transmission electron microscope (TEM) biological objects can be imaged. The image in the plane of the detector is a result of the interaction of the illuminating beam with the object and subsequent deflection by the microscope lenses. Conventionally, electrons are considered particles. However, as DeBroglie confirmed, electrons exhibit wave properties [9]. In this thesis we consider phase contrast microscopy, which is based on the quantum mechanical picture that the electrons from the electron gun can be interpreted as waves that interfere. The interference originates from a phase difference between the waves a result of a change in wavelength. As the wavelength scales with the inverse of the square root of the accelerating voltage, the larger the accelerating voltage, the larger the electron energy and the smaller the wavelength of the electron wave. In regions of positive electrostatic potential, the electrons are further accelerated which means there is a small reduction in the wavelength for waves that traversed regions of high potential and as a result, there is a phase difference with waves that were not accelerated further. In this chapter, first an overview is given of the principles of the image formation and linear systems theory. In the remaining sections we describe how the distribution of intensity in the image plane depends on the object structure using wavefunctions. Additionally we study the influence of (non-ideal) properties of the illumination and microscope lenses on the image contrast. 2-2 Overview of the image formation The image formation can be schematized as in Figure 2-1. At the top, the illuminating electron wave ψ 0 is the input. The interaction of the wave and the object is described by a transmission function t obj. The wavefunction at the exit plane of the object is labelled ψ e.
19 8 Image formation Figure 2-1: Schematic representation of the image formation of phase contrast imaging with a transmission electron microscope. A plane illuminating wave ψ 0 illuminates the object. The wavefunction at the exit plane of the object can be described as the multiplication of ψ 0 and the transmission function of the object, t obj. The phase and amplitude of the exit wave function ψ e are altered by the transfer function H micr. It is not the wavefunction ψ i, but intensities that are detected. The distribution of electrons in the image plane is described by w(r).
20 2-3 Linear system theory 9 The exit wavefunction is deflected by the microscope lenses, which is depicted in Figure 2-1 by the transfer function H micr. The multiplication of the exit wave function with the transfer function in the Fourier domain is equivalent to the convolution with the point spread function in the real domain. The result of the convolution with the point spread function of the microscope is a wavefunction ψ i and the intensity of this wavefunction is recorded at the detector. In the following sections each step of the schematic representation are considered in more detail. First a reprisal of linear systems theory is given (2-3), then the notation of the linear system specific to the TEM is stated (2-4), and in section 2-5 the relationship between image intensity and the wavefunction at the exit plane of the object is outlined. These are the second and third part of the schematic representation depicted in Figure 2-1. The first part, the object transmission function t obj, is considered in sections 2-6 and 2-7. The result of the analysis of section 2-7 is an expression for the image intensity distribution, W (r) that is linear to the projected potential in the Fourier domain. 2-3 Linear system theory The transfer of any linear system can be written in the Fourier domain as [10] F out (k) = H(k) F in (k), (2-1) with F in (k) the input to the linear system; F out (k) the output; and H(k) the transfer function of the system. Each of these functions is expressed in the Fourier domain, in terms of the 2D spatial frequency coordinates k = [k x, k y ]. Or, equivalently by inverse Fourier transformation, this same equation can be written in terms of the real space coordinates r = [x, y], f out (r) = h(r) f in (r), (2-2) in which denotes the convolution. The function h(r) is known as the point-spread function or the impulse response. The point-spread function (PSF) can be interpreted as the image that is obtained when imaging a point source. It is related to H(k) as h(r) = F 1 {H(k)} H(k) = F{h(r)} (2-3) In this equation, the operators F and F 1 denote the continuous forward and inverse Fourier transform, respectively. In the remainder of this thesis the convention will be adopted that capital letters are used to denote Fourier transformed quantities. The transfer function can be split into an amplitude part E(k) and a phase part e iγ(k) H(k) = H(k) e iγ(k) = E(k) e iγ(k). (2-4) The term E(k) in this definition describes the strength with which spatial frequency components of the input signal are transferred by the system and γ(k) is the phase shift of the system.
21 10 Image formation When E(k) = 1 and γ(k) = 0, F out (k) is identical to F in (k). In this case, all spatial frequencies are transferred with equal magnitude to the output. The real space equivalent of this is a delta peak for the point spread function; h(r) = δ(r). The two-dimensional delta function is defined as [30] { δ(r) = δ 2 +, x (x, y) = 2 + y 2 = 0 0. x 2 + y 2 (2-5) 0 Properties of this delta function are δ 2 (x, y)dxdy = 1, (2-6) and δ 2 (x, y) = δ(x)δ(y), (2-7) δ 2 (ax, by) = 1 ab δ2 (x, y) (2-8) Due to lens aberrations, the point spread function of the electron microscope has a finite width. 2-4 Transfer function of the TEM To form a magnified image of the object the exit wave passes through an objective lens and is further magnified by subsequent lenses. However, in this imaging process the image wave, Ψ i does not correspond exactly to the wavefunction at the exit plane, Ψ e of the object, due to non-ideal imaging and aberrations of the lenses [8]. Using the linear system theory introduced in the preceding section, the wavefunctions at the detector plane can be related to that at the exit plane of the object as Ψ i (k) = H micr (k) Ψ e (k), (2-9) with H micr (k) = E micr (k) e iγ micr(k). (2-10) In sections 2-8 and 2-9 the amplitude E micr (k), which is known as the envelope function, and the phase γ micr (k), which is known as the wave aberration function, are considered in more detail. 2-5 Detected image It is the intensity and not the wavefunction that is recorded with the detector of an electron microscope. In the absence of noise, the image intensity distribution is related to the wavefunction at the detector as [19] w(r) = ψ i (r) 2. (2-11)
22 2-6 Phase contrast microscopy 11 The wavefunction can be written as the multiplication of an amplitude and a phase term ψ i (r) = a(r) e iθ(r), (2-12) with a and θ the wave amplitude and phase respectively. Substituting this into the definition for the intensity gives w(r) = a(r) e iθ(r) 2 = a(r) 2. (2-13) Therefore only the amplitude of the wavefunction in the detector plane is recorded and the phase information is lost. Using the linear system theory introduced above, the intensity can be written in terms of the wavefunction at the exit face of the object, ψ e, w(r) = h micr (r) ψ e (r) 2. (2-14) In this equation, h micr (r) is the point spread function of the electron microscope. It is related to the transfer function in the way defined in Eq. (2-3). Thus, h micr (r) = F 1 {H micr (k)}. 2-6 Phase contrast microscopy The expression for the image intensity distribution derived in the preceding section can be approximated for certain classes of objects. In this section the phase object approximation is described that is suitable for describing biological molecules that are mainly composed of atoms that scatter weakly [10]. For this type of objects it can be assumed that the object only affects the phase and not the amplitude of the illuminating plane wave. In the section that follows this section, (section 2-7), an even stronger approximation, the weak phase object approximation is described. For both approximations the image intensity distribution in terms of object and microscope parameters is outlined. In this thesis we assume the Weak Phase Object Approximation is satisfied for GroEL particles Transmission function of a phase object The complex transmission function t obj of a phase object is mathematically denoted as, t obj (r) = e iθ obj(r). (2-15) It is the local change in the phase shift θ obj that causes intensity variations in the recorded image. Phase contrast is based on the quantum mechanical picture that an electron wave interferes with itself. For the interference to occur, a coherent plane wave is required to illuminate the object. Any deviation from perfect coherence is accounted for by the envelope function described in subsection 2-8. Assuming the plane wave has unit amplitude i.e. ψ 0 (r) = 1 and no spatial phase variation, the wavefunction at the exit plane of the object can be written as ψ e (r) = ψ 0 (r) t obj (r) = t obj (r), (2-16) with t obj defined as in Eq. (2-15). In the following, it is shown how the phase shift depends on the object potential.
23 12 Image formation Dependence of the object s phase shift on the projected object potential Each of the incident electrons is described by a wave function ψ 0. The object acts as a medium of variable refractive index for the electron wave, due to the object s atomic potential. In passing through the object, a phase-difference occurs relative to the unobstructed wave. Just as light rays are bent by glass or water, so an electron wave is affected by the change of refractive index due to a change in atomic potential [10]. From the principle of conservation of energy the wavelength of the electron when treated classically is [23] λ 1.2, (2-17) V0 with λ in nm and V 0 the potential energy of the electron in ev. The potential energy (in ev) is equivalent to the accelerating voltage (in V). A typical value for the accelerating voltage is 200V and the wavelength corresponding to this voltage is nm. The constant 1.2 is proportional to Planck s constant divided by the square root of the electron rest mass. Its unit is [ ev nm]. Although at high energies a relativistically corrected value for V 0 should be used, Eq. (2-17) gives an indication. The positive electrostatic potential φ 0 inside the object further accelerates the incident fast electrons, resulting in a small reduction in wavelength inside the object. The refractive index n in the object is calculated by expressing the wavelength in vacuum relative to that in the object n = λ λ = 1.2 / φ 0. (2-18) V0 V0 + φ 0 2V 0 In regions of high atomic potential, the refractive index is high, causing a reduction in the fast electron s wavelength and a phase advance relative to a wave passing through regions of higher atomic potential. The phase shift that an electron experiences because of the atom s potential can be calculated by expressing its phase relative to an electron that does not feel the potential. For an electron passing through a layer of potential φ 0 and thickness t this phase shift is θ obj = 2π(n 1)t λ = πφ 0t λv 0 = σφ 0 t, (2-19) where the definition of the refractive index was used. In this equation the interaction constant was introduced, which is defined as [23] σ = π λv 0. (2-20) The value of σ, for an accelerating voltage of 200kV, is σ m 1 ev 1. Assuming a thin object, such that the defocus difference between the top and the bottom of the object is neglectable, the phase change can be expressed in terms of the local projected potential, θ obj (r) = σφ p (r), (2-21) In this equation, φ p (r) = t/2 t/2 φ(x, y, z)dz is the projected potential, projected in the direction of the optical axis z, with t the thickness of the object [17]. Thus the overall effect of the object on the electron is represented by a phase-shift, θ obj, proportional to the projection of the potential distribution of the object.
24 2-7 Weak phase object approximation 13 Based on the foregoing, it is concluded that the image intensity distribution is related to the projected potential as for phase objects. w(r) = h micr (r) t obj (r) 2 = h micr (r) e iσφp(r) 2, (2-22) 2-7 Weak phase object approximation For objects that only very weakly change the phase of the illumination, the image intensity distribution can be approximated further. For these weak phase objects, θ obj << 1, and the object function t obj can be approximated as t obj (r) = e iθ obj(r) 1 + iθ obj (r) = 1 + iσφ p (r). (2-23) This is the weak phase object approximation (WPOA). The complex amplitude at the exit face of the object is then, ψ e (r) = 1 + iσφ p (r). (2-24) The first term in this equation represents the unscattered beam and the second term describes the part of the beam that was scattered [10]. The intensity at the image plane can be calculated using Eq. (2-14). It follows that [10], w = h micr ψ e 2 = h micr h micr φ p iσ 2 + (h micr φ p iσ) + (h micr φ p iσ). (2-25) In this equation, the notation ( ) is used to denote the complex conjugation. For a complex number a = b + ic the complex conjugate is defined as a = b ic. Using the notation introduced in section 2-3, the first term of Eq. (2-25) can be calculated as h micr (r) 1 = F 1 {H micr (k) δ(k)} = F 1 {E micr (0)e iγ(0) δ(k)} = F 1 {δ(k)} = 1. Further noting that the potential is a real function and neglecting the term that is quadratic in σφ p, Eq. (2-25) can be approximated as w = 1 + (h micr h micr) φ p iσ = 1 2Im(h micr ) φ p σ In this equation, Im(c) = Im(a + bi) = b. It can be shown that if h micr (r) and H micr (k) are a Fourier transform pair [20] h micr (r) h micr(r) = F 1 {H micr (k) H micr( k)}. (2-26)
25 14 Image formation Using Eq. (2-10) it follows that h micr (r) h micr(r) = F 1{ E micr (k)e iγ micr(k) E micr( k)e iγ micr( k) }. The envelope function E micr (k) is a real even function. This implies E micr (k) = E micr( k). From Eq. (2-32) it is seen that the wave aberration function is a real function. If it further holds that γ micr is an even function, then γ micr (k) = γ micr ( k), Im(h micr (r)) = F 1 {Im(H micr (k))}. Using the relation between sine and cosine and the complex exponential function, e iγ micr = cos(γ micr ) + i sin(γ micr ), the image intensity distribution can now be written as w(r) = 1 2σφ p (r) F 1{ sin(γ micr (k))e micr (k) }. (2-27) Fourier transforming this equation gives the intensity in terms of spatial frequencies k [13], W (k) = δ(k) 2σΦ p sin(γ micr (k))e micr (k). (2-28) Eq. (2-28) shows that under the weak phase object approximation, the image contrast is proportional to the projected object potential in the Fourier domain. The function sin ( γ micr (k) ) describes how phase contrast of the object is transferred through the microscope and is referred to as the phase contrast transfer function (PCTF). Eq. (2-28) is a very important equation. We assume that the GroEL chaperone can be considered a weak phase object and that the intensity in the image plane is thus described by Eq. (2-28). In the two sections that follow we consider the formulation and properties of the envelope function and properties of the PCTF of the transmission electron microscope. 2-8 Envelope function of the TEM The image recorded in an electron microscope is a finite time integral of the electron waves in the image plane due to each of the electron waves that reach the image plane within the recording time. The wave functions due to each to the electrons interfering in the image plane are assumed to be independent events. Any difference in imaging conditions between consecutive electrons then implies that the wave fields due to the electrons do not overlap precisely so that blurring occurs. This blurring is described by envelope functions. The effect of the envelope functions is that the contrast is dampened for high spatial frequencies. In phase contrast electron microscopy there are many envelope functions that limit the resolution. One of these factors is partial coherence.
26 2-8 Envelope function of the TEM 15 Figure 2-2: Coherence envelope functions of the TEM, for several defocus settings. The larger the underfocus, the more limiting is E coh. The parameters used to compute this graph are stated in Table 3-1. For phase contrast imaging, a perfectly parallel beam is required to assure perfect coherence. The envelope function E coh (k) describes the reduced transmittance of high frequency components when the illumination is only partially coherent. It is defined as [7, 8], ( E micr (k) = E coh (k) = exp π 2 k0 2 (C s λ 3 k 3 z λ k) 2), (2-29) with k 0 = α λ and α a constant that has a typical value of 0.1mrad for a field emission gun (FEG) [6, 7, 25] and C s the spherical aberration constant. In Figure 2-2 the coherence envelope has been depicted as a function of spatial frequency for three defoci. It is seen in this figure that the effect of partial coherence is that some spatial frequencies are transferred less strongly than others. In fact, for large underfocus, the high spatial frequencies are not transferred at all. The coherence envelope function in this case thus acts as a low-pass filter. Partial coherence is not the only limitation to the resolution with phase contrast imaging. However, in this thesis we only consider the effect of partial coherence. The reason we make this choice is that the coherence envelope function depends on the defocus of the microscope. Other envelope functions like chromatic aberration for example do not depend on the defocus and thus poses a constant limitation on the resolution. Since we focus in this thesis on how the choice of the defocus (and electron dose) effects the quality of the reconstructions, the chromatic aberration envelope function is not so interesting to consider as it does not affect the optimal defocus. Further, for the relative large under-focus values that are used in single particle analysis (between 1 and 3µm), the coherence envelope function limits the resolution more severely than the chromatic aberration.
27 16 Image formation 2-9 Wave aberration function of the TEM The phase shift γ micr (k) introduced by the microscope is a consequence of lens-aberrations and focussing errors. In this section we describe the former with phase shift γ s and the latter with a phase shift γ f. The foremost aberration that lenses in the electron microscope suffer from is spherical aberration. The effect of spherical aberration is that rays leaving the object at large angles are refracted too strongly by the outer zones of the lens and are brought to focus before the image plane (the plane defined by lens law). As a result, the image of a point becomes a blurred disk. This defect can be described by a phase shift [23], γ s (k) = πc s λ 3 k 4 /2, (2-30) with C s the spherical aberration coefficient and λ the electron wavelength. A typical value of C s is 1.2mm. The phase shift γ f for a certain defocus setting z is [23] γ f (k) = π zλk 2. (2-31) In this equation z is the distance from exact focus. It is defined such that it is positive when the microscope is underfocused and negative when the microscope is overfocused. The focus error as a result of the spherical aberration can be partly compensated for by operating the microscope with underfocus [8]. The overall phase shift due to spherical aberration and defocus is γ micr (k) = γ s (k) + γ f (k) = πc s λ 3 k 4 /2 π zλk 2. (2-32) In Figure 2-3, the wave aberration function has been depicted as a function of spatial frequency for three defoci. Properties of the PCTF In section 2-7 the PCTF was defined as follows P CT F (k) = sin(γ micr (k)). (2-33) Based on the definition of γ micr in Eq. (2-32) the PCTF has been plotted for three defoci in Figure 2-4. In this figure we see that some spatial frequencies are transferred less strongly than others to the detected image. Also, due to the oscillating behaviour of the sine, the spatial frequencies are either transferred with a positive or a negative sign. The larger the defocus, the lower the spatial frequency at which the first zero crossing occurs.
28 2-9 Wave aberration function of the TEM 17 Figure 2-3: Wave aberration functions of the TEM, for several defocus settings. The larger the underfocus, the larger the phase-shift of the imaging system. The parameters used to compute this graph are stated in Table 3-1. Figure 2-4: The PCTF as a function of spatial frequency, for several defocus settings. The larger the defocus, the lower the spatial frequency where the PCTF crosses zero the first time. The parameters used to compute this graph are stated in Table 3-1.
29 18 Image formation 2-10 Concluding remarks In this chapter the derivation of an expression for the distribution of the intensity in the image plane for phase contrast microscopy was considered. The derivation is in terms of a few wavefunctions that describe the amplitude and phase of the electron waves in a certain plane, in terms of 2D spatial coordinates. The first assumption is that the object is illuminated by a plane wave. As a result of the interaction with the atoms in the specimen, the phase of the wavefunction in the exit plane of the specimen is not constant. The non-ideal properties of the imaging system are accounted for by a point spread function. The wavefunction in the image plane is the convolution of this point spread function and the wavefunction in the exit face of the specimen. The contrast in the detected images is the amplitude squared of the wavefunction in the image plane. Two object approximations were considered, the phase and the weak phase object approximation (POA and WPOA respectively). In the phase object approximation it is assumed that the object s potential only affects the phase, and not the amplitude of the illumination. For weak phase objects, it is further assumed that the local electrostatic potential only weakly varies and as a result the phase differences between the waves are small. With the WPOA, the distribution of intensity in the image plane is expressed by the convolution of the projected potential of the object and a function that resulted from non-ideal imaging conditions. Similarly in the Fourier domain, the image intensity distribution is linearly related to the projected potential. Disturbances to the imaging system are accounted for by an envelope function and the phase contrast transfer function (PCTF). Both affect the strength with which 2D spatial frequencies are present in the detected images. The envelope function accounts for differences in the imaging conditions for consecutive electrons and the PCTF originates from any additional phase shifts introduced by the imaging system. Important to note is that both the envelope function and the PCTF vary as a function of defocus. As a result, the content of images is dependent on the defocus setting. It is the expression for the intensity according to the WPOA, Eq. (2-28), that is used in the remainder of this thesis. For example, in the simulation study described in chapter 6, we simulate images based on the projected potential of the GroEL chaperone molecule while taking into account the microscope envelope function and the PCTF.
30 Chapter 3 Detected images 3-1 Introduction In the preceding chapter, the image intensity distribution in the detector plane w(r) was derived (Eq. (2-27)) based on the wave property electrons. When imaging with a transmission electron microscope an electron source is employed. From this source a flow of electrons is emitted. With a CCD camera, the number of electrons that arrive within each pixel is counted during the recording time. The distribution of the number of electrons counted is what forms the image. It is thus particles and not waves, that are detected. The intensity distribution distribution derived in chapter 2 describes the probability distribution for the electrons. With the CCD camera, a discrete image is formed from the electron counts. The detected image is discrete. In this chapter, the image intensity distributions of Eq. (2-27) and Eq. (2-28) are discretized. Using the definition of the electron dose as defined in section 3-2, the number of electrons that is expected to be detected at each pixel of the detector can be formulated. This is considered in more detail in subsection The electron counting at the detector is disturbed by Poisson noise. In section 3-6, the statistical properties of the noise are considered in more detail. Also, in this section the circumstances under which the Poisson noise can be approximated as Gaussian are considered. This approximation is useful when analysing the quality measures described in chapter 5 Finally, in section 3-7, the origin of registration errors is briefly introduced. This is a factor that will be discussed in great detail in the next chapter. The registration errors are another disturbance to the particle images in addition to that of the microscope envelope and phase contrast transfer function. 3-2 Electron dose The electron dose is defined as the expected total number of electrons that traverse a unit area of the object during the exposure time. This quantity is denoted by the symbol P A. A
31 20 Detected images typical value for the electron dose used in single particle analysis applications is 10e /Å 2 (or equivalently 100e nm 2 ), with e the charge of an electron in ev. Additionally, the electron dose per pixel P P is defined. Considering an area d 2 of the projection of an object, on average P P will traverse this unit area. This second definition is convenient when working with discrete images. The area d 2 is chosen such that it is the same size as a pixel of the discrete image. Both definitions of the electron dose express the number of electrons that the object is exposed to per unit area. They are related to each other as, P A = P P d 2, (3-1) with d the length of the pixels in object coordinates, in unit Å. For example, when the physical pixel size of the CCD camera is D = 24µm [3] and the magnification is set at M=150k it is easily calculated that d = D M = 1.6Å. There are two constraints on the electron dose. The biological molecules are damaged more when the electron dose per unit area, P A, is large. Thus from radiation damage considerations, P A should be minimised. On the other hand, from signal to noise considerations (the signal to noise ratio will be defined in section 5-2), the total number of electrons detected at each pixel, P P should be maximised. 3-3 Image discretization The image recorded with the CCD camera is discrete. It is for this reason that the expression for the image intensity distribution needs to be discretized. In this section, first Eq. (2-28) is discretized. After this, the definition of the fast Fourier transform operator is stated. This operator is used to relate the discretized spatial frequency intensity distribution to a real space equivalent. Finally, using the derived discretized intensity distribution, the expected electron count for each pixel of the CCD camera is stated Discretized intensity distribution in the Fourier Domain The intensity distribution is discretized as W = δ 2σΦ sin(γ )E, (3-2) with Φ the discretized projected potential. This potential is discussed in more detail in subsection The term δ in Eq. (3-2) is the discrete equivalent of the dirac delta pulse of Eq. (2-5) and is defined as { +N δ = 2, for i, j = c (3-3) 0, else with c the center of a square matrix of size N N, defined as, c = N 2 N is even c = N N is odd. (3-4)
32 3-3 Image discretization 21 We define the discretized envelope and wave aberration function as follows, with k i and k j discrete frequency vectors defined as D Fast Fourier transform E = E micr (k i, k j ), (3-5) γ = γ micr (k i, k j ), (3-6) k i = 1 d N (i N/2) {i = 1...N} k j = 1 d N (j N/2), {j = 1...N}. (3-7) The 2D Fast Fourier transform of a matrix a is computed in Matlab using the command fft2. This transform is defined as  = N N m=1 l=1 ( a ml exp 2πi N [(l 1)(j 1) + (m 1)(i 1) ] ), (3-8) Note that both i and i occur in the definition of the fast Fourier transform. The former is not an index, but the square root of minus one. The size of the matrices a and  is N N. The Fourier transform as it is defined here has the first and the third quadrant switched. This means that the lowest spatial frequencies are in the corners of  and the highest spatial frequencies are at the center of Â. For visual interpretation it is convenient to shift the zero frequency component to the center of the image. This is done using the command fftshift. Applying this command to  will switch the first and the third quadrant and the second and the fourth. Thus, the Fourier transform of a is defined as ) A = fftshift (fft2 (a )) = fftshift (Â. (3-9) The inverse Fourier transform is defined as a = 1 N 2 N N m=1 l=1 (  ml exp + 2πi N [(l 1)(j 1) + (m 1)(i 1) ] ) (3-10) and is computed in Matlab using the command ifft2. The factor 1 is a normalisation factor. N 2 In all the following, the fast Fourier transform relationship between a and A will be denoted as follows A ml = F{a } a = F 1 {A ml }. (3-11) Discretized projected potential The projected potential φ p in Eq. (2-28) is a continuous function in real space coordinates r. We downloaded the 3D potential of the GroEL molecule from the Protein Data Bank (PDB)
33 22 Detected images Figure 3-1: Discrete projected potential of the GroEL particle in the side-view. The colormap on the right, indicates the pixel values of the image. The numbers along the axes of the image are the indices [i, j] of the matrix φ. [29] and projected it to form the projected potential φ p. The discretized potential is related to the continuous in the following way, with discrete spatial frequency vectors defined as φ = φ p (x i, y j ), (3-12) x i = d (i N/2), y j = d (j N/2), {i = 1...N} {j = 1...N}. The variable d in this definition is the sampling distance and N N is the number of pixels of φ. Alternatively the discretized potential can be considered to be related to the continuous as, φ = 1 d 2 xi d x i 1 2 d yj d y j 1 2 d φ p (x, y)dydx, (3-13) The discrete Fourier transformed potential is related to that defined in Eq. (3-12) as Φ = F{φ ml }. (3-14) The projected potential of the GroEL molecule from the PDB is depicted in Figure 3-1. The projected potential corresponds to a side-view of the GroEL particle. The size of the GroEL particle in this view is approximately Å [22]. In the absence of aberrations, the projected potential φ of the GroEL particle has a size of approximately pixels. Each pixel thus corresponds to a length of approximately d = = 1.6Å (3-15)
34 3-3 Image discretization 23 A typical physical size of the pixels of a CCD camera is D=24µm [3]. Thus, the magnification is approximately, Magnification = D = = 150kX. (3-16) d 1.6 The magnitude of the pixel-values of the projected potential had to be normalized to a value that is typical for biological molecules. According to [21] for this type of specimens it holds that c 2 rms = 1 N N N 2 2σφ 2 = 0.05 ev 2 m 2. (3-17) i=1 j=1 In [21] this is referred to as the RMS-contrast. We normalize the projected potential such that Eq. (3-17) is satisfied Discretized intensity distribution Based on the preceding sections, the distribution of the intensity in the image plane is related to that stated in Eq. (3-2) as w = F 1 {W ml } = 1 2σF 1 {Φ ml sin(γ ml )E ml }. (3-18) This equation does not express the magnitude, but it does describe the distribution of the number of electrons detected at each pixel of the CCD camera Expected electron count at the CCD camera The intensity distribution can be interpreted as a probability distribution for each electron when it is normalized such that the total volume under the curve is one. The probability that an electron hits the pixel [i, j] is expressed by the normalized intensity distribution. xi d yj + 1 x i 1 2 d 2 d y j 1 2 w(x, y)dxdy d (3-19) w(x, y)dxdy The expected number of electrons at each pixel is the multiplication of the probability density function and the total number of electrons. The total number of electrons that penetrates the field of view is related to the electron dose per pixel by a multiplication with the total number of pixels within the field of view. P T = N 2 P P (3-20) In this equation, N 2 is the total number of pixels within the field of view. The expected number of electrons per pixel can be approximated by making a few assumptions. The first approximation we make is that the volume under the image intensity distribution surface is the multiplication of the pixel value and the pixel area. xi d yj d x i 1 2 d y j 1 2 d w(x, y)dxdy w d 2 (3-21)
35 24 Detected images Figure 3-2: This is a schematic illustration of the image intensity distribution w(x, y). The intensity distribution is discretized. The value of the discrete intensity distribution is that of the continuous at the center of the pixel. The pixel width is d. As indicated by the dotted line, the volume under the image intensity distribution surface is approximated as d 2 w. This approximation has been schematically illustrated in Figure 3-2. The integral of the curve w(x, y) (which represents a probability distribution and has been indicated in blue) can be approximated by the multiplication of the central pixel-value (dashed line) and the area of the pixel. Defining the spatial average of an image as a = 1 N 2 N i=1 j=1 N a, (3-22) the second approximation we make is that the spatial average of the image intensity distribution is approximately unity. w 1 (3-23) With these assumptions, the expected number of electrons per pixel is related to w and P P in the following way. f = xi d yj + 1 x i 1 2 d 2 d y j 1 2 w(x, y)dxdy d w(x, y)dxdy P T = xi d yj + 1 x i 1 2 d 2 d y j 1 2 N i=1 w(x, y)dxdy d P P N 2 w(x, y)dxdy w d 2 N j=1 w d P 2 P N 2 = w d 2 d 2 N 2 w P P N 2 w d 2 d 2 N 2 P P N 2 = w P P (3-24) The subscripts i and j are used to denote the pixel indices, {f ; i = 1...N, j = 1...N} in which N is the number of pixels along each side of the image. Thus, using the definition of Eq. (3-18), the expected electron count is approximately
36 3-4 Particle images 25 [ ] f = P P w = P P 1 2σF 1 {Φ ml sin(γ ml )E ml }. (3-25) In the following, attention is focussed on the interpretation of Eq. (3-25). First, imagine an object that is described as φ = 0 for all i and j. Then all the electrons penetrate through the object undeflected and the number of electrons counted at each of the detector pixels is P P. For weak phase objects it can be said in general that most electrons pass through the object unaffected by the object potential. Those electrons form a bright background (as described by the first term of Eq. (3-25)). The electrons that are influenced by the potential appear as dark regions in an otherwise bright field. The images are referred to as bright-field images for this reason. To be able to interpret the image intensity distribution as a probability distribution it is essential that the spatial average of w is approximately unity. In some regions w is slightly greater than one and in some regions it is slightly less. Considering Eq. (3-25) this can be interpreted as originating from the deflection of the electrons. The illuminating electrons are deflected by the object, but no electrons are lost in passing through the object. Unless it is assumed that w 1 the number of electrons in the system does not remain constant. 3-4 Particle images In single particle analysis, many particles are detected each recording. For the reconstruction procedure, the particles are boxed into windows that enclose only a single particle image. These windows we refer to as particle images. Each of the particle images is disturbed by noise. The boxed particle images form a dataset from which a reconstruction can be formed. In this thesis we assume that all particle images have the same projected potential. In addition, sub-pixel shifts are not considered and we assume that all particles have identical orientations. Therefore, for certain microscope settings, particle images only differ in their noise realization and all particle images have the same motif φ. In the remainder of this thesis, all the images are particle images Normalization The aim of the 2D single particle analysis is to form a reconstruction of the projected potential of the biological molecule from a group of particle images. The particle images are Poisson noise disturbed realisations of f (Eq. (3-25)) and are bright-field images. We denote the noisy images as f k, with k 1..M. For interpretation, it is useful to perform the following normalization to the simulated noisedisturbed particle images q k = f k /P P 1. (3-26) 2σ The particle images are first normalized for their electron dose. Subsequently, the constant background is subtracted. The motif that is common to all normalized particle images is an image of the projected
37 26 Detected images (a) (b) (c) Figure 3-3: In this figure three examples of aberrated potential p are depicted. The defocus settings for graphs (a), (b) and (c) are z = 120nm, z = 2067nm and z = 3981nm respectively. The colormap on the right of each image, indicates the pixel values of the image. The numbers along the axes of the images are the indices [i, j] of the matrix p. The parameters used to compute this graph are stated in Table 3-1. potential, aberrated by the PCTF and the envelope function. This motif will be referred to in this thesis as the aberrated potential p and is defined as p = 1 f /P P 2σ = F 1{ Φ ml sin(γ ml )E ml }, (3-27) with f as defined in Eq. (3-25). When simulating many particle images f k with the same microscope settings, each of the images will be a noise-disturbed realisation of p. When averaging over many such images, q k (as defined in Eq. (3-26)), in such a way that the motifs overlap perfectly, the average (q ) M = 1 M q k M, (3-28) will become equal to p in the limit of very many particle images. Thus, k=1 lim M (q ) M = p. (3-29) This is an important point. The matrix p is the aberrated potential as defined in Eq. (3-27). Averaging over many particle images, not the projected potential φ, but the aberrated potential is retrieved from many noisy realisations. In Figure 3-3 examples of simulated aberrated potentials for three different defocus settings are depicted. When comparing the graphs of the aberrated projected potentials to the original potential of Figure 3-1, it is seen that the aberrated potentials have both positive and negative values are blurred into an area of the detector that is larger than that of φ have a maximum pixel-value that is lower than that of φ The envelope function and the phase contrast transfer function thus have a spreading effect. It is for this reason that the motif p covers a larger area than φ. The larger the defocus,
38 3-5 Parameters 27 Parameter Symbol Value Defocus z nm Magnification 150k Pixel size in object coordinates 1.6 Å Electron dose per unit area P A 6 30e Å 2 Electron dose per pixel P P 15 77e pixel 2 Spherical aberration constant C s 1.2 mm Accelerating voltage V 0 300kV Electron wavelength λ 2.7 pm Proportionality constant WPOA σ Number of particle images averaged M 800 Table 3-1: Parameters used for all simulations done in this thesis. A range of defoci and electron doses are considered and thus in the figures the electron dose and defocus settings are indicated. the larger the blur. The size of the projected potential and the aberrated potentials depicted in Figure 3-1 and Figure 3-3 is = N N. The size of each f k is then also N N. In section it was stated that the projected potential φ p in the absence of aberrations is approximately 92 pixels wide and long. However, the images have a size N N and thus have a border of b = 32 around the projected potential to account for the blur. The size of this border seems reasonable from inspecting Figure 3-3, since the outer pixels of the aberrated potential only have a weak signal strength. A final remark in this subsection concerns the magnitude of p. In subsection it was stated that for biological molecules it is reasonable to assume that w 1. Since, w 1 2σp, this implies p Parameters The fundamental equation that describes the detected contrast is Eq. (3-27), with the envelope function and wave aberration function as defined in Eq. (2-29) and Eq. (2-32) respectively. The parameters for the simulation of the images are listed in Table 3-1. In all the remainder of this thesis it is these parameters that are used. 3-6 Noise The recorded images are disturbed by noise, due to Poisson counting statistics. Each image that is recorded at the same electron dose and defocus will be different due to this random disturbance. When recording a series of M images, each image f k ; {k = 1...M} can be considered a realisation of the corresponding random variable f. For each pixel [i, j] of this random variable, it holds that the expectation and the variance E[f ] = f, Var(f ) = f, (3-30)
39 28 Detected images with f the expected number of electrons per pixel. Since for biological molecules, the projected potential may be assumed to be weak, Eq. (3-18) can be approximated. E[f ] P P, Var(f ) P P. (3-31) Gaussian additive noise It is convenient to approximate the Poisson noise by Gaussian additive noise. This approximation is a reasonably good approximation as long as it holds for each pixel that [15] Referring to Eq. (3-31), this is approximately equivalent to E[f ] > 10. (3-32) P P > 10. (3-33) In section 3-2 it was stated that a typical electron dose is 10e /Å 2. For a magnification setting of 150k, this corresponds to P P = 16. Thus, for this magnification setting, the criterion of Eq. (3-33) is satisfied. It is assumed that the noise can be approximated by an additive contribution. Thus, q k = p + n k. (3-34) In this equation, p is a signal motif that is common to all images that have the same sin(γ ) and E. The term n k is a realisation specific to image k, of a Gaussian zero-mean noise source n. A suitable choice for the variance of n can be computed by relating the random variable q back to f, using Eq. (3-26). f = ( 2σq + 1) P P (3-35) The variance of f then is Var(f ) = 2 2 P 2 P σ 2 Var(q ) = 4P 2 P σ 2 Var(n ), (3-36) and the mean E[f ] = ( 2σE[q ] + 1) P P = ( 2σp + 1) P P. (3-37) Using Eq. (3-30) we find that Var(n ) = σ 2 n = ( 2σp + 1) P P 4P 2 P σ2 = 2σp + 1 4P P σ 2. (3-38) When it is assumed that p << 1 2σ, this reduces to Var(n ) = σ 2 n 1 4P P σ 2. (3-39) Thus, we assume the variance of the noise of each pixel is the same. When p 0, the spatial variation in the number of electrons expected to be detected is small (f P P ). Thus, the
40 3-6 Noise 29 (a) (b) (c) k are shown that are noise disturbed, for Figure 3-4: In this figure examples of particle images q the same defocus setting as in Figure 3-3, z = 120nm, z = 2067nm and z = 3981nm and with electron dose PP = 40. The colormap on the right of each image, indicates the pixel values of the image. The numbers along the axes of the images are the indices [i, j] of the matrix. The parameters used to compute this graph are stated in Table 3-1. noise variance can be assumed to be the same for each pixel of the image. The approximation of a weak signal strength p is reasonable, since biological molecules scatter only weakly [8]. k is considered a realisation of a random variable q. In the foregoing it was Each image q derived that 1 E[q ] = p Var(q ) = Var(n ) = σn2 (3-40) 4PP σ 2 In all the preceding, σ is the interaction constant, as defined in Eq. (2-20). It is important to realise that Eq. (3-40) states the expected value and variance of q for each pixel and is not the spatial average of a single image. k are depicted. The defocus setting for graphs In Figure 3-4 examples of particle images q (a)-(c) are the same as those in Figure 3-4. Note from these graphs that for low defocus the signal motif is hard to recognise Gaussian additive noise in the Fourier domain The equivalent of Eq. (3-34) in the Fourier domain reads Q = P + N. (3-41) Assuming the variance of q can be approximated as Gaussian with variance σn2 ( Eq. (3-39)) and mean µn = 0 for all pixels, it can be derived that the noise in the Fourier domain also has mean zero and variance, Var(N ) = σn2 N 2. (3-42) In this equation N 2 is the number of pixels and is a consequence of the normalization choice in the definition of the fast Fourier transform, Eq. (3-8) and Eq. (3-9) Noise variance of sample average When simulating a sample of M particle images, a sample average can be computed. Assuming each particle image only differs in its noise realization, the sample average corresponds to
41 30 Detected images (q ) M = 1 M M q k = 1 M k=1 M p + 1 M k=1 M n k = p + (n ) M (3-43) in which (q ) M is the sample mean of M particle images. The average is again a realization of a random variable. The variance of each pixel of the random variable (q ) M is, Var ( ( ) 1 M ) (q ) M = Var q k = 1 ( M M 2 Var M ) n k = 1 M 2 MVar( n k ) k=1 k=1 = 1 M σ2 n = 1 1 M 4P P σ 2. (3-44) It was assumed that the signal motif of the particle images overlaps perfectly. In chapter 4 the reconstruction from particle images for which the signal motif does not overlap perfectly is considered. Further, under the same assumption of perfect overlap, the expectation of the 2D averaged image is E [ [ ] 1 M ] (q ) M = E q k = 1 M E [ q k ] 1 M = p = p. (3-45) M M M k=1 Similarly, for the sample average in the Fourier domain the variance is Var ( (Q ) M ) = Var( 1 M k=1 k=1 k=1 M Q k ) = 1 M M 2 Var( N k ) = 1 M Var(Nk ) k=1 = 1 M σ2 nn 2 = N 2 M k=1 1 4P P σ 2, (3-46) and the expectation is E [ (Q ) M ] = E [ 1 M M k=1 Q k ] = 1 M M k=1 E [ Q k ] 1 = M M P = P. (3-47) k=1 3-7 Registration error With the electron microscope, an image is recorded that contains many particle images. This image is referred to as a micrograph. The locations of the particles in the micrograph are not regularly spaced. Therefore, when creating particle images for each of the particles in the micrograph (section 3-4), first the location of the particles has to be determined. Each particle is boxed into a frame of size N N pixels. In this way, many particle images are created from a single recorded micrograph. Thus far, it was assumed that each of these particle images can be described as the sum of an identical signal and a random noise contribution q k = p + n k. However, when the signal to noise ratio of the recorded micrograph is low, the location cannot be determined accurately
42 3-8 Concluding remarks 31 and some of the aligned particle images may not have the signal exactly in the center of their box. Instead, the signal is shifted (q k ) = p [i s k x,j s k y ] + n k, (3-48) with S k = [s k x, s k y] a registration error specific to image k. In this thesis only shifts that are a multiple of the pixel-size are considered. Although this is an unrealistic assumption it keeps the framework simple. The value of the particle image at pixel [i, j] is again the sum of the projected potential and a noise realization, but the signal component p is misaligned. The misalignment of particle images is considered in greater detail in section 4-3 of the next chapter. 3-8 Concluding remarks In this chapter, attention was focussed on describing a method to simulate discrete images based on the image formation outlined in chapter 2. The main difficulty is that images detected with a CCD camera are discrete while the derivation of the image intensity distribution in chapter 2 was in terms of the continuous variables r and k. First the image intensity distribution was discretized and we derived the expected electron count. The result is stated in Eq. (3-25). An important assumption for the derivation is that no electrons are lost in the imaging process. The number of detected electrons is Poisson noise disturbed. In section 3-6 it was outlined under which circumstances the Poisson noise can be approximated as Gaussian. Under the approximation of Gaussian noise, each normalized particle image can be described as the sum of the aberrated projected potential and a noise contribution. An important conclusion from this section is that each of the normalized particle images has a variance that is inversely proportional to the electron dose per unit area of a pixel. When a low electron dose is used the noise variance is high, some particle images cannot be aligned with high accuracy in this case and registration errors result. With registration errors, every normalized image is again described as the sum of the aberrated projected potential and a noise contribution, but in this case, the aberrated projected potential p is shifted. Finally, it is important to realize that we assume the registration errors are a multiple of the pixel-size.
43 32 Detected images
44 Chapter 4 Image reconstruction 4-1 Introduction In this thesis we consider the defocus as a parameter that can be optimized for the experimental design of single particle analysis. With a simulation study that mimics the actual reconstruction process realistically we are aiming to find the defocus for which the resolution is maximal, constrained to the electron dose setting. With the image formation described in chapter 2 and the discretization considered in chapter 3 we have the tools to simulate images of particles. Starting from a potential projected in a single direction, we create a simulated data set of particle images by convolving the projected potential with the microscope point spread function and adding a noise contribution. In this chapter we consider the procedure for reconstructing the 2D projected potential from a set of particle images. When taking the pixel-wise average over multiple particle images the signal to noise ratio of the reconstruction is higher than that of the individual images. Chapter 3 and this chapter provide the tools for simulating reconstructions in the simulation study. In the last chapter of this thesis, chapter 6, we outline how the quality of the 2D reconstruction varies as a function of defocus based on simulations. The 2D reconstruction procedure can be summarized by the following steps, Choose a setting for the electron dose and defocus. Simulate one reference image, f 0 ; i = 1...N, j = 1...N, that is a Poisson noise-disturbed realization of f as defined in Eq. (3-25) and Eq. (3-30). In the same way, simulate M = 800 images, f k ; i = 1...N, j = 1...N with k = 1...M. Determine the cross-correlation matrix of the images f 0 and f k. From the cross-correlation matrix calculate the required shift to align the particle images.
45 34 Image reconstruction Create aligned particle images (f k )aligned. Normalise the aligned particle images (f k )aligned according to Eq. (3-26). Take the 2D average of the aligned images, (q k )aligned to form the averaged image (q ) M. The first three of these bullet points have been discussed in the foregoing chapters of this thesis. In chapter 2, the influence of the defocus setting on the microscope s envelope and wave aberration function was discussed. The envelope and wave aberration function were discretized in chapter 3. Also, in this chapter, the properties of the particle images f k were discussed and a way to compute them from the projected potential was outlined. Thus, based on chapters 2 and 3, a hypothetical data set of particle images can be formed. In this chapter, the reconstruction procedure is described. First the cross-correlation algorithm is introduced. This algorithm is used to align particle images. In literature, other methods are also used for this purpose, but cross-correlation is the simplest method. Once the particle images are aligned, an average, or 2D reconstruction is computed. As is outlined in section 4-6, the 2D reconstruction can be described as a convolution product. 4-2 Cross-correlating two images With cross-correlation, the reference image f 0 is moved across another image f k. For each position, the pixel-values of the reference and the k th image are multiplied and summed. ρ = N N m=1 l=1 f 0 ml f k [N i+m,n j+l], for { i = 1, 2,.., (2N 1) j = 1, 2,.., (2N 1), with fml k = 0 for m, l < 1 and m, l > N. The size of both f 0 and f k is N N pixels. The size of ρ is (2N 1) (2N 1). When the signal to noise ratios are high, the cross-correlation function will have a maximum for the location where the motifs of the images exactly overlap. By finding the highest peak of ρ, the position of best overlap is found. For images f k with a low signal to noise ratio, the signal contribution to each image f k is very small compared to the noise. In this case, the highest peak may not correspond to the best overlap of the projected particle potential p of each of the particle images. As an example, consider two particle images that have the same motif. When both images are noiseless, the cross-correlation matrix will have a maximum for that pixel [i, j] for which the motifs overlap. In Figure 4-1(a), an example of a central row of the cross-correlation matrix has been depicted. The particle images were of size When the particle images are disturbed with noise, a cross-correlation vector such as that shown in Figure 4-1(b) may result. In this graph, the maximum does not occur for the same value as in (a). Thus, for noise-disturbed particle images, the peak of the cross-correlation matrix may not be at the same pixel as for noiseless particle images.
46 4-3 Aligned particle images 35 (a) (b) Figure 4-1: Example of the central row of a cross-correlation matrix. In graph (a), the particle images that are correlated are noiseless. In graph (b), the images are noise disturbed. For both graph (a) and (b) the motif of the particle images is identical. The x-axis indicates the shift between the particle images. When this shift is zero, the particle images overlap perfectly. 4-3 Aligned particle images The peak of the cross-correlation function determines the position of best overlap of the reference image f 0 with f k. Consider two images with a high SNR. When the two images have an identical noiseless signal, thus p r 1 = pr 2 = p, with p r the noiseless signal of each of the images, then the peak of the cross-correlation matrix occurs at the center. The center of the cross-correlation matrix corresponds to the indices i peak = j peak = N. Still considering images with very high SNR, the peak of the cross-correlation matrix will not occur at the center if one of the images has a noiseless signal that is shifted with respect to the other. For example, consider an image that has noiseless signal p r 1 = p and a second image that has a motif that is shifted with respect to that of the first image p r 2 = p [i+1,j] and pixel value zero for those pixels for which i = N. When cross-correlating the first image to the second, the peak of the cross-correlation function occurs at [i peak, j peak ] = [N + 1, N]. The shift S k = [s k x, s k y] that is required to align the particle images is determined from the location of the peak in the cross-correlation matrix. The shifts in the horizontal and vertical direction are related to the maximum of the cross-correlation matrix as s k x = i k peak N s k y = j k peak N (4-1) with [i k peak, jk peak ] the indices at which the peak of the cross-correlation product occurs. The 2 M vector S k may be considered an array of realisations of a random variable S. This random variable describes the probability that a certain registration error occurs. For the first example given in this section the required shift to align the particle images is S k = [0, 0], while for the second example the shift is S k = [1, 0]. The aligned particle image for the second example is (p r 2 )aligned = p r 2 [i s x,j s y] = pr 2 [i 1,j] = p. (4-2)
47 36 Image reconstruction Returning to the reconstruction procedure as it was outlined in the introduction, we assume the reference particle image f 0 and the particle images to be aligned f k have the same signal motif p and are not misaligned to start off with. When the required shift found from the cross-correlation procedure is S k = [0, 0], the algorithm aligned the images successfully. Any shift other than S k = [0, 0] is a registration error. We could instead have chosen to start with misaligned noisy particle images f k and then apply the registration procedure to result in a data set of aligned particle images that are better aligned relative to each other. However, we expect that the residual alignment error for a certain noisy particle image f k and the reference image f 0 after alignment is the same as that after the alignment of the particle image shifted by a shift [S 1, S 2 ], i.e. f[i S k 1,j S 2 ] and the reference image. Thus, we start with simulated particle images that are perfectly aligned and only differ due to noise and carry out the cross-correlation procedure to study the effect of registration errors on the reconstruction quality. This may be confusing, but the cross-correlation alignment procedure thus in fact has the effect of misaligning the particle images f k. However, it is only in simulations that the exact alignment is known. In practical applications, particle images f 0 and f k are misaligned. The alignment of particle images then needs to be done using a procedure such as that described in section 4-2. The aligned particle images that result after the alignment procedure have registration errors S k. The maximal horizontal and vertical registration error that is taken into consideration is 32 pixels to the left or the right. This choice is made to assure that there is always some overlap between the noiseless signal motif in the reference image and that in the image to be aligned. Effectively, we thus exclude the false detection of particles. To be able to do the shifting without excluding pixels of the original particle images f k, the aligned particle images need to have a larger dimension. To understand that this is the case, a graphical illustration has been depicted in Figure 4-2. In graph (a) an example of an aligned particle image that has a certain registration error S k has been depicted. In graph (b) an aligned particle image with S k = [0, 0] has been drawn. In grey, the original particle image f k is indicated. Due to the registration error, the particle image is shifted by Sk within the aligned particle image. The size of the aligned particle images, (f k )aligned, is N a N a. Taking a maximal shift of b = 32 pixels into consideration, it follows that N a = (2b + N) = 220, with N N is the size of each of the particle images f k. An aligned particle image is related to the noisy particle image f k as follows. (f k [b+s k x+i,b+s k y+j] )aligned = f k for 1 i N and 1 j N. (4-3) The aligned particle image f k of (f k )aligned for is defined for 1 i, j N. Thus, Eq. (4-3) defines the value max(b + s k x, b) i min(b + s k x + N, b + N) max(b + s k y, b) j min(b + s k y + N, b + N). (4-4) The min and max are required in this definition because s k x and s k y may be positive or negative. When there is no registration error, S k = [0, 0]. Filling this into Eq. (4-4), (f k )aligned is thus defined for b < i < (b + N) and b < j < (b + N). Considering Figure 4-2, this corresponds to graph (b).
48 4-4 Normalization of the aligned particle images 37 (a) (b) Figure 4-2: In this figure, two examples of aligned particle images are depicted. The outer frame encloses a particle image, while the inner grey frame indicates the projected potential p that is common to all particle images. When the grey frame is not in the center of the aligned particle image, it has a residual registration error. Thus, the aligned particle image in graph (a) has a registration error, while the particle image in graph (b) does not. The center of the aligned particle images has been indicated by the black dot. The 2D reconstruction is the average over multiple aligned particle images. The remainder of the pixels of (f k )aligned, which are not assigned a value in Eq. (4-3), are filled with Poisson noise with expectation P P. Effectively we thus assume that p = 0 for these pixels. 4-4 Normalization of the aligned particle images The next step in the reconstruction is the normalization of the aligned particle images. This is done in the way described in subsection The normalized aligned particle images are computed as follows. (q k ) aligned = (f k )aligned /P P 1 2σ (4-5) 4-5 The 2D average A reconstruction is the sum of the normalized aligned particle images. (q ) M = 1 M M (q) k aligned (4-6) k=1
49 38 Image reconstruction Each of the (q k )aligned can again be written as the sum of the motif and a noise contribution. Similarly to Eq. (4-3), the aligned motifs are created { (p k p for 1 i N and 1 j N [b+s k x +i,b+sk y +j])aligned = 0 else. (4-7) Referring to the motifs defined in Eq. (4-7) as aligned motifs is in analogy to the terminology aligned particle images the previous section. Again, the term aligned is in fact used to indicate that the motifs may be misaligned. The noise image is defined here as the normalized particle image minus the aligned motif. (n k ) aligned = (q k ) aligned (p k ) aligned. (4-8) The 2D average can be then written as the sum of the aligned particle images and the aligned noise images. (q ) M = 1 M (p k M ) aligned + 1 M (n k M ) aligned (4-9) k=1 In the next section an alternative way to describe the 2D average, or 2D reconstruction, is described. Similarly to Eq. (4-9), a reconstruction in the Fourier domain can be expressed as the sum of aligned particle images. k=1 (Q ) M = 1 M = 1 M M k=1 (Q k ) aligned M (P) k aligned + 1 M k=1 M (N) k aligned (4-10) k=1 In this equation, each of the images is related by the fast Fourier transform relationship, A = F { a ml }. The size of (Q ) M is N a N a. 4-6 Introducing an alternative notation for the 2D average The 2D average can equivalently be written as the convolution of a registration error matrix and the projected potential p. In this section, first the 2D convolution between two images is defined. Subsequently, the registration error matrix is defined. Finally, the definition of the 2D average is stated and an example is given D Convolution of images The 2D convolution of two images g and p is computed as c = N N g [N+1 m,n+1 l] p [i 1+m,j 1+l] (4-11) l=1 m=1
50 4-6 Introducing an alternative notation for the 2D average 39 If the size of g is N g N g and the size of p is N N; the size of c is (N g +N 1) (N g +N 1). The convolution operation is denoted using the symbol. c = g p (4-12) The matrix c in this equation is computed in the way defined in Eq. (4-11) Using the 2D convolution to describe registration errors Each aligned image can be expressed as the convolution of a filter and the aberrated potential p. The filter is a matrix b k specific to the k th image, that is constructed as follows. b k = 1 for [i, j] = [c + s k x, c + s k y] b k = 0 else (4-13) with c the center of a square matrix of size N N as defined in Eq. (3-4). The size of the matrix b k is N g N g = (2b + 1) (2b + 1). The aligned particle image corresponding to the registration error S k is the following (q k ) aligned = b k p + (n k ) aligned. (4-14) When S k = [0, 0], the matrix b k is the discrete equivalent of a delta function and the motif p is simulated in the center of the aligned particle image. The size of p as depicted in Figure 3-1 is N N = Defining a maximum shift b = 32 as before, the width and height of the image (q k )aligned is N a = N g + N 1 = (2b + N) = D Average Not only an aligned particle image, but also the 2D average can be described using the 2D convolution operator. Defining the matrix g as (g ) M = 1 M M b k, (4-15) k=1 the 2D average is (q ) M = c + 1 M M k=1 = (g ) M p + 1 M (n k ) aligned M (n k ) aligned. (4-16) The matrix g contains the registration errors of a group of images. The size of (g ) M is again (2b + 1) (2b + 1) and the size of the 2D average N a N a. k=1
51 40 Image reconstruction Example Each pixel of the reconstruction (q ) M contains information from several pixels of the motif p. Exactly which pixels, depends on the registration errors S k of each of the aligned particle images. Consider the reconstruction from 5 aligned particle images, (q ) 5 = k=1 (q k ) aligned When the registration errors S k of these 5 images are, S 1 = [0, 0] S 2 = [1, 0] S 3 = [0, 1] S 4 = [0, 0] S 5 = [0, 2] the reconstruction can be calculated as the 2D convolution between a filter g and the aberrated potential p. (q ) 5 = (g ) 5 p (n k 5 ) aligned, where denotes the 2D discrete convolution and (g ) 5 is a matrix that accounts for the registration errors. In the next section the definition of the convolution product is stated. In this example (g ) 5 is defined as, (g ) 5 = k=1 1/5 for [i, j] = [b, b + 1] 1/5 for [i, j] = [b + 1, b] 2/5 for [i, j] = [b + 1, b + 1] 1/5 for [i, j] = [b + 3, b + 1] 0 else and has size (2b + 1) (2b + 1). The pixel [i, j] = [b + 1, b + 1] is at the center of the matrix g. 4-7 Fourier transform of the reconstructed image A convolution in the real-domain can be expressed as a multiplication in the Fourier domain. However, for such an element-wise matrix multiplication, the size of the matrix (g ) M should be the same as that of the matrix p. In the following subsection, p, b k and (g ) M are padded, such that their sizes are N a N a.
52 4-7 Fourier transform of the reconstructed image Image padding In the following, the aberrated projected potential, p is padded with a border of zeros of width b pixels. This matrix will be referred to as p padded and is defined as follows. p padded = p for (b + 1) i (b + N) and (b + 1) j (b + N) p padded = 0 else (4-17) Also, b k and g are padded to a size N a N a. (b k ) padded = b k for (N a /2 b) i (N a /2 b + N g 1) and (N a /2 b) j (N a /2 b + N g 1) (b k ) padded = 0 else and (g padded ) M = g for (N a /2 b) i (N a /2 + b) and (N a /2 b) j (N a /2 + b) (g padded ) M = 0 else. The center of an N a N a matrix is N a /2. The matrix (g ) M is placed in the center of the (larger) matrix (g padded ) M Registration error matrix Fourier transforming the matrix b k for a registration error S k, an expression for the Fourier transformed registration matrix of a single image is obtained. (B k ) padded = F{(b k ml )padded } ( = fftshift e 2πi Na [(N a/2+s k y 1)(j 1)+(Na/2+sk x 1)(i 1) ]), (4-18) For the derivation of this equation, the definition of the fast Fourier transform, Eq. (3-8) was used. The size of the matrix (B k ) padded is N a N a. The matrix (B k ) padded is a phase shift specific to image k. Shifting the motif only alters the phase of the Fourier transform. A single aligned particle image can be expressed in the Fourier domain as the sum of the pixel-wise multiplication of the matrix (B k ) padded with (P ) padded and a noise contribution. (Q k ) aligned = (B k ) padded (P ) padded + (N k ) aligned. (4-19)
53 42 Image reconstruction Figure 4-3: The registration error matrix (G padded ) M may be considered an envelope function for the reconstruction. Plotted here is the radial average of the matrix (G padded ) M for positive spatial frequencies, with M = 800. The electron dose for this graph is P P = 15. The parameters used to compute this graph are stated in Table 3-1. The registration error matrix of a group of images is defined similarly to the real-space equivalent. M (G padded ) M = F{(g padded ) M } = (B k ) padded (4-20) Equivalently, this matrix can be calculated as k=1 (G padded ) M = F{(g padded ) M } (4-21) The registration error matrix (G padded ) M can be considered an envelope function for the reconstruction very similar to the coherence envelope. A difference between the two is, however, that partial coherence limits the resolution of each of the detected images while the registration error matrix only limits the resolution of the reconstruction. In Figure 4-3 the envelope function due to registration errors is depicted for several values of the defocus and a certain electron dose for a reconstruction of the GroEL chaperone motif D Average The Fourier transform of the reconstruction can be calculated as (Q ) M = (G padded ) M P padded + 1 M (N k M ) aligned = (G padded ) M P padded where the capital letters represent Fourier transformed quantities. k=1 + (N ) M (4-22) Example In Figure 4-4, the two examples of real-space registration matrices and their Fourier transformed equivalents are drawn for a 2D reconstruction of the GroEL chaperone projected
54 4-8 Correcting for the PCTF 43 (a) (b) (c) (d) Figure 4-4: Examples of the registration error matrices (g ) M and (G padded ) M for the projected potential of the GroEL chaperone, with M = 800. In graphs (a) and (b) examples of real space registration error matrices are shown, while in graphs (c) and (d) the Fourier registration error matrices corresponding to those of graphs (a) and (b) have been depicted. The natural logarithm of the real space registration matrix (g ) M has been drawn in (a) and (b). The colormap indicates the grey values of the graphs and the values along the axes number the pixels of the images. We show in these graphs that the wider the registration error in the real domain, the less wide the Fourier registration matrix and vice versa. The electron dose of graphs (a) and (c) is P P = 15 and for graphs (b) and (d) P P = The defocus is z = 3967nm for all graphs. The parameters used to compute this graph are stated in Table 3-1. potential. We note that the wider the distribution of the registration errors in real space, the less wide the distribution in Fourier space. Further, the distribution of registration errors is asymmetrical. There are larger registration errors in the vertical direction than in the horizontal direction. We expect that this may be consequence of the periodicity of the projected potential in the vertical direction. 4-8 Correcting for the PCTF The images are aberrated by the envelope function and the PCTF, but of these two disturbances the PCTF has the strongest biasing effect. It causes some of the regions for which the intensity was strongly positive to have a negative value; diminished contrast for patches of constant intensity and enhanced edges. All these effects make the interpretation of the images very difficult and for this reason, mostly a correction for the PCTF is performed in
55 44 Image reconstruction single particle applications. There are different approaches for the correction. In one of these approaches, only a correction for the sign of the PCTF is done [8]. This is referred to as phase flipping. For all spatial frequencies for which the PCTF is negative, it is multiplied by minus one. The idea behind this is as follows; the zeros of the PCTF occur at different spatial frequencies, for different defocus settings. When averaging the corrected PCTF s from different defoci, it is assumed that the average over all corrected PCTF s will have a fairly constant (and non-zero) amplitude. Ideally, the corrected PCTF of the reconstruction is one for all spatial frequencies. Another approach is to not only correct for the sign of the PCTF, but additionally for the amplitude. This can be done by applying a Wiener filter [8]. The spatial frequencies for which the particle images do not contain any information related to the object (due to the zeros of the PCTF) cannot be restored. However, the spatial frequencies that are transferred with diminished magnitude are amplified by the Wiener filter. The Wiener filter can either be applied to the images or to the reconstruction. For the reconstructions the filter is defined as follows. Writing the reconstructions as (Q ) M = (G padded ) M E padded sin(γ ) Φ padded + (N ) M = H Φ padded + (N ) M (4-23) with H the multiplication of the disturbances; the envelope functions G and E and the PCTF, the Wiener filter is defined as [8] S = H H H + 1. (4-24) SNR The corrected reconstruction is the multiplication of the filter matrix S and the Fourier transformed reconstruction, ( Q ) Wiener Filtered = S ( Q ) M. (4-25) In the definition of the Wiener filter, Eq. (4-24), the term 1 SNR is there to prevent the noise to be amplified in regions where H 2 is small. When H 2 >> 1 1 SNR for a certain [i, j], the term SNR may be neglected and the filter is approximately S = 1 H and the amplitude of this pixel is restored fully. However, when H 2 << 1 SNR for a certain [i, j], the signal for this pixel of ( Q ) M is very weak and cannot be restored unless the noise is amplified strongly at the same time as well. The Wiener filter thus restores the spatial frequencies that are transferred with a diminished amplitude as long the SNR is sufficiently high. In Figure 4-5 examples are depicted to illustrate the effect of Wiener filtering on reconstructions for two defoci. We conclude that visually the quality of the reconstructions is greatly improved by Wiener filtering for both reconstructions. The highest spatial frequency that can be restored is that spatial frequency for which H 2 is greater than 1/SNR. As is illustrated in Figure 4-6 it is reasonable to assume that this spatial frequency is mainly determined by the envelope functions. Or at least, for those spatial frequencies for which (G padded ) M 2 E padded 2 is smaller than 1/SNR, the spatial frequencies of the image additionally aberrated by the PCTF most certainly is smaller than 1/SNR.
56 4-8 Correcting for the PCTF 45 (a) (b) Figure 4-5: The graphs in this figure are Wiener filtered images. The electron dose of both graphs is P P = 40 and the defocus is z = 2067nm for graph (a) and z = 3981nm for graph (b). Comparing these graphs to the uncorrected images depicted in Figure 3-3 (c) and (d) and the projected potential depicted in Figure 3-1, we conclude that the Wiener filtered images are visually more alike the projected potential. Although still ring effects are seen, the light regions in these graphs mostly correspond to light areas in Figure 3-1 and similarly for dark areas. The parameters used to compute this graph are stated in Table 3-1. Figure 4-6: In this graph radial average of the multiplication of the envelope functions G and E is drawn in blue and the radial average of the function H is depicted in red. From this graph we conclude that the maximum spatial frequency for which the red curve is equal to 1/SNR cannot be larger than that for which the blue curve is equal to 1/SNR.
57 46 Image reconstruction To keep the analysis simple in this thesis we decided to assume that the PCTF can be corrected for fully up to the spatial frequency that the envelope functions become smaller than 1/SNR. From the foregoing discussion and illustrations we find it interesting to focus on this specific case. Although the approximation that the PCTF can be corrected for completely (for example by a Wiener filter) may not be so good in some instances it does mean the framework is much simpler. Since this thesis is the first step towards a full-scale investigation of optimal settings for single particle analysis it is desirable to consider a limited number of parameters and effects. In work following up this thesis it is interesting to investigate how the Wiener filter can best be applied and to again determine an optimal defocus setting given the electron dose. Assuming the PCTF can be fully corrected for, the reconstruction is described as ( Q ) M = (G padded ) M ( P ) padded + ( N ) M, (4-26) with ( P ) padded = (Φ ) padded (E ) padded. In much of what follows we will assume the reconstructions after PCTF-correction are given by Eq. (4-26). 4-9 Concluding remarks In this chapter, the reconstruction procedure was described. To form a 2D reconstruction, the particle images have to be aligned. All particle images are aligned to the same reference using 2D cross-correlation. We choose to use a noise disturbed image from the data-set as a reference. The aligned particle images are averaged pixel-wise to form a reconstruction. The reconstruction can be described as the convolution between a matrix that describes the registration errors and an image of the signal motif common to all particle images, Eq. (4-16). Equivalently, the reconstruction can be described as the multiplication of a matrix that describes the registration errors and an image of the signal motif common to all particle images in the Fourier domain, Eq. (4-22). An important assumption we make is that the PCTF of the reconstruction can be corrected for fully. Thus, after correction, P CT F = 1 for all [i, j]. The motivation for this choice is to keep the framework simple and the number of tuneable parameters limited. After PCTF-correction the reconstruction is assumed to be described by Eq. (4-26).
58 Chapter 5 Measures describing the quality of a reconstruction 5-1 Introduction In this chapter measures that describe the quality of the reconstruction are discussed. The first is the signal to noise ratio (SNR), a measure that describes how strong the object related information is in proportion to the random disturbances present in all the images. Not only does the signal to noise ratio improve when averaging over multiple images, also the setting of the defocus will influence how much contrast there is in the reconstruction. The SNR is defined in section 5-2. Low SNR-images will have registration errors. The magnitude of such registration errors influences the amount of blur in the reconstruction and thus is directly related to the quality of the reconstructions. The severity of the impact of the registration errors on the quality of the reconstructions can be qualified by the variance of the registration errors, but additionally the width of the registration error matrix (G padded ) M is interesting to consider. In section 5-3 the Full Width at Half Maximum (FWHM) is introduced to define the width of the pass-band of a matrix. The mean squared error (MSE) is a measure that is often used in the field of statistical signal processing to define the quality of an estimator. The MSE takes into account both bias and variance aspects of a reconstruction and is defined in section 5-4. The Fourier Ring Correlation (FRC) and the Spectral Signal to Noise Ratio (SSNR) are measures especially common in the field of single particle analysis. The Fourier Ring Correlation (FRC) describes, in the Fourier domain, how well two reconstructions correlate and the Spectral Signal to Noise Ratio (SSNR) expresses, as the name suggests, the signal to noise ratio in the Fourier domain. The reason that these latter two measures are so commonly used is that no knowledge of the true projected potential is required. In subsections and approximate expressions are derived for the FRC and the SSNR. The last quality measure that will be considered is the information limit, a measure that is often used in the high resolution TEM field. The information limit indicates the largest
59 48 Measures describing the quality of a reconstruction spatial frequency component present if the envelope function and noise contributions limit the resolution. In this way, each envelope function is associated with a resolution figure. In the last section of this chapter, the equations for the resolution according to the FRC, SSNR and information limit are compared. In the next chapter (chapter 6) we test how well the approximations derived in this chapter hold for a data-set of simulated images of the GroEL chaperone. Further we will then use the quality measures to see if there is an optimal defocus setting for the data-set given an electron dose. 5-2 The signal to noise ratio There are many definitions for the SNR of images in literature. In [8], the signal to noise ratio is defined as the ratio of the signal variance to the noise variance, SNR = ω2 s ω 2 n (5-1) with ω 2 s the spatial signal variance and ω 2 n the spatial noise variance of a single image. The spatial signal variance ω 2 s is defined as ω 2 s = 1 N 2 N i=1 j=1 with p the noiseless image and the spatial average signal value p = 1 N 2 N [p p ] 2, (5-2) N i=1 j=1 The prefactor is 1 N 2, since the average is taken over N N pixels. The spatial noise variance, ω 2 n, is defined equivalently to ω 2 s. with the spatial average noise value ω 2 n = 1 N 2 N i=1 j=1 n = 1 N 2 N p. (5-3) N [n n ] 2, (5-4) N i=1 j=1 N n. (5-5) It is convenient that the SNR as defined in Eq. (5-1), is quantified by a single value for the entire image. The noise is a stochastic disturbance, that can be assumed to have the same variance for all pixels (Eq. (3-39)). As long as the number of pixels of the image is fairly large, the spatial noise variance of an image is the noise variance of each pixel. ω 2 n σ 2 n = 1 4P P σ 2 (5-6)
60 5-2 The signal to noise ratio 49 The noiseless signal p, however, is deterministic. Its spatial variation across the image is not caused by a random disturbance, but depends on the projected potential distribution and the point spread function of the electron microscope. Referring to Eq. (5-2) as a variance may thus be confusing, since there is no stochastic nature to the variation. We defined each pixel of an image as the sum of a signal and noise component, Eq. (3-34). Thus, in fact the signal to noise ratio may be defined for each pixel as the ratio of the signal power and the noise variance. SNR = E[(q )] 2 (5-7) Var(q ) Based on Eq. (3-40) this can be approximated as SNR = (p ) 2 Var(n ) = (p ) 2 /σ 2 n (p ) 2 4P P σ 2 (5-8) The definition of Eq. (5-7) corresponds to a more conventional approach as that given in Eq. (5-1). Taking the spatial average of Eq. (5-8) according to Eq. (5-3), SNR = (p ) 2 4P P σ 2, (5-9) it is seen that in fact the spatial average of SNR is the same as Frank s definition, Eq. (5-1) when it holds that p 0 and the number of pixels N 2 is large. In this case ω 2 s (p ) 2, (5-10) In the remainder of this thesis we use Eq. (5-1) as the definition of the SNR. It is important to note that the signal to noise ratio is highest when a large electron dose is used SNR of sample average As was stated in section 3-2, the radiation damage is minimised for small electron doses. Small electron doses, however, result in small signal to noise ratios of the particle images q k. When averaging many noise-disturbed images, an average with a higher SNR is obtained. That this is the case can be understood from considering the variance and expectation of the sample average. In section it was derived that Var ( (q ) M ) = 1 M σ2 n, E [ (q ) M ] = p. The variance and expectation of an image q k are Var ( q k ) = σ 2 n E [ q k ] = p. (5-11) Thus, the variance of (q ) M is lower, while the expectation is the same as that of an individual particle image. The signal to noise ratio of the sample mean is thus higher. In all the foregoing it was assumed that for each particle image it holds that q k = p + n k. In other words, the images only differ in their noise realization and have the same signal motif p.
61 50 Measures describing the quality of a reconstruction Figure 5-1: Examples of realizations of three different estimators of the center of the circular disk. The estimator on the left is unbiased and has a small variance. The middle also has a small variance, but is biased, while the right is unbiased but has a larger variance. From [4]. 5-3 Full Width at Half Maximum The resolution of the corrected aberrated potential is limited as a consequence of registration errors and partial coherence. Examples of E and (G padded ) M were depicted in Figure 2-2 and Figure 4-3 respectively. As we see in these figures, the envelope functions are low pass filters. For the partial coherence, the width of the pass-band is directly related to the defocus. The greater the defocus, the smaller the width. For the registration errors, the relation between the defocus and the width of the pass-band is not so straightforward. To be able to quantify the width of the registration error envelope function we introduce the full width at half maximum (FWHM). It is defined as the distance between points on the curve at which the function reaches half its maximum value [31]. 5-4 Mean squared error It is common to quantify the quality of an estimator by the mean squared error (MSE). This measure takes account of both bias and variance aspects. In Figure 5-1, three examples of realizations of an estimator are depicted. Not only the bias, the expectation of the difference between the estimator and the true value, is of importance. Also, when the variation between several realizations of the estimator is large, the precision of the estimator is not very good. An estimator with a low MSE has both low bias and low variance. The quantity being estimated in this thesis is the projected potential. The reconstruction is an estimate of the projected potential. The reconstruction has a bias due to the registration errors of the particle images and the transfer function of the microscope. When forming several reconstructions from the same number of particle images, the reconstructions will be slightly different. For reconstructions from M particle images, the variation is due to the noise and the noise-induced registration error matrices (g ) M.
62 5-4 Mean squared error 51 Definition of the MSE The quality of a reconstruction can be characterised by the mean squared error (MSE). The MSE of an estimator ˆθ M of a quantity θ 0 from M measurements is defined as [4] ] MSE(ˆθ M ) = E [(ˆθ M θ 0 ) 2. (5-12) This can be expanded as [4] ] MSE(ˆθ M ) = E [(ˆθ M E[ˆθ M ] + E[ˆθ M ] θ 0 ) 2 [ 2 ( ) 2 [ = E ˆθ M E[ˆθ M ]] + E[ˆθ M ] θ 0 + 2E (ˆθM E[ˆθ M ] )( ) ] E[ˆθ M ] θ 0 [ 2 ( ) 2 = E ˆθ M E[ˆθ M ]] + E[ˆθ M ] θ (5-13) The second term of the last line is a bias term. The first term expresses the variance of an estimator ˆθ M. Thus, [4] MSE(ˆθ M ) = Var (ˆθM ) + [ Bias (ˆθM )] 2 (5-14) After this general definition of the MSE we will now focus specifically on the bias and variance of reconstructions. In sections and we explain how the bias and variance are computed Bias In line with the above definition of a general estimator ˆθ M, a reconstruction from M particle images can be interpreted as an estimator of the projected potential. The bias of a reconstruction is thus is defined as Bias [ (q ) M ] = E[(q ) M ] (φ ) padded. (5-15) The padded projected potential in this equation is formed by padding the projected potential φ using Eq. (4-17). Since the expectation of the noise is assumed to be zero, the expectation of the reconstruction is E[(q ) M ] = E[g ] p (5-16) This was based on the definition of the reconstruction, Eq. (4-16). The bias then is Bias [ (q ) M ] = E[g ] p (φ ) padded, (5-17) with g the matrix that contains the registration errors of all particle images. Even when there are no registration errors, the reconstruction is still biased. This is due to the transfer function of the microscope. The envelope and phase contrast transfer function introduce a bias for every pixel. A problem with the bias definition of Eq. (5-17), is that the expected
63 52 Measures describing the quality of a reconstruction value of the registration error matrix g is unknown. We approximate the expectation of g by the registration error matrix for a large number of particle images. Thus, Bias [ (q ) M ] (g ) M p (φ ) padded, (5-18) where (g ) M is a registration error matrix for a reconstruction from M particle images (with M large). Each pixel of the reconstruction has a value for the bias that is either positive, negative or zero. Based on Eq. (5-14) we label a reconstruction with a value for the bias squared. All values of the bias matrix are squared and summed. Every pixel that has a bias, either positive or negative, contributes to the overall bias Variance Based on the definition of the MSE in Eq. (5-13), the variance of the reconstruction is defined as follows. Var [ (q ) M ] = E [(q ) M E[(q ) M ]] 2 (5-19) There are two reasons why there is variation between two reconstructions formed from the same number of particle images. The first reason is noise and the second is that the images have registration errors. The variance of each pixel of the reconstruction due to the noise is 1 M σ2 n. The variation as a consequence of the registration errors can not be stated so easily and is more difficult to understand. For each reconstruction the ensemble of registration errors will be slightly different. Convolving with slightly different registration error matrices means the reconstructions will differ thus causing variation. When forming R reconstructions, the expectation of these reconstructions may be approximated as follows. E[(q ) M ] 1 R = 1 R R E[(q r ) M ] Using this approximation, the variance is estimated as follows. Var [ (q ) M ] 1 R R r=1 r=1 R (g) r M p (5-20) r=1 [ (q r ) M 1 R R ] 2 (g) r M p (5-21) For each defocus and electron dose, M = 800 particle images were computed. Every particle image had a value for the registration error and these registration errors were saved as an array, S k, of size 2 M. For the variance calculation R reconstructions are required and we thus created additional groups of M particle images. The simulation of large numbers of particle images is computationally demanding. The alignment using cross-correlation is the step that consumes the most time. Therefore, instead of carrying out the registration procedure for the additional particle r=1
64 5-5 Fourier Ring Correlation 53 images, it is assumed that the matrix S k is representative. If the particle images are most likely to have a certain registration error, then the registration error array will have this value for many k. Thus, we assumed that the probability that a certain registration error results can for large M be reasonably well approximated by the number of times that it occurs in the array S k divided by M. For each defocus, R reconstructions are made. Each reconstruction is formed from M particle images, that have registration errors that are randomly chosen from the array S k. Each reconstruction R differs in its realization of the matrix (g r ) M and a random noise contribution. Both are a source of variation between the reconstructions. The variance is computed using Eq. (5-21). Just as with the bias, the pixels of the variance matrix are summed, to quantify each reconstruction by a single value for the variance Sample variance Although the sample variance is not used in the definition of the MSE, the sample variance is useful later in the definition of the SSNR. The sample variance is a measure that expresses the variation within a data set. The value of a pixel [i, j] of each aligned particle image is different due the noise and registration errors. The sample variance expresses the variation between aligned particle images that are used to form a reconstruction. In this thesis, the sample variance is defined as follows. SampleVar [ (q ) M ] = ( (q k )aligned (q ) M ) 2 = 1 M M k=1 ( (q k ) aligned (q ) M ) 2. (5-22) The difference between variance as it was defined in the preceding section and the sample variance is that the former expresses the variance of the estimator of the projected potential, whereas the sample variance expresses the variability within the data-set. The measures, however, have the same origin, namely noise and noise-induced registration errors. In fact, the sample variance may be used as an approximation of the variance of a random variable that represents a single particle image. Writing an aligned particle image as (q ) aligned = b p + (n ) aligned, (5-23) the variance can be approximated by the sample variance. Thus, ) Var ((q ) aligned 1 M 5-5 Fourier Ring Correlation M k=1 ( (q k ) aligned (q ) M ) 2. (5-24) In this section, first the radial average is defined, subsection This command is used in the computation of both the Fourier Ring Correlation (FRC) and, in the next section, the Spectral Signal to Noise Ratio. The radial average is the average of pixels along rings of a
65 54 Measures describing the quality of a reconstruction 2D image. In subsection 5-5-2, the definition of the FRC is stated and in the subsection that follows two approximations of the FRC are derived. Finally, in subsection an example of an FRC curve is depicted and in subsection it is outlined how an FRC curve can be associated with a single value for the resolution Radial average The radial average is of an N a N a matrix G is defined as radial average RadAvg(G ) = Gm = 1 K round( i 2 +j 2 )=m = G, for m = 1,..., N a 2 (5-25) with K the number of pixels in the ring that has a radius of m pixels. The command round(a) is used to indicate that the argument is rounded to the nearest integer. For example, round(a) = 1 for 0.5 a < 1.5 With the command RadAvg the average of pixels that have the same radial distance to the center is computed. This definition is especially useful when the field G of which the radial average is computed is radially symmetric about the center. The radial average is a way of representing a 2D matrix in 1D. The number of pixels that contribute to the average of a certain spatial frequency, or ring, is not constant. The larger the radius of a ring, the larger the number of pixels over which the average is computed. The corners of a matrix have the largest radial distance to the center of a matrix. However, only the corners of the matrix have this large radial distance and thus the radial average runs over a smaller number of pixels again. We compute the radial average only for round( i 2 + j 2 ) Na 2. Thus, the radial distance cannot be larger than half the number of pixels of the square matrix. Beyond this radial distance, the number of pixels in a ring begins to decrease. The radial average has length Na 2 and corresponds to the positive spatial frequencies, k m+ Na 2 for m = 1,..., N a 2. (5-26) The spatial frequency vector k i was defined in Eq. (3-7) Definition of the FRC The bias definition assumes knowledge about the true image. In practice such a quantity is not known. Different measures for the quality of the reconstruction then are required. In the field of single particle analysis many such measures for the quality of a reconstruction exist. One of these measures is the Fourier Ring Correlation [10]. The FRC expresses the correlation along rings in the Fourier domain between two reconstructions, each computed from half the data-set of particle images.
66 5-5 Fourier Ring Correlation 55 The Fourier Ring Correlation is defined as [10], ( Re [i,j] B (Q1 ) M/2 ((Q 2) ) ) M/2 FRC m = { [i,j] B (Q1 ) M/2 2 } 1/2, (5-27) [i,j] B (Q2 ) M/2 2 with B a ring of Fourier space and (Q r ) M/2 a reconstruction with label r formed from M/2 particle images. The m is an index that corresponds to the frequency band B. The length of the vector FRC m in this definition depends on the width of the frequency bands. We compute the FRC using the definition of the radial average. Using this definition, ( [ Re RadAvg (Q 1 ) M/2 ((Q 2) ) ]) M/2 FRC m = { RadAvg [ (Q 1) ] M/2 2 RadAvg [ (Q 2) ]} 1/2. (5-28) M/ Approximate expressions for the FRC In the following, we derive three different approximations for the FRC. In chapter 6, the validity of the approximations is tested. First approximation Using the definition of Eq. (4-22), each of the reconstructions can be formulated as (Q r ) M/2 = (G padded,r ) M/2 P padded + 1 M/2 (N k M/2 ) aligned (5-29) The multiplication in the numerator of Eq. (5-27) is approximated as ( ) ) (Q 1 ) M/2 (Q 2 ) M/2 P padded 2 (G padded,1 ( ) M/2 (G padded,2 ) M/2. (5-30) In this equation it was assumed that the noise terms N k are independent of each other and zero mean. To approximate the denominator of Eq. (5-27) it is useful to first approximate (Q r ) M/2 2. This we do as follows. k=1 (Q r ) M/2 2 = (G padded,r ) M/2 P padded + 1 M/2 (N k M/2 ) aligned 2 (G padded,r (G padded,r (G padded,r ) M/2 2 P padded 2 + ) M/2 2 P padded 2 + k=1 M/2 1 (M/2) 2 1 (M/2) 2 ) M/2 2 P padded 2 + σn 2 N 2 a M/2 k=1 M/2 (N k ) aligned 2 (N k ) aligned 2 k=1 (5-31)
67 56 Measures describing the quality of a reconstruction In the first line it is assumed that the noise is uncorrelated with the noiseless signal. Subsequently it is assumed that each of the noise realizations N k is uncorrelated with the others. And finally, in the last line the sum of the noise terms is related to the noise variance σn. 2 In section 3-6-2, it was stated that the noise variance in the Fourier domain is scaled by the number of pixels squared; Var ( (N ) aligned) = σn 2 Na 2. Further, we note that 1 (M/2) 2 Var( M/2 k=1 ( N k ) aligned) = 1 M/2 Var( (N k ) aligned). (5-32) The last term of Eq. (5-31) is an approximation of the noise variance, assuming the noise is zero-mean. Using the approximations of Eq. (5-30) and Eq. (5-31), the FRC now reads ( [ Re RadAvg P padded FRC m = { [ (G padded,1 RadAvg 2 (G padded,1 ) M/2 2 P padded ) M/2 ( (G padded,2 ) M/2 ) ]) 2 + σn 2 N 2 a M/2 1 { [ RadAvg (G padded,2 ) M/2 2 P padded 2 + σn 2 ]} 1 2 N 2 a M/2 ]} 1. (5-33) 2 Mind that the second line of this equation is multiplied with the first. Further, the denominator of the first and second line only differ in the matrix (G padded,r ) M/2. In chapter 6 we consider how well Eq. (5-33) approximates the FRC. If it turns out that it is a good approximation, this has computational advantages for the simulations done in this thesis. First of all, the data that has to be stored is greatly reduced. Instead of having to save M particle images, only the shift vector S k has to be saved, for each defocus and electron dose combination. From the shift vectors, the registration error matrices can be computed. Calculating the FRC using the approximate definition also is considerably faster. These computational advantages, however, only hold within this theoretical study, where the true potential and registration errors are known. Second approximation Having derived Eq. (5-33), we wonder how large the influence is of the different G padded,r. When the number of particle images is large (M is large), the registration matrices are very similar. It may thus be suggested that Eq. (5-33) can be approximated as ( [ ( ) Re RadAvg P padded ]) 2 (G padded ) M (G padded ) M FRC m = = [ ] (G padded RadAvg ) M 2 P padded 2 + σn 2 Na 2 M/2 [ ] RadAvg P padded 2 (G padded ) M 2 [ RadAvg (G padded ) M 2 P padded ], (5-34) 2 + σn 2 N 2 a M/2
68 5-5 Fourier Ring Correlation 57 Figure 5-2: The unbroken line is an example of an FRC-curve as a function of spatial frequency. The defocus is z = 3981nm and the electron dose is P P = 40. The dotted line indicates a cut-off of W FRC = 0.5 for determining a single resolution value for the FRC-curve. In this case the resolution is ρ FRC = 1.2nm 1. with (G padded ) M the registration error matrix due to all particle images. Thus, for this approximation we assume that (G padded,1 ) M/2 (G padded ) M and (G padded,2 ) M/2 (G padded ) M. A remark with respect to Eq. (5-34) is that the FRC as it is approximated here is real-valued Example of an FRC-curve The FRC describes the discrepancy between two reconstructions [8]. In this example, two reconstructions are formed, that are each formed from 400 misaligned particle images. The FRC is computed using the definition of Eq. (5-28). In Figure 5-2, an example of the FRC as a function of spatial frequency is plotted. For low spatial frequency, the FRC between two different reconstructions is close to one which implies that the phases of the two reconstructions are highly correlated. On the other hand, for high spatial frequencies, the FRC is zero and thus the phases of the reconstructions are uncorrelated [8]. This is a consequence of the fact that hardly any signal related to the object is present at high spatial frequencies and the noise is uncorrelated Expressing the resolution based on the FRC-curve It is convenient to derive a single value from the FRC-curve that expresses the resolution of the reconstruction. A cut-off value W FRC is defined. The spatial frequency for which FRC m is smaller than W FRC is defined as the resolution. For the FRC, we use a cut-off of W FRC = 0.5. This value is one of the thresholds that is used in literature [8]. For the example outlined in the previous section, Figure 5-2, the resolution, is ρ FRC = 1.2nm 1. Aimed is at the highest resolution in nm 1.
69 58 Measures describing the quality of a reconstruction The lowest m for which FRC m < W FRC (5-35) is determined. This index we refer to as m FRC. The resolution ρ FRC then corresponds to the spatial frequency ρ FRC = k i for i = m FRC. (5-36) In this equation, k i is the discrete spatial frequency vector as defined in Eq. (3-7). When FRC m > W FRC up to a high spatial-frequency, the resolution is good. It is noted that the resolution is dependent on which cut-off value is used. The resolution graphs depicted in the last chapter are specific to the choice W FRC = 0.5 for the threshold. 5-6 Spectral Signal to Noise Ratio This section is structured very similarly to the section about the Fourier Ring Correlation. First the definition of the Spectral Signal to Noise Ratio (SSNR) is stated. A part of the SSNR calculation is the computation of the sample variance. To be able to derive an approximate expression for the SSNR first the sample variance is approximated. Then, in subsection an approximation of the SSNR is derived and in subsection an example of an SSNR curve is given. In the final subsection, it is stated how a resolution figure is computed from an SSNR-curve Definition of the SSNR The Spectral Signal to Noise Ratio was first defined by [26] as, α m = { FR 1, F R > 1 0, F R 1 (5-37) with, In this definition (Ω signal m is the noise variance. (Ω signal m F R = (Ωsignal m ) 2 (Ω noise m ) 2. (5-38) ) 2 is the local signal variance within a frequency band B and (Ω noise m ) 2 ) 2 and (Ω noise m ) 2 are defined as follows. (Ω signal m ) 2 = 1 M (Ω noise m ) 2 = 1 K B [i,j] B 1 M K B [i,j] B k=1 M M k=1 Q k 2 (5-39) Q k (Q ) M 2 (5-40) The denominator of Eq. (5-40) is not in line with the definition in [12, 26], where it reads (M 1). In this thesis, the sample variance was chosen to be defined with a factor M (as was stated in Eq. (5-22)) and it is for this reason that in the definition of the SSNR also a factor M is used. The constant K B is the number of pixels in the frequency band B.
70 5-6 Spectral Signal to Noise Ratio 59 The sum over a band of frequency components is computed using the radial average defined in subsection Thus, the signal and noise variance are computed as follows. (Ω signal m ) 2 = 1 [ M M RadAvg (Q k ) aligned ] 2 k=1 (5-41) (Ω noise m ) 2 = 1 [ M M RadAvg ] (Q k ) aligned (Q ) M 2 k=1 (5-42) Eq. (5-42) is recognised as the sample variance. The pixel-wise variation between the data-set of particle images is, however, not only due to the noise but also due to registration errors. The name noise variance for the variable Ω noise m may thus be misleading Approximate expression for the sample variance of a reconstruction In this subsection, we concentrate on deriving an approximate expression for the sample variance, SampleVar[(Q ) M ] = 1 M M (Q k ) aligned (Q ) M 2 (5-43) The radial average of the sample variance is the noise variance, (Ω noise m ) 2. In section it was stated that the pixels of the sample variance are an estimate of the pixel-wise variation between many aligned particle images. The variation is a consequence of the noise variance and the registration errors. Usually only the noise is considered a source of variation between particle images. As far as we are aware of, considering registration errors as an additional source of variation in the computation of the SSNR is a new concept. Every aligned particle image can be considered a realization of the random variable (Q ) aligned. (Q ) aligned = (B ) padded (P ) padded + (N ) aligned. (5-44) The matrix (B ) padded is directly related to the shift vector S. Assuming S and (N ) aligned are uncorrelated, the variance (Q ) aligned can be expressed linearly in terms of the variance of the registration errors and the noise variance. ) Var ((Q ) aligned k=1 = P padded ( 2 Var (B ) padded) ( + Var (N ) aligned) (5-45) The assumption of independence of (B ) padded and (N ) aligned is reasonable, since a high noise value in a certain pixel [i, j] does not directly imply anything about the value of the matrix (B ) padded. In section it was stated that the variance of the noise is ( Var (N ) aligned) = σn 2 Na 2 (5-46) The variance of (B ) padded is approximated in the next paragraph.
71 60 Measures describing the quality of a reconstruction The expectation and variance of the Fourier transformed registration matrix When a finite number of images is simulated, the mean of M realizations of the random variable (B ) padded corresponds to B = 1 M = 1 M M k=1 k=1 (B k ) padded [ M ( fftshift exp 2πi N [(N/2 + s k y 1)(j 1) + (N/2 + s k x 1)(i 1) ] ) ], (5-47) where we used the definition of (B k ) padded in Eq. (4-18). The sample variance is defined as follows. (B k ) padded B 2 = 1 M M ( k=1 (B k ) padded B )( (B k ) padded B) (5-48) It can be concluded from Eq. (4-20), that B is related to G padded as follows. B = (G padded ) M, (5-49) Eq. (5-48) can be rewritten such that it is a function of B 2 = (G padded ) M 2. Var(B ) (B k ) padded B 2 = 1 M [(B k) padded( (B k) padded) ( M k=1 (B k ) padded) B B k = 1 [ M (B k M ) padded( (B k ) padded) M ((B k ) padded) B k=1 k=1 + M ] B 2 = 1 [ M (B k M ) padded 2 M B B M BB + M ] B 2 k=1 = 1 [ M 1 M B M B M B 2 + M ] B 2 k=1 = 1 [ M 2M B 2 + M ] B 2 M = 1 [ M M ] B 2 M = 1 B 2 = 1 (G padded ) M 2 ( ] B) + B 2 M k=1 (B k ) padded( B ) (5-50)
72 5-6 Spectral Signal to Noise Ratio 61 (a) (b) (c) Figure 5-3: Examples of Re((B k ) padded ). Both the real and imaginary part of this matrix are sinusoids. The direction of the bands for which the real part is positive depends on the size of s k x and s k y. For graphs (a)-(c) the registration errors S k are [-2 2], [2 2] and [0 3] respectively. In this calculation, the fact that (B k ) padded 2 = 1 for all [i, j] was used. The variance of B is thus, according to Eq. (5-50), linearly related to (G padded ) M 2. Examples of (G ) padded 2 M were depicted in Figure 4-4 (c) and (d). The matrix (G ) padded M 2 is maximal for low spatial frequencies and minimal for high spatial frequencies. As a consequence the variance of B is minimal for low and maximal for high spatial frequencies. The origin of this relation may be understood as follows. The real and imaginary part of the registration error matrix, Eq. (4-18), are sinusoidal functions with an oscillation frequency dependent on the registration error S k. In Figure 5-3 three examples of the real part of (B k ) padded have been depicted. The central pixel the matrix (B k ) padded always has the value 1. The variance of this pixel is thus zero. The direction of the indices for which the sinusoids (for example) have a value +1 is different in graphs (a)-(c). As a consequence the variation between Re[(B k ) padded ] is largest for pixels away from the center (high spatial frequencies). For low spatial frequencies the real part of the matrices (B k ) padded has a similar value in each of graphs (a)-(c). The variation between different realizations of (B k ) padded is thus small. Even though only the real part was depicted in Figure 5-3, this may help understand why Var(B ) is minimal for low spatial frequencies and maximal for high spatial frequencies. To conclude this paragraph, we will state the approximate expression for the sample variance of a reconstruction. We derived an expression for the variance of the Fourier transformed registration error matrix in this paragraph. Using Eq. (5-50) in addition to the noise variance, Eq. (5-46), the sample variance was derived to equal the sum of the variation due to
73 62 Measures describing the quality of a reconstruction registration errors and the noise variance. SampleVar[(Q ) M ] = 1 M M Q k (Q ) M 2 k=1 P padded ( 2 Var (B ) padded) + Var ((N ) aligned) P padded 2 (1 (G ) padded M 2) + 1 M (N M ) k aligned N 2 k=1 P padded 2 (1 (G ) padded 2 ) M + σ 2 n Na 2 (5-51) The validity of this approximation will be considered in the next chapter by visually comparing images of the true and approximated sample variance Approximate expressions for the SSNR In the previous subsection the sample variance of a reconstruction was considered in great detail and an approximation was derived. We were interested in this expression to be able to approximate the SSNR which contains the sample variance in its definition. In this subsection we will derive two approximations for the SSNR based on the approximate sample variance. First approximation First we will approximate the signal variance (Ω signal m ) 2 in the definition of the SSNR. (Ω signal m ) 2 = 1 [ M M RadAvg (Q k ) aligned ] 2 k=1 = 1 [ M RadAvg M 2 ] (Q ) M 2 [ = M RadAvg (Q ) M 2] [ = M RadAvg (G ) padded M (P ) padded + (N ) aligned ] 2 [ M RadAvg (G ) padded 2 M (P ) padded 2 + σn 2 N a 2 ] M (5-52) Next, the noise variance (Ω noise m ) 2 which is equivalent to the sample variance is approximated using Eq. (5-51). (Ω noise m ) 2 = 1 [ M M RadAvg ] (Q k ) aligned (Q ) M 2 k=1 [ ( RadAvg P padded 2 1 ) ] (G ) padded 2 M + σn 2 Na 2. (5-53)
74 5-6 Spectral Signal to Noise Ratio 63 Based on these approximations and the definition of the SSNR, Eq. (5-37), the first approximation is [ RadAvg M (G ] ) padded M P padded 2 + σn 2 Na 2 α m [ ( RadAvg P padded 2 1 ) ] (G ) padded 1. (5-54) 2 M + σn 2 Na 2 with σ n as defined in Eq. (3-40). Second approximation We derived that the sample variance of a set of Fourier transformed images has a contribution from the noise and from the registration errors. In theoretical papers published on this topic thus far, only the noise was considered a source of variation and the misalignment of particle images was neglected when considering the SSNR. We would like to find out how large the influence of disregarding this contribution is on the resolution. If there are no registration errors, it holds that G padded 2 1 for all [i, j]. This can be understood from the fact that in this case (b k ) padded = 1 for [i, j] = [ Na ] and zero 2, Na 2 otherwise. As a result ( b k ) padded too is a discrete 2D delta peak, the Fourier transform of which is unity for all pixels. For small registration errors, G padded 2 is close to unity for all spatial frequencies and the term ( P padded 2 1 ) (G ) padded 2 M is neglectable compared to σn 2 Na 2 in the denominator of Eq. (5-54). The second approximation to the SSNR thus is as follows. [ RadAvg M (G ] ) padded M P padded 2 + σn 2 Na 2 α m σn 2 Na 2 1. (5-55) In the next chapter, we consider how well the resolution can be estimated by either of the two approximations Example of an SSNR-curve In Figure 5-4 an example of an SSNR-curve is depicted computed using the definition of the SSNR,Eq. (5-37) for a reconstruction of the GroEL chaperone from M = 800 images. As is seen in Figure 5-4, the spectral signal to noise ratio is highest for low spatial frequencies. This is because the noise variance is the same for all spatial frequencies while the magnitude of object-related information becomes weaker for higher spatial frequencies. The ratio of the magnitude of the signal to the noise variance thus is smaller for high spatial frequencies. The reconstruction in this example was formed from M = 800 particle images Expressing the resolution based on the SSNR-curve The SSNR curve provides useful information on how strongly object related information is present in the reconstruction, for a vector of spatial frequencies. However, just as with the
75 64 Measures describing the quality of a reconstruction Figure 5-4: The unbroken line is an example of a SSNR-curve as a function of spatial frequency. The defocus is z = 3981nm and the electron dose is P P = 40. The dotted line indicates a cut-off of W SSNR = 4 for determining a single resolution value for the SSNR-curve. For this reconstruction, the resolution is ρ SSNR =0.7nm 1. FRC, it is most practical to associate a reconstruction with a single value for the resolution. The resolution should give an estimate of the highest frequency component that is significantly present in the reconstruction. It thus is an indication of the amount of detail in a reconstruction. The lowest m for which α m < W SSNR (5-56) is determined. This index we refer to as m SSNR. The resolution, ρ SSNR then corresponds to the spatial frequency ρ SSNR = k i for i = m SSNR. (5-57) In Figure 5-4 the cut-off W SSNR = 4 has been drawn. The resolution is defined as the spatial frequency where the two lines cross. 5-7 Information limit In section 4-8 we outlined that usually a correction for the PCTF is done. Just as for the PCTF, the particle images could be corrected for their envelope functions. This correction involves restoring the decreased amplitude of the high spatial frequency components. However, the very high-resolution information is so weakly present in the reconstruction, that these spatial frequencies are dominated by noise. Aiming to restore these components may amplify the noise strongly. The amplitude effect of an envelope function can thus only be restored up to a certain spatial frequency. The spatial frequency beyond which this is no longer possible is referred to as the information limit, ρ InfLim,G,E [6]. We interpret the information limit as defined in [14] as follows. The envelope functions of a reconstruction can be corrected for as long as the signal is a factor W InfLim greater than the
76 5-8 Comparing the FRC, SSNR and the information limit 65 noise variance. The signal strength of a reconstruction is computed radially and we label the radial signal strength InfLim m. [ (E InfLim m = RadAvg ) padded (G ) padded M (Φ ) padded 2], (5-58) Using the notation introduced in section 4-8, Eq. (5-58) could equivalently be written as [ InfLim m = RadAvg (G ) padded 2 ( P ) padded 2]. (5-59) The information limit is defined as the maximal spatial frequency for which the radial signal strength is a factor W InfLim greater than the noise variance. The noise variance was shown 1 to equal M σ2 nn 2 in Eq. (3-46), and thus the spatial frequency at the maximal index m for which InfLim m > W InfLim σn 2 Na 2 /M, (5-60) gives the information limit ρ InfLim,G,E of the reconstruction. This index we label m InfLim. The information limit thus corresponds to M ρ InfLim,G,E = k i for i = m InfLim. (5-61) The constant W InfLim can be chosen between 1 and 3 [14]. In the same way as has been outlined above, the envelope functions due to partial coherence and registration errors can each be associated with an information limit. These information limits we label ρ InfLim,E and ρ InfLim,G respectively. The information limit ρ InfLim,E is the (E spatial frequency at which the radial signal RadAvg[ ) padded (Φ ) padded 2] is no longer stronger than the noise variance of the reconstruction. 5-8 Comparing the FRC, SSNR and the information limit The FRC, SSNR and information limit are all used as measures for the resolution. In this section, an approximate expression for the FRC is compared to the expression for the information limit. In subsection the SSNR and the FRC are compared The FRC and the information limit In this subsection, the FRC for a reconstruction which is assumed to be perfectly corrected for the PCTF is considered. When the approximate expression for the FRC, Eq. (5-34), is valid, we can in this case relate the resolution and the information limit to each other. Rewriting Eq. (5-35), with the FRC as defined in Eq. (5-34), [ RadAvg P padded 2 ] (G ) padded 2 M [ < W FRC RadAvg (G ) padded 2 padded P 2 + σn 2 M N 2 a M/2 ]
77 66 Measures describing the quality of a reconstruction [ (1 W FRC ) RadAvg P padded 2 ] (G ) padded 2 M < W FRC σn 2 [ RadAvg P padded 2 ] (G ) padded ( 2 2WFRC ) M < 1 W FRC N 2 a M/2 σn 2 Na 2 M. (5-62) Comparing Eq. (5-60) and Eq. (5-62), we conclude that the FRC is equivalent to the information limit due to the combined effect of the registration errors and the envelope function and W InfLim = 2W FRC 1 W FRC. If W FRC = 0.5, this implies W InfLim = 2 for the two measures to be equivalent The SSNR and the FRC In [8, 12], it is stated that the SSNR and the FRC can be related to each other. However, the registration errors were not considered as a source of variation for the denominator of the SSNR. In this subsection, it is considered if the cut-off for the SSNR can be chosen such that the resolution computed using the FRC or SSNR become equivalent. In the previous subsection it was shown that the information limit and the approximation to the FRC are equivalent when the cut-off for the information limit is W InfLim = 2W FRC 1 W FRC. According to Eq. (5-54) and Eq. (5-56), the resolution of a reconstruction corresponds to the lowest spatial frequency for which, [ RadAvg M (G ) padded M [ RadAvg P padded 2 (1 (G ) padded M ] padded P 2 + σn 2 Na 2 ] 1 < W 2 ) SSNR. + σ 2 n Na 2 This inequality can be rewritten to a form that is similar to that of Eq. (5-62). [ RadAvg M (G ) padded M ] padded P 2 + σn 2 Na 2 [ < (W SSNR + 1) RadAvg P padded 2 (1 (G ) padded M ] 2 ) + σ 2 n Na 2 [( ) RadAvg M + W SSNR + 1 (G ) padded M 2 P padded 2 (W SSNR + 1) padded P ] 2 < W SSNR σ 2 n N 2 a (5-63) This equation differs from Eq. (5-62) because of the additional term (W SSNR + 1) padded P 2. The origin for the discrepancy between the FRC and the SSNR is that the sample variance may not be a good estimate of the noise variance of the reconstruction when registration errors are present. When the second approximations, Eq. (5-34) and Eq. (5-55) can be used to approximate the FRC and SSNR respectively, the resolutions according to either become equivalent.
78 5-9 Concluding remarks 67 The resolution for the FRC in this case corresponds to the lowest m for which, [ RadAvg (G ) padded 2 M ] padded P 2 FRC m = [ RadAvg (G ) padded 2 ] padded < W FRC M P 2 + σn 2 Na 2 M/2 [ RadAvg (G ) padded 2 M ] padded P 2 < W FRC σ 2 Na 2 n 1 W FRC M/2 (5-64) The resolution for the SSNR corresponds to the lowest m for which, [ RadAvg M ] (G ) padded M P padded 2 + σn 2 Na 2 SSNR m = σn 2 Na 2 1 < W SSNR [ ] RadAvg (G ) padded M P padded 2 < W SSNR σn 2 N a 2 M. (5-65) Comparing Eq. (5-64) and Eq. (5-65) it is concluded that these expressions are identical when, 2W FRC 1 W FRC = W SSNR. (5-66) This relationship between the thresholds for the FRC and SSNR is the same as that stated in [8, 12, 18]. If the registration errors are neglectable and the threshold for the FRC is chosen W FRC = 0.5, then the resolutions according to the FRC and SSNR are equivalent when W SSNR = Concluding remarks In this chapter, measures that can be used to quantify the quality of a reconstruction were outlined. First, the definition of the SNR was discussed. From the definition of the SNR we conclude that the larger the electron dose per unit area of a pixel, the smaller the variance of the noise and thus the larger the SNR. This implies that when small electron doses are used, the SNR is low and the particles are hard to localize in an image containing many particles. Some particle images cannot be aligned with high accuracy in this case and registration errors result. Next, the definitions of the mean squared error, Fourier Ring Correlation, Spectral Signal to Noise Ratio and information limit were stated. We derived approximate expressions for the FRC and SSNR. These approximations involved the assumption that the noise of different images is independent and zero mean and has a constant noise variance. In the last section of this chapter, the resolution measures were compared. It is concluded that the FRC and the information limit are equivalent when the threshold for the FRC is W FRC = 0.5 and for the information limit W InfLim = 2W FRC 1 W FRC = 2. The resolution according to the FRC may thus be interpreted as the maximum spatial frequency for which the signal
79 68 Measures describing the quality of a reconstruction amplitude is twice the noise variance. Further, we showed that the SSNR is not equivalent to the FRC and information limit when the particle images are disturbed by registration errors. When the sample variance as a result of the registration errors is neglectable relative to the noise variance the FRC and the SSNR are the same when the threshold for the SSNR is chosen W SSNR W InfLim = 2W FRC 1 W FRC = 2 for W FRC = 0.5. The theoretical relationship between the resolution according to the FRC, SSNR and information limit was discussed in this chapter. We did not derive a relationship between the MSE and the resolution. In the next chapter, we use simulations to study if there is a relationship between the MSE and the resolution measures. So for example, if the MSE is high when the resolution (calculated using either the FRC or SSNR) is low.
80 Chapter 6 Results from simulations 6-1 Introduction The theoretical foundation for the simulation of images recorded with a TEM and the reconstruction procedure were outlined in chapter 2, 3 and 4. In chapter 5, several measures that quantify the quality of a reconstruction were defined. In this chapter, the quality of the reconstructions as a function of defocus is considered for the GroEL chaperone by means of a simulation study in Matlab [16]. First, in section 6-2 the signal to noise ratio (SNR) as a function of defocus is considered. The motivation for considering the SNR is that it may be expected that particle images that have a high signal to noise ratio are most easily aligned. When the SNR is low, the images are very noisy and likely there are registration errors. In section 6-3 it is considered if there is indeed a relation between the SNR and the registration error. In section 6-4 the MSE, bias and variance as a function of defocus are considered. We are especially interested to find out if the variance significantly effects the MSE of a reconstruction. In section 6-5, the sample variance is considered. In the previous chapter, we derived an approximate expression for the sample variance of Fourier transformed particle images. Here we compare the approximate to the actual pixel-wise sample variance. In section 6-6, the results for the resolution measures are outlined. We consider the approximations to the resolution according to the FRC and SSNR and compare these to the information limit. Finally, in section 6-7, we compare the MSE to the resolution, both as a function of defocus to study if a direct relationship between the resolution and MSE of a reconstruction of the GroEL chaperone molecule. The results discussed in this chapter are all specific to the projection of the potential of GroEL chaperone as extracted from the Protein Data Bank and crucially depend on the assumption that the PCTF can be neglected. The motivation for leaving the influence of the PCTF on the quality of the reconstructions out of consideration, is the intuition that there is a way to fully restore the disturbances as a consequence of the PCTF when a large number of images from different defoci are combined to form a 2D reconstruction.
81 70 Results from simulations (a) (b) Figure 6-1: (a) The signal to noise ratio according to the definition of Eq. (5-9) as a function of defocus. The electron dose per unit area of a pixel for computing this graph was P P = 40. (b) The SNR for a reconstruction, at z = 2067nm and electron dose P P = Signal to noise ratio The signal to noise ratio expresses the strength of the signal relative to the noise variance. There are several factors that influence the SNR of the images: The electron dose, P P The defocus, z Window size In section 5-2, we showed that the SNR is inversely proportional to the pixel-wise electron dose. Therefore. increasing the electron dose increases the SNR of the simulated images. In the following, the other two factors are considered Dependence of the SNR on the defocus The SNR of the images q k does not increase linearly when increasing the defocus. Changing the defocus will change the coherence envelope function and the phase contrast transfer function and thus the motif p. We considered defocus settings between 120 and 3967nm with intervals of 33nm. For each value of the defocus we calculated p and the SNR according to definition Eq. (5-9). The SNR as a function of defocus has been plotted in Figure 6-1(a) for a dose setting of P P = 40 (or equivalently P A = 16e /Å 2 ). The SNR values in graph (a) are very low. However, considering the pixel-wise SNR as it was stated in Eq. (5-8) for the same electron dose, the values for some pixels of the reconstruction have a lot higher value for the SNR. An example of SNR is depicted in graph (b). Even though the spatial average SNR is only 0.07, some pixels have a SNR of 2. The relationship between the SNR and the defocus depends on the object being studied. For
82 6-3 Registration error 71 the projected potential of the GroEL the SNR is highest for a defocus of 2000nm. In the following we will try to seek an explanation for the shape of the SNR as a function of defocus by considering the PCTF and characteristics of the GroEL. Although this is more a thought than a prove it may give some insight. Considering Figure 6-2(a) we see that the Fourier transformed aberrated projected potential has strong peaks in the vertical direction for the spatial frequencies ±0.3nm 1. Further we note the rings that result as a consequence of the PCTF. We suggest that the shape of the SNR-curve is related to the magnitude of the PCTF at the low-resolution frequency peaks of the aberrated projected potential. In Figure 6-2(b) the magnitude of the PCTF has been indicated for several defoci. We see in this graph that the magnitude of the PCTF first increases, reaches a maximum and then decreases again. These characteristics correspond to those of the SNR as a function of defocus. The relation between the SNR and the shape of the motif of the images is an interesting topic for future research. We at least conclude from the above idea that the SNR is dependent on the shape characteristics of the projected potential and that all the results presented in this study are specific to GroEL chaperone Signal to noise ratio as a function of the window size We interpreted the SNR as it was defined in Eq. (5-1) as the spatial average of the signal to noise ratios of all pixels, SNR. As a result, the SNR is dependent on the number of (empty) pixels that surround a certain motif. Imagine a square motif with amplitude 1 and a noise variance 1 for all pixels. The signal to noise ratio of all pixels then also is 1. Padding the motif with zeros and adding noise, the signal to noise ratio of the pixels surrounding the motif is zero. Taking the spatial average of SNR of the padded image, the value for the SNR decreases when the size of the empty border is increased. In the simulations the window size is the same for all images and thus the comparison of SNR s is fair. However, for example when Wiener filtering an image, the SNR is required to set a suitable threshold up to which the Wiener filter can be applied without amplifying the noise. We find it surprising that such a threshold would depend on the amount of padding done to the images. 6-3 Registration error As a consequence of the low SNR of the particle images there are registration errors. The registration errors are considered by studying the array S k in real space and the Full Width at Half Maximum (FWHM) of the matrix G padded in Fourier space The registration error matrix in real space We computed the registration errors for a group of 800 aligned particle images. In Figure 6-3 the distribution of the registration errors in the horizontal and vertical direction are depicted for two defocus-settings and a fixed electron dose.
83 72 Results from simulations (a) (b) Figure 6-2: (a) The magnitude of the Fourier transformed aberrated projected potential, P 2 for a defocus z = 120nm. We see that the projected potential has a strong peak in the vertical direction for a spatial frequency of 0.3nm 1. (b) The magnitude of the PCTF for the spatial frequency 0.3nm 1 has been indicated by a red line in this figure. The magnitude of the PCTF first increases, reaches a maximum for z = 2859nm and then decreases again.
84 6-3 Registration error 73 (a) (b) (c) (d) Figure 6-3: In this figure, the registration errors of particle images that together form a reconstruction are summarised by a histogram plot. Two defocus values are considered; graphs (a) and (c) have a defocus of 120nm while graphs (b) and (d) have a defocus of 417nm. The electron dose was P P = 15. The graphs in the top row depict the horizontal registration errors while the graphs in the bottom row depict the vertical registration errors. From these figures we conclude that the mean of the registration errors is approximately zero. Considering Figure 6-3 (b) it is seen that most particle images have a registration error of 0. The width of the distribution of registration errors in the horizontal direction is greater for low than for high defocus. For the vertical direction, the same holds, but in this case minor peaks are encountered for registration errors of +20 and -20. These peaks are a consequence of the periodicity of the projected potential in the vertical direction (see Figure 3-3). The width of the distribution of registration errors in real-space can be quantified by the standard deviation of the registration errors, σ reg. In Figure 6-4(a) the standard deviation in the horizontal direction is depicted as a function of defocus. For the electron doses depicted in this figure, σ reg is greatest for low defocus. When increasing the defocus, the standard deviation of the registration errors decreases; reaches a minimum and then increases again. Considering the SNR as a function of defocus, as was depicted in Figure 6-1, we conclude that there may be a relation between the SNR and σ reg. For small and high defocus, the signal to noise ratio is smallest. Also, intuitively we would expect that the registration errors are greatest when the SNR is small.
85 74 Results from simulations However, σ reg does not only depend on the SNR. In Figure 6-4(a), the standard deviation of the registration errors increases between 1000 < z < 1500 for electron doses P P = 40 and P P = 65 even though the SNR is also an increasing function in this range. We expect that another important factor on which σ reg depends is the amount of fine detail. Two very smooth motifs that are disturbed with noise are harder to align than motifs with sharp edges. As the defocus is increased, the width of the passband of the coherence envelope function becomes smaller. As a consequence, the images are more strongly low-pass-filtered and the fine detail is thus filtered away. Considering Figure 6-4(a) again, it seems that when the SNR is above a certain value, the alignment works. For the electron doses P P = 15, 40 and 65 these are 1500nm, 800nm and 500 nm respectively. For higher defoci, the standard deviation of the registration errors slowly increases as a consequence of the coherence envelope function. The standard deviation of the registration errors and the factors it depends on is an important topic that is interesting for further research. According to [8], the size of the motif to be aligned is also critical for the ability to align noisy images The registration error matrix in Fourier space The width of the Fourier registration error matrix G padded can be quantified by the full width at half maximum (FWHM). The envelope function for registration errors is asymmetrical and therefore the FWHM is different in the horizontal and vertical direction. In Figure 6-4(b), the width in the horizontal direction has been depicted. For low electron dose, the width of the pass band is first increasing and then decreasing. For high electron dose, the width is maximal for low defocus. Remarkable about Figure 6-4(b) is the FWHM for low defoci for electron doses P P = 15 and P P = 65. The maximal positive and negative spatial frequency given the pixel size is 3.1nm 1 and the maximal value of the FWHM is thus 6.2nm 1. When the half maximum of (G ) padded M is not reached at the highest spatial frequencies, the FWHM is set tot 6.2nm 1. This explains why the FWHM is constant for low defocus and electron dose P P = Comparing the width of the real-space and Fourier transformed registration error matrix It is interesting to compare the graphs for the width of the registration error distribution that were depicted in Figure 6-4(a) and (b). For this comparison it is important to note that a good reconstruction has a low value for σ reg and a high value for the FWHM. The standard deviation of the registration errors for an electron dose of P P = 40 is first decreasing, reaches a minimum value and is then from z = 800nm onwards a slowly increasing function. The FWHM is for the same electron dose first an increasing function, reaches a maximum and is then from a defocus of approximately z = 500nm a decreasing function. From this we conclude that σ reg and FWHM have equivalent characteristics. However, we are surprised that images with a standard deviation of the registration errors of approximately 1 pixel (for defoci nm and electron doses P P = 40 and P P = 65) have such a small FWHM. The very small increase in σ reg for z > 1500nm in fact corresponds to a large decrease in FWHM. The explanation for this may be as follows. It is only fair to compare standard deviations when the distribution (for example Gaussian)
86 6-3 Registration error 75 (a) (b) Figure 6-4: (a) The standard deviation, σ reg, of the registration errors in the horizontal direction is depicted as a function of defocus. σ reg is expressed in pixels, with pixel size d=1.6å. (b) The full width at half maximum of the Fourier registration matrix (G ) padded M in the horizontal direction.
87 76 Results from simulations Figure 6-5: In this figure the number of non-zero registration errors as a function of defocus has been plotted, for three electron doses. For each defocus, the array 2 M array S contains the registration errors of all particle images. The rows of this array are the horizontal and vertical registration errors. The number of entries of S that are not equal to 0 are counted in the row corresponding to the horizontal registration errors. of the random variable is the same. It may be concluded from Figure 6-3 that the distribution of the registration errors is dependent on the defocus setting. In Figure 6-3(d) clear peaks are seen at ±20, whereas Figure 6-3(c) such peaks are not seen. If registration errors were the only disturbance to the images, we expect that the particle images that have registration errors as depicted in graph Figure 6-3(d) have a much better quality reconstruction than those of graph Figure 6-3(c). The standard deviations of the registration errors corresponding to graphs Figure 6-3(c) and (d) are 13.6 and This seems like a small difference in standard deviation for two distributions of registration errors that are so different. In Figure 6-3(d) there are many more particle images that have a registration error S k = [0, 0]. In Figure 6-5 the number of nonzero registration errors as a function of defocus has been depicted. The curves of the number of non-zeros as a function of defocus and the FWHM are more equivalent than the σ reg and FWHM. Overall, we conclude that there is an optimum defocus for which the registration errors limit the quality of the reconstructions the least. The higher the electron dose, the lower the defocus for which this optimum occurs. There is a relation between the SNR and the registration errors. However, the variability and magnitude of the registration errors not only depends on the SNR but also on the characteristics of the image such as smoothness of the motif to be aligned.
88 6-4 Mean squared error Mean squared error The mean squared error (MSE) is the sum of the bias squared and the variance. In this section, first the bias squared (simply referred to as the bias) is discussed. In subsection the variance is discussed. In the last subsection, it is discussed whether the bias, or variance dominates the mean squared error of a reconstruction Bias There are several reasons why reconstructions from M aligned particle images are biased. PCTF Coherence envelope function Registration errors The first two of these image degrading effects are disturbances that influence each particle image, while the last is an effect that is introduced in the reconstruction procedure. In the remainder of this subsection both the combined effect of the disturbing influences and the separate effect of each is considered. PCTF and envelope function The coherence envelope function is most limiting for high defocus values (see Figure 2-2). The envelope function acts as a low-pass filter. Thus, the smaller the width of the filter the lower the highest spatial frequency that is transferred. Our intuition was that the bias will be greater for high defocus than it is for low defocus. The bias squared due to the envelope and wave aberration function in the absence of registration errors is for each defocus setting computed as, Bias 2 = N N ( ) 2 N N [ p φ = F 1{ ] } 2 Φ ml sin γ ml E ml φ. (6-1) i=1 j=1 i=1 j=1 In Figure 6-6(a) the bias computed using Eq. (6-1) has been plotted as a function of defocus. The bias is indeed an increasing function for low defocus, but for high defocus the bias decreases. The explanation for this is that the low-resolution information dominates the bias. The strength with which low resolution information is transferred is mainly determined by the PCTF. As a result, the shape of the bias curve is mainly determined by the contrast as a function of defocus. In Figure 6-1(a), the SNR as a function of defocus was depicted. We see that the shape of the bias curve is very similar to that of the SNR curve.
89 78 Results from simulations (a) (b) Figure 6-6: (a) The bias of p from φ. (b) The bias of p from φ. This is the bias when the PCTF is left out of consideration. For both these bias graphs, the registration errors were assumed to be zero. Envelope function In the following the PCTF is left out of consideration. The motif in this hypothetical situation is named, p. p = F 1 {Φ ml E ml } (6-2) The bias is computed as, Bias 2 = N i=1 j=1 N ) 2, ( p φ (6-3) and has been depicted in Figure 6-6 (b). It is seen that the bias now is a monotonically increasing function. Thus, under the assumption that the PCTF can be fully corrected for, the bias is indeed greatest for high defocus. Registration errors and the envelope function In this paragraph the combined bias effect due to the registration errors and the envelope function of the microscope is considered. Defining, p = F 1 {Φ ml E ml } as before, the bias is computed as follows. Bias 2 = N N ((g ) M p (φ ) padded) 2 i=1 j=1 (6-4) The bias as a function of defocus for this situation has been depicted in Figure 6-7. As was seen in Figure 6-4(a), the standard deviation of the registration errors is greatest for low defocus. Thus, the convolution with the registration matrix may be expected to have the greatest influence on the bias for low defocus. When comparing Figure 6-7 to Figure 6-4(a) and Figure 6-5 we conclude that there is great similarity between the bias curves and the standard deviation of the registration errors as a function of defocus.
90 6-4 Mean squared error 79 Figure 6-7: The bias due to the combined effect of the envelope transfer function of the microscope and registration errors has been depicted for three electron doses. We conclude from this figure that the registration errors have a direct influence on the bias of a reconstruction. The bias is the least for high electron dose. Thus, when the PCTF can be fully corrected for we can state the following about the relation between the registration errors, electron dose and the bias. The reconstruction is most biased for low defocus as a result of registration errors, whereas for high electron dose the reconstruction is most biased for high defocus due to both registration errors and the coherence envelope function Variance There are two reasons why there is variance between reconstructions formed from the same number of particle images and for the same microscope settings. Noise Different noise-induced registration matrices In this subsection we will consider the variance as a function of defocus due to both these factors. Just as with the bias we will first consider reconstructions where no correction for the PCTF was done and in the second paragraph, reconstructions where the PCTF was fully corrected for.
91 80 Results from simulations Figure 6-8: For each defocus value, the variance between 80 reconstructions is computed, according to the definition of Eq. (5-21). For the points with marker, the particle images are disturbed by the registration errors, the PCTF, the coherence envelope function and noise. For the points with marker + the particle images are disturbed by the registration errors, the coherence envelope function and noise. Each curve corresponds to a certain setting of the electron dose. Registration errors, the PCTF, the envelope function and noise For every defocus value, 80 reconstructions are computed, each formed from 800 particle images. The variance between the reconstructions is depicted in Figure 6-8 using marker. The variance curve is flat as a function of defocus. Thus, for a certain choice of the electron dose, the variance is not affected by the defocus setting. In section 6-3 we saw that the registration errors are strongly defocus dependent. Therefore, if the variance was due to the registration errors, we would expect that the variance curve is also defocus dependent. But, as the noise variance is the same for all defoci we conclude that the variation between the reconstructions is mainly due to the noise variance. The variance is thus approximately equal to the noise variance of the reconstructions, σn 2 Na 2 /M. Registration errors, the envelope function and noise In this paragraph, the variance is considered when the influence of the PCTF can be neglected. The variance is depicted in Figure 6-8 using the marker +. For this class of particle images, the variance is not only due to the noise variance. For low defocus, the variance curves are decreasing functions. This is a consequence of the difference between the registration error matrices (G ) padded M for different defoci. The registration error matrices affect the variance mainly for low defocus.
92 6-5 Sample variance in Fourier domain 81 It is remarkable that the variation as a consequence of the registration errors is significant only when the PCTF is neglected. We can explain this is as follows. The properties of the noise are the same for both classes of particle images. The noise variance of the reconstructions is thus identical. However, the magnitude of the influence of the registration errors on the variance curve is dependent on the signal strength of the particle images. For particle images disturbed by the PCTF and envelope function, the SNR is lower than that for particle images only disturbed by the envelope function. The smaller the pixel values of the signal, the smaller the influence of the registration errors on the variance. For example, if the signal motif of the particle images is approximately zero for all pixels, the variance is only due to the noise. In line with the foregoing, the fact that the variance curves are flat as a function of defocus when the particle images are disturbed with the PCTF does not imply that the registration error matrices of different reconstructions differ only very little. More likely, the variance curves are flat because the signal strength is very weak. When a reconstruction is described as ( Q ) M = (G ) padded M P padded + ( N ) aligned and the signal is very weak, the reconstruction can be approximated as ( Q ) M ( N ) aligned No matter how different the matrices (G ) padded M are, they are not a source of variance when the signal strength is weak. We conclude this subsection by stating that the variance is fairly independent of defocus for reconstructions formed from 800 particle images. Does the bias or variance dominate the MSE? The bias dominates the MSE. This is true in two respects. First of all, the bias curve has a larger magnitude than the variance curve (for the electron doses considered). Further, since the variance curves are fairly flat, they are not going to influence the best defocus value. Each reconstruction formed from particle images with the same defocus and electron dose setting has a value for the mean squared error. The variance is smallest for high electron dose, but fairly independent of the defocus. Therefore, if a range of defocus values is to be selected for which the MSE is lowest, this corresponds to the range for which the bias is minimal. 6-5 Sample variance in Fourier domain Forming a set of particle images at the same defocus in simulations, a certain pixel [i, j] will differ between the images as a consequence of noise and the registration errors. Both these aspects thus are a source of variation between different aligned particle images. The sample variance is similar to the variance between reconstructions in section 6-4-2, but describes the variation between particle images that together form a reconstruction. In subsection an approximate expression for the sample variance between a set of Fourier
93 82 Results from simulations Figure 6-9: The MSE as a function of defocus for three electron doses. The MSE is the sum of the bias and the variance, but is dominated by the bias. We conclude from this graph that the shape of the curves is very similar to those of Figure 6-7. transformed particle images was derived. The result of this derivation is stated in Eq. (5-51). In this section, we discuss how good this approximation is. In Figure 6-10 both the sample variance calculated using Eq. (6-5) and that estimated using Eq. (5-51) are depicted for electron dose P P = 27.5 and defocus z = 252nm. Although Figure 6-10(a) is more noisy than Figure 6-10(b) we conclude from these graphs that the approximation for the sample variance is good. The sample variance was approximated as, SampleVar[(Q ) M ] P padded 2 (1 (G ) padded M 2) + σnn 2 a 2. (6-5) If the sample variance was a consequence of the noise of particle images only, it would be of magnitude σn 2 Na 2 independent of the defocus setting. The sample variance depicted in Figure 6-10 is not uniform and this is a consequence of the variation caused by the registration errors. The contribution to the sample variance by the registration errors is dependent on the aberrated projected potential. The greater P padded 2, the greater the contribution of the variance due to the registration errors. However, at the same time, the greater the aberrated projected potential, the smaller the registration errors and the smaller 1 G padded 2. When there are no registration errors, (G ) padded M 2 1. The rings are a consequence of the PCTF and the bright spots correspond to the Fourier transformed projected potential. In Figure 6-10(a) the sample variance is fairly constant for high spatial frequencies. It is especially for the bright spots that the sample variance is significantly different from σn 2 Na 2. In Figure 6-10, the electron dose is P P = 27.5 and thus if noise was the only variance source, the sample variance would be uniform and of magnitude σn 2 Na 2 = We conclude that the registration errors cause the sample variance to be significantly different
94 6-6 Resolution 83 (a) (b) Figure 6-10: (a) The sample variance between the Fourier transformed particle images (Q k )padded that are used to form a reconstruction. The sample variance was calculated using Eq. (6-5). (b) An estimate of the sample variance, calculated using Eq. (5-51). We conclude from these images that the sample variance is well approximated by (b). The electron dose was P P = 27.5 and the defocus z = 252nm. from the noise variance at low spatial frequencies. 6-6 Resolution In the preceding section, the MSE and its relation to the SNR and registration errors was discussed. In this section we move to the quality measures that define the resolution of the reconstructed images. The resolution measures that we consider were defined in the previous chapter; the FRC, the SSNR and the information limit. In the subsection 6-6-1, the validity of approximations derived in chapter 5 is discussed. It is especially interesting to find out if the FRC, SSNR and information limit are equivalent resolution measures. In subsection 6-6-2, the influences of the registration errors and the coherence envelope function on the resolution are considered separately. In subsection the combined effect is studied Approximations to the FRC and SSNR In Figure 6-11 the FRC and SSNR and their approximations have been depicted. The approximations were derived in sections and The cut-off for the FRC and SSNR were W FRC = 0.5 and W SSNR = 2 respectively. Approximate FRC For the first approximation, Eq. (5-33), we assumed that the noise of particle images is uncorrelated. Further, we assumed the noise variance has an approximate magnitude of
3. Image formation, Fourier analysis and CTF theory. Paula da Fonseca
 3. Image formation, Fourier analysis and CTF theory Paula da Fonseca EM course 2017 - Agenda - Overview of: Introduction to Fourier analysis o o o o Sine waves Fourier transform (simple examples of 1D
3. Image formation, Fourier analysis and CTF theory Paula da Fonseca EM course 2017 - Agenda - Overview of: Introduction to Fourier analysis o o o o Sine waves Fourier transform (simple examples of 1D
OPTI-521 Graduate Report 2 Matthew Risi Tutorial: Introduction to imaging, and estimate of image quality degradation from optical surfaces
 OPTI-521 Graduate Report 2 Matthew Risi Tutorial: Introduction to imaging, and estimate of image quality degradation from optical surfaces Abstract The purpose of this tutorial is to introduce the concept
OPTI-521 Graduate Report 2 Matthew Risi Tutorial: Introduction to imaging, and estimate of image quality degradation from optical surfaces Abstract The purpose of this tutorial is to introduce the concept
Neurophysical Model by Barten and Its Development
 Chapter 14 Neurophysical Model by Barten and Its Development According to the Barten model, the perceived foveal image is corrupted by internal noise caused by statistical fluctuations, both in the number
Chapter 14 Neurophysical Model by Barten and Its Development According to the Barten model, the perceived foveal image is corrupted by internal noise caused by statistical fluctuations, both in the number
specular diffuse reflection.
 Lesson 8 Light and Optics The Nature of Light Properties of Light: Reflection Refraction Interference Diffraction Polarization Dispersion and Prisms Total Internal Reflection Huygens s Principle The Nature
Lesson 8 Light and Optics The Nature of Light Properties of Light: Reflection Refraction Interference Diffraction Polarization Dispersion and Prisms Total Internal Reflection Huygens s Principle The Nature
Chapter 24. Wave Optics
 Chapter 24 Wave Optics Wave Optics The wave nature of light is needed to explain various phenomena Interference Diffraction Polarization The particle nature of light was the basis for ray (geometric) optics
Chapter 24 Wave Optics Wave Optics The wave nature of light is needed to explain various phenomena Interference Diffraction Polarization The particle nature of light was the basis for ray (geometric) optics
2.710 Optics Spring 09 Solutions to Problem Set #1 Posted Wednesday, Feb. 18, 2009
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY.70 Optics Spring 09 Solutions to Problem Set # Posted Wednesday, Feb. 8, 009 Problem : Spherical waves and energy conservation In class we mentioned that the radiation
MASSACHUSETTS INSTITUTE OF TECHNOLOGY.70 Optics Spring 09 Solutions to Problem Set # Posted Wednesday, Feb. 8, 009 Problem : Spherical waves and energy conservation In class we mentioned that the radiation
Ray Optics I. Last time, finished EM theory Looked at complex boundary problems TIR: Snell s law complex Metal mirrors: index complex
 Phys 531 Lecture 8 20 September 2005 Ray Optics I Last time, finished EM theory Looked at complex boundary problems TIR: Snell s law complex Metal mirrors: index complex Today shift gears, start applying
Phys 531 Lecture 8 20 September 2005 Ray Optics I Last time, finished EM theory Looked at complex boundary problems TIR: Snell s law complex Metal mirrors: index complex Today shift gears, start applying
Diffraction. Single-slit diffraction. Diffraction by a circular aperture. Chapter 38. In the forward direction, the intensity is maximal.
 Diffraction Chapter 38 Huygens construction may be used to find the wave observed on the downstream side of an aperture of any shape. Diffraction The interference pattern encodes the shape as a Fourier
Diffraction Chapter 38 Huygens construction may be used to find the wave observed on the downstream side of an aperture of any shape. Diffraction The interference pattern encodes the shape as a Fourier
An Intuitive Explanation of Fourier Theory
 An Intuitive Explanation of Fourier Theory Steven Lehar slehar@cns.bu.edu Fourier theory is pretty complicated mathematically. But there are some beautifully simple holistic concepts behind Fourier theory
An Intuitive Explanation of Fourier Theory Steven Lehar slehar@cns.bu.edu Fourier theory is pretty complicated mathematically. But there are some beautifully simple holistic concepts behind Fourier theory
Supporting Information for Azimuthal Polarization Filtering for Accurate, Precise, and Robust Single-Molecule Localization Microscopy
 Nano Letters Supporting Information for Azimuthal Polarization Filtering for Accurate, Precise, and Robust Single-Molecule Localization Microscopy Matthew D. Lew, and W. E. Moerner *, Departments of Chemistry
Nano Letters Supporting Information for Azimuthal Polarization Filtering for Accurate, Precise, and Robust Single-Molecule Localization Microscopy Matthew D. Lew, and W. E. Moerner *, Departments of Chemistry
SUPPLEMENTARY INFORMATION
 SUPPLEMENTARY INFORMATION doi:10.1038/nature10934 Supplementary Methods Mathematical implementation of the EST method. The EST method begins with padding each projection with zeros (that is, embedding
SUPPLEMENTARY INFORMATION doi:10.1038/nature10934 Supplementary Methods Mathematical implementation of the EST method. The EST method begins with padding each projection with zeros (that is, embedding
Optics Vac Work MT 2008
 Optics Vac Work MT 2008 1. Explain what is meant by the Fraunhofer condition for diffraction. [4] An aperture lies in the plane z = 0 and has amplitude transmission function T(y) independent of x. It is
Optics Vac Work MT 2008 1. Explain what is meant by the Fraunhofer condition for diffraction. [4] An aperture lies in the plane z = 0 and has amplitude transmission function T(y) independent of x. It is
Dielectric Optical-Controllable Magnifying Lens. by Nonlinear Negative Refraction
 Dielectric Optical-Controllable Magnifying Lens by Nonlinear Negative Refraction Jianjun Cao 1, Ce Shang 2, Yuanlin Zheng 1,Yaming Feng, Xianfeng Chen 1,3, Xiaogan Liang 4 and Wenjie Wan 1,2,3* 1 Key Laboratory
Dielectric Optical-Controllable Magnifying Lens by Nonlinear Negative Refraction Jianjun Cao 1, Ce Shang 2, Yuanlin Zheng 1,Yaming Feng, Xianfeng Chen 1,3, Xiaogan Liang 4 and Wenjie Wan 1,2,3* 1 Key Laboratory
High spatial resolution measurement of volume holographic gratings
 High spatial resolution measurement of volume holographic gratings Gregory J. Steckman, Frank Havermeyer Ondax, Inc., 8 E. Duarte Rd., Monrovia, CA, USA 9116 ABSTRACT The conventional approach for measuring
High spatial resolution measurement of volume holographic gratings Gregory J. Steckman, Frank Havermeyer Ondax, Inc., 8 E. Duarte Rd., Monrovia, CA, USA 9116 ABSTRACT The conventional approach for measuring
Chapter 37. Wave Optics
 Chapter 37 Wave Optics Wave Optics Wave optics is a study concerned with phenomena that cannot be adequately explained by geometric (ray) optics. Sometimes called physical optics These phenomena include:
Chapter 37 Wave Optics Wave Optics Wave optics is a study concerned with phenomena that cannot be adequately explained by geometric (ray) optics. Sometimes called physical optics These phenomena include:
Cover Page. The handle holds various files of this Leiden University dissertation
 Cover Page The handle http://hdl.handle.net/1887/48877 holds various files of this Leiden University dissertation Author: Li, Y. Title: A new method to reconstruct the structure from crystal images Issue
Cover Page The handle http://hdl.handle.net/1887/48877 holds various files of this Leiden University dissertation Author: Li, Y. Title: A new method to reconstruct the structure from crystal images Issue
Chapter 37. Interference of Light Waves
 Chapter 37 Interference of Light Waves Wave Optics Wave optics is a study concerned with phenomena that cannot be adequately explained by geometric (ray) optics These phenomena include: Interference Diffraction
Chapter 37 Interference of Light Waves Wave Optics Wave optics is a study concerned with phenomena that cannot be adequately explained by geometric (ray) optics These phenomena include: Interference Diffraction
COMPUTER SIMULATION TECHNIQUES FOR ACOUSTICAL DESIGN OF ROOMS - HOW TO TREAT REFLECTIONS IN SOUND FIELD SIMULATION
 J.H. Rindel, Computer simulation techniques for the acoustical design of rooms - how to treat reflections in sound field simulation. ASVA 97, Tokyo, 2-4 April 1997. Proceedings p. 201-208. COMPUTER SIMULATION
J.H. Rindel, Computer simulation techniques for the acoustical design of rooms - how to treat reflections in sound field simulation. ASVA 97, Tokyo, 2-4 April 1997. Proceedings p. 201-208. COMPUTER SIMULATION
Structural Information obtained
 Structural Information obtained from Electron Microscopy Christiane Schaffitzel, 09.05.2013 Including slides from John Briggs, Bettina Boettcher, Nicolas Boisset, Andy Hoenger, Michael Schatz, and more
Structural Information obtained from Electron Microscopy Christiane Schaffitzel, 09.05.2013 Including slides from John Briggs, Bettina Boettcher, Nicolas Boisset, Andy Hoenger, Michael Schatz, and more
HW Chapter 20 Q 2,3,4,5,6,10,13 P 1,2,3. Chapter 20. Classic and Modern Optics. Dr. Armen Kocharian
 HW Chapter 20 Q 2,3,4,5,6,10,13 P 1,2,3 Chapter 20 Classic and Modern Optics Dr. Armen Kocharian Electromagnetic waves and matter: A Brief History of Light 1000 AD It was proposed that light consisted
HW Chapter 20 Q 2,3,4,5,6,10,13 P 1,2,3 Chapter 20 Classic and Modern Optics Dr. Armen Kocharian Electromagnetic waves and matter: A Brief History of Light 1000 AD It was proposed that light consisted
Chapter 24. Wave Optics
 Chapter 24 Wave Optics Diffraction Huygen s principle requires that the waves spread out after they pass through slits This spreading out of light from its initial line of travel is called diffraction
Chapter 24 Wave Optics Diffraction Huygen s principle requires that the waves spread out after they pass through slits This spreading out of light from its initial line of travel is called diffraction
Wave Phenomena Physics 15c. Lecture 19 Diffraction
 Wave Phenomena Physics 15c Lecture 19 Diffraction What We Did Last Time Studied interference > waves overlap Amplitudes add up Intensity = (amplitude) does not add up Thin-film interference Reflectivity
Wave Phenomena Physics 15c Lecture 19 Diffraction What We Did Last Time Studied interference > waves overlap Amplitudes add up Intensity = (amplitude) does not add up Thin-film interference Reflectivity
E x Direction of Propagation. y B y
 x E x Direction of Propagation k z z y B y An electromagnetic wave is a travelling wave which has time varying electric and magnetic fields which are perpendicular to each other and the direction of propagation,
x E x Direction of Propagation k z z y B y An electromagnetic wave is a travelling wave which has time varying electric and magnetic fields which are perpendicular to each other and the direction of propagation,
Light. Form of Electromagnetic Energy Only part of Electromagnetic Spectrum that we can really see
 Light Form of Electromagnetic Energy Only part of Electromagnetic Spectrum that we can really see Facts About Light The speed of light, c, is constant in a vacuum. Light can be: REFLECTED ABSORBED REFRACTED
Light Form of Electromagnetic Energy Only part of Electromagnetic Spectrum that we can really see Facts About Light The speed of light, c, is constant in a vacuum. Light can be: REFLECTED ABSORBED REFRACTED
Transmission Electron Microscopy 2. Scattering and Diffraction
 Transmission Electron Microscopy 2. Scattering and Diffraction EMA 6518 Spring 2007 01/07 Outline Why are we interested in electron scattering? Terminology of scattering The characteristics of electron
Transmission Electron Microscopy 2. Scattering and Diffraction EMA 6518 Spring 2007 01/07 Outline Why are we interested in electron scattering? Terminology of scattering The characteristics of electron
IMPORTANT INSTRUCTIONS
 2017 Imaging Science Ph.D. Qualifying Examination June 9, 2017 9:00AM to 12:00PM IMPORTANT INSTRUCTIONS You must complete two (2) of the three (3) questions given for each of the core graduate classes.
2017 Imaging Science Ph.D. Qualifying Examination June 9, 2017 9:00AM to 12:00PM IMPORTANT INSTRUCTIONS You must complete two (2) of the three (3) questions given for each of the core graduate classes.
Formulas of possible interest
 Name: PHYS 3410/6750: Modern Optics Final Exam Thursday 15 December 2011 Prof. Bolton No books, calculators, notes, etc. Formulas of possible interest I = ɛ 0 c E 2 T = 1 2 ɛ 0cE 2 0 E γ = hν γ n = c/v
Name: PHYS 3410/6750: Modern Optics Final Exam Thursday 15 December 2011 Prof. Bolton No books, calculators, notes, etc. Formulas of possible interest I = ɛ 0 c E 2 T = 1 2 ɛ 0cE 2 0 E γ = hν γ n = c/v
Coupling of surface roughness to the performance of computer-generated holograms
 Coupling of surface roughness to the performance of computer-generated holograms Ping Zhou* and Jim Burge College of Optical Sciences, University of Arizona, Tucson, Arizona 85721, USA *Corresponding author:
Coupling of surface roughness to the performance of computer-generated holograms Ping Zhou* and Jim Burge College of Optical Sciences, University of Arizona, Tucson, Arizona 85721, USA *Corresponding author:
Cryo-electron microscopy Cryo-EM. Garry Taylor
 Cryo-electron microscopy Cryo-EM Garry Taylor www.st-andrews.ac.uk/~glt2/bl3301 Electron has a wavelength de Broglie relationship: m v = h / λ or λ = h / mv Accelerate e - in a field of potential V, it
Cryo-electron microscopy Cryo-EM Garry Taylor www.st-andrews.ac.uk/~glt2/bl3301 Electron has a wavelength de Broglie relationship: m v = h / λ or λ = h / mv Accelerate e - in a field of potential V, it
PHYSICS. Chapter 33 Lecture FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E RANDALL D. KNIGHT
 PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 33 Lecture RANDALL D. KNIGHT Chapter 33 Wave Optics IN THIS CHAPTER, you will learn about and apply the wave model of light. Slide
PHYSICS FOR SCIENTISTS AND ENGINEERS A STRATEGIC APPROACH 4/E Chapter 33 Lecture RANDALL D. KNIGHT Chapter 33 Wave Optics IN THIS CHAPTER, you will learn about and apply the wave model of light. Slide
Chapter 12 Notes: Optics
 Chapter 12 Notes: Optics How can the paths traveled by light rays be rearranged in order to form images? In this chapter we will consider just one form of electromagnetic wave: visible light. We will be
Chapter 12 Notes: Optics How can the paths traveled by light rays be rearranged in order to form images? In this chapter we will consider just one form of electromagnetic wave: visible light. We will be
The sources must be coherent. This means they emit waves with a constant phase with respect to each other.
 CH. 24 Wave Optics The sources must be coherent. This means they emit waves with a constant phase with respect to each other. The waves need to have identical wavelengths. Can t be coherent without this.
CH. 24 Wave Optics The sources must be coherent. This means they emit waves with a constant phase with respect to each other. The waves need to have identical wavelengths. Can t be coherent without this.
Chapter 36. Diffraction. Dr. Armen Kocharian
 Chapter 36 Diffraction Dr. Armen Kocharian Diffraction Light of wavelength comparable to or larger than the width of a slit spreads out in all forward directions upon passing through the slit This phenomena
Chapter 36 Diffraction Dr. Armen Kocharian Diffraction Light of wavelength comparable to or larger than the width of a slit spreads out in all forward directions upon passing through the slit This phenomena
Coherent Gradient Sensing Microscopy: Microinterferometric Technique. for Quantitative Cell Detection
 Coherent Gradient Sensing Microscopy: Microinterferometric Technique for Quantitative Cell Detection Proceedings of the SEM Annual Conference June 7-10, 010 Indianapolis, Indiana USA 010 Society for Experimental
Coherent Gradient Sensing Microscopy: Microinterferometric Technique for Quantitative Cell Detection Proceedings of the SEM Annual Conference June 7-10, 010 Indianapolis, Indiana USA 010 Society for Experimental
Edge and local feature detection - 2. Importance of edge detection in computer vision
 Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
Chapter 35 &36 Physical Optics
 Chapter 35 &36 Physical Optics Physical Optics Phase Difference & Coherence Thin Film Interference 2-Slit Interference Single Slit Interference Diffraction Patterns Diffraction Grating Diffraction & Resolution
Chapter 35 &36 Physical Optics Physical Optics Phase Difference & Coherence Thin Film Interference 2-Slit Interference Single Slit Interference Diffraction Patterns Diffraction Grating Diffraction & Resolution
Chapter 24. Wave Optics. Wave Optics. The wave nature of light is needed to explain various phenomena
 Chapter 24 Wave Optics Wave Optics The wave nature of light is needed to explain various phenomena Interference Diffraction Polarization The particle nature of light was the basis for ray (geometric) optics
Chapter 24 Wave Optics Wave Optics The wave nature of light is needed to explain various phenomena Interference Diffraction Polarization The particle nature of light was the basis for ray (geometric) optics
Nicholas J. Giordano. Chapter 24. Geometrical Optics. Marilyn Akins, PhD Broome Community College
 Nicholas J. Giordano www.cengage.com/physics/giordano Chapter 24 Geometrical Optics Marilyn Akins, PhD Broome Community College Optics The study of light is called optics Some highlights in the history
Nicholas J. Giordano www.cengage.com/physics/giordano Chapter 24 Geometrical Optics Marilyn Akins, PhD Broome Community College Optics The study of light is called optics Some highlights in the history
Waves & Oscillations
 Physics 42200 Waves & Oscillations Lecture 41 Review Spring 2016 Semester Matthew Jones Final Exam Date:Tuesday, May 3 th Time:7:00 to 9:00 pm Room: Phys 112 You can bring one double-sided pages of notes/formulas.
Physics 42200 Waves & Oscillations Lecture 41 Review Spring 2016 Semester Matthew Jones Final Exam Date:Tuesday, May 3 th Time:7:00 to 9:00 pm Room: Phys 112 You can bring one double-sided pages of notes/formulas.
(Refer Slide Time: 00:10)
 Fundamentals of optical and scanning electron microscopy Dr. S. Sankaran Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Module 02 Unit-4 Phase contrast, Polarized
Fundamentals of optical and scanning electron microscopy Dr. S. Sankaran Department of Metallurgical and Materials Engineering Indian Institute of Technology, Madras Module 02 Unit-4 Phase contrast, Polarized
dq dt I = Irradiance or Light Intensity is Flux Φ per area A (W/m 2 ) Φ =
 Radiometry (From Intro to Optics, Pedrotti -4) Radiometry is measurement of Emag radiation (light) Consider a small spherical source Total energy radiating from the body over some time is Q total Radiant
Radiometry (From Intro to Optics, Pedrotti -4) Radiometry is measurement of Emag radiation (light) Consider a small spherical source Total energy radiating from the body over some time is Q total Radiant
Single-particle electron microscopy (cryo-electron microscopy) CS/CME/BioE/Biophys/BMI 279 Nov. 16 and 28, 2017 Ron Dror
 Single-particle electron microscopy (cryo-electron microscopy) CS/CME/BioE/Biophys/BMI 279 Nov. 16 and 28, 2017 Ron Dror 1 Last month s Nobel Prize in Chemistry Awarded to Jacques Dubochet, Joachim Frank
Single-particle electron microscopy (cryo-electron microscopy) CS/CME/BioE/Biophys/BMI 279 Nov. 16 and 28, 2017 Ron Dror 1 Last month s Nobel Prize in Chemistry Awarded to Jacques Dubochet, Joachim Frank
Two slit interference - Prelab questions
 Two slit interference - Prelab questions 1. Show that the intensity distribution given in equation 3 leads to bright and dark fringes at y = mλd/a and y = (m + 1/2) λd/a respectively, where m is an integer.
Two slit interference - Prelab questions 1. Show that the intensity distribution given in equation 3 leads to bright and dark fringes at y = mλd/a and y = (m + 1/2) λd/a respectively, where m is an integer.
1. Particle Scattering. Cogito ergo sum, i.e. Je pense, donc je suis. - René Descartes
 1. Particle Scattering Cogito ergo sum, i.e. Je pense, donc je suis. - René Descartes Generally gas and particles do not scatter isotropically. The phase function, scattering efficiency, and single scattering
1. Particle Scattering Cogito ergo sum, i.e. Je pense, donc je suis. - René Descartes Generally gas and particles do not scatter isotropically. The phase function, scattering efficiency, and single scattering
CHEM-E5225 :Electron Microscopy Imaging I
 CHEM-E5225 :Electron Microscopy Imaging I 2018.11 Yanling Ge Outline Amplitude Contrast Phase Contrast Images Thickness and Bending Effects Amplitude Contrast Amplitude phase TEM STEM Incoherent elastic
CHEM-E5225 :Electron Microscopy Imaging I 2018.11 Yanling Ge Outline Amplitude Contrast Phase Contrast Images Thickness and Bending Effects Amplitude Contrast Amplitude phase TEM STEM Incoherent elastic
INTERFERENCE. where, m = 0, 1, 2,... (1.2) otherwise, if it is half integral multiple of wavelength, the interference would be destructive.
 1.1 INTERFERENCE When two (or more than two) waves of the same frequency travel almost in the same direction and have a phase difference that remains constant with time, the resultant intensity of light
1.1 INTERFERENCE When two (or more than two) waves of the same frequency travel almost in the same direction and have a phase difference that remains constant with time, the resultant intensity of light
Lens Design I. Lecture 11: Imaging Herbert Gross. Summer term
 Lens Design I Lecture 11: Imaging 2015-06-29 Herbert Gross Summer term 2015 www.iap.uni-jena.de 2 Preliminary Schedule 1 13.04. Basics 2 20.04. Properties of optical systrems I 3 27.05. 4 04.05. Properties
Lens Design I Lecture 11: Imaging 2015-06-29 Herbert Gross Summer term 2015 www.iap.uni-jena.de 2 Preliminary Schedule 1 13.04. Basics 2 20.04. Properties of optical systrems I 3 27.05. 4 04.05. Properties
Refraction of Light. This bending of the ray is called refraction
 Refraction & Lenses Refraction of Light When a ray of light traveling through a transparent medium encounters a boundary leading into another transparent medium, part of the ray is reflected and part of
Refraction & Lenses Refraction of Light When a ray of light traveling through a transparent medium encounters a boundary leading into another transparent medium, part of the ray is reflected and part of
Supplementary Figure 1 Optimum transmissive mask design for shaping an incident light to a desired
 Supplementary Figure 1 Optimum transmissive mask design for shaping an incident light to a desired tangential form. (a) The light from the sources and scatterers in the half space (1) passes through the
Supplementary Figure 1 Optimum transmissive mask design for shaping an incident light to a desired tangential form. (a) The light from the sources and scatterers in the half space (1) passes through the
dq dt I = Irradiance or Light Intensity is Flux Φ per area A (W/m 2 ) Φ =
 Radiometry (From Intro to Optics, Pedrotti -4) Radiometry is measurement of Emag radiation (light) Consider a small spherical source Total energy radiating from the body over some time is Q total Radiant
Radiometry (From Intro to Optics, Pedrotti -4) Radiometry is measurement of Emag radiation (light) Consider a small spherical source Total energy radiating from the body over some time is Q total Radiant
Physics 123 Optics Review
 Physics 123 Optics Review I. Definitions & Facts concave converging convex diverging real image virtual image real object virtual object upright inverted dispersion nearsighted, farsighted near point,
Physics 123 Optics Review I. Definitions & Facts concave converging convex diverging real image virtual image real object virtual object upright inverted dispersion nearsighted, farsighted near point,
f. (5.3.1) So, the higher frequency means the lower wavelength. Visible part of light spectrum covers the range of wavelengths from
 Lecture 5-3 Interference and Diffraction of EM Waves During our previous lectures we have been talking about electromagnetic (EM) waves. As we know, harmonic waves of any type represent periodic process
Lecture 5-3 Interference and Diffraction of EM Waves During our previous lectures we have been talking about electromagnetic (EM) waves. As we know, harmonic waves of any type represent periodic process
Chapter 7: Geometrical Optics. The branch of physics which studies the properties of light using the ray model of light.
 Chapter 7: Geometrical Optics The branch of physics which studies the properties of light using the ray model of light. Overview Geometrical Optics Spherical Mirror Refraction Thin Lens f u v r and f 2
Chapter 7: Geometrical Optics The branch of physics which studies the properties of light using the ray model of light. Overview Geometrical Optics Spherical Mirror Refraction Thin Lens f u v r and f 2
3DEM > GENERAL METHODS. SINGLE PARTICLE RECONSTRUCTION (SPA): Introduction
 3DEM > GENERAL METHODS SINGLE PARTICLE RECONSTRUCTION (SPA): Introduction SINGLE PARTICLE RECONSTRUCTION > INTRODUCTION General principle of single particle reconstruction o 2D projection images of a 3D
3DEM > GENERAL METHODS SINGLE PARTICLE RECONSTRUCTION (SPA): Introduction SINGLE PARTICLE RECONSTRUCTION > INTRODUCTION General principle of single particle reconstruction o 2D projection images of a 3D
Control of Light. Emmett Ientilucci Digital Imaging and Remote Sensing Laboratory Chester F. Carlson Center for Imaging Science 8 May 2007
 Control of Light Emmett Ientilucci Digital Imaging and Remote Sensing Laboratory Chester F. Carlson Center for Imaging Science 8 May 007 Spectro-radiometry Spectral Considerations Chromatic dispersion
Control of Light Emmett Ientilucci Digital Imaging and Remote Sensing Laboratory Chester F. Carlson Center for Imaging Science 8 May 007 Spectro-radiometry Spectral Considerations Chromatic dispersion
Light: Geometric Optics
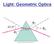 Light: Geometric Optics The Ray Model of Light Light very often travels in straight lines. We represent light using rays, which are straight lines emanating from an object. This is an idealization, but
Light: Geometric Optics The Ray Model of Light Light very often travels in straight lines. We represent light using rays, which are straight lines emanating from an object. This is an idealization, but
Chapter 38 Wave Optics (II)
 Chapter 38 Wave Optics (II) Initiation: Young s ideas on light were daring and imaginative, but he did not provide rigorous mathematical theory and, more importantly, he is arrogant. Progress: Fresnel,
Chapter 38 Wave Optics (II) Initiation: Young s ideas on light were daring and imaginative, but he did not provide rigorous mathematical theory and, more importantly, he is arrogant. Progress: Fresnel,
Scattering/Wave Terminology A few terms show up throughout the discussion of electron microscopy:
 1. Scattering and Diffraction Scattering/Wave Terology A few terms show up throughout the discussion of electron microscopy: First, what do we mean by the terms elastic and inelastic? These are both related
1. Scattering and Diffraction Scattering/Wave Terology A few terms show up throughout the discussion of electron microscopy: First, what do we mean by the terms elastic and inelastic? These are both related
MEASUREMENT OF THE WAVELENGTH WITH APPLICATION OF A DIFFRACTION GRATING AND A SPECTROMETER
 Warsaw University of Technology Faculty of Physics Physics Laboratory I P Irma Śledzińska 4 MEASUREMENT OF THE WAVELENGTH WITH APPLICATION OF A DIFFRACTION GRATING AND A SPECTROMETER 1. Fundamentals Electromagnetic
Warsaw University of Technology Faculty of Physics Physics Laboratory I P Irma Śledzińska 4 MEASUREMENT OF THE WAVELENGTH WITH APPLICATION OF A DIFFRACTION GRATING AND A SPECTROMETER 1. Fundamentals Electromagnetic
Ultrasonic Multi-Skip Tomography for Pipe Inspection
 18 th World Conference on Non destructive Testing, 16-2 April 212, Durban, South Africa Ultrasonic Multi-Skip Tomography for Pipe Inspection Arno VOLKER 1, Rik VOS 1 Alan HUNTER 1 1 TNO, Stieltjesweg 1,
18 th World Conference on Non destructive Testing, 16-2 April 212, Durban, South Africa Ultrasonic Multi-Skip Tomography for Pipe Inspection Arno VOLKER 1, Rik VOS 1 Alan HUNTER 1 1 TNO, Stieltjesweg 1,
Philip E. Plantz. Application Note. SL-AN-08 Revision C. Provided By: Microtrac, Inc. Particle Size Measuring Instrumentation
 A Conceptual, Non-Mathematical Explanation on the Use of Refractive Index in Laser Particle Size Measurement (Understanding the concept of refractive index and Mie Scattering in Microtrac Instruments and
A Conceptual, Non-Mathematical Explanation on the Use of Refractive Index in Laser Particle Size Measurement (Understanding the concept of refractive index and Mie Scattering in Microtrac Instruments and
Condenser Optics for Dark Field X-Ray Microscopy
 Condenser Optics for Dark Field X-Ray Microscopy S. J. Pfauntsch, A. G. Michette, C. J. Buckley Centre for X-Ray Science, Department of Physics, King s College London, Strand, London WC2R 2LS, UK Abstract.
Condenser Optics for Dark Field X-Ray Microscopy S. J. Pfauntsch, A. G. Michette, C. J. Buckley Centre for X-Ray Science, Department of Physics, King s College London, Strand, London WC2R 2LS, UK Abstract.
TEAMS National Competition High School Version Photometry 25 Questions
 TEAMS National Competition High School Version Photometry 25 Questions Page 1 of 14 Telescopes and their Lenses Although telescopes provide us with the extraordinary power to see objects miles away, the
TEAMS National Competition High School Version Photometry 25 Questions Page 1 of 14 Telescopes and their Lenses Although telescopes provide us with the extraordinary power to see objects miles away, the
2012 Imaging Science Ph.D. Comprehensive Examination June 15, :00AM to 1:00PM IMPORTANT INSTRUCTIONS
 2012 Imaging Science Ph.D. Comprehensive Examination June 15, 2012 9:00AM to 1:00PM IMPORTANT INSTRUCTIONS You must complete two (2) of the three (3) questions given for each of the core graduate classes.
2012 Imaging Science Ph.D. Comprehensive Examination June 15, 2012 9:00AM to 1:00PM IMPORTANT INSTRUCTIONS You must complete two (2) of the three (3) questions given for each of the core graduate classes.
12/7/2012. Biomolecular structure. Diffraction, X-ray crystallography, light- and electron microscopy. CD spectroscopy, mass spectrometry
 phase difference at a given distance constructive/destructive interference Biomolecular structure. Diffraction, X-ray crystallography, light- and electron microscopy. CD spectroscopy, mass spectrometry
phase difference at a given distance constructive/destructive interference Biomolecular structure. Diffraction, X-ray crystallography, light- and electron microscopy. CD spectroscopy, mass spectrometry
ISO INTERNATIONAL STANDARD. Particle size analysis Laser diffraction methods. Analyse granulométrique Méthodes par diffraction laser
 INTERNATIONAL STANDARD ISO 13320 First edition 2009-10-01 Corrected version 2009-12-01 Particle size analysis Laser diffraction methods Analyse granulométrique Méthodes par diffraction laser Reference
INTERNATIONAL STANDARD ISO 13320 First edition 2009-10-01 Corrected version 2009-12-01 Particle size analysis Laser diffraction methods Analyse granulométrique Méthodes par diffraction laser Reference
Chapter 24. Wave Optics. Wave Optics. The wave nature of light is needed to explain various phenomena
 Chapter 24 Wave Optics Wave Optics The wave nature of light is needed to explain various phenomena Interference Diffraction Polarization The particle nature of light was the basis for ray (geometric) optics
Chapter 24 Wave Optics Wave Optics The wave nature of light is needed to explain various phenomena Interference Diffraction Polarization The particle nature of light was the basis for ray (geometric) optics
Waves & Oscillations
 Physics 42200 Waves & Oscillations Lecture 42 Review Spring 2013 Semester Matthew Jones Final Exam Date:Tuesday, April 30 th Time:1:00 to 3:00 pm Room: Phys 112 You can bring two double-sided pages of
Physics 42200 Waves & Oscillations Lecture 42 Review Spring 2013 Semester Matthew Jones Final Exam Date:Tuesday, April 30 th Time:1:00 to 3:00 pm Room: Phys 112 You can bring two double-sided pages of
Distortion Correction for Conical Multiplex Holography Using Direct Object-Image Relationship
 Proc. Natl. Sci. Counc. ROC(A) Vol. 25, No. 5, 2001. pp. 300-308 Distortion Correction for Conical Multiplex Holography Using Direct Object-Image Relationship YIH-SHYANG CHENG, RAY-CHENG CHANG, AND SHIH-YU
Proc. Natl. Sci. Counc. ROC(A) Vol. 25, No. 5, 2001. pp. 300-308 Distortion Correction for Conical Multiplex Holography Using Direct Object-Image Relationship YIH-SHYANG CHENG, RAY-CHENG CHANG, AND SHIH-YU
PHYSICS 213 PRACTICE EXAM 3*
 PHYSICS 213 PRACTICE EXAM 3* *The actual exam will contain EIGHT multiple choice quiz-type questions covering concepts from lecture (16 points), ONE essay-type question covering an important fundamental
PHYSICS 213 PRACTICE EXAM 3* *The actual exam will contain EIGHT multiple choice quiz-type questions covering concepts from lecture (16 points), ONE essay-type question covering an important fundamental
Using a multipoint interferometer to measure the orbital angular momentum of light
 CHAPTER 3 Using a multipoint interferometer to measure the orbital angular momentum of light Recently it was shown that the orbital angular momentum of light can be measured using a multipoint interferometer,
CHAPTER 3 Using a multipoint interferometer to measure the orbital angular momentum of light Recently it was shown that the orbital angular momentum of light can be measured using a multipoint interferometer,
1. ABOUT INSTALLATION COMPATIBILITY SURESIM WORKFLOWS a. Workflow b. Workflow SURESIM TUTORIAL...
 SuReSim manual 1. ABOUT... 2 2. INSTALLATION... 2 3. COMPATIBILITY... 2 4. SURESIM WORKFLOWS... 2 a. Workflow 1... 3 b. Workflow 2... 4 5. SURESIM TUTORIAL... 5 a. Import Data... 5 b. Parameter Selection...
SuReSim manual 1. ABOUT... 2 2. INSTALLATION... 2 3. COMPATIBILITY... 2 4. SURESIM WORKFLOWS... 2 a. Workflow 1... 3 b. Workflow 2... 4 5. SURESIM TUTORIAL... 5 a. Import Data... 5 b. Parameter Selection...
6-1 LECTURE #6: OPTICAL PROPERTIES OF SOLIDS. Basic question: How do solids interact with light? The answers are linked to:
 LECTURE #6: OPTICAL PROPERTIES OF SOLIDS Basic question: How do solids interact with light? The answers are linked to: Properties of light inside a solid Mechanisms behind light reflection, absorption
LECTURE #6: OPTICAL PROPERTIES OF SOLIDS Basic question: How do solids interact with light? The answers are linked to: Properties of light inside a solid Mechanisms behind light reflection, absorption
Central Slice Theorem
 Central Slice Theorem Incident X-rays y f(x,y) R x r x Detected p(, x ) The thick line is described by xcos +ysin =R Properties of Fourier Transform F [ f ( x a)] F [ f ( x)] e j 2 a Spatial Domain Spatial
Central Slice Theorem Incident X-rays y f(x,y) R x r x Detected p(, x ) The thick line is described by xcos +ysin =R Properties of Fourier Transform F [ f ( x a)] F [ f ( x)] e j 2 a Spatial Domain Spatial
Module 18: Diffraction-I Lecture 18: Diffraction-I
 Module 18: iffraction-i Lecture 18: iffraction-i Our discussion of interference in the previous chapter considered the superposition of two waves. The discussion can be generalized to a situation where
Module 18: iffraction-i Lecture 18: iffraction-i Our discussion of interference in the previous chapter considered the superposition of two waves. The discussion can be generalized to a situation where
UNIT VI OPTICS ALL THE POSSIBLE FORMULAE
 58 UNIT VI OPTICS ALL THE POSSIBLE FORMULAE Relation between focal length and radius of curvature of a mirror/lens, f = R/2 Mirror formula: Magnification produced by a mirror: m = - = - Snell s law: 1
58 UNIT VI OPTICS ALL THE POSSIBLE FORMULAE Relation between focal length and radius of curvature of a mirror/lens, f = R/2 Mirror formula: Magnification produced by a mirror: m = - = - Snell s law: 1
( ) = First Bessel function, x = π Dθ
 Observational Astronomy Image formation Complex Pupil Function (CPF): (3.3.1) CPF = P( r,ϕ )e ( ) ikw r,ϕ P( r,ϕ ) = Transmittance of the aperture (unobscured P = 1, obscured P = 0 ) k = π λ = Wave number
Observational Astronomy Image formation Complex Pupil Function (CPF): (3.3.1) CPF = P( r,ϕ )e ( ) ikw r,ϕ P( r,ϕ ) = Transmittance of the aperture (unobscured P = 1, obscured P = 0 ) k = π λ = Wave number
Blob-Representation of Multidimensional Objects and Surfaces
 Blob-Representation of Multidimensional Objects and Surfaces Edgar Garduño and Gabor T. Herman Department of Computer Science The Graduate Center City University of New York Presentation Outline Reconstruction
Blob-Representation of Multidimensional Objects and Surfaces Edgar Garduño and Gabor T. Herman Department of Computer Science The Graduate Center City University of New York Presentation Outline Reconstruction
AP* Optics Free Response Questions
 AP* Optics Free Response Questions 1978 Q5 MIRRORS An object 6 centimeters high is placed 30 centimeters from a concave mirror of focal length 10 centimeters as shown above. (a) On the diagram above, locate
AP* Optics Free Response Questions 1978 Q5 MIRRORS An object 6 centimeters high is placed 30 centimeters from a concave mirror of focal length 10 centimeters as shown above. (a) On the diagram above, locate
AP Physics: Curved Mirrors and Lenses
 The Ray Model of Light Light often travels in straight lines. We represent light using rays, which are straight lines emanating from an object. This is an idealization, but is very useful for geometric
The Ray Model of Light Light often travels in straight lines. We represent light using rays, which are straight lines emanating from an object. This is an idealization, but is very useful for geometric
Chapter 3 Geometrical Optics
 Chapter 3 Geometrical Optics Gabriel Popescu University of Illinois at Urbana Champaign Beckman Institute Quantitative Light Imaging Laboratory http://light.ece.uiuc.edu Principles of Optical Imaging Electrical
Chapter 3 Geometrical Optics Gabriel Popescu University of Illinois at Urbana Champaign Beckman Institute Quantitative Light Imaging Laboratory http://light.ece.uiuc.edu Principles of Optical Imaging Electrical
Aberrations in Holography
 Aberrations in Holography D Padiyar, J Padiyar 1070 Commerce St suite A, San Marcos, CA 92078 dinesh@triple-take.com joy@triple-take.com Abstract. The Seidel aberrations are described as they apply to
Aberrations in Holography D Padiyar, J Padiyar 1070 Commerce St suite A, San Marcos, CA 92078 dinesh@triple-take.com joy@triple-take.com Abstract. The Seidel aberrations are described as they apply to
diffraction patterns obtained with convergent electron beams yield more information than patterns obtained with parallel electron beams:
 CBED-Patterns Principle of CBED diffraction patterns obtained with convergent electron beams yield more information than patterns obtained with parallel electron beams: specimen thickness more precise
CBED-Patterns Principle of CBED diffraction patterns obtained with convergent electron beams yield more information than patterns obtained with parallel electron beams: specimen thickness more precise
Simple Spatial Domain Filtering
 Simple Spatial Domain Filtering Binary Filters Non-phase-preserving Fourier transform planes Simple phase-step filters (for phase-contrast imaging) Amplitude inverse filters, related to apodization Contrast
Simple Spatial Domain Filtering Binary Filters Non-phase-preserving Fourier transform planes Simple phase-step filters (for phase-contrast imaging) Amplitude inverse filters, related to apodization Contrast
DESIGNER S NOTEBOOK Proximity Detection and Link Budget By Tom Dunn July 2011
 INTELLIGENT OPTO SENSOR Number 38 DESIGNER S NOTEBOOK Proximity Detection and Link Budget By Tom Dunn July 2011 Overview TAOS proximity sensors operate by flashing an infrared (IR) light towards a surface
INTELLIGENT OPTO SENSOR Number 38 DESIGNER S NOTEBOOK Proximity Detection and Link Budget By Tom Dunn July 2011 Overview TAOS proximity sensors operate by flashing an infrared (IR) light towards a surface
The Death of the Aerial Image
 Tutor50.doc: Version 5/9/05 T h e L i t h o g r a p h y E x p e r t (August 005) The Death of the Aerial Image Chris A. Mack, KLA-Tencor, FINLE Division, Austin, Texas The aerial image is, quite literally,
Tutor50.doc: Version 5/9/05 T h e L i t h o g r a p h y E x p e r t (August 005) The Death of the Aerial Image Chris A. Mack, KLA-Tencor, FINLE Division, Austin, Texas The aerial image is, quite literally,
Be careful not to leave your fingerprints on the optical surfaces of lenses or Polaroid sheets.
 POLARIZATION OF LIGHT REFERENCES Halliday, D. and Resnick, A., Physics, 4 th edition, New York: John Wiley & Sons, Inc, 1992, Volume II, Chapter 48-1, 48-2, 48-3. (2weights) (1weight-exercises 1 and 3
POLARIZATION OF LIGHT REFERENCES Halliday, D. and Resnick, A., Physics, 4 th edition, New York: John Wiley & Sons, Inc, 1992, Volume II, Chapter 48-1, 48-2, 48-3. (2weights) (1weight-exercises 1 and 3
Chapter 25. Wave Optics
 Chapter 25 Wave Optics Interference Light waves interfere with each other much like mechanical waves do All interference associated with light waves arises when the electromagnetic fields that constitute
Chapter 25 Wave Optics Interference Light waves interfere with each other much like mechanical waves do All interference associated with light waves arises when the electromagnetic fields that constitute
Optical Ptychography Imaging
 Optical Ptychography Imaging Summer Project Annafee Azad Supervisors: Dr Fucai Zhang Prof Ian Robinson Summer 2014 23 October 2014 Optical Ptychography Imaging P a g e 2 Abstract This report details a
Optical Ptychography Imaging Summer Project Annafee Azad Supervisors: Dr Fucai Zhang Prof Ian Robinson Summer 2014 23 October 2014 Optical Ptychography Imaging P a g e 2 Abstract This report details a
Chapter 2: Wave Optics
 Chapter : Wave Optics P-1. We can write a plane wave with the z axis taken in the direction of the wave vector k as u(,) r t Acos tkzarg( A) As c /, T 1/ and k / we can rewrite the plane wave as t z u(,)
Chapter : Wave Optics P-1. We can write a plane wave with the z axis taken in the direction of the wave vector k as u(,) r t Acos tkzarg( A) As c /, T 1/ and k / we can rewrite the plane wave as t z u(,)
Physics I : Oscillations and Waves Prof. S Bharadwaj Department of Physics & Meteorology Indian Institute of Technology, Kharagpur
 Physics I : Oscillations and Waves Prof. S Bharadwaj Department of Physics & Meteorology Indian Institute of Technology, Kharagpur Lecture - 20 Diffraction - I We have been discussing interference, the
Physics I : Oscillations and Waves Prof. S Bharadwaj Department of Physics & Meteorology Indian Institute of Technology, Kharagpur Lecture - 20 Diffraction - I We have been discussing interference, the
Chapter 36. Diffraction. Copyright 2014 John Wiley & Sons, Inc. All rights reserved.
 Chapter 36 Diffraction Copyright 36-1 Single-Slit Diffraction Learning Objectives 36.01 Describe the diffraction of light waves by a narrow opening and an edge, and also describe the resulting interference
Chapter 36 Diffraction Copyright 36-1 Single-Slit Diffraction Learning Objectives 36.01 Describe the diffraction of light waves by a narrow opening and an edge, and also describe the resulting interference
CoE4TN4 Image Processing. Chapter 5 Image Restoration and Reconstruction
 CoE4TN4 Image Processing Chapter 5 Image Restoration and Reconstruction Image Restoration Similar to image enhancement, the ultimate goal of restoration techniques is to improve an image Restoration: a
CoE4TN4 Image Processing Chapter 5 Image Restoration and Reconstruction Image Restoration Similar to image enhancement, the ultimate goal of restoration techniques is to improve an image Restoration: a
Figure 1 - Refraction
 Geometrical optics Introduction Refraction When light crosses the interface between two media having different refractive indices (e.g. between water and air) a light ray will appear to change its direction
Geometrical optics Introduction Refraction When light crosses the interface between two media having different refractive indices (e.g. between water and air) a light ray will appear to change its direction
Chapter 7. Widely Tunable Monolithic Laser Diodes
 Chapter 7 Widely Tunable Monolithic Laser Diodes We have seen in Chapters 4 and 5 that the continuous tuning range λ is limited by λ/λ n/n g, where n is the index change and n g the group index of the
Chapter 7 Widely Tunable Monolithic Laser Diodes We have seen in Chapters 4 and 5 that the continuous tuning range λ is limited by λ/λ n/n g, where n is the index change and n g the group index of the
Chapter 8: Physical Optics
 Chapter 8: Physical Optics Whether light is a particle or a wave had puzzled physicists for centuries. In this chapter, we only analyze light as a wave using basic optical concepts such as interference
Chapter 8: Physical Optics Whether light is a particle or a wave had puzzled physicists for centuries. In this chapter, we only analyze light as a wave using basic optical concepts such as interference
Michelson Interferometer
 Michelson Interferometer The Michelson interferometer uses the interference of two reflected waves The third, beamsplitting, mirror is partially reflecting ( half silvered, except it s a thin Aluminum
Michelson Interferometer The Michelson interferometer uses the interference of two reflected waves The third, beamsplitting, mirror is partially reflecting ( half silvered, except it s a thin Aluminum
Fourier Transforms. Laboratory & Computational Physics 2
 Fourier Transforms Laboratory & Computational Physics 2 Last compiled August 8, 2017 1 Contents 1 Introduction 3 1.1 Prelab questions................................ 3 2 Background theory 5 2.1 Physical
Fourier Transforms Laboratory & Computational Physics 2 Last compiled August 8, 2017 1 Contents 1 Introduction 3 1.1 Prelab questions................................ 3 2 Background theory 5 2.1 Physical
THREE-DIMENSIONA L ELECTRON MICROSCOP Y OF MACROMOLECULAR ASSEMBLIE S. Visualization of Biological Molecules in Their Native Stat e.
 THREE-DIMENSIONA L ELECTRON MICROSCOP Y OF MACROMOLECULAR ASSEMBLIE S Visualization of Biological Molecules in Their Native Stat e Joachim Frank CHAPTER 1 Introduction 1 1 The Electron Microscope and
THREE-DIMENSIONA L ELECTRON MICROSCOP Y OF MACROMOLECULAR ASSEMBLIE S Visualization of Biological Molecules in Their Native Stat e Joachim Frank CHAPTER 1 Introduction 1 1 The Electron Microscope and
Fourier Transforms. Laboratory & Comp. Physics 2
 Fourier Transforms Laboratory & Comp. Physics 2 Last compiled August 8, 2017 Contents 1 Introduction 3 1.1 Prelab questions............ 3 2 Background theory 6 2.1 Physical discussion of Fourier transforms.................
Fourier Transforms Laboratory & Comp. Physics 2 Last compiled August 8, 2017 Contents 1 Introduction 3 1.1 Prelab questions............ 3 2 Background theory 6 2.1 Physical discussion of Fourier transforms.................
