Projective spaces and Bézout s theorem
|
|
|
- Emily Maxwell
- 5 years ago
- Views:
Transcription
1 Projective spaces and Bézout s theorem êaû{0 Mijia Lai 5 \ laimijia@sjtu.edu.cn
2 Outline 1. History 2. Projective spaces 3. Conics and cubics 4. Bézout s theorem and the resultant 5. Cayley-Bacharach theorem 6. Pappus s theorem and Pascal s theorem
3 Chronology of developments leading to algebraic geometry (300 B.C.) Greeks: Euclid, Apollonius,... study of conics I (Middle Age) Arabs,... algebra, good notation of algebra, (First half of 17th century) Fermat, Descartes,... analytic geometry, )ÛAÛ (Start of 19th century) Monge, Poncelet, Klein,... projective geometry, KAÛ
4 Chronology of developments leading to algebraic geometry (300 B.C.) Greeks: Euclid, Apollonius,... study of conics I (Middle Age) Arabs,... algebra, good notation of algebra, (First half of 17th century) Fermat, Descartes,... analytic geometry, )ÛAÛ (Start of 19th century) Monge, Poncelet, Klein,... projective geometry, KAÛ
5 Chronology of developments leading to algebraic geometry (300 B.C.) Greeks: Euclid, Apollonius,... study of conics I (Middle Age) Arabs,... algebra, good notation of algebra, (First half of 17th century) Fermat, Descartes,... analytic geometry, )ÛAÛ (Start of 19th century) Monge, Poncelet, Klein,... projective geometry, KAÛ
6 Chronology of developments leading to algebraic geometry (300 B.C.) Greeks: Euclid, Apollonius,... study of conics I (Middle Age) Arabs,... algebra, good notation of algebra, (First half of 17th century) Fermat, Descartes,... analytic geometry, )ÛAÛ (Start of 19th century) Monge, Poncelet, Klein,... projective geometry, KAÛ
7 Main theme of algebraic geometry (Second half of 19th century) Riemann, Plücker, Hilbert, Noether,... Algebraic geometry, êaû Study of the solutions of algebraic equations. The study is naturally connected with commutative algebra, complex analysis, differential geometry, number theory, projective geometry, topology, etc.
8 Main theme of algebraic geometry (Second half of 19th century) Riemann, Plücker, Hilbert, Noether,... Algebraic geometry, êaû Study of the solutions of algebraic equations. The study is naturally connected with commutative algebra, complex analysis, differential geometry, number theory, projective geometry, topology, etc.
9 Main theme of algebraic geometry (Second half of 19th century) Riemann, Plücker, Hilbert, Noether,... Algebraic geometry, êaû Study of the solutions of algebraic equations. The study is naturally connected with commutative algebra, complex analysis, differential geometry, number theory, projective geometry, topology, etc.
10 Plane curves in Cartesian coordinates Lines are of the form ax + by + c = 0.
11 Plane curves in Cartesian coordinates Lines are of the form ax + by + c = 0. Ellipse x 2 a 2 + y 2 b 2 = 1.
12 Plane curves in Cartesian coordinates Lines are of the form ax + by + c = 0. Ellipse Parabola x 2 a 2 + y 2 b 2 = 1. y = ax 2.
13 Plane curves in Cartesian coordinates Lines are of the form ax + by + c = 0. Ellipse Parabola Hyperbola x 2 a 2 + y 2 b 2 = 1. y = ax 2. x 2 a 2 y 2 b 2 = 1.
14 Study from transformation-invariant point view One can choose coordinates freely, e.g., one makes a linear transformation x = ax + by, y = cx + dy. Algebraic equation changes, but the shape does not change. Motivated by Perspective in drawing, which was introduced by Italian Renaissance painters and architects, one could also freely move the plane in R 3 and consider projection of curve onto various planes. In doing so, one should add points at infinity to a plane to make the projection a bijection. This extended plane is called the projective plane RP 2.
15 Study from transformation-invariant point view One can choose coordinates freely, e.g., one makes a linear transformation x = ax + by, y = cx + dy. Algebraic equation changes, but the shape does not change. Motivated by Perspective in drawing, which was introduced by Italian Renaissance painters and architects, one could also freely move the plane in R 3 and consider projection of curve onto various planes. In doing so, one should add points at infinity to a plane to make the projection a bijection. This extended plane is called the projective plane RP 2.
16 Perspective
17
18 Projection between two planes Light coming from O, there is no image for the line m P in Q, similarly, there is no pre-image for the line n Q in P. The solution is adding both planes a line at infinity.
19 Projective spaces A formal definition of RP 2 : R 3 \ (0, 0, 0)/, where (x, y, z) (x, y, z ) if there exists λ 0 such that (x, y, z) = λ(x, y, z ). It can be viewed as the set of all lines in R 3 passing through origin. We use the homogeneous coordinates [x : y : z] to denote a point in the projective plane, where x, y, z are not all zero. Projective plane can be viewed as the union of plane z = 1 and lines that are parallel to z = 1 ( points at infinity ).
20 Plane curve curve in the Projective plane Any polynomial g(x, y) R[x, y] of degree n can be homogenized by z n g( x z, y z ). Examples: g(x, y) = 3x + 5y 2 2, after homogenization, we get f (x, y, z) = 3xz + 5y 2 2z 2, a homogeneous polynomial in x, y, z. f (x, y, z) = 0 RP 2 g(x, y) = 0 {z = 1} points at infinity.
21 Plane curve curve in the Projective plane Any polynomial g(x, y) R[x, y] of degree n can be homogenized by z n g( x z, y z ). Examples: g(x, y) = 3x + 5y 2 2, after homogenization, we get f (x, y, z) = 3xz + 5y 2 2z 2, a homogeneous polynomial in x, y, z. f (x, y, z) = 0 RP 2 g(x, y) = 0 {z = 1} points at infinity.
22 Within this identification, we could study zeros of homogeneous polynomials in RP 2. They are usual plane curves with points at infinity added. Degree one (line): ax + by + cz = 0. Degree two (quadratic curve): ax 2 + by 2 + cz 2 + dxy + exz + fyz = 0. Degree three (cubic curve): ax 3 + by jxyz = 0. }{{} 10 terms
23 Within this identification, we could study zeros of homogeneous polynomials in RP 2. They are usual plane curves with points at infinity added. Degree one (line): ax + by + cz = 0. Degree two (quadratic curve): ax 2 + by 2 + cz 2 + dxy + exz + fyz = 0. Degree three (cubic curve): ax 3 + by jxyz = 0. }{{} 10 terms
24 Classification of quadratic curves in RP 2 x = ax + by + cz, y = dx + ey + fz, z = gx + hy + iz is called a linear transformation from RP 2 RP 2. Theorem Any curve of degree 2 in RP 2 can be transformed into one the following types: x 2 = 0, a double line; x 2 + y 2 = 0, a point; x 2 y 2 = 0, two lines, x 2 + y 2 + z 2 = 0, the empty set; x 2 + y 2 z 2 = 0, the unit circle (conic).
25 Classification of quadratic curves in RP 2 x = ax + by + cz, y = dx + ey + fz, z = gx + hy + iz is called a linear transformation from RP 2 RP 2. Theorem Any curve of degree 2 in RP 2 can be transformed into one the following types: x 2 = 0, a double line; x 2 + y 2 = 0, a point; x 2 y 2 = 0, two lines, x 2 + y 2 + z 2 = 0, the empty set; x 2 + y 2 z 2 = 0, the unit circle (conic).
26 Conics Ellipses, parabolas, hyperbolas are all same as circles. (They all arise as conic sections, i.e., intersection of a plane with a cone in various position, thus from projective point view they are the same) Conic sections
27 Cubics A cubic curve is irreducible if it cannot factor out degree 1 or 2 factors. Theorem Any irreducible cubic curve can be transformed into y 2 = x 3 + ax 2 + bx + c. In complex projective plane, such a curve looks like a torus, so it is called an elliptic curve.
28 Cubics A cubic curve is irreducible if it cannot factor out degree 1 or 2 factors. Theorem Any irreducible cubic curve can be transformed into y 2 = x 3 + ax 2 + bx + c. In complex projective plane, such a curve looks like a torus, so it is called an elliptic curve.
29 Cubics A cubic curve is irreducible if it cannot factor out degree 1 or 2 factors. Theorem Any irreducible cubic curve can be transformed into y 2 = x 3 + ax 2 + bx + c. In complex projective plane, such a curve looks like a torus, so it is called an elliptic curve.
30 Common zeros: solutions of algebraic systems Examples: 3x + 2y 1 = 0 and 3x + 2y 5 = 0 By homogenization, they become 3x + 2y z = 0 and 3x + 2y 5z = 0, by eliminating z, we get 3x + 2y = 0, and z = 0, thus they intersect at [ 2, 3, 0] RP 2. This is a point at infinity. So in projective plane, any two lines intersect at exactly one point. Example: x 2 y 2 = 1, x y = 0 By homogenization, they become x 2 y 2 = z 2 and x y = 0, it follows that z = 0, and x = y, thus they intersect at [1 : 1 : 0], but the intersection has a multiplicity 2.
31 Bézout s theorem Theorem (Bézout) Let f = 0 and g = 0 be two homogeneous polynomials in x, y, z variables of degree n and m respectively, assume they don t have any common component, then they intersect at most m n points in RP 2. Assumption as above, f and g intersect at exactly m n points, counting multiplicities, in the complex projective plane.
32 Resultant Given two polynomials f (x) = a n x n + + a 0 and g(x) = b m x m + + b 0, the resultant R(f, g) is defined to be R(f, g) = a m n b n m (αi β j ), where α i are roots of f (x), and β j are those of g(x). (By fundamental theorem of algebra, α i, β j exist as complex numbers) Proposition R(f, g) = 0 if and only if f and g have a common root.
33 In terms of coefficients, we have a n a n 1 a 0 a n a n 1 a 0 R(f, g) = a n a n 1 a 0 b m b 0 b m b 0 b m b 0
34 Determine a quadratic curve Any two points determine a line uniquely. How many points determine a quadratic curve uniquely? Heuristics: suppose the curve is ax 2 + bxy + cy 2 + dx + ey + f = 0, then plugging given points, we will get a system of linear equations on a, b, c, d, e, f - the six unknowns. Multiplying by a non-zero constant results in the same curve, so in general if given five points, we get five equations for six unknowns, from linear algebra, we know the solution set is at least one-dimensional.
35 Determine a quadratic curve Any two points determine a line uniquely. How many points determine a quadratic curve uniquely? Heuristics: suppose the curve is ax 2 + bxy + cy 2 + dx + ey + f = 0, then plugging given points, we will get a system of linear equations on a, b, c, d, e, f - the six unknowns. Multiplying by a non-zero constant results in the same curve, so in general if given five points, we get five equations for six unknowns, from linear algebra, we know the solution set is at least one-dimensional.
36 Uniqueness Uniqueness of such curve relies on Bézout s theorem (2 2 < 5). Namely, the given five points should be in the general position. Theorem Any five points in RP 2, no three of which are collinear, lie on exactly one conic. Theorem Any five points in RP 2, no four of which are collinear, lie on exactly one quadratic curve.
37 Uniqueness Uniqueness of such curve relies on Bézout s theorem (2 2 < 5). Namely, the given five points should be in the general position. Theorem Any five points in RP 2, no three of which are collinear, lie on exactly one conic. Theorem Any five points in RP 2, no four of which are collinear, lie on exactly one quadratic curve.
38 Uniqueness Uniqueness of such curve relies on Bézout s theorem (2 2 < 5). Namely, the given five points should be in the general position. Theorem Any five points in RP 2, no three of which are collinear, lie on exactly one conic. Theorem Any five points in RP 2, no four of which are collinear, lie on exactly one quadratic curve.
39 Cubic curve For a cubic curve, the same linear algebra reason suggests that any nine points can determine a cubic curve. What about the uniqueness? The issue is subtle as 9 = 3 3. Theorem (Cayley-Bacharach) Let P(x, y) = 0 and Q(x, y) = 0 be two cubic curves that intersect (over C) in precisely nine distinct points p 1,, p 9. Let R(x, y) be a cubic polynomial that vanishes on eight of these points (say p 1,, p 8 ). Then R is a linear combination of P and Q, in particular, R also vanishes on the ninth point p 9.
40 Cubic curve For a cubic curve, the same linear algebra reason suggests that any nine points can determine a cubic curve. What about the uniqueness? The issue is subtle as 9 = 3 3. Theorem (Cayley-Bacharach) Let P(x, y) = 0 and Q(x, y) = 0 be two cubic curves that intersect (over C) in precisely nine distinct points p 1,, p 9. Let R(x, y) be a cubic polynomial that vanishes on eight of these points (say p 1,, p 8 ). Then R is a linear combination of P and Q, in particular, R also vanishes on the ninth point p 9.
41 Pappus theorem Theorem (Pappus) Let l, l be two distinct lines, let A 1, A 2, A 3 be three distinct points on l not on l, and let B 1, B 2, B 3 be three distinct points on l not on l. Suppose that for ij = 12, 23, 31, the line A i B j and A j B i intersect at C ij. Then the three points C 12, C 23 and C 31 are collinear.
42 Pascal s theorem Theorem (Pascal) Let A 1, A 2, A 3, B 1, B 2, B 3 be distinct points on a conic σ. Suppose that for ij = 12, 23, 31, the lines A i B j and A j B i intersect at C ij. Then the points C 12, C 23 and C 31 are collinear.
43 References and further reading topics References: 1. Robert Bix, Conics and Cubics g Úng 2. Frances Kirwan, Complex Algebraic Curves E ê 3. Terence Tao, Pappus s theorem and elliptic curves, His blog: What s new? Figure out the multiplicity mentioned in this lecture. Why certain cubic curves are called Elliptic curves? Resultant
Dubna 2018: lines on cubic surfaces
 Dubna 2018: lines on cubic surfaces Ivan Cheltsov 20th July 2018 Lecture 1: projective plane Complex plane Definition A line in C 2 is a subset that is given by ax + by + c = 0 for some complex numbers
Dubna 2018: lines on cubic surfaces Ivan Cheltsov 20th July 2018 Lecture 1: projective plane Complex plane Definition A line in C 2 is a subset that is given by ax + by + c = 0 for some complex numbers
ADDITION LAW ON ELLIPTIC CURVES
 ADDITION LAW ON ELLIPTIC CURVES JORDAN HISEL Abstract. This paper will explore projective spaces and elliptic curves. Addition on elliptic curves is rather unintuitive, but with a rigorous definition,
ADDITION LAW ON ELLIPTIC CURVES JORDAN HISEL Abstract. This paper will explore projective spaces and elliptic curves. Addition on elliptic curves is rather unintuitive, but with a rigorous definition,
EM225 Projective Geometry Part 2
 EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
EM225 Projective Geometry Part 2 eview In projective geometry, we regard figures as being the same if they can be made to appear the same as in the diagram below. In projective geometry: a projective point
Chapter 15: Functions of Several Variables
 Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
Chapter 15: Functions of Several Variables Section 15.1 Elementary Examples a. Notation: Two Variables b. Example c. Notation: Three Variables d. Functions of Several Variables e. Examples from the Sciences
LECTURE 13, THURSDAY APRIL 1, 2004
 LECTURE 13, THURSDAY APRIL 1, 2004 FRANZ LEMMERMEYER 1. Parametrizing Curves of Genus 0 As a special case of the theorem that curves of genus 0, in particular those with the maximal number of double points,
LECTURE 13, THURSDAY APRIL 1, 2004 FRANZ LEMMERMEYER 1. Parametrizing Curves of Genus 0 As a special case of the theorem that curves of genus 0, in particular those with the maximal number of double points,
Section 12.2: Quadric Surfaces
 Section 12.2: Quadric Surfaces Goals: 1. To recognize and write equations of quadric surfaces 2. To graph quadric surfaces by hand Definitions: 1. A quadric surface is the three-dimensional graph of an
Section 12.2: Quadric Surfaces Goals: 1. To recognize and write equations of quadric surfaces 2. To graph quadric surfaces by hand Definitions: 1. A quadric surface is the three-dimensional graph of an
Manifolds (Relates to text Sec. 36)
 22M:132 Fall 07 J. Simon Manifolds (Relates to text Sec. 36) Introduction. Manifolds are one of the most important classes of topological spaces (the other is function spaces). Much of your work in subsequent
22M:132 Fall 07 J. Simon Manifolds (Relates to text Sec. 36) Introduction. Manifolds are one of the most important classes of topological spaces (the other is function spaces). Much of your work in subsequent
Quadric Surfaces. Philippe B. Laval. Spring 2012 KSU. Philippe B. Laval (KSU) Quadric Surfaces Spring /
 .... Quadric Surfaces Philippe B. Laval KSU Spring 2012 Philippe B. Laval (KSU) Quadric Surfaces Spring 2012 1 / 15 Introduction A quadric surface is the graph of a second degree equation in three variables.
.... Quadric Surfaces Philippe B. Laval KSU Spring 2012 Philippe B. Laval (KSU) Quadric Surfaces Spring 2012 1 / 15 Introduction A quadric surface is the graph of a second degree equation in three variables.
Quadric Surfaces. Philippe B. Laval. Today KSU. Philippe B. Laval (KSU) Quadric Surfaces Today 1 / 24
 Quadric Surfaces Philippe B. Laval KSU Today Philippe B. Laval (KSU) Quadric Surfaces Today 1 / 24 Introduction A quadric surface is the graph of a second degree equation in three variables. The general
Quadric Surfaces Philippe B. Laval KSU Today Philippe B. Laval (KSU) Quadric Surfaces Today 1 / 24 Introduction A quadric surface is the graph of a second degree equation in three variables. The general
Chapter 8.1 Conic Sections/Parabolas. Honors Pre-Calculus Rogers High School
 Chapter 8.1 Conic Sections/Parabolas Honors Pre-Calculus Rogers High School Introduction to Conic Sections Conic sections are defined geometrically as the result of the intersection of a plane with a right
Chapter 8.1 Conic Sections/Parabolas Honors Pre-Calculus Rogers High School Introduction to Conic Sections Conic sections are defined geometrically as the result of the intersection of a plane with a right
Duality of Plane Curves
 Duality of Plane Curves Maria Monks December 1, 2011 Abstract The dual of an algebraic curve C in RP 2 defined by the polynomial equation f(x, y, z) = ( f x ) f f 0 is the locus of points (a, b, c) : (a,
Duality of Plane Curves Maria Monks December 1, 2011 Abstract The dual of an algebraic curve C in RP 2 defined by the polynomial equation f(x, y, z) = ( f x ) f f 0 is the locus of points (a, b, c) : (a,
Some Highlights along a Path to Elliptic Curves
 Some Highlights along a Path to Elliptic Curves Part 6: Rational Points on Elliptic Curves Steven J. Wilson, Fall 016 Outline of the Series 1. The World of Algebraic Curves. Conic Sections and Rational
Some Highlights along a Path to Elliptic Curves Part 6: Rational Points on Elliptic Curves Steven J. Wilson, Fall 016 Outline of the Series 1. The World of Algebraic Curves. Conic Sections and Rational
Triple lines on curves
 Triple lines on curves Frank de Zeeuw EPFL (Switzerland) IPAM: Algebraic Techniques for Combinatorial Geometry - LA - May 13, 2014 Japanese-Swiss Workshop on Combinatorics - Tokyo - June 5, 2014 I will
Triple lines on curves Frank de Zeeuw EPFL (Switzerland) IPAM: Algebraic Techniques for Combinatorial Geometry - LA - May 13, 2014 Japanese-Swiss Workshop on Combinatorics - Tokyo - June 5, 2014 I will
CS-9645 Introduction to Computer Vision Techniques Winter 2019
 Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Name. Center axis. Introduction to Conic Sections
 Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Name Introduction to Conic Sections Center axis This introduction to conic sections is going to focus on what they some of the skills needed to work with their equations and graphs. year, we will only
Perspective Mappings. Contents
 Perspective Mappings David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy
Perspective Mappings David Eberly, Geometric Tools, Redmond WA 98052 https://www.geometrictools.com/ This work is licensed under the Creative Commons Attribution 4.0 International License. To view a copy
Generalizing the Converse to Pascal s Theorem via Hyperplane Arrangements and the Cayley-Bacharach Theorem
 arxiv:1108.3368v1 [math.ag] 16 Aug 2011 Generalizing the Converse to Pascal s Theorem via Hyperplane Arrangements and the Cayley-Bacharach Theorem Will Traves August 18, 2011 Abstract Using a new point
arxiv:1108.3368v1 [math.ag] 16 Aug 2011 Generalizing the Converse to Pascal s Theorem via Hyperplane Arrangements and the Cayley-Bacharach Theorem Will Traves August 18, 2011 Abstract Using a new point
ALGEBRA II UNIT X: Conic Sections Unit Notes Packet
 Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
Name: Period: ALGEBRA II UNIT X: Conic Sections Unit Notes Packet Algebra II Unit 10 Plan: This plan is subject to change at the teacher s discretion. Section Topic Formative Work Due Date 10.3 Circles
Key Idea. It is not helpful to plot points to sketch a surface. Mainly we use traces and intercepts to sketch
 Section 12.7 Quadric surfaces 12.7 1 Learning outcomes After completing this section, you will inshaallah be able to 1. know what are quadric surfaces 2. how to sketch quadric surfaces 3. how to identify
Section 12.7 Quadric surfaces 12.7 1 Learning outcomes After completing this section, you will inshaallah be able to 1. know what are quadric surfaces 2. how to sketch quadric surfaces 3. how to identify
4 = 1 which is an ellipse of major axis 2 and minor axis 2. Try the plane z = y2
 12.6 Quadrics and Cylinder Surfaces: Example: What is y = x? More correctly what is {(x,y,z) R 3 : y = x}? It s a plane. What about y =? Its a cylinder surface. What about y z = Again a cylinder surface
12.6 Quadrics and Cylinder Surfaces: Example: What is y = x? More correctly what is {(x,y,z) R 3 : y = x}? It s a plane. What about y =? Its a cylinder surface. What about y z = Again a cylinder surface
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
 Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Math 1330 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text. We start
Conics on the Cubic Surface
 MAAC 2004 George Mason University Conics on the Cubic Surface Will Traves U.S. Naval Academy USNA Trident Project This talk is a preliminary report on joint work with MIDN 1/c Andrew Bashelor and my colleague
MAAC 2004 George Mason University Conics on the Cubic Surface Will Traves U.S. Naval Academy USNA Trident Project This talk is a preliminary report on joint work with MIDN 1/c Andrew Bashelor and my colleague
1.6 Quadric Surfaces Brief review of Conic Sections 74 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE. Figure 1.18: Parabola y = 2x 2
 7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
7 CHAPTER 1. VECTORS AND THE GEOMETRY OF SPACE Figure 1.18: Parabola y = x 1.6 Quadric Surfaces Figure 1.19: Parabola x = y 1.6.1 Brief review of Conic Sections You may need to review conic sections for
Conic Sections. College Algebra
 Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Conic Sections College Algebra Conic Sections A conic section, or conic, is a shape resulting from intersecting a right circular cone with a plane. The angle at which the plane intersects the cone determines
Geometry: Conic Sections
 Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
Conic Sections Introduction When a right circular cone is intersected by a plane, as in figure 1 below, a family of four types of curves results. Because of their relationship to the cone, they are called
MATH 110 analytic geometry Conics. The Parabola
 1 MATH 11 analytic geometry Conics The graph of a second-degree equation in the coordinates x and y is called a conic section or, more simply, a conic. This designation derives from the fact that the curve
1 MATH 11 analytic geometry Conics The graph of a second-degree equation in the coordinates x and y is called a conic section or, more simply, a conic. This designation derives from the fact that the curve
Partial Derivatives. Partial Derivatives. Partial Derivatives. Partial Derivatives. Partial Derivatives. Partial Derivatives
 In general, if f is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant. By the definition of a derivative, we have Then we are really
In general, if f is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant. By the definition of a derivative, we have Then we are really
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Chapter 9. Linear algebra applications in geometry
 Chapter 9. Linear algebra applications in geometry C.O.S. Sorzano Biomedical Engineering August 25, 2013 9. Linear algebra applications in geometry August 25, 2013 1 / 73 Outline 9 Linear algebra applications
Chapter 9. Linear algebra applications in geometry C.O.S. Sorzano Biomedical Engineering August 25, 2013 9. Linear algebra applications in geometry August 25, 2013 1 / 73 Outline 9 Linear algebra applications
What you will learn today
 What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
What you will learn today Conic Sections (in 2D coordinates) Cylinders (3D) Quadric Surfaces (3D) Vectors and the Geometry of Space 1/24 Parabolas ellipses Hyperbolas Shifted Conics Conic sections result
Algebraic Geometry of Segmentation and Tracking
 Ma191b Winter 2017 Geometry of Neuroscience Geometry of lines in 3-space and Segmentation and Tracking This lecture is based on the papers: Reference: Marco Pellegrini, Ray shooting and lines in space.
Ma191b Winter 2017 Geometry of Neuroscience Geometry of lines in 3-space and Segmentation and Tracking This lecture is based on the papers: Reference: Marco Pellegrini, Ray shooting and lines in space.
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
1 Affine and Projective Coordinate Notation
 CS348a: Computer Graphics Handout #9 Geometric Modeling Original Handout #9 Stanford University Tuesday, 3 November 992 Original Lecture #2: 6 October 992 Topics: Coordinates and Transformations Scribe:
CS348a: Computer Graphics Handout #9 Geometric Modeling Original Handout #9 Stanford University Tuesday, 3 November 992 Original Lecture #2: 6 October 992 Topics: Coordinates and Transformations Scribe:
TNM079 Modeling & Animation Lecture 6 (Implicit surfaces)
 TNM079 Modeling & Animation Lecture 6 (Implicit surfaces) Mark Eric Dieckmann, Media and Information Technology, ITN Linköpings universitet Campus Norrköping SE-60174 Norrköping May 4, 2016 Content of
TNM079 Modeling & Animation Lecture 6 (Implicit surfaces) Mark Eric Dieckmann, Media and Information Technology, ITN Linköpings universitet Campus Norrköping SE-60174 Norrköping May 4, 2016 Content of
Graphing Techniques. Domain (, ) Range (, ) Squaring Function f(x) = x 2 Domain (, ) Range [, ) f( x) = x 2
 Graphing Techniques In this chapter, we will take our knowledge of graphs of basic functions and expand our ability to graph polynomial and rational functions using common sense, zeros, y-intercepts, stretching
Graphing Techniques In this chapter, we will take our knowledge of graphs of basic functions and expand our ability to graph polynomial and rational functions using common sense, zeros, y-intercepts, stretching
f (Pijk ) V. may form the Riemann sum: . Definition. The triple integral of f over the rectangular box B is defined to f (x, y, z) dv = lim
 Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Projective geometry for Computer Vision
 Department of Computer Science and Engineering IIT Delhi NIT, Rourkela March 27, 2010 Overview Pin-hole camera Why projective geometry? Reconstruction Computer vision geometry: main problems Correspondence
Department of Computer Science and Engineering IIT Delhi NIT, Rourkela March 27, 2010 Overview Pin-hole camera Why projective geometry? Reconstruction Computer vision geometry: main problems Correspondence
Interpretations and Models. Chapter Axiomatic Systems and Incidence Geometry
 Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Interpretations and Models Chapter 2.1-2.4 - Axiomatic Systems and Incidence Geometry Axiomatic Systems in Mathematics The gold standard for rigor in an area of mathematics Not fully achieved in most areas
Topic 2.3: Tangent Planes, Differentiability, and Linear Approximations. Textbook: Section 14.4
 Topic 2.3: Tangent Planes, Differentiability, and Linear Approximations Textbook: Section 14.4 Warm-Up: Graph the Cone & the Paraboloid paraboloid f (x, y) = x 2 + y 2 cone g(x, y) = x 2 + y 2 Do you notice
Topic 2.3: Tangent Planes, Differentiability, and Linear Approximations Textbook: Section 14.4 Warm-Up: Graph the Cone & the Paraboloid paraboloid f (x, y) = x 2 + y 2 cone g(x, y) = x 2 + y 2 Do you notice
Unit 12 Topics in Analytic Geometry - Classwork
 Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
Unit 1 Topics in Analytic Geometry - Classwork Back in Unit 7, we delved into the algebra and geometry of lines. We showed that lines can be written in several forms: a) the general form: Ax + By + C =
9.3 Hyperbolas and Rotation of Conics
 9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
9.3 Hyperbolas and Rotation of Conics Copyright Cengage Learning. All rights reserved. What You Should Learn Write equations of hyperbolas in standard form. Find asymptotes of and graph hyperbolas. Use
Generation of lattices of points for bivariate interpolation
 Generation of lattices of points for bivariate interpolation J. M. Carnicer and M. Gasca Departamento de Matemática Aplicada. University of Zaragoza, Spain Abstract. Principal lattices in the plane are
Generation of lattices of points for bivariate interpolation J. M. Carnicer and M. Gasca Departamento de Matemática Aplicada. University of Zaragoza, Spain Abstract. Principal lattices in the plane are
Rational Bezier Curves
 Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
Rational Bezier Curves Use of homogeneous coordinates Rational spline curve: define a curve in one higher dimension space, project it down on the homogenizing variable Mathematical formulation: n P(u)
The Normals to a Parabola and the Real Roots of a Cubic
 The Normals to a Parabola and the Real Roots of a Cubic Manjinder S. Bains CSU, Chico J. B. Thoo Yuba College March 6, 7 Around b.c. Apollonius of Perga wrote Conics, a collection of books that includes
The Normals to a Parabola and the Real Roots of a Cubic Manjinder S. Bains CSU, Chico J. B. Thoo Yuba College March 6, 7 Around b.c. Apollonius of Perga wrote Conics, a collection of books that includes
Provide a drawing. Mark any line with three points in blue color.
 Math 3181 Name: Dr. Franz Rothe August 18, 2014 All3181\3181_fall14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Math 3181 Name: Dr. Franz Rothe August 18, 2014 All3181\3181_fall14h1.tex Homework has to be turned in this handout. For extra space, use the back pages, or blank pages between. The homework can be done
Multivariable Calculus
 Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Multivariable Calculus Chapter 10 Topics in Analytic Geometry (Optional) 1. Inclination of a line p. 5. Circles p. 4 9. Determining Conic Type p. 13. Angle between lines p. 6. Parabolas p. 5 10. Rotation
Part 0. The Background: Projective Geometry, Transformations and Estimation
 Part 0 The Background: Projective Geometry, Transformations and Estimation La reproduction interdite (The Forbidden Reproduction), 1937, René Magritte. Courtesy of Museum Boijmans van Beuningen, Rotterdam.
Part 0 The Background: Projective Geometry, Transformations and Estimation La reproduction interdite (The Forbidden Reproduction), 1937, René Magritte. Courtesy of Museum Boijmans van Beuningen, Rotterdam.
We start by looking at a double cone. Think of this as two pointy ice cream cones that are connected at the small tips:
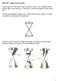 Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Math 1330 Chapter 8 Conic Sections In this chapter, we will study conic sections (or conics). It is helpful to know exactly what a conic section is. This topic is covered in Chapter 8 of the online text.
Surfaces Beyond Classification
 Chapter XII Surfaces Beyond Classification In most of the textbooks which present topological classification of compact surfaces the classification is the top result. However the topology of 2- manifolds
Chapter XII Surfaces Beyond Classification In most of the textbooks which present topological classification of compact surfaces the classification is the top result. However the topology of 2- manifolds
12.6 Cylinders and Quadric Surfaces
 12 Vectors and the Geometry of Space 12.6 and Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and We have already looked at two special types of surfaces:
12 Vectors and the Geometry of Space 12.6 and Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and We have already looked at two special types of surfaces:
Chapter 9 Topics in Analytic Geometry
 Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Chapter 9 Topics in Analytic Geometry What You ll Learn: 9.1 Introduction to Conics: Parabolas 9.2 Ellipses 9.3 Hyperbolas 9.5 Parametric Equations 9.6 Polar Coordinates 9.7 Graphs of Polar Equations 9.1
Chapter 3. Quadric hypersurfaces. 3.1 Quadric hypersurfaces Denition.
 Chapter 3 Quadric hypersurfaces 3.1 Quadric hypersurfaces. 3.1.1 Denition. Denition 1. In an n-dimensional ane space A; given an ane frame fo;! e i g: A quadric hypersurface in A is a set S consisting
Chapter 3 Quadric hypersurfaces 3.1 Quadric hypersurfaces. 3.1.1 Denition. Denition 1. In an n-dimensional ane space A; given an ane frame fo;! e i g: A quadric hypersurface in A is a set S consisting
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS
 CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
CHAPTER 8 QUADRATIC RELATIONS AND CONIC SECTIONS Big IDEAS: 1) Writing equations of conic sections ) Graphing equations of conic sections 3) Solving quadratic systems Section: Essential Question 8-1 Apply
= f (a, b) + (hf x + kf y ) (a,b) +
 Chapter 14 Multiple Integrals 1 Double Integrals, Iterated Integrals, Cross-sections 2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals
Chapter 14 Multiple Integrals 1 Double Integrals, Iterated Integrals, Cross-sections 2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals
Ex. 1-3: Put each circle below in the correct equation form as listed!! above, then determine the center and radius of each circle.
 Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
Day 1 Conics - Circles Equation of a Circle The circle with center (h, k) and radius r is the set of all points (x, y) that satisfies!! (x h) 2 + (y k) 2 = r 2 Ex. 1-3: Put each circle below in the correct
Sung-Eui Yoon ( 윤성의 )
 CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
CS480: Computer Graphics Curves and Surfaces Sung-Eui Yoon ( 윤성의 ) Course URL: http://jupiter.kaist.ac.kr/~sungeui/cg Today s Topics Surface representations Smooth curves Subdivision 2 Smooth Curves and
REVIEW I MATH 254 Calculus IV. Exam I (Friday, April 29) will cover sections
 REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
Homogeneous coordinates, lines, screws and twists
 Homogeneous coordinates, lines, screws and twists In lecture 1 of module 2, a brief mention was made of homogeneous coordinates, lines in R 3, screws and twists to describe the general motion of a rigid
Homogeneous coordinates, lines, screws and twists In lecture 1 of module 2, a brief mention was made of homogeneous coordinates, lines in R 3, screws and twists to describe the general motion of a rigid
RATIONAL CURVES ON SMOOTH CUBIC HYPERSURFACES. Contents 1. Introduction 1 2. The proof of Theorem References 9
 RATIONAL CURVES ON SMOOTH CUBIC HYPERSURFACES IZZET COSKUN AND JASON STARR Abstract. We prove that the space of rational curves of a fixed degree on any smooth cubic hypersurface of dimension at least
RATIONAL CURVES ON SMOOTH CUBIC HYPERSURFACES IZZET COSKUN AND JASON STARR Abstract. We prove that the space of rational curves of a fixed degree on any smooth cubic hypersurface of dimension at least
Notes for Lecture 10
 COS 533: Advanced Cryptography Lecture 10 (October 16, 2017) Lecturer: Mark Zhandry Princeton University Scribe: Dylan Altschuler Notes for Lecture 10 1 Motivation for Elliptic Curves Diffie-Hellman For
COS 533: Advanced Cryptography Lecture 10 (October 16, 2017) Lecturer: Mark Zhandry Princeton University Scribe: Dylan Altschuler Notes for Lecture 10 1 Motivation for Elliptic Curves Diffie-Hellman For
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Sameer Agarwal LECTURE 1 Image Formation 1.1. The geometry of image formation We begin by considering the process of image formation when a
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Sameer Agarwal LECTURE 1 Image Formation 1.1. The geometry of image formation We begin by considering the process of image formation when a
form. We will see that the parametric form is the most common representation of the curve which is used in most of these cases.
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 36 Curve Representation Welcome everybody to the lectures on computer graphics.
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 36 Curve Representation Welcome everybody to the lectures on computer graphics.
SECONDARY DRAFT SYLLABUS. 2. Representation of functions. 3. Types of functions. 4. Composition of functions (two and three)
 et et et CLASS IX Topic :Set Language et et 1. Describing and representing sets SECONDARY DRAFT SYLLABUS Able to describe a set in Descriptive, Set- builder and roster forms and through Venn diagram. Use
et et et CLASS IX Topic :Set Language et et 1. Describing and representing sets SECONDARY DRAFT SYLLABUS Able to describe a set in Descriptive, Set- builder and roster forms and through Venn diagram. Use
Graphics and Interaction Transformation geometry and homogeneous coordinates
 433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
Elementary Functions
 Elementary Functions Part 1, Functions Lecture 1.2a, Graphs of Functions: Introduction Dr. Ken W. Smith Sam Houston State University Spring 2013 Smith (SHSU) Elementary Functions Spring 2013 1 / 37 Representing
Elementary Functions Part 1, Functions Lecture 1.2a, Graphs of Functions: Introduction Dr. Ken W. Smith Sam Houston State University Spring 2013 Smith (SHSU) Elementary Functions Spring 2013 1 / 37 Representing
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates
 COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
Geometric Modeling of Curves
 Curves Locus of a point moving with one degree of freedom Locus of a one-dimensional parameter family of point Mathematically defined using: Explicit equations Implicit equations Parametric equations (Hermite,
Curves Locus of a point moving with one degree of freedom Locus of a one-dimensional parameter family of point Mathematically defined using: Explicit equations Implicit equations Parametric equations (Hermite,
4. Definition: topological space, open set, topology, trivial topology, discrete topology.
 Topology Summary Note to the reader. If a statement is marked with [Not proved in the lecture], then the statement was stated but not proved in the lecture. Of course, you don t need to know the proof.
Topology Summary Note to the reader. If a statement is marked with [Not proved in the lecture], then the statement was stated but not proved in the lecture. Of course, you don t need to know the proof.
x 6 + λ 2 x 6 = for the curve y = 1 2 x3 gives f(1, 1 2 ) = λ actually has another solution besides λ = 1 2 = However, the equation λ
 Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Math 0 Prelim I Solutions Spring 010 1. Let f(x, y) = x3 y for (x, y) (0, 0). x 6 + y (4 pts) (a) Show that the cubic curves y = x 3 are level curves of the function f. Solution. Substituting y = x 3 in
Section 2.5. Functions and Surfaces
 Section 2.5. Functions and Surfaces ² Brief review for one variable functions and curves: A (one variable) function is rule that assigns to each member x in a subset D in R 1 a unique real number denoted
Section 2.5. Functions and Surfaces ² Brief review for one variable functions and curves: A (one variable) function is rule that assigns to each member x in a subset D in R 1 a unique real number denoted
Mid-Chapter Quiz: Lessons 7-1 through 7-3
 Write an equation for and graph a parabola with the given focus F and vertex V 1. F(1, 5), V(1, 3) Because the focus and vertex share the same x coordinate, the graph is vertical. The focus is (h, k +
Write an equation for and graph a parabola with the given focus F and vertex V 1. F(1, 5), V(1, 3) Because the focus and vertex share the same x coordinate, the graph is vertical. The focus is (h, k +
Computer Vision I - Algorithms and Applications: Multi-View 3D reconstruction
 Computer Vision I - Algorithms and Applications: Multi-View 3D reconstruction Carsten Rother 09/12/2013 Computer Vision I: Multi-View 3D reconstruction Roadmap this lecture Computer Vision I: Multi-View
Computer Vision I - Algorithms and Applications: Multi-View 3D reconstruction Carsten Rother 09/12/2013 Computer Vision I: Multi-View 3D reconstruction Roadmap this lecture Computer Vision I: Multi-View
PERIODS OF ALGEBRAIC VARIETIES
 PERIODS OF ALGEBRAIC VARIETIES OLIVIER DEBARRE Abstract. The periods of a compact complex algebraic manifold X are the integrals of its holomorphic 1-forms over paths. These integrals are in general not
PERIODS OF ALGEBRAIC VARIETIES OLIVIER DEBARRE Abstract. The periods of a compact complex algebraic manifold X are the integrals of its holomorphic 1-forms over paths. These integrals are in general not
Computer Vision I - Appearance-based Matching and Projective Geometry
 Computer Vision I - Appearance-based Matching and Projective Geometry Carsten Rother 05/11/2015 Computer Vision I: Image Formation Process Roadmap for next four lectures Computer Vision I: Image Formation
Computer Vision I - Appearance-based Matching and Projective Geometry Carsten Rother 05/11/2015 Computer Vision I: Image Formation Process Roadmap for next four lectures Computer Vision I: Image Formation
Isometries. 1 Identifying Isometries
 Isometries 1 Identifying Isometries 1. Modeling isometries as dynamic maps. 2. GeoGebra files: isoguess1.ggb, isoguess2.ggb, isoguess3.ggb, isoguess4.ggb. 3. Guessing isometries. 4. What can you construct
Isometries 1 Identifying Isometries 1. Modeling isometries as dynamic maps. 2. GeoGebra files: isoguess1.ggb, isoguess2.ggb, isoguess3.ggb, isoguess4.ggb. 3. Guessing isometries. 4. What can you construct
MEI Desmos Tasks for AS Pure
 Task 1: Coordinate Geometry Intersection of a line and a curve 1. Add a quadratic curve, e.g. y = x² 4x + 1 2. Add a line, e.g. y = x 3 3. Select the points of intersection of the line and the curve. What
Task 1: Coordinate Geometry Intersection of a line and a curve 1. Add a quadratic curve, e.g. y = x² 4x + 1 2. Add a line, e.g. y = x 3 3. Select the points of intersection of the line and the curve. What
1. Complex Projective Surfaces
 1. Complex Projective Surfaces 1.1 Notation and preliminaries In this section we fix some notations and some basic results (we do not prove: good references are [Bea78] and [BPV84]) we will use in these
1. Complex Projective Surfaces 1.1 Notation and preliminaries In this section we fix some notations and some basic results (we do not prove: good references are [Bea78] and [BPV84]) we will use in these
Jorg s Graphics Lecture Notes Coordinate Spaces 1
 Jorg s Graphics Lecture Notes Coordinate Spaces Coordinate Spaces Computer Graphics: Objects are rendered in the Euclidean Plane. However, the computational space is better viewed as one of Affine Space
Jorg s Graphics Lecture Notes Coordinate Spaces Coordinate Spaces Computer Graphics: Objects are rendered in the Euclidean Plane. However, the computational space is better viewed as one of Affine Space
Special Quartics with Triple Points
 Journal for Geometry and Graphics Volume 6 (2002), No. 2, 111 119. Special Quartics with Triple Points Sonja Gorjanc Faculty of Civil Engineering, University of Zagreb V. Holjevca 15, 10010 Zagreb, Croatia
Journal for Geometry and Graphics Volume 6 (2002), No. 2, 111 119. Special Quartics with Triple Points Sonja Gorjanc Faculty of Civil Engineering, University of Zagreb V. Holjevca 15, 10010 Zagreb, Croatia
MAT 3271: Selected Solutions to the Assignment 6
 Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
Chapter 2: Major Exercises MAT 3271: Selected Solutions to the Assignment 6 1. Since a projective plan is a model of incidence geometry, Incidence Axioms 1-3 and Propositions 2.1-2.5 (which follow logically
PROJECTIVE SPACE AND THE PINHOLE CAMERA
 PROJECTIVE SPACE AND THE PINHOLE CAMERA MOUSA REBOUH Abstract. Here we provide (linear algebra) proofs of the ancient theorem of Pappus and the contemporary theorem of Desargues on collineations. We also
PROJECTIVE SPACE AND THE PINHOLE CAMERA MOUSA REBOUH Abstract. Here we provide (linear algebra) proofs of the ancient theorem of Pappus and the contemporary theorem of Desargues on collineations. We also
CK 12 Algebra II with Trigonometry Concepts 1
 10.1 Parabolas with Vertex at the Origin Answers 1. up 2. left 3. down 4.focus: (0, 0.5), directrix: y = 0.5 5.focus: (0.0625, 0), directrix: x = 0.0625 6.focus: ( 1.25, 0), directrix: x = 1.25 7.focus:
10.1 Parabolas with Vertex at the Origin Answers 1. up 2. left 3. down 4.focus: (0, 0.5), directrix: y = 0.5 5.focus: (0.0625, 0), directrix: x = 0.0625 6.focus: ( 1.25, 0), directrix: x = 1.25 7.focus:
13.1 2/20/2018. Conic Sections. Conic Sections: Parabolas and Circles
 13 Conic Sections 13.1 Conic Sections: Parabolas and Circles 13.2 Conic Sections: Ellipses 13.3 Conic Sections: Hyperbolas 13.4 Nonlinear Systems of Equations 13.1 Conic Sections: Parabolas and Circles
13 Conic Sections 13.1 Conic Sections: Parabolas and Circles 13.2 Conic Sections: Ellipses 13.3 Conic Sections: Hyperbolas 13.4 Nonlinear Systems of Equations 13.1 Conic Sections: Parabolas and Circles
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS
 Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
SPECIAL TECHNIQUES-II
 SPECIAL TECHNIQUES-II Lecture 19: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Method of Images for a spherical conductor Example :A dipole near aconducting sphere The
SPECIAL TECHNIQUES-II Lecture 19: Electromagnetic Theory Professor D. K. Ghosh, Physics Department, I.I.T., Bombay Method of Images for a spherical conductor Example :A dipole near aconducting sphere The
KEMATH1 Calculus for Chemistry and Biochemistry Students. Francis Joseph H. Campeña, De La Salle University Manila
 KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
KEMATH1 Calculus for Chemistry and Biochemistry Students Francis Joseph H Campeña, De La Salle University Manila January 26, 2015 Contents 1 Conic Sections 2 11 A review of the coordinate system 2 12 Conic
Module 3: Graphing Quadratic Functions
 Haberman MTH 95 Section V Quadratic Equations and Functions Module 3 Graphing Quadratic Functions In this module, we'll review the graphing quadratic functions (you should have studied the graphs of quadratic
Haberman MTH 95 Section V Quadratic Equations and Functions Module 3 Graphing Quadratic Functions In this module, we'll review the graphing quadratic functions (you should have studied the graphs of quadratic
Elements of three dimensional geometry
 Lecture No-3 Elements of three dimensional geometr Distance formula in three dimension Let P( x1, 1, z1) and Q( x2, 2, z 2) be two points such that PQ is not parallel to one of the 2 2 2 coordinate axis
Lecture No-3 Elements of three dimensional geometr Distance formula in three dimension Let P( x1, 1, z1) and Q( x2, 2, z 2) be two points such that PQ is not parallel to one of the 2 2 2 coordinate axis
Know it. Control points. B Spline surfaces. Implicit surfaces
 Know it 15 B Spline Cur 14 13 12 11 Parametric curves Catmull clark subdivision Parametric surfaces Interpolating curves 10 9 8 7 6 5 4 3 2 Control points B Spline surfaces Implicit surfaces Bezier surfaces
Know it 15 B Spline Cur 14 13 12 11 Parametric curves Catmull clark subdivision Parametric surfaces Interpolating curves 10 9 8 7 6 5 4 3 2 Control points B Spline surfaces Implicit surfaces Bezier surfaces
Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane
 Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane Rafikul Alam Department of Mathematics IIT Guwahati Chain rule Theorem-A: Let x : R R n be differentiable at t 0 and f : R n R be differentiable
Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane Rafikul Alam Department of Mathematics IIT Guwahati Chain rule Theorem-A: Let x : R R n be differentiable at t 0 and f : R n R be differentiable
Final Exam Review Algebra Semester 1
 Final Exam Review Algebra 015-016 Semester 1 Name: Module 1 Find the inverse of each function. 1. f x 10 4x. g x 15x 10 Use compositions to check if the two functions are inverses. 3. s x 7 x and t(x)
Final Exam Review Algebra 015-016 Semester 1 Name: Module 1 Find the inverse of each function. 1. f x 10 4x. g x 15x 10 Use compositions to check if the two functions are inverses. 3. s x 7 x and t(x)
The point (x, y) lies on the circle of radius r and center (h, k) iff. x h y k r
 NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
NOTES +: ANALYTIC GEOMETRY NAME LESSON. GRAPHS OF EQUATIONS IN TWO VARIABLES (CIRCLES). Standard form of a Circle The point (x, y) lies on the circle of radius r and center (h, k) iff x h y k r Center:
. As x gets really large, the last terms drops off and f(x) ½x
 Pre-AP Algebra 2 Unit 8 -Lesson 3 End behavior of rational functions Objectives: Students will be able to: Determine end behavior by dividing and seeing what terms drop out as x Know that there will be
Pre-AP Algebra 2 Unit 8 -Lesson 3 End behavior of rational functions Objectives: Students will be able to: Determine end behavior by dividing and seeing what terms drop out as x Know that there will be
Topology of Plane Algebraic Curves. Enrique Acosta Jaramillo
 Topology of Plane Algebraic Curves Enrique Acosta Jaramillo May 11, 2008 Contents 1 The Real Projective Plane RP 2 2 1.1 Real Manifold Structure..................... 4 2 Topology of Curves over the Complex
Topology of Plane Algebraic Curves Enrique Acosta Jaramillo May 11, 2008 Contents 1 The Real Projective Plane RP 2 2 1.1 Real Manifold Structure..................... 4 2 Topology of Curves over the Complex
9.1: GRAPHING QUADRATICS ALGEBRA 1
 9.1: GRAPHING QUADRATICS ALGEBRA 1 OBJECTIVES I will be able to graph quadratics: Given in Standard Form Given in Vertex Form Given in Intercept Form What does the graph of a quadratic look like? https://www.desmos.com/calculator
9.1: GRAPHING QUADRATICS ALGEBRA 1 OBJECTIVES I will be able to graph quadratics: Given in Standard Form Given in Vertex Form Given in Intercept Form What does the graph of a quadratic look like? https://www.desmos.com/calculator
521493S Computer Graphics Exercise 2 Solution (Chapters 4-5)
 5493S Computer Graphics Exercise Solution (Chapters 4-5). Given two nonparallel, three-dimensional vectors u and v, how can we form an orthogonal coordinate system in which u is one of the basis vectors?
5493S Computer Graphics Exercise Solution (Chapters 4-5). Given two nonparallel, three-dimensional vectors u and v, how can we form an orthogonal coordinate system in which u is one of the basis vectors?
Three Dimensional Geometry. Linear Programming
 Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Chapter 10. Exploring Conic Sections
 Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
Chapter 10 Exploring Conic Sections Conics A conic section is a curve formed by the intersection of a plane and a hollow cone. Each of these shapes are made by slicing the cone and observing the shape
POLYHEDRAL GEOMETRY. Convex functions and sets. Mathematical Programming Niels Lauritzen Recall that a subset C R n is convex if
 POLYHEDRAL GEOMETRY Mathematical Programming Niels Lauritzen 7.9.2007 Convex functions and sets Recall that a subset C R n is convex if {λx + (1 λ)y 0 λ 1} C for every x, y C and 0 λ 1. A function f :
POLYHEDRAL GEOMETRY Mathematical Programming Niels Lauritzen 7.9.2007 Convex functions and sets Recall that a subset C R n is convex if {λx + (1 λ)y 0 λ 1} C for every x, y C and 0 λ 1. A function f :
5.1 Introduction to the Graphs of Polynomials
 Math 3201 5.1 Introduction to the Graphs of Polynomials In Math 1201/2201, we examined three types of polynomial functions: Constant Function - horizontal line such as y = 2 Linear Function - sloped line,
Math 3201 5.1 Introduction to the Graphs of Polynomials In Math 1201/2201, we examined three types of polynomial functions: Constant Function - horizontal line such as y = 2 Linear Function - sloped line,
