Branching Algorithms
|
|
|
- Gladys Clark
- 5 years ago
- Views:
Transcription
1 Lecture Branching Algorithms Author: Arkadiusz Soca la 1 Motivation Definition 1. Decision problem L Σ is called NP problem if there exists a predicate ψ P computable in polynomial time such that: 1. x L y y poly x x, y ψ such y is called a witness for x.. x L y x, y ψ. An common example of NP problem is Hamiltonian Cycle Input: A graph G Question: Does there exists a simple cycle of length V G? Suppose we know that y p x for some polynomial p. Then we can check every possible witness y in the total time of p x i poly x O p x poly x. i=0 The general question is how fast we can check entire space of witnesses and how well we can improve it. Also whether we can omit some part of that space. Suppose that we have an algorithm which works in O n time and that on our computer we can solve this problem up to n = 6. Note that if we improve our computer to be four times faster then we will be able to compute the problem up to n = 6 +. But if we improve algorithm to O n/ then we can solve the problem up to n = 5. So to sum up, our motivations are: theoretical question:,,how much we can speed up our algorithm?, solving real problems: it is better to improve algorithm than buy a new hardware, a new different view on algorithms for hard problems. Vertex Cover We study the following problem. Vertex Cover Input: A graph G and an integer k Question: Does there exist a set X V G of size at most k, such that every edge of G has at least one endpoint in G?
2 Theorem. Maximal vertex cover can be found in O n m time where n = V G and m = EG. Proof. For chosen subset of V G we can test if every of EG is covered. Testing every subset of V G can be done in total O n m time. Let s introduce O notation Definition 3. O fn = Ofn polyinput size. We decide to ignore polynomial factors almost always in the analysis, as they are theoretically irrelevant: O n n 100 O.0001 n..1 Fixed parameter tractability. Suppose we want to find a Vertex Cover, but of size not greater than some k. Let s say k = 0. Then we can use different approach than checking any subset not greater than k. Intuition: we want to create a recursion with depth bounded by k. Theorem 4. Vertex Cover can be solved in O k time and polynomial space. Proof. For any edge at least one end must be covered. So if we have any uncovered edge we must add to the cover one of the ends of this edge. We try both possibilities recursively. When we already have maximal number of vertices in the cover i.e. when k = 0 and we still have some edges uncovered then there is no solution in the current branch. The pseudocode of the algorithm: function VCG, k if EG = then return YES if k = 0 then return NO uv any ofeg return VCG u, k 1 or VCG v, k 1 end function Definition 5. Language L Σ is fixed parameter tractable FPT for parameter k : Σ N if it can be solved in Ofkx poly x time, for some computable function f. Parameter k in the definition above can be any function of input. For example it can be size of solution or some measure of the graph. The idea is to find parameters responsible for exponent in the complexity of the problem and separate them by multiplication from size of the input in polynomial. When the parameters are bounded then we can solve our problem fast in polynomial time for fixed parameters. Corollary 6. Vertex Cover is FPT for the size of the cover parameter.
3 Let s compare two algorithms for solving Vertex Cover problem: above algorithm which works in O k n time and checking all k-element possibilities in O n k time. For example if we put k = 10 then first solution works fine even for big values of n, e.g. n = 104. But the second solution even for n = 4 performs over one million operations, and for n = 8 over one billion. We can choose one of them depending on the values of k, n and some constant α : if k α n then VCG, k else Check all k-subsets. Let s analyse this algorithm for α = 3 4. For the first case we have O k O 3 n 4. For the second O n k So we have n 3 4 n = O n3 n! 3 4 n! 1 4 n. To estimate the last expression we can use Stirling s approximation: s s s! = Θ s. e 4 n! = O 1 4 n e n e n 1 4 n 3 4 n e 3 4 n = O Which is better than O n. For α = we can get even O 1.71 n.. Branching. n O 1.76 n. Now let s try another approach. We forget for a while about parameter k. Note that solving our problem for any graph with vertex degree not greater than is simple. Such graphs consist of paths and cycles only. We will use the following notation: Definition 7. v V G Nv = {u V G \ {v} : vu EV } Suppose that we have a vertex of a large degree in G. There are two possibilities: it is in Vertex Cover or all its neighbours are. This leads us to the following algorithm of finding minimal vertex cover: function VCG v vertex of maximal degree in G if degv then solve in polynomial time return min1+vcg v, degv+vcg v Nv end function Let s calculate time complexity of the above algorithm. We know that in the expression VCG v Nv we are deleting at least four vertices. So to obtain an estimation we can use a recursion
4 T n = T n 1 + T n 4. We want to find such x that T n x n. From recursion we have x n = x n 1 + x n 4. We can solve 1 = 1 x + 1 x 4 and get x Currently Oct 01 the best known algorithm works in O 0.88n O 1.3 n [3]. We can also estimate time complexity of VC in terms of parameter k. We have T k = T k 1 + T k 3, which leads us similarly as above to O k. Currently Oct 01 the best known FPT algorithm works in O1.738 k + kn [1]..3 Measure and Conquer. Let s consider slightly modified version of VC function VC3G if v V G degv = 0 then VC3G v else if v V G degv = 1 then 1+VC3G v Nv else v vertex of maximal degree in G if degv then solve in polynomial time else min1+vc3g v, degv+vc3g u Nu end function The idea is to introduce new measure for,,hardness of the instance. Note that vertices of degrees in {0, 1} are easy so we can assign them weight 0. Vertices of degree are a little harder so we assign them weight 1. Finally degree of greater weights are hard, so we assign them weight 1. For v chosen in algorithm we denote d = {u Nv, degu = }, d 3 = {u Nv, degu = 3}, d 4 = {u Nv, degu 4}. Then the recursion has the form T µ = T µ d d T We explain it in details: Expression T µ d d 3 1 µ d d 3 d 4 1. d neighbours of degree have now degree 1 change from weight 1 to weight 0 d 3 neighbours of degree 3 have now degree change from weight 1 to weight 1 1 deleting vertex v from G degv 3 so the weight is 1
5 Expression T µ d d 3 d 4 1 d deleting neighbours of degree with weights 1 d 3 deleting neighbours of degree 3 with weights 1 d 4 deleting neighbours of degree 4 with weights 1 1 deleting vertex v from G degv 3 so the weight is 1 Possibly other vertices the neighbours of the neighbours lose their degrees and weights but this expression is only upper bound so it is OK. For degv 4 in the worst case we have T µ = T µ 1 + T µ 5 when degv = 4 and all neighbours of v are of degree 4. And for degv = 3 the worst case is T µ T µ d 1 + T µ d 1 which is T µ T µ.5 when all neighbours of v are of degree. This leads us to O n. Note that we have chosen our weights basing on our intuition. We can choose them better. For example if we assign to vertices of degree 3 weight 0.99 then we obtain a slightly better complexity. So still we have the same algorithm, but we are improving our analysis of it. The above example and analysis can be found in the book of Fomin and Kratsch [4]. 3 Feedback Vertex Set Feedback Vertex Set Input: A graph G Question: What is a minimal power of X V G such that G \ X is a forest. We will be solving a dual problem of the above: Maximum Induced Forest Input: A graph G Question: What is a maximal power of Y V G such that G[X] is a forest. We will create recursive function MIFG, Y, Ŷ enlarging forest Y by any vertex v Y connected to the connected component of Y Ŷ and by an edge between v and Ŷ. To measure,,hardness of the instance we will take the following function: every v NŶ gets weight 1 every v NŶ gets weight Let s introduce notion of,,generalized neighbourhood N v = {u V G \ Y : in G[Y + v + u] exist path from v to u}. We call MIFG, Y, Ŷ recursively. Depending on N v we have the following cases: 1. For N v = 0 we take Y + = v.. For N v = 1 we also take Y + = v. 3. For N v = we do a branch:
6 Y + = v G = v, Y + = N v. If there is a solution Y which takes u 1 but no v nor u then Y u 1 + v is also a solution. N v = {u 1, u } so v is a leaf in Y u 1 + v. 4. For N v 3 we do a naive branch: Y + = v G = v Cases 1 and are simple. Let s analyse case 3. For simplicity we will be writing 3 instead of We are assuming N v =. Let a of them are in NŶ. Then we can estimate time T N T N 1 a a 1 + T N 1 a a 3. To analyse case 4 we use T N T N 1 degv 1 + T N 1 a a 3. If the current,,active component Ŷ has no neighbours then we select another connected component of G[Y ] as,,active. Every neighbour of the new,,active component lose on weight. If there is no connected component of Y with any neighbour then we take a vertex v of a maximal degree in V \ Y : If its degree is, then there are only cycles and paths in G Y so we can solve the problem in polynomial time. If its degree is 3, then we do a branch: Y + = v and Ŷ = {v} then we lose , because v has at least 3 neighbours, G = v then we lose from µ. By estimating above inequalities we can obtain O n. But this is also estimation for n n 3. The explanation of this fact is still open question Oct 01. The presented algorithm is due to Razgon [5]. Currently the fastest known algorithm for Feedback Vertex Set runs in O n []. References [1] Jianer Chen, Iyad A. Kanj, and Ge Xia. Improved upper bounds for vertex cover. Theor. Comput. Sci., : , 010. [] Fedor V. Fomin, Serge Gaspers, Artem V. Pyatkin, and Igor Razgon. On the minimum feedback vertex set problem: Exact and enumeration algorithms. Algorithmica, 5:93 307, 008. [3] Fedor V. Fomin, Fabrizio Grandoni, and Dieter Kratsch. A measure & conquer approach for the analysis of exact algorithms. J. ACM, 565, 009. [4] Fedor V. Fomin and Dieter Kratsch. Exact Exponential Algorithms. Springer, 010. [5] Igor Razgon. Exact computation of maximum induced forest. In Lars Arge and Rusins Freivalds, editors, SWAT, volume 4059 of Lecture Notes in Computer Science, pages Springer, 006.
Parameterized Algorithm for Eternal Vertex Cover
 Parameterized Algorithm for Eternal Vertex Cover Fedor V. Fomin a,1, Serge Gaspers b, Petr A. Golovach c, Dieter Kratsch d, Saket Saurabh e, a Department of Informatics, University of Bergen, N-5020 Bergen,
Parameterized Algorithm for Eternal Vertex Cover Fedor V. Fomin a,1, Serge Gaspers b, Petr A. Golovach c, Dieter Kratsch d, Saket Saurabh e, a Department of Informatics, University of Bergen, N-5020 Bergen,
On the minimum feedback vertex set problem: Exact and enumeration algorithms
 On the minimum feedback vertex set problem: Exact and enumeration algorithms Fedor V. Fomin Serge Gaspers Artem V. Pyatkin Igor Razgon November 26, 2007 Abstract We present a time O(1.7548 n ) algorithm
On the minimum feedback vertex set problem: Exact and enumeration algorithms Fedor V. Fomin Serge Gaspers Artem V. Pyatkin Igor Razgon November 26, 2007 Abstract We present a time O(1.7548 n ) algorithm
Simplicity is Beauty: Improved Upper Bounds for Vertex Cover
 Simplicity is Beauty: Improved Upper Bounds for Vertex Cover Jianer Chen, Iyad A. Kanj, and Ge Xia Department of Computer Science, Texas A&M University, College Station, TX 77843 email: {chen, gexia}@cs.tamu.edu
Simplicity is Beauty: Improved Upper Bounds for Vertex Cover Jianer Chen, Iyad A. Kanj, and Ge Xia Department of Computer Science, Texas A&M University, College Station, TX 77843 email: {chen, gexia}@cs.tamu.edu
Faster parameterized algorithm for Cluster Vertex Deletion
 Faster parameterized algorithm for Cluster Vertex Deletion Dekel Tsur arxiv:1901.07609v1 [cs.ds] 22 Jan 2019 Abstract In the Cluster Vertex Deletion problem the input is a graph G and an integer k. The
Faster parameterized algorithm for Cluster Vertex Deletion Dekel Tsur arxiv:1901.07609v1 [cs.ds] 22 Jan 2019 Abstract In the Cluster Vertex Deletion problem the input is a graph G and an integer k. The
An Improved Exact Algorithm for Undirected Feedback Vertex Set
 Noname manuscript No. (will be inserted by the editor) An Improved Exact Algorithm for Undirected Feedback Vertex Set Mingyu Xiao Hiroshi Nagamochi Received: date / Accepted: date Abstract A feedback vertex
Noname manuscript No. (will be inserted by the editor) An Improved Exact Algorithm for Undirected Feedback Vertex Set Mingyu Xiao Hiroshi Nagamochi Received: date / Accepted: date Abstract A feedback vertex
Improved Upper Bounds for Partial Vertex Cover
 Improved Upper Bounds for Partial Vertex Cover Joachim Kneis, Alexander Langer, Peter Rossmanith Dept. of Computer Science, RWTH Aachen University, Germany Abstract. The Partial Vertex Cover problem is
Improved Upper Bounds for Partial Vertex Cover Joachim Kneis, Alexander Langer, Peter Rossmanith Dept. of Computer Science, RWTH Aachen University, Germany Abstract. The Partial Vertex Cover problem is
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Dominating Set on Bipartite Graphs
 Dominating Set on Bipartite Graphs Mathieu Liedloff Abstract Finding a dominating set of minimum cardinality is an NP-hard graph problem, even when the graph is bipartite. In this paper we are interested
Dominating Set on Bipartite Graphs Mathieu Liedloff Abstract Finding a dominating set of minimum cardinality is an NP-hard graph problem, even when the graph is bipartite. In this paper we are interested
Linear Kernel for Planar Connected Dominating Set
 Linear Kernel for Planar Connected Dominating Set Daniel Lokshtanov Matthias Mnich Saket Saurabh Abstract We provide polynomial time data reduction rules for Connected Dominating Set on planar graphs and
Linear Kernel for Planar Connected Dominating Set Daniel Lokshtanov Matthias Mnich Saket Saurabh Abstract We provide polynomial time data reduction rules for Connected Dominating Set on planar graphs and
Directed Feedback Vertex Set Problem is FPT
 Directed Feedback Vertex Set Problem is FPT Jianer Chen Yang Liu Songjian Lu Department of Computer Science Texas A&M University College Station, TX 77843, USA {chen,yangliu,sjlu}@cs.tamu.edu Abstract
Directed Feedback Vertex Set Problem is FPT Jianer Chen Yang Liu Songjian Lu Department of Computer Science Texas A&M University College Station, TX 77843, USA {chen,yangliu,sjlu}@cs.tamu.edu Abstract
A Moderately Exponential Time Algorithm for Full Degree Spanning Tree
 A Moderately Exponential Time Algorithm for Full Degree Spanning Tree Serge Gaspers Saket Saurabh Alexey A. Stepanov Abstract We present a moderately exponential time exact algorithm for the wellstudied
A Moderately Exponential Time Algorithm for Full Degree Spanning Tree Serge Gaspers Saket Saurabh Alexey A. Stepanov Abstract We present a moderately exponential time exact algorithm for the wellstudied
New Upper Bounds for MAX-2-SAT and MAX-2-CSP w.r.t. the Average Variable Degree
 New Upper Bounds for MAX-2-SAT and MAX-2-CSP w.r.t. the Average Variable Degree Alexander Golovnev St. Petersburg University of the Russian Academy of Sciences, St. Petersburg, Russia alex.golovnev@gmail.com
New Upper Bounds for MAX-2-SAT and MAX-2-CSP w.r.t. the Average Variable Degree Alexander Golovnev St. Petersburg University of the Russian Academy of Sciences, St. Petersburg, Russia alex.golovnev@gmail.com
Minimal dominating sets in interval graphs and trees
 Minimal dominating sets in interval graphs and trees Petr A. Golovach a, Pinar Heggernes a, Mamadou Moustapha Kanté b, Dieter Kratsch c,, Yngve Villanger a a Department of Informatics, University of Bergen,
Minimal dominating sets in interval graphs and trees Petr A. Golovach a, Pinar Heggernes a, Mamadou Moustapha Kanté b, Dieter Kratsch c,, Yngve Villanger a a Department of Informatics, University of Bergen,
arxiv: v1 [cs.ds] 8 Jan 2019
![arxiv: v1 [cs.ds] 8 Jan 2019 arxiv: v1 [cs.ds] 8 Jan 2019](/thumbs/93/113547113.jpg) Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Fixed-Parameter Algorithm for 2-CNF Deletion Problem
 Fixed-Parameter Algorithm for 2-CNF Deletion Problem Igor Razgon Igor Razgon Computer Science Department University College Cork Ireland A brief introduction to the area of fixed-parameter algorithms 2
Fixed-Parameter Algorithm for 2-CNF Deletion Problem Igor Razgon Igor Razgon Computer Science Department University College Cork Ireland A brief introduction to the area of fixed-parameter algorithms 2
On Structural Parameterizations of the Matching Cut Problem
 On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
A 2k-Kernelization Algorithm for Vertex Cover Based on Crown Decomposition
 A 2k-Kernelization Algorithm for Vertex Cover Based on Crown Decomposition Wenjun Li a, Binhai Zhu b, a Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation, Changsha
A 2k-Kernelization Algorithm for Vertex Cover Based on Crown Decomposition Wenjun Li a, Binhai Zhu b, a Hunan Provincial Key Laboratory of Intelligent Processing of Big Data on Transportation, Changsha
Important separators and parameterized algorithms
 Important separators and parameterized algorithms Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary PCSS 2017 Vienna, Austria September
Important separators and parameterized algorithms Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary PCSS 2017 Vienna, Austria September
Convex Recoloring Revisited: Complexity and Exact Algorithms
 Convex Recoloring Revisited: Complexity and Exact Algorithms Iyad A. Kanj Dieter Kratsch Abstract We take a new look at the convex path recoloring (CPR), convex tree recoloring (CTR), and convex leaf recoloring
Convex Recoloring Revisited: Complexity and Exact Algorithms Iyad A. Kanj Dieter Kratsch Abstract We take a new look at the convex path recoloring (CPR), convex tree recoloring (CTR), and convex leaf recoloring
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Lecture 4: September 11, 2003
 Algorithmic Modeling and Complexity Fall 2003 Lecturer: J. van Leeuwen Lecture 4: September 11, 2003 Scribe: B. de Boer 4.1 Overview This lecture introduced Fixed Parameter Tractable (FPT) problems. An
Algorithmic Modeling and Complexity Fall 2003 Lecturer: J. van Leeuwen Lecture 4: September 11, 2003 Scribe: B. de Boer 4.1 Overview This lecture introduced Fixed Parameter Tractable (FPT) problems. An
Exponential time algorithms for the minimum dominating set problem on some graph classes
 Exponential time algorithms for the minimum dominating set problem on some graph classes Serge Gaspers University of Bergen Department of Informatics N-500 Bergen, Norway. gaspers@ii.uib.no Dieter Kratsch
Exponential time algorithms for the minimum dominating set problem on some graph classes Serge Gaspers University of Bergen Department of Informatics N-500 Bergen, Norway. gaspers@ii.uib.no Dieter Kratsch
A 2lk Kernel for l-component Order Connectivity
 A 2lk Kernel for l-component Order Connectivity Mithilesh Kumar 1 and Daniel Lokshtanov 2 1 Department of Informatics, University of Bergen Norway Mithilesh.Kumar@ii.uib.no 2 Department of Informatics,
A 2lk Kernel for l-component Order Connectivity Mithilesh Kumar 1 and Daniel Lokshtanov 2 1 Department of Informatics, University of Bergen Norway Mithilesh.Kumar@ii.uib.no 2 Department of Informatics,
Improved Parameterized Upper Bounds for Vertex Cover
 Improved Parameterized Upper Bounds for Vertex Cover Jianer Chen 1 Iyad A. Kanj 2 Ge Xia 3 1 Department of Computer Science, Texas A&M University, College Station, TX 77843, USA. This author was supported
Improved Parameterized Upper Bounds for Vertex Cover Jianer Chen 1 Iyad A. Kanj 2 Ge Xia 3 1 Department of Computer Science, Texas A&M University, College Station, TX 77843, USA. This author was supported
Iterative Compression and Exact Algorithms
 Iterative Compression and Exact Algorithms Fedor V Fomin Serge Gaspers Dieter Kratsch Mathieu Liedloff Saket Saurabh Abstract Iterative Compression has recently led to a number of breakthroughs in parameterized
Iterative Compression and Exact Algorithms Fedor V Fomin Serge Gaspers Dieter Kratsch Mathieu Liedloff Saket Saurabh Abstract Iterative Compression has recently led to a number of breakthroughs in parameterized
Further Improvement on Maximum Independent Set in Degree-4 Graphs
 Further Improvement on Maximum Independent Set in Degree-4 Graphs Mingyu Xiao School of Computer Science and Engineering, University of Electronic Science and Technology of China, China, myxiao@gmail.com
Further Improvement on Maximum Independent Set in Degree-4 Graphs Mingyu Xiao School of Computer Science and Engineering, University of Electronic Science and Technology of China, China, myxiao@gmail.com
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees
 Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Algorithm and Complexity of Disjointed Connected Dominating Set Problem on Trees Wei Wang joint with Zishen Yang, Xianliang Liu School of Mathematics and Statistics, Xi an Jiaotong University Dec 20, 2016
Minimal dominating sets in graph classes: combinatorial bounds and enumeration
 Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
CS 231: Algorithmic Problem Solving
 CS 231: Algorithmic Problem Solving Naomi Nishimura Module 7 Date of this version: January 28, 2019 WARNING: Drafts of slides are made available prior to lecture for your convenience. After lecture, slides
CS 231: Algorithmic Problem Solving Naomi Nishimura Module 7 Date of this version: January 28, 2019 WARNING: Drafts of slides are made available prior to lecture for your convenience. After lecture, slides
Solving Dominating Set in Larger Classes of Graphs: FPT Algorithms and Polynomial Kernels
 Solving Dominating Set in Larger Classes of Graphs: FPT Algorithms and Polynomial Kernels Geevarghese Philip, Venkatesh Raman, and Somnath Sikdar The Institute of Mathematical Sciences, Chennai, India.
Solving Dominating Set in Larger Classes of Graphs: FPT Algorithms and Polynomial Kernels Geevarghese Philip, Venkatesh Raman, and Somnath Sikdar The Institute of Mathematical Sciences, Chennai, India.
nonblocker: Parameterized Algorithmics for minimum dominating set
 nonblocker: Parameterized Algorithmics for minimum dominating set Frank Dehne 1, Michael Fellows 2, Henning Fernau 2,3, Elena Prieto 2, Frances Rosamond 2 1 School of Computer Science Carleton University,
nonblocker: Parameterized Algorithmics for minimum dominating set Frank Dehne 1, Michael Fellows 2, Henning Fernau 2,3, Elena Prieto 2, Frances Rosamond 2 1 School of Computer Science Carleton University,
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes
 Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Vertex Cover is Fixed-Parameter Tractable
 Vertex Cover is Fixed-Parameter Tractable CS 511 Iowa State University November 28, 2010 CS 511 (Iowa State University) Vertex Cover is Fixed-Parameter Tractable November 28, 2010 1 / 18 The Vertex Cover
Vertex Cover is Fixed-Parameter Tractable CS 511 Iowa State University November 28, 2010 CS 511 (Iowa State University) Vertex Cover is Fixed-Parameter Tractable November 28, 2010 1 / 18 The Vertex Cover
Approximation slides 1. An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs
 Approximation slides 1 An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs Approximation slides 2 Linear independence A collection of row vectors {v T i } are independent
Approximation slides 1 An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs Approximation slides 2 Linear independence A collection of row vectors {v T i } are independent
10. EXTENDING TRACTABILITY
 0. EXTENDING TRACTABILITY finding small vertex covers solving NP-hard problems on trees circular arc coverings vertex cover in bipartite graphs Lecture slides by Kevin Wayne Copyright 005 Pearson-Addison
0. EXTENDING TRACTABILITY finding small vertex covers solving NP-hard problems on trees circular arc coverings vertex cover in bipartite graphs Lecture slides by Kevin Wayne Copyright 005 Pearson-Addison
NP-Hard (A) (B) (C) (D) 3 n 2 n TSP-Min any Instance V, E Question: Hamiltonian Cycle TSP V, n 22 n E u, v V H
 Hard Problems What do you do when your problem is NP-Hard? Give up? (A) Solve a special case! (B) Find the hidden parameter! (Fixed parameter tractable problems) (C) Find an approximate solution. (D) Find
Hard Problems What do you do when your problem is NP-Hard? Give up? (A) Solve a special case! (B) Find the hidden parameter! (Fixed parameter tractable problems) (C) Find an approximate solution. (D) Find
Adjacent: Two distinct vertices u, v are adjacent if there is an edge with ends u, v. In this case we let uv denote such an edge.
 1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
Dual-Based Approximation Algorithms for Cut-Based Network Connectivity Problems
 Dual-Based Approximation Algorithms for Cut-Based Network Connectivity Problems Benjamin Grimmer bdg79@cornell.edu arxiv:1508.05567v2 [cs.ds] 20 Jul 2017 Abstract We consider a variety of NP-Complete network
Dual-Based Approximation Algorithms for Cut-Based Network Connectivity Problems Benjamin Grimmer bdg79@cornell.edu arxiv:1508.05567v2 [cs.ds] 20 Jul 2017 Abstract We consider a variety of NP-Complete network
Improved induced matchings in sparse graphs
 Improved induced matchings in sparse graphs Rok Erman 1, Lukasz Kowalik 2, Matjaž Krnc 1, Tomasz Waleń 2 August 31, 2009 1 Department of Mathematics, University of Ljubljana Jadranska 21, 1111 Ljubljana,
Improved induced matchings in sparse graphs Rok Erman 1, Lukasz Kowalik 2, Matjaž Krnc 1, Tomasz Waleń 2 August 31, 2009 1 Department of Mathematics, University of Ljubljana Jadranska 21, 1111 Ljubljana,
4 Greedy Approximation for Set Cover
 COMPSCI 532: Design and Analysis of Algorithms October 14, 2015 Lecturer: Debmalya Panigrahi Lecture 12 Scribe: Allen Xiao 1 Overview In this lecture, we introduce approximation algorithms and their analysis
COMPSCI 532: Design and Analysis of Algorithms October 14, 2015 Lecturer: Debmalya Panigrahi Lecture 12 Scribe: Allen Xiao 1 Overview In this lecture, we introduce approximation algorithms and their analysis
Hardness of Subgraph and Supergraph Problems in c-tournaments
 Hardness of Subgraph and Supergraph Problems in c-tournaments Kanthi K Sarpatwar 1 and N.S. Narayanaswamy 1 Department of Computer Science and Engineering, IIT madras, Chennai 600036, India kanthik@gmail.com,swamy@cse.iitm.ac.in
Hardness of Subgraph and Supergraph Problems in c-tournaments Kanthi K Sarpatwar 1 and N.S. Narayanaswamy 1 Department of Computer Science and Engineering, IIT madras, Chennai 600036, India kanthik@gmail.com,swamy@cse.iitm.ac.in
Finding a winning strategy in variations of Kayles
 Finding a winning strategy in variations of Kayles Simon Prins ICA-3582809 Utrecht University, The Netherlands July 15, 2015 Abstract Kayles is a two player game played on a graph. The game can be dened
Finding a winning strategy in variations of Kayles Simon Prins ICA-3582809 Utrecht University, The Netherlands July 15, 2015 Abstract Kayles is a two player game played on a graph. The game can be dened
Modules. 6 Hamilton Graphs (4-8 lectures) Introduction Necessary conditions and sufficient conditions Exercises...
 Modules 6 Hamilton Graphs (4-8 lectures) 135 6.1 Introduction................................ 136 6.2 Necessary conditions and sufficient conditions............. 137 Exercises..................................
Modules 6 Hamilton Graphs (4-8 lectures) 135 6.1 Introduction................................ 136 6.2 Necessary conditions and sufficient conditions............. 137 Exercises..................................
A note on Baker s algorithm
 A note on Baker s algorithm Iyad A. Kanj, Ljubomir Perković School of CTI, DePaul University, 243 S. Wabash Avenue, Chicago, IL 60604-2301. Abstract We present a corrected version of Baker s algorithm
A note on Baker s algorithm Iyad A. Kanj, Ljubomir Perković School of CTI, DePaul University, 243 S. Wabash Avenue, Chicago, IL 60604-2301. Abstract We present a corrected version of Baker s algorithm
Interaction Between Input and Output-Sensitive
 Interaction Between Input and Output-Sensitive Really? Mamadou M. Kanté Université Blaise Pascal - LIMOS, CNRS Enumeration Algorithms Using Structure, Lorentz Institute, August 26 th, 2015 1 Introduction
Interaction Between Input and Output-Sensitive Really? Mamadou M. Kanté Université Blaise Pascal - LIMOS, CNRS Enumeration Algorithms Using Structure, Lorentz Institute, August 26 th, 2015 1 Introduction
Kernelization Upper Bounds for Parameterized Graph Coloring Problems
 Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Greedy Algorithms 1 {K(S) K(S) C} For large values of d, brute force search is not feasible because there are 2 d {1,..., d}.
 Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
Greedy Algorithms 1 Simple Knapsack Problem Greedy Algorithms form an important class of algorithmic techniques. We illustrate the idea by applying it to a simplified version of the Knapsack Problem. Informally,
The 3-Steiner Root Problem
 The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
The 3-Steiner Root Problem Maw-Shang Chang 1 and Ming-Tat Ko 2 1 Department of Computer Science and Information Engineering National Chung Cheng University, Chiayi 621, Taiwan, R.O.C. mschang@cs.ccu.edu.tw
More NP-complete Problems. CS255 Chris Pollett May 3, 2006.
 More NP-complete Problems CS255 Chris Pollett May 3, 2006. Outline More NP-Complete Problems Hamiltonian Cycle Recall a hamiltonian cycle is a permutation of the vertices v i_1,, v i_n of a graph G so
More NP-complete Problems CS255 Chris Pollett May 3, 2006. Outline More NP-Complete Problems Hamiltonian Cycle Recall a hamiltonian cycle is a permutation of the vertices v i_1,, v i_n of a graph G so
Common Induced Subgraph Isomorphism Structural Parameterizations and Exact Algorithms
 Common Induced Subgraph Isomorphism Structural Parameterizations and Exact Algorithms Faisal N. Abu-Khzam Department of Computer Science and Mathematics Lebanese American University Beirut, Lebanon Overview
Common Induced Subgraph Isomorphism Structural Parameterizations and Exact Algorithms Faisal N. Abu-Khzam Department of Computer Science and Mathematics Lebanese American University Beirut, Lebanon Overview
Cluster Editing with Locally Bounded Modifications Revisited
 Cluster Editing with Locally Bounded Modifications Revisited Peter Damaschke Department of Computer Science and Engineering Chalmers University, 41296 Göteborg, Sweden ptr@chalmers.se Abstract. For Cluster
Cluster Editing with Locally Bounded Modifications Revisited Peter Damaschke Department of Computer Science and Engineering Chalmers University, 41296 Göteborg, Sweden ptr@chalmers.se Abstract. For Cluster
val(y, I) α (9.0.2) α (9.0.3)
 CS787: Advanced Algorithms Lecture 9: Approximation Algorithms In this lecture we will discuss some NP-complete optimization problems and give algorithms for solving them that produce a nearly optimal,
CS787: Advanced Algorithms Lecture 9: Approximation Algorithms In this lecture we will discuss some NP-complete optimization problems and give algorithms for solving them that produce a nearly optimal,
9. Parameter Treewidth
 9. Parameter Treewidth COMP6741: Parameterized and Exact Computation Serge Gaspers Semester 2, 2017 Contents 1 Algorithms for trees 1 2 Tree decompositions 2 3 Monadic Second Order Logic 4 4 Dynamic Programming
9. Parameter Treewidth COMP6741: Parameterized and Exact Computation Serge Gaspers Semester 2, 2017 Contents 1 Algorithms for trees 1 2 Tree decompositions 2 3 Monadic Second Order Logic 4 4 Dynamic Programming
Copyright 2000, Kevin Wayne 1
 Guessing Game: NP-Complete? 1. LONGEST-PATH: Given a graph G = (V, E), does there exists a simple path of length at least k edges? YES. SHORTEST-PATH: Given a graph G = (V, E), does there exists a simple
Guessing Game: NP-Complete? 1. LONGEST-PATH: Given a graph G = (V, E), does there exists a simple path of length at least k edges? YES. SHORTEST-PATH: Given a graph G = (V, E), does there exists a simple
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
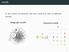 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
The Method of Extremal Structure on the k-maximum CUT Problem
 The Method of Extremal Structure on the k-maximum CUT Problem Elena Prieto School of Electrical Engineering and Computer Science The University of Newcastle Australia Abstract Using the Method of Extremal
The Method of Extremal Structure on the k-maximum CUT Problem Elena Prieto School of Electrical Engineering and Computer Science The University of Newcastle Australia Abstract Using the Method of Extremal
FEDOR V. FOMIN. Lectures on treewidth. The Parameterized Complexity Summer School 1-3 September 2017 Vienna, Austria
 FEDOR V. FOMIN Lectures on treewidth The Parameterized Complexity Summer School 1-3 September 2017 Vienna, Austria Why treewidth? Very general idea in science: large structures can be understood by breaking
FEDOR V. FOMIN Lectures on treewidth The Parameterized Complexity Summer School 1-3 September 2017 Vienna, Austria Why treewidth? Very general idea in science: large structures can be understood by breaking
Treewidth: Preprocessing and Kernelization
 Treewidth: Preprocessing and Kernelization Hans L. Bodlaender Joint work with Arie Koster, Frank van den Eijkhof, Bart Jansen, Stefan Kratsch, Vincent Kreuzen 1 This talk Survey of work on preprocessing
Treewidth: Preprocessing and Kernelization Hans L. Bodlaender Joint work with Arie Koster, Frank van den Eijkhof, Bart Jansen, Stefan Kratsch, Vincent Kreuzen 1 This talk Survey of work on preprocessing
Multicut in trees viewed through the eyes of vertex cover
 Multicut in trees viewed through the eyes of vertex cover Jianer Chen 1 Jia-Hao Fan 1 Iyad A. Kanj 2 Yang Liu 3 Fenghui Zhang 4 1 Department of Computer Science and Engineering, Texas A&M University, College
Multicut in trees viewed through the eyes of vertex cover Jianer Chen 1 Jia-Hao Fan 1 Iyad A. Kanj 2 Yang Liu 3 Fenghui Zhang 4 1 Department of Computer Science and Engineering, Texas A&M University, College
Graph Theory Day Four
 Graph Theory Day Four February 8, 018 1 Connected Recall from last class, we discussed methods for proving a graph was connected. Our two methods were 1) Based on the definition, given any u, v V(G), there
Graph Theory Day Four February 8, 018 1 Connected Recall from last class, we discussed methods for proving a graph was connected. Our two methods were 1) Based on the definition, given any u, v V(G), there
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman, M. S. Ramanujan and Saket Saurabh The Institute of Mathematical Sciences, Chennai, India. {vraman msramanujan saket}@imsc.res.in Abstract. It is well known
Paths, Flowers and Vertex Cover Venkatesh Raman, M. S. Ramanujan and Saket Saurabh The Institute of Mathematical Sciences, Chennai, India. {vraman msramanujan saket}@imsc.res.in Abstract. It is well known
INTRODUCTION. An easy way to express the idea of an algorithm (very much like C/C++, Java, Pascal, Ada, )
 INTRODUCTION Objective: - Algorithms - Techniques - Analysis. Algorithms: Definition: Pseudocode: An algorithm is a sequence of computational steps that tae some value, or set of values, as input and produce
INTRODUCTION Objective: - Algorithms - Techniques - Analysis. Algorithms: Definition: Pseudocode: An algorithm is a sequence of computational steps that tae some value, or set of values, as input and produce
In this lecture, we ll look at applications of duality to three problems:
 Lecture 7 Duality Applications (Part II) In this lecture, we ll look at applications of duality to three problems: 1. Finding maximum spanning trees (MST). We know that Kruskal s algorithm finds this,
Lecture 7 Duality Applications (Part II) In this lecture, we ll look at applications of duality to three problems: 1. Finding maximum spanning trees (MST). We know that Kruskal s algorithm finds this,
Hitting and harvesting pumpkins. Gwenaël Joret Christophe Paul Ignasi Sau Saket Saurabh Stéphan Thomassé
 Hitting and harvesting pumpkins Gwenaël Joret Christophe Paul Ignasi Sau Saket Saurabh Stéphan Thomassé Pumpkins c-pumpkin: c NB: graph = multigraph Graphs with no c-pumpkin minor c = 1: empty graphs c
Hitting and harvesting pumpkins Gwenaël Joret Christophe Paul Ignasi Sau Saket Saurabh Stéphan Thomassé Pumpkins c-pumpkin: c NB: graph = multigraph Graphs with no c-pumpkin minor c = 1: empty graphs c
Sharp Separation and Applications to Exact and Parameterized Algorithms
 Sharp Separation and Applications to Exact and Parameterized Algorithms Fedor V. Fomin 1 Daniel Lokshtanov 1 Fabrizio Grandoni 2 Saket Saurabh 3 1 Department of Informatics, University of Bergen, N-5020
Sharp Separation and Applications to Exact and Parameterized Algorithms Fedor V. Fomin 1 Daniel Lokshtanov 1 Fabrizio Grandoni 2 Saket Saurabh 3 1 Department of Informatics, University of Bergen, N-5020
CMSC 451: Lecture 22 Approximation Algorithms: Vertex Cover and TSP Tuesday, Dec 5, 2017
 CMSC 451: Lecture 22 Approximation Algorithms: Vertex Cover and TSP Tuesday, Dec 5, 2017 Reading: Section 9.2 of DPV. Section 11.3 of KT presents a different approximation algorithm for Vertex Cover. Coping
CMSC 451: Lecture 22 Approximation Algorithms: Vertex Cover and TSP Tuesday, Dec 5, 2017 Reading: Section 9.2 of DPV. Section 11.3 of KT presents a different approximation algorithm for Vertex Cover. Coping
CMPSCI 311: Introduction to Algorithms Practice Final Exam
 CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
Introduction to the Analysis of Algorithms. Algorithm
 Introduction to the Analysis of Algorithms Based on the notes from David Fernandez-Baca Bryn Mawr College CS206 Intro to Data Structures Algorithm An algorithm is a strategy (well-defined computational
Introduction to the Analysis of Algorithms Based on the notes from David Fernandez-Baca Bryn Mawr College CS206 Intro to Data Structures Algorithm An algorithm is a strategy (well-defined computational
Exact Algorithms for Graph Homomorphisms
 Exact Algorithms for Graph Homomorphisms Fedor V. Fomin Pinar Heggernes Dieter Kratsch Abstract Graph homomorphism, also called H-coloring, is a natural generalization of graph coloring: There is a homomorphism
Exact Algorithms for Graph Homomorphisms Fedor V. Fomin Pinar Heggernes Dieter Kratsch Abstract Graph homomorphism, also called H-coloring, is a natural generalization of graph coloring: There is a homomorphism
A Linear Kernel for the Differential of a Graph
 A Linear Kernel for the Differential of a Graph Can we beat combinatorial kernels? Sergio Bermudo Henning Fernau Universidad Pablo de Olavide Universität Trier sbernav@upo.es,fernau@uni-trier.de WorKer,
A Linear Kernel for the Differential of a Graph Can we beat combinatorial kernels? Sergio Bermudo Henning Fernau Universidad Pablo de Olavide Universität Trier sbernav@upo.es,fernau@uni-trier.de WorKer,
CSE 417 Branch & Bound (pt 4) Branch & Bound
 CSE 417 Branch & Bound (pt 4) Branch & Bound Reminders > HW8 due today > HW9 will be posted tomorrow start early program will be slow, so debugging will be slow... Review of previous lectures > Complexity
CSE 417 Branch & Bound (pt 4) Branch & Bound Reminders > HW8 due today > HW9 will be posted tomorrow start early program will be slow, so debugging will be slow... Review of previous lectures > Complexity
Introduction to Graph Theory
 Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
10. EXTENDING TRACTABILITY
 0. EXTENDING TRACTABILITY finding small vertex covers solving NP-hard problems on trees circular arc coverings vertex cover in bipartite graphs Lecture slides by Kevin Wayne Copyright 005 Pearson-Addison
0. EXTENDING TRACTABILITY finding small vertex covers solving NP-hard problems on trees circular arc coverings vertex cover in bipartite graphs Lecture slides by Kevin Wayne Copyright 005 Pearson-Addison
CSE 421: Introduction to Algorithms Complexity
 CSE 421: Introduction to Algorithms Complexity Yin-Tat Lee 1 Defining Efficiency Runs fast on typical real problem instances Pros: Sensible, Bottom-line oriented Cons: Moving target (diff computers, programming
CSE 421: Introduction to Algorithms Complexity Yin-Tat Lee 1 Defining Efficiency Runs fast on typical real problem instances Pros: Sensible, Bottom-line oriented Cons: Moving target (diff computers, programming
Fast algorithms for max independent set
 Fast algorithms for max independent set N. Bourgeois 1 B. Escoffier 1 V. Th. Paschos 1 J.M.M. van Rooij 2 1 LAMSADE, CNRS and Université Paris-Dauphine, France {bourgeois,escoffier,paschos}@lamsade.dauphine.fr
Fast algorithms for max independent set N. Bourgeois 1 B. Escoffier 1 V. Th. Paschos 1 J.M.M. van Rooij 2 1 LAMSADE, CNRS and Université Paris-Dauphine, France {bourgeois,escoffier,paschos}@lamsade.dauphine.fr
Exact algorithms for L(2, 1)-labeling of graphs
 Exact algorithms for L(, 1)-labeling of graphs Frédéric Havet Martin Klazar Jan Kratochvíl Dieter Kratsch Mathieu Liedloff Abstract The notion of distance constrained graph labelings, motivated by the
Exact algorithms for L(, 1)-labeling of graphs Frédéric Havet Martin Klazar Jan Kratochvíl Dieter Kratsch Mathieu Liedloff Abstract The notion of distance constrained graph labelings, motivated by the
Lower Bound on Comparison-based Sorting
 Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
A Linear Vertex Kernel for Maximum Internal Spanning Tree
 A Linear Vertex Kernel for Maximum Internal Spanning Tree Fedor V. Fomin Serge Gaspers Saket Saurabh Stéphan Thomassé Abstract We present a polynomial time algorithm that for any graph G and integer k
A Linear Vertex Kernel for Maximum Internal Spanning Tree Fedor V. Fomin Serge Gaspers Saket Saurabh Stéphan Thomassé Abstract We present a polynomial time algorithm that for any graph G and integer k
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs
 Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Parametric Duality and Kernelization: Lower Bounds and Upper Bounds on Kernel Size
 Parametric Duality and Kernelization: Lower Bounds and Upper Bounds on Kernel Size Jianer Chen 1 Henning Fernau 2 Iyad A. Kanj 3 Ge Xia 1 1 Department of Computer Science, Texas A&M University, College
Parametric Duality and Kernelization: Lower Bounds and Upper Bounds on Kernel Size Jianer Chen 1 Henning Fernau 2 Iyad A. Kanj 3 Ge Xia 1 1 Department of Computer Science, Texas A&M University, College
Computing optimal total vertex covers for trees
 Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Computing optimal total vertex covers for trees Pak Ching Li Department of Computer Science University of Manitoba Winnipeg, Manitoba Canada R3T 2N2 Abstract. Let G = (V, E) be a simple, undirected, connected
Exact Algorithms Lecture 7: FPT Hardness and the ETH
 Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
Exact Algorithms Lecture 7: FPT Hardness and the ETH February 12, 2016 Lecturer: Michael Lampis 1 Reminder: FPT algorithms Definition 1. A parameterized problem is a function from (χ, k) {0, 1} N to {0,
The Parameterized Complexity of the Rainbow Subgraph Problem
 The Parameterized Complexity of the Rainbow Subgraph Problem Falk Hüffner, Christian Komusiewicz, Rolf Niedermeier, and Martin Rötzschke Institut für Softwaretechnik und Theoretische Informatik, TU Berlin,
The Parameterized Complexity of the Rainbow Subgraph Problem Falk Hüffner, Christian Komusiewicz, Rolf Niedermeier, and Martin Rötzschke Institut für Softwaretechnik und Theoretische Informatik, TU Berlin,
Fixed-Parameter Evolutionary Algorithms and the Vertex Cover Problem
 Fixed-Parameter Evolutionary Algorithms and the Vertex Cover Problem Stefan Kratsch Algorithms and Complexity Group Max-Planck-Institut für Informatik Saarbrücken, Germany Frank Neumann Algorithms and
Fixed-Parameter Evolutionary Algorithms and the Vertex Cover Problem Stefan Kratsch Algorithms and Complexity Group Max-Planck-Institut für Informatik Saarbrücken, Germany Frank Neumann Algorithms and
15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018
 15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018 In this lecture, we describe a very general problem called linear programming
15-451/651: Design & Analysis of Algorithms October 11, 2018 Lecture #13: Linear Programming I last changed: October 9, 2018 In this lecture, we describe a very general problem called linear programming
What Makes Equitable Connected Partition Easy
 What Makes Equitable Connected Partition Easy Rosa Enciso 1, Micheal R. Fellows 2, Jiong Guo 3, Iyad Kanj 4, Frances Rosamond 2, and Ondřej Suchý 5 1 School of Electrical Engineering and Computer Science
What Makes Equitable Connected Partition Easy Rosa Enciso 1, Micheal R. Fellows 2, Jiong Guo 3, Iyad Kanj 4, Frances Rosamond 2, and Ondřej Suchý 5 1 School of Electrical Engineering and Computer Science
Greedy algorithms Or Do the right thing
 Greedy algorithms Or Do the right thing March 1, 2005 1 Greedy Algorithm Basic idea: When solving a problem do locally the right thing. Problem: Usually does not work. VertexCover (Optimization Version)
Greedy algorithms Or Do the right thing March 1, 2005 1 Greedy Algorithm Basic idea: When solving a problem do locally the right thing. Problem: Usually does not work. VertexCover (Optimization Version)
Results on the min-sum vertex cover problem
 Results on the min-sum vertex cover problem Ralucca Gera, 1 Craig Rasmussen, Pantelimon Stănică 1 Naval Postgraduate School Monterey, CA 9393, USA {rgera, ras, pstanica}@npsedu and Steve Horton United
Results on the min-sum vertex cover problem Ralucca Gera, 1 Craig Rasmussen, Pantelimon Stănică 1 Naval Postgraduate School Monterey, CA 9393, USA {rgera, ras, pstanica}@npsedu and Steve Horton United
Monotone Paths in Geometric Triangulations
 Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Branch and Recharge: Exact algorithms for generalized domination
 Branch and Recharge: Exact algorithms for generalized domination Fedor V. Fomin Petr A. Golovach Jan Kratochvíl Dieter Kratsch Mathieu Liedloff February 28, 2010 Abstract In this paper we present branching
Branch and Recharge: Exact algorithms for generalized domination Fedor V. Fomin Petr A. Golovach Jan Kratochvíl Dieter Kratsch Mathieu Liedloff February 28, 2010 Abstract In this paper we present branching
Upper bounds and algorithms for parallel knock-out numbers
 Theoretical Computer Science 410 (2009) 1319 1327 Contents lists available at ScienceDirect Theoretical Computer Science journal homepage: www.elsevier.com/locate/tcs Upper bounds and algorithms for parallel
Theoretical Computer Science 410 (2009) 1319 1327 Contents lists available at ScienceDirect Theoretical Computer Science journal homepage: www.elsevier.com/locate/tcs Upper bounds and algorithms for parallel
Important separators and parameterized algorithms
 Important separators and parameterized algorithms Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary School on Parameterized Algorithms
Important separators and parameterized algorithms Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary School on Parameterized Algorithms
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Polynomial-Time Approximation Algorithms
 6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
6.854 Advanced Algorithms Lecture 20: 10/27/2006 Lecturer: David Karger Scribes: Matt Doherty, John Nham, Sergiy Sidenko, David Schultz Polynomial-Time Approximation Algorithms NP-hard problems are a vast
11.1 Facility Location
 CS787: Advanced Algorithms Scribe: Amanda Burton, Leah Kluegel Lecturer: Shuchi Chawla Topic: Facility Location ctd., Linear Programming Date: October 8, 2007 Today we conclude the discussion of local
CS787: Advanced Algorithms Scribe: Amanda Burton, Leah Kluegel Lecturer: Shuchi Chawla Topic: Facility Location ctd., Linear Programming Date: October 8, 2007 Today we conclude the discussion of local
Here is a recursive algorithm that solves this problem, given a pointer to the root of T : MaxWtSubtree [r]
![Here is a recursive algorithm that solves this problem, given a pointer to the root of T : MaxWtSubtree [r] Here is a recursive algorithm that solves this problem, given a pointer to the root of T : MaxWtSubtree [r]](/thumbs/79/79323586.jpg) CSE 101 Final Exam Topics: Order, Recurrence Relations, Analyzing Programs, Divide-and-Conquer, Back-tracking, Dynamic Programming, Greedy Algorithms and Correctness Proofs, Data Structures (Heap, Binary
CSE 101 Final Exam Topics: Order, Recurrence Relations, Analyzing Programs, Divide-and-Conquer, Back-tracking, Dynamic Programming, Greedy Algorithms and Correctness Proofs, Data Structures (Heap, Binary
On Approximating Minimum Vertex Cover for Graphs with Perfect Matching
 On Approximating Minimum Vertex Cover for Graphs with Perfect Matching Jianer Chen and Iyad A. Kanj Abstract It has been a challenging open problem whether there is a polynomial time approximation algorithm
On Approximating Minimum Vertex Cover for Graphs with Perfect Matching Jianer Chen and Iyad A. Kanj Abstract It has been a challenging open problem whether there is a polynomial time approximation algorithm
Solving NP-hard Problems on Special Instances
 Solving NP-hard Problems on Special Instances Solve it in poly- time I can t You can assume the input is xxxxx No Problem, here is a poly-time algorithm 1 Solving NP-hard Problems on Special Instances
Solving NP-hard Problems on Special Instances Solve it in poly- time I can t You can assume the input is xxxxx No Problem, here is a poly-time algorithm 1 Solving NP-hard Problems on Special Instances
NEIGHBOURHOOD SUM CORDIAL LABELING OF GRAPHS
 NEIGHBOURHOOD SUM CORDIAL LABELING OF GRAPHS A. Muthaiyan # and G. Bhuvaneswari * Department of Mathematics, Government Arts and Science College, Veppanthattai, Perambalur - 66, Tamil Nadu, India. P.G.
NEIGHBOURHOOD SUM CORDIAL LABELING OF GRAPHS A. Muthaiyan # and G. Bhuvaneswari * Department of Mathematics, Government Arts and Science College, Veppanthattai, Perambalur - 66, Tamil Nadu, India. P.G.
