Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes
|
|
|
- Kathlyn Robinson
- 5 years ago
- Views:
Transcription
1 Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F Metz France 2 University of Bergen N-5020 Bergen Norway /54 Journées Combinatoires Rhônes-Alpes Auvergne Clermont-Ferrand, 1-2 fevrier, 2012
2 2/54 Contents Exact Exponential Algorithms Input-Sensitive Enumeration Known Algorithms and Combinatorial Bounds Dominating Set Graph Classes Chordal Graphs Cographs Chain Graphs Cobipartite Graphs Open Questions
3 3/54 I. Solving computationally hard problems exactly
4 4/54 How to attack NP-hard problems Various techniques have been developed to attack NP-hard problems : approximation algorithms heuristics parameterized algorithms randomized algorithms restricted inputs exact exponential algorithms
5 5/54 Exact exponential-time algorithms dates back to the early nineteen sixties Davis, Putnam (1960) and Bellmann ; Held, Karp (1962) tries to cope with NP-completeness in a strong sense solves problem exactly worst-case analysis of running time (and space)
6 6/54 Why Study Exponential Algorithms? leads to a better understanding of NP-hard problems initiates interesting new combinatorial and algorithmic challenges Alan Perlis (first Turing Award winner) : for every polynomial-time algorithm you have, there is an exponential algorithm that I would rather run.
7 7/54 II. Why study input-sensitive enumeration algorithms?
8 8/54 Types of problems General decision optimization counting enumeration Example decision problem : Has the graph G a dominating set? optimization problem : Find the minimum size of a dominating set of G. counting problem : Count the number of dominating sets of G of size k. enumeration problem : List all minimal dominating sets of G.
9 9/54 An input-sensitive algorithm solving an enumeration problem... can be used to solve appropriate decision, optimization and counting versions of the problem can be used to solve other NP-hard problems provides an upper bound for the maximum number of enumerated objects
10 10/54 What is the maximum number of vertex sets satisfying a given property in an n-vertex graph? Upper bounds... are crucial for the analysis of the worst-case running time of exact algorithms allow to use enumeration algorithms as subroutines may lead to matching lower and upper bounds (up to a polynomial factor) are of interest in their own in Combinatorics Examples What is the maximum number of maximal independent sets in an n-vertex graph? What is the maximum number of minimal dominating sets in an n-vertex graph?
11 11/54 III. Highlights
12 12/54 Maximal Independent Sets Moon,Moser 1965 The maximum number of maximal independent sets in any graph on n vertices is 3 n/3. Original proof by induction Easy to transform into a branching algorithm enumerating all maximal independent sets of a graph in time O (3 n/3 ) Polynomial-delay algorithm (Tsukiyama, Ide, Ariyoshi, Shirakawa, 1977)
13 13/54 Application in Coloring Algorithms based on dynamic programming over set of all maximal independent sets O( n ) time optimal coloring algorithm (Lawler 1976) improved upper bound on the maximum number of maximal independent sets of small size O( n ) time algorithm to compute an optimal coloring of a graph (Eppstein 2003)
14 14/54 Minimal Feedback Vertex Sets Fomin,Gaspers,Pyatkin,Razgon, 2008 The maximum number of minimal feedback vertex sets in any graph on n vertices is at most n. Proof based on a branching algorithm to enumerate all minimal feedback vertex sets of running time O( n ). Lower Bound : There exists an infinite family of graphs all having 105 n/ n minimal feedback vertex sets. Polynomial-delay algorithm (Schwikowski, Speckenmeyer, 2002)
15 15/54 Minimal Separators and Potential Maximal Cliques Fomin,Villanger, ICALP 2008 and STACS 2010 There is an algorithm to enumerate all potential maximal cliques of a graph in time O( n ). The maximum number of potential maximal cliques in any graph on n vertices is at most O( n ). Every n-vertex graph has at most O( n ) minimal separators. Lower Bound : There exists an infinite family of graphs all having 3 n/ n minimal separators and 3 n/ n maximal potential cliques. Application in Treewidth Algorithms O( n ) algorithm to exactly compute the treewidth of a graph. (Fomin,Villanger, ICALP 2008)
16 16/54 IV. Dominating Set
17 17/54 Fundamental notions dominating set A vertex set S V is a dominating set of G if every vertex of G either belongs to S or has a neighbour in S. Every vertex v of a dominating set dominates the vertices in N[v]. minimal dominating set (mds) A dominating set S is a minimal dominating set (mds) if no proper subset of S is a dominating set. private neighbour If S is a mds, then for every vertex v S, there is a vertex x N[v] which is dominated only by v. Such a vertex x is a private neighbor of v, since x is not adjacent to any vertex in S \ {v}. A vertex in S is its own private neighbor if it is an isolate in G[S].
18 18/54 Number of minimal dominating sets We denote by µ(g) the number of mds of G. Lemma Let G be a graph with connected components G 1, G 2,..., G t. Then µ(g) = t i=1 µ(g i).
19 19/54 Enumerating minimal dominating sets Fomin,Grandoni,Pyatkin,Stepanov, 2008 The maximum number of minimal dominating sets in any graph on n vertices is at most n. Proof based on a branching algorithm to enumerate all minimal dominating sets of running time O( n ). Lower Bound : There exists an infinite family of graphs all having 15 n/ n minimal dominating sets. No algorithm of output-polynomial running time known No polynomial delay algorithm known
20 20/54 V. Graph Classes
21 21/54 Our Goals We provide upper and lower bounds for the maximum number of minimal dominating sets in chordal, cographs, chain, cobipartite graphs... Typically we have either matching upper and lower bounds, using combinatorial arguments or asymptotic bounds proved by using branching algorithms. We obtain algorithms to enumerate all minimal dominating sets for graphs in each of our graph classes.
22 22/54 Summary of Upper and Lower Bounds Graph Class Lower Bound Upper Bound general [FGPS08] n n chordal n n cobipartite n n split n n proper interval n n cograph n n trivially perfect n n threshold ω(g) ω(g) chain n/2 + m n/2 + m
23 Some Lower Bounds Cographs µ(3k 2 ) = 15 µ(t3k 2 ) = 15 t There exists an infinite family of cographs all having 15 n/ n minimal dominating sets. Chordal Graphs 23/54 µ(k 3 ) = 3 µ(tk 3 ) = 3 t There exists an infinite family of chordal graphs all having 3 n/ n minimal dominating sets. Disjoint union of triangles also proper interval, trivially perfect, cograph, permutation graph,...
24 24/54 Output-Sensitive Enumeration Kanté, Limouzy, Mary, Nourine, FCT 2011 Study of the output-sensitive complexity of enumerating all minimal dominating sets in graph classes Polynomial-delay algorithm for split graphs Further classes with polynomial delay algorithm
25 25/54 Branching Algorithms Branching algorithms recursively applied to instances of the problem using Branching rules and Reduction rules. Branching rules : solving the problem by recursively solving smaller instances Reduction rules : - simplify the instance - (typically) reduce the size of the instance
26 26/54 Search Trees Search Tree : used to illustrate and analyse an execution of a Branching algorithm nodes : assigns to each node a solved problem instance root : assigns the input to the root child : each instance (of a subproblem) reached by a branching rule is assigned to a child of the node (of the original instance)
27 27/54 A search tree V1 Select Discard V2 V4 S D S D V3 V5 S D S D
28 28/54 Analysis of the Running Time To obtain an upper bound on the maximum number of nodes of the search tree (for an input of size n) : 1. Define a Measure for a problem instance. 2. Lower bound the progress made by the algorithm at each branching step. 3. Compute the collection of linear recurrences and branching vectors by considering all branching rules. 4. Solve all those recurrences by the computation of the branching number (to obtain an upper bound of the form O(αi n )) for each one. 5. Take the worst case over all solutions : maximum branching number α. Then the maximum number of leaves in any search tree is O(α n ).
29 29/54 V.1. Chordal Graphs
30 0/54 Enumeration via Branching Main Features branching algorithm generates vertex subsets at the leaves of the corresponding search tree every minimal dominating set is assigned to a leaf of the search tree ALLOWED : multiple occurences of mds as well as vertex sets not being mds (at termination simply check each leaf whether its vertex set is indeed a mds) Thus an upper bound on the maximum number of leaves in the search tree for input graph G is also an upper bound for µ(g), i.e., the number of mds of G.
31 31/54 Setting of our Algorithm and its Analysis Invariants INSTANCE of a recursiv call : (G, D) where G is an induced subgraph of the input graph G, and D is a subset of V (G) \ V (G ). D chosen for mds, i.e., D subset of any vertex set of a leaf in the subtree rooted at (G, D) D dominates all vertices of V (G) \ V (G ) ; thus any vertex of G when added to D must have a private neighbour in G. Features Choice of vertex to branch based on structural properties Measure of an instance (G, D) is defined by assigning a weight of 0 or 1 to each vertex and by then taking the sum of the weights over V
32 32/54 Structural Properties of Chordal Graphs Definitions A graph G is chordal if every cycle of length at least 4 has a chord. A vertex x of G is simplicial if its neighbourhood N(x) is a clique. Properties Every chordal graph has a simplicial vertex. If x is a simplicial vertex of G then for all y N(x), N[x] N[y].
33 33/54 Branching 0 (G, D) : Choose simplicial vertex x of G to branch on. Vertices of G are dominated or not, and forbidden or not. Reduction rule : x isolated. There are 3 different branching rules.
34 34/54 Branching 1 Case 1 : x is already dominated. x D. Since x is simplicial and needs a private neighbour in N(x), we can delete x and all its neighbours. x / D. Since it is already dominated, it is safe to delete x. Branching vector (2, 1)
35 35/54 Branching 2 Case 2 : x is not already dominated and N(x) 2 Let y be a neigbour of x. y D. Since x is simplicial, all neighbours of x are dominated by y. We delete x and y. y / D. Since y N(x), any vertex we select later to dominate x will also dominate y. Thus we can delete y. Branching vector (2, 1)
36 36/54 Branching 3 Case 3 : x is not already dominated and N(x) = 1. Let y be the neighbour of x. x D. Since y is the private neighbour of x, we can delete x and y. x / D. The only way to dominate x is to take y into D. Hence y D and we can delete x and y. Branching vector (2, 2)
37 37/54 Analysis Running Time Branching vectors : (2, 1), (2, 1), (2, 2) τ(2, 1) , τ(2, 2) Algorithm to enumerate all mds of a chordal graph runs in time O( n ). Bounds The maximum number of minimal dominating sets in a chordal graph on n vertices is at most O( n ). Lower bound : n
38 38/54 V.2. Cographs
39 39/54 Structural Properties of Cographs Definitions The disjoint union of G 1 and G 2 is the graph G 1 G 2 = (V 1 V 2, E 1 E 2 ). The join of G 1 and G 2 is the graph G 1 G 2 = (V 1 V 2, E 1 E 2 {v 1 v 2 v 1 V 1, v 2 V 2 }). A graph G is a cograph if it can be constructed from isolated vertices by the operations disjoint union and join. Properties Every cograph can be represented by its cotree. A graph is a cograph iff it has no P 4 as induced subgraph.
40 40/54 Proof by induction Theorem Every cograph has at most 15 n 6 minimal dominating sets. Proof by induction. It is easy to enumerate all the cographs with n 6 vertices and to verify that each has at most 15 n 6 minimal dominating sets. Assume the theorem is true for all cographs with less than n vertices. Let G be a cograph with n vertices.
41 40/54 Proof by induction Theorem Every cograph has at most 15 n 6 minimal dominating sets. Proof by induction. It is easy to enumerate all the cographs with n 6 vertices and to verify that each has at most 15 n 6 minimal dominating sets. Assume the theorem is true for all cographs with less than n vertices. Let G be a cograph with n vertices.
42 41/54 Decomposition Decomposition Since every cograph G can be constructed from isolated vertices by disjoint union and by join operation... Cograph G can be decomposed into graphs G 1 with n 1 vertices and G 2 with n 2 vertices such that : 1. either G is a disjoint union of G 1 and G 2 and there is no edge between G 1 and G or G is a join of G 1 and G 2 and all edges with one endpoint in G 1 and one in G 2 are present. Clearly n = n 1 + n 2.
43 42/54 G = G 1 G 2 µ(g) = µ(g 1 ) µ(g 2 ) By induction hypothesis µ(g) 15 n n 2 6 = 15 n 6
44 43/54 G = G 1 G 2 Since x 1 x 2 E(G) for all x 1 V (G 1 ) and for all x 2 V (G 2 ), there are three types of minimal dominating sets of G : minimal dominating set D 1 of G 1, minimal dominating set D 2 of G 2, {x 1, x 2 }, for all x 1 V (G 1 ) and for all x 2 V (G 2 ) Consequently µ(g) = µ(g 1 ) + µ(g 2 ) + n 1 n 2. By induction hypothesis and since n 7, µ(g) 15 n n n 1 n 2 15 n 6.
45 44/54 Upper Bound Matches Lower Bound The maximum number of minimal dominating sets in a cograph on n = 6t vertices is 15 n/6.
46 45/54 V.3. Chain Graphs
47 46/54 Structural Properties of Chain Graphs Definitions A bipartite graph G = (A, B, E) is a chain graph if there is an ordering σ A = a 1, a 2,..., a k of the vertices of A such that N(a 1 ) N(a 2 ) N(a k ), as well as an ordering σ B = b 1, b 2,..., b l of the vertices of B such that N(b 1 ) N(b 2 ) N(b l ). σ A and σ B together chain ordering of G Properties In a disconnected chain graph at most one component contains edges. All isolated vertices belong to every minimal dominating set. (and every maximal independent set). W.l.o.g. chain graph G connected.
48 47/54 A chain graph with n/2 + 1 maximal independent sets a 1 a 2 a 3 a 4 a 5 b 1 b 2 b 3 b 4 b 5
49 48/54 The exact value of the maximum number of mis Maximum number of mis A chain graph has at most n/2 + 1 maximal independent sets, and there are chain graphs that have n/2 + 1 maximal independent sets. Lower Bound For every even n 2, let G n be the chain graph obtained from two independent sets A = {a 1,..., a n/2 } and B = {b 1,..., b n/2 } by making a i adjacent to every vertex in {b 1,..., b i }, for i = 1,..., n/2. For every even n 2, the graph G n contains exactly n/2 + 1 maximal independent sets.
50 49/54 Structure of minimal dominating sets At most one edge in mds For every minimal dominating set S of a chain graph G, the graph G[S] contains at most one edge. Exactly one mds containing edge ab Let ab be an edge of a chain graph G = (A, B, E) with a A and b B. If a or b has degree 1, then there is no minimal dominating set in G containing both a and b. If both a and b have degree at least 2, then there is exactly one minimal dominating set in G containing both a and b.
51 50/54 The exact value of the maximum number of mis Maximum number of minimal dominating sets A chain graph on at least 2 vertices has at most n/2 + m minimal dominating sets, and there are chain graphs with n/2 + m minimal dominating sets. Lower Bound Take graph G n from lower bound for mis, n even. σ A = a 1,..., a k and σ B = b 1,..., b l chain ordering of G n Let G n be the graph obtained from G n by adding the edge a k 1 b l. The graph G n contains exactly n/2 + m mds : one for each of the n/2 maximal independent sets, and one for each edge of G n, apart from the edge a 1 b 1.
52 51/54 V.4. Cobipartite Graphs
53 52/54 Definition A graph G = (V, E) is cobipartite if its vertex set can be partitioned into two cliques X and Y. Lower Bound For n = 5k, two disjoint cliques X and Y, where X = k and Y = 4k. Make every vertex in X adjacent to exactly four vertices in Y, such that every vertex in Y is adjacent to exactly one vertex in X. The graph has 4 n/ n mds being subsets of Y. Upper Bound A cobipartite graph on n vertices has at most O( n ) minimal dominating sets.
54 53/54 Upper Bound X = αn with 0.5 α 1, and Y = (1 α)n polynomial number of mds D with D = 1, or D X = 1 and D Y = 1 number of mds S Y is 2 Y 2 n/2 How many mds D X? Let D = βn, where β α and 2 βn X. 1. every vertex of D X has a private neighbour which must be from Y implies β 1 α 3. number of subsets of X of size βn is ( αn βn 4. for fixed α maximizes with β = α/2 : ( αn α/2 n 5. to optimally choose α : β = α/2 1 α implies α 2/3. 6. Hence number of mds D, with D 2 and D X, is at most ), which is less than or equal to 2 2n/3 ( 2n/3 n/3 ) )
55 54/54 VII. Open Questions Conjecture : maximum number of mds in a general graph is 15 n/6. Conjecture : maximum number of mds in interval and split graphs is 3 n/3. Bipartite graphs : known lower bound 6 n/ n, disjoint union of C 4. Find an upper bound better than n. Find an output-polynomial algorithm to enumerate all mds of chordal graphs. Find an output-polynomial algorithm to enumerate all mds of graphs in general.
Minimal dominating sets in graph classes: combinatorial bounds and enumeration
 Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Minimal dominating sets in graph classes: combinatorial bounds and enumeration Jean-François Couturier 1, Pinar Heggernes 2, Pim van t Hof 2, and Dieter Kratsch 1 1 LITA, Université Paul Verlaine - Metz,
Minimal dominating sets in interval graphs and trees
 Minimal dominating sets in interval graphs and trees Petr A. Golovach a, Pinar Heggernes a, Mamadou Moustapha Kanté b, Dieter Kratsch c,, Yngve Villanger a a Department of Informatics, University of Bergen,
Minimal dominating sets in interval graphs and trees Petr A. Golovach a, Pinar Heggernes a, Mamadou Moustapha Kanté b, Dieter Kratsch c,, Yngve Villanger a a Department of Informatics, University of Bergen,
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Interaction Between Input and Output-Sensitive
 Interaction Between Input and Output-Sensitive Really? Mamadou M. Kanté Université Blaise Pascal - LIMOS, CNRS Enumeration Algorithms Using Structure, Lorentz Institute, August 26 th, 2015 1 Introduction
Interaction Between Input and Output-Sensitive Really? Mamadou M. Kanté Université Blaise Pascal - LIMOS, CNRS Enumeration Algorithms Using Structure, Lorentz Institute, August 26 th, 2015 1 Introduction
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Fast algorithms for max independent set
 Fast algorithms for max independent set N. Bourgeois 1 B. Escoffier 1 V. Th. Paschos 1 J.M.M. van Rooij 2 1 LAMSADE, CNRS and Université Paris-Dauphine, France {bourgeois,escoffier,paschos}@lamsade.dauphine.fr
Fast algorithms for max independent set N. Bourgeois 1 B. Escoffier 1 V. Th. Paschos 1 J.M.M. van Rooij 2 1 LAMSADE, CNRS and Université Paris-Dauphine, France {bourgeois,escoffier,paschos}@lamsade.dauphine.fr
THE LEAFAGE OF A CHORDAL GRAPH
 Discussiones Mathematicae Graph Theory 18 (1998 ) 23 48 THE LEAFAGE OF A CHORDAL GRAPH In-Jen Lin National Ocean University, Taipei, Taiwan Terry A. McKee 1 Wright State University, Dayton, OH 45435-0001,
Discussiones Mathematicae Graph Theory 18 (1998 ) 23 48 THE LEAFAGE OF A CHORDAL GRAPH In-Jen Lin National Ocean University, Taipei, Taiwan Terry A. McKee 1 Wright State University, Dayton, OH 45435-0001,
arxiv: v1 [cs.ds] 8 Jan 2019
![arxiv: v1 [cs.ds] 8 Jan 2019 arxiv: v1 [cs.ds] 8 Jan 2019](/thumbs/93/113547113.jpg) Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Chordal graphs MPRI
 Chordal graphs MPRI 2017 2018 Michel Habib habib@irif.fr http://www.irif.fr/~habib Sophie Germain, septembre 2017 Schedule Chordal graphs Representation of chordal graphs LBFS and chordal graphs More structural
Chordal graphs MPRI 2017 2018 Michel Habib habib@irif.fr http://www.irif.fr/~habib Sophie Germain, septembre 2017 Schedule Chordal graphs Representation of chordal graphs LBFS and chordal graphs More structural
Dominating Set on Bipartite Graphs
 Dominating Set on Bipartite Graphs Mathieu Liedloff Abstract Finding a dominating set of minimum cardinality is an NP-hard graph problem, even when the graph is bipartite. In this paper we are interested
Dominating Set on Bipartite Graphs Mathieu Liedloff Abstract Finding a dominating set of minimum cardinality is an NP-hard graph problem, even when the graph is bipartite. In this paper we are interested
Kernelization Upper Bounds for Parameterized Graph Coloring Problems
 Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
Kernelization Upper Bounds for Parameterized Graph Coloring Problems Pim de Weijer Master Thesis: ICA-3137910 Supervisor: Hans L. Bodlaender Computing Science, Utrecht University 1 Abstract This thesis
arxiv: v1 [cs.ds] 14 Dec 2018
![arxiv: v1 [cs.ds] 14 Dec 2018 arxiv: v1 [cs.ds] 14 Dec 2018](/thumbs/92/109311905.jpg) Graph classes and forbidden patterns on three vertices Laurent Feuilloley 1,2,3 and Michel Habib 1,3 arxiv:1812.05913v1 [cs.ds] 14 Dec 2018 1 IRIF, UMR 8243 CNRS & Paris Diderot University, Paris, France
Graph classes and forbidden patterns on three vertices Laurent Feuilloley 1,2,3 and Michel Habib 1,3 arxiv:1812.05913v1 [cs.ds] 14 Dec 2018 1 IRIF, UMR 8243 CNRS & Paris Diderot University, Paris, France
A Decomposition for Chordal graphs and Applications
 A Decomposition for Chordal graphs and Applications Michel Habib Joint work with Vincent Limouzy and Juraj Stacho Pretty Structure, Existencial Polytime Jack Edmonds Birthday, 7-9 april 2009 Schedule Chordal
A Decomposition for Chordal graphs and Applications Michel Habib Joint work with Vincent Limouzy and Juraj Stacho Pretty Structure, Existencial Polytime Jack Edmonds Birthday, 7-9 april 2009 Schedule Chordal
Certifying Algorithms and Forbidden Induced Subgraphs
 /32 and P. Heggernes 1 D. Kratsch 2 1 Institutt for Informatikk Universitetet i Bergen Norway 2 Laboratoire d Informatique Théorique et Appliquée Université Paul Verlaine - Metz France Dagstuhl - Germany
/32 and P. Heggernes 1 D. Kratsch 2 1 Institutt for Informatikk Universitetet i Bergen Norway 2 Laboratoire d Informatique Théorique et Appliquée Université Paul Verlaine - Metz France Dagstuhl - Germany
Exponential time algorithms for the minimum dominating set problem on some graph classes
 Exponential time algorithms for the minimum dominating set problem on some graph classes Serge Gaspers University of Bergen Department of Informatics N-500 Bergen, Norway. gaspers@ii.uib.no Dieter Kratsch
Exponential time algorithms for the minimum dominating set problem on some graph classes Serge Gaspers University of Bergen Department of Informatics N-500 Bergen, Norway. gaspers@ii.uib.no Dieter Kratsch
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
On Structural Parameterizations of the Matching Cut Problem
 On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
Ton Kloks and Yue-Li Wang. Advances in Graph Algorithms. October 10, y X z
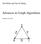 Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Dominating sequences in graphs
 Dominating sequences in graphs Boštjan Brešar a,b Tanja Gologranc b Martin Milanič c,b Douglas F. Rall d Romeo Rizzi e July 18, 2014 a Faculty of Natural Sciences and Mathematics, University of Maribor,
Dominating sequences in graphs Boštjan Brešar a,b Tanja Gologranc b Martin Milanič c,b Douglas F. Rall d Romeo Rizzi e July 18, 2014 a Faculty of Natural Sciences and Mathematics, University of Maribor,
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Preprocessing for treewidth
 Preprocessing for treewidth Bodlaender, H.L.; Jansen, B.M.P.; Kratsch, S. Published in: arxiv Published: 21/04/2011 Please check the document version of this publication: A submitted manuscript is the
Preprocessing for treewidth Bodlaender, H.L.; Jansen, B.M.P.; Kratsch, S. Published in: arxiv Published: 21/04/2011 Please check the document version of this publication: A submitted manuscript is the
Exact Algorithms for Graph Homomorphisms
 Exact Algorithms for Graph Homomorphisms Fedor V. Fomin Pinar Heggernes Dieter Kratsch Abstract Graph homomorphism, also called H-coloring, is a natural generalization of graph coloring: There is a homomorphism
Exact Algorithms for Graph Homomorphisms Fedor V. Fomin Pinar Heggernes Dieter Kratsch Abstract Graph homomorphism, also called H-coloring, is a natural generalization of graph coloring: There is a homomorphism
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs
 Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Efficient Enumeration Algorithm for Dominating Sets in Bounded Degenerate Graphs Kazuhiro Kurita 1, Kunihiro Wasa 2, Hiroki Arimura 1, and Takeaki Uno 2 1 IST, Hokkaido University, Sapporo, Japan 2 National
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Small Survey on Perfect Graphs
 Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Graphs and Discrete Structures
 Graphs and Discrete Structures Nicolas Bousquet Louis Esperet Fall 2018 Abstract Brief summary of the first and second course. É 1 Chromatic number, independence number and clique number The chromatic
Graphs and Discrete Structures Nicolas Bousquet Louis Esperet Fall 2018 Abstract Brief summary of the first and second course. É 1 Chromatic number, independence number and clique number The chromatic
Computing minimum distortion embeddings into a path for bipartite permutation graphs and threshold graphs
 Computing minimum distortion embeddings into a path for bipartite permutation graphs and threshold graphs Pinar Heggernes Daniel Meister Andrzej Proskurowski Abstract The problem of computing minimum distortion
Computing minimum distortion embeddings into a path for bipartite permutation graphs and threshold graphs Pinar Heggernes Daniel Meister Andrzej Proskurowski Abstract The problem of computing minimum distortion
Lecture Notes on Graph Theory
 Lecture Notes on Graph Theory Vadim Lozin 1 Introductory concepts A graph G = (V, E) consists of two finite sets V and E. The elements of V are called the vertices and the elements of E the edges of G.
Lecture Notes on Graph Theory Vadim Lozin 1 Introductory concepts A graph G = (V, E) consists of two finite sets V and E. The elements of V are called the vertices and the elements of E the edges of G.
Vertex coloring, chromatic number
 Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Fully dynamic algorithm for recognition and modular decomposition of permutation graphs
 Fully dynamic algorithm for recognition and modular decomposition of permutation graphs Christophe Crespelle Christophe Paul CNRS - Département Informatique, LIRMM, Montpellier {crespell,paul}@lirmm.fr
Fully dynamic algorithm for recognition and modular decomposition of permutation graphs Christophe Crespelle Christophe Paul CNRS - Département Informatique, LIRMM, Montpellier {crespell,paul}@lirmm.fr
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees
 Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Characterization of Super Strongly Perfect Graphs in Chordal and Strongly Chordal Graphs
 ISSN 0975-3303 Mapana J Sci, 11, 4(2012), 121-131 https://doi.org/10.12725/mjs.23.10 Characterization of Super Strongly Perfect Graphs in Chordal and Strongly Chordal Graphs R Mary Jeya Jothi * and A Amutha
ISSN 0975-3303 Mapana J Sci, 11, 4(2012), 121-131 https://doi.org/10.12725/mjs.23.10 Characterization of Super Strongly Perfect Graphs in Chordal and Strongly Chordal Graphs R Mary Jeya Jothi * and A Amutha
Vertex coloring, chromatic number
 Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
 This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
Treewidth: Preprocessing and Kernelization
 Treewidth: Preprocessing and Kernelization Hans L. Bodlaender Joint work with Arie Koster, Frank van den Eijkhof, Bart Jansen, Stefan Kratsch, Vincent Kreuzen 1 This talk Survey of work on preprocessing
Treewidth: Preprocessing and Kernelization Hans L. Bodlaender Joint work with Arie Koster, Frank van den Eijkhof, Bart Jansen, Stefan Kratsch, Vincent Kreuzen 1 This talk Survey of work on preprocessing
Complexity Results on Graphs with Few Cliques
 Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
Discrete Mathematics and Theoretical Computer Science DMTCS vol. 9, 2007, 127 136 Complexity Results on Graphs with Few Cliques Bill Rosgen 1 and Lorna Stewart 2 1 Institute for Quantum Computing and School
9 About Intersection Graphs
 9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
Eternal Domination: Criticality and Reachability
 Eternal Domination: Criticality and Reachability William F. Klostermeyer School of Computing University of North Florida Jacksonville, FL 32224-2669 wkloster@unf.edu Gary MacGillivray Department of Mathematics
Eternal Domination: Criticality and Reachability William F. Klostermeyer School of Computing University of North Florida Jacksonville, FL 32224-2669 wkloster@unf.edu Gary MacGillivray Department of Mathematics
Emergency Response Sets in Graphs
 Emergency Response Sets in Graphs Jean Blair, US Military Academy Wayne Goddard, Sandra M. Hedetniemi, Stephen T. Hedetniemi Clemson University Fredrik Manne, University of Bergen Douglas Rall, Furman
Emergency Response Sets in Graphs Jean Blair, US Military Academy Wayne Goddard, Sandra M. Hedetniemi, Stephen T. Hedetniemi Clemson University Fredrik Manne, University of Bergen Douglas Rall, Furman
Parameterized coloring problems on chordal graphs
 Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Graphs and Orders Cours MPRI
 Graphs and Orders Cours MPRI 2012 2013 Michel Habib habib@liafa.univ-paris-diderot.fr http://www.liafa.univ-paris-diderot.fr/~habib Chevaleret novembre 2012 Table des Matières Introduction Definitions
Graphs and Orders Cours MPRI 2012 2013 Michel Habib habib@liafa.univ-paris-diderot.fr http://www.liafa.univ-paris-diderot.fr/~habib Chevaleret novembre 2012 Table des Matières Introduction Definitions
A taste of perfect graphs (continued)
 A taste of perfect graphs (continued) Recall two theorems from last class characterizing perfect graphs (and that we observed that the α ω theorem implied the Perfect Graph Theorem). Perfect Graph Theorem.
A taste of perfect graphs (continued) Recall two theorems from last class characterizing perfect graphs (and that we observed that the α ω theorem implied the Perfect Graph Theorem). Perfect Graph Theorem.
Section 3.1: Nonseparable Graphs Cut vertex of a connected graph G: A vertex x G such that G x is not connected. Theorem 3.1, p. 57: Every connected
 Section 3.1: Nonseparable Graphs Cut vertex of a connected graph G: A vertex x G such that G x is not connected. Theorem 3.1, p. 57: Every connected graph G with at least 2 vertices contains at least 2
Section 3.1: Nonseparable Graphs Cut vertex of a connected graph G: A vertex x G such that G x is not connected. Theorem 3.1, p. 57: Every connected graph G with at least 2 vertices contains at least 2
Chordal Graphs: Theory and Algorithms
 Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Minimal Dominating Set Enumeration
 Title: Name: Affil./Addr. Keywords: SumOriWork: Minimal Dominating Set Enumeration Mamadou Moustapha Kanté, Lhouari Nourine Clermont-Université, Université Blaise Pascal, LIMOS, CNRS, France. Enumeration;
Title: Name: Affil./Addr. Keywords: SumOriWork: Minimal Dominating Set Enumeration Mamadou Moustapha Kanté, Lhouari Nourine Clermont-Université, Université Blaise Pascal, LIMOS, CNRS, France. Enumeration;
Math 776 Graph Theory Lecture Note 1 Basic concepts
 Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Exact Algorithms for NP-hard problems
 24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
24 mai 2012 1 Why do we need exponential algorithms? 2 3 Why the P-border? 1 Practical reasons (Jack Edmonds, 1965) For practical purposes the difference between algebraic and exponential order is more
Clique-Width for Four-Vertex Forbidden Subgraphs
 Clique-Width for Four-Vertex Forbidden Subgraphs Andreas Brandstädt 1 Joost Engelfriet 2 Hoàng-Oanh Le 3 Vadim V. Lozin 4 March 15, 2005 1 Institut für Informatik, Universität Rostock, D-18051 Rostock,
Clique-Width for Four-Vertex Forbidden Subgraphs Andreas Brandstädt 1 Joost Engelfriet 2 Hoàng-Oanh Le 3 Vadim V. Lozin 4 March 15, 2005 1 Institut für Informatik, Universität Rostock, D-18051 Rostock,
Necessary edges in k-chordalizations of graphs
 Necessary edges in k-chordalizations of graphs Hans L. Bodlaender Abstract In this note, we look at which edges must always be added to a given graph G = (V, E), when we want to make it a chordal graph
Necessary edges in k-chordalizations of graphs Hans L. Bodlaender Abstract In this note, we look at which edges must always be added to a given graph G = (V, E), when we want to make it a chordal graph
Locally identifying coloring of graphs
 Locally identifying coloring of graphs Louis Esperet Laboratoire G-SCOP Grenoble-INP, CNRS Grenoble, France louis.esperet@g-scop.inpg.fr Mickaël Montassier LaBRI Université de Bordeaux, CNRS Talence, France
Locally identifying coloring of graphs Louis Esperet Laboratoire G-SCOP Grenoble-INP, CNRS Grenoble, France louis.esperet@g-scop.inpg.fr Mickaël Montassier LaBRI Université de Bordeaux, CNRS Talence, France
Fixed-Parameter Algorithms, IA166
 Fixed-Parameter Algorithms, IA166 Sebastian Ordyniak Faculty of Informatics Masaryk University Brno Spring Semester 2013 Introduction Outline 1 Introduction Algorithms on Locally Bounded Treewidth Layer
Fixed-Parameter Algorithms, IA166 Sebastian Ordyniak Faculty of Informatics Masaryk University Brno Spring Semester 2013 Introduction Outline 1 Introduction Algorithms on Locally Bounded Treewidth Layer
Efficient Enumeration of Dominating Sets in Sparse Graphs
 Efficient Enumeration of Dominating Sets in Sparse Graphs Kazuhiro Kurita Kunihiro Wasa Takeaki Uno Hiroki Arimura Abstract A dominating set is one of the fundamental graph structures. However, enumeration
Efficient Enumeration of Dominating Sets in Sparse Graphs Kazuhiro Kurita Kunihiro Wasa Takeaki Uno Hiroki Arimura Abstract A dominating set is one of the fundamental graph structures. However, enumeration
Reachability in K 3,3 -free and K 5 -free Graphs is in Unambiguous Logspace
 CHICAGO JOURNAL OF THEORETICAL COMPUTER SCIENCE 2014, Article 2, pages 1 29 http://cjtcs.cs.uchicago.edu/ Reachability in K 3,3 -free and K 5 -free Graphs is in Unambiguous Logspace Thomas Thierauf Fabian
CHICAGO JOURNAL OF THEORETICAL COMPUTER SCIENCE 2014, Article 2, pages 1 29 http://cjtcs.cs.uchicago.edu/ Reachability in K 3,3 -free and K 5 -free Graphs is in Unambiguous Logspace Thomas Thierauf Fabian
WORM COLORINGS. Wayne Goddard. Dept of Mathematical Sciences, Clemson University Kirsti Wash
 1 2 Discussiones Mathematicae Graph Theory xx (xxxx) 1 14 3 4 5 6 7 8 9 10 11 12 13 WORM COLORINGS Wayne Goddard Dept of Mathematical Sciences, Clemson University e-mail: goddard@clemson.edu Kirsti Wash
1 2 Discussiones Mathematicae Graph Theory xx (xxxx) 1 14 3 4 5 6 7 8 9 10 11 12 13 WORM COLORINGS Wayne Goddard Dept of Mathematical Sciences, Clemson University e-mail: goddard@clemson.edu Kirsti Wash
Tolerance Representations of Graphs in Trees Nancy Eaton. Tolerance Representations of Graphs in Trees Lecture I. Tree Representations of Graphs
 Tolerance Representations of Graphs in Trees Nancy Eaton Tolerance Representations of Graphs in Trees Lecture I Tree Representations of Graphs Tolerance Representations Some background A conjecture on
Tolerance Representations of Graphs in Trees Nancy Eaton Tolerance Representations of Graphs in Trees Lecture I Tree Representations of Graphs Tolerance Representations Some background A conjecture on
Fixed-Parameter Algorithms
 Fixed-Parameter Algorithms Rolf Niedermeier and Jiong Guo Lehrstuhl Theoretische Informatik I / Komplexitätstheorie Institut für Informatik Friedrich-Schiller-Universität Jena niedermr@minet.uni-jena.de
Fixed-Parameter Algorithms Rolf Niedermeier and Jiong Guo Lehrstuhl Theoretische Informatik I / Komplexitätstheorie Institut für Informatik Friedrich-Schiller-Universität Jena niedermr@minet.uni-jena.de
Price of Connectivity for the vertex cover problem and the dominating set problem: conjectures and investigation of critical graphs
 Price of Connectivity for the vertex cover problem and the dominating set problem: conjectures and investigation of critical graphs Eglantine Camby Université Libre de Bruxelles, Brussels, Belgium GERAD
Price of Connectivity for the vertex cover problem and the dominating set problem: conjectures and investigation of critical graphs Eglantine Camby Université Libre de Bruxelles, Brussels, Belgium GERAD
Enumerations, Forbidden Subgraph Characterizations, and the Split-Decomposition
 Enumerations, Forbidden Subgraph Characterizations, and the Split-Decomposition Maryam Bahrani Jérémie Lumbroso Abstract Forbidden characterizations may sometimes be the most natural way to describe families
Enumerations, Forbidden Subgraph Characterizations, and the Split-Decomposition Maryam Bahrani Jérémie Lumbroso Abstract Forbidden characterizations may sometimes be the most natural way to describe families
The domination game on split graphs
 The domination game on split graphs Tijo James a,b Sandi Klavžar c,d,e Ambat Vijayakumar b August 6, 018 a Department of Mathematics, Pavanatma College, Murickassery, India tijojames@gmail.com b Department
The domination game on split graphs Tijo James a,b Sandi Klavžar c,d,e Ambat Vijayakumar b August 6, 018 a Department of Mathematics, Pavanatma College, Murickassery, India tijojames@gmail.com b Department
Covering the edges of a graph by a prescribed tree with minimum overlap
 Covering the edges of a graph by a prescribed tree with minimum overlap Noga Alon Yair Caro Raphael Yuster Abstract Let H = (V H, E H ) be a graph, and let k be a positive integer. A graph G = (V G, E
Covering the edges of a graph by a prescribed tree with minimum overlap Noga Alon Yair Caro Raphael Yuster Abstract Let H = (V H, E H ) be a graph, and let k be a positive integer. A graph G = (V G, E
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
arxiv: v5 [cs.dm] 9 May 2016
![arxiv: v5 [cs.dm] 9 May 2016 arxiv: v5 [cs.dm] 9 May 2016](/thumbs/94/122228531.jpg) Tree spanners of bounded degree graphs Ioannis Papoutsakis Kastelli Pediados, Heraklion, Crete, reece, 700 06 October 21, 2018 arxiv:1503.06822v5 [cs.dm] 9 May 2016 Abstract A tree t-spanner of a graph
Tree spanners of bounded degree graphs Ioannis Papoutsakis Kastelli Pediados, Heraklion, Crete, reece, 700 06 October 21, 2018 arxiv:1503.06822v5 [cs.dm] 9 May 2016 Abstract A tree t-spanner of a graph
The Parameterized Complexity of the Rainbow Subgraph Problem. Falk Hüffner, Christian Komusiewicz *, Rolf Niedermeier and Martin Rötzschke
 Algorithms 2015, 8, 60-81; doi:10.3390/a8010060 OPEN ACCESS algorithms ISSN 1999-4893 www.mdpi.com/journal/algorithms Article The Parameterized Complexity of the Rainbow Subgraph Problem Falk Hüffner,
Algorithms 2015, 8, 60-81; doi:10.3390/a8010060 OPEN ACCESS algorithms ISSN 1999-4893 www.mdpi.com/journal/algorithms Article The Parameterized Complexity of the Rainbow Subgraph Problem Falk Hüffner,
NOTE ON MINIMALLY k-connected GRAPHS
 NOTE ON MINIMALLY k-connected GRAPHS R. Rama a, Suresh Badarla a a Department of Mathematics, Indian Institute of Technology, Chennai, India ABSTRACT A k-tree is either a complete graph on (k+1) vertices
NOTE ON MINIMALLY k-connected GRAPHS R. Rama a, Suresh Badarla a a Department of Mathematics, Indian Institute of Technology, Chennai, India ABSTRACT A k-tree is either a complete graph on (k+1) vertices
Graph Theory S 1 I 2 I 1 S 2 I 1 I 2
 Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Math 778S Spectral Graph Theory Handout #2: Basic graph theory
 Math 778S Spectral Graph Theory Handout #: Basic graph theory Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved the Königsberg Bridge problem: Is it possible
Math 778S Spectral Graph Theory Handout #: Basic graph theory Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved the Königsberg Bridge problem: Is it possible
Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded
 Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded Cemil Dibek Tınaz Ekim Pinar Heggernes Abstract We determine the maximum number of edges that a claw-free
Maximum number of edges in claw-free graphs whose maximum degree and matching number are bounded Cemil Dibek Tınaz Ekim Pinar Heggernes Abstract We determine the maximum number of edges that a claw-free
Conflict Graphs for Combinatorial Optimization Problems
 Conflict Graphs for Combinatorial Optimization Problems Ulrich Pferschy joint work with Andreas Darmann and Joachim Schauer University of Graz, Austria Introduction Combinatorial Optimization Problem CO
Conflict Graphs for Combinatorial Optimization Problems Ulrich Pferschy joint work with Andreas Darmann and Joachim Schauer University of Graz, Austria Introduction Combinatorial Optimization Problem CO
CS261: A Second Course in Algorithms Lecture #16: The Traveling Salesman Problem
 CS61: A Second Course in Algorithms Lecture #16: The Traveling Salesman Problem Tim Roughgarden February 5, 016 1 The Traveling Salesman Problem (TSP) In this lecture we study a famous computational problem,
CS61: A Second Course in Algorithms Lecture #16: The Traveling Salesman Problem Tim Roughgarden February 5, 016 1 The Traveling Salesman Problem (TSP) In this lecture we study a famous computational problem,
{ 1} Definitions. 10. Extremal graph theory. Problem definition Paths and cycles Complete subgraphs
 Problem definition Paths and cycles Complete subgraphs 10. Extremal graph theory 10.1. Definitions Let us examine the following forbidden subgraph problems: At most how many edges are in a graph of order
Problem definition Paths and cycles Complete subgraphs 10. Extremal graph theory 10.1. Definitions Let us examine the following forbidden subgraph problems: At most how many edges are in a graph of order
Characterizing Graphs (3) Characterizing Graphs (1) Characterizing Graphs (2) Characterizing Graphs (4)
 S-72.2420/T-79.5203 Basic Concepts 1 S-72.2420/T-79.5203 Basic Concepts 3 Characterizing Graphs (1) Characterizing Graphs (3) Characterizing a class G by a condition P means proving the equivalence G G
S-72.2420/T-79.5203 Basic Concepts 1 S-72.2420/T-79.5203 Basic Concepts 3 Characterizing Graphs (1) Characterizing Graphs (3) Characterizing a class G by a condition P means proving the equivalence G G
On the minimum feedback vertex set problem: Exact and enumeration algorithms
 On the minimum feedback vertex set problem: Exact and enumeration algorithms Fedor V. Fomin Serge Gaspers Artem V. Pyatkin Igor Razgon November 26, 2007 Abstract We present a time O(1.7548 n ) algorithm
On the minimum feedback vertex set problem: Exact and enumeration algorithms Fedor V. Fomin Serge Gaspers Artem V. Pyatkin Igor Razgon November 26, 2007 Abstract We present a time O(1.7548 n ) algorithm
Coloring edges and vertices of graphs without short or long cycles
 Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
3-colouring AT-free graphs in polynomial time
 3-colouring AT-free graphs in polynomial time Juraj Stacho Wilfrid Laurier University, Department of Physics and Computer Science, 75 University Ave W, Waterloo, ON N2L 3C5, Canada stacho@cs.toronto.edu
3-colouring AT-free graphs in polynomial time Juraj Stacho Wilfrid Laurier University, Department of Physics and Computer Science, 75 University Ave W, Waterloo, ON N2L 3C5, Canada stacho@cs.toronto.edu
The strong chromatic number of a graph
 The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
A New Approach to Graph Recognition and Applications to Distance-Hereditary Graphs
 Nakano S-i, Uehara R, Uno T. A new approach to graph recognition and applications to distance-hereditary graphs. JOUR- NAL OF COMPUTER SCIENCE AND TECHNOLOGY 24(3): 517 533 May 2009 A New Approach to Graph
Nakano S-i, Uehara R, Uno T. A new approach to graph recognition and applications to distance-hereditary graphs. JOUR- NAL OF COMPUTER SCIENCE AND TECHNOLOGY 24(3): 517 533 May 2009 A New Approach to Graph
Abstract. A graph G is perfect if for every induced subgraph H of G, the chromatic number of H is equal to the size of the largest clique of H.
 Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Last course. Last course. Michel Habib 28 octobre 2016
 Last course Michel Habib habib@irif.fr http://www.irif.fr/~habib 28 octobre 2016 Schedule Introduction More structural insights on chordal graphs Properties of reduced clique graphs Exercises Interval
Last course Michel Habib habib@irif.fr http://www.irif.fr/~habib 28 octobre 2016 Schedule Introduction More structural insights on chordal graphs Properties of reduced clique graphs Exercises Interval
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Branch and Recharge: Exact algorithms for generalized domination
 Branch and Recharge: Exact algorithms for generalized domination Fedor V. Fomin Petr A. Golovach Jan Kratochvíl Dieter Kratsch Mathieu Liedloff February 28, 2010 Abstract In this paper we present branching
Branch and Recharge: Exact algorithms for generalized domination Fedor V. Fomin Petr A. Golovach Jan Kratochvíl Dieter Kratsch Mathieu Liedloff February 28, 2010 Abstract In this paper we present branching
arxiv: v3 [cs.ds] 26 Sep 2013
![arxiv: v3 [cs.ds] 26 Sep 2013 arxiv: v3 [cs.ds] 26 Sep 2013](/thumbs/96/129281842.jpg) Preprocessing Subgraph and Minor Problems: When Does a Small Vertex Cover Help?, Fedor V. Fomin a, Bart M. P. Jansen a,, Micha l Pilipczuk a a Department of Informatics, University of Bergen. PO Box 7803,
Preprocessing Subgraph and Minor Problems: When Does a Small Vertex Cover Help?, Fedor V. Fomin a, Bart M. P. Jansen a,, Micha l Pilipczuk a a Department of Informatics, University of Bergen. PO Box 7803,
Parameterized Algorithm for Eternal Vertex Cover
 Parameterized Algorithm for Eternal Vertex Cover Fedor V. Fomin a,1, Serge Gaspers b, Petr A. Golovach c, Dieter Kratsch d, Saket Saurabh e, a Department of Informatics, University of Bergen, N-5020 Bergen,
Parameterized Algorithm for Eternal Vertex Cover Fedor V. Fomin a,1, Serge Gaspers b, Petr A. Golovach c, Dieter Kratsch d, Saket Saurabh e, a Department of Informatics, University of Bergen, N-5020 Bergen,
Common Induced Subgraph Isomorphism Structural Parameterizations and Exact Algorithms
 Common Induced Subgraph Isomorphism Structural Parameterizations and Exact Algorithms Faisal N. Abu-Khzam Department of Computer Science and Mathematics Lebanese American University Beirut, Lebanon Overview
Common Induced Subgraph Isomorphism Structural Parameterizations and Exact Algorithms Faisal N. Abu-Khzam Department of Computer Science and Mathematics Lebanese American University Beirut, Lebanon Overview
arxiv: v1 [cs.dm] 21 Dec 2015
![arxiv: v1 [cs.dm] 21 Dec 2015 arxiv: v1 [cs.dm] 21 Dec 2015](/thumbs/84/90806310.jpg) The Maximum Cardinality Cut Problem is Polynomial in Proper Interval Graphs Arman Boyacı 1, Tinaz Ekim 1, and Mordechai Shalom 1 Department of Industrial Engineering, Boğaziçi University, Istanbul, Turkey
The Maximum Cardinality Cut Problem is Polynomial in Proper Interval Graphs Arman Boyacı 1, Tinaz Ekim 1, and Mordechai Shalom 1 Department of Industrial Engineering, Boğaziçi University, Istanbul, Turkey
Improved Algorithms and Complexity Results for Power Domination in Graphs
 Improved Algorithms and Complexity Results for Power Domination in Graphs Jiong Guo Rolf Niedermeier Daniel Raible July 3, 2007 Abstract The NP-complete Power Dominating Set problem is an electric power
Improved Algorithms and Complexity Results for Power Domination in Graphs Jiong Guo Rolf Niedermeier Daniel Raible July 3, 2007 Abstract The NP-complete Power Dominating Set problem is an electric power
COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES
 Volume 2, Number 1, Pages 61 66 ISSN 1715-0868 COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES MARCIN KAMIŃSKI AND VADIM LOZIN Abstract. Vertex and edge colorability are two graph problems
Volume 2, Number 1, Pages 61 66 ISSN 1715-0868 COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES MARCIN KAMIŃSKI AND VADIM LOZIN Abstract. Vertex and edge colorability are two graph problems
An upper bound for the chromatic number of line graphs
 EuroComb 005 DMTCS proc AE, 005, 151 156 An upper bound for the chromatic number of line graphs A D King, B A Reed and A Vetta School of Computer Science, McGill University, 3480 University Ave, Montréal,
EuroComb 005 DMTCS proc AE, 005, 151 156 An upper bound for the chromatic number of line graphs A D King, B A Reed and A Vetta School of Computer Science, McGill University, 3480 University Ave, Montréal,
Graph Connectivity G G G
 Graph Connectivity 1 Introduction We have seen that trees are minimally connected graphs, i.e., deleting any edge of the tree gives us a disconnected graph. What makes trees so susceptible to edge deletions?
Graph Connectivity 1 Introduction We have seen that trees are minimally connected graphs, i.e., deleting any edge of the tree gives us a disconnected graph. What makes trees so susceptible to edge deletions?
Bayesian Networks, Winter Yoav Haimovitch & Ariel Raviv
 Bayesian Networks, Winter 2009-2010 Yoav Haimovitch & Ariel Raviv 1 Chordal Graph Warm up Theorem 7 Perfect Vertex Elimination Scheme Maximal cliques Tree Bibliography M.C.Golumbic Algorithmic Graph Theory
Bayesian Networks, Winter 2009-2010 Yoav Haimovitch & Ariel Raviv 1 Chordal Graph Warm up Theorem 7 Perfect Vertex Elimination Scheme Maximal cliques Tree Bibliography M.C.Golumbic Algorithmic Graph Theory
Characterizations of Trees
 Characterizations of Trees Lemma Every tree with at least two vertices has at least two leaves. Proof. 1. A connected graph with at least two vertices has an edge. 2. In an acyclic graph, an end point
Characterizations of Trees Lemma Every tree with at least two vertices has at least two leaves. Proof. 1. A connected graph with at least two vertices has an edge. 2. In an acyclic graph, an end point
Vertex Cover Reconfiguration and Beyond
 algorithms Article Vertex Cover Reconfiguration and Beyond Amer E. Mouawad 1, *, Naomi Nishimura 2, Venkatesh Raman 3 and Sebastian Siebertz 4, 1 Department of Informatics, University of Bergen, PB 7803,
algorithms Article Vertex Cover Reconfiguration and Beyond Amer E. Mouawad 1, *, Naomi Nishimura 2, Venkatesh Raman 3 and Sebastian Siebertz 4, 1 Department of Informatics, University of Bergen, PB 7803,
