A taste of perfect graphs (continued)
|
|
|
- Posy Reeves
- 6 years ago
- Views:
Transcription
1 A taste of perfect graphs (continued) Recall two theorems from last class characterizing perfect graphs (and that we observed that the α ω theorem implied the Perfect Graph Theorem). Perfect Graph Theorem. A graph G is perfect if and only if G is perfect. Theorem. A graph G is perfect if and only if every induced subgraph H of G satisfies the inequalilty V (H) α(h)ω(h). We also proved a lemma regarding minimally imperfect graphs that plays a key role in the proof of the α ω theorem. Lemma. Let G be a minimally imperfect graph. Then G contains α(g)ω(g)+1 independent sets S 0, S 1,..., S α(g)ω(g) and α(g)ω(g)+1 cliques C 0, C 1,..., C α(g)ω(g) such that (a) each vertex of G belongs to precisely α(g) of the independent sets S i, (b) each clique C i has ω(g) vertices, (c) C i S i = for 0 i α(g)ω(g), (d) and C i S j = 1 for 0 i < j α(g)ω(g). Math Prof. Kindred - Lecture 24 Page 1
2 Proof of α ω theorem. ( ) Suppose that G is perfect, and let H be an induced subgraph of G. We have ω(h) = χ(h) V (H) α(h) = V (H) α(h)ω(h). ( ) We prove this direction by showing that if G is minimally imperfect, then V (G) α(g)ω(g) + 1. Let n = V (G). Consider the families {S i : 0 i α(g)ω(g)} and {C i : 0 i α(g)ω(g)} of independent sets and cliques described in the previous lemma. Let M S and M C be the n (α(g)ω(g) + 1) incidence matrices of these families. It follows from the lemma that M T S M C = J I. Notice that J I is a nonsingular matrix (with inverse 1 α(g)ω(g) J I). Thus, it must be a full rank matrix, i.e., We have rank(j I) = α(g)ω(g) + 1. α(g)ω(g) + 1 = rank(j I) = rank(m T S M C ) min(rank(m S ), rank(m C )) rank(m S) or rank(m C ) n, where the last inequality follows from the fact that the two matrices have n rows. Thus, we have shown that n α(g)ω(g) + 1. If a graph is perfect, then so are all of its induced subgraphs. This means that we can characterize perfect graphs by describing all minimally imperfect graphs. Math Prof. Kindred - Lecture 24 Page 2
3 Berge (1961) conjectured that the odd cycles (of length at least 5) and their complements were the only minimally imperfect graphs. This conjecture was known as the Strong Perfect Graph Conjecture (and is printed as such in your text). But it was proven in 2002 by Chudnovsky and colleagues. Strong Perfect Graph Theorem. A graph is perfect if and only if it contains no odd cycle of length at least five or its complement as an induced subgraph. The proof of this theorem was a major achievement, as much effort had been expended over the years on attempts to settle the Strong Perfect Graph Conjecture. Furthermore, a polynomial-time recognition algorithm for perfect graphs was developed shortly thereafter by Chudnovsky, et al., (2005). Math Prof. Kindred - Lecture 24 Page 3
4 Chordal graphs Definition A chord of a cycle C is an edge not in C whose endpoints lie in C. A chordless cycle in a graph G is a cycle of length at least 4 in G that has no chord (that is, the cycle is an induced subgraph). G is a chordal graph if it is simple and has no chordless cycle. Being chordal is a hereditary property, inherited by all the induced subgraphs of a chordal graph. Recall the notion of an x, y-cut. Definition Let x, y be nonadjacent vertices of G. An x, y-cut, or x, y-separator, is a set of vertices S such that x and y are in different components of G S. A minimal x, y-cut is an x, y-cut S such that no proper subset of S is an x, y-cut. (Note: a minimal x, y-cut is not necessarily the smallest x, y-cut in G.) Theorem. Let a and b be nonadjacent vertices of a connected chordal graph G, and let S be a minimal a, b-cut. Then S is a clique. Proof. Let S be such a cut, and let G[A], G[B] be components of G S with a A and b B. Every vertex in v S must be adjacent to some vertex of A and to some vertex of B otherwise, S would not be minimal. If S only contains one vertex, then we are done (it is clearly a clique). So assume u, v S. We claim that u v. Suppose not. Then let P be a shortest u, v-path all of whose internal vertices are in A, so P = u a 1 a 2 a s v. Math Prof. Kindred - Lecture 24 Page 4
5 Likewise, let Q be a shortest u, v-path all of whose internal vertices are in B, so Q = u b 1 b 2 b t v. a 1 u b a s A v S b t B Then the union of P and Q is an induced cycle of length at least 4. Hence, it must be that u v for any pair of vertices u, v S, thereby implying that S is a clique. Note that trees are clearly chordal graphs since they are acyclic. It turns out that chordal graphs, in general, have a treelike structure composed of complete graphs (just as trees are composed of copies of K 2.) In this spirit, we generalize the notion of a leaf in a tree to that of a simplicial vertex. Definition A vertex of G is simplicial if its neighborhood in G is a clique. We prove two results for simplicial vertices and chordal graphs that are analogous to the following facts for trees and leaves: If T is a tree with at least 2 vertices, then T has a leaf. If v is a leaf of T, then T v is also a tree. Theorem. If G is a (nonempty) chordal graph, then G has a simplicial vertex. Furthermore, if G is not a complete graph, then G has two nonadjacent simplicial vertices. Math Prof. Kindred - Lecture 24 Page 5
Small Survey on Perfect Graphs
 Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Vertex coloring, chromatic number
 Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Definition For vertices u, v V (G), the distance from u to v, denoted d(u, v), in G is the length of a shortest u, v-path. 1
 Graph fundamentals Bipartite graph characterization Lemma. If a graph contains an odd closed walk, then it contains an odd cycle. Proof strategy: Consider a shortest closed odd walk W. If W is not a cycle,
Graph fundamentals Bipartite graph characterization Lemma. If a graph contains an odd closed walk, then it contains an odd cycle. Proof strategy: Consider a shortest closed odd walk W. If W is not a cycle,
Vertex coloring, chromatic number
 Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
Vertex coloring, chromatic number A k-coloring of a graph G is a labeling f : V (G) S, where S = k. The labels are called colors; the vertices of one color form a color class. A k-coloring is proper if
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
9 About Intersection Graphs
 9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
Algorithm design in Perfect Graphs N.S. Narayanaswamy IIT Madras
 Algorithm design in Perfect Graphs N.S. Narayanaswamy IIT Madras What is it to be Perfect? Introduced by Claude Berge in early 1960s Coloring number and clique number are one and the same for all induced
Algorithm design in Perfect Graphs N.S. Narayanaswamy IIT Madras What is it to be Perfect? Introduced by Claude Berge in early 1960s Coloring number and clique number are one and the same for all induced
Characterizations of graph classes by forbidden configurations
 Characterizations of graph classes by forbidden configurations Zdeněk Dvořák September 14, 2015 We consider graph classes that can be described by excluding some fixed configurations. Let us give some
Characterizations of graph classes by forbidden configurations Zdeněk Dvořák September 14, 2015 We consider graph classes that can be described by excluding some fixed configurations. Let us give some
Colouring graphs with no odd holes
 Colouring graphs with no odd holes Paul Seymour (Princeton) joint with Alex Scott (Oxford) 1 / 17 Chromatic number χ(g): minimum number of colours needed to colour G. 2 / 17 Chromatic number χ(g): minimum
Colouring graphs with no odd holes Paul Seymour (Princeton) joint with Alex Scott (Oxford) 1 / 17 Chromatic number χ(g): minimum number of colours needed to colour G. 2 / 17 Chromatic number χ(g): minimum
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Network flows and Menger s theorem
 Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
THE LEAFAGE OF A CHORDAL GRAPH
 Discussiones Mathematicae Graph Theory 18 (1998 ) 23 48 THE LEAFAGE OF A CHORDAL GRAPH In-Jen Lin National Ocean University, Taipei, Taiwan Terry A. McKee 1 Wright State University, Dayton, OH 45435-0001,
Discussiones Mathematicae Graph Theory 18 (1998 ) 23 48 THE LEAFAGE OF A CHORDAL GRAPH In-Jen Lin National Ocean University, Taipei, Taiwan Terry A. McKee 1 Wright State University, Dayton, OH 45435-0001,
How many colors are needed to color a map?
 How many colors are needed to color a map? Is 4 always enough? Two relevant concepts How many colors do we need to color a map so neighboring countries get different colors? Simplifying assumption (not
How many colors are needed to color a map? Is 4 always enough? Two relevant concepts How many colors do we need to color a map so neighboring countries get different colors? Simplifying assumption (not
DO NOT RE-DISTRIBUTE THIS SOLUTION FILE
 Professor Kindred Math 104, Graph Theory Homework 2 Solutions February 7, 2013 Introduction to Graph Theory, West Section 1.2: 26, 38, 42 Section 1.3: 14, 18 Section 2.1: 26, 29, 30 DO NOT RE-DISTRIBUTE
Professor Kindred Math 104, Graph Theory Homework 2 Solutions February 7, 2013 Introduction to Graph Theory, West Section 1.2: 26, 38, 42 Section 1.3: 14, 18 Section 2.1: 26, 29, 30 DO NOT RE-DISTRIBUTE
Graphs and Discrete Structures
 Graphs and Discrete Structures Nicolas Bousquet Louis Esperet Fall 2018 Abstract Brief summary of the first and second course. É 1 Chromatic number, independence number and clique number The chromatic
Graphs and Discrete Structures Nicolas Bousquet Louis Esperet Fall 2018 Abstract Brief summary of the first and second course. É 1 Chromatic number, independence number and clique number The chromatic
Chordal Graphs: Theory and Algorithms
 Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
Chordal Graphs: Theory and Algorithms 1 Chordal graphs Chordal graph : Every cycle of four or more vertices has a chord in it, i.e. there is an edge between two non consecutive vertices of the cycle. Also
if for every induced subgraph H of G the chromatic number of H is equal to the largest size of a clique in H. The triangulated graphs constitute a wid
 Slightly Triangulated Graphs Are Perfect Frederic Maire e-mail : frm@ccr.jussieu.fr Case 189 Equipe Combinatoire Universite Paris 6, France December 21, 1995 Abstract A graph is triangulated if it has
Slightly Triangulated Graphs Are Perfect Frederic Maire e-mail : frm@ccr.jussieu.fr Case 189 Equipe Combinatoire Universite Paris 6, France December 21, 1995 Abstract A graph is triangulated if it has
MATH 350 GRAPH THEORY & COMBINATORICS. Contents
 MATH 350 GRAPH THEORY & COMBINATORICS PROF. SERGEY NORIN, FALL 2013 Contents 1. Basic definitions 1 2. Connectivity 2 3. Trees 3 4. Spanning Trees 3 5. Shortest paths 4 6. Eulerian & Hamiltonian cycles
MATH 350 GRAPH THEORY & COMBINATORICS PROF. SERGEY NORIN, FALL 2013 Contents 1. Basic definitions 1 2. Connectivity 2 3. Trees 3 4. Spanning Trees 3 5. Shortest paths 4 6. Eulerian & Hamiltonian cycles
Abstract. A graph G is perfect if for every induced subgraph H of G, the chromatic number of H is equal to the size of the largest clique of H.
 Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Abstract We discuss a class of graphs called perfect graphs. After defining them and getting intuition with a few simple examples (and one less simple example), we present a proof of the Weak Perfect Graph
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
EE512 Graphical Models Fall 2009
 EE512 Graphical Models Fall 2009 Prof. Jeff Bilmes University of Washington, Seattle Department of Electrical Engineering Fall Quarter, 2009 http://ssli.ee.washington.edu/~bilmes/ee512fa09 Lecture 11 -
EE512 Graphical Models Fall 2009 Prof. Jeff Bilmes University of Washington, Seattle Department of Electrical Engineering Fall Quarter, 2009 http://ssli.ee.washington.edu/~bilmes/ee512fa09 Lecture 11 -
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Abstract We present two parameterized algorithms for the Minimum Fill-In problem, also known as Chordal
Fast Skew Partition Recognition
 Fast Skew Partition Recognition William S. Kennedy 1, and Bruce Reed 2, 1 Department of Mathematics and Statistics, McGill University, Montréal, Canada, H3A2K6 kennedy@math.mcgill.ca 2 School of Computer
Fast Skew Partition Recognition William S. Kennedy 1, and Bruce Reed 2, 1 Department of Mathematics and Statistics, McGill University, Montréal, Canada, H3A2K6 kennedy@math.mcgill.ca 2 School of Computer
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
K 4 C 5. Figure 4.5: Some well known family of graphs
 08 CHAPTER. TOPICS IN CLASSICAL GRAPH THEORY K, K K K, K K, K K, K C C C C 6 6 P P P P P. Graph Operations Figure.: Some well known family of graphs A graph Y = (V,E ) is said to be a subgraph of a graph
08 CHAPTER. TOPICS IN CLASSICAL GRAPH THEORY K, K K K, K K, K K, K C C C C 6 6 P P P P P. Graph Operations Figure.: Some well known family of graphs A graph Y = (V,E ) is said to be a subgraph of a graph
On a perfect problem
 R u t c o r Research R e p o r t On a perfect problem Igor E. Zverovich a RRR 26-2005, September 2005 RUTCOR Rutgers Center for Operations Research Rutgers University 640 Bartholomew Road Piscataway, New
R u t c o r Research R e p o r t On a perfect problem Igor E. Zverovich a RRR 26-2005, September 2005 RUTCOR Rutgers Center for Operations Research Rutgers University 640 Bartholomew Road Piscataway, New
Claw-Free Graphs With Strongly Perfect Complements. Fractional and Integral Version.
 Claw-Free Graphs With Strongly Perfect Complements. Fractional and Integral Version. Part I. Basic graphs Maria Chudnovsky Department of Industrial Engineering and Operations Research Columbia University,
Claw-Free Graphs With Strongly Perfect Complements. Fractional and Integral Version. Part I. Basic graphs Maria Chudnovsky Department of Industrial Engineering and Operations Research Columbia University,
Block Duplicate Graphs and a Hierarchy of Chordal Graphs
 Block Duplicate Graphs and a Hierarchy of Chordal Graphs Martin Charles Golumbic Uri N. Peled August 18, 1998 Revised October 24, 2000 and March 15, 2001 Abstract A block graph is a graph whose blocks
Block Duplicate Graphs and a Hierarchy of Chordal Graphs Martin Charles Golumbic Uri N. Peled August 18, 1998 Revised October 24, 2000 and March 15, 2001 Abstract A block graph is a graph whose blocks
Math 776 Homework. Austin Mohr. June 15, Theorem 1.1. The following assertions are equivalent for a graph T : (i) T is a tree;
 Math 776 Homework Austin Mohr June 15, 2012 1 Problem 1 Theorem 1.1. The following assertions are equivalent for a graph T : (i) T is a tree; (ii) Any two vertices of T are linked by a unique path in T
Math 776 Homework Austin Mohr June 15, 2012 1 Problem 1 Theorem 1.1. The following assertions are equivalent for a graph T : (i) T is a tree; (ii) Any two vertices of T are linked by a unique path in T
Chordal graphs MPRI
 Chordal graphs MPRI 2017 2018 Michel Habib habib@irif.fr http://www.irif.fr/~habib Sophie Germain, septembre 2017 Schedule Chordal graphs Representation of chordal graphs LBFS and chordal graphs More structural
Chordal graphs MPRI 2017 2018 Michel Habib habib@irif.fr http://www.irif.fr/~habib Sophie Germain, septembre 2017 Schedule Chordal graphs Representation of chordal graphs LBFS and chordal graphs More structural
Mock Exam. Juanjo Rué Discrete Mathematics II, Winter Deadline: 14th January 2014 (Tuesday) by 10:00, at the end of the lecture.
 Mock Exam Juanjo Rué Discrete Mathematics II, Winter 2013-2014 Deadline: 14th January 2014 (Tuesday) by 10:00, at the end of the lecture. Problem 1 (2 points): 1. State the definition of perfect graph
Mock Exam Juanjo Rué Discrete Mathematics II, Winter 2013-2014 Deadline: 14th January 2014 (Tuesday) by 10:00, at the end of the lecture. Problem 1 (2 points): 1. State the definition of perfect graph
9 Connectivity. Contents. 9.1 Vertex Connectivity
 9 Connectivity Contents 9.1 Vertex Connectivity.............................. 205 Connectivity and Local Connectivity............... 206 Vertex Cuts and Menger s Theorem................. 207 9.2 The Fan
9 Connectivity Contents 9.1 Vertex Connectivity.............................. 205 Connectivity and Local Connectivity............... 206 Vertex Cuts and Menger s Theorem................. 207 9.2 The Fan
Bayesian Networks, Winter Yoav Haimovitch & Ariel Raviv
 Bayesian Networks, Winter 2009-2010 Yoav Haimovitch & Ariel Raviv 1 Chordal Graph Warm up Theorem 7 Perfect Vertex Elimination Scheme Maximal cliques Tree Bibliography M.C.Golumbic Algorithmic Graph Theory
Bayesian Networks, Winter 2009-2010 Yoav Haimovitch & Ariel Raviv 1 Chordal Graph Warm up Theorem 7 Perfect Vertex Elimination Scheme Maximal cliques Tree Bibliography M.C.Golumbic Algorithmic Graph Theory
Rigidity, connectivity and graph decompositions
 First Prev Next Last Rigidity, connectivity and graph decompositions Brigitte Servatius Herman Servatius Worcester Polytechnic Institute Page 1 of 100 First Prev Next Last Page 2 of 100 We say that a framework
First Prev Next Last Rigidity, connectivity and graph decompositions Brigitte Servatius Herman Servatius Worcester Polytechnic Institute Page 1 of 100 First Prev Next Last Page 2 of 100 We say that a framework
Skew partitions in perfect graphs
 Discrete Applied Mathematics 156 (2008) 1150 1156 www.elsevier.com/locate/dam Skew partitions in perfect graphs Bruce Reed a,b a McGill University, Montreal, Canada b CNRS, France Received 14 June 2005;
Discrete Applied Mathematics 156 (2008) 1150 1156 www.elsevier.com/locate/dam Skew partitions in perfect graphs Bruce Reed a,b a McGill University, Montreal, Canada b CNRS, France Received 14 June 2005;
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Theorem 3.1 (Berge) A matching M in G is maximum if and only if there is no M- augmenting path.
 3 Matchings Hall s Theorem Matching: A matching in G is a subset M E(G) so that no edge in M is a loop, and no two edges in M are incident with a common vertex. A matching M is maximal if there is no matching
3 Matchings Hall s Theorem Matching: A matching in G is a subset M E(G) so that no edge in M is a loop, and no two edges in M are incident with a common vertex. A matching M is maximal if there is no matching
Approximation slides 1. An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs
 Approximation slides 1 An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs Approximation slides 2 Linear independence A collection of row vectors {v T i } are independent
Approximation slides 1 An optimal polynomial algorithm for the Vertex Cover and matching in Bipartite graphs Approximation slides 2 Linear independence A collection of row vectors {v T i } are independent
Excluding induced subgraphs
 Excluding induced subgraphs Maria Chudnovsky and Paul Seymour Abstract 1 Introduction Given two graphs, G and H, we say that H is an induced subgraph of G if V (H) V (G), and two vertices of H are adjacent
Excluding induced subgraphs Maria Chudnovsky and Paul Seymour Abstract 1 Introduction Given two graphs, G and H, we say that H is an induced subgraph of G if V (H) V (G), and two vertices of H are adjacent
 This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
This article was originally published in a journal published by Elsevier, and the attached copy is provided by Elsevier for the author s benefit and for the benefit of the author s institution, for non-commercial
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
Diskrete Mathematik und Optimierung
 Diskrete Mathematik und Optimierung Stephan Dominique Andres Winfried Hochstättler: A strong perfect digraph theorem Technical Report feu-dmo026.11 Contact: dominique.andres@fernuni-hagen.de, winfried.hochstaettler@fernuni-hagen.de
Diskrete Mathematik und Optimierung Stephan Dominique Andres Winfried Hochstättler: A strong perfect digraph theorem Technical Report feu-dmo026.11 Contact: dominique.andres@fernuni-hagen.de, winfried.hochstaettler@fernuni-hagen.de
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Fundamental Properties of Graphs
 Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
1 Matchings with Tutte s Theorem
 1 Matchings with Tutte s Theorem Last week we saw a fairly strong necessary criterion for a graph to have a perfect matching. Today we see that this condition is in fact sufficient. Theorem 1 (Tutte, 47).
1 Matchings with Tutte s Theorem Last week we saw a fairly strong necessary criterion for a graph to have a perfect matching. Today we see that this condition is in fact sufficient. Theorem 1 (Tutte, 47).
Lecture 4: Walks, Trails, Paths and Connectivity
 Lecture 4: Walks, Trails, Paths and Connectivity Rosa Orellana Math 38 April 6, 2015 Graph Decompositions Def: A decomposition of a graph is a list of subgraphs such that each edge appears in exactly one
Lecture 4: Walks, Trails, Paths and Connectivity Rosa Orellana Math 38 April 6, 2015 Graph Decompositions Def: A decomposition of a graph is a list of subgraphs such that each edge appears in exactly one
Tree Spanners of Simple Graphs
 Tree Spanners of Simple Graphs by Ioannis E. Papoutsakis A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Computer Science University
Tree Spanners of Simple Graphs by Ioannis E. Papoutsakis A thesis submitted in conformity with the requirements for the degree of Doctor of Philosophy Graduate Department of Computer Science University
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees
 Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Contracting Chordal Graphs and Bipartite Graphs to Paths and Trees Pinar Heggernes Pim van t Hof Benjamin Léveque Christophe Paul Abstract We study the following two graph modification problems: given
Minimal comparability completions of arbitrary graphs
 Minimal comparability completions of arbitrary graphs Pinar Heggernes Federico Mancini Charis Papadopoulos Abstract A transitive orientation of an undirected graph is an assignment of directions to its
Minimal comparability completions of arbitrary graphs Pinar Heggernes Federico Mancini Charis Papadopoulos Abstract A transitive orientation of an undirected graph is an assignment of directions to its
arxiv: v2 [math.co] 25 May 2016
![arxiv: v2 [math.co] 25 May 2016 arxiv: v2 [math.co] 25 May 2016](/thumbs/88/117788175.jpg) arxiv:1605.06638v2 [math.co] 25 May 2016 A note on a conjecture of Gyárfás Ryan R. Martin Abstract This note proves that, given one member, T, of a particular family of radius-three trees, every radius-two,
arxiv:1605.06638v2 [math.co] 25 May 2016 A note on a conjecture of Gyárfás Ryan R. Martin Abstract This note proves that, given one member, T, of a particular family of radius-three trees, every radius-two,
RECOGNIZING CHORDAL PROBE GRAPHS AND CYCLE-BICOLORABLE GRAPHS
 SIAM J. DISCRETE MATH. Vol. 21, No. 3, pp. 573 591 c 2007 Society for Industrial and Applied Mathematics RECOGNIZING CHORDAL PROBE GRAPHS AND CYCLE-BICOLORABLE GRAPHS ANNE BERRY, MARTIN CHARLES GOLUMBIC,
SIAM J. DISCRETE MATH. Vol. 21, No. 3, pp. 573 591 c 2007 Society for Industrial and Applied Mathematics RECOGNIZING CHORDAL PROBE GRAPHS AND CYCLE-BICOLORABLE GRAPHS ANNE BERRY, MARTIN CHARLES GOLUMBIC,
Characterizations of Trees
 Characterizations of Trees Lemma Every tree with at least two vertices has at least two leaves. Proof. 1. A connected graph with at least two vertices has an edge. 2. In an acyclic graph, an end point
Characterizations of Trees Lemma Every tree with at least two vertices has at least two leaves. Proof. 1. A connected graph with at least two vertices has an edge. 2. In an acyclic graph, an end point
Independence Number and Cut-Vertices
 Independence Number and Cut-Vertices Ryan Pepper University of Houston Downtown, Houston, Texas 7700 pepperr@uhd.edu Abstract We show that for any connected graph G, α(g) C(G) +1, where α(g) is the independence
Independence Number and Cut-Vertices Ryan Pepper University of Houston Downtown, Houston, Texas 7700 pepperr@uhd.edu Abstract We show that for any connected graph G, α(g) C(G) +1, where α(g) is the independence
Problem Set 3. MATH 776, Fall 2009, Mohr. November 30, 2009
 Problem Set 3 MATH 776, Fall 009, Mohr November 30, 009 1 Problem Proposition 1.1. Adding a new edge to a maximal planar graph of order at least 6 always produces both a T K 5 and a T K 3,3 subgraph. Proof.
Problem Set 3 MATH 776, Fall 009, Mohr November 30, 009 1 Problem Proposition 1.1. Adding a new edge to a maximal planar graph of order at least 6 always produces both a T K 5 and a T K 3,3 subgraph. Proof.
Dirac-type characterizations of graphs without long chordless cycles
 Dirac-type characterizations of graphs without long chordless cycles Vašek Chvátal Department of Computer Science Rutgers University chvatal@cs.rutgers.edu Irena Rusu LIFO Université de Orléans irusu@lifo.univ-orleans.fr
Dirac-type characterizations of graphs without long chordless cycles Vašek Chvátal Department of Computer Science Rutgers University chvatal@cs.rutgers.edu Irena Rusu LIFO Université de Orléans irusu@lifo.univ-orleans.fr
Tolerance Representations of Graphs in Trees Nancy Eaton. Tolerance Representations of Graphs in Trees Lecture I. Tree Representations of Graphs
 Tolerance Representations of Graphs in Trees Nancy Eaton Tolerance Representations of Graphs in Trees Lecture I Tree Representations of Graphs Tolerance Representations Some background A conjecture on
Tolerance Representations of Graphs in Trees Nancy Eaton Tolerance Representations of Graphs in Trees Lecture I Tree Representations of Graphs Tolerance Representations Some background A conjecture on
On Sequential Topogenic Graphs
 Int. J. Contemp. Math. Sciences, Vol. 5, 2010, no. 36, 1799-1805 On Sequential Topogenic Graphs Bindhu K. Thomas, K. A. Germina and Jisha Elizabath Joy Research Center & PG Department of Mathematics Mary
Int. J. Contemp. Math. Sciences, Vol. 5, 2010, no. 36, 1799-1805 On Sequential Topogenic Graphs Bindhu K. Thomas, K. A. Germina and Jisha Elizabath Joy Research Center & PG Department of Mathematics Mary
MAT 145: PROBLEM SET 6
 MAT 145: PROBLEM SET 6 DUE TO FRIDAY MAR 8 Abstract. This problem set corresponds to the eighth week of the Combinatorics Course in the Winter Quarter 2019. It was posted online on Friday Mar 1 and is
MAT 145: PROBLEM SET 6 DUE TO FRIDAY MAR 8 Abstract. This problem set corresponds to the eighth week of the Combinatorics Course in the Winter Quarter 2019. It was posted online on Friday Mar 1 and is
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
ON SOME CONJECTURES OF GRIGGS AND GRAFFITI
 ON SOME CONJECTURES OF GRIGGS AND GRAFFITI ERMELINDA DELAVINA, SIEMION FAJTLOWICZ, BILL WALLER Abstract. We discuss a conjecture of J. R. Griggs relating the maximum number of leaves in a spanning tree
ON SOME CONJECTURES OF GRIGGS AND GRAFFITI ERMELINDA DELAVINA, SIEMION FAJTLOWICZ, BILL WALLER Abstract. We discuss a conjecture of J. R. Griggs relating the maximum number of leaves in a spanning tree
Exercise set 2 Solutions
 Exercise set 2 Solutions Let H and H be the two components of T e and let F E(T ) consist of the edges of T with one endpoint in V (H), the other in V (H ) Since T is connected, F Furthermore, since T
Exercise set 2 Solutions Let H and H be the two components of T e and let F E(T ) consist of the edges of T with one endpoint in V (H), the other in V (H ) Since T is connected, F Furthermore, since T
Excluding induced subgraphs
 Excluding induced subgraphs Maria Chudnovsky and Paul Seymour Abstract In this paper we survey some results concerning the structure and properties of families of graphs defined by excluding certain induced
Excluding induced subgraphs Maria Chudnovsky and Paul Seymour Abstract In this paper we survey some results concerning the structure and properties of families of graphs defined by excluding certain induced
arxiv: v3 [cs.ds] 26 Sep 2013
![arxiv: v3 [cs.ds] 26 Sep 2013 arxiv: v3 [cs.ds] 26 Sep 2013](/thumbs/96/129281842.jpg) Preprocessing Subgraph and Minor Problems: When Does a Small Vertex Cover Help?, Fedor V. Fomin a, Bart M. P. Jansen a,, Micha l Pilipczuk a a Department of Informatics, University of Bergen. PO Box 7803,
Preprocessing Subgraph and Minor Problems: When Does a Small Vertex Cover Help?, Fedor V. Fomin a, Bart M. P. Jansen a,, Micha l Pilipczuk a a Department of Informatics, University of Bergen. PO Box 7803,
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes
 Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
Minimal Dominating Sets in Graphs: Enumeration, Combinatorial Bounds and Graph Classes J.-F. Couturier 1 P. Heggernes 2 D. Kratsch 1 P. van t Hof 2 1 LITA Université de Lorraine F-57045 Metz France 2 University
On the correspondence between tree representations of chordal and dually chordal graphs
 On the correspondence between tree representations of chordal and dually chordal graphs Pablo De Caria, Marisa Gutierrez CONICET/ Departamento de Matemática, Universidad Nacional de La Plata, Calle 50
On the correspondence between tree representations of chordal and dually chordal graphs Pablo De Caria, Marisa Gutierrez CONICET/ Departamento de Matemática, Universidad Nacional de La Plata, Calle 50
Complexity of Disjoint Π-Vertex Deletion for Disconnected Forbidden Subgraphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 18, no. 4, pp. 603 631 (2014) DOI: 10.7155/jgaa.00339 Complexity of Disjoint Π-Vertex Deletion for Disconnected Forbidden Subgraphs Jiong
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 18, no. 4, pp. 603 631 (2014) DOI: 10.7155/jgaa.00339 Complexity of Disjoint Π-Vertex Deletion for Disconnected Forbidden Subgraphs Jiong
1 Matching in Non-Bipartite Graphs
 CS 369P: Polyhedral techniques in combinatorial optimization Instructor: Jan Vondrák Lecture date: September 30, 2010 Scribe: David Tobin 1 Matching in Non-Bipartite Graphs There are several differences
CS 369P: Polyhedral techniques in combinatorial optimization Instructor: Jan Vondrák Lecture date: September 30, 2010 Scribe: David Tobin 1 Matching in Non-Bipartite Graphs There are several differences
The External Network Problem
 The External Network Problem Jan van den Heuvel and Matthew Johnson CDAM Research Report LSE-CDAM-2004-15 December 2004 Abstract The connectivity of a communications network can often be enhanced if the
The External Network Problem Jan van den Heuvel and Matthew Johnson CDAM Research Report LSE-CDAM-2004-15 December 2004 Abstract The connectivity of a communications network can often be enhanced if the
Partitions and Packings of Complete Geometric Graphs with Plane Spanning Double Stars and Paths
 Partitions and Packings of Complete Geometric Graphs with Plane Spanning Double Stars and Paths Master Thesis Patrick Schnider July 25, 2015 Advisors: Prof. Dr. Emo Welzl, Manuel Wettstein Department of
Partitions and Packings of Complete Geometric Graphs with Plane Spanning Double Stars and Paths Master Thesis Patrick Schnider July 25, 2015 Advisors: Prof. Dr. Emo Welzl, Manuel Wettstein Department of
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
NOTE ON MINIMALLY k-connected GRAPHS
 NOTE ON MINIMALLY k-connected GRAPHS R. Rama a, Suresh Badarla a a Department of Mathematics, Indian Institute of Technology, Chennai, India ABSTRACT A k-tree is either a complete graph on (k+1) vertices
NOTE ON MINIMALLY k-connected GRAPHS R. Rama a, Suresh Badarla a a Department of Mathematics, Indian Institute of Technology, Chennai, India ABSTRACT A k-tree is either a complete graph on (k+1) vertices
CLAW-FREE 3-CONNECTED P 11 -FREE GRAPHS ARE HAMILTONIAN
 CLAW-FREE 3-CONNECTED P 11 -FREE GRAPHS ARE HAMILTONIAN TOMASZ LUCZAK AND FLORIAN PFENDER Abstract. We show that every 3-connected claw-free graph which contains no induced copy of P 11 is hamiltonian.
CLAW-FREE 3-CONNECTED P 11 -FREE GRAPHS ARE HAMILTONIAN TOMASZ LUCZAK AND FLORIAN PFENDER Abstract. We show that every 3-connected claw-free graph which contains no induced copy of P 11 is hamiltonian.
arxiv: v1 [cs.ds] 8 Jan 2019
![arxiv: v1 [cs.ds] 8 Jan 2019 arxiv: v1 [cs.ds] 8 Jan 2019](/thumbs/93/113547113.jpg) Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Subset Feedback Vertex Set in Chordal and Split Graphs Geevarghese Philip 1, Varun Rajan 2, Saket Saurabh 3,4, and Prafullkumar Tale 5 arxiv:1901.02209v1 [cs.ds] 8 Jan 2019 1 Chennai Mathematical Institute,
Line Graphs and Circulants
 Line Graphs and Circulants Jason Brown and Richard Hoshino Department of Mathematics and Statistics Dalhousie University Halifax, Nova Scotia, Canada B3H 3J5 Abstract The line graph of G, denoted L(G),
Line Graphs and Circulants Jason Brown and Richard Hoshino Department of Mathematics and Statistics Dalhousie University Halifax, Nova Scotia, Canada B3H 3J5 Abstract The line graph of G, denoted L(G),
5 Matchings in Bipartite Graphs and Their Applications
 5 Matchings in Bipartite Graphs and Their Applications 5.1 Matchings Definition 5.1 A matching M in a graph G is a set of edges of G, none of which is a loop, such that no two edges in M have a common
5 Matchings in Bipartite Graphs and Their Applications 5.1 Matchings Definition 5.1 A matching M in a graph G is a set of edges of G, none of which is a loop, such that no two edges in M have a common
On Cyclically Orientable Graphs
 DIMACS Technical Report 2005-08 February 2005 On Cyclically Orientable Graphs by Vladimir Gurvich RUTCOR, Rutgers University 640 Bartholomew Road Piscataway NJ 08854-8003 gurvich@rutcor.rutgers.edu DIMACS
DIMACS Technical Report 2005-08 February 2005 On Cyclically Orientable Graphs by Vladimir Gurvich RUTCOR, Rutgers University 640 Bartholomew Road Piscataway NJ 08854-8003 gurvich@rutcor.rutgers.edu DIMACS
Number Theory and Graph Theory
 1 Number Theory and Graph Theory Chapter 6 Basic concepts and definitions of graph theory By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: satya8118@gmail.com
1 Number Theory and Graph Theory Chapter 6 Basic concepts and definitions of graph theory By A. Satyanarayana Reddy Department of Mathematics Shiv Nadar University Uttar Pradesh, India E-mail: satya8118@gmail.com
Edge colorings. Definition The minimum k such that G has a proper k-edge-coloring is called the edge chromatic number of G and is denoted
 Edge colorings Edge coloring problems often arise when objects being scheduled are pairs of underlying elements, e.g., a pair of teams that play each other, a pair consisting of a teacher and a class,
Edge colorings Edge coloring problems often arise when objects being scheduled are pairs of underlying elements, e.g., a pair of teams that play each other, a pair consisting of a teacher and a class,
Ton Kloks and Yue-Li Wang. Advances in Graph Algorithms. October 10, y X z
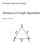 Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Ton Kloks and Yue-Li Wang Advances in Graph Algorithms October 10, 2013 x Z Y < y X z
Preprocessing for treewidth
 Preprocessing for treewidth Bodlaender, H.L.; Jansen, B.M.P.; Kratsch, S. Published in: arxiv Published: 21/04/2011 Please check the document version of this publication: A submitted manuscript is the
Preprocessing for treewidth Bodlaender, H.L.; Jansen, B.M.P.; Kratsch, S. Published in: arxiv Published: 21/04/2011 Please check the document version of this publication: A submitted manuscript is the
Topics in Combinatorics. Dorottya Sziráki Gergő Nemes
 Topics in Combinatorics Dorottya Sziráki Gergő Nemes ii Preface These notes are based on the lectures of the course titled Topics in Combinatorics, which were given by Ervin Győri in the winter trimester
Topics in Combinatorics Dorottya Sziráki Gergő Nemes ii Preface These notes are based on the lectures of the course titled Topics in Combinatorics, which were given by Ervin Győri in the winter trimester
arxiv: v1 [cs.dm] 30 Apr 2014
![arxiv: v1 [cs.dm] 30 Apr 2014 arxiv: v1 [cs.dm] 30 Apr 2014](/thumbs/84/90655931.jpg) The stable set polytope of (P 6,triangle)-free graphs and new facet-inducing graphs Raffaele Mosca arxiv:1404.7623v1 [cs.dm] 30 Apr 2014 May 1, 2014 Abstract The stable set polytope of a graph G, denoted
The stable set polytope of (P 6,triangle)-free graphs and new facet-inducing graphs Raffaele Mosca arxiv:1404.7623v1 [cs.dm] 30 Apr 2014 May 1, 2014 Abstract The stable set polytope of a graph G, denoted
Math 776 Graph Theory Lecture Note 1 Basic concepts
 Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Adjacent: Two distinct vertices u, v are adjacent if there is an edge with ends u, v. In this case we let uv denote such an edge.
 1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
A graph is finite if its vertex set and edge set are finite. We call a graph with just one vertex trivial and all other graphs nontrivial.
 2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
Finding a -regular Supergraph of Minimum Order
 Finding a -regular Supergraph of Minimum Order Hans L. Bodlaender a, Richard B. Tan a,b and Jan van Leeuwen a a Department of Computer Science Utrecht University Padualaan 14, 3584 CH Utrecht The Netherlands
Finding a -regular Supergraph of Minimum Order Hans L. Bodlaender a, Richard B. Tan a,b and Jan van Leeuwen a a Department of Computer Science Utrecht University Padualaan 14, 3584 CH Utrecht The Netherlands
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Lecture Notes on Graph Theory
 Lecture Notes on Graph Theory Vadim Lozin 1 Introductory concepts A graph G = (V, E) consists of two finite sets V and E. The elements of V are called the vertices and the elements of E the edges of G.
Lecture Notes on Graph Theory Vadim Lozin 1 Introductory concepts A graph G = (V, E) consists of two finite sets V and E. The elements of V are called the vertices and the elements of E the edges of G.
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Paths, Flowers and Vertex Cover Venkatesh Raman, M.S. Ramanujan, and Saket Saurabh Presenting: Hen Sender 1 Introduction 2 Abstract. It is well known that in a bipartite (and more generally in a Konig)
Deciding k-colorability of P 5 -free graphs in polynomial time
 Deciding k-colorability of P 5 -free graphs in polynomial time Chính T. Hoàng Marcin Kamiński Vadim Lozin Joe Sawada Xiao Shu April 16, 2008 Abstract The problem of computing the chromatic number of a
Deciding k-colorability of P 5 -free graphs in polynomial time Chính T. Hoàng Marcin Kamiński Vadim Lozin Joe Sawada Xiao Shu April 16, 2008 Abstract The problem of computing the chromatic number of a
A Necessary Condition and a Sufficient Condition for Pairwise Compatibility Graphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 21, no. 3, pp. 341 352 (2017) DOI: 10.7155/jgaa.00419 A Necessary Condition and a Sufficient Condition for Pairwise Compatibility Graphs
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 21, no. 3, pp. 341 352 (2017) DOI: 10.7155/jgaa.00419 A Necessary Condition and a Sufficient Condition for Pairwise Compatibility Graphs
arxiv: v1 [cs.ds] 14 Dec 2018
![arxiv: v1 [cs.ds] 14 Dec 2018 arxiv: v1 [cs.ds] 14 Dec 2018](/thumbs/92/109311905.jpg) Graph classes and forbidden patterns on three vertices Laurent Feuilloley 1,2,3 and Michel Habib 1,3 arxiv:1812.05913v1 [cs.ds] 14 Dec 2018 1 IRIF, UMR 8243 CNRS & Paris Diderot University, Paris, France
Graph classes and forbidden patterns on three vertices Laurent Feuilloley 1,2,3 and Michel Habib 1,3 arxiv:1812.05913v1 [cs.ds] 14 Dec 2018 1 IRIF, UMR 8243 CNRS & Paris Diderot University, Paris, France
Graph Theory S 1 I 2 I 1 S 2 I 1 I 2
 Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Some new results on circle graphs. Guillermo Durán 1
 Some new results on circle graphs Guillermo Durán 1 Departamento de Ingeniería Industrial, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Santiago, Chile gduran@dii.uchile.cl Departamento
Some new results on circle graphs Guillermo Durán 1 Departamento de Ingeniería Industrial, Facultad de Ciencias Físicas y Matemáticas, Universidad de Chile, Santiago, Chile gduran@dii.uchile.cl Departamento
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Parameterized coloring problems on chordal graphs
 Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Parameterized coloring problems on chordal graphs Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary dmarx@cs.bme.hu
Some Upper Bounds for Signed Star Domination Number of Graphs. S. Akbari, A. Norouzi-Fard, A. Rezaei, R. Rotabi, S. Sabour.
 Some Upper Bounds for Signed Star Domination Number of Graphs S. Akbari, A. Norouzi-Fard, A. Rezaei, R. Rotabi, S. Sabour Abstract Let G be a graph with the vertex set V (G) and edge set E(G). A function
Some Upper Bounds for Signed Star Domination Number of Graphs S. Akbari, A. Norouzi-Fard, A. Rezaei, R. Rotabi, S. Sabour Abstract Let G be a graph with the vertex set V (G) and edge set E(G). A function
V10 Metabolic networks - Graph connectivity
 V10 Metabolic networks - Graph connectivity Graph connectivity is related to analyzing biological networks for - finding cliques - edge betweenness - modular decomposition that have been or will be covered
V10 Metabolic networks - Graph connectivity Graph connectivity is related to analyzing biological networks for - finding cliques - edge betweenness - modular decomposition that have been or will be covered
Chapter 8 Independence
 Chapter 8 Independence Section 8.1 Vertex Independence and Coverings Next, we consider a problem that strikes close to home for us all, final exams. At the end of each term, students are required to take
Chapter 8 Independence Section 8.1 Vertex Independence and Coverings Next, we consider a problem that strikes close to home for us all, final exams. At the end of each term, students are required to take
