PSE Game Physics. Session (3) Springs, Ropes, Linear Momentum and Rotations. Oliver Meister, Roland Wittmann
|
|
|
- Mae Adams
- 5 years ago
- Views:
Transcription
1 PSE Game Physics Session (3) Springs, Ropes, Linear Momentum and Rotations Oliver Meister, Roland Wittmann Session (3) Springs, Ropes, Linear Momentum and Rotations,
2 Outline Springs and ropes Overview Springs Ropes Collisions Collision detection Collision resolution Linear momentum Basics Conservation laws Why use the inverse of mass? Rotations Session (3) Springs, Ropes, Linear Momentum and Rotations,
3 Outline Springs and ropes Overview Springs Ropes Collisions Collision detection Collision resolution Linear momentum Basics Conservation laws Why use the inverse of mass? Rotations Session (3) Springs, Ropes, Linear Momentum and Rotations,
4 Springs and Ropes Springs and ropes are so called constraints since they force different objects to behave in a specific way. Other constraints are e. g. a hinge or a wheel attached to a car Springs and ropes are frequently used in games: Ropes and springs to drag & drop something Building bridges out of ropes Setting up a 3rd-person camera with damped spring Connecting 2 objects... For this worksheet, we assume a few simplifications: The spring is attached to the mass center of the object Spring/Rope collisions are not considered Session (3) Springs, Ropes, Linear Momentum and Rotations,
5 Springs (1/2) Object1 Object2 Figure: Spring Create a force acting on both involved objects Force depends on the distance of the spring anchors Hook s law gives us the force acting on each object: F = k d F: Applied force, k: Spring coefficient, d: spring elongation (= length - equilibrium length) Session (3) Springs, Ropes, Linear Momentum and Rotations,
6 Springs (2/2) How to implement this force into our physics engine? This force can be implemented via a soft constraint: We can easily compute the acceleration exceeded by the spring s force for each object within a time-step (use an explicit euler step). Then the change of acceleration can be simply added to the acceleration accumulator during each time-step. The direction is given by the line between the anchor points of both objects. Question: Are there problems with large time-steps and large spring coefficients? How can we handle those? Session (3) Springs, Ropes, Linear Momentum and Rotations,
7 Ropes (1/2) Object1 Object2 Figure: Top image: rope without exceeding its maximum length, Bottom image: Colliding rope We only consider ropes without rope collisions!!! After finishing all worksheets, you ll be able to simulate this as well :-) Session (3) Springs, Ropes, Linear Momentum and Rotations,
8 Ropes (2/2) Object1 Object2 max length interpenetration depth Figure: Colliding details Imagine 2 objects with increasing distance. Once the anchor points of the ropes at the objects exceed a specific rope length an impulse acts onto both attached objects This is similar to applying an impulse during collision handling hard constraint Create a simple collision dataset Session (3) Springs, Ropes, Linear Momentum and Rotations,
9 Outline Springs and ropes Overview Springs Ropes Collisions Collision detection Collision resolution Linear momentum Basics Conservation laws Why use the inverse of mass? Rotations Session (3) Springs, Ropes, Linear Momentum and Rotations,
10 Collision detection Basic algorithmic steps for collision detection: 1. Take any two colliding objects Session (3) Springs, Ropes, Linear Momentum and Rotations,
11 Collision detection Basic algorithmic steps for collision detection: 1. Take any two colliding objects 2. (Optional) Coarse culling: find a lower bound for the distance between the two objects If this lower bound is greater than zero, abort Session (3) Springs, Ropes, Linear Momentum and Rotations,
12 Collision detection Basic algorithmic steps for collision detection: 1. Take any two colliding objects 2. (Optional) Coarse culling: find a lower bound for the distance between the two objects If this lower bound is greater than zero, abort 3. Fine culling: Determine collision points, normal, interpenetration depth (usually goes hand in hand) If interpenetration depth is less than zero, abort Session (3) Springs, Ropes, Linear Momentum and Rotations,
13 Collision detection Basic algorithmic steps for collision detection: 1. Take any two colliding objects 2. (Optional) Coarse culling: find a lower bound for the distance between the two objects If this lower bound is greater than zero, abort 3. Fine culling: Determine collision points, normal, interpenetration depth (usually goes hand in hand) If interpenetration depth is less than zero, abort 4. Set collision parameters and start collision resolution for the two objects Session (3) Springs, Ropes, Linear Momentum and Rotations,
14 Collision detection Basic algorithmic steps for collision detection: 1. Take any two colliding objects 2. (Optional) Coarse culling: find a lower bound for the distance between the two objects If this lower bound is greater than zero, abort 3. Fine culling: Determine collision points, normal, interpenetration depth (usually goes hand in hand) If interpenetration depth is less than zero, abort 4. Set collision parameters and start collision resolution for the two objects 5. Check if any other collisions occured (always necessary?), if yes return to step 1 Session (3) Springs, Ropes, Linear Momentum and Rotations,
15 Collision resolution Goals: No more collision between the two objects, obviously Very little movement, which is visually unpleasant and might cause further collisions Somehow physical behaviour Session (3) Springs, Ropes, Linear Momentum and Rotations,
16 Collision resolution Goals: No more collision between the two objects, obviously Very little movement, which is visually unpleasant and might cause further collisions Somehow physical behaviour Steps: Move the objects apart from each other (along what direction?): m Move Object 1 by 1 m 1 1 +m 2 2 of the interpenetration depth. m Move Object 2 by 2 m 1 1 +m 2 2 of the interpenetration depth. Session (3) Springs, Ropes, Linear Momentum and Rotations,
17 Collision resolution Goals: No more collision between the two objects, obviously Very little movement, which is visually unpleasant and might cause further collisions Somehow physical behaviour Steps: Move the objects apart from each other (along what direction?): m Move Object 1 by 1 m 1 1 +m 2 2 of the interpenetration depth. m Move Object 2 by 2 m 1 1 +m 2 2 of the interpenetration depth. (Later) Update velocities by applying forces to the objects Why the weird inverse masses? Session (3) Springs, Ropes, Linear Momentum and Rotations,
18 Collision resolution Goals: No more collision between the two objects, obviously Very little movement, which is visually unpleasant and might cause further collisions Somehow physical behaviour Steps: Move the objects apart from each other (along what direction?): m Move Object 1 by 1 m 1 1 +m 2 2 of the interpenetration depth. m Move Object 2 by 2 m 1 1 +m 2 2 of the interpenetration depth. (Later) Update velocities by applying forces to the objects Why the weird inverse masses? Design decision: Allow infinite mass, neglect zero mass! Session (3) Springs, Ropes, Linear Momentum and Rotations,
19 Outline Springs and ropes Overview Springs Ropes Collisions Collision detection Collision resolution Linear momentum Basics Conservation laws Why use the inverse of mass? Rotations Session (3) Springs, Ropes, Linear Momentum and Rotations,
20 Linear momentum Once there is a collision, several things have to be done: Resolving the interpenetration (finished during last session) The velocity of at least one object has to be modified according to its current state So far, we only consider elastic collisions! Session (3) Springs, Ropes, Linear Momentum and Rotations,
21 Basics Object 1 V 1 = 1 V 2 = -1 Object 2 m 1 = 2 m 2 = 1 Figure: 2 colliding spheres Relevant object properties for linear momentum in 1D: mass of objects: m 1, m 2 velocity of object before collision: v 1, v 2 velocity of object after collision: v 1, v 2 Closing velocity: v c = v 1 v 2 What s the separating velocity for each object? Session (3) Springs, Ropes, Linear Momentum and Rotations,
22 Force and Linear Impulse A Force leads to change of acceleration. F = ma Is it possible to change the velocity instantaneously? Idea : use the Impulse. t 2 J = m v = F dt t 1 Session (3) Springs, Ropes, Linear Momentum and Rotations,
23 We start with a few basic conservation laws: Energy conservation for elastic collisions: 1 2 m 1v m 2v2 2 = 1 2 m 1v m 2v 2 2 Conservation of momentum: m 1 v 1 + m 2 v 2 = m 1 v 1 + m 2 v 2 Session (3) Springs, Ropes, Linear Momentum and Rotations,
24 We start by rewriting the energy conservation law to m 1 (v 2 1 v 2 1 ) = m 2 (v 2 2 v 2 2 ) and avoid an expression of the velocity with a square exponent: m 1 (v 1 v 1) (v 1 + v }{{} 1) = m 2 (v 2 v 2)(v 2 + v 2) A By rewriting the equation for the conservation of momentum to m 1 (v 1 v 1) = m 2 (v 2 v 2) we can replace (A) by the right side of the upper equation: m 2 (v 2 v 2)(v 1 + v 1) = m 2 (v 2 v 2)(v 2 + v 2) Finally, we get the first result: v 1 + v 1 = v 2 + v 2 or v 1 v 2 = (v 1 v 2 ) where the separating velocity v s = v 1 v 2 is the exact opposite of the closing velocity v c = v 1 v 2. Session (3) Springs, Ropes, Linear Momentum and Rotations,
25 Updated Velocities Using the equation v 1 v 2 = (v 1 v 2 ) of the previous slide, we can rearrange it to v 2 = v 1 v 2 + v 1 By putting this equation in the momentum equation, we get m 1 (v 1 v 1) = m 2 (v 2 (v 1 v 2 +v 1)) = m 2 v 2 +m 2 v 1 m 2 v 2 +m 2 v 1 Extension by 0 {}}{ m 1 v 1 + m 2 v 1 = 2m 2 v 2 m 2 v 1 + m 1 v 1 +m 2 v 1 m 2 v 1 (m 1 + m 2 )v 1 = 2(m 2 v 2 m 2 v 1 ) + (m 1 + m 2 )v 1 By dividing the equation by (m 1 + m 2 ), the velocity of object 1 after collision is given by v 1 = 2 m 2(v 2 v 1 ) m 1 + m 2 m 2 + v 1 = 2 v c + v 1 m 1 + m 2 Session (3) Springs, Ropes, Linear Momentum and Rotations,
26 Normally, collisions are not completely elastic. The coefficient of restitution C r is used to represent the respective deviation depending on the closing and separating velocity: C r = v 2 v 1 v 1 v 2 = v s v c With inclusion of the coefficient of restitution, the velocity of object 1 after collision is given (without proof) by m 2 v 1 = (1 + C r ) v c + v 1 m 1 + m 2 Similarly, the velocity of object 2 after the collision is given by m 1 v 2 = (1 + C r ) v c + v 2 m 1 + m 2 Session (3) Springs, Ropes, Linear Momentum and Rotations,
27 Getting more insight, no formulas Understanding the formulas is crucial. Therefore we have a look at the most important parts: v 1 }{{} new velocity m 2 = (1 + C r ) }{{} m 1 + m 2 1+C r }{{} v c }{{} closing velocity mass fraction + v 1 }{{} old velocity Old/New velocity: Velocity of object 1 before/after the collision Closing velocity: Relative speed of the two objects Mass fraction: The fraction accounts for the change of velocity depending on the fraction m object /m total 1 + C r: Imagine a collision between a moving object 1 with mass 0 and a steady object 2 with mass 1. Then object 2 doesn t move at all. Object 1 reverses its velocity and is slowed down by the factor C r. Therefore v 1 = C r v 1 = (1 + C r )v 1 + v 1 = (1 + C r )v c + v 1. Session (3) Springs, Ropes, Linear Momentum and Rotations,
28 Using inverse mass... Computing v 2 directly, we get problems when the masses of the objects become huge, i.e. approach infinity. Assuming, that m 1 =, we get v 2 = (1 + C r ) v c + v 2 + m }{{ 2 } undefined!!! Without further checks, we run into severe problems due to the fact, that arithmetic datatypes are finite. Therefore we will work with the inverse of the mass: m 1 m 1 + m 2 = m 1 m 1 1 m 1 2 (m 1 + m 2 ) m 1 1 m 1 = 2 m 1 2 m m 1 2 Session (3) Springs, Ropes, Linear Momentum and Rotations,
29 Momentum in 3D closing velocity -n v 1 α closing velocity v 1 collision normal n Ground Figure: Collision involving the collision normal For 3D (any dimension higher than 1D), we have to take the collision normal into account. Only the velocity component parallel to the collision normal may be involved in computing the new velocity (no friction so far!) Thus the collision velocity v is computed by using only the fraction of the velocity in direction of the collision normal. Using the dot product we can compute this fraction by: v = n c v Session (3) Springs, Ropes, Linear Momentum and Rotations,
30 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? Session (3) Springs, Ropes, Linear Momentum and Rotations,
31 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) Session (3) Springs, Ropes, Linear Momentum and Rotations,
32 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) They are perpendicular to the surface (No friction!) Session (3) Springs, Ropes, Linear Momentum and Rotations,
33 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) They are perpendicular to the surface (No friction!) So what are the collision normals for the following cases? Sphere-Sphere: Sphere-Plane: Sphere-Edge: Sphere-Rectangle: Session (3) Springs, Ropes, Linear Momentum and Rotations,
34 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) They are perpendicular to the surface (No friction!) So what are the collision normals for the following cases? Sphere-Sphere: Line connecting sphere centers Sphere-Plane: Sphere-Edge: Sphere-Rectangle: Session (3) Springs, Ropes, Linear Momentum and Rotations,
35 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) They are perpendicular to the surface (No friction!) So what are the collision normals for the following cases? Sphere-Sphere: Line connecting sphere centers Sphere-Plane: Plane normal Sphere-Edge: Sphere-Rectangle: Session (3) Springs, Ropes, Linear Momentum and Rotations,
36 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) They are perpendicular to the surface (No friction!) So what are the collision normals for the following cases? Sphere-Sphere: Line connecting sphere centers Sphere-Plane: Plane normal Sphere-Edge: Shortest line segment connecting sphere center and edge Sphere-Rectangle: Session (3) Springs, Ropes, Linear Momentum and Rotations,
37 Collision normal? Wtf is that? The collision normal describes the direction at which repelling forces act on the two colliding objects upon impact. Imagine two arbitrary objects colliding without any friction. What restrictions must these forces meet at the time of impact? They sum up to zero (Newton s Third law) They are perpendicular to the surface (No friction!) So what are the collision normals for the following cases? Sphere-Sphere: Line connecting sphere centers Sphere-Plane: Plane normal Sphere-Edge: Shortest line segment connecting sphere center and edge Sphere-Rectangle: Two known cases: Sphere-Plane and Sphere-Edge Session (3) Springs, Ropes, Linear Momentum and Rotations,
38 Outline Springs and ropes Overview Springs Ropes Collisions Collision detection Collision resolution Linear momentum Basics Conservation laws Why use the inverse of mass? Rotations Session (3) Springs, Ropes, Linear Momentum and Rotations,
39 Rotations Different approaches to describe rotations: Session (3) Springs, Ropes, Linear Momentum and Rotations,
40 Rotations Different approaches to describe rotations: Angles Matrices (Later) Quaternions Generally, assume there are n N degrees of freedom r R n that describe a rotation. What operators do we need for rotations then? Session (3) Springs, Ropes, Linear Momentum and Rotations,
41 Rotations Different approaches to describe rotations: Angles Matrices (Later) Quaternions Generally, assume there are n N degrees of freedom r R n that describe a rotation. What operators do we need for rotations then? Mapping M, which creates the description r for the rotation. Transformation T r : R d R d, which applies the rotation r to points Concatenation : R n R n R n, which allows to combine two rotations r 1 and r 2 to a new rotation r = r 1 r 2 Session (3) Springs, Ropes, Linear Momentum and Rotations,
42 Rotations in 2D Angles: Session (3) Springs, Ropes, Linear Momentum and Rotations,
43 Rotations in 2D Angles: Store the rotation angle α (1 DoF). Concatenation: Easy, α = α 1 + α 2 :) Transformation: ( Use 2D Rotation ) Matrix cos α sin α R(α) =, then T sin α cos α α (x) = R(α)x Matrices: Session (3) Springs, Ropes, Linear Momentum and Rotations,
44 Rotations in 2D Angles: Store the rotation angle α (1 DoF). Concatenation: Easy, α = α 1 + α 2 :) Transformation: ( Use 2D Rotation ) Matrix cos α sin α R(α) =, then T sin α cos α α (x) = R(α)x Matrices: Store a rotation matrix R (4 DoFs) Concatenation: Matrix multiplication R = R 1 R 2. Transformation: T R (x) = R x Difference to angles? Session (3) Springs, Ropes, Linear Momentum and Rotations,
45 Rotations in 2D Angles: Store the rotation angle α (1 DoF). Concatenation: Easy, α = α 1 + α 2 :) Transformation: ( Use 2D Rotation ) Matrix cos α sin α R(α) =, then T sin α cos α α (x) = R(α)x Matrices: Store a rotation matrix R (4 DoFs) Concatenation: Matrix multiplication R = R 1 R 2. Transformation: T R (x) = R x Difference to angles? ) Example: Rotate vector v = by 90 (= π 2 ) ( 1 0 v new = R(90 ) v = ( ) ( 1 0 ) = ( 0 1 ) (1) Session (3) Springs, Ropes, Linear Momentum and Rotations,
46 Rotations in 3D: it s not that easy... Handling rotations sounds straight-forward, but definitely isn t! Autopilot on F-16 flipped the airplane upside-down when crossed the equator! Session (3) Springs, Ropes, Linear Momentum and Rotations,
47 Euler Angles From 2D rotation...: 1 rotation axis therefore, we use one type of rotation matrix R 2D...to 3D: 3 possible rotation axes (x,y,z) use three rotations to describe any rotation in space Euler angles: Describe rotated position by angles between this position and reference position z y x Session (3) Springs, Ropes, Linear Momentum and Rotations,
48 Euler Angles: Problems Different conventions/ approaches Example: zyx-convention 1. Rotation about z-axis 2. Rotation about y-axis 3. Rotation about x-axis 3 degrees of freedom z y rotate 180 about z, rotate 0 about y, rotate 0 about x x rotate 0 about z, rotate 180 about y, rotate 180 about x Rotational description not unique Session (3) Springs, Ropes, Linear Momentum and Rotations,
49 Euler Angles: Problems - Gimbal Lock (1) Excerpt from the NASA logs and commentary (taken from Visualizing Quaternions, A.J. Hanson,2006):... Stafford had the vehicle in the right attitude 10 minutes early. Cernan asked, You ready? Then he suddenly exclaimed, Son of a bitch! Snoopy seemed to be throwing a fit, lurching wildly about. He later said it was like flying an Immelmann turn in an aircraft, a combination of pitch and yaw. Stafford yelled that they were in gimbal lock that the engine had swiveled over to a stop and stuck- and they almost were. He called out for Cernan to thrust forward. Stafford then hit the switch to get rid of the descent stage and realized they were 30 degrees off from their previous attitude. The lunar module continued its crazy gyrations across the lunar sky, and a warning light indicated that the inertial measuring unit really was about to reach its limits and go into gimbal lock. Stafford then took over in manual control, made a big pitch maneuver, and started working the attitude control switches. Snoopy finally calmed down. Session (3) Springs, Ropes, Linear Momentum and Rotations,
50 Euler Angles: Problems - Gimbal Lock (2) Gimbal Lock: Loss of one degree of freedom in rotations z y rotate α about z, rotate 90 about y, rotate γ about x x Example: z- and x-axis become parallel. Solution: Allow rotations around axes Z, Y, X in different order. Better solution: Use quaternions. Session (3) Springs, Ropes, Linear Momentum and Rotations,
51 Rotations in 3D Angles: Store angles α, β, γ for rotations about unit vectors (3 DoFs) Transformation: T r (x) = R 1 (α)r 2 (β)r 3 (γ)x. Concatenation: Same as 2D, add up angles Each time we rotate around one axis 1, we rotate axes 2 and 3 as well Problem? Session (3) Springs, Ropes, Linear Momentum and Rotations,
52 Rotations in 3D Angles: Store angles α, β, γ for rotations about unit vectors (3 DoFs) Transformation: T r (x) = R 1 (α)r 2 (β)r 3 (γ)x. Concatenation: Same as 2D, add up angles Each time we rotate around one axis 1, we rotate axes 2 and 3 as well Problem? Matrices: Store matrix R (9 DoFs) Similar to 2D, concatenation by matrix multiplication and transformation by matrix-vector product Difference to angles: Imagine many small updates to the rotation. What happens in both cases? Session (3) Springs, Ropes, Linear Momentum and Rotations,
53 Rotations in 3D Angles: Store angles α, β, γ for rotations about unit vectors (3 DoFs) Transformation: T r (x) = R 1 (α)r 2 (β)r 3 (γ)x. Concatenation: Same as 2D, add up angles Each time we rotate around one axis 1, we rotate axes 2 and 3 as well Problem? Matrices: Store matrix R (9 DoFs) Similar to 2D, concatenation by matrix multiplication and transformation by matrix-vector product Difference to angles: Imagine many small updates to the rotation. What happens in both cases? Quaternions: Try and take the best of both approaches Eliminate Gimbal Lock Session (3) Springs, Ropes, Linear Momentum and Rotations,
54 Quaternions: Basics Describe a rotation θ around an arbitrary axis (x, y, z) in space Advantage: 3+1 degrees of freedom Solves the Gimbal Lock-Problem Given rotation axis (x, y, z), with rotation axis length (x, y, z) T = 1 and angle θ, the corresponding quaternion q is given by q := w i j k = cos θ 2 x sin θ 2 y sin θ 2 z sin θ 2 (2) Session (3) Springs, Ropes, Linear Momentum and Rotations,
55 Quaternions: Multiplication Applying two rotations given by quaternions q and p to an object means to apply the multiplication of both quaternions: q p. Multiplication of two quaternions is given by w 1 w 2 w 1 w 2 (i 1 i 2 + j 1 j 2 + k 1 k 2 ) i 1 j 1 i 2 j 2 = w 1 i 2 + w 2 i 1 + j 1 k 2 k 1 j 2 w 1 j 2 + w 2 j 1 + k 1 i 2 i 1 k 2 k 1 k 2 w 1 k 2 + w 2 k 1 + i 1 j 2 j 1 i 2 In this way the rotation of p is applied first, then the rotation expressed with the Quaternion q. Session (3) Springs, Ropes, Linear Momentum and Rotations,
56 Quaternions: Convertion to rotation matrix Convert quaternion back to general rotation matrix R via 1 2(j 2 + k 2 ) 2(ij + kw) 2(ik jw) R = 2(ij kw) 1 2(i 2 + k 2 ) 2(jk + iw) 2(ik + jw) 2(jk iw) 1 2(i 2 + j 2 ) Session (3) Springs, Ropes, Linear Momentum and Rotations,
57 Things, you should remember... Linear transformations: Objects are projected from model-space to world-space by applying the matrix M to the object. We can simply invert the model matrix M to transform backwards from world-space to object-space. Object coordinates are given with homogenous coordinates to account for translations. Use the inverse-transpose M T to transform normals. Use quaternions for rotations to avoid the gimbal-lock. Always draw sketches! Any questions? Session (3) Springs, Ropes, Linear Momentum and Rotations,
Autonomous Navigation for Flying Robots
 Computer Vision Group Prof. Daniel Cremers Autonomous Navigation for Flying Robots Lecture 3.1: 3D Geometry Jürgen Sturm Technische Universität München Points in 3D 3D point Augmented vector Homogeneous
Computer Vision Group Prof. Daniel Cremers Autonomous Navigation for Flying Robots Lecture 3.1: 3D Geometry Jürgen Sturm Technische Universität München Points in 3D 3D point Augmented vector Homogeneous
3D Transformations. CS 4620 Lecture Kavita Bala w/ prior instructor Steve Marschner. Cornell CS4620 Fall 2015 Lecture 11
 3D Transformations CS 4620 Lecture 11 1 Announcements A2 due tomorrow Demos on Monday Please sign up for a slot Post on piazza 2 Translation 3 Scaling 4 Rotation about z axis 5 Rotation about x axis 6
3D Transformations CS 4620 Lecture 11 1 Announcements A2 due tomorrow Demos on Monday Please sign up for a slot Post on piazza 2 Translation 3 Scaling 4 Rotation about z axis 5 Rotation about x axis 6
3D Transformations. CS 4620 Lecture 10. Cornell CS4620 Fall 2014 Lecture Steve Marschner (with previous instructors James/Bala)
 3D Transformations CS 4620 Lecture 10 1 Translation 2 Scaling 3 Rotation about z axis 4 Rotation about x axis 5 Rotation about y axis 6 Properties of Matrices Translations: linear part is the identity
3D Transformations CS 4620 Lecture 10 1 Translation 2 Scaling 3 Rotation about z axis 4 Rotation about x axis 5 Rotation about y axis 6 Properties of Matrices Translations: linear part is the identity
Answers. Chapter 2. 1) Give the coordinates of the following points:
 Answers Chapter 2 1) Give the coordinates of the following points: a (-2.5, 3) b (1, 2) c (2.5, 2) d (-1, 1) e (0, 0) f (2, -0.5) g (-0.5, -1.5) h (0, -2) j (-3, -2) 1 2) List the 48 different possible
Answers Chapter 2 1) Give the coordinates of the following points: a (-2.5, 3) b (1, 2) c (2.5, 2) d (-1, 1) e (0, 0) f (2, -0.5) g (-0.5, -1.5) h (0, -2) j (-3, -2) 1 2) List the 48 different possible
Quaternions & Rotation in 3D Space
 Quaternions & Rotation in 3D Space 1 Overview Quaternions: definition Quaternion properties Quaternions and rotation matrices Quaternion-rotation matrices relationship Spherical linear interpolation Concluding
Quaternions & Rotation in 3D Space 1 Overview Quaternions: definition Quaternion properties Quaternions and rotation matrices Quaternion-rotation matrices relationship Spherical linear interpolation Concluding
CS354 Computer Graphics Rotations and Quaternions
 Slide Credit: Don Fussell CS354 Computer Graphics Rotations and Quaternions Qixing Huang April 4th 2018 Orientation Position and Orientation The position of an object can be represented as a translation
Slide Credit: Don Fussell CS354 Computer Graphics Rotations and Quaternions Qixing Huang April 4th 2018 Orientation Position and Orientation The position of an object can be represented as a translation
Quaternions and Rotations
 CSCI 520 Computer Animation and Simulation Quaternions and Rotations Jernej Barbic University of Southern California 1 Rotations Very important in computer animation and robotics Joint angles, rigid body
CSCI 520 Computer Animation and Simulation Quaternions and Rotations Jernej Barbic University of Southern California 1 Rotations Very important in computer animation and robotics Joint angles, rigid body
Simulation in Computer Graphics. Deformable Objects. Matthias Teschner. Computer Science Department University of Freiburg
 Simulation in Computer Graphics Deformable Objects Matthias Teschner Computer Science Department University of Freiburg Outline introduction forces performance collision handling visualization University
Simulation in Computer Graphics Deformable Objects Matthias Teschner Computer Science Department University of Freiburg Outline introduction forces performance collision handling visualization University
Animation. Computer Graphics COMP 770 (236) Spring Instructor: Brandon Lloyd 4/23/07 1
 Animation Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 4/23/07 1 Today s Topics Interpolation Forward and inverse kinematics Rigid body simulation Fluids Particle systems Behavioral
Animation Computer Graphics COMP 770 (236) Spring 2007 Instructor: Brandon Lloyd 4/23/07 1 Today s Topics Interpolation Forward and inverse kinematics Rigid body simulation Fluids Particle systems Behavioral
Quaternion Rotations AUI Course Denbigh Starkey
 Major points of these notes: Quaternion Rotations AUI Course Denbigh Starkey. What I will and won t be doing. Definition of a quaternion and notation 3 3. Using quaternions to rotate any point around an
Major points of these notes: Quaternion Rotations AUI Course Denbigh Starkey. What I will and won t be doing. Definition of a quaternion and notation 3 3. Using quaternions to rotate any point around an
Motion Control (wheeled robots)
 Motion Control (wheeled robots) Requirements for Motion Control Kinematic / dynamic model of the robot Model of the interaction between the wheel and the ground Definition of required motion -> speed control,
Motion Control (wheeled robots) Requirements for Motion Control Kinematic / dynamic model of the robot Model of the interaction between the wheel and the ground Definition of required motion -> speed control,
Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ x + 5y + 7z 9x + 3y + 11z
 Basic Linear Algebra Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ 1 5 ] 7 9 3 11 Often matrices are used to describe in a simpler way a series of linear equations.
Basic Linear Algebra Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ 1 5 ] 7 9 3 11 Often matrices are used to describe in a simpler way a series of linear equations.
Analysis of Euler Angles in a Simple Two-Axis Gimbals Set
 Vol:5, No:9, 2 Analysis of Euler Angles in a Simple Two-Axis Gimbals Set Ma Myint Myint Aye International Science Index, Mechanical and Mechatronics Engineering Vol:5, No:9, 2 waset.org/publication/358
Vol:5, No:9, 2 Analysis of Euler Angles in a Simple Two-Axis Gimbals Set Ma Myint Myint Aye International Science Index, Mechanical and Mechatronics Engineering Vol:5, No:9, 2 waset.org/publication/358
12.1 Quaternions and Rotations
 Fall 2015 CSCI 420 Computer Graphics 12.1 Quaternions and Rotations Hao Li http://cs420.hao-li.com 1 Rotations Very important in computer animation and robotics Joint angles, rigid body orientations, camera
Fall 2015 CSCI 420 Computer Graphics 12.1 Quaternions and Rotations Hao Li http://cs420.hao-li.com 1 Rotations Very important in computer animation and robotics Joint angles, rigid body orientations, camera
ME5286 Robotics Spring 2014 Quiz 1 Solution. Total Points: 30
 Page 1 of 7 ME5286 Robotics Spring 2014 Quiz 1 Solution Total Points: 30 (Note images from original quiz are not included to save paper/ space. Please see the original quiz for additional information and
Page 1 of 7 ME5286 Robotics Spring 2014 Quiz 1 Solution Total Points: 30 (Note images from original quiz are not included to save paper/ space. Please see the original quiz for additional information and
CS612 - Algorithms in Bioinformatics
 Fall 2017 Structural Manipulation November 22, 2017 Rapid Structural Analysis Methods Emergence of large structural databases which do not allow manual (visual) analysis and require efficient 3-D search
Fall 2017 Structural Manipulation November 22, 2017 Rapid Structural Analysis Methods Emergence of large structural databases which do not allow manual (visual) analysis and require efficient 3-D search
Transformations: 2D Transforms
 1. Translation Transformations: 2D Transforms Relocation of point WRT frame Given P = (x, y), translation T (dx, dy) Then P (x, y ) = T (dx, dy) P, where x = x + dx, y = y + dy Using matrix representation
1. Translation Transformations: 2D Transforms Relocation of point WRT frame Given P = (x, y), translation T (dx, dy) Then P (x, y ) = T (dx, dy) P, where x = x + dx, y = y + dy Using matrix representation
Quaternions and Rotations
 CSCI 420 Computer Graphics Lecture 20 and Rotations Rotations Motion Capture [Angel Ch. 3.14] Rotations Very important in computer animation and robotics Joint angles, rigid body orientations, camera parameters
CSCI 420 Computer Graphics Lecture 20 and Rotations Rotations Motion Capture [Angel Ch. 3.14] Rotations Very important in computer animation and robotics Joint angles, rigid body orientations, camera parameters
ME 597: AUTONOMOUS MOBILE ROBOTICS SECTION 2 COORDINATE TRANSFORMS. Prof. Steven Waslander
 ME 597: AUTONOMOUS MOILE ROOTICS SECTION 2 COORDINATE TRANSFORMS Prof. Steven Waslander OUTLINE Coordinate Frames and Transforms Rotation Matrices Euler Angles Quaternions Homogeneous Transforms 2 COORDINATE
ME 597: AUTONOMOUS MOILE ROOTICS SECTION 2 COORDINATE TRANSFORMS Prof. Steven Waslander OUTLINE Coordinate Frames and Transforms Rotation Matrices Euler Angles Quaternions Homogeneous Transforms 2 COORDINATE
Quaternions and Rotations
 CSCI 480 Computer Graphics Lecture 20 and Rotations April 6, 2011 Jernej Barbic Rotations Motion Capture [Ch. 4.12] University of Southern California http://www-bcf.usc.edu/~jbarbic/cs480-s11/ 1 Rotations
CSCI 480 Computer Graphics Lecture 20 and Rotations April 6, 2011 Jernej Barbic Rotations Motion Capture [Ch. 4.12] University of Southern California http://www-bcf.usc.edu/~jbarbic/cs480-s11/ 1 Rotations
Motion Capture & Simulation
 Motion Capture & Simulation Motion Capture Character Reconstructions Joint Angles Need 3 points to compute a rigid body coordinate frame 1 st point gives 3D translation, 2 nd point gives 2 angles, 3 rd
Motion Capture & Simulation Motion Capture Character Reconstructions Joint Angles Need 3 points to compute a rigid body coordinate frame 1 st point gives 3D translation, 2 nd point gives 2 angles, 3 rd
Introduction to quaternions. Mathematics. Operations
 Introduction to quaternions Topics: Definition Mathematics Operations Euler Angles (optional) intro to quaternions 1 noel.h.hughes@gmail.com Euler's Theorem y y Angle! rotation follows right hand rule
Introduction to quaternions Topics: Definition Mathematics Operations Euler Angles (optional) intro to quaternions 1 noel.h.hughes@gmail.com Euler's Theorem y y Angle! rotation follows right hand rule
Transformation. Jane Li Assistant Professor Mechanical Engineering & Robotics Engineering
 RBE 550 MOTION PLANNING BASED ON DR. DMITRY BERENSON S RBE 550 Transformation Jane Li Assistant Professor Mechanical Engineering & Robotics Engineering http://users.wpi.edu/~zli11 Announcement Project
RBE 550 MOTION PLANNING BASED ON DR. DMITRY BERENSON S RBE 550 Transformation Jane Li Assistant Professor Mechanical Engineering & Robotics Engineering http://users.wpi.edu/~zli11 Announcement Project
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer
 Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Geometric Transformations
 Geometric Transformations CS 4620 Lecture 9 2017 Steve Marschner 1 A little quick math background Notation for sets, functions, mappings Linear and affine transformations Matrices Matrix-vector multiplication
Geometric Transformations CS 4620 Lecture 9 2017 Steve Marschner 1 A little quick math background Notation for sets, functions, mappings Linear and affine transformations Matrices Matrix-vector multiplication
Virtual Environments
 ELG 524 Virtual Environments Jean-Christian Delannoy viewing in 3D world coordinates / geometric modeling culling lighting virtualized reality collision detection collision response interactive forces
ELG 524 Virtual Environments Jean-Christian Delannoy viewing in 3D world coordinates / geometric modeling culling lighting virtualized reality collision detection collision response interactive forces
Fundamentals of Computer Animation
 Fundamentals of Computer Animation Orientation and Rotation University of Calgary GraphicsJungle Project CPSC 587 5 page Motivation Finding the most natural and compact way to present rotation and orientations
Fundamentals of Computer Animation Orientation and Rotation University of Calgary GraphicsJungle Project CPSC 587 5 page Motivation Finding the most natural and compact way to present rotation and orientations
Quaternions and Rotations
 CSCI 520 Computer Animation and Simulation Quaternions and Rotations Jernej Barbic University of Southern California 1 Rotations Very important in computer animation and robotics Joint angles, rigid body
CSCI 520 Computer Animation and Simulation Quaternions and Rotations Jernej Barbic University of Southern California 1 Rotations Very important in computer animation and robotics Joint angles, rigid body
Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation
 Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation and the type of an object. Even simple scaling turns a
Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation and the type of an object. Even simple scaling turns a
Visual Recognition: Image Formation
 Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
The Jello Cube Assignment 1, CSCI 520. Jernej Barbic, USC
 The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC 1 The jello cube Undeformed cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC 1 The jello cube Undeformed cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
10/11/07 1. Motion Control (wheeled robots) Representing Robot Position ( ) ( ) [ ] T
![10/11/07 1. Motion Control (wheeled robots) Representing Robot Position ( ) ( ) [ ] T 10/11/07 1. Motion Control (wheeled robots) Representing Robot Position ( ) ( ) [ ] T](/thumbs/79/79288754.jpg) 3 3 Motion Control (wheeled robots) Introduction: Mobile Robot Kinematics Requirements for Motion Control Kinematic / dynamic model of the robot Model of the interaction between the wheel and the ground
3 3 Motion Control (wheeled robots) Introduction: Mobile Robot Kinematics Requirements for Motion Control Kinematic / dynamic model of the robot Model of the interaction between the wheel and the ground
Geometric transformations in 3D and coordinate frames. Computer Graphics CSE 167 Lecture 3
 Geometric transformations in 3D and coordinate frames Computer Graphics CSE 167 Lecture 3 CSE 167: Computer Graphics 3D points as vectors Geometric transformations in 3D Coordinate frames CSE 167, Winter
Geometric transformations in 3D and coordinate frames Computer Graphics CSE 167 Lecture 3 CSE 167: Computer Graphics 3D points as vectors Geometric transformations in 3D Coordinate frames CSE 167, Winter
3D Transformations World Window to Viewport Transformation Week 2, Lecture 4
 CS 430/536 Computer Graphics I 3D Transformations World Window to Viewport Transformation Week 2, Lecture 4 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory
CS 430/536 Computer Graphics I 3D Transformations World Window to Viewport Transformation Week 2, Lecture 4 David Breen, William Regli and Maxim Peysakhov Geometric and Intelligent Computing Laboratory
Articulated Characters
 Articulated Characters Skeleton A skeleton is a framework of rigid body bones connected by articulated joints Used as an (invisible?) armature to position and orient geometry (usually surface triangles)
Articulated Characters Skeleton A skeleton is a framework of rigid body bones connected by articulated joints Used as an (invisible?) armature to position and orient geometry (usually surface triangles)
Orientation & Quaternions
 Orientation & Quaternions Orientation Position and Orientation The position of an object can be represented as a translation of the object from the origin The orientation of an object can be represented
Orientation & Quaternions Orientation Position and Orientation The position of an object can be represented as a translation of the object from the origin The orientation of an object can be represented
CALCULATING TRANSFORMATIONS OF KINEMATIC CHAINS USING HOMOGENEOUS COORDINATES
 CALCULATING TRANSFORMATIONS OF KINEMATIC CHAINS USING HOMOGENEOUS COORDINATES YINGYING REN Abstract. In this paper, the applications of homogeneous coordinates are discussed to obtain an efficient model
CALCULATING TRANSFORMATIONS OF KINEMATIC CHAINS USING HOMOGENEOUS COORDINATES YINGYING REN Abstract. In this paper, the applications of homogeneous coordinates are discussed to obtain an efficient model
Quaternions and Euler Angles
 Quaternions and Euler Angles Revision #1 This document describes how the VR Audio Kit handles the orientation of the 3D Sound One headset using quaternions and Euler angles, and how to convert between
Quaternions and Euler Angles Revision #1 This document describes how the VR Audio Kit handles the orientation of the 3D Sound One headset using quaternions and Euler angles, and how to convert between
METR 4202: Advanced Control & Robotics
 Position & Orientation & State t home with Homogenous Transformations METR 4202: dvanced Control & Robotics Drs Surya Singh, Paul Pounds, and Hanna Kurniawati Lecture # 2 July 30, 2012 metr4202@itee.uq.edu.au
Position & Orientation & State t home with Homogenous Transformations METR 4202: dvanced Control & Robotics Drs Surya Singh, Paul Pounds, and Hanna Kurniawati Lecture # 2 July 30, 2012 metr4202@itee.uq.edu.au
CS 130 Final. Fall 2015
 CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
CS 130 Final Fall 2015 Name Student ID Signature You may not ask any questions during the test. If you believe that there is something wrong with a question, write down what you think the question is trying
Robots are built to accomplish complex and difficult tasks that require highly non-linear motions.
 Path and Trajectory specification Robots are built to accomplish complex and difficult tasks that require highly non-linear motions. Specifying the desired motion to achieve a specified goal is often a
Path and Trajectory specification Robots are built to accomplish complex and difficult tasks that require highly non-linear motions. Specifying the desired motion to achieve a specified goal is often a
CMPUT 412 Motion Control Wheeled robots. Csaba Szepesvári University of Alberta
 CMPUT 412 Motion Control Wheeled robots Csaba Szepesvári University of Alberta 1 Motion Control (wheeled robots) Requirements Kinematic/dynamic model of the robot Model of the interaction between the wheel
CMPUT 412 Motion Control Wheeled robots Csaba Szepesvári University of Alberta 1 Motion Control (wheeled robots) Requirements Kinematic/dynamic model of the robot Model of the interaction between the wheel
MTRX4700 Experimental Robotics
 MTRX 4700 : Experimental Robotics Lecture 2 Stefan B. Williams Slide 1 Course Outline Week Date Content Labs Due Dates 1 5 Mar Introduction, history & philosophy of robotics 2 12 Mar Robot kinematics &
MTRX 4700 : Experimental Robotics Lecture 2 Stefan B. Williams Slide 1 Course Outline Week Date Content Labs Due Dates 1 5 Mar Introduction, history & philosophy of robotics 2 12 Mar Robot kinematics &
Rotations in 3D Graphics and the Gimbal Lock
 Rotations in 3D Graphics and the Gimbal Lock Valentin Koch Autodesk Inc. January 27, 2016 Valentin Koch (ADSK) IEEE Okanagan January 27, 2016 1 / 37 Presentation Road Map 1 Introduction 2 Rotation Matrices
Rotations in 3D Graphics and the Gimbal Lock Valentin Koch Autodesk Inc. January 27, 2016 Valentin Koch (ADSK) IEEE Okanagan January 27, 2016 1 / 37 Presentation Road Map 1 Introduction 2 Rotation Matrices
Lecture Note 3: Rotational Motion
 ECE5463: Introduction to Robotics Lecture Note 3: Rotational Motion Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio, USA Spring 2018 Lecture 3 (ECE5463
ECE5463: Introduction to Robotics Lecture Note 3: Rotational Motion Prof. Wei Zhang Department of Electrical and Computer Engineering Ohio State University Columbus, Ohio, USA Spring 2018 Lecture 3 (ECE5463
Creating joints for the NovodeX MAX exporter
 Creating joints for the NovodeX MAX exporter (a step-by-step tutorial by Pierre Terdiman) p.terdiman@wanadoo.fr Version 0.3 I) Creating a hinge Here we'll see how to create a hinge joint compatible with
Creating joints for the NovodeX MAX exporter (a step-by-step tutorial by Pierre Terdiman) p.terdiman@wanadoo.fr Version 0.3 I) Creating a hinge Here we'll see how to create a hinge joint compatible with
CS184: Using Quaternions to Represent Rotation
 Page 1 of 5 CS 184 home page A note on these notes: These notes on quaternions were created as a resource for students taking CS184 at UC Berkeley. I am not doing any research related to quaternions and
Page 1 of 5 CS 184 home page A note on these notes: These notes on quaternions were created as a resource for students taking CS184 at UC Berkeley. I am not doing any research related to quaternions and
Animating orientation. CS 448D: Character Animation Prof. Vladlen Koltun Stanford University
 Animating orientation CS 448D: Character Animation Prof. Vladlen Koltun Stanford University Orientation in the plane θ (cos θ, sin θ) ) R θ ( x y = sin θ ( cos θ sin θ )( x y ) cos θ Refresher: Homogenous
Animating orientation CS 448D: Character Animation Prof. Vladlen Koltun Stanford University Orientation in the plane θ (cos θ, sin θ) ) R θ ( x y = sin θ ( cos θ sin θ )( x y ) cos θ Refresher: Homogenous
The jello cube. Undeformed cube. Deformed cube
 The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC Undeformed cube The jello cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
The Jello Cube Assignment 1, CSCI 520 Jernej Barbic, USC Undeformed cube The jello cube Deformed cube The jello cube is elastic, Can be bent, stretched, squeezed,, Without external forces, it eventually
Transformations Week 9, Lecture 18
 CS 536 Computer Graphics Transformations Week 9, Lecture 18 2D Transformations David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 3 2D Affine Transformations
CS 536 Computer Graphics Transformations Week 9, Lecture 18 2D Transformations David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 3 2D Affine Transformations
Hello, welcome to the video lecture series on Digital Image Processing. So in today's lecture
 Digital Image Processing Prof. P. K. Biswas Department of Electronics and Electrical Communications Engineering Indian Institute of Technology, Kharagpur Module 02 Lecture Number 10 Basic Transform (Refer
Digital Image Processing Prof. P. K. Biswas Department of Electronics and Electrical Communications Engineering Indian Institute of Technology, Kharagpur Module 02 Lecture Number 10 Basic Transform (Refer
Centre for Autonomous Systems
 Robot Henrik I Centre for Autonomous Systems Kungl Tekniska Högskolan hic@kth.se 27th April 2005 Outline 1 duction 2 Kinematic and Constraints 3 Mobile Robot 4 Mobile Robot 5 Beyond Basic 6 Kinematic 7
Robot Henrik I Centre for Autonomous Systems Kungl Tekniska Högskolan hic@kth.se 27th April 2005 Outline 1 duction 2 Kinematic and Constraints 3 Mobile Robot 4 Mobile Robot 5 Beyond Basic 6 Kinematic 7
CS 445 / 645 Introduction to Computer Graphics. Lecture 21 Representing Rotations
 CS 445 / 645 Introduction to Computer Graphics Lecture 21 Representing Rotations Parameterizing Rotations Straightforward in 2D A scalar, θ, represents rotation in plane More complicated in 3D Three scalars
CS 445 / 645 Introduction to Computer Graphics Lecture 21 Representing Rotations Parameterizing Rotations Straightforward in 2D A scalar, θ, represents rotation in plane More complicated in 3D Three scalars
Computer Animation II
 Computer Animation II Orientation interpolation Dynamics Some slides courtesy of Leonard McMillan and Jovan Popovic Lecture 13 6.837 Fall 2002 Interpolation Review from Thursday Splines Articulated bodies
Computer Animation II Orientation interpolation Dynamics Some slides courtesy of Leonard McMillan and Jovan Popovic Lecture 13 6.837 Fall 2002 Interpolation Review from Thursday Splines Articulated bodies
Modeling Cloth Using Mass Spring Systems
 Modeling Cloth Using Mass Spring Systems Corey O Connor Keith Stevens May 2, 2003 Abstract We set out to model cloth using a connected mesh of springs and point masses. After successfully implementing
Modeling Cloth Using Mass Spring Systems Corey O Connor Keith Stevens May 2, 2003 Abstract We set out to model cloth using a connected mesh of springs and point masses. After successfully implementing
2D and 3D Transformations AUI Course Denbigh Starkey
 2D and 3D Transformations AUI Course Denbigh Starkey. Introduction 2 2. 2D transformations using Cartesian coordinates 3 2. Translation 3 2.2 Rotation 4 2.3 Scaling 6 3. Introduction to homogeneous coordinates
2D and 3D Transformations AUI Course Denbigh Starkey. Introduction 2 2. 2D transformations using Cartesian coordinates 3 2. Translation 3 2.2 Rotation 4 2.3 Scaling 6 3. Introduction to homogeneous coordinates
Robotics (Kinematics) Winter 1393 Bonab University
 Robotics () Winter 1393 Bonab University : most basic study of how mechanical systems behave Introduction Need to understand the mechanical behavior for: Design Control Both: Manipulators, Mobile Robots
Robotics () Winter 1393 Bonab University : most basic study of how mechanical systems behave Introduction Need to understand the mechanical behavior for: Design Control Both: Manipulators, Mobile Robots
For each question, indicate whether the statement is true or false by circling T or F, respectively.
 True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
3D Game Engine Programming. Understanding Quaternions. Helping you build your dream game engine. Posted on June 25, 2012 by Jeremiah van Oosten
 3D Game Engine Programming Helping you build your dream game engine. Understanding Quaternions Posted on June 25, 2012 by Jeremiah van Oosten Understanding Quaternions In this article I will attempt to
3D Game Engine Programming Helping you build your dream game engine. Understanding Quaternions Posted on June 25, 2012 by Jeremiah van Oosten Understanding Quaternions In this article I will attempt to
Chapter 4 Dynamics. Part Constrained Kinematics and Dynamics. Mobile Robotics - Prof Alonzo Kelly, CMU RI
 Chapter 4 Dynamics Part 2 4.3 Constrained Kinematics and Dynamics 1 Outline 4.3 Constrained Kinematics and Dynamics 4.3.1 Constraints of Disallowed Direction 4.3.2 Constraints of Rolling without Slipping
Chapter 4 Dynamics Part 2 4.3 Constrained Kinematics and Dynamics 1 Outline 4.3 Constrained Kinematics and Dynamics 4.3.1 Constraints of Disallowed Direction 4.3.2 Constraints of Rolling without Slipping
What You ll See in This Chapter. Word Cloud. René Descartes. Introduction. Ian Parberry University of North Texas. Fletcher Dunn
 What You ll See in This Chapter Chapter 1: Cartesian Coordinate Systems Fletcher Dunn Valve Software Ian Parberry University of North Texas This chapter describes the basic concepts of 3D math. It is divided
What You ll See in This Chapter Chapter 1: Cartesian Coordinate Systems Fletcher Dunn Valve Software Ian Parberry University of North Texas This chapter describes the basic concepts of 3D math. It is divided
Transformations. Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico
 Transformations Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico Angel: Interactive Computer Graphics 4E Addison-Wesley 25 1 Objectives
Transformations Ed Angel Professor of Computer Science, Electrical and Computer Engineering, and Media Arts University of New Mexico Angel: Interactive Computer Graphics 4E Addison-Wesley 25 1 Objectives
Today. Today. Introduction. Matrices. Matrices. Computergrafik. Transformations & matrices Introduction Matrices
 Computergrafik Matthias Zwicker Universität Bern Herbst 2008 Today Transformations & matrices Introduction Matrices Homogeneous Affine transformations Concatenating transformations Change of Common coordinate
Computergrafik Matthias Zwicker Universität Bern Herbst 2008 Today Transformations & matrices Introduction Matrices Homogeneous Affine transformations Concatenating transformations Change of Common coordinate
Animation. CS 4620 Lecture 32. Cornell CS4620 Fall Kavita Bala
 Animation CS 4620 Lecture 32 Cornell CS4620 Fall 2015 1 What is animation? Modeling = specifying shape using all the tools we ve seen: hierarchies, meshes, curved surfaces Animation = specifying shape
Animation CS 4620 Lecture 32 Cornell CS4620 Fall 2015 1 What is animation? Modeling = specifying shape using all the tools we ve seen: hierarchies, meshes, curved surfaces Animation = specifying shape
2D/3D Geometric Transformations and Scene Graphs
 2D/3D Geometric Transformations and Scene Graphs Week 4 Acknowledgement: The course slides are adapted from the slides prepared by Steve Marschner of Cornell University 1 A little quick math background
2D/3D Geometric Transformations and Scene Graphs Week 4 Acknowledgement: The course slides are adapted from the slides prepared by Steve Marschner of Cornell University 1 A little quick math background
3-D D Euclidean Space - Vectors
 3-D D Euclidean Space - Vectors Rigid Body Motion and Image Formation A free vector is defined by a pair of points : Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Coordinates of the vector : 3D Rotation
3-D D Euclidean Space - Vectors Rigid Body Motion and Image Formation A free vector is defined by a pair of points : Jana Kosecka http://cs.gmu.edu/~kosecka/cs682.html Coordinates of the vector : 3D Rotation
CS251 Spring 2014 Lecture 7
 CS251 Spring 2014 Lecture 7 Stephanie R Taylor Feb 19, 2014 1 Moving on to 3D Today, we move on to 3D coordinates. But first, let s recap of what we did in 2D: 1. We represented a data point in 2D data
CS251 Spring 2014 Lecture 7 Stephanie R Taylor Feb 19, 2014 1 Moving on to 3D Today, we move on to 3D coordinates. But first, let s recap of what we did in 2D: 1. We represented a data point in 2D data
A simple example. Assume we want to find the change in the rotation angles to get the end effector to G. Effect of changing s
 CENG 732 Computer Animation This week Inverse Kinematics (continued) Rigid Body Simulation Bodies in free fall Bodies in contact Spring 2006-2007 Week 5 Inverse Kinematics Physically Based Rigid Body Simulation
CENG 732 Computer Animation This week Inverse Kinematics (continued) Rigid Body Simulation Bodies in free fall Bodies in contact Spring 2006-2007 Week 5 Inverse Kinematics Physically Based Rigid Body Simulation
Graphics and Interaction Transformation geometry and homogeneous coordinates
 433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
1 Transformations. Chapter 1. Transformations. Department of Computer Science and Engineering 1-1
 Transformations 1-1 Transformations are used within the entire viewing pipeline: Projection from world to view coordinate system View modifications: Panning Zooming Rotation 1-2 Transformations can also
Transformations 1-1 Transformations are used within the entire viewing pipeline: Projection from world to view coordinate system View modifications: Panning Zooming Rotation 1-2 Transformations can also
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates
 COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
521493S Computer Graphics Exercise 2 Solution (Chapters 4-5)
 5493S Computer Graphics Exercise Solution (Chapters 4-5). Given two nonparallel, three-dimensional vectors u and v, how can we form an orthogonal coordinate system in which u is one of the basis vectors?
5493S Computer Graphics Exercise Solution (Chapters 4-5). Given two nonparallel, three-dimensional vectors u and v, how can we form an orthogonal coordinate system in which u is one of the basis vectors?
IntroductionToRobotics-Lecture02
 IntroductionToRobotics-Lecture02 Instructor (Oussama Khatib):Okay. Let's get started. So as always, the lecture starts with a video segment, and today's video segment comes from 1991, and from the group
IntroductionToRobotics-Lecture02 Instructor (Oussama Khatib):Okay. Let's get started. So as always, the lecture starts with a video segment, and today's video segment comes from 1991, and from the group
Transforms. COMP 575/770 Spring 2013
 Transforms COMP 575/770 Spring 2013 Transforming Geometry Given any set of points S Could be a 2D shape, a 3D object A transform is a function T that modifies all points in S: T S S T v v S Different transforms
Transforms COMP 575/770 Spring 2013 Transforming Geometry Given any set of points S Could be a 2D shape, a 3D object A transform is a function T that modifies all points in S: T S S T v v S Different transforms
COMP30019 Graphics and Interaction Three-dimensional transformation geometry and perspective
 COMP30019 Graphics and Interaction Three-dimensional transformation geometry and perspective Department of Computing and Information Systems The Lecture outline Introduction Rotation about artibrary axis
COMP30019 Graphics and Interaction Three-dimensional transformation geometry and perspective Department of Computing and Information Systems The Lecture outline Introduction Rotation about artibrary axis
The Three Dimensional Coordinate System
 The Three-Dimensional Coordinate System The Three Dimensional Coordinate System You can construct a three-dimensional coordinate system by passing a z-axis perpendicular to both the x- and y-axes at the
The Three-Dimensional Coordinate System The Three Dimensional Coordinate System You can construct a three-dimensional coordinate system by passing a z-axis perpendicular to both the x- and y-axes at the
Visualizing Quaternions
 Visualizing Quaternions Andrew J. Hanson Computer Science Department Indiana University Siggraph 1 Tutorial 1 GRAND PLAN I: Fundamentals of Quaternions II: Visualizing Quaternion Geometry III: Quaternion
Visualizing Quaternions Andrew J. Hanson Computer Science Department Indiana University Siggraph 1 Tutorial 1 GRAND PLAN I: Fundamentals of Quaternions II: Visualizing Quaternion Geometry III: Quaternion
3.5 Equations of Lines and Planes
 3.5 Equations of Lines and Planes Objectives Iknowhowtodefinealineinthree-dimensionalspace. I can write a line as a parametric equation, a symmetric equation, and a vector equation. I can define a plane
3.5 Equations of Lines and Planes Objectives Iknowhowtodefinealineinthree-dimensionalspace. I can write a line as a parametric equation, a symmetric equation, and a vector equation. I can define a plane
Sphero Lightning Lab Cheat Sheet
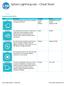 Actions Tool Description Variables Ranges Roll Combines heading, speed and time variables to make the robot roll. Duration Speed Heading (0 to 999999 seconds) (degrees 0-359) Set Speed Sets the speed of
Actions Tool Description Variables Ranges Roll Combines heading, speed and time variables to make the robot roll. Duration Speed Heading (0 to 999999 seconds) (degrees 0-359) Set Speed Sets the speed of
Computer Animation Fundamentals. Animation Methods Keyframing Interpolation Kinematics Inverse Kinematics
 Computer Animation Fundamentals Animation Methods Keyframing Interpolation Kinematics Inverse Kinematics Lecture 21 6.837 Fall 2001 Conventional Animation Draw each frame of the animation great control
Computer Animation Fundamentals Animation Methods Keyframing Interpolation Kinematics Inverse Kinematics Lecture 21 6.837 Fall 2001 Conventional Animation Draw each frame of the animation great control
DD2429 Computational Photography :00-19:00
 . Examination: DD2429 Computational Photography 202-0-8 4:00-9:00 Each problem gives max 5 points. In order to pass you need about 0-5 points. You are allowed to use the lecture notes and standard list
. Examination: DD2429 Computational Photography 202-0-8 4:00-9:00 Each problem gives max 5 points. In order to pass you need about 0-5 points. You are allowed to use the lecture notes and standard list
INSTITUTE OF AERONAUTICAL ENGINEERING
 Name Code Class Branch Page 1 INSTITUTE OF AERONAUTICAL ENGINEERING : ROBOTICS (Autonomous) Dundigal, Hyderabad - 500 0 MECHANICAL ENGINEERING TUTORIAL QUESTION BANK : A7055 : IV B. Tech I Semester : MECHANICAL
Name Code Class Branch Page 1 INSTITUTE OF AERONAUTICAL ENGINEERING : ROBOTICS (Autonomous) Dundigal, Hyderabad - 500 0 MECHANICAL ENGINEERING TUTORIAL QUESTION BANK : A7055 : IV B. Tech I Semester : MECHANICAL
Visualisation Pipeline : The Virtual Camera
 Visualisation Pipeline : The Virtual Camera The Graphics Pipeline 3D Pipeline The Virtual Camera The Camera is defined by using a parallelepiped as a view volume with two of the walls used as the near
Visualisation Pipeline : The Virtual Camera The Graphics Pipeline 3D Pipeline The Virtual Camera The Camera is defined by using a parallelepiped as a view volume with two of the walls used as the near
Lecture VI: Constraints and Controllers. Parts Based on Erin Catto s Box2D Tutorial
 Lecture VI: Constraints and Controllers Parts Based on Erin Catto s Box2D Tutorial Motion Constraints In practice, no rigid body is free to move around on its own. Movement is constrained: wheels on a
Lecture VI: Constraints and Controllers Parts Based on Erin Catto s Box2D Tutorial Motion Constraints In practice, no rigid body is free to move around on its own. Movement is constrained: wheels on a
Rotations (and other transformations) Rotation as rotation matrix. Storage. Apply to vector matrix vector multiply (15 flops)
 Cornell University CS 569: Interactive Computer Graphics Rotations (and other transformations) Lecture 4 2008 Steve Marschner 1 Rotation as rotation matrix 9 floats orthogonal and unit length columns and
Cornell University CS 569: Interactive Computer Graphics Rotations (and other transformations) Lecture 4 2008 Steve Marschner 1 Rotation as rotation matrix 9 floats orthogonal and unit length columns and
3D Rotations and Complex Representations. Computer Graphics CMU /15-662, Fall 2017
 3D Rotations and Complex Representations Computer Graphics CMU 15-462/15-662, Fall 2017 Rotations in 3D What is a rotation, intuitively? How do you know a rotation when you see it? - length/distance is
3D Rotations and Complex Representations Computer Graphics CMU 15-462/15-662, Fall 2017 Rotations in 3D What is a rotation, intuitively? How do you know a rotation when you see it? - length/distance is
Mechanisms. Updated: 18Apr16 v7
 Mechanisms Updated: 8Apr6 v7 Mechanism Converts input motion or force into a desired output with four combinations of input and output motion Rotational to Oscillating Rotational to Rotational Rotational
Mechanisms Updated: 8Apr6 v7 Mechanism Converts input motion or force into a desired output with four combinations of input and output motion Rotational to Oscillating Rotational to Rotational Rotational
Coordinate Transformations. Coordinate Transformation. Problem in animation. Coordinate Transformation. Rendering Pipeline $ = $! $ ! $!
 Rendering Pipeline Another look at rotation Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera tone model reproduction (focuses
Rendering Pipeline Another look at rotation Photography: real scene camera (captures light) photo processing Photographic print processing Computer Graphics: 3D models camera tone model reproduction (focuses
animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time
 animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time computer graphics animation 2009 fabio pellacini 2 animation representation many ways to
animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time computer graphics animation 2009 fabio pellacini 2 animation representation many ways to
Notes on Spherical Geometry
 Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
To do this the end effector of the robot must be correctly positioned relative to the work piece.
 Spatial Descriptions and Transformations typical robotic task is to grasp a work piece supplied by a conveyer belt or similar mechanism in an automated manufacturing environment, transfer it to a new position
Spatial Descriptions and Transformations typical robotic task is to grasp a work piece supplied by a conveyer belt or similar mechanism in an automated manufacturing environment, transfer it to a new position
Computer Graphics with OpenGL ES (J. Han) Chapter IV Spaces and Transforms
 Chapter IV Spaces and Transforms Scaling 2D scaling with the scaling factors, s x and s y, which are independent. Examples When a polygon is scaled, all of its vertices are processed by the same scaling
Chapter IV Spaces and Transforms Scaling 2D scaling with the scaling factors, s x and s y, which are independent. Examples When a polygon is scaled, all of its vertices are processed by the same scaling
Animation. CS 4620 Lecture 33. Cornell CS4620 Fall Kavita Bala
 Animation CS 4620 Lecture 33 Cornell CS4620 Fall 2015 1 Announcements Grading A5 (and A6) on Monday after TG 4621: one-on-one sessions with TA this Friday w/ prior instructor Steve Marschner 2 Quaternions
Animation CS 4620 Lecture 33 Cornell CS4620 Fall 2015 1 Announcements Grading A5 (and A6) on Monday after TG 4621: one-on-one sessions with TA this Friday w/ prior instructor Steve Marschner 2 Quaternions
Lesson 1: Introduction to Pro/MECHANICA Motion
 Lesson 1: Introduction to Pro/MECHANICA Motion 1.1 Overview of the Lesson The purpose of this lesson is to provide you with a brief overview of Pro/MECHANICA Motion, also called Motion in this book. Motion
Lesson 1: Introduction to Pro/MECHANICA Motion 1.1 Overview of the Lesson The purpose of this lesson is to provide you with a brief overview of Pro/MECHANICA Motion, also called Motion in this book. Motion
Camera Model and Calibration
 Camera Model and Calibration Lecture-10 Camera Calibration Determine extrinsic and intrinsic parameters of camera Extrinsic 3D location and orientation of camera Intrinsic Focal length The size of the
Camera Model and Calibration Lecture-10 Camera Calibration Determine extrinsic and intrinsic parameters of camera Extrinsic 3D location and orientation of camera Intrinsic Focal length The size of the
Inertial Measurement Units II!
 ! Inertial Measurement Units II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 10! stanford.edu/class/ee267/!! wikipedia! Polynesian Migration! Lecture Overview! short review of
! Inertial Measurement Units II! Gordon Wetzstein! Stanford University! EE 267 Virtual Reality! Lecture 10! stanford.edu/class/ee267/!! wikipedia! Polynesian Migration! Lecture Overview! short review of
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Answers to practice questions for Midterm 1
 Answers to practice questions for Midterm Paul Hacking /5/9 (a The RREF (reduced row echelon form of the augmented matrix is So the system of linear equations has exactly one solution given by x =, y =,
Answers to practice questions for Midterm Paul Hacking /5/9 (a The RREF (reduced row echelon form of the augmented matrix is So the system of linear equations has exactly one solution given by x =, y =,
Lecture VI: Constraints and Controllers
 Lecture VI: Constraints and Controllers Motion Constraints In practice, no rigid body is free to move around on its own. Movement is constrained: wheels on a chair human body parts trigger of a gun opening
Lecture VI: Constraints and Controllers Motion Constraints In practice, no rigid body is free to move around on its own. Movement is constrained: wheels on a chair human body parts trigger of a gun opening
Game Mathematics. (12 Week Lesson Plan)
 Game Mathematics (12 Week Lesson Plan) Lesson 1: Set Theory Textbook: Chapter One (pgs. 1 15) We begin the course by introducing the student to a new vocabulary and set of rules that will be foundational
Game Mathematics (12 Week Lesson Plan) Lesson 1: Set Theory Textbook: Chapter One (pgs. 1 15) We begin the course by introducing the student to a new vocabulary and set of rules that will be foundational
