CGT 511 Procedural Methods
|
|
|
- Brent Lang
- 5 years ago
- Views:
Transcription
1 3D object representation CGT 511 Procedural Methods Volume representation Voxels 3D object representation Boundary representation Wire frame Procedural Fractals Bedřich Beneš, Ph.D. Purdue University Department of Computer Graphics Technology Oct tree CSG Surfaces Polygonal Free form Bézier surfaces Particle systems Grammars NURBS Implicit surfaces Procedural Techniques Three classes: fractals particle systems grammars Used when shape cannot be represented as a surface (fire, water, smoke, flock of birds, explosions, model of mountain, grass, clouds, plants, etc.) Used for Simulation of Natural Phenomena Procedural Techniques Model is generated by a piece of code Model is not represented as data! The generation can take some time and of course the data can be precalculated 1
2 The Mandelbrot Set the big logo The Mandelbrot set discovered in 1970 by Benoit Mandelbrot It is a non linear deterministic fractal It is graph of a solution of a dynamic system The Mandelbrot Set Take the equation z n+1 = z n2 +c where: z i and c are complex numbers and z 0 =0+i0 Explore c complex numbers from the complex plane Measure the speed of divergence of the z n i.e., measure when z n > 2 (predefined value) The Mandelbrot Set Explore c complex numbers from the complex plane Measure the speed of divergence of the z n i.e., measure when z n > 2 (predefined value) there are two kinds of points: z n < 2 for n >, (stable points) z n > 2 for certain n and n greater (unstable points) The Mandelbrot Set a) stable points displayed in black b) unstable points color=f(n) for every point c in the plane < 2 2i>, <2+2i> do set z = 0+i0 set n=0 while (n<max) and ( z <2) do z=z 2 +c end of while if (n==max) Draw Point(Black) else Draw Point(n) end of for 2
3 The Mandelbrot Set Zooming into the Mandelbrot set The Mandelbrot Set Zooming into the Mandelbrot set The Mandelbrot Set Zooming into the Mandelbrot set The Mandelbrot Set Zooming into the Mandelbrot set 3
4 The Mandelbrot Set Zooming into the Mandelbrot set Dimensions Dimension how long is the coast of Corsica? A stick of 500m will give 700km (not very precise) A stick of 100m will give 1200km (?) What if we use length equal to dl? The length will be Dimensions How long is the coast of Corsica? we have applied n sticks of length N() times the total length is K stick of the length 1m and = 10cm=1/10m we need N() = 10 pieces if =0.5m we need N()=2 K= N() But in the case of Corsica we need to use formula K= D N() to get reasonable results What is this D? (Richardson) Dimensions How long is the coast of Corsica? Having N() = 1/ we get K= D / with >0 (i.e., getting the stick shorter) we get D K lim 0 For the line segment we need to set D=1 it the case of Corsica we need to set non integer The D is so called Hausdorff dimension Sometimes called fractal dimension Fractals do not have dimensions 0,1,2,... 4
5 Fractals Fractals fractal is a set that is self similar, A i ( A) i1 it is a set that is copy of itself here i is transformation scales down scale, denoted by s must be 0 < s < 1 i.e., a contraction Fractal is set that has Hausdorff s dimension greater than its dimension topological Fractals Fractal is a set that is geometrically complex and its structure is given by repetition of a certain shape at different scales. Fractals Fractals Linear Non linear Deterministic Non deterministic Deterministic or exact fractals Non deterministic or random fractals (Based on the type of self similarity (exact, random)) Linear rotation, scale, translation, shear Non linear the others Fractals Fractals Linear Non linear Deterministic Non deterministic Four classes: 1. Linear deterministic, 2. Non linear deterministic, 3. Non linear non deterministic 4. Linear non deterministic In CG we mostly use the last mentioned 5
6 Dimensions Special cases If we use just ONE transformation all the time with fixed and n repetitions the fractal dimension is determined as D=log n/log Linear Deterministic Fractals The Cantor s discontinuum (published in 1883) 1) take a line segment 2) scale it 1/3 3) shift it to the left and right. 4) do it recursively (Georg Cantor ) Linear Deterministic Fractals What is the dimension of the Cantor s discontinuum? scale = 3 n=2 new pieces for this we can use formula D=log n/log D= log 2/ log 3= 0.63 this object is something between a point and a line Linear Deterministic Fractals The Koch s snowflake 1) take a line segment 2) erase the mid third (similar to Cantor) 3) create equilateral triangle 4) repeat this recursively Scale = 3, n = 4, D=log 4 /log 3 = 1.26 Properties: does not have derivative! infinite length zero area the area inside is non zero and non infinity (January 25, 1870 March 11, 1924) 6
7 Linear Deterministic Fractals The Sierpinsky gasket (Wacław Franciszek Sierpiński ) 1) take a triangle 2) erase mid triangle 3) repeat this recursively = 2 n = 3 D=log 3 /log 2 = 1.59 not plane, not line! Linear Deterministic Fractals The Menger sponge (Karl Menger ( )) 1) take a cube 2) erase mid cross of cubes 3) repeat this recursively Scale = 3 n = 20 D=log 20 /log 3 = 2.73 Dust of points! It is invisible! Linear Deterministic Fractals The Peano curve (Guiseppe Peano ) 1) take a line segment 2) substitute it by the lines from the image 3) repeat recursively on each line segment =3 n=9 D=log 9/ log 3= 2 space filling curve Non Linear Deterministic Fractals Quaternions if we apply the formula z n+1 = z n2 +c in quaternion space (hypercomplex numbers 4D) we will get something like this: 7
8 Linear Non Deterministic Fractals random numbers and linear transformations motivation: What would happen if increasing the speed of playing music? Noise? Change of the speed is scaling Linear Non Deterministic Fractals Another motivation: How large is this stone? 10cm? 1m? 10m? Linear Non Deterministic Fractals The way to model Nature is capturing the self similarity with stochastic processes Brownian Motion Brownian motion (Bm) Particles of pollen in water watched under microscope The key for these models are noise functions Noise is (usually) self similar moving because of random hits of molecules of water This is also called the random walk 8
9 Brownian Motion 1D Bm simulation: Random hits have Gaussian random number distribution e x 2 1 ( ) 2 f ( x) 2 2 So we need them... the rand() function generates 0,1,,A (A=2 15 1) suppose we have n of such numbers d i the Gaussian random number W n 1 12 is: W d A n i1 i 3 n Brownian Motion 1D Bm simulation (contd.): let s have func. W( that kicks a point in the y direction it has Gaussian random numbers distribution it is called the white noise the Bm (Brownian function) X( is then simply said, we accumulate the perturbations W( X( X ( W ( s) t s Brownian Motion 1D Bm simulation (contd.): The fractal dimension of this curve is D=1.5 Bm scaling if we scale the Bm in the axis x by coefficient r we have to scale in the y axis by r H, where H is so called Hurst exponent then the fractal dimension of the curve is D=2 H this curve is called Fractional Brownian Motion or fbm H is 0<H<1 so the D is <1,2> (this is NOT Fractal Brownian Motion) Fractional Brownian Motion (fbm) fbm H=0.5 > fbm has D=1.5 i.e., it is Bm H>0.5 > fbm has 1<D<1.5 H<0.5 > fbm has 1.5<D<2 higher D means wilder the curve is autocorrelated H=0.5 autocorrelation is 0 H<0.5 autocorrelation is positive H>0.5 autocorrelation is negative 9
10 Fractional Brownian Motion (fbm) Linear Non Deterministic Fractals In order to generate nice fractals, we need fbm The above described function is good But does not provide adaptive results The Midpoint Displacement Algorithm the MDP is the key algorithm for fractals 1) Take a line segment 2) Find its midpoint (center) 3) Move it randomly in the y direction 4) Apply this step to all lines recursively The Midpoint Displacement Algorithm The random numbers distribution has its and. Scale down the by two in every iteration. (the second level of recursion has /2, the third has /4, the fourth has /8, etc.) Divide the Gaussian random numbers by two (if we divide in each step by 2 H, H is the Hurst exponent we will get fbm with dimension D=2 H) 10
11 The Midpoint Displacement Algorithm Properties very easy to implement it is interpolation of two points, so it is also called the Fractal interpolation just division by two and random numbers call quite realistic The Midpoint Displacement Algorithm Two dimensional fbm works with 2D arrays it is called fbm surface dimension is D=3 H, where 0<H<1 so the D is <2,3> D=2.5 D=2.8 The Midpoint Displacement Algorithm 2D fbm on quadrilaterals (diamond square) having four points P 0,P 1,P 2,P 3 1) Evaluate the midpoint 2) Evaluate points on the edges 3) Evaluate points in the middle 4) Ad 2) etc... The Midpoint Displacement Algorithm 2D fbm on quadrilaterals (diamond square) 11
12 Random Faults Another method for generating fbm 1. take an object 2. divide it into two parts 3. increase the elevation of one and decrease the other one (change color, etc.) 4. apply this step many times 5. in each decrease the intensity of changes 2x 6. the limit of this process is fbm Random Faults Random Faults Implementation Data: 2D array Algorithm: Do this many times: 1) Generate random line (get two random points) 2) For each point in the 2D array I. Check if it is on the left or right (dot produc II. Increase/decrease the value Random Faults Variations Use any 2D object (circle, square) Randomly alter the area inside/outside 12
13 Random Faults on a Sphere 1) Take sphere and divide it randomly into two hemispheres assign to each hemisphere different color 2) Apply the step 1 recursively, but decrease the intensity in each step with 1/2 H Random Faults on a Sphere Diffusion Limited Aggregation DLA 1) Particles (molecules) are floating in the water 2) When a particle approaches an condensation center it is aggregated 3) The process is repeated for many particles Diffusion Limited Aggregation DLA The important part is the way the particles travel i.e., random walk Corals, lightings, frozen ice on a window, etc. 13
14 Diffusion Limited Aggregation DLA Diffusion Limited Aggregation DLA 3D object representation 3D object representation Volume representation Boundary representation Voxels Wire frame Oct tree Surfaces CSG Polygonal Free form Bézier surfaces NURBS Procedural Fractals Particle systems Grammars L systems Lindenmayer's systems Lindenmayer s system or D0L systems [d zero l system] (parallel string rewriting systems) L-system is an ordered triple : L=<V,P,w>, where: V is a finite non-empty set called an alphabet P is a finite set of production rules in the form A->a, where A V and a V* * denotes reflexive transitive closure w V is so called axiom (starting symbol) Aristid Lindenmayer ( ) Implicit surfaces 14
15 L systems Example: F >F+F F+F +, ~ 60 o generates: F >F+F F+F=> => F+F F+F + F+F F+F F+F F+F + F+F F+F => etc. Interpretation makes the Koch s snowflake L systems can generate linear deterministic fractals Peano curve, Sierpinsky gasket, etc. L systems Example: L= < {F,[,],+, }, {F >F[+F]F, [ >[, ] >], + > +, > }, F > products: F > >F[+F]F=> F[+F]F [+ F[+F] F ] F[+F] F=> =>etc //the alphabet //rewriting rules //axiom L systems string is interpreted by the turtle graphics turtle is an abstract geometrical automaton having its state (position and orientation) able to interpret commands symbol from the alphabet has assigned a command usually F go forward + turn right turn left [ save state onto stack ] pop state from the stack bracketed L systems (Prusinkiewicz) L systems the first string from the example is interpreted: F [ + F ] F 15
16 L systems Bracketed rules are useful for generating branching structures F >F[+F][ F]F F >F[[+F] F]F 1L(R)L systems Context sensitive Lindenmayer's systems D0L systems deterministic, zero context can be easily extended by random numbers 1LL systems include context sensitive rewriting 1LL systems one element from the left side is 1L(R)L systems Example P: A<B > A w: ABBBB ABBBB > AABBB > AAABB > AAAAB > AAAAA It simulates propagation of a signal from the root! 1RL systems propagation from leaves down 1L1RL systems both directions pl systems Parametric Lindenmayer's systems pl systems every symbol has parameter Example: F(x) > F(x)[+F(x/2)][ F(x/2)] x is the length of the step F(8) > F(8)[+F(4)][ F(4)] => F(8)[ +F(4)(+F(2)][ F(2))(F(2) ][ F(4)(+F(2)][ F(2))(F(2) ] => the lateral branches are getting smaller 16
17 pl systems Parametric Lindenmayer's systems (contd.) pl systems conditional rule rewriting F(x) (x<=1) > e F(x) (x<=10) > F(x 1) F(5) > F(4) > F(3) > F(2) > F(1) > e shortening the branch pl systems Example: P: A(x) x==0 > FA(x+1) A(x) x==3 > B A(x) x==1 > [ L]FA(x+1) A(x) x==2 > [+L]FA(x+1) w: A(0) A(0) >FA(1)=>F[ L]FA(2)=>F[ L]F[+L]FA(3)=>F[ L]F[+L]FB F ~ stem L ~ leaf B ~ blossom A ~ bud pl systems Open L systems Open L systems Can interact with surrounding environment?e(x 1, x 2, ) query modules set exogenous parameters x can be for example distance from the obstacle A(0)-> FA(1)-> F[-L]FA(2)->F[-L]F[+L]FA(3)->F[-L]F[+L]FB 17
18 Open L systems Example Open L systems P: A>?E(x) x<2 > F(x,y+1)A A>?E(x) x>=2 > e w: F(0,0)A?E(0) F(0,0)A?E(0) > F(0,0)F(0,1)A?E(1) => F(0,0)F(0,1)F(0,2)A?E(2) => F(0,0)F(0,1)F(0,2)?E(3) Particle Systems Introduced by Reeves and Blau in 1983 used in the Star Trek movie for explosion of a planet Particle Systems Particle systems principle Init phase: (a particle has initial speed, color, etc.) The initial values are generated randomly, by user, etc. Loop phase: 1) generate new particles 2) assign velocity, color, lifetime etc. 3) eliminate every particle which should die 4) compute position and color of existing particles 5) display the system 18
19 Particle Systems Particles can interact with environment Particle Systems Particles can interact with each other Particle Systems Particles can be displayed in many ways, the way they move can depend on many things the way they are generated can vary etc. It is extremely versatile modeling tool Newtonian particle systems Applying Newtonian physics to particles Particle is represented by its position x(, velocity v(, and mass m x( y( v( We want to know the change in time i.e., d dt y( d dt x( v( F( v( m 19
20 Newtonian particle systems We must solve ordinary differential equation. A simple way is to use the Euler's method x( t x( tv( F( v( t v( t m Newtonian particle systems Typical forces applied to particles: Gravity F = m g m particle mass, g constant 9.82 Viscosity F = v c v particle velocity, c constant Wind F = F wind F wind wind vector can vary in time F wind (v) Newtonian particle systems Newtonian particle systems Collision detection Particle moves with velocity v to the surface with normal vector n v n New velocity vector: divide velocity to the tangent and normal component v = v t + v n v n =(v*n) n v t = v v n then we change direction of the normal component, v so the new velocity vector is v = v t v n n surface surface 20
21 Newtonian particle systems When is a collision detected? When particle crosses the surface We need a point to surface detection algorithm also condition n * v < 0 must be satisfied (i.e., particle travels to the surface) Newtonian particle systems Putting it all together: Particle: x[3] (position), v[3] (velocity), m (mass), f[3](force accumulator) 1. Initialize particles (set boundary condition for the equation) 2. In every frame do: a. Detect collisions and recalculate the velocity vector b. Clear force accumulators for every particle c. Accumulate the forces d. Solve differential equation (from the forces, velocity, mass, and position evaluate new velocity and position) e. Display particles Summary When and why procedural methods are used? Code instead of data Dimensions and fractals mathematical monsters random linear fractals Bm and fbm the midpoint displacement random faults DLA grammars particles 21
CGT 581 G Procedural Methods Fractals
 CGT 581 G Procedural Methods Fractals Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Procedural Techniques Model is generated by a piece of code. Model is not represented
CGT 581 G Procedural Methods Fractals Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Procedural Techniques Model is generated by a piece of code. Model is not represented
Fractals Week 10, Lecture 19
 CS 430/536 Computer Graphics I Fractals Week 0, Lecture 9 David Breen, William Regli and Maim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Dreel University http://gicl.cs.dreel.edu
CS 430/536 Computer Graphics I Fractals Week 0, Lecture 9 David Breen, William Regli and Maim Peysakhov Geometric and Intelligent Computing Laboratory Department of Computer Science Dreel University http://gicl.cs.dreel.edu
Fractal Geometry. LIACS Natural Computing Group Leiden University
 Fractal Geometry Contents Introduction The Fractal Geometry of Nature Self-Similarity Some Pioneering Fractals Dimension and Fractal Dimension Cellular Automata Particle Systems Scope of Fractal Geometry
Fractal Geometry Contents Introduction The Fractal Geometry of Nature Self-Similarity Some Pioneering Fractals Dimension and Fractal Dimension Cellular Automata Particle Systems Scope of Fractal Geometry
Fractals. Moreno Marzolla Dip. di Informatica Scienza e Ingegneria (DISI) Università di Bologna.
 Fractals Moreno Marzolla Dip. di Informatica Scienza e Ingegneria (DISI) Università di Bologna http://www.moreno.marzolla.name/ 2 Geometric Objects Man-made objects are geometrically simple (e.g., rectangles,
Fractals Moreno Marzolla Dip. di Informatica Scienza e Ingegneria (DISI) Università di Bologna http://www.moreno.marzolla.name/ 2 Geometric Objects Man-made objects are geometrically simple (e.g., rectangles,
Fractals and Multi-Layer Coloring Algorithms
 Fractals and Multi-Layer Coloring Algorithms Javier Barrallo and Santiago Sanchez Mathematics, Physics and Computer Science The University of the Basque Country School of Architecture. Plaza Onati, 2.
Fractals and Multi-Layer Coloring Algorithms Javier Barrallo and Santiago Sanchez Mathematics, Physics and Computer Science The University of the Basque Country School of Architecture. Plaza Onati, 2.
Fractal Geometry. Prof. Thomas Bäck Fractal Geometry 1. Natural Computing Group
 Fractal Geometry Prof. Thomas Bäck Fractal Geometry 1 Contents Introduction The Fractal Geometry of Nature - Self-Similarity - Some Pioneering Fractals - Dimension and Fractal Dimension Scope of Fractal
Fractal Geometry Prof. Thomas Bäck Fractal Geometry 1 Contents Introduction The Fractal Geometry of Nature - Self-Similarity - Some Pioneering Fractals - Dimension and Fractal Dimension Scope of Fractal
8 Special Models for Animation. Chapter 8. Special Models for Animation. Department of Computer Science and Engineering 8-1
 Special Models for Animation 8-1 L-Systems 8-2 L-Systems Branching Structures Botany Display geometric substitution turtle graphics Animating plants, animals 8-3 Plant examples http://algorithmicbotany.org/papers/#abop
Special Models for Animation 8-1 L-Systems 8-2 L-Systems Branching Structures Botany Display geometric substitution turtle graphics Animating plants, animals 8-3 Plant examples http://algorithmicbotany.org/papers/#abop
Fractals. Fractals. Beautiful designs of infinite structure and complexity Qualities of Fractals:
 Fractals Fractals Beautiful designs of infinite structure and complexity Qualities of Fractals: Fractional dimension Self similarity Complex structure at all scales Chaotic dynamical behavior Simple generation
Fractals Fractals Beautiful designs of infinite structure and complexity Qualities of Fractals: Fractional dimension Self similarity Complex structure at all scales Chaotic dynamical behavior Simple generation
Session 27: Fractals - Handout
 Session 27: Fractals - Handout Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. Benoit Mandelbrot (1924-2010)
Session 27: Fractals - Handout Clouds are not spheres, mountains are not cones, coastlines are not circles, and bark is not smooth, nor does lightning travel in a straight line. Benoit Mandelbrot (1924-2010)
Fractals & Iterative Function Systems
 CS 543: Computer Graphics Fractals & Iterative Function Systems Robert W. Lindeman Associate Professor Department of Computer Science Worcester Polytechnic Institute gogo@wpi.edu (with lots of help from
CS 543: Computer Graphics Fractals & Iterative Function Systems Robert W. Lindeman Associate Professor Department of Computer Science Worcester Polytechnic Institute gogo@wpi.edu (with lots of help from
 FRACTALS The term fractal was coined by mathematician Benoit Mandelbrot A fractal object, unlike a circle or any regular object, has complexity at all scales Natural Fractal Objects Natural fractals
FRACTALS The term fractal was coined by mathematician Benoit Mandelbrot A fractal object, unlike a circle or any regular object, has complexity at all scales Natural Fractal Objects Natural fractals
CS 4300 Computer Graphics. Prof. Harriet Fell Fall 2012 Lecture 28 November 8, 2012
 CS 4300 Computer Graphics Prof. Harriet Fell Fall 2012 Lecture 28 November 8, 2012 1 Today s Topics Fractals Mandelbrot Set Julia Sets L-Systems 2 Fractals The term fractal was coined in 1975 by Benoît
CS 4300 Computer Graphics Prof. Harriet Fell Fall 2012 Lecture 28 November 8, 2012 1 Today s Topics Fractals Mandelbrot Set Julia Sets L-Systems 2 Fractals The term fractal was coined in 1975 by Benoît
Mathematics 350 Section 6.3 Introduction to Fractals
 Mathematics 350 Section 6.3 Introduction to Fractals A fractal is generally "a rough or fragmented geometric shape that is self-similar, which means it can be split into parts, each of which is (at least
Mathematics 350 Section 6.3 Introduction to Fractals A fractal is generally "a rough or fragmented geometric shape that is self-similar, which means it can be split into parts, each of which is (at least
CSE 167: Introduction to Computer Graphics Lecture #16: Procedural Modeling
 CSE 167: Introduction to Computer Graphics Lecture #16: Procedural Modeling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013 Announcements Reduced office hours today and tomorrow
CSE 167: Introduction to Computer Graphics Lecture #16: Procedural Modeling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2013 Announcements Reduced office hours today and tomorrow
12.2 Plants. CS Dept, UK
 1 12.2 Plants - modeling and animation of plants represents an interesting and challenging area - exhibit arbitrary complexity while possessing a constrained branching structure - grow from a single source
1 12.2 Plants - modeling and animation of plants represents an interesting and challenging area - exhibit arbitrary complexity while possessing a constrained branching structure - grow from a single source
Procedural modeling and shadow mapping. Computer Graphics CSE 167 Lecture 15
 Procedural modeling and shadow mapping Computer Graphics CSE 167 Lecture 15 CSE 167: Computer graphics Procedural modeling Height fields Fractals L systems Shape grammar Shadow mapping Based on slides
Procedural modeling and shadow mapping Computer Graphics CSE 167 Lecture 15 CSE 167: Computer graphics Procedural modeling Height fields Fractals L systems Shape grammar Shadow mapping Based on slides
Lecture 3: Some Strange Properties of Fractal Curves
 Lecture 3: Some Strange Properties of Fractal Curves I have been a stranger in a strange land. Exodus 2:22 1. Fractal Strangeness Fractals have a look and feel that is very different from ordinary curves.
Lecture 3: Some Strange Properties of Fractal Curves I have been a stranger in a strange land. Exodus 2:22 1. Fractal Strangeness Fractals have a look and feel that is very different from ordinary curves.
Midterm Project: L-systems in Practice and Theory
 Midterm Project: L-systems in Practice and Theory Joey Gonzales-Dones March 28, 2016 1 Introduction Lindenmayer systems, or L-systems, are systems for algorithmically rewriting a string of characters.
Midterm Project: L-systems in Practice and Theory Joey Gonzales-Dones March 28, 2016 1 Introduction Lindenmayer systems, or L-systems, are systems for algorithmically rewriting a string of characters.
Hei nz-ottopeitgen. Hartmut Jürgens Dietmar Sau pe. Chaos and Fractals. New Frontiers of Science
 Hei nz-ottopeitgen Hartmut Jürgens Dietmar Sau pe Chaos and Fractals New Frontiers of Science Preface Authors VU X I Foreword 1 Mitchell J. Feigenbaum Introduction: Causality Principle, Deterministic
Hei nz-ottopeitgen Hartmut Jürgens Dietmar Sau pe Chaos and Fractals New Frontiers of Science Preface Authors VU X I Foreword 1 Mitchell J. Feigenbaum Introduction: Causality Principle, Deterministic
Fractal Coding. CS 6723 Image Processing Fall 2013
 Fractal Coding CS 6723 Image Processing Fall 2013 Fractals and Image Processing The word Fractal less than 30 years by one of the history s most creative mathematician Benoit Mandelbrot Other contributors:
Fractal Coding CS 6723 Image Processing Fall 2013 Fractals and Image Processing The word Fractal less than 30 years by one of the history s most creative mathematician Benoit Mandelbrot Other contributors:
7. Stochastic Fractals
 Stochastic Fractals Christoph Traxler Fractals-Stochastic 1 Stochastic Fractals Simulation of Brownian motion Modelling of natural phenomena, like terrains, clouds, waves,... Modelling of microstructures,
Stochastic Fractals Christoph Traxler Fractals-Stochastic 1 Stochastic Fractals Simulation of Brownian motion Modelling of natural phenomena, like terrains, clouds, waves,... Modelling of microstructures,
CSE 167: Lecture #15: Procedural Modeling. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012
 CSE 167: Introduction to Computer Graphics Lecture #15: Procedural Modeling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Announcements Monday, Nov 26: Midterm review in
CSE 167: Introduction to Computer Graphics Lecture #15: Procedural Modeling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2012 Announcements Monday, Nov 26: Midterm review in
9. Three Dimensional Object Representations
 9. Three Dimensional Object Representations Methods: Polygon and Quadric surfaces: For simple Euclidean objects Spline surfaces and construction: For curved surfaces Procedural methods: Eg. Fractals, Particle
9. Three Dimensional Object Representations Methods: Polygon and Quadric surfaces: For simple Euclidean objects Spline surfaces and construction: For curved surfaces Procedural methods: Eg. Fractals, Particle
Fractals: a way to represent natural objects
 Fractals: a way to represent natural objects In spatial information systems there are two kinds of entity to model: natural earth features like terrain and coastlines; human-made objects like buildings
Fractals: a way to represent natural objects In spatial information systems there are two kinds of entity to model: natural earth features like terrain and coastlines; human-made objects like buildings
Solid models and fractals
 Solid models and fractals COM3404 Richard Everson School of Engineering, Computer Science and Mathematics University of Exeter R.M.Everson@exeter.ac.uk http://www.secamlocal.ex.ac.uk/studyres/com304 Richard
Solid models and fractals COM3404 Richard Everson School of Engineering, Computer Science and Mathematics University of Exeter R.M.Everson@exeter.ac.uk http://www.secamlocal.ex.ac.uk/studyres/com304 Richard
Chapel Hill Math Circle: Symmetry and Fractals
 Chapel Hill Math Circle: Symmetry and Fractals 10/7/17 1 Introduction This worksheet will explore symmetry. To mathematicians, a symmetry of an object is, roughly speaking, a transformation that does not
Chapel Hill Math Circle: Symmetry and Fractals 10/7/17 1 Introduction This worksheet will explore symmetry. To mathematicians, a symmetry of an object is, roughly speaking, a transformation that does not
Outline. Solid models and fractals. Constructive solid geometry. Constructive solid geometry COM3404. Richard Everson
 Outline Solid models and fractals COM School of Engineering, Computer Science and Mathematics University of Exeter Constructive solid geometry Fractals Dimension s Landscape generation L-systems R.M.Everson@exeter.ac.uk
Outline Solid models and fractals COM School of Engineering, Computer Science and Mathematics University of Exeter Constructive solid geometry Fractals Dimension s Landscape generation L-systems R.M.Everson@exeter.ac.uk
CSE 167: Lecture #17: Procedural Modeling. Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011
 CSE 167: Introduction to Computer Graphics Lecture #17: Procedural Modeling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Important dates: Final project outline
CSE 167: Introduction to Computer Graphics Lecture #17: Procedural Modeling Jürgen P. Schulze, Ph.D. University of California, San Diego Fall Quarter 2011 Announcements Important dates: Final project outline
Shape modeling Modeling technique Shape representation! 3D Graphics Modeling Techniques
 D Graphics http://chamilo2.grenet.fr/inp/courses/ensimag4mmgd6/ Shape Modeling technique Shape representation! Part : Basic techniques. Projective rendering pipeline 2. Procedural Modeling techniques Shape
D Graphics http://chamilo2.grenet.fr/inp/courses/ensimag4mmgd6/ Shape Modeling technique Shape representation! Part : Basic techniques. Projective rendering pipeline 2. Procedural Modeling techniques Shape
Fractals: Self-Similarity and Fractal Dimension Math 198, Spring 2013
 Fractals: Self-Similarity and Fractal Dimension Math 198, Spring 2013 Background Fractal geometry is one of the most important developments in mathematics in the second half of the 20th century. Fractals
Fractals: Self-Similarity and Fractal Dimension Math 198, Spring 2013 Background Fractal geometry is one of the most important developments in mathematics in the second half of the 20th century. Fractals
Fractals and L- Systems
 Fractals and L- Systems Sanyam Gupta January 26, 2018 1 Lindenmayer systems Have you ever wondered, how to formulate a mathematical equation for the plant in your verandah or garden? The nature produces
Fractals and L- Systems Sanyam Gupta January 26, 2018 1 Lindenmayer systems Have you ever wondered, how to formulate a mathematical equation for the plant in your verandah or garden? The nature produces
CGT 581 G Geometric Modeling Curves
 CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
CGT 581 G Geometric Modeling Curves Bedrich Benes, Ph.D. Purdue University Department of Computer Graphics Technology Curves What is a curve? Mathematical definition 1) The continuous image of an interval
CSC 470 Computer Graphics. Fractals
 CSC 47 Computer Graphics Fractals 1 This Week Approaches to Infinity Fractals and Self-Similarity Similarity Iterative Function Systems Lindenmayer Systems Curves Natural Images (trees, landscapes..) Introduction
CSC 47 Computer Graphics Fractals 1 This Week Approaches to Infinity Fractals and Self-Similarity Similarity Iterative Function Systems Lindenmayer Systems Curves Natural Images (trees, landscapes..) Introduction
Fun with Fractals Saturday Morning Math Group
 Fun with Fractals Saturday Morning Math Group Alistair Windsor Fractals Fractals are amazingly complicated patterns often produced by very simple processes. We will look at two different types of fractals
Fun with Fractals Saturday Morning Math Group Alistair Windsor Fractals Fractals are amazingly complicated patterns often produced by very simple processes. We will look at two different types of fractals
Interactive Computer Graphics A TOP-DOWN APPROACH WITH SHADER-BASED OPENGL
 International Edition Interactive Computer Graphics A TOP-DOWN APPROACH WITH SHADER-BASED OPENGL Sixth Edition Edward Angel Dave Shreiner Interactive Computer Graphics: A Top-Down Approach with Shader-Based
International Edition Interactive Computer Graphics A TOP-DOWN APPROACH WITH SHADER-BASED OPENGL Sixth Edition Edward Angel Dave Shreiner Interactive Computer Graphics: A Top-Down Approach with Shader-Based
Lecture 6: Fractals from Iterated Function Systems. He draweth also the mighty with his power: Job 24:22
 Lecture 6: Fractals from Iterated Function Systems He draweth also the mighty with his power: Job 24:22 1. Fractals by Iteration The Sierpinski gasket and the Koch snowflake can both be generated in LOGO
Lecture 6: Fractals from Iterated Function Systems He draweth also the mighty with his power: Job 24:22 1. Fractals by Iteration The Sierpinski gasket and the Koch snowflake can both be generated in LOGO
Constructive Solid Geometry and Procedural Modeling. Stelian Coros
 Constructive Solid Geometry and Procedural Modeling Stelian Coros Somewhat unrelated Schedule for presentations February 3 5 10 12 17 19 24 26 March 3 5 10 12 17 19 24 26 30 April 2 7 9 14 16 21 23 28
Constructive Solid Geometry and Procedural Modeling Stelian Coros Somewhat unrelated Schedule for presentations February 3 5 10 12 17 19 24 26 March 3 5 10 12 17 19 24 26 30 April 2 7 9 14 16 21 23 28
lecture 9 Object hierarchies - call trees and GL_MODELVIEW stack - fractals - L systems
 lecture 9 Object hierarchies - call trees and GL_MODELVIEW stack - fractals - L systems Last lecture: - hierarchy of bounding volumes of objects and scenes - spatial partition represented as a tree (BSP
lecture 9 Object hierarchies - call trees and GL_MODELVIEW stack - fractals - L systems Last lecture: - hierarchy of bounding volumes of objects and scenes - spatial partition represented as a tree (BSP
Discovering. Algebra. An Investigative Approach. Condensed Lessons for Make-up Work
 Discovering Algebra An Investigative Approach Condensed Lessons for Make-up Work CONDENSED L E S S O N 0. The Same yet Smaller Previous In this lesson you will apply a recursive rule to create a fractal
Discovering Algebra An Investigative Approach Condensed Lessons for Make-up Work CONDENSED L E S S O N 0. The Same yet Smaller Previous In this lesson you will apply a recursive rule to create a fractal
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a
 The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
Clouds, biological growth, and coastlines are
 L A B 11 KOCH SNOWFLAKE Fractals Clouds, biological growth, and coastlines are examples of real-life phenomena that seem too complex to be described using typical mathematical functions or relationships.
L A B 11 KOCH SNOWFLAKE Fractals Clouds, biological growth, and coastlines are examples of real-life phenomena that seem too complex to be described using typical mathematical functions or relationships.
Computer Graphics (CS 543) Lecture 2c: Fractals. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics (CS 543 Lecture c: Fractals Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI What are Fractals? Mathematical expressions to generate pretty pictures Evaluate
Computer Graphics (CS 543 Lecture c: Fractals Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI What are Fractals? Mathematical expressions to generate pretty pictures Evaluate
Exploring Fractals through Geometry and Algebra. Kelly Deckelman Ben Eggleston Laura Mckenzie Patricia Parker-Davis Deanna Voss
 Exploring Fractals through Geometry and Algebra Kelly Deckelman Ben Eggleston Laura Mckenzie Patricia Parker-Davis Deanna Voss Learning Objective and skills practiced Students will: Learn the three criteria
Exploring Fractals through Geometry and Algebra Kelly Deckelman Ben Eggleston Laura Mckenzie Patricia Parker-Davis Deanna Voss Learning Objective and skills practiced Students will: Learn the three criteria
Developmental Systems
 Developmental Systems 1 Biological systems Early development of the Drosophila fly http://flybase.bio.indiana.edu dorsal view lateral view 2 Biological systems Early development of Drosophila [Slack 2006]
Developmental Systems 1 Biological systems Early development of the Drosophila fly http://flybase.bio.indiana.edu dorsal view lateral view 2 Biological systems Early development of Drosophila [Slack 2006]
Course Review. Computer Animation and Visualisation. Taku Komura
 Course Review Computer Animation and Visualisation Taku Komura Characters include Human models Virtual characters Animal models Representation of postures The body has a hierarchical structure Many types
Course Review Computer Animation and Visualisation Taku Komura Characters include Human models Virtual characters Animal models Representation of postures The body has a hierarchical structure Many types
Fractals in Nature and Mathematics: From Simplicity to Complexity
 Fractals in Nature and Mathematics: From Simplicity to Complexity Dr. R. L. Herman, UNCW Mathematics & Physics Fractals in Nature and Mathematics R. L. Herman OLLI STEM Society, Oct 13, 2017 1/41 Outline
Fractals in Nature and Mathematics: From Simplicity to Complexity Dr. R. L. Herman, UNCW Mathematics & Physics Fractals in Nature and Mathematics R. L. Herman OLLI STEM Society, Oct 13, 2017 1/41 Outline
Journal of Applied Mathematics and Computation (JAMC), 2018, 2(1), 13-20
 Journal of Applied Mathematics and Computation (JAMC), 2018, 2(1), 13-20 http://www.hillpublisher.org/journal/jamc ISSN Online:2576-0645 ISSN Print:2576-0653 Generation of Fractal Vessel Structure Functions
Journal of Applied Mathematics and Computation (JAMC), 2018, 2(1), 13-20 http://www.hillpublisher.org/journal/jamc ISSN Online:2576-0645 ISSN Print:2576-0653 Generation of Fractal Vessel Structure Functions
Computer Graphics 4731 Lecture 5: Fractals. Prof Emmanuel Agu. Computer Science Dept. Worcester Polytechnic Institute (WPI)
 Computer Graphics 4731 Lecture 5: Fractals Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI What are Fractals? Mathematical expressions to generate pretty pictures Evaluate
Computer Graphics 4731 Lecture 5: Fractals Prof Emmanuel Agu Computer Science Dept. Worcester Polytechnic Institute (WPI What are Fractals? Mathematical expressions to generate pretty pictures Evaluate
PITSCO Math Individualized Prescriptive Lessons (IPLs)
 Orientation Integers 10-10 Orientation I 20-10 Speaking Math Define common math vocabulary. Explore the four basic operations and their solutions. Form equations and expressions. 20-20 Place Value Define
Orientation Integers 10-10 Orientation I 20-10 Speaking Math Define common math vocabulary. Explore the four basic operations and their solutions. Form equations and expressions. 20-20 Place Value Define
Fractals. Materials. Pencil Paper Grid made of triangles
 Fractals Overview: Fractals are new on the mathematics scene, however they are in your life every day. Cell phones use fractal antennas, doctors study fractal-based blood flow diagrams to search for cancerous
Fractals Overview: Fractals are new on the mathematics scene, however they are in your life every day. Cell phones use fractal antennas, doctors study fractal-based blood flow diagrams to search for cancerous
Section 9.5. Tessellations. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 9.5 Tessellations What You Will Learn Tessellations 9.5-2 Tessellations A tessellation (or tiling) is a pattern consisting of the repeated use of the same geometric figures to entirely cover a
Section 9.5 Tessellations What You Will Learn Tessellations 9.5-2 Tessellations A tessellation (or tiling) is a pattern consisting of the repeated use of the same geometric figures to entirely cover a
Topics. Recursive tree models. Procedural approach L-systems. Image-based approach. Billboarding
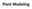 Plant Modeling Topics Recursive tree models Billboarding Procedural approach L-systems Image-based approach Tree Model The structure of a tree Trunk (linkage) Branches (linkage, child of trunk node) Leaves/Buds/flowers/fruit
Plant Modeling Topics Recursive tree models Billboarding Procedural approach L-systems Image-based approach Tree Model The structure of a tree Trunk (linkage) Branches (linkage, child of trunk node) Leaves/Buds/flowers/fruit
Parametric L-Systems and borderline fractals
 1 Parametric L-Systems and borderline fractals A preprint version of a Mathematical graphics column from Mathematica in Education and Research. Mark McClure Department of Mathematics University of North
1 Parametric L-Systems and borderline fractals A preprint version of a Mathematical graphics column from Mathematica in Education and Research. Mark McClure Department of Mathematics University of North
Some geometries to describe nature
 Some geometries to describe nature Christiane Rousseau Since ancient times, the development of mathematics has been inspired, at least in part, by the need to provide models in other sciences, and that
Some geometries to describe nature Christiane Rousseau Since ancient times, the development of mathematics has been inspired, at least in part, by the need to provide models in other sciences, and that
Rendering diffuse objects using particle systems inside voxelized surface geometry. Thorsten Juckel Steffi Beckhaus
 Rendering diffuse objects using particle systems inside voxelized surface geometry Thorsten Juckel Steffi Beckhaus University of Hamburg interactive media / virtual environments 1 Outline 1. Introduction
Rendering diffuse objects using particle systems inside voxelized surface geometry Thorsten Juckel Steffi Beckhaus University of Hamburg interactive media / virtual environments 1 Outline 1. Introduction
Lecture 6: Fractals from Iterated Function Systems. He draweth also the mighty with his power: Job 24:22
 Lecture 6: Fractals from Iterated Function Systems He draweth also the mighty with his power: Job 24:22 1. Generating Fractals by Iterating Transformations The Sierpinski gasket and the Koch snowflake
Lecture 6: Fractals from Iterated Function Systems He draweth also the mighty with his power: Job 24:22 1. Generating Fractals by Iterating Transformations The Sierpinski gasket and the Koch snowflake
Exploring the Effect of Direction on Vector-Based Fractals
 BRIDGES Mathematical Connections in Art, Music, and Science Exploring the Effect of Direction on Vector-Based Fractals Magdy Ibrahim and Robert J. Krawczyk College of Architecture Dlinois Institute of
BRIDGES Mathematical Connections in Art, Music, and Science Exploring the Effect of Direction on Vector-Based Fractals Magdy Ibrahim and Robert J. Krawczyk College of Architecture Dlinois Institute of
Scientific Calculation and Visualization
 Scientific Calculation and Visualization Topic Iteration Method for Fractal 2 Classical Electrodynamics Contents A First Look at Quantum Physics. Fractals.2 History of Fractal.3 Iteration Method for Fractal.4
Scientific Calculation and Visualization Topic Iteration Method for Fractal 2 Classical Electrodynamics Contents A First Look at Quantum Physics. Fractals.2 History of Fractal.3 Iteration Method for Fractal.4
Mathematics. Year 7. Autumn Term
 Mathematics Year 7 Autumn Term Decimals o Use place value with decimals o Add and subtract, multiply and divide decimal numbers Basic Arithmetic o Multiply by a two or three digit number o Divide by a
Mathematics Year 7 Autumn Term Decimals o Use place value with decimals o Add and subtract, multiply and divide decimal numbers Basic Arithmetic o Multiply by a two or three digit number o Divide by a
Birkdale High School - Higher Scheme of Work
 Birkdale High School - Higher Scheme of Work Module 1 - Integers and Decimals Understand and order integers (assumed) Use brackets and hierarchy of operations (BODMAS) Add, subtract, multiply and divide
Birkdale High School - Higher Scheme of Work Module 1 - Integers and Decimals Understand and order integers (assumed) Use brackets and hierarchy of operations (BODMAS) Add, subtract, multiply and divide
Constrained Diffusion Limited Aggregation in 3 Dimensions
 Constrained Diffusion Limited Aggregation in 3 Dimensions Paul Bourke Swinburne University of Technology P. O. Box 218, Hawthorn Melbourne, Vic 3122, Australia. Email: pdb@swin.edu.au Abstract Diffusion
Constrained Diffusion Limited Aggregation in 3 Dimensions Paul Bourke Swinburne University of Technology P. O. Box 218, Hawthorn Melbourne, Vic 3122, Australia. Email: pdb@swin.edu.au Abstract Diffusion
Fractals and the Chaos Game
 Math: Outside the box! Fractals and the Chaos Game Monday February 23, 2009 3:30-4:20 IRMACS theatre, ASB 10900 Randall Pyke Senior Lecturer Department of Mathematics, SFU A Game. Is this a random walk?
Math: Outside the box! Fractals and the Chaos Game Monday February 23, 2009 3:30-4:20 IRMACS theatre, ASB 10900 Randall Pyke Senior Lecturer Department of Mathematics, SFU A Game. Is this a random walk?
CHAPTER 1 Graphics Systems and Models 3
 ?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
?????? 1 CHAPTER 1 Graphics Systems and Models 3 1.1 Applications of Computer Graphics 4 1.1.1 Display of Information............. 4 1.1.2 Design.................... 5 1.1.3 Simulation and Animation...........
More modelling. Ruth Aylett
 More modelling Ruth Aylett Overview The great outdoors: fractals L-systems City Models Procedural generation of models How to make models.. Interactive modeling Human with a software modeling tool Scanning
More modelling Ruth Aylett Overview The great outdoors: fractals L-systems City Models Procedural generation of models How to make models.. Interactive modeling Human with a software modeling tool Scanning
In this lesson, students build fractals and track the growth of fractal measurements using tables and equations. Enduring Understanding
 LessonTitle: Fractal Functions Alg 5.8 Utah State Core Standard and Indicators Algebra Standards 2, 4 Process Standards 1-5 Summary In this lesson, students build fractals and track the growth of fractal
LessonTitle: Fractal Functions Alg 5.8 Utah State Core Standard and Indicators Algebra Standards 2, 4 Process Standards 1-5 Summary In this lesson, students build fractals and track the growth of fractal
DLA Simulations. Jasraj Singh Kohli Gregory Raustad Peter Del Rosso
 DLA Simulations Jasraj Singh Kohli Gregory Raustad Peter Del Rosso Aim To Use Monte-Carlo Method (Random Walkers)/DLA to simulate growth pattern of an air bubble expanding in a Newtonian fluid. To understand
DLA Simulations Jasraj Singh Kohli Gregory Raustad Peter Del Rosso Aim To Use Monte-Carlo Method (Random Walkers)/DLA to simulate growth pattern of an air bubble expanding in a Newtonian fluid. To understand
Making Plant-Like Fractals on GSP by Mike M c Garry
 Making Plant-Like Fractals on GSP by Mike M c Garry athenianmike@yahoo.com Important Idea #1: Control Points When you make a new line segment, circle, etc. on GSP, the points that determine it when it
Making Plant-Like Fractals on GSP by Mike M c Garry athenianmike@yahoo.com Important Idea #1: Control Points When you make a new line segment, circle, etc. on GSP, the points that determine it when it
Interactive Math Glossary Terms and Definitions
 Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Grade 9 Math Terminology
 Unit 1 Basic Skills Review BEDMAS a way of remembering order of operations: Brackets, Exponents, Division, Multiplication, Addition, Subtraction Collect like terms gather all like terms and simplify as
Unit 1 Basic Skills Review BEDMAS a way of remembering order of operations: Brackets, Exponents, Division, Multiplication, Addition, Subtraction Collect like terms gather all like terms and simplify as
A simple problem that has a solution that is far deeper than expected!
 The Water, Gas, Electricity Problem A simple problem that has a solution that is far deeper than expected! Consider the diagram below of three houses and three utilities: water, gas, and electricity. Each
The Water, Gas, Electricity Problem A simple problem that has a solution that is far deeper than expected! Consider the diagram below of three houses and three utilities: water, gas, and electricity. Each
Introduction to Applied and Pre-calculus Mathematics (2008) Correlation Chart - Grade 10 Introduction to Applied and Pre-Calculus Mathematics 2009
 Use words and algebraic expressions to describe the data and interrelationships in a table with rows/columns that are not related recursively (not calculated from previous data) (Applied A-1) Use words
Use words and algebraic expressions to describe the data and interrelationships in a table with rows/columns that are not related recursively (not calculated from previous data) (Applied A-1) Use words
Curve and Surface Basics
 Curve and Surface Basics Implicit and parametric forms Power basis form Bezier curves Rational Bezier Curves Tensor Product Surfaces ME525x NURBS Curve and Surface Modeling Page 1 Implicit and Parametric
Curve and Surface Basics Implicit and parametric forms Power basis form Bezier curves Rational Bezier Curves Tensor Product Surfaces ME525x NURBS Curve and Surface Modeling Page 1 Implicit and Parametric
First of all, we need to know what it means for a parameterize curve to be differentiable. FACT:
 CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
Textures III. Week 10, Wed Mar 24
 University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Textures III Week 10, Wed Mar 24 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 News signup sheet for P3 grading Mon/today/Fri
University of British Columbia CPSC 314 Computer Graphics Jan-Apr 2010 Tamara Munzner Textures III Week 10, Wed Mar 24 http://www.ugrad.cs.ubc.ca/~cs314/vjan2010 News signup sheet for P3 grading Mon/today/Fri
CS 543: Computer Graphics Lecture 3 (Part I): Fractals. Emmanuel Agu
 CS 543: Computer Graphics Lecture 3 (Part I: Fractals Emmanuel Agu What are Fractals? Mathematical expressions Approach infinity in organized way Utilizes recursion on computers Popularized by Benoit Mandelbrot
CS 543: Computer Graphics Lecture 3 (Part I: Fractals Emmanuel Agu What are Fractals? Mathematical expressions Approach infinity in organized way Utilizes recursion on computers Popularized by Benoit Mandelbrot
2.) From the set {A, B, C, D, E, F, G, H}, produce all of the four character combinations. Be sure that they are in lexicographic order.
 Discrete Mathematics 2 - Test File - Spring 2013 Exam #1 1.) RSA - Suppose we choose p = 5 and q = 11. You're going to be sending the coded message M = 23. a.) Choose a value for e, satisfying the requirements
Discrete Mathematics 2 - Test File - Spring 2013 Exam #1 1.) RSA - Suppose we choose p = 5 and q = 11. You're going to be sending the coded message M = 23. a.) Choose a value for e, satisfying the requirements
Number Sense and Operations Curriculum Framework Learning Standard
 Grade 5 Expectations in Mathematics Learning Standards from the MA Mathematics Curriculum Framework for the end of Grade 6 are numbered and printed in bold. The Franklin Public School System s grade level
Grade 5 Expectations in Mathematics Learning Standards from the MA Mathematics Curriculum Framework for the end of Grade 6 are numbered and printed in bold. The Franklin Public School System s grade level
Applications. 44 Stretching and Shrinking
 Applications 1. Look for rep-tile patterns in the designs below. For each design, tell whether the small quadrilaterals are similar to the large quadrilateral. Explain. If the quadrilaterals are similar,
Applications 1. Look for rep-tile patterns in the designs below. For each design, tell whether the small quadrilaterals are similar to the large quadrilateral. Explain. If the quadrilaterals are similar,
Particle Systems. Lecture 8 Taku Komura
 Particle Systems Computer Animation and Visualisation Lecture 8 Taku Komura Overview Particle System Modelling fuzzy objects (fire, smoke) Modelling liquid Modelling cloth Integration : implicit integration,
Particle Systems Computer Animation and Visualisation Lecture 8 Taku Komura Overview Particle System Modelling fuzzy objects (fire, smoke) Modelling liquid Modelling cloth Integration : implicit integration,
Modeling. Michael Kazhdan ( /657) HB FvDFH Modeling Seashells, Fowler et al. 1992
 Modeling Michael Kazhdan (601.457/657) HB 10.18 10.19 FvDFH 20.2 20.4 Modeling Seashells, Fowler et al. 1992 Modeling How do we... Represent 3D objects in a computer? Construct such representations quickly
Modeling Michael Kazhdan (601.457/657) HB 10.18 10.19 FvDFH 20.2 20.4 Modeling Seashells, Fowler et al. 1992 Modeling How do we... Represent 3D objects in a computer? Construct such representations quickly
GTPS Curriculum Mathematics Grade 8
 4.2.8.B2 Use iterative procedures to generate geometric patterns: Fractals (e.g., the Koch Snowflake); Self-similarity; Construction of initial stages; Patterns in successive stages (e.g., number of triangles
4.2.8.B2 Use iterative procedures to generate geometric patterns: Fractals (e.g., the Koch Snowflake); Self-similarity; Construction of initial stages; Patterns in successive stages (e.g., number of triangles
Generation of 3D Fractal Images for Mandelbrot and Julia Sets
 178 Generation of 3D Fractal Images for Mandelbrot and Julia Sets Bulusu Rama #, Jibitesh Mishra * # Department of Computer Science and Engineering, MLR Institute of Technology Hyderabad, India 1 rama_bulusu@yahoo.com
178 Generation of 3D Fractal Images for Mandelbrot and Julia Sets Bulusu Rama #, Jibitesh Mishra * # Department of Computer Science and Engineering, MLR Institute of Technology Hyderabad, India 1 rama_bulusu@yahoo.com
Chapter 12: Fractal Geometry The Koch Snowflake and Self-Similarity
 Chapter 12: Fractal Geometry 12.1 The Koch Snowflake and Self-Similarity Geometric Fractal Our first example of a geometric fractal is a shape known as the Koch snowflake, named after the Swedish mathematician
Chapter 12: Fractal Geometry 12.1 The Koch Snowflake and Self-Similarity Geometric Fractal Our first example of a geometric fractal is a shape known as the Koch snowflake, named after the Swedish mathematician
Solving inequalities Expanding brackets and simplifying the result Graphing quadratic functions in simple cases Interpreting real-life graphs, e.g.
 Grade C Descriptors Estimation and division by a number less than 1 Calculating compound interest - no rounding necessary Using a calculator in complex situations Multiplication and division by a number
Grade C Descriptors Estimation and division by a number less than 1 Calculating compound interest - no rounding necessary Using a calculator in complex situations Multiplication and division by a number
Turtle Graphics and L-systems Informatics 1 Functional Programming: Tutorial 7
 Turtle Graphics and L-systems Informatics 1 Functional Programming: Tutorial 7 Heijltjes, Wadler Due: The tutorial of week 9 (20/21 Nov.) Reading assignment: Chapters 15 17 (pp. 280 382) Please attempt
Turtle Graphics and L-systems Informatics 1 Functional Programming: Tutorial 7 Heijltjes, Wadler Due: The tutorial of week 9 (20/21 Nov.) Reading assignment: Chapters 15 17 (pp. 280 382) Please attempt
o Represent 3D objects in a computer? o Manipulate 3D objects with a computer? o CAD programs o Subdivision surface editors :)
 Modeling How do we... o Represent 3D objects in a computer? Procedural Modeling Adam Finkelstein Princeton University COS 426, Spring 2003 o Construct such representations quickly and/or automatically
Modeling How do we... o Represent 3D objects in a computer? Procedural Modeling Adam Finkelstein Princeton University COS 426, Spring 2003 o Construct such representations quickly and/or automatically
WHOLE NUMBER AND DECIMAL OPERATIONS
 WHOLE NUMBER AND DECIMAL OPERATIONS Whole Number Place Value : 5,854,902 = Ten thousands thousands millions Hundred thousands Ten thousands Adding & Subtracting Decimals : Line up the decimals vertically.
WHOLE NUMBER AND DECIMAL OPERATIONS Whole Number Place Value : 5,854,902 = Ten thousands thousands millions Hundred thousands Ten thousands Adding & Subtracting Decimals : Line up the decimals vertically.
Design considerations
 Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Curves Design considerations local control of shape design each segment independently smoothness and continuity ability to evaluate derivatives stability small change in input leads to small change in
Scope and Sequence for the New Jersey Core Curriculum Content Standards
 Scope and Sequence for the New Jersey Core Curriculum Content Standards The following chart provides an overview of where within Prentice Hall Course 3 Mathematics each of the Cumulative Progress Indicators
Scope and Sequence for the New Jersey Core Curriculum Content Standards The following chart provides an overview of where within Prentice Hall Course 3 Mathematics each of the Cumulative Progress Indicators
Fixed Point Iterative Techniques An Application to Fractals
 Fixed Point Iterative Techniques An Application to Fractals Narayan Partap 1 and Prof. Renu Chugh 2 1 Amity Institute of Applied Sciences, Amity University, Noida, India 2 Department of Mathematics, M.D.
Fixed Point Iterative Techniques An Application to Fractals Narayan Partap 1 and Prof. Renu Chugh 2 1 Amity Institute of Applied Sciences, Amity University, Noida, India 2 Department of Mathematics, M.D.
Hopalong Fractals. Linear complex. Quadratic complex
 Hopalong Fractals Hopalong fractals are created by iterating a more or less simple formula in x and y over and over again. In general three types of behaviour can be distinguished. Often the series will
Hopalong Fractals Hopalong fractals are created by iterating a more or less simple formula in x and y over and over again. In general three types of behaviour can be distinguished. Often the series will
Shape Representation Basic problem We make pictures of things How do we describe those things? Many of those things are shapes Other things include
 Shape Representation Basic problem We make pictures of things How do we describe those things? Many of those things are shapes Other things include motion, behavior Graphics is a form of simulation and
Shape Representation Basic problem We make pictures of things How do we describe those things? Many of those things are shapes Other things include motion, behavior Graphics is a form of simulation and
Chapter 14 Particle Systems & Interactions
 Chapter 14 Particle Systems & Interactions This is probably the nicest and most flexible of the Blender effects. When you turn an object into particles, it can be used to simulate snow, fire, smoke, clouds,
Chapter 14 Particle Systems & Interactions This is probably the nicest and most flexible of the Blender effects. When you turn an object into particles, it can be used to simulate snow, fire, smoke, clouds,
Homework #2. Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves
 Computer Graphics Instructor: Brian Curless CSEP 557 Autumn 2016 Homework #2 Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves Assigned: Wednesday, Nov 16 th Due: Wednesday, Nov 30
Computer Graphics Instructor: Brian Curless CSEP 557 Autumn 2016 Homework #2 Shading, Projections, Texture Mapping, Ray Tracing, and Bezier Curves Assigned: Wednesday, Nov 16 th Due: Wednesday, Nov 30
CMP Book: Investigation Number Objective: PASS: 1.1 Describe data distributions and display in line and bar graphs
 Data About Us (6th Grade) (Statistics) 1.1 Describe data distributions and display in line and bar graphs. 6.5.1 1.2, 1.3, 1.4 Analyze data using range, mode, and median. 6.5.3 Display data in tables,
Data About Us (6th Grade) (Statistics) 1.1 Describe data distributions and display in line and bar graphs. 6.5.1 1.2, 1.3, 1.4 Analyze data using range, mode, and median. 6.5.3 Display data in tables,
Does it Look Square? Hexagonal Bipyramids, Triangular Antiprismoids, and their Fractals
 Does it Look Square? Hexagonal Bipyramids, Triangular Antiprismoids, and their Fractals Hideki Tsuiki Graduate School of Human and Environmental Studies Kyoto University Yoshida-Nihonmatsu, Kyoto 606-8501,
Does it Look Square? Hexagonal Bipyramids, Triangular Antiprismoids, and their Fractals Hideki Tsuiki Graduate School of Human and Environmental Studies Kyoto University Yoshida-Nihonmatsu, Kyoto 606-8501,
Fractal Dimension and the Cantor Set
 Fractal Dimension and the Cantor Set Shailesh A Shirali Shailesh Shirali is Director of Sahyadri School (KFI), Pune, and also Head of the Community Mathematics Centre in Rishi Valley School (AP). He has
Fractal Dimension and the Cantor Set Shailesh A Shirali Shailesh Shirali is Director of Sahyadri School (KFI), Pune, and also Head of the Community Mathematics Centre in Rishi Valley School (AP). He has
1/16. Emergence in Artificial Life. Sebastian Marius Kirsch Back Close
 1/16 Emergence in Artificial Life Sebastian Marius Kirsch skirsch@moebius.inka.de 2/16 Artificial Life not life as it is, but life as it could be very recent field of science first a-life conference in
1/16 Emergence in Artificial Life Sebastian Marius Kirsch skirsch@moebius.inka.de 2/16 Artificial Life not life as it is, but life as it could be very recent field of science first a-life conference in
Central Valley School District Math Curriculum Map Grade 8. August - September
 August - September Decimals Add, subtract, multiply and/or divide decimals without a calculator (straight computation or word problems) Convert between fractions and decimals ( terminating or repeating
August - September Decimals Add, subtract, multiply and/or divide decimals without a calculator (straight computation or word problems) Convert between fractions and decimals ( terminating or repeating
1 Transforming Geometric Objects
 1 Transforming Geometric Objects RIGID MOTION TRANSFORMA- TIONS Rigid Motions Transformations 1 Translating Plane Figures Reflecting Plane Figures Rotating Plane Figures Students will select translations
1 Transforming Geometric Objects RIGID MOTION TRANSFORMA- TIONS Rigid Motions Transformations 1 Translating Plane Figures Reflecting Plane Figures Rotating Plane Figures Students will select translations
