3 Global Properties of Networks
|
|
|
- Jeffry Richard
- 5 years ago
- Views:
Transcription
1 3 Global Properties of Networks Ralf Steuer a and Gorka Zamora-López b a Humboldt University Berlin, Institute for Theoretical Biology, Invalidenstr. 43, Berlin, Germany. b University of Potsdam, Institute for Physics, Nonlinear Dynamics Group, Am Neuen Palais 10, Potsdam, Germany. 3.1 INTRODUCTION Complex dynamical systems are often characterized by a large number of nonlinearly interacting elements, giving rise to emergent properties that transcend the principle of linear superposition. In particular within the biological sciences, one of the primary challenges is to investigate how the collective behavior of cells, tissues or organisms can be understood in terms of the properties of their molecular constituents. To investigate this intricate connectivity of cellular systems, the analysis of complex networks has become an important part of molecular biology. A large number of biological phenomena and processes can be translated into the abstract concept of a complex network, making biological problems mathematically tractable. Prominent examples include the representation of transcriptional regulation as a network, where vertices represent genes or proteins and edges represent regulatory interactions, as well as cellular metabolism, where vertices represent metabolites and edges represent biochemical interconversions. However, beyond these rather straightforward examples, more abstract processes can sometimes also be translated into the language of complex networks. For example, different configurational states of a protein may be represented as vertices, with edges indicating transitions between them. Once a biological process or phenomenon is represented by a network, the tools of complex network theory allow for a systematic characterization of its structural properties. The analysis of network topology then seeks to uncover the functional organization, the underlying design principles and unknown organizing principles of cellular systems. Indeed, as realized only rather recently, many empirically derived complex networks, ranging from technological and sociological to biological examples, share common topological features. The organizing principles of empirical networks often reflect crucial system properties, such as robustness, redundancy or other functional interdependencies between network elements. A quantitative analysis of the large-scale characteristics of complex networks thus contributes to a i
2 ii metabolite metabolite Fig. 3.1 The substrate graph G S of the S. cerevisiae metabolic network [23], consisting of N V = 810 vertices (metabolites) and N E = 3419 edges. Directional information is omitted. Left: A visualization of the substrate graph using the freely available software package Pajek [9]. Right: A visualization of the adjacency matrix, with vertices (metabolites) ranked according to their degree. Each dot indicates whether the corresponding vertices (metabolites) are connected by an edge. The figures are adapted from [61]. better understanding of the organization of cellular functions and has already made significant impact on our current view of molecular biology. While not aiming at a comprehensive review, this chapter seeks to summarize and describe several basic measures and characteristics of network topology. The chapter is organized as follows: The main emphasis is placed on an overview of basic measures and indices that characterize the topology of networks, given within Section 3.2. In Section 3.3, several basic prototype models of complex networks are discussed. The subsequent Section 3.4 is devoted to a brief outline of global features of complex networks, such as hierarchies, modularity, attack tolerance and robustness. Finally, Section 3.5 provides notes on the statistical testing of network properties and describes several known pitfalls and possible misinterpretations in the statistical analysis of network properties. The working example throughout this chapter is a reconstructed version of the S. cerevisiae metabolic network [23], consisting of 810 metabolites and 843 reactions. The original bipartite graph was collapsed, such that two metabolites are connected if they participate in a common reaction. A graphical representation is shown in Fig GLOBAL PROPERTIES OF COMPLEX NETWORKS Following the nomenclature of Chapter 2, a network is formally represented by a graph G = (V, E), consisting of a set V of N V vertices and a set E of N E edges. We distinguish between undirected graphs, whose vertices are connected by edges without any directional information and directed graphs (digraphs), whose
3 GLOBAL PROPERTIES OF COMPLEX NETWORKS iii Fig. 3.2 Representations of complex networks. a) A directed network, consisting of N V = 7 vertices and N E = 13 directed edges. b) The adjacency matrix A of the network. c) The set of adjacency lists, specifying to which other vertices each vertex connects. d) The distance matrix D with elements d ij. Note that the distances are not symmetric and may be infinite, indicating that not all vertices can be reached from all other vertices. e) The input degree ki in and output degree ki out of each vertex. edges posses directional information. Additionally, in weighted graphs, each edge (directed or undirected) is associated with a scalar value, quantifying a possible interaction strength, a cost, or a flow on the respective edge. In most cases, a network is represented by its adjacency matrix A, with entries A ij = 1 indicating that there exists an edge between vertex n i and n j, and A ij = 0 otherwise. For undirected networks, the adjacency matrix is symmetric A ij = A ji. For weighted networks, the elements of the adjacency matrix are replaced by nonbinary scalar values. However, in particular for sparse networks, i.e. networks where the number of edges is much smaller than the number of possible edges N E NV 2, the adjacency matrix becomes computationally inefficient in terms of memory allocation. Alternatively, the network can be specified by a set of adjacency lists, consisting of N V lists that enumerate to which other vertices each vertex connects, see also Chapter 2. The adjacency matrix, as well as the adjacency lists, have their unique advantages and disadvantages in terms of computational efficiency. A schematic example of both representations is given in Fig. 3.2.
4 iv Distance, Average Pathlength and Diameter In a network consisting of N V vertices, the distance d ij between any two vertices n i and n j is given by the length of the shortest path between the vertices, i.e., the minimal number of edges that need to be transversed to travel from vertex n i to n j. The shortest path between two vertices does not have to be unique, often there exist several alternative paths with identical pathlength. For directed networks, the distance between two vertices n i to n j is usually not symmetric d ij d ji. Likewise, for directed, as well as disconnected networks, i.e., networks consisting of two or more isolated components, there might not always be a path that connects vertex n i to n j. In such a case, the distance between the respective vertices is infinite d ij =. See Fig. 3.2 for examples. The diameter d m = max(d ij ) of a network is defined as the maximal distance of any pair of vertices. The average or characteristic pathlength d = d ij of a network is defined as the average distance between all pairs of vertices. In the case of infinite distances, the average inverse pathlengthd eff = 1/d ij, also referred to as efficiency, can be used to specify the average pathlength within the network. In this case, a fully connected network d ij = 1 i, j has an efficiency d eff = 1, whereas large distances and disconnected components (using the limit 1/d ij = 0 for d ij = ) reduce the efficiency of the network. The situation is slightly less straightforward if weighted networks are considered. Then, we are faced with the possibility to take additional information into account. For example, within a network of train connections, the shortest pathlength (distance) between two stations can be defined according to physical distances, or, taking travel time into account, by the total time needed to travel from one station to another. Furthermore, the fastest connection must not always be the cheapest, thus we might wish to define the distance between two stations according to the amount of money needed to travel from one station to another. In either case, the term distance between vertices can be generalized to accommodate additional scalar information, given by a weight factor that is associated with each edge. Computationally, the estimation of the distance between two vertices is not trivial. Within the extensive literature on the shortest paths problem, the most common choices are the Dijkstra and the Floyd-Warshall algorithm [6]. The Dijkstra algorithm returns the lowest cost path between a source vertex n i and all other vertices in the network in O(NV 2 ) time. For efficiency reasons, the algorithm return just one shortest path, enumerating all shortest paths between two vertices is computationally more tricky and expensive. To calculate the all-to-all distances, the Floyd-Warshall algorithm is the method of choice. The algorithm returns the distance matrix in O(NV 3 ). Both algorithms straightforwardly allow to incorporate weighted edges. Negative weights may induce cycles that reduce the cost of a path each time the cycle is traversed. In this case, the definition of the lowest cost path has to be modified. Note that distances, pathlength and diameter also depend on network size and density (number of vertices and links) and are therefore no genuine classifiers that straightforwardly allow to compare different networks.
5 GLOBAL PROPERTIES OF COMPLEX NETWORKS v Six Degrees of Separation: Concepts of a Small World One of the striking properties of almost all empirical networks is that, despite their huge size of sometimes several millions of vertices, the average pathlength is usually surprisingly small. For example within cellular metabolism, represented by a network of metabolites (vertices) linked by biochemical reactions (edges), the average pathlength between two metabolites is only approximately d 3, independent of the specific organism [22, 33, 71]. A recent study of the World-Wide Web (WWW), represented by a network of web documents (vertices) that are connected by directed hyperlinks (URLs), estimated that the average pathlength between any two vertices is only d 16 [1], extrapolated for a network of 200 million documents. The term small world network itself originated in the social sciences, reflecting the assertion that within networks of social acquaintances (or friendships) all people (vertices) on the planet are separated from each other by just a small number of intermediate friends or acquaintances ( six degrees of separation, although the specific value six must not be taken too literally). However, strictly speaking, the term small-world is not a genuine network property, i.e. there is no measure or statistical test that allows to check whether a given specific empirical network belongs to the class of small world networks. As stated above, the average distance between vertices also depends on the size of the network: The more vertices a network has, the more distant the vertices tend to be. The small-world property is thus mainly understood to apply to network models whose average pathlength d increases slower or equal than the logarithm of the network size d log N V for N V. A further distinction includes ultra-small networks [13], whose average pathlength scales as d log log N V The Degree Distribution One of the most basic properties of a vertex n i is its degree k i, defined as the number of edges adjacent to the vertex. In a network without self-loops (edges that connect a vertex to itself) and multiple links (two vertices are connected by more than one edge) the degree equals the number of neighbors of the vertex. In the case of directed networks, we distinguish between the input degree k in i and the output degree k out i. Taking all vertices of a network into account, we can ask for the probability p(k) that the degree of a randomly chosen vertex equals k. The degree distribution p(k) has become one of the most prominent characteristics of network topology. One of the key discoveries that triggered the renewed interest in complex network theory was that the distribution p(k) of many empirical networks approximately follows a power law p(k) k γ, where γ denotes the degree exponent. In contrast to the until then prevailing picture, where vertices are connected randomly and each vertex has approximately the same number of links, many empirical networks are strongly inhomogeneous: While the vast majority of vertices only posses a small number of links, a small number of vertices ( hubs ) are highly connected. Examples of prototypical degree distributions are depicted in Fig Though being one of the most basics characteristics of network architecture, a statisti-
6 vi Fig. 3.3 Degree distributions of complex networks. a) A lattice-like network. Each vertex has the same degree k (for periodic boundary conditions or large networks, such that vertices at the border can be neglected). b) An Erdös-Rényi random network. The degree distribution is homogeneous, the degrees of the vertices are centered around the average value. c) A scale-free network. The degree distribution is highly inhomogeneous and follows a power law of the form p(k) k γ, where γ denotes the degree exponent. While most vertices only have a low number of connections, a smaller number of vertices is highly connected. cally stringent numerical estimation of the degree distribution is far from trivial [25]. In the simplest case, p(k) can be straightforwardly estimated from an (usually binned) histogram of degrees. However, for many real networks with strongly inhomogeneous degree distributions, the simple histogram approach provides insufficient statistics at high degree vertices and is a notorious source of misinterpretations [25]. More reliable in terms of numerical estimation is the cumulative degree distribution p c (k), defined as the probability that a randomly chosen vertex has a degree larger than k. The cumulative degree distribution p c (k) is a monotonously decreasing function of k and its estimation requires no binning. For a power-law distribution p(k) k γ, the cumulative degree distribution is of the form p(k) k (γ 1). An exponential distribution p(k) exp( k) corresponds to an invariant cumulative distribution p c (k) exp( k). Computationally even more straightforward is to rank the vertices according to their degree and plot the degree versus the rank of each vertex. Examples of different representations of the degree distribution are shown in Fig 3.4. It should be noted that all empirical networks necessarily show deviations from an strict mathematical degree distribution. In particular for power-law distributions, the size (number of vertices) of the network puts constraints on the estimation of the degree exponent. Highly connected vertices are rare, and their probability is thus difficult to estimate for small networks. Likewise, the number of vertices with small degree is restricted by network size. Consequently, the formula p k γ often only applies to an intermediate region of the empirical degree distribution and has to be adjusted with an exponential cut-off at high degrees. More importantly, as shown
7 GLOBAL PROPERTIES OF COMPLEX NETWORKS vii a) 10 3 b) 10 0 c) histogram cum. distribution p c (k) γ c = 1.29 degree k γ r degree k degree k node rank Fig. 3.4 Different representations of the degree distribution of the metabolite substrate network described in Fig 3.1. a) A binned histogram. Shown is the number of vertices with a degree k, using a logarithmic binning. b) The cumulative degree distribution p c(k), i.e, the probability that a vertex has a degree larger or equal k. Note that the cumulative distribution does not require binning, but is obtained from the (normalized) number of vertices with degree larger or equal k. c) The rank plot of metabolites, ranked according to their degree k. A power-law of the form p k γr in the rank plot corresponds to a degree exponent γ = γ r 2.3 in the original degree distribution p(k) and γ c 1.3 in the cumulative distribution. The straight lines are not fitted and only serve as a guide to the eye. in the recent literature, the reported degree exponent of many empirical networks correlates with network size and thus might not reflect the actual exponent of the underlying networks [18, 17]. Furthermore, for small degree exponents the variance of the degree distribution is infinite, thus any empirical sample of vertex degree is no typical observation. However, for many biological problem it is often more important to note that the degree distribution is highly inhomogeneous and long-tailed, as opposed to the question whether the degree distribution fits a power-law in a strict statistical sense. For weighted networks, the concept of degree can also be extended to account for the weights of the edges by defining the strength of a vertex as the sum of the absolute values of the weights Assortative Mixing and Degree Correlations Despite its importance in the topological characterization of complex networks, the degree distribution itself does provide only little information about the internal structure and organization of the network. More interesting is thus to look for correlations between the degrees of adjacent vertices. A network is called disassortative if vertices with high degree connect preferentially to vertices with low degree. Vice versa, a network is called assortative if vertices with high degree preferentially also connect to other vertices with high degree. As pointed out in the recent literature [49], social networks tend to be assortative, i.e. persons (vertices) with many friends (connections) tend to be also connected to other persons with many friends, while most technological and biological networks are disassortative.
8 viii Formally, the degree correlation can be obtained from the joint probability distribution p(k i, k j ) that two connected vertices n i and n j have degree k i and k j respectively. For uncorrelated degrees the joint probability is given by the product of the marginal degree distributions p(k i, k j ) = p(k i )p(k j ) A measure for the deviation from statistical independence is given by the mutual information [64, 66]. Unfortunately, a direct numerical estimation of p(k i, k j ) is computationally demanding and often not feasible due to the limited size of the (empirical) network (but see also [66] for the numerical estimation of probability distributions and a discussion of finite size effects). More straightforward is thus to consider the Pearson correlation coefficient between the degree of two adjacent vertices. The correlation coefficient or assortativity coefficient r lies in the range 1 r 1, with r < 0 corresponding to a disassortative network and r > 0 to an assortative network. Note that the assortativity coefficient r, similar to the usual Pearson correlation, has it limits for strongly inhomogeneous degree distributions and fails to correctly quantify nonlinear degree correlations, i.e. networks that are assortative for low degree vertices and disassortative for high degree vertices. Another popular, and closely related, measure to evaluate degree correlations is the average neighbor degree [53]. For each vertex n i the average degree k i,nn = 1 NV k i j=1 A ijk j of its neighbors is calculated. Subsequently, these values are averaged for all vertices having the same degree k, resulting in the average neighbor degree k nn (k). See Fig. 3.5 for examples of vertex degree correlations. To evaluate the degree correlations for weighted and directed networks requires slight modifications in the respective definitions. In the case of directed networks, two distinct correlation indices are most interesting: (i) Do the in-degrees ki in of vertices correlate with their neighbors out-degrees ki out, and (ii) do the out-degrees ki out? In the case of weighted of vertices correlate with their neighbors in-degrees ki in networks, the degrees can again be replaced by their weighted counterparts The Clustering Coefficient Another basic measure that accounts for the internal structure of a network is the clustering coefficient C. The clustering coefficient relates to the local cohesiveness of a network and measures the probability that two vertices with a common neighbor are connected. In the case of undirected networks,given a vertex n i with k i neighbors, there existe max = k i (k i 1)/2 possible edges between the neighbors. The clustering coefficient C i of the vertex n i is then given as the ratio of the actual number of edges E i between the neighbors to the maximal number E max, C i = 2E i k i (k i 1). (3.1) See Fig. 3.6 for a schematic example. Note that, strictly speaking, the clustering coefficient C i is not a property of the vertex n i itself, but rather a property of its neighbors. The global or mean clustering coefficient C = C i of the network is the average cluster coefficient of all vertices.
9 GLOBAL PROPERTIES OF COMPLEX NETWORKS ix average neighbor degree node degree k clustering coefficient C node degree k Fig. 3.5 Vertex degree correlation in the substrate graph. Left: The average neighbor degree k i,nn of each vertex n i, plotted versus the degree k i. The solid line gives the (binned) average over all vertices with the same degree k. For large degrees a weak negative correlation is observed. Right: The clustering coefficient C i of each vertex versus the degree k i. Highly connected vertices exhibit a low clustering coefficient, i.e., highly connected vertices preferentially connect to vertices that are not mutually connected, indicating a hierarchical structure. Many empirical networks exhibit a rather high clustering coefficient, indicating a local cohesiveness and a tendency of vertices to form clusters or groups. Indeed, for example in social networks, it seems intuitive that two persons (vertices) who have a common friend are much more likely to be also friends, as compared to two randomly chosen persons. Interestingly, this also directly relates to the notion of degree correlations and dynamics on networks. As persons that share a common friend are likely to become acquainted themselves, they will acquire new friends over time. In particular, a highly connected person will induce new connections among his friends (neighboring vertices). In this sense, within social networks, a situation with disassortative degree correlations and low clustering coefficients is dynamically unstable and must be expected to evolve gradually towards more clustering and thus assortative degree correlations. However, despite its conceptual simplicity, the interpretation and statistical testing of the clustering coefficient holds some pitfalls, which are discussed in more detail in the Section 3.5. Furthermore, the clustering coefficient depends on the number of edges within the network. To claim a nontrivial local clustering within the network, an estimated value of C thus has to be compared to an appropriate null model to validate whether the value is indeed statistically significant, i.e., whether the respective network indeed exhibits a higher degree of clustering than a corresponding random network. Difficulties also arise for specific types of graphs, such as bipartite graphs, that exhibit a nontrivial clustering coefficient inherent to the bipartite structure [1, 52], see Section 3.5 for a detailed discussion. An alternative, but equivalent, definition of C can be given with respect to the number of triads (triples of vertices where each vertex is connected to both others) within a network. Note that the number of edges between the neighbors of a vertex is equal to the number of triads that vertex is part of. The global clustering coefficient is then
10 x Fig. 3.6 The clustering coefficient relates to the local cohesiveness of a network. a) The clustering coefficient is defined as the probability that two vertices with a common neighbor are connected. b) A highly connected vertex with a low clustering coefficient, indicating a (at least locally) hierarchical structure. c) A a vertex with high clustering coefficient C vertex = 0.8 defined as the proportion of triads in a network with respect to the total number of connected triples (triples where at least one vertex is connected to both others). C = 3 number of triads number of connected triples (3.2) The factor 3 accounts for the fact that each triad contributes to 3 connected triples [1]. A characterization of the clustering coefficient with respect to the number of triads holds some advantages with respect to numerical estimation and can be generalized to other structures, such as the number of squares [31]. Of particular interest is also the correlation of the clustering coefficient C i with other properties of a vertex n i. For example, as described by Newman [49], many empirical networks exhibit a negative correlation between the degrees k i and the clustering coefficients C i, indicating a modular structure of the network. See Fig. 3.5 for an example The Matching Index Within many empirical networks, two vertices that are functionally similar do not necessarily have to be connected. For example, within a network of protein interactions, two proteins that are involved in the regulation of similar processes and should be considered as closely related, must not necessarily bind to each other. Correspondingly, the normalized matching index M ij quantifies the similarity between two vertices based on the number of common neighbors shared by two vertices n i and n j. M ij = common neighbors total number of neighbors = N k,l A ika jl k i + k j N k,l A (3.3) ika jl Note that for the measure to be properly normalized, the denominator only counts the number of distinct neighbors, i.e. neighbors that are shared by both vertices are only counted once. One of the virtues of the matching index is that it can
11 GLOBAL PROPERTIES OF COMPLEX NETWORKS xi Fig. 3.7 Vertices that are functionally related do not necessarily have to be connected. The matching index counts number of common neighbors shared by two vertices, normalized by the total number of distinct neighbors. The right panel shows the adjacency list of the vertices n 1 and n 2, along with the corresponding matching index M 12. be straightforwardly applied to networks consisting of different types of vertices, such as bipartite graphs. For example, two transcription factors may regulate the expression of similar genes, without necessarily regulating (or binding to) each other. A schematic illustration of the matching index is given in Fig 3.7. The matching index can be generalized beyond the immediate neighbors of a vertex or extended to multiple vertices [40]. Furthermore, at the most general level, two vertices can be regarded (or defined) as similar if their distance to all other vertices within the network is approximately the same, irrespective of whether they are directly connected or not [75]. An advantage of this definition lies in the fact that the actual pair-wise similarity of two vertices must not be specified. The definition only draws upon the notion that two entities (vertices) must be considered similar, if they perceive the rest of the world (here the distance to all other vertices within the network) in a similar way Network Centralities Closely related to distance measures, network centrality indices seek to characterize each vertex or edge with respect to their position within the network. Centrality measures will be discussed in more detail in Chapter 4 of this book, here we will only briefly outline some basic features. Intuitively, a basic measure of the importance of a vertex n i is its degree k i (degree centrality). And indeed, several studies on biological network report a significant relationship between vertex degree and functional importance of vertices [2]. For example, within protein interaction networks, the removal of highly connected proteins is more likely to have lethal effects than removal of proteins with only a small number of links [32]. However, the degree is clearly not the only determinant of the functional importance of a vertex. Often more relevant, is the contextual location of the vertex within the network. For example, we can ask from which vertex a signal should be sent to reach all other vertices in minimal time. Or, vice versa, which vertices can be reached fastest from any other vertex within the network? In this respect, the closeness centrality specifies which vertices have the shortest paths to all
12 xii Fig. 3.8 The degree of a vertex does not necessarily reflect importance with respect to function of a network. While vertex n 1 has a high degree, its removal does not necessarily affect communication within the network. However, removal of vertices with low degree may have significant effects on communication or mass flow within the network, as seen for vertex n 2. others, measured for example by the (inverse of the) average distance from a vertex to all other vertices. For detailed definitions see Chapter 4 in this book. Probably the most well-known centrality measure is the betweenness centrality (BC). The betweenness centrality can be defined with respect to vertices and edges, and measures how often a vertex or edge is present in the set of all shortest paths As can be seen in Fig. 3.8, low degree vertices can be crucial to establish communication or mass flow within a network. Thus, with respect to robustness properties of a network, a selective attack on vertices with high BC was often found to be more relevant than a removal of vertices with high degree. Computationally, the estimation of the betweenness centrality is rather demanding and described in Chapter 4 of this book Eigenvalues and Spectral Properties of Networks An important property of network topology are the spectral properties of the adjacency matrix A. Though as yet only hardly used in biological research, the spectra of random graphs are among the oldest characteristics of network topology with a plethora of applications in many branches of physics [1]. For an undirected graph, the symmetric adjacency matrix A has N V real eigenvalues λ i. The spectral density ρ(λ), ρ(λ) = 1 N V N V δ(λ λ i ), (3.4) i=1 approaches a continuous function for increasing network size N V. An extensive amount of work about the mathematical properties of the spectral density is available, including the famous Wigner semicircle law [21, 1]. Of more relevance to the biological sciences, the eigenvalues of network matrices are becoming increasingly important with respect to two different fields of research: First, in networks of coupled oscillators, i.e, in networks where each vertex corre-
13 MODELS OF COMPLEX NETWORKS xiii sponds to an oscillator coupled to other oscillators via an adjacency matrix, the global dynamics of the system are determined by the structure of the adjacency matrix. In particular, the stability of the synchronized state, i.e., the state of the network where almost all vertices oscillate synchronously, can be related to the eigenvalues of the Laplacian matrix of the network [54], defined in close analogy to the adjacency matrix. Recent studies also take into account the effect of weighted edges [74]. Second, along similar lines, the eigenvalues of network matrices determine the stability and local dynamics of networks composed of interacting elements. For example, the vertices of a metabolic network denote metabolites, whose concentrations change according to the adjacent edges (metabolic reactions). Formally this system is represented by a differential equation for all metabolite concentrations. However, at least locally, this (usually unknown) system of differential equations can be approximated by a weighted interaction matrix, denoted as the Jacobian J of the system. The Jacobian matrix already governs essential aspects of the dynamics and predicts specific dynamic behavior even if detailed knowledge about the underlying reactions and interactions is not available [63, 65, 68]. 3.3 MODELS OF COMPLEX NETWORKS The various network indices discussed until now characterize and quantify the topological structure of a given network. However, to understand and elucidate whether an estimated value indeed corresponds to nontrivial structure within the network requires to consider basic prototype models of complex networks. We emphasize that none of the models described below aims to mimic the detailed features of any real network. Rather they represent minimal models, each invented to exhibit distinct generic features of complex networks. The purpose of prototype models is twofold: First, they provide null models to understand whether an observed feature is a generic feature of certain network classes or whether it deviates from what could be expected for a simplistic model. Second, prototype models often provide insight on how certain features of complex networks arise from the construction rules of the prototype models, allowing to probe to what extent (for example evolutionary) mechanisms can account for the observed features of empirical networks. Again, more detailed mathematical treatises on random network models are given elsewhere [1, 17, 50], here we only outline the basic ideas The Erdös-Rényi Model Probably the most basic model of a random network is given by the Erdös-Rényi (ER) network [20]. The ER network consists of N V vertices, connected by N E (undirected) edges which are chosen randomly from the set of N V (N V 1)/2 possible edges (excluding multiple connections and links from a vertex to itself). The 2N E N V (N V 1). probability p that two randomly chosen vertices are connected is thus p = Alternatively, the ER model can be defined as a set of N V vertices, with each pair of vertices connected with an equal probability p 1. The number of edges N E is then
14 xiv a random variable, with the expectation value N E = pn V (N V 1)/2 [1]. The ER model has been the primary subject of random graph theory, resulting in extensive knowledge about its mathematical properties and typical features. Here we only summarize some basic properties. The degree distribution of the ER model is given by a binomial distribution that becomes approximately Poissonian in the limit of large networks (N V ). The probability of a vertex to have degree k is k k k p(k) e k! (3.5) with k = pn V denoting the average degree. A typical realization of the ER model is rather homogeneous, most vertices have a similar degree, distributed approximately symmetrically around the average degree k, as shown in Figure 3.3b. Most analytical work on the ER model has concentrated on questions related to percolation theory, i.e, the connectednes of the network and the emergence of paths that enable a traversal of the whole network. For small p the network is disconnected and consists of a large number of isolated components [50]. At p 1/N V (thus for average degree k 1) a phase transition occurs, giving rise to a giant-component that encompassed most of the vertices of the network. For p log(n V )/N V all vertices are connected for almost all realizations of the random network. The ER model exhibits the small-world property. Above the percolation threshold, the average pathlength is very small and scales as the logarithm of the number of vertices l log N V (with k kept constant for increasing number of vertices). By construction, the clustering coefficient of the ER network C = p = k /N V, i.e. the probability that two vertices with a common neighbor are connected equals the probability that any pair of randomly chosen vertices are connected. The ER model does not show any local cohesiveness. Likewise, the degree of connected vertices is uncorrelated, the ER model does not display degree correlations. The Erdös-Rényi model remains one of the most important prototype models in graph theory. However, the main limitations for a direct comparison of network properties with empirical networks are its homogeneous degree distribution, the absence of local structure and the lack of degree correlations. A close variant of the ER model, the configuration model, will be discussed in Section The Watts-Strogatz Model While the Erdös-Rényi model correctly reproduces the small-world property, it fails to account for the local clustering that characterizes many empirical networks. In particular for social networks, i.e. networks of mutual friendships or acquaintances, most studies indicate a clustering coefficient that is orders of magnitude higher than the value obtained for a corresponding ER network. In one of the seminal papers of complex network theory, Watts and Strogatz proposed a model for coexistence of local structure on the one hand, and a small average pathlength on the other hand [72]. The starting point of the model is the limiting case of
15 MODELS OF COMPLEX NETWORKS xv Fig. 3.9 The Watts-Strogatz model: Starting point is a regular network, constructed such that each vertex is connected to its two nearest neighbors, resulting in a maximal clustering coefficient C = 1. With probability p rew links are randomly rewired. In the limit p rew 1 the ER model is recovered. a regular lattice-like network: Each vertex (arranged on an one-dimensional ring in the original model) is connected to its n/2 nearest neighbors. In social terms, this would resemble a strictly local medieval-like world, where each person only knows people in his or her immediate vicinity, such as neighbors and people in nearby villages. Consequently, the model exhibits strong local cohesiveness (a high clustering coefficient), but the spread of information is slow, i.e. the average pathlength scales linearly with system size. Extending the regular lattice-like network, shortcuts between distant vertices are introduced, i.e. with a probability p rew a link is rewired, such that one end is detached from its original vertex and connected to a randomly chosen vertex. In social terms, this would correspond to a merchant or traveler, who is also acquainted to a small number of more distant people within the country. As the probability p rew increases and more links are rewired, the model approaches a random network of the ER type. In the limit p rew 1 the ER model is recovered. The network thus again exhibits no local structure (small clustering coefficient) and the average pathlength scales as the logarithm of network size. One of the intriguing result of the WS model is that already a very small number of shortcuts (p rew 1) is sufficient to rapidly decrease the average pathlength [28]. On the other hand, for small p rew, the local clustering remains almost unaffected and the clustering coefficient only decreased significantly for p rew 1. Thus for an intermediate region of p rew, the WS model exhibits a coexistence of high local clustering and short average pathlength (small-world property), as also observed in many empirical networks. A schematic representation of the WS model is given in
16 xvi Fig The Barabási-Albert model [7]: Starting with an initial small network, consisting of N 0 unconnected vertices, a new vertex is introduced at each timestep and connected with m < N 0 edges (here shown with m = 2). Fig The main significance of the WS model results from the fact that it emphasizes a difference between local and global properties of networks. The clustering coefficient, a local property, is determined by the immediate neighborhood of a vertex and is almost unaffected by the introduction of additional shortcuts within the network. On the other hand, the average pathlength, a global property, rapidly decreases upon the introduction of just a few shortcuts. This has, for example, profound implications on the spread of infectious diseases across continents. A change in average pathlength to distant vertices is not detectable at the local level, i.e., your social neighborhood might remain almost unaltered, while the distance (in network terms) to infected persons can rapidly decrease with only a small number of transcontinental travellers. However, apart from the coexistence of high local clustering and short average pathlength, the WS models captures almost no other feature found in empirical networks. Its importance as a null model for biological networks thus remains limited The Barabási-Albert Model Among the most important limitations of the models discussed above is that neither captures or accounts for the inhomogeneous degree distribution found in many empirical networks. To this end, Barabási and Albert [7] proposed a simple network model that gives rise to a scale-free degree distribution and still provides the conceptual basis for most current network models described in the literature. Closely related to (and actually a simplification of) an earlier model by Price [4, 16, 45, 50], the BA model is based on two essential ingredients: i) Growth: In contrast to the models discussed above, the BA model does not assume that the number of vertices within the network is fixed. Mimicking the dynamics of many real networks, vertices are continuously added and the network grows as a function of time. ii) Preferential attachment: New edges are not introduced randomly, but the probability that a vertex receives a new edge depends on its present degree k i, again reflecting dynamic properties of real networks. The growth process is organized as follows: Starting with an initial small network, consisting of N 0 unconnected vertices, a new vertex is introduced at each timestep. The new vertex is connected to with m N 0 edges to the already present vertices. The probability ρ(n i ) that analready present vertex n i receives a new edge is
17 MODELS OF COMPLEX NETWORKS xvii proportional to its degree k i : ρ(n i ) = k i j k j. (3.6) After t timesteps, the network consists of N V (t) = N 0 + t vertices, connected by N E (t) = mt edges. Due to the preferential attachment mechanism, older vertices tend to have accumulated more links, and thus have an even higher probability to receive yet more links (a rich-get-richer dynamics). Likewise, new vertices only have a small number of links, and thus a low probability of receiving additional links. A schematic illustration of the growth process is given in Fig In the long time limit t 1, the BA model exhibits a scale-free degree distribution p(k) k γba with a degree exponent γ BA = 3 that is invariant with time. The degree exponent is independent of the free parameters m and N 0. The BA model captures the small world property, BA networks are found to have shorter average pathlength than ER and WS models of the same size and density. The degrees are uncorrelated and analytical estimates of the clustering coefficient are available [36]. One of the merits of the BA model is that it provides a possible mechanism to explain the observed scale-free distribution of many empirical networks. Indeed, the time evolution of many empirical networks is governed by preferential attachment-like processes. For example, within a social network, people (vertices) with already many friends (edges) are more likely to acquire new friends, as compared to people with few edges. Likewise, already famous actors will obtain more offers to act in a new movie than young unknown actors. Scientific papers that are already frequently cited are more likely to be read and cited again than less frequently cited papers. Importantly, the preferential attachment rule also provides several testable predictions for complex networks. For example, if metabolic networks are reported as scale-free, then, according to this growth rule, highly connected metabolites should have an early evolutionary origin. Indeed, as emphasized by Wagner and Fell [71], many of the highly connected metabolites, mainly intermediates of the TCA cycle and glycolysis, as well as some ubiquitous co-factors, are among the evolutionary oldest. However, explanations in terms of evolutionary mechanisms also hold some pitfalls which are unfortunately rarely if ever discussed in the literature. Most importantly, not only the formation of a network itself, but often also the acquisition of data about the network is governed by similar mechanisms. For example, minor movies with famous actors are more likely to be included in the respective databases than local movies starring only unknown actors. Likewise, putative biochemical regulations or reactions adjacent to the TCA cycle are more likely to be investigated, and thus reported in publications, than putative regulations within the outskirts of metabolism. In this sense, an observed feature of an empirical network might also always reflect properties of the data acquisition process, rather than genuine properties of the network itself.
18 xviii Extensions of the BA Model The BA model constitutes the conceptual basis for a large variety of extensions and modifications and has triggered an exceptional amount of further work in the complex network models. Most extensions can roughly be subdivided into two (though often overlapping) categories: i) Modifications that aim to generate networks with specific tunable features, such as different degree exponents, tunable cluster coefficients or degree correlations. ii) Modifications that aim to mimic the evolutionary growth processes of specific networks in more detail, such as aging in social networks or capacity restrictions in transportation networks. For example, the exponential cutoff at high degrees observed in many real networks can be accounted for by aging of vertices, i.e., vertices that have been present for a given time T stop acquiring new edges or are removed from the network [3] as could be expected in social networks. Similar, an airport within a transportation network will not acquire new connections beyond a certain capacity, again resulting in an exponential cutoff at high degrees. Other processes to modify the properties of the network include re-wiring of edges according to defined rules. For example, within a social network people that have a common friend are more likely to become acquainted themselves, resulting in an increased local clustering of the network [15]. Further extensions and modifications include memory effects and high clustering [36], degree correlations [56, 73], tunable degree exponents [38], information accessibility [48], among many more. An overview of early modifications and extensions of the original BA model can also be found in Table III of [1]. 3.4 ADDITIONAL PROPERTIES OF COMPLEX NETWORKS Within the first section, most emphasis was placed on quantitative measures that describe the properties of individual vertices and edges. However, complex networks are also characterized by emergent features that transcend the properties of individual vertices and relate to the organization of the network as a whole. In the following the basic emergent global properties of complex networks, such as robustness or modularity, are outlined Structural Robustness and Attack Tolerance Most biological systems share a common feature: robustness [8, 35, 60, 69]. Constituting one of the fundamental organizing principles of biology, cellular networks must be able to maintain their function in the face of constant perturbations and fluctuations that affect the internal or external parameters of the system. In the context of complex network analysis, robustness is mainly understood as the persistence of topological network properties, such as average pathlength or connectedness, upon removal of vertices or links [1, 2, 10, 33]. Indeed, most empirical networks show a surprising tolerance against removal of vertices. Focusing on topological aspects of robustness only, a number of studies
19 ADDITIONAL PROPERTIES OF COMPLEX NETWORKS xix Fig The robust, yet fragile nature of scale-free networks. Properties of scale-free networks are highly robust against random removal of vertices, but vulnerable against selective intentional removal of vertices. revealed significant differences between distinct network topologies upon removal of vertices or edges [2, 29]. In general, we have to distinguish between random and intentional attacks on network topology. While for ER networks, due to the homogeneity of vertex properties, the response to random and intentional attacks is roughly similar, the situation for scale-free networks is markedly different. Most properties of scale-free networks were found to be exceptionally robust against random removal of vertices. However, at the same time, scale-free networks are vulnerable with respect to intentional attacks. This difference is due to the heterogeneous degree distribution. Low degree vertices are far more frequent than high degree vertices, but only play a minor role in overall network topology. While random attacks will most likely affect low degree vertices, a selective attack on high degree vertices has far more dramatic consequence on global network indices [2, 1, 29]. A schematic illustration is given in Fig In general, the difference between random and intentional attacks is at the core of most current research on network robustness. The robust, yet fragile nature of complex systems refers to the fact that many complex systems are robust against random attacks, while they remain fragile against selective attacks. In particular highly optimized systems are extremely robust against anticipated attacks, while optimization concomitantly leads to vulnerability against unanticipated perturbations, related to the principle of highly optimized tolerance (HOT) [12]. It should be noted though, that the restriction to topological aspects of robustness only allows for a rather restricted view on network robustness. Dynamic aspects of functional robustness thus receive increasing interest recently [35, 47, 60, 63, 65] Modularity, Community Structures and Hierarchies Related to the idea of functional robustness is the notion of modules and community structures within complex networks. In general, it is assumed that many complex networks are built up from (interacting and possibly overlapping) modules or communitites. The detection of such community structures has attracted substantial interest recently and defines an important aspect of complex network analysis [57, 75, 76].
Properties of Biological Networks
 Properties of Biological Networks presented by: Ola Hamud June 12, 2013 Supervisor: Prof. Ron Pinter Based on: NETWORK BIOLOGY: UNDERSTANDING THE CELL S FUNCTIONAL ORGANIZATION By Albert-László Barabási
Properties of Biological Networks presented by: Ola Hamud June 12, 2013 Supervisor: Prof. Ron Pinter Based on: NETWORK BIOLOGY: UNDERSTANDING THE CELL S FUNCTIONAL ORGANIZATION By Albert-László Barabási
Lesson 4. Random graphs. Sergio Barbarossa. UPC - Barcelona - July 2008
 Lesson 4 Random graphs Sergio Barbarossa Graph models 1. Uncorrelated random graph (Erdős, Rényi) N nodes are connected through n edges which are chosen randomly from the possible configurations 2. Binomial
Lesson 4 Random graphs Sergio Barbarossa Graph models 1. Uncorrelated random graph (Erdős, Rényi) N nodes are connected through n edges which are chosen randomly from the possible configurations 2. Binomial
Example for calculation of clustering coefficient Node N 1 has 8 neighbors (red arrows) There are 12 connectivities among neighbors (blue arrows)
 Example for calculation of clustering coefficient Node N 1 has 8 neighbors (red arrows) There are 12 connectivities among neighbors (blue arrows) Average clustering coefficient of a graph Overall measure
Example for calculation of clustering coefficient Node N 1 has 8 neighbors (red arrows) There are 12 connectivities among neighbors (blue arrows) Average clustering coefficient of a graph Overall measure
(Social) Networks Analysis III. Prof. Dr. Daning Hu Department of Informatics University of Zurich
 (Social) Networks Analysis III Prof. Dr. Daning Hu Department of Informatics University of Zurich Outline Network Topological Analysis Network Models Random Networks Small-World Networks Scale-Free Networks
(Social) Networks Analysis III Prof. Dr. Daning Hu Department of Informatics University of Zurich Outline Network Topological Analysis Network Models Random Networks Small-World Networks Scale-Free Networks
Wednesday, March 8, Complex Networks. Presenter: Jirakhom Ruttanavakul. CS 790R, University of Nevada, Reno
 Wednesday, March 8, 2006 Complex Networks Presenter: Jirakhom Ruttanavakul CS 790R, University of Nevada, Reno Presented Papers Emergence of scaling in random networks, Barabási & Bonabeau (2003) Scale-free
Wednesday, March 8, 2006 Complex Networks Presenter: Jirakhom Ruttanavakul CS 790R, University of Nevada, Reno Presented Papers Emergence of scaling in random networks, Barabási & Bonabeau (2003) Scale-free
A Generating Function Approach to Analyze Random Graphs
 A Generating Function Approach to Analyze Random Graphs Presented by - Vilas Veeraraghavan Advisor - Dr. Steven Weber Department of Electrical and Computer Engineering Drexel University April 8, 2005 Presentation
A Generating Function Approach to Analyze Random Graphs Presented by - Vilas Veeraraghavan Advisor - Dr. Steven Weber Department of Electrical and Computer Engineering Drexel University April 8, 2005 Presentation
Constructing a G(N, p) Network
 Random Graph Theory Dr. Natarajan Meghanathan Professor Department of Computer Science Jackson State University, Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Introduction At first inspection, most
Random Graph Theory Dr. Natarajan Meghanathan Professor Department of Computer Science Jackson State University, Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Introduction At first inspection, most
1 Homophily and assortative mixing
 1 Homophily and assortative mixing Networks, and particularly social networks, often exhibit a property called homophily or assortative mixing, which simply means that the attributes of vertices correlate
1 Homophily and assortative mixing Networks, and particularly social networks, often exhibit a property called homophily or assortative mixing, which simply means that the attributes of vertices correlate
Graph Theory. Graph Theory. COURSE: Introduction to Biological Networks. Euler s Solution LECTURE 1: INTRODUCTION TO NETWORKS.
 Graph Theory COURSE: Introduction to Biological Networks LECTURE 1: INTRODUCTION TO NETWORKS Arun Krishnan Koenigsberg, Russia Is it possible to walk with a route that crosses each bridge exactly once,
Graph Theory COURSE: Introduction to Biological Networks LECTURE 1: INTRODUCTION TO NETWORKS Arun Krishnan Koenigsberg, Russia Is it possible to walk with a route that crosses each bridge exactly once,
Constructing a G(N, p) Network
 Random Graph Theory Dr. Natarajan Meghanathan Associate Professor Department of Computer Science Jackson State University, Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Introduction At first inspection,
Random Graph Theory Dr. Natarajan Meghanathan Associate Professor Department of Computer Science Jackson State University, Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Introduction At first inspection,
Complex Networks. Structure and Dynamics
 Complex Networks Structure and Dynamics Ying-Cheng Lai Department of Mathematics and Statistics Department of Electrical Engineering Arizona State University Collaborators! Adilson E. Motter, now at Max-Planck
Complex Networks Structure and Dynamics Ying-Cheng Lai Department of Mathematics and Statistics Department of Electrical Engineering Arizona State University Collaborators! Adilson E. Motter, now at Max-Planck
M.E.J. Newman: Models of the Small World
 A Review Adaptive Informatics Research Centre Helsinki University of Technology November 7, 2007 Vocabulary N number of nodes of the graph l average distance between nodes D diameter of the graph d is
A Review Adaptive Informatics Research Centre Helsinki University of Technology November 7, 2007 Vocabulary N number of nodes of the graph l average distance between nodes D diameter of the graph d is
Summary: What We Have Learned So Far
 Summary: What We Have Learned So Far small-world phenomenon Real-world networks: { Short path lengths High clustering Broad degree distributions, often power laws P (k) k γ Erdös-Renyi model: Short path
Summary: What We Have Learned So Far small-world phenomenon Real-world networks: { Short path lengths High clustering Broad degree distributions, often power laws P (k) k γ Erdös-Renyi model: Short path
TELCOM2125: Network Science and Analysis
 School of Information Sciences University of Pittsburgh TELCOM2125: Network Science and Analysis Konstantinos Pelechrinis Spring 2015 Figures are taken from: M.E.J. Newman, Networks: An Introduction 2
School of Information Sciences University of Pittsburgh TELCOM2125: Network Science and Analysis Konstantinos Pelechrinis Spring 2015 Figures are taken from: M.E.J. Newman, Networks: An Introduction 2
Critical Phenomena in Complex Networks
 Critical Phenomena in Complex Networks Term essay for Physics 563: Phase Transitions and the Renormalization Group University of Illinois at Urbana-Champaign Vikyath Deviprasad Rao 11 May 2012 Abstract
Critical Phenomena in Complex Networks Term essay for Physics 563: Phase Transitions and the Renormalization Group University of Illinois at Urbana-Champaign Vikyath Deviprasad Rao 11 May 2012 Abstract
Graph-theoretic Properties of Networks
 Graph-theoretic Properties of Networks Bioinformatics: Sequence Analysis COMP 571 - Spring 2015 Luay Nakhleh, Rice University Graphs A graph is a set of vertices, or nodes, and edges that connect pairs
Graph-theoretic Properties of Networks Bioinformatics: Sequence Analysis COMP 571 - Spring 2015 Luay Nakhleh, Rice University Graphs A graph is a set of vertices, or nodes, and edges that connect pairs
Structure of biological networks. Presentation by Atanas Kamburov
 Structure of biological networks Presentation by Atanas Kamburov Seminar Gute Ideen in der theoretischen Biologie / Systembiologie 08.05.2007 Overview Motivation Definitions Large-scale properties of cellular
Structure of biological networks Presentation by Atanas Kamburov Seminar Gute Ideen in der theoretischen Biologie / Systembiologie 08.05.2007 Overview Motivation Definitions Large-scale properties of cellular
Erdős-Rényi Model for network formation
 Network Science: Erdős-Rényi Model for network formation Ozalp Babaoglu Dipartimento di Informatica Scienza e Ingegneria Università di Bologna www.cs.unibo.it/babaoglu/ Why model? Simpler representation
Network Science: Erdős-Rényi Model for network formation Ozalp Babaoglu Dipartimento di Informatica Scienza e Ingegneria Università di Bologna www.cs.unibo.it/babaoglu/ Why model? Simpler representation
CAIM: Cerca i Anàlisi d Informació Massiva
 1 / 72 CAIM: Cerca i Anàlisi d Informació Massiva FIB, Grau en Enginyeria Informàtica Slides by Marta Arias, José Balcázar, Ricard Gavaldá Department of Computer Science, UPC Fall 2016 http://www.cs.upc.edu/~caim
1 / 72 CAIM: Cerca i Anàlisi d Informació Massiva FIB, Grau en Enginyeria Informàtica Slides by Marta Arias, José Balcázar, Ricard Gavaldá Department of Computer Science, UPC Fall 2016 http://www.cs.upc.edu/~caim
Advanced Algorithms and Models for Computational Biology -- a machine learning approach
 Advanced Algorithms and Models for Computational Biology -- a machine learning approach Biological Networks & Network Evolution Eric Xing Lecture 22, April 10, 2006 Reading: Molecular Networks Interaction
Advanced Algorithms and Models for Computational Biology -- a machine learning approach Biological Networks & Network Evolution Eric Xing Lecture 22, April 10, 2006 Reading: Molecular Networks Interaction
CSCI5070 Advanced Topics in Social Computing
 CSCI5070 Advanced Topics in Social Computing Irwin King The Chinese University of Hong Kong king@cse.cuhk.edu.hk!! 2012 All Rights Reserved. Outline Graphs Origins Definition Spectral Properties Type of
CSCI5070 Advanced Topics in Social Computing Irwin King The Chinese University of Hong Kong king@cse.cuhk.edu.hk!! 2012 All Rights Reserved. Outline Graphs Origins Definition Spectral Properties Type of
The Complex Network Phenomena. and Their Origin
 The Complex Network Phenomena and Their Origin An Annotated Bibliography ESL 33C 003180159 Instructor: Gerriet Janssen Match 18, 2004 Introduction A coupled system can be described as a complex network,
The Complex Network Phenomena and Their Origin An Annotated Bibliography ESL 33C 003180159 Instructor: Gerriet Janssen Match 18, 2004 Introduction A coupled system can be described as a complex network,
An Introduction to Complex Systems Science
 DEIS, Campus of Cesena Alma Mater Studiorum Università di Bologna andrea.roli@unibo.it Disclaimer The field of Complex systems science is wide and it involves numerous themes and disciplines. This talk
DEIS, Campus of Cesena Alma Mater Studiorum Università di Bologna andrea.roli@unibo.it Disclaimer The field of Complex systems science is wide and it involves numerous themes and disciplines. This talk
CS-E5740. Complex Networks. Scale-free networks
 CS-E5740 Complex Networks Scale-free networks Course outline 1. Introduction (motivation, definitions, etc. ) 2. Static network models: random and small-world networks 3. Growing network models: scale-free
CS-E5740 Complex Networks Scale-free networks Course outline 1. Introduction (motivation, definitions, etc. ) 2. Static network models: random and small-world networks 3. Growing network models: scale-free
Signal Processing for Big Data
 Signal Processing for Big Data Sergio Barbarossa 1 Summary 1. Networks 2.Algebraic graph theory 3. Random graph models 4. OperaGons on graphs 2 Networks The simplest way to represent the interaction between
Signal Processing for Big Data Sergio Barbarossa 1 Summary 1. Networks 2.Algebraic graph theory 3. Random graph models 4. OperaGons on graphs 2 Networks The simplest way to represent the interaction between
Universal Properties of Mythological Networks Midterm report: Math 485
 Universal Properties of Mythological Networks Midterm report: Math 485 Roopa Krishnaswamy, Jamie Fitzgerald, Manuel Villegas, Riqu Huang, and Riley Neal Department of Mathematics, University of Arizona,
Universal Properties of Mythological Networks Midterm report: Math 485 Roopa Krishnaswamy, Jamie Fitzgerald, Manuel Villegas, Riqu Huang, and Riley Neal Department of Mathematics, University of Arizona,
Small World Properties Generated by a New Algorithm Under Same Degree of All Nodes
 Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 950 954 c International Academic Publishers Vol. 45, No. 5, May 15, 2006 Small World Properties Generated by a New Algorithm Under Same Degree of All
Commun. Theor. Phys. (Beijing, China) 45 (2006) pp. 950 954 c International Academic Publishers Vol. 45, No. 5, May 15, 2006 Small World Properties Generated by a New Algorithm Under Same Degree of All
Models of Network Formation. Networked Life NETS 112 Fall 2017 Prof. Michael Kearns
 Models of Network Formation Networked Life NETS 112 Fall 2017 Prof. Michael Kearns Roadmap Recently: typical large-scale social and other networks exhibit: giant component with small diameter sparsity
Models of Network Formation Networked Life NETS 112 Fall 2017 Prof. Michael Kearns Roadmap Recently: typical large-scale social and other networks exhibit: giant component with small diameter sparsity
Chapter 1. Social Media and Social Computing. October 2012 Youn-Hee Han
 Chapter 1. Social Media and Social Computing October 2012 Youn-Hee Han http://link.koreatech.ac.kr 1.1 Social Media A rapid development and change of the Web and the Internet Participatory web application
Chapter 1. Social Media and Social Computing October 2012 Youn-Hee Han http://link.koreatech.ac.kr 1.1 Social Media A rapid development and change of the Web and the Internet Participatory web application
Network Theory: Social, Mythological and Fictional Networks. Math 485, Spring 2018 (Midterm Report) Christina West, Taylor Martins, Yihe Hao
 Network Theory: Social, Mythological and Fictional Networks Math 485, Spring 2018 (Midterm Report) Christina West, Taylor Martins, Yihe Hao Abstract: Comparative mythology is a largely qualitative and
Network Theory: Social, Mythological and Fictional Networks Math 485, Spring 2018 (Midterm Report) Christina West, Taylor Martins, Yihe Hao Abstract: Comparative mythology is a largely qualitative and
Centrality Book. cohesion.
 Cohesion The graph-theoretic terms discussed in the previous chapter have very specific and concrete meanings which are highly shared across the field of graph theory and other fields like social network
Cohesion The graph-theoretic terms discussed in the previous chapter have very specific and concrete meanings which are highly shared across the field of graph theory and other fields like social network
An Evolving Network Model With Local-World Structure
 The Eighth International Symposium on Operations Research and Its Applications (ISORA 09) Zhangjiajie, China, September 20 22, 2009 Copyright 2009 ORSC & APORC, pp. 47 423 An Evolving Network odel With
The Eighth International Symposium on Operations Research and Its Applications (ISORA 09) Zhangjiajie, China, September 20 22, 2009 Copyright 2009 ORSC & APORC, pp. 47 423 An Evolving Network odel With
Attack vulnerability of complex networks
 Attack vulnerability of complex networks Petter Holme and Beom Jun Kim Department of Theoretical Physics, Umeå University, 901 87 Umeå, Sweden Chang No Yoon and Seung Kee Han Department of Physics, Chungbuk
Attack vulnerability of complex networks Petter Holme and Beom Jun Kim Department of Theoretical Physics, Umeå University, 901 87 Umeå, Sweden Chang No Yoon and Seung Kee Han Department of Physics, Chungbuk
1 More configuration model
 1 More configuration model In the last lecture, we explored the definition of the configuration model, a simple method for drawing networks from the ensemble, and derived some of its mathematical properties.
1 More configuration model In the last lecture, we explored the definition of the configuration model, a simple method for drawing networks from the ensemble, and derived some of its mathematical properties.
RANDOM-REAL NETWORKS
 RANDOM-REAL NETWORKS 1 Random networks: model A random graph is a graph of N nodes where each pair of nodes is connected by probability p: G(N,p) Random networks: model p=1/6 N=12 L=8 L=10 L=7 The number
RANDOM-REAL NETWORKS 1 Random networks: model A random graph is a graph of N nodes where each pair of nodes is connected by probability p: G(N,p) Random networks: model p=1/6 N=12 L=8 L=10 L=7 The number
arxiv:cond-mat/ v1 [cond-mat.dis-nn] 3 Aug 2000
![arxiv:cond-mat/ v1 [cond-mat.dis-nn] 3 Aug 2000 arxiv:cond-mat/ v1 [cond-mat.dis-nn] 3 Aug 2000](/thumbs/83/87495160.jpg) Error and attack tolerance of complex networks arxiv:cond-mat/0008064v1 [cond-mat.dis-nn] 3 Aug 2000 Réka Albert, Hawoong Jeong, Albert-László Barabási Department of Physics, University of Notre Dame,
Error and attack tolerance of complex networks arxiv:cond-mat/0008064v1 [cond-mat.dis-nn] 3 Aug 2000 Réka Albert, Hawoong Jeong, Albert-László Barabási Department of Physics, University of Notre Dame,
V 1 Introduction! Mon, Oct 15, 2012! Bioinformatics 3 Volkhard Helms!
 V 1 Introduction! Mon, Oct 15, 2012! Bioinformatics 3 Volkhard Helms! How Does a Cell Work?! A cell is a crowded environment! => many different proteins,! metabolites, compartments,! On a microscopic level!
V 1 Introduction! Mon, Oct 15, 2012! Bioinformatics 3 Volkhard Helms! How Does a Cell Work?! A cell is a crowded environment! => many different proteins,! metabolites, compartments,! On a microscopic level!
Introduction to network metrics
 Universitat Politècnica de Catalunya Version 0.5 Complex and Social Networks (2018-2019) Master in Innovation and Research in Informatics (MIRI) Instructors Argimiro Arratia, argimiro@cs.upc.edu, http://www.cs.upc.edu/~argimiro/
Universitat Politècnica de Catalunya Version 0.5 Complex and Social Networks (2018-2019) Master in Innovation and Research in Informatics (MIRI) Instructors Argimiro Arratia, argimiro@cs.upc.edu, http://www.cs.upc.edu/~argimiro/
The missing links in the BGP-based AS connectivity maps
 The missing links in the BGP-based AS connectivity maps Zhou, S; Mondragon, RJ http://arxiv.org/abs/cs/0303028 For additional information about this publication click this link. http://qmro.qmul.ac.uk/xmlui/handle/123456789/13070
The missing links in the BGP-based AS connectivity maps Zhou, S; Mondragon, RJ http://arxiv.org/abs/cs/0303028 For additional information about this publication click this link. http://qmro.qmul.ac.uk/xmlui/handle/123456789/13070
V2: Measures and Metrics (II)
 - Betweenness Centrality V2: Measures and Metrics (II) - Groups of Vertices - Transitivity - Reciprocity - Signed Edges and Structural Balance - Similarity - Homophily and Assortative Mixing 1 Betweenness
- Betweenness Centrality V2: Measures and Metrics (II) - Groups of Vertices - Transitivity - Reciprocity - Signed Edges and Structural Balance - Similarity - Homophily and Assortative Mixing 1 Betweenness
Networks in economics and finance. Lecture 1 - Measuring networks
 Networks in economics and finance Lecture 1 - Measuring networks What are networks and why study them? A network is a set of items (nodes) connected by edges or links. Units (nodes) Individuals Firms Banks
Networks in economics and finance Lecture 1 - Measuring networks What are networks and why study them? A network is a set of items (nodes) connected by edges or links. Units (nodes) Individuals Firms Banks
Basics of Network Analysis
 Basics of Network Analysis Hiroki Sayama sayama@binghamton.edu Graph = Network G(V, E): graph (network) V: vertices (nodes), E: edges (links) 1 Nodes = 1, 2, 3, 4, 5 2 3 Links = 12, 13, 15, 23,
Basics of Network Analysis Hiroki Sayama sayama@binghamton.edu Graph = Network G(V, E): graph (network) V: vertices (nodes), E: edges (links) 1 Nodes = 1, 2, 3, 4, 5 2 3 Links = 12, 13, 15, 23,
A Study of Random Duplication Graphs and Degree Distribution Pattern of Protein-Protein Interaction Networks
 A Study of Random Duplication Graphs and Degree Distribution Pattern of Protein-Protein Interaction Networks by Zheng Ma A thesis presented to the University of Waterloo in fulfillment of the thesis requirement
A Study of Random Duplication Graphs and Degree Distribution Pattern of Protein-Protein Interaction Networks by Zheng Ma A thesis presented to the University of Waterloo in fulfillment of the thesis requirement
Nick Hamilton Institute for Molecular Bioscience. Essential Graph Theory for Biologists. Image: Matt Moores, The Visible Cell
 Nick Hamilton Institute for Molecular Bioscience Essential Graph Theory for Biologists Image: Matt Moores, The Visible Cell Outline Core definitions Which are the most important bits? What happens when
Nick Hamilton Institute for Molecular Bioscience Essential Graph Theory for Biologists Image: Matt Moores, The Visible Cell Outline Core definitions Which are the most important bits? What happens when
Epidemic spreading on networks
 Epidemic spreading on networks Due date: Sunday October 25th, 2015, at 23:59. Always show all the steps which you made to arrive at your solution. Make sure you answer all parts of each question. Always
Epidemic spreading on networks Due date: Sunday October 25th, 2015, at 23:59. Always show all the steps which you made to arrive at your solution. Make sure you answer all parts of each question. Always
arxiv:cond-mat/ v1 21 Oct 1999
 Emergence of Scaling in Random Networks Albert-László Barabási and Réka Albert Department of Physics, University of Notre-Dame, Notre-Dame, IN 46556 arxiv:cond-mat/9910332 v1 21 Oct 1999 Systems as diverse
Emergence of Scaling in Random Networks Albert-László Barabási and Réka Albert Department of Physics, University of Notre-Dame, Notre-Dame, IN 46556 arxiv:cond-mat/9910332 v1 21 Oct 1999 Systems as diverse
Heuristics for the Critical Node Detection Problem in Large Complex Networks
 Heuristics for the Critical Node Detection Problem in Large Complex Networks Mahmood Edalatmanesh Department of Computer Science Submitted in partial fulfilment of the requirements for the degree of Master
Heuristics for the Critical Node Detection Problem in Large Complex Networks Mahmood Edalatmanesh Department of Computer Science Submitted in partial fulfilment of the requirements for the degree of Master
An introduction to the physics of complex networks
 An introduction to the physics of complex networks Alain Barrat CPT, Marseille, France ISI, Turin, Italy http://www.cpt.univ-mrs.fr/~barrat http://www.cxnets.org http://www.sociopatterns.org REVIEWS: Statistical
An introduction to the physics of complex networks Alain Barrat CPT, Marseille, France ISI, Turin, Italy http://www.cpt.univ-mrs.fr/~barrat http://www.cxnets.org http://www.sociopatterns.org REVIEWS: Statistical
Mathematics of networks. Artem S. Novozhilov
 Mathematics of networks Artem S. Novozhilov August 29, 2013 A disclaimer: While preparing these lecture notes, I am using a lot of different sources for inspiration, which I usually do not cite in the
Mathematics of networks Artem S. Novozhilov August 29, 2013 A disclaimer: While preparing these lecture notes, I am using a lot of different sources for inspiration, which I usually do not cite in the
Response Network Emerging from Simple Perturbation
 Journal of the Korean Physical Society, Vol 44, No 3, March 2004, pp 628 632 Response Network Emerging from Simple Perturbation S-W Son, D-H Kim, Y-Y Ahn and H Jeong Department of Physics, Korea Advanced
Journal of the Korean Physical Society, Vol 44, No 3, March 2004, pp 628 632 Response Network Emerging from Simple Perturbation S-W Son, D-H Kim, Y-Y Ahn and H Jeong Department of Physics, Korea Advanced
Graph Theory for Network Science
 Graph Theory for Network Science Dr. Natarajan Meghanathan Professor Department of Computer Science Jackson State University, Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Networks or Graphs We typically
Graph Theory for Network Science Dr. Natarajan Meghanathan Professor Department of Computer Science Jackson State University, Jackson, MS E-mail: natarajan.meghanathan@jsums.edu Networks or Graphs We typically
Comparison of Centralities for Biological Networks
 Comparison of Centralities for Biological Networks Dirk Koschützki and Falk Schreiber Bioinformatics Center Gatersleben-Halle Institute of Plant Genetics and Crop Plant Research Corrensstraße 3 06466 Gatersleben,
Comparison of Centralities for Biological Networks Dirk Koschützki and Falk Schreiber Bioinformatics Center Gatersleben-Halle Institute of Plant Genetics and Crop Plant Research Corrensstraße 3 06466 Gatersleben,
Eciency of scale-free networks: error and attack tolerance
 Available online at www.sciencedirect.com Physica A 320 (2003) 622 642 www.elsevier.com/locate/physa Eciency of scale-free networks: error and attack tolerance Paolo Crucitti a, Vito Latora b, Massimo
Available online at www.sciencedirect.com Physica A 320 (2003) 622 642 www.elsevier.com/locate/physa Eciency of scale-free networks: error and attack tolerance Paolo Crucitti a, Vito Latora b, Massimo
Overlay (and P2P) Networks
 Overlay (and P2P) Networks Part II Recap (Small World, Erdös Rényi model, Duncan Watts Model) Graph Properties Scale Free Networks Preferential Attachment Evolving Copying Navigation in Small World Samu
Overlay (and P2P) Networks Part II Recap (Small World, Erdös Rényi model, Duncan Watts Model) Graph Properties Scale Free Networks Preferential Attachment Evolving Copying Navigation in Small World Samu
Master s Thesis. Title. Supervisor Professor Masayuki Murata. Author Yinan Liu. February 12th, 2016
 Master s Thesis Title A Study on the Effect of Physical Topology on the Robustness of Fractal Virtual Networks Supervisor Professor Masayuki Murata Author Yinan Liu February 12th, 2016 Department of Information
Master s Thesis Title A Study on the Effect of Physical Topology on the Robustness of Fractal Virtual Networks Supervisor Professor Masayuki Murata Author Yinan Liu February 12th, 2016 Department of Information
Failure in Complex Social Networks
 Journal of Mathematical Sociology, 33:64 68, 2009 Copyright # Taylor & Francis Group, LLC ISSN: 0022-250X print/1545-5874 online DOI: 10.1080/00222500802536988 Failure in Complex Social Networks Damon
Journal of Mathematical Sociology, 33:64 68, 2009 Copyright # Taylor & Francis Group, LLC ISSN: 0022-250X print/1545-5874 online DOI: 10.1080/00222500802536988 Failure in Complex Social Networks Damon
Characteristics of Preferentially Attached Network Grown from. Small World
 Characteristics of Preferentially Attached Network Grown from Small World Seungyoung Lee Graduate School of Innovation and Technology Management, Korea Advanced Institute of Science and Technology, Daejeon
Characteristics of Preferentially Attached Network Grown from Small World Seungyoung Lee Graduate School of Innovation and Technology Management, Korea Advanced Institute of Science and Technology, Daejeon
Empirical analysis of online social networks in the age of Web 2.0
 Physica A 387 (2008) 675 684 www.elsevier.com/locate/physa Empirical analysis of online social networks in the age of Web 2.0 Feng Fu, Lianghuan Liu, Long Wang Center for Systems and Control, College of
Physica A 387 (2008) 675 684 www.elsevier.com/locate/physa Empirical analysis of online social networks in the age of Web 2.0 Feng Fu, Lianghuan Liu, Long Wang Center for Systems and Control, College of
Supplementary material to Epidemic spreading on complex networks with community structures
 Supplementary material to Epidemic spreading on complex networks with community structures Clara Stegehuis, Remco van der Hofstad, Johan S. H. van Leeuwaarden Supplementary otes Supplementary ote etwork
Supplementary material to Epidemic spreading on complex networks with community structures Clara Stegehuis, Remco van der Hofstad, Johan S. H. van Leeuwaarden Supplementary otes Supplementary ote etwork
Complex-Network Modelling and Inference
 Complex-Network Modelling and Inference Lecture 8: Graph features (2) Matthew Roughan http://www.maths.adelaide.edu.au/matthew.roughan/notes/ Network_Modelling/ School
Complex-Network Modelling and Inference Lecture 8: Graph features (2) Matthew Roughan http://www.maths.adelaide.edu.au/matthew.roughan/notes/ Network_Modelling/ School
arxiv:cond-mat/ v5 [cond-mat.dis-nn] 16 Aug 2006
![arxiv:cond-mat/ v5 [cond-mat.dis-nn] 16 Aug 2006 arxiv:cond-mat/ v5 [cond-mat.dis-nn] 16 Aug 2006](/thumbs/77/74621232.jpg) arxiv:cond-mat/0505185v5 [cond-mat.dis-nn] 16 Aug 2006 Characterization of Complex Networks: A Survey of measurements L. da F. Costa F. A. Rodrigues G. Travieso P. R. Villas Boas Instituto de Física de
arxiv:cond-mat/0505185v5 [cond-mat.dis-nn] 16 Aug 2006 Characterization of Complex Networks: A Survey of measurements L. da F. Costa F. A. Rodrigues G. Travieso P. R. Villas Boas Instituto de Física de
Complex Networks: Ubiquity, Importance and Implications. Alessandro Vespignani
 Contribution : 2005 NAE Frontiers of Engineering Complex Networks: Ubiquity, Importance and Implications Alessandro Vespignani School of Informatics and Department of Physics, Indiana University, USA 1
Contribution : 2005 NAE Frontiers of Engineering Complex Networks: Ubiquity, Importance and Implications Alessandro Vespignani School of Informatics and Department of Physics, Indiana University, USA 1
CSCI5070 Advanced Topics in Social Computing
 CSCI5070 Advanced Topics in Social Computing Irwin King The Chinese University of Hong Kong king@cse.cuhk.edu.hk!! 2012 All Rights Reserved. Outline Scale-Free Networks Generation Properties Analysis Dynamic
CSCI5070 Advanced Topics in Social Computing Irwin King The Chinese University of Hong Kong king@cse.cuhk.edu.hk!! 2012 All Rights Reserved. Outline Scale-Free Networks Generation Properties Analysis Dynamic
arxiv:cond-mat/ v3 [cond-mat.dis-nn] 30 Jun 2005
![arxiv:cond-mat/ v3 [cond-mat.dis-nn] 30 Jun 2005 arxiv:cond-mat/ v3 [cond-mat.dis-nn] 30 Jun 2005](/thumbs/72/67577111.jpg) arxiv:cond-mat/0505185v3 [cond-mat.dis-nn] 30 Jun 2005 Characterization of Complex Networks: A Survey of measurements L. da F. Costa F. A. Rodrigues G. Travieso P. R. Villas Boas Instituto de Física de
arxiv:cond-mat/0505185v3 [cond-mat.dis-nn] 30 Jun 2005 Characterization of Complex Networks: A Survey of measurements L. da F. Costa F. A. Rodrigues G. Travieso P. R. Villas Boas Instituto de Física de
Preliminaries: networks and graphs
 978--52-8795-7 - Dynamical Processes on Complex Networks Preliminaries: networks and graphs In this chapter we introduce the reader to the basic definitions of network and graph theory. We define metrics
978--52-8795-7 - Dynamical Processes on Complex Networks Preliminaries: networks and graphs In this chapter we introduce the reader to the basic definitions of network and graph theory. We define metrics
V 2 Clusters, Dijkstra, and Graph Layout
 Bioinformatics 3 V 2 Clusters, Dijkstra, and Graph Layout Mon, Oct 31, 2016 Graph Basics A graph G is an ordered pair (V, E) of a set V of vertices and a set E of edges. Degree distribution P(k) Random
Bioinformatics 3 V 2 Clusters, Dijkstra, and Graph Layout Mon, Oct 31, 2016 Graph Basics A graph G is an ordered pair (V, E) of a set V of vertices and a set E of edges. Degree distribution P(k) Random
CS224W: Analysis of Networks Jure Leskovec, Stanford University
 CS224W: Analysis of Networks Jure Leskovec, Stanford University http://cs224w.stanford.edu 11/13/17 Jure Leskovec, Stanford CS224W: Analysis of Networks, http://cs224w.stanford.edu 2 Observations Models
CS224W: Analysis of Networks Jure Leskovec, Stanford University http://cs224w.stanford.edu 11/13/17 Jure Leskovec, Stanford CS224W: Analysis of Networks, http://cs224w.stanford.edu 2 Observations Models
Phase Transitions in Random Graphs- Outbreak of Epidemics to Network Robustness and fragility
 Phase Transitions in Random Graphs- Outbreak of Epidemics to Network Robustness and fragility Mayukh Nilay Khan May 13, 2010 Abstract Inspired by empirical studies researchers have tried to model various
Phase Transitions in Random Graphs- Outbreak of Epidemics to Network Robustness and fragility Mayukh Nilay Khan May 13, 2010 Abstract Inspired by empirical studies researchers have tried to model various
An Exploratory Journey Into Network Analysis A Gentle Introduction to Network Science and Graph Visualization
 An Exploratory Journey Into Network Analysis A Gentle Introduction to Network Science and Graph Visualization Pedro Ribeiro (DCC/FCUP & CRACS/INESC-TEC) Part 1 Motivation and emergence of Network Science
An Exploratory Journey Into Network Analysis A Gentle Introduction to Network Science and Graph Visualization Pedro Ribeiro (DCC/FCUP & CRACS/INESC-TEC) Part 1 Motivation and emergence of Network Science
My favorite application using eigenvalues: partitioning and community detection in social networks
 My favorite application using eigenvalues: partitioning and community detection in social networks Will Hobbs February 17, 2013 Abstract Social networks are often organized into families, friendship groups,
My favorite application using eigenvalues: partitioning and community detection in social networks Will Hobbs February 17, 2013 Abstract Social networks are often organized into families, friendship groups,
MIDTERM EXAMINATION Networked Life (NETS 112) November 21, 2013 Prof. Michael Kearns
 MIDTERM EXAMINATION Networked Life (NETS 112) November 21, 2013 Prof. Michael Kearns This is a closed-book exam. You should have no material on your desk other than the exam itself and a pencil or pen.
MIDTERM EXAMINATION Networked Life (NETS 112) November 21, 2013 Prof. Michael Kearns This is a closed-book exam. You should have no material on your desk other than the exam itself and a pencil or pen.
Random Graph Model; parameterization 2
 Agenda Random Graphs Recap giant component and small world statistics problems: degree distribution and triangles Recall that a graph G = (V, E) consists of a set of vertices V and a set of edges E V V.
Agenda Random Graphs Recap giant component and small world statistics problems: degree distribution and triangles Recall that a graph G = (V, E) consists of a set of vertices V and a set of edges E V V.
Graph Theory Review. January 30, Network Science Analytics Graph Theory Review 1
 Graph Theory Review Gonzalo Mateos Dept. of ECE and Goergen Institute for Data Science University of Rochester gmateosb@ece.rochester.edu http://www.ece.rochester.edu/~gmateosb/ January 30, 2018 Network
Graph Theory Review Gonzalo Mateos Dept. of ECE and Goergen Institute for Data Science University of Rochester gmateosb@ece.rochester.edu http://www.ece.rochester.edu/~gmateosb/ January 30, 2018 Network
- relationships (edges) among entities (nodes) - technology: Internet, World Wide Web - biology: genomics, gene expression, proteinprotein
 Complex networks Phys 7682: Computational Methods for Nonlinear Systems networks are everywhere (and always have been) - relationships (edges) among entities (nodes) explosion of interest in network structure,
Complex networks Phys 7682: Computational Methods for Nonlinear Systems networks are everywhere (and always have been) - relationships (edges) among entities (nodes) explosion of interest in network structure,
Gaussian and Exponential Architectures in Small-World Associative Memories
 and Architectures in Small-World Associative Memories Lee Calcraft, Rod Adams and Neil Davey School of Computer Science, University of Hertfordshire College Lane, Hatfield, Herts AL1 9AB, U.K. {L.Calcraft,
and Architectures in Small-World Associative Memories Lee Calcraft, Rod Adams and Neil Davey School of Computer Science, University of Hertfordshire College Lane, Hatfield, Herts AL1 9AB, U.K. {L.Calcraft,
The quantitative analysis of interactions takes bioinformatics to the next higher dimension: we go from 1D to 2D with graph theory.
 1 The human protein-protein interaction network of aging-associated genes. A total of 261 aging-associated genes were assembled using the GenAge Human Database. Protein-protein interactions of the human
1 The human protein-protein interaction network of aging-associated genes. A total of 261 aging-associated genes were assembled using the GenAge Human Database. Protein-protein interactions of the human
Higher order clustering coecients in Barabasi Albert networks
 Physica A 316 (2002) 688 694 www.elsevier.com/locate/physa Higher order clustering coecients in Barabasi Albert networks Agata Fronczak, Janusz A. Ho lyst, Maciej Jedynak, Julian Sienkiewicz Faculty of
Physica A 316 (2002) 688 694 www.elsevier.com/locate/physa Higher order clustering coecients in Barabasi Albert networks Agata Fronczak, Janusz A. Ho lyst, Maciej Jedynak, Julian Sienkiewicz Faculty of
V4 Matrix algorithms and graph partitioning
 V4 Matrix algorithms and graph partitioning - Community detection - Simple modularity maximization - Spectral modularity maximization - Division into more than two groups - Other algorithms for community
V4 Matrix algorithms and graph partitioning - Community detection - Simple modularity maximization - Spectral modularity maximization - Division into more than two groups - Other algorithms for community
1. Performance Comparison of Interdependent and Isolated Systems
 Supplementary Information for: Fu, G., Dawson, R., Khoury, M., & Bullock, S. (2014) Interdependent networks: Vulnerability analysis and strategies to limit cascading failure, European Physical Journal
Supplementary Information for: Fu, G., Dawson, R., Khoury, M., & Bullock, S. (2014) Interdependent networks: Vulnerability analysis and strategies to limit cascading failure, European Physical Journal
SELECTION OF A MULTIVARIATE CALIBRATION METHOD
 SELECTION OF A MULTIVARIATE CALIBRATION METHOD 0. Aim of this document Different types of multivariate calibration methods are available. The aim of this document is to help the user select the proper
SELECTION OF A MULTIVARIATE CALIBRATION METHOD 0. Aim of this document Different types of multivariate calibration methods are available. The aim of this document is to help the user select the proper
ECS 253 / MAE 253, Lecture 8 April 21, Web search and decentralized search on small-world networks
 ECS 253 / MAE 253, Lecture 8 April 21, 2016 Web search and decentralized search on small-world networks Search for information Assume some resource of interest is stored at the vertices of a network: Web
ECS 253 / MAE 253, Lecture 8 April 21, 2016 Web search and decentralized search on small-world networks Search for information Assume some resource of interest is stored at the vertices of a network: Web
γ : constant Goett 2 P(k) = k γ k : degree
 Goett 1 Jeffrey Goett Final Research Paper, Fall 2003 Professor Madey 19 December 2003 Abstract: Recent observations by physicists have lead to new theories about the mechanisms controlling the growth
Goett 1 Jeffrey Goett Final Research Paper, Fall 2003 Professor Madey 19 December 2003 Abstract: Recent observations by physicists have lead to new theories about the mechanisms controlling the growth
Structural Analysis of Paper Citation and Co-Authorship Networks using Network Analysis Techniques
 Structural Analysis of Paper Citation and Co-Authorship Networks using Network Analysis Techniques Kouhei Sugiyama, Hiroyuki Ohsaki and Makoto Imase Graduate School of Information Science and Technology,
Structural Analysis of Paper Citation and Co-Authorship Networks using Network Analysis Techniques Kouhei Sugiyama, Hiroyuki Ohsaki and Makoto Imase Graduate School of Information Science and Technology,
1 Degree Distributions
 Lecture Notes: Social Networks: Models, Algorithms, and Applications Lecture 3: Jan 24, 2012 Scribes: Geoffrey Fairchild and Jason Fries 1 Degree Distributions Last time, we discussed some graph-theoretic
Lecture Notes: Social Networks: Models, Algorithms, and Applications Lecture 3: Jan 24, 2012 Scribes: Geoffrey Fairchild and Jason Fries 1 Degree Distributions Last time, we discussed some graph-theoretic
Graph Structure Over Time
 Graph Structure Over Time Observing how time alters the structure of the IEEE data set Priti Kumar Computer Science Rensselaer Polytechnic Institute Troy, NY Kumarp3@rpi.edu Abstract This paper examines
Graph Structure Over Time Observing how time alters the structure of the IEEE data set Priti Kumar Computer Science Rensselaer Polytechnic Institute Troy, NY Kumarp3@rpi.edu Abstract This paper examines
CS249: SPECIAL TOPICS MINING INFORMATION/SOCIAL NETWORKS
 CS249: SPECIAL TOPICS MINING INFORMATION/SOCIAL NETWORKS Overview of Networks Instructor: Yizhou Sun yzsun@cs.ucla.edu January 10, 2017 Overview of Information Network Analysis Network Representation Network
CS249: SPECIAL TOPICS MINING INFORMATION/SOCIAL NETWORKS Overview of Networks Instructor: Yizhou Sun yzsun@cs.ucla.edu January 10, 2017 Overview of Information Network Analysis Network Representation Network
Topic II: Graph Mining
 Topic II: Graph Mining Discrete Topics in Data Mining Universität des Saarlandes, Saarbrücken Winter Semester 2012/13 T II.Intro-1 Topic II Intro: Graph Mining 1. Why Graphs? 2. What is Graph Mining 3.
Topic II: Graph Mining Discrete Topics in Data Mining Universität des Saarlandes, Saarbrücken Winter Semester 2012/13 T II.Intro-1 Topic II Intro: Graph Mining 1. Why Graphs? 2. What is Graph Mining 3.
The Topology and Dynamics of Complex Man- Made Systems
 The Topology and Dynamics of Complex Man- Made Systems Dan Braha New England Complex Institute Cambridge, MA, USA University of Massachusetts Dartmouth, MA, USA braha@necsi.edu http://necsi.edu/affiliates/braha/dan_braha-description.htm
The Topology and Dynamics of Complex Man- Made Systems Dan Braha New England Complex Institute Cambridge, MA, USA University of Massachusetts Dartmouth, MA, USA braha@necsi.edu http://necsi.edu/affiliates/braha/dan_braha-description.htm
CSE 258 Lecture 12. Web Mining and Recommender Systems. Social networks
 CSE 258 Lecture 12 Web Mining and Recommender Systems Social networks Social networks We ve already seen networks (a little bit) in week 3 i.e., we ve studied inference problems defined on graphs, and
CSE 258 Lecture 12 Web Mining and Recommender Systems Social networks Social networks We ve already seen networks (a little bit) in week 3 i.e., we ve studied inference problems defined on graphs, and
Modeling and Simulating Social Systems with MATLAB
 Modeling and Simulating Social Systems with MATLAB Lecture 8 Introduction to Graphs/Networks Olivia Woolley, Stefano Balietti, Lloyd Sanders, Dirk Helbing Chair of Sociology, in particular of Modeling
Modeling and Simulating Social Systems with MATLAB Lecture 8 Introduction to Graphs/Networks Olivia Woolley, Stefano Balietti, Lloyd Sanders, Dirk Helbing Chair of Sociology, in particular of Modeling
Smallest small-world network
 Smallest small-world network Takashi Nishikawa, 1, * Adilson E. Motter, 1, Ying-Cheng Lai, 1,2 and Frank C. Hoppensteadt 1,2 1 Department of Mathematics, Center for Systems Science and Engineering Research,
Smallest small-world network Takashi Nishikawa, 1, * Adilson E. Motter, 1, Ying-Cheng Lai, 1,2 and Frank C. Hoppensteadt 1,2 1 Department of Mathematics, Center for Systems Science and Engineering Research,
Case Studies in Complex Networks
 Case Studies in Complex Networks Introduction to Scientific Modeling CS 365 George Bezerra 08/27/2012 The origin of graph theory Königsberg bridge problem Leonard Euler (1707-1783) The Königsberg Bridge
Case Studies in Complex Networks Introduction to Scientific Modeling CS 365 George Bezerra 08/27/2012 The origin of graph theory Königsberg bridge problem Leonard Euler (1707-1783) The Königsberg Bridge
Homophily-Based Network Formation Models
 Homophily-Based Network Formation Models Senior Honors Project Final Report Scott Linderman School of Electrical and Computer Engineering Cornell University Frank H T Rhodes Hall Ithaca, NY 14853 swl28@cornell.edu
Homophily-Based Network Formation Models Senior Honors Project Final Report Scott Linderman School of Electrical and Computer Engineering Cornell University Frank H T Rhodes Hall Ithaca, NY 14853 swl28@cornell.edu
Spatial Patterns Point Pattern Analysis Geographic Patterns in Areal Data
 Spatial Patterns We will examine methods that are used to analyze patterns in two sorts of spatial data: Point Pattern Analysis - These methods concern themselves with the location information associated
Spatial Patterns We will examine methods that are used to analyze patterns in two sorts of spatial data: Point Pattern Analysis - These methods concern themselves with the location information associated
Distributed Detection in Sensor Networks: Connectivity Graph and Small World Networks
 Distributed Detection in Sensor Networks: Connectivity Graph and Small World Networks SaeedA.AldosariandJoséM.F.Moura Electrical and Computer Engineering Department Carnegie Mellon University 5000 Forbes
Distributed Detection in Sensor Networks: Connectivity Graph and Small World Networks SaeedA.AldosariandJoséM.F.Moura Electrical and Computer Engineering Department Carnegie Mellon University 5000 Forbes
Network Thinking. Complexity: A Guided Tour, Chapters 15-16
 Network Thinking Complexity: A Guided Tour, Chapters 15-16 Neural Network (C. Elegans) http://gephi.org/wp-content/uploads/2008/12/screenshot-celegans.png Food Web http://1.bp.blogspot.com/_vifbm3t8bou/sbhzqbchiei/aaaaaaaaaxk/rsc-pj45avc/
Network Thinking Complexity: A Guided Tour, Chapters 15-16 Neural Network (C. Elegans) http://gephi.org/wp-content/uploads/2008/12/screenshot-celegans.png Food Web http://1.bp.blogspot.com/_vifbm3t8bou/sbhzqbchiei/aaaaaaaaaxk/rsc-pj45avc/
V 2 Clusters, Dijkstra, and Graph Layout"
 Bioinformatics 3! V 2 Clusters, Dijkstra, and Graph Layout" Mon, Oct 21, 2013" Graph Basics" A graph G is an ordered pair (V, E) of a set V of vertices and a set E of edges." Degree distribution P(k)!
Bioinformatics 3! V 2 Clusters, Dijkstra, and Graph Layout" Mon, Oct 21, 2013" Graph Basics" A graph G is an ordered pair (V, E) of a set V of vertices and a set E of edges." Degree distribution P(k)!
V 2 Clusters, Dijkstra, and Graph Layout
 Bioinformatics 3 V 2 Clusters, Dijkstra, and Graph Layout Fri, Oct 19, 2012 Graph Basics A graph G is an ordered pair (V, E) of a set V of vertices and a set E of edges. Degree distribution P(k) Random
Bioinformatics 3 V 2 Clusters, Dijkstra, and Graph Layout Fri, Oct 19, 2012 Graph Basics A graph G is an ordered pair (V, E) of a set V of vertices and a set E of edges. Degree distribution P(k) Random
Degree Distribution: The case of Citation Networks
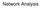 Network Analysis Degree Distribution: The case of Citation Networks Papers (in almost all fields) refer to works done earlier on same/related topics Citations A network can be defined as Each node is a
Network Analysis Degree Distribution: The case of Citation Networks Papers (in almost all fields) refer to works done earlier on same/related topics Citations A network can be defined as Each node is a
The Mathematical Description of Networks
 Modelling Complex Systems University of Manchester, 21 st 23 rd June 2010 Tim Evans Theoretical Physics The Mathematical Description of Networs Page 1 Notation I will focus on Simple Graphs with multiple
Modelling Complex Systems University of Manchester, 21 st 23 rd June 2010 Tim Evans Theoretical Physics The Mathematical Description of Networs Page 1 Notation I will focus on Simple Graphs with multiple
