Parallelism; Parallel Collections
|
|
|
- Marianna Bradley
- 5 years ago
- Views:
Transcription
1 Parallelism; Parallel Collections COS 326 Andrew W. Appel Princeton University slides copyright David Walker and Andrew W. Appel
2 let x = in 3 + x Visualizing Computational Costs
3 Visualizing Computational Costs x = cost = 1 let x = in 3 + x 3 + x cost = 1
4 Visualizing Computational Costs x = cost = 1 let x = in 3 + x 3 + x cost = 1 dependence: x = happens before 3 + x
5 Visualizing Computational Costs let x = in 3 + x x = x cost = 1 cost = 1 total cost = = 2
6 Visualizing Computational Costs (1 + 2 f 3) parallel pair: compute both left and right-hand sides independently return pair of values
7 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1
8 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 1 processor. How much time does this computation take?
9 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 1 processor. How much time does this computation take? Scheduld A-B-C-D:
10 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 1 processor. How much time does this computation take? Schedule A-C-B-D:
11 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 2 processors. How much time does this computation take?
12 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 2 processors. How much time does this computation take? Schedule A-CB-D: 1 + max(1,7) + 1 = 9
13 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 3 processors. How much time does this computation take?
14 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have 3 processors. How much time does this computation take? Schedule A-BC-D: 1 + max(1,7) + 1 = 9
15 Visualizing Computational Costs A cost = 1 cost = 1 (1 + 2 f 3) B C f 3 cost = 7 D (, ) cost = 1 Suppose we have infinite processors. How much time does this computation take? Schedule A-BC-D: 1 + max(1,7) + 1 = 9
16 Work and Span Understanding the complexity of a parallel program is a little more complex than a sequential program the number of processors has a significant effect One way to approximate the cost is to consider of a parallel algorithm independently of the machine it runs on is to consider two metrics: Work: The cost of executing a program with just 1 processor. Span: The cost of executing a program with an infinite number of processors Always good to minimize work Every instruction executed consumes energy Minimize span as a second consideration Communication costs are also crucial (we are ignoring them)
17 Parallelism The parallelism of an algorithm is an estimate of the maximum number of processors an algorithm can profit from. parallelism = work / span If work = span then parallelism = 1. We can only use 1 processor It's a sequential algorithm If span = ½ work then parallelism = 2 We can use up to 2 processors If work = 100, span = 1 All operations are independent & can be executed in parallel We can use up to 100 processors
18 Series-Parallel Graphs one operation two operations in sequence e1; e2 two operations in parallel (e1 e2) Series-parallel graphs arise from execution of functional programs with parallel pairs. Also known as well-structured, nested parallelism.
19 Series-Parallel Graphs Compose one operation two graphs in sequence two graphs in parallel In general, a series-parallel graph has a source and a sink and is: a single node two series-parallel graphs in sequence two series-parallel graphs in parallel
20 Not a Series-Parallel Graph However: The results about greedy schedulers (next few slides) do apply to DAG schedules as well as series-parallel schedules!
21 Work and Span of Series-Parallel Graphs Let's assume each node costs 1. Work: sum the nodes. Span: longest path from source to sink.
22 Work and Span of Acyclic Graphs Let's assume each node costs 1. Work: sum the nodes. Span: longest path from source to sink. work = 10 span = 5
23 Scheduling Let's assume each node costs 1. A Let's assume we have 2 processors. How do we schedule computation? B G C D H I E J F
24 Scheduling Let's assume each node costs 1. A Let's assume we have 2 processors. How do we schedule computation? C B D H G I Option 1: A B G C D E J F
25 Scheduling Let's assume each node costs 1. A Let's assume we have 2 processors. How do we schedule computation? C B D H G I Option 1: A B G C D E H I J F E J F
26 Scheduling Let's assume each node costs 1. A Let's assume we have 2 processors. How do we schedule computation? C B D H G I Option 1: A B G C D E H H I I E J J F F E J F
27 Scheduling Let's assume each node costs 1. A Let's assume we have 2 processors. How do we schedule computation? C B D H G I Option 1: A B G C D E H H I I E J J F F E J F Conclusion: How you schedule jobs can have an impact on performance
28 Greedy Schedulers Greedy schedulers will schedule some task to a processor as soon as that processor is free. Doesn't sound so smart! Properties (for p processors): T(p) < work/p + span T(p) >= max(work/p, span) can't do better than perfect division between processors (work/p) can't be faster than span
29 Properties (for p processors): Greedy Schedulers max(work/p, span) <= T(p) < work/p + span Consequences: as span gets small relative to work/p work/p + span ==> work/p max(work/p, span) ==> work/p so T(p) ==> work/p -- greedy schedulers converge to the optimum! if span approaches the work work/p + span ==> span max(work/p, span) ==> span so T(p) ==> span greedy schedulers converge to the optimum!
30 COMPLEXITY OF PARALLEL PROGRAMS
31 Divide-and-Conquer Parallel Algorithms Split your input in 2 or more subproblems Solve the subproblems recursively in parallel Combine the results to solve the overall problem split recur in parallel merge
32 Mergesort (on lists) let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 ;; for sequential mergesort, replace with: (mergesort sorted1, mergesort sorted2)
33 Mergesort (on lists) let rec split l = match l with [] -> ([], []) [x] -> ([x], []) x :: y :: xs -> let (pile1, pile2) = split xs in (x :: pile1, y :: pile2) let rec merge l1 l2 = match (l1, l2) with ([], l2) -> l2 (l1, []) -> l1 (x :: xs, y :: ys) -> if x < y then x :: merge xs l2 else y :: merge l1 ys
34 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: work_mergesort(n) = work_split(n) + 2*work_mergesort(n/2) + work_merge(n)
35 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: work_mergesort(n) = work_split(n) + 2*work_mergesort(n/2) + work_merge(n) read this as "approximately equal to" = k1*n + 2*work_mergesort(n/2) + k2*n
36 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: work_mergesort(n) = work_split(n) + 2*work_mergesort(n/2) + work_merge(n) = k*n + 2*work_mergesort(n/2)
37 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: work_mergesort(n) = work_split(n) + 2*work_mergesort(n/2) + work_merge(n) = k*n + 2*work_mergesort(n/2) = O(n log n)
38 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: span_mergesort(n) = span_split(n) + max(span_mergesort(n/2), span_mergesort(n/2)) + span_merge(n)
39 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: span_mergesort(n) = k*n + span_mergesort(n/2)
40 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: span_mergesort(n) = k*n + k*(n/2 + n/4 + n/8 +...)
41 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Assume input list of size n: span_mergesort(n) = 2*k*n = O(n)
42 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Summary for input list of size n: work_mergesort(n) = k*n*log n span_mergesort(n) = k*n parallelism?
43 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Summary for input list of size n: work_mergesort(n) = k*n*log n span_mergesort(n) = k*n parallelism? parallelism = work/span = n*log n / n = log n when sorting 10 billion entries, can only make use of 30 machines
44 Complexity let rec mergesort (l : int list) : int list = match l with [] -> [] [x] -> [x] _ -> let (pile1,pile2) = split l in let (sorted1,sorted2) = both mergesort pile1 mergesort pile2 in merge sorted1 sorted2 Summary for input list of size n: work_mergesort(n) = k*n*log n span_mergesort(n) = k*n splitting and merging take linear time too long to get good speedups parallelism? parallelism = work/span = n*log n / n = log n when sorting 10 billion entries, can only make use of 30 machines
45 Complexity when sorting 10 billion entries, can only make use of 30 machines/cores data centers have 10s of 1000s of machines or more Problem: splitting and merging take linear time too long to get good speedups Problem: cutting a list in half takes at least time proportional to n/2 Problem: stitching 2 lists together of size n/2 takes n/2 time Conclusion: lists are a bad data structure to choose
46 Complexity Consider balanced trees: splitting is pretty easy in constant time merging is harder, but can be done in poly-log time
47 Parallel TreeSort type tree = Empty Node of tree * int * tree let node left i right = Node (left, i, right) let one i = node Empty i Empty Problem: Given a balanced tree t, return a balanced tree with the same elements, in order: elements in the left subtree are less than the root elements in the right subtree are greater than the root
48 Parallel TreeSort type tree = Empty Node of tree * int * tree let node left i right = Node (left, i, right) let one i = node Empty i Empty let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in rebalance(merge (merge l' r') (one i)) We are going to ignore this.
49 Parallel TreeSort type tree = Empty Node of tree * int * tree let node left i right = Node (left, i, right) let one i = node Empty i Empty let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in merge (merge l' r') (one i)
50 Merging trees Subproblem: Given two sorted, balanced trees, l and r, create a new tree with the same elements that is also balanced and whose elements are in order. Uses split_at t i divides t into items less than i and items greater than i let rec merge (t1:tree) (t2:tree) : tree = match t1 with Empty -> t2 Node (l1, i, r1) -> let (l2, r2) = split_at t2 i in let (t1', t2') = both (merge l1) l2 (merge r1) r2 in Node (t1', i, t2')
51 Splitting a tree Sub-problem: Divide t in to items less than i and items greater than i let rec split_at t bound = match t with Empty -> (Empty, Empty) Node (l, i, r) -> if bound < i then let (ll, lr) = split_at l bound in (ll, Node (lr, i, r)) else let (rl, rr) = split_at r bound in (Node (l, i, rl), rr)
52 Splitting a tree Sub-problem: Divide t in to items less than i and items greater than i let rec split_at t bound = match t with Empty -> (Empty, Empty) Node (l, i, r) -> if bound < i then let (ll, lr) = split_at l bound in (ll, Node (lr, i, r)) else let (rl, rr) = split_at r bound in (Node (l, i, rl), rr) span (h) = k*h where h is the height of the tree t h = log(n) if t is balanced with n nodes
53 Span of Merge let rec merge (t1:tree) (t2:tree) : tree = match t1 with Empty -> t2 Node (l1, i, r1) -> let (l2, r2) = split_at t2 i in let (t1', t2') = both (merge l1) l2 (merge r1) r2 in Node (t1', i, t2') let's assume t1 and t2 are balanced and have heights h1, h2 and h1 >= h2: span_merge(h1,h2) = span_split(h2) + max(span_merge(h1-1), span_merge(h2-1)) = k*h2 + span_merge(h1-1) = k*h2*h1
54 Span of Parallel TreeSort let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in merge (merge l' r') (one i) let's assume: t is balanced with n nodes and height h = log n tsort returns balanced trees (l', r') merge returns balanced trees
55 Span of Parallel TreeSort let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in merge (merge l' r') (one i) let's assume: t is balanced with n nodes and height h = log n tsort returns balanced trees (l', r') merge returns balanced trees span_tsort(h) = max(span_tsort(h-1), span_tsort(h-1)) + span_merge(h-1,h-1) + span_merge(h,1)
56 Span of Parallel TreeSort let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in merge (merge l' r') (one i) let's assume: t is balanced with n nodes and height h = log n tsort returns balanced trees (l', r') merge returns balanced trees span_tsort(h) = max(span_tsort(h-1), span_tsort(h-1)) + span_merge(h-1,h-1) + span_merge(h,1) = span_tsort(h-1) + k*(h-1)*(h-1) + k*h
57 Span of Parallel TreeSort let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in merge (merge l' r') (one i) let's assume: t is balanced with n nodes and height h = log n tsort returns balanced trees (l', r') merge returns balanced trees span_tsort(h) = max(span_tsort(h-1), span_tsort(h-1)) + span_merge(h-1,h-1) + span_merge(h,1) = span_tsort(h-1) + k*(h-1)*(h-1) + k*h = k*h*h*h
58 Span of Parallel TreeSort let rec tsort t = match t with Empty -> Empty Node (l, i, r) -> let (l', r') = both tsort l tsort r in merge (merge l' r') (one i) let's assume: t is balanced with n nodes and height h = log n tsort returns balanced trees (l', r') merge returns balanced trees = k*h 3 = O(log 3 n) span_tsort(h) = max(span_tsort(h-1), span_tsort(h-1)) + span_merge(h-1,h-1) + span_merge(h,1) = span_tsort(h-1) + k*(h-1)*(h-1) + k*h = k*h*h*h
59 Summary of Parallel Sorting Exercise Both parallel list sort and parallel tree sort follow a traditional parallel divide-and-conquer strategy. By changing data structures from lists to trees, we were able to: split our data in half in constant span instead of linear span merge our data back together in log 3 n span instead of linear span We get more parallelism: with lists: work/span = log n make use of 30 machines when sorting 10 billion items with trees: work/span = n log n/log 3 n = n/log 2 n make use of millions* of machines when sorting 10 billion items caveat: we didn't factor in data communication costs! *Well, almost. What is log 2 (10,000,000,000)?
60 Summary: Work, Span, Parallelism Series parallel-graphs describe the kinds of control structures that arise in pure functional programs with structured, parallel fork-join execution Work: total number/cost of operations time program execution takes with 1 processor Work( e1 e2 ) = Work(e1) + Work(e2) + 1 Span: length of the longest dependency chain time program execution takes with infinite processors Span ( e1 e2 ) = max (Span e1, Span e2) + 1 Parallelism: Work / Span Many parallel algorithms follow a divide-and-conquer strategy efficient algorithms divide quickly and merge quickly
61 Parallel Collections COS 326 Andrew W. Appel Princeton University slides copyright David Walker and Andrew W. Appel
62 Parallel Collections One way to give programmers access to parallelism in a functional style (even in an imperative language) is to develop a library for programming parallel collections Example collections: sets, tables, dictionaries, sequences Example bulk operations: create, map, reduce, join, filter
63 Parallel sequences Parallel Sequences < e1, e2, e3,..., en > Languages: Nesl [Blelloch] Data-parallel Haskell
64 Parallel Sequences: Selected Operations tabulate : (int -> 'a) -> int -> 'a seq tabulate f n == <f 0, f 1,..., f (n-1)> work = O(n) span = O(1)
65 Parallel Sequences: Selected Operations tabulate : (int -> 'a) -> int -> 'a seq tabulate f n == <f 0, f 1,..., f (n-1)> work = O(n work(f)) span = O(1 span(f)) nth : 'a seq -> int -> 'a nth <e0, e1,..., e(n-1)> i == ei work = O(1) span = O(1)
66 Parallel Sequences: Selected Operations tabulate : (int -> 'a) -> int -> 'a seq tabulate f n == <f 0, f 1,..., f (n-1)> work = O(n work(f)) span = O(1 span(f)) nth : 'a seq -> int -> 'a nth <e0, e1,..., e(n-1)> i == ei work = O(1) span = O(1) length : 'a seq -> int length <e0, e1,..., e(n-1)> == n work = O(1) span = O(1)
67 Problems Write a function that creates the sequence <0,..., n-1> Write a function such that given a sequence <v0,..., vn-1>, maps f over each element of the sequence. Work = O(n); Span = O(1) (if f is a constant-work function) Write a function such that given a sequence <v1,..., vn-1>, reverses the sequence. Work = O(n); Span = O(1) Operations: Try it! tabulate f n nth i s length s
68 Solutions (* create n == <0, 1,..., n-1> *) let create n = tabulate (fun i -> i) n (* map f <v0,..., vn-1> == <f v0,..., f vn-1> *) let map f s = tabulate (fun i -> nth s i) (length s) (* reverse <v0,..., vn-1> == <vn-1,..., v0> *) let map f s = let n = length s in tabulate (fun i -> nth s (n-i-1)) n
69 One more problem Consider the problem of determining whether a sequence of parentheses is balanced or not. For example: balanced: ()()(()) not balanced: ( or ) or ())) Try formulating a divide-and-conquer parallel algorithm to solve this problem efficiently: type paren = L R (* L(eft) or R(ight) paren *) let balanced (ps : paren list) : bool =... You will need another function on sequences: (* split s n divides s into (s1, s2) such that s1 is the first n elements of s and s2 is the rest Work = O(n) Span = O(1) *) split : 'a sequence -> int -> 'a sequence * 'a sequence
Parallelism and Concurrency (Part II) COS 326 David Walker Princeton University
 Parallelism and Concurrency (Part II) COS 326 David Walker Princeton University let x = 1 + 2 in 3 + x Visualizing ComputaConal Costs Visualizing ComputaConal Costs x = 1 + 2 let x = 1 + 2 in 3 + x 3 +
Parallelism and Concurrency (Part II) COS 326 David Walker Princeton University let x = 1 + 2 in 3 + x Visualizing ComputaConal Costs Visualizing ComputaConal Costs x = 1 + 2 let x = 1 + 2 in 3 + x 3 +
Merge Sort fi fi fi 4 9. Merge Sort Goodrich, Tamassia
 Merge Sort 7 9 4 fi 4 7 9 7 fi 7 9 4 fi 4 9 7 fi 7 fi 9 fi 9 4 fi 4 Merge Sort 1 Divide-and-Conquer ( 10.1.1) Divide-and conquer is a general algorithm design paradigm: Divide: divide the input data S
Merge Sort 7 9 4 fi 4 7 9 7 fi 7 9 4 fi 4 9 7 fi 7 fi 9 fi 9 4 fi 4 Merge Sort 1 Divide-and-Conquer ( 10.1.1) Divide-and conquer is a general algorithm design paradigm: Divide: divide the input data S
Lecture 6: Sequential Sorting
 15-150 Lecture 6: Sequential Sorting Lecture by Dan Licata February 2, 2012 Today s lecture is about sorting. Along the way, we ll learn about divide and conquer algorithms, the tree method, and complete
15-150 Lecture 6: Sequential Sorting Lecture by Dan Licata February 2, 2012 Today s lecture is about sorting. Along the way, we ll learn about divide and conquer algorithms, the tree method, and complete
Quick-Sort fi fi fi 7 9. Quick-Sort Goodrich, Tamassia
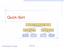 Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Quick-Sort 7 4 9 6 2 fi 2 4 6 7 9 4 2 fi 2 4 7 9 fi 7 9 2 fi 2 9 fi 9 Quick-Sort 1 Quick-Sort ( 10.2 text book) Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm: x
Sorting Goodrich, Tamassia Sorting 1
 Sorting Put array A of n numbers in increasing order. A core algorithm with many applications. Simple algorithms are O(n 2 ). Optimal algorithms are O(n log n). We will see O(n) for restricted input in
Sorting Put array A of n numbers in increasing order. A core algorithm with many applications. Simple algorithms are O(n 2 ). Optimal algorithms are O(n log n). We will see O(n) for restricted input in
Algorithm classification
 Types of Algorithms Algorithm classification Algorithms that use a similar problem-solving approach can be grouped together We ll talk about a classification scheme for algorithms This classification scheme
Types of Algorithms Algorithm classification Algorithms that use a similar problem-solving approach can be grouped together We ll talk about a classification scheme for algorithms This classification scheme
DIVIDE AND CONQUER ALGORITHMS ANALYSIS WITH RECURRENCE EQUATIONS
 CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
CHAPTER 11 SORTING ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY M. AMATO AND
Merge Sort Goodrich, Tamassia Merge Sort 1
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Merge Sort 1 Review of Sorting Selection-sort: Search: search through remaining unsorted elements for min Remove: remove
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Merge Sort 1 Review of Sorting Selection-sort: Search: search through remaining unsorted elements for min Remove: remove
CSE 530A. B+ Trees. Washington University Fall 2013
 CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
Lecture 19 Sorting Goodrich, Tamassia
 Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
Lecture 19 Sorting 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 2004 Goodrich, Tamassia Outline Review 3 simple sorting algorithms: 1. selection Sort (in previous course) 2. insertion Sort (in previous
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, Merge Sort & Quick Sort
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort & Quick Sort 1 Divide-and-Conquer Divide-and conquer is a general algorithm
15 150: Principles of Functional Programming Sorting Integer Lists
 15 150: Principles of Functional Programming Sorting Integer Lists Michael Erdmann Spring 2018 1 Background Let s define what we mean for a list of integers to be sorted, by reference to datatypes and
15 150: Principles of Functional Programming Sorting Integer Lists Michael Erdmann Spring 2018 1 Background Let s define what we mean for a list of integers to be sorted, by reference to datatypes and
Sorting. Data structures and Algorithms
 Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
Sorting Data structures and Algorithms Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++ Goodrich, Tamassia and Mount (Wiley, 2004) Outline Bubble
CSE 332: Data Structures & Parallelism Lecture 15: Analysis of Fork-Join Parallel Programs. Ruth Anderson Autumn 2018
 CSE 332: Data Structures & Parallelism Lecture 15: Analysis of Fork-Join Parallel Programs Ruth Anderson Autumn 2018 Outline Done: How to use fork and join to write a parallel algorithm Why using divide-and-conquer
CSE 332: Data Structures & Parallelism Lecture 15: Analysis of Fork-Join Parallel Programs Ruth Anderson Autumn 2018 Outline Done: How to use fork and join to write a parallel algorithm Why using divide-and-conquer
SORTING, SETS, AND SELECTION
 CHAPTER 11 SORTING, SETS, AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM
CHAPTER 11 SORTING, SETS, AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM
A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 2 Analysis of Fork-Join Parallel Programs
 A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 2 Analysis of Fork-Join Parallel Programs Dan Grossman Last Updated: January 2016 For more information, see http://www.cs.washington.edu/homes/djg/teachingmaterials/
A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 2 Analysis of Fork-Join Parallel Programs Dan Grossman Last Updated: January 2016 For more information, see http://www.cs.washington.edu/homes/djg/teachingmaterials/
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort 2015 Goodrich and Tamassia Merge Sort 1 Application: Internet Search
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Merge Sort 2015 Goodrich and Tamassia Merge Sort 1 Application: Internet Search
What next? CSE332: Data Abstractions Lecture 20: Parallel Prefix and Parallel Sorting. The prefix-sum problem. Parallel prefix-sum
 What next? CSE332: Data Abstractions Lecture 20: Parallel Prefix and Parallel Sorting Dan Grossman Spring 2010 Done: Simple ways to use parallelism for counting, summing, finding Even though in practice
What next? CSE332: Data Abstractions Lecture 20: Parallel Prefix and Parallel Sorting Dan Grossman Spring 2010 Done: Simple ways to use parallelism for counting, summing, finding Even though in practice
A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 3 Parallel Prefix, Pack, and Sorting
 A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 3 Parallel Prefix, Pack, and Sorting Dan Grossman Last Updated: November 2012 For more information, see http://www.cs.washington.edu/homes/djg/teachingmaterials/
A Sophomoric Introduction to Shared-Memory Parallelism and Concurrency Lecture 3 Parallel Prefix, Pack, and Sorting Dan Grossman Last Updated: November 2012 For more information, see http://www.cs.washington.edu/homes/djg/teachingmaterials/
15 210: Parallel and Sequential Data Structures and Algorithms
 Full Name: Andrew ID: Section: 15 210: Parallel and Sequential Data Structures and Algorithms Practice Exam I February 2017 There are 11 pages in this examination, comprising 6 questions worth a total
Full Name: Andrew ID: Section: 15 210: Parallel and Sequential Data Structures and Algorithms Practice Exam I February 2017 There are 11 pages in this examination, comprising 6 questions worth a total
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
11. Divide and Conquer
 The whole is of necessity prior to the part. Aristotle 11. Divide and Conquer 11.1. Divide and Conquer Many recursive algorithms follow the divide and conquer philosophy. They divide the problem into smaller
The whole is of necessity prior to the part. Aristotle 11. Divide and Conquer 11.1. Divide and Conquer Many recursive algorithms follow the divide and conquer philosophy. They divide the problem into smaller
Comparison Sorts. Chapter 9.4, 12.1, 12.2
 Comparison Sorts Chapter 9.4, 12.1, 12.2 Sorting We have seen the advantage of sorted data representations for a number of applications Sparse vectors Maps Dictionaries Here we consider the problem of
Comparison Sorts Chapter 9.4, 12.1, 12.2 Sorting We have seen the advantage of sorted data representations for a number of applications Sparse vectors Maps Dictionaries Here we consider the problem of
Quick-Sort. Quick-sort is a randomized sorting algorithm based on the divide-and-conquer paradigm:
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 2014 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9
Next. 1. Covered basics of a simple design technique (Divideand-conquer) 2. Next, more sorting algorithms.
 Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
SORTING AND SELECTION
 2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
2 < > 1 4 8 6 = 9 CHAPTER 12 SORTING AND SELECTION ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 2016)
15-853:Algorithms in the Real World. Outline. Parallelism: Lecture 1 Nested parallelism Cost model Parallel techniques and algorithms
 :Algorithms in the Real World Parallelism: Lecture 1 Nested parallelism Cost model Parallel techniques and algorithms Page1 Andrew Chien, 2008 2 Outline Concurrency vs. Parallelism Quicksort example Nested
:Algorithms in the Real World Parallelism: Lecture 1 Nested parallelism Cost model Parallel techniques and algorithms Page1 Andrew Chien, 2008 2 Outline Concurrency vs. Parallelism Quicksort example Nested
1. Covered basics of a simple design technique (Divideand-conquer) 2. Next, more sorting algorithms.
 Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Next 1. Covered basics of a simple design technique (Divideand-conquer) Ch. 2 of the text. 2. Next, more sorting algorithms. Sorting Switch from design paradigms to applications. Sorting and order statistics
Quick-Sort. Quick-Sort 1
 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Quick-Sort 1 Outline and Reading Quick-sort ( 4.3) Algorithm Partition step Quick-sort tree Execution example Analysis of quick-sort (4.3.1) In-place
Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Quick-Sort 1 Outline and Reading Quick-sort ( 4.3) Algorithm Partition step Quick-sort tree Execution example Analysis of quick-sort (4.3.1) In-place
Parallel and Sequential Data Structures and Algorithms Lecture (Spring 2012) Lecture 16 Treaps; Augmented BSTs
 Lecture 16 Treaps; Augmented BSTs Parallel and Sequential Data Structures and Algorithms, 15-210 (Spring 2012) Lectured by Margaret Reid-Miller 8 March 2012 Today: - More on Treaps - Ordered Sets and Tables
Lecture 16 Treaps; Augmented BSTs Parallel and Sequential Data Structures and Algorithms, 15-210 (Spring 2012) Lectured by Margaret Reid-Miller 8 March 2012 Today: - More on Treaps - Ordered Sets and Tables
Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu
 Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Merge sort Quick sort Radix sort Summary We will see more complex techniques
Algorithms and Data Structures (INF1) Lecture 7/15 Hua Lu Department of Computer Science Aalborg University Fall 2007 This Lecture Merge sort Quick sort Radix sort Summary We will see more complex techniques
CSC Design and Analysis of Algorithms
 CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
Lecture 23: Parallelism. To Use Library. Getting Good Results. CS 62 Fall 2016 Kim Bruce & Peter Mawhorter
 Lecture 23: Parallelism CS 62 Fall 2016 Kim Bruce & Peter Mawhorter Some slides based on those from Dan Grossman, U. of Washington To Use Library Getting Good Results Create a ForkJoinPool Instead of subclass
Lecture 23: Parallelism CS 62 Fall 2016 Kim Bruce & Peter Mawhorter Some slides based on those from Dan Grossman, U. of Washington To Use Library Getting Good Results Create a ForkJoinPool Instead of subclass
Lecture 6 Sequences II. Parallel and Sequential Data Structures and Algorithms, (Fall 2013) Lectured by Danny Sleator 12 September 2013
 Lecture 6 Sequences II Parallel and Sequential Data Structures and Algorithms, 15-210 (Fall 2013) Lectured by Danny Sleator 12 September 2013 Material in this lecture: Today s lecture is about reduction.
Lecture 6 Sequences II Parallel and Sequential Data Structures and Algorithms, 15-210 (Fall 2013) Lectured by Danny Sleator 12 September 2013 Material in this lecture: Today s lecture is about reduction.
CSC Design and Analysis of Algorithms. Lecture 7. Transform and Conquer I Algorithm Design Technique. Transform and Conquer
 // CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more
// CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more
Lecture 6: Divide-and-Conquer
 Lecture 6: Divide-and-Conquer COSC242: Algorithms and Data Structures Brendan McCane Department of Computer Science, University of Otago Types of Algorithms In COSC242, we will be looking at 3 general
Lecture 6: Divide-and-Conquer COSC242: Algorithms and Data Structures Brendan McCane Department of Computer Science, University of Otago Types of Algorithms In COSC242, we will be looking at 3 general
1 Dynamic Programming
 Recitation 13 Dynamic Programming Parallel and Sequential Data Structures and Algorithms, 15-210 (Fall 2013) November 20, 2013 1 Dynamic Programming Dynamic programming is a technique to avoid needless
Recitation 13 Dynamic Programming Parallel and Sequential Data Structures and Algorithms, 15-210 (Fall 2013) November 20, 2013 1 Dynamic Programming Dynamic programming is a technique to avoid needless
Algorithms (IX) Guoqiang Li. School of Software, Shanghai Jiao Tong University
 Algorithms (IX) Guoqiang Li School of Software, Shanghai Jiao Tong University Q: What we have learned in Algorithm? Algorithm Design Algorithm Design Basic methodologies: Algorithm Design Algorithm Design
Algorithms (IX) Guoqiang Li School of Software, Shanghai Jiao Tong University Q: What we have learned in Algorithm? Algorithm Design Algorithm Design Basic methodologies: Algorithm Design Algorithm Design
Recitation 12. Dynamic Programming Announcements. SegmentLab has been released and is due Apr 14.
 Recitation 12 Dynamic Programming 12.1 Announcements SegmentLab has been released and is due Apr 14. 73 74 RECITATION 12. DYNAMIC PROGRAMMING 12.2 Matrix Chain Product Definition 12.1. In the matrix chain
Recitation 12 Dynamic Programming 12.1 Announcements SegmentLab has been released and is due Apr 14. 73 74 RECITATION 12. DYNAMIC PROGRAMMING 12.2 Matrix Chain Product Definition 12.1. In the matrix chain
QuickSort
 QuickSort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 1 QuickSort QuickSort on an input sequence S with n elements consists of three steps: n n n Divide: partition S into two sequences S 1 and S 2 of about
QuickSort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 1 QuickSort QuickSort on an input sequence S with n elements consists of three steps: n n n Divide: partition S into two sequences S 1 and S 2 of about
Parallel Sorting Algorithms
 CSC 391/691: GPU Programming Fall 015 Parallel Sorting Algorithms Copyright 015 Samuel S. Cho Sorting Algorithms Review Bubble Sort: O(n ) Insertion Sort: O(n ) Quick Sort: O(n log n) Heap Sort: O(n log
CSC 391/691: GPU Programming Fall 015 Parallel Sorting Algorithms Copyright 015 Samuel S. Cho Sorting Algorithms Review Bubble Sort: O(n ) Insertion Sort: O(n ) Quick Sort: O(n log n) Heap Sort: O(n log
Parallel Functional Programming Data Parallelism
 Parallel Functional Programming Data Parallelism Mary Sheeran http://www.cse.chalmers.se/edu/course/pfp Data parallelism Introduce parallel data structures and make operations on them parallel Often data
Parallel Functional Programming Data Parallelism Mary Sheeran http://www.cse.chalmers.se/edu/course/pfp Data parallelism Introduce parallel data structures and make operations on them parallel Often data
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 2015 Goodrich and Tamassia
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 Quick-Sort 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 2015 Goodrich and Tamassia
Merge Sort Goodrich, Tamassia. Merge Sort 1
 Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort 1 Divide-and-Conquer ( 10.1.1) Divide-and conquer is a general algorithm design paradigm: Divide: divide the input data S in two disjoint
Merge Sort 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Merge Sort 1 Divide-and-Conquer ( 10.1.1) Divide-and conquer is a general algorithm design paradigm: Divide: divide the input data S in two disjoint
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 03 / 25 / 2013 Instructor: Michael Eckmann Today s Topics Comments/Questions? More on Recursion Including Dynamic Programming technique Divide and Conquer techniques
CS 206 Introduction to Computer Science II 03 / 25 / 2013 Instructor: Michael Eckmann Today s Topics Comments/Questions? More on Recursion Including Dynamic Programming technique Divide and Conquer techniques
Shell CSCE 314 TAMU. Functions continued
 1 CSCE 314: Programming Languages Dr. Dylan Shell Functions continued 2 Outline Defining Functions List Comprehensions Recursion 3 A Function without Recursion Many functions can naturally be defined in
1 CSCE 314: Programming Languages Dr. Dylan Shell Functions continued 2 Outline Defining Functions List Comprehensions Recursion 3 A Function without Recursion Many functions can naturally be defined in
Info 2950, Lecture 16
 Info 2950, Lecture 16 28 Mar 2017 Prob Set 5: due Fri night 31 Mar Breadth first search (BFS) and Depth First Search (DFS) Must have an ordering on the vertices of the graph. In most examples here, the
Info 2950, Lecture 16 28 Mar 2017 Prob Set 5: due Fri night 31 Mar Breadth first search (BFS) and Depth First Search (DFS) Must have an ordering on the vertices of the graph. In most examples here, the
Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION
 DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
DESIGN AND ANALYSIS OF ALGORITHMS Unit 6 Chapter 15 EXAMPLES OF COMPLEXITY CALCULATION http://milanvachhani.blogspot.in EXAMPLES FROM THE SORTING WORLD Sorting provides a good set of examples for analyzing
Programming Languages and Techniques (CIS120)
 Programming Languages and Techniques (CIS120) Lecture 7 January 26, 2018 Binary Search Trees: Inserting and Deleting (Chapters 7 & 8) Announcements Read Chapters 7 & 8 Binary Search Trees Next up: generics
Programming Languages and Techniques (CIS120) Lecture 7 January 26, 2018 Binary Search Trees: Inserting and Deleting (Chapters 7 & 8) Announcements Read Chapters 7 & 8 Binary Search Trees Next up: generics
Sorting. Divide-and-Conquer 1
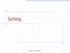 Sorting Divide-and-Conquer 1 Divide-and-Conquer 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Divide-and-Conquer 2 Divide-and-Conquer Divide-and conquer is a general algorithm design paradigm: Divide:
Sorting Divide-and-Conquer 1 Divide-and-Conquer 7 2 9 4 2 4 7 9 7 2 2 7 9 4 4 9 7 7 2 2 9 9 4 4 Divide-and-Conquer 2 Divide-and-Conquer Divide-and conquer is a general algorithm design paradigm: Divide:
Dynamic Programming Group Exercises
 Name: Name: Name: Dynamic Programming Group Exercises Adapted from material by Cole Frederick Please work the following problems in groups of 2 or 3. Use additional paper as needed, and staple the sheets
Name: Name: Name: Dynamic Programming Group Exercises Adapted from material by Cole Frederick Please work the following problems in groups of 2 or 3. Use additional paper as needed, and staple the sheets
CSE373: Data Structures & Algorithms Lecture 22: Parallel Reductions, Maps, and Algorithm Analysis. Kevin Quinn Fall 2015
 CSE373: Data Structures & Algorithms Lecture 22: Parallel Reductions, Maps, and Algorithm Analysis Kevin Quinn Fall 2015 Outline Done: How to write a parallel algorithm with fork and join Why using divide-and-conquer
CSE373: Data Structures & Algorithms Lecture 22: Parallel Reductions, Maps, and Algorithm Analysis Kevin Quinn Fall 2015 Outline Done: How to write a parallel algorithm with fork and join Why using divide-and-conquer
CSE 3101: Introduction to the Design and Analysis of Algorithms. Office hours: Wed 4-6 pm (CSEB 3043), or by appointment.
 CSE 3101: Introduction to the Design and Analysis of Algorithms Instructor: Suprakash Datta (datta[at]cse.yorku.ca) ext 77875 Lectures: Tues, BC 215, 7 10 PM Office hours: Wed 4-6 pm (CSEB 3043), or by
CSE 3101: Introduction to the Design and Analysis of Algorithms Instructor: Suprakash Datta (datta[at]cse.yorku.ca) ext 77875 Lectures: Tues, BC 215, 7 10 PM Office hours: Wed 4-6 pm (CSEB 3043), or by
UNIT 5B Binary Search
 205/09/30 UNIT 5B Binary Search Course Announcements Written exam next week (Wed. Oct 7 ) Practice exam available on the Resources page Exam reviews: Sunday afternoon; watch Piazza for times and places
205/09/30 UNIT 5B Binary Search Course Announcements Written exam next week (Wed. Oct 7 ) Practice exam available on the Resources page Exam reviews: Sunday afternoon; watch Piazza for times and places
Programming Languages and Techniques (CIS120)
 Programming Languages and Techniques () Lecture 6 January 24, 2018 Binary Search Trees (Lecture notes Chapter 7) Announcements Homework 2: Computing Human Evolution due Tuesday, September 19 th Reading:
Programming Languages and Techniques () Lecture 6 January 24, 2018 Binary Search Trees (Lecture notes Chapter 7) Announcements Homework 2: Computing Human Evolution due Tuesday, September 19 th Reading:
Spring 2018 Lecture 8. Sorting Integer Trees
 15-150 Spring 2018 Lecture 8 Sorting Integer Trees assessment msort(l) has O(n log n) work, where n is the length of L msort(l) has O(n) span So the speed-up factor obtainable by exploiting parallelism
15-150 Spring 2018 Lecture 8 Sorting Integer Trees assessment msort(l) has O(n log n) work, where n is the length of L msort(l) has O(n) span So the speed-up factor obtainable by exploiting parallelism
1 Dynamic Programming
 Recitation 13 Dynamic Programming Parallel and Sequential Data Structures and Algorithms, 15-210 (Spring 2013) April 17, 2013 1 Dynamic Programming Dynamic programming is a technique to avoid needless
Recitation 13 Dynamic Programming Parallel and Sequential Data Structures and Algorithms, 15-210 (Spring 2013) April 17, 2013 1 Dynamic Programming Dynamic programming is a technique to avoid needless
PROGRAMMING IN HASKELL. CS Chapter 6 - Recursive Functions
 PROGRAMMING IN HASKELL CS-205 - Chapter 6 - Recursive Functions 0 Introduction As we have seen, many functions can naturally be defined in terms of other functions. factorial :: Int Int factorial n product
PROGRAMMING IN HASKELL CS-205 - Chapter 6 - Recursive Functions 0 Introduction As we have seen, many functions can naturally be defined in terms of other functions. factorial :: Int Int factorial n product
Programming in Haskell Aug-Nov 2015
 Programming in Haskell Aug-Nov 2015 LECTURE 11 SEPTEMBER 10, 2015 S P SURESH CHENNAI MATHEMATICAL INSTITUTE Measuring efficiency Measuring efficiency Computation is reduction Application of definitions
Programming in Haskell Aug-Nov 2015 LECTURE 11 SEPTEMBER 10, 2015 S P SURESH CHENNAI MATHEMATICAL INSTITUTE Measuring efficiency Measuring efficiency Computation is reduction Application of definitions
Programming II (CS300)
 1 Programming II (CS300) Chapter 12: Sorting Algorithms MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Outline 2 Last week Implementation of the three tree depth-traversal algorithms Implementation of the BinarySearchTree
1 Programming II (CS300) Chapter 12: Sorting Algorithms MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Outline 2 Last week Implementation of the three tree depth-traversal algorithms Implementation of the BinarySearchTree
Lectures 17 and 18: Cost Semantics, Sequences, n-body Simulation
 15-150 Lectures 17 and 18: Cost Semantics, Sequences, n-body Simulation Lectures by Dan Licata March 20 and 22, 2012 Before we start, let s think about the big picture of parallelism Parallelism is relevant
15-150 Lectures 17 and 18: Cost Semantics, Sequences, n-body Simulation Lectures by Dan Licata March 20 and 22, 2012 Before we start, let s think about the big picture of parallelism Parallelism is relevant
2. (a) Explain when the Quick sort is preferred to merge sort and vice-versa.
 Code No: RR210504 Set No. 1 1. (a) Order the following functions according to their order of growth (from the lowest to the highest). (n-2)!, 5 log (n+100) 10,2 2n, 0.001n 4 +3n 3 +1, ln 2 n, n 1/3, 3
Code No: RR210504 Set No. 1 1. (a) Order the following functions according to their order of growth (from the lowest to the highest). (n-2)!, 5 log (n+100) 10,2 2n, 0.001n 4 +3n 3 +1, ln 2 n, n 1/3, 3
Sorting isn't only relevant to records and databases. It turns up as a component in algorithms in many other application areas surprisingly often.
 Sorting isn't only relevant to records and databases. It turns up as a component in algorithms in many other application areas surprisingly often. There are many graph algorithms which include sorting
Sorting isn't only relevant to records and databases. It turns up as a component in algorithms in many other application areas surprisingly often. There are many graph algorithms which include sorting
Divide & Conquer Algorithms
 Divide & Conquer Algorithms Outline MergeSort Finding the middle point in the alignment matrix in linear space Linear space sequence alignment Block Alignment Four-Russians speedup Constructing LCS in
Divide & Conquer Algorithms Outline MergeSort Finding the middle point in the alignment matrix in linear space Linear space sequence alignment Block Alignment Four-Russians speedup Constructing LCS in
Data Structures and Algorithms Chapter 4
 Data Structures and Algorithms Chapter. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Chapter Divide and conquer
Data Structures and Algorithms Chapter. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Chapter Divide and conquer
Chapter 4: Sorting. Spring 2014 Sorting Fun 1
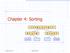 Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Chapter 4: Sorting 7 4 9 6 2 2 4 6 7 9 4 2 2 4 7 9 7 9 2 2 9 9 Spring 2014 Sorting Fun 1 What We ll Do! Quick Sort! Lower bound on runtimes for comparison based sort! Radix and Bucket sort Spring 2014
Friday Four Square! 4:15PM, Outside Gates
 Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Search Trees. Computer Science S-111 Harvard University David G. Sullivan, Ph.D. Binary Search Trees
 Unit 9, Part 2 Search Trees Computer Science S-111 Harvard University David G. Sullivan, Ph.D. Binary Search Trees Search-tree property: for each node k: all nodes in k s left subtree are < k all nodes
Unit 9, Part 2 Search Trees Computer Science S-111 Harvard University David G. Sullivan, Ph.D. Binary Search Trees Search-tree property: for each node k: all nodes in k s left subtree are < k all nodes
CSE 332: Analysis of Fork-Join Parallel Programs. Richard Anderson Spring 2016
 CSE 332: Analysis of Fork-Join Parallel Programs Richard Anderson Spring 2016 1 New Story: Shared Memory with Threads Threads, each with own unshared call stack and program counter Heap for all objects
CSE 332: Analysis of Fork-Join Parallel Programs Richard Anderson Spring 2016 1 New Story: Shared Memory with Threads Threads, each with own unshared call stack and program counter Heap for all objects
Course goals. exposure to another language. knowledge of specific data structures. impact of DS design & implementation on program performance
 Course goals exposure to another language C++ Object-oriented principles knowledge of specific data structures lists, stacks & queues, priority queues, dynamic dictionaries, graphs impact of DS design
Course goals exposure to another language C++ Object-oriented principles knowledge of specific data structures lists, stacks & queues, priority queues, dynamic dictionaries, graphs impact of DS design
Sorting and Selection
 Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Sorting and Selection Introduction Divide and Conquer Merge-Sort Quick-Sort Radix-Sort Bucket-Sort 10-1 Introduction Assuming we have a sequence S storing a list of keyelement entries. The key of the element
Divide and Conquer Algorithms
 Divide and Conquer Algorithms T. M. Murali February 19, 2009 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Divide and Conquer Algorithms T. M. Murali February 19, 2009 Divide and Conquer Break up a problem into several parts. Solve each part recursively. Solve base cases by brute force. Efficiently combine
Stacks and queues (chapters 6.6, 15.1, 15.5)
 Stacks and queues (chapters 6.6, 15.1, 15.5) So far... Complexity analysis For recursive and iterative programs Sorting algorithms Insertion, selection, quick, merge, (intro, dual-pivot quick, natural
Stacks and queues (chapters 6.6, 15.1, 15.5) So far... Complexity analysis For recursive and iterative programs Sorting algorithms Insertion, selection, quick, merge, (intro, dual-pivot quick, natural
1 The smallest free number
 1 The smallest free number Introduction Consider the problem of computing the smallest natural number not in a given finite set X of natural numbers. The problem is a simplification of a common programming
1 The smallest free number Introduction Consider the problem of computing the smallest natural number not in a given finite set X of natural numbers. The problem is a simplification of a common programming
Functional Programming. Pure Functional Programming
 Functional Programming Pure Functional Programming Computation is largely performed by applying functions to values. The value of an expression depends only on the values of its sub-expressions (if any).
Functional Programming Pure Functional Programming Computation is largely performed by applying functions to values. The value of an expression depends only on the values of its sub-expressions (if any).
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
COMP4128 Programming Challenges
 COMP4128 Challenges School of Computer Science and Engineering UNSW Australia 2D Table of Contents 2 2D 1 2 3 4 5 6 2D 7 Divide 3 2D Wikipedia: an algorithm design paradigm based on multi-branched recursion
COMP4128 Challenges School of Computer Science and Engineering UNSW Australia 2D Table of Contents 2 2D 1 2 3 4 5 6 2D 7 Divide 3 2D Wikipedia: an algorithm design paradigm based on multi-branched recursion
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
CSci 231 Final Review
 CSci 231 Final Review Here is a list of topics for the final. Generally you are responsible for anything discussed in class (except topics that appear italicized), and anything appearing on the homeworks.
CSci 231 Final Review Here is a list of topics for the final. Generally you are responsible for anything discussed in class (except topics that appear italicized), and anything appearing on the homeworks.
CSE373: Data Structures & Algorithms Lecture 28: Final review and class wrap-up. Nicki Dell Spring 2014
 CSE373: Data Structures & Algorithms Lecture 28: Final review and class wrap-up Nicki Dell Spring 2014 Final Exam As also indicated on the web page: Next Tuesday, 2:30-4:20 in this room Cumulative but
CSE373: Data Structures & Algorithms Lecture 28: Final review and class wrap-up Nicki Dell Spring 2014 Final Exam As also indicated on the web page: Next Tuesday, 2:30-4:20 in this room Cumulative but
15.4 Longest common subsequence
 15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
15.4 Longest common subsequence Biological applications often need to compare the DNA of two (or more) different organisms A strand of DNA consists of a string of molecules called bases, where the possible
Lecture 7. Transform-and-Conquer
 Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1
![1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1](/thumbs/85/92778785.jpg) Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 2. O(n) 2. [1 pt] What is the solution to the recurrence T(n) = T(n/2) + n, T(1)
Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 2. O(n) 2. [1 pt] What is the solution to the recurrence T(n) = T(n/2) + n, T(1)
Chapter 6. Dynamic Programming
 Chapter 6 Dynamic Programming CS 573: Algorithms, Fall 203 September 2, 203 6. Maximum Weighted Independent Set in Trees 6..0. Maximum Weight Independent Set Problem Input Graph G = (V, E) and weights
Chapter 6 Dynamic Programming CS 573: Algorithms, Fall 203 September 2, 203 6. Maximum Weighted Independent Set in Trees 6..0. Maximum Weight Independent Set Problem Input Graph G = (V, E) and weights
Data Structures and Algorithms Week 4
 Data Structures and Algorithms Week. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Week Divide and conquer Merge
Data Structures and Algorithms Week. About sorting algorithms. Heapsort Complete binary trees Heap data structure. Quicksort a popular algorithm very fast on average Previous Week Divide and conquer Merge
Greedy algorithms is another useful way for solving optimization problems.
 Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
Programming II (CS300)
 1 Programming II (CS300) Chapter 12: Sorting Algorithms MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Outline 2 Last week Implementation of the three tree depth-traversal algorithms Implementation of the BinarySearchTree
1 Programming II (CS300) Chapter 12: Sorting Algorithms MOUNA KACEM mouna@cs.wisc.edu Spring 2018 Outline 2 Last week Implementation of the three tree depth-traversal algorithms Implementation of the BinarySearchTree
CPE702 Algorithm Analysis and Design Week 7 Algorithm Design Patterns
 CPE702 Algorithm Analysis and Design Week 7 Algorithm Design Patterns Pruet Boonma pruet@eng.cmu.ac.th Department of Computer Engineering Faculty of Engineering, Chiang Mai University Based on Slides by
CPE702 Algorithm Analysis and Design Week 7 Algorithm Design Patterns Pruet Boonma pruet@eng.cmu.ac.th Department of Computer Engineering Faculty of Engineering, Chiang Mai University Based on Slides by
The divide-and-conquer paradigm involves three steps at each level of the recursion: Divide the problem into a number of subproblems.
 2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
2.3 Designing algorithms There are many ways to design algorithms. Insertion sort uses an incremental approach: having sorted the subarray A[1 j - 1], we insert the single element A[j] into its proper
A Second Look At ML. Chapter Seven Modern Programming Languages, 2nd ed. 1
 A Second Look At ML Chapter Seven Modern Programming Languages, 2nd ed. 1 Outline Patterns Local variable definitions A sorting example Chapter Seven Modern Programming Languages, 2nd ed. 2 Two Patterns
A Second Look At ML Chapter Seven Modern Programming Languages, 2nd ed. 1 Outline Patterns Local variable definitions A sorting example Chapter Seven Modern Programming Languages, 2nd ed. 2 Two Patterns
Data Structures and Algorithms. Roberto Sebastiani
 Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 0 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
Data Structures and Algorithms Roberto Sebastiani roberto.sebastiani@disi.unitn.it http://www.disi.unitn.it/~rseba - Week 0 - B.S. In Applied Computer Science Free University of Bozen/Bolzano academic
CS584/684 Algorithm Analysis and Design Spring 2017 Week 3: Multithreaded Algorithms
 CS584/684 Algorithm Analysis and Design Spring 2017 Week 3: Multithreaded Algorithms Additional sources for this lecture include: 1. Umut Acar and Guy Blelloch, Algorithm Design: Parallel and Sequential
CS584/684 Algorithm Analysis and Design Spring 2017 Week 3: Multithreaded Algorithms Additional sources for this lecture include: 1. Umut Acar and Guy Blelloch, Algorithm Design: Parallel and Sequential
Tree Data Structures CSC 221
 Tree Data Structures CSC 221 BSTree Deletion - Merging template // LOOK AT THIS PARAMETER!!! void BST::deleteByMerging(BSTNode* & nodepointer) { BSTNode* temp= nodepointer;
Tree Data Structures CSC 221 BSTree Deletion - Merging template // LOOK AT THIS PARAMETER!!! void BST::deleteByMerging(BSTNode* & nodepointer) { BSTNode* temp= nodepointer;
Jana Kosecka. Linear Time Sorting, Median, Order Statistics. Many slides here are based on E. Demaine, D. Luebke slides
 Jana Kosecka Linear Time Sorting, Median, Order Statistics Many slides here are based on E. Demaine, D. Luebke slides Insertion sort: Easy to code Fast on small inputs (less than ~50 elements) Fast on
Jana Kosecka Linear Time Sorting, Median, Order Statistics Many slides here are based on E. Demaine, D. Luebke slides Insertion sort: Easy to code Fast on small inputs (less than ~50 elements) Fast on
Recursive Sorts. Recursive Sorts. Divide-and-Conquer. Divide-and-Conquer. Divide-and-conquer paradigm:
 Recursive Sorts Recursive Sorts Recursive sorts divide the data roughly in half and are called again on the smaller data sets. This is called the Divide-and-Conquer paradigm. We will see 2 recursive sorts:
Recursive Sorts Recursive Sorts Recursive sorts divide the data roughly in half and are called again on the smaller data sets. This is called the Divide-and-Conquer paradigm. We will see 2 recursive sorts:
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
15110 Principles of Computing, Carnegie Mellon University - CORTINA. Binary Search. Required: List L of n unique elements.
 UNIT 5B Binary Search 1 Binary Search Required: List L of n unique elements. The elements must be sorted in increasing order. Result: The index of a specific element (called the key) or None if the key
UNIT 5B Binary Search 1 Binary Search Required: List L of n unique elements. The elements must be sorted in increasing order. Result: The index of a specific element (called the key) or None if the key
Chapter 10. Sorting and Searching Algorithms. Fall 2017 CISC2200 Yanjun Li 1. Sorting. Given a set (container) of n elements
 Chapter Sorting and Searching Algorithms Fall 2017 CISC2200 Yanjun Li 1 Sorting Given a set (container) of n elements Eg array, set of words, etc Suppose there is an order relation that can be set across
Chapter Sorting and Searching Algorithms Fall 2017 CISC2200 Yanjun Li 1 Sorting Given a set (container) of n elements Eg array, set of words, etc Suppose there is an order relation that can be set across
Programming Languages 3. Definition and Proof by Induction
 Programming Languages 3. Definition and Proof by Induction Shin-Cheng Mu Oct. 22, 2015 Total Functional Programming The next few lectures concerns inductive definitions and proofs of datatypes and programs.
Programming Languages 3. Definition and Proof by Induction Shin-Cheng Mu Oct. 22, 2015 Total Functional Programming The next few lectures concerns inductive definitions and proofs of datatypes and programs.
Tuples. CMSC 330: Organization of Programming Languages. Examples With Tuples. Another Example
 CMSC 330: Organization of Programming Languages OCaml 2 Higher Order Functions Tuples Constructed using (e1,..., en) Deconstructed using pattern matching Patterns involve parens and commas, e.g., (p1,p2,
CMSC 330: Organization of Programming Languages OCaml 2 Higher Order Functions Tuples Constructed using (e1,..., en) Deconstructed using pattern matching Patterns involve parens and commas, e.g., (p1,p2,
