Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance

Transcription

1 Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI Tampere, Finland jussi.kujala@tut.fi, elomaa@cs.tut.fi Abstract. We introduce a new O(lg lg n)-competitive binary search tree data structure called poketree that has the advantage of attaining, under worst-case analysis, O(lg n) cost per operation, including updates. Previous O(lg lg n)-competitive binary search tree data structures have not achieved O(lg n) worst-case cost per operation. A standard data structure such as red-black tree or deterministic skip list can be augmented with the dynamic links of a poketree to make it O(lg lg n)-competitive. Our approach also uses less memory per node than previous competitive data structures supporting updates. 1 Introduction Among the most widely used data structures are different binary search trees (BSTs). They support a variety of operations, usually at least searching for a key as well as updating the set of stored items through insertions and deletions. A successful search for a key stored into the BST is called an access. BST data structures are mostly studied by analyzing the cost of serving an arbitrary sequence of operation requests. Moreover, the realistic online BST algorithms, which cannot see future requests, are often contrasted in competitive analysis against offline BST algorithms that have the unrealistic advantage of knowing future requests. Examples of BST algorithms include 2-3 trees, red-black trees [1], B-trees [2], splay trees [3], and an alternative to using the tree structure, skip lists [4,5]. In an attempt to make some progress in resolving the dynamic optimality conjecture of Sleator and Tarjan [3], Demaine et al. [6] recently introduced Tango, an online BST data structure effectively designed to reverse engineer Wilber s [7] first lower bound on the cost of optimal offline BST. Broadly taken the dynamic optimality conjecture proposes that some (self-adjusting) BST data structure working online, possibly splay tree, would be competitive up to a constant factor with the best offline algorithm for any access sequence. Tango does not quite attain constant competitiveness, but Demaine et al. showed an asymptotically small competitive ratio of O(lg lg n) for Tango in a static universe of n keys.

2 Table 1. Known asymptotic upper bounds on the performance of competitive BST algorithms. Memory is given in bits, where letter w is a shorthand for words. Tango MST Poketree Poketree(RB) Poketree(skip) Search, worst-case O(lg lg n lg n) O(lg 2 n) O(lg n) O(lg n) O(lg n) Search, amortized O(lg lg n lg n) O(lg n) O(lg n) O(lg n) O(lg n) insert/delete N/A O(lg 2 n) N/A O(lg n) O(lg 2 n) memory per node 4w+2lg w+2 7w+lg w+1 6w+1 6w+2 4w+lg lg w Prior to this result the best known competitive factor for an online BST data structure was the trivial O(lg n) achieved by any balanced BST. 1 Tango only stores a static set of keys, it does not support update operations on stored data items. It has O(lg n lg lg n) worst-case access cost and cannot guarantee better performance under amortized analysis for all access sequences. 2 Wang, Derryberry, and Sleator [8] put forward a somewhat more practical BST data structure, in the sense that it supports update operations as well, multisplay trees (MST) a hybrid of Tango and splay trees which also attains the double logarithmic competitive ratio O(lg lg n). The worst-case complexity of a MST is O(lg 2 n), but it achieves O(lg n) amortized access cost. The costs for update operations in a MST are similar. MSTs inherit some interesting properties from splay trees; it is, e.g., shown that the sequential access lemma [9] holds for MSTs. In this paper we introduce poketree, which is a generic scheme for attaining O(lg lg n)-competitive BST data structures with different static data structures underlying it. As static data structures we use red-black trees [1] and deterministic skip lists [5]. By using different static data structures we can balance between the amount of augmented information in the nodes and efficiency of operations. In contrast to Tango and MST, poketree has O(lg n) cost per operation under worst-case analysis. The O(lg 2 n) update cost with skip lists can be, in practice, lowered to O(lg n) cost per update [5]. See Table 1 for a summary of the characteristic costs of Tango, MST, and poketree. The contribution of this paper is a dynamically O(lg lg n)-optimal data structure that has the best combination of space and cost requirements with updates supported. Poketree is not a strict binary search tree, because nodes in it can have up to one additional pointer, but it supports the same set of operations. As a side result we give a lower bound to the cost of BST algorithms, proven in a similar manner to the bound of Demaine et al. [6], which has a small increase in the additive term from the previous best of n 2r [8] to n/2 r/2. The remainder of this paper is organized as follows. In Section 2 we explain the lower bound on the cost of offline BST algorithms that we use. It is slightly tighter than the one in [6] and formulated to support other than strict 2-trees. In Section 3 we demonstrate the idea behind poketree in case where the static 1 By lg n, for a positive integer n, we denote log 2 n and define lg 0 = lg 1 = 1. 2 Subsequent manuscripts available at the Internet mention that Tango can be modified to support O(lg n) worst-case access.

3 structure is a perfectly balanced BST with no update operations supported. In Sections 4 and 5 we generalize to other static structures, now supporting update operations. The concluding remarks of this paper are presented in Section 6. 2 Cost Model and the Interleave Bound Because we want to compare the costs of online and offline BST algorithms, we need a formal model of cost. Earlier work [3,7,6,8] has mostly used a model which charges one unit of cost for each node accessed and for each rotation. However, a simpler cost model was used by Demaine et al. [6] in proving a lower bound. They only counted the number of nodes touched in serving an access. A node is touched during an access if the data structure reads or writes information on the node. These two models, and several others, differ at most by a constant factor because a BST can be transformed to any other one containing the same set of keys using a number of rotations that is twice the number of nodes in the tree [10]. We adopt the latter model and take care that no computation is too costly when compared to the number of nodes accessed. Wilber [7] gave two lower bounds on the cost of dynamic BST algorithms; the first of these is also known as the interleave bound. It has been used to prove the O(lg lg n)-competitiveness of the recent online BST algorithms [6,8]. We will also use it to show the O(lg lg n)-competitiveness of poketree. Let us describe the interleave bound briefly. Let P be a static BST on the items that are accessed. The BST P is called a reference tree. It may be a proper BST, 2-3 tree, or any * tree. Using BSTs results in the tightest bound and, hence, they have been used previously. However, we do not necessarily need as tight results as possible, therefore, we give a slightly different version of the interleave bound. We are given an access sequence σ = σ 1,..., σ m that is served using P. For each item i in P define the preferred child of i as the child into whose subtree the most recent access to the subtree of i was directed. Let IB(σ, P, i) be the number of switches of preferred child of i in serving σ. The interleave bound IB(σ, P) is the sum of these over all the nodes of P: i P IB(σ, P, i). Let r be the number of rotations in P while serving σ. Theorem 1. Any dynamic binary search tree algorithm serving an access sequence σ has a cost of at least IB(σ, P)/2 + m n/2 r/2. This bound is slightly tighter than previously known best lower bound IB(σ, P)/2 +m n 2r by Wang, Derryberry, and Sleator [8]. The proof for the new bound is given is given in Appendix B. 3 Poketree A Dynamic Data Structure Let P t be the state of the reference tree P at time t. In addition to P, P t contains information on preferred children. Preferred paths follow preferred child pointers in P t. Both Tango and MST keep each preferred path of a reference

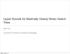
4 tree P t on a separate tree; these trees make up a tree of trees. When the interleave bound on P increases by k, then exactly k subtrees are touched. Moreover, the algorithms provide an efficient way to update the structure to correspond to the new reference tree P t+1. Thus the access cost is at most k lg(# of items on a path) k lg lg n when the data structure for subtrees is chosen suitably. We, rather, augment a standard balanced search structure with dynamic links to support a kind of binary search on preferred paths. The balanced search structure corresponds to the structure of the reference tree, which is used to provide a lower bound on the cost. In our approach we take advantage of the static links in searching for an item, whereas Tango and MST maintain the reference tree information but do not really use it in searching. This enables us to implement update operations using less space than MST. We first describe how our method, called poketree, works on a perfectly balanced tree. In the following sections we relax these assumptions and generalize it to handle trees with less balance and to support update operations insert and delete. Interpreted most strictly, poketree is not really a BST, because items are not necessarily searched through a search tree, but using dynamic links. However, this is rather a philosophical than a practical point, since the same operations are supported in any case. The nodes of a poketree are augmented with a dynamic link to make it dynamically competitive. The idea is to follow a dynamic link whenever possible, and descend via a static link otherwise. Dynamic links allow to efficiently find a desired location on a preferred path and they can be efficiently updated to match the new reference tree P t+1. We consider later the requirement of inserting (removing) an item to the head of a preferred path brought along by supporting insertion (deletion). Let us fix a preferred path a = a 1,..., a l and note that a l is always a leaf in the static tree but a 1 is not necessarily its root. If the dynamic links would implement a binary search on the path a, then it would be possible to travel from a 1 to any a i in lg l lg lg n time. However, this idea does not work as such, because updating dynamic links would be difficult and, even worse, since the preferred path a is a path in a BST, it is not necessarily ordered, making it impossible to carry out binary search on it. For now we just augment each node to contain the smallest and the largest item in the subtree rooted at the node (we later lift this requirement in Section 5). We still have to set the dynamic links to implement a kind of binary search including quick updates to the structure of the preferred paths in P. There are two types of nodes, of type SDD and S. Define a static successor of a node N to be the child in which the last search through N went. The dynamic link of a node of type SDD leads to the same node as following two dynamic links starting from its static successor. A node of type S, on the other hand, has its dynamic link pointing to its static successor. Note that the dynamic links always point lower in the tree, except in the special case of a leaf node. The key trick is to choose the type of a node. The rule for this is as follows. A node is of type SDD if the length of the dynamic link of its successor equals the

5 Fig.1. An example of dynamic links. Static links are omitted, they point always to the next item in the list. The round nodes are of type SDD and the square ones of type S. The node with label 0 is a leaf. length of the dynamic link of the dynamic link of the successor. Otherwise, the node is of type S or a leaf node, which does not have a dynamic link. Observe that to satisfy this requirement, links have to be set up from a leaf to the root. An example of the resulting structure is given in Figure 1. Intuitively, dynamic links let us recursively split a path into two parts and have one dynamic link arc over the first part and another one over the second part. The two Ds in SDD stand for these arcs. Now note that if these links are set from the last item to the first one, the distance that a dynamic link traverses is a function of its distance to the end of the preferred path. Every possible path starting from a particular node is of the same length because we have assumed that a poketree is perfectly balanced. These facts together make it possible to update dynamic links quickly when a preferred path in P changes direction. We describe next the search operation and how to update the structure corresponding to P t to correspond to P t+1. The search attempts at each node to use the dynamic link to potentially skip a number of static links. However, if following the dynamic link leads to a node that does not contain the searched item in the range of items in its subtree, we say that the dynamic link fails. If the dynamic link fails, then the search backtracks to the node where the dynamic link was used and resorts to using the appropriate static pointer. Using a dynamic link has a cost, because an additional node has to be visited. It is possible to augment the parent of a dynamic link with the range information of the dynamic link, but this costs more space. After the searched item has been found, we may have to update those nodes in which a static link was used, because the preferred path may have changed. Assume that we know whether a node is of type S or SDD, for example by reading a bit that contains this information. After performing a search, in going from the bottom to the top, the dynamic link in each node can be (re)set because the the links in the subtree rooted at the preferred child have already been set up. Let us start by stating the most obvious result. Theorem 2. The worst-case cost for any search in a poketree is O(lg n). Proof. Clearly, in the worst case all dynamic links fail because otherwise some static link can be skipped with no cost. Thus, the worst-case cost is bounded to be a constant factor away from the number of static links traversed. This bound is of the order O(lg n) because the static structure is balanced and a constant amount of work is done during each static link.

6 The following theorem states that dynamic links are fast enough. Theorem 3. No more than O(lg lg n) time is spent on a preferred path on the way to the accessed element. The proof is given in Appendix A. Each change in the preferred paths, and subsequently in dynamic links, corresponds to one switch in dynamic pointers. Poketree does at most a constant amount of work for each switch in the dynamic links. Thus, by Theorems 3 and 1, it follows: Theorem 4. Poketree is O(lg lg n)-competitive among the class of all binary search tree algorithms. 4 Insertions and Deletions: Poketree(RB) In previous section we assumed that each root-to-leaf path has the same length. In reality, a data structure must support insertions and deletions and, thus, we cannot rely on idealized perfect balance to make things easy for us. Nevertheless, it is possible to retain the use of dynamic links while supporting these important operations. Some data structures are in a sense always perfectly balanced. For example, in a red-black tree [1,11] every root-to-leaf path has the same number of black nodes and in balanced 2-3 tree implementations the nodes (each containing one or two items) are always in perfect balance. In order to argue competitiveness, we need a cost model that can handle updates. During updates the structure of the reference tree changes to correspond to the static structure of the poketree. An insertion causes a search and insertion to the location in the reference tree where the item should be, and a deletion causes a search to both the deleted item and its successor in the key space, after which the item is deleted as usual. The actual cost charged from an offline BST algorithm is the number of preferred child pointers that switch, more precisely a constant factor of that number. Wang et al. [8] implement updates and use a similar model, which however is not as tight, because in a deletion they search for both predecessor and successor as well as rotate the item in the offline BST to a leaf. We now describe how to support insertion and deletion by using a red-black tree as the static structure. A red-black tree can be viewed as a tree, where a node of the tree corresponds to a black node and its red children. We choose the reference tree P to be the tree of the red-black tree. In the red-black tree the dynamic links point only from black nodes to black nodes. First, note that in the tree view of a red-black tree, the tree increases height only from the top, and when splitting nodes the distance from nodes to leaves stays the same (in the tree). Second, during updates nodes in the red-black tree may switch nodes in the tree, because there might be repaints. Third, it is known that during an update to a red-black tree the amortized number of repaints and the worst-case number of rotations are both constants [12]. The resulting algorithm,

7 poketree(rb), has the same asymptotic competitiveness properties as a perfectly balanced poketree, but now with updates supported. Note that the competitive ratio is not exactly the same, because red nodes are without dynamic links and, thus, there is a constant factor overhead in the competitive ratio. On the other hand, less unnecessary work is done if the access sequence does not conform to a structure that allows a BST algorithm to serve it in less than Θ(m lg n) cost. To support update operations, we must be able to decide the type of a new root S or SDD assuming that the types in the subtree rooted at the root are set up correctly. If we are given such a node, then it is possible to count the number of consecutive SDD nodes its static successor and dynamic link of the static successor have. If these are equal, then the node is of type SDD, otherwise it is of type S. This holds, because the rule for choosing the type of a node depends on the fact that the length of the dynamic link in its successor and in the dynamic link of the successor are the same, which is true if the same number of SDD nodes have been chosen in a row in those two locations. Leaf nodes (tails in a preferred path) make an exception, because they do not have a dynamic link. In poketree each node carries information about the interval of keys in its subtree. In poketree(rb) these bounds are maintained in the form of strict lower and upper bounds, i.e., a lower bound cannot be the smallest key in the tree, but could be the predecessor to the smallest key. The reason is that these bounds can be efficiently handled during updates. To insert a key to a poketree(rb) we need to search for its predecessor and successor (note that there is no need to actually know their values), actually insert it and set the lower and upper bound in the corresponding node, update the dynamic links, and finally fix any violations to red-black invariants while taking care in each repaint of the nodes that the poketree invariant holds in the tree at the level of the current operation. In general a repaint from black to red deletes the dynamic link and a repaint from red to black sets the dynamic link according to the type of the node which can either be obtained from some other node or as described above in the case of a new root node. For completeness we describe what to do during the fixup of the red-black tree as it might not be obvious. These cases correspond to ones in [11, pp ]. Unfortunately, the page limit does not allow for a more complete presentation. Case 1: Swap memory locations of the A and C nodes and set static pointers and dynamic pointer in A. This ensures that dynamic links upper in the tree point to a correct node. Then set the type of D to be the type of C and remove dynamic link in C and set the dynamic link in D. This case represents a split of a node in the tree view. Case 2: Do nothing. Case 3: Swap memory locations of B and C and set the static pointers. Thus B obtains the dynamic link that was in C and dynamic links upper in the tree point to a correct node.

8 Finally, if the root was repainted from red to black, obtain a new type using the procedure described above and set the type info and dynamic link accordingly. Note that we may need to update information about lower and upper bounds on the nodes. The total time of insertion is O(lg n), because the type-procedure needs to be called at most once at the root. A deletion can be implemented using the same ideas as the insertion, but the details are slightly more complicated. In a deletion the following sequence of operations is executed: find the item to be deleted; find its successor by using dynamic links, bound information, and comparing the lower bound to the deleted item; set dynamic links; delete the item as usual; finally, call the RB-fixup to fix possible invariant violations. In fixup there are several cases to consider, but the general idea is that in the tree there might be an extra black with an associated memory address (because a node further up in the tree may point to it through a dynamic link), which floats upper in the tree, and the address might change, until it is assigned in another location. Things to consider during RB-fixup: Case 1: Swap memory locations of B and D items and set the static pointers. Case 2: (There is no dynamic link pointing to D). Delete dynamic information on D. Swap memory location and type of A with the extra black. This represents a merge of two nodes in the tree. Case 3: Swap memory locations of C and D items and set the static pointers. Case 4: Set static pointers, delete dynamic information on D, set type of E to type of D and set the dynamic pointer, swap memory location and type of A with extra black, set memory location and type of B to those of the extra black, set static pointers and update the dynamic pointer on B and A accordingly. If there is an extra black in the root, just delete it and set the type to be the type of a black child node before the update. Note that the lower bound must be set on the nodes along the dynamic links on the preferred path from the successor node to the location where the successor previously was. This ensures that the dynamic links pointing from above of the successor to its subtree do not make a mistake if the successor is later accessed. All operations done during updates have a cost of O(lg lg n) per switch of preferred child pointer in the reference tree. We conclude that poketree(rb) is O(lg lg n)-competitive, even when updates to the tree are taken into account. 5 Reducing Memory Consumption: Poketree(skip) So far we have augmented each node in a poketree with a lower bound and an upper bound on key values in its subtree. This constitutes a problem, since each node consumes two words of precious memory. It is no surprise that it is possible to fare better, as a part of the information about lower and upper bounds seems to be redundant between nodes. We suggest a poketree based on a variant of a deterministic skip list by Munro, Papadakis, and Sedgewick [5].

9 In a skip list items form a list. A node of this list is an array that contains a key, a pointer to the next item in the list, and a varying number of links that point progressively further in the list. More precisely, each additional link on an item points about twice as far as the previous link. The number of additional links on an item is referred to as its height. Approximately 1/2 h th part of the nodes have h additional links and links of same height are nearly uniformly distributed in the list. Thus, the search cost is logarithmic and the total space consumed is upper bound by n + n + n i=1 1/2i = 3n. What makes this structure desirable for us is that if we search for an item and can see only a node of the list, then it is easy to check whether the searched item is between the current node and a node pointed by a link of some particular height. Hence, we can lower the memory overhead of storing bounds for keys in subtrees, but have to fetch one additional node to see its key. A deterministic skip list corresponds to a perfectly balanced 2-3 tree [5]. Using this correspondence, it is possible to relate the performance of a skip list augmented with dynamic links to BST algorithms. More specifically, if there is a dynamic link for each additional static link, then it is possible to associate each dynamic link to a node in the 2-3 tree view. Items between an item and a particular static link on it correspond to a subtree rooted to a node in the 2-3 tree. The dynamic link associated with this static link corresponds to the dynamic link of that node in the 2-3 tree. We do not go into the details, because of lack of space. Insertion and deletion can be implemented similarly as in a poketree(rb). Unfortunately, an insertion takes O(lg 2 n)-time in a deterministic skip list, so we have a trade-off here. However, Munro et al. [5] argue that in practice the update operation can be implemented in O(lg n)-time if memory for nodes is allocated in powers of two. 6 Conclusions We have presented poketree algorithm, which is O(lg lg n)-competitive against the best dynamic offline BST algorithm and that is founded on same ideas as previous such algorithms, like Tango [6]. Our implementation supports update operations, like MST [8] does, and has better worst case performance. Acknowledgments This work was supported by Academy of Finland project INTENTS: Intelligent Online Data Structures. Moreover, the work of J. Kujala is financially supported by Tampere Graduate School in Information Science and Engineering (TISE). References 1. Bayer, R.: Symmetric binary B-trees: Data structure and maintenance algorithms. Acta Informatica 1 (1972)

10 2. Bayer, R., McCreight, E.M.: Organization and maintenance of large ordered indices. Acta Informatica 1 (1972) Sleator, D.D., Tarjan, R.E.: Self-adjusting binary search trees. Journal of the ACM 32(3) (1985) Pugh, W.: Skip lists: A probabilistic alternative to balanced trees. Communications of the ACM 33(6) (1990) Munro, I., Papadakis, T., Sedgewick, R.: Deterministic skip lists. In: Proceedings of the 3rd Annual ACM-SIAM Symposium on Discrete Algorithms, SIAM (1992) Demaine, E.D., Harmon, D., Iacono, J., Pǎtraşcu, M.: Dynamic optimality almost. In: Proceedings of the 45th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press (2004) Wilber, R.: Lower bounds for accessing binary search trees with rotations. SIAM Journal on Computing 18(1) (1989) Wang, C.C., Derryberry, J., Sleator, D.D.: O(log log n)-competitive dynamic binary search trees. In: Proceedings of the 17th Annual ACM-SIAM Symposium on Discrete Algorithms, ACM Press (2006) Tarjan, R.E.: Sequential access in splay trees takes linear time. Combinatorica 5(4) (1985) Culik II, K., Wood, D.: A note on some tree similarity measures. Information Processing Letters 15(1) (1982) Cormen, T.H., Leiserson, C.E., Rivest, R.L., Stein, C.: Introduction to Algorithms. Second edn. McGraw-Hill (2001) 12. Tarjan, R.E.: Data Structures and Network Algorithms. SIAM (1983) A Proof of Theorem 3 The definition of dynamic links gives the following recursive rule for the length L(m) of the dynamic link of the mth item counted from the tail of a preferred path. 0 m 1 L(m) = 1 + 2L(m 1) if L(m 1) = L(m 1 L(m 1)) 1 otherwise. Let b 1,...,b j be the items accessed on the preferred path when searching for b j, or the place where the search deviates from the path, and the first item on the path is b 1. Associate to each b i a the length of its dynamic link k i. We will prove that the sequence K = k 1,..., k j is of the form where it first increases and then decreases and, moreover, that no number appears more than twice in a row. Together with the fact that numbers k i are of form L(N) = {0, 1, 3, 7, 15, 31, 63,..., 2 i 1,...} and a maximal k i is at most a length of a root-to-leaf path l this implies that j can be at most 4 lg l 4 lg lg n, if l lg n. As a tool we use a more intuitive presentation of the sequence L(m): L(m) is the mth item in a sequence 0, S, where S is a infinite sequence. Let S 1:i be the prefix of S containing the first i numbers. The sequence S has been generated by repeatedly applying a rule to generate a longer prefix of S: S 1 1:2 = 1, 1 S k 1:2(i+1) = Sk 1 1:i, (i + 1), S k 1 1:i, (i + 1).

11 Here the superscript k counts how many times this rule has been used. Equivalence of these two presentations can be verified by simple induction on k. In induction step assume that numbers in S1:i k equal numbers given by the function L, i.e. S1:i k = L(2),..., L(i + 1). By inductive assumption S k = S k 1, L(i+1), S k 1, L(i+1) and by definition the first i numbers in S k+1 equal S k and S k+1 i+1 = 2L(i+1)+1 = L(i+2). Now, L(i+3) = 1 because L(i+2) must be larger than numbers in L(1),..., L(i+1), and L(i+3) = 1 because L(i+1) > 1 and L(i+2) = 1. In fact, L(2),...,L(i+2) = L(i+3),...,L(2i+3), because L(i+2) is larger than numbers in L(2),..., L(i+1) and thus it behaves like 0 in the definition of L until the number L(i + 2) itself is generated again, which is not until L(2i + 3). Thus L(i + 3),..., L(2i + 4) = S k, 2i + 1 and we can conclude that the correspondence between L and S holds. Let us denote by k M the maximal element in the sequence K. The prefix of K that is k 1,..., k i+1, k i+2,...,k M is a non-decreasing sequence with at most two repetitions of the same value because of the following structure in a subsequence of S: k M,...,k i+1 or k i+2, 1, 1,..., k }{{} i, }{{}..., k i, 2k i + 1. k i 1 items k i 1 items Now the subscript in the item marked by k = (k i+1 or k i+2 ) depends on which k i corresponds to the actual item that is visited during k i in K (we use k i as both an item in the sequence K and a numerical value). Due to the rule generating S, k must be either 0, which is impossible in our case, 2k i +1, or a larger value. On the other hand, k M,...,k i,...,k j is a non-increasing sequence with at most two repetitions of same value, because we can again write a subsequence S as:..., 1, 1,..., k }{{} i, 1, 1,..., k }{{} i, 2k i + 1,...,k M,.... k j is here or here Here the parts indicated by underbraces are of length k i 1. B Proof of Theorem 1 A BST algorithm serving σ = σ 1,..., σ m defines a sequence of trees T 0,...,T m and touches items during each access, let these be connected subtrees S 1,..., S m. In the spirit of Demaine et al. [6], we will play with marbles. Our argument is similar, but not quite the same as theirs. More precisely, for each change of a preferred child, we will place a marble on an item. They are placed so that at any time there is at most one marble on an item. Furthermore, no more than two marbles per item in S j σ j are discarded during σ j. Two can be discarded because after the first discard a new marble might be placed and then discarded. Thus, half of the number of the marbles discarded is a lower bound on the cost of the BST algorithm minus m. The number of marbles discarded can be at most that of marbles placed M placed and is at least M placed n, because there is

12 at most one marble on an item at any given time. So the total cost of any BST algorithm is at least M placed /2 n/2 + m. Note that in our argument the trees T i are BSTs, but P can have nodes with several items. As such, this is not an improvement to the results of Demaine et al., because if for example a 2-3 tree P is given as a BST it gives a tighter bound, but we are able to get a smaller additive term of n/2 to the bound. Let us now describe a method of placing marbles. On an access σ j we first discard marbles on S j σ j. Then for each switch in preferred children a marble is placed. It is placed to the least common ancestor (LCA) in T j of items in the subtree of formerly preferred child. Note that T j is the tree after an access σ j. After placing marbles, again discard marbles on S j σ j. Why are two marbles never on the same item? First, note that distinct subtrees rooted at items in P form continuous intervals in key values. Thus their LCAs must be distinct, because the LCA of a continuous interval belongs to that interval. This implies that marbles placed during the same time step do not mix; the previously preferred subtrees are distinct, so their LCAs are distinct too. Second, marbles placed at different time steps do not mix. To see why, assume that there is an item a that already has a marble when we try to place another on it. Preferred child pointer of a node v changes; it previously pointed to subtree P a of P containing a. Let s 1 be the access during which the first marble was placed and s 2 the access trying to place the second marble. There are two separate cases depending on where the first marble has been placed: above of v in P or on v or below it. In the first case we must either have touched a during the access to s 2, because a must have been an ancestor of s 2, or a must have been touched while it was rotated from being an ancestor to s 2. In the second case the first marble has been placed on v or in P a and a has been touched when an item in P a was last accessed, which must be after or during s 1 because the preferred child pointer of v points to P a and s 1 is in P a. In any case, a cannot hold the first marble anymore and the second marble can be safely inserted to a. Assume now that we may do rotations on BST P. What happens if we rotate an item a above of b? If before the rotation tree P was safe in the sense that an access to any item would not place two marbles on the same item, then by removing a marble from a certain item on P, we can guarantee that after the rotation the new tree P is safe as well. To find this item, note that preferred child pointers of a and b point to two subtrees and it is safe to switch the pointers to these subtrees and place a marble to the LCA of those subtrees. After the rotation, if the preferred child pointers are set to their natural places, at most one of these two pointers points to a different tree (this can be verified by going through all four eight, counting the mirror images possible cases). If we remove the marble on the LCA of the items in this tree, then P is safe. This implies a lower bound of (IB(σ, P) n r)/2 + m, where r is the number of rotations. This is the tightest known bound formulated using a reference tree P.