Lecture 11: Multiway and (2,4) Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
|
|
|
- Melinda Welch
- 6 years ago
- Views:
Transcription
1 Lecture 11: Multiway and (2,4) Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie
2 Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary ADT Searching in multiway trees (2,4) trees: a special case of multiway trees Height properties p Insertion Deletion 2
3 Review: Binary Search Tree < 6 2 > 1 4 = 8 9 Question: can we generalize binary search trees to hold more than 1 entry per node? Answer: yes, with multiway search tree Why should we care? New type of search tree Smaller height ht (but not necessarily more efficient) i 3
4 Multi-Way Search Tree Multi-way search tree is not binary (more than two children are allowed) Each node can store more than one ordered entries keys between 2 and 6 keys between 6 and 8
5 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 11 key-value items (k i, o i ), where d is the number of children For a node with children v 1 v 2 v d storing keys k 1 k 2 k d 1 keys in the subtree of v 1 are less than k 1 keys in the subtree of v i are between k i 1 and k i (i = 2,, d 1) keys in the subtree of v d are greater than k d 1 The leaves store no items and serve as placeholders 5
6 Multi-Way Search Tree For node with children v 1 v 2 v d storing keys k 1 k 2 k d 1 keys in the subtree of v 1 are less than k 1 keys in the subtree of v i are between k i 1 and k i (i = 2,, d 1) keys in the subtree of v d are greater than k d 1 k 1 k 2 k v 1 v 2 v 3 v 4 3 between 2 and 6 between 6 and 8 6
7 Multi-Way Inorder Traversal We can extend the notion of inorder traversal from binary trees to multi-way search trees Namely, we visit item (k i, o i ) of node v between the recursive traversals of the subtrees of v rooted at children v i and v i + 1 An inorder traversal of a multi-way search tree visits the keys in increasing order
8 Multi-Way Searching Similar to search in a binary search tree An internal node with children v 1 v 2 v d and keys k 1 k 2 k d 1 k = k i (i = 1,, d 1): the search terminates successfully k < k 1 : we continue the search in child v 1 k i 1 < k < k i (i = 2,, d 1): we continue the search in child v i k > k d 1 : we continue the search in child v d Reaching an external node terminates the search unsuccessfully Assuming d is a constant independent of number of nodes, examining each node during search takes O(1) ( ) time, thus time to search is proportional to the multiway tree height Example: search for
9 Multi-Way Searching: Another Example Search for key 7 Search terminates at a leaf child, which implies that there is no entry with key 7 in the tree
10 (2,4) Trees A (2,4) tree (also called 2-4 tree or tree) is a multi-way search tree with the following properties Node-Size Property: every internal node has at most four children Depth Property: all the external nodes have the same depth Recall that in a multiway tree, the minimum number of children for an internal node is 2. Thus an internal node can have 2, 3, or 4 children The depth property together th with the requirement that t every internal node has at least 2 children, will guarantee logarithmic height (in the number of entries) for the tree, as we shall see later 10
11 (2,4) Trees Internal node can have 2, 3, or 4 children Depending on the number of children, an internal node of a (2,4) tree is called a 2-node, 3-node or 4- node 11
12 Height of a (2,4) Tree Theorem: A (2,4) tree storing n entries has height O(log n) Proof: Let h be the height of a (2,4) tree with n entries Since each internal node holds at least one entry, n number of internal nodes By depth property, no external nodes at depths i = 0,, h 1 By multiway tree property, each hinternal node has at tleast t2 children, there are at least 2 i entries at depth i = 0,, h 1 and no items at depth h, we have n number of internal nodes h 1 = 2 h 1 Thus, h log (n + 1), and therefore h is O(log n) depth 0 1 # of entries 1 2 h h 1 h 0
13 Other Operations in a (2,4) Tree Thus searching in a (2,4) tree with n items takes O(log n) time Now we have to show how to insert and remove entries in a (2,4) tree while preserving the node-size and the depth properties Insertion into (2,4) tree is easier than into AVL tree Removal is slightly more complicated than the insertion 13
14 Insertion Suppose we need to insert a new entry (k, o) in the (2,4)-tree Always insert at a node only with leaf children (a node at level h-1, where h is the maximum depth of the tree) Suppose we know the correct node v to insert in. put (k, o) ) in the correct place (keys have to stay in order at node v) since the number of entries increased, for the tree to stay a multiway tree, we must add 1 more leaf child to v (in the correct place, after the inserted entry) v insert 30 v v insert 40 v
15 Insertion How to find the correct node v to insert? i.e. inserting in v preserves the multiway tree search order There are 2 cases: Case 1: The key k is not in the tree. Then v is the parent of the leaf reached by searching for k Example: insert v v
16 Insertion Case 2: The key k is already in the tree. Solve it in a way similar to the binary search trees Perform search. When reach node v containing entry with key k i = k, continue search in the left subtree v i (could, equivalently go in the right subtree v i+1 ). Stop when reached the node with only leaf children. Example: insert v v
17 Insertion The procedure on the previous slides preserves: Multiway search tree order Depth property (all external nodes have the same depth) But it may violate the node size property Overflow occurs when a 4-node becomes 5-node (illegal in (2,4)-tree) v v overflow
18 Insertion: Overflow and Split u v u v' v" v 1 v 2 v 3 v 4 v v 5 1 v 2 v 3 v 4 v 5 overflow split We handle an overflow at a 5-node v with a split operation: let v 1 v 5 be the children of v and k 1 k 4 be the keys of v node v is replaced by nodes v' and v" v' is a 3-node with keys k 1 k 2 and children v 1 v 2 v 3 v" is a 2-node with key k 4 and children v 4 v 5 key k 3 is inserted into the parent u of v (a new root may be created) If v was child i of u, v and v become children i and i +1 of u, respectively The overflow may propagate to the parent node u
19 Insertion Example overflow overflow
20 Analysis of Insertion Algorithm insert(k, o) 1. v = search(root, k) while (! v has only external children) v = search(v.childtotheleft(k)) 2. We add the new entry (k, o) at node v 3. while overflow(v) if isroot(v) create a new empty root above v v split(v) search(node, k) returns the node which has entry with key k or, if key k is not in tree, the parent of the leaf reached when searching for k v.childtotheleft(k)) ( returns the child immediately to the left of key k split(v) performs the split on node v and returns the parent of node v Let T be a (2,4) tree with n items Tree T has O(log n) height Step 1 takes O(log n) time because we visit O(log n) nodes Step 2 takes O(1) time Step 3 takes O(log n) time because each split takes O(1) time and we may perform up to O(log n) splits Thus, an insertion in a (2,4) tree takes O(log n) time 20
21 Deletion: Step 1 Like in AVL trees, first ensure that entry that needs to be deleted is at the node with leaf children If an entry is an internal node with no leaf children replace the entry with its inorder successor (or, equivalently, with its inorder predecessor) and delete the latter entry and one leaf Example: to delete key 24, we replace it with 27 (inorder successor)
22 Step 2: Underflow and Transfer Now assume that entry to be deleted is at node v with leaf children Deletion from v can cause an underflow (if v becomes a 1-node) To handle an underflow at node v with parent u, we consider two cases (note that underflow node v has no entries) Case 1: an adjacent sibling w of v is a 3-node or a 4-node Transfer operation: 1. we move a child of w to v 2. we move an entry from u (the entry between w and v) to v 3. we move an entry from w (the entry with key closest to the deleted key in u at step 2) to replace the missing entry of u After a transfer, no new underflow occurs 2 u w v 2 u w 9 v
23 Step 2: Underflow and Fusion Case 2: all adjacent siblings of v are 2-nodes Cannot do transfer in this case, will do fusion Fusion operation: we merge v with an adjacent sibling w and move an entry from u (the entry between w and v) to the merged node v' After a fusion, the underflow may propagate to the parent u If underflow propagates all the way to the root, we simply delete the root in which h case, height ht of the tree decreases by 1 u w v u v'
24 Another Fusion Example u 9 9 delete w 2 v underflow v u 2 9 underflow 2 9
25 Comments on Deletions Either case 1 or case 2 must always hold Let v be the node from which we deleted an entry No underflow before deletion in the tree Thus parent of v must be at least 2-node(but could be also a 3 node or a 4 node) Thus node at which deletion occurs must have at least 1 sibling which is at least a 2-node (but could be also a 3 node or a 4 node) u w v
26 Deletion Example 9 14 delete underflow! transfer 7 14 delete underflow! fusion
27 Deletion Algorithm delete(k) search for key k to locate the deletion node v if v is not internal node with leaf children then swap(entry at v,, entry at inorder successor of (v,k)), v = position of inorder successor of (v,k) Delete the entry with key k from v while underflow(v) if isroot(v) = true make (the only) child of v the new root else if there is a 3-4 node immediate sibling s transfer(v,s) else s = immediate sibling of v v = fusion(v,s) ( ) O(log n) O(log ( n) ) O(1) transfer(v s) O(log n) Inorder successor(v,k) is the smallest entry in the subtree to the right of key k in node v Thus, deleting an item from a (2,4) tree takes O(log n) time Assume fusion(v,s) returns the parent of v 27
28 Analysis of Deletion (repeated) Let T be a (2,4) tree with n items Tree T has O(log n) height In a deletion operation We visit O(log n) nodes to locate the node from which to delete the entry We handle an underflow with a series of O(log n) fusions, followed by at most one transfer Each fusion and transfer takes O(1) time Thus, deleting an item from a (2,4) tree takes O(log n) time 28
29 Implementing a Dictionary Comparison of efficient dictionary implementations Search Insert Delete Notes Hash Table 1 expected 1 expected 1 expected no ordered dictionary methods simple to implement AVL Tree log n worst-case log n worst-case log n worst-case complex to implement (2,4) Tree log n worst-case log n worst-case log n worst-case complex to implement 29
30 AVL vs (2,4) Trees Advantages of (2,4) trees over AVL trees Easier to understand In general, fewer nodes (smaller height) Advantages of AVL trees over (2,4) trees More efficient (by a constant factor, both trees have O(log n) basic operations complexity) Easier to implement ( I think ) Only 1 type of nodes to maintain, as opposed to 23 2,3,4 nodes of f(2 (2,4) tree 30
31 Another Insertion Example insert split split
32 Another Deletion Example 22 delete fusion transfer underflow
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
(2,4) Trees Goodrich, Tamassia. (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 (2,4) Trees 1 Multi-Way Search Tree ( 9.4.1) A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 1 key-element items
(2,4) Trees 9 2 5 7 10 14 (2,4) Trees 1 Multi-Way Search Tree ( 9.4.1) A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 1 key-element items
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Data Structure: Search Trees 2. Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering
 Data Structure: Search Trees 2 2017 Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered
Data Structure: Search Trees 2 2017 Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered
Multi-Way Search Tree
 Presentation for se with the textbook Data Strctres and Algorithms in Jaa, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 204 (2,4) Trees 9 2 5 7 0 4 204 Goodrich, Tamassia,
Presentation for se with the textbook Data Strctres and Algorithms in Jaa, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 204 (2,4) Trees 9 2 5 7 0 4 204 Goodrich, Tamassia,
Multi-Way Search Tree
 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two and at most d children and stores d -1 data items (k i, D i ) Rule: Number of children = 1
Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two and at most d children and stores d -1 data items (k i, D i ) Rule: Number of children = 1
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
M-ary Search Tree. B-Trees. B-Trees. Solution: B-Trees. B-Tree: Example. B-Tree Properties. Maximum branching factor of M Complete tree has height =
 M-ary Search Tree B-Trees Section 4.7 in Weiss Maximum branching factor of M Complete tree has height = # disk accesses for find: Runtime of find: 2 Solution: B-Trees specialized M-ary search trees Each
M-ary Search Tree B-Trees Section 4.7 in Weiss Maximum branching factor of M Complete tree has height = # disk accesses for find: Runtime of find: 2 Solution: B-Trees specialized M-ary search trees Each
B-Trees. Disk Storage. What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree. Deletion in a B-tree
 B-Trees Disk Storage What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree Deletion in a B-tree Disk Storage Data is stored on disk (i.e., secondary memory) in blocks. A block is
B-Trees Disk Storage What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree Deletion in a B-tree Disk Storage Data is stored on disk (i.e., secondary memory) in blocks. A block is
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
M-ary Search Tree. B-Trees. Solution: B-Trees. B-Tree: Example. B-Tree Properties. B-Trees (4.7 in Weiss)
 M-ary Search Tree B-Trees (4.7 in Weiss) Maximum branching factor of M Tree with N values has height = # disk accesses for find: Runtime of find: 1/21/2011 1 1/21/2011 2 Solution: B-Trees specialized M-ary
M-ary Search Tree B-Trees (4.7 in Weiss) Maximum branching factor of M Tree with N values has height = # disk accesses for find: Runtime of find: 1/21/2011 1 1/21/2011 2 Solution: B-Trees specialized M-ary
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
B-Trees. Version of October 2, B-Trees Version of October 2, / 22
 B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
Multiway Search Trees
 Multiway Search Trees Intuitive Definition A multiway search tree is one with nodes that have two or more children. Within each node is stored a given key, which is associated to an item we wish to access
Multiway Search Trees Intuitive Definition A multiway search tree is one with nodes that have two or more children. Within each node is stored a given key, which is associated to an item we wish to access
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Red-Black Trees. 2/24/2006 Red-Black Trees 1
 Red-Black Trees 3 8 //00 Red-Black Trees 1 Outline and Reading From (,) trees to red-black trees ( 10.5) Red-black tree ( 10.5.1) Definition Height Insertion restructuring recoloring Deletion restructuring
Red-Black Trees 3 8 //00 Red-Black Trees 1 Outline and Reading From (,) trees to red-black trees ( 10.5) Red-black tree ( 10.5.1) Definition Height Insertion restructuring recoloring Deletion restructuring
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Red-Black Trees Goodrich, Tamassia. Red-Black Trees 1
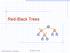 Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Module 4: Dictionaries and Balanced Search Trees
 Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CSC Design and Analysis of Algorithms
 CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
CSC : Lecture 7 CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique CSC : Lecture 7 Transform and Conquer This group of techniques solves a problem by a
Binary search trees. Binary search trees are data structures based on binary trees that support operations on dynamic sets.
 COMP3600/6466 Algorithms 2018 Lecture 12 1 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees are data structures based on binary trees that support operations on dynamic
COMP3600/6466 Algorithms 2018 Lecture 12 1 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees are data structures based on binary trees that support operations on dynamic
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
2-3 Tree. Outline B-TREE. catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS
 Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Heaps 2. Recall Priority Queue ADT. Heaps 3/19/14
 Heaps 3// Presentation for use with the textbook Data Structures and Algorithms in Java, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 Heaps Heaps Recall Priority Queue ADT
Heaps 3// Presentation for use with the textbook Data Structures and Algorithms in Java, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 Heaps Heaps Recall Priority Queue ADT
Multiway searching. In the worst case of searching a complete binary search tree, we can make log(n) page faults Everyone knows what a page fault is?
 Multiway searching What do we do if the volume of data to be searched is too large to fit into main memory Search tree is stored on disk pages, and the pages required as comparisons proceed may not be
Multiway searching What do we do if the volume of data to be searched is too large to fit into main memory Search tree is stored on disk pages, and the pages required as comparisons proceed may not be
CSC Design and Analysis of Algorithms. Lecture 7. Transform and Conquer I Algorithm Design Technique. Transform and Conquer
 // CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more
// CSC - Design and Analysis of Algorithms Lecture 7 Transform and Conquer I Algorithm Design Technique Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
2-3 and Trees. COL 106 Shweta Agrawal, Amit Kumar, Dr. Ilyas Cicekli
 2-3 and 2-3-4 Trees COL 106 Shweta Agrawal, Amit Kumar, Dr. Ilyas Cicekli Multi-Way Trees A binary search tree: One value in each node At most 2 children An M-way search tree: Between 1 to (M-1) values
2-3 and 2-3-4 Trees COL 106 Shweta Agrawal, Amit Kumar, Dr. Ilyas Cicekli Multi-Way Trees A binary search tree: One value in each node At most 2 children An M-way search tree: Between 1 to (M-1) values
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Module 4: Priority Queues
 Module 4: Priority Queues CS 240 Data Structures and Data Management T. Biedl K. Lanctot M. Sepehri S. Wild Based on lecture notes by many previous cs240 instructors David R. Cheriton School of Computer
Module 4: Priority Queues CS 240 Data Structures and Data Management T. Biedl K. Lanctot M. Sepehri S. Wild Based on lecture notes by many previous cs240 instructors David R. Cheriton School of Computer
CSE 326: Data Structures B-Trees and B+ Trees
 Announcements (2/4/09) CSE 26: Data Structures B-Trees and B+ Trees Midterm on Friday Special office hour: 4:00-5:00 Thursday in Jaech Gallery (6 th floor of CSE building) This is in addition to my usual
Announcements (2/4/09) CSE 26: Data Structures B-Trees and B+ Trees Midterm on Friday Special office hour: 4:00-5:00 Thursday in Jaech Gallery (6 th floor of CSE building) This is in addition to my usual
Stores a collection of elements each with an associated key value
 CH9. PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 201) PRIORITY QUEUES Stores a collection
CH9. PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN JAVA, GOODRICH, TAMASSIA AND GOLDWASSER (WILEY 201) PRIORITY QUEUES Stores a collection
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES
 HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
Multi-way Search Trees! M-Way Search! M-Way Search Trees Representation!
 Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
A set of nodes (or vertices) with a single starting point
 Binary Search Trees Understand tree terminology Understand and implement tree traversals Define the binary search tree property Implement binary search trees Implement the TreeSort algorithm 2 A set of
Binary Search Trees Understand tree terminology Understand and implement tree traversals Define the binary search tree property Implement binary search trees Implement the TreeSort algorithm 2 A set of
CMPS 2200 Fall 2015 Red-black trees Carola Wenk
 CMPS 2200 Fall 2015 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/9/15 CMPS 2200 Intro. to Algorithms 1 ADT Dictionary / Dynamic Set Abstract data type
CMPS 2200 Fall 2015 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/9/15 CMPS 2200 Intro. to Algorithms 1 ADT Dictionary / Dynamic Set Abstract data type
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
From (2,4) to Red-Black Trees
 Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Binary search trees 3. Binary search trees. Binary search trees 2. Reading: Cormen et al, Sections 12.1 to 12.3
 Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees 3 Binary search trees are data structures based on binary trees that support operations on dynamic sets. Each element
Binary search trees Reading: Cormen et al, Sections 12.1 to 12.3 Binary search trees 3 Binary search trees are data structures based on binary trees that support operations on dynamic sets. Each element
CH 8. HEAPS AND PRIORITY QUEUES
 CH 8. HEAPS AND PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CH 8. HEAPS AND PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Balanced Search Trees
 Balanced Search Trees Computer Science E-22 Harvard Extension School David G. Sullivan, Ph.D. Review: Balanced Trees A tree is balanced if, for each node, the node s subtrees have the same height or have
Balanced Search Trees Computer Science E-22 Harvard Extension School David G. Sullivan, Ph.D. Review: Balanced Trees A tree is balanced if, for each node, the node s subtrees have the same height or have
CH. 8 PRIORITY QUEUES AND HEAPS
 CH. 8 PRIORITY QUEUES AND HEAPS ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CH. 8 PRIORITY QUEUES AND HEAPS ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Sorted Arrays. Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min
 Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CS127: B-Trees. B-Trees
 CS127: B-Trees B-Trees 1 Data Layout on Disk Track: one ring Sector: one pie-shaped piece. Block: intersection of a track and a sector. Disk Based Dictionary Structures Use a disk-based method when the
CS127: B-Trees B-Trees 1 Data Layout on Disk Track: one ring Sector: one pie-shaped piece. Block: intersection of a track and a sector. Disk Based Dictionary Structures Use a disk-based method when the
Lecture 7. Transform-and-Conquer
 Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
SFU CMPT Lecture: Week 9
 SFU CMPT-307 2008-2 1 Lecture: Week 9 SFU CMPT-307 2008-2 Lecture: Week 9 Ján Maňuch E-mail: jmanuch@sfu.ca Lecture on July 8, 2008, 5.30pm-8.20pm SFU CMPT-307 2008-2 2 Lecture: Week 9 Binary search trees
SFU CMPT-307 2008-2 1 Lecture: Week 9 SFU CMPT-307 2008-2 Lecture: Week 9 Ján Maňuch E-mail: jmanuch@sfu.ca Lecture on July 8, 2008, 5.30pm-8.20pm SFU CMPT-307 2008-2 2 Lecture: Week 9 Binary search trees
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Heaps. 2/13/2006 Heaps 1
 Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
The B-Tree. Yufei Tao. ITEE University of Queensland. INFS4205/7205, Uni of Queensland
 Yufei Tao ITEE University of Queensland Before ascending into d-dimensional space R d with d > 1, this lecture will focus on one-dimensional space, i.e., d = 1. We will review the B-tree, which is a fundamental
Yufei Tao ITEE University of Queensland Before ascending into d-dimensional space R d with d > 1, this lecture will focus on one-dimensional space, i.e., d = 1. We will review the B-tree, which is a fundamental
Material You Need to Know
 Review Quiz 2 Material You Need to Know Normalization Storage and Disk File Layout Indexing B-trees and B+ Trees Extensible Hashing Linear Hashing Decomposition Goals: Lossless Joins, Dependency preservation
Review Quiz 2 Material You Need to Know Normalization Storage and Disk File Layout Indexing B-trees and B+ Trees Extensible Hashing Linear Hashing Decomposition Goals: Lossless Joins, Dependency preservation
CMPS 2200 Fall 2017 Red-black trees Carola Wenk
 CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
CSC Design and Analysis of Algorithms. Lecture 7. Transform and Conquer I Algorithm Design Technique. Transform and Conquer
 CSC 83- Design and Analysis of Algorithms Lecture 7 Transform and Conuer I Algorithm Design Techniue Transform and Conuer This group of techniues solves a problem by a transformation to a simpler/more
CSC 83- Design and Analysis of Algorithms Lecture 7 Transform and Conuer I Algorithm Design Techniue Transform and Conuer This group of techniues solves a problem by a transformation to a simpler/more
CS 3343 Fall 2007 Red-black trees Carola Wenk
 CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
What is a Multi-way tree?
 B-Tree Motivation for studying Multi-way and B-trees A disk access is very expensive compared to a typical computer instruction (mechanical limitations) -One disk access is worth about 200,000 instructions.
B-Tree Motivation for studying Multi-way and B-trees A disk access is very expensive compared to a typical computer instruction (mechanical limitations) -One disk access is worth about 200,000 instructions.
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Heaps Goodrich, Tamassia. Heaps 1
 Heaps Heaps 1 Recall Priority Queue ADT A priority queue stores a collection of entries Each entry is a pair (key, value) Main methods of the Priority Queue ADT insert(k, x) inserts an entry with key k
Heaps Heaps 1 Recall Priority Queue ADT A priority queue stores a collection of entries Each entry is a pair (key, value) Main methods of the Priority Queue ADT insert(k, x) inserts an entry with key k
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
Multi-Way Search Tree ( ) (2,4) Trees. Multi-Way Inorder Traversal. Multi-Way Search Tree ( ) Multi-Way Searching. Multi-Way Searching
 Mlti-Way Search Tree ( 0..) (,) Trees 9 5 7 0 (,) Trees (,) Trees Mlti-Way Search Tree ( 0..) A mlti-ay search tree is an ordered tree sch that Each internal node has at least to children and stores d
Mlti-Way Search Tree ( 0..) (,) Trees 9 5 7 0 (,) Trees (,) Trees Mlti-Way Search Tree ( 0..) A mlti-ay search tree is an ordered tree sch that Each internal node has at least to children and stores d
Physical Level of Databases: B+-Trees
 Physical Level of Databases: B+-Trees Adnan YAZICI Computer Engineering Department METU (Fall 2005) 1 B + -Tree Index Files l Disadvantage of indexed-sequential files: performance degrades as file grows,
Physical Level of Databases: B+-Trees Adnan YAZICI Computer Engineering Department METU (Fall 2005) 1 B + -Tree Index Files l Disadvantage of indexed-sequential files: performance degrades as file grows,
Motivation for B-Trees
 1 Motivation for Assume that we use an AVL tree to store about 20 million records We end up with a very deep binary tree with lots of different disk accesses; log2 20,000,000 is about 24, so this takes
1 Motivation for Assume that we use an AVL tree to store about 20 million records We end up with a very deep binary tree with lots of different disk accesses; log2 20,000,000 is about 24, so this takes
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Binary Trees. BSTs. For example: Jargon: Data Structures & Algorithms. root node. level: internal node. edge.
 Binary Trees 1 A binary tree is either empty, or it consists of a node called the root together with two binary trees called the left subtree and the right subtree of the root, which are disjoint from
Binary Trees 1 A binary tree is either empty, or it consists of a node called the root together with two binary trees called the left subtree and the right subtree of the root, which are disjoint from
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Lower Bound on Comparison-based Sorting
 Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lecture 3: B-Trees. October Lecture 3: B-Trees
 October 2017 Remarks Search trees The dynamic set operations search, minimum, maximum, successor, predecessor, insert and del can be performed efficiently (in O(log n) time) if the search tree is balanced.
October 2017 Remarks Search trees The dynamic set operations search, minimum, maximum, successor, predecessor, insert and del can be performed efficiently (in O(log n) time) if the search tree is balanced.
Hash Tables. CS 311 Data Structures and Algorithms Lecture Slides. Wednesday, April 22, Glenn G. Chappell
 Hash Tables CS 311 Data Structures and Algorithms Lecture Slides Wednesday, April 22, 2009 Glenn G. Chappell Department of Computer Science University of Alaska Fairbanks CHAPPELLG@member.ams.org 2005
Hash Tables CS 311 Data Structures and Algorithms Lecture Slides Wednesday, April 22, 2009 Glenn G. Chappell Department of Computer Science University of Alaska Fairbanks CHAPPELLG@member.ams.org 2005
Trees. Truong Tuan Anh CSE-HCMUT
 Trees Truong Tuan Anh CSE-HCMUT Outline Basic concepts Trees Trees A tree consists of a finite set of elements, called nodes, and a finite set of directed lines, called branches, that connect the nodes
Trees Truong Tuan Anh CSE-HCMUT Outline Basic concepts Trees Trees A tree consists of a finite set of elements, called nodes, and a finite set of directed lines, called branches, that connect the nodes
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
CS 234. Module 6. October 25, CS 234 Module 6 ADT Dictionary 1 / 22
 CS 234 Module 6 October 25, 2016 CS 234 Module 6 ADT Dictionary 1 / 22 Case study Problem: Find a way to store student records for a course, wit unique IDs for eac student, were records can be accessed,
CS 234 Module 6 October 25, 2016 CS 234 Module 6 ADT Dictionary 1 / 22 Case study Problem: Find a way to store student records for a course, wit unique IDs for eac student, were records can be accessed,
Lec 17 April 8. Topics: binary Trees expression trees. (Chapter 5 of text)
 Lec 17 April 8 Topics: binary Trees expression trees Binary Search Trees (Chapter 5 of text) Trees Linear access time of linked lists is prohibitive Heap can t support search in O(log N) time. (takes O(N)
Lec 17 April 8 Topics: binary Trees expression trees Binary Search Trees (Chapter 5 of text) Trees Linear access time of linked lists is prohibitive Heap can t support search in O(log N) time. (takes O(N)
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
B-trees. It also makes sense to have data structures that use the minimum addressable unit as their base node size.
 B-trees Balanced BSTs such as RBTs are great for data structures that can fit into the main memory of the computer. But what happens when we need to use external storage? Here are some approximate speeds
B-trees Balanced BSTs such as RBTs are great for data structures that can fit into the main memory of the computer. But what happens when we need to use external storage? Here are some approximate speeds
Binary Search Trees > = 2014 Goodrich, Tamassia, Goldwasser. Binary Search Trees 1
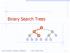 Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Programming II (CS300)
 1 Programming II (CS300) Chapter 11: Binary Search Trees MOUNA KACEM mouna@cs.wisc.edu Fall 2018 General Overview of Data Structures 2 Introduction to trees 3 Tree: Important non-linear data structure
1 Programming II (CS300) Chapter 11: Binary Search Trees MOUNA KACEM mouna@cs.wisc.edu Fall 2018 General Overview of Data Structures 2 Introduction to trees 3 Tree: Important non-linear data structure
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Binary Trees
 Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
Binary Trees 4-7-2005 Opening Discussion What did we talk about last class? Do you have any code to show? Do you have any questions about the assignment? What is a Tree? You are all familiar with what
a graph is a data structure made up of nodes in graph theory the links are normally called edges
 1 Trees Graphs a graph is a data structure made up of nodes each node stores data each node has links to zero or more nodes in graph theory the links are normally called edges graphs occur frequently in
1 Trees Graphs a graph is a data structure made up of nodes each node stores data each node has links to zero or more nodes in graph theory the links are normally called edges graphs occur frequently in
Balanced Search Trees
 Balanced Search Trees Michael P. Fourman February 2, 2010 To investigate the efficiency of binary search trees, we need to establish formulae that predict the time required for these dictionary or set
Balanced Search Trees Michael P. Fourman February 2, 2010 To investigate the efficiency of binary search trees, we need to establish formulae that predict the time required for these dictionary or set
CSCI 136 Data Structures & Advanced Programming. Lecture 25 Fall 2018 Instructor: B 2
 CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
