Maximum flows & Maximum Matchings
|
|
|
- Shonda Walton
- 5 years ago
- Views:
Transcription
1 Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings are analyzed in order to prove that flows and matchings are closely related. We will result into the fact that maximum flow algorithms can be used in order to find maximum matchings. 9. Flows 9.. Definition of Flows A network flow graph is can be defined as a graph G = (V, E) and a capacity function c: V V R+ that satisfies all the following conditions:. For each (u, v) E, c(u, v) > If (u, v) E, then c(u, v) = There is a source s and a sink t. 4. Each vertex is on a directed path from s to t. Due to the fourth condition, in a network flow graph for each node there is a path from source to sink through u therefore the graph is connected. We can consider that in this kind of networks, flow is produced at the source node and consumed at the sink node. All the other nodes are just used in order to move flow from source to sink and never store flow. Note: Capacity function c is defined independently for the two directions of an edge A flow in a network flow graph is a function f : V V R+ such that :. For all (u, v) E, f(u, v) c(u, v) (Capacity constraint : the network flow from one vertex to another must not exceed the given capacity) 2. For all (u, v) V, f(u, v) = - f(v, u) (Skew symmetry : flow from one vertex u to a vertex v is the negative of the flow in the reverse direction) 3. For all u V {s, t}, f ( u, v) = 0 (Flow conservation : the total flow out of a v V vertex other than the sink or source is 0) We should note here that there could be no flow between two nodes that are not connected (there is no edge between them). Flow is only defined across an edge.
2 The value of the flow passing from source s to sink t though (al least one) intermediate node v is : f = v V f ( s, v) = f ( v, t) (9.) As we can see the value of the flow is the total outgoing flow of the source or the incoming flow of the sink. Also note that the flow value is constant, meaning that the flow that is produced from the source at each moment is equal to the flow that is consumed at the sink. This is true, since every other node except source or sink has a net flow value of 0 (due to flow conservation). So the non-zero incoming flow of the sink should match the nonzero outgoing flow of the source Maximum flows A maximum flow in a flow network is a feasible flow (a flow that satisfies the flow conservation) such that the value of the flow is as large as possible. In the maximum flow problem we are given a flow network G with source s and sink t and we wish to find a flow of maximum value from s to t. This maximum value depends both on the structure of the network and on the various capacities of its connections. We can consider the problem as finding the maximum quantity of material that we can transfer through a network without exceeding the maximum transfer rate of the network. Assume that we want to provide a city with water, transferring it from a lake through a network of water pipes. Pulping more water that the maximum flow can harm the network while pulping less will not utilize the network at 00%. Also we are not concerned with the time that it takes for the water that is pulped to reach the city, but we should be sure that the amount of water that is pulped per moment is equal to the amount of water that reaches the city per moment Network with multiple sources and sinks We have considered the maximum flow problem as if there is one source leading to one sink. In the case that there are multiple source or sinks, we reduce the problem to the single sink problem by adding a single source at the beginning (supersource) and one at the end (supersink). These nodes are connected to the other, through edges that their capacity is. Now in order to computer the whole flow, we should compute the flow from the supersource to the supersink. Also using edges with capacity, does not affect the value of the total flow More definitions When we think of a maximum flow we can suppose that there exists no path that can carry any more flow though the network. If there existed one we could ship more flow through it so the flow is not maximum. So while computing the maximum flow we try to find edges that are not fully utilized and create a path through them. We call residual capacity c f (u, v) of an edge (u, v) on a flow network G the additional amount of flow that can be send from u to v before exceeding the capacity of the edge c(u, v). So v V c f (u, v)= c(u, v) - f(u, v) (9.2) All these edges constitute the residual network: Given a flow f on a flow network G the residual network G f of G (induced by f) is a flow graph on G with flows capacities c f (u,v). The residual network is the actual network that will be used in order to compute the maximum flow. Note that due to the skew symmetry condition (f(u, v) = - f(v, u)) an edge that
3 exist in the residual network may not be an edge of the flow network! For each edge of the flow network, there may be created at most one more edge in the residual network. So the maximum number of edges that a residual network may contain is two times the number of edges in the flow network. We have noted that our purpose is to find more paths from source to sink that provide us with more flow, not utilized until now. These paths are called augmenting paths: Given a graph G =(V, E) and a flow f in G, an augmenting path p is a simple (directed) path connection source s to sink t in the residual graph G f. Because of the definition of residual network, each edge permits some additional net flow through each edge without violating the capacity constraint. So the maximum amount of flow that we can ship among an augmenting edge is equal to the residual capacity of the edge. The amount of flow that we will ship through the whole augmenting path is the minimum residual capacity of the edges of path. Considering all these, it turn out that if an augmenting path exist in the residual network we can improve the flow of the network. So in order to achieve maximum flow we should search for augmenting paths. Finally we will define cut of flow networks : An (S, T) - cut in a flow network G = (V, E), is a partition of V to S and T = V S such that s S and t T. The flow across a (S, T) - cut is f(s, T) = f ( u, v) (9.3) u S v T The capacity of the cut is c(s, T) = c ( u, v) (9.4) u S v T Cuts in flow networks are very useful. A property of a cut is that the value of the flow across the cuts is equal to the flow of the network. Also this shows that in a flow network, the flow of the network is bounded by the capacity of any cut of the network Max flow Min cut Theorem Theorem 9. Let f be a flow from s to t in G. The following conditions are equivalent ) F is a maximum flow 2) The residual graph G f allows no augmenting paths 3) f = c(s, T) for some (S, T) cut Proof. ( a ) () (2) Let F be a maximum flow in a flow network. If the residual graph of the flow network G f has an augmenting path, the flow f can be improved though that path so flow is not maximum. So there exist no augmenting paths. ( b ) (2) (3) We construct an (S, T) - cut as follows : Let S = {u V there is a path from s to u in G f } and let T = V S. This partition defines an (S, T) cut : s S, t T otherwise there is an augmenting path in G f. For each u S and v T we have f(u, v) = c(u, v) otherwise edge (u, v) E f and u S. Then f(s, T) = c(s, T) so f = f(s, T) = c(s, T) ( c ) (3) () We have proved that for any (S, T) cut, f c(s, T) thus if f = c(s, T) for some cut, f is a maximum flow.
4 9..6 Maximum flows algorithms The Ford Fulkerson method can be used to solve the maximum flow problem. The method is iterative. It proceeds by finding an augmenting path in the residual network through which we can ship more flow. This is ended when no augmenting path can be found and we have achieved maximum flow. There are many implementations of this method and differs in the way that augmenting paths are discovered. Ford Fulkerson Input: a graph G, a source s and a sink t in the graph Output: a maximum flow for this graph from source to sink Ford Fulkerson (G, s, t) for each edge (u, v) Edges[G] 2 do f [u, v] 0 3 f [u, v] 0 4 while there exist a path p from s to t in the residual network G f 5 do c f min {c f (u, v) : (u, v) is in p} 6 for each edge (u, v) in p 7 do f [u, v] f [u, v] + c f (p) 8 f [u, v] f [u, v] At each iteration of the while loop we find an augmenting path in the residual network and ship more flow through the edges until there exist no more augmenting paths. The running time of the algorithm depends on the implementation. If augmenting paths are found using a BFS search then the algorithm runs in polynomial time. The exact time of the execution in this case is O( V E 2 ) and is called Edmonds - Karp algorithm. Example Given the graph shown in Figure 9. (a) we will run the algorithm. The first augmenting path that we find is a b c d (Figure 9. (b)). The flow that we can ship through is 4 and so we update the network. In the second iteration (Figure 9. (c)) we find a b d. Edge (a, b) can carry only 4 additional units of flow so this is the maximum flow through this path. Finally, (Figure 9. (d)), we navigate through a c d by adding 2 units of flow since edge (c, d) can t carry any more. Now our network has no augmenting paths so the algorithm terminates and we have found the maximum flow for the flow network a b d 4/8 b 7 a 4/4 d 5 c 6 5 c 4/6 8/8 b 4/7 a 4/4 d 8/8 b 4/7 a 4/4 d 5 c 4/6 2/5 c 6/6 Figure 9.: A Ford - Fulkerson algorithm example
5 9.2 Matchings 9.2. Definitions A matching in a graph G=(V, E), is a set of edges (links) no two of which have a common end (vertex). In the most practical problems we want to find the matching for the most elements of the graph. Such a matching is called maximum matching. A matching is also called an independent edge set. An edge in a matching of a graph is a matched edge. All the edges of the graph that are not in the matching are called free edges. A vertex incident to an edge of the matching is called matched vertex (with respect to the matching), on the other side every other vertex is an exposed vertex (with respect to the matching). In the most practical problems we want to find the matching for the most elements of the graph, such matching is called maximum matching (also known as maximum cardinality matching). Formal Definition: Given a graph G=(V, E) a set of edges M is a matching if. M E 2. No two edges of M share the same node. A maximum matching in G is a matching M with maximal cardinality. That means that for every other maximal matching M' of the graph G: M > M'. In a bipartite graph G = (X, Y, E), a matching is a complete matching from X to Y if every vertex in X is incident to an edge of the matching. The necessary and sufficient condition for the existence of such a complete matching is that f(a) A for every subset A of X, where f(a) is the set of vertices that are adjacent to at least one vertex in A. A matching in a graph is a perfect matching if every vertex in the graph is incident to an edge in the matching. Given an arbitrary graph G = (V, E), we want to find out if all the vertices of V can be grouped in pairs using this matching. According to the Konig s Marriage Theorem: If a bipartite graph G = (X, Y, E) is k-regular (where k is positive), there is a perfect matching in the graph. If a graph has a perfect matching M then M = V /2, that means practically that each vertex has its unique pair. Theorem 9.2 (Tutte) The graph G = (V, E) has a perfect matching if and only if the number of odd components of (G S) does not exceed S for every S V Building a Matching Before continuing with methods and algorithms for finding the maximum matching, we must introduce some definitions of terms. Given a matching M in G, a simple path P of G: P = u, u 2, u 3, u 4,, u k is the path that connects u with u k.
6 An alternating path with respect to M is the path P that all its odd edges are not in M and also all its even edges are in M (Figure 9.2). u u2 u3 u4 u5 u6 u7 u8 u9 P = u, u2,u3,u4, u5, u6 M = (u2,u3), (u4,u5), (u7,u8) Figure 9.2 : Paths & alternating paths An alternating path P is an augmenting path with respect to M if its first and its last node are not covered by M. An augmenting path has odd number of edges. The idea of the augmenting path is one of the fundamental ideas of matching theory. A path or a circuit P in a graph G is said to be alternating with respect to a matching M if its edges alternately are in and not in M (an alternating circuit will have an even number of edges). If the end nodes (first and last) of a path P are not saturated by M then P is called an augmenting path. Removing the even edges of P from M and adding the odd edges of P to M increases the size of the matching by one (covering two more vertices). Theorem 9.3 (Berge 957) A matching M in a graph G is maximum iff there is no augmenting path in G with respect to M. Proof. (a) Augmenting path not maximum: If there is an augmenting path then M is not the maximum matching since we can use the path to get a larger matching. (b) Not maximum augmenting path. Assume that M is not the maximum. we need to show that there is an augmenting path with respect to M. Let M be a matching in G such that M > M consider the graph H = (V, M M ) The degrees in this graph are 0,, and 2. The connected components in the graph are either paths or cycles (circuits), since there are no cycles with odd number of edges, there must be at least one connected component (path) with mode one edge of M than M. This component is an augmenting path A generalized Matching Algorithm
7 Main steps:. M 0; 2. while there are augmenting paths with respect to M 3. extend the matching using an augmenting path. The analysis of this algorithm is very complex. Here we will emphasize in a solution for bi-partite graphs only. In a bipartite graph the search for an augmenting path, which is the most difficult step in the generalized algorithm above, can be done by a variation of the Ford - Fulkenson method which we saw in the Maximum flows. u u2 u u2 u3 u5 u6 u4 s u3 u5 u6 u4 t u7 u8 u7 u8 u9 u9 (a) (b) Figure 9.3 : Conversion of an undirected bi-partite graph in a flow network in order to find matchings Given an undirected bi-partite graph G=(V, E), (Figure 9.3 (a)) we must construct a flow network in which the flows will correspond to the matchings. Let G = (V, E ) be the corresponding flow network for G (Figure 9.3 (b)) (according to super-source and super-sink theory section 9..3) We define two new vertices a source s and a sink t not in V, and we let: V = V {s, t} For the original graph G if V = L R where L is the left partition, and R is the right partition of the bi-partite graph G, then the directed edges of G are given by: E = {(s, u): u L} {(u, v): u L, v R, and (u, v) E} {(v, t) : v R, } The last step to finish the directed weighted graph G is to assign unit capacity to every edge in E. (Figure 9.4)
8 u2 s u3 u7 u u5 u4 u6 u8 u9 t P = u, u2,u3,u4, u5, u6 M = (u2,u3), (u4,u5), (u7,u8) Figure 9.4 : Last step of conversion, each edge has capacity and the graph has been transformed to an flow network The following show that a matching in G corresponds to a flow in G network flow. We say a flow f on a flow network G = (V, E) is integer-valued if f(u, v) is an integer for all (u, v) V x V. Lemma 9.4: Let G = (V, E) be a bi-partite graph with vertex partition V = L R and let G = ( V, E ) be its corresponding flow network. If M is a matching in G, then there is an integer-valued flow g in G with value f = M. Conversely, if f is an integer-valued flow in G, then there is a matching M in G with cardinality M = f. Proof. We must show that a matching M in G corresponds to an integer flow in G. If (u, v) M, then f(s, u) = f(u, v) = f(v, t) = and f(u, s) = f(v, u) = f(t, v) = - For all other edges of E we define f(u, v) = 0. Since the graph is bi-partite we observe that for each path from s to t: s u v t with u L, v R the capacity is. Since each vertex in L has incoming capacity there can be at most edge (u, v) leaving L to R. The set of edges (u,v) therefore corresponds a matching M. To see that M = f where f the number of flows, we observe that for every matched vertex u L we have f(s, u) = and for every edge (u, v) E - M,we have f(u, v) = 0. Consequently we obtain : M = f(l,r) = f(l, V ) - f(l, L) f(l, s) f(l, t) = f(s, L) - 0 = f(s,v ) = f The above shows that we can use an algorithm for finding maximum flows to find the maximum matching of a Graph G.
9 Bibliography [] Thomas H Cormen, Charles E. Leiserson, Ronald L. Rivest. Introduction to Algorithms. MIT Press, Cambridge Massachusetts, 990 [2] R. L. Graham, M. Grotchel L.Lovasz. Handbook of Combinatorics Vol. MIT Press, Cambridge Massachusetts, 995 [3] V. K. Balakrishnan. Graph Theory. McGraw-Hill, New York 997 [4] R. Diestel. Graph Theory. Springer, New York 997
Maximum Flow. Flow Networks. Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms. Example Flow Network
 Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Jessica Su (some parts copied from CLRS / last quarter s notes)
 1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Graphs and Network Flows IE411. Lecture 13. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Matching Algorithms. Proof. If a bipartite graph has a perfect matching, then it is easy to see that the right hand side is a necessary condition.
 18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
18.433 Combinatorial Optimization Matching Algorithms September 9,14,16 Lecturer: Santosh Vempala Given a graph G = (V, E), a matching M is a set of edges with the property that no two of the edges have
Problem Set 7 Solutions
 Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching. 1 Primal/Dual Algorithm for weighted matchings in Bipartite Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 009) Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching Lecturer: Mohammad R. Salavatipour Date: Sept 15 and 17, 009
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 009) Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching Lecturer: Mohammad R. Salavatipour Date: Sept 15 and 17, 009
Network Flow. November 23, CMPE 250 Graphs- Network Flow November 23, / 31
 Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Lecture 11: Maximum flow and minimum cut
 Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Graph Algorithms Matching
 Chapter 5 Graph Algorithms Matching Algorithm Theory WS 2012/13 Fabian Kuhn Circulation: Demands and Lower Bounds Given: Directed network, with Edge capacities 0and lower bounds l for Node demands for
Chapter 5 Graph Algorithms Matching Algorithm Theory WS 2012/13 Fabian Kuhn Circulation: Demands and Lower Bounds Given: Directed network, with Edge capacities 0and lower bounds l for Node demands for
Solution for Homework set 3
 TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
CS 217 Algorithms and Complexity Homework Assignment 2
 CS 217 Algorithms and Complexity Homework Assignment 2 Shanghai Jiaotong University, Fall 2015 Handed out on 2015-10-19 Due on 2015-10-26 You can hand in your solution either as a printed file or hand-written
CS 217 Algorithms and Complexity Homework Assignment 2 Shanghai Jiaotong University, Fall 2015 Handed out on 2015-10-19 Due on 2015-10-26 You can hand in your solution either as a printed file or hand-written
Network flows and Menger s theorem
 Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
Source. Sink. Chapter 10: Iterative Programming Maximum Flow Problem. CmSc250 Intro to Algorithms
 Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Notes for Lecture 20
 U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
Tutorial for Algorithm s Theory Problem Set 5. January 17, 2013
 Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Graphs. Edges may be directed (from u to v) or undirected. Undirected edge eqvt to pair of directed edges
 (p 186) Graphs G = (V,E) Graphs set V of vertices, each with a unique name Note: book calls vertices as nodes set E of edges between vertices, each encoded as tuple of 2 vertices as in (u,v) Edges may
(p 186) Graphs G = (V,E) Graphs set V of vertices, each with a unique name Note: book calls vertices as nodes set E of edges between vertices, each encoded as tuple of 2 vertices as in (u,v) Edges may
2. Lecture notes on non-bipartite matching
 Massachusetts Institute of Technology 18.433: Combinatorial Optimization Michel X. Goemans February 15th, 013. Lecture notes on non-bipartite matching Given a graph G = (V, E), we are interested in finding
Massachusetts Institute of Technology 18.433: Combinatorial Optimization Michel X. Goemans February 15th, 013. Lecture notes on non-bipartite matching Given a graph G = (V, E), we are interested in finding
CSE 417 Network Flows (pt 4) Min Cost Flows
 CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
Sources for this lecture. 3. Matching in bipartite and general graphs. Symmetric difference
 S-72.2420 / T-79.5203 Matching in bipartite and general graphs 1 3. Matching in bipartite and general graphs Let G be a graph. A matching M in G is a set of nonloop edges with no shared endpoints. Let
S-72.2420 / T-79.5203 Matching in bipartite and general graphs 1 3. Matching in bipartite and general graphs Let G be a graph. A matching M in G is a set of nonloop edges with no shared endpoints. Let
Network Flow I. Lecture Overview The Network Flow Problem
 Lecture Network Flow I. Overview In these next two lectures we are going to talk about an important algorithmic problem called the Network Flow Problem. Network flow is important because it can be used
Lecture Network Flow I. Overview In these next two lectures we are going to talk about an important algorithmic problem called the Network Flow Problem. Network flow is important because it can be used
CS612 Algorithms for Electronic Design Automation
 CS612 Algorithms for Electronic Design Automation Lecture 8 Network Flow Based Modeling 1 Flow Network Definition Given a directed graph G = (V, E): Each edge (u, v) has capacity c(u,v) 0 Each edge (u,
CS612 Algorithms for Electronic Design Automation Lecture 8 Network Flow Based Modeling 1 Flow Network Definition Given a directed graph G = (V, E): Each edge (u, v) has capacity c(u,v) 0 Each edge (u,
and 6.855J March 6, Maximum Flows 2
 5.08 and.855j March, 00 Maximum Flows Network Reliability Communication Network What is the maximum number of arc disjoint paths from s to t? How can we determine this number? Theorem. Let G = (N,A) be
5.08 and.855j March, 00 Maximum Flows Network Reliability Communication Network What is the maximum number of arc disjoint paths from s to t? How can we determine this number? Theorem. Let G = (N,A) be
Network Design and Optimization course
 Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
1 Matchings in Graphs
 Matchings in Graphs J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 Definition Two edges are called independent if they are not adjacent
Matchings in Graphs J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 Definition Two edges are called independent if they are not adjacent
Minimum Cost Edge Disjoint Paths
 Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
Algorithm Circle Extra Lecture: Solving the Assignment Problem with Network Flow
 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Algorithm Circle Extra Lecture: Solving the with Network Flow 17 September 2012 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline
The Network Flow Minimum-Cost Maximum Flow Shameless Plug Algorithm Circle Extra Lecture: Solving the with Network Flow 17 September 2012 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline
GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS. March 3, 2016
 GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS ZOÉ HAMEL March 3, 2016 1. Introduction Let G = (V (G), E(G)) be a graph G (loops and multiple edges not allowed) on the set of vertices V (G) and the set
GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS ZOÉ HAMEL March 3, 2016 1. Introduction Let G = (V (G), E(G)) be a graph G (loops and multiple edges not allowed) on the set of vertices V (G) and the set
Matching. Algorithms and Networks
 Matching Algorithms and Networks This lecture Matching: problem statement and applications Bipartite matching (recap) Matching in arbitrary undirected graphs: Edmonds algorithm Diversion: generalized tic-tac-toe
Matching Algorithms and Networks This lecture Matching: problem statement and applications Bipartite matching (recap) Matching in arbitrary undirected graphs: Edmonds algorithm Diversion: generalized tic-tac-toe
1 Introduction. 2 The Generic Push-Relabel Algorithm. Improvements on the Push-Relabel Method: Excess Scaling. 2.1 Definitions CMSC 29700
 CMSC 9700 Supervised Reading & Research Week 6: May 17, 013 Improvements on the Push-Relabel Method: Excess Scaling Rahul Mehta 1 Introduction We now know about both the methods based on the idea of Ford
CMSC 9700 Supervised Reading & Research Week 6: May 17, 013 Improvements on the Push-Relabel Method: Excess Scaling Rahul Mehta 1 Introduction We now know about both the methods based on the idea of Ford
CS261: Problem Set #1
 CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
Maximum Flow Algorithms
 Maximum Flow Algorithms Network Algorithms Georgia Kaouri Contents Applications, special cases Flow networks Ford Fulkerson algorithm Preflow push algorithms Lift to front algorithm Material flows Applications
Maximum Flow Algorithms Network Algorithms Georgia Kaouri Contents Applications, special cases Flow networks Ford Fulkerson algorithm Preflow push algorithms Lift to front algorithm Material flows Applications
5.1 Min-Max Theorem for General Matching
 CSC5160: Combinatorial Optimization and Approximation Algorithms Topic: General Matching Date: 4/01/008 Lecturer: Lap Chi Lau Scribe: Jennifer X.M. WU In this lecture, we discuss matchings in general graph.
CSC5160: Combinatorial Optimization and Approximation Algorithms Topic: General Matching Date: 4/01/008 Lecturer: Lap Chi Lau Scribe: Jennifer X.M. WU In this lecture, we discuss matchings in general graph.
Matchings. Examples. K n,m, K n, Petersen graph, Q k ; graphs without perfect matching. A maximal matching cannot be enlarged by adding another edge.
 Matchings A matching is a set of (non-loop) edges with no shared endpoints. The vertices incident to an edge of a matching M are saturated by M, the others are unsaturated. A perfect matching of G is a
Matchings A matching is a set of (non-loop) edges with no shared endpoints. The vertices incident to an edge of a matching M are saturated by M, the others are unsaturated. A perfect matching of G is a
CSE 417 Network Flows (pt 3) Modeling with Min Cuts
 CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
1 Matching in Non-Bipartite Graphs
 CS 369P: Polyhedral techniques in combinatorial optimization Instructor: Jan Vondrák Lecture date: September 30, 2010 Scribe: David Tobin 1 Matching in Non-Bipartite Graphs There are several differences
CS 369P: Polyhedral techniques in combinatorial optimization Instructor: Jan Vondrák Lecture date: September 30, 2010 Scribe: David Tobin 1 Matching in Non-Bipartite Graphs There are several differences
Datenstrukturen & Algorithmen Solution of Sheet 11 FS 14
 Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 14th May
Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 14th May
Minimum Spanning Tree (undirected graph)
 1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
GRAPH THEORY and APPLICATIONS. Matchings
 GRAPH THEORY and APPLICATIONS Matchings Definition Matching of a graph G: Any subset of edges M E such that no two elements of M are adjacent. Example: {e} {e,e5,e0} {e2,e7,e0} {e4,e6,e8} e4 e7 e8 e e2
GRAPH THEORY and APPLICATIONS Matchings Definition Matching of a graph G: Any subset of edges M E such that no two elements of M are adjacent. Example: {e} {e,e5,e0} {e2,e7,e0} {e4,e6,e8} e4 e7 e8 e e2
Homework 3 Solutions
 CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
11.1. Definitions. 11. Domination in Graphs
 11. Domination in Graphs Some definitions Minimal dominating sets Bounds for the domination number. The independent domination number Other domination parameters. 11.1. Definitions A vertex v in a graph
11. Domination in Graphs Some definitions Minimal dominating sets Bounds for the domination number. The independent domination number Other domination parameters. 11.1. Definitions A vertex v in a graph
Lecture 14: Linear Programming II
 A Theorist s Toolkit (CMU 18-859T, Fall 013) Lecture 14: Linear Programming II October 3, 013 Lecturer: Ryan O Donnell Scribe: Stylianos Despotakis 1 Introduction At a big conference in Wisconsin in 1948
A Theorist s Toolkit (CMU 18-859T, Fall 013) Lecture 14: Linear Programming II October 3, 013 Lecturer: Ryan O Donnell Scribe: Stylianos Despotakis 1 Introduction At a big conference in Wisconsin in 1948
Network Flow. The network flow problem is as follows:
 Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
1. Lecture notes on bipartite matching February 4th,
 1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
Lecture 10,11: General Matching Polytope, Maximum Flow. 1 Perfect Matching and Matching Polytope on General Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
CSC 8301 Design & Analysis of Algorithms: Linear Programming
 CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
PERFECT MATCHING THE CENTRALIZED DEPLOYMENT MOBILE SENSORS THE PROBLEM SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS OF MOBILE SENSORS
 SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING 1 2 ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms
SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING 1 2 ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Hamiltonian cycles in bipartite quadrangulations on the torus
 Hamiltonian cycles in bipartite quadrangulations on the torus Atsuhiro Nakamoto and Kenta Ozeki Abstract In this paper, we shall prove that every bipartite quadrangulation G on the torus admits a simple
Hamiltonian cycles in bipartite quadrangulations on the torus Atsuhiro Nakamoto and Kenta Ozeki Abstract In this paper, we shall prove that every bipartite quadrangulation G on the torus admits a simple
CMPSCI 311: Introduction to Algorithms Practice Final Exam
 CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
CMPSCI 311: Introduction to Algorithms Practice Final Exam Name: ID: Instructions: Answer the questions directly on the exam pages. Show all your work for each question. Providing more detail including
Today. Maximum flow. Maximum flow. Problem
 5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
Paths, Trees, and Flowers by Jack Edmonds
 Paths, Trees, and Flowers by Jack Edmonds Xiang Gao ETH Zurich Distributed Computing Group www.disco.ethz.ch Introduction and background Edmonds maximum matching algorithm Matching-duality theorem Matching
Paths, Trees, and Flowers by Jack Edmonds Xiang Gao ETH Zurich Distributed Computing Group www.disco.ethz.ch Introduction and background Edmonds maximum matching algorithm Matching-duality theorem Matching
Graph Algorithms Maximum Flow Applications
 Chapter 5 Graph Algorithms Maximum Flow Applications Algorithm Theory WS 202/3 Fabian Kuhn Maximum Flow Applications Maximum flow has many applications Reducing a problem to a max flow problem can even
Chapter 5 Graph Algorithms Maximum Flow Applications Algorithm Theory WS 202/3 Fabian Kuhn Maximum Flow Applications Maximum flow has many applications Reducing a problem to a max flow problem can even
Network Flow. By: Daniel Pham, Anthony Huber, Shaazan Wirani
 Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Network Flow and Matching
 Chapter 4 Network Flow and Matching In this chapter, we examine the network flow problem, a graph problem to which many problems can be reduced. In fact, some problems that don t even appear to be graph
Chapter 4 Network Flow and Matching In this chapter, we examine the network flow problem, a graph problem to which many problems can be reduced. In fact, some problems that don t even appear to be graph
Taking Stock. Last Time Flows. This Time Review! 1 Characterize the structure of an optimal solution
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 26 Jeff Linderoth Last Time Department of Industrial and Systems Engineering Lehigh University April 2, 2007 This Time Review! Jeff Linderoth
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 26 Jeff Linderoth Last Time Department of Industrial and Systems Engineering Lehigh University April 2, 2007 This Time Review! Jeff Linderoth
Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model
 Dhaka Univ. J. Sci. (): 9-, 3 (January) Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model Sohana Jahan, Marzia Yesmin and Fatima Tuj Jahra Department of Mathematics,University
Dhaka Univ. J. Sci. (): 9-, 3 (January) Application of Bounded Variable Simplex Algorithm in Solving Maximal Flow Model Sohana Jahan, Marzia Yesmin and Fatima Tuj Jahra Department of Mathematics,University
PERFECT MATCHING THE CENTRALIZED DEPLOYMENT MOBILE SENSORS THE PROBLEM SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS OF MOBILE SENSORS
 SECOND PART: WIRELESS NETWORKS.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms A.y.
SECOND PART: WIRELESS NETWORKS.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms A.y.
Theorem 3.1 (Berge) A matching M in G is maximum if and only if there is no M- augmenting path.
 3 Matchings Hall s Theorem Matching: A matching in G is a subset M E(G) so that no edge in M is a loop, and no two edges in M are incident with a common vertex. A matching M is maximal if there is no matching
3 Matchings Hall s Theorem Matching: A matching in G is a subset M E(G) so that no edge in M is a loop, and no two edges in M are incident with a common vertex. A matching M is maximal if there is no matching
Matching Theory. Amitava Bhattacharya
 Matching Theory Amitava Bhattacharya amitava@math.tifr.res.in Definition: A simple graph is a triple G = (V, E, φ), where V is a finite set of vertices, E is a finite set of edges, and φ is a function
Matching Theory Amitava Bhattacharya amitava@math.tifr.res.in Definition: A simple graph is a triple G = (V, E, φ), where V is a finite set of vertices, E is a finite set of edges, and φ is a function
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Module 7. Independent sets, coverings. and matchings. Contents
 Module 7 Independent sets, coverings Contents and matchings 7.1 Introduction.......................... 152 7.2 Independent sets and coverings: basic equations..... 152 7.3 Matchings in bipartite graphs................
Module 7 Independent sets, coverings Contents and matchings 7.1 Introduction.......................... 152 7.2 Independent sets and coverings: basic equations..... 152 7.3 Matchings in bipartite graphs................
SOLVING THE TRANSPORTATION PROBLEM WITH PIECEWISE-LINEAR CONCAVE COST FUNCTIONS
 Review of the Air Force Academy No.2 (34)/2017 SOLVING THE TRANSPORTATION PROBLEM WITH PIECEWISE-LINEAR CONCAVE COST FUNCTIONS Tatiana PAȘA, Valeriu UNGUREANU Universitatea de Stat, Chișinău, Moldova (pasa.tatiana@yahoo.com,
Review of the Air Force Academy No.2 (34)/2017 SOLVING THE TRANSPORTATION PROBLEM WITH PIECEWISE-LINEAR CONCAVE COST FUNCTIONS Tatiana PAȘA, Valeriu UNGUREANU Universitatea de Stat, Chișinău, Moldova (pasa.tatiana@yahoo.com,
CS 125 Section #5 Graph Traversal and Linear Programs October 6, 2016
 CS 125 Section #5 Graph Traversal and Linear Programs October 6, 2016 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there
CS 125 Section #5 Graph Traversal and Linear Programs October 6, 2016 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
7. NETWORK FLOW II. Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 2013 Kevin Wayne
 7. NETWORK FLOW II Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 203 Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos bipartite matching disjoint paths extensions
7. NETWORK FLOW II Lecture slides by Kevin Wayne Copyright 2005 Pearson-Addison Wesley Copyright 203 Kevin Wayne http://www.cs.princeton.edu/~wayne/kleinberg-tardos bipartite matching disjoint paths extensions
Design And Analysis of Algorithms Lecture 6: Combinatorial Matching Algorithms.
 Design And Analysis of Algorithms Lecture 6: Combinatorial Matching Algorithms. February 14, 2018 In this lecture, we will study algorithms for constructing matchings on graphs. A matching M E has maximum
Design And Analysis of Algorithms Lecture 6: Combinatorial Matching Algorithms. February 14, 2018 In this lecture, we will study algorithms for constructing matchings on graphs. A matching M E has maximum
1 Bipartite maximum matching
 Cornell University, Fall 2017 Lecture notes: Matchings CS 6820: Algorithms 23 Aug 1 Sep These notes analyze algorithms for optimization problems involving matchings in bipartite graphs. Matching algorithms
Cornell University, Fall 2017 Lecture notes: Matchings CS 6820: Algorithms 23 Aug 1 Sep These notes analyze algorithms for optimization problems involving matchings in bipartite graphs. Matching algorithms
Solving problems on graph algorithms
 Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Lecture 10: Strongly Connected Components, Biconnected Graphs
 15-750: Graduate Algorithms February 8, 2016 Lecture 10: Strongly Connected Components, Biconnected Graphs Lecturer: David Witmer Scribe: Zhong Zhou 1 DFS Continued We have introduced Depth-First Search
15-750: Graduate Algorithms February 8, 2016 Lecture 10: Strongly Connected Components, Biconnected Graphs Lecturer: David Witmer Scribe: Zhong Zhou 1 DFS Continued We have introduced Depth-First Search
Network Flows. 1. Flows deal with network models where edges have capacity constraints. 2. Shortest paths deal with edge costs.
 Network Flows. Flows deal with network models where edges have capacity constraints. 2. Shortest paths deal with edge costs. 4 u v 2 5 s 6 5 t 4 x 2 y 3 3. Network flow formulation: A network G = (V, E).
Network Flows. Flows deal with network models where edges have capacity constraints. 2. Shortest paths deal with edge costs. 4 u v 2 5 s 6 5 t 4 x 2 y 3 3. Network flow formulation: A network G = (V, E).
Ma/CS 6b Class 2: Matchings
 Ma/CS 6b Class 2: Matchings By Adam Sheffer Send anonymous suggestions and complaints from here. Email: adamcandobetter@gmail.com Password: anonymous2 There aren t enough crocodiles in the presentations
Ma/CS 6b Class 2: Matchings By Adam Sheffer Send anonymous suggestions and complaints from here. Email: adamcandobetter@gmail.com Password: anonymous2 There aren t enough crocodiles in the presentations
1 Linear programming relaxation
 Cornell University, Fall 2010 CS 6820: Algorithms Lecture notes: Primal-dual min-cost bipartite matching August 27 30 1 Linear programming relaxation Recall that in the bipartite minimum-cost perfect matching
Cornell University, Fall 2010 CS 6820: Algorithms Lecture notes: Primal-dual min-cost bipartite matching August 27 30 1 Linear programming relaxation Recall that in the bipartite minimum-cost perfect matching
Matching 4/21/2016. Bipartite Matching. 3330: Algorithms. First Try. Maximum Matching. Key Questions. Existence of Perfect Matching
 Bipartite Matching Matching 3330: Algorithms A graph is bipartite if its vertex set can be partitioned into two subsets A and B so that each edge has one endpoint in A and the other endpoint in B. A B
Bipartite Matching Matching 3330: Algorithms A graph is bipartite if its vertex set can be partitioned into two subsets A and B so that each edge has one endpoint in A and the other endpoint in B. A B
Notes on Minimum Cuts and Modular Functions
 Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
COMP260 Spring 2014 Notes: February 4th
 COMP260 Spring 2014 Notes: February 4th Andrew Winslow In these notes, all graphs are undirected. We consider matching, covering, and packing in bipartite graphs, general graphs, and hypergraphs. We also
COMP260 Spring 2014 Notes: February 4th Andrew Winslow In these notes, all graphs are undirected. We consider matching, covering, and packing in bipartite graphs, general graphs, and hypergraphs. We also
Matchings. Saad Mneimneh
 Matchings Saad Mneimneh 1 Stable matching Consider n men and n women. A matching is a one to one correspondence between the men and the women. In finding a matching, however, we would like to respect the
Matchings Saad Mneimneh 1 Stable matching Consider n men and n women. A matching is a one to one correspondence between the men and the women. In finding a matching, however, we would like to respect the
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
Assignment 1 Introduction to Graph Theory CO342
 Assignment 1 Introduction to Graph Theory CO342 This assignment will be marked out of a total of thirty points, and is due on Thursday 18th May at 10am in class. Throughout the assignment, the graphs are
Assignment 1 Introduction to Graph Theory CO342 This assignment will be marked out of a total of thirty points, and is due on Thursday 18th May at 10am in class. Throughout the assignment, the graphs are
Parametric Maximum Flow Problem: Techniques and Algorithms. Deepika Sareen, Dr Deepak Garg. Thapar University, Patiala
 Parametric Maximum Flow Problem: Techniques and Algorithms Deepika Sareen, Dr Deepak Garg Thapar University, Patiala sareendeepika@yahoo.co.in, dgarg@thapar.edu Abstract We encounter many different types
Parametric Maximum Flow Problem: Techniques and Algorithms Deepika Sareen, Dr Deepak Garg Thapar University, Patiala sareendeepika@yahoo.co.in, dgarg@thapar.edu Abstract We encounter many different types
Paths, Flowers and Vertex Cover
 Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
Paths, Flowers and Vertex Cover Venkatesh Raman M. S. Ramanujan Saket Saurabh Abstract It is well known that in a bipartite (and more generally in a König) graph, the size of the minimum vertex cover is
1. Lecture notes on bipartite matching
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Discrete Mathematics and Probability Theory Fall 2013 Vazirani Note 7
 CS 70 Discrete Mathematics and Probability Theory Fall 2013 Vazirani Note 7 An Introduction to Graphs A few centuries ago, residents of the city of Königsberg, Prussia were interested in a certain problem.
CS 70 Discrete Mathematics and Probability Theory Fall 2013 Vazirani Note 7 An Introduction to Graphs A few centuries ago, residents of the city of Königsberg, Prussia were interested in a certain problem.
Graph Algorithms. A Brief Introduction. 高晓沨 (Xiaofeng Gao) Department of Computer Science Shanghai Jiao Tong Univ.
 Graph Algorithms A Brief Introduction 高晓沨 (Xiaofeng Gao) Department of Computer Science Shanghai Jiao Tong Univ. 目录 2015/5/7 1 Graph and Its Applications 2 Introduction to Graph Algorithms 3 References
Graph Algorithms A Brief Introduction 高晓沨 (Xiaofeng Gao) Department of Computer Science Shanghai Jiao Tong Univ. 目录 2015/5/7 1 Graph and Its Applications 2 Introduction to Graph Algorithms 3 References
Transportation Planning: The maximum flow problem
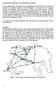 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
CS 5540 Spring 2013 Assignment 3, v1.0 Due: Apr. 24th 11:59PM
 1 Introduction In this programming project, we are going to do a simple image segmentation task. Given a grayscale image with a bright object against a dark background and we are going to do a binary decision
1 Introduction In this programming project, we are going to do a simple image segmentation task. Given a grayscale image with a bright object against a dark background and we are going to do a binary decision
γ(ɛ) (a, b) (a, d) (d, a) (a, b) (c, d) (d, d) (e, e) (e, a) (e, e) (a) Draw a picture of G.
 MAD 3105 Spring 2006 Solutions for Review for Test 2 1. Define a graph G with V (G) = {a, b, c, d, e}, E(G) = {r, s, t, u, v, w, x, y, z} and γ, the function defining the edges, is given by the table ɛ
MAD 3105 Spring 2006 Solutions for Review for Test 2 1. Define a graph G with V (G) = {a, b, c, d, e}, E(G) = {r, s, t, u, v, w, x, y, z} and γ, the function defining the edges, is given by the table ɛ
Computational Methods in IS Research Fall Graph Algorithms Network Flow Problems
 Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
MTL 776: Graph Algorithms Lecture : Matching in Graphs
 MTL 776: Graph Algorithms Lecture : Matching in Graphs Course Coordinator: Prof. B. S. Panda Note: The note is based on the lectures taken in the class. It is a draft version and may contain errors. It
MTL 776: Graph Algorithms Lecture : Matching in Graphs Course Coordinator: Prof. B. S. Panda Note: The note is based on the lectures taken in the class. It is a draft version and may contain errors. It
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
CS261: Problem Set #2
 CS261: Problem Set #2 Due by 11:59 PM on Tuesday, February 9, 2016 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Submission instructions:
CS261: Problem Set #2 Due by 11:59 PM on Tuesday, February 9, 2016 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Submission instructions:
Bipartite Matching & the Hungarian Method
 Bipartite Matching & the Hungarian Method Last Revised: 15/9/7 These notes follow formulation originally developed by Subhash Suri in http://www.cs.ucsb.edu/ suri/cs/matching.pdf We previously saw how
Bipartite Matching & the Hungarian Method Last Revised: 15/9/7 These notes follow formulation originally developed by Subhash Suri in http://www.cs.ucsb.edu/ suri/cs/matching.pdf We previously saw how
Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R + Goal: find a tour (Hamiltonian cycle) of minimum cost
 Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R + Goal: find a tour (Hamiltonian cycle) of minimum cost Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R
Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R + Goal: find a tour (Hamiltonian cycle) of minimum cost Traveling Salesman Problem (TSP) Input: undirected graph G=(V,E), c: E R
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret
 Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Graph Theory: Matchings and Factors
 Graph Theory: Matchings and Factors Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Matchings A matching of size k in a graph G is a set of k
Graph Theory: Matchings and Factors Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Matchings A matching of size k in a graph G is a set of k
