Network Flow. The network flow problem is as follows:
|
|
|
- Amice Wilson
- 5 years ago
- Views:
Transcription
1 Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished vertices, s and t, called the source and the sink, such that the source only has out-edges and the sink only has inedges, find the maximum amount of some commodity that can flow through the network from source to sink. One way to imagine the situation is imagining each edge as a pipe that allows a certain flow of a liquid per second. The source is where the liquid is pouring from, and the sink is where it ends up. Each edge weight specifies the maximal amount of liquid that can flow through that pipe per second. Given that information, what is the most liquid that can flow from source to sink per second, in the steady state? Here is an example of an empty flow graph: Here is an example of some flow going through the flow graph specified above:
2 In the picture on the previous page, the first number on each edge represents the current flow going through that edge and the second value represents the capacity of the edge, the maximum amount of flow that could be going through that edge. In this picture above, we have 19 units of flow going from the source (S) to the sink (T). In order for the assignment of flows to be valid, we must have the sum of flow coming into a vertex equal to the flow coming out of a vertex, for each vertex in the graph except the source and the sink. This is the conservation rule. Also, each flow must be less than or equal to the capacity of the edge. This is the capacity rule. The flow of the network is defined as the flow from the source, or into the sink. For the situation above, the network flow is 19. Cuts A cut is a partition of vertices (Vs, Vt) such that the s Vs and t Vt. An edge that goes from u to v is a forward edge if u Vs and v Vt. If the opposite is true, then it is a backward edge. Also let F equal the flow of a network. For any cut, define the flow across the cut to be the sum of the flows of the forward edges minus the sum of the flows of the backwards edges. The flow across any cut equals the flow of a network. In our previous example, the flow was 19. Consider the flow across the cut Vs = {s, a, b}. We have three forward edges with flows of 8, 4, and 15 and two backward edges with flows of 1 and 7. Summing, we have = 19, as desired. Basically, we have a total of 27 units going from the side with S to the side with T and 8 units going from the side with T to the the side with S, for a net positive flow of 19 units from the side with S to the side with T. Note the following observations: 1) The sum of the flows of all the vertices in Vs is the flow of the network because this sum is 0 for all non-source vertices in Vs, and equal to the flow at the source. 2) We need only to show that the flow NOT across Vs is 0. This is true simply because no edge in Vs leads into s. They all lead to each other. Thus, the net flow of all the edges within Vs is 0, because for two different vertices in Vs we add and subtract the same flow for an edge. We can use this to show that the flow of a network can not exceed the capacity of any cut. Simply put, our best case is if we don't have any edges with flow from the side with T to the side with S. In this case, we are simply left with forward edges, each with a particular capacity. The sum of these capacities is the capacity of the cut, and an upper bound on the flow of that cut.
3 Finding the Maximum Flow in a Flow Network We will use two ideas to help us determine whether or not a flow is maximum. Namely, we must show that absolutely no more flow could be added, no matter how we adjust each edge. The ideas we will look are residual capacity and augmenting paths. The residual capacity of an edge from vertex u to vertex v is simply its unused capacity - the difference between its capacity and its flow in the direction of the edge. In the opposite direction (from v to u), this value is defined as the flow of the edge. The idea with this second statement is that if flow is going from u to v, there s no reason we can t unsend those units of flow. Mathematically, this means subtracting from the flow in the forward direction. Also, the residual capacity of a path is defined as the minimum of the residual capacities of the edges on that path. This particular value is the maximum excess flow we can push down that particular path. Thus, an augmenting path is defined as one where you have a path from the source to the sink where every edge has a non-zero residual capacity. Namely, where for every edge on the path flow is less than capacity for each forward edge, AND flow is greater than 0 for each backward edge. In our example below, consider the following path: s a c b t The forward edges on this path are sa, ac, and bt. The backward edge is cb. Thus, the minimum residual capacity of the path is 4, which is the limit given to us by cb, since we can push back at most 4 units of flow from vertex c to vertex b. From s to a, we could push forward up to 5 units of flow, from a to c we could push 10 units of flow, and from b to t we could also push up to 5 units of flow. Thus, our limiting factor for this specific augmenting path is edge cb, where we can push back at most 4 units of flow.
4 Now, let's augment this path: Hopefully it should be clear that if we find an augmenting path, adding the minimal residual capacity of that path to each edge on that path yields another valid flow. In essence, what we are doing is simply adding some fluid to a particular path in the network. On a backwards edge, we are actually taking away fluid. Intuitively, what using a backwards edge is doing is fixing a previous mistake. Before we added this last piece of flow, we had been sending 4 units of flow from B to C, and then C to D, where it was essentially getting stuck. So, by directing those 4 units from B to T (instead of through C), we were able to free up 4 more units to come from S to A to C to D. If one doesn t use any backwards edges in their search for augmenting paths, they lose the ability to fix errors that naturally occur when we guess suboptimal augmenting paths. Essentially, there s no way to know in advance what all the augmenting paths with no backward edges might look like. But, the algorithm allows us to correct our mistakes as we go, by taking backwards edges and this is the essence of how it works. Now, we will show that if a flow network has no augmenting path, then it has a cut of maximum capacity. If no augmenting path exists, then that means for all paths from source to sink, there is at least one edge without any residual capacity. Now, consider partitioning the vertices according to this rule: Place in Vs all vertices v that DO have augmenting paths from the source s. Then place all other vertices in Vt. (Note that the sink t must be in this set since there is no augmenting path to t.) Now, consider all the edges with respect to this cut. Clearly, NONE of these edges have any residual capacity. If they did, then we would have added the vertex that they reach to the set Vs. Thus, for this particular cut, the flow at each forward edge is to its capacity and the flow at each backwards edge is 0. As we showed before, this situation represents the maximal flow possible.
5 Now, based upon the fact that augmenting paths can always be used to increase flow, and that the minimum capacity of a cut constrains the maximal flow, we can now claim the following: The Max-Flow, Min-Cut Theorem: The value of the maximal flow in a flow network equals the value of the minimum cut. With our example, we can see that there is no augmenting path from s to t. If there were, it would have to go through b and utilize edge bt. But all three edges leading to bt have no residual capacity. Now, consider forming the set of vertices that do have augmenting paths from s. This set includes {s, a, c, d} As mentioned before, it is impossible to reach b on an augmenting path since all edges leading to b are at full capacity already. Now, if we look at this cut, we find that the maximal value of this cut is the sum of the capacities of the edges ab, db, and dt which is = 23. (Notice that we did not add or subtract anything for edge bc with capacity 9, since it is a backwards edge.)
6 Ford-Fulkerson Algorithm The Ford-Fulkerson Algorithm is a basic consequent of the work above. In its simplest form, we do the following: While there exists an augmenting path Add the appropriate flow to that augmenting path We can check the existence of an augmenting path by doing any graph traversal on the network (with all full capacity edges removed.) Typically, DFS is used for Ford- Fulkerson. This graph, a subgraph with all edges of full capacity removed is called a residual graph. It is difficult to analyze the true running time of this algorithm because it is unclear exactly how many augmenting paths can be found in an arbitrary flow network. In the worst case, each augmenting path adds 1 to the flow of a network, and each search for an augmenting path takes O(E) time, where E is the number of edges in the graph. Thus, at worst-case, the algorithm takes O( f E) time, where f is the maximal flow of the network. The Edmonds-Karp Algorithm This algorithm is a variation on the Ford-Fulkerson method which is intended to increase the speed of the first algorithm. The idea is to try to choose good augmenting paths. In this algorithm, the augmenting path suggested is the augmenting path with the minimal number of edges. (We can find this using BFS, since this finds all paths of a certain length before moving on to longer paths.) The total number of iterations of the algorithm using this strategy is O(VE). Thus, its total running time when storing the graph as an adjacency matrix is O(V 3 E).
7 Applications of Network Flow Obvious applications of network flow involve physical situations, such as a set of pipes moving water, or traffic in a network. For these situations, the translation of the input data into an appropriate graph is fairly intuitive. However, a vast majority of the applications of network flow pertain to problems that don't seem to involve the physical movement of items through networks. While we don't have time to look at all the types of applications of network flow, we will analyze one specific problem, bipartite matching, that can be solved using network flow, along with a few extra sample problems that can be solved with network flow. Bipartite Matching The bipartite matching problem is as follows: Input: two mutually exclusive sets of equal size U and V, along with a list of ordered pairs of the form (u, v) where u U and v V, indicating pairs of members, one of each set that can be "paired" together. Output: True, if there exists a way to pair up each item in U with an item in V such that each item in both sets appears in exactly one pairing, and false otherwise. Solution: Let n = the size of each input set. Set up a graph with 2n+2 vertices. Create one vertex for each item in each set and add source and sink vertices. Add an edge from the source to each item in set U with capacity 1. Add an edge from each item in set V to the sink with capacity 1. Add an edge between each item in set U and set V that are in the set of ordered pairs with capacity 1. Calculate the maximal flow of this network. If the answer is n, then a complete matching exists, otherwise a complete matching doesn't exist. If you want the matching, keep track of each "edge" added during each iteration of the algorithm. (Note: some edges change as well.)
8 Instance of Bipartite Matching Set of companies:{google,microsoft, Facebook, Amazon, Lockheed} Set of students: {Amanda, Belinda, Cameron, David, Elyse} Set of offers: {(Google, Belinda), (Google, Elyse), (Microsoft, Amanda), (Microsoft, Cameron), (Facebook, Amanda), (Facebook, David), (Facebook, Elyse), (Amazon, Amanda), (Amazon, Elyse), (Lockheed, Belinda) } Second Instance of Bipartite Matching Set of boys: {Bob, Dave, Fred, Harvey} Set of girls: {Alice, Carol, Elaina, Giselle} Set of ordered pairs: { (Bob, Elaina), (Bob, Giselle), (Dave, Elaina), (Fred, Alice), (Fred, Carol), (Fred, Giselle), (Harvey, Giselle) } Note: More generally, if we relax the restriction on the sizes of the two sets being equal, we can calculate the maximum number of pairs that we can form by running a Network Flow algorithm on a graph of the form described above.
9 Indirect use of bipartite matching In some problems we might be asked to pick a maximum number of items so that no two items from two distinct sets conflict. So, perhaps set A is Mrs. Weaver s class and set B is Mr. Gordon s class. We want to get the maximum number of kids in a single group from both classes so that no two kids hate each other. All the kids in each class like the other kids in their class, but they may hate some of the kids in the other class. For this type of scenario, it helps to solve the opposite problem: Find the maximum number of pairs of kids, one from each class, such that each pair hates each other. Note that in finding this maximum matching, which is equal to the maximum flow through the network created by linking edges between pairs of kids that hate each other, we are showing that for each of these pairs, at most one kid can be chosen. Since this matching is maximum, we CAN T add a new pair to it. Thus, this means it s safe to add ALL the other kids not involved in any pair AND then add one person from each of these pairs. Thus, the total number of students we can choose is equal to the total number of kids in both classes minus the maximum number of pairs we can create who hate each other. Cow Steeplechase Problem (from USACO) Utilizes bipartite matching indirectly Given a list of horizontal line segments (none of which intersect each other) and vertical line segments (none of which intersect each other), calculate the minimum number of line segments that must be removed, so that no two lines intersect each other, or alternatively, the most number of line segments that mutually don't intersect one another. Solution We can create a bipartite matching solution. Our goal is to match horizontal line segments to vertical line segments in such a way that each pair intersects. We know that if we have a set of these intersecting pairs, at the very least, one item in each pair must be removed. Thus, what we really want is the maximum matching. Once we have this (say there are 7 matching pairs in our maximal matching), then we have proof that 7 of the segments must be removed. No other matching forces us to remove more. Thus, that how many we are forced to remove to create no intersecting line segments. Alternatively, we can calculate the maximum set of segments we can have without any two intersecting by taking the total number and subtracting out this maximum matching.
10 Network Flow for other matching problems In other matching problems, we aren t always making one to one matchings. Instead, we might be matching several items in several groups to other items grouped together differently. In the two example problems shown below, the capacities of our edges are not always one, and these capacities indicate the number of items from one set that we can match elsewhere. These sorts of problems take many different forms, so it s best just to understand the basic structure of setting up an flow graph and be flexible to edit that structure for each new problem that you see. Example Problem: Grand Dinner Problem (from ACMUVA) N teams attend a dinner. Team i has ti members. There are M tables at the dinner, with M N. Table i can has si chairs. We wish to seat all teams such that no two team members are at the same table, so that we maximum students getting to meet members of other teams. Can we do so? Solution using Network Flow Create a flow network with N + M + 2 vertices. Create one vertex for each team and one for each table. Create extra source and sink vertices. Create edges from the source to each team with a capacity of ti. Create edges from each table vertex to the sink vertex with capacity si. Finally, add edges from each team to each table, with capacity 1, since each team can provide at most one person per table. Run the network flow algorithm. If the maximal flow equals the sum of the number of team members, the seating can be done. Otherwise, it can not be.
11 Museum Guard Problem: 2009 South East Regional A museum employs guards that work in 30 minute shifts: 12am - 12:30am, 12:30am- 1am,..., 11:30pm-12 am. Each guard has a list of times he/she can NOT work. (For example, a particular guard might not be able to work from 3:30 am to 7:30am and from 4:29pm to 8:01pm. In this case, the guard could work the 3am-3:30am and 7:30am-8am shifts, but not the 4pm - 4:30pm shift or 8pm-8:30pm shift.) Furthermore, each guard has a maximum number of hours they can work in a single day. Determine the maximum number of guards we can have scheduled to cover each shift without violating any of the constraints. Solution using a flow network As usual, we create an extra source and sink. Each guard will be a vertex in the flow network. From the source, we connect an edge to each guard with an integer representing the maximum number of shifts that guard can work. Each shift (there are 48) will become a node in the flow network. Add an edge with capacity 1 from each guard to each shift where the guard is able to work that shift. Finally, if we are to set the capacities from all the shifts to the sink to 1, and we run the network flow algorithm at obtain 48, we know that we can post 1 guard for each slot. We can re-run the algorithm with all of these capacities set to 2 and see if the resulting flow is 96 or not. If so, we move onto 3, and so forth. Since there are at most 50 guards, our answer will never exceed 50 and this will run in time. A more clever approach involves a binary search. Try capacities at 25 for each of these edges. If this doesn't work, go to 12, If it does, go to 37, and so on. Basically, rather than checking if 1 works, then 2, then 3, etc. a binary search will hone in on the answer a bit more quickly, especially in the cases that the answer is closer to 50.
Network Flow. November 23, CMPE 250 Graphs- Network Flow November 23, / 31
 Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Source. Sink. Chapter 10: Iterative Programming Maximum Flow Problem. CmSc250 Intro to Algorithms
 Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
CSE 417 Network Flows (pt 3) Modeling with Min Cuts
 CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
Tutorial for Algorithm s Theory Problem Set 5. January 17, 2013
 Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Network Flow I. Lecture Overview The Network Flow Problem
 Lecture Network Flow I. Overview In these next two lectures we are going to talk about an important algorithmic problem called the Network Flow Problem. Network flow is important because it can be used
Lecture Network Flow I. Overview In these next two lectures we are going to talk about an important algorithmic problem called the Network Flow Problem. Network flow is important because it can be used
CSE 417 Network Flows (pt 4) Min Cost Flows
 CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
COMP4128 Programming Challenges
 Network Networks Network COMP4128 Programming Challenges School of Computer Science and Engineering UNSW Australia Table of Contents 2 Network 1 Networks Networks 2 3 4 5 6 networks 3 Network Networks
Network Networks Network COMP4128 Programming Challenges School of Computer Science and Engineering UNSW Australia Table of Contents 2 Network 1 Networks Networks 2 3 4 5 6 networks 3 Network Networks
Maximum flows & Maximum Matchings
 Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Network Flow and Matching
 Chapter 4 Network Flow and Matching In this chapter, we examine the network flow problem, a graph problem to which many problems can be reduced. In fact, some problems that don t even appear to be graph
Chapter 4 Network Flow and Matching In this chapter, we examine the network flow problem, a graph problem to which many problems can be reduced. In fact, some problems that don t even appear to be graph
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Notes for Lecture 20
 U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
Maximum Flow. Flow Networks. Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms. Example Flow Network
 Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Jessica Su (some parts copied from CLRS / last quarter s notes)
 1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching
 Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS. March 3, 2016
 GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS ZOÉ HAMEL March 3, 2016 1. Introduction Let G = (V (G), E(G)) be a graph G (loops and multiple edges not allowed) on the set of vertices V (G) and the set
GRAPH DECOMPOSITION BASED ON DEGREE CONSTRAINTS ZOÉ HAMEL March 3, 2016 1. Introduction Let G = (V (G), E(G)) be a graph G (loops and multiple edges not allowed) on the set of vertices V (G) and the set
Graphs and Network Flows IE411. Lecture 13. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Problem Set 7 Solutions
 Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
Maximum Flow Algorithms
 Maximum Flow Algorithms Network Algorithms Georgia Kaouri Contents Applications, special cases Flow networks Ford Fulkerson algorithm Preflow push algorithms Lift to front algorithm Material flows Applications
Maximum Flow Algorithms Network Algorithms Georgia Kaouri Contents Applications, special cases Flow networks Ford Fulkerson algorithm Preflow push algorithms Lift to front algorithm Material flows Applications
Lecture 11: Maximum flow and minimum cut
 Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Answers to specimen paper questions. Most of the answers below go into rather more detail than is really needed. Please let me know of any mistakes.
 Answers to specimen paper questions Most of the answers below go into rather more detail than is really needed. Please let me know of any mistakes. Question 1. (a) The degree of a vertex x is the number
Answers to specimen paper questions Most of the answers below go into rather more detail than is really needed. Please let me know of any mistakes. Question 1. (a) The degree of a vertex x is the number
Network Flow. By: Daniel Pham, Anthony Huber, Shaazan Wirani
 Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
1 Shortest Paths. 1.1 Breadth First Search (BFS) CS 124 Section #3 Shortest Paths and MSTs 2/13/2018
 CS Section # Shortest Paths and MSTs //08 Shortest Paths There are types of shortest paths problems: Single source single destination Single source to all destinations All pairs shortest path In today
CS Section # Shortest Paths and MSTs //08 Shortest Paths There are types of shortest paths problems: Single source single destination Single source to all destinations All pairs shortest path In today
Transportation Planning: The maximum flow problem
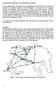 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Graphs. Edges may be directed (from u to v) or undirected. Undirected edge eqvt to pair of directed edges
 (p 186) Graphs G = (V,E) Graphs set V of vertices, each with a unique name Note: book calls vertices as nodes set E of edges between vertices, each encoded as tuple of 2 vertices as in (u,v) Edges may
(p 186) Graphs G = (V,E) Graphs set V of vertices, each with a unique name Note: book calls vertices as nodes set E of edges between vertices, each encoded as tuple of 2 vertices as in (u,v) Edges may
Solutions to Final. Solutions to Final. May 18th CS170 David Wolfe ALWAYS TRUE SOMETIMES TRUE NEVER TRUE
 Solutions to Final May 18th 1995 CS170 David Wolfe 1. (30 points) Check one box for each of the following. ALWAYS TRUE SOMETIMES TRUE NEVER TRUE In a connected graph, E=O(V) In a connected graph, E=Ω(V)
Solutions to Final May 18th 1995 CS170 David Wolfe 1. (30 points) Check one box for each of the following. ALWAYS TRUE SOMETIMES TRUE NEVER TRUE In a connected graph, E=O(V) In a connected graph, E=Ω(V)
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem
 Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
COT 6936: Topics in Algorithms! Giri Narasimhan. ECS 254A / EC 2443; Phone: x3748
 COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COMP3121/3821/9101/ s1 Assignment 1
 Sample solutions to assignment 1 1. (a) Describe an O(n log n) algorithm (in the sense of the worst case performance) that, given an array S of n integers and another integer x, determines whether or not
Sample solutions to assignment 1 1. (a) Describe an O(n log n) algorithm (in the sense of the worst case performance) that, given an array S of n integers and another integer x, determines whether or not
1 Matchings in Graphs
 Matchings in Graphs J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 Definition Two edges are called independent if they are not adjacent
Matchings in Graphs J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 J J 2 J 3 J 4 J 5 J J J 6 8 7 C C 2 C 3 C 4 C 5 C C 7 C 8 6 Definition Two edges are called independent if they are not adjacent
Topological Sort. Here a topological sort would label A with 1, B and C with 2 and 3, and D with 4.
 Topological Sort The goal of a topological sort is given a list of items with dependencies, (ie. item 5 must be completed before item 3, etc.) to produce an ordering of the items that satisfies the given
Topological Sort The goal of a topological sort is given a list of items with dependencies, (ie. item 5 must be completed before item 3, etc.) to produce an ordering of the items that satisfies the given
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret
 Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Advanced Algorithms Class Notes for Monday, October 23, 2012 Min Ye, Mingfu Shao, and Bernard Moret Greedy Algorithms (continued) The best known application where the greedy algorithm is optimal is surely
Homework 3 Solutions
 CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
COMP 251 Winter 2017 Online quizzes with answers
 COMP 251 Winter 2017 Online quizzes with answers Open Addressing (2) Which of the following assertions are true about open address tables? A. You cannot store more records than the total number of slots
COMP 251 Winter 2017 Online quizzes with answers Open Addressing (2) Which of the following assertions are true about open address tables? A. You cannot store more records than the total number of slots
Computational Methods in IS Research Fall Graph Algorithms Network Flow Problems
 Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Minimum Spanning Tree (undirected graph)
 1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
Network flows and Menger s theorem
 Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
ELEC-270 Solutions to Assignment 5
 ELEC-270 Solutions to Assignment 5 1. How many positive integers less than 1000 (a) are divisible by 7? (b) are divisible by 7 but not by 11? (c) are divisible by both 7 and 11? (d) are divisible by 7
ELEC-270 Solutions to Assignment 5 1. How many positive integers less than 1000 (a) are divisible by 7? (b) are divisible by 7 but not by 11? (c) are divisible by both 7 and 11? (d) are divisible by 7
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems. Problems, Hints, and Solutions
 Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
Dr. Amotz Bar-Noy s Compendium of Algorithms Problems Problems, Hints, and Solutions Chapter 1 Searching and Sorting Problems 1 1.1 Array with One Missing 1.1.1 Problem Let A = A[1],..., A[n] be an array
2. CONNECTIVITY Connectivity
 2. CONNECTIVITY 70 2. Connectivity 2.1. Connectivity. Definition 2.1.1. (1) A path in a graph G = (V, E) is a sequence of vertices v 0, v 1, v 2,..., v n such that {v i 1, v i } is an edge of G for i =
2. CONNECTIVITY 70 2. Connectivity 2.1. Connectivity. Definition 2.1.1. (1) A path in a graph G = (V, E) is a sequence of vertices v 0, v 1, v 2,..., v n such that {v i 1, v i } is an edge of G for i =
2. True or false: even though BFS and DFS have the same space complexity, they do not always have the same worst case asymptotic time complexity.
 1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
Weekly Assignment nr.4
 UNIVERSITY OF OSLO, INSTITUTE OF INFORMATICS Weekly Assignment nr.4 1 FLOW NETWORKS Prerequisites: Graphs(directed, undirected) Degrees, neighbours, paths Depth-first, Breadth-first Lesson Plan: 1. Flow
UNIVERSITY OF OSLO, INSTITUTE OF INFORMATICS Weekly Assignment nr.4 1 FLOW NETWORKS Prerequisites: Graphs(directed, undirected) Degrees, neighbours, paths Depth-first, Breadth-first Lesson Plan: 1. Flow
CS261: Problem Set #1
 CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
Test 1 Last 4 Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. 2 points each t 1
 CSE 0 Name Test Fall 00 Last Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. points each t. What is the value of k? k=0 A. k B. t C. t+ D. t+ +. Suppose that you have
CSE 0 Name Test Fall 00 Last Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. points each t. What is the value of k? k=0 A. k B. t C. t+ D. t+ +. Suppose that you have
22 Elementary Graph Algorithms. There are two standard ways to represent a
 VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
VI Graph Algorithms Elementary Graph Algorithms Minimum Spanning Trees Single-Source Shortest Paths All-Pairs Shortest Paths 22 Elementary Graph Algorithms There are two standard ways to represent a graph
Lecture and notes by: Sarah Fletcher and Michael Xu November 3rd, Multicommodity Flow
 Multicommodity Flow 1 Introduction Suppose we have a company with a factory s and a warehouse t. The quantity of goods that they can ship from the factory to the warehouse in a given time period is limited
Multicommodity Flow 1 Introduction Suppose we have a company with a factory s and a warehouse t. The quantity of goods that they can ship from the factory to the warehouse in a given time period is limited
Greedy algorithms is another useful way for solving optimization problems.
 Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
Greedy Algorithms Greedy algorithms is another useful way for solving optimization problems. Optimization Problems For the given input, we are seeking solutions that must satisfy certain conditions. These
Primal Dual Schema Approach to the Labeling Problem with Applications to TSP
 1 Primal Dual Schema Approach to the Labeling Problem with Applications to TSP Colin Brown, Simon Fraser University Instructor: Ramesh Krishnamurti The Metric Labeling Problem has many applications, especially
1 Primal Dual Schema Approach to the Labeling Problem with Applications to TSP Colin Brown, Simon Fraser University Instructor: Ramesh Krishnamurti The Metric Labeling Problem has many applications, especially
Suggested problems - solutions
 Suggested problems - solutions Examples and models Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section 2.2,
Suggested problems - solutions Examples and models Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section 2.2,
Algorithm Circle Extra Lecture: Solving the Assignment Problem with Network Flow
 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Algorithm Circle Extra Lecture: Solving the with Network Flow 17 September 2012 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline
The Network Flow Minimum-Cost Maximum Flow Shameless Plug Algorithm Circle Extra Lecture: Solving the with Network Flow 17 September 2012 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline
Lecture 3: Totally Unimodularity and Network Flows
 Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
CS261: A Second Course in Algorithms Lecture #3: The Push-Relabel Algorithm for Maximum Flow
 CS26: A Second Course in Algorithms Lecture #3: The Push-Relabel Algorithm for Maximum Flow Tim Roughgarden January 2, 206 Motivation The maximum flow algorithms that we ve studied so far are augmenting
CS26: A Second Course in Algorithms Lecture #3: The Push-Relabel Algorithm for Maximum Flow Tim Roughgarden January 2, 206 Motivation The maximum flow algorithms that we ve studied so far are augmenting
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Shortest Paths. Nishant Mehta Lectures 10 and 11
 Shortest Paths Nishant Mehta Lectures 0 and Finding the Fastest Way to Travel between Two Intersections in Vancouver Granville St and W Hastings St Homer St and W Hastings St 6 Granville St and W Pender
Shortest Paths Nishant Mehta Lectures 0 and Finding the Fastest Way to Travel between Two Intersections in Vancouver Granville St and W Hastings St Homer St and W Hastings St 6 Granville St and W Pender
CSC 8301 Design & Analysis of Algorithms: Linear Programming
 CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
Network Design and Optimization course
 Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
Bipartite Matching & the Hungarian Method
 Bipartite Matching & the Hungarian Method Last Revised: 15/9/7 These notes follow formulation originally developed by Subhash Suri in http://www.cs.ucsb.edu/ suri/cs/matching.pdf We previously saw how
Bipartite Matching & the Hungarian Method Last Revised: 15/9/7 These notes follow formulation originally developed by Subhash Suri in http://www.cs.ucsb.edu/ suri/cs/matching.pdf We previously saw how
Solving problems on graph algorithms
 Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Notes on Network Optimization CE 4920 Stephen Boyles Fall 2009
 Notes on Network Optimization CE 9 Stephen Boyles Fall 9 Introduction and Preliminaries From this point on, the remaining course material takes on a more tangible form than nonlinear or linear programming
Notes on Network Optimization CE 9 Stephen Boyles Fall 9 Introduction and Preliminaries From this point on, the remaining course material takes on a more tangible form than nonlinear or linear programming
Minimum Cost Edge Disjoint Paths
 Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
1 5,9,2,7,6,10,4,3,8,1 The first number (5) is automatically the first number of the sorted list
 Algorithms One of the more challenging aspects of Computer Science are algorithms. An algorithm is a plan that solves a problem. When assembling a bicycle based on the included instructions, in this case,
Algorithms One of the more challenging aspects of Computer Science are algorithms. An algorithm is a plan that solves a problem. When assembling a bicycle based on the included instructions, in this case,
Vertex-Colouring Edge-Weightings
 Vertex-Colouring Edge-Weightings L. Addario-Berry a, K. Dalal a, C. McDiarmid b, B. A. Reed a and A. Thomason c a School of Computer Science, McGill University, University St. Montreal, QC, H3A A7, Canada
Vertex-Colouring Edge-Weightings L. Addario-Berry a, K. Dalal a, C. McDiarmid b, B. A. Reed a and A. Thomason c a School of Computer Science, McGill University, University St. Montreal, QC, H3A A7, Canada
Shortest Paths. Nishant Mehta Lectures 10 and 11
 Shortest Paths Nishant Mehta Lectures 0 and Communication Speeds in a Computer Network Find fastest way to route a data packet between two computers 6 Kbps 4 0 Mbps 6 6 Kbps 6 Kbps Gbps 00 Mbps 8 6 Kbps
Shortest Paths Nishant Mehta Lectures 0 and Communication Speeds in a Computer Network Find fastest way to route a data packet between two computers 6 Kbps 4 0 Mbps 6 6 Kbps 6 Kbps Gbps 00 Mbps 8 6 Kbps
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
GRAPHS Lecture 17 CS2110 Spring 2014
 GRAPHS Lecture 17 CS2110 Spring 2014 These are not Graphs 2...not the kind we mean, anyway These are Graphs 3 K 5 K 3,3 = Applications of Graphs 4 Communication networks The internet is a huge graph Routing
GRAPHS Lecture 17 CS2110 Spring 2014 These are not Graphs 2...not the kind we mean, anyway These are Graphs 3 K 5 K 3,3 = Applications of Graphs 4 Communication networks The internet is a huge graph Routing
CSE 5311 Notes 9: Maximum Flows
 CSE 5311 Notes 9: Maximum Flows (Last updated 3/1/17 1:8 PM) Goldberg and Tarjan, http://dl.acm.org.ezproxy.uta.edu/citation.cfm?doid=63661.68036 CLRS, Chapter 6 FORD-FULKERSON (review) Network Flow Concepts:
CSE 5311 Notes 9: Maximum Flows (Last updated 3/1/17 1:8 PM) Goldberg and Tarjan, http://dl.acm.org.ezproxy.uta.edu/citation.cfm?doid=63661.68036 CLRS, Chapter 6 FORD-FULKERSON (review) Network Flow Concepts:
4 Integer Linear Programming (ILP)
 TDA6/DIT37 DISCRETE OPTIMIZATION 17 PERIOD 3 WEEK III 4 Integer Linear Programg (ILP) 14 An integer linear program, ILP for short, has the same form as a linear program (LP). The only difference is that
TDA6/DIT37 DISCRETE OPTIMIZATION 17 PERIOD 3 WEEK III 4 Integer Linear Programg (ILP) 14 An integer linear program, ILP for short, has the same form as a linear program (LP). The only difference is that
Module 7. Independent sets, coverings. and matchings. Contents
 Module 7 Independent sets, coverings Contents and matchings 7.1 Introduction.......................... 152 7.2 Independent sets and coverings: basic equations..... 152 7.3 Matchings in bipartite graphs................
Module 7 Independent sets, coverings Contents and matchings 7.1 Introduction.......................... 152 7.2 Independent sets and coverings: basic equations..... 152 7.3 Matchings in bipartite graphs................
Computational Geometry
 Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
Motivation Motivation Polygons and visibility Visibility in polygons Triangulation Proof of the Art gallery theorem Two points in a simple polygon can see each other if their connecting line segment is
PERFECT MATCHING THE CENTRALIZED DEPLOYMENT MOBILE SENSORS THE PROBLEM SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS OF MOBILE SENSORS
 SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING 1 2 ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms
SECOND PART: WIRELESS NETWORKS 2.B. SENSOR NETWORKS THE CENTRALIZED DEPLOYMENT OF MOBILE SENSORS I.E. THE MINIMUM WEIGHT PERFECT MATCHING 1 2 ON BIPARTITE GRAPHS Prof. Tiziana Calamoneri Network Algorithms
Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching. 1 Primal/Dual Algorithm for weighted matchings in Bipartite Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 009) Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching Lecturer: Mohammad R. Salavatipour Date: Sept 15 and 17, 009
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 009) Lecture 4: Primal Dual Matching Algorithm and Non-Bipartite Matching Lecturer: Mohammad R. Salavatipour Date: Sept 15 and 17, 009
Retiming. Adapted from: Synthesis and Optimization of Digital Circuits, G. De Micheli Stanford. Outline. Structural optimization methods. Retiming.
 Retiming Adapted from: Synthesis and Optimization of Digital Circuits, G. De Micheli Stanford Outline Structural optimization methods. Retiming. Modeling. Retiming for minimum delay. Retiming for minimum
Retiming Adapted from: Synthesis and Optimization of Digital Circuits, G. De Micheli Stanford Outline Structural optimization methods. Retiming. Modeling. Retiming for minimum delay. Retiming for minimum
Graph Algorithms Matching
 Chapter 5 Graph Algorithms Matching Algorithm Theory WS 2012/13 Fabian Kuhn Circulation: Demands and Lower Bounds Given: Directed network, with Edge capacities 0and lower bounds l for Node demands for
Chapter 5 Graph Algorithms Matching Algorithm Theory WS 2012/13 Fabian Kuhn Circulation: Demands and Lower Bounds Given: Directed network, with Edge capacities 0and lower bounds l for Node demands for
V1.0: Seth Gilbert, V1.1: Steven Halim August 30, Abstract. d(e), and we assume that the distance function is non-negative (i.e., d(x, y) 0).
 CS4234: Optimisation Algorithms Lecture 4 TRAVELLING-SALESMAN-PROBLEM (4 variants) V1.0: Seth Gilbert, V1.1: Steven Halim August 30, 2016 Abstract The goal of the TRAVELLING-SALESMAN-PROBLEM is to find
CS4234: Optimisation Algorithms Lecture 4 TRAVELLING-SALESMAN-PROBLEM (4 variants) V1.0: Seth Gilbert, V1.1: Steven Halim August 30, 2016 Abstract The goal of the TRAVELLING-SALESMAN-PROBLEM is to find
Integers. N = sum (b i * 2 i ) where b i = 0 or 1. This is called unsigned binary representation. i = 31. i = 0
 Integers So far, we've seen how to convert numbers between bases. How do we represent particular kinds of data in a certain (32-bit) architecture? We will consider integers floating point characters What
Integers So far, we've seen how to convert numbers between bases. How do we represent particular kinds of data in a certain (32-bit) architecture? We will consider integers floating point characters What
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
Important separators and parameterized algorithms
 Important separators and parameterized algorithms Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary School on Parameterized Algorithms
Important separators and parameterized algorithms Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary School on Parameterized Algorithms
(Refer Slide Time: 00:02:00)
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 18 Polyfill - Scan Conversion of a Polygon Today we will discuss the concepts
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 18 Polyfill - Scan Conversion of a Polygon Today we will discuss the concepts
Basic Combinatorics. Math 40210, Section 01 Fall Homework 4 Solutions
 Basic Combinatorics Math 40210, Section 01 Fall 2012 Homework 4 Solutions 1.4.2 2: One possible implementation: Start with abcgfjiea From edge cd build, using previously unmarked edges: cdhlponminjkghc
Basic Combinatorics Math 40210, Section 01 Fall 2012 Homework 4 Solutions 1.4.2 2: One possible implementation: Start with abcgfjiea From edge cd build, using previously unmarked edges: cdhlponminjkghc
Approximation Algorithms
 Approximation Algorithms Subhash Suri June 5, 2018 1 Figure of Merit: Performance Ratio Suppose we are working on an optimization problem in which each potential solution has a positive cost, and we want
Approximation Algorithms Subhash Suri June 5, 2018 1 Figure of Merit: Performance Ratio Suppose we are working on an optimization problem in which each potential solution has a positive cost, and we want
CS4800: Algorithms & Data Jonathan Ullman
 CS4800: Algorithms & Data Jonathan Ullman Lecture 12: Graph Search: BFS Applications, DFS Feb 20, 2018 BFS Review BFS Algorithm: Input: source node! " # =! " % = all neighbors of " # " & = all neighbors
CS4800: Algorithms & Data Jonathan Ullman Lecture 12: Graph Search: BFS Applications, DFS Feb 20, 2018 BFS Review BFS Algorithm: Input: source node! " # =! " % = all neighbors of " # " & = all neighbors
CS521 \ Notes for the Final Exam
 CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
s-t Graph Cuts for Binary Energy Minimization
 s-t Graph Cuts for Binary Energy Minimization E data term ( L) = D ( ) + ( ) P Lp λ Ι Lp Lq p prior term Now that we have an energy function, the big question is how do we minimize it? pq N n Exhaustive
s-t Graph Cuts for Binary Energy Minimization E data term ( L) = D ( ) + ( ) P Lp λ Ι Lp Lq p prior term Now that we have an energy function, the big question is how do we minimize it? pq N n Exhaustive
1 Shortest Paths. 1.1 Breadth First Search (BFS) CS 124 Section #3 Shortest Paths and MSTs 2/13/2018
 CS 4 Section # Shortest Paths and MSTs //08 Shortest Paths There are types of shortest paths problems: Single source single destination Single source to all destinations All pairs shortest path In today
CS 4 Section # Shortest Paths and MSTs //08 Shortest Paths There are types of shortest paths problems: Single source single destination Single source to all destinations All pairs shortest path In today
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/27/17
 01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
Mathematics Masters Examination
 Mathematics Masters Examination OPTION 4 March 30, 2004 COMPUTER SCIENCE 2 5 PM NOTE: Any student whose answers require clarification may be required to submit to an oral examination. Each of the fourteen
Mathematics Masters Examination OPTION 4 March 30, 2004 COMPUTER SCIENCE 2 5 PM NOTE: Any student whose answers require clarification may be required to submit to an oral examination. Each of the fourteen
Lecture 6: Shortest distance, Eulerian cycles, Maxflow
 DD2458, Problem Solving and Programming Under Pressure Lecture 6: Shortest distance, Eulerian cycles, Maxflow Date: 2008-10-06 Scribe(s): Adam Kull, David Vuorio Lecturer: Douglas Wikström 1 Shortest path
DD2458, Problem Solving and Programming Under Pressure Lecture 6: Shortest distance, Eulerian cycles, Maxflow Date: 2008-10-06 Scribe(s): Adam Kull, David Vuorio Lecturer: Douglas Wikström 1 Shortest path
Worst-case Ethernet Network Latency for Shaped Sources
 Worst-case Ethernet Network Latency for Shaped Sources Max Azarov, SMSC 7th October 2005 Contents For 802.3 ResE study group 1 Worst-case latency theorem 1 1.1 Assumptions.............................
Worst-case Ethernet Network Latency for Shaped Sources Max Azarov, SMSC 7th October 2005 Contents For 802.3 ResE study group 1 Worst-case latency theorem 1 1.1 Assumptions.............................
The Simplex Algorithm for LP, and an Open Problem
 The Simplex Algorithm for LP, and an Open Problem Linear Programming: General Formulation Inputs: real-valued m x n matrix A, and vectors c in R n and b in R m Output: n-dimensional vector x There is one
The Simplex Algorithm for LP, and an Open Problem Linear Programming: General Formulation Inputs: real-valued m x n matrix A, and vectors c in R n and b in R m Output: n-dimensional vector x There is one
Maximal Monochromatic Geodesics in an Antipodal Coloring of Hypercube
 Maximal Monochromatic Geodesics in an Antipodal Coloring of Hypercube Kavish Gandhi April 4, 2015 Abstract A geodesic in the hypercube is the shortest possible path between two vertices. Leader and Long
Maximal Monochromatic Geodesics in an Antipodal Coloring of Hypercube Kavish Gandhi April 4, 2015 Abstract A geodesic in the hypercube is the shortest possible path between two vertices. Leader and Long
NETWORK OPTIMIZATION MODELS
 NETWORK OPTIMIZATION MODELS Network models Transportation, electrical and communication networks pervade our daily lives. Network representation are widely used in: Production, distribution, project planning,
NETWORK OPTIMIZATION MODELS Network models Transportation, electrical and communication networks pervade our daily lives. Network representation are widely used in: Production, distribution, project planning,
On Universal Cycles of Labeled Graphs
 On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
On Universal Cycles of Labeled Graphs Greg Brockman Harvard University Cambridge, MA 02138 United States brockman@hcs.harvard.edu Bill Kay University of South Carolina Columbia, SC 29208 United States
CSE 417 Network Flows (pt 2) Modeling with Max Flow
 CSE 47 Network Flows (pt 2) Modeling with Max Flow Reminders > HW6 is due on Friday start early may take time to figure out the sub-structure Review of last lecture > Defined the maximum flow problem find
CSE 47 Network Flows (pt 2) Modeling with Max Flow Reminders > HW6 is due on Friday start early may take time to figure out the sub-structure Review of last lecture > Defined the maximum flow problem find
Problem Set 7 Solutions
 " [ Introduction to Algorithms November 29, 200 Massachusetts Institute of Technology 6046J/18410J Professors Shafi Goldwasser and Silvio Micali Handout 27 Problem Set 7 Solutions Problem 7-1 Shortest
" [ Introduction to Algorithms November 29, 200 Massachusetts Institute of Technology 6046J/18410J Professors Shafi Goldwasser and Silvio Micali Handout 27 Problem Set 7 Solutions Problem 7-1 Shortest
1 Definition of Reduction
 1 Definition of Reduction Problem A is reducible, or more technically Turing reducible, to problem B, denoted A B if there a main program M to solve problem A that lacks only a procedure to solve problem
1 Definition of Reduction Problem A is reducible, or more technically Turing reducible, to problem B, denoted A B if there a main program M to solve problem A that lacks only a procedure to solve problem
6.4 Maximum Flow. overview Ford-Fulkerson implementations applications
 6.4 Maximum Flow overview Ford-Fulkerson implementations applications Algorithms, 4 th Edition Robert Sedgewick and Kevin Wayne Copyright 2002 2010 April 18, 2011 11:02:27 AM Mincut problem Given. A weighted
6.4 Maximum Flow overview Ford-Fulkerson implementations applications Algorithms, 4 th Edition Robert Sedgewick and Kevin Wayne Copyright 2002 2010 April 18, 2011 11:02:27 AM Mincut problem Given. A weighted
Today. Maximum flow. Maximum flow. Problem
 5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
