Algorithm Circle Extra Lecture: Solving the Assignment Problem with Network Flow
|
|
|
- Willa Stanley
- 5 years ago
- Views:
Transcription
1 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Algorithm Circle Extra Lecture: Solving the with Network Flow 17 September 2012
2 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline 1 The 2 Network Flow 3 Minimum-Cost Maximum Flow
3 The Network Flow Minimum-Cost Maximum Flow Shameless Plug The Problem We are given two groups of N objects. Each object in the first group must be assigned to a distinct object in the second group. Each assignment between a pair of elements has an associated cost. We need to find the set of assignments that minimises the total cost.
4 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Minimum Weight Bipartite Matching We can recast this problem as finding the minimum weight matching in a complete bipartite graph Weighted bipartite matching [1]
5 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Minimum Weight Bipartite Matching We can recast this problem as finding the minimum weight matching in a complete bipartite graph Weighted bipartite matching [1]
6 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline 1 The 2 Network Flow 3 Minimum-Cost Maximum Flow
7 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Network Flow We will solve this matching problem by reducing it to a problem in graph theory concerning flow through a graph. A flow network is a directed graph (V, E) where each edge (u, v) E has a numerical capacity c(u, v). Two vertices s, t V play a special role: s is the source vertex and t is the sink. We are often concerned with finding a flow through this network.
8 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Network Flow We will solve this matching problem by reducing it to a problem in graph theory concerning flow through a graph. A flow network is a directed graph (V, E) where each edge (u, v) E has a numerical capacity c(u, v). Two vertices s, t V play a special role: s is the source vertex and t is the sink. We are often concerned with finding a flow through this network.
9 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Network Flow We can think of flow networks as being a network of pipes. Water enters the network at the source and exits at the sink. The amount of water flowing through each edge gives the flow through the network. The capacities of the edges represent the maximum amount of water that can flow through a given edge per second.
10 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Network Flow More formally, we can see that the flow through an edge f (u, v) must satisfy the following: Capacity Constraints: f (u, v) c(u, v) Reverse flow: f (u, v) = f (v, u) Additionally for a vertex v other than source and sink, flow must be conserved. Conservation of flow: f (v, w) = 0. w V Here we use the convention that if two vertices u, v are not connected by an edge then f (u, v) = c(u, v) = 0.
11 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow The archetypical problem in network flow is determining the maximum possible total flow through a network. This can be solved by the Ford-Fulkerson algorithm. We consider the residual capacity of each edge r(u, v) = c(u, v) f (u, v). A path from source to sink that only uses edges of positive residual capacity is called an augmenting path.
12 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow The archetypical problem in network flow is determining the maximum possible total flow through a network. This can be solved by the Ford-Fulkerson algorithm. We consider the residual capacity of each edge r(u, v) = c(u, v) f (u, v). A path from source to sink that only uses edges of positive residual capacity is called an augmenting path.
13 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow Ford-Fulkerson Initially, there is no flow through the network. While we can find an augmenting path, we send flow along that path, add this to the total flow and update the residual capacities. When there are no more augmenting paths, the algorithm terminates and we have found the maximum flow. This algorithm is greedy, but there is an important subtlety that allows it to get the correct result. Flow may be sent backwards through an edge reducing the flow through that edge in order to increase flow elsewhere.
14 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow Ford-Fulkerson Initially, there is no flow through the network. While we can find an augmenting path, we send flow along that path, add this to the total flow and update the residual capacities. When there are no more augmenting paths, the algorithm terminates and we have found the maximum flow. This algorithm is greedy, but there is an important subtlety that allows it to get the correct result. Flow may be sent backwards through an edge reducing the flow through that edge in order to increase flow elsewhere.
15 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow Ford-Fulkerson Initially, there is no flow through the network. While we can find an augmenting path: Let f be the flow we may send along that path. Increment the flow along each edge of the path, and decrement the flow along each reverse edge, by f. Increment the total flow by f. When there are no more augmenting paths, the algorithm terminates and we have found the maximum flow. This algorithm is greedy, but there is an important subtlety that allows it to get the correct result. Flow may be sent backwards through an edge reducing the flow through that edge in order to increase flow elsewhere.
16 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow Ford-Fulkerson Initially, there is no flow through the network. While we can find an augmenting path: Let f be the flow we may send along that path. Increment the flow along each edge of the path, and decrement the flow along each reverse edge, by f. Increment the total flow by f. When there are no more augmenting paths, the algorithm terminates and we have found the maximum flow. This algorithm is greedy, but there is an important subtlety that allows it to get the correct result. Flow may be sent backwards through an edge reducing the flow through that edge in order to increase flow elsewhere.
17 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Maximum Flow Ford-Fulkerson Correctness of this algorithm follows from the Max-flow Min-cut theorem which we will not discuss here. For termination, we assume the weights are integers. Then on each iteration we increase the flow by 1. Thus, the algorithm terminates after at most f iterations where f is the maximum flow. Each iteration takes O(E) time so the total runtime is O(Ef ).
18 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Bipartite Matching as Maximum Flow We will illustrate the Ford-Fulkerson algorithm by considering the following problem. Consider the assignment problem, but suppose that all the costs are all either 0 or. We may represent this as a graph by including edges only where the cost is 0. The resulting matching problem can be solved by finding the maximum flow.
19 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Bipartite Matching as Maximum Flow Example Bipartite matching flow network [2]
20 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Bipartite Matching as Maximum Flow Example Bipartite matching flow network [2]
21 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
22 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
23 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
24 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
25 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
26 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
27 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Ford-Fulkerson Example A X B Y C Z Bipartite matching augmenting paths [3] D W
28 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Outline 1 The 2 Network Flow 3 Minimum-Cost Maximum Flow
29 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Minimum-Cost Maximum Flow Now we can finally generalise the Maximum Flow problem to be able to solve our original problem. We consider a weighted flow network, where w(u, v) denotes the weight of each edge in the graph. The Minimum-Cost Maximum Flow problem is to find, out of all possible the assignments of flows that give the maximum total flow, the one that minimises the following quantity f (u, v) w(u, v). (u,v) E
30 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Minimum-Cost Maximum Flow The solution is given by a simple modification of the Ford-Fulkerson algorithm. In the standard algorithm, it is not specified how augmenting paths are found, but generally depth first search is used. Instead, we use a shortest path algorithm, such as Bellman-Ford, to find the augmenting path of the least weight. We weight the back-edges going in the reverse direction with the negative of the weight of the forward direction. This is why we need a shortest path algorithm that can handle negative weight edges.
31 The Network Flow Minimum-Cost Maximum Flow Shameless Plug The The Solution As before we use network flow to find a matching of the graph associated with the assignment problem. But this time, we weight the edges according to the cost of the assignment. The runtime of this algorithm is Θ(V EV ) = Θ(V 4 ). There is a way to dynamically reassign weights to the graph so that we can use Dijkstra s to find the shortest path. This gives a runtime of Θ(V 3 ). This is out of the scope of the lecture, but the re-weighting is very similar to that used in Johnson s algorithm for negative-edge-weight all-pairs shortest paths.
32 The Network Flow Minimum-Cost Maximum Flow Shameless Plug The The Solution As before we use network flow to find a matching of the graph associated with the assignment problem. But this time, we weight the edges according to the cost of the assignment. The runtime of this algorithm is Θ(V EV ) = Θ(V 4 ). There is a way to dynamically reassign weights to the graph so that we can use Dijkstra s to find the shortest path. This gives a runtime of Θ(V 3 ). This is out of the scope of the lecture, but the re-weighting is very similar to that used in Johnson s algorithm for negative-edge-weight all-pairs shortest paths.
33 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Algorithm Circle Haskell Course Algorithm Circle is holding a Haskell course that will run on Saturday the 22 nd of September and Saturday 27 nd of September. Haskell is a purely functional programming language with non-strict semantics 1. The following Haskell code generates an infinite list containing the Fibonacci numbers: let fib = 0:1: zipwith (+) fib (tail fib) 1 It is also the best programming language.
34 The Network Flow Minimum-Cost Maximum Flow Shameless Plug ACM ICPC The Southern African Regionals of the ACM Intercollegiate Programming Contest will be taking place on Saturday the 20 th of October. There will be an information session this Wednesday in Meridian. Training sessions will be held on the 23 rd and 30 th of September and another date to be announced.
35 The Network Flow Minimum-Cost Maximum Flow Shameless Plug Licensing These lecture slides were created by for UCT Algorithm Circle and are licensed under the Creative Commons Attribution-ShareAlike 3.0 Unported License. I made use of the following content from Bruce Merry s Algorithm Circle lecture on Matching Problems: 1 Weighted bipartite matching diagram 2 Bipartite matching flow network 3 Bipartite matching augmenting paths
Maximum flows & Maximum Matchings
 Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
Chapter 9 Maximum flows & Maximum Matchings This chapter analyzes flows and matchings. We will define flows and maximum flows and present an algorithm that solves the maximum flow problem. Then matchings
CSE 417 Network Flows (pt 4) Min Cost Flows
 CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
CSE 417 Network Flows (pt 4) Min Cost Flows Reminders > HW6 is due Monday Review of last three lectures > Defined the maximum flow problem find the feasible flow of maximum value flow is feasible if it
Network Flow. November 23, CMPE 250 Graphs- Network Flow November 23, / 31
 Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Network Flow November 23, 2016 CMPE 250 Graphs- Network Flow November 23, 2016 1 / 31 Types of Networks Internet Telephone Cell Highways Rail Electrical Power Water Sewer Gas... CMPE 250 Graphs- Network
Graphs and Network Flows IE411. Lecture 13. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Graphs and Network Flows IE411 Lecture 13 Dr. Ted Ralphs IE411 Lecture 13 1 References for Today s Lecture IE411 Lecture 13 2 References for Today s Lecture Required reading Sections 21.1 21.2 References
Lecture 18 Solving Shortest Path Problem: Dijkstra s Algorithm. October 23, 2009
 Solving Shortest Path Problem: Dijkstra s Algorithm October 23, 2009 Outline Lecture 18 Focus on Dijkstra s Algorithm Importance: Where it has been used? Algorithm s general description Algorithm steps
Solving Shortest Path Problem: Dijkstra s Algorithm October 23, 2009 Outline Lecture 18 Focus on Dijkstra s Algorithm Importance: Where it has been used? Algorithm s general description Algorithm steps
Computational Methods in IS Research Fall Graph Algorithms Network Flow Problems
 Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Computational Methods in IS Research Fall 2017 Graph Algorithms Network Flow Problems Nirmalya Roy Department of Information Systems University of Maryland Baltimore County www.umbc.edu Network Flow Problems
Minimum Spanning Tree (undirected graph)
 1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
1 Minimum Spanning Tree (undirected graph) 2 Path tree vs. spanning tree We have constructed trees in graphs for shortest path to anywhere else (from vertex is the root) Minimum spanning trees instead
Jessica Su (some parts copied from CLRS / last quarter s notes)
 1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
1 Max flow Consider a directed graph G with positive edge weights c that define the capacity of each edge. We can identify two special nodes in G: the source node s and the sink node t. We want to find
Maximum Flow. Flow Networks. Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms. Example Flow Network
 Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Flow Networks Ford-Fulkerson Method Edmonds-Karp Algorithm Push-Relabel Algorithms Maximum Flow Flow Networks A flow network is a directed graph where: Each edge (u,v) has a capacity c(u,v) 0. If (u,v)
Lecture 3: Graphs and flows
 Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Chapter 3 Lecture 3: Graphs and flows Graphs: a useful combinatorial structure. Definitions: graph, directed and undirected graph, edge as ordered pair, path, cycle, connected graph, strongly connected
Source. Sink. Chapter 10: Iterative Programming Maximum Flow Problem. CmSc250 Intro to Algorithms
 Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Chapter 10: Iterative Programming Maximum Flow Problem CmSc20 Intro to Algorithms A flow network is a model of a system where some material is produced at its source, travels through the system, and is
Network Design and Optimization course
 Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
Effective maximum flow algorithms Modeling with flows Network Design and Optimization course Lecture 5 Alberto Ceselli alberto.ceselli@unimi.it Dipartimento di Tecnologie dell Informazione Università degli
and 6.855J March 6, Maximum Flows 2
 5.08 and.855j March, 00 Maximum Flows Network Reliability Communication Network What is the maximum number of arc disjoint paths from s to t? How can we determine this number? Theorem. Let G = (N,A) be
5.08 and.855j March, 00 Maximum Flows Network Reliability Communication Network What is the maximum number of arc disjoint paths from s to t? How can we determine this number? Theorem. Let G = (N,A) be
CSC 8301 Design & Analysis of Algorithms: Linear Programming
 CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
CSC 8301 Design & Analysis of Algorithms: Linear Programming Professor Henry Carter Fall 2016 Iterative Improvement Start with a feasible solution Improve some part of the solution Repeat until the solution
Solving problems on graph algorithms
 Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Solving problems on graph algorithms Workshop Organized by: ACM Unit, Indian Statistical Institute, Kolkata. Tutorial-3 Date: 06.07.2017 Let G = (V, E) be an undirected graph. For a vertex v V, G {v} is
Problem Set 7 Solutions
 Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
Design and Analysis of Algorithms March 0, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 7 Solutions Problem Set 7 Solutions
Lecture 6: Shortest distance, Eulerian cycles, Maxflow
 DD2458, Problem Solving and Programming Under Pressure Lecture 6: Shortest distance, Eulerian cycles, Maxflow Date: 2008-10-06 Scribe(s): Adam Kull, David Vuorio Lecturer: Douglas Wikström 1 Shortest path
DD2458, Problem Solving and Programming Under Pressure Lecture 6: Shortest distance, Eulerian cycles, Maxflow Date: 2008-10-06 Scribe(s): Adam Kull, David Vuorio Lecturer: Douglas Wikström 1 Shortest path
Minimum Cost Edge Disjoint Paths
 Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
Minimum Cost Edge Disjoint Paths Theodor Mader 15.4.2008 1 Introduction Finding paths in networks and graphs constitutes an area of theoretical computer science which has been highly researched during
Network Flow I. Lecture Overview The Network Flow Problem
 Lecture Network Flow I. Overview In these next two lectures we are going to talk about an important algorithmic problem called the Network Flow Problem. Network flow is important because it can be used
Lecture Network Flow I. Overview In these next two lectures we are going to talk about an important algorithmic problem called the Network Flow Problem. Network flow is important because it can be used
Lecture 3: Totally Unimodularity and Network Flows
 Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Lecture 3: Totally Unimodularity and Network Flows (3 units) Outline Properties of Easy Problems Totally Unimodular Matrix Minimum Cost Network Flows Dijkstra Algorithm for Shortest Path Problem Ford-Fulkerson
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem
 Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
Outline: Finish uncapacitated simplex method Negative cost cycle algorithm The max-flow problem Max-flow min-cut theorem Uncapacitated Networks: Basic primal and dual solutions Flow conservation constraints
CS261: Problem Set #2
 CS261: Problem Set #2 Due by 11:59 PM on Tuesday, February 9, 2016 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Submission instructions:
CS261: Problem Set #2 Due by 11:59 PM on Tuesday, February 9, 2016 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Submission instructions:
Maximum Flow Algorithms
 Maximum Flow Algorithms Network Algorithms Georgia Kaouri Contents Applications, special cases Flow networks Ford Fulkerson algorithm Preflow push algorithms Lift to front algorithm Material flows Applications
Maximum Flow Algorithms Network Algorithms Georgia Kaouri Contents Applications, special cases Flow networks Ford Fulkerson algorithm Preflow push algorithms Lift to front algorithm Material flows Applications
CS 125 Section #5 Graph Traversal and Linear Programs October 6, 2016
 CS 125 Section #5 Graph Traversal and Linear Programs October 6, 2016 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there
CS 125 Section #5 Graph Traversal and Linear Programs October 6, 2016 1 Depth first search 1.1 The Algorithm Besides breadth first search, which we saw in class in relation to Dijkstra s algorithm, there
Tutorial for Algorithm s Theory Problem Set 5. January 17, 2013
 Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
Tutorial for Algorithm s Theory Problem Set 5 January 17, 2013 Exercise 1: Maximum Flow Algorithms Consider the following flow network: a) Solve the maximum flow problem on the above network by using the
COMP 251 Winter 2017 Online quizzes with answers
 COMP 251 Winter 2017 Online quizzes with answers Open Addressing (2) Which of the following assertions are true about open address tables? A. You cannot store more records than the total number of slots
COMP 251 Winter 2017 Online quizzes with answers Open Addressing (2) Which of the following assertions are true about open address tables? A. You cannot store more records than the total number of slots
CS261: Problem Set #1
 CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
CS261: Problem Set #1 Due by 11:59 PM on Tuesday, April 21, 2015 Instructions: (1) Form a group of 1-3 students. You should turn in only one write-up for your entire group. (2) Turn in your solutions by
Single Source Shortest Path: The Bellman-Ford Algorithm. Slides based on Kevin Wayne / Pearson-Addison Wesley
 Single Source Shortest Path: The Bellman-Ford Algorithm Slides based on Kevin Wayne / Pearson-Addison Wesley Single Source Shortest Path Problem Shortest path network. Directed graph G = (V, E, w). Weight
Single Source Shortest Path: The Bellman-Ford Algorithm Slides based on Kevin Wayne / Pearson-Addison Wesley Single Source Shortest Path Problem Shortest path network. Directed graph G = (V, E, w). Weight
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn
 Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Chapter 5 Graph Algorithms Algorithm Theory WS 2012/13 Fabian Kuhn Graphs Extremely important concept in computer science Graph, : node (or vertex) set : edge set Simple graph: no self loops, no multiple
Copyright 2007 Pearson Addison-Wesley. All rights reserved. A. Levitin Introduction to the Design & Analysis of Algorithms, 2 nd ed., Ch.
 Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Iterative Improvement Algorithm design technique for solving optimization problems Start with a feasible solution Repeat the following step until no improvement can be found: change the current feasible
Network flows and Menger s theorem
 Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
Network flows and Menger s theorem Recall... Theorem (max flow, min cut strong duality). Let G be a network. The maximum value of a flow equals the minimum capacity of a cut. We prove this strong duality
1. Let n and m be positive integers with n m. a. Write the inclusion/exclusion formula for the number S(n, m) of surjections from {1, 2,...
 MATH 3012, Quiz 3, November 24, 2015, WTT Student Name and ID Number 1. Let n and m be positive integers with n m. a. Write the inclusion/exclusion formula for the number S(n, m) of surjections from {1,
MATH 3012, Quiz 3, November 24, 2015, WTT Student Name and ID Number 1. Let n and m be positive integers with n m. a. Write the inclusion/exclusion formula for the number S(n, m) of surjections from {1,
CSE 417 Network Flows (pt 3) Modeling with Min Cuts
 CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
CSE 417 Network Flows (pt 3) Modeling with Min Cuts Reminders > HW6 is due on Friday start early bug fixed on line 33 of OptimalLineup.java: > change true to false Review of last two lectures > Defined
Homework 3 Solutions
 CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
CS3510 Design & Analysis of Algorithms Section A Homework 3 Solutions Released: 7pm, Wednesday Nov 8, 2017 This homework has a total of 4 problems on 4 pages. Solutions should be submitted to GradeScope
COMP4128 Programming Challenges
 Network Networks Network COMP4128 Programming Challenges School of Computer Science and Engineering UNSW Australia Table of Contents 2 Network 1 Networks Networks 2 3 4 5 6 networks 3 Network Networks
Network Networks Network COMP4128 Programming Challenges School of Computer Science and Engineering UNSW Australia Table of Contents 2 Network 1 Networks Networks 2 3 4 5 6 networks 3 Network Networks
LECTURES 3 and 4: Flows and Matchings
 LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
LECTURES 3 and 4: Flows and Matchings 1 Max Flow MAX FLOW (SP). Instance: Directed graph N = (V,A), two nodes s,t V, and capacities on the arcs c : A R +. A flow is a set of numbers on the arcs such that
Routing Protocols and the IP Layer
 Routing Protocols and the IP Layer CS244A Review Session 2/0/08 Ben Nham Derived from slides by: Paul Tarjan Martin Casado Ari Greenberg Functions of a router Forwarding Determine the correct egress port
Routing Protocols and the IP Layer CS244A Review Session 2/0/08 Ben Nham Derived from slides by: Paul Tarjan Martin Casado Ari Greenberg Functions of a router Forwarding Determine the correct egress port
Network Flow. The network flow problem is as follows:
 Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Network Flow The network flow problem is as follows: Given a connected directed graph G with non-negative integer weights, (where each edge stands for the capacity of that edge), and two distinguished
Solution for Homework set 3
 TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
TTIC 300 and CMSC 37000 Algorithms Winter 07 Solution for Homework set 3 Question (0 points) We are given a directed graph G = (V, E), with two special vertices s and t, and non-negative integral capacities
CS612 Algorithms for Electronic Design Automation
 CS612 Algorithms for Electronic Design Automation Lecture 8 Network Flow Based Modeling 1 Flow Network Definition Given a directed graph G = (V, E): Each edge (u, v) has capacity c(u,v) 0 Each edge (u,
CS612 Algorithms for Electronic Design Automation Lecture 8 Network Flow Based Modeling 1 Flow Network Definition Given a directed graph G = (V, E): Each edge (u, v) has capacity c(u,v) 0 Each edge (u,
Mathematics for Decision Making: An Introduction. Lecture 18
 Mathematics for Decision Making: An Introduction Lecture 18 Matthias Köppe UC Davis, Mathematics March 5, 2009 18 1 Augmenting Circuit Algorithm for Min Cost Flow Augmenting Circuit Algorithm, Kantoróvich
Mathematics for Decision Making: An Introduction Lecture 18 Matthias Köppe UC Davis, Mathematics March 5, 2009 18 1 Augmenting Circuit Algorithm for Min Cost Flow Augmenting Circuit Algorithm, Kantoróvich
TIE Graph algorithms
 TIE-20106 1 1 Graph algorithms This chapter discusses the data structure that is a collection of points (called nodes or vertices) and connections between them (called edges or arcs) a graph. The common
TIE-20106 1 1 Graph algorithms This chapter discusses the data structure that is a collection of points (called nodes or vertices) and connections between them (called edges or arcs) a graph. The common
Lecture 11: Maximum flow and minimum cut
 Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Optimisation Part IB - Easter 2018 Lecture 11: Maximum flow and minimum cut Lecturer: Quentin Berthet 4.4. The maximum flow problem. We consider in this lecture a particular kind of flow problem, with
Graph Algorithms (part 3 of CSC 282),
 Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/11cs8 Homework problem sessions are in CSB 601, 6:1-7:1pm on Oct. (Wednesday), Oct. 1 (Wednesday), and on Oct. 19 (Wednesday);
Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/11cs8 Homework problem sessions are in CSB 601, 6:1-7:1pm on Oct. (Wednesday), Oct. 1 (Wednesday), and on Oct. 19 (Wednesday);
Introduction to Algorithms. Lecture 11
 Introduction to Algorithms Lecture 11 Last Time Optimization Problems Greedy Algorithms Graph Representation & Algorithms Minimum Spanning Tree Prim s Algorithm Kruskal s Algorithm 2 Today s Topics Shortest
Introduction to Algorithms Lecture 11 Last Time Optimization Problems Greedy Algorithms Graph Representation & Algorithms Minimum Spanning Tree Prim s Algorithm Kruskal s Algorithm 2 Today s Topics Shortest
Cuts, Connectivity, and Flow
 Cuts, Connectivity, and Flow Vertex Cut and Connectivity A separating set or vertex cut of a graph G is a set S V(G) such that G S G S has more than one component A graph G is k-connected if every vertex
Cuts, Connectivity, and Flow Vertex Cut and Connectivity A separating set or vertex cut of a graph G is a set S V(G) such that G S G S has more than one component A graph G is k-connected if every vertex
Chapter 7. Network Flow. Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved.
 Chapter 7 Network Flow Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 * 7.13 Assignment Problem Assignment Problem Assignment problem. Input: weighted, complete bipartite
Chapter 7 Network Flow Slides by Kevin Wayne. Copyright 2005 Pearson-Addison Wesley. All rights reserved. 1 * 7.13 Assignment Problem Assignment Problem Assignment problem. Input: weighted, complete bipartite
1 Weighted matchings in bipartite graphs
 Praktikum Algorithmen-Entwurf (Teil ) 19.11.1 1 1 Weighted matchings in bipartite graphs LetG = (V,E)beanundirectedgraphwithintegeredgeweightsw : E Z.Amatching in G is a subset M E of edges such that no
Praktikum Algorithmen-Entwurf (Teil ) 19.11.1 1 1 Weighted matchings in bipartite graphs LetG = (V,E)beanundirectedgraphwithintegeredgeweightsw : E Z.Amatching in G is a subset M E of edges such that no
Discrete Optimization 2010 Lecture 5 Min-Cost Flows & Total Unimodularity
 Discrete Optimization 2010 Lecture 5 Min-Cost Flows & Total Unimodularity Marc Uetz University of Twente m.uetz@utwente.nl Lecture 5: sheet 1 / 26 Marc Uetz Discrete Optimization Outline 1 Min-Cost Flows
Discrete Optimization 2010 Lecture 5 Min-Cost Flows & Total Unimodularity Marc Uetz University of Twente m.uetz@utwente.nl Lecture 5: sheet 1 / 26 Marc Uetz Discrete Optimization Outline 1 Min-Cost Flows
Algorithms for Data Science
 Algorithms for Data Science CSOR W4246 Eleni Drinea Computer Science Department Columbia University Thursday, October 1, 2015 Outline 1 Recap 2 Shortest paths in graphs with non-negative edge weights (Dijkstra
Algorithms for Data Science CSOR W4246 Eleni Drinea Computer Science Department Columbia University Thursday, October 1, 2015 Outline 1 Recap 2 Shortest paths in graphs with non-negative edge weights (Dijkstra
Data Structures and Algorithms
 Data Structures and Algorithms Session 9. April 6, 009 Instructor: Bert Huang http://www.cs.columbia.edu/~bert/courses/7 Announcements Homework due by midnight tonight Homework 5 assigned Review Topological
Data Structures and Algorithms Session 9. April 6, 009 Instructor: Bert Huang http://www.cs.columbia.edu/~bert/courses/7 Announcements Homework due by midnight tonight Homework 5 assigned Review Topological
Today. Maximum flow. Maximum flow. Problem
 5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
5 Maximum Flow (slides 1 4) Today Maximum flow Algorithms and Networks 2008 Maximum flow problem Applications Briefly: Ford-Fulkerson; min cut max flow theorem Preflow push algorithm Lift to front algorithm
Material handling and Transportation in Logistics. Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena
 Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
Material handling and Transportation in Logistics Paolo Detti Dipartimento di Ingegneria dell Informazione e Scienze Matematiche Università di Siena Introduction to Graph Theory Graph Theory As Mathematical
CS 341: Algorithms. Douglas R. Stinson. David R. Cheriton School of Computer Science University of Waterloo. February 26, 2019
 CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
CS 341: Algorithms Douglas R. Stinson David R. Cheriton School of Computer Science University of Waterloo February 26, 2019 D.R. Stinson (SCS) CS 341 February 26, 2019 1 / 296 1 Course Information 2 Introduction
Lecture 6 Basic Graph Algorithms
 CS 491 CAP Intro to Competitive Algorithmic Programming Lecture 6 Basic Graph Algorithms Uttam Thakore University of Illinois at Urbana-Champaign September 30, 2015 Updates ICPC Regionals teams will be
CS 491 CAP Intro to Competitive Algorithmic Programming Lecture 6 Basic Graph Algorithms Uttam Thakore University of Illinois at Urbana-Champaign September 30, 2015 Updates ICPC Regionals teams will be
Student Name and ID Number. MATH 3012, Quiz 3, April 16, 2018, WTT
 MATH 3012, Quiz 3, April 16, 2018, WTT Student Name and ID Number 1. A graph with weights on edges is shown below. In the space to the right of the figure, list in order the edges which make up a minimum
MATH 3012, Quiz 3, April 16, 2018, WTT Student Name and ID Number 1. A graph with weights on edges is shown below. In the space to the right of the figure, list in order the edges which make up a minimum
CS599: Convex and Combinatorial Optimization Fall 2013 Lecture 14: Combinatorial Problems as Linear Programs I. Instructor: Shaddin Dughmi
 CS599: Convex and Combinatorial Optimization Fall 2013 Lecture 14: Combinatorial Problems as Linear Programs I Instructor: Shaddin Dughmi Announcements Posted solutions to HW1 Today: Combinatorial problems
CS599: Convex and Combinatorial Optimization Fall 2013 Lecture 14: Combinatorial Problems as Linear Programs I Instructor: Shaddin Dughmi Announcements Posted solutions to HW1 Today: Combinatorial problems
I ACCEPT NO RESPONSIBILITY FOR ERRORS ON THIS SHEET. I assume that E = (V ).
 1 I ACCEPT NO RESPONSIBILITY FOR ERRORS ON THIS SHEET. I assume that E = (V ). Data structures Sorting Binary heas are imlemented using a hea-ordered balanced binary tree. Binomial heas use a collection
1 I ACCEPT NO RESPONSIBILITY FOR ERRORS ON THIS SHEET. I assume that E = (V ). Data structures Sorting Binary heas are imlemented using a hea-ordered balanced binary tree. Binomial heas use a collection
The Shortest Path Problem. The Shortest Path Problem. Mathematical Model. Integer Programming Formulation
 The Shortest Path Problem jla,jc@imm.dtu.dk Department of Management Engineering Technical University of Denmark The Shortest Path Problem Given a directed network G = (V,E,w) for which the underlying
The Shortest Path Problem jla,jc@imm.dtu.dk Department of Management Engineering Technical University of Denmark The Shortest Path Problem Given a directed network G = (V,E,w) for which the underlying
s-t Graph Cuts for Binary Energy Minimization
 s-t Graph Cuts for Binary Energy Minimization E data term ( L) = D ( ) + ( ) P Lp λ Ι Lp Lq p prior term Now that we have an energy function, the big question is how do we minimize it? pq N n Exhaustive
s-t Graph Cuts for Binary Energy Minimization E data term ( L) = D ( ) + ( ) P Lp λ Ι Lp Lq p prior term Now that we have an energy function, the big question is how do we minimize it? pq N n Exhaustive
Graph Algorithms. A Brief Introduction. 高晓沨 (Xiaofeng Gao) Department of Computer Science Shanghai Jiao Tong Univ.
 Graph Algorithms A Brief Introduction 高晓沨 (Xiaofeng Gao) Department of Computer Science Shanghai Jiao Tong Univ. 目录 2015/5/7 1 Graph and Its Applications 2 Introduction to Graph Algorithms 3 References
Graph Algorithms A Brief Introduction 高晓沨 (Xiaofeng Gao) Department of Computer Science Shanghai Jiao Tong Univ. 目录 2015/5/7 1 Graph and Its Applications 2 Introduction to Graph Algorithms 3 References
Graph Algorithms (part 3 of CSC 282),
 Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/10cs8 1 Schedule Homework is due Thursday, Oct 1. The QUIZ will be on Tuesday, Oct. 6. List of algorithms covered in the
Graph Algorithms (part of CSC 8), http://www.cs.rochester.edu/~stefanko/teaching/10cs8 1 Schedule Homework is due Thursday, Oct 1. The QUIZ will be on Tuesday, Oct. 6. List of algorithms covered in the
Shortest Path Algorithms
 Shortest Path Algorithms Andreas Klappenecker [based on slides by Prof. Welch] 1 Single Source Shortest Path Given: a directed or undirected graph G = (V,E) a source node s in V a weight function w: E
Shortest Path Algorithms Andreas Klappenecker [based on slides by Prof. Welch] 1 Single Source Shortest Path Given: a directed or undirected graph G = (V,E) a source node s in V a weight function w: E
2. True or false: even though BFS and DFS have the same space complexity, they do not always have the same worst case asymptotic time complexity.
 1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
1. T F: Consider a directed graph G = (V, E) and a vertex s V. Suppose that for all v V, there exists a directed path in G from s to v. Suppose that a DFS is run on G, starting from s. Then, true or false:
Fundamental Algorithms CSCI-GA /Summer Solution to Homework 8
 Fundamental Algorithms CSCI-GA.70-00/Summer 206 Solution to Homework 8 Problem (CLRS 23.-6). ( point) Show that a graph has a unique minimum spanning tree if, for every cut of the graph, there is a unique
Fundamental Algorithms CSCI-GA.70-00/Summer 206 Solution to Homework 8 Problem (CLRS 23.-6). ( point) Show that a graph has a unique minimum spanning tree if, for every cut of the graph, there is a unique
Dynamic-Programming algorithms for shortest path problems: Bellman-Ford (for singlesource) and Floyd-Warshall (for all-pairs).
 Lecture 13 Graph Algorithms I 13.1 Overview This is the first of several lectures on graph algorithms. We will see how simple algorithms like depth-first-search can be used in clever ways (for a problem
Lecture 13 Graph Algorithms I 13.1 Overview This is the first of several lectures on graph algorithms. We will see how simple algorithms like depth-first-search can be used in clever ways (for a problem
CSC 373 Lecture # 3 Instructor: Milad Eftekhar
 Huffman encoding: Assume a context is available (a document, a signal, etc.). These contexts are formed by some symbols (words in a document, discrete samples from a signal, etc). Each symbols s i is occurred
Huffman encoding: Assume a context is available (a document, a signal, etc.). These contexts are formed by some symbols (words in a document, discrete samples from a signal, etc). Each symbols s i is occurred
CSC 373: Algorithm Design and Analysis Lecture 8
 CSC 373: Algorithm Design and Analysis Lecture 8 Allan Borodin January 23, 2013 1 / 19 Lecture 8: Announcements and Outline Announcements No lecture (or tutorial) this Friday. Lecture and tutorials as
CSC 373: Algorithm Design and Analysis Lecture 8 Allan Borodin January 23, 2013 1 / 19 Lecture 8: Announcements and Outline Announcements No lecture (or tutorial) this Friday. Lecture and tutorials as
CS/COE 1501 cs.pitt.edu/~bill/1501/ Network Flow
 CS/COE 1501 cs.pitt.edu/~bill/1501/ Network Flow Defining network flow Consider a directed, weighted graph G(V, E) Weights are applied to edges to state their capacity c(u, w) is the capacity of edge (u,
CS/COE 1501 cs.pitt.edu/~bill/1501/ Network Flow Defining network flow Consider a directed, weighted graph G(V, E) Weights are applied to edges to state their capacity c(u, w) is the capacity of edge (u,
All Shortest Paths. Questions from exercises and exams
 All Shortest Paths Questions from exercises and exams The Problem: G = (V, E, w) is a weighted directed graph. We want to find the shortest path between any pair of vertices in G. Example: find the distance
All Shortest Paths Questions from exercises and exams The Problem: G = (V, E, w) is a weighted directed graph. We want to find the shortest path between any pair of vertices in G. Example: find the distance
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching
 Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Advanced Algorithm Design and Analysis (Lecture 5) SW5 fall 2007 Simonas Šaltenis
 Advanced Algorithm Design and Analysis (Lecture 5) SW5 fall 2007 Simonas Šaltenis 3.2.12 simas@cs.aau.dk All-pairs shortest paths Main goals of the lecture: to go through one more example of dynamic programming
Advanced Algorithm Design and Analysis (Lecture 5) SW5 fall 2007 Simonas Šaltenis 3.2.12 simas@cs.aau.dk All-pairs shortest paths Main goals of the lecture: to go through one more example of dynamic programming
COT 6936: Topics in Algorithms! Giri Narasimhan. ECS 254A / EC 2443; Phone: x3748
 COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
COT 6936: Topics in Algorithms! Giri Narasimhan ECS 254A / EC 2443; Phone: x3748 giri@cs.fiu.edu http://www.cs.fiu.edu/~giri/teach/cot6936_s12.html https://moodle.cis.fiu.edu/v2.1/course/view.php?id=174
Title. Ferienakademie im Sarntal Course 2 Distance Problems: Theory and Praxis. Nesrine Damak. Fakultät für Informatik TU München. 20.
 Title Ferienakademie im Sarntal Course 2 Distance Problems: Theory and Praxis Nesrine Damak Fakultät für Informatik TU München 20. September 2010 Nesrine Damak: Classical Shortest-Path Algorithms 1/ 35
Title Ferienakademie im Sarntal Course 2 Distance Problems: Theory and Praxis Nesrine Damak Fakultät für Informatik TU München 20. September 2010 Nesrine Damak: Classical Shortest-Path Algorithms 1/ 35
Network Flow. By: Daniel Pham, Anthony Huber, Shaazan Wirani
 Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Network Flow By: Daniel Pham, Anthony Huber, Shaazan Wirani Questions 1. What is a network flow? 2. What is the Big O notation of the Ford-Fulkerson method? 3. How to test if the Hungarian algorithm is
Today: Amortized Analysis (examples) Multithreaded Algs.
 Today: Amortized Analysis (examples) Multithreaded Algs. COSC 581, Algorithms March 11, 2014 Many of these slides are adapted from several online sources Reading Assignments Today s class: Chapter 17 (Amortized
Today: Amortized Analysis (examples) Multithreaded Algs. COSC 581, Algorithms March 11, 2014 Many of these slides are adapted from several online sources Reading Assignments Today s class: Chapter 17 (Amortized
College of Computer & Information Science Fall 2007 Northeastern University 14 September 2007
 College of Computer & Information Science Fall 2007 Northeastern University 14 September 2007 CS G399: Algorithmic Power Tools I Scribe: Eric Robinson Lecture Outline: Linear Programming: Vertex Definitions
College of Computer & Information Science Fall 2007 Northeastern University 14 September 2007 CS G399: Algorithmic Power Tools I Scribe: Eric Robinson Lecture Outline: Linear Programming: Vertex Definitions
Analysis of Algorithms, I
 Analysis of Algorithms, I CSOR W4231.002 Eleni Drinea Computer Science Department Columbia University Thursday, March 8, 2016 Outline 1 Recap Single-source shortest paths in graphs with real edge weights:
Analysis of Algorithms, I CSOR W4231.002 Eleni Drinea Computer Science Department Columbia University Thursday, March 8, 2016 Outline 1 Recap Single-source shortest paths in graphs with real edge weights:
Shortest path problems
 Next... Shortest path problems Single-source shortest paths in weighted graphs Shortest-Path Problems Properties of Shortest Paths, Relaxation Dijkstra s Algorithm Bellman-Ford Algorithm Shortest-Paths
Next... Shortest path problems Single-source shortest paths in weighted graphs Shortest-Path Problems Properties of Shortest Paths, Relaxation Dijkstra s Algorithm Bellman-Ford Algorithm Shortest-Paths
Lecture #7. 1 Introduction. 2 Dijkstra s Correctness. COMPSCI 330: Design and Analysis of Algorithms 9/16/2014
 COMPSCI 330: Design and Analysis of Algorithms 9/16/2014 Lecturer: Debmalya Panigrahi Lecture #7 Scribe: Nat Kell 1 Introduction In this lecture, we will further examine shortest path algorithms. We will
COMPSCI 330: Design and Analysis of Algorithms 9/16/2014 Lecturer: Debmalya Panigrahi Lecture #7 Scribe: Nat Kell 1 Introduction In this lecture, we will further examine shortest path algorithms. We will
Tutorial 4: Flow Artificial Intelligence
 Tutorial 4: Flow Artificial Intelligence G.Guérard Les étudiants doivent faire des groupes de 3-4 afin de faire un brainstorming pour chaque exercice. Il n est pas demandé aux étudiants d avoir une connaissance
Tutorial 4: Flow Artificial Intelligence G.Guérard Les étudiants doivent faire des groupes de 3-4 afin de faire un brainstorming pour chaque exercice. Il n est pas demandé aux étudiants d avoir une connaissance
1 Dynamic Programming
 CS161 Lecture 13 Dynamic Programming and Greedy Algorithms Scribe by: Eric Huang Date: May 13, 2015 1 Dynamic Programming The idea of dynamic programming is to have a table of solutions of subproblems
CS161 Lecture 13 Dynamic Programming and Greedy Algorithms Scribe by: Eric Huang Date: May 13, 2015 1 Dynamic Programming The idea of dynamic programming is to have a table of solutions of subproblems
Graphs. Part II: SP and MST. Laura Toma Algorithms (csci2200), Bowdoin College
 Laura Toma Algorithms (csci2200), Bowdoin College Topics Weighted graphs each edge (u, v) has a weight denoted w(u, v) or w uv stored in the adjacency list or adjacency matrix The weight of a path p =
Laura Toma Algorithms (csci2200), Bowdoin College Topics Weighted graphs each edge (u, v) has a weight denoted w(u, v) or w uv stored in the adjacency list or adjacency matrix The weight of a path p =
Introduction to Algorithms
 Introduction to Algorithms 6.046J/18.401J LECTURE 13 Graph algorithms Graph representation Minimum spanning trees Greedy algorithms Optimal substructure Greedy choice Prim s greedy MST algorithm Prof.
Introduction to Algorithms 6.046J/18.401J LECTURE 13 Graph algorithms Graph representation Minimum spanning trees Greedy algorithms Optimal substructure Greedy choice Prim s greedy MST algorithm Prof.
Artificial Intelligence
 Artificial Intelligence Shortest Path Problem G. Guérard Department of Nouvelles Energies Ecole Supérieur d Ingénieurs Léonard de Vinci Lecture 3 GG A.I. 1/42 Outline 1 The Shortest Path Problem Introduction
Artificial Intelligence Shortest Path Problem G. Guérard Department of Nouvelles Energies Ecole Supérieur d Ingénieurs Léonard de Vinci Lecture 3 GG A.I. 1/42 Outline 1 The Shortest Path Problem Introduction
Transportation Planning: The maximum flow problem
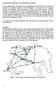 Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Transportation lanning: The maximum flow problem In many applications, and especially in the planning of Transportation and Logistics of materials, one important problem is that of finding how much material
Matching. Algorithms and Networks
 Matching Algorithms and Networks This lecture Matching: problem statement and applications Bipartite matching (recap) Matching in arbitrary undirected graphs: Edmonds algorithm Diversion: generalized tic-tac-toe
Matching Algorithms and Networks This lecture Matching: problem statement and applications Bipartite matching (recap) Matching in arbitrary undirected graphs: Edmonds algorithm Diversion: generalized tic-tac-toe
Taking Stock. Last Time Flows. This Time Review! 1 Characterize the structure of an optimal solution
 Taking Stock IE170: Algorithms in Systems Engineering: Lecture 26 Jeff Linderoth Last Time Department of Industrial and Systems Engineering Lehigh University April 2, 2007 This Time Review! Jeff Linderoth
Taking Stock IE170: Algorithms in Systems Engineering: Lecture 26 Jeff Linderoth Last Time Department of Industrial and Systems Engineering Lehigh University April 2, 2007 This Time Review! Jeff Linderoth
n 2 ( ) ( ) + n is in Θ n logn
 CSE Test Spring Name Last Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. points each. The time to multiply an m n matrix and a n p matrix is in: A. Θ( n) B. Θ( max(
CSE Test Spring Name Last Digits of Mav ID # Multiple Choice. Write your answer to the LEFT of each problem. points each. The time to multiply an m n matrix and a n p matrix is in: A. Θ( n) B. Θ( max(
Notes for Lecture 20
 U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
U.C. Berkeley CS170: Intro to CS Theory Handout N20 Professor Luca Trevisan November 13, 2001 Notes for Lecture 20 1 Duality As it turns out, the max-flow min-cut theorem is a special case of a more general
Lecture and notes by: Sarah Fletcher and Michael Xu November 3rd, Multicommodity Flow
 Multicommodity Flow 1 Introduction Suppose we have a company with a factory s and a warehouse t. The quantity of goods that they can ship from the factory to the warehouse in a given time period is limited
Multicommodity Flow 1 Introduction Suppose we have a company with a factory s and a warehouse t. The quantity of goods that they can ship from the factory to the warehouse in a given time period is limited
CSE 101. Algorithm Design and Analysis Miles Jones Office 4208 CSE Building Lecture 8: Negative Edges
 CSE 101 Algorithm Design and Analysis Miles Jones mej016@eng.ucsd.edu Office 4208 CSE Building Lecture 8: Negative Edges DIJKSTRA S ALGORITHM WITH DIFFERENT PRIORITY QUEUES. Runtime of Array: O V 2 Runtime
CSE 101 Algorithm Design and Analysis Miles Jones mej016@eng.ucsd.edu Office 4208 CSE Building Lecture 8: Negative Edges DIJKSTRA S ALGORITHM WITH DIFFERENT PRIORITY QUEUES. Runtime of Array: O V 2 Runtime
Lecture 11: Analysis of Algorithms (CS ) 1
 Lecture 11: Analysis of Algorithms (CS583-002) 1 Amarda Shehu November 12, 2014 1 Some material adapted from Kevin Wayne s Algorithm Class @ Princeton 1 2 Dynamic Programming Approach Floyd-Warshall Shortest
Lecture 11: Analysis of Algorithms (CS583-002) 1 Amarda Shehu November 12, 2014 1 Some material adapted from Kevin Wayne s Algorithm Class @ Princeton 1 2 Dynamic Programming Approach Floyd-Warshall Shortest
Problem set 2. Problem 1. Problem 2. Problem 3. CS261, Winter Instructor: Ashish Goel.
 CS261, Winter 2017. Instructor: Ashish Goel. Problem set 2 Electronic submission to Gradescope due 11:59pm Thursday 2/16. Form a group of 2-3 students that is, submit one homework with all of your names.
CS261, Winter 2017. Instructor: Ashish Goel. Problem set 2 Electronic submission to Gradescope due 11:59pm Thursday 2/16. Form a group of 2-3 students that is, submit one homework with all of your names.
Datenstrukturen & Algorithmen Solution of Sheet 11 FS 14
 Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 14th May
Eidgenössische Technische Hochschule Zürich Ecole polytechnique fédérale de Zurich Politecnico federale di Zurigo Federal Institute of Technology at Zurich Institut für Theoretische Informatik 14th May
CS490 Quiz 1. This is the written part of Quiz 1. The quiz is closed book; in particular, no notes, calculators and cell phones are allowed.
 CS490 Quiz 1 NAME: STUDENT NO: SIGNATURE: This is the written part of Quiz 1. The quiz is closed book; in particular, no notes, calculators and cell phones are allowed. Not all questions are of the same
CS490 Quiz 1 NAME: STUDENT NO: SIGNATURE: This is the written part of Quiz 1. The quiz is closed book; in particular, no notes, calculators and cell phones are allowed. Not all questions are of the same
Lecture 19 Shortest Path vs Spanning Tree Max-Flow Problem. October 25, 2009
 Shortest Path vs Spanning Tree Max-Flow Problem October 25, 2009 Outline Lecture 19 Undirected Network Illustration of the difference between the shortest path tree and the spanning tree Modeling Dilemma:
Shortest Path vs Spanning Tree Max-Flow Problem October 25, 2009 Outline Lecture 19 Undirected Network Illustration of the difference between the shortest path tree and the spanning tree Modeling Dilemma:
10. EXTENDING TRACTABILITY
 0. EXTENDING TRACTABILITY finding small vertex covers solving NP-hard problems on trees circular arc coverings vertex cover in bipartite graphs Lecture slides by Kevin Wayne Copyright 005 Pearson-Addison
0. EXTENDING TRACTABILITY finding small vertex covers solving NP-hard problems on trees circular arc coverings vertex cover in bipartite graphs Lecture slides by Kevin Wayne Copyright 005 Pearson-Addison
Lecture 10,11: General Matching Polytope, Maximum Flow. 1 Perfect Matching and Matching Polytope on General Graphs
 CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
CMPUT 675: Topics in Algorithms and Combinatorial Optimization (Fall 2009) Lecture 10,11: General Matching Polytope, Maximum Flow Lecturer: Mohammad R Salavatipour Date: Oct 6 and 8, 2009 Scriber: Mohammad
CS483 Design and Analysis of Algorithms
 CS483 Design and Analysis of Algorithms Review: Chapters 4-8, DPV Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: STII, Room 443, Friday 4:00pm - 6:00pm or by appointments Course
CS483 Design and Analysis of Algorithms Review: Chapters 4-8, DPV Instructor: Fei Li lifei@cs.gmu.edu with subject: CS483 Office hours: STII, Room 443, Friday 4:00pm - 6:00pm or by appointments Course
