a 1 (x ) a 1 (x ) a 1 (x ) ) a 2 3 (x Input Variable x
|
|
|
- Bernadette Arnold
- 5 years ago
- Views:
Transcription
1 Support Vector Learning for Fuzzy Rule-Base Classification Systems Yixin Chen, Stuent Member, IEEE, James Z. Wang, Member, IEEE Abstract To esign a fuzzy rule-base classification system (fuzzy classifier) with goo generalization ability in a high imensional feature space has been an active research topic for a long time. As a powerful machine learning approach for pattern recognition problems, support vector machine (SVM) is known to have goo generalization ability. More importantly, an SVM can work very well on a high (or even infinite) imensional feature space. This paper investigates the connection between fuzzy classifiers an kernel machines, establishes a link between fuzzy rules an kernels, an proposes a learning algorithm for fuzzy classifiers. We first show that a fuzzy classifier implicitly efines a translation invariant kernel uner the assumption that all membership functions associate with the same input variable are generate from location transformation of a reference function. Fuzzy inference on the IF-part of a fuzzy rule can be viewe as evaluating the kernel function. The kernel function is then proven to be a Mercer kernel if the reference functions meet certain spectral requirement. The corresponing fuzzy classifier is name positive efinite fuzzy classifier (PDFC). A PDFC can be built from the given training samples base on a support vector learning approach with the IF-part fuzzy rules given by the support vectors. Since the learning process minimizes an upper boun on the expecte risk (expecte preiction error) instea of the empirical risk (training error), the resulting PDFC usually has goo generalization. Moreover, because of the sparsity properties of the SVMs, the number of fuzzy rules is irrelevant to the imension of input space. In this sense, we avoi the curse of imensionality." Finally, PDFCs with ifferent reference functions are constructe using the support vector learning approach. The performance of the PDFCs is illustrate by extensive experimental results. Comparisons with other methos are also provie. Keywors Fuzzy systems, statistical learning theory, support vector machines, fuzzy classifier, kernel methos, pattern classification. I. Introuction Since the publication of L.A. Zaeh's seminal paper on fuzzy sets [64], fuzzy set theory an its escenant, fuzzy logic, have evolve into powerful tools for managing uncertainties inherent in complex systems. In the recent twenty years, fuzzy methoology has been successfully applie to a variety of areas incluing control an system ientification [7], [3], [48], [57], [65], signal an image processing [36], [39], [47], pattern classification [], [7], [], [6], an information retrieval [8], [34]. In general, builing a fuzzy system consists of three basic steps [6]: structure ientification (variable selection, partitioning input an Yixin Chen is with the Department of Computer Science an Engineering, The Pennsylvania State University, University Park, PA 68, USA ( yixchen@cse.psu.eu). James Z. Wang is with the School of Information Sciences an Technology an the Department of Computer Science an Engineering, The Pennsylvania State University, University Park, PA 68, USA ( jwang@ist.psu.eu). output spaces, specifying the number of fuzzy rules, an choosing a parametric/nonparametric form of membership functions), parameter estimation (obtaining unknown parameters in fuzzy rules via optimizing a given criterion), an moel valiation (performance evaluation an moel simplification). There are numerous stuies on all these subjects. Space limitation preclues the possibility of a comprehensive survey. Instea, we only review some of those results that are most relate to ours. A. Structure Ientification an Parameter Estimation Deciing the number of input variables is referre to the problem of variable selection, i.e., selecting input variables that are most preictive of a given outcome. It is relate to the problems of input imensionality reuction an parameter pruning. Emami et al. [4] present a simple metho of ientifying non-significant input variables in a fuzzy system base on the istribution of egree of memberships over the omain. Recently, Silipo et al. [44] propose a metho that quantifies the iscriminative power of the input features in a fuzzy moel base on information gain. Selecting input variables accoring to their information gains may improve the preiction performance of the fuzzy system an provies a better unerstaning of the unerlying concept that generates the ata. Given a set of input an output variables, a fuzzy partition associates fuzzy sets (or linguistic labels) with each variable. There are roughly two ways of oing it: ata inepenent partition an ata epenent partition. The former approach partitions the input space in a preetermine fashion. The partition of the output space then follows from supervise learning. One of the commonly use strategies is to assign a fixe number of linguistic labels to each input variable [56]. Although this scheme is not ifficult to implement, it has two serious rawbacks: ffl The information in the given ata (patterns) is not fully exploite. The performance of the resulting system maybe poor if the input space partition is quite istinct from the true istribution of ata. Optimizing output space partition alone is not sufficient. ffl The scheme suffers from the curse of imensionality. If each input variable is allocate m fuzzy sets, a fuzzy system with n inputs an one output nees on the orer of m n rules. Various ata epenent partition methos have been propose to alleviate these rawbacks. Dickerson et al. [] use an unsupervise competitive learning algorithm to fin the mean an covariance matrix of each ata cluster in the input/output space. Each ata cluster forms an ellipsoial fuzzy rule patch. Thawonmas et al. [5] escribe a simple
2 heuristic for unsupervise iterative ata partition. At each iteration, an input imension, which gives the maximum intra-class ifference between the maximum an the minimum values of the ata along that imension, is selecte. The partition is performe perpenicular to the selecte imension. Two ata group representations, hyper-box an ellipsoial representations, are compare. In [4], a supervise clustering algorithm is use to group input/output ata pairs into a preetermine number of fuzzy clusters. Each cluster correspons to a fuzzy IF-THEN rule. Univariate membership functions can then be obtaine by projecting fuzzy clusters onto corresponing coorinate axes. Although a fuzzy partition can generate fuzzy rules, results are usually very coarse with many parameters to be learne an tune. Various optimization techniques are propose to solve this problem. Genetic algorithms [9], [49], [59] an artificial neural networks [], [4], [6] are two of the most popular an effective approaches. B. Generalization Performance After going through the long journey of structure ientification an parameter estimation, can we infer that we get a goo fuzzy moel? In orer to raw a conclusion, the following two questions must be answere: ffl How capable can a fuzzy moel be? ffl How well can the moel, built on finite amount of ata, capture the concept unerlying the ata? The first question coul be answere from the perspective of function approximation. Several types of fuzzy moels are proven to be universal approximators" [8], [38], [58], [63], i.e., we can always fin a moel from a given fuzzy moel set so that the moel can uniformly approximate any continuous function on a compact omain to any egree of accuracy. The secon question is about the generalization performance, which is closely relate to several well-known problems in the statistics an machine learning literature, such as the structural risk minimization [5], the bias variance ilemma [5], an the overfitting phenomena []. Loosely speaking, a moel, buil on finite amount of given ata (training patterns), generalizes the best if the right traeoff is foun between the training (learning) accuracy an the capacity" of the moel set from which the moel is chosen. On one han, a low capacity" moel set may not contain any moel that fits the training ata well. On the other han, too much freeom may eventually generate a moel behaving like a refine look-up-table: perfect for the training ata but (maybe) poor on generalization. Researchers in the fuzzy systems community attempt to tackle this problem with roughly two approaches:() use the iea of cross-valiation to select a moel that has the best ability to generalize [46]; () focus on moel reuction, which is usually achieve by rule base reuction [43], [6], to simplify the moel. In statistical learning literature, the Vapnik-Chervonenkis (VC) theory [5], [53] provies a general measure of moel set complexity. Base on the VC theory, support vector machines (SVM) [5], [53] can be esigne for classification problems. In many real applications, the SVMs give excellent performance []. C. Our Approach However, no effort has been mae to analyze the relationship between fuzzy rule-base classification systems an kernel machines. The work presente here attempts to brige this gap. We relate aitive fuzzy systems to kernel machines, an emonstrate that, uner a general assumption on membership functions, an aitive fuzzy rule-base classification system can be constructe irectly from the given training samples using the support vector learning approach. Such aitive fuzzy rule-base classification systems are name the positive efinite fuzzy classifiers (PDFC). Using the SVM approach to buil PDFCs has following avantages: ffl Fuzzy rules are extracte irectly from the given training ata. The number of fuzzy rules is irrelevant to the imension of the input space. It is no greater (usually much less) than the number of training samples. In this sense, we avoi the curse of imensionality". ffl The VC theory establishes the theoretical founation for goo generalization of the resulting PDFC. ffl The global solution of an SVM optimization problem can be foun efficiently using specifically esigne quaratic programming algorithms. The remainer of the paper is organize as follows. In Section II, a brief overview of the VC theory an SVMs is presente. Section III escribes the PDFCs, a class of aitive fuzzy rule-base classification systems with positive efinite membership functions, prouct fuzzy conjunction operator, an center of area (COA) efuzzification with thresholing unit. We show that the ecision bounary of a PDFC can be viewe as ahyperplane in the feature space inuce by the kernel. In Section IV, an algorithm is provie to construct PDFC: first, an optimal separating hyperplane is foun using the support vector learning approach, fuzzy rules are then extracte from the hyperplane. Section V emonstrates the experiments we have performe, an provies the results. A escription of the relationship between PDFCs an SVMs with raial basis function (RBF) kernels an a iscussion on the avantages of relating fuzzy systems to kernel machines are presente in Section VI. An finally, we conclue in Section VII together with a iscussion of future work. II. VC Theory an Support Vector Machines This section presents the basic concepts of the VC theory an SVMs. For gentle tutorials of VC theory an SVMs, we refer intereste reaers to Burges [5] an Müller et al. [35]. More exhaustive treatments can be foun in the books by Vapnik [5], [53]. A. VC Theory Let's consier a two-class classification problem of assigning class label y f+; g to input feature vector ~x R n. We are given a set of training samples f(~x ;y ); ;(~x l ;y l )gρr n f+; g that are rawn inepenently from some unknown cumulative probability istribution P (~x; y). The learning task is formulate as fining a machine (a function f : R n! f+; g) that
3 3 best" approximates the mapping generating the training set. In orer to make learning feasible, we nee to specify a function space, H, from which a machine is chosen. An ieal measure of generalization performance for a selecte machine f is expecte risk (or the prob- of misclassification) efine as R P (~x;y) (f) = Rability R n f+; g I ff (~x)6=yg(~x; y)p (~x; y) where I A (z) is an inicator function such that I A (z) = for all z A, an I A (z) = for all z = A. Unfortunately, this is more an elegant way of writing the error probability than practical usefulness because P (~x; y) is usually unknown. However, there is a family of bouns on the expecte risk, which emonstrates funamental principles of builing machines with goo generalization. Here we present one result from the VC theory ue to Vapnik an Chervonenkis [54]: given a set of l training samples an function space H, with probability, for any f H the expecte risk is boune above by R P (~x;y) (f)» R emp (f)+ s h(+ln l h ) ln 4 l for any istribution P (~x; y) on R n f+; g. Here R emp (f) iscalle the empirical risk (or training error), h is a non-negative integer calle the Vapnik Chervonenkis (VC) imension. The VC imension is a measure of the capacity ofaf+; g-value function space. Given a training set of size l, () emonstrates a strategy to control expecte risk by controlling two quantities: the empirical risk an the VC imension. Next we will iscuss an application of this iea: the SVM learning strategy. B. Support Vector Machines Let f(~x ;y ); ; (~x l ;y l )gρr n f+; g be a training set. The SVM learning approach attempts to fin a canonical hyperplane f~x R n : h ~w; ~xi + b =; ~w R n ; b Rg that maximally separates two classes of training samples. Here h ; i is an inner prouct in R n. The corresponing ecision function (or classifier) f : R n!f+; g is then given by f(~x) = sgn (h ~w;~xi + b). Consiering that the training set may not be linearly separable, the optimal ecision function is foun by solving the following quaratic program: minimize J( ~w; ~ ο)= h ~w; ~wi + C lx subject to i= () ο i () y i (h ~w; ~x i i + b) ο i ; ο i ; i =; ;l where ο ~ =[ο ; ;ο l ] T are slack variables introuce to allow for the possibility of misclassification of training samples, C>is some constant. How oes minimizing () relate to our ultimate goal of optimizing the generalization? To answer this question, we nee to introuce a theorem about the VC imension of canonical hyperplanes [5], which is state A hyperplane f~x R n : h ~w; ~xi + b =; ~w R n ; b Rg is calle canonical for a given training set if an only if ~w an b satisfy min i=; ;l jh ~w; ~x i i + bj =. as follows. For a given set of l training samples, let R be the raius of the smallest ball containing all l training samples, an Λ ρ R n R be the set of coefficients of canonical hyperplanes efine on the training set. The VC imension h of the function space H = ff(~x) = sgn (h ~w; ~xi + b) :(~w; b) Λ; k ~wk»a; ~x R n g is boune above by h» min R A ;n +. Thus minimizing the h ~w; ~wi term in () amounts to minimizing the VC imension of H, therefore P the secon term of the boun (). l On the other han, ο i= i is an upper boun on the number of misclassifications on the training set,thus controls the empirical risk term in (). For an aequate positive constant C, minimizing () can inee ecrease the upper boun on the expecte risk. Applying the Karush-Kuhn-Tucker complementarity conitions, one can show that a ~w, which minimizes (), P l can be written as ~w = y i= iff i ~x i. This is calle the ual representation of ~w. An ~x j with nonzero ff j is calle a support vector. Let S be the inex set of support vectors, then the optimal ecision function becomes f(~x) = sgn ψ X is y i ff i h~x; ~x i i + b where the coefficients ff i can be foun by solving the ual problem of (): maximize W (~ff) = subject to lx i= ff i lx i;j= C ff i ; i =; ;l; an! (3) ff i ff j y i y j h~x i ;~x j i(4) lx i= ff i y i =: The ecision bounary given by (3) is a hyperplane in R n. More complex ecision surfaces can be generate by employing a nonlinear mapping Φ : R n! F to map the ata into a new feature space F (usually has imension higher than n), an fining the maximal separating hyperplane in F. Note that in (4) ~x i never appears isolate but always in the form of inner prouct h~x i ;~x j i. This implies that there is no nee to evaluate the nonlinear mapping Φ as long as we know the inner prouct in F for any given ~x; ~z R n. So for computational purposes, instea of efining Φ : R n! F explicitly, a function K : R n R n! R is introuce to irectly efine an inner prouct in F. Such a function K is also calle the Mercer kernel [], [5], [53]. Substituting K(~x i ;~x j ) for h~x i ;~x j i in (4) prouces a new optimization problem maximize W (~ff) = subject to lx i= ff i lx i;j= C ff i ; i =; ;l; an ff i ff j y i y j K(~x i ;~x j (5) ) lx i= ff i y i =: A training feature vector ~x i is misclassifie if an only if ο i < or equivalently ο i >. Let t be the number of misclassifications on the training set. We have t» P l i= ο i since ο i for all i an ο i > for misclassifications.
4 4 Solving (5) for ~ff gives a ecision function of the form f(~x) = sgn ψ X is y i ff i K(~x; ~x i )+b! ; (6) whose ecision bounary is a hyperplane in F, an translates to nonlinear bounaries in the original space. Several techniques of solving quaratic programming problems arising in SVM algorithms are escribe in [3], [5], [37]. Details of calculating b can be foun in [7]. III. Aitive Fuzzy Rule-Base Classification Systems an Positive Definite Fuzzy Classifiers This section starts with a short escription of an aitive fuzzy moel, base on which binary fuzzy classifiers an stanar binary fuzzy classifiers are efine. We then introuce the concept of positive efinite functions, an efine positive efinite fuzzy classifiers (PDFC) accoringly. Finally, some nice properties of the PDFCs are iscusse. A. Aitive Fuzzy Rule-Base Classification Systems Depening on the THEN-part of fuzzy rules an the way to combine fuzzy rules, a fuzzy rule-base classification system can take many ifferent forms [9]. In this paper, we consier the aitive fuzzy rule-base classification systems (or in short fuzzy classifier) with constant THEN-parts. Although the iscussions in this section an Section IV focus on binary classifiers. The results can be extene to multiclass problems by combining several binary classifiers. Consier a fuzzy moel with m fuzzy rules of the form Rule j : IF A j AND A j AND AND A n j THEN b j (7) where A k j is a fuzzy set with membership function ak j : R! [; ], j = ; ;m, k = ; ;n, b j R. If we choose prouct as the fuzzy conjunction operator, aition for fuzzy rule aggregation (that is what aitive" means), an COA efuzzification, then the moel becomes a special form of the Takagi-Sugeno (TS) fuzzy moel [48], an the input output mapping, F : R n! R, of the moel is efine as P m Q j= F (~x) = b n j k= ak j (x k ) Q n k= ak j (x (8) k) P m j= where ~x = [x ; ;x n ] T R n is P the input. Note that (8) is not well-efine on R n m Q if n j= k= ak j (x k) = for some ~x R n, which coul happen if the input space is not wholly covere by fuzzy rule patches". However, there are several easy fixes for this problem. For example, Qwe can force the output to some constant when n k= ak j (x k) =, or a a fuzzy rule so that the P m j= enominator P m j= Q n k= ak j (x k) > for all ~x R n. Here we take the secon approach for analytical simplicity. The following rule is ae: Rule : IF A AND A AND AND A n THEN b (9) where b R, the membership functions a k (x k ) for k = ; ;n an any x k R. Consequently, the input output mapping becomes F (~x) = b + P m j= b j Q n k= ak j (x k) + P m j= Q n k= ak j (x k) : () A classifier associates class labels with input features, i.e., it is essentially a mapping from the input space to the set of class labels. In binary case, thresholing is one of the simplest ways to transform F (~x) to class labels + or. In this article, we are intereste in binary fuzzy classifiers efine as follows. Definition III.: (Binary Fuzzy Classifier) Consier a fuzzy system with m+ fuzzy rules where Rule is given by (9), Rule j; j =; ;m, has the form of (7). If the system uses prouct for fuzzy conjunction, aition for rule aggregation, an COA efuzzification, then the system inuces a binary fuzzy classifier, f, with ecision rule, f(~x) = sign (F (~x)+t) () where F (~x) is efine in (), t R is a threshol. The following corollary states that we can assume t = without loss of generality. Corollary III.: For any binary fuzzy classifier given by Definition III. with nonzero threshol t, there exists a binary fuzzy classifier that has the same ecision rule but zero threshol. Proof: Given a binary fuzzy classifier, f, with t 6=. From () an (), we have f(~x) = sign ψ (b + t)+ P m j= (b j + t) Q n + P m j= Q n k= ak j (x k) k= ak j (x k) which is ientical to the ecision rule of a binary fuzzy classifier with b j + t as the THEN-part of jth fuzzy rule (j =; ;m) an zero threshol. The membership functions for a binary fuzzy classifier efine above coul be any function from R to [; ]. However, too much flexibility on the moel coul make effective learning (or training) unfeasible. So we narrow our interests to a class of membership functions, which are generate from location transformation of reference functions [], an the classifiers efine on them. Definition III.3: (Reference Function, []) A function μ : R! [; ] isareference function if an only if ffl μ(x) =μ( x); ffl μ() = ; an ffl μ is nonincreasing on [; ). Definition III.4: (Stanar Binary Fuzzy Classifier) A binary fuzzy classifier given by Definition III. is a stanar binary fuzzy classifier if for the kth input, k f; ;ng, the membership functions, a k j : R! [; ], j = ; ;m, are generate from a reference function a k through location transformation, i.e., a k j (x k)=a k (x k zj k) for some location parameter zj k R. A simple example will be helpful for illustrating an unerstaning the basic iea of the above efinition. Let's! ;
5 5 Degree of Membership Degree of Membership a (x ) a (x ) a (x ) a (x ) Input Variable x a a (x ) (x ) a (x ) a 3 (x ) Input Variable x Fig.. IF-part membership functions for a stanar binary fuzzy classifier. Two thick curves enote the reference functions a (x ) an a (x ) for inputs x an x, respectively. a (x )=a (x + 6), a (x )=a (x + 3), an a 3 (x )=a (x 5) are membership functions associate with x. a (x )=a (x + 5), a (x )=a (x 3), an a 3 (x )=a (x 7) are membership functions associate with x. Clearly, a (x ), a (x ), an a 3 (x ) are location transforme versions of a (x ), an a (x ), a (x ), an a 3 (x ) are location transforme versions of a (x ). consier a stanar binary fuzzy classifier with two inputs (x an x ) an three fuzzy rules (excluing Rule ) Rule : IF A AND A THEN b Rule : IF A AND A THEN b Rule 3 : IF A 3 AND A 3 THEN b 3 where a (x ) = e x 4 an a (x ) = max( j x j; ) are 3 reference functions for inputs x an x, respectively, a k j is the membership function of A k j, j =; ; 3, k =;. As shown in Figure, the membership functions a, a, an a 3 belong to one location family generate by a, the membership functions a, a, an a 3 belong the other location family generate by a. Corollary III.5: The ecision rule of a stanar binary fuzzy classifier given by Definition III.4 can be written as f(~x) = sign m j= b j K(~x; ~z j )+b A () where ~x =[x ;x ; ;x n ] T R n, ~z j =[zj ;z j ; ;zn j ] T R n contains the location parameters of a k j ; k = ; ;n, K : R n R n! [; ] is a translation invariant kernel 3 3 Akernel K(~x;~z) is translation invariant if K(~x; ~z) = K(~x ~z), i.e., it epens only on ~x ~z, but not on ~x an ~z themselves. efine as K(~x; ~z j )= ny k= a k (x k z k j ) : (3) Proof: From (), (), an Corollary III., the ecision rule of a binary fuzzy classifier is f(~x) = sign ψ P m Q b + P b n j= j k= ak j (x k ) m Q + n j= k= ak j (x k) P m Q Since + n j= k= ak j (x k) >, we have mx f(~x) = sign@ b + j= b j n Y k=! a k j (x k ) A : (4) From the efinition of stanar binary fuzzy classifier, a k j (x k ) = a k (x k z k j ), k = ; ;n, j = ; ;m. Substituting them into (4) completes the proof. The ecision rule (3) is not merely a ifferent representation form of (), it provies us with a novel perspective on binary fuzzy classifiers (Section III-B, III-C), an accoringly leas to a new esign algorithm for binary fuzzy classifiers (Section IV). B. Positive Definite Fuzzy Classifiers One particular kin of kernel, Mercer kernel, has receive consierable attention in the machine learning literature [], [6], [5], [53] because it is an efficient way of extening linear learning machines to nonlinear ones. Is the kernel efine by (3) a Mercer kernel? Before answering this question, we first quote a theorem. Theorem III.6: (Mercer Theorem [], [3]) Let X be a compact subset of R n. Suppose K isacontinuous symmetric function such that the integral operator T K : L (X)! L (X), Z (T K f)( ) = X K( ;~x)f(~x)~x is positive, that is Z K(~x; ~z)f(~x)f(~z)~x~z (5) X X for all f L (X). Then we can expan K(~x; ~z) in a uniformly convergent series (on X X) in terms of T K 's eigen-functions ffi i L (X), normalize in such a way that kffi i k L =, an positive associate eigenvalues j >, K(~x; ~z) = X i= k ffi i (~x)ffi i (~z) : (6) The positivity conition (5) is also calle the Mercer conition. A kernel satisfying the Mercer conition is name a Mercer kernel. An equivalent form of the Mercer conition, which proves most useful in constructing Mercer kernels, is given by the following lemma []. Lemma III.7: (Positivity Conition for Mercer Kernels []) For a kernel K : R n R n! R, the Mercer conition (5) hols if an only if the matrix [K(~x i ;~x j )] :
6 6 is positive semi-efinite for all choices of points f~x ; ;~x n gρx an all n =; ;. For most nontrivial kernels, irectly checking the Mercer conitions in (5) or Lemma III.7 is not an easy task. Nevertheless, for the class of translation invariant kernels, to which the kernels efine by (3) belong, there is an equivalent yet practically more powerful criterion base the spectral property of the kernel [45]. Lemma III.8: (Mercer Conitions for Translation Invariant Kernels, Smola et al. [45]) Atranslation invariant kernel K(~x; ~z) =K(~x ~z) is a Mercer kernel if an only if the Fourier transform R n n F[K](~!) = (ß) n Z R n K(~x)e ih~!;~xi ~x is nonnegative. Kernels efine by (3) o not, in general, have nonnegative Fourier transforms. However, if we assume that the reference functions are positive efinite functions, which are efine by the following efinition, then we o get a Mercer kernel (given in Theorem III.). Definition III.9: (Positive Definite Function [8]) A function f : R! R is sai to be a positive efinite function if the matrix [f(x i x j )] R n n is positive semiefinite for all choices of points fx ; ;x n gρ R an all n =; ;. Corollary III.: A function f : R! R is positive efinite if an only if the Fourier transform F[f](!) = p ß Z f(x)e i!x x is nonnegative. Proof: Given any function f : R! R, we can efine a translation invariant kernel K : R R! R as K(x; z) =f(x z) : From Lemma III.8, K is a Mercer kernel if an only if the Fourier transform of f is nonnegative. Thus from Lemma III.7 an Definition III.9, we conclue that f is a positive efinite function if an only if its Fourier transform is nonnegative. Theorem III.: (Positive Definite Fuzzy Classifier, PDFC) A stanar binary classifier given by Definition III.4 is calle a positive efinite fuzzy classifier (PDFC) if the reference functions, a k : R! [; ]; k = ; ;n, are positive efinite functions (they o not nee to be the same function). The translation invariant kernel (3) is then a Mercer kernel. Proof: From Lemma III.8, it suffices to show that the translation invariant kernel efine by (3) has nonnegative Fourier transform. Rewrite (3) as K(~x; ~z) =K(~u) = ny k= a k (u k ) where ~x = [x ; ;x n ] T, ~z = [z ; ;z n ] T R n, ~u = [u ; ;u n ] T = ~x ~z. Then F[K](~!) = = = (ß) n (ß) n ny k= Z Z R n e ih~!;~ui ny R n k= ny k= a k (u k )~u a k (u k )e i! ku k ~u p ß ZR ak (u k )e i! ku k u k which is nonnegative since a k ;k = ; ;n, are positive efinite functions (Corollary III.). It might seem that the positive efinite assumption on reference functions is quite restrictive. In fact, many commonly use reference functions are inee positive efinite. An incomplete list is given in Table I. More generally, the weighte summation (with positive weights) an the prouct of positive efinite functions are still positive efinite (a irect conclusion from the linearity an prouct/convolution properties of the Fourier transform). So we can get a class of positive efinite membership functions from those liste above. It is worthwhile noting that the asymmetric triangle an the trapezoi membership functions are not positive efinite. C. The PDFC an Mercer Features Recall the expansion (6) given by the Mercer Theorem. Let F be an l space. If we efine a nonlinear mapping Φ:X! F as Φ(~x) =[ p ffi (~x); ; p k ffi i (~x); ] T ; (7) an efine an inner prouct in F as Ω [u ; ;u i ; ] T ; [v ; ;v i ; ] Tff F = X then (6) becomes i= u i v i ; (8) K(~x; ~z) =hφ(~x); Φ(~z)i F : (9) Φ(~x) F is sometimes referre to as the Mercer features. Equation (9) isplays a nice property of Mercer kernels: a Mercer kernel implicitly efines a nonlinear mapping Φ such that the kernel computes the inner prouct in the space Φ maps to. Therefore a Mercer kernel enables a classifier, in the form of (), to work on Mercer features (which usually resie in a space with imension much higher than that of the input space) without explicitly evaluating the Mercer features (which is computationally very expensive). The following theorem illustrates the relationship between the PDFCs an Mercer features. Theorem III.: Given n positive efinite reference functions, a k : R! [; ], k =; ;n, an a compact set X ρ R n, we efine a Mercer kernel K(~x; ~z) = Q n k= ak (x k z k ) where ~x = [x ; ;x n ] T ;~z = [z ; ;z n ] T X. Let F be an l space, Φ : X! F be the nonlinear mapping
7 7 TABLE I A list of positive efinite reference functions an their Fourier transform. Reference Function Fourier Transform Symmetric Triangle μ(x) = max( jxj ; ); > F[μ](!) = p sin (! ) ß (! ) Gaussian μ(x) =e x ; > F[μ](!) = p e! 4 q Cauchy μ(x) = +x ß ; > F[μ](!) = Laplace μ(x) =e jxj ; > F[μ](!) = Hyperbolic Secant μ(x) = e x +e x ; > F[μ](!) = Square sinc q ß μ(x) = sin (x) x ; > F[μ](!) = max( q p j!j e +! ß ß! e ß! +e q ß ( j!j ); ) given by (7), an h ; i F be an inner prouct in F efine by (8). Given a set of points f~z ; ;~z m g ρ X, we efine a subspace W ρ F as W = SpanfΦ(~z ); ; Φ(~z m )g, an a function space H on F as H = fh : h(~u) = sign(h ~w;~ui F + b ); ~w W ; ~u F; b Rg. Then we have the following results:. For any g H, there exists a PDFC with a k ; k = ; ; n,asreference functions such that the ecision rule, f, of the PDFC satisfies f(~x) =g(φ(~x)); 8~x X.. For any PDFC using a k ; k = ; ;n, as reference functions, if ~z j contains location parameters of the IF-part membership functions associate with the jth fuzzy rule for j =; ;m (as efine incorollary III.5), then there exists g H such that the ecision rule, f, of the PDFC satisfies f(~x) =g(φ(~x)); 8~x X. Proof:. Given g H, we have g(~u) = sign(h ~w;~ui F + b ). Since ~w W, it P can be written as a linear combination of Φ(~z j )'s, m i.e., ~w = j= b jφ(~z j ). Thus g(~u) becomes g(~u) = sign = sign * j= m j= b j Φ(~z j );~u + F + b A b j hφ(~z j );~ui F + b A : Now we can efine a PDFC using a k ; k =; ;n, as reference functions. For j =; ;m, let ~z j contain location parameters of the IF-part membership functions associate with the jth fuzzy rule (as efine in Corollary III.5), an b j be the THEN-part of the jth fuzzy rule. The THENpart of Rule is b. Then from () an (9), the ecision rule is f(~x) = sign = sign m j= b j K(~x; ~z j )+b A j= m b j hφ(~x); Φ(~z j )i F + b A Clearly, f(~x) =g(φ(~x)); 8~x X.. For a PDFC escribe in the theorem, let b j be the THEN-part of the jth fuzzy rule, an b be the THENpart of Rule. Then from () an (9), the ecision rule is f(~x) = sign = sign m j= * j= b j hφ(~x); Φ(~z j )i F + b A b j Φ(~z j ); Φ(~x) + F + b A : () Let ~w = P m j= b jφ(~z j ) an g(~u) = sign(h ~w;~ui F + b ), then g H an f(~x) =g(φ(~x)); 8~x X. This completes the proof. Remark III.3: The compactness of the input omain X is require for purely theoretical reason: it ensures that the expansion (6) can be written in a form of countable sum, thus the nonlinear mapping (7) can be efine. In practice, we on't nee to worry about it provie that all input features (both training an testing) are within certain range (which can be satisfie via ata preprocessing). Consequently, it is reasonable to assume that ~z j is also in X for j =; ; m because this essentially requires that all fuzzy rule patches" center insie the input omain. Remark III.4: Since g(~u) = sign(h ~w;~ui F + b) =efines a hyperplane in F, Theorem III. relates the ecision bounary of a PDFC inxto a hyperplane in F. The theorem implies that given any hyperplane in F, if its orientation (normal irection pointe by ~w) is a linear combination of vectors that have preimage (uner Φ) inx, then the hyperplane transforms to a ecision bounary of a PDFC. Conversely, given a PDFC, one can fin a hyperplane in F that transforms to the ecision bounary of the given PDFC. Therefore, we can alternatively consier the ecision bounary of a PDFC as a hyperplane in the feature space F, which correspons to a nonlinear ecision bounary in X. Constructing a PDFC is then converte to fining a hyperplane in F. Remark III.5: A hyperplane in F is efine by its normal irection ~w an the istance to the origin, which is etermine by b for fixe ~w. Accoring to P the proof of m Theorem III., ~w an b are efine as ~w = b j= jφ(~z j ) an b = b, respectively, where f~z ; ;~z m g ρ X is the set of location parameters of the IF-part fuzzy rules, an fb ; ;b m gρr is the set of constants in the THEN-part fuzzy rules. This implies that the IF-part an THEN-part
8 8 of fuzzy rules play ifferent roles in moeling the hyperplane. The IF-part parameters, f~z ; ;~z m g, efines a set of feasible orientations, W = SpanfΦ(~z ); ; Φ(~z m )g, of the hyperplane. The P THEN-part parameters fb ; ;b m g m select an orientation, b j= jφ(~z j ),from W. The istance to the origin is then etermine by the THEN-part of Rule, i.e., b = b. IV. An SVM Approach to Buil PDFCs A PDFC with n inputs an m, which is unknown, fuzzy rules is parameterize by n, possibly ifferent, positive efinite reference functions (a k : R! [; ], k = ; :::n), a set of location parameters (f~z ; ;~z m g ρ X) for the membership functions of the IF-part fuzzy rules, an a set of real numbers (fb ; ;b m g ρ R) for the constants in the THEN-part fuzzy rules. Which reference functions to choose is an interesting research topic by itself [33]. But it is out of the scope of this article. Here we assume that the reference functions a i : R! [; ]; i =; ;n are preetermine. So the remaining question is how to fin a set of fuzzy rules (f~z ; ;~z m g an fb ; ;b m g) from the given training samples f(~x ;y ); ;(~x l ;y l )gρx f+; g so that the PDFC has goo generalization. As given in (3), for a PDFC, a Mercer kernel can be constructe from the positive efinite reference functions. The kernel implicitly efines a nonlinear mapping Φ that maps X into a kernel-inuce feature space F. Theorem III. states that the ecision rule of a PDFC can be viewe as a hyperplane in F. Therefore, the original question transforms to: given training samples f(φ(~x );y ); ;(Φ(~x l );y l )gρf f+; g, how to fin a separating hyperplane in F that yiels goo generalization, an how to extract fuzzy rules from the obtaine optimal hyperplane. We have seen in Section II-B that the SVM algorithm fins a separating hyperplane (in the input space or the kernel inuce feature space) with goo generalization by reucing the empirical risk an, at the same time, controlling the hyperplane margin. Thus we can use the SVM algorithm to fin an optimal hyperplane in F. Once we get such a hyperplane, fuzzy rules can be easily extracte. The whole proceure is escribe by the following algorithm. Algorithm IV.: SVM Learning for PDFC Inputs: Positive efinite reference functions a k (x k ), k = ; ; n, associate with n input variables, an a set of training samples f(~x ;y ); ;(~x l ;y l )g. Outputs: A set of fuzzy rules parameterize by~z j, b j, an m. ~z j (j =; ;m) contains the location parameters of the IF-part membership functions of the jth fuzzy rule, b j (j =; ;m) is the THEN-part constant of the jth fuzzy rule, an m + is the number of fuzzy rules. Steps: Construct a Mercer kernel, K, from the given positive efinite reference functions accoring to (3). Construct an SVM to get a ecision rule of the form (6): ) Assign some positive number to C, an solve the quaratic program efine by (5) to get the Lagrange multipliers ~ff. ) Fin b (etails can be foun in, for example, [7]). 3 Extracting fuzzy rules from the ecision rule of the SVM: b ψ b j ψ FOR i =TO l IF ff i > ~z j ψ ~x i b j ψ y i ff i j ψ j + END IF END FOR m ψ j It is straightforwar to check that the ecision rule of the resulting PDFC is ientical to (6). Once reference functions are fixe, the only free parameter in the above algorithm is C. Accoring to the optimization criterion in (), C weights the classification error versus the upper boun on the VC imension. Another way of interpreting C is that it affects the sparsity of ~ff (the number of nonzero entries in ~ff) [4]. Unfortunately, there is no general rule for picking C. Typically, a range of values of C shoul be trie before the best one can be selecte. The above learning algorithm has several nice properties: ffl The shape of the reference functions an C parameter are the only prior information neee by the algorithm. ffl The algorithm automatically generates a set of fuzzy rules. The number of fuzzy rules is irrelevant to the imension of the input space. It equals the number of nonzero Lagrange multipliers. In this sense, the curse of imensionality" is avoie. In aition, ue to the sparsity of ~ff, the number of fuzzy rules is usually much less than the number of training samples. ffl Each fuzzy rule is parameterize by a training sample (~x j ;y j ) an the associate nonzero Lagrange multiplier ff j where ~x j specifies the location of the IF-part membership functions, an y j ff j gives the THEN-part constant. ffl The global solution for the optimization problem can always be foun efficiently because of the convexity of the objective function an of the feasible region. Algorithms esigne specifically for the quaratic programming problems in SVMs make large-scale training (for example ; samples with 4; input variables) practical [3], [5], [37]. The computational complexity of classification operation is etermine by the cost of kernel evaluation an the number of support vectors. ffl Since the goal of optimization is to lower an upper boun on the expecte risk (not just the empirical risk), the resulting PDFC usually has goo generalization, which will be emonstrate in the coming section. V. Experimental Results Using Algorithm IV., we esign PDFCs with ifferent choices of reference functions 4. Base on the IRIS ata 4 The SVMLight [3] is use to implement the SVMs. This software is available at
9 9 set [3] an the USPS ata set 5, we evaluate the performance of PDFCs in terms of generalization (classification rate) an number of fuzzy rules. Comparisons with fuzzy classifiers escribe in [9] an results in [35] are also provie. A. IRIS Data Set The IRIS ata set consists of 5 samples belonging to 3 classes of iris plants namely Setosa, Versicolor, an Verginica. Each class contains 5 samples, an each sample is represente by four input features (sepal length, sepal with, petal length, an petal with) an the associate class label. The Setosa class is linearly separable from the Versicolor an Verginica classes, the latter are not linearly separable from each other. Clearly, this is a multi-class classification problem. But the Algorithm IV. only works for binary classifiers. So we esign three PDFCs, each of which separates one class from the rest two classes. The final preicte class label is ecie by the winner of three PDFCs, i.e., one with the maximum un-threshole output. The generalization performance is evaluate via -fol cross-valiation. The IRIS ata set is ranomly ivie into two subsets of equal size (75 samples). A PDFC is traine times, each time with a ifferent subset hel out as a valiation set. The classification rate is then efine as the number of correctly classifie valiation samples ivie by the size of the valiation set. We repeat the -fol cross-valiation times using ifferent partitions of the IRIS ata set, an compute the mean of the classification rates. This quantity is viewe as an estimation of the generalization performance. For all input variables, we use the Gaussian reference function given in Table I. PDFCs are esigne for ifferent values of C (in Algorithm IV.) an (of the Gaussian reference function). The mean classification rate an the mean number of fuzzy rules for ifferent values of C an are plotte in Figure. Separating the Setosa class from the other two classes is relatively easy since they are linearly separable. Consequently, as shown in Figure (a), the PDFCs generalizes perfectly for all values of C an. Separating the Versicolor (or Verginica) class from the rest two classes requires slightly more efforts. Figure (b) an (c) show that the generalization performance epens on the choices of C an. However, for ifferent values of C, we get very similar generalization performance by picking a proper value. In Figure (b), the maximum mean classification rates for C =,, an are 96:8% ( = ), 96:6% ( = ), an 96:45% ( = ), respectively. In Figure (c), the maximum mean classification rates for C =,, an are 96:57% ( = ), 6 96:6% ( = ), an 96:56% ( = ), respectively Moreover, Figure (), (e), an (f) emonstrate that C affects the number of fuzzy rules. For a fixe value of, a larger C value correspons to a smaller mean number of fuzzy rules. This complies with the observation in 5 The USPS ata set is available at the SVM literature that the number of support vectors ecreases when C is large. To get the final multi-class classifier, we nee to combine three PDFCs (each one is esigne to separate one class from the rest two classes). Here we use the following strategy: ffl Pick three PDFCs with the same C an values. ffl The preicte class label is given by the PDFC with the maximum un-threshole output. This strategy is by no means optimal. But it is very simple, an works very well. The results for C =, =,,, 4, an are summarize in Table II, where we also cite the 8 6 results reporte by Ishibuchi et al. [9]. In their approach, input features are normalize to the interval [; ], an each axis of the input space is assigne M uniformly istribute fuzzy sets. The rule weights an THEN-part of fuzzy rules are etermine by a rewar-an-punishment scheme [9]. Clearly, the number of fuzzy rules for such a system is M 4. From Table II we can see that the classification rates of classifiers built on PDFCs (with a range of values) are higher than those of the classifiers constructe from Ishibuchi's approach. Moreover, the number of fuzzy rules use by PDFCs is less than that of Ishibuchi's approach (except for M = which gives a less favorable classification rate of 9:73%). In aition, for a PDFC, the number of fuzzy rules is boune above by the number of training samples since each fuzzy rule is parameterize by a training sample with nonzero Lagrange multiplier. While, using Ishibuchi's approach, the number of fuzzy rules increases exponentially as M 4. B. USPS Data Set The USPS ata set contains 998 grayscale images of hanwritten igits. The images are size normalize to fit in a 6 6 pixel box while preserving their aspect ratio. The ata set is ivie into a training set of 79 samples an a testing set of 7 samples. For each sample, the input feature vector consists of 56 grayscale values. In this experiment, we test the performance of PDFCs for ifferent choices of reference functions given in Table I. For ifferent input variables, the reference functions are chosen to be ientical. Ten PDFCs are esigne, each of which separates one igit from the rest nine igits. The final preicte class label is ecie by the PDFC with the maximum un-threshole output. Base on the training set, we use 5-fol cross-valiation to etermine the parameter of reference functions an the C parameter in support vector learning (for each PDFC) where C takes values from f; ; g, an takes values from f : n =; ; g. For each pair of an C, the average n cross-valiation error is compute. The optimal an C are the values that gives the minimal mean cross-valiation error. Base on the selecte parameter, the PDFCs are constructe an evaluate on the testing set. The whole process is repeate 5 times. The mean classification rate (an the stanar eviation) on the testing set an the mean number of fuzzy rules (for one PDFC) are liste in Table III. For comparison purpose, we also cite the results
10 Mean Classification Rate.95 Mean Classification Rate Mean Classification Rate C= C= C= C= C= C= C= C= C= (a) Setosa versus the rest. (b) Versicolor versus the rest. (c) Verginica versus the rest C= C= C= C= C= C= C= 5 C= 5 C= Mean Number of Fuzzy Rules 8 Mean Number of Fuzzy Rules Mean Number of Fuzzy Rules () Setosa versus the rest. (e) Versicolor versus the rest. (f) Verginica versus the rest. Fig.. Performance of PDFCs in terms of the mean classification rate an the mean number of fuzzy rules for the IRIS ata set. (a) an () give the mean classification rate an the mean number of fuzzy rules, respectively, of PDFCs esigne to separate Setosa class from the other two classes. (b) an (e) give the mean classification rate an the mean number of fuzzy rules, respectively, of PDFCs esigne to separate Versicolor class from the other two classes. (c) an (f) give the mean classification rate an the mean number of fuzzy rules, respectively, of PDFCs esigne to separate Verginica class from the other two classes. TABLE II Mean classification rate r an mean number of fuzzy rules m (for multi-class classifiers). A comparison of multi-class classifiers constructe from three PDFCs an fuzzy classifiers built from Ishibuchi's approach using the IRIS ata set. Combining 3 PDFCs (C = ) Ishibuchi's Approach [9] = = = = =: M = M =3 M =4 M =5 M = r 95:46% 96:% 96:38% 95:97% 95:55% 9:73% 94:8% 94:53% 94:8% 95:37% m 6:49 47:5 35:46 8:695 6: TABLE III USPS ata set. Mean classification rate r ± stanar eviation an mean number of fuzzy rules m (for one PDFC) using ifferent reference functions. Gaussian Cauchy Laplace S-Triangle H-Secant Sinc r 95:% ± :3% 95:% ± :3% 94:7% ± :4% 95:% ± :3% 95:% ± :3% 95:% ± :% m
11 from [35]: linear SVM (classification rate 9:3%), k-nearest neighbor (classification rate 94:3%), SVM with Gaussian kernel (classification rate 95:8%), an virtual SVM (classification rate 97:%). Note that the Gaussian reference function correspons to the Gaussian RBF kernel use in the SVM literature. For the USPS ata, all six reference functions achieve similar classification rates. The number of fuzzy rules varies significantly. The number of fuzzy rules neee by the square sinc reference function is only 68:% of that neee by the Gaussian reference function. Compare with the linear SVM an k-nearest neighbor approach [35], the PDFCs achieve a better classification rate. SVMs can be improve by using prior knowlege. For instance the virtual SVM [35] performs better than current PDFCs. However, same approach can be applie to buil PDFCs, i.e., PDFCs can also benefit from the same prior knowlege. VI. Discussion A. The Relationship between PDFC kernels an RBF Kernels In the literature, it is well-known that a Gaussian RBF network can be traine via support vector learning using a Gaussian RBF kernel [4]. While the functional equivalence between fuzzy inference systems an Gaussian RBF networks is establishe in [] where the membership functions within each rule must be Gaussian functions with ientical variance. So connection between such fuzzy systems an SVMs with Gaussian RBF kernels can be establishe. The following iscussion compares the kernels efine by PDFCs an RBF kernels commonly use in SVMs. The kernels of PDFCs are constructe from positive efinite reference functions. These kernels are translation invariant, symmetric with respect to a set of orthogonal axes, an tailing off graually. In this sense, they appear to be very similar to the general RBF kernels [6]. In fact, the Gaussian reference function efines the Gaussian RBF kernel. However, in general, the kernels of PDFCs are not RBF kernels. Accoring to the efinition, an RBF kernel, K(~x; ~z), epens only on the norm of ~x ~z, i.e., K(~x ~z) =K RBF (k~x ~zk). It can be shown that for a kernel, K(~x; ~z), efine by (3) using symmetric triangle, Cauchy, Laplace, hyperbolic secant, or square sinc reference functions (even with ientical for all input variables), there exists ~x, ~x, ~z, an ~z such that k~x ~z k = k~x ~z k an K(~x ;~z ) 6= K(~x ;~z ). Moreover, a general RBF kernels (even if it is a Mercer kernel) may not be a PDFC kernel, i.e., it can not be in general ecompose as prouct of positive efinite reference functions. It is worth noting that the kernel efine by symmetric triangle reference functions is ientical to the B n -splines (or orer ) kernel that is commonly use in the SVM literature [55]. B. Avantages of Connecting Fuzzy Systems to Kernel Machines Kernel methos represent one of the most important irections both in theory an application of machine learning. While fuzzy classifier was regare as a metho that are cumbersome to use in high imensions or on complex problems or in problems with ozens or hunres of features (pp. 94, [3])." Establishing the connection between fuzzy systems an kernel machines has the following avantages: ffl A novel kernel perspective of fuzzy classifiers is provie. Through reference functions, fuzzy rules are relate to translation invariant kernels. Fuzzy inference on the IFpart of a fuzzy rule is equivalenttoevaluating the kernel. If the reference functions are restricte to the class of positive efinite functions then the kernel turns out to be a Mercer kernel, an the corresponing fuzzy classifier becomes a PDFC. Since Mercer kernel inuces a feature space, we can consier the ecision bounary of a PDFC asahyperplane in that space. The esign of a PDFC is then equivalent to fining an optimal" hyperplane. ffl A new approach to buil fuzzy classifiers is propose. Base on the link between fuzzy systems an kernel machines, a support vector learning approach is propose to construct PDFCs so that a fuzzy classifier can have goo generalization ability in a high imensional feature space. The resulting fuzzy rules are etermine by support vectors, corresponing Lagrange multipliers, an associate class labels. ffl It points out a future irection of applying techniques in fuzzy systems literature to improve the performance of kernel methos. The link between fuzzy systems an kernel machines implies that a class of kernel machines, such as those using Gaussian kernels, can be interprete by a set of fuzzy IF-THEN rules. This opens interesting connections between fuzzy rule base reuction techniques [43] an computational complexity issues in SVMs [6] an kernel PCA [4]: The computational complexity of an SVM scales with the number of support vectors. One way of ecreasing the complexity is to reuce the number of support-vector-like vectors in the ecision rule (6). For the class of kernels, which can be interprete by a set of fuzzy IF-THEN rules, this can be viewe as fuzzy rule base simplification. In kernel PCA [4], given a test point ~x, the kth nonlinear P principal component, fi k, is compute by fi k = l i= ffk i K(~x; ~x i) where l is the number of ata points in a given ata set (etails of calculating ff k i R can be foun in [4]). Therefore, the computational complexity of computing fi k scales with l. For the class of kernels iscusse in this paper, it is not ifficult to erive that fi k can be equivalently viewe as the output of an aitive fuzzy system using first orer moment efuzzification without thresholing unit. Here ~x i an ff k i parameterize the IF-part an THEN-part of the ith fuzzy rule (i =; ;l), respectively. As a result, fuzzy rule base reuction techniques may be applie to increase the spee of nonlinear principal components calculation.
IEEE TRANSACTIONS ON FUZZY SYSTEMS, VOL. 11, NO. 6, DECEMBER Support Vector Learning for Fuzzy Rule-Based Classification Systems
 TRANSACTIONS ON FUZZY SYSTEMS, VOL. 11, NO. 6, DECEMBER 2003 1 Support Vector Learning for Fuzzy Rule-Based Classification Systems Yixin Chen, Student Member,, and James Z. Wang, Member, Abstract To design
TRANSACTIONS ON FUZZY SYSTEMS, VOL. 11, NO. 6, DECEMBER 2003 1 Support Vector Learning for Fuzzy Rule-Based Classification Systems Yixin Chen, Student Member,, and James Z. Wang, Member, Abstract To design
Classifying Facial Expression with Radial Basis Function Networks, using Gradient Descent and K-means
 Classifying Facial Expression with Raial Basis Function Networks, using Graient Descent an K-means Neil Allrin Department of Computer Science University of California, San Diego La Jolla, CA 9237 nallrin@cs.ucs.eu
Classifying Facial Expression with Raial Basis Function Networks, using Graient Descent an K-means Neil Allrin Department of Computer Science University of California, San Diego La Jolla, CA 9237 nallrin@cs.ucs.eu
1 Surprises in high dimensions
 1 Surprises in high imensions Our intuition about space is base on two an three imensions an can often be misleaing in high imensions. It is instructive to analyze the shape an properties of some basic
1 Surprises in high imensions Our intuition about space is base on two an three imensions an can often be misleaing in high imensions. It is instructive to analyze the shape an properties of some basic
Particle Swarm Optimization Based on Smoothing Approach for Solving a Class of Bi-Level Multiobjective Programming Problem
 BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 17, No 3 Sofia 017 Print ISSN: 1311-970; Online ISSN: 1314-4081 DOI: 10.1515/cait-017-0030 Particle Swarm Optimization Base
BULGARIAN ACADEMY OF SCIENCES CYBERNETICS AND INFORMATION TECHNOLOGIES Volume 17, No 3 Sofia 017 Print ISSN: 1311-970; Online ISSN: 1314-4081 DOI: 10.1515/cait-017-0030 Particle Swarm Optimization Base
6 Gradient Descent. 6.1 Functions
 6 Graient Descent In this topic we will iscuss optimizing over general functions f. Typically the function is efine f : R! R; that is its omain is multi-imensional (in this case -imensional) an output
6 Graient Descent In this topic we will iscuss optimizing over general functions f. Typically the function is efine f : R! R; that is its omain is multi-imensional (in this case -imensional) an output
Learning convex bodies is hard
 Learning convex boies is har Navin Goyal Microsoft Research Inia navingo@microsoftcom Luis Raemacher Georgia Tech lraemac@ccgatecheu Abstract We show that learning a convex boy in R, given ranom samples
Learning convex boies is har Navin Goyal Microsoft Research Inia navingo@microsoftcom Luis Raemacher Georgia Tech lraemac@ccgatecheu Abstract We show that learning a convex boy in R, given ranom samples
Skyline Community Search in Multi-valued Networks
 Syline Community Search in Multi-value Networs Rong-Hua Li Beijing Institute of Technology Beijing, China lironghuascut@gmail.com Jeffrey Xu Yu Chinese University of Hong Kong Hong Kong, China yu@se.cuh.eu.h
Syline Community Search in Multi-value Networs Rong-Hua Li Beijing Institute of Technology Beijing, China lironghuascut@gmail.com Jeffrey Xu Yu Chinese University of Hong Kong Hong Kong, China yu@se.cuh.eu.h
Exercises of PIV. incomplete draft, version 0.0. October 2009
 Exercises of PIV incomplete raft, version 0.0 October 2009 1 Images Images are signals efine in 2D or 3D omains. They can be vector value (e.g., color images), real (monocromatic images), complex or binary
Exercises of PIV incomplete raft, version 0.0 October 2009 1 Images Images are signals efine in 2D or 3D omains. They can be vector value (e.g., color images), real (monocromatic images), complex or binary
Online Appendix to: Generalizing Database Forensics
 Online Appenix to: Generalizing Database Forensics KYRIACOS E. PAVLOU an RICHARD T. SNODGRASS, University of Arizona This appenix presents a step-by-step iscussion of the forensic analysis protocol that
Online Appenix to: Generalizing Database Forensics KYRIACOS E. PAVLOU an RICHARD T. SNODGRASS, University of Arizona This appenix presents a step-by-step iscussion of the forensic analysis protocol that
BIJECTIONS FOR PLANAR MAPS WITH BOUNDARIES
 BIJECTIONS FOR PLANAR MAPS WITH BOUNDARIES OLIVIER BERNARDI AND ÉRIC FUSY Abstract. We present bijections for planar maps with bounaries. In particular, we obtain bijections for triangulations an quarangulations
BIJECTIONS FOR PLANAR MAPS WITH BOUNDARIES OLIVIER BERNARDI AND ÉRIC FUSY Abstract. We present bijections for planar maps with bounaries. In particular, we obtain bijections for triangulations an quarangulations
The Reconstruction of Graphs. Dhananjay P. Mehendale Sir Parashurambhau College, Tilak Road, Pune , India. Abstract
 The Reconstruction of Graphs Dhananay P. Mehenale Sir Parashurambhau College, Tila Roa, Pune-4030, Inia. Abstract In this paper we iscuss reconstruction problems for graphs. We evelop some new ieas lie
The Reconstruction of Graphs Dhananay P. Mehenale Sir Parashurambhau College, Tila Roa, Pune-4030, Inia. Abstract In this paper we iscuss reconstruction problems for graphs. We evelop some new ieas lie
Image Segmentation using K-means clustering and Thresholding
 Image Segmentation using Kmeans clustering an Thresholing Preeti Panwar 1, Girhar Gopal 2, Rakesh Kumar 3 1M.Tech Stuent, Department of Computer Science & Applications, Kurukshetra University, Kurukshetra,
Image Segmentation using Kmeans clustering an Thresholing Preeti Panwar 1, Girhar Gopal 2, Rakesh Kumar 3 1M.Tech Stuent, Department of Computer Science & Applications, Kurukshetra University, Kurukshetra,
Here are a couple of warnings to my students who may be here to get a copy of what happened on a day that you missed.
 Preface Here are my online notes for my Calculus I course that I teach here at Lamar University. Despite the fact that these are my class notes, they shoul be accessible to anyone wanting to learn Calculus
Preface Here are my online notes for my Calculus I course that I teach here at Lamar University. Despite the fact that these are my class notes, they shoul be accessible to anyone wanting to learn Calculus
Non-homogeneous Generalization in Privacy Preserving Data Publishing
 Non-homogeneous Generalization in Privacy Preserving Data Publishing W. K. Wong, Nios Mamoulis an Davi W. Cheung Department of Computer Science, The University of Hong Kong Pofulam Roa, Hong Kong {wwong2,nios,cheung}@cs.hu.h
Non-homogeneous Generalization in Privacy Preserving Data Publishing W. K. Wong, Nios Mamoulis an Davi W. Cheung Department of Computer Science, The University of Hong Kong Pofulam Roa, Hong Kong {wwong2,nios,cheung}@cs.hu.h
Classical Mechanics Examples (Lagrange Multipliers)
 Classical Mechanics Examples (Lagrange Multipliers) Dipan Kumar Ghosh Physics Department, Inian Institute of Technology Bombay Powai, Mumbai 400076 September 3, 015 1 Introuction We have seen that the
Classical Mechanics Examples (Lagrange Multipliers) Dipan Kumar Ghosh Physics Department, Inian Institute of Technology Bombay Powai, Mumbai 400076 September 3, 015 1 Introuction We have seen that the
THE BAYESIAN RECEIVER OPERATING CHARACTERISTIC CURVE AN EFFECTIVE APPROACH TO EVALUATE THE IDS PERFORMANCE
 БСУ Международна конференция - 2 THE BAYESIAN RECEIVER OPERATING CHARACTERISTIC CURVE AN EFFECTIVE APPROACH TO EVALUATE THE IDS PERFORMANCE Evgeniya Nikolova, Veselina Jecheva Burgas Free University Abstract:
БСУ Международна конференция - 2 THE BAYESIAN RECEIVER OPERATING CHARACTERISTIC CURVE AN EFFECTIVE APPROACH TO EVALUATE THE IDS PERFORMANCE Evgeniya Nikolova, Veselina Jecheva Burgas Free University Abstract:
Lecture 1 September 4, 2013
 CS 84r: Incentives an Information in Networks Fall 013 Prof. Yaron Singer Lecture 1 September 4, 013 Scribe: Bo Waggoner 1 Overview In this course we will try to evelop a mathematical unerstaning for the
CS 84r: Incentives an Information in Networks Fall 013 Prof. Yaron Singer Lecture 1 September 4, 013 Scribe: Bo Waggoner 1 Overview In this course we will try to evelop a mathematical unerstaning for the
Loop Scheduling and Partitions for Hiding Memory Latencies
 Loop Scheuling an Partitions for Hiing Memory Latencies Fei Chen Ewin Hsing-Mean Sha Dept. of Computer Science an Engineering University of Notre Dame Notre Dame, IN 46556 Email: fchen,esha @cse.n.eu Tel:
Loop Scheuling an Partitions for Hiing Memory Latencies Fei Chen Ewin Hsing-Mean Sha Dept. of Computer Science an Engineering University of Notre Dame Notre Dame, IN 46556 Email: fchen,esha @cse.n.eu Tel:
Generalized Edge Coloring for Channel Assignment in Wireless Networks
 TR-IIS-05-021 Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu, Pangfeng Liu, Da-Wei Wang, Jan-Jan Wu December 2005 Technical Report No. TR-IIS-05-021 http://www.iis.sinica.eu.tw/lib/techreport/tr2005/tr05.html
TR-IIS-05-021 Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu, Pangfeng Liu, Da-Wei Wang, Jan-Jan Wu December 2005 Technical Report No. TR-IIS-05-021 http://www.iis.sinica.eu.tw/lib/techreport/tr2005/tr05.html
MANJUSHA K.*, ANAND KUMAR M., SOMAN K. P.
 Journal of Engineering Science an echnology Vol. 13, No. 1 (2018) 141-157 School of Engineering, aylor s University IMPLEMENAION OF REJECION SRAEGIES INSIDE MALAYALAM CHARACER RECOGNIION SYSEM BASED ON
Journal of Engineering Science an echnology Vol. 13, No. 1 (2018) 141-157 School of Engineering, aylor s University IMPLEMENAION OF REJECION SRAEGIES INSIDE MALAYALAM CHARACER RECOGNIION SYSEM BASED ON
Transient analysis of wave propagation in 3D soil by using the scaled boundary finite element method
 Southern Cross University epublications@scu 23r Australasian Conference on the Mechanics of Structures an Materials 214 Transient analysis of wave propagation in 3D soil by using the scale bounary finite
Southern Cross University epublications@scu 23r Australasian Conference on the Mechanics of Structures an Materials 214 Transient analysis of wave propagation in 3D soil by using the scale bounary finite
Generalized Edge Coloring for Channel Assignment in Wireless Networks
 Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu Institute of Information Science Acaemia Sinica Taipei, Taiwan Da-wei Wang Jan-Jan Wu Institute of Information Science
Generalize Ege Coloring for Channel Assignment in Wireless Networks Chun-Chen Hsu Institute of Information Science Acaemia Sinica Taipei, Taiwan Da-wei Wang Jan-Jan Wu Institute of Information Science
Throughput Characterization of Node-based Scheduling in Multihop Wireless Networks: A Novel Application of the Gallai-Edmonds Structure Theorem
 Throughput Characterization of Noe-base Scheuling in Multihop Wireless Networks: A Novel Application of the Gallai-Emons Structure Theorem Bo Ji an Yu Sang Dept. of Computer an Information Sciences Temple
Throughput Characterization of Noe-base Scheuling in Multihop Wireless Networks: A Novel Application of the Gallai-Emons Structure Theorem Bo Ji an Yu Sang Dept. of Computer an Information Sciences Temple
Modifying ROC Curves to Incorporate Predicted Probabilities
 Moifying ROC Curves to Incorporate Preicte Probabilities Cèsar Ferri DSIC, Universitat Politècnica e València Peter Flach Department of Computer Science, University of Bristol José Hernánez-Orallo DSIC,
Moifying ROC Curves to Incorporate Preicte Probabilities Cèsar Ferri DSIC, Universitat Politècnica e València Peter Flach Department of Computer Science, University of Bristol José Hernánez-Orallo DSIC,
Kinematic Analysis of a Family of 3R Manipulators
 Kinematic Analysis of a Family of R Manipulators Maher Baili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S. 6597 1, rue e la Noë, BP 92101,
Kinematic Analysis of a Family of R Manipulators Maher Baili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S. 6597 1, rue e la Noë, BP 92101,
Cluster Center Initialization Method for K-means Algorithm Over Data Sets with Two Clusters
 Available online at www.scienceirect.com Proceia Engineering 4 (011 ) 34 38 011 International Conference on Avances in Engineering Cluster Center Initialization Metho for K-means Algorithm Over Data Sets
Available online at www.scienceirect.com Proceia Engineering 4 (011 ) 34 38 011 International Conference on Avances in Engineering Cluster Center Initialization Metho for K-means Algorithm Over Data Sets
Coupling the User Interfaces of a Multiuser Program
 Coupling the User Interfaces of a Multiuser Program PRASUN DEWAN University of North Carolina at Chapel Hill RAJIV CHOUDHARY Intel Corporation We have evelope a new moel for coupling the user-interfaces
Coupling the User Interfaces of a Multiuser Program PRASUN DEWAN University of North Carolina at Chapel Hill RAJIV CHOUDHARY Intel Corporation We have evelope a new moel for coupling the user-interfaces
A Classification of 3R Orthogonal Manipulators by the Topology of their Workspace
 A Classification of R Orthogonal Manipulators by the Topology of their Workspace Maher aili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S.
A Classification of R Orthogonal Manipulators by the Topology of their Workspace Maher aili, Philippe Wenger an Damien Chablat Institut e Recherche en Communications et Cybernétique e Nantes, UMR C.N.R.S.
A shortest path algorithm in multimodal networks: a case study with time varying costs
 A shortest path algorithm in multimoal networks: a case stuy with time varying costs Daniela Ambrosino*, Anna Sciomachen* * Department of Economics an Quantitative Methos (DIEM), University of Genoa Via
A shortest path algorithm in multimoal networks: a case stuy with time varying costs Daniela Ambrosino*, Anna Sciomachen* * Department of Economics an Quantitative Methos (DIEM), University of Genoa Via
On the Role of Multiply Sectioned Bayesian Networks to Cooperative Multiagent Systems
 On the Role of Multiply Sectione Bayesian Networks to Cooperative Multiagent Systems Y. Xiang University of Guelph, Canaa, yxiang@cis.uoguelph.ca V. Lesser University of Massachusetts at Amherst, USA,
On the Role of Multiply Sectione Bayesian Networks to Cooperative Multiagent Systems Y. Xiang University of Guelph, Canaa, yxiang@cis.uoguelph.ca V. Lesser University of Massachusetts at Amherst, USA,
Handling missing values in kernel methods with application to microbiology data
 an Machine Learning. Bruges (Belgium), 24-26 April 2013, i6oc.com publ., ISBN 978-2-87419-081-0. Available from http://www.i6oc.com/en/livre/?gcoi=28001100131010. Hanling missing values in kernel methos
an Machine Learning. Bruges (Belgium), 24-26 April 2013, i6oc.com publ., ISBN 978-2-87419-081-0. Available from http://www.i6oc.com/en/livre/?gcoi=28001100131010. Hanling missing values in kernel methos
Characterizing Decoding Robustness under Parametric Channel Uncertainty
 Characterizing Decoing Robustness uner Parametric Channel Uncertainty Jay D. Wierer, Wahee U. Bajwa, Nigel Boston, an Robert D. Nowak Abstract This paper characterizes the robustness of ecoing uner parametric
Characterizing Decoing Robustness uner Parametric Channel Uncertainty Jay D. Wierer, Wahee U. Bajwa, Nigel Boston, an Robert D. Nowak Abstract This paper characterizes the robustness of ecoing uner parametric
Kernel Methods & Support Vector Machines
 & Support Vector Machines & Support Vector Machines Arvind Visvanathan CSCE 970 Pattern Recognition 1 & Support Vector Machines Question? Draw a single line to separate two classes? 2 & Support Vector
& Support Vector Machines & Support Vector Machines Arvind Visvanathan CSCE 970 Pattern Recognition 1 & Support Vector Machines Question? Draw a single line to separate two classes? 2 & Support Vector
Using Vector and Raster-Based Techniques in Categorical Map Generalization
 Thir ICA Workshop on Progress in Automate Map Generalization, Ottawa, 12-14 August 1999 1 Using Vector an Raster-Base Techniques in Categorical Map Generalization Beat Peter an Robert Weibel Department
Thir ICA Workshop on Progress in Automate Map Generalization, Ottawa, 12-14 August 1999 1 Using Vector an Raster-Base Techniques in Categorical Map Generalization Beat Peter an Robert Weibel Department
SURVIVABLE IP OVER WDM: GUARANTEEEING MINIMUM NETWORK BANDWIDTH
 SURVIVABLE IP OVER WDM: GUARANTEEEING MINIMUM NETWORK BANDWIDTH Galen H Sasaki Dept Elec Engg, U Hawaii 2540 Dole Street Honolul HI 96822 USA Ching-Fong Su Fuitsu Laboratories of America 595 Lawrence Expressway
SURVIVABLE IP OVER WDM: GUARANTEEEING MINIMUM NETWORK BANDWIDTH Galen H Sasaki Dept Elec Engg, U Hawaii 2540 Dole Street Honolul HI 96822 USA Ching-Fong Su Fuitsu Laboratories of America 595 Lawrence Expressway
State Indexed Policy Search by Dynamic Programming. Abstract. 1. Introduction. 2. System parameterization. Charles DuHadway
 State Inexe Policy Search by Dynamic Programming Charles DuHaway Yi Gu 5435537 503372 December 4, 2007 Abstract We consier the reinforcement learning problem of simultaneous trajectory-following an obstacle
State Inexe Policy Search by Dynamic Programming Charles DuHaway Yi Gu 5435537 503372 December 4, 2007 Abstract We consier the reinforcement learning problem of simultaneous trajectory-following an obstacle
A Neural Network Model Based on Graph Matching and Annealing :Application to Hand-Written Digits Recognition
 ITERATIOAL JOURAL OF MATHEMATICS AD COMPUTERS I SIMULATIO A eural etwork Moel Base on Graph Matching an Annealing :Application to Han-Written Digits Recognition Kyunghee Lee Abstract We present a neural
ITERATIOAL JOURAL OF MATHEMATICS AD COMPUTERS I SIMULATIO A eural etwork Moel Base on Graph Matching an Annealing :Application to Han-Written Digits Recognition Kyunghee Lee Abstract We present a neural
Optimal Oblivious Path Selection on the Mesh
 Optimal Oblivious Path Selection on the Mesh Costas Busch Malik Magon-Ismail Jing Xi Department of Computer Science Rensselaer Polytechnic Institute Troy, NY 280, USA {buschc,magon,xij2}@cs.rpi.eu Abstract
Optimal Oblivious Path Selection on the Mesh Costas Busch Malik Magon-Ismail Jing Xi Department of Computer Science Rensselaer Polytechnic Institute Troy, NY 280, USA {buschc,magon,xij2}@cs.rpi.eu Abstract
Figure 1: Schematic of an SEM [source: ]
![Figure 1: Schematic of an SEM [source: ] Figure 1: Schematic of an SEM [source: ]](/thumbs/85/92721477.jpg) EECI Course: -9 May 1 by R. Sanfelice Hybri Control Systems Eelco van Horssen E.P.v.Horssen@tue.nl Project: Scanning Electron Microscopy Introuction In Scanning Electron Microscopy (SEM) a (bunle) beam
EECI Course: -9 May 1 by R. Sanfelice Hybri Control Systems Eelco van Horssen E.P.v.Horssen@tue.nl Project: Scanning Electron Microscopy Introuction In Scanning Electron Microscopy (SEM) a (bunle) beam
Multilevel Linear Dimensionality Reduction using Hypergraphs for Data Analysis
 Multilevel Linear Dimensionality Reuction using Hypergraphs for Data Analysis Haw-ren Fang Department of Computer Science an Engineering University of Minnesota; Minneapolis, MN 55455 hrfang@csumneu ABSTRACT
Multilevel Linear Dimensionality Reuction using Hypergraphs for Data Analysis Haw-ren Fang Department of Computer Science an Engineering University of Minnesota; Minneapolis, MN 55455 hrfang@csumneu ABSTRACT
A Multi-class SVM Classifier Utilizing Binary Decision Tree
 Informatica 33 (009) 33-41 33 A Multi-class Classifier Utilizing Binary Decision Tree Gjorgji Mazarov, Dejan Gjorgjevikj an Ivan Chorbev Department of Computer Science an Engineering Faculty of Electrical
Informatica 33 (009) 33-41 33 A Multi-class Classifier Utilizing Binary Decision Tree Gjorgji Mazarov, Dejan Gjorgjevikj an Ivan Chorbev Department of Computer Science an Engineering Faculty of Electrical
Learning Subproblem Complexities in Distributed Branch and Bound
 Learning Subproblem Complexities in Distribute Branch an Boun Lars Otten Department of Computer Science University of California, Irvine lotten@ics.uci.eu Rina Dechter Department of Computer Science University
Learning Subproblem Complexities in Distribute Branch an Boun Lars Otten Department of Computer Science University of California, Irvine lotten@ics.uci.eu Rina Dechter Department of Computer Science University
FINDING OPTICAL DISPERSION OF A PRISM WITH APPLICATION OF MINIMUM DEVIATION ANGLE MEASUREMENT METHOD
 Warsaw University of Technology Faculty of Physics Physics Laboratory I P Joanna Konwerska-Hrabowska 6 FINDING OPTICAL DISPERSION OF A PRISM WITH APPLICATION OF MINIMUM DEVIATION ANGLE MEASUREMENT METHOD.
Warsaw University of Technology Faculty of Physics Physics Laboratory I P Joanna Konwerska-Hrabowska 6 FINDING OPTICAL DISPERSION OF A PRISM WITH APPLICATION OF MINIMUM DEVIATION ANGLE MEASUREMENT METHOD.
Almost Disjunct Codes in Large Scale Multihop Wireless Network Media Access Control
 Almost Disjunct Coes in Large Scale Multihop Wireless Network Meia Access Control D. Charles Engelhart Anan Sivasubramaniam Penn. State University University Park PA 682 engelhar,anan @cse.psu.eu Abstract
Almost Disjunct Coes in Large Scale Multihop Wireless Network Meia Access Control D. Charles Engelhart Anan Sivasubramaniam Penn. State University University Park PA 682 engelhar,anan @cse.psu.eu Abstract
MORA: a Movement-Based Routing Algorithm for Vehicle Ad Hoc Networks
 : a Movement-Base Routing Algorithm for Vehicle A Hoc Networks Fabrizio Granelli, Senior Member, Giulia Boato, Member, an Dzmitry Kliazovich, Stuent Member Abstract Recent interest in car-to-car communications
: a Movement-Base Routing Algorithm for Vehicle A Hoc Networks Fabrizio Granelli, Senior Member, Giulia Boato, Member, an Dzmitry Kliazovich, Stuent Member Abstract Recent interest in car-to-car communications
Considering bounds for approximation of 2 M to 3 N
 Consiering bouns for approximation of to (version. Abstract: Estimating bouns of best approximations of to is iscusse. In the first part I evelop a powerseries, which shoul give practicable limits for
Consiering bouns for approximation of to (version. Abstract: Estimating bouns of best approximations of to is iscusse. In the first part I evelop a powerseries, which shoul give practicable limits for
Solution Representation for Job Shop Scheduling Problems in Ant Colony Optimisation
 Solution Representation for Job Shop Scheuling Problems in Ant Colony Optimisation James Montgomery, Carole Faya 2, an Sana Petrovic 2 Faculty of Information & Communication Technologies, Swinburne University
Solution Representation for Job Shop Scheuling Problems in Ant Colony Optimisation James Montgomery, Carole Faya 2, an Sana Petrovic 2 Faculty of Information & Communication Technologies, Swinburne University
Design of Policy-Aware Differentially Private Algorithms
 Design of Policy-Aware Differentially Private Algorithms Samuel Haney Due University Durham, NC, USA shaney@cs.ue.eu Ashwin Machanavajjhala Due University Durham, NC, USA ashwin@cs.ue.eu Bolin Ding Microsoft
Design of Policy-Aware Differentially Private Algorithms Samuel Haney Due University Durham, NC, USA shaney@cs.ue.eu Ashwin Machanavajjhala Due University Durham, NC, USA ashwin@cs.ue.eu Bolin Ding Microsoft
New Version of Davies-Bouldin Index for Clustering Validation Based on Cylindrical Distance
 New Version of Davies-Boulin Inex for lustering Valiation Base on ylinrical Distance Juan arlos Roas Thomas Faculta e Informática Universia omplutense e Mari Mari, España correoroas@gmail.com Abstract
New Version of Davies-Boulin Inex for lustering Valiation Base on ylinrical Distance Juan arlos Roas Thomas Faculta e Informática Universia omplutense e Mari Mari, España correoroas@gmail.com Abstract
AnyTraffic Labeled Routing
 AnyTraffic Labele Routing Dimitri Papaimitriou 1, Pero Peroso 2, Davie Careglio 2 1 Alcatel-Lucent Bell, Antwerp, Belgium Email: imitri.papaimitriou@alcatel-lucent.com 2 Universitat Politècnica e Catalunya,
AnyTraffic Labele Routing Dimitri Papaimitriou 1, Pero Peroso 2, Davie Careglio 2 1 Alcatel-Lucent Bell, Antwerp, Belgium Email: imitri.papaimitriou@alcatel-lucent.com 2 Universitat Politècnica e Catalunya,
On the Placement of Internet Taps in Wireless Neighborhood Networks
 1 On the Placement of Internet Taps in Wireless Neighborhoo Networks Lili Qiu, Ranveer Chanra, Kamal Jain, Mohamma Mahian Abstract Recently there has emerge a novel application of wireless technology that
1 On the Placement of Internet Taps in Wireless Neighborhoo Networks Lili Qiu, Ranveer Chanra, Kamal Jain, Mohamma Mahian Abstract Recently there has emerge a novel application of wireless technology that
WLAN Indoor Positioning Based on Euclidean Distances and Fuzzy Logic
 WLAN Inoor Positioning Base on Eucliean Distances an Fuzzy Logic Anreas TEUBER, Bern EISSFELLER Institute of Geoesy an Navigation, University FAF, Munich, Germany, e-mail: (anreas.teuber, bern.eissfeller)@unibw.e
WLAN Inoor Positioning Base on Eucliean Distances an Fuzzy Logic Anreas TEUBER, Bern EISSFELLER Institute of Geoesy an Navigation, University FAF, Munich, Germany, e-mail: (anreas.teuber, bern.eissfeller)@unibw.e
Algebraic transformations of Gauss hypergeometric functions
 Algebraic transformations of Gauss hypergeometric functions Raimunas Viūnas Faculty of Mathematics, Kobe University Abstract This article gives a classification scheme of algebraic transformations of Gauss
Algebraic transformations of Gauss hypergeometric functions Raimunas Viūnas Faculty of Mathematics, Kobe University Abstract This article gives a classification scheme of algebraic transformations of Gauss
EXACT SIMULATION OF A BOOLEAN MODEL
 Original Research Paper oi:10.5566/ias.v32.p101-105 EXACT SIMULATION OF A BOOLEAN MODEL CHRISTIAN LANTUÉJOULB MinesParisTech 35 rue Saint-Honoré 77305 Fontainebleau France e-mail: christian.lantuejoul@mines-paristech.fr
Original Research Paper oi:10.5566/ias.v32.p101-105 EXACT SIMULATION OF A BOOLEAN MODEL CHRISTIAN LANTUÉJOULB MinesParisTech 35 rue Saint-Honoré 77305 Fontainebleau France e-mail: christian.lantuejoul@mines-paristech.fr
Feature Extraction and Rule Classification Algorithm of Digital Mammography based on Rough Set Theory
 Feature Extraction an Rule Classification Algorithm of Digital Mammography base on Rough Set Theory Aboul Ella Hassanien Jafar M. H. Ali. Kuwait University, Faculty of Aministrative Science, Quantitative
Feature Extraction an Rule Classification Algorithm of Digital Mammography base on Rough Set Theory Aboul Ella Hassanien Jafar M. H. Ali. Kuwait University, Faculty of Aministrative Science, Quantitative
Bayesian localization microscopy reveals nanoscale podosome dynamics
 Nature Methos Bayesian localization microscopy reveals nanoscale poosome ynamics Susan Cox, Ewar Rosten, James Monypenny, Tijana Jovanovic-Talisman, Dylan T Burnette, Jennifer Lippincott-Schwartz, Gareth
Nature Methos Bayesian localization microscopy reveals nanoscale poosome ynamics Susan Cox, Ewar Rosten, James Monypenny, Tijana Jovanovic-Talisman, Dylan T Burnette, Jennifer Lippincott-Schwartz, Gareth
Support Vector Machines
 Support Vector Machines . Importance of SVM SVM is a discriminative method that brings together:. computational learning theory. previously known methods in linear discriminant functions 3. optimization
Support Vector Machines . Importance of SVM SVM is a discriminative method that brings together:. computational learning theory. previously known methods in linear discriminant functions 3. optimization
Intensive Hypercube Communication: Prearranged Communication in Link-Bound Machines 1 2
 This paper appears in J. of Parallel an Distribute Computing 10 (1990), pp. 167 181. Intensive Hypercube Communication: Prearrange Communication in Link-Boun Machines 1 2 Quentin F. Stout an Bruce Wagar
This paper appears in J. of Parallel an Distribute Computing 10 (1990), pp. 167 181. Intensive Hypercube Communication: Prearrange Communication in Link-Boun Machines 1 2 Quentin F. Stout an Bruce Wagar
Object Recognition Using Colour, Shape and Affine Invariant Ratios
 Object Recognition Using Colour, Shape an Affine Invariant Ratios Paul A. Walcott Centre for Information Engineering City University, Lonon EC1V 0HB, Englan P.A.Walcott@city.ac.uk Abstract This paper escribes
Object Recognition Using Colour, Shape an Affine Invariant Ratios Paul A. Walcott Centre for Information Engineering City University, Lonon EC1V 0HB, Englan P.A.Walcott@city.ac.uk Abstract This paper escribes
Learning Polynomial Functions. by Feature Construction
 I Proceeings of the Eighth International Workshop on Machine Learning Chicago, Illinois, June 27-29 1991 Learning Polynomial Functions by Feature Construction Richar S. Sutton GTE Laboratories Incorporate
I Proceeings of the Eighth International Workshop on Machine Learning Chicago, Illinois, June 27-29 1991 Learning Polynomial Functions by Feature Construction Richar S. Sutton GTE Laboratories Incorporate
Distributed Decomposition Over Hyperspherical Domains
 Distribute Decomposition Over Hyperspherical Domains Aron Ahmaia 1, Davi Keyes 1, Davi Melville 2, Alan Rosenbluth 2, Kehan Tian 2 1 Department of Applie Physics an Applie Mathematics, Columbia University,
Distribute Decomposition Over Hyperspherical Domains Aron Ahmaia 1, Davi Keyes 1, Davi Melville 2, Alan Rosenbluth 2, Kehan Tian 2 1 Department of Applie Physics an Applie Mathematics, Columbia University,
A fast embedded selection approach for color texture classification using degraded LBP
 A fast embee selection approach for color texture classification using egrae A. Porebski, N. Vanenbroucke an D. Hama Laboratoire LISIC - EA 4491 - Université u Littoral Côte Opale - 50, rue Ferinan Buisson
A fast embee selection approach for color texture classification using egrae A. Porebski, N. Vanenbroucke an D. Hama Laboratoire LISIC - EA 4491 - Université u Littoral Côte Opale - 50, rue Ferinan Buisson
A Framework for Dialogue Detection in Movies
 A Framework for Dialogue Detection in Movies Margarita Kotti, Constantine Kotropoulos, Bartosz Ziólko, Ioannis Pitas, an Vassiliki Moschou Department of Informatics, Aristotle University of Thessaloniki
A Framework for Dialogue Detection in Movies Margarita Kotti, Constantine Kotropoulos, Bartosz Ziólko, Ioannis Pitas, an Vassiliki Moschou Department of Informatics, Aristotle University of Thessaloniki
Table-based division by small integer constants
 Table-base ivision by small integer constants Florent e Dinechin, Laurent-Stéphane Diier LIP, Université e Lyon (ENS-Lyon/CNRS/INRIA/UCBL) 46, allée Italie, 69364 Lyon Ceex 07 Florent.e.Dinechin@ens-lyon.fr
Table-base ivision by small integer constants Florent e Dinechin, Laurent-Stéphane Diier LIP, Université e Lyon (ENS-Lyon/CNRS/INRIA/UCBL) 46, allée Italie, 69364 Lyon Ceex 07 Florent.e.Dinechin@ens-lyon.fr
CS 106 Winter 2016 Craig S. Kaplan. Module 01 Processing Recap. Topics
 CS 106 Winter 2016 Craig S. Kaplan Moule 01 Processing Recap Topics The basic parts of speech in a Processing program Scope Review of syntax for classes an objects Reaings Your CS 105 notes Learning Processing,
CS 106 Winter 2016 Craig S. Kaplan Moule 01 Processing Recap Topics The basic parts of speech in a Processing program Scope Review of syntax for classes an objects Reaings Your CS 105 notes Learning Processing,
Rough Set Approach for Classification of Breast Cancer Mammogram Images
 Rough Set Approach for Classification of Breast Cancer Mammogram Images Aboul Ella Hassanien Jafar M. H. Ali. Kuwait University, Faculty of Aministrative Science, Quantitative Methos an Information Systems
Rough Set Approach for Classification of Breast Cancer Mammogram Images Aboul Ella Hassanien Jafar M. H. Ali. Kuwait University, Faculty of Aministrative Science, Quantitative Methos an Information Systems
Fast Fractal Image Compression using PSO Based Optimization Techniques
 Fast Fractal Compression using PSO Base Optimization Techniques A.Krishnamoorthy Visiting faculty Department Of ECE University College of Engineering panruti rishpci89@gmail.com S.Buvaneswari Visiting
Fast Fractal Compression using PSO Base Optimization Techniques A.Krishnamoorthy Visiting faculty Department Of ECE University College of Engineering panruti rishpci89@gmail.com S.Buvaneswari Visiting
Animated Surface Pasting
 Animate Surface Pasting Clara Tsang an Stephen Mann Computing Science Department University of Waterloo 200 University Ave W. Waterloo, Ontario Canaa N2L 3G1 e-mail: clftsang@cgl.uwaterloo.ca, smann@cgl.uwaterloo.ca
Animate Surface Pasting Clara Tsang an Stephen Mann Computing Science Department University of Waterloo 200 University Ave W. Waterloo, Ontario Canaa N2L 3G1 e-mail: clftsang@cgl.uwaterloo.ca, smann@cgl.uwaterloo.ca
Short-term prediction of photovoltaic power based on GWPA - BP neural network model
 Short-term preiction of photovoltaic power base on GWPA - BP neural networ moel Jian Di an Shanshan Meng School of orth China Electric Power University, Baoing. China Abstract In recent years, ue to China's
Short-term preiction of photovoltaic power base on GWPA - BP neural networ moel Jian Di an Shanshan Meng School of orth China Electric Power University, Baoing. China Abstract In recent years, ue to China's
arxiv: v1 [math.co] 15 Dec 2017
![arxiv: v1 [math.co] 15 Dec 2017 arxiv: v1 [math.co] 15 Dec 2017](/thumbs/95/123306327.jpg) Rectilinear Crossings in Complete Balance -Partite -Uniform Hypergraphs Rahul Gangopahyay Saswata Shannigrahi arxiv:171.05539v1 [math.co] 15 Dec 017 December 18, 017 Abstract In this paper, we stuy the
Rectilinear Crossings in Complete Balance -Partite -Uniform Hypergraphs Rahul Gangopahyay Saswata Shannigrahi arxiv:171.05539v1 [math.co] 15 Dec 017 December 18, 017 Abstract In this paper, we stuy the
2-connected graphs with small 2-connected dominating sets
 2-connecte graphs with small 2-connecte ominating sets Yair Caro, Raphael Yuster 1 Department of Mathematics, University of Haifa at Oranim, Tivon 36006, Israel Abstract Let G be a 2-connecte graph. A
2-connecte graphs with small 2-connecte ominating sets Yair Caro, Raphael Yuster 1 Department of Mathematics, University of Haifa at Oranim, Tivon 36006, Israel Abstract Let G be a 2-connecte graph. A
Figure 1: 2D arm. Figure 2: 2D arm with labelled angles
 2D Kinematics Consier a robotic arm. We can sen it commans like, move that joint so it bens at an angle θ. Once we ve set each joint, that s all well an goo. More interesting, though, is the question of
2D Kinematics Consier a robotic arm. We can sen it commans like, move that joint so it bens at an angle θ. Once we ve set each joint, that s all well an goo. More interesting, though, is the question of
5th International Conference on Advanced Design and Manufacturing Engineering (ICADME 2015)
 5th International Conference on Avance Design an Manufacturing Engineering (ICADME 25) Research on motion characteristics an application of multi egree of freeom mechanism base on R-W metho Xiao-guang
5th International Conference on Avance Design an Manufacturing Engineering (ICADME 25) Research on motion characteristics an application of multi egree of freeom mechanism base on R-W metho Xiao-guang
Variable Independence and Resolution Paths for Quantified Boolean Formulas
 Variable Inepenence an Resolution Paths for Quantifie Boolean Formulas Allen Van Geler http://www.cse.ucsc.eu/ avg University of California, Santa Cruz Abstract. Variable inepenence in quantifie boolean
Variable Inepenence an Resolution Paths for Quantifie Boolean Formulas Allen Van Geler http://www.cse.ucsc.eu/ avg University of California, Santa Cruz Abstract. Variable inepenence in quantifie boolean
New Geometric Interpretation and Analytic Solution for Quadrilateral Reconstruction
 New Geometric Interpretation an Analytic Solution for uarilateral Reconstruction Joo-Haeng Lee Convergence Technology Research Lab ETRI Daejeon, 305 777, KOREA Abstract A new geometric framework, calle
New Geometric Interpretation an Analytic Solution for uarilateral Reconstruction Joo-Haeng Lee Convergence Technology Research Lab ETRI Daejeon, 305 777, KOREA Abstract A new geometric framework, calle
Frequent Pattern Mining. Frequent Item Set Mining. Overview. Frequent Item Set Mining: Motivation. Frequent Pattern Mining comprises
 verview Frequent Pattern Mining comprises Frequent Pattern Mining hristian Borgelt School of omputer Science University of Konstanz Universitätsstraße, Konstanz, Germany christian.borgelt@uni-konstanz.e
verview Frequent Pattern Mining comprises Frequent Pattern Mining hristian Borgelt School of omputer Science University of Konstanz Universitätsstraße, Konstanz, Germany christian.borgelt@uni-konstanz.e
Adjacency Matrix Based Full-Text Indexing Models
 1000-9825/2002/13(10)1933-10 2002 Journal of Software Vol.13, No.10 Ajacency Matrix Base Full-Text Inexing Moels ZHOU Shui-geng 1, HU Yun-fa 2, GUAN Ji-hong 3 1 (Department of Computer Science an Engineering,
1000-9825/2002/13(10)1933-10 2002 Journal of Software Vol.13, No.10 Ajacency Matrix Base Full-Text Inexing Moels ZHOU Shui-geng 1, HU Yun-fa 2, GUAN Ji-hong 3 1 (Department of Computer Science an Engineering,
Distributed Line Graphs: A Universal Technique for Designing DHTs Based on Arbitrary Regular Graphs
 IEEE TRANSACTIONS ON KNOWLEDE AND DATA ENINEERIN, MANUSCRIPT ID Distribute Line raphs: A Universal Technique for Designing DHTs Base on Arbitrary Regular raphs Yiming Zhang an Ling Liu, Senior Member,
IEEE TRANSACTIONS ON KNOWLEDE AND DATA ENINEERIN, MANUSCRIPT ID Distribute Line raphs: A Universal Technique for Designing DHTs Base on Arbitrary Regular raphs Yiming Zhang an Ling Liu, Senior Member,
Offloading Cellular Traffic through Opportunistic Communications: Analysis and Optimization
 1 Offloaing Cellular Traffic through Opportunistic Communications: Analysis an Optimization Vincenzo Sciancalepore, Domenico Giustiniano, Albert Banchs, Anreea Picu arxiv:1405.3548v1 [cs.ni] 14 May 24
1 Offloaing Cellular Traffic through Opportunistic Communications: Analysis an Optimization Vincenzo Sciancalepore, Domenico Giustiniano, Albert Banchs, Anreea Picu arxiv:1405.3548v1 [cs.ni] 14 May 24
Bends, Jogs, And Wiggles for Railroad Tracks and Vehicle Guide Ways
 Ben, Jogs, An Wiggles for Railroa Tracks an Vehicle Guie Ways Louis T. Klauer Jr., PhD, PE. Work Soft 833 Galer Dr. Newtown Square, PA 19073 lklauer@wsof.com Preprint, June 4, 00 Copyright 00 by Louis
Ben, Jogs, An Wiggles for Railroa Tracks an Vehicle Guie Ways Louis T. Klauer Jr., PhD, PE. Work Soft 833 Galer Dr. Newtown Square, PA 19073 lklauer@wsof.com Preprint, June 4, 00 Copyright 00 by Louis
An Algorithm for Building an Enterprise Network Topology Using Widespread Data Sources
 An Algorithm for Builing an Enterprise Network Topology Using Wiesprea Data Sources Anton Anreev, Iurii Bogoiavlenskii Petrozavosk State University Petrozavosk, Russia {anreev, ybgv}@cs.petrsu.ru Abstract
An Algorithm for Builing an Enterprise Network Topology Using Wiesprea Data Sources Anton Anreev, Iurii Bogoiavlenskii Petrozavosk State University Petrozavosk, Russia {anreev, ybgv}@cs.petrsu.ru Abstract
Research Article Inviscid Uniform Shear Flow past a Smooth Concave Body
 International Engineering Mathematics Volume 04, Article ID 46593, 7 pages http://x.oi.org/0.55/04/46593 Research Article Invisci Uniform Shear Flow past a Smooth Concave Boy Abullah Mura Department of
International Engineering Mathematics Volume 04, Article ID 46593, 7 pages http://x.oi.org/0.55/04/46593 Research Article Invisci Uniform Shear Flow past a Smooth Concave Boy Abullah Mura Department of
Queueing Model and Optimization of Packet Dropping in Real-Time Wireless Sensor Networks
 Queueing Moel an Optimization of Packet Dropping in Real-Time Wireless Sensor Networks Marc Aoun, Antonios Argyriou, Philips Research, Einhoven, 66AE, The Netherlans Department of Computer an Communication
Queueing Moel an Optimization of Packet Dropping in Real-Time Wireless Sensor Networks Marc Aoun, Antonios Argyriou, Philips Research, Einhoven, 66AE, The Netherlans Department of Computer an Communication
Threshold Based Data Aggregation Algorithm To Detect Rainfall Induced Landslides
 Threshol Base Data Aggregation Algorithm To Detect Rainfall Inuce Lanslies Maneesha V. Ramesh P. V. Ushakumari Department of Computer Science Department of Mathematics Amrita School of Engineering Amrita
Threshol Base Data Aggregation Algorithm To Detect Rainfall Inuce Lanslies Maneesha V. Ramesh P. V. Ushakumari Department of Computer Science Department of Mathematics Amrita School of Engineering Amrita
A FUZZY FRAMEWORK FOR SEGMENTATION, FEATURE MATCHING AND RETRIEVAL OF BRAIN MR IMAGES
 A FUZZY FRAMEWORK FOR SEGMENTATION, FEATURE MATCHING AND RETRIEVAL OF BRAIN MR IMAGES Archana.S 1 an Srihar.S 2 1 Department of Information Science an Technology, College of Engineering, Guiny archana.santhira@gmail.com
A FUZZY FRAMEWORK FOR SEGMENTATION, FEATURE MATCHING AND RETRIEVAL OF BRAIN MR IMAGES Archana.S 1 an Srihar.S 2 1 Department of Information Science an Technology, College of Engineering, Guiny archana.santhira@gmail.com
A Revised Simplex Search Procedure for Stochastic Simulation Response Surface Optimization
 272 INFORMS Journal on Computing 0899-1499 100 1204-0272 $05.00 Vol. 12, No. 4, Fall 2000 2000 INFORMS A Revise Simplex Search Proceure for Stochastic Simulation Response Surface Optimization DAVID G.
272 INFORMS Journal on Computing 0899-1499 100 1204-0272 $05.00 Vol. 12, No. 4, Fall 2000 2000 INFORMS A Revise Simplex Search Proceure for Stochastic Simulation Response Surface Optimization DAVID G.
On Effectively Determining the Downlink-to-uplink Sub-frame Width Ratio for Mobile WiMAX Networks Using Spline Extrapolation
 On Effectively Determining the Downlink-to-uplink Sub-frame With Ratio for Mobile WiMAX Networks Using Spline Extrapolation Panagiotis Sarigianniis, Member, IEEE, Member Malamati Louta, Member, IEEE, Member
On Effectively Determining the Downlink-to-uplink Sub-frame With Ratio for Mobile WiMAX Networks Using Spline Extrapolation Panagiotis Sarigianniis, Member, IEEE, Member Malamati Louta, Member, IEEE, Member
Random Clustering for Multiple Sampling Units to Speed Up Run-time Sample Generation
 DEIM Forum 2018 I4-4 Abstract Ranom Clustering for Multiple Sampling Units to Spee Up Run-time Sample Generation uzuru OKAJIMA an Koichi MARUAMA NEC Solution Innovators, Lt. 1-18-7 Shinkiba, Koto-ku, Tokyo,
DEIM Forum 2018 I4-4 Abstract Ranom Clustering for Multiple Sampling Units to Spee Up Run-time Sample Generation uzuru OKAJIMA an Koichi MARUAMA NEC Solution Innovators, Lt. 1-18-7 Shinkiba, Koto-ku, Tokyo,
filtering LETTER An Improved Neighbor Selection Algorithm in Collaborative Taek-Hun KIM a), Student Member and Sung-Bong YANG b), Nonmember
 107 IEICE TRANS INF & SYST, VOLE88 D, NO5 MAY 005 LETTER An Improve Neighbor Selection Algorithm in Collaborative Filtering Taek-Hun KIM a), Stuent Member an Sung-Bong YANG b), Nonmember SUMMARY Nowaays,
107 IEICE TRANS INF & SYST, VOLE88 D, NO5 MAY 005 LETTER An Improve Neighbor Selection Algorithm in Collaborative Filtering Taek-Hun KIM a), Stuent Member an Sung-Bong YANG b), Nonmember SUMMARY Nowaays,
Image compression predicated on recurrent iterated function systems
 2n International Conference on Mathematics & Statistics 16-19 June, 2008, Athens, Greece Image compression preicate on recurrent iterate function systems Chol-Hui Yun *, Metzler W. a an Barski M. a * Faculty
2n International Conference on Mathematics & Statistics 16-19 June, 2008, Athens, Greece Image compression preicate on recurrent iterate function systems Chol-Hui Yun *, Metzler W. a an Barski M. a * Faculty
A Plane Tracker for AEC-automation Applications
 A Plane Tracker for AEC-automation Applications Chen Feng *, an Vineet R. Kamat Department of Civil an Environmental Engineering, University of Michigan, Ann Arbor, USA * Corresponing author (cforrest@umich.eu)
A Plane Tracker for AEC-automation Applications Chen Feng *, an Vineet R. Kamat Department of Civil an Environmental Engineering, University of Michigan, Ann Arbor, USA * Corresponing author (cforrest@umich.eu)
Holy Halved Heaquarters Riddler
 Holy Halve Heaquarters Riler Anonymous Philosopher June 206 Laser Larry threatens to imminently zap Riler Heaquarters (which is of regular pentagonal shape with no courtyar or other funny business) with
Holy Halve Heaquarters Riler Anonymous Philosopher June 206 Laser Larry threatens to imminently zap Riler Heaquarters (which is of regular pentagonal shape with no courtyar or other funny business) with
Analysis of half-space range search using the k-d search skip list. Here we analyse the expected time for half-space
 Analysis of half-space range search using the k- search skip list Mario A. Lopez Brafor G. Nickerson y 1 Abstract We analyse the average cost of half-space range reporting for the k- search skip list.
Analysis of half-space range search using the k- search skip list Mario A. Lopez Brafor G. Nickerson y 1 Abstract We analyse the average cost of half-space range reporting for the k- search skip list.
Robust Camera Calibration for an Autonomous Underwater Vehicle
 obust Camera Calibration for an Autonomous Unerwater Vehicle Matthew Bryant, Davi Wettergreen *, Samer Aballah, Alexaner Zelinsky obotic Systems Laboratory Department of Engineering, FEIT Department of
obust Camera Calibration for an Autonomous Unerwater Vehicle Matthew Bryant, Davi Wettergreen *, Samer Aballah, Alexaner Zelinsky obotic Systems Laboratory Department of Engineering, FEIT Department of
Iterative Computation of Moment Forms for Subdivision Surfaces
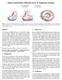 Iterative Computation of Moment Forms for Subivision Surfaces Jan P. Hakenberg ETH Zürich Ulrich Reif TU Darmstat Figure : Solis boune by Catmull-Clark an Loop subivision surfaces with centrois inicate
Iterative Computation of Moment Forms for Subivision Surfaces Jan P. Hakenberg ETH Zürich Ulrich Reif TU Darmstat Figure : Solis boune by Catmull-Clark an Loop subivision surfaces with centrois inicate
I. Introuction With the evolution of imaging technology, an increasing number of image moalities becomes available. In remote sensing, sensors are use
 A multivalue image wavelet representation base on multiscale funamental forms P. Scheuners Vision Lab, Department ofphysics, University ofantwerp, Groenenborgerlaan 7, 00 Antwerpen, Belgium Tel.: +3/3/8
A multivalue image wavelet representation base on multiscale funamental forms P. Scheuners Vision Lab, Department ofphysics, University ofantwerp, Groenenborgerlaan 7, 00 Antwerpen, Belgium Tel.: +3/3/8
Nearest Neighbor Search using Additive Binary Tree
 Nearest Neighbor Search using Aitive Binary Tree Sung-Hyuk Cha an Sargur N. Srihari Center of Excellence for Document Analysis an Recognition State University of New York at Buffalo, U. S. A. E-mail: fscha,sriharig@cear.buffalo.eu
Nearest Neighbor Search using Aitive Binary Tree Sung-Hyuk Cha an Sargur N. Srihari Center of Excellence for Document Analysis an Recognition State University of New York at Buffalo, U. S. A. E-mail: fscha,sriharig@cear.buffalo.eu
Fuzzy Clustering in Parallel Universes
 Fuzzy Clustering in Parallel Universes Bern Wisweel an Michael R. Berthol ALTANA-Chair for Bioinformatics an Information Mining Department of Computer an Information Science, University of Konstanz 78457
Fuzzy Clustering in Parallel Universes Bern Wisweel an Michael R. Berthol ALTANA-Chair for Bioinformatics an Information Mining Department of Computer an Information Science, University of Konstanz 78457
Fast Window Based Stereo Matching for 3D Scene Reconstruction
 The International Arab Journal of Information Technology, Vol. 0, No. 3, May 203 209 Fast Winow Base Stereo Matching for 3D Scene Reconstruction Mohamma Mozammel Chowhury an Mohamma AL-Amin Bhuiyan Department
The International Arab Journal of Information Technology, Vol. 0, No. 3, May 203 209 Fast Winow Base Stereo Matching for 3D Scene Reconstruction Mohamma Mozammel Chowhury an Mohamma AL-Amin Bhuiyan Department
A PSO Optimized Layered Approach for Parametric Clustering on Weather Dataset
 Vol.3, Issue.1, Jan-Feb. 013 pp-504-508 ISSN: 49-6645 A PSO Optimize Layere Approach for Parametric Clustering on Weather Dataset Shikha Verma, 1 Kiran Jyoti 1 Stuent, Guru Nanak Dev Engineering College
Vol.3, Issue.1, Jan-Feb. 013 pp-504-508 ISSN: 49-6645 A PSO Optimize Layere Approach for Parametric Clustering on Weather Dataset Shikha Verma, 1 Kiran Jyoti 1 Stuent, Guru Nanak Dev Engineering College
