Coding of Fractal Binary Images with Contractive Set Mappings Composed of Affine Transformations
|
|
|
- Candice Reed
- 5 years ago
- Views:
Transcription
1 Linköping Studies in Science and Technology Dissertation No. 700 Coding of Fractal Binary Images with Contractive Set Mappings Composed of Affine Transformations Niclas Wadströmer Department of Electrical Engineering Linköping University, SE Linköping, Sweden Linköping 2001
2
3 Linköping Studies in Science and Technology Dissertation No. 700 Coding of Fractal Binary Images with Contractive Set Mappings Composed of Affine Transformations Niclas Wadströmer Department of Electrical Engineering Linköping University, SE Linköping, Sweden Linköping 2001
4
5 to granny and grandpa
6
7 Abstract There are several efficient algorithms by which one can generate approximations of binary attractors induced from contractive set mappings which are composed of affine mappings. There are also complex attractors resembling natural-looking images where the attractors are induced from only a few affine mappings which can be represented with a few bits. Thus it is more efficient to store and transmit the affine mappings than the image itself. For set mappings to be useful for image coding, it is also necessary to have an algorithm which can find a set mapping that defines an attractor image which is close to the given image. In the present thesis, we will describe and analyse two algorithms for this problem, usually called an inverse problem. One algorithm is based on a full search through the parameter space of the affine mappings. The other is based on a gradient search in the parameter space of the affine mappings where the gradient is obtained by the Kantorovich metric. We describe some variants of these attractor coding methods and compare them with non-fractal coding methods for binary images. We have found that the gradient search algorithm can be used to improve a good initial solution. A disadvantage of this algorithm is that the number of mappings must be given. Thus, it is less suitable for encoding images. The full search algorithm with its variants can be used to encode binary images. It also has an inverse property regarding the number of affine mappings, which means that if the given image was generated by a set mapping, then under some conditions the algorithm can recover the mappings that generated the given image. The Kantorovich distance has a high computational complexity and takes considerable time to compute even for small images. We have implemented two algorithms with some variants for the computation of the distance and compared them. We found that they can be used to compute the distance between images. The underlying notion behind the attractor-based techniques described here is that using a larger parameter space for the affine mappings in the spatial domain should give a better image coding in a rate distortion sense. We have also made some experiments on grey scale images along this line of thought.
8
9 Acknowledgements First I would like to thank my supervisors Dr. Robert Forchheimer and Dr. Thomas Kaijser for supporting me throughout this work. I also thank Prof. Ingemar Ingemarsson and Dr. Viiveke Fåk who supervised me writing my licentiate thesis. I would also like to thank all present and previous collegues and friends in the Image Coding, Information Theory and Data Transmission groups at the Dept. of Electrical Engineering. Many thanks goes to my family Stina, Valdemar, Dorotea and Zackarias for their love and support and for letting me work strange hours. I dedicate my thesis to granny and grandpa who also made a long journey though not only in mind but also in the world. Linköping, April 2001 Niclas Wadströmer
10
11 Contents 1 Introduction Background Image coding Contractive set mappings Image coding with contractive set mappings Distance measures Outline Models of fractal binary images Representations of real world black and white images Fractal binary images A metric space and two theorems Iterated function systems Recurrent iterated function systems Local iterated function systems Iterated digital set mappings Image generation Iterated function systems Recurrent iterated function systems Local iterated function systems Digital set mappings Conclusion Inverse problems of IFS s 37 5 An automatisation of Barnsley s algorithm Barnsley s algorithm An automatisation of Barnsley s algorithm Results Conclusion xi
12 xii Contents 6 A gradient search algorithm The Kantorovich distance Gradient search About the gradient Results Conclusion Coding of binary images The Hamming distance Local iterated function systems Recurrent iterated function systems Non-attractor coding methods Results Conclusion Coding of grey scale images Measures and iterated function systems with probabilities Functions and affine operators Vectors and affine mappings Comparison Results Conclusion Computing the Kantorovich distance for images The Kantorovich distance and the transportation problem The primal-dual algorithm Computing the Kantorovich distance for images Implementation Results Conclusion Conclusions 141 References 143
13 Chapter 1 Introduction Vari det, för att läsaren inte skall invaggas i några falska förhoppningar vad gäller denna lilla boks underhållningsvärde, från början slås fast att handlingen i sagda bok snarast är av psykologisk karaktär, eller att den med andra ord och sanningen att säga utgör en ganska tråkig läsning. Efter att sålunda förvarnat läsaren övergår berättelsen till att skildra ett oväntat och lägligt telefonsamtal. ur Francisco Santis långa natt av Humberto Costantini This thesis deals with methods for efficient representation of fractal binary images. By efficiency, we mean the average number of bits required for the representation of an image. Efficient representation of images is needed for transmission and storage of images where the storage or transmission capacity is limited, e.g. downloading of images to a mobile telephone. The problem is to find a representation of images which yields a minimum average number of bits per image of acceptable quality. Another problem is to find algorithms of acceptable computational complexity which will translate from images to the representation (coding) and back again (decoding). The number of bits required for the representation is called rate, usually measured in bits per pixel. The methods will primarily be assessed by the rate, but the computational complexity of the coding and decoding algorithms will also be considered. If some distortion is allowed in the decoded image compared with the given image, then the rate can be considerably reduced. In this case the methods will be assessed by the rate for a given level of distortion. Most methods considered in this work give rise to variable rate and distortion and must thus be assessed by the relationship between the two properties. We will view a real world image as a subset of the plane, called image support, from which light is radiating with spatially varying intensity and spectral content. The radiating light will be described by the visual dimensions of the image. The image has a limited spatial extension, here usually to a square. We will consider two representations of the intensity. It can be represented by a real valued function 1
14 2 Chapter 1 Introduction defined on the image support. The value of the function represents the intensity of each point. The intensity can also be represented by a real valued measure defined on the image support. The measure represents the total intensity emitted by each measurable subset. The second representation will be used in Chapter 8 to represent grey scale images. A digital image is usually represented by a finite number of pixels, each of which has an address (position) in the digital image. A value of one or several dimensions is associated with each pixel. The value represents the intensity and colour of either a point or a small area in the image. A binary image is an image where the visual dimension only has two possible values, usually black and white. A fractal binary image will typically have the following properties (Falconer [15]): details on arbitrarily small scales; be too irregular to be described with traditional geometric language; have some form of self-similarity; and have a fractal dimension which is larger than the topological dimension. Figure 1.1 shows examples of binary images. Some are natural, with certain fractal properties, and some are artificial, i.e. defined by contractive set mappings (described in Ch. 2), and are fractal by definition. There are complex and natural-looking binary images, see e.g. Barnsley [6], called attractors, which are defined by contractive set mappings with very few parameters. These set mappings can be represented by few bits, thus a very low rate is achieved. Mandelbrot [34] was among the first to recognise that many phenomena in nature, e.g. coastlines, mountains, clouds etc., have fractal properties and sug- Figure 1.1 Some fractal binary images.
15 gested that contractive set mappings might provide an efficient representation of them. Barnsley and Sloan [8] presented the first image coding method based on the new ideas. In the present work our goal is to find out whether contractive set mappings give an efficient representation of fractal binary images in terms of the relationship between rate and distortion. We will investigate three particular methods, each based on a class of contractive set mappings composed of affine transformations. The three classes of set mappings are iterated function systems (IFS), recurrent iterated function systems (RIFS) and local iterated function systems (LIFS). Each method consists of a class of set mappings, and associated coding and decoding algorithms. There are many decoding algorithms which generate binary images from set mappings in the classes we will consider, see e.g. Dubuc and Elqortobi [13], Hepting, Prusinkiewicz and Saupe [21], Monro and Dudbridge [36]. The algorithms have different properties, and most of them are very efficient in terms of accuracy and computational complexity. The coding problem is related to the inverse problem of fractal sets, see e.g. Barnsley et. al. [4], Forte and Vrscay [17], Mantica [35]. The inverse problem is how to find a set mapping which defines an attractor (in this case the decoded image) that is closer than a given limit to the given image. The inverse problem is part of the coding problem, but here also the length of the description of the set mapping needs to be considered. There are many set mappings that define attractors which are arbitrarily close to the given image. However, most of these set mappings need a longer description than the image itself and are not good for image coding. Finding coding algorithms for the proposed classes of set mappings is the main issue of the present work. The existing fractal coding systems, e.g. Jacquin [26], Fisher [16], Novak [39], mostly developed for grey scale images, are also based on affine transformations on the plane. To reduce the encoding time, the class of mappings is reduced to a small subclass. Our goal is to find an encoding algorithm that can use a wider class of mappings. Although most of our work is oriented towards binary images, we believe that our ideas have bearing also on the coding of grey scale images. The main contributions of the present thesis can be summarised as; A presentation of two new algorithms for the inverse problem of IFS s suited to image coding purposes, an automatisation of Barnsley s algorithm and a gradient search algorithm based on the Kantorovich metric. A comparison of an attractor coding method for binary images with some nonfractal coding methods for binary images. An approach to encoding grey scale images based on a larger class of spatial mappings than what is usual in block-based attractor coding. A description of an implementation and a comparison of two algorithms for the computation of the Kantorovich metric for images. Parts of the present thesis have been published in [46][47][48][49][50][51]. 3
16 4 Chapter 1 Introduction 1.1 Background The starting point of image coding with attractors (fractals) is usually dated to an article in Byte Magazine 1988 by Barnsley and Sloan [8], where they claimed that image compression ratios of 10,000 to 1 could be obtained. In the article they showed a class of complex attractors defined by a few parameters, but little was said about how to find the parameters from a given image. In 1990 Jacquin [25] presented block-based fractal coding, which used a limited class of affine image transformations with corresponding attractors to model grey scale images. The transforms in the spatial domain, i.e. of the image support, were limited to a small subclass of the affine mappings. Jacquin also presented a procedure for how to code the images. The compression ratios achieved by Jacquin s method were only moderate, similar to conventional coding techniques, and with the disadvantage of very high encoding time. Following Jacquin, many researchers have contributed to the development of block-based fractal coding. Both the compression ratio and the coding time have been improved and can now be compared to the best coding methods, see e.g. Gharavi-Alkhansari [18]. One of the problems of representing images with attractors is that the encoding involves an extensive search. To cope with this search, the set of mappings is usually reduced. This means that if the images are of fractal nature, the encoding cannot utilise the fractal property because the set of functions is too limited. It is an experience that fractal coding schemes for grey scale images the show worst performance in what appears to be fractal parts of images. An issue which we will address is to what extent the performance will improve if the class of mappings is extended. The present work started with the notion that it might be possible to find a solution to the inverse problem of iterated function systems by using a gradient search algorithm based on the Kantorovich metric. In the beginning, the problem was the long computation time for the Kantorovich distance measure. The distance could only be computed for images of too low resolution. The problem with the computation of the Kantorovich distance triggered the work to find faster algorithms. These algorithms made it possible to compute the Kantorovich distance for images of higher resolution, and the gradient search algorithm performed much better. However, we found that the gradient search could be used mainly to improve a rather good initial guess of the affine mappings. The full search algorithm started off as a way to find such an initial guess for the gradient search. However, we found that the search algorithm could give a solution that was sufficient for image coding, thus the gradient search was not needed. The full search algorithm also solved the problem of determining the number of affine mappings which the gradient search algorithm could not solve. An underlying notion behind our approach to attractor (fractal) coding is that the parameter space of the spatial mappings should be large to yield better coding. This is the reason why we also applied the idea to grey scale images.
17 1.2 Image coding Image coding A general model of a source coding system consists of a source of symbols, an encoder, a decoder and a receiver (Fig. 1.2). Traditionally, one views the source as a stochastic process yielding a sequence of independent symbols. The encoder replaces each symbol with a sequence of binary symbols. The length of the sequence is variable and depends on the input symbol. We assume that the storage/transmission of the data does not compromise them in any way. In a more general model we would have to accept some probability of errors during storage/transmission of the data. The decoder estimates which symbols were sent from the stored/transmitted data. Let us temporarily describe the encoder and decoder with tables which associate each symbol with a binary codeword and each codeword with a symbol. The problem is to construct tables such that the mean number of bits per symbol, called mean rate, is minimised. If some distortion, in some measure, is allowed at the receiver (by allowing different symbols to share the same codeword), then the mean number of bits per symbol should be minimised for that level of distortion. Shannon [43] used statistical models of the source, i.e. he assumed knowledge of the probability distribution of the source symbols. He found that the source can be characterised by a number called entropy, which is a function of the probability distribution. The entropy determines the minimum rate required to be able to represent the data without errors. If fewer bits are used, there will inevitably be errors. Shannon also derived a lower limit to the rate when a given level of distortion is accepted. The limit to the rate is given by the mutual information between the source of symbols and the receivers distorted symbols under the condition that the distortion is at most the acceptable level. Huffman, among others, constructed an algorithm which, from the probability distribution, generates a table associating each source symbol with a codeword. The mean rate given by this code is very close to the entropy of the source if the symbols are independent of each other. However, there are two problems with this model when applied to images. Consider e.g. a source of digital binary images of size pixels. The number of possible images is = , hence it is practically impossible to represent the code as a table. The second problem is that little is known about the probability distribution. Since this model of the source does not lead to a practical coding method, one often takes another view. Let us consider the source as producing digital images with source encoder decoder receiver Figure 1.2 A model of an image transmission system.
18 6 Chapter 1 Introduction the pixel values in some known order. The symbol alphabet, i.e. the number of possible values of a pixel, is small, and the probability distribution can thus be estimated. The reduction in rate with methods based on this model is, however, very small compared with using a large group of pixels at a time [38]. The problem is that most of the statistical redundancy lies in the strong dependency between the values of neighbouring pixels. Many different techniques have been proposed to decorrelate the values, e.g. predictive coding, subband coding, wavelet coding, geometrical models, and other descriptions of the image. The coding is often based on a model, i.e. a simplified description of the class of images. The model has some parameters that determine its state and thus the current model image. The idea is that the model image is an accurate description of the given image and that the parameters are easier to encode than the given image. Usually the model is constructed so that all images can be described as accurately as required. Another idea is that the quantisation and coding of the parameters can utilise statistical redundancy and subjective properties. Thus the coding problem is divided into two parts: first, how to find the model parameters and second, how to encode the parameters. The model is constructed such that it can describe the current class of images accurately. During the model construction, the parameter coding is not considered. There could be dependencies, but we will disregard them. Source coding can be viewed as removing redundancy, and Shannon s remarkable finding is that there is a lower limit to the rate achievable with coding, which only depends on the probability distribution of the symbols. This limit does not require any essential degradation in quality. The cost of the coding is a delay due to the encoder and decoder, and some computational complexity. There is also a delay due to the simultaneous coding of long blocks of symbols. There could also be other more evident kinds of redundancy, e.g. with respect to a human observer. There could also be redundancy with respect to a distortion measure used to evaluate the system. If there are several images which are equivalent with respect to the distance measure, it is only necessary to transmit one representative image, not each one in the equivalent set. Since the description of the encoder and decoder as tables is practically impossible to use, we will describe them with algorithms instead. This will, however, yield new problems. We need to consider the computational complexity of the algorithms, though in our case this will be secondary to the rate. Most algorithms we will consider will have a variable rate and distortion, thus they must be assessed by the relation between rate and distortion. Although the computational complexity will be secondary to the rate, we will only consider algorithms that are practically computable. We will use the available computing resources to find as good rate distortion relationships as possible.
19 1.3 Contractive set mappings Contractive set mappings A contractive function maps points onto new points such that when applied to any two points the distance between the new points will be less than the distance between the original points. Each contractive function on a complete metric space has a unique fixed point, i.e. a point which is invariant under the function. The fixed point is also defined as the limit when the function is iterated recursively starting with any point. The fixed point is also called an attractor. A set mapping is a function that maps sets onto other sets. In our case it is composed of functions which are applied to every point of the input set. The union of the function values is the output set. A characteristic of the functions used in this work is that if they are applied to a finite set, then the resulting set will have more points than the given set. In the next chapter a space of binary images and some classes of contractive set mappings on the space will be defined. Then we will see that there are complex and natural-looking attractors (images) that are defined by very few parameters which can be represented by very few bits. Since digital images require many bits for their representation, a very efficient representation can be achieved if these images are represented by their set mappings. The attractors described above are by definition fractal. They fulfil all the criteria for fractal images, hence our assumption is that it is possible to represent fractal images with functions that define attractors. Most of the mappings on the space of images considered in this work are composed of a number N of functions w 1,, w N. Likewise, the image W( A) is composed of the images w 1 ( A),, w N ( A). The subimages w i ( A) are called fragments, and the composite image W( A) is called the collage. The Collage theorem will be very useful in the coding procedure. Assume that there is an image that is to be represented by a contractive set mapping and that there is a mapping such that the distance between the image and the collage is small. Then the theorem states that the distance between the given image and the fixed point of the mapping is also small. This is useful because, in the attractor, every part of the image depends on all the parameters of the mapping, but in the collage most parts only depend on a small subset of the parameters. This will make the coding procedure less complex. For these ideas to be useful for image coding, we need to find a space where each point in the space can represent an image. Furthermore, we have to find a class of contractive mappings on this space where the mappings have a more compact representation than the fixed point (image) of the function. In Chapter 2 and 8 we will define spaces and classes of contractive mappings on these spaces where the points represent images.
20 8 Chapter 1 Introduction 1.4 Image coding with contractive set mappings The objective when coding images with attractors is to find a contractive mapping with an attractor that is close to the given image. The mapping should be possible to represent with a small number of bits. At present there are no practical algorithms that can solve this problem directly for a general case. We will therefore deal with the problem of finding a collage that is close to the given image with a small number of submappings. The collage approach reduces the dependencies between the parameters, and the rough measure of the rate as proportional to the number of submappings also simplifies the problem. If we let the mappings use an adaptive number of bits, the search for the mappings will again be too complicated. An attractor can be generated at any resolution. This does not mean that a large magnification can be used to show new details, but in some applications this can be a useful feature as an interpolation technique. Some caution is needed when discussing the compression of attractor images. Because the attractor can be generated at any scale and resolution, the compression will seem larger if the decoded image is large. 1.5 Distance measures An important factor in the construction and assessment of image coding algorithms is the distance measure. The distance measure is used to compute the distortion. The allowed distortion controls the performance of the coding system. An often occurring problem is that theoretical or practical considerations may give a distance measure which does not coincide with the user s subjective perception of quality. In particular for image coding based on the Collage theorem, the distance measure should be such that one can determine whether or not image transformations are contractive. In this work we will use three distance measures, the Hamming, the Hausdorff and the Kantorovich distance. Some distance measures (e.g. the Hamming distance) are separable in the image support. This means that if two images are divided into some parts, then the distance between the two images can be computed from the distance between the parts. This also makes it possible to measure whether subimages are close to some part of a full image. The Hamming distance is an often occurring distance measure. The Hausdorff distance comes from the theory of attractors where it is used to show that image transformations are contractive. In this context the Kantorovich (or Hutchinson) distance has its origin in the theory of fractals. Its relation to subjective perception of quality is not yet determined.
21 1.6 Outline Outline In Chapter 2 we describe three classes of contractive set mappings induced from IFS, RIFS and LIFS, which are used to model fractal binary images. Chapter 3 deals with algorithms for reconstructing binary images from the mapping parameters. We give an overview of algorithms that generate digital binary images approximating attractors which are induced by IFS s. The most important parameters of the algorithms are the accuracy and the computational complexity. We also describe how these algorithms can be applied to RIFS and LIFS and how they perform in terms of accuracy and computational complexity. Finally we consider the reconstruction of images defined by digital set mappings. In Chapter 4 some inverse problems related to IFS s are described, and a short overview of solutions found in the literature is given. In Chapter 5 we describe a search algorithm for the solution of the inverse problem of IFS s. In Chapter 6 a gradient search algorithm for the solution of the inverse problem of IFS s is described and tested. The gradient is based on the Kantorovich distance. In Chapter 7 we investigate the coding of general binary images. The search algorithm from Chapter 5 is extended to a subclass of RIFS and a subclass of LIFS mappings. The coding result of these algorithms is compared to some non-fractal coding schemes. In Chapter 8 we consider the coding of grey scale images. We define three models of fractal grey scale images, review some efficient algorithms that generate images from the mappings and briefly describe some coding algorithms for the three models. We describe some experiments from which we argue that higher resolution in the parameters of the spatial mappings give better coding in a rate distortion sense. In Chapter 9 two algorithms for the computation of the Kantorovich distance for images are described and compared. Chapter 10 contains our conclusions.
22 10 Chapter 1 Introduction
23 Chapter 2 Models of fractal binary images In which we describe three models of fractal binary images, i.e. basically classes of contractive set mappings on a complete metric space. We will also describe a digital model which can be used to approximate fractal binary images 1. Real world images are assumed to have the following properties (Barnsley and Hurd [7]): 1. They have a rectangular support and physical dimensions. 2. They possess chromatic attributes. 3. They are resolution independent. 4. The set of real world images is closed under the application of invertible affine mappings applied to clipped parallelograms within images chosen so as to yield rectangular images. In our case we will only consider black and white images, which means that the chromatic attributes are confined to two values. There are many examples of black and white images in the real world, e.g. some black and white photographs, fax images, laser printed pages (although they may seem to have many shades, this is the effect of a varying density of small dots) etc. Such images will be represented by binary images. We will discuss what is meant by fractal binary images and then define three related models of such images. 1. Most of the concepts described in this chapter come from the work of Barnsley et al. [5][6][7]. 11
24 12 Chapter 2 Models of fractal binary images 2.1 Representations of real world black and white images First in this section a mathematical representation of real world black and white images will be defined. The representation basically follows Barnsley and Hurd [7, p. 26, model (i)]. The representation has properties corresponding to the properties of real world images listed above. Real world black and white images will be represented by binary valued functions. The image support, or the domain of the functions, is defined in Definition 2.1 The image support D is a rectangular subset of. The image support is the set on which the binary valued functions are defined. It will typically be a square, e.g. [ 0.5, 0.5] 2. The image support should not be confused with the mathematical meaning of the support of a function, which is the closure of the set of all points at which the function is non-zero [40, p. 246]. Definition 2.2 With binary image we mean a binary valued function f : D { 01, } defined on the image support D. We will think of the binary image as containing a black object on a white background. Usually 0 will stand for white and 1 for black. Any set A D defines a binary image in the following way f A 2 1 : x A f A ( x) =ˆ x D. (2.1) 0 : x A Images treated by computers are usually spatially discrete besides being discrete in the grey scale. Binary computer images will be represented by digital binary images. Digital binary images will be used to approximate binary images. Thus, if D is the image support of binary images, then the corresponding support of digital binary images is defined in Definition 2.3 The digital image support D is a finite subset of D. The digital image support will typically be points in a square grid. The minimum distance between two points in the digital image support will be denoted δ. Usually there is a one-to-one correspondence between the points of the digital image support and the pixels of a computer image. Definition 2.4 With digital binary image we mean a binary valued function f : D { 01, } defined on the digital image support D.
25 2.2 Fractal binary images 13 A set A D defines a digital binary image f A according to (2.1) if in (2.1) D is replaced by D and A is replaced by A. Definition 2.5 The digital approximation [ A] D of a binary image A with reference to the digital image support D is the nearest digital binary image as measured by the Hausdorff metric (Def. 2.8). If there are several digital binary images that are nearest, then the one of them with the largest set is chosen. 2.2 Fractal binary images A set A defining a fractal binary image typically has most of the following properties (Falconer [15, pp. xx]). (i) A has a fine structure, i.e. details on arbitrary small scales. (ii) (iii) (iv) (v) A is too irregular to be described in traditional geometrical language both locally and globally. A has some form of self-similarity, perhaps approximate or statistical. The fractal dimension of A (defined in some way) is greater than its topological dimension. A is defined in a very simple way, perhaps recursively. According to Falconer it seems difficult to make an unambiguous definition of what fractal means. When we refer to an image as fractal, it will fulfil most of the above properties. Property (v) is interesting from an image coding point of view. It suggests that fractal images have simple descriptions, which implies that they can be represented by a small number of bits. Attractors defined by contractive set mappings are, with few exceptions, fractal, i.e. they fulfil all the properties listed above. A fractal dimension The fractal dimension can be used as an indication of whether or not an image is fractal. The fractal dimension can also be used to restrict the search space for the inverse problem of IFS s by requiring that the attractor of the IFS has the same fractal dimension as the given binary image. The use of the fractal dimension will not be pursued any further in this thesis. However, because fractal dimension is a key property of fractal binary images, we will give the definition of a fractal dimension. Let ( X, d) be a complete metric space and let ( X) be the set of all compact non-empty subsets of X. Let A ( X) and let N( A, ε) denote the smallest number
26 14 Chapter 2 Models of fractal binary images of closed balls of radius ε needed to cover A. The intuitive idea behind fractal dimension is that a set A has fractal dimension D if N( A, ε) Cε D (2.2) for some positive constant C when ε is small, which leads to Definition 2.6 (Barnsley [6, p. 174]) Let ( X, d) be a metric space and let A ( X). Let N( A, ε) denote the smallest number of closed balls of radius ε needed to cover A. If D = ln( N( A, ε) ) lim ln( 1 ε) ε 0 (2.3) exists, then D is called the fractal dimension of A. It can be difficult to compute an approximation of the fractal dimension based on this definition due to the requirement to find the minimum number of balls of some size which cover the object. The next theorem, formulated for sets in m, tells us that, for sets in 2, the same result is obtained if the object is covered with a crossruled paper and the number of squares which intersect the object is counted. Theorem 2.1 Box Counting Theorem (see e.g. Barnsley [6, pp. 176]) Let A ( m ), where the Euclidean metric is used. Cover m by closed just-touching square boxes of side length ( 2 n ). Let N n ( A) denote the number of boxes of side length ( 2 n ) which intersects A. If D = ln( N n ( A) ) lim ln( 2 n ) n (2.4) then A has fractal dimension D. Proof: See Barnsley [6, pp. 177]. An estimation of the fractal dimension for a set A can be computed [6] by first computing some points ( ln( N n ( A) ), ln( 2 n )) for different n and then fitting a line by least squares method to the points. The slope of the line is then an approximation of the fractal dimension.
27 2.3 A metric space and two theorems A metric space and two theorems A metric space of sets and two theorems are behind the theory of attractors, as used for image coding. The elements of a metric space of sets can be used to represent binary images. The fixed point theorem shows that there is a unique point associated with every contractive function. The Collage theorem will simplify the encoding. A metric space of binary images The metric space of sets can be constructed in the following way. Let ( X, d) be a metric space. Let ( X) be the set of all compact non-empty subsets of X. The Hausdorff distance. This is a distance measure between sets of points, e.g. elements in ( X). It is defined in two steps. The distance from a set to another set is defined in Definition 2.7 (Barnsley [6, p. 31]) Let A, B ( X). The distance from A to B denoted d * H is defined by d H * ( A, B) =ˆ sup dab (, ). (2.5) Note that if A B and B \ A, then d * H ( A, B) = 0 and d H* ( B, A) > 0, hence d * H ( A, B) is not symmetric and thus not a metric. The distance between two sets is defined in Definition 2.8 (Barnsley [6, p. 34]) Let A, B ( X). The Hausdorff distance ( A, B) is defined by d H d H The Hausdorff distance is a metric [6, p. 34]. Thus, ( ( X), d H ) is a metric space. a A b B * ( A, B) =ˆ max( d H ( A, B), d * H ( B, A) ). (2.6) Remark. A binary image f A defined by the set A ( 2 ) can be represented by a set mapping W : ( 2 ) ( 2 ) if W( A) = A and A is the only fixed point of W. Theorem 2.2 (Barnsley [6, pp. 37]) If ( X, d) is a complete metric space, then ( ( X), d H ) is a complete metric space. inf
28 16 Chapter 2 Models of fractal binary images The fixed point theorem Let ( X, d) be a complete metric space. Definition 2.9 (Barnsley [6, p. 75]) A function f : X X on a metric space ( X, d) is called contractive if there is a constant s [ 01, ) such that d( f( a), f( b) ) sd( a, b) ab, X. (2.7) Any such number s is called a contractivity factor for f. The n-fold recursive application of f is denoted f ( n) () =ˆ f( f( f ( () ))) n times. (2.8) Banach s fixed point theorem can be formulated as follows (Barnsley [6]). Theorem 2.3 Let ( X, d) be a complete metric space and f : X X a contractive function. Then there exists a unique point x such that f( x * ) = x * and lim n f ( n) ( x 0 ) = x (2.9) for any initial point X. x 0 Definition 2.10 of the mapping. We will call the fixed point of a contractive mapping the attractor Remark. From Theorem 2.2 and Theorem 2.3 it follows that every contractive set mapping W : ( 2 ) ( 2 ) has a unique fixed point x * ( 2 ), thus W can be used to represent x *. The Collage theorem Theorem 2.4 (The Collage theorem (Barnsley [6, p. 96]) Let ( X, d) be a complete metric space. For any point x X and any contractive mapping f with fixed point x * it holds that d( x, x * 1 ) d( x, f( x) ) 1 s (2.10) where s is a contractivity factor for f.
29 2.4 Iterated function systems 17 There is a very short proof of the Collage theorem. Proof: (Dekking [11]) We have from which the statement follows. d( x, x * ) = d( x, f( x * )) d( x, f( x) ) + d( f( x), f( x * )) d( x, f( x) ) + sd( x, x * ) (2.11) Remark. Let A be a given set and W a contractive set mapping such that d H ( AWA, ( )) is small. Then it follows from Theorem 2.4 that the fixed point x * of W is also close to A. In later chapters we will see that the Collage theorem can be used to simplify image encoding algorithms. 2.4 Iterated function systems Iterated function systems (IFS) will be used for modelling fractal binary images. Definition 2.11 (Barnsley [6, p. 82]) An iterated function system (IFS) consists of a finite set of N contractive mappings { w i : X X, i = 1,, N } on a complete metric space ( X, d). A contractivity factor for the IFS is s = max{ s i, i = 1,, N }, where s i is a contractivity factor for w i. We denote an IFS by W = { X; w i, i = 1,, N }. by Let W be an IFS. The IFS W induces a set mapping N W m ( A) =ˆ w i ( A) i = 1 W m : ( X) ( X) defined (2.12) where as usual w i ( A) =ˆ w i ( x). (2.13) x A We will call W m ( A) the collage of A induced by W and w i ( A) a fragment of A induced by. We will use the notation W( A) =ˆ W m ( A). w i
30 18 Chapter 2 Models of fractal binary images Theorem 2.5 (Barnsley [6, pp. 82]) Let W = { X; w i, i = 1,, N } be an IFS with contractivity factor s. Then, the set mapping W m : ( X) ( X) induced by the IFS is a contraction mapping on ( ( X), d H ) with contractivity factor s. From Theorem 2.5 and the fixed point theorem it follows that the set mapping induced from an IFS has a unique fixed set, which can be interpreted as a binary image. Hence the IFS can be used to represent the binary image. 2.5 Recurrent iterated function systems Recurrent iterated function systems (RIFS s) will be used for modelling fractal binary images and define a wider class of attractors than IFS s. RIFS generalise the IFS structure to multiple spaces and set mappings. Let ( X, d) be a compact metric space and let ( H, d H ) be the associated metric space of non-empty compact subsets of X with the Hausdorff metric. Let =ˆ H, i = 1,, N. H i Definition 2.12 (Barnsley et al. [5]) A recurrent iterated function system (RIFS) consists of a set of contractive set mappings { W ij : H j H i, ( i, j) I}, where I is a set of pairs of indices such that for each i 1,, N there is a j 1,, N, where ( i, j) I. Acontractivity factor of the RIFS is s = max{ s ij : ( i, j) I}, where s ij is a contractivity factor for the set mapping W ij. We denote an RIFS by W = { H; W ij : H j H i, ( i, j) I}. Let H = H 1 H N, where H i =ˆ H, i = 1,, N. Let A, B H. Define the metric according to d H d H ( A, B) =ˆ max{ d H ( A i, B i )} i = 1. (2.14) If ( H i, d H ), i = 1,, N are N compact metric spaces, then ( H, d H ) is a compact metric space [5, pp. 13]. An RIFS W induces a set mapping W : H H defined by W( A) =ˆ ( W 1 j ( A j ),, W Nj ( A j )). (2.15) j : ( 1, j) I j: ( N, j) I Theorem 2.6 (Barnsley et al. [5]) Let W be an RIFS with contractivity factor s. Then, the set mapping W : H H induced from the RIFS has contractivity factor s on ( H, d H ). From Theorem 2.6, the fixed point theorem and the fact that a compact metric space is complete it follows that W has a unique fixed point A H. The union of the N
31 2.5 Recurrent iterated function systems 19 components from the fixed point, i.e. image. A = N i = 1 A i, can be interpreted as a binary Remark. A function f is called eventually contractive and has a unique fixed point if f ( n) is contractive for some n [16]. It is not necessary that every set mapping in an RIFS is contractive for the set mapping induced by the RIFS to be eventually contractive. If e.g. an expansive mapping is followed by only contractive mappings, then the composed mapping induced by the RIFS can be eventually contractive. In this work we will only consider set mappings W ij induced from sets of contractive mappings as follows: { w ijt : H j H i, t = 1, N ij } induce the set mapping W ij : H j H i defined by N ij W ij ( A) =ˆ w ijt ( x). (2.16) t = 1 x A Examples. In Figure 2.1 there is an example of an RIFS with five mappings on a space H = ( H 1, H 2 ) with two components. The set mappings are induced from sets of similitudes where each similitude is denoted by ( α, st, x, t y ) as shorthand for w( p) s cosα sinα t p x = +. (2.17) sinα cosα t y H 1 H 2 W H 1 H 2 Figure 2.1 An example of an RIFS and the corresponding attractor. The RIFS is defined on a space with two components and has five affine mappings.
32 20 Chapter 2 Models of fractal binary images H 1 H 2 H 1 H 2 A 0 A 1 A 2 A 3 A 15 Figure 2.2 An example of an image of the attractor induced from an RIFS with four affine mappings on a space with two components. The rows show the initial image, the first three and the fifteenth iteration.
33 2.5 Recurrent iterated function systems 21 The four set mappings induced from five similitudes are W 11 = {( 0, 0.5, 128, 128), ( 0, 0.5, 128, 128) } W 12 = {( 0, 0.8, 256, 0) }. (2.18) W 21 = {( 0, 0.1, 215, 215) } W 22 = {( 0.52, 0.9, 76, 2) } Figure 2.2 is another example of an RIFS, which is defined on a space H = ( H 1, H 2 ) with two components and has four affine mappings, where each mapping is denoted by abe cd f (2.19) as shorthand for wx ( ) = ab x e +. (2.20) cd f The four set mappings of the RIFS are induced from the sets of affine mappings W =, W = (2.21) W = There is another definition of RIFS, slightly less general than the RIFS defined above. If the set mappings of the RIFS above are induced from contractive mappings as in (2.16), then these contractive mappings can be used in an RIFS as defined below. If the RIFS as defined below fulfil a condition, then the two RIFS s give the same attractor. Definition 2.13 (Barnsley et al. [5]) A single space recurrent iterated function system (ssrifs) consists of a set of N contractive mappings { w i : X X, i = 1,, N } on a complete metric space ( X, d) and a N N row stochastic matrix P r = ( p ij ).
34 22 Chapter 2 Models of fractal binary images We say that there is a connection from w j to w i if p ji > 0. An ssrifs has complete connections if it is possible to connect every mapping w j to every mapping w i through one or several mappings. The ssrifs induces a Markov random model. If there are complete connections, then the Markov model induces a unique probability distribution. We will only consider the support of the probability distribution. The support is also called the attractor of the ssrifs. If there are not complete connections, then there may be several different attractors, each generated by a subset of the mappings. We will be interested in the largest attractor, which is the union of all attractors. An RIFS W can be obtained from an ssrifs W ss = { Xw ; i, p ij, i, j = 1,, N } in the following way. Assume that ( X, d) is a compact metric space. Let H = H 1,, H N where H i = X, i = 1,, N, let I = {( i, j) : p ji > 0} and let W ij = w i, ( i, j) I. The RIFS W has a unique fixed point B = ( B 1,, B N ) such that B = W( B) with B i = W ( ), thus B i = w i ( B x ). x : ( i, x) I ix B x x : p xi > 0 Theorem 2.7 (Barnsley et al. [6]) Let ( X, d) be a complete metric space. Let W ss = { Xw ; i, p ij, i, j = 1,, N } be an ssrifs. Let A be the attractor defined by W ss. Then there exist unique compact sets A i A with = A such that A i A i = j: p ji > 0 w i ( A j ). (2.22) It follows from the construction of the RIFS and Theorem 2.7 that A i = B i, i = 1,, N. The subsets A i, i = 1,, N can be determined by making a random walk according to the Markov model defined by the ssrifs. The points which were last mapped by the mapping belong to the set. w i A i 2.6 Local iterated function systems Local iterated function systems (LIFS s) define a wider class of attractors than IFS and also a class of attractors partially different from those defined by RIFS. The locally contractive mappings of an LIFS are defined on arbitrary subsets of a space instead of on the whole space as for the contractive mappings of IFS s and RIFS s. LIFS are also called partitioned IFS (PIFS) [16]. Definition 2.14 (Barnsley and Hurd [7]) Let ( X, d) be a compact metric space. Let R be a non-empty subset of X. A function f : R X is called locally contractive or a local contraction mapping if there is a constant s [ 01, ) such that d( f( a), f( b) ) sd( a, b) ab, R. (2.23)
35 2.6 Local iterated function systems 23 Any such number is called a contractivity factor for f. Definition 2.15 (Barnsley and Hurd [7]) Let ( X, d) be a compact metric space and let R i X, i = 1,, N. A local iterated function system (LIFS) consists of a finite set of locally contractive mappings { w i : R i X, i = 1,, N }. A contractivity factor for the LIFS is s = max{ s i, i = 1,, N } where s i is a contractivity factor for w i. We denote an LIFS by W = { X; w i : R i X, i = 1,, N } Let S denote the set of all subsets of X. An LIFS W induces a set mapping W m : S S defined by N W m ( A) =ˆ w i ( R i A). (2.24) i = 1 We will use the notation W( A) =ˆ W m ( A). We follow Barnsley and Hurd [7] closely. Let W be an LIFS and suppose that R i, i = 1,, N are compact subsets of X. Let A n, i = 01,, be a sequence of compact subsets of X defined by A 0 = X and A n = W m ( A n 1 ). Then A 0 A 1 A 2, i.e. a decreasing set of compact subsets. There exists a compact set A X such that lim A n n = A (2.25) and A = W m ( A). If A is not empty, then it is the largest attractor for the LIFS W. If there is a non-empty compact subset B such that W( B) B then the attractor of W is non-empty. The attractor is also non-empty if w i ( R i ) R i for any i [7, p. 179]. An LIFS may have no attractor or it may have many [7, pp. 177]. When we speak of the attractor of an LIFS, we mean the largest one which is the union of all attractors of the LIFS. Remark. The set mapping induced from an LIFS can be eventually contractive even though not every mapping of the LIFS is contractive. Example. Figure 2.3 shows a schematic example of an LIFS. Figure 2.4 shows another example of an LIFS with four mappings
36 24 Chapter 2 Models of fractal binary images w 1 = ( 1.57, 0.36, 0.13, 0.31) w 2 = ( 1.57, 0.36, 0.18, 0.27) w 3 = ( 0.19, 0.7, 0, 0.08) w 4 = (2.26) with the corresponding domain regions D 1 = D 3 = [ 0.5, 0.5] [ 0.5, 0.5] D 2 = D 4 = [ 0.5, 0] [ 0.5, 0.5]. (2.27) Some iterations from the generation process are also shown. 2.7 Iterated digital set mappings We will use digital set mappings as approximations of set mappings induced by IFS, RIFS and LIFS. The digital image support is a subset of the image support, thus the set mappings induced from IFS, RIFS and LIFS can be applied to digital binary images. The resulting images, however, will generally not be digital binary images, but binary images. Thus the application of the set mappings is not closed on the space of digital binary Figure 2.3 An example of an LIFS with five mappings defined on four subsets of the image support. The image shows a representation of the mappings.
37 2.7 Iterated digital set mappings 25 A 0 w 1 ( A 0 ) w 2 ( A 0 ) w 3 ( A 0 ) w 4 ( A 0 ) A 1 = W( A) = w i ( A 0 ) w 1 ( A 1 ) w 2 ( A 1 ) w 3 ( A 1 ) w 4 ( A 1 ) A 2 A 3 A 4 A 5 A 8 Figure 2.4 An example of an image of the attractor induced from an LIFS with four affine mappings. In the top row the initial image is shown. In the second row the images resulting from applying the four mappings to the initial image are shown. The third row shows the union of the four images from the previous row. On the third to fifth row the second iteration are shown. The last row shows iterations 3, 4, 5, and 8.
38 26 Chapter 2 Models of fractal binary images images. Here we will define digital set mappings, which are closed on the space of digital binary images. Let D be the support of digital binary images and let D * be the set of all nonempty subsets of D. The sets of D * are used to define digital binary images. Let W be a set mapping, in our case induced from an IFS, RIFS or LIFS. The digital set mapping W D : D * D * is defined as W D ( A) =ˆ [ W ( A) ] D (2.28) where A D * is a digital binary image. (See Definition 2.5 for a definition of [] D.) We will call W D the digital approximation of W. Let A 0 = D and define A n = W D ( A n 1 ), i = 12,,. Then A n is a sequence of sets with non-increasing number of points. There is an n such that An = A n 1. Then A n is a fixed set of the digital binary set mapping W D. There can also be other sets with fewer points that are invariant to the digital binary set mapping.
39 Chapter 3 Image generation In which we describe and compare some algorithms which generate approximations of attractors induced from IFS, RIFS and LIFS. In this chapter we describe a tree algorithm which generates digital binary images approximating the attractors induced from IFS s and single space RIFS s. The computational complexity is proportional to the number of points in the digital image support. Some other algorithms for the generation of digital binary images approximating attractors induced from IFS, RIFS and LIFS are described for comparison. 3.1 Iterated function systems Let W = { 2 ; w i, i = 1,, N } be an IFS with contractivity factor s and the attractor A. Let D be the digital image support and let δ denote the minimum L 1 distance between the points in the digital image support. The Hausdorff distance used is based on the -metric. L 1 The Tree algorithm A S x * where x * : w i ( x * ) = x * for some w i W while S do begin take any x S S S \ x for i = 1 N do 27
40 28 Chapter 3 Image generation end if [ w i ( x) ] D A then begin end A A [ w i ( x) ] D S S w i ( x) The Tree algorithm is illustrated in Figure 3.1. Theorem 3.1 The distance between the set A given by the Tree algorithm and the attractor A is limited by d H * ( A, A) δ (3.1) and Figure 3.1 An illustration of the Tree algorithm. The squares correspond to the pixels of a low resolution digital binary image. The grey fern image is an approximation of an attractor. The algorithm starts with the point in the uppermost marked square. The point is the fixed point of one of the mappings. The lines show points which follow by application of one of the affine mappings. One square is reached by the mapping of two points, which illustrates the stop criterion. When a point is mapped to a pixel which already has a point, then this branch is ended.
41 3.1 Iterated function systems 29 d H * 2δ ( A, A) δ. (3.2) 1 s Proof: Let à be the points that in the algorithm are approximated to become A. First we prove (3.1). Note that x * is such that w i ( x * ) = x * for some w i W and thus by Theorem 2.3 x * A. Theorem 2.3 and x * A give that W( { x * }) A and W ( 2) x * * ({ }) A and so on, thus à A. Since à A, then d H ( Ã, A) = 0. Thus * * d H ( A, A) = d H ([ Ã] D, A) δ. Then we prove (3.2). The algorithm gives d H* ( W( Ã), Ã) 2δ and further by the contractivity of W d H* ( W ( 2) ( à ), W( Ã) ) s2δ, d H* ( W ( 3) ( Ã), W ( 2) ( Ã) ) s 2 2δ and so forth. Thus by d * H ( AC, ) d * H ( A, B) + d H* ( BC, ) [6, p. 34] it follows that d H * ( A, Ã) d * H ( W i ( Ã), W i 1 ( Ã) ) i = 1 Finally we use the triangle inequality again to get = 2δ (3.3) 1 s d H * ( A, A) d * H ( A, Ã) + d * H ( Ã, A) = 2δ δ 1 s (3.4) The computational complexity of the algorithm is proportional to the number of points in A. A variant of the Tree algorithm, the Graphic algorithm, is described by Dubuc and Elqortobi [13]. The Graphic algorithm is obtained from the Tree algorithm by changing S x * to S [ x * ] D and S S w i ( x) to S S [ w i ( x) ] D. Let A be the set given by the Graphic algorithm. Then d H where s is a contractivity factor of W [13]. ( A, A) δ, (3.5) s Remark. The algorithms have the same computational complexity. The Graphic algorithm has the best bound of the Hausdorff distance between the attractor and the * approximation. However, the Tree algorithm has d H ( A, A) = δ, which is better than * the Graphic algorithm s d H ( A, A) = δ ( 1 s).
42 30 Chapter 3 Image generation The Stochastic Algorithm (Barnsley and Demko [3]) The Stochastic algorithm is suggested by Barnsley [6] as a way of generating an approximation of the attractor induced from an IFS. Let { Φ n } n 1 be a sequence of independent random integer variables with values in { 1,, N }. For any i { 1,, N } and any integer n, pr( Φ n = i) > 0. Choose a starting point x 0 2. Define a sequence of points x n = w Φn ( x n 1 ), i = 12,,. Except for the first few points, x n is close to the attractor A. If the x 0 is chosen to be the fixed point of one of the contractive mappings, then x n An, = 01,,. There are two problems with this algorithm. How should the probabilities be chosen, and how is a suitable stopping rule constructed if an approximation of the attractor with a given accuracy is demanded? A lower bound on the computational complexity is ON ( logn), where N is the number of points in the digital binary image approximating the attractor [36]. The Iterative algorithm (Hutchinson [23]) The Iterative algorithm is an application of (2.9) in Theorem 2.3. Let B 0 ( 2 ) be any initial set and let B n = W( B n 1 ), i = 12,,. (3.6) If B 0 A, e.g. the fixed point of one of the contractive mappings, then B n = B n 1 W( B n 1 ). is an approximation of A with B n d H where s is a contractivity for W and 1 ( A, B n ) d, (3.7) 1 s H ( B n, B n + 1 ) d H ( A, B n ) s n d H ( A, B 0 ). (3.8) A problem with this algorithm when applied to finite sets is that the number of points in B n grows exponentially with n. For example, if an IFS has four mappings, s = 0.8 and it is required that d H ( A, B n ) 0.01d H ( A, B 0 ), then 21 iterations are needed and the number of points will increase by a factor of
43 3.1 Iterated function systems 31 The Escape time algorithm Let B A. The attractor is the set of points which do not diverge to infinity when the inverse function W 1 is applied iteratively starting from the points [6]. A B p B d 0 ( W 1 ) ( n) = \ : lim (, ( p) ) n (3.9) Let a bound δ be given as a distance from the origin within which the attractor is found. Let n be the chosen number of iterations. If a point is within the bound after n iterations, then the point is considered as belonging to the attractor. An approximation of the attractor is given by à = { x D : B ( W 1 ) ( n) }. (3.10) The Escape time algorithm is most practical to apply to IFS s if the fragments are separate and the regions of the fragments are known. Then it is known which inverse mapping to apply, and the iterations will give a sequence of points. If the regions are not known, every mapping has to be applied in every step, which will result in a tree of points. When a point is outside the limit, then that branch can be stopped. A point is in the attractor if at least one branch of points does not diverge. The Escape time algorithm is computationally unstable since the inverse function is expansive, which means that a small error in the computation is enlarged in the following iterations. Most points will eventually diverge due to small error occurring in the calculations. The Transform composition algorithm (Williams [52]) be the set of all composi- Let W be an IFS, i.e. a set of N affine mappings. Let tions of n functions W n { ( w 1 w ) w W i 1 n n :, =,, } i (3.11) and let W * = W n. Let W ( ε ) be the set of compositions with contractivity n = 1 factor smaller than or equal to ε and such that if the last mapping is removed, then the contractivity factor increases above ε. The set B = { Fix( g) : g W( ε) } where Fix( g) is the fixed point of g is an approximation of the attractor A. Let A be the attractor induced by a given IFS W, and let B be the set of fixed points as described above. Then d( A, B) εdiam( A), where diam( A) = sup{ d( x, y) : x, y A} [13]. It is not necessary to compute the fixed points of the composed mappings. Assume that the attractor is a subset of S 2. Then the fixed point of the mappings
44 32 Chapter 3 Image generation must be within the transformed subset S. Thus taking any point within the boundary of the attractor and transforming it with all mappings in the set B, the resulting points are very close to the attractor. The computational complexity is determined by the contraction factors of the affine mappings and the resolution of the generated image. Let a contractivity factor ε be given. V { w i, i = 1,, N } while u V with contractivity factor s > ε V ( V \ u) { u w i, i = 1,, N } Ã = x 2 : wx ( ) = x w V Then ( A, Ã) εdiam( A) where diam( A) = sup{ d( x, y) : x, y A} [13]. d H Let a region of interest I 2 and a spatial bound B A of the attractor be given. V { w W : wb ( ) I } while u V with contractivity factor s > ε V ( V \ u) { u w: ( w W) ( u w( B) I ) } Ã = wb ( ) w V Then 3.2. d H ( A I, Ã I) εd H ( A I, B I). The algorithm is illustrated in Figure Remark The algorithms above generate digital approximations of approximations of the attractor. In general it is not possible to generate the digital approximation of an attractor because 1; the attractor is an infinite set of points and can thus not be practically generated, 2; an approximation of an attractor with the corresponding uncertainty does not generally give a unique digital approximation for all possible outcomes of the attractor within the uncertainty. 3.2 Recurrent iterated function systems The attractor of multiple space RIFS s can be approximated by the Iterative, Transform composition and Escape time algorithms. It is not necessary that an RIFS is recurrent, thus there can be several attractors, each within a subset of the components of the space. The Tree algorithm can be used if an initial point in each separate attractor is chosen. A point in the attractor can be found as the fixed point of a recurrent sequence of mappings.
45 3.3 Local iterated function systems 33 The Stochastic algorithm cannot be used because there may be dead ends, i.e. components of the space which has no mapping defined on them. The attractor of a singe space RIFS can be approximated by the Stochastic, Transform composition and the Escape time algorithms. For the Stochastic algorithm it is preferable to start with an initial point which is a member of the attractor. A point of the attractor can be found as the fixed point of a recurrent sequence of mappings. A single space RIFS can be viewed as a multiple space RIFS by using a component space for each mapping. Thus, it is possible to generate an approximation of the attractor by using the algorithms applicable to multiple space RIFS. 3.3 Local iterated function systems If the LIFS has several attractors, the result of the Iterative algorithm depends on the initial set. The Stochastic algorithm will get stuck on one of the attractors. If a spatial bound of the attractor is known, then the Iterative algorithm starting with any set which includes the attractor will converge towards the attractor Figure 3.2 Illustration of the transform composition algorithm. Assume the attractor is confined within the square in image 0. Application of the set mapping once gives that the attractor is confined within the two squares in image 1, and so forth until the individual squares are small enough to give the required accuracy.
46 34 Chapter 3 Image generation 3.4 Digital set mappings Let W D be the digital approximation the set mapping W induced from an IFS, RIFS or LIFS. Let A denote the attractor of W and let s denote the contractivity factor of W. Here we describe an efficient implementation of the iterations used in Section 2.7 to show that there is a largest digital fixed set for every digital set mapping. d H n p = { q D : p W( { q} )}, p D S { x D : n x = 0} for all x S do begin for all y W( { x} ) do begin end end S S \ x A = { x D : n x > 0} n y n y 1 if n y = 0 then S S y Let A be the digital binary image generated by the algorithm above. Then ( A, W ( A) ) δ, which by the Collage theorem gives d H ( A, A) δ. (3.12) s The algorithm gives the digital binary image A with the largest set such that W D ( A) = A. The computational complexity is proportional to the number of points in the digital image support. 3.5 Conclusion The Tree algorithm is fast and yields a high accuracy, which is determined by the contractivity factor of the IFS and the resolution of the generated digital binary image. The Tree algorithm can also be used for single space RIFS. However, if the connections are incomplete, there is a risk that only a part of the attractor will be generated. In such a case, the complete attractor can be generated by starting with several initial points.
47 3.5 Conclusion 35 For both RIFS and LIFS there is a risk of dead ends. Complete connections are necessary in some cases, e.g. for the Stochastic algorithm. An RIFS attractor can be generated in only one image plane by the Stochastic algorithm, but it requires complete connections. It is an advantage to start with a fixed point, but this is more difficult than in the IFS case. In all the above cases it is necessary to know a spatial bound of the attractor. If some part of the attractor is outside the image support, then all ancestors or descendants of the points of the attractor being outside of the image support will be missing. Hence there will be errors everywhere in the image. The Stochastic algorithm does not have this problem. The stochastic jumping point defined by the stochastic model will cover the attractor. If a small part of the attractor is outside of the image support, then there are no problems. But if only a small part of the attractor is to be approximated, then algorithm will take much unnecessary time because many of the generated points will be outside of the area of interest. If only a small part of the attractor is to be generated, then the Transform composition algorithm can be used. Iterating the digital set mapping can generate IFS, RIFS and LIFS attractors.
48 36 Chapter 3 Image generation
49 Chapter 4 Inverse problems of IFS s In which we describe some inverse problems related to IFS s, make some remarks on the existence and characteristics of solutions, and give an overview of solutions presented in the literature. Inverse problem 1 (Image representation problem). Let A be a given binary image. Given ε > 0, find an IFS W with the attractor A W * such that d H ( A, A W * ) ε. For any given binary image there is a solution to Inverse problem 1 [15, pp. 134]. A solution is obtained by covering the given binary image with many small fragments. There is a requirement that the contractivity factors of the mappings are small enough. The translation of each mapping is given by the solution. However, there is no other requirement on the mappings. If affine mappings are used, then the parameters determining the deformation can be chosen arbitrarily as long as the contractivity factors are small enough. Thus, if the given image is the attractor induced from an IFS W, then it is not likely that the solution obtained is close to W or any solution with compositions of mappings from W. If the given binary image is an attractor induced from an IFS, then this IFS is a solution to Inverse problem 1. However, the attractor induced from an IFS cannot be given to a computer for the solution of the inverse problem in a form which preserves the meaning of the inverse problem. A binary image can be given to a computer as a finite list of points, but most attractors, including those that we are concerned with in this thesis, are infinite sets of points. A binary image can also be given as a method for generating the points. However, if the method includes the mappings, then there is no inverse problem. If the given binary image is an approximation of the attractor induced by an IFS, then the IFS is a solution if ε is not too small. Inverse problem 2 (Image coding problem). Let A be a given binary image. Given ε > 0, find an IFS W with as few mappings as possible and an attractor A W * such that ( A, A W * ) ε. d H 37
50 38 Chapter 4 Inverse problems of IFS s The solution is an IFS with a subset of the set of all contractive mappings inducing a fragment that is close enough to the given image. The solution is the smallest set such that the induced collage is close enough to the given image. No efficient algorithm is known which solves this problem. We have chosen to formulate the Image coding problem as to minimise the number of mappings instead of as to minimise the number of bits, which perhaps would have been more appropriate. Binary images generated from IFS s with few mappings can be efficiently represented by the IFS. However, it is not known whether the IFS is the solution to the Image coding problem. Inverse problem 3 (Inverse problem of IFS s). Let A be a given digital binary image approximating the attractor induced from an IFS W with N mappings. Given an arbitrary ε > 0, find an IFS W with N or fewer mappings and an attractor A W * such that ( A, A W * ) ε. d H A partial solution to Inverse problem 3 can be obtained by using the Collage theorem (Theorem 2.4). The Collage theorem states that if there is an IFS W such that * d H ( AW, ( A) ) ε, then the attractor A W induced from the IFS W is such that d H ( A, A W * ) ε ( 1 s), where s is a contractivity factor for the IFS W. The Collage theorem together with the Hausdorff metric relax the dependence between the parameters of the IFS. Most of the points in the attractor depend on all parameters of the IFS, whereas each point in the collage only depends on the parameters of one of the affine mappings. If the given digital binary image is an approximation of the attractor induced from an IFS, then the IFS is a solution if ε is not too small. Since every binary image can be represented by an IFS it is not possible to make a distinction between images generated from IFS s and other images. Image coding is about the trade-off between rate and distortion. However, the inverse problem of IFS s does not imply any such trade-off. The inverse problem of IFS s with probabilities assigned to the mappings is closely related and treated in many papers, e.g. [12], [17], [33]. An IFS with probabilities induces a probability distribution. The inverse problem is to find the IFS and the probabilities from a given probability distribution. The images treated in this work can be viewed as the support of probability distributions induced from IFS s with probabilities. Under some conditions these methods can be used for binary IFS images. Previous solutions to inverse problems of IFS s Most previous work on the inverse problem has been concentrated on the problem of finding a collage that is within some given arbitrary, small distance, from the given image and only to a lesser degree considered minimising the number of mappings.
51 Also much of the previous work concerns the inverse problem of IFS s with probabilities. In this case a probability measure is given, and in addition to finding the affine mappings a probability for each mapping has to be found. In some cases a solution to this problem could be useful for our problem. In that case an assumption has to be made about the probabilities. In one case the solution for the inverse problem of IFS s with probabilities is divided into two parts, where the first part is the same as our problem and in the second part the probabilities are determined. A solution of this kind can be used for our problem. The first to mention the inverse problem of IFS s with probabilities and to present a solution were Barnsley and Demko [3] in They show an example where an approximation of the parameters of an IFS with two mapping defining a twin dragon is found from the image by moment equations. They do not mention the image coding related problem of finding a minimum number of affine mappings. In 1986 Diaconis and Shahshahani [12] gave the moment equations which solve the inverse problem in one dimension. They conclude that the equations extend to higher dimensions, but the algebraic manipulations are significantly more complex and the applicability of their procedure to actual problems was not tested by them. In 1986 Barnsley et. al. [4] presented the Collage theorem as a solution to the inverse problem. The Collage theorem states that if there is a collage that is close to the given image, then the attractor defined by the collage mapping is also close to the given image. However, no indication is given of how to find the collage. Levy-Vehel and Lutton [31] (1994) propose genetic algorithms to solve the inverse problem, Their goal is to find n contractions such that the attractor of the IFS is close to the given image in the Hausdorff metric. They propose to use a fractal dimension for a lower bound on the number of mappings. They claim that the distance function between an attractor and an attractor where the IFS is perturbed with a small number is fractal. Thus they propose genetic algorithms to find the minimum of this distance. They provide arguments for their choices of parameters for the genetic algorithm. The fern mappings were found by their algorithm in four hours of computing time. Hart et. al. [19] (1995) propose similarity hashing to solve the inverse problem. They first look for a set of feature points in the image. For all pairs of line segments defined by quartettes of feature points they find the scaling and rotation that relate the two line segments. By plotting the scale and rotation parameters in a diagram there will be a high concentration of points at the parameters of the self-similarity of the image. This can be extended to all parameters of the affine mappings. They show a few examples of IFS images with manually chosen feature points where similarity hashing is used to find the parameters. Hocevar and Kropatsch [22] (1995) show that knowledge of the fixed points of the individual affine maps can be used to find the other parameters of the affine maps of a non-convex, undistorted, connected attractor. They take the set difference between the attractor and a copy of the attractor rotated around the fixed point of an affine mapping. The connected attractor will be split in several disconnected components. There are some demands on the rotation angle. The transformation is given as the mapping that maps the largest component on the second largest component. They 39
52 40 Chapter 4 Inverse problems of IFS s do not show how to find the fixed points, how to automatically determine the two largest components or how to find the mapping. Forte and Vrscay [17] (1995) describe an algorithm that, to an arbitrary accuracy, approximates a probability measure with the attractor of an IFS with probabilities. They use a fixed set of mappings and let only the probability vary. They prove a collage theorem for moments, which makes it possible to minimise the distance between moment vectors. Luenberger [33] (1995) considers the inverse problem of iterated function systems with probabilities. An image is considered to be a measure and an approximation of the Kantorovich metric is used as a fidelity criterion. To simplify the search, Luenberger reduces the class of functions to a small set (a fractal library) and only lets the probability of each function vary. If the spatial mappings are given, then the probabilities of the mappings are given by an optimisation procedure. Ibenthal and Grigat [24] (1997) presents a method to find contraction factors and rotation which works by applying the Fourier transform to the image followed by taking the logarithm of the Fourier transformed coordinates followed by a second Fourier transform. The contraction factor appears as peaks in the resulting image. The results presented concern only global contraction factors and the factors of simple IFS images. Berkner [10] (1997) presents a method based on the continuous wavelet transform, of finding the number of transforms in a one-dimensional fractal IFS function.. With certain conditions on the wavelet transform it is possible to find the end points of the intervals. This method can be extended to images, but it is unclear how it works on approximate IFS functions. Several methods have been proposed, but none provides an ideal solution to the inverse problem for image coding purposes. In some cases there are steps in the algorithms which are not fully automated, and it is not clear how to do them. Ideally, there should not be any limitations on the mappings. The algorithm should fulfil the inverse property concerning the number of mappings, and the computation time should be tractable.
53 Chapter 5 An automatisation of Barnsley s algorithm In which we describe a search algorithm for the inverse problem of IFS s. The search algorithm can be viewed as an automatisation of Barnsley s algorithm. In most of our experiments, when the given digital binary image is generated from an IFS, the algorithm gives an approximation of the IFS that was used to generate the given digital binary image as solution 1. In this chapter we describe a search algorithm for the inverse problem of IFS s with affine mappings and investigate to what extent it gives a solution that can be used for image coding. 5.1 Barnsley s algorithm Barnsley [6] proposed that the fragments for the solution of the inverse problem of IFS s could be identified manually, either by visually finding the fragments and then computing the parameters of the mappings or by trying parameters and visually comparing the induced fragment with the given image. Hence, the class of mappings has to be restricted to mappings that can be visually recognised. Barnsley restricted the class to affine mappings and also proposed that the Hausdorff metric could be used to measure closeness. When the fragments have been identified, three pairs of points are needed for each affine mapping to be able to determine the parameters of the affine mapping. Each of the pairs consists of a point in the given image and the corresponding point in the fragment, see Figure 5.1. The points of each pair are chosen such that the point in the 1. Parts of this work have been published in [49]. 41
54 42 Chapter 5 An automatisation of Barnsley s fragment is assumed to be the result of applying the sought affine mapping to the point in the given image. The three points in the given image must be linearly independent to give a unique solution. An affine transformation in two dimensions is determined by three such pairs of points. Let X be a vector with the points in the given image and Y a vector with the points in the fragment. It is assumed that Y = w i X + t i, where w i is the deformation part and t i is the translation part of an affine mapping. The solution is given by solving Y = w i X + t i. The procedure for recovering the IFS from an image described above, will be referred to as Barnsley s algorithm. However, it is sometimes difficult to measure the points accurately enough to get a mapping with a collage that is close enough to the given image. The difficulties can be due to a limited resolution of the given digital binary image or practical measuring difficulties. To get a collage that is closer to the given image, more pairs of points can be measured and the over-determined equation Y = w i X + t i can be solved by minimising w i X + t i Y. The given image for the inverse problem of IFS s is supposed to be generated from an IFS, but what happens if it is not? In that case the method for the solution can be described as tiling the given image into tiles, which may overlap, where each tile can be approximated by a fragment. 5.2 An automatisation of Barnsley s algorithm Let A be a given digital binary image generated from an IFS W. Choose an ε, and the search algorithm will find an IFS W with affine mappings such that d H ( A, [ W ( A) ]) ε with few mappings. Then, by the Collage theorem the attractor A W * of W is such that d H ( A, A W * ) ε ( 1 s), where s is a contractivity factor for W. The algorithm will search a finite set of points P from the parameter space P of the contractive affine mappings. Figure 5.1 An illustration of Barnsley s algorithm. Left is the given image. Right is the given image where three fragments have been identified and for two of the fragments three pairs of corresponding points have been identified. The parameters of the mappings can be determined from these points.
55 5.2 An automatisation of Barnsley s algorithm 43 The algorithm has two phases. In the first phase mappings with decreasing contractivity factor are collected until the collage is close to the given image. In the second phase the number of mappings is reduced while keeping the small distance between the collage and the given image. Mappings collected in the first phase are removed if the removal does not increase the distance above the threshold. The collected mappings are tested in order of increasing contractivity factor. The main running variable of the algorithm is the approximate IFS W. There is also an auxiliary variable, the current collage C, which simplifies the computations. The current collage is a function of the approximate IFS W. The IFS contains the continuous mappings while the collage contains the digital binary image. At the end of the algorithm these two variables contain the result. These variables are initialised to W C 0 In the first phase the parameter space of the affine mappings is traversed in order of decreasing size of the induced fragment. Fragments that are close to the given image and extend the current collage are added to the current collage, and the mapping is added to the current IFS. This can be written as for all w P (in order of increasing contractivity) do if d * H ([ w( A) ] D, A) ε and d * H ([ w( A) ] D, C) > ρ then begin W W w C C [ w( A) ] D if d H* ( C, A) ε then exit end The search is ready when the collage is close to the given image. ρ is a priori known bound of the minimum distance between fragments in the given image. If ρ is known, it can be used to reduce the search time. The second phase can be described as, for all w W (in order from last found to first found) do if d * H ( A, [( W \ w) ( A) ] D ) ε then W W \ w ( W \ w) means the IFS W without the mapping w. The search algorithm gives an IFS W with a collage [ W ( A) ] D such that d H ( A, [ W ( A) ] D ) ε if P is dense enough. If ε is not chosen too small and P densely
56 44 Chapter 5 An automatisation of Barnsley s enough, the nearest approximation of W in P is a solution to the inverse problem of IFS s. If the mappings are restricted to affine, then a pixel size resolution of the translation and a contractivity factor contracting the image to a point are sufficient to always find a solution. Rotation and scaling of the image is computationally more expensive than translation, which is why the parameters are searched in the following order, for s = [ n s 1,, 0]0.9 ( n s 1) do for α = [ 0,, n α 1] ( 2π) n α do for t x = [ 0,, n t 1] n t 0.5 do for ( t y = [ 0,, n t 1] n t ) 0.5 do w() ssinα ssinα t () x + ssinα scosα t y. To keep the number of mappings low, those with large contractivity factor (large fragments) are searched first. With the full search algorithm it is possible to control the accuracy of the solution, and the rate is given by the solution. However the algorithm does not allow the rate to be controlled other than in an indirect way by trying different accuracies until the desired rate is achieved. Remark 1. The Hausdorff distance based on the L 1 -metric can be computed for digital binary images by first computing two distance maps [44]. Let A be a digital binary image. A distance map is an image A map : D, which for each point in the image support gives the minimum distance to a point in the set defining the image A, i.e. A map ( p) =ˆ min d( x, p), (5.1) x A where d is the distance measure that underlies the Hausdorff metric, in this case the L 1 -metric. The d * H -distance can be computed as d H * ( B, A) = max A map ( x). (5.2) x B The distance map for digital binary images on a support with a square grid of points requires two scans of the image to be computed if based on the L 1 -metric. Finally the Hausdorff distance is computed by scanning the two distance maps. The computational complexity is proportional to the number of points in the digital image support. The distance map of the given digital binary image needs only be computed once, and the distance map of the current collage needs only be computed when the current collage has changed.
57 5.2 An automatisation of Barnsley s algorithm 45 Remark 2. There are two observations behind the search algorithm. The first concerns the Hausdorff metric. By using the Collage theorem and the Hausdorff metric it is possible to search for one fragment at a time and thereby reduce the search space to P. In the algorithm we use Remark 4. The Kantorovich distance (Ch. 6) could also be interesting as an alternative to the Hausdorff metric. The Collage theorem can be formulated with the Kantorovich distance [6], and the distance measure seems to have some geometrical meaning. However, the computational complexity is high, and the measure is not sepd H * i ( w i ( A), A) = max { ( w i ( A), A) }, (5.3) i i.e., if the collage is close to the given image, then every fragment is close to the given image. Hence as the parameter space is searched, every fragment that is close to the given image is a potential member of the collage. The other observation is that if a smaller fragment is a subset (or close to) of a larger fragment, the smaller fragment is redundant. An IFS with N affine mappings has the following property. Every fragment w i ( A) can be expressed as a set of N smaller fragments: N t = 1 w i ( A) = w i ( w t ( A) ) = ( w i w t )( A). (5.4) Assume that the only fragments that are close to the given image are induced by mappings that are close to mappings in the given IFS or a composition of some of these mappings. Hence one may search through the fragments in order of decreasing size. The mappings must be tried in order of decreasing size to yield a collage with a minimum number of mappings because when w i ( A) w j ( A), can be discarded. Remark 3. The Hamming metric (Def. 7.2) could be interesting as an alternative to the Hausdorff metric in the search algorithm. The Hamming metric has low computational complexity and is a common distance measure for binary images. However, there are some problems with the use of the Hamming metric. The Collage theorem can not be expressed with the Hamming distance. Hence, that a collage is close to the given image has no implication on the distance between the attractor of the corresponding IFS and the given image. The Hamming distance measure is not separable in the fragments as is the Hausdorff distance measure. If the distance measure is not separable, it is not possible to search for the fragments on at a time. A limit to the Hamming distance between the collage and the given image does not have any useful implication on the distance between each of the fragments and the given image. It is not possible to give a limit to the distance between the collage and the given image for which the IFS that generated the given image is a solution. The Hamming metric does not have a geometrical meaning. d H * N t = 1 w i
58 46 Chapter 5 An automatisation of Barnsley s arable in the fragments. A limit to the distance between the given image and the collage only has a limited implication on the distance between each of the fragments and the given image. It is possible to give a limit to the distance between the given image and the collage for which the IFS that generated the given image is a solution. However, from some experiments this limit seems to be loose. Remark 5. A matching pursuit algorithm [18] would be a way to simultaneously control rate and distortion. The basic idea behind this technique is to find the fragment that reduces the distance between the given image and the collage as much as possible and then continue the search until the desired accuracy is reached. But the problem is that the fragment that reduces the distance the most may not be a fragment that is close to the given image. It may even be that the largest fragment that is close to the given image does not decrease the Hausdorff distance at all. Another disadvantage with matching pursuit is that the search needs to be through P for every affine mapping. 5.3 Results Here we present the results of trying the automatic search algorithm on some images. IFS s with mappings restricted to similitudes First, three digital binary images generated from IFS s. The algorithm is expected to find an approximation of the IFS s that generated these images. These are the wellknown fern image [6] and two other images chosen by us. One has overlapping fragments. For these images, rate-distortion analysis is not meaningful. The left row in Figure 5.2 shows three images defined by IFS s composed of a few similitudes. In the middle row are representations of the mappings which define the images. Right are the images reconstructed from the approximative IFS s found by the full search algorithm. Table 5.1 summarises the distances between the given Table 5.1 The coding result of the full search algorithm. ε d H ( A, Ã) fern 2 4 image image image and the collage and between the given image and the attractor as defined by the
59 5.3 Results 47 Figure 5.2 Three images generated from IFS s. From left to right; the given image generated from the given IFS, the mappings of the given IFS, an image generated from the found IFS and the mappings of the found IFS. Figure 5.3 Found mappings for the fern image with the Hausdorff error limit for the collage set too small.
60 48 Chapter 5 An automatisation of Barnsley s Table 5.2 The original mappings and the mappings resulting from the search algorithm. original mapping found mapping fern ( ) ( ) ( ) ( ) ( ) ( ) image 2 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) image 3 ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) found approximation. In Table 5.2 the original mappings and the found approximations are shown. If the error limit of the collage is set too small, the search algorithm will find an IFS but possibly with more mappings, see Figure 5.3. IFS approximation of the dragon image In this section we present the result of the IFS coding of the dragon image (Figure 5.4) [14] also used in [20]. The dragon image is expected to be approximately self-similar under affine mappings. For this image we will try different parameters and get a rate-distortion trade off. The parameters of the coding algorithm are the following: n α - the number of rotation angles. They are equally spaced between 0 and 360 degrees. - the number of scaling factors. n s
61 5.3 Results 49 Figure 5.4 The dragon image, size pixels. Figure 5.5 The dragon image represented with an IFS with 37 similitudes. Left: The reconstructed image. Right: The 37 mappings. Figure 5.6 The dragon image represented with an IFS with 6541 similitudes. Left: The reconstructed image. Right: The 6541 mappings. The square frame is mapped by each of the mappings. For 4273 of the mappings the result is just a point.
62 50 Chapter 5 An automatisation of Barnsley s s max - the maximum scaling factor. The scaling factors are equally spaced between s max and 0. ε - the chosen accuracy of the collage in the Hausdorff metric. The result is expressed by the following data. W - the number of mappings. R - the rate in bits per pixel. d H - the Hausdorff distance between the reconstructed image and the given image. Parameters of the search algorithm and the result of the search are shown in Table 5.4. In Figure 5.5 an approximation of the dragon image generated from an IFS Table 5.3 The result of IFS approximations of the dragon image. n α n s s max ε W pt maps R [bpp] d H with 37 similitudes is shown. A representation of the mappings is found to the right in the Figure. Figure 5.6 shows an approximation of the dragon image generated from an IFS with 6541 similitudes. Here the distance between the given image and the collage is d H ( A, [ W ( A) ]) = 0, which gives an uninteresting rate but low distortion. We conclude that the dragon image is not an IFS image. When the parameter resolution is increased, several bits per mapping is required for the representation of each mapping. At the same time fewer mappings are needed for the image and the total number of bits per image does not increase after a particular level. IFS approximation of a Julia set We will now try to approximate an image that is not induced by an IFS with affine mappings. A Julia set is defined by an equation f λ ( z) = z 2 λ on the complex
63 5.3 Results 51 plane. It is specified by a complex number λ. Two examples are shown in Figure 5.7. The left Julia set ( λ = ( 0.1, 0.7) ) seems possible to approximate with an IFS, but the right set ( λ = ( 0.2, 0.7) ) seems more difficult. It may be possible if the set is filled. We will try to approximate the left Julia set. In Figure 5.8 six approximations are shown. In Figure 5.9 the mappings of the worst and the best approximation are shown.the Julia set is pixels. The parameter space has 360 rotation angles, 128 scaling factors between 0.9 and 0 and a translation step of 1 pixel. Given different ε, the result is shown in Table 5.4. Table 5.4 Results of the IFS approximations of the Julia set. ε d H maps R [bpp] IFS based on affine mappings Consider the Spiral in Figure 5.10 [6], which has been coded in two ways. First the search algorithm was extended to search for affine mappings, which have six parameters, instead of similitudes, which have four parameters. As before, the search is done in order of increasing contractivity, i.e. starts with large fragments and progresses towards smaller fragments. Let s max be the maximum allowed expansion in one direction. In the examples we choose smax = 1.1. Below we only show the order in which the variables are iterated. The rest of the algorithm is as before. Figure 5.7 Two Julia sets.
64 52 Chapter 5 An automatisation of Barnsley s Figure 5.8 IFS approximation of the Julia set. Figure 5.9 The mappings of the best and the worst approximation of the Julia set.
65 5.3 Results 53 for s = [ n s 1,, 0]0.9 ( n s 1) do for α = [ 0,, n α 1] ( 2π) n α do for β = [ 0,, n β 1] ( 2π) n β do for s 1 = s max,, s step 0.9 ( n s 1) do for t x = [ 0,, n t 1] n t 0.5 do for t y = [ 0,, n t 1] n t 0.5 do w() cosα sinα s 1 0 cosβ sinβ t () x + sinα cosα 0 s 2 sinβ cosβ t y The result of the use of the extended search algorithm on the fern image [6, p. 99] is shown in Figure As a reference we also solved the inverse problem manually using Barnsley s algorithm. The mappings are identified manually, and three pair of points are determined that give the parameters of the mappings. But in this case it was not possible to measure closely enough to yield an accurate solution. So we determined seven and eight pairs of points for each transformation. Then we computed the mapping, giving the minimum squared error of the transformed points. The result is shown in Figure The measured points (see Figure 5.12) for the two transforms are Reconstructed Given image (light), reconst. (dark), common black) Figure 5.11 Manual coding of a spiral image ( pixels).
66 54 Chapter 5 An automatisation of Barnsley s The given image Collage Reconstructed Given image (light), collage (dark), common (black) Given image (light), reconst. (dark), common (black) Figure 5.10 algorithm. Encoding of a spiral image ( pixels) by the search
67 5.3 Results 55 X 1 = p 1 p 2 p 3 p 4 p 5 p 6 p 7 p = (5.5) Y 1 = p 1 p 3 p 4 p 5 p 6 p 7 p 8 p = (5.6) Figure 5.12 The measured points for the manual coding.
68 56 Chapter 5 An automatisation of Barnsley s X 2 = p 1 p 2 p 3 p 4 p 5 p 6 p = (5.7) Y 2 = p 2 p 11 p 12 p 13 p 14 p 15 p = (5.8) The solution, i.e. the two mappings is w 1 = w 2 = (5.9) 5.4 Conclusion The IFS that induced the given digital binary image is a solution to the inverse problem of IFS s if the required accuracy is chosen not smaller than a limit and the discrete parameter space is dense enough. In most of our experiments the search algorithm give, for given digital binary images generated from IFS s, an approximation of the IFS that generated the given image as result. In our experiment Barnsley s algorithm gave better results than the automatic search algorithm in the sense that the reconstructed image is closer to the given image.
69 Chapter 6 A gradient search algorithm In which we describe a novel approach to the inverse problem of iterated function systems. Starting with a rough initial approximation of the IFS the algorithm will follow the gradient in the parameter space of the IFS obtained by the Kantorovich metric to a minimum point, which can be the solution to the inverse problem or a local minimum point. In this chapter we will describe an attempt to solve the inverse problem of iterated function systems. The parameter space of IFS s has a varying number of too many dimensions to make a blind search practically feasible. For the algorithm presented here the number of mappings has to be given. The idea is to start with a given rough initial approximation of the parameters of the IFS and then improve the approximation by moving the parameters in the direction of the gradient in the parameter space obtained by the Kantorovich distance measure. Our hypothesis is that there are few local minimum points, so the gradient search has some chance of reaching the minimum point. The disadvantage of this algorithm is the high computational complexity of the Kantorovich metric and the fact that the number of affine mappings in the IFS has to be given. This algorithm cannot find the minimum number of affine maps. 6.1 The Kantorovich distance The Kantorovich (Hutchinson, Vaserstein) metric has been introduced several times in connection with attractors (fractals) but has not been used in practical applications because of the high computational complexity. A short background can be found in Kaijser [29]. In Chapter 9 we describe our implementation and comparison of two recent algorithms for the computation of the Kantorovich distance for images. In this section we essentially follow Kaijser [29]. In this chapter we will consider digital images, where each pixel has a weight (or mass) assigned to it and a position in the plane. For binary images the weight can be a unit weight. Later, we will see 57
70 58 Chapter 6 A gradient search algorithm that integer mass is needed for binary images. Let A = { u i 2, i = 1,, k} and B = { v j 2, j = 1,, l} be the points of two images, and let A( p) denote the weight of p A. A transportation plan (also called a coupling) T between A and B is a set of triplets {( s i, t i, m i ), i = 1,, n} where s i A, t i B, m i 0 and there are no triplets with the same ( s i, t i ). The triplets are such that m i i : s i = p A( p) p A (6.1) and m i i: t i = p B( p) p B. (6.2) We will call a transportation plan complete if there is equality in (6.1) or (6.2) or both. Let Θ( A, B) be the set of all complete transportation plans between A and B. Let d : 2 2 be a distance measure, called inner distance measure. The cost of a transportation plan T is defined as n ct ( ) =ˆ m i ds ( i, t i ). (6.3) i = 1 Definition 6.1 The d * K distance between two images is the cost of the complete transportation plan with minimum cost. Let A, B be images. Define d K * ( A, B) =ˆ min{ ct ( ): T Θ( A, B) }. (6.4) Definition 6.2 Let A, B be images with equal total weight. The Kantorovich distance is defined by d K ( A, B) =ˆ min{ ct ( ): T Θ( A, B) }. (6.5) The Kantorovich distance can be computed by solving a balanced minimum cost transportation problem with k supplies and l demands. The transportation problem is defined by a set of supplies with magnitudes { a i = Au ( i ), i = 1,, k}, a set of demands with magnitudes { b j = Bv ( j ), j = 1,, l} and a set of costs { c ij = du ( i, v j ), u i Av, j B}. The solution implies a set of flows (also called arcs) F = { f ij } where f ij is the flow from supply u i to demand v j. The problem is to
71 6.2 Gradient search 59 minimise subject to k l i = 1 j = 1 l j = 1 k i = 1 f ij f ij f ij 0 c ij f ij = i = 1,, k a i = j = 1,, l b j (6.6) In general, images have different total grey mass. If so, the masses have to be normalised to give the images the same total mass to be able to compute the Kantorovich distance between the images. We will normalise the masses by scaling each mass with the total mass of the other image. Let S A = a i and let S B = b i. Then let A' = { s B a i } and let B' = { S A b i }. In the sequel we will assume that images A and B have equal total mass. Thus the Kantorovich distance is insensitive to differences between images obtained by scaling the grey scale of the whole image. Figure 6.1 shows two images and two couplings obtained by computing the Kantorovich distance between the images. The two couplings correspond to different inner distance measures. 6.2 Gradient search Let A be a given digital binary image which is generated from an IFS with N affine mappings and assume the N is given. The problem is to find the parameters of the IFS, with N affine mappings, that minimise the distance between the given image and the collage. To facilitate the discussion we define the function f A ( W ) =ˆ d K ( A, [ W ( A) ] D ). (6.7) Thus the problem is to find the parameters of the IFS W, with N mappings, which minimise f A ( W ). The parameter space in which the solution can be found has many dimensions. However, if the Kantorovich metric gives the function f A a smooth descent towards the minimum value of f A, then it should be possible to solve the problem by a gradient search algorithm. Let us find out if the sequence W t = W t 1 c f A ( W t 1) (6.8)
72 60 Chapter 6 A gradient search algorithm converges towards the minimum value of f A. A gradient search algorithm requires an initial approximation of the IFS and a way to calculate or approximate the gradient. In this algorithm the number of mappings of the IFS has to be given. There is no way known to us of finding the number of mappings of an IFS from a given image except by also finding the IFS. In this case the gradient search algorithm will not be needed. A tedious way to find the number of mappings could be by finding the best approximation of an IFS with few mappings by means of the gradient search algorithm. If the collage is not close enough to the given image, then the number of mappings of the IFS is increased, and the gradient algorithm is used again to find the best approximation of the IFS. The process is iterated until the collage is close enough to the given image. How close to the given image the resulting collage can be expected to come is determined by the accuracy of the given image. If A is generated from W, then the result of the algorithm can be expected to come at least within f A ( W ) of the given image. Figure 6.1 Top: Two fern images of size pixels. Bottom left: The transportation plan (coupling) obtained from the Kantorovich distance measure based on the L 1 inner distance measure. Bottom right: The transportation plan based on the square of the L 2 inner distance measure.
73 6.3 About the gradient 61 which results in the translation that minimises the cost given that the connections between points are kept and the lengths of the arcs are allowed to change. The dis- The evaluation of the function f A implies the solution of a minimum cost transportation problem to which a coupling (transportation plan) between the given image and the collage is associated. The coupling is a set of arcs, where each arc is a connection between a point in the given image and a point in the collage. Every point in both images is connected to at least one point in the other image. A change in the IFS means that the points of the collage will be displaced. In general this will result in f A implying another coupling with different arcs. However, for small changes of the IFS the coupling will often contain the same arcs but with the location of the collage points somewhat displaced. If the IFS is changed along a line in the parameter space, there will be points where the coupling changes. This observation lies behind the idea that it might be possible to calculate an approximation of the gradient of f A from the coupling by letting the collage points move according to the change in the IFS while the arcs are kept. 6.3 About the gradient The gradient f A is given by the operators W =,,, w 1 w 2 wn (6.9) and w i = w ( a) i,,,,, w ( b) i w ( c) i w ( d) i w ( f ) i w ( f ) i. (6.10) w i The affine mapping consists of two parts, a translation and a deformation. Given a coupling, the translation that minimises the cost of the given coupling between points can easily be calculated. However, a recoupling may give lower cost. The translation giving the minimum cost is found by taking the partial derivatives of the distance with respect to the translation parameters and solving the equations w ( e) i f A ( W ) = 0 (6.11) w ( f ) i f A ( W ) = 0, (6.12)
74 62 Chapter 6 A gradient search algorithm tance between two images is the cost of the cheapest coupling. Translating an image while keeping the coupling does not necessarily give the cheapest coupling. To get the minimum cost with the translated image it is necessary to make a new computation to find the coupling with minimum cost. The translation parameter can be minimised simultaneously for the translation of all affine maps in the IFS. We will only consider translations that are integer valued. Let A be a given digital binary image and let B = [ W ( A) ] D be the collage. Let {( a i, b i, m i ), i = 1, n} be a coupling between the images A and B. If the fragments of the collage are disjoint, [ w i ( A) ] D [ w j ( A) ] D = if i j. Then for each arc i point b i in the collage can be uniquely associated with an affine mapping 1 v i where v i W and a point a' i = v i ( b i ). The point a' i is close to a point in A but in general it is not a point in the digital image support of A. Then b i v ( a ) v i ( a' i ) i v ( b) i a'i ( x) v ( e) = = + i = v ( c ) i v ( d) i a' ( y) i v ( f ) i v ( a ) i a' x i v ( c ) i a' x i + + ( ) v ( b ) i a' ( y) i v ( e) i + + ( ) v ( d ) i a' ( y) i v ( f ) i. (6.13) Let a b = a ( x) b ( x) + a ( y) b( y), ab, 2 denote the L 1 -distance.the distance between the given image and the collage is f A ( W ) = d K ( A, [ W ( A) ] D ) = d K ( A, B) = = n i = 1 n i = 1 m i a i m i a i x v i ( a' i ) ( + + ) + ( ) v ( a ) i a' ( x) i v( b ) i a' ( y) i v ( e ) i + m i a ( y) i ( v ( c ) i a' ( x) i + v ( d ) i a' ( y) i + v ( f ) i ). (6.14) The partial derivative of with respect to w ( e ) i is f A f A w ( e) i = n i = 1 m i a ( x) i w ( a ) i a' ( x) i w ( b ) i a' ( y) i w e : ( + + ( ) i ) > 0. (6.15) a ( x) i ( w ( a ) i a' ( x) i + w ( b ) i a' ( y) i + w ( e : ) i ) < 0 m i Then find the translation w ( e) i where f A w ( e) I changes sign. This can be done by sorting the m i values according to which value of w ( e) i that the contribution to f A w ( e) I changes from negative to positive. Then find the value for which the sum of the m i values on either side is as equal as possible. Let us consider the parameters of the mappings in two groups, the deformation and the translation. The deformation changes the size of the fragments, whereas the translation only changes their location. If the translational parameters change a little,
75 6.4 Results 63 the connections between the points will probably stay the same. Only the lengths of the arcs will change. In some cases the coupling will change, with the result that the distance decreases more than if only the lengths of the arcs had changed. But if the size of the fragments change, then the weight of the arcs will change and thus the connections. The partial derivatives of f A with respect to each of the deformation parameters can be approximated by differences. Let w be one of the deformation parameters of W, let w be a unit vector which points in the direction of w in the parameter space and let h > 0 be a small number. Then, f A ( W + h w ) f A ( W ) ( W ) (6.16) w h A distance calculation is necessary for each parameter. The difference h W has to be chosen carefully as there are some quantisation problems. The distance does not vary continuously with the parameters of W because we work with images which are defined on a finite set of points and not on true attractors which are defined on 2. The algorithm has two steps. The first is to minimise the distance with respect to the translation; the second is to change the deformation parameters of the IFS according to the gradient. The two steps are iterated until the distance converges to a minimum value. The optimisation is based on a gradient search. An initial guess of the IFS is made and then improved iteratively along the gradient. The metric must be such that the distance between the given image and the collage image has few local minimum points when the parameters of the approximate IFS vary. The deformation parameters cannot be minimised independently of each other because a change in one of them may change the relative weight between the fragments and thus the minimum value for other parameters. 6.4 Results In this section we show examples of how the gradient search algorithm performs. In the experiments we limit the affine mappings to similitudes. We compute the Kantorovich distance based on the L 1 inner distance measure. The given fern image, size pixels, is shown in Figure 6.3a. In the search we assume knowledge of the number of mappings. Figure 6.3b shows the collage induced from the initial guess of the IFS. Figure 6.3c shows the last approximation of the collage and, finally in Figure 6.3d is the fern image generated from the final approximation of the IFS shown. Figure 6.5 shows a second example with a different initial guess of the IFS. In this case the fragments have the same size. Figure 6.2 shows how the distance decreases with the number of iterations in the two examples.
76 64 Chapter 6 A gradient search algorithm The bottom curve shows the distance change when the initial guess is the IFS that generated the given image. The parameters of an affine map w i ( p) = ab p + e cd f will be written as abe. (6.17) cd f The IFS that generated the given fern is W = ,, (6.18) The last approximation of the IFS in Example 1 is W 1 = ,,. (6.19) The last approximation of the IFS in Example 2 is W =,,. (6.20) The examples were executed on a Sun Sparc station. The total execution time for Example 1 was 59 hours. The distance converged to its minimum after 40 hours. The second example gave a total execution time of 37 hours and convergence after 14 hours. The c value, see Eq. (6.8), that determines how far the IFS is moved in the parameter space for each iteration was constant in these examples. It had to be rather small to permit the approximate IFS to come close to the given IFS. However, a small c results in slow convergence. Varying c would give convergence in fewer iterations and also a possibility to get closer to the given IFS. The two initial approximations of the IFS are both close to the given image. 6.5 Conclusion The gradient search algorithm can be used to improve a rather good initial approximation. The number of mappings must be given. The algorithm is best at finding the translation. In our experiments there were often problems with local minimum points
77 6.5 Conclusion 65 with regard to the scaling and the rotation parameters. Even then the gradient is rather smooth, which is necessary if the algorithm is to work at all. A major obstacle is the computational complexity of the Kantorovich distance measure. In the beginning of the work several different ways of computing an approximation of the gradient from the coupling were tried but none worked very well. The algorithm described here became possible to use due to a recent algorithm for the computation of the Kantorovich distance measure developed by Kaijser [29] Gradient search Kantorovich distance Iteration nr Figure 6.2 A plot of the distance between the given image and the collage during the gradient search. The top curve corresponds to the example shown in Fig. 6.3 and the middle curve to Fig The bottom curve shows the case when the initial guess is the IFS which generated the given image.
78 66 Chapter 6 A gradient search algorithm (a) (b) (c) (d) Figure 6.3 (a) The given fern image. (b) The collage of the initial approximation of the IFS. (c) The collage of the final approximation of the IFS. (d) The attractor of the final approximation of the IFS.
79 6.5 Conclusion 67 Figure 6.4 Two couplings induced by the Kantorovich distance between two pairs of fern images. The Kantorovich distance is based on the L 1 -metric. Right of each coupling is the two images shown.
80 68 Chapter 6 A gradient search algorithm (a) (b) (c) (d) Figure 6.5 (a) The given image. (b) The collage of the first approximation of the IFS. (c) The collage of the second approximation of the IFS. (d) The collage of the final approximation of the IFS. (e) The attractor of the final approximation of the IFS. (e)
81 Chapter 7 Coding of binary images In which we compare three attractor based coding methods for binary images with some non-fractal coding methods. The comparison is made with the Hamming, the Hausdorff and the Kantorovich distance measures. In this chapter we will study coding methods for digital binary images, both fractal and others. The latter images are expected to be approximately self-similar but not on a global scale like the attractor of an IFS. Instead small parts of the image transformed by contractive affine transformations are expected to be approximately similar to other parts of the image. We will compare IFS coding of approximately self-similar images with two other attractor coding methods for binary images. These two latter methods are described in this chapter and are based on RIFS and LIFS (described in Chapter 2). The two latter methods are built on mappings defined on parts of the image. Affine mappings defined on parts of the image are a way to make use of the piecewise self-similarity. The three attractor coding methods for binary images will be compared to a quadtree coding method and a method based on subsampling followed by standard JBIG coding for binary images. The IFS coding algorithm described in Chapter 5 is based on the Hausdorff distance measure. Another distance measure for digital binary images is the Hamming distance. One of the attractor coding methods described in this chapter is based on the Hamming distance. The other is built on the Hausdorff metric. The Hausdorff metric is motivated by its use in the theory of binary attractors. It is the metric by which the contractivity of the mappings is shown, demonstrating the existence of a unique attractor. The collage bound (Theorem 2.4) is also expressed in the Hausdorff metric. It is not meaningful to use the Hamming metric for the same purpose. The affine mappings on the plane are generally not contractive under the Hamming metric. Thus, if the collage is close to the given image in the Hamming metric, the Collage theorem has no implication on the Hamming distance between the given image and the attractor. The Hamming metric and the related signal-to- 69
82 70 Chapter 7 Coding of binary images noise ratio are motivated because they are used in coding methods and to evaluate the performance of such methods. When we consider the attractor coding methods using RIFS and LIFS, we will keep the inverse property in mind. If the image is generated with a mapping from the same class that the coding algorithm uses, then preferably the algorithm should find an approximation of the mapping that generated the image. The most important requirement is that it has the same number of affine mappings. In Chapter 5 we saw that the IFS coding algorithm has this inverse property. Many coding algorithms present a way to control the trade-off between rate and distortion. In the IFS algorithm we choose to control the accuracy to be able to give the algorithm the inverse property. We will do the same for the LIFS and RIFS coding algorithms. An alternative would be to control the rate. We will see that with some algorithms this is straightforward whereas with others it is more difficult. One of the differences between the proposed LIFS and RIFS attractor classes is that the LIFS class allows overlapping fragments whereas the RIFS class does not. Each range region in the RIFS attractor is described by only one fragment. In the comparison of the different coding methods we will take the above mentioned distance measures into account as well as the Kantorovich distance measure. In this work we have not considered any entropy coding of the parameters of the function systems. The bit rates are based on a fixed length binary representation of the discrete parameters. 7.1 The Hamming distance The Hamming distance between two digital binary images is the number of positions where the images differ. Definition 7.1 Let A, B D. The d * h distance from A to B is defined by d h * ( A, B) =ˆ A \ B, (7.1) which is the number of points of A that are not in B. Note that if A B and B\ A, then d h* ( A, B) = 0 and d h* ( A, B) > 0. Hence d h* ( A, B) is not symmetric. Definition 7.2 Let A, B D. The Hamming distance d h ( A, B) is defined by d h ( A, B) =ˆ d * h ( A, B) + d * h ( B, A). (7.2) The computational complexity is proportional to the number of points in the digital image support.
83 7.2 Local iterated function systems 71 Signal-to-noise ratio (SNR). The signal-to-noise ratio is measured between a digital binary image A D and a distorted version à D of the image. The SNR is defined as A SNR( A, Ã) =ˆ 10 log (7.3) ( A, Ã) Peak SNR (PSNR). A common distortion measure for grey scale images is PSNR, where the noise is related to the peak signal. The corresponding distortion measure for digital binary images is defined as D PSNR( A, Ã) =ˆ 10 log (7.4) ( A, Ã) Both SNR and PSNR measures can be viewed as normalised Hamming distances. PSNR is the Hamming distance related to the number of points in the digital image support, and SNR is the Hamming distance related to the number of points in the undistorted image. d h d h 7.2 Local iterated function systems An anticipated problem with the coding of images with IFS s is that few images are expected to be self-similar on a global scale. A solution is to define the affine mappings not on the whole image support but on subsets of it. Thus, we let every affine mapping be defined on any subset of the image support (see Definition 2.15 of local iterated function systems). Each affine mapping must be accompanied by a description of the subset, also called domain, on which the mapping is defined. The problem with the coding algorithm is that while the IFS coding algorithm has to search the space of the affine mappings once, the LIFS algorithm has to search the space of the mappings once for every possible domain. To cope with the search problem we will only consider a limited number of domains, a number of square nonoverlapping subsets of the image support. The subsets have the same size. The LIFS coding problem is to find the smallest set of fragments that gives the required accuracy. Consider the set of all fragments defined by the current class of affine mappings and the current set of domains. The coding problem can be solved by a search through all subsets of fragments to find the smallest subset with the required accuracy. However, this solution is not computationally tractable. We will use a search algorithm similar to the IFS search algorithm but with two modifications. First, the set of possible mappings must be searched, for every domain. Second, it is not enough to order the mappings according to decreasing contractivity factor. Consider two fragments with different domains, one with many points and the other with few points. Assume that the fragment with many points is
84 72 Chapter 7 Coding of binary images induced by a mapping with a small contractivity factor and that the fragment with few points is induced by a mapping with a large contractivity factor. Thus, if selected by the contractivity factor the fragment with few points would be chosen. However, it is likely that fewer fragments is needed if fragments with many points are chosen before those with few points. Thus, the mappings and their accompanying domains will be sorted according to the number of points in the induced fragment. As with the IFS search algorithm it is suitable to use the Hausdorff metric since this makes it possible to control the accuracy. We will see that the proposed search algorithm has the inverse property. It is also possible to use the Hamming distance. The d * h -distance (Def. 2.5) from a fragment to the given image is a function of the number of points of the fragment that are not in the given image. We will normalise the distance with the number of points in the fragment since the fragments have different sizes. If two fragments have the same number of points outside of the given image, the distance should be such that the fragment with most points is considered to be closest. A limit on the maximum number of errors per fragment would not make it possible to control the accuracy of the collage with the suggested search algorithm since the number of mappings in that case is given. Moreover the collage s number of errors cannot be computed from the fragments number of errors since the erroneous bits are not mutually exclusive. Instead this would lead to a more complex algorithm. A limit on the error frequency is also difficult to control since the fragments may overlap. If the accuracy is given as the number of tolerable pixel errors, then the question is how to distribute these errors to get a small number of mappings. If the Hamming distance is used, it is not possible to give a requirement on the distance between the given image and the collage image such that if the limit is achieved it will lead to the inverse property. If the Hausdorff distance is used and a sufficiently large class of mappings is allowed, the LIFS coding of an IFS image will give at most the number of mappings of the original IFS times the number of possible domain regions. The LIFS search algorithm. The algorithm (Fig. 7.1) consists of two phases. In the first phase the parameter space of the affine mappings is searched, and fragments are collected. Fragments which are close to the given image and extend the current collage are kept. At the end of phase one the collage and the given image are close to each other as measured by the Hausdorff distance. However the LIFS can have redundant mappings. In the second phase the number of redundant mappings is reduced. The mappings of the LIFS are tested, and those mappings are discarded which, when removed, do not increase the distance between the collage and the given image. If the distance increases, the mapping is necessary in the collage and is left in the LIFS. In the first phase the fragments are tried out in order of decreasing size. Thus the domain regions and the scaling factors are ordered according to the size of the fragments. During the search, one domain and scaling is taken at a time. and the remaining parameters are varied. In phase two the mappings and their accompanied regions of the LIFS are tested in order of increasing size of the fragment induced from the mapping.
85 7.3 Recurrent iterated function systems 73 In the first phase the algorithm searches the fragments in order of decreasing size to keep the number of mappings in the approximate LIFS low. The parameter resolution should be such that a collage close enough to the given image can be found. Therefore we choose the translation resolution the same as the pixel size. The number of contraction factors are chosen to be the same as the domain block diameter in pixels and the number of rotation angles the same as the boundary length of the domain block. If this kind of LIFS is to be able to represent any image at an arbitrary accuracy in the Hausdorff metric sense, then one way to assure this is to include translation resolution of pixel size and allow contraction down to a point. This is equivalent to a range size of one pixel per mapping. If there is a part of the image which requires this kind of coding to give low enough error, the coding is probably not very efficient. A solution could be to extend LIFS coding with condensation sets, which is generated by a mapping which gives the same output set irrespective of the input set. The condensation set could be coded with some other image coding method. 7.3 Recurrent iterated function systems The coding of a given digital binary image with an RIFS can be divided into two steps. First the number of required subspaces must be determined, and the image must be divided into the subspaces. The union of the images from the subspaces should be the given binary image. Images from different subspaces need not be disjunctive. The second step is to find the contractive set mappings needed to give the W C 0 for all ( w, R) P { R i, i = 1,, N } (order increasing size of [ w( A R) ] D ) do * * if d H ([ w( A R) ] D, A) ε and d H ([ w( A R) ] D, C) > δ then begin W W ( w, R) C C [ w( A R) ] D end for all ( w, R) W (in order from last found to first found) do * if d H ( A, [( W \ ( w, R) )( A) ]D ) ε then W W \ ( w, R) Figure 7.1 Search algorithm for LIFS.
86 74 Chapter 7 Coding of binary images image in each subspace by mappings of the binary images in the subspaces. This can be done with an algorithm like the search algorithm for IFS s. To our knowledge there is no computationally tractable algorithm that solves the coding problem for RIFS s as given above. If the first step is solved, it is possible to use a search algorithm like the search algorithm for IFS s to solve the second problem. But a search through all divisions of the given binary image into subimages in the composed space has too high computational complexity to be of practical use. One way to handle the coding problem is to consider a subclass of RIFS. The image support is divided into non-overlapping regions, and each region is given a subspace where the binary image from the region is put. Usually the image support is divided into squares which can be of different size in a hierarchical way. A subclass of RIFS of this kind was first introduced for image coding of grey scale images by Jacquin [25]. The image range is divided into non-overlapping squares of different sizes, and the mappings are scalings by factors of 2 i, eight isometries and translation by a factor of the pixel size. This mapping can be seen as an RIFS where each square pixel region is a component in the extended space. This limited set of mappings is a way to reduce the search problem. The algorithm can be applied to binary images. However, this class of RIFS cannot with good coding results represent general IFS and RIFS images. The problem is the very coarse quantisation of the scaling and rotation parameters. Generally, it will not be possible to find fragments which fit. However, it is possible to represent any attractor defined by an IFS, and any other image, to any desired accuracy in the Hausdorff distance if pixel size resolution of the translation is used and mappings are allowed to contract any image to a point. This is equivalent to describing the position of the pixel and can, of course, be applied to every pixel in the given image. However, the coding performance is then only good for very sparse images. It can nevertheless be useful, together with attractor coding, to describe a few isolated pixels which are important for the quality. We have implemented two variants of this algorithm, one which uses the Hausdorff distance and one which uses the Hamming distance. In the Hausdorff case it can be shown that the mappings are contractive. However, the Hamming metric can no be used to show that the mappings are contractive. Instead the mappings will be chosen from a set of contractive mappings when the Hamming metric is used. The RIFS search algorithm. The method is similar to block-based attractor coding for grey scale images, see e.g. Jacquin [27], Fisher et al. [16]. Block-based coding has also been tried for binary images by Barnsley and Hurd [7] and Hart [20]. The given binary image is subdivided hierarchically into square blocks, where the largest block is one quarter of the given binary image, and the smallest block is determined such that fewer bits are needed to send the pixels uncoded than by a contractive set mapping. In our case we will set the smallest size to 4 by 4 pixels. A block is divided when the best source block, yields more errors than a prescribed limit. If there are few points in a block it needs not be coded and the division is stopped at that level for this block.
87 7.3 Recurrent iterated function systems 75 The parameters of the algorithm are the maximum range block size, the minimum range block size, the tolerance limit in errors per pixel and the translation resolution. The sizes and the translation are both factors of two. The contractivity is always 0.5. The domain image is first shrunk by taking the union of four pixels. Then the mapping is done from this image. This is equivalent to restricting the translation space to even addresses. There can be a larger library if odd and even addresses are distinguished. However, the coding result was not improved by using a full translation space. How could the rate/distortion of the coding be controlled? Here we use two ways. One is to restrict the smallest allowed block size, the other is to restrict the allowed number of errors per pixel. Neither method makes it possible to exactly control the rate or the distortion. RIFS coding is different from IFS and LIFS coding. In RIFS coding each range block is described by only one domain block. For RIFS coding, the range image is divided into disjunctive blocks, whereas for our LIFS coding the domain image is divided into disjunctive blocks. But for general LIFS coding, the domain blocks need not be disjunctive. An algorithm of this kind has been tested by Hart [20] with negative results. He found that very small range blocks were required, which implies a high data rate. If contraction factor one is used, then it is necessary to avoid the transform of a block onto itself. In the presented algorithm the accuracy is controlled through a maximum limit on the mean number of errors. Range blocks with more errors than the limit are divided procedure encode(b) begin if d h ( B, 0) = 0 then empty block else if size of B is small then send block uncoded else begin w find_map( B) if d h ( BwA, ( )) > εn then split block and encode subblocks else send code end end Figure 7.2 Coding algorithm for RIFS.
88 76 Chapter 7 Coding of binary images into four blocks unless the block already is of minimum size, in which case the block is represented by the best fragment. Another alternative would be to divide the block with maximum number of errors until sufficient accuracy or rate is achieved. It is also possible to divide the block which gives the best increase in rate-distortion sense, but in this case all blocks of one size smaller than the current coding also have to be tested. Every block is temporarily split into its four subblocks. For each of these blocks the best coding is searched. When this has been done for all blocks, it can be determined which block should be split to give the best increase in rate distortion performance. A block can be coded in two ways. It can be split into four equal-sized smaller blocks which are coded individually or the block itself could be represented. There are three alternatives for the coded blocks: 1) the block could be empty if there are no points in it; 2) the block can be coded by giving the mapping which transforms some other part of the image into an approximation of the block; 3) if the block is so small that the actual image data need fewer bits to be described than the mapping would need, the block is sent uncoded. For the blocks to be coded, the following expression shows how the mappings are found. w = arg min w : w 1 ( K B ) K A, dh( w ( A w 1 ( K B ))) > 0 K B d h ([ w( A w 1 ( ))] D, B) (7.5) K A where A is the given image, is the image support, B is the image block to be coded and K B is the image support of the block. Data can be stored hierarchically. Starting with the largest blocks a bit is needed to indicate split or no split, and for each encoded block a bit is needed to say whether there is a transform or an empty block. Some practical details on the implementation follow here. Before the search, the image is contracted, and all isometries are computed. All the domain images are searched for every range block. If no contraction is allowed, all mappings that map any part of a domain back onto itself must be discarded. In this implementation we use square blocks with a contraction that is a power of two. The size of the blocks will also be a power of two. The smallest range blocks can be 2, 4 or 8 pixels in square. The corresponding mapping must use at most 4, 16 or 64 bits for its representation. If the mappings need more bits for its representation, it is more efficient to send the block uncoded. Sixteen bits per block are too few to expect that a mapping will give an efficient representation since we will use full resolution of the translation parameter, giving 16 bits. For this method to be of interest it must be possible to describe most areas of size pixels or larger with a similitude or affine mapping. We have also tried this algorithm with the Hausdorff distance, but there is a difficulty since the Hausdorff distance cannot be measured separately for disjunctive blocks. In our RIFS coding case the image is divided into disjunctive blocks, each of which is encoded separately. The distance from a fragment to a block of the given
89 7.4 Non-attractor coding methods 77 image is measurable. However it is not possible to get the distance from the full given image to a fragment by measuring the distance from a block of the given image to the fragment. The true distance depends on the surrounding blocks. In the algorithm we have used the Hausdorff distance locally on each block, thus the collage might be closer to the given image than what is measured by the local Hausdorff distance. 7.4 Non-attractor coding methods The Hamming distance has an advantage over the Hausdorff and the Kantorovich distance. The image plane can be divided into disjunctive regions, and each region can be independently measured. These distances can be used to compute the distance between the full images. The Hamming metric is the sum of the differences over the image, thus the distance can be measured over regions separately. If the mappings are separable over regions, which is true for block-based mappings, the coding can be done separately for the blocks. Generally it is easier to encode independent parameters separately than to encode dependent parameters simultaneously. The disadvantage of the block division approach is that it often leads to block artifacts in the decoded image. In this section two non-attractor coding methods will be presented. The first is a combination of subsampling and the JBIG international coding standard for binary images. The second method is a quad-tree description of the image. Subsampling with the Hausdorff Metric. If the Hausdorff metric is used as a quality measure, then subsampling will yield high compression. The subsampling can of course be extended with coding of the subsampled images to give even better compression. Let be ε be the acceptable error in the Hausdorff distance. Then the image can be represented by an image with a point per ε 2 area. For the integer case a compression of 2ε( 1 + ε) + 1 to 1 is obtained, if the edge effects at the borders of the image support are disregarded, which will reduce the coding ratio to some extent. The subsampling regions are squares turned 45 degrees. The corresponding ratio for square blocks is ( ε 2) 2 4 to 1. Thus large compression can be achieved with only subsampling when the Hausdorff distance is used. On top of this any entropy coding technique can be applied. However, the relationship to the Hamming distance is very weak. For practical reasons we have only tested square subsampling where the regions are aligned with the image boundary: Thus it is possible to do somewhat better. There are many ways to do the reconstruction if the only criterion is the Hausdorff distance between the given image and the reconstructed image. We will reconstruct with a black or white box depending on whether the point is in the image or not. In this case the reconstructed image will cover the given image. The other extreme is to put just one point in the middle of the region.
90 78 Chapter 7 Coding of binary images JBIG. The international coding standard for binary images [55] is primarily for graphics. The compression is lossless, which is a main difference compared to attractor coding. We have coded the images with the implementation described in [30] as a comparison. The algorithm uses a combination of a Quad-tree representation of the image and a predictive coder. Quad-tree coding. Quad-tree coding is a hierarchical description of the image. A square region of the image could be either split into four equally sized squares or the Figure 7.3 Subsampling based on the Hausdorff distance. 10 Distortion [Hausdorff distance] Rate [bit/pixel] Figure 7.4 Rate-distortion for the subsampling scheme. Solid line = square regions, dashed line = square regions turned 45 degrees.
91 7.4 Non-attractor coding methods 79 area could be described as either white or black. The smallest squares allowed are 2 by 2 pixels and are encoded directly by their four pixel values. This method is considered because we wanted an algorithm with variable distortion and because we wanted to have an algorithm that is suited for the Hamming distance. We are interested in finding all pairs of rate and distortion, in the Hamming distance sense, that are obtainable with such a tree code. These can be found through a recursive procedure (Fig. 7.5) starting with the smallest blocks and working its way up to the largest block. Consider a square where the rate-distortion pairs for each of the four subsquares are known. The rate distortion pairs for the main block are given by all combinations of one pair each from the subsquares with one bit added to indicate the division of the main block. This is what the combine procedure does (see Fig. 7.5). The block could also be either completely black or white, adding another pair, depending on which of the two cases gives lowest distortion. From the large set of pairs, the meaningless pairs are removed, i.e. those pairs which are worse in both rate and distortion than another pair. If the coding of a given rate or distortion is needed, it can be found with a recursive procedure, i.e. an extension to the described procedure. Assume the requested rate or distortion for a block is given. We first find the rate-distortion pairs for this block. Then we look for the pair with the requested rate or distortion. Associated with the rate-distortion pair is the rate-distortion pair for each of the quadrants. Thus it is possible to know how to distribute the rate or distortion among the subsquares. It is then possible to encode each of the subsquares. encode(b) begin if size B = min_size then end return else ( B, 0) return ((1, B ), (1, size*size - B ), combine(encode( B( 0.0) ), encode( B( 01, )), encode( B( 10, )), encode( B( 11, )) )+ 1 bit) Figure 7.5 Computation of the rate-distortion curve for Quad-tree coding. The combine procedure merges rate-distortion curves by giving as output all combinations of the sum of rate and distortion from each of the input curves.
92 80 Chapter 7 Coding of binary images 7.5 Results The given images (Fig. 7.6) used in the experiments are of size pixels. The fern image is generated from an IFS with three similitudes. The snowflake [9] is an image of a natural snowflake and the dragon image [14] comes from a sketch. The Sierpinski-spiral (Fig. 2.1) is generated from an RIFS on a two element space and with five mappings. We will give some results of the coding of these images with the proposed methods. Parameters for the algorithms will be presented together with coding result. In the last subsection the result for these different methods will be compared. We will see in this chapter that the Hausdorff metric is not suitable for image quality measures. Our main measure will be the Hamming metric, which for binary images is equivalent to the RMS metric usually used for grey scale images. In the result tables we present the following data. W - the number of mappings. R - the rate in bits per pixel. d H d h - the Hausdorff distance between the reconstructed image and the given image. - the normalised Hamming distance between the given image and the reconstructed image. SNR - the signal-to-noise ratio. k 1 k 2 - the Kantorovich distance based on Manhattan distance and - the Kantorovich distance based on the squared Euclidean distance. Figure 7.6 The given images, size pixels. From left: The fern, the snowflake, the dragon and the Sierpinski-spiral images.
93 7.5 Results 81 LIFS In this section we give the result of the LIFS coding of the test images. Some of the results could be seen as IFS coding. The difference is given by the size of the domain blocks. The parameters of the coding algorithm are the following n α - the number of rotation angles. They are equally spaced between 0 and 360 degrees. n s - the number of scaling factors. s max - the maximum scaling factor. The scaling factors are equally spaced between s max and 0. blksize - the domain size. ε - the chosen accuracy of the collage, measured either in the Hausdorff metric or normalised Hamming distance. Under some conditions LIFS coding can be used to represent RIFS images, as shown in Figure 7.7. It is then necessary that the domain block division is coherent with the RIFS subspaces. An IFS image can always be LIFS coded with the proposed algorithm as shown in Figure 7.7. The number of mappings will at most increase by a factor that equals the number of domain blocks in the LIFS code. If the parameter resolution is sufficient, the LIFS that generated the given image is a solution. In Table 7.1 the result of some LIFS coded images is shown. In Figure 7.11 some examples of reconstructed dragon images are shown at different rates. RIFS Consider the encoding of the fern image with a typical fractal block coder, see Fig Due to the restricted set of affine mappings of the spatial part, it will not be possible to achieve good encoding. Hence the class of mappings usually used should be extended to include any affine mapping. In this section we give some results from RIFS coding of the dragon image and the snowflake image. There are two variants of the algorithm: one based on the Hamming distance, and the other based on the Hausdorff distance. The algorithm is controlled by the distortion and by the maximum and minimum range block size. Tables 7.2 and 7.3 show the coding results. In Figure 7.11 examples of reconstructed dragon images are shown at different rates. Figure 7.9 shows a rate-distortion curve for the RIFS coding of the dragon image. Extension of address space to odd addresses gives no improvement in the coding result, as mentioned earlier.
94 82 Chapter 7 Coding of binary images Table 7.2 The result of coding the snowflake image with RIFS. W R [bpp] d H d h SNR [db] k 1 k (8) (767) Figure 7.7 Above left: The given Sierpinski-spiral image. Above right: The Sierpinski-spiral image reconstructed from an LIFS. Below left: The given fern image and its affine mappings. Below right: The fern image reconstructed from an LIFS.
95 image n α n s s max blksize ε no maps R [bpp] d H d h SNR [db] k 1 k snowflake dragon Sierpinski-spiral Table 7.1 The result of coding the dragon image and the snowflake image with LIFS. 7.5 Results 83
96 84 Chapter 7 Coding of binary images Subsampling and JBIG Table 7.4 shows the result of subsampling and subsequent JBIG coding. The Kantorovich distances were computed on images of reduced size, pixels. The shrinking was done by taking the union of four pixels. This is the reason for the zero Kantorovich distance when subsampling with a factor of 4. Square blocks were chosen for practical reasons. Square regions rotated 45 degrees give a better rate at the same distortion, see Section 7.4. Figure 7.8 An illustration of the difficulty encoding fractal images with square blocks and right-angle rotations. A fern image encoded with pixel destination blocks and pixel source blocks, 8 isometries and pixel size resolution of translation. Top row: given image and attractor as digital images. Bottom row: approximation of attractor and the collage.
97 7.5 Results 85 Table 7.3 The result of coding the dragon image with RIFS based on the Hausdorff distance and RIFS based on the Hamming distance. Metric W R [bpp] d H d h SNR [db] k 1 k 2 dim Hausdorff Hamming Quad-tree Coding In Fig we show the rate-distortion curve for quad-tree coding with the Hamming distance. For a few cases we have coded and decoded the image to be able to compare the result by the Hausdorff distance and the Kantorovich distance, see Table 7.5. Comparison Last in this section we make a comparison of the different coding methods. In Figure 7.11 some examples of the result of the five proposed methods are shown. The 0.35 Hamming distance range block size pixels 32-8 pixels 32-4 pixels Rate [bit/pixel] Figure 7.9 Rate-distortion curve for block based coding with the Hamming distance. Range block size 32-16, 32-8 and 32-4 pixels.
98 86 Chapter 7 Coding of binary images Table 7.4 Coding results, subsampling and JBIG. ( k 1 and k 2 are calculated on images reduced to pixels.) Image R [bpp] d H d h SNR [db] k 1 k dragon snowflake fern Hamming distance dragon snowflake fern Rate [db] Sierpinskispiral Figure 7.10 Rate-distortion curve for quad-tree coding with optimal division based on the Hamming metric.
99 7.6 Conclusion 87 Table 7.5 Quad-tree approximation of the dragon image. ( k 1 and k 2 are calculated on images reduced to 128x128 pixels.) R [bpp] d H d h SNR [db] k 1 k compression for most methods is around 5, 10 and 100 times, that is 0.2, 0.1, and 0.01 bits per pixel. In the following three Figures, 7.12 to 7.14, rate-distortion results are shown. All methods are compared by all current metrics. Some algorithms need only search the parameter space once, whereas other methods have to search the parameter space once for each included mapping. 7.6 Conclusion The attractor coding methods are competitive when the Hausdorff metric is used. LIFS coding and block coding based on the Hausdorff metric give the best result. These methods perform best at low rates. At high rates the non-attractor methods perform best among the five tested methods. If the result is evaluated in the Hamming metric, the non-attractor methods are best, both quad-tree and subsampling with JBIG. The best attractor method is block coding based on the Hamming metric. In the Kantorovich metric the attractor methods based on the Hausdorff metric and subsampling are the best. Visually the Hausdorff based methods and the subsampling look best at low rates. In brief, the conclusion is that the coding method should be based on the metric that will be used to evaluate the coding. Attractor coding methods perform best at low rates. For high quality images there are other methods that perform better than attractor coding. How to find the best set of fragments for a given accuracy is still an open question. A solution to this problem would further improve the coding performance.
100 88 Chapter 7 Coding of binary images 1: (0.22, 0.20) 2: (0.11, 0.22) 3: (0.01, 0.39) 5: (0.20, 0.16) 6: (0.11, 0.21) 7: (0.01, 0.27) 4: (1, 0), Given image 8: (0.34, 0.17) 9: (0.13, 0.19) 10: (0.10, 0.24) 11: (0.015, 0.35) 12: (0.20, 0.10) 13: (0.1, 0.14) 14: (0.01, 0.21) Subsampling Quad-tree Block-code, Hausdorff Block-code, Hamming LIFS 15: (0.14, 0.17) 16: (0.04, 0.31) 17: (0.01, 0.41) 18: (0.004, 0.53) Figure 7.11 Some examples of the reconstructed dragon image from the five proposed coding methods. Below the images are the rate in bit/pixel and the distortion in the Hamming metric distance.
101 7.6 Conclusion Hausdorff distance Quad-tree - Subsampling + JBIG - LIFS - Block code, Hamming - Block code, Hausdorff Rate [bit/pixel] 0.45 Hamming distance Quad-tree - Subsampling + JBIG - LIFS - Block code, Hamming - Block code, Hausdorff Rate [bit/pixel] Figure 7.12 Comparison of the five proposed coding methods for the dragon image. Top: Distortion measured with the Hausdorff metric. Below: Distortion measured with the normalised Hamming distance.
102 90 Chapter 7 Coding of binary images 0.16 Kantorovich distance (Manhattan distance) Quad-tree - Subsampling + JBIG - LIFS - Block code, Hamming - Block code, Hausdorff Rate [bit/pixel] Kantorovich distance (squared Euclidean distance) Quad-tree - Subsampling + JBIG - LIFS - Block code, Hamming - Block code, Hausdorff Rate [bit/pixel] Figure 7.13 Comparison of the five proposed coding methods for the dragon image. Distortion measured with the Kantorovich distance. Top: Manhattan metric as inner metric. Below: Square of the Euclidean inner distance measure.
103 7.6 Conclusion SNR [db] Quad-tree - Subsampling + JBIG - LIFS - Block code, Hamming - Block code, Hausdorff Rate [bit/pixel] Figure 7.14 Comparison of the five proposed coding methods for the dragon image. Distortion measured with signal-to-noise ratio (SNR).
104 92 Chapter 7 Coding of binary images
105 Chapter 8 Coding of grey scale images In which we discuss possible improvements of the coding performance for block-based attractor coders, in terms of rate and distortion, by enlarging the set of spatial mappings. We review three models of fractal grey scale images. Each of the models consists of a mathematical representation of images, a class of contractive image transformations and algorithms for encoding and reconstruction of images. The performance of attractor coding methods for grey scale images in terms of rate and distortion is good, close to other state-of-the-art coding methods [18], [53]. But there is hope that improvements are possible because the extremely good rate-distortion performance previously believed to be reachable has not yet been reached. It is also experienced that fractal looking parts of images get the worst coding performance, which seems unintuitive when an attractor based method is used. Attractor coding methods often suffer from a high computational complexity which is reduced by using only a small subset of the affine transformations in the spatial domain. In this chapter we discuss possible gains in the rate-distortion sense by enlarging the set of spatial mappings. We will describe some experiments which support our idea. However, attractor coding methods are complex, with many parameters. Here, we will compare the coding result of our coding methods with the coding result of a baseline block-based attractor coder [16]. The attractor coders that give the best result include many features and optimised parameters. We have not included such extensions in our coder. By grey scale images we mean real world grey scale images, which can be represented by measures, functions or vectors [34]. By vector image, for example, we mean a vector that represents a grey scale image. For each of the representations, a class of contractive image transformations whose attractors can be used to represent grey scale images will be considered. Why do we need three different models of fractal grey scale images? Most attractor coding methods are described in terms of a vector model of images. Because of the high computational complexity of the encoding a very restricted set of mappings 93
106 94 Chapter 8 Coding of grey scale images in the spatial domain is used. This set of mappings can be described within the vector model. Our idea is to extend the set of mappings. However, by doing so they do not fit the vector model very well. The extended set of mappings is better described with a spatially continuous representation of images. Fractal images exist in some spatially continuous space of images. The images in the spatially discrete space can therefore only approximate fractal images. One characteristic of fractal images is details on every scale, which a spatially discrete image with limited resolution cannot have. However, the spatially discrete images may be self-similar, which is another characteristic of fractal images. As in Chapter 2 a real world image will be viewed as a plane from which light is radiating with spatially varying intensity and spectral content. We will describe three models of fractal grey scale images. The models will use different representations of real world images. Two of the representations basically follow Barnsley and Hurd [7, pp. 28, model (ii) and model (iii)], and the third representation is a common vector representation of grey scale images. Barnsley and Hurd [7] assume the existence of a class of real world images with properties listed in Chapter 2, p. 11. Following Barnsley and Hurd [7] we define two representations which have properties corresponding to the listed properties of real world grey scale images. The characteristics of fractal grey scale images are similar to the characteristics of fractal binary images, i.e. details on many scales, self-similarity, and they are too irregular to be described in traditional geometrical language. It is an advantage if the models are complete in the sense that any image in the corresponding space can be represented at arbitrarily high accuracy by a mapping. This means that any image can be represented by the model, although it does not say anything about the corresponding bit rate. 8.1 Measures and iterated function systems with probabilities Grey scale images can be represented by normalised real-valued Borel measures on the plane [7, pp. 29]. We will only consider measures with support that is spatially bounded, thus the images can be viewed as enclosed within the image support. The value of each measurable subset represents the total intensity emitted by the subset. Let ( Dd, ) be a compact metric space. Let ( D) denote the set of normalised Borel measures on D and let d K denote the Kantorovich metric. Then, ( ( D), d K ) is a compact metric space [6, p. 355]. Definition 8.1 (Barnsley [6, p. 334]) An iterated function system with probabilities (IFSP) consists of a set of N contractive mappings { w i : D D, i = 1,, N } on a complete metric space ( Dd, ) and a set of N probabilities { p i, i = 1,, N } with N p i = 1 and p. i= 1 i > 0, i = 1,, N The IFSP W induces a Markov operator on ( ( D), d K ) defined by
107 8.1 Measures and iterated function systems with probabilities 95 N µ ( A) =ˆ p i µ ( w 1 i ( A) ) i = 1 (8.1) for all µ ( D). If the IFS corresponding to the IFSP W has a contractivity factor s [ 01, ), the induced Markov operator : ( D) ( D) has a contractivity factor s with respect to the Kantorovich metric [6, p. 357]. Any given image can be represented by an IFSP to any given accuracy by covering the given image with a large number of small fragments and giving each fragment the mass of the corresponding part of the given image. But this description is likely to need very many mappings which take little account of the fine structure of the given image except on the scale at which the solution was constructed. The solution means covering the given image with small fragments where the deformation part of the mapping is irrelevant except for the contractivity factor. If the given image was generated by an IFSP, then a solution of this kind is not likely to be able to recover the IFSP that generated the image. Image generation We will describe a stochastic algorithm and a tree algorithm. These algorithms are also applicable to ssrifs. The stochastic algorithm is based on a randomly jumping point and a counting of how many times the point hits every area that is to be measured. The stochastic jumps are controlled by a Markov model induced from the IFSP. An approximation of the accuracy after a given number of steps will have a probabilistic form. Let { x n } n = 0 with x n = w σn ( x n 1 ) denote an orbit of the IFS produced by the random iteration algorithm, starting with x 0. The maps are chosen independently according to the probabilities, p 1,, p n for n = 12,,. Let µ be the unique invariant measure for the IFSP. Then, with probability one n 1 lim f( x 1 + n k ) = f( x) dµ ( x) n k = 0 X (8.2) for all continuous functions f : X and all x 0 [6, pp. 370]. If a spatial bound of the attractor is known, the deterministic transform composition algorithm (Chapter 3.1) has a deterministic number of steps for a given accuracy and vice versa; for a given number of steps the accuracy can be determined. Let S be the set of all compositions of affine mappings from W. Let S( ε) be a set of maps with contractivity factor smaller than or equal to ε. Let ε i be the contraction of map s i S( ε) and p i the probability of the map. Let W be an IFS with probabilities. The set S( ε) can be constructed by starting with the maps of W and exchanging the maps with too large contractivity factor until all maps have contractivity factor
108 96 Chapter 8 Coding of grey scale images smaller than ε. If s i has too large contractivity, it is exchanged for { s i w j } W j = 1. Finally the approximate measure B is given by summing up the measure of all the fragments. The probability mass p i is added to the area s i ( Ã), where à is a bound for the support of the measure. The Kantorovich distance between the attractor and the approximation is bounded by d K ( A, B) n i = ε, (8.3) 2 i p i diam( A) where diam( A) is the largest distance between two points in A. The tree algorithm can generate parts of the attractor without increasing the computational complexity. The stochastic algorithm can also generate parts of the attractor, but the complexity will be much higher since the stochastic walk passes through the complete image. An example of a measure is shown in Figure 8.1. A problem seems to be that much of the probability mass gathers together in a few places. The span of the measure between small unit areas is very large. Coding There are many different coding methods suggested for this model, e.g. [17], [33]. But to our knowledge there is no algorithm suited for image coding. Many algorithms solve the problem of finding a mapping with an attractor that is sufficiently close to the given image but with little consideration of the importance of minimising the number of mappings to get a low rate. Also, many algorithms only use a limited set of spatial mappings and then find the probabilities that minimise the distance. In this case many more mappings are needed, which could lead to worse coding performance. Figure 8.1 A measure whose support is a fern.
109 8.2 Functions and affine operators 97 In one sense the coding problem for this model is more difficult than for the other models. The probabilities should sum to one, thus they cannot be determined one at a time. The probabilities all depend on each other. One suggestion is to first find the spatial mappings [31]. This can be done with the full search algorithm for the IFS inverse problem. When the spatial mappings are known, it is not very difficult to find the probabilities. 8.2 Functions and affine operators Grey scale images can be represented by real valued functions defined on the image support [7, p. 28]. The value of the function represents the intensity of each point of the image. Let =ˆ { f : D } be the space of functions that represents images. The -metric is defined by d d ( f, g) =ˆ sup x X d( f( x), gx ( )) (8.4) The operator, transforming images denoted W, of interest consists of two parts: a spatial transformation ω and a grey scale transformation with two parts a and b. The mappings of the functions that we will consider are defined in the following way. The value in the point p 2 of the image f transformed by W is given by ( Wf )( p) = a( p)f ( ω 1 ( p) ) + b( p). (8.5) Usually a(), b() and ω 1 () are chosen to be piecewise constant over square regions. This is a special case of the Read-Bajraktarevic operator T [11] defined by Tf ( x) =ˆ vx (, fmx ( ( ))) x X (8.6) where mx ( ) = ω 1 ( x). m is a mapping on the image support, and for each point in the support there is a mapping v on the grey scale dimension. A function vx (, ) is called uniformly contractive if there exists an s [ 01), such that d ( vxg (, ), vxh (, )) sd ( gh, ) x X. (8.7) If vx (, ) is uniformly contractive, then T is contractive under the d -metric [11]: Thus the contractivity is determined by the grey scale mapping, and the spatial mapping is irrelevant to the contractivity.
110 98 Chapter 8 Coding of grey scale images Image generation We will consider four ways of generating an approximation of the attractor from an affine operator. First, there is a choice of generating subsamples or the total value of small areas. Second, there is a choice of mapping forward or backward. With forward iteration the initial points or regions can be chosen, and the final points or regions are given by the algorithm. In the backward iteration the final points or regions can be chosen, and the initial points or regions are given by the algorithm. If the iteration is done a sufficient number of times, then the influence from the initial point or region will become negligible. We will describe two alternatives. One (subsampling) is used to generate a set of samples from the image, the other is used to generate the total value of small areas. The subsampling algorithm has low complexity. The other has high complexity since the areas split into smaller areas, generally polygons, for every iteration. The subsampling algorithm can be described by the following recursive formulas: T n f( x) = vxt (, n 1 f( m( x) )) (8.8) and T 0 f( x) = f( x). (8.9) Thus, in general we have Tf ( x) = vx (, fmx ( ( ))). (8.10) Inserting affine mappings yields Tf ( x) = ax ( )f( m( x) ) + bx ( ) (8.11) T ( 2) f( x) = ax ( )Tf ( m( x) ) + bx ( ) = ax ( )( amx ( ( ))f( m ( 2) ( x ))) + bmx ( ( ))) + bx ( ) = ax ( )amx ( ( ))f( m ( 2) ( x) ) + ax ( )bmx ( ( )) + bx ( ) (8.12) and so forth until the first term is small enough. The influence of the initial image decreases with the number of iterations. Figure 8.2 shows an example of an enlargement of a small area in the reconstructed image. Here we have computed an approximation of a number of samples located within a small area with the size of a pixel in the given image. We have used the backwards iterating algorithm.
111 8.2 Functions and affine operators 99 Figure 8.2 The Lenna image, pixels, viewed as a function and coded with affine operators. The transformation performed by the affine operator is similar to the transformation performed by a block-based attractor coder. Left: The reconstructed image. Right: A small area, corresponding to a pixel in the given image, reconstructed with high resolution, 1 pixel in the given image corresponds to pixels. As is seen, the area contains details although they are not fractal. Coding If the spatial mapping is given for some region over which a and b should be constant, then the values of a and b which minimise the d can be computed by an optimisation algorithm. The minimisation also gives the distance. A simple and frequently used technique is to divide the image into square regions of different sizes. The coding algorithm starts by trying to code large regions. If the distortion is too high, the regions are divided into four equally large regions which are coded independently. The recursive division goes on until the distortion is low enough or until the rate is the chosen one. Typically, distortion is measured as the mean squared error. We have not seen the d distance measure used even though it is the distance measure in which the Collage theorem is expressed. How are a and b found that minimise the d distance? If a is given, then the b that minimises the distance can be found by a search. Starting with any a, one can find the largest and smallest limiting lines. It is then possible to determine in what direction to go to decrease the distance and to find the next break point. The iteration is continued until the minimum is found.
112 100 Chapter 8 Coding of grey scale images 8.3 Vectors and affine mappings Grey scale images can be represented by real valued vectors [16], [32], [53]. This model will be used to approximate the two previous models, thus only a subset of the possible mappings will be considered. The vectors will also be referred to as digital grey scale images. The elements of such a vector are referred to as pixels. Every pixel has an address, i.e. its location in a two-dimensional array. The value of the pixel could correspond to the grey value of a point in the image or to the total intensity of a small region. Let f N and g N. The L 2 metric is defined as d( f, g) N f. (8.13) N ( i g i ) =ˆ i = 1 The metric space in this model is ( N, d). We will consider affine mappings on this vector space, i.e. Wx + t where W is an N N matrix and t is an N 1 column vector. We will only consider a subclass of these mappings, viz. those with only a few values on each row of the matrix W. The mappings form discretized approximations of the two earlier models. An affine mapping is contractive when [16] s = sup Wx < 1 x. (8.14) x Any digital image can be represented by this model by letting W be the all zero matrix and t the given image. However, in this case we cannot talk about efficient representation. Efficiency is only obtained if the matrix and the vector have some structure which makes it possible to represent them in an efficient way. Image generation In many cases it is enough to iterate the mapping starting with any image. In such cases the contraction is so high that only a few iterations are needed to get very close to the attractor. There are also many tricks available that make the image generation less complex, see e.g. [16], [32]. Coding We will use a class of affine mappings which is a spatially discrete approximation of the affine operators of the function image model. A range region corresponds to a set of pixels. Each such set is described by a spatial and a visual mapping. Every pixel is the mapping of one or a few source pixels depending on the contraction factor and the
113 8.4 Comparison 101 contraction method. Both subsampling and mean value of neighbouring pixels are common. The mapping in the visual dimension is usually affine but other mappings occur. We will only consider affine mappings. If the spatial mapping is given, then the parameters of the affine mapping that minimise the distance can be computed together with the distance. The spatial mapping is found by searching. A hierarchical division of the pixels is common. The algorithms start with large range regions, and if the distortion is not low enough the regions are divided into four equally large squares which are coded individually. 8.4 Comparison In the case of images represented by functions and measures, we will consider a pixel to be a small square area. If the spatial mappings used in the function and measure models are such that every domain pixel is mapped within a range pixel, then the vector model can be used instead. Often the spatial contraction is chosen to be a power of two. Let the pixel values of the vector model represent the total measure of the corresponding pixel area in a measure image. For function images the pixel values of the vector model can represent either the sum of the image function over the pixel area or the value of a specific sampling point. If the value of a pixel represents the value of a point, then whenever an image is transformed with mappings from the larger class, the value of some points has to be interpolated. The common block-based attractor coding method as described by Jacquin [26] can also be described with functions and affine operators [11]. The spatial mappings in a common block-based attractor coder are such that also the vector model can be used. Often the vector model is used as an approximation of the other two models. If the vector image approximates a function image, we will consider each value of the vector image to be the average of the value of the function image over a small region corresponding to a pixel. If a measure image is approximated, then each value of the vector image corresponds to the total measure of the pixel region. The spatial mapping is constrained to eight isometries, and the translation is constrained to pixel size resolution at most. These constraints make it straightforward to model the earlier models with vectors and affine mappings on the vector space. The range blocks are usually square and hierarchically subdivided into four equally large areas when needed to reduce the distortion. It should also be noted that there is a connection between binary images defined by RIFS and grey scale images defined by block-based attractor codes where the range blocks are mapped within domain blocks. If the mappings from the blockbased attractor code are viewed as set mappings in three dimensions, they can also be considered as an RIFS defined on a three-dimensional space. An RIFS needs to have
114 102 Chapter 8 Coding of grey scale images Figure 8.3 A typical division into destination blocks. contractive mappings and complete connections to define a unique fixed set. The contractivity is fulfilled if the mappings are contractive in both the spatial and the visual dimensions. There can be two cases. In the first case there is at least a subset of the mappings with complete connections, hence a part of the image is given as a fixed set. The rest of the image is given as a mapping of the fixed set. The other case is that there is at least one mapping which is a condensation set, i.e. a constant set. The rest of the image can be a mapping of this set. 8.5 Results The idea that we want to test is whether a larger class of spatial transforms will give better coding performance. The reason for keeping the spatial transform class restricted is to reduce coding time. The only way of coding known so far is to search for the best source block for every destination block. The search time can be reduced by classification schemes and restrictions of the number of possible source blocks. In our experiments we will view the given images as sampled functions, and the image transformations will be viewed as affine operators. However, for the first two experiments we will only use transformations which scale the domain blocks to half the size and apply the usual eight symmetry operations. The translations will be
115 8.5 Results 103 allowed to have pixel size resolution or some multiple thereof. If a given resolution for the reconstructed images is considered, the vector model can also be used to describe the operations. For the subclasses of image transformations used here the functions with affine operators will give the same result as vectors with affine mappings. In the third experiment, where we consider a larger set of rotation angles and scaling factors, we will use the model based on functions and affine operators. The given image is considered to be samples from a grey scale image. When the value for a point between the given sampled points is needed, we will use bilinear interpolation. In a typical block-based attractor coder a library of blocks is formed by choosing a set of blocks from the domain image. For each of the range blocks one of the domain blocks is transformed to the range block by an affine mapping. The affine mappings are of the form w( p) = Ap + t. The matrix is usually chosen from a set of eight matrices, and the translation is chosen from some set of vectors. In our view we will not consider the library explicitly but rather view the class of mappings. We will vary the set from which A and t are taken to see how the coding performance is affected. Block-splitting criteria and optimality of the split We will consider a block-based attractor coder with hierarchical splitting of the range blocks. The range blocks are split if no available domain block gives low enough error. The two questions which we will address in this section are what splitting criterion to use and how close the hierarchical splitting is to an optimal splitting, with reference to the relation between the rate and the distortion. Hierarchical splits of the above-mentioned kinds require a search for a domain block for every block in the tree. There are also many other alternatives both with higher and lower computational complexity, e.g. to determine the division into blocks based only on the range blocks and searching only for the final blocks or for every sub-block of the current division and then choosing to split the block which gains the most. Is it possible to get a complete rate-distortion curve for a fractal coder? Since an attractor coder is expensive in coding it could be very time-consuming. But a common coder works by successively improving the coding by splitting blocks which do not have good enough quality. This seems like a good start for a rate-distortion curve. However, we cannot be sure that this algorithm gives the optimal division. In particular, the division is based on the collage distance, which is not the same as the distance between the given and reconstructed image. How about the division into blocks? Several models have been tried but here we will only consider the most common one, division into hierarchical square blocks. The most common way to do the division is to decide upon a threshold for the RMS error of each block. If there is a block where no map can satisfy the condition, then the block is subdivided into equally sized blocks. The other way is to decided on an acceptable total amount of error and divide the block with the largest total error.
116 104 Chapter 8 Coding of grey scale images This alternative is somewhat more complex to implement since the code is not available until the whole image is encoded. In the previous case the code can be output block by block. Another alterative would be to split the block with the lowest ratio between the change in rate and distortion, i.e. the block with the highest reduction in distortion per extra bit for the code. But this requires that all blocks are coded one level below the final level, which means a substantial increase in computing time. We will try two common splitting rules. One is to split the block with maximum total error and the other is to split the block with maximum mean error. These two rules are compared to an optimal splitting in a rate-distortion sense for quad-tree division. We assume that all mappings need the same number of bits for their representation. Finding the optimal division is a much more computationally complex problem. There is also a considerable difference between computing the rate-distortion curve and finding the actual code for a given point somewhere on the curve. See [42]. The rate-distortion curve is computed by first finding the best affine map for each range block of every interesting size. That is, for every range block the domain block is selected that fits best. Furthermore, we assume the rate-distortion curve for every quadrant of a block is known. The rate-distortion curve is made up of all combinations of these curves, and the rate-distortion is achieved if the block is coded with one transform. The unnecessary points can be removed, that is points which have both worse rate and worse distortion than another point. The rate-distortion curve generated with this algorithm does not present the actual division of the range blocks for different points on the curve. There are two ways to get the code and division into blocks for a point on the rate-distortion curve. One way is with a recursive procedure which on each level in the splitting tree first finds the rate-distortion curve and then decides how to split the current block. If the block is split, the procedure continues to decide whether and how to split the blocks on the level below. The other way is to keep pointers in the tree while the rate-distortion curve is computed. Then it is possible to follow these pointers when the rate-distortion point is decided. The above reasoning about the rate-distortion optimised coding presumes that the coding cost of the w is known beforehand. The experiments are done on the Lenna image, size pixels. The translation is done with pixel size resolution, and all eight isometries are used. The subdivision of the destination blocks is done down to 2 2 pixel blocks which are transmitted uncoded. The rate of 2 2 pixel blocks is about the same as for the attractor code of a block of the same size. Hence the distortion will approach zero at a rate slightly higher than the given image. Splitting the block with maximum total error is best. The other rule, to split the block with maximum mean error, is an implicit secondary condition that the error should be spread out in the image. In Figure 8.4 we can see that the splitting by the maximum total error gives results very close to the optimal case in the rate 0 to 1 bit per pixel. In Figure 8.4 and 8.5 we can see that the attractor follows the collage distance diagram.
117 8.5 Results 105 Translation resolution First we will apply different resolutions of the translation parameters of the spatial transform to find out how the coding performance in a rate-distortion sense is affected. Here we will only use eight geometric transforms and block scaling to half the size together with the eight symmetry operations. The range image is hierarchically divided into smaller blocks as necessary to give smaller distance than the required maximum distance between the collage and the given image. Translation resolutions of 1, 2, 4 and 8 pixels have been tried, meaning that the distance between the position of two neighbouring domain blocks corresponds to these numbers of pixels. As is shown in Figures 8.6 and 8.7 there is a significant difference in coding performance between the resolutions factors for rates of 0.6 bit/ pixel and above. For rates lower than 0.6 bit/pixel the difference is very small. Similar results have been obtained by e.g. Fisher [16], who tried several strategies for selecting addresses, including fixed step-size independent of block size as well as block-size-dependent step size, and found that fixed resolution gave the best rate-distortion relationship. When comparing the spacing of two and four pixels, he found that the difference was small, with the spacing of two being slightly better. PSNR [db] split by mean error Performance for two block splitting rules split by total error optimal split τ = 0 τ = Rate [bit/pixel] Figure 8.4 A comparison of two splitting rules. The translation resolution is 2 τ.
118 106 Chapter 8 Coding of grey scale images Collage vs attractor performance optimal split collage attractor PSNR [db] Rate [bit/pixel] 38 Performance for different resolutions of the translation parameters PSNR [db] optimal split 0 τ = 1 τ = 3 τ = 2 τ = Rate [bit/pixel] Figure 8.5 Top: Collage distance compared to attractor distance. Bottom: Collage distance with different resolution of translation. The translation resolution is 2 τ.
119 8.5 Results Performance for different resolutions of the translation parameters PSNR [db] * Rate [bit/pixel] 32 Performance for different limitations of splitting depth 30 PSNR [db] * Rate [bit/pixel] Figure 8.6 Top: Coding result for the Lenna image with different resolutions of the translation parameter. Bottom: Coding result for the Lenna image with different limitations to the splitting depth. The number shows the smallest range block.
120 108 Chapter 8 Coding of grey scale images 38 Performance for different resolutions of the translation parameters 36 PSNR [db] * Rate [bit/pixel] Figure 8.7 Coding result for the Lenna image with different resolutions of the translation parameter. Scale and rotation resolution The domain image is usually divided into blocks in some way, and these blocks make up the domain pool or library. The range image is similarly divided into blocks, usually spatially smaller than the domain blocks. Thus there are usually very few scaling factors and rotation angles involved. Only those represented by a scaling to half the size and the eight symmetries are used. According to Lu [32, pp. 130], the performance improves remarkably by introducing skewing transforms in the spatial domain. The most commonly used scaling factor is two, though other factors have been tried [53]. While the symmetry operations introduced by Jacquin are widely used, there are conflicting reports as to whether they improve the coding performance or not [53]. Increasing the number of scaling factors beyond powers of two and rotation angles beyond right angles has not, to our knowledge, been reported before. Figures 8.8 and 8.9 show two examples of coding with increased resolution in rotation angle and scaling factor. Figure 8.10 shows the coding performance in a rate-dis-
121 8.5 Results 109 Figure 8.8 Encoding Lenna ( ) with 80 destination blocks, 32 rotation angles and 8 scaling factors between 0 and 0.5. Given image, initial image, iterations 1, 2 and the reconstructed image.
122 110 Chapter 8 Coding of grey scale images Figure 8.9 Encoding Lenna ( ) with 400 destination blocks, 32 rotation angles and 8 scaling factors between 0 and 0.5. Iteration 2, 3 and the reconstructed image. tortion sense for different resolutions in scaling factor and rotation angle. Transforming the image requires some kind of interpolation because the points of the discrete image are not typically transformed onto another point. In the examples we have used bilinear interpolation to get image values between pixel points. 8.6 Conclusion The experiments show better coding results when the translation step size of a blockbased attractor coder is decreased. For low rates the difference is small, whereas for higher rates there is a significant difference.
123 8.6 Conclusion 111 The experiments also show better coding results when the number of scaling factors and rotation angles is increased beyond those given by shrinking to half the size and the eight isometries usually used. The difference is small but clear. It should again be stressed that no entropy coding has been applied to the generated parameters. Thus, the quantitative performance can be different if such methods are applied. However, the qualitative result that a larger parameter space is better is still believed to be true. PSNR [db] Rate [bits/pixel] Figure 8.10 A comparison of encoding the Lenna ( ) image with different resolutions of the rotation angle and the scaling factor. Squares: scaling = 0.5 and angles = 8 isometries. Circles: scaling 2-8 factors with a maximum of 0.5 and 8-32 angles.
124 112 Chapter 8 Coding of grey scale images
125 Chapter 9 Computing the Kantorovich distance for images In which we compare two algorithms for the computation of the Kantorovich distance for images. Kaijsers s algorithm needs considerably shorter computation times than Atkinson and Vaidya s algorithm for the test images though the algorithms seem to have about the same computational complexity. The Kantorovich distance was briefly introduced in Chapter 6. In this chapter we repeat the description and continue by describing our implementation and comparison of two algorithms for the computation of the Kantorovich distance for images. 9.1 The Kantorovich distance and the transportation problem In this section we essentially follow Kaijser [29]. In this chapter we will consider digital images, where each pixel has a weight (or mass) assigned to it and a position in the plane. For grey scale images the weight can be the grey level; for binary images the weight can be a unit weight. Later we will see that also for binary images integer mass is needed. Let A = { u i 2, i = 1,, k} and B = { v j 2, j = 1,, l} be images, and let A( p) denote the weight of p A. A transportation plan T between A and B is a set of triplets {( s i, t i, m i ), i = 1,, n T }, where s i A, t i B, m i 0 and there are no triplets with the same ( s i, t i ). The triplets are such that m i i: s i = p A( p) p A (9.1) 113
126 114 Chapter 9 Computing the Kantorovich and m i i: t i = p B( p) p B. (9.2) We will call a transportation plan complete if there is equality in (9.1) or (9.2) or both. Let Θ( A, B) be the set of all complete transportation plans between A and B. Let d be a distance measure, called inner distance measure. The cost of a transportation plan T is defined to be n T ct ( ) =ˆ m i ds ( i, t i ). (9.3) i = 1 Definition 9.1 The d * K distance between two images is the cost of the complete transportation plan with minimum cost. Let A, B be images. Define d K * ( A, B) =ˆ min{ ct ( ): T Θ( A, B) }. (9.4) Definition 9.2 Let A, B be images with equal total weight. The Kantorovich distance is defined by d K ( A, B) =ˆ min{ ct ( ): T Θ( A, B) }. (9.5) The computation of the Kantorovich distance implies the solution of a balanced minimum cost transportation problem with k supplies and l demands. The transportation problem is defined by a set of supplies with magnitudes { a i = Au ( i ), i = 1,, k}, a set of demands with magnitudes { b j = Bv ( j ), j = 1,, l} and a set of costs { c ij = du ( i, v j ), u i Av, j B}. The solution implies a set of flows F = { f ij } where f ij is the flow from supply u i to demand. The problem is to v j
127 9.1 The Kantorovich distance and the transportation problem Figure 9.1 An illustration of the Kantorovich metric for binary images, in this example two fern images. In the middle row the binary values have been interpreted as height or mass. The total mass of the images is normalised to give the same mass for both images. The bottom row shows the arcs of the transportation plan between the two images. The mass that each arc carries is not illustrated. The left transportation plan is based on the L 1 -metric and the right on the square of the L 2 - metric.
128 116 Chapter 9 Computing the Kantorovich minimise subject to k zf ( ) = c ij f ij l i = 1 j = 1 l j = 1 k i = 1 f ij f ij f ij 0 = i = 1,, k a i = j = 1,, l b j (9.6) The dual problem is to maximise k i = 1 a i α i + l j = 1 subject to α i + β j c ij b j β j for all i, j (9.7) where { α i, i = 1,, k} and { β j, j = 1,, l} are auxiliary dual variables. The dual variable α i is associated with u i and the dual variable β j is associated with v j. The orthogonality conditions that are necessary and sufficient for optimality of primal and dual solutions are [1] ( 1) f ij > 0 α i + β j = c ij ( 2) α i 0 ( 3) β j 0 l = i = 1,, k f ij j = 1 k f ij i = 1 a i = j = 1,, l b j (9.8) In general, images have different total grey mass. In this case we will normalise the mass before computing the Kantorovich distance between the images. Thus the Kantorovich distance is insensitive to differences between images by scaling the grey scale of the whole image. 9.2 The primal-dual algorithm We will use the primal-dual algorithm (following the description by Murty [37]) to solve the balanced min-cost flow problem. Consider one image as supply, with k
129 9.2 The primal-dual algorithm 117 nodes, and the other image as demand, with l nodes. Usually k and l are the same and equal to the number of pixels in the images. All mass at the supplies should be transported to the demands at minimum cost. We assume that the total supply exactly corresponds to the total demand. This is called a balanced problem. The algorithm starts with a dual feasible solution, i.e. a solution which satisfies the constraints of the dual problem. A max flow problem is solved for each setting of dual variables, and then the dual variables are changed to allow more flow to pass through. The algorithm continues until primal feasibility, i.e. until the constraints of the primal problem are satisfied. The primal-dual algorithm is, in brief, procedure primal-dual algorithm begin initiate α i, β j, f ij while flow is not maximum solve max-flow problem on admissible arcs calculate δ and update α i and β j, see Equation (9.10) end An arc ( u i, v j ) with α i + β j = c ij is called admissible. The first step in the algorithm is to initialise the dual variables and the flow to some feasible value. Set e.g. α i = 0 i = 1,, k β j = min i = 1,, k { c ij } j = 1,, l (9.9) The supply nodes with remaining mass are called surplus nodes, whereas the demand nodes with remaining demand are called deficit nodes. The flow can be initialised by the following procedure; traverse the admissible arcs ( u i, v j ) and set the flow to f ij min{ a i, b j }. Reduce the available supply (surplus) a i a i f ij and the remaining demand (deficit) b j b j f ij. The algorithm has two main steps. One step is to maximise the flow on the admissible arcs; the other is to update the dual variables to find new admissible arcs. The steps are repeated until all the supplies are used and demands are fulfilled. The maximise flow procedure is, in brief, procedure maximise flow begin label while there is a breakthrough do begin increase flow label end end
130 118 Chapter 9 Computing the Kantorovich where label is a procedure which tries to find a path along which the flow can be increased. If such a path is found, it is called a breakthrough. The flow is increased by finding a path from a surplus node to a deficit node. The path goes from a surplus node via an admissible arc to a deficit node and backwards via an arc with positive flow to a supply node and so on until a deficit node is reached. Then the flow is increased as much as possible, limited by the surplus, deficit and the arc in the path with the smallest positive backwards flow. To find the path, a labelling procedure is used. The labels are also used when the dual variables are changed to allow new admissible arcs. The last part is the update of the dual variables to give new admissible arcs. Let S be the labelled supply nodes and T be the labelled demand nodes, and let δ = min u i S, v j T { du ( i, v j ) α i β j }. (9.10) Then change the dual variables to α i α i + δ i: ui S β j β j δ j: vj T (9.11) Below we will describe the labelling, flow change routine and dual variable update procedures. Labelling procedure. The labelling procedure will find a path from a surplus node to a deficit node, along which the flow can be increased. First all labels (if there are any) are removed. (i) All nodes with surplus are labelled. (ii) If supply u i is labelled and demand v j is not labelled yet and ( u i, v j ) is an admissible arc, then demand v j is labelled, and together with the label it is noted at which node the supply is available. (iii) If demand v j is labelled and supply u i is not yet labelled and f ij > 0, then supply v j is labelled together with a notation of the node where supply is available. The algorithm starts with (i), then goes through (ii) and (iii) iteratively as long as possible. If a demand node with deficit is labelled, then there is a path along which the flow can be increased. This is also called a breakthrough. The labelling algorithm is terminated and the algorithm continues with the flow change routine. The labelling is also terminated if no more nodes can be marked. Then the algorithm continues with the dual variable update procedure to get new admissible arcs. The procedure is shown in Fig S is the surplus nodes, F is the deficit nodes, F i is the set of demand nodes reachable from u i through admissible arcs, and A j is the set of supply nodes with positive flow to. v j
131 9.2 The primal-dual algorithm 119 Flow change routine. This routine is called when there is a path from a surplus node to a deficit node along which the flow can be increased. A path is a set of arcs from a supply to a demand node. The path is found by backtracing the labels from the deficit node where the breakthrough occurred. The flow from supply to demand is increased as much as possible. The flow increase is limited by the supply, the demand and the flow on reverse arcs along the path. On every second arc the flow in the direction from supply to demand will be increased by reducing the flow on the arc. Thus the flow on these arcs will limit the possible flow increase. Dual variable update. The dual variables are updated after non-breakthrough. The first step of the dual variable update is a search for the minimum reduced cost δ for the labelled supply nodes and unlabelled demand nodes (Eq. 9.10). This is followed by increasing the dual variables of the labelled supplies with δ and reducing the dual variables of the labelled demands with δ (Eq. 9.11). The current flow is not affected. But there will be some new admissible arcs. The change occurs among the labelled supplies and unlabelled demands. procedure label begin mark all surplus nodes for u i S do mark u i S' S while S' do begin F' for u i S' do for v j F i do if v i not marked then begin if then exit with breakthrough mark v ivi append to F' end S' for v j F' do for v i A j do end end if v j not marked then begin mark v jv append j to end Figure 9.2 The labelling procedure. S'
132 120 Chapter 9 Computing the Kantorovich In the labelling procedure the algorithm alternates between tracing arcs with nonzero flow and admissible arcs. Later we will see that the number of arcs with non- Unbalanced transportation problem. The computation of the d * K -distance implies the solution of an unbalanced transportation problem which can also be solved with the primal-dual algorithm [37, pp. 326] by introducing an extra slack node that takes up the unbalanced mass. The cost between the slack node and all other nodes is set to 0. The standard primal-dual algorithm can also be used without the slack node if the stop criterion of the loop is changed to stop when any of the images is empty and the dual variables of the image with excess mass are initialised to the same value. In every iteration the nodes with excess mass have the same dual value. All other nodes will at most have the same dual value. Then it would, in the end, be possible to introduce a slack node with this negative dual value and let this node take the excess mass. Performance. The complexity of the primal-dual algorithm is On ( 2 A) [1], where A is the sum of all supplies and n is the number of points. There is also a problem with the size of the cost and flow matrices. If the images are of size pixels, then the matrices will have 2 32 elements, which requires at least 4 Gb of memory. It is not common to have that amount of primary memory in a computer today. In the next section we describe some modifications to the algorithm which make it possible to solve the transportation problem for images. 9.3 Computing the Kantorovich distance for images This section describes the modifications to the primal-dual algorithm introduced by Kaijser [29] and the modification introduced by Atkinson and Vaidya [1], which makes it possible to substantially decrease the computational complexity. The characteristics of the transportation problem for images are the very large number of nodes, the full connections between the nodes, that the nodes are located in a square grid on the plane and that the distances are defined by a distance measure on the plane. Let A and B be images with N nodes each. Let R( p) = min( A( p), B( p) ) p. If the inner distance measure is a metric, then d K ( A, B) = d K ( A R, B R) [28], i.e. mass that is common to a supply node and a demand node in the same position can be discarded. If the inner distance measure is the L 1 -metric, then the dual variables can be initialised to α i = 0 i = 1,, N β j = 1 j = 1,, N (9.12) Finding admissible arcs
133 9.3 Computing the Kantorovich distance for images 121 zero flow can be kept very low, at most one less than the number of nodes. The basic algorithm contains no other way to look for admissible arcs than to search through all arcs. Below we will use some observations by Kaijser [29] to reduce this search to a much smaller number. Let the inner distance function be a metric. Let the dual variables α i and β j be such that for each point u i there exists a point v j such that du ( i, v j ) α i β j = 0 and vice versa. Then α s α t du ( s, u t ) and β s β t dv ( s, v t ) [29, p. 187]. A node u is called low with respect to v if α u < c uv β v. Suppose that the distance function is the L 1 -metric. Let u be a pixel in U, let α u be a dual variable such that duv (, 0 ) α u β v0 = 0 for some v 0. Furthermore assume that for each v V there exists a pixel u' U such that du' (, v) α u' β v = 0. Now suppose that v 1 V and that v 1 is low with respect to u. Then if v 1 is northeast of u and v is northeast of v 1, v is low and for the other three directions [29, p. 188]. The above theorem is illustrated in Figure 9.3. When the inner distance measure is the square of the L 2 -metric, then the following proposition will speed up the search for admissible arcs. Similarly, with the case of the L 1 -metric, the search can be stopped on each row as soon as the reduced cost increases. Suppose that q 1 and q 2 obtained after the dual variable change routine are close to each other, that both are low with respect to p and that q 1 is strictly lower than q 2. Then if q 2 is east of q 1, all pixels east of q 2 will be low. If q 2 is west of q 1, all pixel west of q 2 will be low [29]. A procedure that finds the admissible arcs for a supply node is shown in Figure 9.4. A full β-matrix must exist with a border with infinite value. This is to reduce the number of comparisons. A corresponding procedure for square of the L 2 - metric is shown in Figure 9.5. In most cases the dual variable change will be 1. Hence it is not necessary to look for the minimum value. In some cases the flow change and labelling routine will be done unnecessarily, but this will not introduce errors. A full β matrix is needed in the algorithm that finds admissible arcs even though the β values exist only in some points of the image. Missing values can be interpolated. The matrix should have a border with infinite value as a stopper in the search algorithm for admissible arcs. The extra values should be as small as possible to ensure the early interruption of the search. c ij α i β j Figure 9.3 Illustration of growth of β j for a given α i. j
134 122 Chapter 9 Computing the Kantorovich Comparison with the method by Atkinson and Vaidya There are four improvements to the standard algorithm (Atkinson and Vaidya [1]). 1, scaling supplies and demands, 2, maintaining flows without cycles, 3, using special data structures to facilitate computation of δ and 4, improved handling of changes in dual variables. Let n be the number of non-zero nodes. Let Σ be sum of all supplies. Let M be the maximum magnitude of a supply or a demand. The most important is the data strucprocedure find_on_row( ( x 0, y 0 ), u) begin ( x, y) ( x 0, y 0 ) + ( 10, ) while β( x, y) = du (, ( xy, )) α( u) do begin if ( x, y) V then (x, y) is admissible x x + 1 end ( x, y) ( x 0, y 0 ) ( 10, ) while β( x, y) = du (, ( xy, )) α( u) do begin if ( x, y) V then (x, y) is admissible x x 1 end end procedure find_admissible_arcs(u) begin if u V then u is admissible find_on_row(u, u) ( x, y) u + ( 01, ) while β( x, y) = d( ( x, y), u) α( u) do begin if ( x, y) V then (x, y) is admissible find_on_row((x, y), u) y y + 1 end ( x, y) u ( 01, ) while β( x, y) = d( ( x, y), u) α( u) do begin if ( x, y) U then (x, y) is admissible find_on_row((x, y), u) y y 1 end end Figure 9.4 The procedure find_admissible_arcs. The procedure finds the admissible arcs for a given source node in the case of L 1 -metric.
135 9.3 Computing the Kantorovich distance for images 123 tures that allow δ to be calculated in O( logn) instead of On ( ). Scaling turns a factor A into a factor nlogm. As long as Σ = ω( nlogm), i.e. Σ grows asymptotically faster than nlogm, scaling gives an improvement in time complexity. Atkinson and Vaidya treats problems with points on the plane. Our problem concerns images where supplies and demands are located on a square grid. procedure find_on_row( ( x 0, y 0 ), u) begin rc prev = rc( uu, ) for x = x 0 + 1,, x max do begin if rc( u, ( x, y 0 )) = 0 then ( x, y 0 ) is admissible if rc( u, ( x, y 0 )) > rc prev and rc prev > 0 then end for loop else rc prev = rc( u, ( x, y 0 )) end rc prev = rc( uu, ) for x = x 0 1,, x min do begin if rc( u, ( x, y 0 )) = 0 then ( x, y 0 ) is admissible if rc( u, ( x, y 0 )) > rc prev and rc prev > 0 then end for loop else rc prev = rc( u, ( x, y 0 )) end end procedure find_admissible_arcs(u) begin ( x 0, y 0 ) = u if rc( uu, ) = 0 then u is admissible find_on_row(u, u) for y = y 0 + 1,, y max do begin if rc( u, ( x 0, y) ) = 0 then ( x 0, y) is admissible find_on_row( ( x 0, y), u) end for y = y 0 1,, y min do begin if rc( u, ( x 0, y) ) = 0 then ( x 0, y) is admissible find_on_row( ( x 0, y), u) end end Figure 9.5 The procedure find_admissible_arcs. The procedure finds the admissible arcs for a given source node in the case of square of the L 2 - metric.
136 124 Chapter 9 Computing the Kantorovich Scaling. In our application we assume that the maximum pixel value M is constant. Hence Σ will at least not grow faster than nlogm. Thus it is doubtful whether scaling will decrease the complexity. On the other hand, if the normalisation is taken into account, then Σ will grow with the square of the number of pixels. Also, M grows with the number of pixels. Hence Σ grows faster than nlogm, therefore the scaling should be useful. Avoiding cycles. A cycle is a set of arcs with non-zero flow connected in a cycle. If the arcs are part of an optimal transportation plan, the cost of sending mass around the cycle must be zero, otherwise it would be possible to reduce the cost by decreasing flow on the cycle. The flow along the cycle can be reduced until the cycle opens up and at least one arc gets zero flow. A cycle is a symptom of more arcs than necessary, and too many arcs will increase the computational complexity. Cycles can be avoided if the labelling starts by labelling all surplus nodes and then always first using all arcs with positive flow that can be used for labelling and only using an arc with zero flow when there is no arc with positive flow. However, labelling the positive flow first makes it necessary to store both incoming and outgoing flow from all nodes. In the basic algorithm, labelling is done on positive flow from demands and on admissible arcs from supplies. In this case the flow arcs need only be stored with the supply nodes. In the algorithm by Atkinson and Vaidya the flow must be kept at both nodes. This makes a difference in the computation time. A breakthrough occurs when the labelling reaches a node with a deficit. Then there is a path along which the flow can be increased. The positive flows from a non-empty supply form a tree. No cycles can be formed if the search for breakthrough goes from tree to tree. There will be no arcs within a tree and no arcs back to a tree. Therefore arcs with positive flow should be labelled first. When no further labelling is possible, an admissible arc is searched for. Then all flow from this node is labelled. When a breakthrough is found, the rest of the tree with positive flow is marked. Since we only want one breakthrough per source, the labelling is stopped before nodes with unfulfilled demand. Finding admissible arcs. We only consider range trees for the L 1 case. Admissible arcs can also be found for the square of the L 2 -metric case with Voronoi-diagrams and somewhat higher complexity. The storage space is On ( logn). We use a twolevel tree of nodes that are sorted according to the dual variable and the distance to a point. At the top node is the arc with least reduced cost. Insertion and deletion takes O( ( logn) 3 ) steps, while initialisation takes On ( ( logn) 3 ) steps. The sorting only takes unmarked nodes into account. As soon as a node is marked, it is withdrawn from the list. Among all unused admissible arcs we want to find the one with the lowest reduced cost. For this we divide the image support with a vertical line. This splits the arcs into three groups, those within the left side, those crossing the vertical line and those within the right half. The shortest arc within the right and left sides can be
137 9.3 Computing the Kantorovich distance for images 125 found with the same procedure. The shortest arc that crosses the line can be found by dividing the area with a horizontal line. Now again we have three parts, arcs within the upper and lower half can be found by the same procedure. The arcs on the diagonal are found in the following way. We sort the arcs within each quadrant, sources and destination separately according to the distance to the crossing of the line reduced by the dual variable. This will give us eight queues. Range trees [45] are used to sort the nodes in order to find the arc with the lowest reduced cost. Assume that the arc with the lowest reduced cost that is crossing a vertical line is wanted. This is found by dividing the region with a horizontal line. The nodes are sorted in eight groups, one for each quadrant. Supplies and demands are separated according to ascending cost from the node to the crossing of the two lines reduced with the dual variable of the node. From these lists the shortest diagonal arc can be found. The shortest arc crossing the vertical line in the upper part can be found with a similar method as the shortest arc crossing the lower part. To find the shortest arc within the region, the shortest arc within left and right regions must also be found. This is done by a similar structure for the left and the right region. The splitting is stopped when all the nodes are on a line or when there are too few of either supply or demand nodes. The range tree can be updated, i.e. nodes can be deleted or added. This will be used to keep the tree up-to-date during the labelling. Improving the dual variable handling. Atkinson and Vaidya define a variable to keep a running total of dual variable changes. and w combine to give an implicit representation of the dual variables. At the end of a search the proper dual variables are recovered by setting α i α i β j β j = wu ( i ) + for u i in S = wu ( i ) for u i not in S = wv ( j ) for v j in T = wv ( j ) for v j not in T (9.13) There are On ( ) dual variable changes per search and On ( ) labelled nodes whose values must be altered. Now each of the On ( ) dual variable changes during a phase takes O( 1) time. Thus the dual variable changes take On ( ) time per augmentation. In the basic algorithm each phase consists of first maximising the flow on the admissible arcs and subsequently changing the dual variables to allow new admissible arcs. The change is the minimum reduced cost greater than zero on the marked supplies and unmarked demands. In the case of images and the L 1 -metric we have seen in our experiments that most changes will be 1. In most changes of the dual variables there will be new admissible arcs with the given change. Thus the complexity is almost On ( ) per augmentation.
138 126 Chapter 9 Computing the Kantorovich Computational complexity Our problem is generally too large to make it possible to store the full cost matrix C and the full flow matrix F. The cost matrix need not be stored since the distance can be calculated from the coordinates of each point. Only the arcs with non-zero flow need to be stored. The number of arcs with non-zero flow is much less than the number of admissible arcs. For both Atkinson and Vaidya s as well as Kaijser s algorithm we will keep a list for each demand node with the non-zero flows. For some variants of Kaijser s algorithm this is sufficient, whereas for others, including Atkinson and Vaidya s algorithms, it is also necessary to keep a list of non-zero flow from the supply node. For Kaijser s algorithm we also need a list with the admissible arcs for each supply node, while for Atkinson and Vaidya s algorithm we need the nodes sorted in the range tree. The maximum decrement of the reduced cost will be one in most cases. Hence, in Kaijser s algorithm we do not search for the maximum decrement of the reduced cost but only decrement by one. In some cases the flow change and labelling routines will be executed some unnecessary times. The basic primal-dual algorithm has computational complexity On ( 2 log A), where n is the number of points and A is the total mass. The computational complexity of Atkinson and Vaidya s [1] algorithm is proved to be On ( 2 ( logn) 3 logn ), where n is the number of points and N is the largest mass of a point. Kaijser [29] has indications from computer experiments that his algorithm has a computational complexity of roughly On ( 2.2 ). 9.4 Implementation The problem in implementing the above algorithms is to find a data structure for the nodes and arcs which enables efficient computation. The core of the algorithms is the labelling and subsequent updating of the flow. The labelling goes from node to node through admissible arcs and arcs with positive flow. As we can see from the experiments, labelling takes a large amount of the execution time, in particular for Kaijser s algorithms. Thus we need a data structure such that one quickly finds the admissible arcs or arcs with positive flow from a given node. We have implemented three versions based on Kaijser s algorithm and one version based on Atkinson and Vaidya s algorithm. The algorithms are as follows: Ka1: L 1 -metric. Ka2: L 1 -metric, cycle free. Ka3: square of the L 2 -metric. AV: L 1 -metric, cycle free. The storage of the arcs and flows is the main problem. While the arcs and flows should be easily accessible from a given node, they are connected to two nodes,
139 9.5 Results 127 which makes it somewhat difficult. The main storage choice is between linked lists and static lists. The first one needs more time and less data space. The second needs less time but more space as the storage space must be predetermined. As we shall see this is where the problem is, namely how to find a trade-off between computation time and space. The basic algorithm uses a label to mark the nodes, but some of the algorithms need two different labels. In some variants of the algorithms the flows are needed in both directions. In other algorithms it is sufficient if the flows are linked to one of the nodes. Flows connected to both nodes cost twice as much to store as flows connected to one node. 9.5 Results Below, we describe the results when the algorithms are applied to three different pairs of images. fern - fern2 (ff2): Two binary images generated from two IFS s with only a small difference. These images are represented as grey scale images with grey scale values 0 and 1. The number of non-zero points differ between the images, thus the mass has to be normalised. (See also Table 9.1.) Lenna - attractor coded Lenna (tm): Two close grey scale (range 0 to 255) images. The difference is barely perceptible. These images have been manipulated to have the same total mass for each size. The maximum pixel value when common mass has been removed will approach (with image size) 255. (See also Table 9.2.) Lenna - baboon (lb): Two clearly different grey scale (range 0 to 255) images with different total mass. The normalisation will give these images a large total mass and an increasing (with image size) maximum pixel value. (See also Table 9.3.)
140 128 Chapter 9 Computing the Kantorovich In the tables below we have summarised some data, e. g. total mass, number of nonzero points and maximum pixel value from the images which are relevant with respect to the computational time and complexity. Table 9.1 Data about the fern and fern2 images (ff2). image size total mass bits reduced mass bits nodes src dst , , , , , ,104, , Table 9.2 Data about the Lenna and attractor-coded Lenna images (tm). image size total mass bits reduced mass bits nodes src dst , , , , , ,615, , Table 9.3 Data about the Lenna and baboon images (lb). image size total mass bits reduced mass bits nodes src dst ,175, ,040, ,507,724, ,805,250, ,512,241, ,457,209, ,246,330,129, ,106,931, Table 9.4 shows the Kantorovich distances between the images. The distances have been normalised to unit mass and unit image size. See also Figures 9.11, 9.10 and 9.9 where the images and the couplings resulting from computation of the Kantorovich distance are shown. There is only a small difference between the couplings that may have cycles and the cycle-free coupling. However, there is a significant difference in the number of arcs, see Tables 9.8 to There is a clear difference
141 9.5 Results 129 between the couplings based on L 1 inner distance measure and couplings based on square of the L 2 inner distance measure. Table 9.4 Kantorovich distances between the images of size The distances have been normalised to unit mass and unit image size. inner distance measure ff2 tm lb L square of the L The computational times for the algorithms are collected in Tables 9.5 and 9.6. See also Figures 9.6, 9.7 and 9.8, where the computational times are displayed in graphs. The computation time is not symmetric in the two images. Below we have chosen the order which gives the shortest computation times. The difference is most clear where there is a significant difference in number of points with non-zero mass. Table 9.5 Computation times for the AV and Ka1 algorithms. image size AV Ka1 ff2 tm lb ff2 tm lb Table 9.6 Computation times for the Ka2 and Ka3 algorithms. image size Ka2 Ka3 ff2 tm lb ff2 tm lb We observe that the computational time is significantly longer for the AV algorithm compared to the Ka1, Ka2 and Ka3 algorithms. The Ka1 algorithm has the
142 130 Chapter 9 Computing the Kantorovich shortest computation time for all three image pairs and image sizes except for the Lenna-baboon image pair of size 128 pixels, where the Ka2 algorithm is slightly faster. According to Atkinson and Vaidya [1] it is necessary that the algorithm throughout the computation maintains a set of arcs with non-zero flow that is cyclefree. This requirement is necessary in their proof of the computational complexity. There is a time penalty for keeping the cycle-free set of arcs, and for our test image sizes the cost is larger than the gain. Comparing the Ka1 with the Ka3 algorithm (Figure 9.8) we find the Ka1 to be faster if the comparison is made based on the size of the image support. However, if the comparison is based on the number of points with non-zero mass, then it is not certain that one algorithm will always have the shortest computation time. The computational complexity has been estimated from the above numbers (restricted to image sizes to pixels). The estimation was done by fitting (minimising the square error) a straight line to the points ( logn, logt) where n is the number of points and t is the computation time. The time is exponential in the number of non-zero points, t cn D where D is the estimated computational complexity. Table 9.7 Computational complexity as estimated from the three largest images. image AV Ka1 Ka2 Ka3 ff tm lb We note that the computational complexity of the AV algorithms seems to be fairly independent of the images. The Ka1, Ka2 and Ka3 algorithms have lower computational complexity than the AV algorithm if the images are close but worse computational complexity for images far apart. The algorithms with the L 1 inner metric will have approximately half as many points as those based on the square of the L 2 -metric due to the reduction of common mass in the first case. The maximum mass of a point will not increase with image size for the tm image pair since they have been manipulated to have equal total mass. However, because of the small image sizes the reduction of common mass will result in a smaller maximum mass which grows with image size up to the maximum value of 255. For the binary images there will be a significant difference between the image size, i.e. the number of points of the image support, and the number of points with non zero-mass. For grey scale images this different is negligible. The main parts of the Ka1, Ka2 and Ka3 algorithms are proportional to the number of points with nonzero mass, but there are also parts of these algorithms which are proportional to the number of points of the image support.
143 9.5 Results 131 The computational complexity of the AV algorithms is proportional to the number of non-zero points. In the tables below we give some more details about the performance of the different algorithms. Table 9.8 Data from the computation of the AV algorithm on images of size ff2 tm lb total time [s] label, no label, time [s] dual variable changes range tree init [s] arcs, no For the AV algorithm we observe that most of the time is spent on initialising the range trees. This is partly due to a less good implementation of the procedure. But even if all of this time is disregarded, the AV algorithm has still longer computation times than both the Ka1 and Ka2 algorithms. Table 9.9 Data from the computation of Ka1 algorithm on images of size ff2 tm lb total time [s] label, no label, time [s] dual variable changes find adm, time [s] arcs, no
144 132 Chapter 9 Computing the Kantorovich Table 9.10 Data from the computation of Ka2 algorithm on images of size ff2 tm lb total time [s] labelling, no labelling, time [s] dual variable changes find admissible arcs, time arcs, no For the Ka1 and Ka2 algorithms, between 50% and 90% of the time is spent on labelling. The main part of the remaining time is spent on finding new admissible arcs. Table 9.11 Data from the computation of Ka3 algorithm on images of size ff2 tm lb total time [s] labelling, no labelling, time [s] dual variable changes find admissible arcs, time [s] arcs, no Discussion We have tried to extend the Ka1 algorithm with scaling of the supplies and the demands, but this leads to longer computation times for our test images. We have also tried the AV algorithm without the scaling, which turned out to lead to longer computation times. In all the algorithms the labelling is done many more times than the dual variable update. In the Ka algorithms the dual variables are changed by one each time. If the dual variables could have been changed with a larger number, then changing it one at a time means that the labelling will sometimes be done unnecessarily. Thus, for our examples we conclude that the possible unnecessary labellings are few. The range tree in the AV algorithm has two purposes. One is to facilitate the computation of the minimum reduced cost by which the dual variables should be changed; the other is to facilitate the labelling by providing admissible arcs. The cost of maintaining the range tree is the initial sorting of the nodes and the updating of the range tree during the labelling algorithm. Since most changes of the dual variables
145 9.6 Conclusion 133 are by one, this purpose of the range tree seems unnecessary. The other purpose of the range tree, i.e. providing admissible arcs during labelling, is more difficult to evaluate. It should be compared with the efficient algorithm to find admissible arcs and the list with the admissible arcs for each node used in the Ka algorithms. The disadvantage of Ka algorithms is that the lists of admissible arcs are only updated after each dual variable change. Many supply nodes can have an admissible arc to the same demand node. This means that after the demand node is labelled, the other supply nodes might make unsuccessful attempts to label the demand node since there is no updating of the lists of admissible arcs after each labelling. This problem is more profound for the L 1 inner distance measure since there are many more admissible arcs than e.g. when the square of the L 2 inner distance measure is used. Altogether this means that the extra effort that the AV s algorithm spends to find the change value of the dual variables is wasted. The Ka algorithms use the knowledge that the change in most cases is by one and in a few cases a little larger. The disadvantage will be an extra unnecessary labelling for each dual variable change. Apparently, this gives better performance. 9.6 Conclusion We have implemented two basic algorithms and some variants of them. Kaijser s algorithm is faster in all examples. In the fastest version it uses much memory but the algorithm can easily be adapted to use less memory than AV s algorithm at the cost of longer computation time. The computation time depends on the distance and the inner metric. The algorithms based on the L 1 -metric is faster than those based on the square of the L 2 -metric.
146 134 Chapter 9 Computing the Kantorovich 10 6 Ka Ka time [s] 10 2 time [s] number of nodes number of nodes 10 6 Ka AV time [s] 10 2 time [s] number of nodes number of nodes Figure 9.6 A comparison of the computation time for different image sizes for each algorithm. - baboon - Lenna, - fern, - Lenna - fractal coded Lenna.
147 9.6 Conclusion fern fern time [s] number of nodes 10 6 Lenna attractor coded Lenna 10 6 Baboon Lenna time [s] 10 2 time [s] number of nodes number of nodes Figure 9.7 A comparison of algorithms based on the L 1 -metric. * - AV, - Ka2, - Ka1.
148 136 Chapter 9 Computing the Kantorovich 10 6 fern fern fern fern time [s] 10 2 time [s] number of points in the image support number of nodes 10 6 Lenna attractor coded Lenna 10 6 Lenna attractor coded Lenna time [s] 10 2 time [s] number of points in the image support number of nodes 10 6 Baboon Lenna 10 6 Baboon Lenna time [s] 10 2 time [s] number of points in the image support number of nodes Figure 9.8 A comparison of the square of the L 2 -metric with the L 1 -metric, * - Ka3, - Ka1.
149 9.6 Conclusion 137 Figure 9.9 Top left: An optimal coupling based on the square of the L 2 -metric. Top right: An optimal coupling based on the L 1 -metric. Centre: An optimal cycle-free coupling based on the L 1 -metric. Bottom left: A fern image ( pixels). Bottom right: Another fern image.
Iterated Functions Systems and Fractal Coding
 Qing Jun He 90121047 Math 308 Essay Iterated Functions Systems and Fractal Coding 1. Introduction Fractal coding techniques are based on the theory of Iterated Function Systems (IFS) founded by Hutchinson
Qing Jun He 90121047 Math 308 Essay Iterated Functions Systems and Fractal Coding 1. Introduction Fractal coding techniques are based on the theory of Iterated Function Systems (IFS) founded by Hutchinson
A Review of Image Compression Techniques
 A Review of Image Compression Techniques Rajesh, Gagan Kumar Computer Science and Engineering Department, MIET College, Mohri, Kurukshetra, Haryana, India Abstract: The demand for images, video sequences
A Review of Image Compression Techniques Rajesh, Gagan Kumar Computer Science and Engineering Department, MIET College, Mohri, Kurukshetra, Haryana, India Abstract: The demand for images, video sequences
Fractal Image Compression
 Ball State University January 24, 2018 We discuss the works of Hutchinson, Vrscay, Kominek, Barnsley, Jacquin. Mandelbrot s Thesis 1977 Traditional geometry with its straight lines and smooth surfaces
Ball State University January 24, 2018 We discuss the works of Hutchinson, Vrscay, Kominek, Barnsley, Jacquin. Mandelbrot s Thesis 1977 Traditional geometry with its straight lines and smooth surfaces
Fractal Compression. Related Topic Report. Henry Xiao. Queen s University. Kingston, Ontario, Canada. April 2004
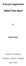 Fractal Compression Related Topic Report By Henry Xiao Queen s University Kingston, Ontario, Canada April 2004 Fractal Introduction Fractal is first introduced in geometry field. The birth of fractal geometry
Fractal Compression Related Topic Report By Henry Xiao Queen s University Kingston, Ontario, Canada April 2004 Fractal Introduction Fractal is first introduced in geometry field. The birth of fractal geometry
5.7. Fractal compression Overview
 5.7. Fractal compression Overview 1. Introduction 2. Principles 3. Encoding 4. Decoding 5. Example 6. Evaluation 7. Comparison 8. Literature References 1 Introduction (1) - General Use of self-similarities
5.7. Fractal compression Overview 1. Introduction 2. Principles 3. Encoding 4. Decoding 5. Example 6. Evaluation 7. Comparison 8. Literature References 1 Introduction (1) - General Use of self-similarities
Lecture : Topological Space
 Example of Lecture : Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Example of 1 2 3 Example of 4 5 6 Example of I Topological spaces and continuous
Example of Lecture : Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Example of 1 2 3 Example of 4 5 6 Example of I Topological spaces and continuous
CHAPTER 4 FRACTAL IMAGE COMPRESSION
 49 CHAPTER 4 FRACTAL IMAGE COMPRESSION 4.1 INTRODUCTION Fractals were first introduced in the field of geometry. The birth of fractal geometry is traced back to the IBM mathematician B. Mandelbrot and
49 CHAPTER 4 FRACTAL IMAGE COMPRESSION 4.1 INTRODUCTION Fractals were first introduced in the field of geometry. The birth of fractal geometry is traced back to the IBM mathematician B. Mandelbrot and
STORING IMAGES WITH FRACTAL IMAGE COMPRESSION
 STORING IMAGES WITH FRACTAL IMAGE COMPRESSION TYLER MCMILLEN 1. Introduction and Motivation One of the obvious limitations to the storage of images in a form a computer can read is storage space, memory.
STORING IMAGES WITH FRACTAL IMAGE COMPRESSION TYLER MCMILLEN 1. Introduction and Motivation One of the obvious limitations to the storage of images in a form a computer can read is storage space, memory.
Mr.Pratyush Tripathi, Ravindra Pratap Singh
 International Refereed Journal of Engineering and Science (IRJES) ISSN (Online) 319-183X, (Print) 319-181 Volume 1, Issue 4(December 01), PP.07-15 Fractal Image Compression With Spiht lgorithm Mr.Pratyush
International Refereed Journal of Engineering and Science (IRJES) ISSN (Online) 319-183X, (Print) 319-181 Volume 1, Issue 4(December 01), PP.07-15 Fractal Image Compression With Spiht lgorithm Mr.Pratyush
Fractal Coding. CS 6723 Image Processing Fall 2013
 Fractal Coding CS 6723 Image Processing Fall 2013 Fractals and Image Processing The word Fractal less than 30 years by one of the history s most creative mathematician Benoit Mandelbrot Other contributors:
Fractal Coding CS 6723 Image Processing Fall 2013 Fractals and Image Processing The word Fractal less than 30 years by one of the history s most creative mathematician Benoit Mandelbrot Other contributors:
M3P1/M4P1 (2005) Dr M Ruzhansky Metric and Topological Spaces Summary of the course: definitions, examples, statements.
 M3P1/M4P1 (2005) Dr M Ruzhansky Metric and Topological Spaces Summary of the course: definitions, examples, statements. Chapter 1: Metric spaces and convergence. (1.1) Recall the standard distance function
M3P1/M4P1 (2005) Dr M Ruzhansky Metric and Topological Spaces Summary of the course: definitions, examples, statements. Chapter 1: Metric spaces and convergence. (1.1) Recall the standard distance function
Error-Correcting Codes
 Error-Correcting Codes Michael Mo 10770518 6 February 2016 Abstract An introduction to error-correcting codes will be given by discussing a class of error-correcting codes, called linear block codes. The
Error-Correcting Codes Michael Mo 10770518 6 February 2016 Abstract An introduction to error-correcting codes will be given by discussing a class of error-correcting codes, called linear block codes. The
However, this is not always true! For example, this fails if both A and B are closed and unbounded (find an example).
 98 CHAPTER 3. PROPERTIES OF CONVEX SETS: A GLIMPSE 3.2 Separation Theorems It seems intuitively rather obvious that if A and B are two nonempty disjoint convex sets in A 2, then there is a line, H, separating
98 CHAPTER 3. PROPERTIES OF CONVEX SETS: A GLIMPSE 3.2 Separation Theorems It seems intuitively rather obvious that if A and B are two nonempty disjoint convex sets in A 2, then there is a line, H, separating
Symmetric Product Graphs
 Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 5-20-2015 Symmetric Product Graphs Evan Witz Follow this and additional works at: http://scholarworks.rit.edu/theses
Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 5-20-2015 Symmetric Product Graphs Evan Witz Follow this and additional works at: http://scholarworks.rit.edu/theses
Product constructions for transitive decompositions of graphs
 116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
MA651 Topology. Lecture 4. Topological spaces 2
 MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
MA651 Topology. Lecture 4. Topological spaces 2 This text is based on the following books: Linear Algebra and Analysis by Marc Zamansky Topology by James Dugundgji Fundamental concepts of topology by Peter
Lecture 17. Lower bound for variable-length source codes with error. Coding a sequence of symbols: Rates and scheme (Arithmetic code)
 Lecture 17 Agenda for the lecture Lower bound for variable-length source codes with error Coding a sequence of symbols: Rates and scheme (Arithmetic code) Introduction to universal codes 17.1 variable-length
Lecture 17 Agenda for the lecture Lower bound for variable-length source codes with error Coding a sequence of symbols: Rates and scheme (Arithmetic code) Introduction to universal codes 17.1 variable-length
Fractal Geometry. Prof. Thomas Bäck Fractal Geometry 1. Natural Computing Group
 Fractal Geometry Prof. Thomas Bäck Fractal Geometry 1 Contents Introduction The Fractal Geometry of Nature - Self-Similarity - Some Pioneering Fractals - Dimension and Fractal Dimension Scope of Fractal
Fractal Geometry Prof. Thomas Bäck Fractal Geometry 1 Contents Introduction The Fractal Geometry of Nature - Self-Similarity - Some Pioneering Fractals - Dimension and Fractal Dimension Scope of Fractal
2. Metric and Topological Spaces
 2 Metric and Topological Spaces Topology begins where sets are implemented with some cohesive properties enabling one to define continuity Solomon Lefschetz In order to forge a language of continuity,
2 Metric and Topological Spaces Topology begins where sets are implemented with some cohesive properties enabling one to define continuity Solomon Lefschetz In order to forge a language of continuity,
On Soft Topological Linear Spaces
 Republic of Iraq Ministry of Higher Education and Scientific Research University of AL-Qadisiyah College of Computer Science and Formation Technology Department of Mathematics On Soft Topological Linear
Republic of Iraq Ministry of Higher Education and Scientific Research University of AL-Qadisiyah College of Computer Science and Formation Technology Department of Mathematics On Soft Topological Linear
Mathematical Morphology and Distance Transforms. Robin Strand
 Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
Mathematical Morphology and Distance Transforms Robin Strand robin.strand@it.uu.se Morphology Form and structure Mathematical framework used for: Pre-processing Noise filtering, shape simplification,...
QED Q: Why is it called the triangle inequality? A: Analogue with euclidean distance in the plane: picture Defn: Minimum Distance of a code C:
 Lecture 3: Lecture notes posted online each week. Recall Defn Hamming distance: for words x = x 1... x n, y = y 1... y n of the same length over the same alphabet, d(x, y) = {1 i n : x i y i } i.e., d(x,
Lecture 3: Lecture notes posted online each week. Recall Defn Hamming distance: for words x = x 1... x n, y = y 1... y n of the same length over the same alphabet, d(x, y) = {1 i n : x i y i } i.e., d(x,
Lecture 9 - Matrix Multiplication Equivalences and Spectral Graph Theory 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanfordedu) February 6, 2018 Lecture 9 - Matrix Multiplication Equivalences and Spectral Graph Theory 1 In the
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanfordedu) February 6, 2018 Lecture 9 - Matrix Multiplication Equivalences and Spectral Graph Theory 1 In the
MATH 54 - LECTURE 10
 MATH 54 - LECTURE 10 DAN CRYTSER The Universal Mapping Property First we note that each of the projection mappings π i : j X j X i is continuous when i X i is given the product topology (also if the product
MATH 54 - LECTURE 10 DAN CRYTSER The Universal Mapping Property First we note that each of the projection mappings π i : j X j X i is continuous when i X i is given the product topology (also if the product
Convexity Theory and Gradient Methods
 Convexity Theory and Gradient Methods Angelia Nedić angelia@illinois.edu ISE Department and Coordinated Science Laboratory University of Illinois at Urbana-Champaign Outline Convex Functions Optimality
Convexity Theory and Gradient Methods Angelia Nedić angelia@illinois.edu ISE Department and Coordinated Science Laboratory University of Illinois at Urbana-Champaign Outline Convex Functions Optimality
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY
 A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
A GRAPH FROM THE VIEWPOINT OF ALGEBRAIC TOPOLOGY KARL L. STRATOS Abstract. The conventional method of describing a graph as a pair (V, E), where V and E repectively denote the sets of vertices and edges,
Observing Information: Applied Computational Topology.
 Observing Information: Applied Computational Topology. Bangor University, and NUI Galway April 21, 2008 What is the geometric information that can be gleaned from a data cloud? Some ideas either already
Observing Information: Applied Computational Topology. Bangor University, and NUI Galway April 21, 2008 What is the geometric information that can be gleaned from a data cloud? Some ideas either already
Fractal Image Coding (IFS) Nimrod Peleg Update: Mar. 2008
 Fractal Image Coding (IFS) Nimrod Peleg Update: Mar. 2008 What is a fractal? A fractal is a geometric figure, often characterized as being self-similar : irregular, fractured, fragmented, or loosely connected
Fractal Image Coding (IFS) Nimrod Peleg Update: Mar. 2008 What is a fractal? A fractal is a geometric figure, often characterized as being self-similar : irregular, fractured, fragmented, or loosely connected
PATTERN CLASSIFICATION AND SCENE ANALYSIS
 PATTERN CLASSIFICATION AND SCENE ANALYSIS RICHARD O. DUDA PETER E. HART Stanford Research Institute, Menlo Park, California A WILEY-INTERSCIENCE PUBLICATION JOHN WILEY & SONS New York Chichester Brisbane
PATTERN CLASSIFICATION AND SCENE ANALYSIS RICHARD O. DUDA PETER E. HART Stanford Research Institute, Menlo Park, California A WILEY-INTERSCIENCE PUBLICATION JOHN WILEY & SONS New York Chichester Brisbane
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS
 Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Topology notes. Basic Definitions and Properties.
 Topology notes. Basic Definitions and Properties. Intuitively, a topological space consists of a set of points and a collection of special sets called open sets that provide information on how these points
Topology notes. Basic Definitions and Properties. Intuitively, a topological space consists of a set of points and a collection of special sets called open sets that provide information on how these points
Sample Based Texture extraction for Model based coding
 DEPARTMENT OF APPLIED PHYSICS AND ELECTRONICS UMEÅ UNIVERISTY, SWEDEN DIGITAL MEDIA LAB Sample Based Texture extraction for Model based coding Zhengrong Yao 1 Dept. Applied Physics and Electronics Umeå
DEPARTMENT OF APPLIED PHYSICS AND ELECTRONICS UMEÅ UNIVERISTY, SWEDEN DIGITAL MEDIA LAB Sample Based Texture extraction for Model based coding Zhengrong Yao 1 Dept. Applied Physics and Electronics Umeå
(i =0..N-1) : with S = {W 0. }. See {1][2][3][4][5]. For the case where the contraction maps are affine transformations, as per W x ,W 3 ,W 2 ,W 5
![(i =0..N-1) : with S = {W 0. }. See {1][2][3][4][5]. For the case where the contraction maps are affine transformations, as per W x ,W 3 ,W 2 ,W 5 (i =0..N-1) : with S = {W 0. }. See {1][2][3][4][5]. For the case where the contraction maps are affine transformations, as per W x ,W 3 ,W 2 ,W 5](/thumbs/89/99785765.jpg) Harvey A. Cohen, Map Colour Rendering of IFS Fractals, Proceedings, Australian Pattern Recognition Society orkshop on Colour Imaging and Applications, Canberra 5-7 December, 1994, pp 43-48. This is the
Harvey A. Cohen, Map Colour Rendering of IFS Fractals, Proceedings, Australian Pattern Recognition Society orkshop on Colour Imaging and Applications, Canberra 5-7 December, 1994, pp 43-48. This is the
Tilings of the Euclidean plane
 Tilings of the Euclidean plane Yan Der, Robin, Cécile January 9, 2017 Abstract This document gives a quick overview of a eld of mathematics which lies in the intersection of geometry and algebra : tilings.
Tilings of the Euclidean plane Yan Der, Robin, Cécile January 9, 2017 Abstract This document gives a quick overview of a eld of mathematics which lies in the intersection of geometry and algebra : tilings.
Morphological Image Processing
 Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
Morphological Image Processing Binary image processing In binary images, we conventionally take background as black (0) and foreground objects as white (1 or 255) Morphology Figure 4.1 objects on a conveyor
FRACTAL IMAGE COMPRESSION OF GRAYSCALE AND RGB IMAGES USING DCT WITH QUADTREE DECOMPOSITION AND HUFFMAN CODING. Moheb R. Girgis and Mohammed M.
 322 FRACTAL IMAGE COMPRESSION OF GRAYSCALE AND RGB IMAGES USING DCT WITH QUADTREE DECOMPOSITION AND HUFFMAN CODING Moheb R. Girgis and Mohammed M. Talaat Abstract: Fractal image compression (FIC) is a
322 FRACTAL IMAGE COMPRESSION OF GRAYSCALE AND RGB IMAGES USING DCT WITH QUADTREE DECOMPOSITION AND HUFFMAN CODING Moheb R. Girgis and Mohammed M. Talaat Abstract: Fractal image compression (FIC) is a
Lossless Compression Algorithms
 Multimedia Data Compression Part I Chapter 7 Lossless Compression Algorithms 1 Chapter 7 Lossless Compression Algorithms 1. Introduction 2. Basics of Information Theory 3. Lossless Compression Algorithms
Multimedia Data Compression Part I Chapter 7 Lossless Compression Algorithms 1 Chapter 7 Lossless Compression Algorithms 1. Introduction 2. Basics of Information Theory 3. Lossless Compression Algorithms
ARTICLE IN PRESS. Topology and its Applications ( )
 S0166-8641(05)0018-7/FLA AID:2822 Vol. ( ) [DTD5] P.1 (1-13) TOPOL:m1a v 1.42 Prn:11/08/2005; 10:03 top2822 by:rita p. 1 Topology and its Applications ( ) www.elsevier.com/locate/topol The topological
S0166-8641(05)0018-7/FLA AID:2822 Vol. ( ) [DTD5] P.1 (1-13) TOPOL:m1a v 1.42 Prn:11/08/2005; 10:03 top2822 by:rita p. 1 Topology and its Applications ( ) www.elsevier.com/locate/topol The topological
BEHIND THE INTUITION OF TILINGS
 BEHIND THE INTUITION OF TILINGS EUGENIA FUCHS Abstract. It may seem visually intuitive that certain sets of tiles can be used to cover the entire plane without gaps or overlaps. However, it is often much
BEHIND THE INTUITION OF TILINGS EUGENIA FUCHS Abstract. It may seem visually intuitive that certain sets of tiles can be used to cover the entire plane without gaps or overlaps. However, it is often much
Lecture 2 Convex Sets
 Optimization Theory and Applications Lecture 2 Convex Sets Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Fall 2016 2016/9/29 Lecture 2: Convex Sets 1 Outline
Optimization Theory and Applications Lecture 2 Convex Sets Prof. Chun-Hung Liu Dept. of Electrical and Computer Engineering National Chiao Tung University Fall 2016 2016/9/29 Lecture 2: Convex Sets 1 Outline
Chapter 5 VARIABLE-LENGTH CODING Information Theory Results (II)
 Chapter 5 VARIABLE-LENGTH CODING ---- Information Theory Results (II) 1 Some Fundamental Results Coding an Information Source Consider an information source, represented by a source alphabet S. S = { s,
Chapter 5 VARIABLE-LENGTH CODING ---- Information Theory Results (II) 1 Some Fundamental Results Coding an Information Source Consider an information source, represented by a source alphabet S. S = { s,
Fractal Geometry. LIACS Natural Computing Group Leiden University
 Fractal Geometry Contents Introduction The Fractal Geometry of Nature Self-Similarity Some Pioneering Fractals Dimension and Fractal Dimension Cellular Automata Particle Systems Scope of Fractal Geometry
Fractal Geometry Contents Introduction The Fractal Geometry of Nature Self-Similarity Some Pioneering Fractals Dimension and Fractal Dimension Cellular Automata Particle Systems Scope of Fractal Geometry
Modified SPIHT Image Coder For Wireless Communication
 Modified SPIHT Image Coder For Wireless Communication M. B. I. REAZ, M. AKTER, F. MOHD-YASIN Faculty of Engineering Multimedia University 63100 Cyberjaya, Selangor Malaysia Abstract: - The Set Partitioning
Modified SPIHT Image Coder For Wireless Communication M. B. I. REAZ, M. AKTER, F. MOHD-YASIN Faculty of Engineering Multimedia University 63100 Cyberjaya, Selangor Malaysia Abstract: - The Set Partitioning
2.8. Connectedness A topological space X is said to be disconnected if X is the disjoint union of two non-empty open subsets. The space X is said to
 2.8. Connectedness A topological space X is said to be disconnected if X is the disjoint union of two non-empty open subsets. The space X is said to be connected if it is not disconnected. A subset of
2.8. Connectedness A topological space X is said to be disconnected if X is the disjoint union of two non-empty open subsets. The space X is said to be connected if it is not disconnected. A subset of
Discrete mathematics , Fall Instructor: prof. János Pach
 Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
THE GRAPH OF FRACTAL DIMENSIONS OF JULIA SETS Bünyamin Demir 1, Yunus Özdemir2, Mustafa Saltan 3. Anadolu University Eskişehir, TURKEY
 International Journal of Pure and Applied Mathematics Volume 70 No. 3 2011, 401-409 THE GRAPH OF FRACTAL DIMENSIONS OF JULIA SETS Bünyamin Demir 1, Yunus Özdemir2, Mustafa Saltan 3 1,2,3 Department of
International Journal of Pure and Applied Mathematics Volume 70 No. 3 2011, 401-409 THE GRAPH OF FRACTAL DIMENSIONS OF JULIA SETS Bünyamin Demir 1, Yunus Özdemir2, Mustafa Saltan 3 1,2,3 Department of
Mesh Based Interpolative Coding (MBIC)
 Mesh Based Interpolative Coding (MBIC) Eckhart Baum, Joachim Speidel Institut für Nachrichtenübertragung, University of Stuttgart An alternative method to H.6 encoding of moving images at bit rates below
Mesh Based Interpolative Coding (MBIC) Eckhart Baum, Joachim Speidel Institut für Nachrichtenübertragung, University of Stuttgart An alternative method to H.6 encoding of moving images at bit rates below
A Connection between Network Coding and. Convolutional Codes
 A Connection between Network Coding and 1 Convolutional Codes Christina Fragouli, Emina Soljanin christina.fragouli@epfl.ch, emina@lucent.com Abstract The min-cut, max-flow theorem states that a source
A Connection between Network Coding and 1 Convolutional Codes Christina Fragouli, Emina Soljanin christina.fragouli@epfl.ch, emina@lucent.com Abstract The min-cut, max-flow theorem states that a source
DISCRETE DOMAIN REPRESENTATION FOR SHAPE CONCEPTUALIZATION
 DISCRETE DOMAIN REPRESENTATION FOR SHAPE CONCEPTUALIZATION Zoltán Rusák, Imre Horváth, György Kuczogi, Joris S.M. Vergeest, Johan Jansson Department of Design Engineering Delft University of Technology
DISCRETE DOMAIN REPRESENTATION FOR SHAPE CONCEPTUALIZATION Zoltán Rusák, Imre Horváth, György Kuczogi, Joris S.M. Vergeest, Johan Jansson Department of Design Engineering Delft University of Technology
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3.
 TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
Encoding Time in seconds. Encoding Time in seconds. PSNR in DB. Encoding Time for Mandrill Image. Encoding Time for Lena Image 70. Variance Partition
 Fractal Image Compression Project Report Viswanath Sankaranarayanan 4 th December, 1998 Abstract The demand for images, video sequences and computer animations has increased drastically over the years.
Fractal Image Compression Project Report Viswanath Sankaranarayanan 4 th December, 1998 Abstract The demand for images, video sequences and computer animations has increased drastically over the years.
Generation of 3D Fractal Images for Mandelbrot and Julia Sets
 178 Generation of 3D Fractal Images for Mandelbrot and Julia Sets Bulusu Rama #, Jibitesh Mishra * # Department of Computer Science and Engineering, MLR Institute of Technology Hyderabad, India 1 rama_bulusu@yahoo.com
178 Generation of 3D Fractal Images for Mandelbrot and Julia Sets Bulusu Rama #, Jibitesh Mishra * # Department of Computer Science and Engineering, MLR Institute of Technology Hyderabad, India 1 rama_bulusu@yahoo.com
Filling Space with Random Line Segments
 Filling Space with Random Line Segments John Shier Abstract. The use of a nonintersecting random search algorithm with objects having zero width ("measure zero") is explored. The line length in the units
Filling Space with Random Line Segments John Shier Abstract. The use of a nonintersecting random search algorithm with objects having zero width ("measure zero") is explored. The line length in the units
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
2 A topological interlude
 2 A topological interlude 2.1 Topological spaces Recall that a topological space is a set X with a topology: a collection T of subsets of X, known as open sets, such that and X are open, and finite intersections
2 A topological interlude 2.1 Topological spaces Recall that a topological space is a set X with a topology: a collection T of subsets of X, known as open sets, such that and X are open, and finite intersections
ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING WITH UNCERTAINTY
 ALGEBRAIC METHODS IN LOGIC AND IN COMPUTER SCIENCE BANACH CENTER PUBLICATIONS, VOLUME 28 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1993 ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING
ALGEBRAIC METHODS IN LOGIC AND IN COMPUTER SCIENCE BANACH CENTER PUBLICATIONS, VOLUME 28 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1993 ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING
 FRACTALS The term fractal was coined by mathematician Benoit Mandelbrot A fractal object, unlike a circle or any regular object, has complexity at all scales Natural Fractal Objects Natural fractals
FRACTALS The term fractal was coined by mathematician Benoit Mandelbrot A fractal object, unlike a circle or any regular object, has complexity at all scales Natural Fractal Objects Natural fractals
Morphological Image Processing
 Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
Morphological Image Processing Morphology Identification, analysis, and description of the structure of the smallest unit of words Theory and technique for the analysis and processing of geometric structures
demand point given tracks
 2 Introduction Establishing stops (or stations) within a transportation network is fundamental for offering public transportation service, since stops are an important part of the PTN. But it is not clear
2 Introduction Establishing stops (or stations) within a transportation network is fundamental for offering public transportation service, since stops are an important part of the PTN. But it is not clear
Chapter 11. Topological Spaces: General Properties
 11.1. Open Sets, Closed Sets, Bases, and Subbases 1 Chapter 11. Topological Spaces: General Properties Section 11.1. Open Sets, Closed Sets, Bases, and Subbases Note. In this section, we define a topological
11.1. Open Sets, Closed Sets, Bases, and Subbases 1 Chapter 11. Topological Spaces: General Properties Section 11.1. Open Sets, Closed Sets, Bases, and Subbases Note. In this section, we define a topological
Fractal Image Denoising
 1560 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 12, NO. 12, DECEMBER 2003 Fractal Image Denoising Mohsen Ghazel, George H. Freeman, and Edward R. Vrscay Abstract Over the past decade, there has been significant
1560 IEEE TRANSACTIONS ON IMAGE PROCESSING, VOL. 12, NO. 12, DECEMBER 2003 Fractal Image Denoising Mohsen Ghazel, George H. Freeman, and Edward R. Vrscay Abstract Over the past decade, there has been significant
THREE LECTURES ON BASIC TOPOLOGY. 1. Basic notions.
 THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
Chapter 2 Notes on Point Set Topology
 Chapter 2 Notes on Point Set Topology Abstract The chapter provides a brief exposition of point set topology. In particular, it aims to make readers from the engineering community feel comfortable with
Chapter 2 Notes on Point Set Topology Abstract The chapter provides a brief exposition of point set topology. In particular, it aims to make readers from the engineering community feel comfortable with
INTRODUCTION TO TOPOLOGY
 INTRODUCTION TO TOPOLOGY MARTINA ROVELLI These notes are an outline of the topics covered in class, and are not substitutive of the lectures, where (most) proofs are provided and examples are discussed
INTRODUCTION TO TOPOLOGY MARTINA ROVELLI These notes are an outline of the topics covered in class, and are not substitutive of the lectures, where (most) proofs are provided and examples are discussed
4. Simplicial Complexes and Simplicial Homology
 MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
MATH41071/MATH61071 Algebraic topology Autumn Semester 2017 2018 4. Simplicial Complexes and Simplicial Homology Geometric simplicial complexes 4.1 Definition. A finite subset { v 0, v 1,..., v r } R n
Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal Class D 2
 Symmetry 2011, 3, 325-364; doi:10.3390/sym3020325 OPEN ACCESS symmetry ISSN 2073-8994 www.mdpi.com/journal/symmetry Article Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal
Symmetry 2011, 3, 325-364; doi:10.3390/sym3020325 OPEN ACCESS symmetry ISSN 2073-8994 www.mdpi.com/journal/symmetry Article Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal
Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal Class D 2
 Symmetry 2011, 3, 325-364; doi:10.3390/sym3020325 OPEN ACCESS symmetry ISSN 2073-8994 www.mdpi.com/journal/symmetry Article Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal
Symmetry 2011, 3, 325-364; doi:10.3390/sym3020325 OPEN ACCESS symmetry ISSN 2073-8994 www.mdpi.com/journal/symmetry Article Polyominoes and Polyiamonds as Fundamental Domains for Isohedral Tilings of Crystal
A new fractal algorithm to model discrete sequences
 A new fractal algorithm to model discrete sequences Zhai Ming-Yue( 翟明岳 ) a) Heidi Kuzuma b) and James W. Rector b)c) a) School of EE Engineering North China Electric Power University Beijing 102206 China
A new fractal algorithm to model discrete sequences Zhai Ming-Yue( 翟明岳 ) a) Heidi Kuzuma b) and James W. Rector b)c) a) School of EE Engineering North China Electric Power University Beijing 102206 China
Topology - I. Michael Shulman WOMP 2004
 Topology - I Michael Shulman WOMP 2004 1 Topological Spaces There are many different ways to define a topological space; the most common one is as follows: Definition 1.1 A topological space (often just
Topology - I Michael Shulman WOMP 2004 1 Topological Spaces There are many different ways to define a topological space; the most common one is as follows: Definition 1.1 A topological space (often just
Lecture 13. Types of error-free codes: Nonsingular, Uniquely-decodable and Prefix-free
 Lecture 13 Agenda for the lecture Introduction to data compression Fixed- and variable-length codes Types of error-free codes: Nonsingular, Uniquely-decodable and Prefix-free 13.1 The data compression
Lecture 13 Agenda for the lecture Introduction to data compression Fixed- and variable-length codes Types of error-free codes: Nonsingular, Uniquely-decodable and Prefix-free 13.1 The data compression
Notes on point set topology, Fall 2010
 Notes on point set topology, Fall 2010 Stephan Stolz September 3, 2010 Contents 1 Pointset Topology 1 1.1 Metric spaces and topological spaces...................... 1 1.2 Constructions with topological
Notes on point set topology, Fall 2010 Stephan Stolz September 3, 2010 Contents 1 Pointset Topology 1 1.1 Metric spaces and topological spaces...................... 1 1.2 Constructions with topological
Manifolds. Chapter X. 44. Locally Euclidean Spaces
 Chapter X Manifolds 44. Locally Euclidean Spaces 44 1. Definition of Locally Euclidean Space Let n be a non-negative integer. A topological space X is called a locally Euclidean space of dimension n if
Chapter X Manifolds 44. Locally Euclidean Spaces 44 1. Definition of Locally Euclidean Space Let n be a non-negative integer. A topological space X is called a locally Euclidean space of dimension n if
Topology and Topological Spaces
 Topology and Topological Spaces Mathematical spaces such as vector spaces, normed vector spaces (Banach spaces), and metric spaces are generalizations of ideas that are familiar in R or in R n. For example,
Topology and Topological Spaces Mathematical spaces such as vector spaces, normed vector spaces (Banach spaces), and metric spaces are generalizations of ideas that are familiar in R or in R n. For example,
Consistency and Set Intersection
 Consistency and Set Intersection Yuanlin Zhang and Roland H.C. Yap National University of Singapore 3 Science Drive 2, Singapore {zhangyl,ryap}@comp.nus.edu.sg Abstract We propose a new framework to study
Consistency and Set Intersection Yuanlin Zhang and Roland H.C. Yap National University of Singapore 3 Science Drive 2, Singapore {zhangyl,ryap}@comp.nus.edu.sg Abstract We propose a new framework to study
Math 5593 Linear Programming Lecture Notes
 Math 5593 Linear Programming Lecture Notes Unit II: Theory & Foundations (Convex Analysis) University of Colorado Denver, Fall 2013 Topics 1 Convex Sets 1 1.1 Basic Properties (Luenberger-Ye Appendix B.1).........................
Math 5593 Linear Programming Lecture Notes Unit II: Theory & Foundations (Convex Analysis) University of Colorado Denver, Fall 2013 Topics 1 Convex Sets 1 1.1 Basic Properties (Luenberger-Ye Appendix B.1).........................
Lecture 15: The subspace topology, Closed sets
 Lecture 15: The subspace topology, Closed sets 1 The Subspace Topology Definition 1.1. Let (X, T) be a topological space with topology T. subset of X, the collection If Y is a T Y = {Y U U T} is a topology
Lecture 15: The subspace topology, Closed sets 1 The Subspace Topology Definition 1.1. Let (X, T) be a topological space with topology T. subset of X, the collection If Y is a T Y = {Y U U T} is a topology
USING FRACTAL CODING FOR PROGRESSIVE IMAGE TRANSMISSION
 USING FRACTAL CODING FOR PROGRESSIVE IMAGE TRANSMISSION Y.-Kheong Chee Internal Report 4-95 e-mail: kheong@rafael.ece.curtin.edu.au School of Elec. and Computer Engineering Curtin University of Technology
USING FRACTAL CODING FOR PROGRESSIVE IMAGE TRANSMISSION Y.-Kheong Chee Internal Report 4-95 e-mail: kheong@rafael.ece.curtin.edu.au School of Elec. and Computer Engineering Curtin University of Technology
Cluster Analysis. Angela Montanari and Laura Anderlucci
 Cluster Analysis Angela Montanari and Laura Anderlucci 1 Introduction Clustering a set of n objects into k groups is usually moved by the aim of identifying internally homogenous groups according to a
Cluster Analysis Angela Montanari and Laura Anderlucci 1 Introduction Clustering a set of n objects into k groups is usually moved by the aim of identifying internally homogenous groups according to a
Final Exam, F11PE Solutions, Topology, Autumn 2011
 Final Exam, F11PE Solutions, Topology, Autumn 2011 Question 1 (i) Given a metric space (X, d), define what it means for a set to be open in the associated metric topology. Solution: A set U X is open if,
Final Exam, F11PE Solutions, Topology, Autumn 2011 Question 1 (i) Given a metric space (X, d), define what it means for a set to be open in the associated metric topology. Solution: A set U X is open if,
Generell Topologi. Richard Williamson. May 27, 2013
 Generell Topologi Richard Williamson May 27, 2013 1 1 Tuesday 15th January 1.1 Topological spaces definition, terminology, finite examples Definition 1.1. A topological space is a pair (X, O) of a set
Generell Topologi Richard Williamson May 27, 2013 1 1 Tuesday 15th January 1.1 Topological spaces definition, terminology, finite examples Definition 1.1. A topological space is a pair (X, O) of a set
ˆf(S) = N. ˆf k (S). (1) k=1. Corollary: From Banach s Fixed Point Theorem, there exists a unique set A H(D) which is the fixed point of ˆf, i.e.
 Lecture 35 Iterated Function Systems (cont d) Application of Banach s Fixed Point Theorem to IFS (conclusion) In the previous lecture, we focussed on the idea of the parallel operator ˆf associated with
Lecture 35 Iterated Function Systems (cont d) Application of Banach s Fixed Point Theorem to IFS (conclusion) In the previous lecture, we focussed on the idea of the parallel operator ˆf associated with
The Farey Tessellation
 The Farey Tessellation Seminar: Geometric Structures on manifolds Mareike Pfeil supervised by Dr. Gye-Seon Lee 15.12.2015 Introduction In this paper, we are going to introduce the Farey tessellation. Since
The Farey Tessellation Seminar: Geometric Structures on manifolds Mareike Pfeil supervised by Dr. Gye-Seon Lee 15.12.2015 Introduction In this paper, we are going to introduce the Farey tessellation. Since
Lecture 5: Duality Theory
 Lecture 5: Duality Theory Rajat Mittal IIT Kanpur The objective of this lecture note will be to learn duality theory of linear programming. We are planning to answer following questions. What are hyperplane
Lecture 5: Duality Theory Rajat Mittal IIT Kanpur The objective of this lecture note will be to learn duality theory of linear programming. We are planning to answer following questions. What are hyperplane
Optimality certificates for convex minimization and Helly numbers
 Optimality certificates for convex minimization and Helly numbers Amitabh Basu Michele Conforti Gérard Cornuéjols Robert Weismantel Stefan Weltge May 10, 2017 Abstract We consider the problem of minimizing
Optimality certificates for convex minimization and Helly numbers Amitabh Basu Michele Conforti Gérard Cornuéjols Robert Weismantel Stefan Weltge May 10, 2017 Abstract We consider the problem of minimizing
CITS 4402 Computer Vision
 CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
CITS 4402 Computer Vision A/Prof Ajmal Mian Adj/A/Prof Mehdi Ravanbakhsh, CEO at Mapizy (www.mapizy.com) and InFarm (www.infarm.io) Lecture 02 Binary Image Analysis Objectives Revision of image formation
Bases of topologies. 1 Motivation
 Bases of topologies 1 Motivation In the previous section we saw some examples of topologies. We described each of them by explicitly specifying all of the open sets in each one. This is not be a feasible
Bases of topologies 1 Motivation In the previous section we saw some examples of topologies. We described each of them by explicitly specifying all of the open sets in each one. This is not be a feasible
Points covered an odd number of times by translates
 Points covered an odd number of times by translates Rom Pinchasi August 5, 0 Abstract Let T be a fixed triangle and consider an odd number of translated copies of T in the plane. We show that the set of
Points covered an odd number of times by translates Rom Pinchasi August 5, 0 Abstract Let T be a fixed triangle and consider an odd number of translated copies of T in the plane. We show that the set of
Separators in High-Genus Near-Planar Graphs
 Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 12-2016 Separators in High-Genus Near-Planar Graphs Juraj Culak jc1789@rit.edu Follow this and additional works
Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 12-2016 Separators in High-Genus Near-Planar Graphs Juraj Culak jc1789@rit.edu Follow this and additional works
Image Compression - An Overview Jagroop Singh 1
 www.ijecs.in International Journal Of Engineering And Computer Science ISSN: 2319-7242 Volume 5 Issues 8 Aug 2016, Page No. 17535-17539 Image Compression - An Overview Jagroop Singh 1 1 Faculty DAV Institute
www.ijecs.in International Journal Of Engineering And Computer Science ISSN: 2319-7242 Volume 5 Issues 8 Aug 2016, Page No. 17535-17539 Image Compression - An Overview Jagroop Singh 1 1 Faculty DAV Institute
Fractal Image Compression on a Pseudo Spiral Architecture
 Fractal Image Compression on a Pseudo Spiral Huaqing Wang, Meiqing Wang, Tom Hintz, Xiangjian He, Qiang Wu Faculty of Information Technology, University of Technology, Sydney PO Box 123, Broadway 2007,
Fractal Image Compression on a Pseudo Spiral Huaqing Wang, Meiqing Wang, Tom Hintz, Xiangjian He, Qiang Wu Faculty of Information Technology, University of Technology, Sydney PO Box 123, Broadway 2007,
Open and Closed Sets
 Open and Closed Sets Definition: A subset S of a metric space (X, d) is open if it contains an open ball about each of its points i.e., if x S : ɛ > 0 : B(x, ɛ) S. (1) Theorem: (O1) and X are open sets.
Open and Closed Sets Definition: A subset S of a metric space (X, d) is open if it contains an open ball about each of its points i.e., if x S : ɛ > 0 : B(x, ɛ) S. (1) Theorem: (O1) and X are open sets.
Basics of Graph Theory
 Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Basics of Graph Theory 1 Basic notions A simple graph G = (V, E) consists of V, a nonempty set of vertices, and E, a set of unordered pairs of distinct elements of V called edges. Simple graphs have their
Image Sampling and Quantisation
 Image Sampling and Quantisation Introduction to Signal and Image Processing Prof. Dr. Philippe Cattin MIAC, University of Basel 1 of 46 22.02.2016 09:17 Contents Contents 1 Motivation 2 Sampling Introduction
Image Sampling and Quantisation Introduction to Signal and Image Processing Prof. Dr. Philippe Cattin MIAC, University of Basel 1 of 46 22.02.2016 09:17 Contents Contents 1 Motivation 2 Sampling Introduction
Interpolation is a basic tool used extensively in tasks such as zooming, shrinking, rotating, and geometric corrections.
 Image Interpolation 48 Interpolation is a basic tool used extensively in tasks such as zooming, shrinking, rotating, and geometric corrections. Fundamentally, interpolation is the process of using known
Image Interpolation 48 Interpolation is a basic tool used extensively in tasks such as zooming, shrinking, rotating, and geometric corrections. Fundamentally, interpolation is the process of using known
Context based optimal shape coding
 IEEE Signal Processing Society 1999 Workshop on Multimedia Signal Processing September 13-15, 1999, Copenhagen, Denmark Electronic Proceedings 1999 IEEE Context based optimal shape coding Gerry Melnikov,
IEEE Signal Processing Society 1999 Workshop on Multimedia Signal Processing September 13-15, 1999, Copenhagen, Denmark Electronic Proceedings 1999 IEEE Context based optimal shape coding Gerry Melnikov,
A Image Comparative Study using DCT, Fast Fourier, Wavelet Transforms and Huffman Algorithm
 International Journal of Engineering Research and General Science Volume 3, Issue 4, July-August, 15 ISSN 91-2730 A Image Comparative Study using DCT, Fast Fourier, Wavelet Transforms and Huffman Algorithm
International Journal of Engineering Research and General Science Volume 3, Issue 4, July-August, 15 ISSN 91-2730 A Image Comparative Study using DCT, Fast Fourier, Wavelet Transforms and Huffman Algorithm
Image Sampling & Quantisation
 Image Sampling & Quantisation Biomedical Image Analysis Prof. Dr. Philippe Cattin MIAC, University of Basel Contents 1 Motivation 2 Sampling Introduction and Motivation Sampling Example Quantisation Example
Image Sampling & Quantisation Biomedical Image Analysis Prof. Dr. Philippe Cattin MIAC, University of Basel Contents 1 Motivation 2 Sampling Introduction and Motivation Sampling Example Quantisation Example
Compression of RADARSAT Data with Block Adaptive Wavelets Abstract: 1. Introduction
 Compression of RADARSAT Data with Block Adaptive Wavelets Ian Cumming and Jing Wang Department of Electrical and Computer Engineering The University of British Columbia 2356 Main Mall, Vancouver, BC, Canada
Compression of RADARSAT Data with Block Adaptive Wavelets Ian Cumming and Jing Wang Department of Electrical and Computer Engineering The University of British Columbia 2356 Main Mall, Vancouver, BC, Canada
1 Counting triangles and cliques
 ITCSC-INC Winter School 2015 26 January 2014 notes by Andrej Bogdanov Today we will talk about randomness and some of the surprising roles it plays in the theory of computing and in coding theory. Let
ITCSC-INC Winter School 2015 26 January 2014 notes by Andrej Bogdanov Today we will talk about randomness and some of the surprising roles it plays in the theory of computing and in coding theory. Let
