IFS Documentation Cycle CY25r1 IFS DOCUMENTATION PROCEDURES (CY25R1) (Operational implementation 9 April 2002) Edited by Peter W.
|
|
|
- Rosamond Watts
- 5 years ago
- Views:
Transcription
1 IFS Documentation Cycle CY25r IFS DOCUMENTATION Part III: DYNAMICS AND NUMERICAL PROCEDURES (CY25R) (Operational implementation 9 April 2002) Edited by Peter W. White (Text written and updated by members of the ECMWF Research Department) Table of contents Chapter. Introduction Chapter 2. Basic equations and discretization Chapter 3. Semi-Lagrangian formulation Chapter 4. Computational details REFERENCES IFS Documentationn Cycle CY25r (Edited 2003)
2 Part III: Dynamics and numerical procedures (CY25R) Copyright ECMWF, All information, text, and electronic images contained within this document are the intellectual property of the European Centre for Medium-Range Weather Forecasts and may not be reproduced or used in any way (other than for personal use) without permission. Any user of any information, text, or electronic images contained within this document accepts all responsibility for the use. In particular, no claims of accuracy or precision of the forecasts will be made which is inappropriate to their scientific basis. 2 IFS Documentation Cycle CY25r (Edited 2003)
3 IFS Documentation Cycle CY25r Part III: DYNAMICS AND NUMERICAL PROCEDURES CHAPTER Introduction Table of contents. Overview. OVERVIEW Since the original demonstration of the efficiency advantage of the semi-lagrangian semi-implicit method over a decade ago by André Robert, this numerical integration scheme is being used in an increasing range of atmospheric models. Most of the applications have been in grid-point models. Shallow-water-equations studies have included three-time-level versions by Robert (98, 982) and Staniforth and Temperton (986), and two-time-level schemes by Temperton and Staniforth (987), Purser and Leslie (988), McDonald and Bates (989), and Côté and Staniforth (990). There also have been various applications in baroclinic grid-point models. Three-time-level sigma-coordinate versions have been presented by Robert et al. (985) and Tanguay et al. (989), and the extension of the three-time-level approach to a non-hydrostatic coordinate has been demonstrated by Tanguay et al. (990). Bates and McDonald (982), McDonald (986), Leslie and Purser (99), McDonald and Haugen (992), and Bates et al. (993) have developed two-time-level sigma-coordinate schemes, McDonald and Haugen (993) have presented the two-time-level extension to a hybrid vertical coordinate, and Golding (992) has applied a split twotime-level semi-lagrangian scheme in a non-hydrostatic model. For spectral models, a semi-lagrangian semi-implicit shallow-water equation model was presented by Ritchie (988) for a three-time-level version, and adapted by Côté and Staniforth (988) for a two-time-level scheme. Baroclinic three-time-level spectral model formulations have been demonstrated by Ritchie (99) for operational numerical weather prediction in a sigma-coordinate model, and recently by Williamson and Olson (994) for climate simulations with a hybrid coordinate model. In a broader context, the semi-lagrangian scheme, as incorporated in spectral numerical weather prediction models, may be considered as an economical variant of the spectral Lagrange-Galerkin method (Süli and Ware, 99). Experience at ECMWF (Simmons et al., 989) suggests that the accuracy of medium-range forecasts has steadily improved with increasing resolution. Consequently, in its four-year plan for the period , ECMWF proposed development of a high-resolution version of its forecast model. A target resolution of a spectral representation with a triangular truncation of 23 waves in the horizontal and 3 levels in the vertical (T23/L3) was set, entailing a doubling of the horizontal resolution and an approximate doubling of the vertical resolution in the troposphere compared to the T06/L9 configuration that was operational at the time (Simmons et al., 989). In view of the anticipated computer resources, it was clear that major efficiency gains would be necessary in order to attain this objective. These gains have been provided by the introduction of the semi-lagrangian treatment of advection permitting a substantial increase in the size of the time-step, the use of a reduced Gaussian grid giving a further advantage of about 25%, the introduction of economies in the Legendre transforms, and improvements to the model's basic architecture. The layout for the remainder of the document is as follows. In Chapter 2 Basic equations and discretization we present the reformulation of the Eulerian model in order to transform the vorticitydivergence formulation into a IFS Documentationn Cycle CY25r (Edited 2003)
4 Part III: Dynamics and numerical procedures momentum-equation version in preparation for a subsequent semi-lagrangian vector treatment of the equations of motion. The vertical discretization of the ECMWF hybrid coordinate on a staggered grid is also considered. The semi-lagrangian treatment is discussed in some detail in Chapter 3 Semi-Lagrangian formulation, including the adaptation to accommodate the reduced Gaussian grid. Several important computational details relevant for efficient execution of the high resolution model on a modestly parallel supercomputer are discussed in Chapter 4 Computational details. 2 IFS Documentation Cycle CY25r (Edited 2003)
5 IFS Documentation Cycle CY25r Part III: DYNAMICS AND NUMERICAL PROCEDURES CHAPTER 2 Basic equations and discretization Table of contents 2. Eulerian reformulation of the continuous equations 2.2 Discretization 2.2. Vertical discretization Finite-element vertical discretization Time discretization Horizontal grid Time-stepping procedure Time filtering Remarks as spectral variable T v 2. EULERIAN REFORMULATION OF THE CONTINUOUS EQUATIONS Following Ritchie (988,99), the first step in developing a semi-lagrangian version of the ECMWF spectral model was to convert the existing Eulerian ζ D (vorticitydivergence) model to a U V formulation, where Uand Vare the wind images defined by U ucosθ, V vcosθ ( u and v are the components of the horizontal wind in spherical coordinates, and θ is latitude). In this section we describe the Eulerian U V model. First we set out the continuous equations in ( λθη,, ) coordinates, where λ is longitude and η is the hybrid vertical coordinate introduced by Simmons and Burridge (98); thus η( p, p surf ) is a monotonic function of the pressure p, and also depends on the surface pressure in such a way that The momentum equations are p surf η( 0, p surf ) 0 and η( p surf, p surf ). U t acos θ U U λ v θ U U cos θ η η φ (fv) R a λ dry T v ( ln p) λ P U K U (2.) IFS Documentationn Cycle CY25r (Edited 2003) 3
6 Part III: Dynamics and numerical procedures V t acos θ U V λ V θ V θ U 2 V 2 V cos sin ( ) θ η η, (2.2) cosθ φ f U R a θ dry T v ( ln p) θ P V K V where a is the radius of the earth, η is the η-coordinate vertical velocity ( η dη dt ), φ is geopotential, is the gas constant for dry air, and is the virtual temperature defined by R dry where T is temperature, q is specific humidity and R vap is the gas constant for water vapour. P U and P V represent the contributions of the parametrized physical processes, while K U and K V are the horizontal diffusion terms. The thermodynamic equation is T v T v T[ { R vap ( R dry ) }q] T t acos θ U T θ V θ T T κt cos θ η v ω P η ( ( δ )q)p T K T (2.3) where κ R dry c pdry ( c pdry is the specific heat of dry air at constant pressure), ω is the ρ-coordinate vertical velocity ( ω d p dt ), and δ c pvap c pdry ( c pvap is the specific heat of water vapour at constant pressure). The moisture equation is q t U q V cosθ q acos 2 θ λ θ η q P η q K q (2.4) In (2.2) and (2.3), P T and P q represent the contributions of the parametrized physical processes, while K T and are the horizontal diffusion terms. K q The continuity equation is p t η. v p η p 0 H η η η (2.5) where is the horizontal gradient operator in spherical coordinates and v H ( uv, ) is the horizontal wind. The geopotential φ which appears in (2.) and (2.2) is defined by the hydrostatic equation φ η R dry T v p p η (2.6) while the vertical velocity ω in (2.3) is given by η p ω. v H η d η vh. p 0 (2.7) 4 IFS Documentation Cycle CY25r (Edited 2003)
7 Chapter 2 Basic equations and discretization Expressions for the rate of change of surface pressure, and for the vertical velocity η, are obtained by integrating (2.5), using the boundary conditions η 0 at η 0 and at η p surf p v t H dη η 0 (2.8) η p η η p p v η H dη η 0 (2.9) Since we use ln( ) rather than as the surface pressure variable, it is convenient to rewrite (2.8) as p surf p surf ---- ( ln p t surf ) p v H dη η p s 0 (2.0) 2.2 DISCRETIZATION 2.2. Vertical discretization To represent the vertical variation of the dependent variables U, V, T and q, the atmosphere is divided into NLEV layers. These layers are defined by the pressures at the interfaces between them (the half-levels ), and these pressures are given by p k 2 A k 2 B k 2 p surf (2.) for 0 k NLEV. The A k 2 and B k 2 are constants whose values effectively define the vertical coordinate and is the surface pressure field. p surf Ak 2 The values of the and B k 2 for all 0 k NLEV are stored in the GRIB header of all fields archived on model levels to allow the reconstruction of the full-level pressure p k associated with each model level (middle of layer) from p k -- ( p ( )by using (2.) and the surface pressure field. 2 k 2 p k 2 ) k NLEV The prognostic variables are represented by their values at full-level pressures p k. Values for p k are not explicitly required by the model s vertical finite-difference scheme, which is described below. The discrete analogue of the surface pressure tendency equation (2.0) is ---- ( ln p t surf ) NLEV ( v H p k ) p surf k (2.2) where p k p k 2 p k 2. (2.3) IFS Documentation Cycle CY25r (Edited 2003) 5
8 Part III: Dynamics and numerical procedures From (2.) we obtain ---- ( ln p t surf ) NLEV D p k p k ( v k. ln p surf ) B k surf k (2.4) where is the divergence at level k, D k D k U k cosθ V k acos 2 θ λ θ (2.5) and B k B k 2 B k 2. (2.6) The discrete analogue of (2.9) is η p η k 2 p k 2. ( v t j p j ) k j (2.7) and from (2.) we obtain η p η k 2 k p surf B k ( 2) ---- ( ln p t surf ) D p j p j ( v j. ln p surf ) B j surf j (2.8) where t( ln p surf ) is given by (2.4). Vertical advection of a variable X is now given by η x η k η p 2 p k η k ( X k X k ) η p η k 2 ( X k X k ) (2.9) The discrete analogue of the hydrostatic equation (2.6) is p R dry ( T v ) k 2 k ln φ k 2 φ k 2 p k 2 (2.20) which gives φ surf R dry ( T v ) ln φ k 2 NLEV j k p j 2 p j 2 (2.2) φ surf where is the geopotential at the surface. Full-level values of the geopotential, as required in the momentum equations (2.) and (2.2), are given by 6 IFS Documentation Cycle CY25r (Edited 2003)
9 Chapter 2 Basic equations and discretization φ k φ k 2 α k R dry ( T v ) k (2.22) where α ln 2 and, for k >, p k 2 α k p k p k 2 p k 2 ln , (2.23) The remaining part of the pressure gradient terms in (2.) and (2.2) is given by R dry ( T v ) R dry ( T v ln p) k k p k p k 2 p k 2 ln p k 2 α k p ( k ) (2.24) with given by (2.23) for all. α k Finally, the energy conversion term in the thermodynamic equation (2.3) is discretized as κt v ω ( ( δ )q)p κ( T v ) k ( δ )q k k p ( k 2 ln ) ( D p k p j p j p surf ( v j. ln p surf ) B j j ) k 2 j (2.25) α k ( D k p k p surf ( v k. ln p surf ) B k )} p surf C k p B p k k 2 ln k p k p ( vk. ln p surf )} k 2 where α ln2, α k, is defined by (2.23) for k >, and C k A k 2 B k 2 A k 2 B k 2. (2.26) The reasons behind the various choices made in this vertical discretization scheme are discussed by Simmons and Burridge (98); basically the scheme is designed to conserve angular momentum and energy, for frictionless adiabatic flow Finite-element vertical discretization In CY24R3 the vertical discretization has been changed in the operational model from the finite-difference discretization in Lorenz staggering described in the previous subsection to a finite-element discretization using cubic B- splines as basis functions. For the finite-element (FE) discretization, all variables (even pressure) are kept at the same levels (full levels), i.e. the values of pressure at full levels and not at half levels are required. Also, the values of the derivatives da dη and db dη at full levels are now needed, from which the vertical derivative of pressure can be computed according to p η ( da dη) ( db dη)p s. In the semi-lagrangian version of the evolution equations these are the only vertical derivatives required. They are constant in time and linked to the definition of the vertical coordinate. It is therefore convenient to change the definition of the vertical coordinate and supply ( da dη) k and ( db dη) k at full levels (instead of A k 2 and B k 2 at half levels) such that IFS Documentation Cycle CY25r (Edited 2003) 7
10 Part III: Dynamics and numerical procedures p η k da dη k db dη p s k (2.27) and da dη dη db 0, dη dη 0 0 (2.28) The two conditions of Eq.(2.28) above ensure that the integral of pressure from the top of the atmosphere to the surface yields exactly the surface pressure. These conditions have to be fulfilled to a good approximation with the numerical integration scheme used. Pressure at any full level can then be obtained by integrating Eq. (2.27) from the top of the atmosphere to the level in question. The only operation in the vertical which has to be evaluated is the vertical integration. An integral operator based on a finite-element representation will be derived next. Most of the integrals we have to evaluate are integrals from the top of the atmosphere to the individual model levels and to the surface. We therefore derive an operator in finite-element representation for this type of integral, i.e. an operator which returns the integral from the top of the atmosphere to each of the model levels η k and to the surface ( η ). The vertical integral in the hydrostatic equation (i.e. from the surface upwards) can be constructed by taking the difference of the integral from the top of the atmosphere to the model level in question minus the integral from the top to the surface. K 2 Let { d i ( η) } i K and { ei ( η) } i M be two sets of linearly independent functions of compact support which can be used as basis functions to expand any function of the vertical coordinate η given in the domain [0,]. The vertical integral can then be approximated as M 2 η F( η) f( x) dx 0 K 2 M 2 η C i d i ( η ) c i e i ( x) dx i K i M 0 (2.29) where C i are the coefficients of the expansion of F( η) as a linear combination of the basis functions { d i ( η) } and are the coefficients of the expansion of f ( η) as a linear combination of the basis functions { e i ( η) }. c i We can then apply the Galerkin procedure to Eq. (2.29) by multiplying both sides of this equation by each function N from a complete set of test functions { t j } 2 j N and integrating over the vertical domain: 8 IFS Documentation Cycle CY25r (Edited 2003)
11 Chapter 2 Basic equations and discretization K 2 M 2 x C i d i ( x )t j ( x) dx c i t j ( x) e i ( y) dy i K i M In matrix form this can be expressed as ÃC c > C Ã. B c B Incorporating into the above expression also the transformations from physical space to finite-element space and back, i.e. c and, we obtain. Here and denote vectors in physical space composed mainly of the values of f and F, respectively, at the model levels: f i f ( η i ), F i F( η i ), i N. The set of values F also includes the value at the surface of the model. Details of the basis functions S f F C F Ã P P f Ĩ f f F B S chosen to implement the scheme as well as how to compute the projection matrices and are given in Untch S P and Hortal (2002). Matrix Ĩ Ã is the integration operator in finite-element formulation which, applied to a function given P B S at full model levels, yields the integrals of this function from the top of the atmosphere to each individual full model level and to the surface. All the finite sums on the vertical levels in subsection 2.2. are replaced by vertical integrals computed by applying the matrix integration operator I. Moreover the quantities α k are no longer needed as the integration operator gives directly the value of the integral at the model levels (the half levels do not have any meaning in the FE discretization). dx Time discretization To introduce a discretization in time, together with a semi-implicit correction, we define the operators δ t X ( X X )/2 t, tt X ( X 2 X X ) where X represents the value of a variable at time t, X the value at time ( t t), and X the value at ( t t). In preparation for the semi-lagrangian treatment to be developed in section 3, we also introduce the three-dimensional advection operator A( X) U x V cosθ----- x acos 2 θ λ θ η x η (2.30) Introducing the semi-implicit correction terms, Eqs. (2.)(2.4) become: φ δ t U A( U) fv R a λ dry T v ln p ) λ P U K U β a tt [ γ ] T R λ dry T ref ( ln p λ surf ) (2.3) IFS Documentation Cycle CY25r (Edited 2003) 9
12 Part III: Dynamics and numerical procedures sinθ δ t V A( V) ( U 2 V 2 ) fu cosθ φ R a cos 2 a θ dry T v ( ln p) θ θ βcosθ P V K V 2a [ γ ] T R tt θ dry T ref ( ln p θ surf ) κt δ t T A( T) v ω β P ( ( δ )q)p T K T -- 2 tt ([ τ]d) δ t q A( q) P q K q (2.32) (2.33) (2.34) where β is a parameter of the semi-implicit scheme; the classical scheme (Robert 969) is recovered with β. The semi-implicit correction terms are linearized versions of the pressure gradient terms in (2.)(2.2) and the energy conversion term in (2.3). Thus T ref is a reference temperature (here chosen to be independent of vertical level), while [ γ ] and [ τ] are matrices such that NLEV ([ γ ]T) k α ref k R dry T k R dry T j ln p j , (2.35) ref j k ref p j 2 ([ τ]d) k κt ref ref p k ref ln p k ref p k 2 k j ref ( D j p j ) α ref k D k. (2.36) where the half-level pressures appearing in (2.35) and (2.35) are reference values obtained from (2.) by choosing ref ref a reference value p surf of p surf, and the coefficients α k are based on these reference values. The reference values adopted for the semi-implicit scheme are T ref ref 300 K and p surf 800 hpa. The integrated surface pressure tendency equation (2.4) becomes δ t ( ln p surf ) NLEV k D p k p k ( v k. ln p surf ) B k surf β -- 2 tt [ ν]d (2.37) where [ ν]d NLEV ref D j p surf ref p surf j (2.38) Horizontal grid A novel feature of the model is the optional use of a reduced Gaussian grid, as described by Hortal and Simmons (99). Thus, the number of points on each latitude row is chosen so that the local eastwest grid length remains approximately constant, with the restriction that the number should be suitable for the FFT ( N 2 p 3 q 5 r ). After some experimentation, the fully reduced grid option of Hortal and Simmons was implemented; all possible wavenumbers (up to the model s truncation limit) are used in the Legendre transforms. A small amount of noise in the 0 IFS Documentation Cycle CY25r (Edited 2003)
13 Chapter 2 Basic equations and discretization immediate vicinity of the poles was removed by increasing the number of grid points in the three most northerly and southerly rows of the grid (from 6, 2 and 8 points in the original design of the T23 grid to 2, 6 and 20 points respectively). Courtier and Naughton (994) have very recently reconsidered the design of reduced Gaussian grids Time-stepping procedure The time-stepping procedure for the Eulerian U V version of the model follows closely that outlined by Temperton (99) for the shallow-water equations. At the start of a time-step, the model state at time ( t t) is defined by the values of U, V, T, q and ln p surf on the Gaussian grid. To compute the semi-implicit corrections, the ( t t) values of divergence D, P/ λ and P/ µ are also held on the grid, where µ sinθ and P [ γ ]T R dry T ref ln p surf. (2.39) The model state at time t is defined by the spectral coefficients of ζ, D, T, q and ln p surf. Legendre transforms followed by Fourier transforms are then used to compute ζ, D, U, V, T, T/ µ, ln p surf and ( ln p surf )/ µ at time t on the model grid. Additional Fourier transforms are used to compute the corresponding values of U/ λ, V / λ. T/ λ, q/ λ and ( ln p surf )/ λ. The meridional gradients of U and V are obtained using the relationships cosθ V ad cos 2 θ U θ λ cosθ U θ V ζ cos 2 θ λ. All the information is then available to evaluate the terms at time t on the left-hand sides of (2.3)(2.34) and (2.37), and thus to compute provisional tendencies of the model variables. These tendencies (together with values of the variables at ( t t) are supplied to the physical parametrization routines, which increment the tendencies with their respective contributions. The semi-implicit correction terms evaluated at time-levels ( t t ) and t are then added to the tendencies. Ignoring the horizontal diffusion terms (which are handled later in spectral space), and grouping together the terms which have been computed on the grid, (2.3)(2.34) and (2.37) can be written in the form U β t p R a λ (2.40) V β t cosθ p R a θ 2 (2.4) T β t [ τ]d R 3 (2.42) q R 4 (2.43) ( ln p surf ) β t [ ν]d R 5 (2.44) The right-hand sides R R 5 are transformed to spectral space via Fourier transforms followed by Gaussian integration. The curl and divergence of (2.40) and (2.4) are then computed in spectral space, leading to IFS Documentation Cycle CY25r (Edited 2003)
14 Part III: Dynamics and numerical procedures ζ curl ( R,R 2 ) (2.45) D β t 2 p div( R, R 2 ). (2.46) Eqs. (2.42), (2.44) and (2.46) can then be combined with the aid of (2.39) to obtain an equation of the form nn ( ) [ I] [ Γ] m ( Dn ) m ( D ) n a 2 (2.47) for each zonal wavenumber m and total wavenumber n, where the matrix [ Γ] β 2 ( t) 2 ([ γ ][ τ] R dry T ref [ ν] ) (2.48) couples all the NLEV values of ( ) in a vertical column. Once D has been found, the calculation of T and ( ln p surf ) can be completed, while q and ζ have already been obtained from (2.43) and (2.45). D n m Finally, a fractional step approach is used to implement the horizontal diffusion of vorticity, divergence, temperature and specific humidity. A simple linear diffusion of order 2r is applied along the hybrid coordinate surfaces: K X ( ) r K 2r X (2.49) where X ζ, D or q. It is applied in spectral space to the ( t t) values such that if X m n is the spectral m coefficient of X prior to diffusion, then the diffused value X n is given by X n m 2 t K nn ( ) r a 2 X n m (2.50) A modified form of (2.50) is also used for the temperature T, to approximate diffusion on surfaces of constant pressure rather than on the sloping hybrid coordinate surfaces (Simmons, 987). The operational version of the model uses fourth-order horizontal diffusion ( r 2) Time filtering To avoid decoupling of the solutions at odd and even time steps, a Robert filter (Asselin 972) is applied at each timestep. The time-filtering is defined by X f X ε ( X f 2 X X ) (2.5) where the subscript f denotes a filtered value, and X, X and X represent values at ( t t), t and ( t t), respectively. Because of the scanning structure of the model (see Chapter 4 Computational details ), it is convenient to apply the time-filtering in grid-point space, and to split (2.5) into two parts: X f X ε( X f 2 X ) (2.52) 2 IFS Documentation Cycle CY25r (Edited 2003)
15 Chapter 2 Basic equations and discretization X f X f ε X (2.53) The partially filtered values computed by (2.52) are stored on a grid-point work file and passed from one timestep to the next. Thus, the information available after the transforms to grid-point space consists of partially filtered values at time ( t t) together with unfiltered values at time t. The filtering of the( t t) fields can then be completed via (2.53), which after shifting by one timestep becomes: X f X f ε X. (2.54) The computations described in Section are performed using these fully filtered values at time ( t t) and the unfiltered values at time t. Once (2.54) has been implemented, values of X f are also available to implement (2.52) for the partially filtered values to be passed on to the next timestep Remarks Ritchie (988) noted that for a spectral model of the shallow-water equations, the U V form and the ζ D form gave identical results (apart from round-off error). In extending this work to a multi-level model, Ritchie (99) found that this equivalence was not maintained. This was in fact a result of some analytic manipulations in the vertical, used to eliminate between the variables in solving the equations of the semi-implicit scheme, which were not exactly matched by the finite-element vertical discretization of Ritchie s model. In the case of the model described here, the corresponding elimination between the variables is purely algebraic, and the equivalence between the U V form and the ζ D form is maintained apart from one small exception due to the use of the hybrid vertical coordinate. In the U V model, the gradients of the geopotential φ are computed in grid-point space (from the spectrally computed gradients of T, q and ln p surf ), while in the ζ D model φ itself is computed and transformed separately into spectral space, where its Laplacian is added into the divergence equation. Since φ is not a quadratic function of the model variables there is some aliasing, which is different for the two versions of the model. In practice the differences between the ζ D model and the U V model were found to be very small, and in the case of a pure sigma-coordinate the two models would be algebraically equivalent. The U V model is nevertheless considerably more economical than its ζ D counterpart in terms of the number of Legendre transforms required. In addition to the transform of φ referred to above, four Legendre transforms are saved in the treatment of the wind fields using the procedures described by Temperton (99) for the shallow-water equations. The number of multi-level Legendre transforms is thereby reduced from 7 to 2 per time-step. T v as spectral variable In preparation for a further reduction in the number of Legendre transforms required by the semi-lagrangian version of the model, the modified Eulerian version includes an option to keep the virtual temperature T v, rather than the temperature T, as the spectral variable. In the time-stepping procedure, Legendre transforms followed by Fourier transforms are used to compute T v, T v / µ and T v / λ at time t on the model grid; the corresponding values of T, T/ µ and T/ λ are then computed using the corresponding values of q, q/ µ and q/ λ. The thermodynamic equation (2.3) is then stepped forward in time exactly as before. After the physical parametrization routines, the provisional value of T( t t) is combined with qt ( t) to compute a provisional value of T v ( t t). The semi-implicit correction terms evaluated at time-levels ( t t) and T v ( t t) are then added to the provisional value of T v ( t t), just before the transform back to spectral space. There are corresponding slight changes in the semi-implicit correction terms. The linearized hydrostatic matrix [ γ ] IFS Documentation Cycle CY25r (Edited 2003) 3
16 Part III: Dynamics and numerical procedures in (2.3)(2.32) and (2.39) now operates on T v rather than on T. From the point of view of the semi-implicit scheme, (2.33) has implicitly been replaced by an equation of the form δ t T v β -- 2 tt ([ τ]d) (2.55) although as explained above it is not necessary to formulate or compute the missing terms explicitly. Hence, (2.42) is replaced by T v β t[ τ]d R 3 (2.56) and the solution of the semi-implicit equations in spectral space proceeds just as before. This change of spectral variable results in only insignificant changes to a 0-day model forecast, but permits useful economies in the semi-lagrangian version to be described in the next chapter. 4 IFS Documentation Cycle CY25r (Edited 2003)
17 IFS Documentation Cycle CY25r IFS documentation Part III: DYNAMICS AND NUMERICAL PROCEDURES CHAPTER 3 Semi-Lagrangian formulation Table of contents 3. General description 3.2 Finding the departure point 3.3 Non-interpolating scheme in the vertical 3.4 Semi-Lagrangian discretization 3.5 Comparison with other schemes 3.6 Time-stepping procedure 3.7 Optimization of vertically non-interpolating scheme 3.8 Modified semi-lagrangian equations 3.8. Momentum equations Continuity equation Thermodynamic equation 3.9 Two-time-level semi-lagrangian scheme 3.9. Stable Extrapolation Two-Time-Level Scheme (SETTLS) 3.0 Numerical coupling of the physical parameterizations to the dynamical equations (SLAVEPP) 3.0. Moisture adjustment and first time-step treatment 3. GENERAL DESCRIPTION The general form of the model equations is dx dt X A( X) R L N t (3.) where the three-dimensional advection operator A was defined in (2.30), L is the linearized part of R and N is the remainder or non-linear terms. An explicit three-time-level semi-lagrangian treatment of (3.) is obtained by finding the approximate trajectory, over the time interval [ t t,t t], of a particle which arrives at each grid point at time ( t t). Equation (3.) is then approximated by X X R 0 2 t (3.2) where the superscripts, 0 and, respectively denote evaluation at the arrival point (, t t), the mid-point IFS Documentationn Cycle CY25r (Edited 2003) 5
18 Part III: Dynamics and numerical procedures of the trajectory (, t), and the departure point (, t t). Since the mid-point and the departure point α 2α will not in general coincide with model grid points, X and R 0 must be determined by interpolation. It is more economical (and, as discussed later, gives better results in some circumstances; see also Tanguay et al., 992) to evaluate the right-hand side of (3.2) as R 0 -- { (, t) (, t) } 2 R 2α R (3.3) since only a single interpolation (of the combined field X( t t) tr() t at the point ( )) is then required 2α in order to determine X. The right-hand sides of the time-discretized model equations also contain semi-implicit correction terms, which in the Eulerian model took the form tt X ( X 2 X 0 X ) where the superscripts refer to time-levels, and to a single common grid point. In the semi-lagrangian version of the model, the semi-implicit correction terms take the form tt X ( X(, t t) X(, t) ) ( X(, t t) X(, t) ) 2α 2α (3.4) and again the terms to be evaluated at the departure point ( ) can be added to other right-hand side terms 2α before interpolation. Notice that the evaluation of tt X, and both ways of evaluating R 0, are all centred in space and time. To obtain accurate results from a semi-lagrangian integration scheme, it is necessary to choose the order of interpolation carefully (see for example Staniforth and Côté 99). In practice it has been found (for the model described here) that linear interpolation is adequate for the terms evaluated at the midpoint of the trajectory, but that cubic interpolation is essential for the terms evaluated at the departure point. Cubic interpolation in three dimensions is expensive, and fortunately a quasi-cubic interpolation (suggested by Courtier) was found to give essentially equivalent results. The technique can be illustrated by two-dimensional interpolation on a regular grid. The target point is at ( x I α, y J β). In the first step, four interpolations are performed in the x -direction: linear (rather than the usual cubic) interpolations to the points ( x I α, y J ) and ( x I α, y J2 ), and cubic interpolations to the points ( x I α, y J ) and ( x I α, y J ). In the second step, one cubic interpolation is performed in the y -direction, to evaluate the field at the target point. The number of neighbours contributing to the result is reduced from 6 to 2. The generalization to three dimensions is straightforward and results in a significant saving, the number of neighbours being reduced from 64 to 32, and the computation being reduced from 2 one-dimensional cubic interpolations to 7 cubic plus 0 linear one-dimensional interpolations. For the reduced Gaussian grid described in Subsection 2.2.4, the mesh is no longer regular. However, it is easily seen that the extra complication is relatively minor provided that the first step in the interpolation is performed in the λ -direction. The order of the interpolation in the vertical is reduced to linear when the evaluation point lies between the two highest model levels, or between the lowest two model levels. Extrapolation beyond the top or bottom levels is not allowed. 6 IFS Documentation Cycle CY25r (Edited 2003)
19 Chapter 3 Semi-Lagrangian formulation 3.2 FINDING THE DEPARTURE POINT Extending the procedure of Robert (98) to three dimensions, the midpoint ( ) and the departure point α ( ) of the trajectory for each arrival point are found by iteratively solving the equation 2α α tṽ(, t) α (3.5) where ṽ in (3.5) is the three-dimensional wind field ( u, v, η ). Since η was never explicitly required in the Eulerian version of the model (see Eqs. (2.8)(2.9) for the Eulerian discretization of vertical advection), it is necessary to construct this field for the trajectory calculations. As η is already specified at the upper and lower boundaries ( η 0, at η 0 and at η ) it would be natural to construct η at the half-levels (i.e. vertically staggered with respect to u and v), and indeed a preliminary version of the model was coded that way. However, it is more convenient to hold the three velocity components at the same set of points (which also coincide with the arrival points), so the formulation was changed to use η at the full levels. Thus, the vertical velocity used in (3.5) is defined by η k -- η p 2 η k η p 2 -- η k p η k (3.6) where η p/ η is already defined by (2.8) and p η k p k A p k p surf B k η surf k A k p 0 B k (3.7) In deriving (3.7) we have used (2.) together with a formal definition of by the discretized Eulerian dynamics): η itself (which again was not required η k A k / p 0 B k where is a constant pressure (chosen to be hpa ). p 0 (3.8) σ -coordinate model. Giv- The iterative procedure for solving (3.5) is analogous to that used by Ritchie (99) in a ( k) en an estimate after k iterations, the next iteration is given by α α ( k) ( k tṽ( α ), t) (3.9) where the vertical ( η) component of the displacement is found first. The vertical component of on the righthand side of (3.9) is then updated before the horizontal components are found taking into account the spherical α geometry following Ritchie (987, 988). The first guess is given by ( k) α ( 0) tṽ(, t) (3.0) The calculations include approximations to the spherical geometry away from the poles, following Ritchie and Beaudoin (994). In agreement with previous work (reviewed by Staniforth and Côté 99), little sensitivity was found to the order of interpolation used in the trajectory calculations, and linear interpolation appears to be sufficiently accurate. After providing a first guess via (3.0), a single further iteration was found to be adequate. IFS Documentation Cycle CY25r (Edited 2003) 7
20 Part III: Dynamics and numerical procedures If the vertical velocity (or the time-step) is sufficiently small, then the modified departure point lies on the same model level as the arrival point, η * is zero and the treatment of vertical advection becomes purely Eulerian. In general there is an Eulerian treatment of the advection by the residual vertical velocity ( η η * ), which is small enough to guarantee that the Eulerian CFL criterion for vertical advection is respected. Thus, the non-interpolat- Once the midpoint ( ) of the trajectory has been found, the departure point ( ) is immediately obtained α 2α (in the horizontal, the backward extension of the trajectory is along a great circle). In the vertical, if the departure point is then above the first (or below the last) mode level, it is modified to lie on the first (last) level. In solving (3.9), it is necessary to convert between a displacement in terms of the spatial coordinates and the corresponding displacement in terms of grid lengths, in order to select the correct three-dimensional block of points for the interpolation routine. This is simple in the horizontal, since the mesh length is constant in the λ -direction (at a given latitude), and almost constant in the θ -direction. It is more difficult in the vertical, where the grid spacing changes rapidly, and the conversion algorithm for the vertical displacement makes use of an auxiliary grid defined with high uniform resolution. 3.3 NON-INTERPOLATING SCHEME IN THE VERTICAL An alternative formulation of the semi-lagrangian scheme in three dimensions was suggested by Ritchie (99). Equation (3.) can be rewritten as d H X η * X R η X η * X dt η η η (3.) where d H X dt X A t H ( X ) and A H is the horizontal part of the advection operator defined in (2.30).In(3.), η * is defined to be a vertical velocity which would lead to the departure point of the trajectory at time ( t t) lying exactly on a model level. This model level is chosen to be the one closest to the true departure point. Equation (3.) is then approximated by X X R η X 2 t η 0 η * X η (3.2) where the superscripts, 0, respectively denote evaluation at the arrival point (, t t), the midpoint (, t) and the departure point (, t t) of the modified trajectory. Since the modified departure point α 2α lies by definition on a model level, no vertical interpolation is required to evaluate X. As discussed in Subsection 3. above, it is also possible to evaluate the terms on the right-hand side of (3.2) by averaging the values at (, t) and (, t) ; in this case no vertical interpolation at all is required. Notice that a separate interpolation 2α is required to evaluate the second term on the right-hand side of (3.2) since the quantity η *, defined by η * η η t (3.3) where η and η are respectively the arrival and departure levels of the modified trajectory, is meaningful only at each grid point. 8 IFS Documentation Cycle CY25r (Edited 2003)
21 Chapter 3 Semi-Lagrangian formulation ing scheme maintains the desirable stability properties of the fully interpolating scheme. There is a subtle, but important, difference in the way the iterative scheme (3.9) is implemented to determine the modified trajectory in the non-interpolating scheme. As before, the first step at each iteration is to update the estimate of the vertical component of the displacement.the implied updated departure point is then moved to the closest model level. In the second step, the horizontal components are then updated using the winds evaluated at the midpoint of the modified trajectory. Notice that this gives a result different from that obtained by simply carrying out the trajectory calculation of the fully interpolating scheme and then projecting the departure point to the nearest model level. The modified procedure described above is easily seen to be more consistent by considering the case in which the vertical velocity is not zero, but is small enough for the modified trajectory to be horizontal ( η * 0) ). The discretization is then equivalent to a purely two-dimensional semi-lagrangian scheme, the trajectory being computed using the horizontal wind field evaluated on a single model level. An incidental advantage of the non-interpolating scheme over the fully interpolating scheme is that it resolves any ambiguities about the treatment of departure points above the top model level or below the bottom model level; the modified departure points automatically lie on the top or bottom level. The treatment of vertical advection becomes Eulerian, which is well-defined at the top and bottom levels. Thus, the non-interpolating scheme removes the need for artificial nudging of the departure points or the extrapolation of quantities to points above or below the domain of the model levels. Smolarkiewicz and Rasch (99) have extended the principle of the non-interpolating semi-lagrangian formulation to generate a broader class of stable and accurate advection schemes. 3.4 SEMI-LAGRANGIAN DISCRETIZATION Here we describe in detail only the fully interpolating version of the semi-lagrangian discretization; the modifications necessary for the non-interpolating in the vertical version become evident by comparing the right-hand side of (3.2) with that of (3.2). Following Ritchie (988, 99), the momentum equations are integrated in vector form to avoid an instability of the metric term near the poles. Using the notation of (3.2) and defining the horizontal wind vector v H ( u, v), the semi-lagrangian equivalent of (2.3)(2.32) is v H v H [ fk x v 2 t H φ R dry T v ln p] 0 β P v K v -- 2 tt { [ γ]t R dry T v ln p surf } (3.4) where k is the vertically directed unit vector and is the horizontal gradient operator in spherical coordinates. On the right-hand side of (3.4), P v and K v respectively denote the contributions of the physical parametrization schemes and horizontal diffusion, to be discussed in Subsection 3.6, while the semi-implicit correction terms are evaluated as in (3.4). For the momentum equations, it was found advantageous to evaluate the time-level t terms [] 0 as an average between the values at the departure and arrival points of the trajectory, as in (3.3). The pressure gradient terms are discretized in exactly the same way as for the Eulerian model (see Subsection 2.2.). Since (3.4) is in vector form, it is important to account for the change in the orientation of the coordinate system as the particle follows the trajectory; the manipulations required are as set out by Ritchie (988) and simplified by Ritchie and Beaudoin (994). The thermodynamic and moisture equations (2.33)(2.34) become IFS Documentation Cycle CY25r (Edited 2003) 9
22 Part III: Dynamics and numerical procedures T T κt v ω β t ( ( δ )q)p P T K T -- 2 tt ([ τ]d) 0 (3.5) q q P 2 t q K q (3.6) In (3.5), the {} 0 term is discretized as in (2.25), and evaluated at the midpoint of the trajectory, while the semiimplicit correction terms are evaluated as in (3.4). The η -coordinate continuity equation (2.5) can be rewritten as d p p D η dt η η η (3.7) Setting p A( η) B( η)p surf and noting that ---- A A p surf 0, t η η η we also have d p B d p surf η p. (3.8) dt η η dt η η Combining (3.7) and (3.8). Now introducing the vertical discretization, (3.9) becomes B d p surf p D η p 0. (3.9) η dt η η η d p B k surf p. (3.20) dt k D k η p η k η p η k the vertical discretization of η p/ η having been defined in (2.8). Changing the prognostic variable to η p/ η, d B k ---- ( ln p dt surf ) p p k D k η p surf η k η p 2 -- η k (3.2) Combining (3.2) with the discrete definition of η p/ η given by (2.8), 20 IFS Documentation Cycle CY25r (Edited 2003)
23 Chapter 3 Semi-Lagrangian formulation d ( ln p B k ---- ( ln p dt surf ) B surf ) k v t k. ln p surf 0 (3.22) where ( ln p surf )/ t is given by (2.4). Noting that NLEV B k, k and including the semi-implicit correction terms, the semi-lagrangian discretization of the continuity equation finally becomes NLEV ( ln p surf ) B k ( ln p surf ) 2 t ( ln p surf) 0 NLEV β t v t k. ln p surf ref tt p ref ( j D j ) p surf k j (3.23) ( ) (Since there is no vertical advection term in (3.23), no modification is required for the vertically non-interpolating scheme). It is important to bear in mind that each contribution to the sum on the right-hand side of (3.23) involves a different trajectory. The interpolations for ln p surf and the semi-implicit correction terms are however twodimensional, since these quantities are independent of vertical level. The {} 0 term is evaluated at the midpoint of the trajectory, and requires a three-dimensional interpolation. In summary, the semi-lagrangian discretization is given by Equations (3.4)(3.6)together with (3.23). 3.5 COMPARISON WITH OTHER SCHEMES The semi-lagrangian formulation presented above differs in some respects from those proposed by other authors. Perhaps the most notable difference lies in the treatment of the conversion ω term in the thermodynamic equation (3.5), and of the right-hand side of the continuity equation (3.23). Both involve terms of the form v. ln p surf, which in our scheme are computed in a purely Eulerian fashion. This may appear somewhat inconsistent; indeed McDonald and Haugen (993) state as a specific design objective of their scheme that the operator v. should not appear explicitly. The alternative approach, also taken by Williamson and Olson (994), is to use the continuity equation in its semi-implicit semi-lagrangian form to derive a consistent equation for predicting η p/ η, which can then be used to eliminate the v. ln p surf terms. In the σ -coordinate system, Bates et al. (993) and McDonald and Haugen (992) used a similar approach to derive a prognostic equation for σ. A possible disadvantage of such an approach is that η p/ η (or σ ) then follows an independent evolution, no longer satisfying a diagnostic relationship of the form (2.8). Our Eulerian treatment of the v. ln p surf terms avoids this disadvantage and seems to work well, but further study is required to determine whether this difference in formulation is important or not. Another aspect of our semi-lagrangian discretization of the continuity equation, which differs from that in other models, concerns the definition of the trajectory; in our scheme this is the same (three-dimensional) trajectory as used for the other variables. In the continuous form of the equation, (3.9), the advective part of the total derivative d p dt may be regarded either as two-dimensional or as three-dimensional (since p surf / η is zero). However the vertically discretized form, (3.20), is well-defined only at discrete model levels, implying that for consistency the semi-lagrangian discretization (3.23) should be based on horizontal trajectories. Correcting this inconsistency IFS Documentation Cycle CY25r (Edited 2003) 2
24 Part III: Dynamics and numerical procedures in our scheme by computing horizontal trajectories for the continuity equation, based on the horizontal wind at each model level, made very little difference to the results, and for the time being we have allowed the inconsistency to remain. (As discussed later, in the case of the vertically non-interpolating scheme the modified trajectories are nearly always horizontal anyway.) In the case of the fully interpolating scheme, recomputing the trajectories represents a significant expense; Bates et al. (993) and McDonald and Haugen (992) used a simple projection of the three-dimensional trajectory onto the model level of the arrival point. In our model this approach resulted in poor mass conservation, though Bates et al. (993) came to the opposite conclusion. Again, the importance or otherwise of these differences in formulation is not yet firmly established. 3.6 TIME-STEPPING PROCEDURE The general outline of the time-stepping procedure for the semi-lagrangian version is similar to that described for the Eulerian model in Subsection Thus at the start of a timestep, the model state at time ( t t) is defined by the values of U, V, T, q and ln p surf on the Gaussian grid. To complete the semi-implicit corrections, the ( t t) values of D, p/ λ and p/ µ are also held on the grid. The model state at time t is defined by the spectral coefficients of ζ, D, T, q and ln p surf. Legendre transforms followed by Fourier transforms are then used to compute D, U, V, T, T/ µ, q, q/ µ, ln p surf, and ( ln p surf )/ µ at time t on the model grid; additional Fourier transforms are used to compute the corresponding values of T/ λ, q/ λ, and ( ln p surf )/ λ. Since ζ and the horizontal gradients of U and V are no longer required on the model grid, one multi-level Legendre transform and three multi-level Fourier transforms are saved in comparison with the Eulerian version. Since the advection of moisture is handled by the semi-lagrangian discretization (3.6), the horizontal gradients of q are only needed in order to compute the horizontal gradients of the virtual temperature T v (which in turn are required to compute the φ term in (3.4)). If T v is chosen as the spectral variable as in Subsection 2.2.8, these gradients are available directly, and there is then no need to transform q/ µ (or q/ λ ) to the model grid. The number of multi-level Legendre transforms per time-step is further reduced to 0. In passing, all the ingredients are then in place for a semi-lagrangian treatment in which the moisture field is never transformed to spectral space (Williamson and Rasch, 994), and only 8 multi-level Legendre transforms are required per time-step (compared with 7 in the original ζ D Eulerian model). After the transforms to the model grid, all the information is then available to compute the trajectories for each grid point, and to evaluate the dynamical contributions to the semi-lagrangian discretization. Ignoring for a moment the contributions of the physical parametrization schemes and of the horizontal diffusion, each equation is either of the form or X ( ) X. (3.24) ( ) t{ R 2α 0 ( ) R 2α 0 ( x) } S ( ) S 2α ( ) X ( ) X ( ) 2 tr 2α 0 S ( ) S 2α ( ) (3.25) depending on whether the R 0 terms are averaged between the end points of the trajectory or evaluated at the midpoints. In (3.24) and (3.25), the S terms represent the semi-implicit corrections; S includes contributions from time-levels ( t t) and t, while S includes contributions from time-levels t and ( t t). In the first part of the calculation for equations of the form (3.24), the combined field X tr 0 S is computed, and the value of this combined field at each departure point( ) is then found by interpolation. Adding 2α 22 IFS Documentation Cycle CY25r (Edited 2003)
IFS DOCUMENTATION CY28r1
 IFS Documentation Cycle CY28r1 IFS DOCUMENTATION CY28r1 III: DYNAMICS AND NUMERICAL PROCEDURES (Operational implementation 9 March 2004) Table of contents Chapter 1. Introduction Chapter 2. Basic equations
IFS Documentation Cycle CY28r1 IFS DOCUMENTATION CY28r1 III: DYNAMICS AND NUMERICAL PROCEDURES (Operational implementation 9 March 2004) Table of contents Chapter 1. Introduction Chapter 2. Basic equations
PART III: DYNAMICS AND NUMERICAL PROCEDURES
 IFS DOCUMENTATION Cy40r1 Operational implementation 22 November 2013 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations
IFS DOCUMENTATION Cy40r1 Operational implementation 22 November 2013 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations
PART III: DYNAMICS AND NUMERICAL PROCEDURES
 IFS DOCUMENTATION Cy43r1 Operational implementation 22 Nov 2016 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations and discretisation
IFS DOCUMENTATION Cy43r1 Operational implementation 22 Nov 2016 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations and discretisation
A mass-conservative version of the semi- Lagrangian semi-implicit HIRLAM using Lagrangian vertical coordinates
 A mass-conservative version of the semi- Lagrangian semi-implicit HIRLAM using Lagrangian vertical coordinates Peter Hjort Lauritzen Atmospheric Modeling & Predictability Section National Center for Atmospheric
A mass-conservative version of the semi- Lagrangian semi-implicit HIRLAM using Lagrangian vertical coordinates Peter Hjort Lauritzen Atmospheric Modeling & Predictability Section National Center for Atmospheric
Chapter 6. Semi-Lagrangian Methods
 Chapter 6. Semi-Lagrangian Methods References: Durran Chapter 6. Review article by Staniford and Cote (1991) MWR, 119, 2206-2223. 6.1. Introduction Semi-Lagrangian (S-L for short) methods, also called
Chapter 6. Semi-Lagrangian Methods References: Durran Chapter 6. Review article by Staniford and Cote (1991) MWR, 119, 2206-2223. 6.1. Introduction Semi-Lagrangian (S-L for short) methods, also called
Two dynamical core formulation flaws exposed by a. baroclinic instability test case
 Two dynamical core formulation flaws exposed by a baroclinic instability test case David L. Williamson, Jerry G. Olson National Center for Atmospheric Research, Boulder, CO, USA Christiane Jablonowski
Two dynamical core formulation flaws exposed by a baroclinic instability test case David L. Williamson, Jerry G. Olson National Center for Atmospheric Research, Boulder, CO, USA Christiane Jablonowski
Global Numerical Weather Predictions and the semi-lagrangian semi-implicit dynamical 1 / 27. ECMWF forecast model
 Global Numerical Weather Predictions and the semi-lagrangian semi-implicit dynamical core of the ECMWF forecast model Michail Diamantakis ECMWF Symposium on Modelling and Computations in Atmospheric Sciences
Global Numerical Weather Predictions and the semi-lagrangian semi-implicit dynamical core of the ECMWF forecast model Michail Diamantakis ECMWF Symposium on Modelling and Computations in Atmospheric Sciences
Interpolation of gridded data using Geostrophic Balance. Lennon O Naraigh *
 Interpolation of gridded data using Geostrophic Balance Lennon O Naraigh * Date: 6 th September 2004 Abstract: In this report, a method of interpolating data from the grid of a global climate model (GCM)
Interpolation of gridded data using Geostrophic Balance Lennon O Naraigh * Date: 6 th September 2004 Abstract: In this report, a method of interpolating data from the grid of a global climate model (GCM)
An explicit and conservative remapping strategy for semi-lagrangian advection
 An explicit and conservative remapping strategy for semi-lagrangian advection Sebastian Reich Universität Potsdam, Potsdam, Germany January 17, 2007 Abstract A conservative semi-lagrangian advection scheme
An explicit and conservative remapping strategy for semi-lagrangian advection Sebastian Reich Universität Potsdam, Potsdam, Germany January 17, 2007 Abstract A conservative semi-lagrangian advection scheme
An explicit and conservative remapping strategy for semi-lagrangian advection
 ATMOSPHERIC SCIENCE LETTERS Atmos. Sci. Let. 8: 58 63 (2007) Published online 22 May 2007 in Wiley InterScience (www.interscience.wiley.com).151 An explicit and conservative remapping strategy for semi-lagrangian
ATMOSPHERIC SCIENCE LETTERS Atmos. Sci. Let. 8: 58 63 (2007) Published online 22 May 2007 in Wiley InterScience (www.interscience.wiley.com).151 An explicit and conservative remapping strategy for semi-lagrangian
Semi-Lagrangian Advection. The Basic Idea. x 1.
 3.2.6. Semi-Lagrangian Advection We have studied the Eulerian leapfrog scheme and found it to be conditionally stable. The criterion for stability was the CFL condition µ c t x 1. For high spatial resolution
3.2.6. Semi-Lagrangian Advection We have studied the Eulerian leapfrog scheme and found it to be conditionally stable. The criterion for stability was the CFL condition µ c t x 1. For high spatial resolution
Regional Cooperation for Limited Area Modeling in Central Europe. Dynamics in LACE. Petra Smolíková thanks to many colleagues
 Dynamics in LACE Petra Smolíková thanks to many colleagues Outline 1 1. VFE NH Design of vertical finite elements scheme for NH version of the model 2. SL scheme Application of ENO technique to SL interpolations
Dynamics in LACE Petra Smolíková thanks to many colleagues Outline 1 1. VFE NH Design of vertical finite elements scheme for NH version of the model 2. SL scheme Application of ENO technique to SL interpolations
M.Sc. in Computational Science. Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
Multi-Domain Pattern. I. Problem. II. Driving Forces. III. Solution
 Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
ATM 298, Spring 2013 Lecture 4 Numerical Methods: Horizontal DiscreDzaDons April 10, Paul A. Ullrich (HH 251)
 ATM 298, Spring 2013 Lecture 4 Numerical Methods: Horizontal DiscreDzaDons April 10, 2013 Paul A. Ullrich (HH 251) paullrich@ucdavis.edu Outline 1. Introduction / Motivation 2. Finite Difference Methods
ATM 298, Spring 2013 Lecture 4 Numerical Methods: Horizontal DiscreDzaDons April 10, 2013 Paul A. Ullrich (HH 251) paullrich@ucdavis.edu Outline 1. Introduction / Motivation 2. Finite Difference Methods
CS205b/CME306. Lecture 9
 CS205b/CME306 Lecture 9 1 Convection Supplementary Reading: Osher and Fedkiw, Sections 3.3 and 3.5; Leveque, Sections 6.7, 8.3, 10.2, 10.4. For a reference on Newton polynomial interpolation via divided
CS205b/CME306 Lecture 9 1 Convection Supplementary Reading: Osher and Fedkiw, Sections 3.3 and 3.5; Leveque, Sections 6.7, 8.3, 10.2, 10.4. For a reference on Newton polynomial interpolation via divided
Advanced Numerical Methods for Numerical Weather Prediction
 Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Numerical Methods for (Time-Dependent) HJ PDEs
 Numerical Methods for (Time-Dependent) HJ PDEs Ian Mitchell Department of Computer Science The University of British Columbia research supported by National Science and Engineering Research Council of
Numerical Methods for (Time-Dependent) HJ PDEs Ian Mitchell Department of Computer Science The University of British Columbia research supported by National Science and Engineering Research Council of
Impact of Consistent Semi-Lagrangian Trajectory Calculations on Numerical Weather Prediction Performance
 OCTOBER 2017 H U S A I N A N D G I R A R D 4127 Impact of Consistent Semi-Lagrangian Trajectory Calculations on Numerical Weather Prediction Performance SYED ZAHID HUSAIN AND CLAUDE GIRARD Atmospheric
OCTOBER 2017 H U S A I N A N D G I R A R D 4127 Impact of Consistent Semi-Lagrangian Trajectory Calculations on Numerical Weather Prediction Performance SYED ZAHID HUSAIN AND CLAUDE GIRARD Atmospheric
A Spectral Element Eulerian-Lagrangian Atmospheric Model (SEELAM)
 A Spectral Element Eulerian-Lagrangian Atmospheric Model SEELAM Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943 E-mail: giraldo@nrlmry.navy.mil A new dynamical core for numerical weather
A Spectral Element Eulerian-Lagrangian Atmospheric Model SEELAM Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943 E-mail: giraldo@nrlmry.navy.mil A new dynamical core for numerical weather
Recent research for dynamical cores of nonhydrostatic, deep-atmosphere, unified models
 Recent research for dynamical cores of nonhydrostatic, deep-atmosphere, unified models Andrew Staniforth and Nigel Wood Met Office, FitzRoy Road, Exeter EX1 3PB, United Kingdom Andrew.Staniforth@metoffice.gov.uk,
Recent research for dynamical cores of nonhydrostatic, deep-atmosphere, unified models Andrew Staniforth and Nigel Wood Met Office, FitzRoy Road, Exeter EX1 3PB, United Kingdom Andrew.Staniforth@metoffice.gov.uk,
The semi-lagrangian technique: current status and future 4 September developments / 42
 The semi-lagrangian technique: current status and future developments Michail Diamantakis ECMWF 4 September 2013 (thanks to: Adrian Simmons, Niels Borman and Richard Forbes) The semi-lagrangian technique:
The semi-lagrangian technique: current status and future developments Michail Diamantakis ECMWF 4 September 2013 (thanks to: Adrian Simmons, Niels Borman and Richard Forbes) The semi-lagrangian technique:
The 3D DSC in Fluid Simulation
 The 3D DSC in Fluid Simulation Marek K. Misztal Informatics and Mathematical Modelling, Technical University of Denmark mkm@imm.dtu.dk DSC 2011 Workshop Kgs. Lyngby, 26th August 2011 Governing Equations
The 3D DSC in Fluid Simulation Marek K. Misztal Informatics and Mathematical Modelling, Technical University of Denmark mkm@imm.dtu.dk DSC 2011 Workshop Kgs. Lyngby, 26th August 2011 Governing Equations
A Test Suite for GCMs: An Intercomparison of 11 Dynamical Cores
 A Test Suite for GCMs: An Intercomparison of 11 Dynamical Cores Christiane Jablonowski 1, Peter Lauritzen 2, Mark 3 Taylor, Ram Nair 2 1 University of Michigan, 2 National Center for Atmospheric Research,
A Test Suite for GCMs: An Intercomparison of 11 Dynamical Cores Christiane Jablonowski 1, Peter Lauritzen 2, Mark 3 Taylor, Ram Nair 2 1 University of Michigan, 2 National Center for Atmospheric Research,
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Computation in Astrophysics Seminar (Spring 2006) L. J. Dursi
 Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Advanced Numerical Methods for Numerical Weather Prediction
 Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models
 Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models B Y CHRISTIANE JABLONOWSKI 1, ROBERT C. OEHMKE 2, QUENTIN F. STOUT 1 1 University of Michigan, 2455 Hayward
Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models B Y CHRISTIANE JABLONOWSKI 1, ROBERT C. OEHMKE 2, QUENTIN F. STOUT 1 1 University of Michigan, 2455 Hayward
Skåne University Hospital Lund, Lund, Sweden 2 Deparment of Numerical Analysis, Centre for Mathematical Sciences, Lund University, Lund, Sweden
 Volume Tracking: A New Method for Visualization of Intracardiac Blood Flow from Three-Dimensional, Time-Resolved, Three-Component Magnetic Resonance Velocity Mapping Appendix: Theory and Numerical Implementation
Volume Tracking: A New Method for Visualization of Intracardiac Blood Flow from Three-Dimensional, Time-Resolved, Three-Component Magnetic Resonance Velocity Mapping Appendix: Theory and Numerical Implementation
An inherently mass-conservative semi-implicit semi-lagrangian model. Peter Hjort Lauritzen
 An inherently mass-conservative semi-implicit semi-lagrangian model by Peter Hjort Lauritzen ph.d. thesis Department of Geophysics University of Copenhagen Denmark September, 2005 Abstract A locally mass-conservative
An inherently mass-conservative semi-implicit semi-lagrangian model by Peter Hjort Lauritzen ph.d. thesis Department of Geophysics University of Copenhagen Denmark September, 2005 Abstract A locally mass-conservative
An Orthogonal Curvilinear Terrain-Following Coordinate for Atmospheric Models!
 Solution of Partial Differential Equations on the Sphere! An Orthogonal Curvilinear Terrain-Following Coordinate for Atmospheric Models! Yiyuan Li 1, Bin Wang 1, Donghai Wang 2! 1. Institute of Atmospheric
Solution of Partial Differential Equations on the Sphere! An Orthogonal Curvilinear Terrain-Following Coordinate for Atmospheric Models! Yiyuan Li 1, Bin Wang 1, Donghai Wang 2! 1. Institute of Atmospheric
CS321 Introduction To Numerical Methods
 CS3 Introduction To Numerical Methods Fuhua (Frank) Cheng Department of Computer Science University of Kentucky Lexington KY 456-46 - - Table of Contents Errors and Number Representations 3 Error Types
CS3 Introduction To Numerical Methods Fuhua (Frank) Cheng Department of Computer Science University of Kentucky Lexington KY 456-46 - - Table of Contents Errors and Number Representations 3 Error Types
Diffusion Wavelets for Natural Image Analysis
 Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Modeling icing using cartesian grids, penalization & level sets
 Introduction State of the art The proposed approach Proof of concept Modeling icing using cartesian grids, penalization & level sets Héloïse Beaugendre IMB Institut de Mathématiques de Bordeaux - INRIA
Introduction State of the art The proposed approach Proof of concept Modeling icing using cartesian grids, penalization & level sets Héloïse Beaugendre IMB Institut de Mathématiques de Bordeaux - INRIA
Optimised corrections for finite-difference modelling in two dimensions
 Optimized corrections for 2D FD modelling Optimised corrections for finite-difference modelling in two dimensions Peter M. Manning and Gary F. Margrave ABSTRACT Finite-difference two-dimensional correction
Optimized corrections for 2D FD modelling Optimised corrections for finite-difference modelling in two dimensions Peter M. Manning and Gary F. Margrave ABSTRACT Finite-difference two-dimensional correction
The CSLaM transport scheme & new numerical mixing diagnostics
 The CSLaM transport scheme & new numerical mixing diagnostics CESM Ocean Model Working Group Meeting 14 15 December, 2011 Peter Hjort Lauritzen Outline: Two parts Briefly introduce the CSLaM scheme (Conservative
The CSLaM transport scheme & new numerical mixing diagnostics CESM Ocean Model Working Group Meeting 14 15 December, 2011 Peter Hjort Lauritzen Outline: Two parts Briefly introduce the CSLaM scheme (Conservative
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
3-D Wind Field Simulation over Complex Terrain
 3-D Wind Field Simulation over Complex Terrain University Institute for Intelligent Systems and Numerical Applications in Engineering Congreso de la RSME 2015 Soluciones Matemáticas e Innovación en la
3-D Wind Field Simulation over Complex Terrain University Institute for Intelligent Systems and Numerical Applications in Engineering Congreso de la RSME 2015 Soluciones Matemáticas e Innovación en la
Edge and local feature detection - 2. Importance of edge detection in computer vision
 Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
C. A. D. Fraga Filho 1,2, D. F. Pezzin 1 & J. T. A. Chacaltana 1. Abstract
 Advanced Computational Methods and Experiments in Heat Transfer XIII 15 A numerical study of heat diffusion using the Lagrangian particle SPH method and the Eulerian Finite-Volume method: analysis of convergence,
Advanced Computational Methods and Experiments in Heat Transfer XIII 15 A numerical study of heat diffusion using the Lagrangian particle SPH method and the Eulerian Finite-Volume method: analysis of convergence,
Theoretical Background for OpenLSTO v0.1: Open Source Level Set Topology Optimization. M2DO Lab 1,2. 1 Cardiff University
 Theoretical Background for OpenLSTO v0.1: Open Source Level Set Topology Optimization M2DO Lab 1,2 1 Cardiff University 2 University of California, San Diego November 2017 A brief description of theory
Theoretical Background for OpenLSTO v0.1: Open Source Level Set Topology Optimization M2DO Lab 1,2 1 Cardiff University 2 University of California, San Diego November 2017 A brief description of theory
Long time integrations of a convective PDE on the sphere by RBF collocation
 Long time integrations of a convective PDE on the sphere by RBF collocation Bengt Fornberg and Natasha Flyer University of Colorado NCAR Department of Applied Mathematics Institute for Mathematics Applied
Long time integrations of a convective PDE on the sphere by RBF collocation Bengt Fornberg and Natasha Flyer University of Colorado NCAR Department of Applied Mathematics Institute for Mathematics Applied
Fluent User Services Center
 Solver Settings 5-1 Using the Solver Setting Solver Parameters Convergence Definition Monitoring Stability Accelerating Convergence Accuracy Grid Independence Adaption Appendix: Background Finite Volume
Solver Settings 5-1 Using the Solver Setting Solver Parameters Convergence Definition Monitoring Stability Accelerating Convergence Accuracy Grid Independence Adaption Appendix: Background Finite Volume
AMR Multi-Moment FVM Scheme
 Chapter 4 AMR Multi-Moment FVM Scheme 4.1 Berger s AMR scheme An AMR grid with the hierarchy of Berger s AMR scheme proposed in [13] for CFD simulations is given in Fig.4.1 as a simple example for following
Chapter 4 AMR Multi-Moment FVM Scheme 4.1 Berger s AMR scheme An AMR grid with the hierarchy of Berger s AMR scheme proposed in [13] for CFD simulations is given in Fig.4.1 as a simple example for following
J. Vira, M. Sofiev SILAM winter school, February 2013, FMI
 Numerical aspects of the advection-diffusion equation J. Vira, M. Sofiev SILAM winter school, February 2013, FMI Outline Intro Some common requirements for numerical transport schemes Lagrangian approach
Numerical aspects of the advection-diffusion equation J. Vira, M. Sofiev SILAM winter school, February 2013, FMI Outline Intro Some common requirements for numerical transport schemes Lagrangian approach
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
Conservative Semi-Lagrangian solvers on mapped meshes
 Conservative Semi-Lagrangian solvers on mapped meshes M. Mehrenberger, M. Bergot, V. Grandgirard, G. Latu, H. Sellama, E. Sonnendrücker Université de Strasbourg, INRIA Grand Est, Projet CALVI, ANR GYPSI
Conservative Semi-Lagrangian solvers on mapped meshes M. Mehrenberger, M. Bergot, V. Grandgirard, G. Latu, H. Sellama, E. Sonnendrücker Université de Strasbourg, INRIA Grand Est, Projet CALVI, ANR GYPSI
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras. Lecture - 36
 Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Lecture - 36 In last class, we have derived element equations for two d elasticity problems
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Lecture - 36 In last class, we have derived element equations for two d elasticity problems
NUMERICAL ANALYSIS OF WIND EFFECT ON HIGH-DENSITY BUILDING AERAS
 NUMERICAL ANALYSIS OF WIND EFFECT ON HIGH-DENSITY BUILDING AERAS Bin ZHAO, Ying LI, Xianting LI and Qisen YAN Department of Thermal Engineering, Tsinghua University Beijing, 100084, P.R. China ABSTRACT
NUMERICAL ANALYSIS OF WIND EFFECT ON HIGH-DENSITY BUILDING AERAS Bin ZHAO, Ying LI, Xianting LI and Qisen YAN Department of Thermal Engineering, Tsinghua University Beijing, 100084, P.R. China ABSTRACT
Advective and conservative semi-lagrangian schemes on uniform and non-uniform grids
 Advective and conservative semi-lagrangian schemes on uniform and non-uniform grids M. Mehrenberger Université de Strasbourg and Max-Planck Institut für Plasmaphysik 5 September 2013 M. Mehrenberger (UDS
Advective and conservative semi-lagrangian schemes on uniform and non-uniform grids M. Mehrenberger Université de Strasbourg and Max-Planck Institut für Plasmaphysik 5 September 2013 M. Mehrenberger (UDS
PTE 519 Lecture Note Finite Difference Approximation (Model)
 PTE 519 Lecture Note 3 3.0 Finite Difference Approximation (Model) In this section of the lecture material, the focus is to define the terminology and to summarize the basic facts. The basic idea of any
PTE 519 Lecture Note 3 3.0 Finite Difference Approximation (Model) In this section of the lecture material, the focus is to define the terminology and to summarize the basic facts. The basic idea of any
Application of ENO technique to semi-lagrangian interpolations. RC LACE stay report Scientific supervisors: Petra Smolíková and Ján Mašek
 Application of ENO technique to semi-lagrangian interpolations RC LACE stay report Scientific supervisors: Petra Smolíková and Ján Mašek Alexandra Crăciun NMA, Romania CHMI, Prague 09.05-03.06.2016 1 Introduction
Application of ENO technique to semi-lagrangian interpolations RC LACE stay report Scientific supervisors: Petra Smolíková and Ján Mašek Alexandra Crăciun NMA, Romania CHMI, Prague 09.05-03.06.2016 1 Introduction
LONG-TIME SIMULATIONS OF VORTEX SHEET DYNAMICS
 LONG-TIME SIMULATIONS OF VORTEX SHEET DYNAMICS BY DANIEL SOLANO 1, LING XU 2, AND SILAS ALBEN 2 1 Rutgers University, New Brunswick, NJ 891, USA. 2 University of Michigan, Ann Arbor, MI 4819, USA. Abstract.
LONG-TIME SIMULATIONS OF VORTEX SHEET DYNAMICS BY DANIEL SOLANO 1, LING XU 2, AND SILAS ALBEN 2 1 Rutgers University, New Brunswick, NJ 891, USA. 2 University of Michigan, Ann Arbor, MI 4819, USA. Abstract.
How to run OpenIFS as a shallow water model
 How to run OpenIFS as a shallow water model OpenIFS includes a number of idealised configurations. In this article we explain how to: setup and run a shallow-water model set idealized (e.g. Rossby-Haurwitz
How to run OpenIFS as a shallow water model OpenIFS includes a number of idealised configurations. In this article we explain how to: setup and run a shallow-water model set idealized (e.g. Rossby-Haurwitz
Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative
 Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative Pedro S. Peixoto College of Engineering, Mathematics and Physical Sciences - University of Exeter Instituto
Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative Pedro S. Peixoto College of Engineering, Mathematics and Physical Sciences - University of Exeter Instituto
used to describe all aspects of imaging process: input scene f, imaging system O, and output image g.
 SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
Post Processing, Visualization, and Sample Output
 Chapter 7 Post Processing, Visualization, and Sample Output Upon successful execution of an ADCIRC run, a number of output files will be created. Specifically which files are created depends upon how the
Chapter 7 Post Processing, Visualization, and Sample Output Upon successful execution of an ADCIRC run, a number of output files will be created. Specifically which files are created depends upon how the
The new ECMWF interpolation package MIR
 from Newsletter Number 152 Summer 2017 COMPUTING The new ECMWF interpolation package MIR Hurricane Patricia off the coast of Mexico on 23 October 2015 ( 2015 EUMETSAT) doi:10.21957/h20rz8 This article
from Newsletter Number 152 Summer 2017 COMPUTING The new ECMWF interpolation package MIR Hurricane Patricia off the coast of Mexico on 23 October 2015 ( 2015 EUMETSAT) doi:10.21957/h20rz8 This article
VI Workshop Brasileiro de Micrometeorologia
 Validation of a statistic algorithm applied to LES model Eduardo Bárbaro, Amauri Oliveira, Jacyra Soares November 2009 Index Objective 1 Objective 2 3 Vertical Profiles Flow properties 4 Objective 1 The
Validation of a statistic algorithm applied to LES model Eduardo Bárbaro, Amauri Oliveira, Jacyra Soares November 2009 Index Objective 1 Objective 2 3 Vertical Profiles Flow properties 4 Objective 1 The
Realtime Water Simulation on GPU. Nuttapong Chentanez NVIDIA Research
 1 Realtime Water Simulation on GPU Nuttapong Chentanez NVIDIA Research 2 3 Overview Approaches to realtime water simulation Hybrid shallow water solver + particles Hybrid 3D tall cell water solver + particles
1 Realtime Water Simulation on GPU Nuttapong Chentanez NVIDIA Research 2 3 Overview Approaches to realtime water simulation Hybrid shallow water solver + particles Hybrid 3D tall cell water solver + particles
Chapter 1 - Basic Equations
 2.20 Marine Hydrodynamics, Fall 2017 Lecture 2 Copyright c 2017 MIT - Department of Mechanical Engineering, All rights reserved. 2.20 Marine Hydrodynamics Lecture 2 Chapter 1 - Basic Equations 1.1 Description
2.20 Marine Hydrodynamics, Fall 2017 Lecture 2 Copyright c 2017 MIT - Department of Mechanical Engineering, All rights reserved. 2.20 Marine Hydrodynamics Lecture 2 Chapter 1 - Basic Equations 1.1 Description
University of Reading. Discretization On Non-uniform Meshes: Tests solving shallow-water equations
 University of Reading School of Mathematics, Meteorology and Physics Discretization On Non-uniform Meshes: Tests solving shallow-water equations By FAWZI B ALBUSAIDI August 2008 This dissertation is submitted
University of Reading School of Mathematics, Meteorology and Physics Discretization On Non-uniform Meshes: Tests solving shallow-water equations By FAWZI B ALBUSAIDI August 2008 This dissertation is submitted
CFD MODELING FOR PNEUMATIC CONVEYING
 CFD MODELING FOR PNEUMATIC CONVEYING Arvind Kumar 1, D.R. Kaushal 2, Navneet Kumar 3 1 Associate Professor YMCAUST, Faridabad 2 Associate Professor, IIT, Delhi 3 Research Scholar IIT, Delhi e-mail: arvindeem@yahoo.co.in
CFD MODELING FOR PNEUMATIC CONVEYING Arvind Kumar 1, D.R. Kaushal 2, Navneet Kumar 3 1 Associate Professor YMCAUST, Faridabad 2 Associate Professor, IIT, Delhi 3 Research Scholar IIT, Delhi e-mail: arvindeem@yahoo.co.in
SLICE-3D: A three-dimensional conservative semi-lagrangian scheme for transport problems. Mohamed Zerroukat. Met Office, Exeter, UK
 SLICE-D: A three-dimensional conservative semi-lagrangian scheme for transport problems Mohamed Zerroukat (Nigel wood & Andrew Staniforth) Met Office, Exeter, UK SRNWP-NT, Zagreb, c Crown Copyright Content
SLICE-D: A three-dimensional conservative semi-lagrangian scheme for transport problems Mohamed Zerroukat (Nigel wood & Andrew Staniforth) Met Office, Exeter, UK SRNWP-NT, Zagreb, c Crown Copyright Content
Technical Report TR
 Technical Report TR-2015-09 Boundary condition enforcing methods for smoothed particle hydrodynamics Arman Pazouki 1, Baofang Song 2, Dan Negrut 1 1 University of Wisconsin-Madison, Madison, WI, 53706-1572,
Technical Report TR-2015-09 Boundary condition enforcing methods for smoothed particle hydrodynamics Arman Pazouki 1, Baofang Song 2, Dan Negrut 1 1 University of Wisconsin-Madison, Madison, WI, 53706-1572,
Physics 235 Chapter 6. Chapter 6 Some Methods in the Calculus of Variations
 Chapter 6 Some Methods in the Calculus of Variations In this Chapter we focus on an important method of solving certain problems in Classical Mechanics. In many problems we need to determine how a system
Chapter 6 Some Methods in the Calculus of Variations In this Chapter we focus on an important method of solving certain problems in Classical Mechanics. In many problems we need to determine how a system
Introduction to Computational Fluid Dynamics Mech 122 D. Fabris, K. Lynch, D. Rich
 Introduction to Computational Fluid Dynamics Mech 122 D. Fabris, K. Lynch, D. Rich 1 Computational Fluid dynamics Computational fluid dynamics (CFD) is the analysis of systems involving fluid flow, heat
Introduction to Computational Fluid Dynamics Mech 122 D. Fabris, K. Lynch, D. Rich 1 Computational Fluid dynamics Computational fluid dynamics (CFD) is the analysis of systems involving fluid flow, heat
Solving a Two Dimensional Unsteady-State. Flow Problem by Meshless Method
 Applied Mathematical Sciences, Vol. 7, 203, no. 49, 242-2428 HIKARI Ltd, www.m-hikari.com Solving a Two Dimensional Unsteady-State Flow Problem by Meshless Method A. Koomsubsiri * and D. Sukawat Department
Applied Mathematical Sciences, Vol. 7, 203, no. 49, 242-2428 HIKARI Ltd, www.m-hikari.com Solving a Two Dimensional Unsteady-State Flow Problem by Meshless Method A. Koomsubsiri * and D. Sukawat Department
Continued Investigation of Small-Scale Air-Sea Coupled Dynamics Using CBLAST Data
 Continued Investigation of Small-Scale Air-Sea Coupled Dynamics Using CBLAST Data Dick K.P. Yue Center for Ocean Engineering Department of Mechanical Engineering Massachusetts Institute of Technology Cambridge,
Continued Investigation of Small-Scale Air-Sea Coupled Dynamics Using CBLAST Data Dick K.P. Yue Center for Ocean Engineering Department of Mechanical Engineering Massachusetts Institute of Technology Cambridge,
Parameterization of triangular meshes
 Parameterization of triangular meshes Michael S. Floater November 10, 2009 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to
Parameterization of triangular meshes Michael S. Floater November 10, 2009 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to
Migration from a non-flat datum via reverse-time extrapolation
 Stanford Exploration Project, Report 84, May 9, 2001, pages 1 50 Migration from a non-flat datum via reverse-time extrapolation Gopal Palacharla 1 ABSTRACT Land surveys usually have elevation changes,
Stanford Exploration Project, Report 84, May 9, 2001, pages 1 50 Migration from a non-flat datum via reverse-time extrapolation Gopal Palacharla 1 ABSTRACT Land surveys usually have elevation changes,
INTERNATIONAL JOURNAL OF CIVIL AND STRUCTURAL ENGINEERING Volume 2, No 3, 2012
 INTERNATIONAL JOURNAL OF CIVIL AND STRUCTURAL ENGINEERING Volume 2, No 3, 2012 Copyright 2010 All rights reserved Integrated Publishing services Research article ISSN 0976 4399 Efficiency and performances
INTERNATIONAL JOURNAL OF CIVIL AND STRUCTURAL ENGINEERING Volume 2, No 3, 2012 Copyright 2010 All rights reserved Integrated Publishing services Research article ISSN 0976 4399 Efficiency and performances
A brief description of the particle finite element method (PFEM2). Extensions to free surface
 A brief description of the particle finite element method (PFEM2). Extensions to free surface flows. Juan M. Gimenez, L.M. González, CIMEC Universidad Nacional del Litoral (UNL) Santa Fe, Argentina Universidad
A brief description of the particle finite element method (PFEM2). Extensions to free surface flows. Juan M. Gimenez, L.M. González, CIMEC Universidad Nacional del Litoral (UNL) Santa Fe, Argentina Universidad
Chapter 18. Geometric Operations
 Chapter 18 Geometric Operations To this point, the image processing operations have computed the gray value (digital count) of the output image pixel based on the gray values of one or more input pixels;
Chapter 18 Geometric Operations To this point, the image processing operations have computed the gray value (digital count) of the output image pixel based on the gray values of one or more input pixels;
NUMERICAL VISCOSITY. Convergent Science White Paper. COPYRIGHT 2017 CONVERGENT SCIENCE. All rights reserved.
 Convergent Science White Paper COPYRIGHT 2017 CONVERGENT SCIENCE. All rights reserved. This document contains information that is proprietary to Convergent Science. Public dissemination of this document
Convergent Science White Paper COPYRIGHT 2017 CONVERGENT SCIENCE. All rights reserved. This document contains information that is proprietary to Convergent Science. Public dissemination of this document
Commutative filters for LES on unstructured meshes
 Center for Turbulence Research Annual Research Briefs 1999 389 Commutative filters for LES on unstructured meshes By Alison L. Marsden AND Oleg V. Vasilyev 1 Motivation and objectives Application of large
Center for Turbulence Research Annual Research Briefs 1999 389 Commutative filters for LES on unstructured meshes By Alison L. Marsden AND Oleg V. Vasilyev 1 Motivation and objectives Application of large
CONSERVATIVE AND NON-CONSERVATIVE METHODS BASED ON HERMITE WEIGHTED ESSENTIALLY-NON-OSCILLATORY RECONSTRUCTION FOR VLASOV EQUATIONS
 CONSERVATIVE AND NON-CONSERVATIVE METHODS BASED ON HERMITE WEIGHTED ESSENTIALLY-NON-OSCILLATORY RECONSTRUCTION FOR VLASOV EQUATIONS CHANG YANG AND FRANCIS FILBET Abstract. We develop weighted essentially
CONSERVATIVE AND NON-CONSERVATIVE METHODS BASED ON HERMITE WEIGHTED ESSENTIALLY-NON-OSCILLATORY RECONSTRUCTION FOR VLASOV EQUATIONS CHANG YANG AND FRANCIS FILBET Abstract. We develop weighted essentially
Trajectory Calculations for Spherical Geodesic Grids in Cartesian Space
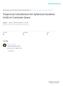 See discussions, stats, author profiles for this publication at: http://www.researchgate.net/publication/4961110 Trajectory Calculations for Spherical Geodesic Grids in Cartesian Space ARTICLE in MONTHLY
See discussions, stats, author profiles for this publication at: http://www.researchgate.net/publication/4961110 Trajectory Calculations for Spherical Geodesic Grids in Cartesian Space ARTICLE in MONTHLY
Adarsh Krishnamurthy (cs184-bb) Bela Stepanova (cs184-bs)
 OBJECTIVE FLUID SIMULATIONS Adarsh Krishnamurthy (cs184-bb) Bela Stepanova (cs184-bs) The basic objective of the project is the implementation of the paper Stable Fluids (Jos Stam, SIGGRAPH 99). The final
OBJECTIVE FLUID SIMULATIONS Adarsh Krishnamurthy (cs184-bb) Bela Stepanova (cs184-bs) The basic objective of the project is the implementation of the paper Stable Fluids (Jos Stam, SIGGRAPH 99). The final
IMPROVING THE NUMERICAL ACCURACY OF HYDROTHERMAL RESERVOIR SIMULATIONS USING THE CIP SCHEME WITH THIRD-ORDER ACCURACY
 PROCEEDINGS, Thirty-Seventh Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, California, January 30 - February 1, 2012 SGP-TR-194 IMPROVING THE NUMERICAL ACCURACY OF HYDROTHERMAL
PROCEEDINGS, Thirty-Seventh Workshop on Geothermal Reservoir Engineering Stanford University, Stanford, California, January 30 - February 1, 2012 SGP-TR-194 IMPROVING THE NUMERICAL ACCURACY OF HYDROTHERMAL
CME 345: MODEL REDUCTION
 CME 345: MODEL REDUCTION Parameterized Partial Differential Equations Charbel Farhat Stanford University cfarhat@stanford.edu 1 / 19 Outline 1 Initial Boundary Value Problems 2 Typical Parameters of Interest
CME 345: MODEL REDUCTION Parameterized Partial Differential Equations Charbel Farhat Stanford University cfarhat@stanford.edu 1 / 19 Outline 1 Initial Boundary Value Problems 2 Typical Parameters of Interest
Supplemental Material Deep Fluids: A Generative Network for Parameterized Fluid Simulations
 Supplemental Material Deep Fluids: A Generative Network for Parameterized Fluid Simulations 1. Extended Results 1.1. 2-D Smoke Plume Additional results for the 2-D smoke plume example are shown in Figures
Supplemental Material Deep Fluids: A Generative Network for Parameterized Fluid Simulations 1. Extended Results 1.1. 2-D Smoke Plume Additional results for the 2-D smoke plume example are shown in Figures
IMPROVED WALL BOUNDARY CONDITIONS WITH IMPLICITLY DEFINED WALLS FOR PARTICLE BASED FLUID SIMULATION
 6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7) 1115 June 2018, Glasgow, UK IMPROVED WALL BOUNDARY CONDITIONS WITH IMPLICITLY
6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7) 1115 June 2018, Glasgow, UK IMPROVED WALL BOUNDARY CONDITIONS WITH IMPLICITLY
Overview of Traditional Surface Tracking Methods
 Liquid Simulation With Mesh-Based Surface Tracking Overview of Traditional Surface Tracking Methods Matthias Müller Introduction Research lead of NVIDIA PhysX team PhysX GPU acc. Game physics engine www.nvidia.com\physx
Liquid Simulation With Mesh-Based Surface Tracking Overview of Traditional Surface Tracking Methods Matthias Müller Introduction Research lead of NVIDIA PhysX team PhysX GPU acc. Game physics engine www.nvidia.com\physx
used to describe all aspects of imaging process: input scene f, imaging system O, and output image g.
 SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
SIMG-716 Linear Imaging Mathematics I 03 1 Representations of Functions 1.1 Functions Function: rule that assigns one numerical value (dependent variable) to each of a set of other numerical values (independent
Water. Notes. Free surface. Boundary conditions. This week: extend our 3D flow solver to full 3D water We need to add two things:
 Notes Added a 2D cross-section viewer for assignment 6 Not great, but an alternative if the full 3d viewer isn t working for you Warning about the formulas in Fedkiw, Stam, and Jensen - maybe not right
Notes Added a 2D cross-section viewer for assignment 6 Not great, but an alternative if the full 3d viewer isn t working for you Warning about the formulas in Fedkiw, Stam, and Jensen - maybe not right
Introduction to C omputational F luid Dynamics. D. Murrin
 Introduction to C omputational F luid Dynamics D. Murrin Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer, chemical reactions, and related phenomena
Introduction to C omputational F luid Dynamics D. Murrin Computational fluid dynamics (CFD) is the science of predicting fluid flow, heat transfer, mass transfer, chemical reactions, and related phenomena
The Immersed Interface Method
 The Immersed Interface Method Numerical Solutions of PDEs Involving Interfaces and Irregular Domains Zhiiin Li Kazufumi Ito North Carolina State University Raleigh, North Carolina Society for Industrial
The Immersed Interface Method Numerical Solutions of PDEs Involving Interfaces and Irregular Domains Zhiiin Li Kazufumi Ito North Carolina State University Raleigh, North Carolina Society for Industrial
Physics Tutorial 2: Numerical Integration Methods
 Physics Tutorial 2: Numerical Integration Methods Summary The concept of numerically solving differential equations is explained, and applied to real time gaming simulation. Some objects are moved in a
Physics Tutorial 2: Numerical Integration Methods Summary The concept of numerically solving differential equations is explained, and applied to real time gaming simulation. Some objects are moved in a
CONFORMAL MAPPING POTENTIAL FLOW AROUND A WINGSECTION USED AS A TEST CASE FOR THE INVISCID PART OF RANS SOLVERS
 European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006 P. Wesseling, E. Oñate and J. Périaux (Eds) c TU Delft, The Netherlands, 2006 CONFORMAL MAPPING POTENTIAL FLOW AROUND A WINGSECTION
European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006 P. Wesseling, E. Oñate and J. Périaux (Eds) c TU Delft, The Netherlands, 2006 CONFORMAL MAPPING POTENTIAL FLOW AROUND A WINGSECTION
New formulations of the semi-lagrangian method for Vlasov-type equations
 New formulations of the semi-lagrangian method for Vlasov-type equations Eric Sonnendrücker IRMA Université Louis Pasteur, Strasbourg projet CALVI INRIA Nancy Grand Est 17 September 2008 In collaboration
New formulations of the semi-lagrangian method for Vlasov-type equations Eric Sonnendrücker IRMA Université Louis Pasteur, Strasbourg projet CALVI INRIA Nancy Grand Est 17 September 2008 In collaboration
Parallel Adaptive Tsunami Modelling with Triangular Discontinuous Galerkin Schemes
 Parallel Adaptive Tsunami Modelling with Triangular Discontinuous Galerkin Schemes Stefan Vater 1 Kaveh Rahnema 2 Jörn Behrens 1 Michael Bader 2 1 Universität Hamburg 2014 PDES Workshop 2 TU München Partial
Parallel Adaptive Tsunami Modelling with Triangular Discontinuous Galerkin Schemes Stefan Vater 1 Kaveh Rahnema 2 Jörn Behrens 1 Michael Bader 2 1 Universität Hamburg 2014 PDES Workshop 2 TU München Partial
CS 450 Numerical Analysis. Chapter 7: Interpolation
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
The impact of background error on incomplete observations for 4-D Var data assimilation with the FSU GSM
 The impact of background error on incomplete observations for 4-D Var data assimilation with the FSU GSM Zhuo Liu and I.M. Navon (Department of Mathematics and School of Computational Science and Information
The impact of background error on incomplete observations for 4-D Var data assimilation with the FSU GSM Zhuo Liu and I.M. Navon (Department of Mathematics and School of Computational Science and Information
Partial Differential Equations
 Simulation in Computer Graphics Partial Differential Equations Matthias Teschner Computer Science Department University of Freiburg Motivation various dynamic effects and physical processes are described
Simulation in Computer Graphics Partial Differential Equations Matthias Teschner Computer Science Department University of Freiburg Motivation various dynamic effects and physical processes are described
Robust Ring Detection In Phase Correlation Surfaces
 Griffith Research Online https://research-repository.griffith.edu.au Robust Ring Detection In Phase Correlation Surfaces Author Gonzalez, Ruben Published 2013 Conference Title 2013 International Conference
Griffith Research Online https://research-repository.griffith.edu.au Robust Ring Detection In Phase Correlation Surfaces Author Gonzalez, Ruben Published 2013 Conference Title 2013 International Conference
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
Driven Cavity Example
 BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
. Tutorial Class V 3-10/10/2012 First Order Partial Derivatives;...
 Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Three-Dimensional Oceanic Flows from Eulerian Velocity Data
 Second-year Ph.D. student, Applied Math and Scientific Computing Project Advisor: Kayo Ide Department of Atmospheric and Oceanic Science Center for Scientific Computation and Mathematical Modeling Earth
Second-year Ph.D. student, Applied Math and Scientific Computing Project Advisor: Kayo Ide Department of Atmospheric and Oceanic Science Center for Scientific Computation and Mathematical Modeling Earth
