PART III: DYNAMICS AND NUMERICAL PROCEDURES
|
|
|
- Naomi Willis
- 5 years ago
- Views:
Transcription
1 IFS DOCUMENTATION Cy40r1 Operational implementation 22 November 2013 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations and discretisation Semi-Lagrangian formulation c Copyright 2014 European Centre for Medium-Range Weather Forecasts Shinfield Park, Reading, RG2 9AX, England Literary and scientific copyrights belong to ECMWF and are reserved in all countries. This publication is not to be reprinted or translated in whole or in part without the written permission of the Director. Appropriate non-commercial use will normally be granted under the condition that reference is made to ECMWF. The information within this publication is given in good faith and considered to be true, but ECMWF accepts no liability for error, omission and for loss or damage arising from its use. IFS Documentation Cy40r1 1
2
3 Chapter 1 Introduction Table of contents 1.1 Overview 1.2 Structure of document 1.1 OVERVIEW Since the original demonstration of the efficiency advantage of the semi-lagrangian semi-implicit method over a decade ago by André Robert, this numerical integration scheme is being used in an increasing range of atmospheric models. Most of the applications have been in grid-point models. Shallow-water-equations studies have included three-time-level versions by Robert 1981,1982) and Staniforth and Temperton 1986), and two-time-level schemes by Temperton and Staniforth 1987), Purser and Leslie 1988), McDonald and Bates 1989), and Côté and Staniforth 1990). There also have been various applications in baroclinic grid-point models. Three-time-level sigma-coordinate versions have been presented by Robert et al. 1985) and Tanguay et al. 1989), and the extension of the threetime-level approach to a non-hydrostatic coordinate has been demonstrated by Tanguay et al. 1990). Bates and McDonald 1982), McDonald 1986), Leslie and Purser 1991), McDonald and Haugen 1992), and Bates et al. 1993) have developed two-time-level sigma-coordinate schemes, McDonald and Haugen 1993) have presented the two-time-level extension to a hybrid vertical coordinate, and Golding 1992) has applied a split two-time-level semi-lagrangian scheme in a non-hydrostatic model. For spectral models, a semi-lagrangian semi-implicit shallow-water equation model was presented by Ritchie 1988) for a three-time-level version, and adapted by Côté and Staniforth 1988) for a two-time-level scheme. Baroclinic three-time-level spectral model formulations have been demonstrated by Ritchie 1991) for operational numerical weather prediction in a sigma-coordinate model, and recently by Williamson and Olson 1994) for climate simulations with a hybrid coordinate model. In a broader context, the semi-lagrangian scheme, as incorporated in spectral numerical weather prediction models, may be considered as an economical variant of the spectral Lagrange-Galerkin method Süli and Ware, 1991). Experience at ECMWF Simmons et al., 1989) suggests that the accuracy of medium-range forecasts has steadily improved with increasing resolution. Consequently, in its four-year plan for the period , ECMWF proposed development of a high-resolution version of its forecast model. A target resolution of a spectral representation with a triangular truncation of 213 waves in the horizontal and 31 levels in the vertical T213/L31) was set, entailing a doubling of the horizontal resolution and an approximate doubling of the vertical resolution in the troposphere compared to the T106/L19 configuration that was operational at the time Simmons et al., 1989). In view of the anticipated computer resources, it was clear that major efficiency gains would be necessary in order to attain this objective. These gains have been provided by the introduction of the semi-lagrangian treatment of advection permitting a substantial increase in the size of the time-step, the use of a reduced Gaussian grid giving a further advantage of about 25%, the introduction of economies in the Legendre transforms, and improvements to the model s basic architecture. IFS Documentation Cy40r1 3
4 Chapter 1: Introduction 1.2 STRUCTURE OF DOCUMENT The layout for the remainder of the document is as follows. In Chapter 2 Basic equations and discretization we present the reformulation of the Eulerian model in order to transform the vorticitydivergence formulation into a momentum-equation version in preparation for a subsequent semi- Lagrangian vector treatment of the equations of motion. The vertical discretization of the ECMWF hybrid coordinate on a staggered grid is also considered. The semi-lagrangian treatment is discussed in some detail in Chapter 3 Semi-Lagrangian formulation, including the adaptation to accommodate the reduced Gaussian grid. 4 IFS Documentation Cy40r1
5 Chapter 2 Basic equations and discretisation Table of contents 2.1 Eulerian reformulation of the continuous equations 2.2 Discretisation Vertical discretisation Finite-element vertical discretisation Time discretisation Horizontal grid Time-stepping procedure Time filtering Remarks T v as spectral variable Horizontal diffusion and de-aliasing 2.1 EULERIAN REFORMULATION OF THE CONTINUOUS EQUATIONS Following Ritchie 1988,1991), the first step in developing a semi-lagrangian version of the ECMWF spectral model was to convert the existing Eulerian ζ D vorticity divergence) model to a U V formulation, where U and V are the wind images defined by U = u cos θ, V = v cos θ u and v are the components of the horizontal wind in spherical coordinates, and θ is latitude). In this section we describe the Eulerian U V model. First we set out the continuous equations in λ, θ, η) coordinates, where λ is longitude and η is the hybrid vertical coordinate introduced by Simmons and Burridge 1981); thus ηp, p s ) is a monotonic function of the pressure p, and also depends on the surface pressure p s in such a way that The momentum equations are U t + 1 a cos 2 θ { V t + 1 a cos 2 U V θ λ { U U + V cos θ U λ θ η0, p s ) = 0 and ηp s, p s ) = 1 } + V cos θ V θ + sin θu2 + V 2 ) } + η U fv + 1 { } φ a λ + R dryt v ln p) = P U + K U 2.1) λ + η V + fu + cos θ a { φ θ + R dryt v ln p) θ } = P V + K V 2.2) where a is the radius of the earth, η is the η-coordinate vertical velocity η = dη/dt), φ is geopotential, R dry is the gas constant for dry air, and T v is the virtual temperature defined by T v = T[1 + {R vap /R dry ) 1}q] where T is temperature, q is specific humidity and R vap is the gas constant for water vapour. P U and P V represent the contributions of the parametrized physical processes, while K U and K V are the horizontal diffusion terms. IFS Documentation Cy40r1 5
6 Chapter 2: Basic equations and discretisation The thermodynamic equation is T t + 1 a cos 2 θ { U T + V cos θ T λ θ } + η T κt v ω 1 + δ 1)q)p = P T + K T 2.3) where κ = R dry /c pdry with c pdry the specific heat of dry air at constant pressure), ω is the pressurecoordinate vertical velocity ω = dp/dt), and δ = c pvap /c pdry with c pvap the specific heat of water vapour at constant pressure). The moisture equation is { q t + 1 a cos 2 U q } + V cos θ q + η q θ λ θ = P q + K q 2.4) In 2.2) and 2.3), P T and P q represent the contributions of the parametrized physical processes, while K T and K q are the horizontal diffusion terms. The continuity equation is ) ) p p + v H + η p ) = 0 2.5) t where is the horizontal gradient operator in spherical coordinates and v H = u, v) is the horizontal wind. The geopotential φ which appears in 2.1) and 2.2) is defined by the hydrostatic equation φ = R dryt v p p 2.6) while the vertical velocity ω in 2.3) is given by ω = η 0 ) p v H dη + v H p 2.7) Expressions for the rate of change of surface pressure, and for the vertical velocity η, are obtained by integrating 2.5), using the boundary conditions η = 0 at η = 0 and at η = 1 p 1 s t = η p = p t 0 η 0 ) p v H dη 2.8) ) p v H dη 2.9) Since we use lnp s ) rather than p s as the surface pressure variable, it is convenient to rewrite 2.8) as t ln p s) = 1 1 ) p v H dη 2.10) p s DISCRETISATION Vertical discretisation To represent the vertical variation of the dependent variables U, V, T and q, the atmosphere is divided into NLEV layers. These layers are defined by the pressures at the interfaces between them the half-levels ), and these pressures are given by p k+1/2 = A k+1/2 + B k+1/2 p s 2.11) for 0 k NLEV. The A k+1/2 and B k+1/2 are constants whose values effectively define the vertical coordinate and p s is the surface pressure field. The values of the A k+1/2 and B k+1/2 for all 0 k NLEV are stored in the GRIB header of all fields archived on model levels to allow the reconstruction of the full-level pressure p k associated with each 6 IFS Documentation Cy40r1
7 model level middle of layer) from p k = 1 2 p k 1/2 + p k+1/2 ) with 1 k NLEV by using 2.11) and the surface pressure field. The prognostic variables are represented by their values at full-level pressures p k. Values for p k are not explicitly required by the model s vertical finite-difference scheme, which is described below. The discrete analogue of the surface pressure tendency equation 2.10) is t ln p s) = 1 NLEV v k p k ) 2.12) p s k=1 where From 2.11) we obtain t ln p s) = p k = p k+1/2 p k 1/2 2.13) NLEV k=1 { } 1 D k p k + v k ln p s ) B k p s 2.14) where D k is the divergence at level k given by ) 1 Uk D k = a cos 2 θ λ + cos θ V k θ 2.15) and The discrete analogue of 2.9) is B k = B k+1/2 B k 1/2 2.16) η p ) = p k+1/2 k+1/2 t k v j p j ) 2.17) j=1 and from 2.11) we obtain η p ) [ = p s B k+1/2 k+1/2 t ln p s) + where / tln p s ) is given by 2.14). Vertical advection of a variable X is now given by η X ) = 1 { η p ) 2 p k k k { }] 1 D j p j + v j ln p s ) B j p s j=1 X k+1 X k ) + k+1/2 The discrete analogue of the hydrostatic equation 2.6) is φ k+1/2 φ k 1/2 = R dry T v ) k ln η p ) } X k X k 1 ) k 1/2 pk+1/2 p k 1/2 ) 2.18) 2.19) 2.20) which gives NLEV φ k+1/2 = φ s + j=k+1 R dry T v ) j ln pj+1/2 p j 1/2 ) 2.21) where φ s is the geopotential at the surface. Full-level values of the geopotential, as required in the momentum equations 2.1) and 2.2), are given by φ k = φ k+1/2 + α k R dry T v ) k 2.22) IFS Documentation Cy40r1 7
8 Chapter 2: Basic equations and discretisation where α 1 = ln 2 and, for k > 1, α k = 1 p k 1/2 p k ln pk+1/2 p k 1/2 The remaining part of the pressure gradient terms in 2.1) and 2.2) is given by R dry T v ln p) k = R { ) } dryt v ) k pk+1/2 ln p k 1/2 + α k p k ) p k p k 1/2 ) 2.23) 2.24) with α k given by 2.23) for all k. Finally, the energy conversion term in the thermodynamic equation 2.3) is discretised as ) { κt v ω κt v ) k = 1 [ ln 1 + δ 1)q)p k 1 + δ 1)q k p k ] + α k D k p k + p s v k ln p s ) B k ) ) k 1 pk+1/2 p k 1/2 + p s p k j=1 D j p j + p s v j ln p s ) B j ) [ B k + C k p k ln pk+1/2 p k 1/2 )] } v k ln p s ) 2.25) where α 1 = ln 2, α k is defined by 2.23) for k > 1, and C k = A k+1/2 B k 1/2 A k 1/2 B k+1/ ) The reasons behind the various choices made in this vertical discretisation scheme are discussed by Simmons and Burridge 1981); basically the scheme is designed to conserve angular momentum and energy, for frictionless adiabatic flow Finite-element vertical discretisation In Cy24r3 the vertical discretisation has been changed in the operational model from the finite-difference discretisation in Lorenz staggering described in the previous subsection to a finite-element discretisation using cubic B-splines as basis functions. For the finite-element FE) discretisation, all variables even pressure) are kept at the same levels full levels), i.e. the values of pressure at full levels and not at half levels are required. Also, the values of the derivatives da/dη and db/dη at full levels are now needed, from which the vertical derivative of pressure can be computed according to p/ = da/dη) + db/dη)p s. In the semi-lagrangian version of the evolution equations these are the only vertical derivatives required. They are constant in time and linked to the definition of the vertical coordinate. It is therefore convenient to change the definition of the vertical coordinate and supply da/dη) k and db/dη) k at full levels instead of A k+1/2 and B k+1/2 at half levels) such that and 1 0 ) p = k da dη dη = 0 ) da + dη k and ) db p s 2.27) dη k 1 0 db dη dη = ) The two conditions of 2.28) ensure that the integral of pressure from the top of the atmosphere to the surface yields exactly the surface pressure. These conditions have to be fulfilled to a good approximation with the numerical integration scheme used. Pressure at any full level can then be obtained by integrating 2.27) from the top of the atmosphere to the level in question. The only operation in the vertical which has to be evaluated is the vertical integration. An integral operator based on a finite-element representation will be derived next. Most of the integrals that have to be evaluated are integrals from the top of the atmosphere to the individual model levels and to the surface. We therefore derive an operator in finite-element representation for this type of integral, i.e. an operator which returns the integral from the top of the atmosphere to each of the model levels η k and to the surface η = 1). The vertical integral in the hydrostatic equation 8 IFS Documentation Cy40r1
9 i.e. from the surface upwards) can be constructed by taking the difference of the integral from the top of the atmosphere to the model level in question minus the integral from the top to the surface. Let {d i η)} K2 i=k 1 and {e i η)} M2 i=m 1 be two sets of linearly independent functions of compact support which can be used as basis functions to expand any function of the vertical coordinate η given in the domain [0, 1]. The vertical integral can then be approximated as K 2 i=k 1 C i d i η) = η Fη) = fx) dx 0 M 2 i=m 1 c i η 0 e i x) dx 2.29) where C i are the coefficients of the expansion of Fη) as a linear combination of the basis functions {d i η)} and c i are the coefficients of the expansion of fη) as a linear combination of the basis functions {e i η)}. We can then apply the Galerkin procedure to 2.29) by multiplying both sides of this equation by each function from a complete set of test functions {t j } N2 j=n 1 and integrating over the vertical domain: K 2 i=k 1 C i 1 0 d i x)t j x) dx = M 2 i=m 1 c i In matrix form this can be expressed as A C = B c C = A 1 B c. 1 0 [ x ] t j x) e i y) dy dx 0 Incorporating into the above expression also the transformations from physical space to finite-element space and back, i.e. c = S 1 f and F = P C, we obtain F = PA 1 BS 1 f I f. Here f and F denote vectors in physical space composed mainly of the values of f and F, respectively, at the model levels: f i = fη i ), F i = Fη i ), 1 i N. The set of values F also includes the value at the surface of the model. Details of the basis functions chosen to implement the scheme as well as how to compute the projection matrices S and P are given in Untch and Hortal 2004). Matrix I PA 1 BS 1 is the integration operator in finite-element formulation which, applied to a function given at full model levels, yields the integrals of this function from the top of the atmosphere to each individual full model level and to the surface. All the finite sums on the vertical levels in Subsection are replaced by vertical integrals computed by applying the matrix integration operator I. Moreover the quantities α k are no longer needed as the integration operator gives directly the value of the integral at the model levels the half levels do not have any meaning in the FE discretisation) Time discretisation To introduce a discretisation in time, together with a semi-implicit correction, we define the operators δ t X = X + X )/2 t tt X = X + 2X + X ) where X represents the value of a variable at time t, X + the value at time t + t), and X the value at t t). In preparation for the semi-lagrangian treatment to be developed in Chapter 3, we also introduce the three-dimensional advection operator AX) = 1 a cos 2 θ U x + V cos θ x λ θ ) + η x 2.30) IFS Documentation Cy40r1 9
10 Chapter 2: Basic equations and discretisation Introducing the semi-implicit correction terms, 2.1) to 2.4) become: δ t U + AU) fv + 1 { } φ a λ + R dryt v ln p) λ = P U + K U β { 2a tt [γ] T } λ + R dryt ref λ ln p s) δ t V + AV ) + sin θ a cos 2 θ U2 + V 2 ) + fu + cos θ a = P V + K V β cos θ 2a tt { φ θ + R dryt v θ ) [γ] T θ + R dryt ref θ ln p s) } ln p) 2.31) 2.32) δ t T + AT) κt v ω 1 + δ 1)q)p = P T + K T β 2 tt[τ]d) 2.33) δ t q + Aq) = P q + K q 2.34) where β is a parameter of the semi-implicit scheme; the classical scheme Robert, 1969) is recovered with β = 1. The semi-implicit correction terms are linearised versions of the pressure gradient terms in 2.1) and 2.2) and the energy conversion term in 2.3). Thus T ref is a reference temperature here chosen to be independent of vertical level), while [γ] and [τ] are matrices such that NLEV [γ]t) k = α ref k R dry T k + { 1 [τ]d) k = κt ref p ref ln k j=k+1 ) k 1 k+1/2 p ref k 1/2 j=1 p ref p ref R dry T j ln j+1/2 p ref j 1/2 ) } D j p ref j ) + α ref k D k 2.35) 2.36) where the half-level pressures appearing in 2.35) and 2.36) are reference values obtained from 2.11) by choosing a reference value p ref s of p s, and the coefficients α ref k are based on these reference values. The reference values adopted for the semi-implicit scheme are T ref = 300 K and p ref s = 800 hpa. The integrated surface pressure tendency equation 2.14) becomes δ t ln p s ) + NLEV k=1 { } 1 D k p k + v k ln p s ) B k = β p s 2 tt[ν]d 2.37) where [ν]d = 1 NLEV p ref D j p ref s 2.38) s j= Horizontal grid A novel feature of the model is the optional use of a reduced Gaussian grid, as described by Hortal and Simmons 1991). Thus, the number of points on each latitude row is chosen so that the local east west grid length remains approximately constant, with the restriction that the number should be suitable for the FFT N = 2 p 3 q 5 r ). After some experimentation, the fully reduced grid option of Hortal and Simmons was implemented; all possible wavenumbers up to the model s truncation limit) are used in the Legendre transforms. A small amount of noise in the immediate vicinity of the poles was removed by increasing the number of grid points in the three most northerly and southerly rows of the grid from 6, 12 and 18 points in the original design of the T213 grid to 12, 16 and 20 points respectively). Courtier and Naughton 1994) have reconsidered the design of reduced Gaussian grids and this procedure is now applied for all operational horizontal resolutions N >= IFS Documentation Cy40r1
11 2.2.5 Time-stepping procedure The time-stepping procedure for the Eulerian U V version of the model follows closely that outlined by Temperton 1991) for the shallow-water equations. At the start of a time-step, the model state at time t t) is defined by the values of U, V, T, q and ln p s on the Gaussian grid. To compute the semi-implicit corrections, the t t) values of divergence D, P/ λ and P/ µ are also held on the grid, where µ = sin θ and P = [γ]t + R dry T ref ln p s 2.39) The model state at time t is defined by the spectral coefficients of ζ, D, T, q and ln p s. Legendre transforms followed by Fourier transforms are then used to compute ζ, D, U, V, T, T/ µ, ln p s and ln p s )/ µ at time t on the model grid. Additional Fourier transforms are used to compute the corresponding values of U/ λ, V/ λ. T/ λ, q/ λ and ln p s )/ λ. The meridional gradients of U and V are obtained using the relationships cos θ V θ = ad cos2 θ U λ cos θ U θ = V λ aζ cos2 θ All the information is then available to evaluate the terms at time t on the left-hand sides of 2.31) to 2.34) and 2.37), and thus to compute provisional tendencies of the model variables. These tendencies together with values of the variables at t t) are supplied to the physical parametrization routines, which increment the tendencies with their respective contributions. The semi-implicit correction terms evaluated at time-levels t t) and t are then added to the tendencies. Ignoring the horizontal diffusion terms which are handled later in spectral space), and grouping together the terms which have been computed on the grid, 2.31) to 2.34) and 2.37) can be written in the form U + + β t a P + λ = R ) V + + β t + cos θ P a θ = R ) T + + β t[τ]d + = R ) q + = R ) ln p s ) + + β t[ν]d + = R ) The right-hand sides R 1 R 5 are transformed to spectral space via Fourier transforms followed by Gaussian integration. The curl and divergence of 2.40) and 2.41) are then computed in spectral space, leading to ζ + = curlr 1, R 2 ) 2.45) D + + β t 2 P + = divr 1, R 2 ) 2.46) Equations 2.42), 2.44) and 2.46) can then be combined with the aid of 2.39) to obtain an equation of the form ) nn + 1) [I] + a 2 [Γ] Dn m ) + = D) m n 2.47) for each zonal wavenumber m and total wavenumber n, where the matrix [Γ] = β 2 t) 2 [γ][τ] + R dry T ref [ν]) 2.48) couples all the NLEV values of D m n ) + in a vertical column. Once D + has been found, the calculation of T + and ln p s ) + can be completed, while q + and ζ + have already been obtained from 2.43) and 2.45) Time filtering To avoid decoupling of the solutions at odd and even time steps in the three-time-level scheme, a Robert filter Asselin, 1972) is applied at each timestep. The time-filtering is defined by X f = X + εx f 2X + X + ) 2.49) IFS Documentation Cy40r1 11
12 Chapter 2: Basic equations and discretisation where the subscript f denotes a filtered value, and X, X and X + represent values at t t), t and t + t), respectively. Because of the scanning structure of the model, it is convenient to apply the time-filtering in grid-point space, and to split 2.57) into two parts: X f = X + εx f 2X) 2.50) X f = X f + εx ) The partially filtered values computed by 2.50) are stored on a grid-point work file and passed from one time-step to the next. Thus, the information available after the transforms to grid-point space consists of partially filtered values at time t t) together with unfiltered values at time t. The filtering of the t t) fields can then be completed via 2.51), which after shifting by one timestep becomes: X f = X f + εx 2.52) The computations described in Subsection are performed using these fully filtered values at time t t) and the unfiltered values at time t. Once 2.52) has been implemented, values of X f are also available to implement 2.50) for the partially filtered values to be passed on to the next timestep Remarks Ritchie 1988) noted that for a spectral model of the shallow-water equations, the U V form and the ζ D form gave identical results apart from round-off error). In extending this work to a multi-level model, Ritchie 1991) found that this equivalence was not maintained. This was in fact a result of some analytic manipulations in the vertical, used to eliminate between the variables in solving the equations of the semi-implicit scheme, which were not exactly matched by the finite-element vertical discretisation of Ritchie s model. In the case of the model described here, the corresponding elimination between the variables is purely algebraic, and the equivalence between the U V form and the ζ D form is maintained apart from one small exception due to the use of the hybrid vertical coordinate. In the U V model, the gradients of the geopotential φ are computed in grid-point space from the spectrally computed gradients of T, q and ln p s ), while in the ζ D model φ itself is computed and transformed separately into spectral space, where its Laplacian is added into the divergence equation. Since φ is not a quadratic function of the model variables there is some aliasing, which is different for the two versions of the model. In practice the differences between the ζ D model and the U V model were found to be very small, and in the case of a pure sigma-coordinate the two models would be algebraically equivalent. The U V model is nevertheless considerably more economical than its ζ D counterpart in terms of the number of Legendre transforms required. In addition to the transform of φ referred to above, four Legendre transforms are saved in the treatment of the wind fields using the procedures described by Temperton 1991) for the shallow-water equations. The number of multi-level Legendre transforms is thereby reduced from 17 to 12 per time-step T v as spectral variable In preparation for a further reduction in the number of Legendre transforms required by the semi- Lagrangian version of the model, the modified Eulerian version includes an option to keep the virtual temperature T v, rather than the temperature T, as the spectral variable. In the time-stepping procedure, Legendre transforms followed by Fourier transforms are used to compute T v, T v / µ and T v / λ at time t on the model grid; the corresponding values of T, T/ µ, and T/ λ are then computed using the corresponding values of q, q/ µ, and q/ λ. The thermodynamic equation 2.3) is then stepped forward in time exactly as before. After the physical parametrization routines, the provisional value of Tt + t) is combined with qt + t) to compute a provisional value of T v t + t). The semi-implicit correction terms evaluated at time-levels t t) and t are then added to the provisional value of T v t + t), just before the transform back to spectral space. There are corresponding slight changes in the semi-implicit correction terms. The linearised hydrostatic matrix [γ] in 2.31) and 2.32) and 2.39) now operates on T v rather than on T. From the point of view 12 IFS Documentation Cy40r1
13 of the semi-implicit scheme, 2.33) has implicitly been replaced by an equation of the form δ t T v =... β 2 tt[τ]d) 2.53) although as explained above it is not necessary to formulate or compute the missing terms explicitly. Hence, 2.42) is replaced by T + v + β t[τ]d + = R ) and the solution of the semi-implicit equations in spectral space proceeds just as before. This change of spectral variable results in only insignificant changes to a 10-day model forecast, but permits useful economies in the semi-lagrangian version to be described in Chapter Horizontal diffusion and de-aliasing Horizontal diffusion is applied for three reasons: firstly to sufficiently dampen the accumulation of kinetic energy and enstrophy at the smallest resolved scales, secondly, to use as an effective absorber for vertically propagating gravity waves at the top of the model sponge ), and thirdly in the spirit of an eddy viscosity term to represent unresolved sub-gridscale mixing. A fractional step approach is used to implement the horizontal diffusion of vorticity, divergence, and temperature. A simple linear diffusion of order 2r is applied along the hybrid coordinate surfaces: K X = 1) r K 2r X 2.55) where X = ζ, D or q. It is applied in spectral space to the t + t) values such that if X m n is the spectral coefficient of X prior to diffusion, then the diffused value X m n is given by: { X n m = tk nn + 1) a 2 ) r } 1 X m n 2.56) A modified form of 2.56) is also used for the temperature, T, to approximate diffusion on surfaces of constant pressure rather than on the sloping hybrid coordinate surfaces Simmons, 1987). The operational version of the model uses fourth-order horizontal diffusion r = 2) with the diffusion coefficient defined as K = τ 1 a 2 ) r 2.57) NN + 1) and timescale τ = 6 t. Inside the sponge layer this is augmented by an additional function Fn, k, t). In the IFS aliasing will show up as spectral blocking, a build up of energy at the smallest scales that may ultimately lead to instability. For example, quadratic terms i.e. products of prognostic variables such as the pressure gradient term in the momentum equation) cannot be represented accurately beyond 2/3N, as quadratic interactions will alias onto waves beyond 2/3N. A procedure that is devised to systematically eliminate quadratic aliasing makes use of the 2/3 rule. This rule is to filter all waves n > 2/3)N since the quadratic interaction of two wavenumbers n 2/3)N will alias only to wavenumbers that will be purged by the filter. Using a quadratic grid with 3N + 1 gridpoints for N wave modes does this automatically, but with the obvious disadvantage of lowering the effective spectral resolution or, conversely, increasing substantially the number of gridpoints and thus the computational cost. East-west aliasing is mostly eliminated on the reduced linear grid due to the choices made in the grid creation. The number of gridpoints used at each reduced latitude is chosen to be 3N r + 1 for N r waves, see Courtier and Naughton 1994) for details. The term most responsible for the aliasing noise is the pressure gradient term in the momentum equation, although higher-order) aliasing also exists due to the right-hand-side of the thermodynamic equation. In the IFS a de-aliasing procedure is applied where the difference between a filtered pressure gradient term and the unfiltered pressure gradient term is subtracted at every timestep from the right-hand-side of the momentum equation. The filtered term is obtained by computing the rotational and divergent components of the pressure gradient term in spectral space, smoothly truncate only the rotational component at approximately 2/3 of the maximum truncation wavenumber N and transforming the result back to gridpoint space. IFS Documentation Cy40r1 13
14
15 Chapter 3 Semi-Lagrangian formulation Table of contents 3.1 General description 3.2 Finding the departure point 3.3 Semi-Lagrangian discretization 3.4 Comparison with other schemes 3.5 Time-stepping procedure 3.6 Modified semi-lagrangian equations Momentum equations Continuity equation Thermodynamic equation 3.7 Two-time-level semi-lagrangian scheme Formal two-time-level scheme Stable Extrapolation Two-Time-Level Scheme SETTLS) 3.8 Numerical coupling of the physical parametrizations to the dynamical equations SLAVEPP) SLAVEPP scheme Moisture adjustment and first time-step treatment 3.1 GENERAL DESCRIPTION The general form of the model equations is dx dt X + AX) = R L + N 3.1) t where the three-dimensional advection operator A was defined in 2.30), L is the linearized part of R and N is the remainder or non-linear terms. An explicit three-time-level semi-lagrangian treatment of 3.1) is obtained by finding the approximate trajectory, over the time interval [t t, t + t], of a particle which arrives at each grid point x at time t + t). Equation 3.1) is then approximated by X + X = R 0 3.2) 2 t where the superscripts +, 0, and, respectively denote evaluation at the arrival point x, t + t), the mid-point of the trajectory x α, t), and the departure point x 2α, t t). Since the mid-point and the departure point will not in general coincide with model grid points, X and R 0 must be determined by interpolation. It is more economical and, as discussed later, gives better results in some circumstances; see also Tanguay et al., 1992) to evaluate the right-hand side of 3.2) as R 0 = 1 2 {Rx 2α, t) + Rx, t)} 3.3) since only a single interpolation of the combined field Xt t) + trt) at the point x 2α)) is then required in order to determine X +. At ECMWF the three-time-level semi-lagrangian scheme uses 3.3) but the interpolation of R to the departure point is done with the tri-linear interpolation while the interpolation of X is of a higher order. IFS Documentation Cy40r1 15
16 Chapter 3: Semi-Lagrangian formulation The right-hand sides of the time-discretized model equations also contain semi-implicit correction terms, which in the Eulerian model took the form tt X = X + 2X 0 + X) where the superscripts refer to time-levels, and to a single common grid point. In the semi-lagrangian version of the model, the semi-implicit correction terms take the form tt X = Xx, t + t) Xx, t)) + Xx 2α, t t) Xx 2α, t)) 3.4) and again the terms to be evaluated at the departure point x 2α) can be added to other right-hand side terms before interpolation. Notice that the evaluation of tt X, and both ways of evaluating R 0, are all centred in space and time. To obtain accurate results from a semi-lagrangian integration scheme, it is necessary to choose the order of interpolation carefully see for example Staniforth and Côté, 1991). In practice it has been found for the model described here) that linear interpolation is adequate for the right-hand side of the equations, but that cubic interpolation is essential for the advected field evaluated at the departure point. Cubic interpolation in three dimensions is expensive, and fortunately a quasi-cubic interpolation suggested by Courtier) was found to give essentially equivalent results. The technique can be illustrated by twodimensional interpolation on a regular grid. The target point is at x I + α, y J + β). In the first step, four interpolations are performed in the x-direction: linear rather than the usual cubic) interpolations to the points x I + α, y J 1 ) and x I + α, y J+2 ), and cubic interpolations to the points x I + α, y J ) and x I + α, y J+1 ). In the second step, one cubic interpolation is performed in the y-direction, to evaluate the field at the target point. The number of neighbours contributing to the result is reduced from 16 to 12. The generalization to three dimensions is straightforward and results in a significant saving, the number of neighbours being reduced from 64 to 32, and the computation being reduced from 21 one-dimensional cubic interpolations to 7 cubic plus 10 linear one-dimensional interpolations. For the reduced Gaussian grid described in Subsection 2.2.4, the mesh is no longer regular. However, it is easily seen that the extra complication is relatively minor provided that the first step in the interpolation is performed in the λ-direction. The order of the interpolation in the vertical is reduced to linear when the evaluation point lies between the two highest model levels, or between the lowest two model levels. Extrapolation beyond the top or bottom levels is not allowed. All the cubic interpolations, except for the vertical interpolations in the thermodynamic and the momentum equations are quasi-monotone interpolations. That means that, after the interpolation itself, the interpolated value is compared with the values of the interpolated function at the two closest points used in the interpolation. The interpolated value is then restricted to stay within the interval defined by the values at these two points. If it is larger than both of them it is reset to the larger value and if it is smaller than both it is reset to the lower value. 3.2 FINDING THE DEPARTURE POINT Extending the procedure of Robert 1981) to three dimensions, the midpoint x α) and the departure point x 2α) of the trajectory for each arrival point x are found by iteratively solving the equation α = tv x α, t) 3.5) where v in 3.5) is the three-dimensional wind field u, v, η). Since η was never explicitly required in the Eulerian version of the model see 2.18) and 2.19) for the Eulerian discretization of vertical advection), it is necessary to construct this field for the trajectory calculations. As η is already specified at the upper and lower boundaries η = 0, at η = 1 and at η = 1) it would be natural to construct η at the half-levels i.e. vertically staggered with respect to u and v), and indeed a preliminary version of the model was coded that way. However, it is more convenient to hold the three velocity components at the same set of points which also coincide with the arrival points), so the formulation was changed to use η at the full 16 IFS Documentation Cy40r1
17 levels. Thus, the vertical velocity used in 3.5) is defined in the finite-difference version of the model by [ ) ) ] 1 2 η p + η p k η k = 1 2 k+ 1 2 ) 3.6) p where η p/ is already defined by 2.18) and ) p = p k A k /p s + B K = p s 3.7) η k A k /p 0 + B k k In deriving 3.7) we have used 2.11) together with a formal definition of η itself which again was not required by the discretized Eulerian dynamics): where p 0 is a constant pressure chosen to be hpa). k η k+1/2 = A k+1/2 /p 0 + B k+1/2 3.8) The iterative procedure for solving 3.5) is analogous to that used by Ritchie 1991) in a σ-coordinate model. Given an estimate α k) after k iterations, the next iteration is given by α k+1) = tv x α k), t) 3.9) The horizontal components of 3.9) are found taking into account the spherical geometry following Ritchie 1987,1988). The first guess is given by α 0) = tv x, t) 3.10) The calculations can include approximations to the spherical geometry away from the poles, following Ritchie and Beaudoin 1994). In agreement with previous work reviewed by Staniforth and Côté, 1991), little sensitivity was found to the order of interpolation used in the trajectory calculations, and linear interpolation appears to be sufficiently accurate. After providing a first guess via 3.10), only two further iterations were found to be adequate. Once the midpoint x α) of the trajectory has been found, the departure point x 2α) is immediately obtained in the horizontal, the backward extension of the trajectory is along a great circle). In the vertical, if the departure point is then above the first or below the last) mode level, it is modified to lie on the first last) level. In solving 3.9), it is necessary to convert between a displacement in terms of the spatial coordinates and the corresponding displacement in terms of grid lengths, in order to select the correct three-dimensional block of points for the interpolation routine. This is simple in the horizontal, since the mesh length is constant in the λ-direction at a given latitude), and almost constant in the θ-direction. It is more difficult in the vertical, where the grid spacing changes rapidly, and the conversion algorithm for the vertical displacement makes use of an auxiliary grid defined with high uniform resolution. At high horizontal resolutions a positive feedback mechanism, between the computation of the departure point of the trajectories and the solution of the momentum equations, can lead to instability, which results in noisy forecast fields in the winter stratosphere. In order to break the positive feedback loop, a smoothing interpolation is applied to the vertical velocity in the computation of the trajectory. This smoothing interpolation uses the same set of points around the departure point as the cubic interpolation, but the horizontal interpolations are substituted by least squares linear fits to the corresponding four points. The procedure is applied to both the arrival and the departure points of the trajectory. As the procedure is not an interpolatory procedure, the value at the arrival point is substituted by a smoothed value, as is also the case for the value at the departure point. 3.3 SEMI-LAGRANGIAN DISCRETIZATION Following Ritchie 1988, 1991), the momentum equations are integrated in vector form to avoid an instability of the metric term near the poles. Using the notation of 3.2) and defining the horizontal IFS Documentation Cy40r1 17
18 Chapter 3: Semi-Lagrangian formulation wind vector v H = u, v), the semi-lagrangian equivalent of 2.31) and 2.32) is v + H v H 2 t + [fk v H + φ + R dry T v ln p] 0 = P v + K v β 2 tt {[γ]t + R dry T v ln p s } 3.11) where k is the vertically directed unit vector and is the horizontal gradient operator in spherical coordinates. On the right-hand side of 3.11), P v, and K v respectively denote the contributions of the physical parametrization schemes and horizontal diffusion, to be discussed in Section 3.5, while the semi-implicit correction terms are evaluated as in 3.4). For the momentum equations, it was found advantageous to evaluate the time-level t terms [ ] 0 as an average between the values at the departure and arrival points of the trajectory, as in 3.3). The pressure gradient terms are discretized in exactly the same way as for the Eulerian model see Subsection 2.2.1). Since 3.11) is in vector form, it is important to account for the change in the orientation of the coordinate system as the particle follows the trajectory; the manipulations required are as set out by Ritchie 1988) and simplified by Ritchie and Beaudoin 1994). The thermodynamic and moisture equations 2.33) and 2.34) become T + T 2 t { κt v ω 1 + δ 1)q)p q + q 2 t } 0 = P T + K T β 2 tt[τ]d) 3.12) = P q + K q 3.13) In 3.12, the { } 0 term is discretized as in 2.25), and evaluated at the midpoint of the trajectory, while the semi-implicit correction terms are evaluated as in 3.4). The η-coordinate continuity equation 2.5) can be rewritten as ) d p + p D + η ) = ) dt Setting and noting that we also have Combining 3.14) and 3.15) t d dt p = Aη) + Bη)p s ) A = ) A = p s = 0 ) p = B dp s dt + η ) p 3.15) B dp s dt + p D + η p ) = ) Now introducing the vertical discretization, 3.16) becomes dp s B k dt + p kd k + η p ) η p ) = ) k+ 1 2 k 1 2 the vertical discretization of η p/ having been defined in 2.18). Changing the prognostic variable to η p/ gives { p k D k + B k d dt ln p s) + 1 p s η p ) η p ) } = ) k+ 1 2 k 1 2 Combining 3.18) with the discrete definition of η p/ given by 2.18) leads to { } d ln B k dt ln p ps ) s) B k + v k ln p s ) = ) t 18 IFS Documentation Cy40r1
19 where ln p s )/ t is given by 2.14). Noting that NLEV k=1 B k = 1 and including the semi-implicit correction terms, the semi-lagrangian discretization of the continuity equation finally becomes NLEV ln p s ) + = k=1 { ln B k [ln p s ) ps ) + 2 t t + v k ln p s } 0 β t p ref s { NLEV tt j=1 }] p ref j D j ) 3.20) Since there is no vertical advection term in 3.20), no modification is required for the vertically noninterpolating scheme.) It is important to bear in mind that each contribution to the sum on the right-hand side of 3.20) involves a different trajectory. The interpolations for ln p s ) and the semi-implicit correction terms are however two-dimensional, since these quantities are independent of vertical level. The { } 0 term is evaluated at the midpoint of the trajectory, and requires a three-dimensional interpolation. In summary, the semi-lagrangian discretization is given by 3.11) to 3.13) together with 3.20). 3.4 COMPARISON WITH OTHER SCHEMES The semi-lagrangian formulation presented above differs in some respects from those proposed by other authors. Perhaps the most notable difference lies in the treatment of the conversion ω term in the thermodynamic equation 3.12), and of the right-hand side of the continuity equation 3.20). Both involve terms of the form v ln p s, which in our scheme are computed in a purely Eulerian fashion. This may appear somewhat inconsistent; indeed McDonald and Haugen 1993) state as a specific design objective of their scheme that the operator v should not appear explicitly. The alternative approach, also taken by Williamson and Olson 1994), is to use the continuity equation in its semi-implicit semi-lagrangian form to derive a consistent equation for predicting η p/, which can then be used to eliminate the v ln p s terms. In the σ-coordinate system, Bates et al. 1993) and McDonald and Haugen 1992) used a similar approach to derive a prognostic equation for σ. A possible disadvantage of such an approach is that η p/ or σ) then follows an independent evolution, no longer satisfying a diagnostic relationship of the form 2.18). Our Eulerian treatment of the v ln p s, terms avoids this disadvantage and seems to work well, but further study is required to determine whether this difference in formulation is important or not. Another aspect of our semi-lagrangian discretization of the continuity equation, which differs from that in other models, concerns the definition of the trajectory; in our scheme this is the same threedimensional) trajectory as used for the other variables. In the continuous form of the equation, 3.16), the advective part of the total derivative dp/dt may be regarded either as two-dimensional or as threedimensional since p s / is zero). However the vertically discretized form, 3.17), is well-defined only at discrete model levels, implying that for consistency the semi-lagrangian discretization 3.20) should be based on horizontal trajectories. Correcting this inconsistency in our scheme by computing horizontal trajectories for the continuity equation, based on the horizontal wind at each model level, made very little difference to the results, and for the time being we have allowed the inconsistency to remain. As discussed later, in the case of the vertically non-interpolating scheme the modified trajectories are nearly always horizontal anyway.) In the case of the fully interpolating scheme, recomputing the trajectories represents a significant expense; Bates et al. 1993) and McDonald and Haugen 1992) used a simple projection of the three-dimensional trajectory onto the model level of the arrival point. In our model this approach resulted in poor mass conservation, though Bates et al. 1993) came to the opposite conclusion. Again, the importance or otherwise of these differences in formulation is not yet firmly established. 3.5 TIME-STEPPING PROCEDURE The general outline of the time-stepping procedure for the semi-lagrangian version is similar to that described for the Eulerian model in Subsection Thus at the start of a timestep, the model state at IFS Documentation Cy40r1 19
20 Chapter 3: Semi-Lagrangian formulation time t t) is defined by the values of U, V, T, q and ln p s, on the Gaussian grid. To complete the semiimplicit corrections, the t t) values of D, P/ µ and P/ µ are also held on the grid. The model state at time t is defined by the spectral coefficients of ζ, D, T, q and ln p s. Legendre transforms followed by Fourier transforms are then used to compute D, U, V, T, T/ µ, q, q/ µ, ln p s, and ln p s )/ µ at time t on the model grid; additional Fourier transforms are used to compute the corresponding values of T/ λ, q/ λ, and ln p s )/ λ. Since ζ and the horizontal gradients of U and V are no longer required on the model grid, one multi-level Legendre transform and three multi-level Fourier transforms are saved in comparison with the Eulerian version. Since the advection of moisture is handled by the semi-lagrangian discretization 3.13), the horizontal gradients of q are only needed in order to compute the horizontal gradients of the virtual temperature T v which in turn are required to compute the φ term in 3.11)). If T v is chosen as the spectral variable as in Subsection 2.2.8, these gradients are available directly, and there is then no need to transform q/ µ or q/ λ) to the model grid. The number of multi-level Legendre transforms per time-step is further reduced to 10. In passing, all the ingredients are then in place for a semi-lagrangian treatment in which the moisture field is never transformed to spectral space Williamson and Rasch, 1994), and only 8 multilevel Legendre transforms are required per time-step compared with 17 in the original ζ D Eulerian model). After the transforms to the model grid, all the information is then available to compute the trajectories for each grid point, and to evaluate the dynamical contributions to the semi-lagrangian discretization. Ignoring for a moment the contributions of the physical parametrization schemes and of the horizontal diffusion, each equation is either of the form or X + x ) = X x 2α) + t{r 0 x 2α) + R 0 x )} + S x 2α) + S + x ) 3.21) X + x ) = X x 2α) + 2 tr 0 x α) + S x 2α) + S + x ) 3.22) depending on whether the R 0 terms are averaged between the end points of the trajectory or evaluated at the midpoints. In 3.21) and 3.22), the S terms represent the semi-implicit corrections; S includes contributions from time-levels t t) and t, while S + includes contributions from time-levels t and t + t). In the first part of the calculation for equations of the form 3.21), the combined field X + + tr 0 + S is computed, and the value of this combined field at each departure point x 2α) is then found by interpolation. Adding the uninterpolated) value tr 0 results in a provisional value X + at each grid point, incorporating all the terms in 3.21) except for S +. The calculation for equations of the form 3.22) proceeds similarly, except that two interpolations are required, one for X + S at x 2α), and one for 2 tr 0 at x α). A provisional value X + is now available at each grid point for each variable, and is used together with X at the same grid point to compute an Eulerian tendency. These fields and their tendencies are then supplied to the physical parametrization routines, which increment the tendencies with their respective contributions, just as in the Eulerian version except that, to avoid extra interpolations, the S terms have been included in the supplied dynamical tendencies). If T v is chosen as the spectral variable, a provisional value of T + v is computed at this point. The contributions from the S terms at time t are now added in, resulting in a set of equations of the form U + + β t P + a λ = Q ) V + + β t + cos θ P a θ = Q ) T + + β t[τ]d + = Q ) q + = Q ) ln p s ) + + β t[v]d + = Q ) 20 IFS Documentation Cy40r1
21 where the right-hand sides Q 1 Q 5 include all the terms which have been computed on the grid, and T + v replaces T + if T v is the spectral variable. Equations 3.23) to 3.27) have exactly the same form as 2.40) to 2.44) of the Eulerian model and are solved in exactly the same way, by first transforming to spectral space. After finding the new spectral coefficients at time t + t), horizontal diffusion is also applied in the same way as for the Eulerian version. The implementation of the time-filtering for the semi-lagrangian model is identical to that for the Eulerian version, as described in Subsection MODIFIED SEMI-LAGRANGIAN EQUATIONS Momentum equations The momentum equations are treated in vector form see 3.11)). Following Rochas 1990) and Temperton 1997), the Coriolis terms can be incorporated in the semi-lagrangian advection. Thus, the advected variable becomes v H + 2Ω r where Ω is the earth s rotation and r is the radial position vector, while the Coriolis terms are dropped from the right-hand side. As described by Temperton 1997), this reformulation is beneficial provided that the spherical geometry is treated accurately in determining the departure point and in rotating the vectors to account for the change in the orientation of the coordinate system as the particle follows the trajectory. The discretization of the momentum equations in the notation of 3.1) is then X = v H + 2Ω r 3.28) L = [γ]t v + R dry T ref ln p s ) 3.29) N = φ + R dry T v ln p s ) L 3.30) where R dry is the gas constant for dry air, T ref is a reference temperature, φ is geopotential and [γ] is the linearized hydrostatic integration matrix defined in Eq. 2.32) of Ritchie et al. 1995). In component form, 2Ω r is just 2Ωa cos θ, 0) where a is the earth s radius and θ is latitude. Since the latitude of the departure point is known, the term 2Ω r in the advected variable X is computed analytically rather than interpolated. An alternative semi-implicit treatment of the Coriolis terms has also been developed Temperton, 1997) Continuity equation Modelling flow over mountains with a semi-lagrangian integration scheme can lead to problems in the form of a spurious resonant response to steady orographic forcing. The mechanism was clarified by Rivest et al. 1994). Strictly speaking, the problem has little to do with the semi-lagrangian scheme itself; rather, it is a result of the long time steps permitted by the scheme, such that the Courant number becomes greater than 1. Recently, Ritchie and Tanguay 1996) proposed a modification to the semi-lagrangian scheme which alleviates the problem. It turned out that their suggestion was easy to implement in the ECMWF model, and had additional benefits besides improving the forecast of flow over orography. Although Ritchie and Tanguay start by introducing a change of variables in the semi-implicit time discretization, this is not necessary and a slightly different derivation is presented here. The continuity equation is written in the form d dt ln p s) = [RHS] 3.31) where [RHS] represents right-hand-side terms. The total derivative on the left-hand side is discretized in a semi-lagrangian fashion, and the final form of the discretized equation involves a vertical summation. Now split ln p s into two parts: ln p s = l + l 3.32) where the time-independent part l depends on the underlying orography φ s such that l = φ s )/R dry T) 3.33) IFS Documentation Cy40r1 21
IFS DOCUMENTATION CY28r1
 IFS Documentation Cycle CY28r1 IFS DOCUMENTATION CY28r1 III: DYNAMICS AND NUMERICAL PROCEDURES (Operational implementation 9 March 2004) Table of contents Chapter 1. Introduction Chapter 2. Basic equations
IFS Documentation Cycle CY28r1 IFS DOCUMENTATION CY28r1 III: DYNAMICS AND NUMERICAL PROCEDURES (Operational implementation 9 March 2004) Table of contents Chapter 1. Introduction Chapter 2. Basic equations
IFS Documentation Cycle CY25r1 IFS DOCUMENTATION PROCEDURES (CY25R1) (Operational implementation 9 April 2002) Edited by Peter W.
 IFS Documentation Cycle CY25r IFS DOCUMENTATION Part III: DYNAMICS AND NUMERICAL PROCEDURES (CY25R) (Operational implementation 9 April 2002) Edited by Peter W. White (Text written and updated by members
IFS Documentation Cycle CY25r IFS DOCUMENTATION Part III: DYNAMICS AND NUMERICAL PROCEDURES (CY25R) (Operational implementation 9 April 2002) Edited by Peter W. White (Text written and updated by members
PART III: DYNAMICS AND NUMERICAL PROCEDURES
 IFS DOCUMENTATION Cy43r1 Operational implementation 22 Nov 2016 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations and discretisation
IFS DOCUMENTATION Cy43r1 Operational implementation 22 Nov 2016 PART III: DYNAMICS AND NUMERICAL PROCEDURES Table of contents Chapter 1 Chapter 2 Chapter 3 References Introduction Basic equations and discretisation
Chapter 6. Semi-Lagrangian Methods
 Chapter 6. Semi-Lagrangian Methods References: Durran Chapter 6. Review article by Staniford and Cote (1991) MWR, 119, 2206-2223. 6.1. Introduction Semi-Lagrangian (S-L for short) methods, also called
Chapter 6. Semi-Lagrangian Methods References: Durran Chapter 6. Review article by Staniford and Cote (1991) MWR, 119, 2206-2223. 6.1. Introduction Semi-Lagrangian (S-L for short) methods, also called
Interpolation of gridded data using Geostrophic Balance. Lennon O Naraigh *
 Interpolation of gridded data using Geostrophic Balance Lennon O Naraigh * Date: 6 th September 2004 Abstract: In this report, a method of interpolating data from the grid of a global climate model (GCM)
Interpolation of gridded data using Geostrophic Balance Lennon O Naraigh * Date: 6 th September 2004 Abstract: In this report, a method of interpolating data from the grid of a global climate model (GCM)
A mass-conservative version of the semi- Lagrangian semi-implicit HIRLAM using Lagrangian vertical coordinates
 A mass-conservative version of the semi- Lagrangian semi-implicit HIRLAM using Lagrangian vertical coordinates Peter Hjort Lauritzen Atmospheric Modeling & Predictability Section National Center for Atmospheric
A mass-conservative version of the semi- Lagrangian semi-implicit HIRLAM using Lagrangian vertical coordinates Peter Hjort Lauritzen Atmospheric Modeling & Predictability Section National Center for Atmospheric
Two dynamical core formulation flaws exposed by a. baroclinic instability test case
 Two dynamical core formulation flaws exposed by a baroclinic instability test case David L. Williamson, Jerry G. Olson National Center for Atmospheric Research, Boulder, CO, USA Christiane Jablonowski
Two dynamical core formulation flaws exposed by a baroclinic instability test case David L. Williamson, Jerry G. Olson National Center for Atmospheric Research, Boulder, CO, USA Christiane Jablonowski
Semi-Lagrangian Advection. The Basic Idea. x 1.
 3.2.6. Semi-Lagrangian Advection We have studied the Eulerian leapfrog scheme and found it to be conditionally stable. The criterion for stability was the CFL condition µ c t x 1. For high spatial resolution
3.2.6. Semi-Lagrangian Advection We have studied the Eulerian leapfrog scheme and found it to be conditionally stable. The criterion for stability was the CFL condition µ c t x 1. For high spatial resolution
Global Numerical Weather Predictions and the semi-lagrangian semi-implicit dynamical 1 / 27. ECMWF forecast model
 Global Numerical Weather Predictions and the semi-lagrangian semi-implicit dynamical core of the ECMWF forecast model Michail Diamantakis ECMWF Symposium on Modelling and Computations in Atmospheric Sciences
Global Numerical Weather Predictions and the semi-lagrangian semi-implicit dynamical core of the ECMWF forecast model Michail Diamantakis ECMWF Symposium on Modelling and Computations in Atmospheric Sciences
Regional Cooperation for Limited Area Modeling in Central Europe. Dynamics in LACE. Petra Smolíková thanks to many colleagues
 Dynamics in LACE Petra Smolíková thanks to many colleagues Outline 1 1. VFE NH Design of vertical finite elements scheme for NH version of the model 2. SL scheme Application of ENO technique to SL interpolations
Dynamics in LACE Petra Smolíková thanks to many colleagues Outline 1 1. VFE NH Design of vertical finite elements scheme for NH version of the model 2. SL scheme Application of ENO technique to SL interpolations
An explicit and conservative remapping strategy for semi-lagrangian advection
 An explicit and conservative remapping strategy for semi-lagrangian advection Sebastian Reich Universität Potsdam, Potsdam, Germany January 17, 2007 Abstract A conservative semi-lagrangian advection scheme
An explicit and conservative remapping strategy for semi-lagrangian advection Sebastian Reich Universität Potsdam, Potsdam, Germany January 17, 2007 Abstract A conservative semi-lagrangian advection scheme
Numerical Methods for (Time-Dependent) HJ PDEs
 Numerical Methods for (Time-Dependent) HJ PDEs Ian Mitchell Department of Computer Science The University of British Columbia research supported by National Science and Engineering Research Council of
Numerical Methods for (Time-Dependent) HJ PDEs Ian Mitchell Department of Computer Science The University of British Columbia research supported by National Science and Engineering Research Council of
ATM 298, Spring 2013 Lecture 4 Numerical Methods: Horizontal DiscreDzaDons April 10, Paul A. Ullrich (HH 251)
 ATM 298, Spring 2013 Lecture 4 Numerical Methods: Horizontal DiscreDzaDons April 10, 2013 Paul A. Ullrich (HH 251) paullrich@ucdavis.edu Outline 1. Introduction / Motivation 2. Finite Difference Methods
ATM 298, Spring 2013 Lecture 4 Numerical Methods: Horizontal DiscreDzaDons April 10, 2013 Paul A. Ullrich (HH 251) paullrich@ucdavis.edu Outline 1. Introduction / Motivation 2. Finite Difference Methods
Impact of Consistent Semi-Lagrangian Trajectory Calculations on Numerical Weather Prediction Performance
 OCTOBER 2017 H U S A I N A N D G I R A R D 4127 Impact of Consistent Semi-Lagrangian Trajectory Calculations on Numerical Weather Prediction Performance SYED ZAHID HUSAIN AND CLAUDE GIRARD Atmospheric
OCTOBER 2017 H U S A I N A N D G I R A R D 4127 Impact of Consistent Semi-Lagrangian Trajectory Calculations on Numerical Weather Prediction Performance SYED ZAHID HUSAIN AND CLAUDE GIRARD Atmospheric
An explicit and conservative remapping strategy for semi-lagrangian advection
 ATMOSPHERIC SCIENCE LETTERS Atmos. Sci. Let. 8: 58 63 (2007) Published online 22 May 2007 in Wiley InterScience (www.interscience.wiley.com).151 An explicit and conservative remapping strategy for semi-lagrangian
ATMOSPHERIC SCIENCE LETTERS Atmos. Sci. Let. 8: 58 63 (2007) Published online 22 May 2007 in Wiley InterScience (www.interscience.wiley.com).151 An explicit and conservative remapping strategy for semi-lagrangian
CS205b/CME306. Lecture 9
 CS205b/CME306 Lecture 9 1 Convection Supplementary Reading: Osher and Fedkiw, Sections 3.3 and 3.5; Leveque, Sections 6.7, 8.3, 10.2, 10.4. For a reference on Newton polynomial interpolation via divided
CS205b/CME306 Lecture 9 1 Convection Supplementary Reading: Osher and Fedkiw, Sections 3.3 and 3.5; Leveque, Sections 6.7, 8.3, 10.2, 10.4. For a reference on Newton polynomial interpolation via divided
Recent research for dynamical cores of nonhydrostatic, deep-atmosphere, unified models
 Recent research for dynamical cores of nonhydrostatic, deep-atmosphere, unified models Andrew Staniforth and Nigel Wood Met Office, FitzRoy Road, Exeter EX1 3PB, United Kingdom Andrew.Staniforth@metoffice.gov.uk,
Recent research for dynamical cores of nonhydrostatic, deep-atmosphere, unified models Andrew Staniforth and Nigel Wood Met Office, FitzRoy Road, Exeter EX1 3PB, United Kingdom Andrew.Staniforth@metoffice.gov.uk,
M.Sc. in Computational Science. Fundamentals of Atmospheric Modelling
 M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
M.Sc. in Computational Science Fundamentals of Atmospheric Modelling Peter Lynch, Met Éireann Mathematical Computation Laboratory (Opp. Room 30) Dept. of Maths. Physics, UCD, Belfield. January April, 2004.
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Computation in Astrophysics Seminar (Spring 2006) L. J. Dursi
 Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Lagrangian methods and Smoothed Particle Hydrodynamics (SPH) Eulerian Grid Methods The methods covered so far in this course use an Eulerian grid: Prescribed coordinates In `lab frame' Fluid elements flow
Multi-Domain Pattern. I. Problem. II. Driving Forces. III. Solution
 Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
Multi-Domain Pattern I. Problem The problem represents computations characterized by an underlying system of mathematical equations, often simulating behaviors of physical objects through discrete time
PTE 519 Lecture Note Finite Difference Approximation (Model)
 PTE 519 Lecture Note 3 3.0 Finite Difference Approximation (Model) In this section of the lecture material, the focus is to define the terminology and to summarize the basic facts. The basic idea of any
PTE 519 Lecture Note 3 3.0 Finite Difference Approximation (Model) In this section of the lecture material, the focus is to define the terminology and to summarize the basic facts. The basic idea of any
The semi-lagrangian technique: current status and future 4 September developments / 42
 The semi-lagrangian technique: current status and future developments Michail Diamantakis ECMWF 4 September 2013 (thanks to: Adrian Simmons, Niels Borman and Richard Forbes) The semi-lagrangian technique:
The semi-lagrangian technique: current status and future developments Michail Diamantakis ECMWF 4 September 2013 (thanks to: Adrian Simmons, Niels Borman and Richard Forbes) The semi-lagrangian technique:
A Spectral Element Eulerian-Lagrangian Atmospheric Model (SEELAM)
 A Spectral Element Eulerian-Lagrangian Atmospheric Model SEELAM Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943 E-mail: giraldo@nrlmry.navy.mil A new dynamical core for numerical weather
A Spectral Element Eulerian-Lagrangian Atmospheric Model SEELAM Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943 E-mail: giraldo@nrlmry.navy.mil A new dynamical core for numerical weather
Advanced Numerical Methods for Numerical Weather Prediction
 Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Edge and local feature detection - 2. Importance of edge detection in computer vision
 Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
Edge and local feature detection Gradient based edge detection Edge detection by function fitting Second derivative edge detectors Edge linking and the construction of the chain graph Edge and local feature
Parameterization of triangular meshes
 Parameterization of triangular meshes Michael S. Floater November 10, 2009 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to
Parameterization of triangular meshes Michael S. Floater November 10, 2009 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to
A Test Suite for GCMs: An Intercomparison of 11 Dynamical Cores
 A Test Suite for GCMs: An Intercomparison of 11 Dynamical Cores Christiane Jablonowski 1, Peter Lauritzen 2, Mark 3 Taylor, Ram Nair 2 1 University of Michigan, 2 National Center for Atmospheric Research,
A Test Suite for GCMs: An Intercomparison of 11 Dynamical Cores Christiane Jablonowski 1, Peter Lauritzen 2, Mark 3 Taylor, Ram Nair 2 1 University of Michigan, 2 National Center for Atmospheric Research,
Physics Tutorial 2: Numerical Integration Methods
 Physics Tutorial 2: Numerical Integration Methods Summary The concept of numerically solving differential equations is explained, and applied to real time gaming simulation. Some objects are moved in a
Physics Tutorial 2: Numerical Integration Methods Summary The concept of numerically solving differential equations is explained, and applied to real time gaming simulation. Some objects are moved in a
Optimised corrections for finite-difference modelling in two dimensions
 Optimized corrections for 2D FD modelling Optimised corrections for finite-difference modelling in two dimensions Peter M. Manning and Gary F. Margrave ABSTRACT Finite-difference two-dimensional correction
Optimized corrections for 2D FD modelling Optimised corrections for finite-difference modelling in two dimensions Peter M. Manning and Gary F. Margrave ABSTRACT Finite-difference two-dimensional correction
Advanced Numerical Methods for Numerical Weather Prediction
 Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
Advanced Numerical Methods for Numerical Weather Prediction Francis X. Giraldo Naval Research Laboratory Monterey, CA 93943-5502 phone: (831) 656-4882 fax: (831) 656-4769 e-mail: giraldo@nrlmry.navy.mil
University of Reading. Discretization On Non-uniform Meshes: Tests solving shallow-water equations
 University of Reading School of Mathematics, Meteorology and Physics Discretization On Non-uniform Meshes: Tests solving shallow-water equations By FAWZI B ALBUSAIDI August 2008 This dissertation is submitted
University of Reading School of Mathematics, Meteorology and Physics Discretization On Non-uniform Meshes: Tests solving shallow-water equations By FAWZI B ALBUSAIDI August 2008 This dissertation is submitted
Solving a Two Dimensional Unsteady-State. Flow Problem by Meshless Method
 Applied Mathematical Sciences, Vol. 7, 203, no. 49, 242-2428 HIKARI Ltd, www.m-hikari.com Solving a Two Dimensional Unsteady-State Flow Problem by Meshless Method A. Koomsubsiri * and D. Sukawat Department
Applied Mathematical Sciences, Vol. 7, 203, no. 49, 242-2428 HIKARI Ltd, www.m-hikari.com Solving a Two Dimensional Unsteady-State Flow Problem by Meshless Method A. Koomsubsiri * and D. Sukawat Department
The new ECMWF interpolation package MIR
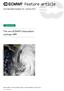 from Newsletter Number 152 Summer 2017 COMPUTING The new ECMWF interpolation package MIR Hurricane Patricia off the coast of Mexico on 23 October 2015 ( 2015 EUMETSAT) doi:10.21957/h20rz8 This article
from Newsletter Number 152 Summer 2017 COMPUTING The new ECMWF interpolation package MIR Hurricane Patricia off the coast of Mexico on 23 October 2015 ( 2015 EUMETSAT) doi:10.21957/h20rz8 This article
J. Vira, M. Sofiev SILAM winter school, February 2013, FMI
 Numerical aspects of the advection-diffusion equation J. Vira, M. Sofiev SILAM winter school, February 2013, FMI Outline Intro Some common requirements for numerical transport schemes Lagrangian approach
Numerical aspects of the advection-diffusion equation J. Vira, M. Sofiev SILAM winter school, February 2013, FMI Outline Intro Some common requirements for numerical transport schemes Lagrangian approach
How to run OpenIFS as a shallow water model
 How to run OpenIFS as a shallow water model OpenIFS includes a number of idealised configurations. In this article we explain how to: setup and run a shallow-water model set idealized (e.g. Rossby-Haurwitz
How to run OpenIFS as a shallow water model OpenIFS includes a number of idealised configurations. In this article we explain how to: setup and run a shallow-water model set idealized (e.g. Rossby-Haurwitz
3-D Wind Field Simulation over Complex Terrain
 3-D Wind Field Simulation over Complex Terrain University Institute for Intelligent Systems and Numerical Applications in Engineering Congreso de la RSME 2015 Soluciones Matemáticas e Innovación en la
3-D Wind Field Simulation over Complex Terrain University Institute for Intelligent Systems and Numerical Applications in Engineering Congreso de la RSME 2015 Soluciones Matemáticas e Innovación en la
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Diffusion Wavelets for Natural Image Analysis
 Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
Diffusion Wavelets for Natural Image Analysis Tyrus Berry December 16, 2011 Contents 1 Project Description 2 2 Introduction to Diffusion Wavelets 2 2.1 Diffusion Multiresolution............................
CS321 Introduction To Numerical Methods
 CS3 Introduction To Numerical Methods Fuhua (Frank) Cheng Department of Computer Science University of Kentucky Lexington KY 456-46 - - Table of Contents Errors and Number Representations 3 Error Types
CS3 Introduction To Numerical Methods Fuhua (Frank) Cheng Department of Computer Science University of Kentucky Lexington KY 456-46 - - Table of Contents Errors and Number Representations 3 Error Types
Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models
 Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models B Y CHRISTIANE JABLONOWSKI 1, ROBERT C. OEHMKE 2, QUENTIN F. STOUT 1 1 University of Michigan, 2455 Hayward
Block-structured Adaptive Meshes and Reduced Grids for Atmospheric General Circulation Models B Y CHRISTIANE JABLONOWSKI 1, ROBERT C. OEHMKE 2, QUENTIN F. STOUT 1 1 University of Michigan, 2455 Hayward
Skåne University Hospital Lund, Lund, Sweden 2 Deparment of Numerical Analysis, Centre for Mathematical Sciences, Lund University, Lund, Sweden
 Volume Tracking: A New Method for Visualization of Intracardiac Blood Flow from Three-Dimensional, Time-Resolved, Three-Component Magnetic Resonance Velocity Mapping Appendix: Theory and Numerical Implementation
Volume Tracking: A New Method for Visualization of Intracardiac Blood Flow from Three-Dimensional, Time-Resolved, Three-Component Magnetic Resonance Velocity Mapping Appendix: Theory and Numerical Implementation
Commutative filters for LES on unstructured meshes
 Center for Turbulence Research Annual Research Briefs 1999 389 Commutative filters for LES on unstructured meshes By Alison L. Marsden AND Oleg V. Vasilyev 1 Motivation and objectives Application of large
Center for Turbulence Research Annual Research Briefs 1999 389 Commutative filters for LES on unstructured meshes By Alison L. Marsden AND Oleg V. Vasilyev 1 Motivation and objectives Application of large
Application of ENO technique to semi-lagrangian interpolations. RC LACE stay report Scientific supervisors: Petra Smolíková and Ján Mašek
 Application of ENO technique to semi-lagrangian interpolations RC LACE stay report Scientific supervisors: Petra Smolíková and Ján Mašek Alexandra Crăciun NMA, Romania CHMI, Prague 09.05-03.06.2016 1 Introduction
Application of ENO technique to semi-lagrangian interpolations RC LACE stay report Scientific supervisors: Petra Smolíková and Ján Mašek Alexandra Crăciun NMA, Romania CHMI, Prague 09.05-03.06.2016 1 Introduction
Parameterization. Michael S. Floater. November 10, 2011
 Parameterization Michael S. Floater November 10, 2011 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to generate from point
Parameterization Michael S. Floater November 10, 2011 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to generate from point
An Orthogonal Curvilinear Terrain-Following Coordinate for Atmospheric Models!
 Solution of Partial Differential Equations on the Sphere! An Orthogonal Curvilinear Terrain-Following Coordinate for Atmospheric Models! Yiyuan Li 1, Bin Wang 1, Donghai Wang 2! 1. Institute of Atmospheric
Solution of Partial Differential Equations on the Sphere! An Orthogonal Curvilinear Terrain-Following Coordinate for Atmospheric Models! Yiyuan Li 1, Bin Wang 1, Donghai Wang 2! 1. Institute of Atmospheric
. Tutorial Class V 3-10/10/2012 First Order Partial Derivatives;...
 Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
C. A. D. Fraga Filho 1,2, D. F. Pezzin 1 & J. T. A. Chacaltana 1. Abstract
 Advanced Computational Methods and Experiments in Heat Transfer XIII 15 A numerical study of heat diffusion using the Lagrangian particle SPH method and the Eulerian Finite-Volume method: analysis of convergence,
Advanced Computational Methods and Experiments in Heat Transfer XIII 15 A numerical study of heat diffusion using the Lagrangian particle SPH method and the Eulerian Finite-Volume method: analysis of convergence,
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
Adarsh Krishnamurthy (cs184-bb) Bela Stepanova (cs184-bs)
 OBJECTIVE FLUID SIMULATIONS Adarsh Krishnamurthy (cs184-bb) Bela Stepanova (cs184-bs) The basic objective of the project is the implementation of the paper Stable Fluids (Jos Stam, SIGGRAPH 99). The final
OBJECTIVE FLUID SIMULATIONS Adarsh Krishnamurthy (cs184-bb) Bela Stepanova (cs184-bs) The basic objective of the project is the implementation of the paper Stable Fluids (Jos Stam, SIGGRAPH 99). The final
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras. Lecture - 36
 Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Lecture - 36 In last class, we have derived element equations for two d elasticity problems
Finite Element Analysis Prof. Dr. B. N. Rao Department of Civil Engineering Indian Institute of Technology, Madras Lecture - 36 In last class, we have derived element equations for two d elasticity problems
Table of contents for: Waves and Mean Flows by Oliver Bühler Cambridge University Press 2009 Monographs on Mechanics. Contents.
 Table of contents for: Waves and Mean Flows by Oliver Bühler Cambridge University Press 2009 Monographs on Mechanics. Preface page 2 Part I Fluid Dynamics and Waves 7 1 Elements of fluid dynamics 9 1.1
Table of contents for: Waves and Mean Flows by Oliver Bühler Cambridge University Press 2009 Monographs on Mechanics. Preface page 2 Part I Fluid Dynamics and Waves 7 1 Elements of fluid dynamics 9 1.1
Trajectory Calculations for Spherical Geodesic Grids in Cartesian Space
 See discussions, stats, author profiles for this publication at: http://www.researchgate.net/publication/4961110 Trajectory Calculations for Spherical Geodesic Grids in Cartesian Space ARTICLE in MONTHLY
See discussions, stats, author profiles for this publication at: http://www.researchgate.net/publication/4961110 Trajectory Calculations for Spherical Geodesic Grids in Cartesian Space ARTICLE in MONTHLY
Continued Investigation of Small-Scale Air-Sea Coupled Dynamics Using CBLAST Data
 Continued Investigation of Small-Scale Air-Sea Coupled Dynamics Using CBLAST Data Dick K.P. Yue Center for Ocean Engineering Department of Mechanical Engineering Massachusetts Institute of Technology Cambridge,
Continued Investigation of Small-Scale Air-Sea Coupled Dynamics Using CBLAST Data Dick K.P. Yue Center for Ocean Engineering Department of Mechanical Engineering Massachusetts Institute of Technology Cambridge,
Driven Cavity Example
 BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
BMAppendixI.qxd 11/14/12 6:55 PM Page I-1 I CFD Driven Cavity Example I.1 Problem One of the classic benchmarks in CFD is the driven cavity problem. Consider steady, incompressible, viscous flow in a square
Parallel Adaptive Tsunami Modelling with Triangular Discontinuous Galerkin Schemes
 Parallel Adaptive Tsunami Modelling with Triangular Discontinuous Galerkin Schemes Stefan Vater 1 Kaveh Rahnema 2 Jörn Behrens 1 Michael Bader 2 1 Universität Hamburg 2014 PDES Workshop 2 TU München Partial
Parallel Adaptive Tsunami Modelling with Triangular Discontinuous Galerkin Schemes Stefan Vater 1 Kaveh Rahnema 2 Jörn Behrens 1 Michael Bader 2 1 Universität Hamburg 2014 PDES Workshop 2 TU München Partial
1.2 Numerical Solutions of Flow Problems
 1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
1.2 Numerical Solutions of Flow Problems DIFFERENTIAL EQUATIONS OF MOTION FOR A SIMPLIFIED FLOW PROBLEM Continuity equation for incompressible flow: 0 Momentum (Navier-Stokes) equations for a Newtonian
Realtime Water Simulation on GPU. Nuttapong Chentanez NVIDIA Research
 1 Realtime Water Simulation on GPU Nuttapong Chentanez NVIDIA Research 2 3 Overview Approaches to realtime water simulation Hybrid shallow water solver + particles Hybrid 3D tall cell water solver + particles
1 Realtime Water Simulation on GPU Nuttapong Chentanez NVIDIA Research 2 3 Overview Approaches to realtime water simulation Hybrid shallow water solver + particles Hybrid 3D tall cell water solver + particles
Introduction to ANSYS CFX
 Workshop 03 Fluid flow around the NACA0012 Airfoil 16.0 Release Introduction to ANSYS CFX 2015 ANSYS, Inc. March 13, 2015 1 Release 16.0 Workshop Description: The flow simulated is an external aerodynamics
Workshop 03 Fluid flow around the NACA0012 Airfoil 16.0 Release Introduction to ANSYS CFX 2015 ANSYS, Inc. March 13, 2015 1 Release 16.0 Workshop Description: The flow simulated is an external aerodynamics
Post Processing, Visualization, and Sample Output
 Chapter 7 Post Processing, Visualization, and Sample Output Upon successful execution of an ADCIRC run, a number of output files will be created. Specifically which files are created depends upon how the
Chapter 7 Post Processing, Visualization, and Sample Output Upon successful execution of an ADCIRC run, a number of output files will be created. Specifically which files are created depends upon how the
The 3D DSC in Fluid Simulation
 The 3D DSC in Fluid Simulation Marek K. Misztal Informatics and Mathematical Modelling, Technical University of Denmark mkm@imm.dtu.dk DSC 2011 Workshop Kgs. Lyngby, 26th August 2011 Governing Equations
The 3D DSC in Fluid Simulation Marek K. Misztal Informatics and Mathematical Modelling, Technical University of Denmark mkm@imm.dtu.dk DSC 2011 Workshop Kgs. Lyngby, 26th August 2011 Governing Equations
Long time integrations of a convective PDE on the sphere by RBF collocation
 Long time integrations of a convective PDE on the sphere by RBF collocation Bengt Fornberg and Natasha Flyer University of Colorado NCAR Department of Applied Mathematics Institute for Mathematics Applied
Long time integrations of a convective PDE on the sphere by RBF collocation Bengt Fornberg and Natasha Flyer University of Colorado NCAR Department of Applied Mathematics Institute for Mathematics Applied
Measuring Lengths The First Fundamental Form
 Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
An inherently mass-conservative semi-implicit semi-lagrangian model. Peter Hjort Lauritzen
 An inherently mass-conservative semi-implicit semi-lagrangian model by Peter Hjort Lauritzen ph.d. thesis Department of Geophysics University of Copenhagen Denmark September, 2005 Abstract A locally mass-conservative
An inherently mass-conservative semi-implicit semi-lagrangian model by Peter Hjort Lauritzen ph.d. thesis Department of Geophysics University of Copenhagen Denmark September, 2005 Abstract A locally mass-conservative
cuibm A GPU Accelerated Immersed Boundary Method
 cuibm A GPU Accelerated Immersed Boundary Method S. K. Layton, A. Krishnan and L. A. Barba Corresponding author: labarba@bu.edu Department of Mechanical Engineering, Boston University, Boston, MA, 225,
cuibm A GPU Accelerated Immersed Boundary Method S. K. Layton, A. Krishnan and L. A. Barba Corresponding author: labarba@bu.edu Department of Mechanical Engineering, Boston University, Boston, MA, 225,
Conservative high order semi-lagrangian finite difference WENO methods for advection in incompressible flow. Abstract
 Conservative high order semi-lagrangian finite difference WENO methods for advection in incompressible flow Jing-Mei Qiu 1 and Chi-Wang Shu Abstract In this paper, we propose a semi-lagrangian finite difference
Conservative high order semi-lagrangian finite difference WENO methods for advection in incompressible flow Jing-Mei Qiu 1 and Chi-Wang Shu Abstract In this paper, we propose a semi-lagrangian finite difference
The Immersed Interface Method
 The Immersed Interface Method Numerical Solutions of PDEs Involving Interfaces and Irregular Domains Zhiiin Li Kazufumi Ito North Carolina State University Raleigh, North Carolina Society for Industrial
The Immersed Interface Method Numerical Solutions of PDEs Involving Interfaces and Irregular Domains Zhiiin Li Kazufumi Ito North Carolina State University Raleigh, North Carolina Society for Industrial
Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative
 Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative Pedro S. Peixoto College of Engineering, Mathematics and Physical Sciences - University of Exeter Instituto
Accuracy analysis of mimetic finite volume operators on geodesic grids and a consistent alternative Pedro S. Peixoto College of Engineering, Mathematics and Physical Sciences - University of Exeter Instituto
Chapter 18. Geometric Operations
 Chapter 18 Geometric Operations To this point, the image processing operations have computed the gray value (digital count) of the output image pixel based on the gray values of one or more input pixels;
Chapter 18 Geometric Operations To this point, the image processing operations have computed the gray value (digital count) of the output image pixel based on the gray values of one or more input pixels;
Chapter 1 - Basic Equations
 2.20 Marine Hydrodynamics, Fall 2017 Lecture 2 Copyright c 2017 MIT - Department of Mechanical Engineering, All rights reserved. 2.20 Marine Hydrodynamics Lecture 2 Chapter 1 - Basic Equations 1.1 Description
2.20 Marine Hydrodynamics, Fall 2017 Lecture 2 Copyright c 2017 MIT - Department of Mechanical Engineering, All rights reserved. 2.20 Marine Hydrodynamics Lecture 2 Chapter 1 - Basic Equations 1.1 Description
COMPUTER AIDED ENGINEERING DESIGN (BFF2612)
 COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
COMPUTER AIDED ENGINEERING DESIGN (BFF2612) BASIC MATHEMATICAL CONCEPTS IN CAED by Dr. Mohd Nizar Mhd Razali Faculty of Manufacturing Engineering mnizar@ump.edu.my COORDINATE SYSTEM y+ y+ z+ z+ x+ RIGHT
CS 450 Numerical Analysis. Chapter 7: Interpolation
 Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Lecture slides based on the textbook Scientific Computing: An Introductory Survey by Michael T. Heath, copyright c 2018 by the Society for Industrial and Applied Mathematics. http://www.siam.org/books/cl80
Supplemental Material Deep Fluids: A Generative Network for Parameterized Fluid Simulations
 Supplemental Material Deep Fluids: A Generative Network for Parameterized Fluid Simulations 1. Extended Results 1.1. 2-D Smoke Plume Additional results for the 2-D smoke plume example are shown in Figures
Supplemental Material Deep Fluids: A Generative Network for Parameterized Fluid Simulations 1. Extended Results 1.1. 2-D Smoke Plume Additional results for the 2-D smoke plume example are shown in Figures
3. Lifting Scheme of Wavelet Transform
 3. Lifting Scheme of Wavelet Transform 3. Introduction The Wim Sweldens 76 developed the lifting scheme for the construction of biorthogonal wavelets. The main feature of the lifting scheme is that all
3. Lifting Scheme of Wavelet Transform 3. Introduction The Wim Sweldens 76 developed the lifting scheme for the construction of biorthogonal wavelets. The main feature of the lifting scheme is that all
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CONFORMAL MAPPING POTENTIAL FLOW AROUND A WINGSECTION USED AS A TEST CASE FOR THE INVISCID PART OF RANS SOLVERS
 European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006 P. Wesseling, E. Oñate and J. Périaux (Eds) c TU Delft, The Netherlands, 2006 CONFORMAL MAPPING POTENTIAL FLOW AROUND A WINGSECTION
European Conference on Computational Fluid Dynamics ECCOMAS CFD 2006 P. Wesseling, E. Oñate and J. Périaux (Eds) c TU Delft, The Netherlands, 2006 CONFORMAL MAPPING POTENTIAL FLOW AROUND A WINGSECTION
Conservative Semi-Lagrangian solvers on mapped meshes
 Conservative Semi-Lagrangian solvers on mapped meshes M. Mehrenberger, M. Bergot, V. Grandgirard, G. Latu, H. Sellama, E. Sonnendrücker Université de Strasbourg, INRIA Grand Est, Projet CALVI, ANR GYPSI
Conservative Semi-Lagrangian solvers on mapped meshes M. Mehrenberger, M. Bergot, V. Grandgirard, G. Latu, H. Sellama, E. Sonnendrücker Université de Strasbourg, INRIA Grand Est, Projet CALVI, ANR GYPSI
SLICE-3D: A three-dimensional conservative semi-lagrangian scheme for transport problems. Mohamed Zerroukat. Met Office, Exeter, UK
 SLICE-D: A three-dimensional conservative semi-lagrangian scheme for transport problems Mohamed Zerroukat (Nigel wood & Andrew Staniforth) Met Office, Exeter, UK SRNWP-NT, Zagreb, c Crown Copyright Content
SLICE-D: A three-dimensional conservative semi-lagrangian scheme for transport problems Mohamed Zerroukat (Nigel wood & Andrew Staniforth) Met Office, Exeter, UK SRNWP-NT, Zagreb, c Crown Copyright Content
Overview of Traditional Surface Tracking Methods
 Liquid Simulation With Mesh-Based Surface Tracking Overview of Traditional Surface Tracking Methods Matthias Müller Introduction Research lead of NVIDIA PhysX team PhysX GPU acc. Game physics engine www.nvidia.com\physx
Liquid Simulation With Mesh-Based Surface Tracking Overview of Traditional Surface Tracking Methods Matthias Müller Introduction Research lead of NVIDIA PhysX team PhysX GPU acc. Game physics engine www.nvidia.com\physx
Using a Single Rotating Reference Frame
 Tutorial 9. Using a Single Rotating Reference Frame Introduction This tutorial considers the flow within a 2D, axisymmetric, co-rotating disk cavity system. Understanding the behavior of such flows is
Tutorial 9. Using a Single Rotating Reference Frame Introduction This tutorial considers the flow within a 2D, axisymmetric, co-rotating disk cavity system. Understanding the behavior of such flows is
A METHOD TO MODELIZE THE OVERALL STIFFNESS OF A BUILDING IN A STICK MODEL FITTED TO A 3D MODEL
 A METHOD TO MODELIE THE OVERALL STIFFNESS OF A BUILDING IN A STICK MODEL FITTED TO A 3D MODEL Marc LEBELLE 1 SUMMARY The aseismic design of a building using the spectral analysis of a stick model presents
A METHOD TO MODELIE THE OVERALL STIFFNESS OF A BUILDING IN A STICK MODEL FITTED TO A 3D MODEL Marc LEBELLE 1 SUMMARY The aseismic design of a building using the spectral analysis of a stick model presents
Modeling icing using cartesian grids, penalization & level sets
 Introduction State of the art The proposed approach Proof of concept Modeling icing using cartesian grids, penalization & level sets Héloïse Beaugendre IMB Institut de Mathématiques de Bordeaux - INRIA
Introduction State of the art The proposed approach Proof of concept Modeling icing using cartesian grids, penalization & level sets Héloïse Beaugendre IMB Institut de Mathématiques de Bordeaux - INRIA
21. Efficient and fast numerical methods to compute fluid flows in the geophysical β plane
 12th International Conference on Domain Decomposition Methods Editors: Tony Chan, Takashi Kako, Hideo Kawarada, Olivier Pironneau, c 2001 DDM.org 21. Efficient and fast numerical methods to compute fluid
12th International Conference on Domain Decomposition Methods Editors: Tony Chan, Takashi Kako, Hideo Kawarada, Olivier Pironneau, c 2001 DDM.org 21. Efficient and fast numerical methods to compute fluid
Math D Printing Group Final Report
 Math 4020 3D Printing Group Final Report Gayan Abeynanda Brandon Oubre Jeremy Tillay Dustin Wright Wednesday 29 th April, 2015 Introduction 3D printers are a growing technology, but there is currently
Math 4020 3D Printing Group Final Report Gayan Abeynanda Brandon Oubre Jeremy Tillay Dustin Wright Wednesday 29 th April, 2015 Introduction 3D printers are a growing technology, but there is currently
Water. Notes. Free surface. Boundary conditions. This week: extend our 3D flow solver to full 3D water We need to add two things:
 Notes Added a 2D cross-section viewer for assignment 6 Not great, but an alternative if the full 3d viewer isn t working for you Warning about the formulas in Fedkiw, Stam, and Jensen - maybe not right
Notes Added a 2D cross-section viewer for assignment 6 Not great, but an alternative if the full 3d viewer isn t working for you Warning about the formulas in Fedkiw, Stam, and Jensen - maybe not right
 Set No. 1 IV B.Tech. I Semester Regular Examinations, November 2010 FINITE ELEMENT METHODS (Mechanical Engineering) Time: 3 Hours Max Marks: 80 Answer any FIVE Questions All Questions carry equal marks
Set No. 1 IV B.Tech. I Semester Regular Examinations, November 2010 FINITE ELEMENT METHODS (Mechanical Engineering) Time: 3 Hours Max Marks: 80 Answer any FIVE Questions All Questions carry equal marks
AMR Multi-Moment FVM Scheme
 Chapter 4 AMR Multi-Moment FVM Scheme 4.1 Berger s AMR scheme An AMR grid with the hierarchy of Berger s AMR scheme proposed in [13] for CFD simulations is given in Fig.4.1 as a simple example for following
Chapter 4 AMR Multi-Moment FVM Scheme 4.1 Berger s AMR scheme An AMR grid with the hierarchy of Berger s AMR scheme proposed in [13] for CFD simulations is given in Fig.4.1 as a simple example for following
IMPROVED WALL BOUNDARY CONDITIONS WITH IMPLICITLY DEFINED WALLS FOR PARTICLE BASED FLUID SIMULATION
 6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7) 1115 June 2018, Glasgow, UK IMPROVED WALL BOUNDARY CONDITIONS WITH IMPLICITLY
6th European Conference on Computational Mechanics (ECCM 6) 7th European Conference on Computational Fluid Dynamics (ECFD 7) 1115 June 2018, Glasgow, UK IMPROVED WALL BOUNDARY CONDITIONS WITH IMPLICITLY
NUMERICAL INVESTIGATION OF THE FLOW BEHAVIOR INTO THE INLET GUIDE VANE SYSTEM (IGV)
 University of West Bohemia» Department of Power System Engineering NUMERICAL INVESTIGATION OF THE FLOW BEHAVIOR INTO THE INLET GUIDE VANE SYSTEM (IGV) Publication was supported by project: Budování excelentního
University of West Bohemia» Department of Power System Engineering NUMERICAL INVESTIGATION OF THE FLOW BEHAVIOR INTO THE INLET GUIDE VANE SYSTEM (IGV) Publication was supported by project: Budování excelentního
The CSLaM transport scheme & new numerical mixing diagnostics
 The CSLaM transport scheme & new numerical mixing diagnostics CESM Ocean Model Working Group Meeting 14 15 December, 2011 Peter Hjort Lauritzen Outline: Two parts Briefly introduce the CSLaM scheme (Conservative
The CSLaM transport scheme & new numerical mixing diagnostics CESM Ocean Model Working Group Meeting 14 15 December, 2011 Peter Hjort Lauritzen Outline: Two parts Briefly introduce the CSLaM scheme (Conservative
Computational Simulation of the Wind-force on Metal Meshes
 16 th Australasian Fluid Mechanics Conference Crown Plaza, Gold Coast, Australia 2-7 December 2007 Computational Simulation of the Wind-force on Metal Meshes Ahmad Sharifian & David R. Buttsworth Faculty
16 th Australasian Fluid Mechanics Conference Crown Plaza, Gold Coast, Australia 2-7 December 2007 Computational Simulation of the Wind-force on Metal Meshes Ahmad Sharifian & David R. Buttsworth Faculty
Efficiency of adaptive mesh algorithms
 Efficiency of adaptive mesh algorithms 23.11.2012 Jörn Behrens KlimaCampus, Universität Hamburg http://www.katrina.noaa.gov/satellite/images/katrina-08-28-2005-1545z.jpg Model for adaptive efficiency 10
Efficiency of adaptive mesh algorithms 23.11.2012 Jörn Behrens KlimaCampus, Universität Hamburg http://www.katrina.noaa.gov/satellite/images/katrina-08-28-2005-1545z.jpg Model for adaptive efficiency 10
THE preceding chapters were all devoted to the analysis of images and signals which
 Chapter 5 Segmentation of Color, Texture, and Orientation Images THE preceding chapters were all devoted to the analysis of images and signals which take values in IR. It is often necessary, however, to
Chapter 5 Segmentation of Color, Texture, and Orientation Images THE preceding chapters were all devoted to the analysis of images and signals which take values in IR. It is often necessary, however, to
99 International Journal of Engineering, Science and Mathematics
 Journal Homepage: Applications of cubic splines in the numerical solution of polynomials Najmuddin Ahmad 1 and Khan Farah Deeba 2 Department of Mathematics Integral University Lucknow Abstract: In this
Journal Homepage: Applications of cubic splines in the numerical solution of polynomials Najmuddin Ahmad 1 and Khan Farah Deeba 2 Department of Mathematics Integral University Lucknow Abstract: In this
SHAPE, SPACE & MEASURE
 STAGE 1 Know the place value headings up to millions Recall primes to 19 Know the first 12 square numbers Know the Roman numerals I, V, X, L, C, D, M Know the % symbol Know percentage and decimal equivalents
STAGE 1 Know the place value headings up to millions Recall primes to 19 Know the first 12 square numbers Know the Roman numerals I, V, X, L, C, D, M Know the % symbol Know percentage and decimal equivalents
CONSERVATIVE AND NON-CONSERVATIVE METHODS BASED ON HERMITE WEIGHTED ESSENTIALLY-NON-OSCILLATORY RECONSTRUCTION FOR VLASOV EQUATIONS
 CONSERVATIVE AND NON-CONSERVATIVE METHODS BASED ON HERMITE WEIGHTED ESSENTIALLY-NON-OSCILLATORY RECONSTRUCTION FOR VLASOV EQUATIONS CHANG YANG AND FRANCIS FILBET Abstract. We develop weighted essentially
CONSERVATIVE AND NON-CONSERVATIVE METHODS BASED ON HERMITE WEIGHTED ESSENTIALLY-NON-OSCILLATORY RECONSTRUCTION FOR VLASOV EQUATIONS CHANG YANG AND FRANCIS FILBET Abstract. We develop weighted essentially
A High Quality, Eulerian 3D Fluid Solver in C++ A Senior Project. presented to. the Faculty of the Computer Science Department of
 A High Quality, Eulerian 3D Fluid Solver in C++ A Senior Project presented to the Faculty of the Computer Science Department of California Polytechnic State University, San Luis Obispo In Partial Fulfillment
A High Quality, Eulerian 3D Fluid Solver in C++ A Senior Project presented to the Faculty of the Computer Science Department of California Polytechnic State University, San Luis Obispo In Partial Fulfillment
Advective and conservative semi-lagrangian schemes on uniform and non-uniform grids
 Advective and conservative semi-lagrangian schemes on uniform and non-uniform grids M. Mehrenberger Université de Strasbourg and Max-Planck Institut für Plasmaphysik 5 September 2013 M. Mehrenberger (UDS
Advective and conservative semi-lagrangian schemes on uniform and non-uniform grids M. Mehrenberger Université de Strasbourg and Max-Planck Institut für Plasmaphysik 5 September 2013 M. Mehrenberger (UDS
Polynomial Approximation and Interpolation Chapter 4
 4.4 LAGRANGE POLYNOMIALS The direct fit polynomial presented in Section 4.3, while quite straightforward in principle, has several disadvantages. It requires a considerable amount of effort to solve the
4.4 LAGRANGE POLYNOMIALS The direct fit polynomial presented in Section 4.3, while quite straightforward in principle, has several disadvantages. It requires a considerable amount of effort to solve the
Advanced Numerical Methods for NWP Models
 Advanced Numerical Methods for NWP Models Francis X. Giraldo Naval Postgraduate School Monterey, CA 93943-5502 phone: (831) 656-2293 fax: (831) 656-2355 e-mail: fxgirald@nps.edu Award #: N0001406WX20257
Advanced Numerical Methods for NWP Models Francis X. Giraldo Naval Postgraduate School Monterey, CA 93943-5502 phone: (831) 656-2293 fax: (831) 656-2355 e-mail: fxgirald@nps.edu Award #: N0001406WX20257
Optimization of a two-link Robotic Manipulator
 Optimization of a two-link Robotic Manipulator Zachary Renwick, Yalım Yıldırım April 22, 2016 Abstract Although robots are used in many processes in research and industry, they are generally not customized
Optimization of a two-link Robotic Manipulator Zachary Renwick, Yalım Yıldırım April 22, 2016 Abstract Although robots are used in many processes in research and industry, they are generally not customized
