11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will
|
|
|
- Conrad Skinner
- 5 years ago
- Views:
Transcription
1 11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will be necessary. This firstly pertains to the basic concepts from the plane geometry and the space geometry. From the field of planimetry one should be familiar with all the facts and theorems about the triangle that are included in the standard high school program. The same is valid for spatial geometry, where it is required to have a solid knowledge on the mutual positions of lines and planes in space, with special emphasis on parallelism and perpendicularity. In the proofs of theorems and the solutions of problems we tried to use the geometrical (synthetic) method wherever possible. Sometimes, however, we were not able to evade the usage of trigonometry or, in certain cases, the very nature of a problem or a theorem required such an approach. Therefore it is assumed that the reader has mastered the basic concepts of trigonometrical functions and trigonometrical facts about the triangle. In the same way, a necessity of vector algebra quite naturally occurs in the text. Hence, the reader should be familiar with the concepts of vector addition and subtraction, as well as with multiplication of a vector by a scalar, furthermore with linear independency of vectors, inner product, vector product and mixed product of vectors. In several problems, a tetrahedron is given by the coordinates of its vertices in a coordinate system in space. That requires elementary knowledge of analytical geometry of space, such as distance between two points in space, equation of a plane, distance between a point and a plane and so on. We also use some theorems and formulas of elementary mathematics which either rarely occur or do not occur at all in high school programs in mathematics.
2 12 1. INTRODUCTORY PART Such theorems and formulas will be explicitly stated and some of the proofs will be given, too. There is a well-known Heron s formula for the area of a triangle with given sidelengths a, b and c. That formula reads P = s(s a)(s b)(s c),where s denotes the semiperimeter of the triangle. This formula may be written in another form: P = 1 4 (a2 + b 2 + c 2 ) 2 2(a 4 + b 4 + c 4 ). (F1) The formula (F1) is suitable if sidelengths are real numbers or algebraic expressions under the square root sign, which is the reason why it will be repeatedly used in such cases. The proof of the formula may be found in [2]. We are going to point out three particular theorems for the triangle. The first reason for that is that these theorems are used in some proofs, and the second reason is that there exist analogous theorems for the tetrahedron, more of which will be said later on in the book. Th1. Let P, Q, R be given points on the respective sides BC, CA and AB of a triangle ABC. The lines AP, BQ and CR intersect in one point if and only if AR BP CQ = BR CP AQ (Fig. 1.1.). Fig This is Ceva s theorem. It was stated and proved by the Italian mathematician Giovanni Ceva ( ). Th2. If a line intersects the sides BC, CA and AB of a triangle ABC in respective points P, Q and R, then it holds: AR BP CQ = BR CP QA (Fig. 1.2.).
3 1. INTRODUCTORY PART 13 Fig This theorem is named after the ancient Greek mathematician Menelaus. The following one is Van Aubel s theorem. Th. If P, Q, R are points on the respective sides BC, CA and AB of a triangle ABC chosen in such a way that the lines AP, BQ and CR intersect at a point O, then it holds CO = CQ OR QA + CP PB (Fig. 1.1.). Let us observe certain connections between the above theorems. Ceva s and Menelaus theorem are so-called dual theorems and are expressed by the same formula. Furthermore, the assumptions on the triangle in both Ceva s and Van Aubel s theorem are identical. Proofs of these theorems may be found in [2]. (In that book, several proofs are supplied for each theorem. In the case of Ceva s theorem, for instance, seven different proofs are given). There is also a certain less known theorem on the orthocentre of a triangle, which is used in the book: Th4. The orthocentre of a triangle divides each of its altitudes into two segments whose product is constant and equal to 4R 2 cos α cos β cos γ,where R is the circumradius and α, β, γ the angles of the triangle. The proof is given in [2]. A theorem concerning a particular position of lines in space is known as the Theorem of three perpendiculars and reads as follows: Th5. Let a and b be two mutually perpendicular lines of a plane π,let A be their intersection point and let c be the line perpendicular to the plane π, passing through a point O of the line a, with O A.
4 14 1. INTRODUCTORY PART Proof. If C is any point on c, then the lines CA and b are perpendicular, too. Fig Since the line c is perpendicular to the plane π, c is also perpendicular to any line in that plane, including the line b (Fig. 1.3.). We see that the line b is perpendicular to the lines a and c. Therefore, b is perpendicular to any line in the plane determined by a and c, hence perpendicular to the line CA, too, which is the assertion of the theorem. Q.E.D. Next theorem will be frequently used in the proofs of some theorems, as well as in the solutions of several problems. Therefore, we are going to prove it. The theorem reads as follows: Th6. Let ϕ be the angle between the planes 1 and 2. If a polygon of area P is situated in the plane 1 and the orthogonal projection of that polygon to the plane 2 is a polygon of area Q,then Q = P cos ϕ. Proof. We use the notation as in fig. 1.4 Every polygon may be decomposed into a finite number of triangles. The area of a triangle does not depend on its position in the plane 1, so that the same holds for its orthogonal projection. Therefore it suffices to prove that the theorem is valid for a triangle in such a position as shown in the figure. Let the triangle ABC be positioned in the plane 1 in such a way that its side AB lies in the intersection of the planes and its vertex C is in any point of 1. If C is the orthogonal projection of C onto the plane 2, then the triangle ABC is the orthogonal projection of the triangle ABC.IfD is the foot of the altitude of the triangle ABC from vertex C,then P = 1 2 AB DC.
5 1. INTRODUCTORY PART 15 Fig According to the Theorem of three perpendiculars (see Th5.), DC is perpendicular to AB, which means that DC is the altitude of the triangle ABC from vertex C. Therefore Q = 1 2 AB DC = 1 AB DC cos ϕ 2 = P cos ϕ. Q.E.D. Now we are going to explore a very important notion of the geometry of space. That notion and the theorems which are directly related thereto will be frequently used in the following text. It is the trihedron. D1. Let a, b and c be three rays in space which do not lie in the same plane and which have a common origin O. The part of space bounded by the three angles determined by those rays in pairs is called a trihedron. Fig The point O is the vertex and the rays a, b, c are the edges of the trihedron. The parts of planes determined by pairs of edges are the faces of the trihedron. A trihedron is represented in a plane by its projection, as
6 16 1. INTRODUCTORY PART in Fig Trihedron is important in the study of the tetrahedron. Let us state an analogy between the triangle and the tetrahedron. If an angle with vertex A is intersected by a line that meets the sides of the angle in the points B and C, then the angle is divided into two parts, one bounded and one unbounded. The bounded part is the triangle ABC with vertices A, B and C. Fig We could define the tetrahedron in a similar way: if a trihedron with vertex O is divided into two parts by a plane which intersects its edges in the points A, B and C, then the bounded part is a tetrahedron with vertices O, A, B and C, as shown in Fig There are two types of angles defined in a trihedron: 1. Angles determined by two edges are called face angles of a trihedron. There are three such angles in a trihedron. 2. Angles between two faces, or dihedral angles, determined by two faces of a trihedron. A tetrahedron obviously has three such angles. At this point I have to say that, unfortunately, in the Croatian mathematical terminology there is no full accordance with regard to these angles. When we talk about the angle at a certain edge of a trihedron, we mean the angle between the two faces having that edge in common. To each face angle we associate the angle between those two faces which share the edge that is not an edge of that face angle. We say that to each face angle we asociate the opposite angle of two faces of the trihedron.
7 1. INTRODUCTORY PART 17 In a trihedron with vertex O and edges a, b and c, we will denote face angles by α 1, β 1, γ 1, and angles between faces (dihedral angles) by α 1, β 1, γ 1 as it is shown in Fig Fig We can see, for instance, that the face angle α is situated opposite to the edge a, and the corresponding dihedral angle at that edge is denoted by α 1. An analogous accordance of notation holds for other edges and angles. The following theorems are valid for the face angles of a trihedron: Th7. Each face angle is smaller than the sum of the other two face angles and greater than the difference of the other two face angles. This proposition is easily proved in such a manner that one edge is orthogonally projected onto the opposite face, so that the opposite angle is divided into two parts, each of them smaller than the corresponding face angle. Th8. If two face angles in a trihedron are equal, then their opposite dihedral angles are equal, too. Hint for a proof: Project orthogonally the edge that the equal face angles have in common onto the opposite face and also project any point of that edge onto the other two edges. Th9. If the face angles of a trihedron satisfy the relation α < β < γ, then for the opposite dihedral angles the relation α 1 < β 1 < γ 1 is valid. This assertion, too, is easily proved by projecting orthogonally one edge of the trihedron onto the plane of its opposite face.
8 18 1. INTRODUCTORY PART The previous theorems remind us of some assertions about the interior angles of a triangle. We know that the sum of such angles equals 180. However, the sum of face angles of a trihedron is not constant and the following theorem holds. Th10. The sum of the face angles of a trihedron is smaller than 360. Proof. We observe the intersection of a trihedron with the vertex O and the face angles α, β and γ by any plane, in such a way that it intersects the edges of the trihedron in the points A, B and C, as shown in Fig Fig If O is the orthogonal projection of the vertex O onto the plane ABC, then it obviously holds α = <)BOC <<)BO C, β = <)COA <<)CO A, γ = <)AOB <<)AO B. Therefrom one gets α + β + γ <<)BO C + <)CO A + <)AO B,or α + β + γ < 360. Q.E.D. Similarly, the sum of dihedral angles of a trihedron is not constant, but the following theorem holds. Th11. Dihedral angles of a trihedron satisfy the relation: 180 < α 1 + β 1 + γ 1 < 540. Proof. Consider a trihedron with vertex in the point O. Let O be any point inside the trihedron and A, B, C projections of the point O onto the faces of the trihedron. The perpendiculars from those points onto the edges of the trihedron mutually intersect in pairs on the edges, in the points A, B and C, as represented in Fig Dihedral angles of our trihedron are: α 1 = <)C AB, β 1 = <)A BC, γ 1 = <)B CA. If we denote the face angles of the trihedron A B C O by α, β, γ then α 1 + α = 180, β 1 + β = 180, γ 1 + γ = 180.
9 1. INTRODUCTORY PART 19 Fig By adding up one gets (α 1 + β 1 + γ 1 )+(α + β + γ )=540. An application of the theorem Th10. to the tetrahedron A B C O directly yields the assertion of the theorem. Q.E.D. The following theorem shows how to calculate the dihedral angles of a trihedron if the values of face angles are given. Th12. If α, β and γ are face angles, and α 1, β 1 and γ 1 are dihedral angles of a trihedron, then cos α cos β cos γ cos β cos γ cos α cos α 1 =, cos β 1 =, sin β sin γ sin γ sin α cos γ cos α cos β cos γ 1 =. sin α sin β Proof. On the edges of a trihedron with vertex in the point O determine the points A, B and C such that the vectors e 1 = OA, e 2 = OB, e 3 = OC be unit vectors. Let D and E be the feet of the perpendiculars from the points B and C to the line OA. Then, by definition of a dihedral angle, α 1 = <)( DB, EC ) (Fig ). It holds DB = DO + e 2, EC = EO + e 3. Since DO e 3 = DO 1 cos( β) = cos γ cos β, EO e 2 = cos β cos γ,itfollows DB EC = cos γ cos β cos β cos γ cos β cos γ + cos α. Finally, owing to DB EC = sin γ sin β cos α 1, we obtain cos α 1 =
10 20 1. INTRODUCTORY PART cos α cos β cos γ. The other two formulas of the theorem can be proved sin β sin γ in an analogous manner. Q.E.D. Fig Let us state the formula for the volume of a tetrahedron determined by vectors of its edges with the origin in a common vertex: a x a y a z V = 1 ( a 6 ) b c = 1 6 b x b y b z. (F2) c x c y c z
SOAR2001 GEOMETRY SUMMER 2001
 SR2001 GEMETRY SUMMER 2001 1. Introduction to plane geometry This is the short version of the notes for one of the chapters. The proofs are omitted but some hints are given. Try not to use the hints first,
SR2001 GEMETRY SUMMER 2001 1. Introduction to plane geometry This is the short version of the notes for one of the chapters. The proofs are omitted but some hints are given. Try not to use the hints first,
A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY
 i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
Spherical Geometry MATH430
 Spherical Geometry MATH430 Fall 014 In these notes we summarize some results about the geometry of the sphere that complement should the textbook. Most notions we had on the plane (points, lines, angles,
Spherical Geometry MATH430 Fall 014 In these notes we summarize some results about the geometry of the sphere that complement should the textbook. Most notions we had on the plane (points, lines, angles,
<Outline> Mathematical Training Program for Laotian Teachers
 Mathematical Training Program for Laotian Teachers Euclidean Geometry Analytic Geometry Trigonometry Dr Wattana Toutip Department of Mathematics Faculty of Science Khon Kaen University February
Mathematical Training Program for Laotian Teachers Euclidean Geometry Analytic Geometry Trigonometry Dr Wattana Toutip Department of Mathematics Faculty of Science Khon Kaen University February
LINES AND ANGLES CHAPTER 6. (A) Main Concepts and Results. (B) Multiple Choice Questions
 CHAPTER 6 LINES AND ANGLES (A) Main Concepts and Results Complementary angles, Supplementary angles, Adjacent angles, Linear pair, Vertically opposite angles. If a ray stands on a line, then the adjacent
CHAPTER 6 LINES AND ANGLES (A) Main Concepts and Results Complementary angles, Supplementary angles, Adjacent angles, Linear pair, Vertically opposite angles. If a ray stands on a line, then the adjacent
Mathematical Analysis of Tetrahedron (solid angle subtended by any tetrahedron at its vertex)
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter March 29, 2015 Mathematical Analysis of Tetrahedron solid angle subtended by any tetrahedron at its vertex) Harish Chandra Rajpoot Rajpoot,
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter March 29, 2015 Mathematical Analysis of Tetrahedron solid angle subtended by any tetrahedron at its vertex) Harish Chandra Rajpoot Rajpoot,
Unit 6: Connecting Algebra and Geometry Through Coordinates
 Unit 6: Connecting Algebra and Geometry Through Coordinates The focus of this unit is to have students analyze and prove geometric properties by applying algebraic concepts and skills on a coordinate plane.
Unit 6: Connecting Algebra and Geometry Through Coordinates The focus of this unit is to have students analyze and prove geometric properties by applying algebraic concepts and skills on a coordinate plane.
Math 311. Trees Name: A Candel CSUN Math
 1. A simple path in a graph is a path with no repeated edges. A simple circuit is a circuit without repeated edges. 2. Trees are special kinds of graphs. A tree is a connected graph with no simple circuits.
1. A simple path in a graph is a path with no repeated edges. A simple circuit is a circuit without repeated edges. 2. Trees are special kinds of graphs. A tree is a connected graph with no simple circuits.
11 The Regular Pentagon
 11 The Regular Pentagon 11.1 The Euclidean construction with the Golden Ratio The figure on page 561 shows an easy Euclidean construction of a regular pentagon. The justification of the construction begins
11 The Regular Pentagon 11.1 The Euclidean construction with the Golden Ratio The figure on page 561 shows an easy Euclidean construction of a regular pentagon. The justification of the construction begins
8 Standard Euclidean Triangle Geometry
 8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
Problem 2.1. Complete the following proof of Euclid III.20, referring to the figure on page 1.
 Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
The angle measure at for example the vertex A is denoted by m A, or m BAC.
 MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
MT 200 ourse notes on Geometry 5 2. Triangles and congruence of triangles 2.1. asic measurements. Three distinct lines, a, b and c, no two of which are parallel, form a triangle. That is, they divide the
Activity 21 OBJECTIVE. MATERIAL REQUIRED Cardboard, white paper, adhesive, pens, geometry box, eraser, wires, paper arrow heads.
 Activity 21 OBJECTIVE To verify that angle in a semi-circle is a right angle, using vector method. MATERIAL REQUIRED Cardboard, white paper, adhesive, pens, geometry box, eraser, wires, paper arrow heads.
Activity 21 OBJECTIVE To verify that angle in a semi-circle is a right angle, using vector method. MATERIAL REQUIRED Cardboard, white paper, adhesive, pens, geometry box, eraser, wires, paper arrow heads.
2 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 6, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Solution of Homework
Definition 2 (Projective plane). A projective plane is a class of points, and a class of lines satisfying the axioms:
 Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Math 3181 Name: Dr. Franz Rothe January 30, 2014 All3181\3181_spr14h2.tex Homework has to be turned in this handout. The homework can be done in groups up to three due February 11/12 2 Homework 1 Definition
Problem 3.1 (Building up geometry). For an axiomatically built-up geometry, six groups of axioms needed:
 Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Math 3181 Dr. Franz Rothe September 29, 2016 All3181\3181_fall16h3.tex Names: Homework has to be turned in this handout. For extra space, use the back pages, or put blank pages between. The homework can
Transformations and Isometries
 Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
Transformations and Isometries Definition: A transformation in absolute geometry is a function f that associates with each point P in the plane some other point P in the plane such that (1) f is one-to-one
Parallel and perspective projections such as used in representing 3d images.
 Chapter 5 Rotations and projections In this chapter we discuss Rotations Parallel and perspective projections such as used in representing 3d images. Using coordinates and matrices, parallel projections
Chapter 5 Rotations and projections In this chapter we discuss Rotations Parallel and perspective projections such as used in representing 3d images. Using coordinates and matrices, parallel projections
SECONDARY DRAFT SYLLABUS. 2. Representation of functions. 3. Types of functions. 4. Composition of functions (two and three)
 et et et CLASS IX Topic :Set Language et et 1. Describing and representing sets SECONDARY DRAFT SYLLABUS Able to describe a set in Descriptive, Set- builder and roster forms and through Venn diagram. Use
et et et CLASS IX Topic :Set Language et et 1. Describing and representing sets SECONDARY DRAFT SYLLABUS Able to describe a set in Descriptive, Set- builder and roster forms and through Venn diagram. Use
Basics of Computational Geometry
 Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Pi at School. Arindama Singh Department of Mathematics Indian Institute of Technology Madras Chennai , India
 Pi at School rindama Singh epartment of Mathematics Indian Institute of Technology Madras Chennai-600036, India Email: asingh@iitm.ac.in bstract: In this paper, an attempt has been made to define π by
Pi at School rindama Singh epartment of Mathematics Indian Institute of Technology Madras Chennai-600036, India Email: asingh@iitm.ac.in bstract: In this paper, an attempt has been made to define π by
CBSE X Mathematics 2012 Solution (SET 1) Section C
 CBSE X Mathematics 01 Solution (SET 1) Q19. Solve for x : 4x 4ax + (a b ) = 0 Section C The given quadratic equation is x ax a b 4x 4ax a b 0 4x 4ax a b a b 0 4 4 0. 4 x [ a a b b] x ( a b)( a b) 0 4x
CBSE X Mathematics 01 Solution (SET 1) Q19. Solve for x : 4x 4ax + (a b ) = 0 Section C The given quadratic equation is x ax a b 4x 4ax a b 0 4x 4ax a b a b 0 4 4 0. 4 x [ a a b b] x ( a b)( a b) 0 4x
1 Appendix to notes 2, on Hyperbolic geometry:
 1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
8.B. The result of Regiomontanus on tetrahedra
 8.B. The result of Regiomontanus on tetrahedra We have already mentioned that Plato s theory that the five regular polyhedra represent the fundamental elements of nature, and in supplement (3.D) to the
8.B. The result of Regiomontanus on tetrahedra We have already mentioned that Plato s theory that the five regular polyhedra represent the fundamental elements of nature, and in supplement (3.D) to the
with slopes m 1 and m 2 ), if and only if its coordinates satisfy the equation y y 0 = 0 and Ax + By + C 2
 CHAPTER 10 Straight lines Learning Objectives (i) Slope (m) of a non-vertical line passing through the points (x 1 ) is given by (ii) If a line makes an angle α with the positive direction of x-axis, then
CHAPTER 10 Straight lines Learning Objectives (i) Slope (m) of a non-vertical line passing through the points (x 1 ) is given by (ii) If a line makes an angle α with the positive direction of x-axis, then
Education Resources. This section is designed to provide examples which develop routine skills necessary for completion of this section.
 Education Resources Straight Line Higher Mathematics Supplementary Resources Section A This section is designed to provide examples which develop routine skills necessary for completion of this section.
Education Resources Straight Line Higher Mathematics Supplementary Resources Section A This section is designed to provide examples which develop routine skills necessary for completion of this section.
Notes on Spherical Geometry
 Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Notes on Spherical Geometry Abhijit Champanerkar College of Staten Island & The Graduate Center, CUNY Spring 2018 1. Vectors and planes in R 3 To review vector, dot and cross products, lines and planes
Geometric Constructions
 HISTORY OF MATHEMATICS Spring 2005 Geometric Constructions Notes, activities, assignment; #3 in a series. Note: I m not giving a specific due date for this somewhat vague assignment. The idea is that it
HISTORY OF MATHEMATICS Spring 2005 Geometric Constructions Notes, activities, assignment; #3 in a series. Note: I m not giving a specific due date for this somewhat vague assignment. The idea is that it
Solutions to the Test. Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written?
 Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Solutions to the Test Problem 1. 1) Who is the author of the first comprehensive text on geometry? When and where was it written? Answer: The first comprehensive text on geometry is called The Elements
Gergonne and Nagel Points for Simplices in the n-dimensional Space
 Journal for Geometry and Graphics Volume 4 (2000), No. 2, 119 127. Gergonne and Nagel Points for Simplices in the n-dimensional Space Edwin Koźniewsi 1, Renata A. Górsa 2 1 Institute of Civil Engineering,
Journal for Geometry and Graphics Volume 4 (2000), No. 2, 119 127. Gergonne and Nagel Points for Simplices in the n-dimensional Space Edwin Koźniewsi 1, Renata A. Górsa 2 1 Institute of Civil Engineering,
GEOMETRY WITH GEOGEBRA
 GEOMETRY WITH GEOGEBRA PART ONE: TRIANGLES Notations AB ( AB ) [ AB ] ] AB [ [ AB ) distance between the points A and B line through the points A and B segment between the two points A and B (A and B included)
GEOMETRY WITH GEOGEBRA PART ONE: TRIANGLES Notations AB ( AB ) [ AB ] ] AB [ [ AB ) distance between the points A and B line through the points A and B segment between the two points A and B (A and B included)
3 Solution of Homework
 Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
Math 3181 Name: Dr. Franz Rothe February 25, 2014 All3181\3181_spr14h3.tex Homework has to be turned in this handout. The homework can be done in groups up to three due March 11/12 3 Solution of Homework
Cyclic Quadrilaterals
 Cyclic Quadrilaterals Definition: Cyclic quadrilateral a quadrilateral inscribed in a circle (Figure 1). Construct and Investigate: 1. Construct a circle on the Voyage 200 with Cabri screen, and label
Cyclic Quadrilaterals Definition: Cyclic quadrilateral a quadrilateral inscribed in a circle (Figure 1). Construct and Investigate: 1. Construct a circle on the Voyage 200 with Cabri screen, and label
I I I.7 : Areas and volumes
 I I I.7 : Areas and volumes Most upper level undergraduate textbooks in geometry do not cover these topics, but for the sake of completeness we shall explain how they fit into the setting of these notes.
I I I.7 : Areas and volumes Most upper level undergraduate textbooks in geometry do not cover these topics, but for the sake of completeness we shall explain how they fit into the setting of these notes.
Mathematical derivations of some important formula in 2D-Geometry by HCR
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Summer March 31, 2018 Mathematical derivations of some important formula in 2D-Geometry by HCR Harish Chandra Rajpoot, HCR Available at: https://works.bepress.com/harishchandrarajpoot_hcrajpoot/61/
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Summer March 31, 2018 Mathematical derivations of some important formula in 2D-Geometry by HCR Harish Chandra Rajpoot, HCR Available at: https://works.bepress.com/harishchandrarajpoot_hcrajpoot/61/
And Now From a New Angle Special Angles and Postulates LEARNING GOALS
 And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
Basic Euclidean Geometry
 hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
TRIGONOMETRIC FUNCTIONS
 Chapter TRIGONOMETRIC FUNCTIONS.1 Introduction A mathematician knows how to solve a problem, he can not solve it. MILNE The word trigonometry is derived from the Greek words trigon and metron and it means
Chapter TRIGONOMETRIC FUNCTIONS.1 Introduction A mathematician knows how to solve a problem, he can not solve it. MILNE The word trigonometry is derived from the Greek words trigon and metron and it means
Circular inversions = hyperbolic isometries
 Circular inversions = hyperbolic isometries Recall how all isometries of the Euclidean plane are products of at most three line reflections. In the (Beltrami-Poincaré model of the) hyperbolic plane, we
Circular inversions = hyperbolic isometries Recall how all isometries of the Euclidean plane are products of at most three line reflections. In the (Beltrami-Poincaré model of the) hyperbolic plane, we
 1 www.gradestack.com/ssc Dear readers, ADVANCE MATHS - GEOMETRY DIGEST Geometry is a very important topic in numerical ability section of SSC Exams. You can expect 14-15 questions from Geometry in SSC
1 www.gradestack.com/ssc Dear readers, ADVANCE MATHS - GEOMETRY DIGEST Geometry is a very important topic in numerical ability section of SSC Exams. You can expect 14-15 questions from Geometry in SSC
I I I.7 : Areas and volumes
 I I I.7 : Areas and volumes Most upper level undergraduate textbooks in geometry do not cover these topics, but for the sake of completeness we shall explain how they fit into the setting of these notes.
I I I.7 : Areas and volumes Most upper level undergraduate textbooks in geometry do not cover these topics, but for the sake of completeness we shall explain how they fit into the setting of these notes.
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: a b 1.
 ASSIGNMENT ON STRAIGHT LINES LEVEL 1 (CBSE/NCERT/STATE BOARDS) 1 Find the angle between the lines joining the points (0, 0), (2, 3) and the points (2, 2), (3, 5). 2 What is the value of y so that the line
ASSIGNMENT ON STRAIGHT LINES LEVEL 1 (CBSE/NCERT/STATE BOARDS) 1 Find the angle between the lines joining the points (0, 0), (2, 3) and the points (2, 2), (3, 5). 2 What is the value of y so that the line
Analytic Spherical Geometry:
 Analytic Spherical Geometry: Begin with a sphere of radius R, with center at the origin O. Measuring the length of a segment (arc) on a sphere. Let A and B be any two points on the sphere. We know that
Analytic Spherical Geometry: Begin with a sphere of radius R, with center at the origin O. Measuring the length of a segment (arc) on a sphere. Let A and B be any two points on the sphere. We know that
EXTREME POINTS AND AFFINE EQUIVALENCE
 EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
Geometry IB Date: 2/18/2013 ID Check Objective: Students will identify and use medians and altitudes in triangles. Bell Ringer: Complete Constructions
 Geometry IB Date: 2/18/2013 ID Check Objective: Students will identify and use medians and altitudes in triangles. Bell Ringer: Complete Constructions HW Requests: pg 327 #17-25 odds 45, 46, pg 338 #11,
Geometry IB Date: 2/18/2013 ID Check Objective: Students will identify and use medians and altitudes in triangles. Bell Ringer: Complete Constructions HW Requests: pg 327 #17-25 odds 45, 46, pg 338 #11,
Elementary Planar Geometry
 Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Building a Geometry Vocabulary
 7-4127_EZGeoCh1-4 1/21/09 2:25 PM Page 1 1 Building a Geometry Vocabulary WHAT YOU WILL LEARN Studying geometry is very different from studying elementary algebra. In geometry we are concerned with developing
7-4127_EZGeoCh1-4 1/21/09 2:25 PM Page 1 1 Building a Geometry Vocabulary WHAT YOU WILL LEARN Studying geometry is very different from studying elementary algebra. In geometry we are concerned with developing
Lectures on Challenging Mathematics. Integrated Mathematics 3. Idea Math. Geometry (Part 2) Summer Internal Use
 Lectures on Challenging Mathematics c Copyright 2008 2018 Integrated Mathematics 3 Geometry (Part 2) Summer 2018 Zuming Feng Phillips Exeter cademy and IDE Math zfeng@exeter.edu Copyright c 2008 2018 IDE
Lectures on Challenging Mathematics c Copyright 2008 2018 Integrated Mathematics 3 Geometry (Part 2) Summer 2018 Zuming Feng Phillips Exeter cademy and IDE Math zfeng@exeter.edu Copyright c 2008 2018 IDE
All numbered readings are from Stillwell s The four pillars of geometry.
 MATH 350. Assigned readings and homework All numbered readings are from Stillwell s The four pillars of geometry. Reading Jan 30, Feb 1: Chapters 1.1 1.4 Feb 6, 8: Chapters 1.5 2.2 Feb 13, 15: Chapters
MATH 350. Assigned readings and homework All numbered readings are from Stillwell s The four pillars of geometry. Reading Jan 30, Feb 1: Chapters 1.1 1.4 Feb 6, 8: Chapters 1.5 2.2 Feb 13, 15: Chapters
7th Bay Area Mathematical Olympiad
 7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
Mathematical Techniques Chapter 10
 PART FOUR Formulas FM 5-33 Mathematical Techniques Chapter 10 GEOMETRIC FUNCTIONS The result of any operation performed by terrain analysts will only be as accurate as the measurements used. An interpretation
PART FOUR Formulas FM 5-33 Mathematical Techniques Chapter 10 GEOMETRIC FUNCTIONS The result of any operation performed by terrain analysts will only be as accurate as the measurements used. An interpretation
Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points.
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance.
 Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
No triangle can be decomposed into seven congruent triangles
 No triangle can be decomposed into seven congruent triangles Michael Beeson November 27, 2008 Abstract We investigate the problem of cutting a triangle into N congruent triangles. While this can be done
No triangle can be decomposed into seven congruent triangles Michael Beeson November 27, 2008 Abstract We investigate the problem of cutting a triangle into N congruent triangles. While this can be done
The Monge Point and the 3(n+1) Point Sphere of an n-simplex
 Journal for Geometry and Graphics Volume 9 (2005), No. 1, 31 36. The Monge Point and the 3(n+1) Point Sphere of an n-simplex Ma lgorzata Buba-Brzozowa Department of Mathematics and Information Sciences,
Journal for Geometry and Graphics Volume 9 (2005), No. 1, 31 36. The Monge Point and the 3(n+1) Point Sphere of an n-simplex Ma lgorzata Buba-Brzozowa Department of Mathematics and Information Sciences,
Boardworks Ltd KS3 Mathematics. S1 Lines and Angles
 1 KS3 Mathematics S1 Lines and Angles 2 Contents S1 Lines and angles S1.1 Labelling lines and angles S1.2 Parallel and perpendicular lines S1.3 Calculating angles S1.4 Angles in polygons 3 Lines In Mathematics,
1 KS3 Mathematics S1 Lines and Angles 2 Contents S1 Lines and angles S1.1 Labelling lines and angles S1.2 Parallel and perpendicular lines S1.3 Calculating angles S1.4 Angles in polygons 3 Lines In Mathematics,
Grade VIII. Mathematics Geometry Notes. #GrowWithGreen
 Grade VIII Mathematics Geometry Notes #GrowWithGreen Polygons can be classified according to their number of sides (or vertices). The sum of all the interior angles of an n -sided polygon is given by,
Grade VIII Mathematics Geometry Notes #GrowWithGreen Polygons can be classified according to their number of sides (or vertices). The sum of all the interior angles of an n -sided polygon is given by,
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Geometric and Algebraic Connections
 Geometric and Algebraic Connections Geometric and Algebraic Connections Triangles, circles, rectangles, squares... We see shapes every day, but do we know much about them?? What characteristics do they
Geometric and Algebraic Connections Geometric and Algebraic Connections Triangles, circles, rectangles, squares... We see shapes every day, but do we know much about them?? What characteristics do they
Mathematical Analysis of Spherical Rectangle by H.C. Rajpoot
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter February 9, 2015 Mathematical Analysis of Spherical Rectangle by H.C. Rajpoot Harish Chandra Rajpoot Rajpoot, HCR Available at: https://works.bepress.com/harishchandrarajpoot_hcrajpoot/30/
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Winter February 9, 2015 Mathematical Analysis of Spherical Rectangle by H.C. Rajpoot Harish Chandra Rajpoot Rajpoot, HCR Available at: https://works.bepress.com/harishchandrarajpoot_hcrajpoot/30/
Euclidean and non-euclidean Geometry 2018
 r. ernd Kreussler Mini rojects MH 4757 1 uclidean and non-uclidean Geometry 2018 1. xternal tangents to two unequal circles (week 8) Given two circles of different radius not containing each other. xplain
r. ernd Kreussler Mini rojects MH 4757 1 uclidean and non-uclidean Geometry 2018 1. xternal tangents to two unequal circles (week 8) Given two circles of different radius not containing each other. xplain
INTRODUCTION TO THREE DIMENSIONAL GEOMETRY
 Chapter 1 INTRODUCTION TO THREE DIMENSIONAL GEOMETRY Mathematics is both the queen and the hand-maiden of all sciences E.T. BELL 1.1 Introduction You may recall that to locate the position of a point in
Chapter 1 INTRODUCTION TO THREE DIMENSIONAL GEOMETRY Mathematics is both the queen and the hand-maiden of all sciences E.T. BELL 1.1 Introduction You may recall that to locate the position of a point in
COORDINATE GEOMETRY. 7.1 Introduction
 COORDINATE GEOMETRY 55 COORDINATE GEOMETRY 7 7. Introduction In Class IX, you have studied that to locate the position of a point on a plane, we require a pair of coordinate axes. The distance of a point
COORDINATE GEOMETRY 55 COORDINATE GEOMETRY 7 7. Introduction In Class IX, you have studied that to locate the position of a point on a plane, we require a pair of coordinate axes. The distance of a point
The statement implies that any three intersection points of two distinct planes lie on a line.
 Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Math 3181 Dr. Franz Rothe February 23, 2015 All3181\3181_spr15ts1.tex 1 Solution of Test Name: Problem 1.1. The second part of Hilbert s Proposition 1 states: Any two different planes have either no point
Math 489 Project 1: Explore a Math Problem L. Hogben 1 Possible Topics for Project 1: Explore a Math Problem draft 1/13/03
 Math 489 Project 1: Explore a Math Problem L. Hogben 1 Possible Topics for Project 1: Explore a Math Problem draft 1/13/03 Number Base and Regularity We use base 10. The Babylonians used base 60. Discuss
Math 489 Project 1: Explore a Math Problem L. Hogben 1 Possible Topics for Project 1: Explore a Math Problem draft 1/13/03 Number Base and Regularity We use base 10. The Babylonians used base 60. Discuss
Module Four: Connecting Algebra and Geometry Through Coordinates
 NAME: Period: Module Four: Connecting Algebra and Geometry Through Coordinates Topic A: Rectangular and Triangular Regions Defined by Inequalities Lesson 1: Searching a Region in the Plane Lesson 2: Finding
NAME: Period: Module Four: Connecting Algebra and Geometry Through Coordinates Topic A: Rectangular and Triangular Regions Defined by Inequalities Lesson 1: Searching a Region in the Plane Lesson 2: Finding
10-1. Three Trigonometric Functions. Vocabulary. Lesson
 Chapter 10 Lesson 10-1 Three Trigonometric Functions BIG IDEA The sine, cosine, and tangent of an acute angle are each a ratio of particular sides of a right triangle with that acute angle. Vocabulary
Chapter 10 Lesson 10-1 Three Trigonometric Functions BIG IDEA The sine, cosine, and tangent of an acute angle are each a ratio of particular sides of a right triangle with that acute angle. Vocabulary
9.2 SECANT AND TANGENT
 TOPICS PAGES. Circles -5. Constructions 6-. Trigonometry -0 4. Heights and Distances -6 5. Mensuration 6-9 6. Statistics 40-54 7. Probability 55-58 CIRCLES 9. CIRCLE A circle is the locus of a points which
TOPICS PAGES. Circles -5. Constructions 6-. Trigonometry -0 4. Heights and Distances -6 5. Mensuration 6-9 6. Statistics 40-54 7. Probability 55-58 CIRCLES 9. CIRCLE A circle is the locus of a points which
Grade IX. Mathematics Geometry Notes. #GrowWithGreen
 Grade IX Mathematics Geometry Notes #GrowWithGreen The distance of a point from the y - axis is called its x -coordinate, or abscissa, and the distance of the point from the x -axis is called its y-coordinate,
Grade IX Mathematics Geometry Notes #GrowWithGreen The distance of a point from the y - axis is called its x -coordinate, or abscissa, and the distance of the point from the x -axis is called its y-coordinate,
MATHEMATICS 105 Plane Trigonometry
 Chapter I THE TRIGONOMETRIC FUNCTIONS MATHEMATICS 105 Plane Trigonometry INTRODUCTION The word trigonometry literally means triangle measurement. It is concerned with the measurement of the parts, sides,
Chapter I THE TRIGONOMETRIC FUNCTIONS MATHEMATICS 105 Plane Trigonometry INTRODUCTION The word trigonometry literally means triangle measurement. It is concerned with the measurement of the parts, sides,
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot. Harish Chandra Rajpoot Rajpoot, HCR. Summer April 6, 2015
 From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Summer April 6, 2015 Mathematical Analysis of Uniform Polyhedron Trapezohedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices
From the SelectedWorks of Harish Chandra Rajpoot H.C. Rajpoot Summer April 6, 2015 Mathematical Analysis of Uniform Polyhedron Trapezohedron having 2n congruent right kite faces, 4n edges & 2n+2 vertices
Any questions about the material so far? About the exercises?
 Any questions about the material so far? About the exercises? Here is a question for you. In the diagram on the board, DE is parallel to AC, DB = 4, AB = 9 and BE = 8. What is the length EC? Polygons Definitions:
Any questions about the material so far? About the exercises? Here is a question for you. In the diagram on the board, DE is parallel to AC, DB = 4, AB = 9 and BE = 8. What is the length EC? Polygons Definitions:
CS 177 Homework 1. Julian Panetta. October 22, We want to show for any polygonal disk consisting of vertex set V, edge set E, and face set F:
 CS 177 Homework 1 Julian Panetta October, 009 1 Euler Characteristic 1.1 Polyhedral Formula We want to show for any polygonal disk consisting of vertex set V, edge set E, and face set F: V E + F = 1 First,
CS 177 Homework 1 Julian Panetta October, 009 1 Euler Characteristic 1.1 Polyhedral Formula We want to show for any polygonal disk consisting of vertex set V, edge set E, and face set F: V E + F = 1 First,
Mathematics High School Geometry
 Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
Mathematics High School Geometry An understanding of the attributes and relationships of geometric objects can be applied in diverse contexts interpreting a schematic drawing, estimating the amount of
An Approach to Geometry (stolen in part from Moise and Downs: Geometry)
 An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
An Approach to Geometry (stolen in part from Moise and Downs: Geometry) Undefined terms: point, line, plane The rules, axioms, theorems, etc. of elementary algebra are assumed as prior knowledge, and apply
Convex Geometry arising in Optimization
 Convex Geometry arising in Optimization Jesús A. De Loera University of California, Davis Berlin Mathematical School Summer 2015 WHAT IS THIS COURSE ABOUT? Combinatorial Convexity and Optimization PLAN
Convex Geometry arising in Optimization Jesús A. De Loera University of California, Davis Berlin Mathematical School Summer 2015 WHAT IS THIS COURSE ABOUT? Combinatorial Convexity and Optimization PLAN
Chapter 1-2 Points, Lines, and Planes
 Chapter 1-2 Points, Lines, and Planes Undefined Terms: A point has no size but is often represented by a dot and usually named by a capital letter.. A A line extends in two directions without ending. Lines
Chapter 1-2 Points, Lines, and Planes Undefined Terms: A point has no size but is often represented by a dot and usually named by a capital letter.. A A line extends in two directions without ending. Lines
Sequence of Geometry Modules Aligned with the Standards
 Sequence of Geometry Modules Aligned with the Standards Module 1: Congruence, Proof, and Constructions Module 2: Similarity, Proof, and Trigonometry Module 3: Extending to Three Dimensions Module 4: Connecting
Sequence of Geometry Modules Aligned with the Standards Module 1: Congruence, Proof, and Constructions Module 2: Similarity, Proof, and Trigonometry Module 3: Extending to Three Dimensions Module 4: Connecting
Section A1: Gradients of straight lines
 Time To study this unit will take you about 10 hours. Trying out and evaluating the activities with your pupils in the class will be spread over the weeks you have planned to cover the topic. 31 Section
Time To study this unit will take you about 10 hours. Trying out and evaluating the activities with your pupils in the class will be spread over the weeks you have planned to cover the topic. 31 Section
Mathematics For Class IX Lines and Angles
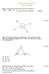 Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Analytical Solid Geometry
 Analytical Solid Geometry Distance formula(without proof) Division Formula Direction cosines Direction ratios Planes Straight lines Books Higher Engineering Mathematics by B S Grewal Higher Engineering
Analytical Solid Geometry Distance formula(without proof) Division Formula Direction cosines Direction ratios Planes Straight lines Books Higher Engineering Mathematics by B S Grewal Higher Engineering
The uses of homogeneous barycentric coordinates in plane euclidean geometry
 The uses of homogeneous barycentric coordinates in plane euclidean geometry Paul Yiu Abstract. The notion of homogeneous barycentric coordinates provides a powerful tool of analysing problems in plane
The uses of homogeneous barycentric coordinates in plane euclidean geometry Paul Yiu Abstract. The notion of homogeneous barycentric coordinates provides a powerful tool of analysing problems in plane
definition. An angle is the union of two rays with a common end point.
 Chapter 3 Angles What s the secret for doing well in geometry? Knowing all the angles. As we did in the last chapter, we will introduce new terms and new notations, the building blocks for our success.
Chapter 3 Angles What s the secret for doing well in geometry? Knowing all the angles. As we did in the last chapter, we will introduce new terms and new notations, the building blocks for our success.
THE DNA INEQUALITY POWER ROUND
 THE DNA INEQUALITY POWER ROUND Instructions Write/draw all solutions neatly, with at most one question per page, clearly numbered. Turn in the solutions in numerical order, with your team name at the upper
THE DNA INEQUALITY POWER ROUND Instructions Write/draw all solutions neatly, with at most one question per page, clearly numbered. Turn in the solutions in numerical order, with your team name at the upper
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1
 Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Grad operator, triple and line integrals. Notice: this material must not be used as a substitute for attending the lectures
 Grad operator, triple and line integrals Notice: this material must not be used as a substitute for attending the lectures 1 .1 The grad operator Let f(x 1, x,..., x n ) be a function of the n variables
Grad operator, triple and line integrals Notice: this material must not be used as a substitute for attending the lectures 1 .1 The grad operator Let f(x 1, x,..., x n ) be a function of the n variables
UNIT III: COORDINATE GEOMETRY
 4. ARITHMETIC PROGRESSIONS (8) Periods Motivation for studying Arithmetic Progression Derivation of the n th term and sum of the first n terms of A.P. and their application in solving daily life problems.
4. ARITHMETIC PROGRESSIONS (8) Periods Motivation for studying Arithmetic Progression Derivation of the n th term and sum of the first n terms of A.P. and their application in solving daily life problems.
Topics in geometry Exam 1 Solutions 7/8/4
 Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования
 ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» V.V. Konev MATHEMATICS PREPARATORY COURSE: TRIGONOMETRY
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ Государственное образовательное учреждение высшего профессионального образования «ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» V.V. Konev MATHEMATICS PREPARATORY COURSE: TRIGONOMETRY
Analytical Solid Geometry
 Analytical Solid Geometry Distance formula(without proof) Division Formula Direction cosines Direction ratios Planes Straight lines Books Higher Engineering Mathematics By B S Grewal Higher Engineering
Analytical Solid Geometry Distance formula(without proof) Division Formula Direction cosines Direction ratios Planes Straight lines Books Higher Engineering Mathematics By B S Grewal Higher Engineering
Vectors. Section 1: Lines and planes
 Vectors Section 1: Lines and planes Notes and Examples These notes contain subsections on Reminder: notation and definitions Equation of a line The intersection of two lines Finding the equation of a plane
Vectors Section 1: Lines and planes Notes and Examples These notes contain subsections on Reminder: notation and definitions Equation of a line The intersection of two lines Finding the equation of a plane
Euclid s Axioms. 1 There is exactly one line that contains any two points.
 11.1 Basic Notions Euclid s Axioms 1 There is exactly one line that contains any two points. Euclid s Axioms 1 There is exactly one line that contains any two points. 2 If two points line in a plane then
11.1 Basic Notions Euclid s Axioms 1 There is exactly one line that contains any two points. Euclid s Axioms 1 There is exactly one line that contains any two points. 2 If two points line in a plane then
Geometry Where everything is made up and the points matter
 Geometry Where everything is made up and the points matter Based on LAMC handouts by Po-Shen Loh and Alin Galatan Math Circle April 15th, 2018 Today we will be returning to the roots of mathematics. Euclidean
Geometry Where everything is made up and the points matter Based on LAMC handouts by Po-Shen Loh and Alin Galatan Math Circle April 15th, 2018 Today we will be returning to the roots of mathematics. Euclidean
Introduction to Complex Analysis
 Introduction to Complex Analysis George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 413 George Voutsadakis (LSSU) Complex Analysis October 2014 1 / 50 Outline
Introduction to Complex Analysis George Voutsadakis 1 1 Mathematics and Computer Science Lake Superior State University LSSU Math 413 George Voutsadakis (LSSU) Complex Analysis October 2014 1 / 50 Outline
GEOMETRY. Changes to the original 2010 COS is in red. If it is red and crossed out, it has been moved to another course.
 The Geometry course builds on Algebra I concepts and increases students knowledge of shapes and their properties through geometry-based applications, many of which are observable in aspects of everyday
The Geometry course builds on Algebra I concepts and increases students knowledge of shapes and their properties through geometry-based applications, many of which are observable in aspects of everyday
Mgr. ubomíra Tomková GEOMETRY
 GEOMETRY NAMING ANGLES: any angle less than 90º is an acute angle any angle equal to 90º is a right angle any angle between 90º and 80º is an obtuse angle any angle between 80º and 60º is a reflex angle
GEOMETRY NAMING ANGLES: any angle less than 90º is an acute angle any angle equal to 90º is a right angle any angle between 90º and 80º is an obtuse angle any angle between 80º and 60º is a reflex angle
(1) Page #1 24 all. (2) Page #7-21 odd, all. (3) Page #8 20 Even, Page 35 # (4) Page #1 8 all #13 23 odd
 Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
Geometry/Trigonometry Unit 1: Parallel Lines Notes Name: Date: Period: # (1) Page 25-26 #1 24 all (2) Page 33-34 #7-21 odd, 23 28 all (3) Page 33-34 #8 20 Even, Page 35 #40 44 (4) Page 60 61 #1 8 all #13
