Bayesian model selection applied to artificial neural networks used for water resources modeling
|
|
|
- Laurel McKenzie
- 5 years ago
- Views:
Transcription
1 WATER RESOURCES RESEARCH, VOL. 44,, doi: /2007wr006155, 2008 Bayesian model selection applied to artificial neural networks used for water resources modeling Greer B. Kingston, 1,2 Holger R. Maier, 1 and Martin F. Lambert 1 Received 7 May 2007; revised 4 December 2007; accepted 14 December 2007; published 12 April [1] Artificial neural networks (ANNs) have proven to be extremely valuable tools in the field of water resources engineering. However, one of the most difficult tasks in developing an ANN is determining the optimum level of complexity required to model a given problem, as there is no formal systematic model selection method. This paper presents a Bayesian model selection (BMS) method for ANNs that provides an objective approach for comparing models of varying complexity in order to select the most appropriate ANN structure. The approach uses Markov Chain Monte Carlo posterior simulations to estimate the evidence in favor of competing models and, in this study, three known methods for doing this are compared in terms of their suitability for being incorporated into the proposed BMS framework for ANNs. However, it is acknowledged that it can be particularly difficult to accurately estimate the evidence of ANN models. Therefore, the proposed BMS approach for ANNs incorporates a further check of the evidence results by inspecting the marginal posterior distributions of the hidden-to-output layer weights, which unambiguously indicate any redundancies in the hidden layer nodes. The fact that this check is available is one of the greatest advantages of the proposed approach over conventional model selection methods, which do not provide such a test and instead rely on the modeler s subjective choice of selection criterion. The advantages of a total Bayesian approach to ANN development, including training and model selection, are demonstrated on two synthetic and one real world water resources case study. Citation: Kingston, G. B., H. R. Maier, and M. F. Lambert (2008), Bayesian model selection applied to artificial neural networks used for water resources modeling, Water Resour. Res., 44,, doi: /2007wr Introduction [2] The popularity of artificial neural networks (ANNs) in water resources modeling has increased dramatically since their introduction to this field in the early 1990s. They have now been used successfully for a varied range of applications, including rainfall-runoff modeling, streamflow prediction, river basin classification, water quality forecasting and regionalization of hydrological model parameters (see Maier and Dandy [2000] and American Society of Civil Engineers Task Committee on Application of Artificial Neural Networks in Hydrology [2000] for a review), and as a result have become well established as a valuable prediction tool in the field of water resources engineering. The versatility of ANNs can partly be attributed to the flexible and model-free structure of ANNs, which enables such relationships to be modeled without any restrictive assumptions about the functional form of the underlying process and, thus, gives them more general appeal than less flexible statistical models. In fact, the flexibility of ANNs 1 School of Civil and Environmental Engineering, The University of Adelaide, Adelaide, South Australia, Australia. 2 Now at HR Wallingford Ltd., Wallingford, UK. Copyright 2008 by the American Geophysical Union /08/2007WR makes it possible to model any continuous function, whether linear or nonlinear, to an arbitrary degree of accuracy [Zhang et al., 1998], and as such, it is often claimed that ANNs are universal function approximators [Cheng and Titterington, 1994; Bishop, 1995]. [3] However, despite the noted advantages of ANNs, they also suffer from a number of limitations; one of these being the lack of ANN development theory and the fact that model complexity selection is still a difficult and somewhat subjective matter. The flexibility in ANN complexity selection primarily lies in selecting the appropriate number of hidden layer nodes, which determine the number of weights, or free parameters, in the model. In doing this, a balance is required between having too few hidden nodes, such that there are insufficient degrees of freedom to adequately capture the underlying relationship, and having too many hidden nodes, such that the model fits to noise in the individual data points rather than the general trend underlying the data as a whole. The latter case is referred to as overfitting, which is often difficult to detect but can significantly impair the generalizability of an ANN. Methods can be employed during training to prevent overfitting (e.g., cross validation, weight regularization); however, these methods are not without their own limitations and they often result in inefficient use of the available data [Ripley, 1994; Bishop, 1995]. Furthermore, apart from being more susceptible to overfitting, large ANNs with many hidden 1of12
2 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING nodes are inefficient to calibrate, the parameters and resulting predictions have a higher degree of associated uncertainty and it is more complicated to extract information about the modeled function from the parameters. Therefore, selection of the minimum number of necessary hidden nodes can be crucial to the performance of an ANN and its value as a prediction tool, particularly in cases where the available data are limited. This can be extremely important in water resources modeling, as the predictions made by ANNs will ultimately be used for making design or management decisions. [4] The most commonly used method for selecting the number of hidden layer nodes is by trial and error [Maier and Dandy, 2000], where a number of networks are trained, while the number of hidden nodes is systematically increased or decreased until the network with the best generalizability is found. The generalizability of an ANN can be estimated by evaluating its out-of-sample performance on an independent test data set (which is also independent of the validation set required for assessing the performance of the final selected model) using some error, or goodness of fit, measure (e.g., root-mean-square error (RMSE), r 2 ). However, this may not be practical if there are limited data available, since the test data cannot be used for training. Furthermore, if the test data are not a representative subset, the evaluation may be biased. Alternatively, information criteria (e.g., Akaike information criterion (AIC) and Bayesian information criterion (BIC)) which measure insample fit (i.e., fit to the training data), but penalize model complexity, can be used to estimate an ANN s generalizability. However, there is currently no consensus as to which criterion, if any, is best suited to ANN model selection. A further limitation of traditional in-sample and out-of-sample model selection methods is that they assume a globally optimal solution (i.e., weight vector) has been found during training. In reality, ANNs may be sensitive to initial conditions (i.e., initial weights) and training parameters (e.g., learning rate) and can often become trapped in local minima in weight space. Therefore, evaluation of the model structure may be incorrectly biased by the weights obtained. [5] A number of studies are now advocating the use of Bayesian techniques for the appropriate selection of hydrological and water resources models, as such methods offer an objective and principled way to compare models of varying complexity [Berger and Rios Insua, 1998; Whiting et al., 2004; Marshall et al., 2005]. Because of the difficulty in applying Bayesian methods to complex models, the adoption of such techniques has not yet been extended to applications of ANNs in water resources modeling. Recently, however, Kingston et al. [2005] developed a relatively simple, yet effective, Bayesian training approach for ANNs, based on Markov Chain Monte Carlo (MCMC) sampled draws from the posterior weight distribution. This paper follows on from that of Kingston et al. [2005] by proposing a Bayesian model selection (BMS) method that uses these MCMC sampled weight vectors to estimate the evidence in support of a given ANN structure. An advantage of the Bayesian approach is that it is based on the posterior weight distribution and, thus, is not reliant on finding a single optimum weight vector. Furthermore, the evidence of a model is evaluated using only the training data and therefore, there is no need to use an independent test set. However, the main advantage of the proposed method is considered to be the objective and unambiguous check of redundancy in the model structure that the posterior weight distributions provide. In this paper, the BMS approach is assessed by applying it to two synthetic data sets for which the optimal ANN sizes are determined and by comparing it to standard deterministic model selection criteria. The benefits of the proposed BMS approach are then demonstrated when applied to a real-world water resources case study. The methods presented are suitable for multilayer perceptrons (MLPs) with a single hidden layer, which are the most popular type of ANN used for the prediction of water resources variables [Maier and Dandy, 2000]. 2. Bayesian Model Selection 2.1. Background [6] The concept behind the Bayesian modeling framework is Bayes theorem, which states that any prior beliefs regarding an uncertain quantity are updated, on the basis of new information, to yield a posterior probability of the unknown quantity. MacKay [1995] describes two levels of Bayesian inference that can be performed in ANN modeling: the first involves inference of the network weights under the assumption that the chosen ANN structure is true, while the second involves model comparison in light of the data and the estimated weight distributions. At the first level of inference, Bayes theorem is used to estimate the posterior distribution of the network weights w ={w 1,..., w d } given a set of N target data y ={y 1,..., y N } and an assumed model structure H, as follows: pðwjy; HÞ ¼ pðyjh pðyjw; HÞpðwjHÞ Þ ¼ R pðyjw; HÞpðwjHÞdw ; ð1þ where p(wjh) is the prior distribution; p(yjw, H) is the likelihood function; and p(yjh) is a normalizing constant known as the marginal likelihood, or evidence, of the model. When estimating the posterior of the weights, it is common to ignore the evidence term, instead writing (1) as the proportionality p(wjy, H) / p(yjw, H)p(wjH) (see Kingston et al. [2005] for further details). However, at the second level of inference, when Bayesian methods are used for model selection, the model evidence becomes very important. [7] Given a set of H competing models {H i ;i =1,..., H}, Bayes theorem can be rewritten to infer the posterior probability that, of the H models, H i is the true model of the system given the observed data, as follows: pðh i jyþ ¼ pðyjh i pðyþ ¼ P H j¼1 p yjh j ÞpðH i Þ ; ð2þ p Hj where p(h i ) is the prior probability assigned to H i and p(yjh) is the denominator from (1), or evidence. Although, it is unlikely that any model will actually be true, the Bayesian approach enables the relative merits of the competing models to be compared, which is worthwhile assuming that at least one of the models is approximately correct [Wasserman, 2000]. It is also generally assumed that 2of12
3 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING the prior probabilities assigned to the different models are approximately equal, as a model thought to be highly implausible would not even be considered in the comparison [Neal, 1993]. Therefore, (2) can be simplified to: pðh i jyþ ¼ p ð yjh iþ pðyþ / pðyjh i Þ; ð3þ which states that the relative probabilities of the competing models can be compared on the basis of their evidence [Bishop, 1995]. As discussed by MacKay [1995], the evidence of a model automatically incorporates Occam s razor, which is a principle that states the preference for simple theories. Thus, this data-based term can be used to rank a number of competing models in order of plausibility without the need to specify a prior that gives preference to simple models. The evidence ratio of a pair of competing models is generally referred to as the Bayes factor Proposed BMS Framework [8] For all but the simplest of models, the integral in (1) is analytically intractable and alternative methods are needed to estimate p(yjh). However, traditional estimation methods based on the assumption of a Gaussian posterior distribution are generally not suitable for ANNs, as the weights of an ANN are typically non-gaussian and multimodal [Neal, 1996]. An alternative is to approximate the evidence of a given ANN model using methods based on simulated observations from the posterior. Posterior simulation methods have greatly enhanced the applicability of the first level of Bayesian inference, as they allow the evaluation of (1), while avoiding the need to calculate the intractable evidence term or make incorrect simplifying assumptions. As such, the Markov Chain Monte Carlo Bayesian training approach proposed by Kingston et al. [2005] is used for posterior simulation in this study. For the second level of inference (i.e., BMS), a number of methods have been proposed for estimating the evidence based on posterior simulations [see DiCiccio et al., 1997]. The suitability of these methods for model selection is generally application dependent; therefore, in this paper, three such methods are compared for their suitability in an ANN BMS approach, in conjunction with the MCMC Bayesian training approach used. However, the aim here is not to thoroughly analyze each of the estimators in order to recommend a single method for use in the proposed BMS framework, as this may introduce as much bias into the results of the model selection as the choice of a more conventional model selection criterion could (even though the evidence estimators are based on the posterior distribution of the weights). Rather, it is proposed that estimates of the evidence be used to guide the selection of the appropriate model structure, while a more objective check be performed to select the final model. It is this check, which is based on the posterior weight distributions obtained from the MCMC simulation, that is the main emphasis of the proposed BMS framework, since it provides an unambiguous way to assess redundancies in an ANN model. [9] To apply the proposed BMS approach, the following steps should therefore be taken. First, train a number of ANN models, of which the number of hidden layer nodes are increased systematically (in increments of 1 2), using the MCMC training method, until the model with the maximum evidence has been identified, as estimated on the basis of the posterior simulations. Then, for the ANN with the maximum evidence, inspect the marginal posterior weight distributions of the hidden-output layer weights to identify whether there are any redundant hidden nodes in the model (as described in section 2.2.5). If any redundant hidden nodes are identified, these should be removed from the model. It should be noted that if a model with the required number of hidden nodes was not developed in step 1, such a model will need to be trained from scratch. If no hidden nodes are found to be redundant, inspect the marginal posterior hidden-output weight distributions for the model containing the next increment number of hidden nodes (i.e., 1 2 more hidden nodes) to verify that the maximum evidence model contains the optimal number of hidden nodes, or to determine that a slightly larger model is, in fact, necessary. The details of the specific methods used in this study are given in the following sections MCMC Bayesian Training [10] The MCMC Bayesian training approach developed by Kingston et al. [2005] involves a two-step iterative procedure, where ANN weight vectors are sampled from the posterior distribution using the adaptive Metropolis algorithm [Haario et al., 2001] and the likelihood and prior variance hyperparameters are sampled using the Gibbs sampler. It is assumed that the residuals between the observed data y and the model outputs ^y are normally and independently distributed with zero mean and constant variance s y 2 ; thus, the likelihood function is given by: p yjw; s 2 y ; H ¼ 1 qffiffiffiffiffiffiffiffiffiffiffi 2Ps 2 y Y N i¼1 ( ) ½ exp y i ^y i Š 2 : ð4þ 2s 2 y A hierarchical prior distribution is chosen to reflect the lack of prior knowledge about the weights and to help prevent overfitting of the data. Given by (5), this prior is the product of four different normal distributions, each with a mean of zero, corresponding to four different groups of weights: the input-hidden layer weights, the hidden layer biases, the hidden-output layer weights and the output layer biases; where s 2 wg and d g are the variance and dimension of the gth weight group, respectively. P pðwþ ¼ Y4 dg! dg=2 2Ps 2 i w g exp g¼1 w2 i g 2s g¼1 2 : ð5þ w g [11] Both s 2 y and s 2 w ={s 2 w1,..., s 2 w4 } in (3) and (5), respectively, are treated as unknown hyperparameters with rather noninformative inverse chi-squared hyperprior distributions, which allows their values to be determined from the data. In terms of the prior distribution, this encourages unnecessary weights to take values close to zero, since a small variance will result in a greater prior probability for such weights Gelfand-Dey Evidence Estimator [12] Importance sampling is a useful method for computing the expectation of a function using samples generated from an importance sampling density Q*. In terms of the 3of12
4 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING evidence of an ANN model, importance sampling can be used to estimate the integral in (1) in the form of: P ns i¼1 ^p ðyjhþ ¼ q ipðyjw i ; HÞ P ns i¼1 q ; ð6þ i where ns is the number of samples generated from Q* and q i = p(w i )/Q*(w i ). As such, Gelfand and Dey [1994] proposed the following estimator for p(yjh): ^p ðyjhþ ¼ 1 ns ( ) X ns 1 tðw i Þ ; ð7þ i¼1 pðyjw i ; HÞpðw i jhþ where w i are sampled draws from the posterior distribution and t(w) plays the role of the importance sampling density. In order to obtain accurate results with this estimator, t(w) should be chosen so that it approximates the posterior distribution. However, this is not a trivial task, and a bad choice of t(w) can produce very poor results [Kass and Raftery, 1995]. Nevertheless, the Gelfand-Dey (G-D) estimator seems well suited for application in conjunction with the Bayesian training method proposed by Kingston et al. [2005]. This is because, by using this posterior simulation technique, the proposal distribution employed by the MCMC algorithm is adapted toward the posterior throughout the simulation and, thus, a reasonable choice for t is determined automatically. In this study, t(w) was set equal to Q(w i j~w) N(~w, S f ), where Q(w i j~w) is the proposal distribution for the transition from ~w, the median of the posterior distribution, to w i ; and S f is the covariance of the proposal at the final iteration of the MCMC algorithm. One of the main advantages of the G-D estimator, when used in conjunction with MCMC sampling, is that it uses sampled draws from the posterior directly and requires no further samples to be generated from any other distribution. However, it is acknowledged that the use of a Gaussian t(w) distribution, when the posterior weight distribution is typically non-gaussian, may introduce inaccuracies into the evidence estimates Chib-Jeliazkov Evidence Estimator [13] By rearranging the general Bayes theorem expression given by (1) and taking the logarithm at some fixed point w, the following expression for log p(yjh) is obtained: log pðyjhþ ¼ log pðyjw; HÞþlog pðwjhþ log pðwjy; HÞ: ð8þ If w is a sampled draw from the posterior distribution, the only unknown in this equation is log p(wjy, H). Therefore, estimation of the evidence is reduced to estimating the posterior weight density at a single point w. Chib and Jeliazkov [2001] proposed the following equation for doing this: P ns i¼1 ^p ðwjy; HÞ ¼ a ð wjw iþqðwjw i Þ P ns j¼1 a w ; ð9þ jjw where w i are sampled draws from the posterior distribution; w j are sampled draws from Q(w i jw), the proposal density for the transition from w to w i ; and a(wjw) is the acceptance probability for a transition from w to w. While the choice of w is arbitrary, for estimation efficiency it is appropriate to choose a point that has high posterior density [Chib and Jeliazkov, 2001]. In this study, w was set equal to the median of the posterior distribution, ~w. [14] The Chib-Jeliazkov (C-J) estimator has an advantage over the G-D method in that the t() function, which is often difficult to select, is not required. However, samples are required from both the proposal and posterior distributions, which increases the computational cost of the overall algorithm. Furthermore, evaluation of a(wjw i ), Q(wjw i ) and a(w j jw) are required for i, j =1,..., ns in order to calculate ^p(yjh) The 1/2BIC Evidence Estimator [15] The Bayesian information criterion [Schwarz, 1978] gives a rough approximation to the logarithm of the Bayes factor for comparing a model to the null model. Under this approximation, it holds that: ^p ðyjhþ exp 1 2 BIC ; ð10þ where BIC = 2log p(yjw, H) +d log N, d is the dimension of w and N is the size of the training data set. While it is noted that this approximation is rough, the BIC estimator has been shown to be asymptotically (i.e., as N!1) consistent for model selection and has been found to work well in practice [Lee, 2001, 2002]. [16] As mentioned, the BIC can be sensitive to the weights obtained; therefore, in this study, the 1/2BIC values were evaluated for each sampled weight vector w 1,..., w ns, resulting in a distribution of 1/2BIC values that accounts for such variability. The maximum value of this distribution (corresponding to the maximum likelihood value) gives the value of ^p(yjh), which can then be used for comparing models of different sizes. If the likelihood values p(yjw i, H) are recorded throughout the posterior simulation, subtraction of the constant d 2 log N from each negative log likelihood value is all that is required to evaluate the distribution for ^p(yjh). This is much simpler than either the G-D or the C-J estimators; however, as the 1/2BIC estimator given by (10) is a large sample approximation, it is not expected to be as accurate when limited data are available Checking Evidence Estimates With Posterior Weight Distributions [17] It is important to keep in mind that the evidence estimates provided by each of the estimators presented in sections are simply that, estimates. Furthermore, as discussed by Lee [2002], it can be difficult to obtain accurate estimates of p(yjh) on the basis of posterior simulations, and this is particularly the case for ANNs. As mentioned, it is therefore proposed that the approximated evidence values be used as a guide for model selection, but a final check of the results be carried out using the posterior weight distributions. If the marginal posterior distribution of a hidden-output layer weight includes the value zero within the 95% highest density region, this suggests that the associated hidden node may be pruned from the network, with a 95% level of credibility that model performance will not be affected (i.e., the node and its associated weights are redundant). If there are more than one hidden-output layer weights with marginal posterior distributions that include 4of12
5 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Figure 1. Examples of a pair of hidden-output layer weights with marginal posterior distributions that include zero within the 95% highest density regions, (a) where the joint distribution passes through (0, 0) and (b) where it does not. zero within the 95% highest density region, these weights should be inspected in a pairwise manner, by means of their respective scatterplots (e.g., w i versus w j, w i versus w k, w j versus w k ), to determine whether the joint distribution of the weights passes through the origin (0, 0), which would indicate that both weights in the pair, and the corresponding hidden nodes, are redundant. Otherwise, if the joint distribution does not pass through (0, 0), only one of the hidden nodes in the pair is redundant. This is illustrated in Figure 1, where two different examples of a pair of hidden-output layer weights for which the marginal posterior distributions include zero within the 95% highest density regions are shown. In Figure 1a, the scatterplot of hidden-output weight 1 versus hidden-output weight 2 passes though (0, 0), indicating that both hidden nodes are not required in the model. However, in Figure 1b, the scatterplot does not pass through the origin, indicating that at least one of the hidden nodes in the pair is required. When considering more than two weights with marginal posterior distributions that include zero within the 95% highest density region, it is important to inspect all pairs of weights before determining a hidden node to be unnecessary. In this study, histograms of the hidden-output weight probability density functions were constructed, from which the 95% highest density regions were estimated Assessment Using Synthetic Data Data and Methods [18] In order to assess the proposed BMS approach, it was first applied to two synthetically generated data sets for which the optimum network sizes could be determined. The first data set was generated from the following linear time series model: y t ¼ 0:3y t 1 0:6y t 4 0:5y t 9 þ ; ð11þ where is a Gaussian random variate with a mean of zero and standard deviation of one. The second data set was also generated by the above time series model, but with the linear addition of an independent nonlinear component sin(2x t ), as shown in (12), where x is an independent random variable uniformly distributed between p and p. y t ¼ 0:3y t 1 0:6y t 4 0:5y t 9 þ sinð2x t Þþ: ð12þ A total of 800 and 1000 data points were generated by (11) and (12), respectively. To reduce the effects of random initialization, the first 100 points were discarded from each set, leaving 700 and 900 points in data sets I and II, respectively. In each case, 80% of these data were used for training and 20% were used for testing. [19] The optimum ANN for modeling a set of data should be that which, when trained until convergence using the correct model inputs and error function, has residuals that closely resemble the random noise in the data. The advantage of synthetic data is that, unlike real data, the inputs and noise model used in the generation of the data are known and, therefore, it is possible to determine what size network is necessary for an appropriate mapping of the data. For each synthetic data set, 10 ANN models, containing between 1 and 10 hidden nodes, were trained by multistart backpropagation until convergence (i.e., overfitting was not prevented) and the resulting model residuals ^ were compared to the noise added to the training data in terms of their variance and mean absolute values (MAV). The network for which these values matched most closely was considered to provide the optimum level of complexity. The in-sample AIC and BIC values and out-of-sample RMSE values were also calculated to compare the results obtained using the BMS approach to standard deterministic model selection methods. 5of12
6 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Table 1. Residuals Variance s^ 2 and MAV^ Results Used to Determine the Optimal Number of Hidden Nodes for Modeling Data Sets I and II Together With Deterministic Model Selection Criteria AIC, BIC, and RMSE Data Set I Data Set II Hidden Nodes s^ 2 MAV^ AIC BIC RMSE s^ 2 MAV^ AIC BIC RMSE [20] The MCMC Bayesian training approach described in section was then used to fit the 10 networks to each data set, taking particular care to ensure that (approximate) convergence of the algorithm was achieved. This was checked by tracking the mean log posterior density throughout the simulation [see Kingston et al., 2005]. Each of the evidence estimators discussed in section 2.2 was used to evaluate the evidence of the models, in order to select the network with the greatest posterior probability for each data set. By comparing these results to the actual optimum network sizes (determined as described above), it was possible to assess which estimator, if any, was most appropriate for BMS within the proposed framework. Inspection of marginal posterior distributions was carried out, as described in section 2.2.5, to check or confirm the results of the evidence comparisons Results [21] The residual variance and MAV results used to determine the optimum network sizes for modeling data sets I and II are shown in Table 1. For the training subset of data set I, the variance and MAV of were equal to and 0.767, respectively. As highlighted in bold in Table 1, a 1 hidden node ANN was the smallest network able to model the data such that both the variance s 2 and MAV of the residuals ^ were approximately equal to the corresponding values of. This result is intuitive, since the data generating function given by (11) is linear and, as such, an ANN containing one hidden node is sufficient. For the training subset of data set II, the variance and MAV of were and 0.797, respectively. As highlighted in bold in Table 1, a 3 hidden node ANN was the smallest network able to model the data such that s 2 and MAV of ^ approximated the corresponding values of. It is also intuitive that data set II would require a network containing at least two (sigmoidal) hidden nodes, as the data generating function given by (12) includes a nonlinear, nonmonotonic component. Therefore, it was concluded that these results were accurate and the networks found to be optimal were considered the actual optimum network sizes for modeling data sets I and II. [22] Also shown in Table 1 are the RMSE, AIC, and BIC values calculated for each deterministic network. It is interesting to note that the minimum (best) values of these deterministic model selection criteria, which are highlighted in italics, are not in agreement for either data set. Given that different deterministic model selection criteria are often used in different studies for no obvious reason, and considering that an optimal model structure may be selected on the basis of only a marginal improvement in the chosen criterion, these results demonstrate the difficulty in consistently selecting the optimum ANN model using such deterministic criteria. In Table 1, it is apparent that the insample AIC underpenalizes model complexity, which is in agreement with the findings of Faraway and Chatfield [1998], while the out-of-sample RMSE results indicate that the best out-of-sample fit is not necessarily obtained using a model of optimum complexity. In each case, the in-sample BIC was able to successfully identify the optimum models; however, there has been some debate regarding the appropriateness of this criterion for ANN model selection in the past [Qi and Zhang, 2001]. Furthermore, as previously mentioned, each of these criteria is heavily dependent on the single set of optimum weights found during training. [23] The resulting log evidence values for all of the 10 different network sizes applied to data sets I and II are plotted in Figures 2a and 2b, respectively. All three evidence estimators correctly identified the optimum network size for both data sets; however, the G-D and C-J estimates, although very similar, have greater variability than the 1/ 2BIC estimates and appear to be less stable for model selection purposes. Since the evidence of a model automatically incorporates a preference for simpler models and because simpler ANN models are always nested in more complex ANNs when only the number of hidden layer nodes is varied, it would be expected that any additional complexity over that required (e.g., 1 hidden node for data set I and 3 hidden nodes for data set II) would result in a reduction in the evidence. However, as can be seen in Figure 2, this was not the case beyond 5 and 6 hidden nodes for both the G-D and C-J estimates when the models were applied to data sets I and II, respectively. The 1/2BIC estimates, on the other hand, indicate a more logical ordering of the models considered for each data set. [24] Since these data were synthetic, it was possible to check that the optimum network sizes identified using the evidence estimators were correct; however, in a real world study this would not be the case. As discussed in section 2.2.5, the marginal posterior weight distributions for the hidden-output weights provide a worthwhile check of the evidence estimates. For data set I, the marginal posterior distributions for the hidden-output weights of the 1 and 2 hidden node models are displayed in Figures 3a and 3b, respectively. As the distribution in Figure 3a does not 6of12
7 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Figure 2. set II. Evidence estimates for the 1,..., 10 hidden node ANNs applied to (a) data set I and (b) data include the value zero, it is indicated that at least one hidden node is required to model data set I. On the other hand, the 95% highest density regions of both marginal posterior distributions shown in Figure 3b do include zero, indicating that at least one of the nodes is not necessary. As the scatterplot in Figure 3b does not pass through the origin, it can be determined that only one of the hidden nodes may be removed from the network. This leaves a 1 hidden node network, which reinforces the evidence results. [25] For data set II, the marginal posterior distributions of the hidden-output weights of the 3 and 4 hidden nodes networks are displayed in Figures 4a and 4b, respectively. In Figure 4a, it can be seen that none of the distributions include zero, indicating that all three of the hidden nodes are needed for modeling data set II, whereas the 95% highest density region of the distribution for hidden-output weight 2, shown in Figure 4b, does include zero, which indicates that this node may be removed from the network without loss of predictive performance. Again, these results reinforce the results obtained with the evidence estimators. 3. Salinity Case Study [26] The aim of model selection is to enable generalization to new cases. In this case study, the performance of the proposed BMS method was assessed on data sampled from a different domain of the data-generating distribution than the training data. In other words, the BMS method was considered with respect to extrapolations or novel predictions. The case study chosen for this purpose was that of forecasting salinity concentrations in the River Murray at Figure 3. Marginal posterior hidden-output weight distribution for the (a) 1 hidden node and (b) 2 hidden node ANNs applied to data set I, showing 95% highest density regions. 7of12
8 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Figure 4. Marginal posterior hidden-output weight distributions for the (a) 3 hidden node and (b) 4 hidden node ANNs applied to data set II, showing 95% highest density regions. Murray Bridge, South Australia, 14 days in advance. This is a benchmark case study to which ANN models have been applied previously by Bowden et al. [2002, 2005] and Kingston et al. [2005]. In each of these studies, approximately half of the available data (1964 data points from 1 December 1986 to 30 June 1992) were used to develop the ANN models, while the remaining data (2028 data points from 1 July 1992 to 1 April 1998) were reserved to simulate a real-time forecasting situation using the developed ANNs. By clustering the data, Bowden et al. [2002] identified that the data set used to perform the real-time simulation contained two regions of uncharacteristic data that were outside the domain of the data used to develop the model. Therefore, it was known that the model would have to extrapolate in these regions if the same data were used for model development and real-time forecasting in this study. In Kingston et al. [2005] and Bowden et al. [2005], only 64% (1257 data points) of the model development data were used for training, while the remaining data were used for cross validation (314 data points) and independent evaluation (393 data points) of the ANN models developed. Although these processes were not carried out in this study, for comparative purposes, only 64% of the model development data were used for training in this study also. These data were sampled over the entire period of the model development data in order to obtain a representative training sample. The 13 model inputs used by Kingston et al. [2005] and Bowden et al. [2005] were also used in this study and included salinity, river level and flow data at various lags and locations in the river. [27] Using a trial and error model selection approach based on the out-of-sample RMSE, Kingston et al. [2005] found that an ANN containing 4 hidden nodes (61 weights = 20.6 training samples per weight) was the most appropriate for modeling the salinity data. On the other hand, Bowden et al. [2005] found that an ANN containing 32 hidden nodes (494 weights = only 2.5 training samples per weight) performed the best; however, a less systematic approach was used to achieve this result. Therefore, the result obtained by Kingston et al. [2005] was used to guide BMS in this study. Initially, networks with 2, 4,...,10 hidden nodes were developed using the MCMC Bayesian training approach of Kingston et al. [2005]; again, taking particular care to ensure that convergence was achieved. The 1/2BIC, G-D, and C-J evidence estimators were used to evaluate the evidence values of each network, in order to determine which of the initial models had the greatest posterior probability. According to the findings of the assessment carried out in section 2.3, the 1/2BIC estimator was given the most weight in terms of model selection, while the G-D and C-J estimators were primarily used for comparative purposes. The marginal distributions for the hidden-output weights of the ANN model with the highest posterior probability were then inspected to determine whether any of the hidden nodes could be pruned from the model as described in section The same distributions were also inspected for the model containing two more hidden nodes than the ANN with the highest posterior probability, in order to verify that one or both of the two additional hidden nodes were unnecessary and could therefore be pruned from the network Results [28] The log evidence values estimated with the 1/2BIC, G-D, and C-J estimators for the 2, 4,..., 10 hidden node ANNs are plotted in Figure 5, where it can be seen that the 4 hidden node ANN had the greatest evidence according to all three estimators. To check this result, the marginal posterior distributions for the hidden-output weights of the 4 and 6 hidden node ANNs were inspected. These are shown in Figures 6a and 6b, respectively. It can be seen in Figure 6a that, for the 4 hidden node model, all of the hidden nodes are necessary, as zero is not included within the 95% highest 8of12
9 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Figure 5. Evidence estimates for the 2, 4,..., 10 hidden node ANNs for the salinity case study. density regions of any of the weight distributions. It can also be seen in Figure 6b that, for the 6 hidden node model, zero is included in the 95% highest density regions of the distributions for hidden-output weights 2 and 6, indicating that at least one of the corresponding nodes could be pruned from the network. By inspection of the scatterplot for hidden-output weight 2 versus hidden-output weight 6, shown in Figure 7, it was evident that both nodes could be pruned, as the joint distribution was found to pass through the origin; thus leaving a network with 4 hidden nodes. [29] To verify that 4 hidden nodes provided the optimal ANN structure for obtaining 14-day salinity forecasts, and to further check the model selection results, networks with 3 and 5 hidden nodes were trained and assessed under the BMS approach. The resulting log evidence values estimated with the 1/2BIC, G-D, and C-J estimators are plotted in Figure 7. Scatterplot of hidden-output weight 2 versus hidden-output weight 6 for the 6 hidden node ANN for the salinity case study. Figure 8, together with those obtained for the five original models. Again, it can be seen that the 4 hidden node ANN had the greatest overall evidence according to all of the estimators. The marginal posterior distributions for the hidden-output weights of the 3 and 5 hidden node ANNs are shown in Figures 9a and 9b, respectively. It can be seen in Figure 9a that all of the hidden nodes are needed in the 3 hidden node model, as none of the distributions are close to zero. However, as can be seen in Figure 9b, the distribution for hidden-output weight 3 includes zero within the 95% highest density region, indicating that the corresponding hidden node is unnecessary, and hence it can again be concluded that a 4 hidden node ANN is more optimal. [30] For comparison of these results with standard model selection methods, the in-sample AIC and BIC and out-of- Figure 6. Marginal posterior hidden-output weight distributions of the (a) 4 hidden node and (b) 6 hidden node ANNs for the salinity case study, showing 95% highest density regions. 9of12
10 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Table 2. Standard Model Selection Criteria Results for 2, 4,..., 10 Hidden Node Deterministic ANNs for the Salinity Case Study Hidden Nodes AIC BIC RMSE (Electrical Conductivity Units) Figure 8. Estimated evidence values including those estimated for the 3 and 5 hidden node ANNs for the salinity case study. sample RMSE results obtained for the 2, 4,..., 10 hidden node ANNs when trained deterministically are given in Table 2. As can be seen in Table 2 and as found by Kingston et al. [2005], the out-of-sample RMSE results indicate that the 4 hidden node ANN is optimal for modeling the salinity data, which is in agreement with the BMS results. On the other hand, the in-sample AIC and BIC results incorrectly indicate that, of the models considered, the 10 hidden node ANN is optimal. Unlike the BMS approach, there is no way to check the accuracy of these deterministic criteria and the optimal network selected is dependent on the subjective choice of criterion. As demonstrated, this can result in inappropriate complexity selection, as each of these criteria is susceptible to erroneous results. [31] Finally, to determine whether the ANN model selected using the proposed BMS approach had better generalizability than those models incorrectly identified as optimal using standard model selection procedures, the predictive performance of the 4 hidden node Bayesian ANN was compared to that of the 10 hidden node ANN determined to be optimal using the deterministic in-sample AIC and BIC and the 32 hidden node ANN developed by Bowden et al. [2005], when applied to the real-time forecasting data. Furthermore, to verify that any improvement in generalizability could be somewhat attributed to appropriate model selection and was not simply due to the use of Bayesian training, which itself improves generalizability, the performance of the 4 and 10 hidden node ANNs were assessed when trained both deterministically and using the MCMC Bayesian approach. Random samples of 10,000 weight vectors from the posterior distributions of the 4 and 10 hidden node Bayesian ANNs were used to calculate predictive distributions for the model development and realtime forecasting data. From these, mean predictions were evaluated and RMSE results were obtained on the basis of these mean predictions when applied to both the model development and real-time forecasting data. For all of the deterministic ANN models, cross validation was employed during training to prevent overfitting and RMSE results were again obtained for the model development and real- Figure 9. Marginal posterior hidden-output weight distributions for the (a) 3 hidden node and (b) 5 hidden node ANNs for the salinity case study, showing 95% highest density regions. 10 of 12
11 KINGSTON ET AL.: BMS OF ANNS IN WATER RESOURCES MODELING Table 3. Comparison of RMSEs (Electrical Conductivity Units) Obtained by Models of Different Complexity Trained Using Different Algorithms for the Salinity Case Study Model Development Data Real-Time Forecasting Data 4 hidden nodes a hidden nodes b hidden nodes a hidden nodes b hidden nodes b,c a Bayesian training. b Deterministically trained. c Developed by Bowden et al. [2005]; contained direct input-output connections, which is potentially why a better fit to the data was obtained than with the deterministic models developed in this study. time forecasting data. These results are presented in Table 3. Overall, the real-time forecasting results show that the generalizability of the 4 hidden node ANN model developed using the proposed BMS approach was significantly better than that of the deterministic ANN models developed in this study and by Bowden et al. [2005], and was also moderately better than that of the 10 hidden node ANN developed using Bayesian training. For the deterministic models, while the generalizability of the 4 hidden node ANN was greater than the 10 hidden node model, the 32 hidden node ANN developed by Bowden et al. [2005] had the greatest generalizability, even though it was the most complex. This may be explained by the fact that, unlike the models developed in this study, it contained direct inputoutput connections; however, it also highlights the potential for obtaining suboptimal results when deterministic methods are used for developing ANNs, regardless of whether the optimum complexity is determined. Therefore, it can be concluded that, by using a total Bayesian approach to objectively select the optimum complexity required, whilst accounting for all plausible weight vectors, a model may be developed that is less susceptible to overfitting and more broadly influenced by the overall information contained in the data and, as such, a more generalized mapping of the underlying relationship can be achieved. This can be seen in Figure 10, where the 4 hidden node Bayesian ANN gives a significantly better fit to the real-time forecasting data than the 10 hidden node model developed using deterministic methods, indicating that although this model did not fit the model development data quite as well as the larger deterministic ANN, it enabled better generalization and extrapolation. In comparison to the 4 hidden node Bayesian ANN, the 10 hidden node deterministic model results in noisier forecasts as well as significantly over predicting some peaks, while significantly under predicting others. Even on the model development data, the performance of the 4 hidden node Bayesian ANN was similar to that of the 32 hidden node deterministic ANN developed by Bowden et al. [2005], which contained 433 more weights. These results highlight the importance of appropriate model selection techniques, as smaller models are less susceptible to overfitting, more efficient to train, have a smaller degree of uncertainty associated with the weights and resulting predictions and are easier to interpret. 4. Conclusions [32] It was shown in this paper that the proposed BMS method is a simple and objective method for accurately selecting the optimal complexity of an ANN model when used in conjunction with the Bayesian training procedure developed by Kingston et al. [2005]. In this study, it was apparent that the 1/2BIC evidence estimator was most consistently able to select the optimum complexity of an ANN; however, it is acknowledged that all evidence estimates based on posterior simulations may be subject to potential inaccuracies (e.g., the BIC estimate may be particularly inaccurate when limited data are available). Therefore, whichever evidence estimator is used within the framework, it is of utmost importance that the estimator be used to guide selection, while inspection of the marginal posterior hidden-output weight distributions should be performed to determine the final optimal network. The ability to carry out this check is considered to be one of the greatest advantages of the proposed Bayesian approach over conventional model selection methods, which do not provide such a statistical and unambiguous test, but instead rely on the modeler s subjective choice of selection criterion. It is also worth noting, however, that each of the evidence estimators considered in this study was able to correctly identify the optimum complexity of the ANN models Figure 10. Mean predictions and 95% prediction limits obtained with the 4 hidden node Bayesian ANN in comparison to the predictions obtained using the 10 hidden node deterministic ANN when applied to the real-time forecasting data. 11 of 12
A Bayesian approach to artificial neural network model selection
 A Bayesian approach to artificial neural network model selection Kingston, G. B., H. R. Maier and M. F. Lambert Centre for Applied Modelling in Water Engineering, School of Civil and Environmental Engineering,
A Bayesian approach to artificial neural network model selection Kingston, G. B., H. R. Maier and M. F. Lambert Centre for Applied Modelling in Water Engineering, School of Civil and Environmental Engineering,
Overview. Monte Carlo Methods. Statistics & Bayesian Inference Lecture 3. Situation At End Of Last Week
 Statistics & Bayesian Inference Lecture 3 Joe Zuntz Overview Overview & Motivation Metropolis Hastings Monte Carlo Methods Importance sampling Direct sampling Gibbs sampling Monte-Carlo Markov Chains Emcee
Statistics & Bayesian Inference Lecture 3 Joe Zuntz Overview Overview & Motivation Metropolis Hastings Monte Carlo Methods Importance sampling Direct sampling Gibbs sampling Monte-Carlo Markov Chains Emcee
FMA901F: Machine Learning Lecture 3: Linear Models for Regression. Cristian Sminchisescu
 FMA901F: Machine Learning Lecture 3: Linear Models for Regression Cristian Sminchisescu Machine Learning: Frequentist vs. Bayesian In the frequentist setting, we seek a fixed parameter (vector), with value(s)
FMA901F: Machine Learning Lecture 3: Linear Models for Regression Cristian Sminchisescu Machine Learning: Frequentist vs. Bayesian In the frequentist setting, we seek a fixed parameter (vector), with value(s)
Bayesian Estimation for Skew Normal Distributions Using Data Augmentation
 The Korean Communications in Statistics Vol. 12 No. 2, 2005 pp. 323-333 Bayesian Estimation for Skew Normal Distributions Using Data Augmentation Hea-Jung Kim 1) Abstract In this paper, we develop a MCMC
The Korean Communications in Statistics Vol. 12 No. 2, 2005 pp. 323-333 Bayesian Estimation for Skew Normal Distributions Using Data Augmentation Hea-Jung Kim 1) Abstract In this paper, we develop a MCMC
Discussion on Bayesian Model Selection and Parameter Estimation in Extragalactic Astronomy by Martin Weinberg
 Discussion on Bayesian Model Selection and Parameter Estimation in Extragalactic Astronomy by Martin Weinberg Phil Gregory Physics and Astronomy Univ. of British Columbia Introduction Martin Weinberg reported
Discussion on Bayesian Model Selection and Parameter Estimation in Extragalactic Astronomy by Martin Weinberg Phil Gregory Physics and Astronomy Univ. of British Columbia Introduction Martin Weinberg reported
Computer vision: models, learning and inference. Chapter 10 Graphical Models
 Computer vision: models, learning and inference Chapter 10 Graphical Models Independence Two variables x 1 and x 2 are independent if their joint probability distribution factorizes as Pr(x 1, x 2 )=Pr(x
Computer vision: models, learning and inference Chapter 10 Graphical Models Independence Two variables x 1 and x 2 are independent if their joint probability distribution factorizes as Pr(x 1, x 2 )=Pr(x
What is machine learning?
 Machine learning, pattern recognition and statistical data modelling Lecture 12. The last lecture Coryn Bailer-Jones 1 What is machine learning? Data description and interpretation finding simpler relationship
Machine learning, pattern recognition and statistical data modelling Lecture 12. The last lecture Coryn Bailer-Jones 1 What is machine learning? Data description and interpretation finding simpler relationship
MCMC Diagnostics. Yingbo Li MATH Clemson University. Yingbo Li (Clemson) MCMC Diagnostics MATH / 24
 MCMC Diagnostics Yingbo Li Clemson University MATH 9810 Yingbo Li (Clemson) MCMC Diagnostics MATH 9810 1 / 24 Convergence to Posterior Distribution Theory proves that if a Gibbs sampler iterates enough,
MCMC Diagnostics Yingbo Li Clemson University MATH 9810 Yingbo Li (Clemson) MCMC Diagnostics MATH 9810 1 / 24 Convergence to Posterior Distribution Theory proves that if a Gibbs sampler iterates enough,
MCMC Methods for data modeling
 MCMC Methods for data modeling Kenneth Scerri Department of Automatic Control and Systems Engineering Introduction 1. Symposium on Data Modelling 2. Outline: a. Definition and uses of MCMC b. MCMC algorithms
MCMC Methods for data modeling Kenneth Scerri Department of Automatic Control and Systems Engineering Introduction 1. Symposium on Data Modelling 2. Outline: a. Definition and uses of MCMC b. MCMC algorithms
A noninformative Bayesian approach to small area estimation
 A noninformative Bayesian approach to small area estimation Glen Meeden School of Statistics University of Minnesota Minneapolis, MN 55455 glen@stat.umn.edu September 2001 Revised May 2002 Research supported
A noninformative Bayesian approach to small area estimation Glen Meeden School of Statistics University of Minnesota Minneapolis, MN 55455 glen@stat.umn.edu September 2001 Revised May 2002 Research supported
Nested Sampling: Introduction and Implementation
 UNIVERSITY OF TEXAS AT SAN ANTONIO Nested Sampling: Introduction and Implementation Liang Jing May 2009 1 1 ABSTRACT Nested Sampling is a new technique to calculate the evidence, Z = P(D M) = p(d θ, M)p(θ
UNIVERSITY OF TEXAS AT SAN ANTONIO Nested Sampling: Introduction and Implementation Liang Jing May 2009 1 1 ABSTRACT Nested Sampling is a new technique to calculate the evidence, Z = P(D M) = p(d θ, M)p(θ
Machine Learning Techniques for Data Mining
 Machine Learning Techniques for Data Mining Eibe Frank University of Waikato New Zealand 10/25/2000 1 PART VII Moving on: Engineering the input and output 10/25/2000 2 Applying a learner is not all Already
Machine Learning Techniques for Data Mining Eibe Frank University of Waikato New Zealand 10/25/2000 1 PART VII Moving on: Engineering the input and output 10/25/2000 2 Applying a learner is not all Already
Neural Networks. CE-725: Statistical Pattern Recognition Sharif University of Technology Spring Soleymani
 Neural Networks CE-725: Statistical Pattern Recognition Sharif University of Technology Spring 2013 Soleymani Outline Biological and artificial neural networks Feed-forward neural networks Single layer
Neural Networks CE-725: Statistical Pattern Recognition Sharif University of Technology Spring 2013 Soleymani Outline Biological and artificial neural networks Feed-forward neural networks Single layer
A Model Selection Criterion for Classification: Application to HMM Topology Optimization
 A Model Selection Criterion for Classification Application to HMM Topology Optimization Alain Biem IBM T. J. Watson Research Center P.O Box 218, Yorktown Heights, NY 10549, USA biem@us.ibm.com Abstract
A Model Selection Criterion for Classification Application to HMM Topology Optimization Alain Biem IBM T. J. Watson Research Center P.O Box 218, Yorktown Heights, NY 10549, USA biem@us.ibm.com Abstract
Level-set MCMC Curve Sampling and Geometric Conditional Simulation
 Level-set MCMC Curve Sampling and Geometric Conditional Simulation Ayres Fan John W. Fisher III Alan S. Willsky February 16, 2007 Outline 1. Overview 2. Curve evolution 3. Markov chain Monte Carlo 4. Curve
Level-set MCMC Curve Sampling and Geometric Conditional Simulation Ayres Fan John W. Fisher III Alan S. Willsky February 16, 2007 Outline 1. Overview 2. Curve evolution 3. Markov chain Monte Carlo 4. Curve
Adaptive spatial resampling as a Markov chain Monte Carlo method for uncertainty quantification in seismic reservoir characterization
 1 Adaptive spatial resampling as a Markov chain Monte Carlo method for uncertainty quantification in seismic reservoir characterization Cheolkyun Jeong, Tapan Mukerji, and Gregoire Mariethoz Department
1 Adaptive spatial resampling as a Markov chain Monte Carlo method for uncertainty quantification in seismic reservoir characterization Cheolkyun Jeong, Tapan Mukerji, and Gregoire Mariethoz Department
Artificial Neural Network based Curve Prediction
 Artificial Neural Network based Curve Prediction LECTURE COURSE: AUSGEWÄHLTE OPTIMIERUNGSVERFAHREN FÜR INGENIEURE SUPERVISOR: PROF. CHRISTIAN HAFNER STUDENTS: ANTHONY HSIAO, MICHAEL BOESCH Abstract We
Artificial Neural Network based Curve Prediction LECTURE COURSE: AUSGEWÄHLTE OPTIMIERUNGSVERFAHREN FÜR INGENIEURE SUPERVISOR: PROF. CHRISTIAN HAFNER STUDENTS: ANTHONY HSIAO, MICHAEL BOESCH Abstract We
Estimation of Item Response Models
 Estimation of Item Response Models Lecture #5 ICPSR Item Response Theory Workshop Lecture #5: 1of 39 The Big Picture of Estimation ESTIMATOR = Maximum Likelihood; Mplus Any questions? answers Lecture #5:
Estimation of Item Response Models Lecture #5 ICPSR Item Response Theory Workshop Lecture #5: 1of 39 The Big Picture of Estimation ESTIMATOR = Maximum Likelihood; Mplus Any questions? answers Lecture #5:
4.12 Generalization. In back-propagation learning, as many training examples as possible are typically used.
 1 4.12 Generalization In back-propagation learning, as many training examples as possible are typically used. It is hoped that the network so designed generalizes well. A network generalizes well when
1 4.12 Generalization In back-propagation learning, as many training examples as possible are typically used. It is hoped that the network so designed generalizes well. A network generalizes well when
Issues in MCMC use for Bayesian model fitting. Practical Considerations for WinBUGS Users
 Practical Considerations for WinBUGS Users Kate Cowles, Ph.D. Department of Statistics and Actuarial Science University of Iowa 22S:138 Lecture 12 Oct. 3, 2003 Issues in MCMC use for Bayesian model fitting
Practical Considerations for WinBUGS Users Kate Cowles, Ph.D. Department of Statistics and Actuarial Science University of Iowa 22S:138 Lecture 12 Oct. 3, 2003 Issues in MCMC use for Bayesian model fitting
Homework. Gaussian, Bishop 2.3 Non-parametric, Bishop 2.5 Linear regression Pod-cast lecture on-line. Next lectures:
 Homework Gaussian, Bishop 2.3 Non-parametric, Bishop 2.5 Linear regression 3.0-3.2 Pod-cast lecture on-line Next lectures: I posted a rough plan. It is flexible though so please come with suggestions Bayes
Homework Gaussian, Bishop 2.3 Non-parametric, Bishop 2.5 Linear regression 3.0-3.2 Pod-cast lecture on-line Next lectures: I posted a rough plan. It is flexible though so please come with suggestions Bayes
An Efficient Model Selection for Gaussian Mixture Model in a Bayesian Framework
 IEEE SIGNAL PROCESSING LETTERS, VOL. XX, NO. XX, XXX 23 An Efficient Model Selection for Gaussian Mixture Model in a Bayesian Framework Ji Won Yoon arxiv:37.99v [cs.lg] 3 Jul 23 Abstract In order to cluster
IEEE SIGNAL PROCESSING LETTERS, VOL. XX, NO. XX, XXX 23 An Efficient Model Selection for Gaussian Mixture Model in a Bayesian Framework Ji Won Yoon arxiv:37.99v [cs.lg] 3 Jul 23 Abstract In order to cluster
Slides for Data Mining by I. H. Witten and E. Frank
 Slides for Data Mining by I. H. Witten and E. Frank 7 Engineering the input and output Attribute selection Scheme-independent, scheme-specific Attribute discretization Unsupervised, supervised, error-
Slides for Data Mining by I. H. Witten and E. Frank 7 Engineering the input and output Attribute selection Scheme-independent, scheme-specific Attribute discretization Unsupervised, supervised, error-
Probabilistic Graphical Models
 Overview of Part Two Probabilistic Graphical Models Part Two: Inference and Learning Christopher M. Bishop Exact inference and the junction tree MCMC Variational methods and EM Example General variational
Overview of Part Two Probabilistic Graphical Models Part Two: Inference and Learning Christopher M. Bishop Exact inference and the junction tree MCMC Variational methods and EM Example General variational
Sampling informative/complex a priori probability distributions using Gibbs sampling assisted by sequential simulation
 Sampling informative/complex a priori probability distributions using Gibbs sampling assisted by sequential simulation Thomas Mejer Hansen, Klaus Mosegaard, and Knud Skou Cordua 1 1 Center for Energy Resources
Sampling informative/complex a priori probability distributions using Gibbs sampling assisted by sequential simulation Thomas Mejer Hansen, Klaus Mosegaard, and Knud Skou Cordua 1 1 Center for Energy Resources
1 Methods for Posterior Simulation
 1 Methods for Posterior Simulation Let p(θ y) be the posterior. simulation. Koop presents four methods for (posterior) 1. Monte Carlo integration: draw from p(θ y). 2. Gibbs sampler: sequentially drawing
1 Methods for Posterior Simulation Let p(θ y) be the posterior. simulation. Koop presents four methods for (posterior) 1. Monte Carlo integration: draw from p(θ y). 2. Gibbs sampler: sequentially drawing
3 Nonlinear Regression
 CSC 4 / CSC D / CSC C 3 Sometimes linear models are not sufficient to capture the real-world phenomena, and thus nonlinear models are necessary. In regression, all such models will have the same basic
CSC 4 / CSC D / CSC C 3 Sometimes linear models are not sufficient to capture the real-world phenomena, and thus nonlinear models are necessary. In regression, all such models will have the same basic
3 Nonlinear Regression
 3 Linear models are often insufficient to capture the real-world phenomena. That is, the relation between the inputs and the outputs we want to be able to predict are not linear. As a consequence, nonlinear
3 Linear models are often insufficient to capture the real-world phenomena. That is, the relation between the inputs and the outputs we want to be able to predict are not linear. As a consequence, nonlinear
Markov Random Fields and Gibbs Sampling for Image Denoising
 Markov Random Fields and Gibbs Sampling for Image Denoising Chang Yue Electrical Engineering Stanford University changyue@stanfoed.edu Abstract This project applies Gibbs Sampling based on different Markov
Markov Random Fields and Gibbs Sampling for Image Denoising Chang Yue Electrical Engineering Stanford University changyue@stanfoed.edu Abstract This project applies Gibbs Sampling based on different Markov
Tutorial using BEAST v2.4.1 Troubleshooting David A. Rasmussen
 Tutorial using BEAST v2.4.1 Troubleshooting David A. Rasmussen 1 Background The primary goal of most phylogenetic analyses in BEAST is to infer the posterior distribution of trees and associated model
Tutorial using BEAST v2.4.1 Troubleshooting David A. Rasmussen 1 Background The primary goal of most phylogenetic analyses in BEAST is to infer the posterior distribution of trees and associated model
7. Decision or classification trees
 7. Decision or classification trees Next we are going to consider a rather different approach from those presented so far to machine learning that use one of the most common and important data structure,
7. Decision or classification trees Next we are going to consider a rather different approach from those presented so far to machine learning that use one of the most common and important data structure,
Reddit Recommendation System Daniel Poon, Yu Wu, David (Qifan) Zhang CS229, Stanford University December 11 th, 2011
 Reddit Recommendation System Daniel Poon, Yu Wu, David (Qifan) Zhang CS229, Stanford University December 11 th, 2011 1. Introduction Reddit is one of the most popular online social news websites with millions
Reddit Recommendation System Daniel Poon, Yu Wu, David (Qifan) Zhang CS229, Stanford University December 11 th, 2011 1. Introduction Reddit is one of the most popular online social news websites with millions
Sistemática Teórica. Hernán Dopazo. Biomedical Genomics and Evolution Lab. Lesson 03 Statistical Model Selection
 Sistemática Teórica Hernán Dopazo Biomedical Genomics and Evolution Lab Lesson 03 Statistical Model Selection Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires Argentina 2013 Statistical
Sistemática Teórica Hernán Dopazo Biomedical Genomics and Evolution Lab Lesson 03 Statistical Model Selection Facultad de Ciencias Exactas y Naturales Universidad de Buenos Aires Argentina 2013 Statistical
Annotated multitree output
 Annotated multitree output A simplified version of the two high-threshold (2HT) model, applied to two experimental conditions, is used as an example to illustrate the output provided by multitree (version
Annotated multitree output A simplified version of the two high-threshold (2HT) model, applied to two experimental conditions, is used as an example to illustrate the output provided by multitree (version
Sampling PCA, enhancing recovered missing values in large scale matrices. Luis Gabriel De Alba Rivera 80555S
 Sampling PCA, enhancing recovered missing values in large scale matrices. Luis Gabriel De Alba Rivera 80555S May 2, 2009 Introduction Human preferences (the quality tags we put on things) are language
Sampling PCA, enhancing recovered missing values in large scale matrices. Luis Gabriel De Alba Rivera 80555S May 2, 2009 Introduction Human preferences (the quality tags we put on things) are language
Chapter 7: Dual Modeling in the Presence of Constant Variance
 Chapter 7: Dual Modeling in the Presence of Constant Variance 7.A Introduction An underlying premise of regression analysis is that a given response variable changes systematically and smoothly due to
Chapter 7: Dual Modeling in the Presence of Constant Variance 7.A Introduction An underlying premise of regression analysis is that a given response variable changes systematically and smoothly due to
Using Excel for Graphical Analysis of Data
 Using Excel for Graphical Analysis of Data Introduction In several upcoming labs, a primary goal will be to determine the mathematical relationship between two variable physical parameters. Graphs are
Using Excel for Graphical Analysis of Data Introduction In several upcoming labs, a primary goal will be to determine the mathematical relationship between two variable physical parameters. Graphs are
Dynamic Thresholding for Image Analysis
 Dynamic Thresholding for Image Analysis Statistical Consulting Report for Edward Chan Clean Energy Research Center University of British Columbia by Libo Lu Department of Statistics University of British
Dynamic Thresholding for Image Analysis Statistical Consulting Report for Edward Chan Clean Energy Research Center University of British Columbia by Libo Lu Department of Statistics University of British
Automatic basis selection for RBF networks using Stein s unbiased risk estimator
 Automatic basis selection for RBF networks using Stein s unbiased risk estimator Ali Ghodsi School of omputer Science University of Waterloo University Avenue West NL G anada Email: aghodsib@cs.uwaterloo.ca
Automatic basis selection for RBF networks using Stein s unbiased risk estimator Ali Ghodsi School of omputer Science University of Waterloo University Avenue West NL G anada Email: aghodsib@cs.uwaterloo.ca
A Visualization Tool to Improve the Performance of a Classifier Based on Hidden Markov Models
 A Visualization Tool to Improve the Performance of a Classifier Based on Hidden Markov Models Gleidson Pegoretti da Silva, Masaki Nakagawa Department of Computer and Information Sciences Tokyo University
A Visualization Tool to Improve the Performance of a Classifier Based on Hidden Markov Models Gleidson Pegoretti da Silva, Masaki Nakagawa Department of Computer and Information Sciences Tokyo University
Clustering Sequences with Hidden. Markov Models. Padhraic Smyth CA Abstract
 Clustering Sequences with Hidden Markov Models Padhraic Smyth Information and Computer Science University of California, Irvine CA 92697-3425 smyth@ics.uci.edu Abstract This paper discusses a probabilistic
Clustering Sequences with Hidden Markov Models Padhraic Smyth Information and Computer Science University of California, Irvine CA 92697-3425 smyth@ics.uci.edu Abstract This paper discusses a probabilistic
Kernel-based online machine learning and support vector reduction
 Kernel-based online machine learning and support vector reduction Sumeet Agarwal 1, V. Vijaya Saradhi 2 andharishkarnick 2 1- IBM India Research Lab, New Delhi, India. 2- Department of Computer Science
Kernel-based online machine learning and support vector reduction Sumeet Agarwal 1, V. Vijaya Saradhi 2 andharishkarnick 2 1- IBM India Research Lab, New Delhi, India. 2- Department of Computer Science
error low bias high variance test set training set high low Model Complexity Typical Behaviour 2 CSC2515 Machine Learning high bias low variance
 CSC55 Machine Learning Sam Roweis high bias low variance Typical Behaviour low bias high variance Lecture : Overfitting and Capacity Control error training set test set November, 6 low Model Complexity
CSC55 Machine Learning Sam Roweis high bias low variance Typical Behaviour low bias high variance Lecture : Overfitting and Capacity Control error training set test set November, 6 low Model Complexity
low bias high variance high bias low variance error test set training set high low Model Complexity Typical Behaviour Lecture 11:
 Lecture 11: Overfitting and Capacity Control high bias low variance Typical Behaviour low bias high variance Sam Roweis error test set training set November 23, 4 low Model Complexity high Generalization,
Lecture 11: Overfitting and Capacity Control high bias low variance Typical Behaviour low bias high variance Sam Roweis error test set training set November 23, 4 low Model Complexity high Generalization,
Using Machine Learning to Optimize Storage Systems
 Using Machine Learning to Optimize Storage Systems Dr. Kiran Gunnam 1 Outline 1. Overview 2. Building Flash Models using Logistic Regression. 3. Storage Object classification 4. Storage Allocation recommendation
Using Machine Learning to Optimize Storage Systems Dr. Kiran Gunnam 1 Outline 1. Overview 2. Building Flash Models using Logistic Regression. 3. Storage Object classification 4. Storage Allocation recommendation
Recitation Supplement: Creating a Neural Network for Classification SAS EM December 2, 2002
 Recitation Supplement: Creating a Neural Network for Classification SAS EM December 2, 2002 Introduction Neural networks are flexible nonlinear models that can be used for regression and classification
Recitation Supplement: Creating a Neural Network for Classification SAS EM December 2, 2002 Introduction Neural networks are flexible nonlinear models that can be used for regression and classification
Response to API 1163 and Its Impact on Pipeline Integrity Management
 ECNDT 2 - Tu.2.7.1 Response to API 3 and Its Impact on Pipeline Integrity Management Munendra S TOMAR, Martin FINGERHUT; RTD Quality Services, USA Abstract. Knowing the accuracy and reliability of ILI
ECNDT 2 - Tu.2.7.1 Response to API 3 and Its Impact on Pipeline Integrity Management Munendra S TOMAR, Martin FINGERHUT; RTD Quality Services, USA Abstract. Knowing the accuracy and reliability of ILI
NOTE: Any use of trade, product or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government.
 U.S. Geological Survey (USGS) MMA(1) NOTE: Any use of trade, product or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. NAME MMA, A Computer Code for
U.S. Geological Survey (USGS) MMA(1) NOTE: Any use of trade, product or firm names is for descriptive purposes only and does not imply endorsement by the U.S. Government. NAME MMA, A Computer Code for
Image Compression: An Artificial Neural Network Approach
 Image Compression: An Artificial Neural Network Approach Anjana B 1, Mrs Shreeja R 2 1 Department of Computer Science and Engineering, Calicut University, Kuttippuram 2 Department of Computer Science and
Image Compression: An Artificial Neural Network Approach Anjana B 1, Mrs Shreeja R 2 1 Department of Computer Science and Engineering, Calicut University, Kuttippuram 2 Department of Computer Science and
Discovery of the Source of Contaminant Release
 Discovery of the Source of Contaminant Release Devina Sanjaya 1 Henry Qin Introduction Computer ability to model contaminant release events and predict the source of release in real time is crucial in
Discovery of the Source of Contaminant Release Devina Sanjaya 1 Henry Qin Introduction Computer ability to model contaminant release events and predict the source of release in real time is crucial in
CLASSIFICATION WITH RADIAL BASIS AND PROBABILISTIC NEURAL NETWORKS
 CLASSIFICATION WITH RADIAL BASIS AND PROBABILISTIC NEURAL NETWORKS CHAPTER 4 CLASSIFICATION WITH RADIAL BASIS AND PROBABILISTIC NEURAL NETWORKS 4.1 Introduction Optical character recognition is one of
CLASSIFICATION WITH RADIAL BASIS AND PROBABILISTIC NEURAL NETWORKS CHAPTER 4 CLASSIFICATION WITH RADIAL BASIS AND PROBABILISTIC NEURAL NETWORKS 4.1 Introduction Optical character recognition is one of
Graphical Analysis of Data using Microsoft Excel [2016 Version]
![Graphical Analysis of Data using Microsoft Excel [2016 Version] Graphical Analysis of Data using Microsoft Excel [2016 Version]](/thumbs/72/67574169.jpg) Graphical Analysis of Data using Microsoft Excel [2016 Version] Introduction In several upcoming labs, a primary goal will be to determine the mathematical relationship between two variable physical parameters.
Graphical Analysis of Data using Microsoft Excel [2016 Version] Introduction In several upcoming labs, a primary goal will be to determine the mathematical relationship between two variable physical parameters.
Frequently Asked Questions Updated 2006 (TRIM version 3.51) PREPARING DATA & RUNNING TRIM
 Frequently Asked Questions Updated 2006 (TRIM version 3.51) PREPARING DATA & RUNNING TRIM * Which directories are used for input files and output files? See menu-item "Options" and page 22 in the manual.
Frequently Asked Questions Updated 2006 (TRIM version 3.51) PREPARING DATA & RUNNING TRIM * Which directories are used for input files and output files? See menu-item "Options" and page 22 in the manual.
Chapter 1. Introduction
 Chapter 1 Introduction A Monte Carlo method is a compuational method that uses random numbers to compute (estimate) some quantity of interest. Very often the quantity we want to compute is the mean of
Chapter 1 Introduction A Monte Carlo method is a compuational method that uses random numbers to compute (estimate) some quantity of interest. Very often the quantity we want to compute is the mean of
Expectation-Maximization Methods in Population Analysis. Robert J. Bauer, Ph.D. ICON plc.
 Expectation-Maximization Methods in Population Analysis Robert J. Bauer, Ph.D. ICON plc. 1 Objective The objective of this tutorial is to briefly describe the statistical basis of Expectation-Maximization
Expectation-Maximization Methods in Population Analysis Robert J. Bauer, Ph.D. ICON plc. 1 Objective The objective of this tutorial is to briefly describe the statistical basis of Expectation-Maximization
( ) = Y ˆ. Calibration Definition A model is calibrated if its predictions are right on average: ave(response Predicted value) = Predicted value.
 Calibration OVERVIEW... 2 INTRODUCTION... 2 CALIBRATION... 3 ANOTHER REASON FOR CALIBRATION... 4 CHECKING THE CALIBRATION OF A REGRESSION... 5 CALIBRATION IN SIMPLE REGRESSION (DISPLAY.JMP)... 5 TESTING
Calibration OVERVIEW... 2 INTRODUCTION... 2 CALIBRATION... 3 ANOTHER REASON FOR CALIBRATION... 4 CHECKING THE CALIBRATION OF A REGRESSION... 5 CALIBRATION IN SIMPLE REGRESSION (DISPLAY.JMP)... 5 TESTING
Simple Model Selection Cross Validation Regularization Neural Networks
 Neural Nets: Many possible refs e.g., Mitchell Chapter 4 Simple Model Selection Cross Validation Regularization Neural Networks Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University February
Neural Nets: Many possible refs e.g., Mitchell Chapter 4 Simple Model Selection Cross Validation Regularization Neural Networks Machine Learning 10701/15781 Carlos Guestrin Carnegie Mellon University February
Chapter 5. Track Geometry Data Analysis
 Chapter Track Geometry Data Analysis This chapter explains how and why the data collected for the track geometry was manipulated. The results of these studies in the time and frequency domain are addressed.
Chapter Track Geometry Data Analysis This chapter explains how and why the data collected for the track geometry was manipulated. The results of these studies in the time and frequency domain are addressed.
A Course in Machine Learning
 A Course in Machine Learning Hal Daumé III 13 UNSUPERVISED LEARNING If you have access to labeled training data, you know what to do. This is the supervised setting, in which you have a teacher telling
A Course in Machine Learning Hal Daumé III 13 UNSUPERVISED LEARNING If you have access to labeled training data, you know what to do. This is the supervised setting, in which you have a teacher telling
Simplifying OCR Neural Networks with Oracle Learning
 SCIMA 2003 - International Workshop on Soft Computing Techniques in Instrumentation, Measurement and Related Applications Provo, Utah, USA, 17 May 2003 Simplifying OCR Neural Networks with Oracle Learning
SCIMA 2003 - International Workshop on Soft Computing Techniques in Instrumentation, Measurement and Related Applications Provo, Utah, USA, 17 May 2003 Simplifying OCR Neural Networks with Oracle Learning
An Introduction to Markov Chain Monte Carlo
 An Introduction to Markov Chain Monte Carlo Markov Chain Monte Carlo (MCMC) refers to a suite of processes for simulating a posterior distribution based on a random (ie. monte carlo) process. In other
An Introduction to Markov Chain Monte Carlo Markov Chain Monte Carlo (MCMC) refers to a suite of processes for simulating a posterior distribution based on a random (ie. monte carlo) process. In other
Variational Methods for Graphical Models
 Chapter 2 Variational Methods for Graphical Models 2.1 Introduction The problem of probabb1istic inference in graphical models is the problem of computing a conditional probability distribution over the
Chapter 2 Variational Methods for Graphical Models 2.1 Introduction The problem of probabb1istic inference in graphical models is the problem of computing a conditional probability distribution over the
Random projection for non-gaussian mixture models
 Random projection for non-gaussian mixture models Győző Gidófalvi Department of Computer Science and Engineering University of California, San Diego La Jolla, CA 92037 gyozo@cs.ucsd.edu Abstract Recently,
Random projection for non-gaussian mixture models Győző Gidófalvi Department of Computer Science and Engineering University of California, San Diego La Jolla, CA 92037 gyozo@cs.ucsd.edu Abstract Recently,
Bootstrapping Method for 14 June 2016 R. Russell Rhinehart. Bootstrapping
 Bootstrapping Method for www.r3eda.com 14 June 2016 R. Russell Rhinehart Bootstrapping This is extracted from the book, Nonlinear Regression Modeling for Engineering Applications: Modeling, Model Validation,
Bootstrapping Method for www.r3eda.com 14 June 2016 R. Russell Rhinehart Bootstrapping This is extracted from the book, Nonlinear Regression Modeling for Engineering Applications: Modeling, Model Validation,
Bayesian Robust Inference of Differential Gene Expression The bridge package
 Bayesian Robust Inference of Differential Gene Expression The bridge package Raphael Gottardo October 30, 2017 Contents Department Statistics, University of Washington http://www.rglab.org raph@stat.washington.edu
Bayesian Robust Inference of Differential Gene Expression The bridge package Raphael Gottardo October 30, 2017 Contents Department Statistics, University of Washington http://www.rglab.org raph@stat.washington.edu
Regression on SAT Scores of 374 High Schools and K-means on Clustering Schools
 Regression on SAT Scores of 374 High Schools and K-means on Clustering Schools Abstract In this project, we study 374 public high schools in New York City. The project seeks to use regression techniques
Regression on SAT Scores of 374 High Schools and K-means on Clustering Schools Abstract In this project, we study 374 public high schools in New York City. The project seeks to use regression techniques
Research Article Forecasting SPEI and SPI Drought Indices Using the Integrated Artificial Neural Networks
 Computational Intelligence and Neuroscience Volume 2016, Article ID 3868519, 17 pages http://dx.doi.org/10.1155/2016/3868519 Research Article Forecasting SPEI and SPI Drought Indices Using the Integrated
Computational Intelligence and Neuroscience Volume 2016, Article ID 3868519, 17 pages http://dx.doi.org/10.1155/2016/3868519 Research Article Forecasting SPEI and SPI Drought Indices Using the Integrated
Classification: Linear Discriminant Functions
 Classification: Linear Discriminant Functions CE-725: Statistical Pattern Recognition Sharif University of Technology Spring 2013 Soleymani Outline Discriminant functions Linear Discriminant functions
Classification: Linear Discriminant Functions CE-725: Statistical Pattern Recognition Sharif University of Technology Spring 2013 Soleymani Outline Discriminant functions Linear Discriminant functions
Analytical model A structure and process for analyzing a dataset. For example, a decision tree is a model for the classification of a dataset.
 Glossary of data mining terms: Accuracy Accuracy is an important factor in assessing the success of data mining. When applied to data, accuracy refers to the rate of correct values in the data. When applied
Glossary of data mining terms: Accuracy Accuracy is an important factor in assessing the success of data mining. When applied to data, accuracy refers to the rate of correct values in the data. When applied
A faster model selection criterion for OP-ELM and OP-KNN: Hannan-Quinn criterion
 A faster model selection criterion for OP-ELM and OP-KNN: Hannan-Quinn criterion Yoan Miche 1,2 and Amaury Lendasse 1 1- Helsinki University of Technology - ICS Lab. Konemiehentie 2, 02015 TKK - Finland
A faster model selection criterion for OP-ELM and OP-KNN: Hannan-Quinn criterion Yoan Miche 1,2 and Amaury Lendasse 1 1- Helsinki University of Technology - ICS Lab. Konemiehentie 2, 02015 TKK - Finland
Exploring Econometric Model Selection Using Sensitivity Analysis
 Exploring Econometric Model Selection Using Sensitivity Analysis William Becker Paolo Paruolo Andrea Saltelli Nice, 2 nd July 2013 Outline What is the problem we are addressing? Past approaches Hoover
Exploring Econometric Model Selection Using Sensitivity Analysis William Becker Paolo Paruolo Andrea Saltelli Nice, 2 nd July 2013 Outline What is the problem we are addressing? Past approaches Hoover
Probabilistic Graphical Models
 Overview of Part One Probabilistic Graphical Models Part One: Graphs and Markov Properties Christopher M. Bishop Graphs and probabilities Directed graphs Markov properties Undirected graphs Examples Microsoft
Overview of Part One Probabilistic Graphical Models Part One: Graphs and Markov Properties Christopher M. Bishop Graphs and probabilities Directed graphs Markov properties Undirected graphs Examples Microsoft
Deep Boltzmann Machines
 Deep Boltzmann Machines Sargur N. Srihari srihari@cedar.buffalo.edu Topics 1. Boltzmann machines 2. Restricted Boltzmann machines 3. Deep Belief Networks 4. Deep Boltzmann machines 5. Boltzmann machines
Deep Boltzmann Machines Sargur N. Srihari srihari@cedar.buffalo.edu Topics 1. Boltzmann machines 2. Restricted Boltzmann machines 3. Deep Belief Networks 4. Deep Boltzmann machines 5. Boltzmann machines
1. Estimation equations for strip transect sampling, using notation consistent with that used to
 Web-based Supplementary Materials for Line Transect Methods for Plant Surveys by S.T. Buckland, D.L. Borchers, A. Johnston, P.A. Henrys and T.A. Marques Web Appendix A. Introduction In this on-line appendix,
Web-based Supplementary Materials for Line Transect Methods for Plant Surveys by S.T. Buckland, D.L. Borchers, A. Johnston, P.A. Henrys and T.A. Marques Web Appendix A. Introduction In this on-line appendix,
( ylogenetics/bayesian_workshop/bayesian%20mini conference.htm#_toc )
 (http://www.nematodes.org/teaching/tutorials/ph ylogenetics/bayesian_workshop/bayesian%20mini conference.htm#_toc145477467) Model selection criteria Review Posada D & Buckley TR (2004) Model selection
(http://www.nematodes.org/teaching/tutorials/ph ylogenetics/bayesian_workshop/bayesian%20mini conference.htm#_toc145477467) Model selection criteria Review Posada D & Buckley TR (2004) Model selection
Variable selection is intended to select the best subset of predictors. But why bother?
 Chapter 10 Variable Selection Variable selection is intended to select the best subset of predictors. But why bother? 1. We want to explain the data in the simplest way redundant predictors should be removed.
Chapter 10 Variable Selection Variable selection is intended to select the best subset of predictors. But why bother? 1. We want to explain the data in the simplest way redundant predictors should be removed.
Quantitative Biology II!
 Quantitative Biology II! Lecture 3: Markov Chain Monte Carlo! March 9, 2015! 2! Plan for Today!! Introduction to Sampling!! Introduction to MCMC!! Metropolis Algorithm!! Metropolis-Hastings Algorithm!!
Quantitative Biology II! Lecture 3: Markov Chain Monte Carlo! March 9, 2015! 2! Plan for Today!! Introduction to Sampling!! Introduction to MCMC!! Metropolis Algorithm!! Metropolis-Hastings Algorithm!!
CSEP 573: Artificial Intelligence
 CSEP 573: Artificial Intelligence Machine Learning: Perceptron Ali Farhadi Many slides over the course adapted from Luke Zettlemoyer and Dan Klein. 1 Generative vs. Discriminative Generative classifiers:
CSEP 573: Artificial Intelligence Machine Learning: Perceptron Ali Farhadi Many slides over the course adapted from Luke Zettlemoyer and Dan Klein. 1 Generative vs. Discriminative Generative classifiers:
Bayesian Statistics Group 8th March Slice samplers. (A very brief introduction) The basic idea
 Bayesian Statistics Group 8th March 2000 Slice samplers (A very brief introduction) The basic idea lacements To sample from a distribution, simply sample uniformly from the region under the density function
Bayesian Statistics Group 8th March 2000 Slice samplers (A very brief introduction) The basic idea lacements To sample from a distribution, simply sample uniformly from the region under the density function
Robust Signal-Structure Reconstruction
 Robust Signal-Structure Reconstruction V. Chetty 1, D. Hayden 2, J. Gonçalves 2, and S. Warnick 1 1 Information and Decision Algorithms Laboratories, Brigham Young University 2 Control Group, Department
Robust Signal-Structure Reconstruction V. Chetty 1, D. Hayden 2, J. Gonçalves 2, and S. Warnick 1 1 Information and Decision Algorithms Laboratories, Brigham Young University 2 Control Group, Department
10.4 Linear interpolation method Newton s method
 10.4 Linear interpolation method The next best thing one can do is the linear interpolation method, also known as the double false position method. This method works similarly to the bisection method by
10.4 Linear interpolation method The next best thing one can do is the linear interpolation method, also known as the double false position method. This method works similarly to the bisection method by
A Fast Learning Algorithm for Deep Belief Nets
 A Fast Learning Algorithm for Deep Belief Nets Geoffrey E. Hinton, Simon Osindero Department of Computer Science University of Toronto, Toronto, Canada Yee-Whye Teh Department of Computer Science National
A Fast Learning Algorithm for Deep Belief Nets Geoffrey E. Hinton, Simon Osindero Department of Computer Science University of Toronto, Toronto, Canada Yee-Whye Teh Department of Computer Science National
DESIGN AND ANALYSIS OF ALGORITHMS. Unit 1 Chapter 4 ITERATIVE ALGORITHM DESIGN ISSUES
 DESIGN AND ANALYSIS OF ALGORITHMS Unit 1 Chapter 4 ITERATIVE ALGORITHM DESIGN ISSUES http://milanvachhani.blogspot.in USE OF LOOPS As we break down algorithm into sub-algorithms, sooner or later we shall
DESIGN AND ANALYSIS OF ALGORITHMS Unit 1 Chapter 4 ITERATIVE ALGORITHM DESIGN ISSUES http://milanvachhani.blogspot.in USE OF LOOPS As we break down algorithm into sub-algorithms, sooner or later we shall
Learning from Data: Adaptive Basis Functions
 Learning from Data: Adaptive Basis Functions November 21, 2005 http://www.anc.ed.ac.uk/ amos/lfd/ Neural Networks Hidden to output layer - a linear parameter model But adapt the features of the model.
Learning from Data: Adaptive Basis Functions November 21, 2005 http://www.anc.ed.ac.uk/ amos/lfd/ Neural Networks Hidden to output layer - a linear parameter model But adapt the features of the model.
Recent Design Optimization Methods for Energy- Efficient Electric Motors and Derived Requirements for a New Improved Method Part 3
 Proceedings Recent Design Optimization Methods for Energy- Efficient Electric Motors and Derived Requirements for a New Improved Method Part 3 Johannes Schmelcher 1, *, Max Kleine Büning 2, Kai Kreisköther
Proceedings Recent Design Optimization Methods for Energy- Efficient Electric Motors and Derived Requirements for a New Improved Method Part 3 Johannes Schmelcher 1, *, Max Kleine Büning 2, Kai Kreisköther
On-line Estimation of Power System Security Limits
 Bulk Power System Dynamics and Control V, August 26-31, 2001, Onomichi, Japan On-line Estimation of Power System Security Limits K. Tomsovic A. Sittithumwat J. Tong School of Electrical Engineering and
Bulk Power System Dynamics and Control V, August 26-31, 2001, Onomichi, Japan On-line Estimation of Power System Security Limits K. Tomsovic A. Sittithumwat J. Tong School of Electrical Engineering and
Rank Measures for Ordering
 Rank Measures for Ordering Jin Huang and Charles X. Ling Department of Computer Science The University of Western Ontario London, Ontario, Canada N6A 5B7 email: fjhuang33, clingg@csd.uwo.ca Abstract. Many
Rank Measures for Ordering Jin Huang and Charles X. Ling Department of Computer Science The University of Western Ontario London, Ontario, Canada N6A 5B7 email: fjhuang33, clingg@csd.uwo.ca Abstract. Many
Machine Learning: An Applied Econometric Approach Online Appendix
 Machine Learning: An Applied Econometric Approach Online Appendix Sendhil Mullainathan mullain@fas.harvard.edu Jann Spiess jspiess@fas.harvard.edu April 2017 A How We Predict In this section, we detail
Machine Learning: An Applied Econometric Approach Online Appendix Sendhil Mullainathan mullain@fas.harvard.edu Jann Spiess jspiess@fas.harvard.edu April 2017 A How We Predict In this section, we detail
Chapter 2 Basic Structure of High-Dimensional Spaces
 Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Optimization Methods for Machine Learning (OMML)
 Optimization Methods for Machine Learning (OMML) 2nd lecture Prof. L. Palagi References: 1. Bishop Pattern Recognition and Machine Learning, Springer, 2006 (Chap 1) 2. V. Cherlassky, F. Mulier - Learning
Optimization Methods for Machine Learning (OMML) 2nd lecture Prof. L. Palagi References: 1. Bishop Pattern Recognition and Machine Learning, Springer, 2006 (Chap 1) 2. V. Cherlassky, F. Mulier - Learning
DESIGN AND EVALUATION OF MACHINE LEARNING MODELS WITH STATISTICAL FEATURES
 EXPERIMENTAL WORK PART I CHAPTER 6 DESIGN AND EVALUATION OF MACHINE LEARNING MODELS WITH STATISTICAL FEATURES The evaluation of models built using statistical in conjunction with various feature subset
EXPERIMENTAL WORK PART I CHAPTER 6 DESIGN AND EVALUATION OF MACHINE LEARNING MODELS WITH STATISTICAL FEATURES The evaluation of models built using statistical in conjunction with various feature subset
Fast Automated Estimation of Variance in Discrete Quantitative Stochastic Simulation
 Fast Automated Estimation of Variance in Discrete Quantitative Stochastic Simulation November 2010 Nelson Shaw njd50@uclive.ac.nz Department of Computer Science and Software Engineering University of Canterbury,
Fast Automated Estimation of Variance in Discrete Quantitative Stochastic Simulation November 2010 Nelson Shaw njd50@uclive.ac.nz Department of Computer Science and Software Engineering University of Canterbury,
Post-Processing for MCMC
 ost-rocessing for MCMC Edwin D. de Jong Marco A. Wiering Mădălina M. Drugan institute of information and computing sciences, utrecht university technical report UU-CS-23-2 www.cs.uu.nl ost-rocessing for
ost-rocessing for MCMC Edwin D. de Jong Marco A. Wiering Mădălina M. Drugan institute of information and computing sciences, utrecht university technical report UU-CS-23-2 www.cs.uu.nl ost-rocessing for
CS6220: DATA MINING TECHNIQUES
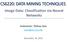 CS6220: DATA MINING TECHNIQUES Image Data: Classification via Neural Networks Instructor: Yizhou Sun yzsun@ccs.neu.edu November 19, 2015 Methods to Learn Classification Clustering Frequent Pattern Mining
CS6220: DATA MINING TECHNIQUES Image Data: Classification via Neural Networks Instructor: Yizhou Sun yzsun@ccs.neu.edu November 19, 2015 Methods to Learn Classification Clustering Frequent Pattern Mining
Approximate Bayesian Computation. Alireza Shafaei - April 2016
 Approximate Bayesian Computation Alireza Shafaei - April 2016 The Problem Given a dataset, we are interested in. The Problem Given a dataset, we are interested in. The Problem Given a dataset, we are interested
Approximate Bayesian Computation Alireza Shafaei - April 2016 The Problem Given a dataset, we are interested in. The Problem Given a dataset, we are interested in. The Problem Given a dataset, we are interested
7. Collinearity and Model Selection
 Sociology 740 John Fox Lecture Notes 7. Collinearity and Model Selection Copyright 2014 by John Fox Collinearity and Model Selection 1 1. Introduction I When there is a perfect linear relationship among
Sociology 740 John Fox Lecture Notes 7. Collinearity and Model Selection Copyright 2014 by John Fox Collinearity and Model Selection 1 1. Introduction I When there is a perfect linear relationship among
Climate Precipitation Prediction by Neural Network
 Journal of Mathematics and System Science 5 (205) 207-23 doi: 0.7265/259-529/205.05.005 D DAVID PUBLISHING Juliana Aparecida Anochi, Haroldo Fraga de Campos Velho 2. Applied Computing Graduate Program,
Journal of Mathematics and System Science 5 (205) 207-23 doi: 0.7265/259-529/205.05.005 D DAVID PUBLISHING Juliana Aparecida Anochi, Haroldo Fraga de Campos Velho 2. Applied Computing Graduate Program,
Expectation and Maximization Algorithm for Estimating Parameters of a Simple Partial Erasure Model
 608 IEEE TRANSACTIONS ON MAGNETICS, VOL. 39, NO. 1, JANUARY 2003 Expectation and Maximization Algorithm for Estimating Parameters of a Simple Partial Erasure Model Tsai-Sheng Kao and Mu-Huo Cheng Abstract
608 IEEE TRANSACTIONS ON MAGNETICS, VOL. 39, NO. 1, JANUARY 2003 Expectation and Maximization Algorithm for Estimating Parameters of a Simple Partial Erasure Model Tsai-Sheng Kao and Mu-Huo Cheng Abstract
Approximate (Monte Carlo) Inference in Bayes Nets. Monte Carlo (continued)
 Approximate (Monte Carlo) Inference in Bayes Nets Basic idea: Let s repeatedly sample according to the distribution represented by the Bayes Net. If in 400/1000 draws, the variable X is true, then we estimate
Approximate (Monte Carlo) Inference in Bayes Nets Basic idea: Let s repeatedly sample according to the distribution represented by the Bayes Net. If in 400/1000 draws, the variable X is true, then we estimate
ADAPTIVE METROPOLIS-HASTINGS SAMPLING, OR MONTE CARLO KERNEL ESTIMATION
 ADAPTIVE METROPOLIS-HASTINGS SAMPLING, OR MONTE CARLO KERNEL ESTIMATION CHRISTOPHER A. SIMS Abstract. A new algorithm for sampling from an arbitrary pdf. 1. Introduction Consider the standard problem of
ADAPTIVE METROPOLIS-HASTINGS SAMPLING, OR MONTE CARLO KERNEL ESTIMATION CHRISTOPHER A. SIMS Abstract. A new algorithm for sampling from an arbitrary pdf. 1. Introduction Consider the standard problem of
