Computational Intelligence Lecture 10:Fuzzy Sets
|
|
|
- Vanessa Horton
- 6 years ago
- Views:
Transcription
1 Computational Intelligence Lecture 10:Fuzzy Sets Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2011 arzaneh Abdollahi Computational Intelligence Lecture 10 1/26
2 Classical Set Fuzzy Set Basic Concepts in Fuzzy Sets Operations on Fuzzy Sets Fuzzy Complement Fuzzy Union Fuzzy Intersection Averaging Operator Farzaneh Abdollahi Computational Intelligence Lecture 10 2/26
3 Classical Set A classical (crisp) set A in the universe of discourse U: can be defined by List method: listing all of its members Rule method: specifying the properties that must be satisfied by the members of the set A = {x U x meets some conditions} Membership method: introduces a zero-one membership function (also called characteristic function, discrimination function, or indicator function) { 1 ifx A µ A = 0 ifx / A Farzaneh Abdollahi Computational Intelligence Lecture 10 3/26
4 Example: cars in Tehran The universe of discourse U. Set A is the cars with 4 cylinders: A = {x U xhas 4 cylinders} OR { 1 ifx U&x has 4 cylinders µ A = 0 ifx U&x does not have 4 cylinders Set D is the car made in Iran BUT the distinction between an Iranian car and a non-iranian a car is not crisp:( Most of them are not completely made in Iran So what should we do??!! Farzaneh Abdollahi Computational Intelligence Lecture 10 4/26
5 Fuzzy Set some sets do not have clear boundaries. Fuzzy set: in a universe of discourse U is characterized by a membership function µ A (x) that takes values in the interval [0, 1]. In classical sets the membership function of a classical set can only take zero and one In fuzzy set the membership function is a continuous function with range [0, 1]. A fuzzy set A in U is represented by: a set of ordered pairs of a generic element x and its membership value: A = {(x, µ A (x)) x U} for continuous U: A = U µ A(x)/x. for discrete U: µ A (x): A = U µ A(x)/x and do not represent integral and summation. They denote collection of all points x U with the associated membership function µ A (x) Farzaneh Abdollahi Computational Intelligence Lecture 10 5/26
6 Example: cars in Tehran (Cont d) D: The set Iranian cars in Iran, µ D = p(x) p(x) is the percentage of the parts of car x made in Iran it takes values from 0% to 100%. F : The set non-iranian cars in Iran, µ F (x) = 1 p(x) Farzaneh Abdollahi Computational Intelligence Lecture 10 6/26
7 Different membership functions can be defined to characterize the same description. The membership functions are not fuzzy, themselves. They are precise mathematical functions. Fuzzy sets are used to defuzzify the world. How to determine the membership functions? Formulate human knowledge Usually, gives a rough formula of the membership function fine-tuning is required. Data collected from various sensors specify the structures of the membership functions and then fine-tune the parameters based on the data. A fuzzy set has a one-to-one correspondence with its membership function Farzaneh Abdollahi Computational Intelligence Lecture 10 7/26
8 Example: Old and Young [?] U is in the interval of [0, 100] young = 25 x 25 (1 + ( 5 ) 2 ) 1 /x old = 100 x (1 + ( 5 ) 2 ) 1 /x 0 1/x Farzaneh Abdollahi Computational Intelligence Lecture 10 8/26
9 Example: A Digital Thermometer T : the set for desirable temperature U [18, 33] µ T = Farzaneh Abdollahi Computational Intelligence Lecture 10 9/26
10 Basic Concepts in Fuzzy Sets Support of a fuzzy set A in the universe of discourse U is a crisp set that contains all the elements of U that have nonzero membership values in A: supp A = {x U µ A > 0} In the digital thermometer example: supp A = [21, 30] empty fuzzy set: support is empty fuzzy singleton: support is a single point Center of a fuzzy set: If the mean value of all points at which the membership function of the fuzzy set achieves its maximum value is finite, then this mean value is the center If the mean value equals positive (negative) infinite, then the center is the smallest (largest) among all points that achieve the maximum membership value. Farzaneh Abdollahi Computational Intelligence Lecture 10 10/26
11 Crossover point of a fuzzy set: the point in U whose membership value in A equals 0.5. Height of a fuzzy set: the largest membership value attained by any point. Normal fuzzy set: the height of fuzzy set equals to one (digital thermometer). α-cut of a fuzzy set A a crisp set A α contains all the elements in U that have membership values in A greater than or equal to α: A α = {x U µ A (x) α} In digital thermometer for α = 0.7, Tα = [23, 24, 25, 26, 27] A fuzzy set A is convex iff its α-cut is a convex set for α (0, 1]. Farzaneh Abdollahi Computational Intelligence Lecture 10 11/26
12 Crossover point of a fuzzy set: the point in U whose membership value in A equals 0.5. Height of a fuzzy set: the largest membership value attained by any point. Normal fuzzy set: the height of fuzzy set equals to one (digital thermometer). α-cut of a fuzzy set A a crisp set A α contains all the elements in U that have membership values in A greater than or equal to α: A α = {x U µ A (x) α} In digital thermometer for α = 0.7, Tα = [23, 24, 25, 26, 27] A fuzzy set A is convex iff its α-cut is a convex set for α (0, 1]. In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object. arzaneh Abdollahi Computational Intelligence Lecture 10 11/26
13 Crossover point of a fuzzy set: the point in U whose membership value in A equals 0.5. Height of a fuzzy set: the largest membership value attained by any point. Normal fuzzy set: the height of fuzzy set equals to one (digital thermometer). α-cut of a fuzzy set A a crisp set A α contains all the elements in U that have membership values in A greater than or equal to α: A α = {x U µ A (x) α} In digital thermometer for α = 0.7, Tα = [23, 24, 25, 26, 27] A fuzzy set A is convex iff its α-cut is a convex set for α (0, 1]. Let C be a set in a real or complex vector space. C is convex if, x, y C and all λ [0, 1], λx + (1 λ)y C Farzaneh Abdollahi Computational Intelligence Lecture 10 11/26
14 Crossover point of a fuzzy set: the point in U whose membership value in A equals 0.5. Height of a fuzzy set: the largest membership value attained by any point. Normal fuzzy set: the height of fuzzy set equals to one (digital thermometer). α-cut of a fuzzy set A a crisp set A α contains all the elements in U that have membership values in A greater than or equal to α: A α = {x U µ A (x) α} In digital thermometer for α = 0.7, Tα = [23, 24, 25, 26, 27] A fuzzy set A is convex iff its α-cut is a convex set for α (0, 1]. Lemma: A fuzzy set A R n is convex iff µ A [λx 1 + (1 λ)x 2 ] min[µ A (x 1 ), µ A (x 2 )] x 1, x 2 R n, λ [0, 1]. Farzaneh Abdollahi Computational Intelligence Lecture 10 11/26
15 Operations on Fuzzy Sets Sets F and D are equal iff µ F (x) = µ D (x), x U Set D contains set F (F D), iff µ F (x) µ D (x), x U Complement of F is a fuzzy set F U whose membership function is µ F (x) = 1 µ F (x) Union of sets F and D (F D) is a fuzzy set in U: µ F D = max[µ F (x), µ D (x)] F D is the smallest fuzzy set containing both F and D. Intersection of F and D (F D) is a fuzzy set in U:µ F D = min[µ F (x), µ D (x)] F D is the smallest fuzzy set contained by F and D. arzaneh Abdollahi Computational Intelligence Lecture 10 12/26
16 The De Morgan s Laws are true for fuzzy sets: F D = F D F D = F D For Iranian Cars example: { µd if 0 p(x) 0.5 µ F D = { µ F if 0.5 p(x) 1 µf if 0 p(x) 0.5 µf B = µ D if 0.5 p(x) 1 Farzaneh Abdollahi Computational Intelligence Lecture 10 13/26
17 Further Operations An other difference between fuzzy sets and crisp sets: for crisp sets only one type of operation is defined for complement, union, and intersection for fuzzy sets, we can define several operations for them based on the given axioms. Why do we need different type of operations? Some operations may not be satisfactory in some situations. Farzaneh Abdollahi Computational Intelligence Lecture 10 14/26
18 Fuzzy Complement Let c : [0, 1] [0, 1] be a mapping that transforms the membership function of fuzzy set A into the membership function of the complement of A: c[µ A (x)] = µā(x) It was defined: c[µ A (x)] = 1 µ A Let a = µ A (x 1 ) and b = µ A (x 2 ) the function c is qualified as a complement if: Axiom c1: c(0) = 1 and c(1) = 0 (boundary condition) Axiom c2: a, b [0, 1], if a < b, then c(a) c(b) (nonincreasing condition) an increase in membership value must result in a decrease or no change in membership value for the complement Farzaneh Abdollahi Computational Intelligence Lecture 10 15/26
19 Fuzzy Complement Let c : [0, 1] [0, 1] be a mapping that transforms the membership function of fuzzy set A into the membership function of the complement of A: c[µ A (x)] = µā(x) It was defined: c[µ A (x)] = 1 µ A Let a = µ A (x 1 ) and b = µ A (x 2 ) the function c is qualified as a complement if: Axiom c1: c(0) = 1 and c(1) = 0 (boundary condition) Axiom c2: a, b [0, 1], if a < b, then c(a) c(b) (nonincreasing condition) an increase in membership value must result in a decrease or no change in membership value for the complement Some types of fuzzy complement: Sugeno class: cλ (a) = 1 a 1+λa, λ ( 1, ) λ = 0 basic fuzzy complement Yager class: cw (a) = (1 a w ) 1/w, w (0, ) w = 1 basic fuzzy complement Farzaneh Abdollahi Computational Intelligence Lecture 10 15/26
20 Fuzzy set-s Norm Let s : [0, 1] [0, 1] [0, 1] be a mapping that transforms the membership functions of fuzzy sets A and B into the membership function of the union of A and B, that s[µ A (x), µ B (x)] = µ A B. the function S to be qualified as an union Let a = µ A (x) and b = µ B (x) Axiom s1.s(1, 1) = 1, s(0, a) = s(a, 0) = a (boundary condition). Axiom s2. s(a, b) = s(b, a) (commutative condition). Axiom s3. If a a and b b, then s(a, b) s(a, b ) (nondecreasing condition). Axiom s4. s(s(a, b), c) = s(a, s(b, c)) (associative condition). Popular types of s-norm 1 Dombi class: s λ (a, b) =, λ (0, ) 1+[( 1 a 1) λ +( 1 b 1) λ ] 1/λ Dobios-Prade class: sα (a, b) = a+b ab min(a,b,1 α) max(1 a,1 b,α), α [0, 1] Yager class: sw (a, b) = min[1, (a w + b w ) 1/w ], w (0, ) Farzaneh Abdollahi Computational Intelligence Lecture 10 16/26
21 Other type of s-norm a if b = 0 Drastic sum: s ds (a, b) = b if a = 0 1 otherwise Einstein sum: s es (a, b) = a+b 1+ab Algebric sum: sas (a, b) = a + b ab Theorem: For any s-norm s, that is for any function s : [0, 1] [0, 1] [0, 1] that satisfies Axioms s1-s4, the smallest s-norm is maximum and the largest is drastic s-norm Proof: Axioms s1 and s3 s(a, b) s(a, 0) = a Axiom s2 s(a, b) = s(b, a) s(b, 0) = b s(a, b) max(a, b) If b = 0, Axiom s1 s(a, b) = s(a, 0) = a s(a, b) = s ds (a, b) If a = 0, Axiom s2 s(a, b) = s ds (a, b) If a 0&b 0, s ds (a, b) = 1 s(a, b) s(a, b) sds (a, b), a, b [0, 1] Farzaneh Abdollahi Computational Intelligence Lecture 10 17/26
22 Example: The Iranian cars Using Algebric sum: µ F D = p(x) + (1 p(x)) p(x)(1 p(x)) = 1 p(x)+p(x) 2 Using Yager s-norm, w = 3: µ F D = min[1, (p(x) 3 + (1 p(x)) 3 ) 1/3 ] Algebric Yager max arzaneh Abdollahi Computational Intelligence Lecture 10 18/26
23 Classical Set Lemma 1: For Dombi class s-norm and Drastic class s-norm it can be defined lim λ(a, b) λ = max(a, b) lim λ(a, b) λ 0 = s ds (a, b) Lemma 2: For Yager class s-norm and Drastic class s-norm it can be defined lim w (a, b) w = max(a, b) lim w (a, b) w 0 = s ds (a, b) Farzaneh Abdollahi Computational Intelligence Lecture 10 19/26
24 Fuzzy Intersection- T-Norm Let t : [0, 1] [0, 1] [0, 1] be a mapping that transforms the membership functions of fuzzy sets A and B into the membership function of the union of A and B, that t[µ A (x), µ B (x)] = µ A B. the function T to be qualified as an intersection Axiom t1.t(0, 0) = 0, t(1, a) = t(a, 1) = 1 (boundary condition). Axiom t2. t(a, b) = t(b, a) (commutative condition). Axiom t3. If a a and b b, then t(a, b) t(a, b ) (nondecreasing condition). Axiom t4. t(t(a, b), c) = t(a, t(b, c)) (associative condition). Popular types of t-norm Dombi class: 1 tλ (a, b) =, λ (0, ) 1+[( 1 a 1)λ +( 1 b 1)λ ] 1/λ Dobios-Prade class: ab tα (a, b) = max(a,b,α), α [0, 1] Yager class: t w (a, b) = 1 min[1, ((1 a) w + (1 b) w ) 1/w ], w (0, ) Farzaneh Abdollahi Computational Intelligence Lecture 10 20/26
25 Other type of t-norm a if b = 1 Drastic product: tds (a, b) = b if a = 1 0 otherwise Einstein product: ab tep (a, b) = 2 (a+b ab) Algebric product: tap (a, b) = ab Theorem: For any t-norm t, that is for any function t : [0, 1] [0, 1] [0, 1] that satisfies Axioms t1-t4, the largest t-norm is minimum and the smallest is drastic t-norm prove it. Lemma 3: For Dombi class t-norm and Drastic class t-norm it can be defined lim λ(a, b) λ = min(a, b) lim λ(a, b) λ 0 = t dp (a, b) Farzaneh Abdollahi Computational Intelligence Lecture 10 21/26
26 Example: One more time, the Iranian cars Using Algebric product: µ F D = p(x)(1 p(x)) Using Yager t-norm, w = 3: µ F D = 1 min[1, ((1 p(x)) 3 +p(x) 3 ) 1/3 ] Algebric Yager arzaneh Abdollahi Computational Intelligence Lecture 10 22/26 min
27 If the s-norm s(a, b), t-norm t(a, b) and fuzzy complement c(a) satisfy the following equation, they form an associated class (DeMorgan s Law) c[s(a, b)] = t[c(a), c(b)] Example: Show that the Yager s-norm and t-norm with the basic complement are associated c[sw (a, b)] = 1 min[1, (a w + b w ) 1/w ] tw [c(a), c(b)] = 1 min[1, ((1 1 + a) w + (1 1 + b) w ) 1/w ] Farzaneh Abdollahi Computational Intelligence Lecture 10 23/26
28 Farzaneh Abdollahi Computational Intelligence Lecture 10 24/26
29 Averaging Operator This operator fills the gap between min(a, b), and max(a, b) Some average operators: Max-min average: v λ (a, b) = λ max(a, b) + (1 λ) min(a, b), λ [0, 1] Generalized means: v α (a, b) = ( aα +b α 2 ) 1/α, α R, α 0 Fuzzy and: v p (a, b) = pmin(a, b) + (1 p)(a+b) 2, p = [0, 1] Fuzzy or: v γ (a, b) = γ max(a, b) + (1 γ)(a+b) 2, γ [0, 1] Farzaneh Abdollahi Computational Intelligence Lecture 10 25/26
30 Full Scope of Fuzzy Operators Farzaneh Abdollahi Computational Intelligence Lecture 10 26/26
Chapter 2: FUZZY SETS
 Ch.2: Fuzzy sets 1 Chapter 2: FUZZY SETS Introduction (2.1) Basic Definitions &Terminology (2.2) Set-theoretic Operations (2.3) Membership Function (MF) Formulation & Parameterization (2.4) Complement
Ch.2: Fuzzy sets 1 Chapter 2: FUZZY SETS Introduction (2.1) Basic Definitions &Terminology (2.2) Set-theoretic Operations (2.3) Membership Function (MF) Formulation & Parameterization (2.4) Complement
Computational Intelligence Lecture 12:Linguistic Variables and Fuzzy Rules
 Computational Intelligence Lecture 12:Linguistic Variables and Fuzzy Rules Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2011 Farzaneh Abdollahi Computational
Computational Intelligence Lecture 12:Linguistic Variables and Fuzzy Rules Farzaneh Abdollahi Department of Electrical Engineering Amirkabir University of Technology Fall 2011 Farzaneh Abdollahi Computational
Fuzzy Sets and Systems. Lecture 1 (Introduction) Bu- Ali Sina University Computer Engineering Dep. Spring 2010
 Fuzzy Sets and Systems Lecture 1 (Introduction) Bu- Ali Sina University Computer Engineering Dep. Spring 2010 Fuzzy sets and system Introduction and syllabus References Grading Fuzzy sets and system Syllabus
Fuzzy Sets and Systems Lecture 1 (Introduction) Bu- Ali Sina University Computer Engineering Dep. Spring 2010 Fuzzy sets and system Introduction and syllabus References Grading Fuzzy sets and system Syllabus
Study of Fuzzy Set Theory and Its Applications
 IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 12, Issue 4 Ver. II (Jul. - Aug.2016), PP 148-154 www.iosrjournals.org Study of Fuzzy Set Theory and Its Applications
IOSR Journal of Mathematics (IOSR-JM) e-issn: 2278-5728, p-issn: 2319-765X. Volume 12, Issue 4 Ver. II (Jul. - Aug.2016), PP 148-154 www.iosrjournals.org Study of Fuzzy Set Theory and Its Applications
Fuzzy Sets and Systems. Lecture 2 (Fuzzy Sets) Bu- Ali Sina University Computer Engineering Dep. Spring 2010
 Fuzzy Sets and Systems Lecture 2 (Fuzzy Sets) Bu- Ali Sina University Computer Engineering Dep. Spring 2010 Fuzzy Sets Formal definition: A fuzzy set A in X (universal set) is expressed as a set of ordered
Fuzzy Sets and Systems Lecture 2 (Fuzzy Sets) Bu- Ali Sina University Computer Engineering Dep. Spring 2010 Fuzzy Sets Formal definition: A fuzzy set A in X (universal set) is expressed as a set of ordered
Introduction to Fuzzy Logic. IJCAI2018 Tutorial
 Introduction to Fuzzy Logic IJCAI2018 Tutorial 1 Crisp set vs. Fuzzy set A traditional crisp set A fuzzy set 2 Crisp set vs. Fuzzy set 3 Crisp Logic Example I Crisp logic is concerned with absolutes-true
Introduction to Fuzzy Logic IJCAI2018 Tutorial 1 Crisp set vs. Fuzzy set A traditional crisp set A fuzzy set 2 Crisp set vs. Fuzzy set 3 Crisp Logic Example I Crisp logic is concerned with absolutes-true
Lecture 15: The subspace topology, Closed sets
 Lecture 15: The subspace topology, Closed sets 1 The Subspace Topology Definition 1.1. Let (X, T) be a topological space with topology T. subset of X, the collection If Y is a T Y = {Y U U T} is a topology
Lecture 15: The subspace topology, Closed sets 1 The Subspace Topology Definition 1.1. Let (X, T) be a topological space with topology T. subset of X, the collection If Y is a T Y = {Y U U T} is a topology
Chapter 2 The Operation of Fuzzy Set
 Chapter 2 The Operation of Fuzzy Set Standard operations of Fuzzy Set! Complement set! Union Ma[, ]! Intersection Min[, ]! difference between characteristics of crisp fuzzy set operator n law of contradiction
Chapter 2 The Operation of Fuzzy Set Standard operations of Fuzzy Set! Complement set! Union Ma[, ]! Intersection Min[, ]! difference between characteristics of crisp fuzzy set operator n law of contradiction
Why Fuzzy Fuzzy Logic and Sets Fuzzy Reasoning. DKS - Module 7. Why fuzzy thinking?
 Fuzzy Systems Overview: Literature: Why Fuzzy Fuzzy Logic and Sets Fuzzy Reasoning chapter 4 DKS - Module 7 1 Why fuzzy thinking? Experts rely on common sense to solve problems Representation of vague,
Fuzzy Systems Overview: Literature: Why Fuzzy Fuzzy Logic and Sets Fuzzy Reasoning chapter 4 DKS - Module 7 1 Why fuzzy thinking? Experts rely on common sense to solve problems Representation of vague,
Fuzzy Logic : Introduction
 Fuzzy Logic : Introduction Debasis Samanta IIT Kharagpur dsamanta@iitkgp.ac.in 23.01.2018 Debasis Samanta (IIT Kharagpur) Soft Computing Applications 23.01.2018 1 / 69 What is Fuzzy logic? Fuzzy logic
Fuzzy Logic : Introduction Debasis Samanta IIT Kharagpur dsamanta@iitkgp.ac.in 23.01.2018 Debasis Samanta (IIT Kharagpur) Soft Computing Applications 23.01.2018 1 / 69 What is Fuzzy logic? Fuzzy logic
Fuzzy Convex Invariants and Product Spaces
 International Mathematical Forum, Vol. 6, 2011, no. 57, 2815-2822 Fuzzy Convex Invariants and Product Spaces Lissy Jacob Department of Mathematics Bharata Mata College, Thrikkakara, Kerala, India, PIN-682021
International Mathematical Forum, Vol. 6, 2011, no. 57, 2815-2822 Fuzzy Convex Invariants and Product Spaces Lissy Jacob Department of Mathematics Bharata Mata College, Thrikkakara, Kerala, India, PIN-682021
2.1 Sets 2.2 Set Operations
 CSC2510 Theoretical Foundations of Computer Science 2.1 Sets 2.2 Set Operations Introduction to Set Theory A set is a structure, representing an unordered collection (group, plurality) of zero or more
CSC2510 Theoretical Foundations of Computer Science 2.1 Sets 2.2 Set Operations Introduction to Set Theory A set is a structure, representing an unordered collection (group, plurality) of zero or more
REVIEW OF FUZZY SETS
 REVIEW OF FUZZY SETS CONNER HANSEN 1. Introduction L. A. Zadeh s paper Fuzzy Sets* [1] introduces the concept of a fuzzy set, provides definitions for various fuzzy set operations, and proves several properties
REVIEW OF FUZZY SETS CONNER HANSEN 1. Introduction L. A. Zadeh s paper Fuzzy Sets* [1] introduces the concept of a fuzzy set, provides definitions for various fuzzy set operations, and proves several properties
Chapter 4 Fuzzy Logic
 4.1 Introduction Chapter 4 Fuzzy Logic The human brain interprets the sensory information provided by organs. Fuzzy set theory focus on processing the information. Numerical computation can be performed
4.1 Introduction Chapter 4 Fuzzy Logic The human brain interprets the sensory information provided by organs. Fuzzy set theory focus on processing the information. Numerical computation can be performed
Unit V. Neural Fuzzy System
 Unit V Neural Fuzzy System 1 Fuzzy Set In the classical set, its characteristic function assigns a value of either 1 or 0 to each individual in the universal set, There by discriminating between members
Unit V Neural Fuzzy System 1 Fuzzy Set In the classical set, its characteristic function assigns a value of either 1 or 0 to each individual in the universal set, There by discriminating between members
Partition of a Nonempty Fuzzy Set in Nonempty Convex Fuzzy Subsets
 Applied Mathematical Sciences, Vol. 6, 2012, no. 59, 2917-2921 Partition of a Nonempty Fuzzy Set in Nonempty Convex Fuzzy Subsets Omar Salazar Morales Universidad Distrital Francisco José de Caldas, Bogotá,
Applied Mathematical Sciences, Vol. 6, 2012, no. 59, 2917-2921 Partition of a Nonempty Fuzzy Set in Nonempty Convex Fuzzy Subsets Omar Salazar Morales Universidad Distrital Francisco José de Caldas, Bogotá,
Semantics of Fuzzy Sets in Rough Set Theory
 Semantics of Fuzzy Sets in Rough Set Theory Y.Y. Yao Department of Computer Science University of Regina Regina, Saskatchewan Canada S4S 0A2 E-mail: yyao@cs.uregina.ca URL: http://www.cs.uregina.ca/ yyao
Semantics of Fuzzy Sets in Rough Set Theory Y.Y. Yao Department of Computer Science University of Regina Regina, Saskatchewan Canada S4S 0A2 E-mail: yyao@cs.uregina.ca URL: http://www.cs.uregina.ca/ yyao
Discrete Mathematics Lecture 4. Harper Langston New York University
 Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING WITH UNCERTAINTY
 ALGEBRAIC METHODS IN LOGIC AND IN COMPUTER SCIENCE BANACH CENTER PUBLICATIONS, VOLUME 28 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1993 ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING
ALGEBRAIC METHODS IN LOGIC AND IN COMPUTER SCIENCE BANACH CENTER PUBLICATIONS, VOLUME 28 INSTITUTE OF MATHEMATICS POLISH ACADEMY OF SCIENCES WARSZAWA 1993 ROUGH MEMBERSHIP FUNCTIONS: A TOOL FOR REASONING
VHDL framework for modeling fuzzy automata
 Doru Todinca Daniel Butoianu Department of Computers Politehnica University of Timisoara SYNASC 2012 Outline Motivation 1 Motivation Why fuzzy automata? Why a framework for modeling FA? Why VHDL? 2 Fuzzy
Doru Todinca Daniel Butoianu Department of Computers Politehnica University of Timisoara SYNASC 2012 Outline Motivation 1 Motivation Why fuzzy automata? Why a framework for modeling FA? Why VHDL? 2 Fuzzy
CSC Discrete Math I, Spring Sets
 CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
CSC 125 - Discrete Math I, Spring 2017 Sets Sets A set is well-defined, unordered collection of objects The objects in a set are called the elements, or members, of the set A set is said to contain its
[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics
![[Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics [Ch 6] Set Theory. 1. Basic Concepts and Definitions. 400 lecture note #4. 1) Basics](/thumbs/82/86066673.jpg) 400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
400 lecture note #4 [Ch 6] Set Theory 1. Basic Concepts and Definitions 1) Basics Element: ; A is a set consisting of elements x which is in a/another set S such that P(x) is true. Empty set: notated {
Introduction to Intelligent Control Part 3
 ECE 4951 - Spring 2010 Introduction to Part 3 Prof. Marian S. Stachowicz Laboratory for Intelligent Systems ECE Department, University of Minnesota Duluth January 26-29, 2010 Part 1: Outline TYPES OF UNCERTAINTY
ECE 4951 - Spring 2010 Introduction to Part 3 Prof. Marian S. Stachowicz Laboratory for Intelligent Systems ECE Department, University of Minnesota Duluth January 26-29, 2010 Part 1: Outline TYPES OF UNCERTAINTY
OPERATIONS RESEARCH. Linear Programming Problem
 OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
OPERATIONS RESEARCH Chapter 1 Linear Programming Problem Prof. Bibhas C. Giri Department of Mathematics Jadavpur University Kolkata, India Email: bcgiri.jumath@gmail.com 1.0 Introduction Linear programming
MATH 54 - LECTURE 4 DAN CRYTSER
 MATH 54 - LECTURE 4 DAN CRYTSER Introduction In this lecture we review properties and examples of bases and subbases. Then we consider ordered sets and the natural order topology that one can lay on an
MATH 54 - LECTURE 4 DAN CRYTSER Introduction In this lecture we review properties and examples of bases and subbases. Then we consider ordered sets and the natural order topology that one can lay on an
Best proximation of fuzzy real numbers
 214 (214) 1-6 Available online at www.ispacs.com/jfsva Volume 214, Year 214 Article ID jfsva-23, 6 Pages doi:1.5899/214/jfsva-23 Research Article Best proximation of fuzzy real numbers Z. Rohani 1, H.
214 (214) 1-6 Available online at www.ispacs.com/jfsva Volume 214, Year 214 Article ID jfsva-23, 6 Pages doi:1.5899/214/jfsva-23 Research Article Best proximation of fuzzy real numbers Z. Rohani 1, H.
Open and Closed Sets
 Open and Closed Sets Definition: A subset S of a metric space (X, d) is open if it contains an open ball about each of its points i.e., if x S : ɛ > 0 : B(x, ɛ) S. (1) Theorem: (O1) and X are open sets.
Open and Closed Sets Definition: A subset S of a metric space (X, d) is open if it contains an open ball about each of its points i.e., if x S : ɛ > 0 : B(x, ɛ) S. (1) Theorem: (O1) and X are open sets.
CHAPTER 3 FUZZY RELATION and COMPOSITION
 CHAPTER 3 FUZZY RELATION and COMPOSITION Crisp relation! Definition (Product set) Let A and B be two non-empty sets, the prod uct set or Cartesian product A B is defined as follows, A B = {(a, b) a A,
CHAPTER 3 FUZZY RELATION and COMPOSITION Crisp relation! Definition (Product set) Let A and B be two non-empty sets, the prod uct set or Cartesian product A B is defined as follows, A B = {(a, b) a A,
Information Granulation and Approximation in a Decision-theoretic Model of Rough Sets
 Information Granulation and Approximation in a Decision-theoretic Model of Rough Sets Y.Y. Yao Department of Computer Science University of Regina Regina, Saskatchewan Canada S4S 0A2 E-mail: yyao@cs.uregina.ca
Information Granulation and Approximation in a Decision-theoretic Model of Rough Sets Y.Y. Yao Department of Computer Science University of Regina Regina, Saskatchewan Canada S4S 0A2 E-mail: yyao@cs.uregina.ca
FUZZY SYSTEMS: Basics using MATLAB Fuzzy Toolbox. Heikki N. Koivo
 FUZZY SYSTEMS: Basics using MATLAB Fuzzy Toolbox By Heikki N. Koivo 200 2.. Fuzzy sets Membership functions Fuzzy set Universal discourse U set of elements, {u}. Fuzzy set F in universal discourse U: Membership
FUZZY SYSTEMS: Basics using MATLAB Fuzzy Toolbox By Heikki N. Koivo 200 2.. Fuzzy sets Membership functions Fuzzy set Universal discourse U set of elements, {u}. Fuzzy set F in universal discourse U: Membership
Numerical Optimization
 Convex Sets Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Let x 1, x 2 R n, x 1 x 2. Line and line segment Line passing through x 1 and x 2 : {y
Convex Sets Computer Science and Automation Indian Institute of Science Bangalore 560 012, India. NPTEL Course on Let x 1, x 2 R n, x 1 x 2. Line and line segment Line passing through x 1 and x 2 : {y
What is all the Fuzz about?
 What is all the Fuzz about? Fuzzy Systems CPSC 433 Christian Jacob Dept. of Computer Science Dept. of Biochemistry & Molecular Biology University of Calgary Fuzzy Systems in Knowledge Engineering Fuzzy
What is all the Fuzz about? Fuzzy Systems CPSC 433 Christian Jacob Dept. of Computer Science Dept. of Biochemistry & Molecular Biology University of Calgary Fuzzy Systems in Knowledge Engineering Fuzzy
Walheer Barnabé. Topics in Mathematics Practical Session 2 - Topology & Convex
 Topics in Mathematics Practical Session 2 - Topology & Convex Sets Outline (i) Set membership and set operations (ii) Closed and open balls/sets (iii) Points (iv) Sets (v) Convex Sets Set Membership and
Topics in Mathematics Practical Session 2 - Topology & Convex Sets Outline (i) Set membership and set operations (ii) Closed and open balls/sets (iii) Points (iv) Sets (v) Convex Sets Set Membership and
Advanced Operations Research Techniques IE316. Quiz 1 Review. Dr. Ted Ralphs
 Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
Advanced Operations Research Techniques IE316 Quiz 1 Review Dr. Ted Ralphs IE316 Quiz 1 Review 1 Reading for The Quiz Material covered in detail in lecture. 1.1, 1.4, 2.1-2.6, 3.1-3.3, 3.5 Background material
A Decision-Theoretic Rough Set Model
 A Decision-Theoretic Rough Set Model Yiyu Yao and Jingtao Yao Department of Computer Science University of Regina Regina, Saskatchewan, Canada S4S 0A2 {yyao,jtyao}@cs.uregina.ca Special Thanks to Professor
A Decision-Theoretic Rough Set Model Yiyu Yao and Jingtao Yao Department of Computer Science University of Regina Regina, Saskatchewan, Canada S4S 0A2 {yyao,jtyao}@cs.uregina.ca Special Thanks to Professor
EC 521 MATHEMATICAL METHODS FOR ECONOMICS. Lecture 2: Convex Sets
 EC 51 MATHEMATICAL METHODS FOR ECONOMICS Lecture : Convex Sets Murat YILMAZ Boğaziçi University In this section, we focus on convex sets, separating hyperplane theorems and Farkas Lemma. And as an application
EC 51 MATHEMATICAL METHODS FOR ECONOMICS Lecture : Convex Sets Murat YILMAZ Boğaziçi University In this section, we focus on convex sets, separating hyperplane theorems and Farkas Lemma. And as an application
Some traffic control proposals by means of fuzzy sets theory
 Some traffic control proposals by means of fuzzy sets theory Jan Piecha, Paweł Gnyla Informatics Systems Department of Transport Faculty of Transport, Silesian University of Technology ul. Krasinskiego
Some traffic control proposals by means of fuzzy sets theory Jan Piecha, Paweł Gnyla Informatics Systems Department of Transport Faculty of Transport, Silesian University of Technology ul. Krasinskiego
CHAPTER 5 FUZZY LOGIC CONTROL
 64 CHAPTER 5 FUZZY LOGIC CONTROL 5.1 Introduction Fuzzy logic is a soft computing tool for embedding structured human knowledge into workable algorithms. The idea of fuzzy logic was introduced by Dr. Lofti
64 CHAPTER 5 FUZZY LOGIC CONTROL 5.1 Introduction Fuzzy logic is a soft computing tool for embedding structured human knowledge into workable algorithms. The idea of fuzzy logic was introduced by Dr. Lofti
7. The Gauss-Bonnet theorem
 7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
7. The Gauss-Bonnet theorem 7.1 Hyperbolic polygons In Euclidean geometry, an n-sided polygon is a subset of the Euclidean plane bounded by n straight lines. Thus the edges of a Euclidean polygon are formed
2 Review of Set Theory
 2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
2 Review of Set Theory Example 2.1. Let Ω = {1, 2, 3, 4, 5, 6} 2.2. Venn diagram is very useful in set theory. It is often used to portray relationships between sets. Many identities can be read out simply
Figure-12 Membership Grades of x o in the Sets A and B: μ A (x o ) =0.75 and μb(xo) =0.25
 Membership Functions The membership function μ A (x) describes the membership of the elements x of the base set X in the fuzzy set A, whereby for μ A (x) a large class of functions can be taken. Reasonable
Membership Functions The membership function μ A (x) describes the membership of the elements x of the base set X in the fuzzy set A, whereby for μ A (x) a large class of functions can be taken. Reasonable
Lecture 2 - Introduction to Polytopes
 Lecture 2 - Introduction to Polytopes Optimization and Approximation - ENS M1 Nicolas Bousquet 1 Reminder of Linear Algebra definitions Let x 1,..., x m be points in R n and λ 1,..., λ m be real numbers.
Lecture 2 - Introduction to Polytopes Optimization and Approximation - ENS M1 Nicolas Bousquet 1 Reminder of Linear Algebra definitions Let x 1,..., x m be points in R n and λ 1,..., λ m be real numbers.
Contents. The Definition of Fuzzy Logic Rules. Fuzzy Logic and Functions. Fuzzy Sets, Statements, and Rules
 Fuzzy Logic and Functions The Definition of Fuzzy Logic Membership Function Evolutionary Algorithms Constructive Induction Fuzzy logic Neural Nets Decision Trees and other Learning A person's height membership
Fuzzy Logic and Functions The Definition of Fuzzy Logic Membership Function Evolutionary Algorithms Constructive Induction Fuzzy logic Neural Nets Decision Trees and other Learning A person's height membership
Convexity: an introduction
 Convexity: an introduction Geir Dahl CMA, Dept. of Mathematics and Dept. of Informatics University of Oslo 1 / 74 1. Introduction 1. Introduction what is convexity where does it arise main concepts and
Convexity: an introduction Geir Dahl CMA, Dept. of Mathematics and Dept. of Informatics University of Oslo 1 / 74 1. Introduction 1. Introduction what is convexity where does it arise main concepts and
L. A. Zadeh: Fuzzy Sets. (1965) A review
 POSSIBILISTIC INFORMATION: A Tutorial L. A. Zadeh: Fuzzy Sets. (1965) A review George J. Klir Petr Osička State University of New York (SUNY) Binghamton, New York 13902, USA gklir@binghamton.edu Palacky
POSSIBILISTIC INFORMATION: A Tutorial L. A. Zadeh: Fuzzy Sets. (1965) A review George J. Klir Petr Osička State University of New York (SUNY) Binghamton, New York 13902, USA gklir@binghamton.edu Palacky
AN APPROXIMATION APPROACH FOR RANKING FUZZY NUMBERS BASED ON WEIGHTED INTERVAL - VALUE 1.INTRODUCTION
 Mathematical and Computational Applications, Vol. 16, No. 3, pp. 588-597, 2011. Association for Scientific Research AN APPROXIMATION APPROACH FOR RANKING FUZZY NUMBERS BASED ON WEIGHTED INTERVAL - VALUE
Mathematical and Computational Applications, Vol. 16, No. 3, pp. 588-597, 2011. Association for Scientific Research AN APPROXIMATION APPROACH FOR RANKING FUZZY NUMBERS BASED ON WEIGHTED INTERVAL - VALUE
Convex sets and convex functions
 Convex sets and convex functions Convex optimization problems Convex sets and their examples Separating and supporting hyperplanes Projections on convex sets Convex functions, conjugate functions ECE 602,
Convex sets and convex functions Convex optimization problems Convex sets and their examples Separating and supporting hyperplanes Projections on convex sets Convex functions, conjugate functions ECE 602,
Convex sets and convex functions
 Convex sets and convex functions Convex optimization problems Convex sets and their examples Separating and supporting hyperplanes Projections on convex sets Convex functions, conjugate functions ECE 602,
Convex sets and convex functions Convex optimization problems Convex sets and their examples Separating and supporting hyperplanes Projections on convex sets Convex functions, conjugate functions ECE 602,
Fuzzy Reasoning. Outline
 Fuzzy Reasoning Outline Introduction Bivalent & Multivalent Logics Fundamental fuzzy concepts Fuzzification Defuzzification Fuzzy Expert System Neuro-fuzzy System Introduction Fuzzy concept first introduced
Fuzzy Reasoning Outline Introduction Bivalent & Multivalent Logics Fundamental fuzzy concepts Fuzzification Defuzzification Fuzzy Expert System Neuro-fuzzy System Introduction Fuzzy concept first introduced
Introduction to Fuzzy Logic and Fuzzy Systems Adel Nadjaran Toosi
 Introduction to Fuzzy Logic and Fuzzy Systems Adel Nadjaran Toosi Fuzzy Slide 1 Objectives What Is Fuzzy Logic? Fuzzy sets Membership function Differences between Fuzzy and Probability? Fuzzy Inference.
Introduction to Fuzzy Logic and Fuzzy Systems Adel Nadjaran Toosi Fuzzy Slide 1 Objectives What Is Fuzzy Logic? Fuzzy sets Membership function Differences between Fuzzy and Probability? Fuzzy Inference.
Digital convex fuzzy hull
 Digital convex fuzzy hull Slobodan Dražić, Svetlana Jakšić, Ljubo Nedović, Nebojša M. Ralević Faculty of Engineering, University of Novi Sad Trg Dositeja Obradovića 6, 21000 Novi Sad, Serbia and Montenegro
Digital convex fuzzy hull Slobodan Dražić, Svetlana Jakšić, Ljubo Nedović, Nebojša M. Ralević Faculty of Engineering, University of Novi Sad Trg Dositeja Obradovića 6, 21000 Novi Sad, Serbia and Montenegro
ARTIFICIAL INTELLIGENCE. Uncertainty: fuzzy systems
 INFOB2KI 2017-2018 Utrecht University The Netherlands ARTIFICIAL INTELLIGENCE Uncertainty: fuzzy systems Lecturer: Silja Renooij These slides are part of the INFOB2KI Course Notes available from www.cs.uu.nl/docs/vakken/b2ki/schema.html
INFOB2KI 2017-2018 Utrecht University The Netherlands ARTIFICIAL INTELLIGENCE Uncertainty: fuzzy systems Lecturer: Silja Renooij These slides are part of the INFOB2KI Course Notes available from www.cs.uu.nl/docs/vakken/b2ki/schema.html
FUZZY SETS. Precision vs. Relevancy LOOK OUT! A 1500 Kg mass is approaching your head OUT!!
 FUZZY SETS Precision vs. Relevancy A 5 Kg mass is approaching your head at at 45.3 45.3 m/sec. m/s. OUT!! LOOK OUT! 4 Introduction How to simplify very complex systems? Allow some degree of uncertainty
FUZZY SETS Precision vs. Relevancy A 5 Kg mass is approaching your head at at 45.3 45.3 m/sec. m/s. OUT!! LOOK OUT! 4 Introduction How to simplify very complex systems? Allow some degree of uncertainty
Convex Geometry arising in Optimization
 Convex Geometry arising in Optimization Jesús A. De Loera University of California, Davis Berlin Mathematical School Summer 2015 WHAT IS THIS COURSE ABOUT? Combinatorial Convexity and Optimization PLAN
Convex Geometry arising in Optimization Jesús A. De Loera University of California, Davis Berlin Mathematical School Summer 2015 WHAT IS THIS COURSE ABOUT? Combinatorial Convexity and Optimization PLAN
Lecture-12: Closed Sets
 and Its Examples Properties of Lecture-12: Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Introduction and Its Examples Properties of 1 Introduction
and Its Examples Properties of Lecture-12: Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Introduction and Its Examples Properties of 1 Introduction
1.1 - Introduction to Sets
 1.1 - Introduction to Sets Math 166-502 Blake Boudreaux Department of Mathematics Texas A&M University January 18, 2018 Blake Boudreaux (Texas A&M University) 1.1 - Introduction to Sets January 18, 2018
1.1 - Introduction to Sets Math 166-502 Blake Boudreaux Department of Mathematics Texas A&M University January 18, 2018 Blake Boudreaux (Texas A&M University) 1.1 - Introduction to Sets January 18, 2018
MTAEA Convexity and Quasiconvexity
 School of Economics, Australian National University February 19, 2010 Convex Combinations and Convex Sets. Definition. Given any finite collection of points x 1,..., x m R n, a point z R n is said to be
School of Economics, Australian National University February 19, 2010 Convex Combinations and Convex Sets. Definition. Given any finite collection of points x 1,..., x m R n, a point z R n is said to be
Topological properties of convex sets
 Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 5: Topological properties of convex sets 5.1 Interior and closure of convex sets Let
Division of the Humanities and Social Sciences Ec 181 KC Border Convex Analysis and Economic Theory Winter 2018 Topic 5: Topological properties of convex sets 5.1 Interior and closure of convex sets Let
However, this is not always true! For example, this fails if both A and B are closed and unbounded (find an example).
 98 CHAPTER 3. PROPERTIES OF CONVEX SETS: A GLIMPSE 3.2 Separation Theorems It seems intuitively rather obvious that if A and B are two nonempty disjoint convex sets in A 2, then there is a line, H, separating
98 CHAPTER 3. PROPERTIES OF CONVEX SETS: A GLIMPSE 3.2 Separation Theorems It seems intuitively rather obvious that if A and B are two nonempty disjoint convex sets in A 2, then there is a line, H, separating
Math Introduction to Advanced Mathematics
 Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
SINGLE VALUED NEUTROSOPHIC SETS
 Fuzzy Sets, Rough Sets and Multivalued Operations and pplications, Vol 3, No 1, (January-June 2011): 33 39; ISSN : 0974-9942 International Science Press SINGLE VLUED NEUTROSOPHIC SETS Haibin Wang, Yanqing
Fuzzy Sets, Rough Sets and Multivalued Operations and pplications, Vol 3, No 1, (January-June 2011): 33 39; ISSN : 0974-9942 International Science Press SINGLE VLUED NEUTROSOPHIC SETS Haibin Wang, Yanqing
Topology I Test 1 Solutions October 13, 2008
 Topology I Test 1 Solutions October 13, 2008 1. Do FIVE of the following: (a) Give a careful definition of connected. A topological space X is connected if for any two sets A and B such that A B = X, we
Topology I Test 1 Solutions October 13, 2008 1. Do FIVE of the following: (a) Give a careful definition of connected. A topological space X is connected if for any two sets A and B such that A B = X, we
Lagrangian Relaxation: An overview
 Discrete Math for Bioinformatics WS 11/12:, by A. Bockmayr/K. Reinert, 22. Januar 2013, 13:27 4001 Lagrangian Relaxation: An overview Sources for this lecture: D. Bertsimas and J. Tsitsiklis: Introduction
Discrete Math for Bioinformatics WS 11/12:, by A. Bockmayr/K. Reinert, 22. Januar 2013, 13:27 4001 Lagrangian Relaxation: An overview Sources for this lecture: D. Bertsimas and J. Tsitsiklis: Introduction
2. Metric and Topological Spaces
 2 Metric and Topological Spaces Topology begins where sets are implemented with some cohesive properties enabling one to define continuity Solomon Lefschetz In order to forge a language of continuity,
2 Metric and Topological Spaces Topology begins where sets are implemented with some cohesive properties enabling one to define continuity Solomon Lefschetz In order to forge a language of continuity,
Fuzzy Set-Theoretical Approach for Comparing Objects with Fuzzy Attributes
 Fuzzy Set-Theoretical Approach for Comparing Objects with Fuzzy Attributes Y. Bashon, D. Neagu, M.J. Ridley Department of Computing University of Bradford Bradford, BD7 DP, UK e-mail: {Y.Bashon, D.Neagu,
Fuzzy Set-Theoretical Approach for Comparing Objects with Fuzzy Attributes Y. Bashon, D. Neagu, M.J. Ridley Department of Computing University of Bradford Bradford, BD7 DP, UK e-mail: {Y.Bashon, D.Neagu,
REDUNDANCY OF MULTISET TOPOLOGICAL SPACES
 Iranian Journal of Fuzzy Systems Vol. 14, No. 4, (2017) pp. 163-168 163 REDUNDANCY OF MULTISET TOPOLOGICAL SPACES A. GHAREEB Abstract. In this paper, we show the redundancies of multiset topological spaces.
Iranian Journal of Fuzzy Systems Vol. 14, No. 4, (2017) pp. 163-168 163 REDUNDANCY OF MULTISET TOPOLOGICAL SPACES A. GHAREEB Abstract. In this paper, we show the redundancies of multiset topological spaces.
2.8. Connectedness A topological space X is said to be disconnected if X is the disjoint union of two non-empty open subsets. The space X is said to
 2.8. Connectedness A topological space X is said to be disconnected if X is the disjoint union of two non-empty open subsets. The space X is said to be connected if it is not disconnected. A subset of
2.8. Connectedness A topological space X is said to be disconnected if X is the disjoint union of two non-empty open subsets. The space X is said to be connected if it is not disconnected. A subset of
Algorithms for the Construction of Digital Convex Fuzzy Hulls
 lgorithms for the Construction of Digital Convex Fuzzy Hulls Nebojša M. Ralević Faculty of Engineering, University of Novi Sad Trg Dositeja Obradovića 6, 000 Novi Sad, Serbia nralevic@uns.ns.ac.yu Lidija
lgorithms for the Construction of Digital Convex Fuzzy Hulls Nebojša M. Ralević Faculty of Engineering, University of Novi Sad Trg Dositeja Obradovića 6, 000 Novi Sad, Serbia nralevic@uns.ns.ac.yu Lidija
2. Sets. 2.1&2.2: Sets and Subsets. Combining Sets. c Dr Oksana Shatalov, Fall
 c Dr Oksana Shatalov, Fall 2014 1 2. Sets 2.1&2.2: Sets and Subsets. Combining Sets. Set Terminology and Notation DEFINITIONS: Set is well-defined collection of objects. Elements are objects or members
c Dr Oksana Shatalov, Fall 2014 1 2. Sets 2.1&2.2: Sets and Subsets. Combining Sets. Set Terminology and Notation DEFINITIONS: Set is well-defined collection of objects. Elements are objects or members
Musikasuwan, Salang (2013) Novel fuzzy techniques for modelling human decision making. PhD thesis, University of Nottingham.
 Musikasuwan, Salang (213) Novel fuzzy techniques for modelling human decision making. PhD thesis, University of Nottingham. Access from the University of Nottingham repository: http://eprints.nottingham.ac.uk/13161/1/salang-phd-thesis.pdf
Musikasuwan, Salang (213) Novel fuzzy techniques for modelling human decision making. PhD thesis, University of Nottingham. Access from the University of Nottingham repository: http://eprints.nottingham.ac.uk/13161/1/salang-phd-thesis.pdf
Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103. Chapter 2. Sets
 Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103 Chapter 2 Sets Slides are adopted from Discrete Mathematics and It's Applications Kenneth H.
Taibah University College of Computer Science & Engineering Course Title: Discrete Mathematics Code: CS 103 Chapter 2 Sets Slides are adopted from Discrete Mathematics and It's Applications Kenneth H.
Simple Linear Interpolation Explains All Usual Choices in Fuzzy Techniques: Membership Functions, t-norms, t-conorms, and Defuzzification
 Simple Linear Interpolation Explains All Usual Choices in Fuzzy Techniques: Membership Functions, t-norms, t-conorms, and Defuzzification Vladik Kreinovich, Jonathan Quijas, Esthela Gallardo, Caio De Sa
Simple Linear Interpolation Explains All Usual Choices in Fuzzy Techniques: Membership Functions, t-norms, t-conorms, and Defuzzification Vladik Kreinovich, Jonathan Quijas, Esthela Gallardo, Caio De Sa
Lecture : Topological Space
 Example of Lecture : Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Example of 1 2 3 Example of 4 5 6 Example of I Topological spaces and continuous
Example of Lecture : Dr. Department of Mathematics Lovely Professional University Punjab, India October 18, 2014 Outline Example of 1 2 3 Example of 4 5 6 Example of I Topological spaces and continuous
Topology 550A Homework 3, Week 3 (Corrections: February 22, 2012)
 Topology 550A Homework 3, Week 3 (Corrections: February 22, 2012) Michael Tagare De Guzman January 31, 2012 4A. The Sorgenfrey Line The following material concerns the Sorgenfrey line, E, introduced in
Topology 550A Homework 3, Week 3 (Corrections: February 22, 2012) Michael Tagare De Guzman January 31, 2012 4A. The Sorgenfrey Line The following material concerns the Sorgenfrey line, E, introduced in
Introduction to Modern Control Systems
 Introduction to Modern Control Systems Convex Optimization, Duality and Linear Matrix Inequalities Kostas Margellos University of Oxford AIMS CDT 2016-17 Introduction to Modern Control Systems November
Introduction to Modern Control Systems Convex Optimization, Duality and Linear Matrix Inequalities Kostas Margellos University of Oxford AIMS CDT 2016-17 Introduction to Modern Control Systems November
Multi objective linear programming problem (MOLPP) is one of the popular
 CHAPTER 5 FUZZY MULTI OBJECTIVE LINEAR PROGRAMMING PROBLEM 5.1 INTRODUCTION Multi objective linear programming problem (MOLPP) is one of the popular methods to deal with complex and ill - structured decision
CHAPTER 5 FUZZY MULTI OBJECTIVE LINEAR PROGRAMMING PROBLEM 5.1 INTRODUCTION Multi objective linear programming problem (MOLPP) is one of the popular methods to deal with complex and ill - structured decision
CHAPTER 4 FREQUENCY STABILIZATION USING FUZZY LOGIC CONTROLLER
 60 CHAPTER 4 FREQUENCY STABILIZATION USING FUZZY LOGIC CONTROLLER 4.1 INTRODUCTION Problems in the real world quite often turn out to be complex owing to an element of uncertainty either in the parameters
60 CHAPTER 4 FREQUENCY STABILIZATION USING FUZZY LOGIC CONTROLLER 4.1 INTRODUCTION Problems in the real world quite often turn out to be complex owing to an element of uncertainty either in the parameters
c) the set of students at your school who either are sophomores or are taking discrete mathematics
 Exercises Exercises Page 136 1. Let A be the set of students who live within one mile of school and let B be the set of students who walk to classes. Describe the students in each of these sets. a) A B
Exercises Exercises Page 136 1. Let A be the set of students who live within one mile of school and let B be the set of students who walk to classes. Describe the students in each of these sets. a) A B
Shiqian Ma, MAT-258A: Numerical Optimization 1. Chapter 2. Convex Optimization
 Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 2 Convex Optimization Shiqian Ma, MAT-258A: Numerical Optimization 2 2.1. Convex Optimization General optimization problem: min f 0 (x) s.t., f i
Shiqian Ma, MAT-258A: Numerical Optimization 1 Chapter 2 Convex Optimization Shiqian Ma, MAT-258A: Numerical Optimization 2 2.1. Convex Optimization General optimization problem: min f 0 (x) s.t., f i
Lecture notes. Com Page 1
 Lecture notes Com Page 1 Contents Lectures 1. Introduction to Computational Intelligence 2. Traditional computation 2.1. Sorting algorithms 2.2. Graph search algorithms 3. Supervised neural computation
Lecture notes Com Page 1 Contents Lectures 1. Introduction to Computational Intelligence 2. Traditional computation 2.1. Sorting algorithms 2.2. Graph search algorithms 3. Supervised neural computation
Dinner for Two, Reprise
 Fuzzy Logic Toolbox Dinner for Two, Reprise In this section we provide the same two-input, one-output, three-rule tipping problem that you saw in the introduction, only in more detail. The basic structure
Fuzzy Logic Toolbox Dinner for Two, Reprise In this section we provide the same two-input, one-output, three-rule tipping problem that you saw in the introduction, only in more detail. The basic structure
Sets. Mukulika Ghosh. Fall Based on slides by Dr. Hyunyoung Lee
 Sets Mukulika Ghosh Fall 2018 Based on slides by Dr. Hyunyoung Lee Sets Sets A set is an unordered collection of objects, called elements, without duplication. We write a A to denote that a is an element
Sets Mukulika Ghosh Fall 2018 Based on slides by Dr. Hyunyoung Lee Sets Sets A set is an unordered collection of objects, called elements, without duplication. We write a A to denote that a is an element
Introduction 2 Fuzzy Sets & Fuzzy Rules. Aleksandar Rakić Contents
 Beograd ETF Fuzzy logic Introduction 2 Fuzzy Sets & Fuzzy Rules Aleksandar Rakić rakic@etf.rs Contents Characteristics of Fuzzy Sets Operations Properties Fuzzy Rules Examples 2 1 Characteristics of Fuzzy
Beograd ETF Fuzzy logic Introduction 2 Fuzzy Sets & Fuzzy Rules Aleksandar Rakić rakic@etf.rs Contents Characteristics of Fuzzy Sets Operations Properties Fuzzy Rules Examples 2 1 Characteristics of Fuzzy
About the Tutorial. Audience. Prerequisites. Disclaimer& Copyright. Fuzzy Logic
 About the Tutorial Fuzzy Logic resembles the human decision-making methodology and deals with vague and imprecise information. This is a very small tutorial that touches upon the very basic concepts of
About the Tutorial Fuzzy Logic resembles the human decision-making methodology and deals with vague and imprecise information. This is a very small tutorial that touches upon the very basic concepts of
Epimorphisms in the Category of Hausdorff Fuzzy Topological Spaces
 Annals of Pure and Applied Mathematics Vol. 7, No. 1, 2014, 35-40 ISSN: 2279-087X (P), 2279-0888(online) Published on 9 September 2014 www.researchmathsci.org Annals of Epimorphisms in the Category of
Annals of Pure and Applied Mathematics Vol. 7, No. 1, 2014, 35-40 ISSN: 2279-087X (P), 2279-0888(online) Published on 9 September 2014 www.researchmathsci.org Annals of Epimorphisms in the Category of
Locally convex topological vector spaces
 Chapter 4 Locally convex topological vector spaces 4.1 Definition by neighbourhoods Let us start this section by briefly recalling some basic properties of convex subsets of a vector space over K (where
Chapter 4 Locally convex topological vector spaces 4.1 Definition by neighbourhoods Let us start this section by briefly recalling some basic properties of convex subsets of a vector space over K (where
4 Mathematical Data Types
 mcs 2015/5/18 1:43 page 81 #89 4 Mathematical Data Types We have assumed that you ve already been introduced to the concepts of sets, sequences, and functions, and we ve used them informally several times
mcs 2015/5/18 1:43 page 81 #89 4 Mathematical Data Types We have assumed that you ve already been introduced to the concepts of sets, sequences, and functions, and we ve used them informally several times
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Sets and set operations. Lecture 5 ICOM 4075
 Sets and set operations Lecture 5 ICOM 4075 Reviewing sets s defined in a previous lecture, a setis a collection of objects that constitute the elementsof the set We say that a set containsits elements,
Sets and set operations Lecture 5 ICOM 4075 Reviewing sets s defined in a previous lecture, a setis a collection of objects that constitute the elementsof the set We say that a set containsits elements,
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS
 Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3.
 TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
Lecture 17: Continuous Functions
 Lecture 17: Continuous Functions 1 Continuous Functions Let (X, T X ) and (Y, T Y ) be topological spaces. Definition 1.1 (Continuous Function). A function f : X Y is said to be continuous if the inverse
Lecture 17: Continuous Functions 1 Continuous Functions Let (X, T X ) and (Y, T Y ) be topological spaces. Definition 1.1 (Continuous Function). A function f : X Y is said to be continuous if the inverse
Lecture 2 September 3
 EE 381V: Large Scale Optimization Fall 2012 Lecture 2 September 3 Lecturer: Caramanis & Sanghavi Scribe: Hongbo Si, Qiaoyang Ye 2.1 Overview of the last Lecture The focus of the last lecture was to give
EE 381V: Large Scale Optimization Fall 2012 Lecture 2 September 3 Lecturer: Caramanis & Sanghavi Scribe: Hongbo Si, Qiaoyang Ye 2.1 Overview of the last Lecture The focus of the last lecture was to give
Three Dimensional Geometry. Linear Programming
 Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
Three Dimensional Geometry Linear Programming A plane is determined uniquely if any one of the following is known: The normal to the plane and its distance from the origin is given, i.e. equation of a
CHAPTER 8. Copyright Cengage Learning. All rights reserved.
 CHAPTER 8 RELATIONS Copyright Cengage Learning. All rights reserved. SECTION 8.3 Equivalence Relations Copyright Cengage Learning. All rights reserved. The Relation Induced by a Partition 3 The Relation
CHAPTER 8 RELATIONS Copyright Cengage Learning. All rights reserved. SECTION 8.3 Equivalence Relations Copyright Cengage Learning. All rights reserved. The Relation Induced by a Partition 3 The Relation
Introduction 3 Fuzzy Inference. Aleksandar Rakić Contents
 Beograd ETF Fuzzy logic Introduction 3 Fuzzy Inference Aleksandar Rakić rakic@etf.rs Contents Mamdani Fuzzy Inference Fuzzification of the input variables Rule evaluation Aggregation of rules output Defuzzification
Beograd ETF Fuzzy logic Introduction 3 Fuzzy Inference Aleksandar Rakić rakic@etf.rs Contents Mamdani Fuzzy Inference Fuzzification of the input variables Rule evaluation Aggregation of rules output Defuzzification
Lecture 4: examples of topological spaces, coarser and finer topologies, bases and closed sets
 Lecture 4: examples of topological spaces, coarser and finer topologies, bases and closed sets Saul Glasman 14 September 2016 Let s give the definition of an open subset of R. Definition 1. Let U R. We
Lecture 4: examples of topological spaces, coarser and finer topologies, bases and closed sets Saul Glasman 14 September 2016 Let s give the definition of an open subset of R. Definition 1. Let U R. We
A Communications Network???
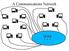 A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
A Communications Network??? A Communications Network What are the desirable properties of the switching box? 1. Every two users must be connected at a switch. 2. Every switch must "look alike". 3. The
CS522: Advanced Algorithms
 Lecture 1 CS5: Advanced Algorithms October 4, 004 Lecturer: Kamal Jain Notes: Chris Re 1.1 Plan for the week Figure 1.1: Plan for the week The underlined tools, weak duality theorem and complimentary slackness,
Lecture 1 CS5: Advanced Algorithms October 4, 004 Lecturer: Kamal Jain Notes: Chris Re 1.1 Plan for the week Figure 1.1: Plan for the week The underlined tools, weak duality theorem and complimentary slackness,
CHAPTER 3 FUZZY RELATION and COMPOSITION
 CHAPTER 3 FUZZY RELATION and COMPOSITION The concept of fuzzy set as a generalization of crisp set has been introduced in the previous chapter. Relations between elements of crisp sets can be extended
CHAPTER 3 FUZZY RELATION and COMPOSITION The concept of fuzzy set as a generalization of crisp set has been introduced in the previous chapter. Relations between elements of crisp sets can be extended
