Spherical Blend Skinning: A Real-time Deformation of Articulated Models
|
|
|
- Hollie Kelley
- 5 years ago
- Views:
Transcription
1 Spherical Blend Skinning: A Real-time Deformation of Articulated Models Ladislav Kavan Jiří Žára Czech Technical University in Prague Abstract Skin deformation based on an underlying skeleton is a common method to animate believable organic models. The most widely used skeletal animation algorithm, linear blend skinning, is also known as skeleton subspace deformation, vertex blending, or enveloping. It runs in real-time even on a low-end hardware but it is also notorious for its failures, such as the collapsing-joints artifacts. We present a new algorithm which removes these shortcomings while maintaining almost the same time and memory complexity as the linear blend skinning. Unlike other approaches, our method works with exactly the same input data as the popular linear version. This minimizes the cost of upgrade from linear to spherical blend skinning in many existing applications: the data structures and models need no change at all. The paper discusses also theoretical properties of rotation interpolation, essential to spherical blend skinning. CR Categories: I.3.7 [Computer Graphics]: Three-Dimensional Graphics and Realism Animation Keywords: skinning, deformation, skeletal animation Introduction Real-time animation of deformable objects is always a compromise between visual fidelity and computation complexity. Other aspects are quite important as well, for example the amount of artists work necessary to design the model. Therefore, there exist many algorithms for modeling deformable objects in the literature. They differ by the intended area of application and generality of allowed models. We focus on the real-time animation systems in this paper. Its most popular representative, known generally as the skeletal animation, is based on simple but versatile structure. It consists of joints, given by their position and orientation. The segments connecting the joints are conveniently interpreted as bones. Theskeleton is, formally speaking, a tree whose nodes are identified with the joints and edges with the bones. The only displayed element is a skin, a 3D polygonal mesh, usually equipped with normal and texture data. Although the terminology is adopted from the virtual humanoid modeling, the skeletal animation is not limited to character animation it can be applied to a wide range of soft objects, including imaginary (cartoon) creatures, plants, furniture, etc. This is an apparent advantage over complex systems which rely on explicit anatomy. kavanl@fel.cvut.cz The skeleton simplifies the animation task considerably: instead of animating each vertex individually, it is sufficient to manipulate the skeleton, and the skin deforms automatically. The skeletal animation in general does not specify how exactly the skeleton posture should be propagated to the skin. However, there is an established standard used in majority of real-time 3D applications. It comes by many names, all relating to the same algorithm: linear blend skinning (LBS), skeleton subspace deformation, vertex blending, enveloping, or simply skinning. Basically, this algorithm blends between rigidly transformed vertices using vertex weights, which denote the amount of influence of individual joints. Although LBS is very fast and advantageous to graphics hardware, it suffers from inherent artifacts, known as collapsing joints, twisting elbow problem or a candy-wrapper artifact. In general, the mesh deformed by LBS loses volume as the joint rotation increases. The cause of this phenomena is explained in section 3, together with the LBS algorithm itself. The structure of the paper is as follows: in the next section, we summarize the previous work concerning real-time skin deformation and sketch our solution. In section 3, we analyze the problems of the LBS algorithm. Our approach to resolve these problems is presented in section 4. In section 5, we compare the results and discuss possible enhancements. 2 Related Work An early contribution concerning the animation of deformable objects is [Magnenat-Thalmann et al. 988], which considers the movement of a human hand. First 3D characters used in numerous computer games were animated by simple, often unpublished algorithms. Later on, the basic principles of LBS were described by the game development community [Lander 998; Lander 999]. The artifacts of LBS were discovered soon [Weber 2000]. An improvement based on addition of auxiliary joints has been also proposed in [Weber 2000]. Although this reduces the artifacts, the skin to joints relationship must be re-designed after joint addition. The number and location of the additional joints remains questionable. Another problem is how the movement of the original skeleton should be propagated into the augmented one. More formal articles consider skin deformation as an interpolation problem, such as [Lewis et al. 2000]. They use radial basis functions to interpolate between example skins with different shapes. Similar method is presented in [Sloan et al. 200] and [Kry et al. 2002]. The latter de-correlates the deformation displacements using principal component analysis, which reduces the memory requirements considerably. The advantage of example based methods is that they capture the designed shape, including effects like muscle bulging. The drawback is the necessity of acquiring the example skins. An interesting generalization of LBS is called multi-weight enveloping [Wang and Phillips 2002]. It introduces more parameters and therefore greater flexibility to the deformation algorithm. Instead of one weight per influence (joint) as in LBS, the multiweight enveloping uses twelve. These numerous parameters are derived from examples using the least squares optimization. The
2 disadvantage is obvious: while the LBS models can be weighted manually by artists [Steed 2002], this is questionable with multiweight enveloping. Tools that help animators to design the vertex weights are described in [Mohr et al. 2003]. This article is interesting also from the theoretical point of view, because it describes how to explore the space of all possible LBS deformations. Another deformation algorithm [Bloomenthal 2002] uses a complex auxiliary structure a medial. An idea similar to spherical blend skinning (SBS) is bones blending proposed by [Kavan and Žára 2003]. However, bones blending is limited to vertices attached to only two joints. In addition, it requires hand-tuning of special parameters. Another algorithm removes the LBS artifacts by adding additional joints, and computes the vertex weights automatically using examples [Mohr and Gleicher 2003]. A recent skin deformation algorithm presented in [Magnenat-Thalmann et al. 2004] seems to give results competitive to SBS, although it is based on a different mathematical fundament [Alexa 2002]. However, this method is considerably slower than LBS and therefore [Magnenat-Thalmann et al. 2004] recommends to use rather the standard LBS if the joint rotations are small. To conclude, there are many methods correcting the problems of LBS, but none of them is superior to LBS in all aspects. As a result, the linear blend skinning is still widely used in many applications, in spite of the artifacts. 2. Our Contribution We observed that the artifacts of LBS are caused by the straightforward, linear interpolation of vertex positions. Intuitively, a linear blending is not suitable to capture deformations induced by skeleton, because their nature is rather spherical. Our basic idea is to change the interpolation domain: we interpolate transformations itself instead of transformed vertex positions. Because we consider transformations consisting of a translation and rotation, we suggest to use a quaternion representation. The transition to non-linear interpolation domain is not elementary. In order to achieve our goal, we cope with two main problems: determination of the center of rotation, and interpolation of multiple quaternions. The first problem follows from the fact that the choice of the center of rotation influences the result of interpolation considerably. We show how to compute a convenient center of rotation in real-time. The second problem is simple in the case of two quaternions [Shoemake 985], but gets considerably harder for more than two rotations [Buss and Fillmore 200; Park et al. 2002; Alexa 2002]. Because the previous methods are not efficient enough for our purpose, we use a simple linear quaternion averaging. We justify both theoretically and experimentally that this solution is appropriate for our task (and probably for many others). Resolving those problems, we obtain a skin animation algorithm that deforms the mesh in much more plausible way then LBS. Because we change only the interpolation domain and not the input data, our program works with exactly the same models as LBS. The proposed algorithm improves a deformed shape even of models that have been designed and carefully tuned for LBS. Considering the high speed and low memory demands of SBS, it provides an attractive alternative to classic LBS. 2.2 Conventions Let us denote matrices by capital letters, while vectors and quaternions by bold. Vectors are considered column vectors, therefore a multiplication of vector v by matrix M is written as Mv. We do not introduce a different notation for the R 3 vectors and their homogeneous R 4 counterparts with last coordinate equal to. The same convention is used for matrices. We denote the dot product of two vectors v,v 2 as (v,v 2 ) and the norm v as a shortcut for (v,v ). 3 Linear Blend Skinning The input to LBS consists of a polygonal mesh representing the digital skin, a skeleton, and vertex weights for every vertex of the skin. The polygonal mesh and the skeleton are designed in a reference position, e.g. virtual characters are often posed in the da Vinci posture [Steed 2002]. Let us label the joints by integer numbers, assigning zero to the root. Each joint in the reference posture is associated with a homogeneous matrix, describing its position and orientation in the world coordinate system. For j-th joint, we denote this matrix by A j, like absolute (or reference) position. This matrix is computed by multiplying all the transformations of individual joints in the chain from root to joint j. To compute the shape of the deformed skin, we need yet another set of matrices, describing the position and orientation of joints in the actual, animated posture. We call them F j, standing for the final placement of joint j. Matrices F j are computed in a similar way as the absolute matrices, but including the actual rotation of each joint in the chain (we do not consider translating and scaling joints). The most simple skin deformation algorithm computes v = F j A j v where v is a vertex in the reference skin associated with joint j and v is its position in the deformed mesh. The interpretation is following: the first matrix A j transforms v to the position with joint j s coordinate system aligned to the world coordinate system. The following transformation F j returns the vertex to its current position induced by the animated skeleton. Because these transformations usually occur together, we define the complete matrix C j = F j A j. Some older computer games animated characters in this way, even though it does not produce nice, smooth deformations. The linear blend skinning allows assignment of one vertex to multiple bones. Assume that vertex v is attached to joints j,..., j n with weights w,...,w n. The weights are coefficients of a convex combination, i.e. non-negative and n i= w i =. The weight w i represents the amount of influence of joint. The vertex position in the mesh deformed by LBS is then computed as v n = w i C ji v () i= that is to say, making a convex combination of individual vertex transformations. For example if n = 2thenvertexv lies on the line segment connecting C j v and C j2 v. The actual position on the segment is given by weight w (or w 2, because w +w 2 = ). As explained in the next section, the SBS works on a circular arc instead of segment, see Figure. If the joint rotations are large, the LBS produces non-natural deformations. In the extremal case of rotation by 80 degrees, the skin can collapse to a single point. It is the notorious candy-wrapper artifact, which is demonstrated in Figure 2. The right shoulder of
3 mesh bone joint j j 2 vertex v C v j 2 C j v LBS workspace SBS workspace Figure : The set of possible results of LBS is a line segment, while SBS gives a circular arc. Figure 2: Up an extreme shoulder twist deformed by LBS, down the same posture deformed by SBS the model is twisted by 80 degrees, while the left shoulder is left in the reference pose. To understand why this undesirable effect occurs, it is sufficient to re-arrange the equation () v = ( n i=w i C ji ) v (2) This formula is less efficient, because it blends matrices instead of vectors, but gives us a valuable insight. It is well known that the component-wise interpolation of matrices produces odd results: it does not preserve the orthogonality of the rotational part of the matrix. In some situations, it does not preserve even the rank of the interpolated matrices. This is exactly what happens in the candywrapper problem: the single point the skin collapses to is a result of transformation by a singular matrix. A similar defect is visible also in the proximity of the singular configuration. Although the matrix is regular, it involves a non-uniform scaling and skewing, which is responsible for the loss of volume of the deformed skin even for small rotations. 4 Spherical Blend Skinning Instead of trying to correct the bad results of LBS, we propose to change the interpolation method in (2). We focus on the interpolation of rotations the linear interpolation of the translation part of C ji matrices is all right. An established interpolation of two rotations is spherical linear interpolation (SLERP) [Shoemake 985]. Its key of success is the use of quaternions to represent rotations. Unfortunately, it is not possible to simply replace matrices C ji in (2) with corresponding pairs quaternion-translation. One of the problems is that the linear interpolation of quaternions is not equivalent to SLERP. However, this is not the most serious difficulty, and we address it in section 4.. The more important problem is to compute a convenient center of the interpolated rotations. We show that this is really an important problem on an example of human arm. Consider that the arm geometry is influenced by two joints j and j 2, such that j is a parent of j 2, as in Figure. The transformation of the whole mesh by C j is illustrated in the top row of Figure 3 and the transformation of the same geometry by C j2 in the bottom row (note that the results are identical in both columns of these rows). The rows in the middle show the progress of interpolation between C j to C j2. The only difference between the two columns in Figure 3 is in the choice of the center of rotation. In the left column, the rotation center r c is set to the translation part of matrix A j2 (the position of joint j 2 in the reference posture). Note that C j r c = C j2 r c, therefore also the transformed rotation center is constant during the interpolation. In the right column of the figure, the rotation center r c is set to the translation part of A j. Because C j r c C j2 r c, the transformed rotation center is linearly interpolated from C j r c to C j2 r c. By comparison with the starting mesh (drawn gray in each frame), it is obvious that the center of rotation choice in the left column is much more advantageous. In this case, the interpolation of every single point is a circular arc (as in Figure ), whereas a disturbing drift is inherent to any other choice of rotation center (such as r c ). Unfortunately, the condition of zero translation cannot be always satisfied, typically for more than two influencing joints. But even if the vertex is attached to only two joints k and l that are not neighbours of each other, some translation may be inevitable. For example consider that there is no relative rotation between C k and C l,but there is a relative translation induced by the joints in the chain between k and l. Clearly no choice of the center of rotation can avoid this translation, because the rotation is identity. Anyway, it is possible to define the rotation center as the point whose transformations by associated matrices are as close as possible. This minimizes the drift and works even if the vertex is assigned to n joints j,..., j n. We find the center of rotation r c as the
4 C j C j r c C j C j r c If we stack all these equations to one matrix D and the right-hand sides to vector e, we can write the whole system as Dr c = e where D is a 3 ( n 2) 3matrix,rc is a 3-dimensional unknown vector and e is 3 ( n 2) -dimensional vector. In general, we cannot make any assumptions about the rank of matrix D, which can vary from 0 to 3 (consider for example n = 2andC j = C j2 ). We search the optimal solution r c in the least-squares sense. If there are multiple solutions giving the minimal Dr c e, ther c with the minimal norm is chosen. This can be done in a robust way using the singular value decomposition (SVD), followed by computation of pseudo-inverse matrix. To perform these computations, we use the LAPACK software [Anderson et al. 999]. Even though LAPACK routines are efficient, computation of the center of rotation per each vertex would not result in a real-time algorithm. Fortunately, the center of rotation depends only on the transformations of the joints j,..., j n and not the vertex itself. Therefore, if we encounter another vertex assigned to the same set of joints j,..., j n, we can re-use the center of rotation computed formerly (cached). Moreover, if there is only one, or two neighboring joints that influence the vertex, we can determine the center of rotation precisely (as indicated in the beginning of this section) and omit the SVD computation at all. It turns out that the number of different non-trivial joint sets, and therefore the number of running the SVD, is surprisingly small for common models about several tens. This enables the real-time performance. 4. Interpolation of Multiple Rotations C j2 r c C j2 rc C j2 Figure 3: The correct center of rotation is chosen in the left column, while the sub-optimal in the right column. In the middle rows, notice the difference of the elbow position with respect to the original skin. least-squares solution of the system of ( n 2) linear vector equations C a r c = C b r c, a < b, a,b {j,..., j n } Each homogeneous matrix C i has structure ( C rot C i = i C tr ) i where Ci rot is a 3 3 orthogonal matrix and C tr i is a translation vector. This enables us to re-write the linear system to (C rot a Ca rot r c + C tr r c + C tr b a = Cb rot Cb rot c = C tr b Ctr a C j2 As mentioned in the introduction, the interpolation of multiple rotations has already received some attention [Buss and Fillmore 200; Park et al. 2002] as well as interpolation of multiple general transformations [Alexa 2002]. Unfortunately, all these methods are substantially slower then the simple linear interpolation used in LBS. Since our goal is an algorithm with comparable time complexity as LBS, we propose an approximate but fast linear quaternion blending. For the case of two rotations, we compare our method with the established SLERP. Recall that a rotation around axis a (unit length vector) with angle 2α corresponds to quaternion q = cosα + asinα. However, this correspondence is not unique, because both quaternions q and q represent the same rotation. The SLERP of two unit quaternions p,q assumes that their dot product (p,q) 0. If the dot product (p,q) < 0, we use p instead of p, which is possible because both p and p represent the same rotation. The SLERP of p,q with interpolation parameter t 0, is given by the following formula, see for example [Eberly 200]. sin(( t)θ)p + sin(tθ)q s(t;p,q)= (3) sinθ where θ is the angle inclined by quaternions p,q, i.e. cosθ =(p,q). The linear interpolation of quaternions (QLERP) is computed as l(t;p,q)= ( t)p +tq ( t)p +tq The difference to SLERP is obvious: QLERP interpolates along the shortest segment, and then projects to arc, which does not result in the uniform interpolation of the arc. In spite of this, we claim that QLERP is sufficient for our task. In order to justify this statement, we face an interesting question by itself: how big can be the difference between QLERP and SLERP for the same input rotations? (4)
5 For t = 0, both QLERP and SLERP return of course p. Fort > 0, we can imagine that both QLERP and SLERP work by concatenating p with some rotation (multiplying p with some quaternion). For SLERP, we denote this quaternion as r s (t). It can be expressed as p s(t;p,q), because pr s (t)=pp s(t;p,q)=s(t;p,q) SLERP The rotation r s (t) can be written out as r s (t)=p s(t;p,q)= sin(( t)θ) + sin(tθ)p q (5) sinθ The quaternion represents the identity (zero angle rotation). From the definition of quaternion multiplication it can be seen that the real part of p q equals (p,q) =cosθ. Since p q is a unit quaternion, we can express it as p q = cosθ + usinθ for some axis of rotation u. If we substitute this into equation (5), we obtain sin(( t)θ)+sin(tθ)cosθ r s (t)= + usin(tθ) sinθ which means that the direction of the axis u is independent on t. Let us examine the rotation r l (t) following p in QLERP: r l (t) = p l(t;p,q)= ( t) +tp q ( t)p +tq = = ( t +t cosθ) ( t)p +tq + u t sinθ ( t)p +tq which shows that the axis of rotation has the same direction. We can conclude with an important property: the SLERP can be written as pr s (t) and QLERP as pr l (t), where the rotations r s (t) and r l (t) have the same axis. Moreover, this axis is constant, i.e. independent on the interpolation parameter t. It follows that the only difference between QLERP and SLERP is in the angle of rotations r s (t) and r l (t). Note that both r s (t) and r l (t) have a form of linear combination of quaternions and p q. It means that the results of both r s (t) and r l (t) always end up in certain 2D subspace of R 4. We can restrict our attention to this subspace (the linear hull of and p q). Since SLERP assumes cosθ =(p,q) 0, the angle θ cannot exceed π/2. To obtain an upper bound of the maximal difference in the angle, we consider the extremal case with θ = π/2, depicted in Figure 4. The angle α(t) on the picture can be computed by atan, andβ(t) by simple linear interpolation of the right angle, which yields the difference function ( ) t d(t)=α(t) β(t)=atan π t 2 t It remains to find the extremes of d(t) on the interval 0,. The elementary mathematical analysis discovers the global extremes in points /2 ± (/π /4). The absolute value of d(t) in these points is approximately 0.07 radians (4.07 degrees). As mentioned in the introduction of this section the angle of rotation is twice the angle inclined by quaternions. To conclude: both SLERP and QLERP interpolate by multiplying the first quaternion with a rotation with the same, fixed axis. The difference between SLERP and QLERP is only in the angle of this t (t) (t) -t QLERP Figure 4: The difference between QLERP angle α(t) and SLERP β(t) rotation, and is strictly less then 0.43 radians (8.5 degrees) for any interpolation parameter t 0,. This is an upper bound; practical results are much smaller and could hardly cause an observable defect in the deformed skin. The big advantage of QLERP is that it can be easily generalized to interpolate multiple rotations it suffices to make a convex combination and re-normalization of multiple quaternions. 4.2 Algorithm Overview Now we have prepared all the ingredients to describe how the SBS algorithm works. The task is to transform a vertex v influenced by joints j,..., j n with convex weights W =(w,...,w n ) to its position v in the animated skin. In order to obtain an appealing deformation, it is necessary to respect the computed center of rotation r c. To achieve this, we extend the QLERP scheme to homogeneous matrices C ji. We denote the interpolation of matrices C ji with weights W as ( ) Q m q(w;c j,...,c jn )= 0 T (6) and compute Q and m as follows. First, the rotation submatrices C rot are converted to quaternions q ji. One of them, for example q j, is chosen as pivot. If (q j,q ji ) < 0foranyi = 2,...,n, we replace q ji with q ji (by analogy to SLERP). Then the QLERP computes s = w q j w n q jn, which is subsequently normalized to s n = s/ s. Finally, s n is converted to the rotation matrix Q. The translation part is just linearly interpolated, m = n i= w ic tr. In order to change the center of rotation from the origin to r c,we define a homogeneous matrix ( ) I rc T = 0 T (7) where I is a 3 3 identity matrix. Then the interpolation of homogeneous matrices with respect to the center of rotation r c can be written as Tq(W;T C j T,...,T C jn T )T (8) Note that the shift of the center of rotation does not influence the interpolated rotation it manifests only in the translation part. The desired transformation of vertex v is v = Tq(W;T C j T,...,T C jn T )T v
6 = n Q(v r c )+ w i C ji r c (9) i= A detailed derivation of this formula can be found in appendix A. The latter addend represents the translation induced by the new center of rotation. The equation (9) has to be evaluated once per each vertex, and therefore should be as efficient as possible. The basic optimization is to pre-compute the quaternions q ji, because they do not depend on the actual vertex only on the joint s transformation, similarly as the rotation centers r c. Nonetheless, QLERP has to be executed for each vertex, since weights w,...,w n can vary. In order to challenge the speed of LBS, we apply a following trick. The vertex v can be represented by a quaternion with zero real part. In this representation, its rotation by quaternion q can be expressed as q vq, which is a quaternion with zero real part as well [Eberly 200]. Although this expression is not efficient for computation (because of slow quaternion multiplication), it enables us to write out the rotation of v by quaternion s n as s n vs n = s 2 svs = (s,s) svs This suggests to convert already the quaternion s to matrix Q and normalize subsequently by dividing (s, s). Therefore, we can compute the Q matrix from (9) as Q = Q and save the sqrt operation. (s,s) Some attention must be paid because standard routines for quaternion to matrix conversion assume a unit-length quaternion. The conversion of an arbitrary length q = w + xi + yj+ zk leads to the following matrix: x2 + w 2 y 2 z 2 2xy 2wz 2xz + 2wy 2xy + 2wz y 2 + w 2 x 2 z 2 2yz 2wx 2xz 2wy 2yz + 2wx z 2 + w 2 x 2 y 2 Vertex normal v n is transformed in a similar way as vertex position, but ignoring the translation v n = Qv n Using the formula (9) we can verify our previous intuitive thinking. First, if we substitute r c in place of v, no rotation occurs, which means that r c is indeed a center of rotation. Second, if n = 2and C j r c = C j2 r c (as in the beginning of section 4), the translation part becomes w C j r c + w 2 C j2 r c =(w + w 2 )C j r c = C j r c which is independent of interpolation parameters (weights), i.e. the translation during interpolation is constant indeed. Third, the equation (9) is nothing but a generalization of LBS to an arbitrary method of rotation interpolation. The choice of QLERP is not important for (9), the matrix Q can be replaced by matrix resulting from any other interpolation scheme, such as [Buss and Fillmore 200]. If we substitute Q = w i C rot, i.e. a simple linear combination of rotation matrices, we obtain v = Q(v r c )+ w i C ji r c = w i C rot v w i C rot r c + w i C rot r c + w i C tr = w i C rot v + w i C tr = w i C ji v which is exactly the LBS equation (). This also shows that LBS is a special case, which is independent of the center of rotation. The whole algorithm can be summarized in the following steps: Figure 5: 3D models used for testing Hand Woman Creature vertices triangles joints Table : Complexities of example models compute matrices C i for all joints and convert their rotation parts to quaternions q i for each vertex v influenced by joints j,..., j n compute (or re-use a cached) center of rotation r c according to section 4 blend quaternions q j,...q jn using QLERP and convert the result to matrix Q compute the position of vertex v in the deformed skin using the equation (9) 5 Results and Comparison We tested the SBS algorithm on three models, see Figure 5 and Table. We compare the shape of the deformed skin on the model of woman, because human eye is most sensitive to the deformations of human body. Figure 6 presents results of LBS and SBS executed on the same posture of the model. Another example has been presented already in Figure 2. For small deformations, both algorithms produce similar results, as in the second row of Figure 6 (although a small loss of volume is noticeable even there). It is remarkable that the results of SBS are better even though the models have been optimised to work with the LBS algorithm. The performance of both algorithms is compared in Table 2. The measured value is an average time in milliseconds necessary to deform one model on a 2.5GHz Athlon PC (rendering time not included). In the last row of the table the number of different nontrivial joint sets is reported (trivial joint set consists of only one joint
7 LBS time SBS time SVD executions Hand Woman Creature Table 2: First two rows: run-time of LBS and SBS algorithms in milliseconds; last row: number of SVD executions only approximates SLERP results). On the one hand, the difference in the deformed skin was barely observable, according to the results from section 4.. On the other hand, the increase in the execution time was quite substantial. For the woman model, the time increased from original 4.54ms to 22.74ms. This only confirmed our choice of QLERP. 5. Conclusion and Future Work The proposed skin deformation system is by no means perfect; it cannot compete with complex, layered models. However, the SBS algorithm offers reasonable price for elimination of the notorious LBS artifacts. The time and memory complexity of both algorithms is comparable. The overhead of replacing an existing LBS implementation by SBS is minimal, because the input data, as well as the internal data structures, are the same. In contrast to other methods, the SBS does not need any additional information, such as the example skins. The presented algorithm opens many questions and suggests several directions of future work. First of all, we worked only with vertex weights optimised for LBS. These weights are designed to suppress the LBS artifacts, even though they cannot remove them. It would be interesting to find out how much can be the SBS results improved by a set of weights especially designed for SBS. In order to accomplish this, a tool to explore the space of SBS deformations would help considerably. This tool has been presented for LBS in [Mohr et al. 2003], but the situation of SBS is somewhat more complex, because our interpolation method is non-linear. Similarly, it would be possible to estimate the SBS vertex weights from examples, as was done for LBS in [Mohr and Gleicher 2003]. This could also cover additional effects like muscle bulging. 6 Figure 6: Comparison of deformations by LBS (left) and SBS (right) or two neighboring joints). Put in another way, it is exactly the number of singular-value decompositions performed by the SBS algorithm. This number participates considerably on the difference between times for LBS and SBS. Theoretically, the number of different non-trivial joint sets could be very high. Fortunately, this number is surprisingly small in practice, because the joint influences tend to be local (e.g. it is unlikely to find vertices influenced by both left and right wrist). The additional memory needed for SBS is dominated by caching the computed centers of rotation. However, this amount of memory is negligible, considering the number of different non-trivial joint sets. In order to test the accuracy of QLERP, we experimented with spherical weighted averages presented in [Buss and Fillmore 200]. The algorithm proposed in [Buss and Fillmore 200] behaves like SLERP for the case of two rotations (in contrast to QLERP, which Acknowledgments This work has been partly supported by the Ministry of Education, Youth and Sports of the Czech Republic under research program No.Y04/98: (Research in the area of information technologies and communications). We thank to Samuel Buss for providing the algorithm for spherical weighted averages [Buss and Fillmore 200] and to LAPACK developers for their software. We would also like to thank to Jaroslav Semanc ı k and the anonymous reviewers for valuable comments and to Adam J. Sporka for help with the accompanying video. A Interpolation of Rotations with an Arbitrary Center In this appendix we derive the formula (9), which describes the interpolation of rotations with respect to rc a custom center of rotation. Let us denote by K the coordinate system with origin in rc and identical basis vectors as the world coordinate system. Then
8 the matrix T (7) can be interpreted as a transformation from K to the world coordinate system. By analogy, the inverse matrix ( ) T I rc = represents the transformation from the world coordinate system to K. It follows that T C ji T is the transformation C ji expressed with respect to K. By interpolating these matrices with QLERP q(w;t C j T,...,T C jn T ) we obtain a matrix working also on vectors in K coordinates. We can express this matrix with respect to the world coordinate system easily Tq(W;T C j T,...,T C jn T )T which is exactly the formula (8). Recall that the matrix C ji has structure ( C rot C ji = C tr which enables us to write out ( C T rot ) C ji T = C ji r c r c as can be simply verified. Please note that the change of the coordinate system did not influence the rotation part C rot at all. Therefore the result of QLERP will be, according to equation (6) ( q(w;t C j T,...,T Q rc + n C jn T )= i= w ) ic ji r c where Q stands for the interpolation of pure rotations, computed as indicated in section 4.2. Using T v = v r c and T x = x + r c,we see that v = Tq(W;T C j T,...,T C jn T )T v ( Q rc + n = T i= w )( ic ji r c v rc n = Q(v r c )+ w i C ji r c i= is true for any vector v. This is exactly the equation (9). References ALEXA, M Linear combination of transformations. In SIGGRAPH 02: Proceedings of the 29th annual conference on Computer graphics and interactive techniques, ACM Press, ANDERSON, E.,BAI, Z.,BISCHOF, C.,BLACKFORD, S.,DEM- MEL, J., DONGARRA, J., DU CROZ, J., GREENBAUM, A., HAMMARLING, S., MCKENNEY, A., AND SORENSEN, D LAPACK Users Guide, third ed. Society for Industrial and Applied Mathematics, Philadelphia, PA. BLOOMENTHAL, J Medial-based vertex deformation. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation, ACM Press, ) ) BUSS, S. R., AND FILLMORE, J. P Spherical averages and applications to spherical splines and interpolation. ACM Trans. Graph. 20, 2, EBERLY, D D game engine design: a practical approach to real-time computer graphics. Morgan Kaufmann Publishers Inc. KAVAN, L., AND ŽÁRA, J Real-time skin deformation with bones blending. In WSCG Short Papers Proceedings. KRY, P. G., JAMES, D. L., AND PAI, D. K Eigenskin: real time large deformation character skinning in hardware. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation, ACM Press, LANDER, J Skin them bones: Game programming for the web generation. Game Developer Magazine (May), 6. LANDER, J Over my dead, polygonal body. Game Developer Magazine (October), LEWIS, J. P., CORDNER, M., AND FONG, N Pose space deformation: a unified approach to shape interpolation and skeleton-driven deformation. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques, ACM Press/Addison-Wesley Publishing Co., MAGNENAT-THALMANN, N., LAPERRIÈRE, R., AND THAL- MANN, D Joint-dependent local deformations for hand animation and object grasping. In Proceedings on Graphics interface 88, Canadian Information Processing Society, MAGNENAT-THALMANN, N.,CORDIER, F.,SEO, H.,AND PA- PAGIANAKIS, G Modeling of bodies and clothes for virtual environments. In CW 04: Proceedings of the 2004 International Conference on Cyberworlds (CW 04), IEEE Computer Society, MOHR, A., AND GLEICHER, M Building efficient, accurate character skins from examples. ACM Trans. Graph. 22, 3, MOHR, A., TOKHEIM, L., AND GLEICHER, M Direct manipulation of interactive character skins. In Proceedings of the 2003 symposium on Interactive 3D graphics, ACM Press, PARK, S. I., SHIN, H. J., AND SHIN, S. Y On-line locomotion generation based on motion blending. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation, ACM Press, 05. SHOEMAKE, K Animating rotation with quaternion curves. In Proceedings of the 2th annual conference on Computer graphics and interactive techniques, ACM Press, SLOAN, P.-P. J., ROSE, III, C. F., AND COHEN, M. F Shape by example. In Proceedings of the 200 symposium on Interactive 3D graphics, ACM Press, STEED, P Animating Real-Time Game Characters with CDROM. Charles River Media, Inc. WANG, X. C., AND PHILLIPS, C Multi-weight enveloping: least-squares approximation techniques for skin animation. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation, ACM Press, WEBER, J Run-time skin deformation. In Proceedings of Game Developers Conference.
Real Time Skin Deformation with Bones Blending
 Real Time Skin Deformation with Bones Blending Ladislav Kavan Charles University Faculty of Mathematics and Physics Malostranske nam. 25 118 00 Prague 1, Czech Republic lkav8604@ss1000.ms.mff.cuni.cz Jiří
Real Time Skin Deformation with Bones Blending Ladislav Kavan Charles University Faculty of Mathematics and Physics Malostranske nam. 25 118 00 Prague 1, Czech Republic lkav8604@ss1000.ms.mff.cuni.cz Jiří
Rigging / Skinning. based on Taku Komura, Jehee Lee and Charles B.Own's slides
 Rigging / Skinning based on Taku Komura, Jehee Lee and Charles B.Own's slides Skeletal Animation Victoria 2 CSE 872 Dr. Charles B. Owen Advanced Computer Graphics Skinning http://www.youtube.com/watch?
Rigging / Skinning based on Taku Komura, Jehee Lee and Charles B.Own's slides Skeletal Animation Victoria 2 CSE 872 Dr. Charles B. Owen Advanced Computer Graphics Skinning http://www.youtube.com/watch?
05 Mesh Animation. Steve Marschner CS5625 Spring 2016
 05 Mesh Animation Steve Marschner CS5625 Spring 2016 Basic surface deformation methods Blend shapes: make a mesh by combining several meshes Mesh skinning: deform a mesh based on an underlying skeleton
05 Mesh Animation Steve Marschner CS5625 Spring 2016 Basic surface deformation methods Blend shapes: make a mesh by combining several meshes Mesh skinning: deform a mesh based on an underlying skeleton
Applications of Dual Quaternions in Three Dimensional Transformation and Interpolation
 Applications of Dual Quaternions in Three Dimensional Transformation and Interpolation November 11, 2013 Matthew Smith mrs126@uclive.ac.nz Department of Computer Science and Software Engineering University
Applications of Dual Quaternions in Three Dimensional Transformation and Interpolation November 11, 2013 Matthew Smith mrs126@uclive.ac.nz Department of Computer Science and Software Engineering University
CMSC 425: Lecture 10 Skeletal Animation and Skinning
 CMSC 425: Lecture 10 Skeletal Animation and Skinning Reading: Chapt 11 of Gregory, Game Engine Architecture. Recap: Last time we introduced the principal elements of skeletal models and discussed forward
CMSC 425: Lecture 10 Skeletal Animation and Skinning Reading: Chapt 11 of Gregory, Game Engine Architecture. Recap: Last time we introduced the principal elements of skeletal models and discussed forward
Spherical Blend Skinning on GPU
 Spherical Blend Skinning on GPU Kasper Amstrup Andersen Dept. of Computer Science, University of Copenhagen Figure 1: Two animated characters using spherical blend skinning on GPU. Abstract Skeletal animation
Spherical Blend Skinning on GPU Kasper Amstrup Andersen Dept. of Computer Science, University of Copenhagen Figure 1: Two animated characters using spherical blend skinning on GPU. Abstract Skeletal animation
Graphics and Interaction Transformation geometry and homogeneous coordinates
 433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
433-324 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates
 COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
Animation of 3D surfaces.
 Animation of 3D surfaces Motivations When character animation is controlled by skeleton set of hierarchical joints joints oriented by rotations the character shape still needs to be visible: visible =
Animation of 3D surfaces Motivations When character animation is controlled by skeleton set of hierarchical joints joints oriented by rotations the character shape still needs to be visible: visible =
CS 775: Advanced Computer Graphics. Lecture 4: Skinning
 CS 775: Advanced Computer Graphics Lecture 4: http://www.okino.com/conv/skinning.htm Binding Binding Always done in a standard rest or bind pose. Binding Always done in a standard rest or bind pose. Associate
CS 775: Advanced Computer Graphics Lecture 4: http://www.okino.com/conv/skinning.htm Binding Binding Always done in a standard rest or bind pose. Binding Always done in a standard rest or bind pose. Associate
Deformation Sensitive Decimation
 Deformation Sensitive Decimation Alex Mohr Michael Gleicher University of Wisconsin, Madison Abstract In computer graphics, many automatic methods for simplifying polygonal meshes have been developed.
Deformation Sensitive Decimation Alex Mohr Michael Gleicher University of Wisconsin, Madison Abstract In computer graphics, many automatic methods for simplifying polygonal meshes have been developed.
Pose Space Deformation A unified Approach to Shape Interpolation and Skeleton-Driven Deformation
 Pose Space Deformation A unified Approach to Shape Interpolation and Skeleton-Driven Deformation J.P. Lewis Matt Cordner Nickson Fong Presented by 1 Talk Outline Character Animation Overview Problem Statement
Pose Space Deformation A unified Approach to Shape Interpolation and Skeleton-Driven Deformation J.P. Lewis Matt Cordner Nickson Fong Presented by 1 Talk Outline Character Animation Overview Problem Statement
animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time
 animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time computer graphics animation 2009 fabio pellacini 2 animation representation many ways to
animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time computer graphics animation 2009 fabio pellacini 2 animation representation many ways to
animation computer graphics animation 2009 fabio pellacini 1
 animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time computer graphics animation 2009 fabio pellacini 2 animation representation many ways to
animation computer graphics animation 2009 fabio pellacini 1 animation shape specification as a function of time computer graphics animation 2009 fabio pellacini 2 animation representation many ways to
Computer Animation Fundamentals. Animation Methods Keyframing Interpolation Kinematics Inverse Kinematics
 Computer Animation Fundamentals Animation Methods Keyframing Interpolation Kinematics Inverse Kinematics Lecture 21 6.837 Fall 2001 Conventional Animation Draw each frame of the animation great control
Computer Animation Fundamentals Animation Methods Keyframing Interpolation Kinematics Inverse Kinematics Lecture 21 6.837 Fall 2001 Conventional Animation Draw each frame of the animation great control
Animation. CS 4620 Lecture 33. Cornell CS4620 Fall Kavita Bala
 Animation CS 4620 Lecture 33 Cornell CS4620 Fall 2015 1 Announcements Grading A5 (and A6) on Monday after TG 4621: one-on-one sessions with TA this Friday w/ prior instructor Steve Marschner 2 Quaternions
Animation CS 4620 Lecture 33 Cornell CS4620 Fall 2015 1 Announcements Grading A5 (and A6) on Monday after TG 4621: one-on-one sessions with TA this Friday w/ prior instructor Steve Marschner 2 Quaternions
Matrices. Chapter Matrix A Mathematical Definition Matrix Dimensions and Notation
 Chapter 7 Introduction to Matrices This chapter introduces the theory and application of matrices. It is divided into two main sections. Section 7.1 discusses some of the basic properties and operations
Chapter 7 Introduction to Matrices This chapter introduces the theory and application of matrices. It is divided into two main sections. Section 7.1 discusses some of the basic properties and operations
CS 523: Computer Graphics, Spring Shape Modeling. Skeletal deformation. Andrew Nealen, Rutgers, /12/2011 1
 CS 523: Computer Graphics, Spring 2011 Shape Modeling Skeletal deformation 4/12/2011 1 Believable character animation Computers games and movies Skeleton: intuitive, low-dimensional subspace Clip courtesy
CS 523: Computer Graphics, Spring 2011 Shape Modeling Skeletal deformation 4/12/2011 1 Believable character animation Computers games and movies Skeleton: intuitive, low-dimensional subspace Clip courtesy
CS 445 / 645 Introduction to Computer Graphics. Lecture 21 Representing Rotations
 CS 445 / 645 Introduction to Computer Graphics Lecture 21 Representing Rotations Parameterizing Rotations Straightforward in 2D A scalar, θ, represents rotation in plane More complicated in 3D Three scalars
CS 445 / 645 Introduction to Computer Graphics Lecture 21 Representing Rotations Parameterizing Rotations Straightforward in 2D A scalar, θ, represents rotation in plane More complicated in 3D Three scalars
Introduction to Computer Graphics. Animation (1) May 19, 2016 Kenshi Takayama
 Introduction to Computer Graphics Animation (1) May 19, 2016 Kenshi Takayama Skeleton-based animation Simple Intuitive Low comp. cost https://www.youtube.com/watch?v=dsonab58qva 2 Representing a pose using
Introduction to Computer Graphics Animation (1) May 19, 2016 Kenshi Takayama Skeleton-based animation Simple Intuitive Low comp. cost https://www.youtube.com/watch?v=dsonab58qva 2 Representing a pose using
Visual Recognition: Image Formation
 Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Skeletal deformation
 CS 523: Computer Graphics, Spring 2009 Shape Modeling Skeletal deformation 4/22/2009 1 Believable character animation Computers games and movies Skeleton: intuitive, low dimensional subspace Clip courtesy
CS 523: Computer Graphics, Spring 2009 Shape Modeling Skeletal deformation 4/22/2009 1 Believable character animation Computers games and movies Skeleton: intuitive, low dimensional subspace Clip courtesy
Animation. CS 4620 Lecture 32. Cornell CS4620 Fall Kavita Bala
 Animation CS 4620 Lecture 32 Cornell CS4620 Fall 2015 1 What is animation? Modeling = specifying shape using all the tools we ve seen: hierarchies, meshes, curved surfaces Animation = specifying shape
Animation CS 4620 Lecture 32 Cornell CS4620 Fall 2015 1 What is animation? Modeling = specifying shape using all the tools we ve seen: hierarchies, meshes, curved surfaces Animation = specifying shape
Animation of 3D surfaces
 Animation of 3D surfaces 2013-14 Motivations When character animation is controlled by skeleton set of hierarchical joints joints oriented by rotations the character shape still needs to be visible: visible
Animation of 3D surfaces 2013-14 Motivations When character animation is controlled by skeleton set of hierarchical joints joints oriented by rotations the character shape still needs to be visible: visible
Analysis of Euler Angles in a Simple Two-Axis Gimbals Set
 Vol:5, No:9, 2 Analysis of Euler Angles in a Simple Two-Axis Gimbals Set Ma Myint Myint Aye International Science Index, Mechanical and Mechatronics Engineering Vol:5, No:9, 2 waset.org/publication/358
Vol:5, No:9, 2 Analysis of Euler Angles in a Simple Two-Axis Gimbals Set Ma Myint Myint Aye International Science Index, Mechanical and Mechatronics Engineering Vol:5, No:9, 2 waset.org/publication/358
Basics of Computational Geometry
 Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a
 The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
The goal is the definition of points with numbers and primitives with equations or functions. The definition of points with numbers requires a coordinate system and then the measuring of the point with
Human Character Animation in 3D-Graphics: The EMOTE System as a Plug-in for Maya
 Hartmann - 1 Bjoern Hartman Advisor: Dr. Norm Badler Applied Senior Design Project - Final Report Human Character Animation in 3D-Graphics: The EMOTE System as a Plug-in for Maya Introduction Realistic
Hartmann - 1 Bjoern Hartman Advisor: Dr. Norm Badler Applied Senior Design Project - Final Report Human Character Animation in 3D-Graphics: The EMOTE System as a Plug-in for Maya Introduction Realistic
COMPUTER ANIMATION 3 KEYFRAME ANIMATION, RIGGING, SKINNING AND CHARACTER ANIMATION. Rémi Ronfard, Animation, M2R MOSIG
 COMPUTER ANIMATION 3 KEYFRAME ANIMATION, RIGGING, SKINNING AND CHARACTER ANIMATION Rémi Ronfard, Animation, M2R MOSIG 2 Outline Principles of animation Keyframe interpolation Rigging, skinning and walking
COMPUTER ANIMATION 3 KEYFRAME ANIMATION, RIGGING, SKINNING AND CHARACTER ANIMATION Rémi Ronfard, Animation, M2R MOSIG 2 Outline Principles of animation Keyframe interpolation Rigging, skinning and walking
Planar Robot Kinematics
 V. Kumar lanar Robot Kinematics The mathematical modeling of spatial linkages is quite involved. t is useful to start with planar robots because the kinematics of planar mechanisms is generally much simpler
V. Kumar lanar Robot Kinematics The mathematical modeling of spatial linkages is quite involved. t is useful to start with planar robots because the kinematics of planar mechanisms is generally much simpler
Example-Based Skeleton Extraction. Scott Schaefer Can Yuksel
 Example-Based Skeleton Extraction Scott Schaefer Can Yuksel Example-Based Deformation Examples Previous Work Mesh-based Inverse Kinematics [Sumner et al. 2005], [Der et al. 2006] Example-based deformation
Example-Based Skeleton Extraction Scott Schaefer Can Yuksel Example-Based Deformation Examples Previous Work Mesh-based Inverse Kinematics [Sumner et al. 2005], [Der et al. 2006] Example-based deformation
For each question, indicate whether the statement is true or false by circling T or F, respectively.
 True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
Question 2: Linear algebra and transformations matrices rotation vectors linear transformation T=U*D*VT
 You must answer all questions. For full credit, an answer must be both correct and well-presented (clear and concise). If you feel a question is ambiguous, state any assumptions that you need to make.
You must answer all questions. For full credit, an answer must be both correct and well-presented (clear and concise). If you feel a question is ambiguous, state any assumptions that you need to make.
3D Modelling: Animation Fundamentals & Unit Quaternions
 3D Modelling: Animation Fundamentals & Unit Quaternions CITS3003 Graphics & Animation Thanks to both Richard McKenna and Marco Gillies for permission to use their slides as a base. Static objects are boring
3D Modelling: Animation Fundamentals & Unit Quaternions CITS3003 Graphics & Animation Thanks to both Richard McKenna and Marco Gillies for permission to use their slides as a base. Static objects are boring
Robots are built to accomplish complex and difficult tasks that require highly non-linear motions.
 Path and Trajectory specification Robots are built to accomplish complex and difficult tasks that require highly non-linear motions. Specifying the desired motion to achieve a specified goal is often a
Path and Trajectory specification Robots are built to accomplish complex and difficult tasks that require highly non-linear motions. Specifying the desired motion to achieve a specified goal is often a
Fundamentals of Computer Animation
 Fundamentals of Computer Animation Quaternions as Orientations () page 1 Multiplying Quaternions q1 = (w1, x1, y1, z1); q = (w, x, y, z); q1 * q = ( w1.w - v1.v, w1.v + w.v1 + v1 X v) where v1 = (x1, y1,
Fundamentals of Computer Animation Quaternions as Orientations () page 1 Multiplying Quaternions q1 = (w1, x1, y1, z1); q = (w, x, y, z); q1 * q = ( w1.w - v1.v, w1.v + w.v1 + v1 X v) where v1 = (x1, y1,
Introduction to Homogeneous coordinates
 Last class we considered smooth translations and rotations of the camera coordinate system and the resulting motions of points in the image projection plane. These two transformations were expressed mathematically
Last class we considered smooth translations and rotations of the camera coordinate system and the resulting motions of points in the image projection plane. These two transformations were expressed mathematically
Geometric Skinning with Approximate Dual Quaternion Blending
 Geometric Skinning with Approximate Dual Quaternion Blending 15 LADISLAV KAVAN and STEVEN COLLINS Trinity College Dublin JIŘÍ ŽÁRA Czech Technical University in Prague and CAROL O SULLIVAN Trinity College
Geometric Skinning with Approximate Dual Quaternion Blending 15 LADISLAV KAVAN and STEVEN COLLINS Trinity College Dublin JIŘÍ ŽÁRA Czech Technical University in Prague and CAROL O SULLIVAN Trinity College
Computer Animation. Algorithms and Techniques. z< MORGAN KAUFMANN PUBLISHERS. Rick Parent Ohio State University AN IMPRINT OF ELSEVIER SCIENCE
 Computer Animation Algorithms and Techniques Rick Parent Ohio State University z< MORGAN KAUFMANN PUBLISHERS AN IMPRINT OF ELSEVIER SCIENCE AMSTERDAM BOSTON LONDON NEW YORK OXFORD PARIS SAN DIEGO SAN FRANCISCO
Computer Animation Algorithms and Techniques Rick Parent Ohio State University z< MORGAN KAUFMANN PUBLISHERS AN IMPRINT OF ELSEVIER SCIENCE AMSTERDAM BOSTON LONDON NEW YORK OXFORD PARIS SAN DIEGO SAN FRANCISCO
EXTREME POINTS AND AFFINE EQUIVALENCE
 EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
EXTREME POINTS AND AFFINE EQUIVALENCE The purpose of this note is to use the notions of extreme points and affine transformations which are studied in the file affine-convex.pdf to prove that certain standard
Preliminaries: Size Measures and Shape Coordinates
 2 Preliminaries: Size Measures and Shape Coordinates 2.1 Configuration Space Definition 2.1 The configuration is the set of landmarks on a particular object. The configuration matrix X is the k m matrix
2 Preliminaries: Size Measures and Shape Coordinates 2.1 Configuration Space Definition 2.1 The configuration is the set of landmarks on a particular object. The configuration matrix X is the k m matrix
CS184: Using Quaternions to Represent Rotation
 Page 1 of 5 CS 184 home page A note on these notes: These notes on quaternions were created as a resource for students taking CS184 at UC Berkeley. I am not doing any research related to quaternions and
Page 1 of 5 CS 184 home page A note on these notes: These notes on quaternions were created as a resource for students taking CS184 at UC Berkeley. I am not doing any research related to quaternions and
Reusable Skinning Templates Using Cage-based Deformations
 Reusable Skinning Templates Using Cage-based Deformations Tao Ju 1 Qian-Yi Zhou 2 Michiel van de Panne 3 Daniel Cohen-Or 4 Ulrich Neumann 2 1 Washington Univ. in St. Louis 2 Univ. of Southern California
Reusable Skinning Templates Using Cage-based Deformations Tao Ju 1 Qian-Yi Zhou 2 Michiel van de Panne 3 Daniel Cohen-Or 4 Ulrich Neumann 2 1 Washington Univ. in St. Louis 2 Univ. of Southern California
Triangulation: A new algorithm for Inverse Kinematics
 Triangulation: A new algorithm for Inverse Kinematics R. Müller-Cajar 1, R. Mukundan 1, 1 University of Canterbury, Dept. Computer Science & Software Engineering. Email: rdc32@student.canterbury.ac.nz
Triangulation: A new algorithm for Inverse Kinematics R. Müller-Cajar 1, R. Mukundan 1, 1 University of Canterbury, Dept. Computer Science & Software Engineering. Email: rdc32@student.canterbury.ac.nz
This week. CENG 732 Computer Animation. Warping an Object. Warping an Object. 2D Grid Deformation. Warping an Object.
 CENG 732 Computer Animation Spring 2006-2007 Week 4 Shape Deformation Animating Articulated Structures: Forward Kinematics/Inverse Kinematics This week Shape Deformation FFD: Free Form Deformation Hierarchical
CENG 732 Computer Animation Spring 2006-2007 Week 4 Shape Deformation Animating Articulated Structures: Forward Kinematics/Inverse Kinematics This week Shape Deformation FFD: Free Form Deformation Hierarchical
Quaternion Rotations AUI Course Denbigh Starkey
 Major points of these notes: Quaternion Rotations AUI Course Denbigh Starkey. What I will and won t be doing. Definition of a quaternion and notation 3 3. Using quaternions to rotate any point around an
Major points of these notes: Quaternion Rotations AUI Course Denbigh Starkey. What I will and won t be doing. Definition of a quaternion and notation 3 3. Using quaternions to rotate any point around an
S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T
 S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T Copyright 2018 Sung-eui Yoon, KAIST freely available on the internet http://sglab.kaist.ac.kr/~sungeui/render
S U N G - E U I YO O N, K A I S T R E N D E R I N G F R E E LY A VA I L A B L E O N T H E I N T E R N E T Copyright 2018 Sung-eui Yoon, KAIST freely available on the internet http://sglab.kaist.ac.kr/~sungeui/render
CSC 2521 Final Project Report. Hanieh Bastani
 CSC 2521 Final Project Report Hanieh Bastani December, 2007 NPR Renderer: Overview I implemented a 3D NPR renderer which supports contours, suggestive contours, and toon shading. For this implementation,
CSC 2521 Final Project Report Hanieh Bastani December, 2007 NPR Renderer: Overview I implemented a 3D NPR renderer which supports contours, suggestive contours, and toon shading. For this implementation,
A Powell Optimization Approach for Example-Based Skinning in a Production Animation Environment
 A Powell Optimization Approach for Example-Based Skinning in a Production Animation Environment Xiao Xian Nanyang Technological University Seah Hock Soon Nanyang Technological University Tian Feng Nanyang
A Powell Optimization Approach for Example-Based Skinning in a Production Animation Environment Xiao Xian Nanyang Technological University Seah Hock Soon Nanyang Technological University Tian Feng Nanyang
a a= a a =a a 1 =1 Division turned out to be equivalent to multiplication: a b= a b =a 1 b
 MATH 245 Extra Effort ( points) My assistant read through my first draft, got half a page in, and skipped to the end. So I will save you the flipping. Here is the assignment. Do just one of them. All the
MATH 245 Extra Effort ( points) My assistant read through my first draft, got half a page in, and skipped to the end. So I will save you the flipping. Here is the assignment. Do just one of them. All the
DIMENSIONAL SYNTHESIS OF SPATIAL RR ROBOTS
 DIMENSIONAL SYNTHESIS OF SPATIAL RR ROBOTS ALBA PEREZ Robotics and Automation Laboratory University of California, Irvine Irvine, CA 9697 email: maperez@uci.edu AND J. MICHAEL MCCARTHY Department of Mechanical
DIMENSIONAL SYNTHESIS OF SPATIAL RR ROBOTS ALBA PEREZ Robotics and Automation Laboratory University of California, Irvine Irvine, CA 9697 email: maperez@uci.edu AND J. MICHAEL MCCARTHY Department of Mechanical
Animations. Hakan Bilen University of Edinburgh. Computer Graphics Fall Some slides are courtesy of Steve Marschner and Kavita Bala
 Animations Hakan Bilen University of Edinburgh Computer Graphics Fall 2017 Some slides are courtesy of Steve Marschner and Kavita Bala Animation Artistic process What are animators trying to do? What tools
Animations Hakan Bilen University of Edinburgh Computer Graphics Fall 2017 Some slides are courtesy of Steve Marschner and Kavita Bala Animation Artistic process What are animators trying to do? What tools
Coordinate Free Perspective Projection of Points in the Conformal Model Using Transversions
 Coordinate Free Perspective Projection of Points in the Conformal Model Using Transversions Stephen Mann Abstract Goldman presented a method for computing a versor form of the perspective projection of
Coordinate Free Perspective Projection of Points in the Conformal Model Using Transversions Stephen Mann Abstract Goldman presented a method for computing a versor form of the perspective projection of
Chapter 5.2 Character Animation
 Chapter 5.2 Character Animation Overview Fundamental Concepts Animation Storage Playing Animations Blending Animations Motion Extraction Mesh Deformation Inverse Kinematics Attachments & Collision Detection
Chapter 5.2 Character Animation Overview Fundamental Concepts Animation Storage Playing Animations Blending Animations Motion Extraction Mesh Deformation Inverse Kinematics Attachments & Collision Detection
A skeleton/cage hybrid paradigm for digital animation
 A skeleton/cage hybrid paradigm for digital animation Fabrizio Corda 1 1 Università degli studi di Cagliari Abstract. Digital animators require simple tools and techniques that allow them to create computer
A skeleton/cage hybrid paradigm for digital animation Fabrizio Corda 1 1 Università degli studi di Cagliari Abstract. Digital animators require simple tools and techniques that allow them to create computer
Rotation with Quaternions
 Rotation with Quaternions Contents 1 Introduction 1.1 Translation................... 1. Rotation..................... 3 Quaternions 5 3 Rotations Represented as Quaternions 6 3.1 Dynamics....................
Rotation with Quaternions Contents 1 Introduction 1.1 Translation................... 1. Rotation..................... 3 Quaternions 5 3 Rotations Represented as Quaternions 6 3.1 Dynamics....................
Video based Animation Synthesis with the Essential Graph. Adnane Boukhayma, Edmond Boyer MORPHEO INRIA Grenoble Rhône-Alpes
 Video based Animation Synthesis with the Essential Graph Adnane Boukhayma, Edmond Boyer MORPHEO INRIA Grenoble Rhône-Alpes Goal Given a set of 4D models, how to generate realistic motion from user specified
Video based Animation Synthesis with the Essential Graph Adnane Boukhayma, Edmond Boyer MORPHEO INRIA Grenoble Rhône-Alpes Goal Given a set of 4D models, how to generate realistic motion from user specified
Measuring Lengths The First Fundamental Form
 Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
3D Kinematics. Consists of two parts
 D Kinematics Consists of two parts D rotation D translation The same as D D rotation is more complicated than D rotation (restricted to z-ais) Net, we will discuss the treatment for spatial (D) rotation
D Kinematics Consists of two parts D rotation D translation The same as D D rotation is more complicated than D rotation (restricted to z-ais) Net, we will discuss the treatment for spatial (D) rotation
Articulated Characters
 Articulated Characters Skeleton A skeleton is a framework of rigid body bones connected by articulated joints Used as an (invisible?) armature to position and orient geometry (usually surface triangles)
Articulated Characters Skeleton A skeleton is a framework of rigid body bones connected by articulated joints Used as an (invisible?) armature to position and orient geometry (usually surface triangles)
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer
 Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Homogeneous Coordinates and Transformations of the Plane
 2 Homogeneous Coordinates and Transformations of the Plane 2. Introduction In Chapter planar objects were manipulated by applying one or more transformations. Section.7 identified the problem that the
2 Homogeneous Coordinates and Transformations of the Plane 2. Introduction In Chapter planar objects were manipulated by applying one or more transformations. Section.7 identified the problem that the
Chapter 2 Basic Structure of High-Dimensional Spaces
 Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Chapter 9 Animation System
 Chapter 9 Animation System 9.1 Types of Character Animation Cel Animation Cel animation is a specific type of traditional animation. A cel is a transparent sheet of plastic on which images can be painted
Chapter 9 Animation System 9.1 Types of Character Animation Cel Animation Cel animation is a specific type of traditional animation. A cel is a transparent sheet of plastic on which images can be painted
Inverse Kinematics Analysis for Manipulator Robot With Wrist Offset Based On the Closed-Form Algorithm
 Inverse Kinematics Analysis for Manipulator Robot With Wrist Offset Based On the Closed-Form Algorithm Mohammed Z. Al-Faiz,MIEEE Computer Engineering Dept. Nahrain University Baghdad, Iraq Mohammed S.Saleh
Inverse Kinematics Analysis for Manipulator Robot With Wrist Offset Based On the Closed-Form Algorithm Mohammed Z. Al-Faiz,MIEEE Computer Engineering Dept. Nahrain University Baghdad, Iraq Mohammed S.Saleh
Rotational Joint Limits in Quaternion Space. Gino van den Bergen Dtecta
 Rotational Joint Limits in Quaternion Space Gino van den Bergen Dtecta Rotational Joint Limits: 1 DoF Image: Autodesk, Creative Commons Rotational Joint Limits: 3 DoFs Image: Autodesk, Creative Commons
Rotational Joint Limits in Quaternion Space Gino van den Bergen Dtecta Rotational Joint Limits: 1 DoF Image: Autodesk, Creative Commons Rotational Joint Limits: 3 DoFs Image: Autodesk, Creative Commons
Animation. Keyframe animation. CS4620/5620: Lecture 30. Rigid motion: the simplest deformation. Controlling shape for animation
 Keyframe animation CS4620/5620: Lecture 30 Animation Keyframing is the technique used for pose-to-pose animation User creates key poses just enough to indicate what the motion is supposed to be Interpolate
Keyframe animation CS4620/5620: Lecture 30 Animation Keyframing is the technique used for pose-to-pose animation User creates key poses just enough to indicate what the motion is supposed to be Interpolate
CHAPTER 6 Parametric Spline Curves
 CHAPTER 6 Parametric Spline Curves When we introduced splines in Chapter 1 we focused on spline curves, or more precisely, vector valued spline functions. In Chapters 2 and 4 we then established the basic
CHAPTER 6 Parametric Spline Curves When we introduced splines in Chapter 1 we focused on spline curves, or more precisely, vector valued spline functions. In Chapters 2 and 4 we then established the basic
3D Computer Graphics. Jared Kirschner. November 8, 2010
 3D Computer Graphics Jared Kirschner November 8, 2010 1 Abstract We are surrounded by graphical displays video games, cell phones, television sets, computer-aided design software, interactive touch screens,
3D Computer Graphics Jared Kirschner November 8, 2010 1 Abstract We are surrounded by graphical displays video games, cell phones, television sets, computer-aided design software, interactive touch screens,
Shape Blending Using the Star-Skeleton Representation
 Shape Blending Using the Star-Skeleton Representation Michal Shapira Ari Rappoport Institute of Computer Science, The Hebrew University of Jerusalem Jerusalem 91904, Israel. arir@cs.huji.ac.il Abstract:
Shape Blending Using the Star-Skeleton Representation Michal Shapira Ari Rappoport Institute of Computer Science, The Hebrew University of Jerusalem Jerusalem 91904, Israel. arir@cs.huji.ac.il Abstract:
Animation space: a truly linear framework for character animation
 Animation space: a truly linear framework for character animation BRUCE MERRY, PARICK MARAIS and JAMES GAIN University of Cape own Skeletal subspace deformation (SSD), a simple method of character animation
Animation space: a truly linear framework for character animation BRUCE MERRY, PARICK MARAIS and JAMES GAIN University of Cape own Skeletal subspace deformation (SSD), a simple method of character animation
Inverse Kinematics. Given a desired position (p) & orientation (R) of the end-effector
 Inverse Kinematics Given a desired position (p) & orientation (R) of the end-effector q ( q, q, q ) 1 2 n Find the joint variables which can bring the robot the desired configuration z y x 1 The Inverse
Inverse Kinematics Given a desired position (p) & orientation (R) of the end-effector q ( q, q, q ) 1 2 n Find the joint variables which can bring the robot the desired configuration z y x 1 The Inverse
A Multiresolutional Approach for Facial Motion Retargetting Using Subdivision Wavelets
 A Multiresolutional Approach for Facial Motion Retargetting Using Subdivision Wavelets Kyungha Min and Moon-Ryul Jung Dept. of Media Technology, Graduate School of Media Communications, Sogang Univ., Seoul,
A Multiresolutional Approach for Facial Motion Retargetting Using Subdivision Wavelets Kyungha Min and Moon-Ryul Jung Dept. of Media Technology, Graduate School of Media Communications, Sogang Univ., Seoul,
Transformations: 2D Transforms
 1. Translation Transformations: 2D Transforms Relocation of point WRT frame Given P = (x, y), translation T (dx, dy) Then P (x, y ) = T (dx, dy) P, where x = x + dx, y = y + dy Using matrix representation
1. Translation Transformations: 2D Transforms Relocation of point WRT frame Given P = (x, y), translation T (dx, dy) Then P (x, y ) = T (dx, dy) P, where x = x + dx, y = y + dy Using matrix representation
Visualization and Analysis of Inverse Kinematics Algorithms Using Performance Metric Maps
 Visualization and Analysis of Inverse Kinematics Algorithms Using Performance Metric Maps Oliver Cardwell, Ramakrishnan Mukundan Department of Computer Science and Software Engineering University of Canterbury
Visualization and Analysis of Inverse Kinematics Algorithms Using Performance Metric Maps Oliver Cardwell, Ramakrishnan Mukundan Department of Computer Science and Software Engineering University of Canterbury
Animation. Traditional Animation Keyframe Animation. Interpolating Rotation Forward/Inverse Kinematics
 Animation Traditional Animation Keyframe Animation Interpolating Rotation Forward/Inverse Kinematics Overview Animation techniques Performance-based (motion capture) Traditional animation (frame-by-frame)
Animation Traditional Animation Keyframe Animation Interpolating Rotation Forward/Inverse Kinematics Overview Animation techniques Performance-based (motion capture) Traditional animation (frame-by-frame)
Animation. CS 465 Lecture 22
 Animation CS 465 Lecture 22 Animation Industry production process leading up to animation What animation is How animation works (very generally) Artistic process of animation Further topics in how it works
Animation CS 465 Lecture 22 Animation Industry production process leading up to animation What animation is How animation works (very generally) Artistic process of animation Further topics in how it works
Visualizing Quaternions
 Visualizing Quaternions Andrew J. Hanson Computer Science Department Indiana University Siggraph 1 Tutorial 1 GRAND PLAN I: Fundamentals of Quaternions II: Visualizing Quaternion Geometry III: Quaternion
Visualizing Quaternions Andrew J. Hanson Computer Science Department Indiana University Siggraph 1 Tutorial 1 GRAND PLAN I: Fundamentals of Quaternions II: Visualizing Quaternion Geometry III: Quaternion
Rotations in 3D Graphics and the Gimbal Lock
 Rotations in 3D Graphics and the Gimbal Lock Valentin Koch Autodesk Inc. January 27, 2016 Valentin Koch (ADSK) IEEE Okanagan January 27, 2016 1 / 37 Presentation Road Map 1 Introduction 2 Rotation Matrices
Rotations in 3D Graphics and the Gimbal Lock Valentin Koch Autodesk Inc. January 27, 2016 Valentin Koch (ADSK) IEEE Okanagan January 27, 2016 1 / 37 Presentation Road Map 1 Introduction 2 Rotation Matrices
Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation
 Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation and the type of an object. Even simple scaling turns a
Geometric transformations assign a point to a point, so it is a point valued function of points. Geometric transformation may destroy the equation and the type of an object. Even simple scaling turns a
IMAGE-BASED RENDERING AND ANIMATION
 DH2323 DGI17 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION IMAGE-BASED RENDERING AND ANIMATION Christopher Peters CST, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
DH2323 DGI17 INTRODUCTION TO COMPUTER GRAPHICS AND INTERACTION IMAGE-BASED RENDERING AND ANIMATION Christopher Peters CST, KTH Royal Institute of Technology, Sweden chpeters@kth.se http://kth.academia.edu/christopheredwardpeters
Animating orientation. CS 448D: Character Animation Prof. Vladlen Koltun Stanford University
 Animating orientation CS 448D: Character Animation Prof. Vladlen Koltun Stanford University Orientation in the plane θ (cos θ, sin θ) ) R θ ( x y = sin θ ( cos θ sin θ )( x y ) cos θ Refresher: Homogenous
Animating orientation CS 448D: Character Animation Prof. Vladlen Koltun Stanford University Orientation in the plane θ (cos θ, sin θ) ) R θ ( x y = sin θ ( cos θ sin θ )( x y ) cos θ Refresher: Homogenous
COMP 558 lecture 19 Nov. 17, 2010
 COMP 558 lecture 9 Nov. 7, 2 Camera calibration To estimate the geometry of 3D scenes, it helps to know the camera parameters, both external and internal. The problem of finding all these parameters is
COMP 558 lecture 9 Nov. 7, 2 Camera calibration To estimate the geometry of 3D scenes, it helps to know the camera parameters, both external and internal. The problem of finding all these parameters is
Lesson 28: When Can We Reverse a Transformation?
 Lesson 8 M Lesson 8: Student Outcomes Students determine inverse matrices using linear systems. Lesson Notes In the final three lessons of this module, students discover how to reverse a transformation
Lesson 8 M Lesson 8: Student Outcomes Students determine inverse matrices using linear systems. Lesson Notes In the final three lessons of this module, students discover how to reverse a transformation
Animation Curves and Splines 2
 Animation Curves and Splines 2 Animation Homework Set up Thursday a simple avatar E.g. cube/sphere (or square/circle if 2D) Specify some key frames (positions/orientations) Associate Animation a time with
Animation Curves and Splines 2 Animation Homework Set up Thursday a simple avatar E.g. cube/sphere (or square/circle if 2D) Specify some key frames (positions/orientations) Associate Animation a time with
Example Examination 2IV
 Example Examination IV60-04071 (translated version IV10 4 july 01, 14:00-17:00) This examination consist of four questions with in total 16 subquestion. Each subquestion weighs equally. In all cases: EXPLAIN
Example Examination IV60-04071 (translated version IV10 4 july 01, 14:00-17:00) This examination consist of four questions with in total 16 subquestion. Each subquestion weighs equally. In all cases: EXPLAIN
Quaternions and Rotations
 CSCI 520 Computer Animation and Simulation Quaternions and Rotations Jernej Barbic University of Southern California 1 Rotations Very important in computer animation and robotics Joint angles, rigid body
CSCI 520 Computer Animation and Simulation Quaternions and Rotations Jernej Barbic University of Southern California 1 Rotations Very important in computer animation and robotics Joint angles, rigid body
Stretchable and Twistable Bones for Skeletal Shape Deformation
 Stretchable and Twistable Bones for Skeletal Shape Deformation Alec Jacobson Olga Sorkine New York University & ETH Zurich Original LBS DQS STBS Figure 1: Left to right: the Beast model is rigged to a
Stretchable and Twistable Bones for Skeletal Shape Deformation Alec Jacobson Olga Sorkine New York University & ETH Zurich Original LBS DQS STBS Figure 1: Left to right: the Beast model is rigged to a
Equations and Functions, Variables and Expressions
 Equations and Functions, Variables and Expressions Equations and functions are ubiquitous components of mathematical language. Success in mathematics beyond basic arithmetic depends on having a solid working
Equations and Functions, Variables and Expressions Equations and functions are ubiquitous components of mathematical language. Success in mathematics beyond basic arithmetic depends on having a solid working
Visualizing Quaternions
 Visualizing Quaternions Andrew J. Hanson Computer Science Department Indiana University Siggraph 25 Tutorial OUTLINE I: (45min) Twisting Belts, Rolling Balls, and Locking Gimbals: Explaining Rotation Sequences
Visualizing Quaternions Andrew J. Hanson Computer Science Department Indiana University Siggraph 25 Tutorial OUTLINE I: (45min) Twisting Belts, Rolling Balls, and Locking Gimbals: Explaining Rotation Sequences
5. GENERALIZED INVERSE SOLUTIONS
 5. GENERALIZED INVERSE SOLUTIONS The Geometry of Generalized Inverse Solutions The generalized inverse solution to the control allocation problem involves constructing a matrix which satisfies the equation
5. GENERALIZED INVERSE SOLUTIONS The Geometry of Generalized Inverse Solutions The generalized inverse solution to the control allocation problem involves constructing a matrix which satisfies the equation
An Introduction to animation and motion blending
 An Introduction to animation and motion blending Stuart Bryson - 98082365 Information Technology Research Preparation University Technology, Sydney 14/06/2005 An introduction to animation and motion blending
An Introduction to animation and motion blending Stuart Bryson - 98082365 Information Technology Research Preparation University Technology, Sydney 14/06/2005 An introduction to animation and motion blending
10 - ARAP and Linear Blend Skinning
 10 - ARAP and Linear Blend Skinning Acknowledgements: Olga Sorkine-Hornung As Rigid As Possible Demo Libigl demo 405 As-Rigid-As-Possible Deformation Preserve shape of cells covering the surface Ask each
10 - ARAP and Linear Blend Skinning Acknowledgements: Olga Sorkine-Hornung As Rigid As Possible Demo Libigl demo 405 As-Rigid-As-Possible Deformation Preserve shape of cells covering the surface Ask each
UNIT 2 2D TRANSFORMATIONS
 UNIT 2 2D TRANSFORMATIONS Introduction With the procedures for displaying output primitives and their attributes, we can create variety of pictures and graphs. In many applications, there is also a need
UNIT 2 2D TRANSFORMATIONS Introduction With the procedures for displaying output primitives and their attributes, we can create variety of pictures and graphs. In many applications, there is also a need
2D/3D Geometric Transformations and Scene Graphs
 2D/3D Geometric Transformations and Scene Graphs Week 4 Acknowledgement: The course slides are adapted from the slides prepared by Steve Marschner of Cornell University 1 A little quick math background
2D/3D Geometric Transformations and Scene Graphs Week 4 Acknowledgement: The course slides are adapted from the slides prepared by Steve Marschner of Cornell University 1 A little quick math background
Transformations Week 9, Lecture 18
 CS 536 Computer Graphics Transformations Week 9, Lecture 18 2D Transformations David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 3 2D Affine Transformations
CS 536 Computer Graphics Transformations Week 9, Lecture 18 2D Transformations David Breen, William Regli and Maxim Peysakhov Department of Computer Science Drexel University 1 3 2D Affine Transformations
Point Multiplication and Soft Caching: An Approach for Accelerating Calculations in Graphics
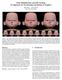 Point Multiplication and Soft Caching: An Approach for Accelerating Calculations in Graphics Mark Meyer John Anderson Pixar Animation Studios Figure 1: An example of the point multiplication technique
Point Multiplication and Soft Caching: An Approach for Accelerating Calculations in Graphics Mark Meyer John Anderson Pixar Animation Studios Figure 1: An example of the point multiplication technique
Parallel and perspective projections such as used in representing 3d images.
 Chapter 5 Rotations and projections In this chapter we discuss Rotations Parallel and perspective projections such as used in representing 3d images. Using coordinates and matrices, parallel projections
Chapter 5 Rotations and projections In this chapter we discuss Rotations Parallel and perspective projections such as used in representing 3d images. Using coordinates and matrices, parallel projections
Synthesizing Realistic Facial Expressions from Photographs
 Synthesizing Realistic Facial Expressions from Photographs 1998 F. Pighin, J Hecker, D. Lischinskiy, R. Szeliskiz and D. H. Salesin University of Washington, The Hebrew University Microsoft Research 1
Synthesizing Realistic Facial Expressions from Photographs 1998 F. Pighin, J Hecker, D. Lischinskiy, R. Szeliskiz and D. H. Salesin University of Washington, The Hebrew University Microsoft Research 1
CS 4620 Program #2: Character Animation
 Cornell University CS 4620 Program #2: Character Animation Forward and Inverse Kinematics out: Tuesday 28 September 2010 due: Tuesday 19 October 2010 Author: Prof. Doug James In this second programming
Cornell University CS 4620 Program #2: Character Animation Forward and Inverse Kinematics out: Tuesday 28 September 2010 due: Tuesday 19 October 2010 Author: Prof. Doug James In this second programming
