Algorithm Theory. 8 Treaps. Christian Schindelhauer
|
|
|
- Bryce Alexander
- 5 years ago
- Views:
Transcription
1 Algorithm Theory 8 Treaps Institut für Informatik Wintersemester 2007/08
2 The Dictionary Problem Given: Universe (U,<) of keys with a total order Goal: Maintain a set S U under the following operations Search(x,S): Is x S? Insert(x,S): Insert x into S if not already in S. Delete(x,S): Delete x from S 2
3 Extended Set of Operations Minimum(S): Return smallest key Maximum(S): Return largest key List(S): Output elements of S in increasing order by key Union(S 1,S 2 ): Merge S 1 and S 2. Condition: x 1 S 1, x 2 S 2 : x 1 < x 2 Split(S,x,S 1,S 2 ): Split S into S 1 and S 2 x 1 S 1, x 2 S 2 : x 1 x and x 2 > x 3
4 Known Solutions Binary search trees d b g a c h Disadvantage: Sequence of insertions may lead to a linear list a, b, c, d, e, f Height balanced trees: AVL-trees, (a,b)-trees Disadvantage: complex algorithms or high memory 4
5 Approach for Randomized Search Trees If n elements are inserted in random order into a binary search tree, the expected depth is 1.39 log n. Idea: Each element x is assigned a priority chosen uniformly at random prio(x) R The goal is to establish the following property (*) The search tree has the structure that would result if elements were inserted in the order of their priorities 5
6 Treaps (Tree + Heap) Definition: A Treap is a binary tree. Each node contains one element x with key(x) U and prio(x) R. The following properties hold. Search tree property For each element x: - elements y in the left subtree x satisfy: key(y) < key(x) - elements y in the right subtree x satisfy: key(y) > key(x) Heap property For all elements x,y: if y is a child of x then prio(y) > prio(x). All priorities are pairwise distinct. 6
7 Example Key Priority a b c d e f g d 1 a 3 f 2 c 4 e 5 g 6 b 7 7
8 Uniqueness of Treaps Lemma: For elements x 1,..., x n with key(x i ) and prio(x i ), there exists a unique treap. It satisfies property (*). Proof: n=1: ok n>1: at the root there is only one choice: key with minimal prio(xr) the left tree and the right tree is determined by induction assumption 8
9 Search for an Element d 1 a 3 f 2 c 4 e 5 g 6 b 7 9
10 Search for Element with Key k 1 v := root; 2 while v nil do 3 case key(v) = k : stop; element found (successful search) 4 key(v) < k : v:= RightChild(v); 5 key(v) > k : v:= LeftChild(v); 6 endcase; 7 endwhile; 8 element not found (failed search) Runtime: O(# elements on the search path) 10
11 Analysis of the Search Path Elements x 1,, x n x i has i-th smallest key Let M be a subset of the elements. P min (M) = element in M with lowest priority Lemma: a) Sei i<m. x i is ancestor of x m iff P min ({x i,,x m }) = x i b) Sei m<i. x i is ancestor of x m iff P min ({x m,,x i }) = x i 11
12 Analysis of the Search Path Proof: a) Use (*). Elements are inserted in order of increasing priorities. P min ({x i,,x m }) = x i x i is inserted first among {x i,,x m }. When x i is inserted, the tree contains only keys k with k < key(x i ) or k > key(x m ) When elements xj {xi,...,xm} is inserted it traverses the same path as xi. xi is an ancester of xj xi is ancestor of xm k key(x i ) > k k key(x i ) < k 12
13 Analysis of the Search Path Beweis: a) (Let i<m. x i is ancestor of x m iff P min ({x i,,x m }) = x i ) Let x j = P min ({x i,,x m }). To prove x i = x j Assume: x i x j Use (*) and consider the search path when xj is inserted. As before we can show that any xk {xi,...,xm} traverses the same search path as xj xj is ancestor of xk Case 1: x j = x m xm is ancestor of xi Contradiction! Case 2: x j x m key(xi) < key(xj) xi in left subtree key(xi) > key(xj) xk in right subtree Part b) follows analogously. 13
14 Analysis of the Search Operation Let T be a treap with elements x 1,, x n x i has i-th smallest key n-th Harmonic number Lemma: 1. Successful Search: The expected number of nodes x m on the path is H m + H n-m Failed Search: Let m be the number of keys being smaller than the search key k. The expected number of nodes on the search path is H m + H n-m. 14
15 Analysis of the Search Operation Beweis: Part 1 else is ancestor of X m = # nodes on the path from the root to x m (incl. x m ) 15
16 Analysis of the Search Operation i < m : is ancestor of All elements of {x i,, x m } have the same probability of being the one with the smallest priority Prob[P min ({x i,,x m }) = x i ] = 1/(m-i+1) i > m : 16
17 Analysis of the Search Operation Teil 2 analog 17
18 1. Choose prio(x). Inserting a New Element x 2. Search for the position of x in the tree. 3. Insert x as a leaf 4. Restore the heap property. while prio(parent(x)) > prio(x) do if x is left child then RotateRight(parent(x)) endif endwhile; else RotateLeft(parent(x)); 18
19 Rotations y RotateRight x x RotateLeft y C A A B B C The rotations maintain the search tree property and restore the heap property. 19
20 Deleting an Element x 1. Find x in the tree. 2. while x is not a leaf do u := child with smaller priority; if u is left child then RotateRight(x)) else RotateLeft(x); endif; endwhile; 3. Delete x; 20
21 Rotations x Rotate Right u u Rotate Left x C A A B B C 21
22 Analysis of Insert and Delete Operations Lemma: The expected running time of insert and delete operations is O(log n). The expected number of rotations is 2. Proof: Analysis of insert (delete is the inverse operation) #rotations = depth of x after being inserted as a leaf (1) - depth of x after rotations (2) Let x = x m (2) Expected depth is H m + H n-m+1 1 (1) Expected detph is H m-1 + H n-m + 1 The tree contains n-1 elements, m-1 of them are smaller. #rotations = H m-1 + H n-m + 1 (H m + H n-m+1 1) < 2 22
23 Extended Set of Operations n = number elements in treap T Minimum(S): Return smallest key O(log n) Maximum(S): Return largest key O(log n) List(S): Output elements of S in increasing order by key O(n) Union(S 1,S 2 ): Merge S 1 and S 2. Condition: x 1 S 1, x 2 S 2 : x 1 < x 2 Split(S,x,S 1,S 2 ): Split S into S 1 and S 2 x 1 S 1, x 2 S 2 : x 1 x and x 2 > x 23
24 The Split Operation Split(T,k,T 1,T 2 ): Split T into T 1 and T 2. x 1 T 1, x 2 T 2 : key(x 1 ) k und key(x 2 ) > k W.l.o.g key k is not in T. Otherwise delete the element with key k and re-insert it into T 1 after the split operation. 1. Generate a new element x with key(x)=k and prio(x) = Insert x into T. 3. Delet the new root. The left subtree is T 1, the right subtree is T 2. 24
25 The Union Operation Union(T 1,T 2 ): Merge T 1 and T 2. Condition: x 1 T 1, x 2 T 2 : key(x 1 ) < key(x 2 ) 1. Determine key k with key(x 1 ) < k < key(x 2 ) for all x 1 T 1 and x 2 T Generate element x with key(x)=k and prio(x) = Generate treap T with root x, left subtree T 1 and right subtree T Delete x from T. 25
26 Analysis Lemma: The expected running time of Union and Split is O(log n). 26
27 Implementation Priorities from [0,1) Priorities are used only when two elements are compared to find out which of them has the higher priority In case of equality, extend both priorities by bits chosen uniformly at random until two bits differ. p 1 = 0, p 1 = 0, p 2 = 0, p 2 = 0,
28 Algorithm Theory 8 Treaps Institut für Informatik Wintersemester 2007/08
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Binary Tree. Preview. Binary Tree. Binary Tree. Binary Search Tree 10/2/2017. Binary Tree
 0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
CS102 Binary Search Trees
 CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
Data Structures in Java
 Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
CSE100. Advanced Data Structures. Lecture 8. (Based on Paul Kube course materials)
 CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
Binary Trees. Recursive definition. Is this a binary tree?
 Binary Search Trees Binary Trees Recursive definition 1. An empty tree is a binary tree 2. A node with two child subtrees is a binary tree 3. Only what you get from 1 by a finite number of applications
Binary Search Trees Binary Trees Recursive definition 1. An empty tree is a binary tree 2. A node with two child subtrees is a binary tree 3. Only what you get from 1 by a finite number of applications
CS Fall 2010 B-trees Carola Wenk
 CS 3343 -- Fall 2010 B-trees Carola Wenk 10/19/10 CS 3343 Analysis of Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CS 3343 -- Fall 2010 B-trees Carola Wenk 10/19/10 CS 3343 Analysis of Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
Randomized incremental construction. Trapezoidal decomposition: Special sampling idea: Sample all except one item
 Randomized incremental construction Special sampling idea: Sample all except one item hope final addition makes small or no change Method: process items in order average case analysis randomize order to
Randomized incremental construction Special sampling idea: Sample all except one item hope final addition makes small or no change Method: process items in order average case analysis randomize order to
Orthogonal range searching. Range Trees. Orthogonal range searching. 1D range searching. CS Spring 2009
 CS 5633 -- Spring 2009 Orthogonal range searching Range Trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 5633 Analysis of Algorithms 1 Input: n points in d dimensions
CS 5633 -- Spring 2009 Orthogonal range searching Range Trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 5633 Analysis of Algorithms 1 Input: n points in d dimensions
Data structures. Organize your data to support various queries using little time and/or space
 Data structures Organize your data to support various queries using little time and/or space Given n elements A[1..n] Support SEARCH(A,x) := is x in A? Trivial solution: scan A. Takes time Θ(n) Best possible
Data structures Organize your data to support various queries using little time and/or space Given n elements A[1..n] Support SEARCH(A,x) := is x in A? Trivial solution: scan A. Takes time Θ(n) Best possible
Design and Analysis of Algorithms Lecture- 9: Binary Search Trees
 Design and Analysis of Algorithms Lecture- 9: Binary Search Trees Dr. Chung- Wen Albert Tsao 1 Binary Search Trees Data structures that can support dynamic set operations. Search, Minimum, Maximum, Predecessor,
Design and Analysis of Algorithms Lecture- 9: Binary Search Trees Dr. Chung- Wen Albert Tsao 1 Binary Search Trees Data structures that can support dynamic set operations. Search, Minimum, Maximum, Predecessor,
An AVL tree with N nodes is an excellent data. The Big-Oh analysis shows that most operations finish within O(log N) time
 B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
CSE2331/5331. Topic 6: Binary Search Tree. Data structure Operations CSE 2331/5331
 CSE2331/5331 Topic 6: Binary Search Tree Data structure Operations Set Operations Maximum Extract-Max Insert Increase-key We can use priority queue (implemented by heap) Search Delete Successor Predecessor
CSE2331/5331 Topic 6: Binary Search Tree Data structure Operations Set Operations Maximum Extract-Max Insert Increase-key We can use priority queue (implemented by heap) Search Delete Successor Predecessor
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
Range Searching and Windowing
 CS 6463 -- Fall 2010 Range Searching and Windowing Carola Wenk 1 Orthogonal range searching Input: n points in d dimensions E.g., representing a database of n records each with d numeric fields Query:
CS 6463 -- Fall 2010 Range Searching and Windowing Carola Wenk 1 Orthogonal range searching Input: n points in d dimensions E.g., representing a database of n records each with d numeric fields Query:
Algorithms, Probability & Computing. Emo Welzl Ueli Maurer Angelika Steger Peter Widmayer Thomas Holenstein
 Algorithms, Probability & Computing Emo Welzl Ueli Maurer Angelika Steger Peter Widmayer Thomas Holenstein Contents Random(ized) Search Trees Point Location Network Flows Minimum Cut Randomized Algebraic
Algorithms, Probability & Computing Emo Welzl Ueli Maurer Angelika Steger Peter Widmayer Thomas Holenstein Contents Random(ized) Search Trees Point Location Network Flows Minimum Cut Randomized Algebraic
Heaps Goodrich, Tamassia. Heaps 1
 Heaps Heaps 1 Recall Priority Queue ADT A priority queue stores a collection of entries Each entry is a pair (key, value) Main methods of the Priority Queue ADT insert(k, x) inserts an entry with key k
Heaps Heaps 1 Recall Priority Queue ADT A priority queue stores a collection of entries Each entry is a pair (key, value) Main methods of the Priority Queue ADT insert(k, x) inserts an entry with key k
AVL Trees. Version of September 6, AVL Trees Version of September 6, / 22
 VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
Algorithms. Red-Black Trees
 Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Dictionaries. Priority Queues
 Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
Lecture 5 Using Data Structures to Improve Dijkstra s Algorithm. (AM&O Sections and Appendix A)
 Lecture Using Data Structures to Improve Dijkstra s Algorithm (AM&O Sections 4.6 4.8 and Appendix A) Manipulating the Data in Dijkstra s Algorithm The bottleneck operation in Dijkstra s Algorithm is that
Lecture Using Data Structures to Improve Dijkstra s Algorithm (AM&O Sections 4.6 4.8 and Appendix A) Manipulating the Data in Dijkstra s Algorithm The bottleneck operation in Dijkstra s Algorithm is that
Balanced Binary Search Trees. Victor Gao
 Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Algorithms and Theory of Computation. Lecture 5: Minimum Spanning Tree
 Algorithms and Theory of Computation Lecture 5: Minimum Spanning Tree Xiaohui Bei MAS 714 August 31, 2017 Nanyang Technological University MAS 714 August 31, 2017 1 / 30 Minimum Spanning Trees (MST) A
Algorithms and Theory of Computation Lecture 5: Minimum Spanning Tree Xiaohui Bei MAS 714 August 31, 2017 Nanyang Technological University MAS 714 August 31, 2017 1 / 30 Minimum Spanning Trees (MST) A
Heaps. 2/13/2006 Heaps 1
 Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Algorithms and Theory of Computation. Lecture 5: Minimum Spanning Tree
 Algorithms and Theory of Computation Lecture 5: Minimum Spanning Tree Xiaohui Bei MAS 714 August 31, 2017 Nanyang Technological University MAS 714 August 31, 2017 1 / 30 Minimum Spanning Trees (MST) A
Algorithms and Theory of Computation Lecture 5: Minimum Spanning Tree Xiaohui Bei MAS 714 August 31, 2017 Nanyang Technological University MAS 714 August 31, 2017 1 / 30 Minimum Spanning Trees (MST) A
Heaps 2. Recall Priority Queue ADT. Heaps 3/19/14
 Heaps 3// Presentation for use with the textbook Data Structures and Algorithms in Java, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 Heaps Heaps Recall Priority Queue ADT
Heaps 3// Presentation for use with the textbook Data Structures and Algorithms in Java, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 Heaps Heaps Recall Priority Queue ADT
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
Algorithms for Memory Hierarchies Lecture 2
 Algorithms for emory Hierarchies Lecture Lecturer: odari Sitchianva Scribes: Robin Rehrmann, ichael Kirsten Last Time External memory (E) model Scan(): O( ) I/Os Stacks / queues: O( 1 ) I/Os / elt ergesort:
Algorithms for emory Hierarchies Lecture Lecturer: odari Sitchianva Scribes: Robin Rehrmann, ichael Kirsten Last Time External memory (E) model Scan(): O( ) I/Os Stacks / queues: O( 1 ) I/Os / elt ergesort:
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
Binary search trees. Support many dynamic-set operations, e.g. Search. Minimum. Maximum. Insert. Delete ...
 Binary search trees Support many dynamic-set operations, e.g. Search Minimum Maximum Insert Delete... Can be used as dictionary, priority queue... you name it Running time depends on height of tree: 1
Binary search trees Support many dynamic-set operations, e.g. Search Minimum Maximum Insert Delete... Can be used as dictionary, priority queue... you name it Running time depends on height of tree: 1
Bioinformatics Programming. EE, NCKU Tien-Hao Chang (Darby Chang)
 Bioinformatics Programming EE, NCKU Tien-Hao Chang (Darby Chang) 1 Tree 2 A Tree Structure A tree structure means that the data are organized so that items of information are related by branches 3 Definition
Bioinformatics Programming EE, NCKU Tien-Hao Chang (Darby Chang) 1 Tree 2 A Tree Structure A tree structure means that the data are organized so that items of information are related by branches 3 Definition
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Trees. A tree is a directed graph with the property
 2: Trees Trees A tree is a directed graph with the property There is one node (the root) from which all other nodes can be reached by exactly one path. Seen lots of examples. Parse Trees Decision Trees
2: Trees Trees A tree is a directed graph with the property There is one node (the root) from which all other nodes can be reached by exactly one path. Seen lots of examples. Parse Trees Decision Trees
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Section 1: True / False (1 point each, 15 pts total)
 Section : True / False ( point each, pts total) Circle the word TRUE or the word FALSE. If neither is circled, both are circled, or it impossible to tell which is circled, your answer will be considered
Section : True / False ( point each, pts total) Circle the word TRUE or the word FALSE. If neither is circled, both are circled, or it impossible to tell which is circled, your answer will be considered
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
CS 380 ALGORITHM DESIGN AND ANALYSIS
 CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
CMPS 2200 Fall 2017 B-trees Carola Wenk
 CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
AVL Trees Heaps And Complexity
 AVL Trees Heaps And Complexity D. Thiebaut CSC212 Fall 14 Some material taken from http://cseweb.ucsd.edu/~kube/cls/0/lectures/lec4.avl/lec4.pdf Complexity Of BST Operations or "Why Should We Use BST Data
AVL Trees Heaps And Complexity D. Thiebaut CSC212 Fall 14 Some material taken from http://cseweb.ucsd.edu/~kube/cls/0/lectures/lec4.avl/lec4.pdf Complexity Of BST Operations or "Why Should We Use BST Data
Algorithms and Theory of Computation. Lecture 7: Priority Queue
 Algorithms and Theory of Computation Lecture 7: Priority Queue Xiaohui Bei MAS 714 September 5, 2017 Nanyang Technological University MAS 714 September 5, 2017 1 / 15 Priority Queues Priority Queues Store
Algorithms and Theory of Computation Lecture 7: Priority Queue Xiaohui Bei MAS 714 September 5, 2017 Nanyang Technological University MAS 714 September 5, 2017 1 / 15 Priority Queues Priority Queues Store
Trees and Graphs Shabsi Walfish NYU - Fundamental Algorithms Summer 2006
 Trees and Graphs Basic Definitions Tree: Any connected, acyclic graph G = (V,E) E = V -1 n-ary Tree: Tree s/t all vertices of degree n+1 A root has degree n Binary Search Tree: A binary tree such that
Trees and Graphs Basic Definitions Tree: Any connected, acyclic graph G = (V,E) E = V -1 n-ary Tree: Tree s/t all vertices of degree n+1 A root has degree n Binary Search Tree: A binary tree such that
Search Trees (Ch. 9) > = Binary Search Trees 1
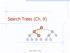 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
EE 368. Weeks 5 (Notes)
 EE 368 Weeks 5 (Notes) 1 Chapter 5: Trees Skip pages 273-281, Section 5.6 - If A is the root of a tree and B is the root of a subtree of that tree, then A is B s parent (or father or mother) and B is A
EE 368 Weeks 5 (Notes) 1 Chapter 5: Trees Skip pages 273-281, Section 5.6 - If A is the root of a tree and B is the root of a subtree of that tree, then A is B s parent (or father or mother) and B is A
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics
 CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
CS2223: Algorithms Sorting Algorithms, Heap Sort, Linear-time sort, Median and Order Statistics 1 Sorting 1.1 Problem Statement You are given a sequence of n numbers < a 1, a 2,..., a n >. You need to
Binary Search Trees, etc.
 Chapter 12 Binary Search Trees, etc. Binary Search trees are data structures that support a variety of dynamic set operations, e.g., Search, Minimum, Maximum, Predecessors, Successors, Insert, and Delete.
Chapter 12 Binary Search Trees, etc. Binary Search trees are data structures that support a variety of dynamic set operations, e.g., Search, Minimum, Maximum, Predecessors, Successors, Insert, and Delete.
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Heaps Outline and Required Reading: Heaps ( 7.3) COSC 2011, Fall 2003, Section A Instructor: N. Vlajic
 1 Heaps Outline and Required Reading: Heaps (.3) COSC 2011, Fall 2003, Section A Instructor: N. Vlajic Heap ADT 2 Heap binary tree (T) that stores a collection of keys at its internal nodes and satisfies
1 Heaps Outline and Required Reading: Heaps (.3) COSC 2011, Fall 2003, Section A Instructor: N. Vlajic Heap ADT 2 Heap binary tree (T) that stores a collection of keys at its internal nodes and satisfies
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
Binary search trees :
 Binary search trees Binary search trees : Search trees are data structures that generally offer the following dynamic-set operations : SEARCH MINIMUM MAXIMUM PREDECESSOR SUCCESSOR INSERT DELETE Basic operations
Binary search trees Binary search trees : Search trees are data structures that generally offer the following dynamic-set operations : SEARCH MINIMUM MAXIMUM PREDECESSOR SUCCESSOR INSERT DELETE Basic operations
B-Trees. Version of October 2, B-Trees Version of October 2, / 22
 B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
Binary Search Trees > = 2014 Goodrich, Tamassia, Goldwasser. Binary Search Trees 1
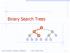 Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Data Structures and Algorithms Lecture 7 DCI FEEI TUKE. Balanced Trees
 Balanced Trees AVL trees reconstruction of perfect balance can be quite expensive operation less rigid criteria of balance (e.g. AVL) [2] inorder, self-balancing binary search tree (BST) Definition: AVL
Balanced Trees AVL trees reconstruction of perfect balance can be quite expensive operation less rigid criteria of balance (e.g. AVL) [2] inorder, self-balancing binary search tree (BST) Definition: AVL
Searching: Introduction
 Searching: Introduction Searching is a major topic in data structures and algorithms Applications: Search for students transcripts from ARR Search for faculty contact email address, office Search for books,
Searching: Introduction Searching is a major topic in data structures and algorithms Applications: Search for students transcripts from ARR Search for faculty contact email address, office Search for books,
COMP : Trees. COMP20012 Trees 219
 COMP20012 3: Trees COMP20012 Trees 219 Trees Seen lots of examples. Parse Trees Decision Trees Search Trees Family Trees Hierarchical Structures Management Directories COMP20012 Trees 220 Trees have natural
COMP20012 3: Trees COMP20012 Trees 219 Trees Seen lots of examples. Parse Trees Decision Trees Search Trees Family Trees Hierarchical Structures Management Directories COMP20012 Trees 220 Trees have natural
Trees. Q: Why study trees? A: Many advance ADTs are implemented using tree-based data structures.
 Trees Q: Why study trees? : Many advance DTs are implemented using tree-based data structures. Recursive Definition of (Rooted) Tree: Let T be a set with n 0 elements. (i) If n = 0, T is an empty tree,
Trees Q: Why study trees? : Many advance DTs are implemented using tree-based data structures. Recursive Definition of (Rooted) Tree: Let T be a set with n 0 elements. (i) If n = 0, T is an empty tree,
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Fundamental Algorithms
 WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
Sample Exam 1 Questions
 CSE 331 Sample Exam 1 Questions Name DO NOT START THE EXAM UNTIL BEING TOLD TO DO SO. If you need more space for some problem, you can link to extra space somewhere else on this exam including right here.
CSE 331 Sample Exam 1 Questions Name DO NOT START THE EXAM UNTIL BEING TOLD TO DO SO. If you need more space for some problem, you can link to extra space somewhere else on this exam including right here.
CS711008Z Algorithm Design and Analysis
 CS711008Z Algorithm Design and Analysis Lecture 7. Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 108 Outline
CS711008Z Algorithm Design and Analysis Lecture 7. Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / 108 Outline
Geometric Data Structures
 Geometric Data Structures 1 Data Structure 2 Definition: A data structure is a particular way of organizing and storing data in a computer for efficient search and retrieval, including associated algorithms
Geometric Data Structures 1 Data Structure 2 Definition: A data structure is a particular way of organizing and storing data in a computer for efficient search and retrieval, including associated algorithms
CS711008Z Algorithm Design and Analysis
 CS700Z Algorithm Design and Analysis Lecture 7 Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / Outline Introduction
CS700Z Algorithm Design and Analysis Lecture 7 Binary heap, binomial heap, and Fibonacci heap Dongbo Bu Institute of Computing Technology Chinese Academy of Sciences, Beijing, China 1 / Outline Introduction
Sample Solutions CSC 263H. June 9, 2016
 Sample Solutions CSC 263H June 9, 2016 This document is a guide for what I would consider a good solution to problems in this course. You may also use the TeX file to build your solutions. 1. Consider
Sample Solutions CSC 263H June 9, 2016 This document is a guide for what I would consider a good solution to problems in this course. You may also use the TeX file to build your solutions. 1. Consider
CMSC 341 Lecture 15 Leftist Heaps
 Based on slides from previous iterations of this course CMSC 341 Lecture 15 Leftist Heaps Prof. John Park Review of Heaps Min Binary Heap A min binary heap is a Complete binary tree Neither child is smaller
Based on slides from previous iterations of this course CMSC 341 Lecture 15 Leftist Heaps Prof. John Park Review of Heaps Min Binary Heap A min binary heap is a Complete binary tree Neither child is smaller
CS521 \ Notes for the Final Exam
 CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
CS521 \ Notes for final exam 1 Ariel Stolerman Asymptotic Notations: CS521 \ Notes for the Final Exam Notation Definition Limit Big-O ( ) Small-o ( ) Big- ( ) Small- ( ) Big- ( ) Notes: ( ) ( ) ( ) ( )
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
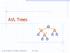 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Sorting and Searching
 Sorting and Searching Lecture 2: Priority Queues, Heaps, and Heapsort Lecture 2: Priority Queues, Heaps, and Heapsort Sorting and Searching 1 / 24 Priority Queue: Motivating Example 3 jobs have been submitted
Sorting and Searching Lecture 2: Priority Queues, Heaps, and Heapsort Lecture 2: Priority Queues, Heaps, and Heapsort Sorting and Searching 1 / 24 Priority Queue: Motivating Example 3 jobs have been submitted
Height of a Heap. Heaps. 1. Insertion into a Heap. Heaps and Priority Queues. The insertion algorithm consists of three steps
 Heaps A heap is a binary tree storing keys at its nodes and satisfying the folloing properties:! Heap-Order: " for every internal node v other than the root, key(v)! key(parent(v))! Complete Binary Tree:
Heaps A heap is a binary tree storing keys at its nodes and satisfying the folloing properties:! Heap-Order: " for every internal node v other than the root, key(v)! key(parent(v))! Complete Binary Tree:
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Announcements. Problem Set 2 is out today! Due Tuesday (Oct 13) More challenging so start early!
 CSC263 Week 3 Announcements Problem Set 2 is out today! Due Tuesday (Oct 13) More challenging so start early! NOT This week ADT: Dictionary Data structure: Binary search tree (BST) Balanced BST - AVL tree
CSC263 Week 3 Announcements Problem Set 2 is out today! Due Tuesday (Oct 13) More challenging so start early! NOT This week ADT: Dictionary Data structure: Binary search tree (BST) Balanced BST - AVL tree
CMSC 341 Lecture 15 Leftist Heaps
 Based on slides from previous iterations of this course CMSC 341 Lecture 15 Leftist Heaps Prof. John Park Review of Heaps Min Binary Heap A min binary heap is a Complete binary tree Neither child is smaller
Based on slides from previous iterations of this course CMSC 341 Lecture 15 Leftist Heaps Prof. John Park Review of Heaps Min Binary Heap A min binary heap is a Complete binary tree Neither child is smaller
Data Structure - Advanced Topics in Tree -
 Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Data Structure - Advanced Topics in Tree - AVL, Red-Black, B-tree Hanyang University Jong-Il Park AVL TREE Division of Computer Science and Engineering, Hanyang University Balanced binary trees Non-random
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 and External Memory 1 1 (2, 4) Trees: Generalization of BSTs Each internal node
Lecture 7. Transform-and-Conquer
 Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Lecture 7 Transform-and-Conquer 6-1 Transform and Conquer This group of techniques solves a problem by a transformation to a simpler/more convenient instance of the same problem (instance simplification)
Algorithm Theory, Winter Term 2015/16 Problem Set 5 - Sample Solution
 Albert-Ludwigs-Universität, Inst. für Informatik Prof. Dr. Fabian Kuhn M. Ahmadi, O. Saukh, A. R. Molla November, 20 Algorithm Theory, Winter Term 20/6 Problem Set - Sample Solution Exercise : Amortized
Albert-Ludwigs-Universität, Inst. für Informatik Prof. Dr. Fabian Kuhn M. Ahmadi, O. Saukh, A. R. Molla November, 20 Algorithm Theory, Winter Term 20/6 Problem Set - Sample Solution Exercise : Amortized
CH 8. HEAPS AND PRIORITY QUEUES
 CH 8. HEAPS AND PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CH 8. HEAPS AND PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
B-Trees and External Memory
 Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Presentation for use with the textbook, Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015 B-Trees and External Memory 1 (2, 4) Trees: Generalization of BSTs Each internal
Orthogonal Range Search and its Relatives
 Orthogonal Range Search and its Relatives Coordinate-wise dominance and minima Definition: dominates Say that point (x,y) dominates (x', y') if x
Orthogonal Range Search and its Relatives Coordinate-wise dominance and minima Definition: dominates Say that point (x,y) dominates (x', y') if x
CS 361, Lecture 21. Outline. Things you can do. Things I will do. Evaluation Results
 HW Difficulty CS 361, Lecture 21 Jared Saia University of New Mexico The HW in this class is inherently difficult, this is a difficult class. You need to be able to solve problems as hard as the problems
HW Difficulty CS 361, Lecture 21 Jared Saia University of New Mexico The HW in this class is inherently difficult, this is a difficult class. You need to be able to solve problems as hard as the problems
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
CH. 8 PRIORITY QUEUES AND HEAPS
 CH. 8 PRIORITY QUEUES AND HEAPS ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CH. 8 PRIORITY QUEUES AND HEAPS ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Sorting and Searching
 Sorting and Searching Lecture 2: Priority Queues, Heaps, and Heapsort Lecture 2: Priority Queues, Heaps, and Heapsort Sorting and Searching 1 / 24 Priority Queue: Motivating Example 3 jobs have been submitted
Sorting and Searching Lecture 2: Priority Queues, Heaps, and Heapsort Lecture 2: Priority Queues, Heaps, and Heapsort Sorting and Searching 1 / 24 Priority Queue: Motivating Example 3 jobs have been submitted
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Advanced algorithms. topological ordering, minimum spanning tree, Union-Find problem. Jiří Vyskočil, Radek Mařík 2012
 topological ordering, minimum spanning tree, Union-Find problem Jiří Vyskočil, Radek Mařík 2012 Subgraph subgraph A graph H is a subgraph of a graph G, if the following two inclusions are satisfied: 2
topological ordering, minimum spanning tree, Union-Find problem Jiří Vyskočil, Radek Mařík 2012 Subgraph subgraph A graph H is a subgraph of a graph G, if the following two inclusions are satisfied: 2
CSE 202: Design and Analysis of Algorithms Lecture 3
 CSE 202: Design and Analysis of Algorithms Lecture 3 Instructor: Kamalika Chaudhuri Announcement Homework 1 out Due on Mon April 11 in class No late homeworks will be accepted Greedy Algorithms Direct
CSE 202: Design and Analysis of Algorithms Lecture 3 Instructor: Kamalika Chaudhuri Announcement Homework 1 out Due on Mon April 11 in class No late homeworks will be accepted Greedy Algorithms Direct
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Foundations of Computer Science Spring Mathematical Preliminaries
 Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
