On Separating the EREW and CREW PRAM Models
|
|
|
- Paulina Burns
- 5 years ago
- Views:
Transcription
1 On Separating the EREW and CREW PRAM Models by E. Gafni, J. saor, and P. Ragde Department of Computer Science Stanford University Stanford, California 94305
2 On Separating the EREW and CREW PRAM Models Eli Gafni * Joseph Naor t Prabhakar Ragde $ Abstract In [6], Snir proposed the Selection Problem (seaxching in a sorted table) to show that the CREW PRAM is strictly more powerful than the EREW PRAM. This problem defines a partial function, that is, one thak is defined only on a restricted set of inputs. Recognizing whether an arbitrary input belongs to this restricted set is hard for both CREW and ER.EW PRAMS. The existence of a total function that exhibits the power of the CREW model over the EREW model was an open problem. Here we solve this problem by generalizing the Selection problem to a Decision Tree problem which is defined on a, full domain a,nd to which Snir s lower bound ampplies. *Dt\ljartnlent of Computer Science, University of Calil ornia.,~ Los Angeles,--CR ~Depa.rtment of Computer Science, Stanford Universitsy, Stanford, CA Support,ecl by contract ONR N %K : Department of Computer Science, University of FVa &loo, \\ a terloo, Ontario, Canada. N2L 3G 1 0
3 1 Introduction Consider the Selection problem, which we denote (S): given an input vector X = (x1,x2,..., ~~-1) and an input y, where all inputs are integers, find the index i such that z; < y 2 x;+l. (By definition x0 = -oo and x,+1 = DO). Problem (S) is just the problem of searching in a sorted table of integers. Snir [6] considered this problem in the context of parallel computation in two different PRAM models. A PRAM consists of a set of processors PO,.&... which communicate by means of cells A,&,, A&,... of shared memory. One step of computation consists of three phases. In the read phase, each processor may choose one cell to read from. In the compute phase, an arbitrary amount of local computation can take place. In the write phase, each processor may choose one cell to write into. The models that Snir considered differ in the degree of simultaneous access to shared memory that is allowed. In the EREW PRAM, no two processors may simultaneously read or write into the same cell. In the CREW PRAM, simultaneous read access is permitted, but not simultaneous write access. It is easy to see that the complexity of problem (S) on a CREW PRAM is O( 1), and Snir [6] proved an O( d&-g) upper and lower bound on solving the problem in the EREW model. His proof proceeds by using Ramsey s Theorem to restrict the set of inputs so that the behaviour of an algorithm solving the problem depends only on the relative order of the input values. Essentially, processors may only make comparisons and gather input va,lues, and an information-theoretic argument shows that this cannot be done quickly. The use of Ramsey s Theorem means that the lower - bound holds only if the input numbers are drawn from a large enough range. A more serious problem with this lower bound proof than the size of the range needed is that the problem is only defined on a restricted set of inputs (termed a deft domain in [4]). Tle 1 xoj 1 1em of testing whether the input is valid (that is, the x s are sorted) requires O(log n) time in the CREW model. (This follows from the lower bound of [I] on the computation of the OR of 12 bits). It could be argued tl1a.t knowing that the input is of a specia.1 form gives information to the CRE\V PRAM that the EREW PRAM cannot use, and thus the comparison is unfair. Examples have been given of PRAM models which can be separated by the use of functions defined on partial domains, but which a,re equal or incomparable when considering functions on full doma.ins ([Z], [:3]).
4 3 In the next section we show how the Selection problem (S) can be reformulated as a. Decision Tree problem, such that the output is well defined for any input. 2 Generalization of the Selection Problem to a Decision Tree Problem Let T be a complete rooted binary tree of size 72 such that n = 2-1 where h is a.n integer. An input variable is associated with each node of T. The variable 5,/z is associated with the root, x,i4 and x3,i4 with the left and right child of the root respectively, and so on. More precisely, if a node has xi associated with it, and i = (2X: + 1) 2, then the left child of the node has xj associated with it, and the right child has xk associated with it, where j = (2k - i)2b and k = (2k + 3>2. We number the nodes, giving a. node the same index as the variable associakecl with it. We now sta,te the Decision Tree problem, denoted problem (D): A pa.th from each node to one of the leaves is defined inductively. The successor of internal node i is the. left child of 1: if y <.c; and the right child of i if y 2 z;. There is a. unique root-leaf pa.th terminaking a.t some leaof j. The output of the problem is j - 1 if?j < x; and j if y > r;. Theorem 2. l P~mdlent (S) can be solved log n) time in the CREW model. Proof: technique. Problem (S) is solved in the CREW model by using the pakh doubling A processor P; is associated with each node i in the tree. P; rea.ds y and x;, t hereby determining the successor of node i. This informakion is stored in memory, sa.y in location i of a,rray S. For a leaf j, let S(j) = j. Then, in pa.ra.llel, each processor 1 ; executes the instruction S(i) +-- S( S(i)), a. total of log log n -times.,4fter t.his is done, S(n/2) = j means that node j is the 1ea.f at, t,he end of the pa.th front t,lle root. 111 O(l) steps the answer can be computed. To set that a. CREW PRAM requires O(log log 11,) time to solve problem (D), we invoke a. result of Simon [5], which states thak any nonclegenera.te Boolean function on 71 \:a.riables requires fl(log log?a) steps to compute on CREW. Our problem does not define a. 1300lean function, since inputs a,re tuples of integers, but we can construct a. BOO1ea.n function 9 by letting y = 1, restricting 21, X2,... :r,,-l lo ha.ve value O-or 1, a.nd defining the output of y to be f (mod 2). Tl le resulting y is at least, as ea.sy to comput.e as.f, a.nd is a, nonclegenerake Boolean function of 71-1 \-ariahles. 2
5 Theorem 2.2 Problem (D) requires O( J&j%) time to solve in the EREW model. Proof: The purpose of demonstrating an 0( JG) algorithm is to show that the lower bound of Snir is the best possible, as the lower bound model does not charge for local computation. As before, a processor P; is associated with node i. In the first step of the algorithm, P; rea,ds 5; and stores this value in node i. We note that in O(1) steps a processor at a node can read any information stored in its left and right children and coalesce this information along with any information it has. Thus, in O(Jlogn> steps, a node v that is at level kdi + 1 for some integer k can gather the values of all variables associated with nodes in the subtree of height Jlogn below node v. Knowing these values and the value of y, a processor can determine in one step the node that is l/l- levels below v on the path from v. In effect, the binary tree has been compressed so that it is now a tree of height l/rogn and fanout 26. The naive sequential algorithm to find the bottom of the root-leaf path can now be run, taking O(Jlogn) steps. To prove the lower bound, we show that problem (S) is reducible to problem (D) in time 0( 1). In fact, problem (S) is just problem (D) restricted to inputs in which t,he x s are sorted. The root-leaf path defined by problem (D) is just the sequence of variables that would be queried by binary search. Another way of stating the sepa,ra.tion implied by the previous two theorems is that for each integer T, there exists a problem which can be solved in T steps in the CREW model, but which requires 2 tt) steps on the EREW model. 3 Separations on Boolean input and output These results can be extended slightly to show a. lower bound for a problem with integer input but Boolean output. The l)rol)lem is just, problem (D), but the output. - is taken to be the output of problem (D) mod 2. To see that Snir s lower bound applies to this problem, one mllst esa,mine Snir s proof. He shows that if o(dz) P steps a.re used by some algorithm, there exist two inputs in the restricted domain and an integer i such that the outputs of problem (S) on t hose two inputs are i and i + 1 respectively, and the computakion of the EREW PRAM on the two inputs is identical. For two such inputs, the output of problem (D) mod 2 would also differ, and the lower bound follows.
6 In [6], Snir gives a lower bound for a problem with Boolean input and output. The problem is to identify the switching index when the input is a string of O s followed by a string of 1%. A lower bound of n(log(n/p)) t ime in the EREW model is proven, where p is the number of processors. The problem can be solved in O(log n/logp) time in the CREW model. In the same vein as in the previous section, it is easy to see that if we modify problem (D) to restrict the inputs to being Boolean, and further fix y = 1, then Snir s problem is just the modified problem defined on a restricted set of inputs. Thus the modified problem (D) takes time at least n(log(n./p)) time in the EREW model. Problem (D) can be solved in time 0( (log n/logp) log logp) in the CREW model. The p processors are assigned to nodes in the first log p levels of the tree and in O(log logp) steps can find out which node at the lowest level is reached by the root-leaf path. This procedure is then repeated log n/ log p times until the bottom of the tree is rea.ch4. References M S. Cook, R. R.eischul; and C. Dwork, Upper and lower bounds for pa.rallel random access mxhines without. simultaneous writes, SI;1:11 J. C~omputing, 15 (19SS) S7-97. F.E. Fich, P. R.a.gde, and A. Wigderson, Relations between colzcul-rent-,rlll-ite models of para,llel computation, SIAM J. C omputing 17 (19SS) V. Grolmusz and P. Ra.gde, I~~.co,lnpnlnbility in parallel compuitrfio~, Proc. 2Sth IEEE Symposium on Foundakions of Computer Science, 1 CJs7. R. Reischuk, Simulta.neous writes do not help to compute simple nrithmet,ic functions, 5 1.4Jf J. Computin~q 16 (19S7). H.-U. Simon, A tight Q(log log n) bound on the time for pa.ra.llel RAMS to compute nonclegenera.tecl Boo1ca.n functions, Info,rmation and C o~~./rol 55 (1982) M. Snir, On paxallel seaxhing, SIAM J. Conzputin,g 14 (19S5) GSS-70s.
Optimal Parallel Randomized Renaming
 Optimal Parallel Randomized Renaming Martin Farach S. Muthukrishnan September 11, 1995 Abstract We consider the Renaming Problem, a basic processing step in string algorithms, for which we give a simultaneously
Optimal Parallel Randomized Renaming Martin Farach S. Muthukrishnan September 11, 1995 Abstract We consider the Renaming Problem, a basic processing step in string algorithms, for which we give a simultaneously
CS256 Applied Theory of Computation
 CS256 Applied Theory of Computation Parallel Computation IV John E Savage Overview PRAM Work-time framework for parallel algorithms Prefix computations Finding roots of trees in a forest Parallel merging
CS256 Applied Theory of Computation Parallel Computation IV John E Savage Overview PRAM Work-time framework for parallel algorithms Prefix computations Finding roots of trees in a forest Parallel merging
Parallel Random Access Machine (PRAM)
 PRAM Algorithms Parallel Random Access Machine (PRAM) Collection of numbered processors Access shared memory Each processor could have local memory (registers) Each processor can access any shared memory
PRAM Algorithms Parallel Random Access Machine (PRAM) Collection of numbered processors Access shared memory Each processor could have local memory (registers) Each processor can access any shared memory
CS 598: Communication Cost Analysis of Algorithms Lecture 15: Communication-optimal sorting and tree-based algorithms
 CS 598: Communication Cost Analysis of Algorithms Lecture 15: Communication-optimal sorting and tree-based algorithms Edgar Solomonik University of Illinois at Urbana-Champaign October 12, 2016 Defining
CS 598: Communication Cost Analysis of Algorithms Lecture 15: Communication-optimal sorting and tree-based algorithms Edgar Solomonik University of Illinois at Urbana-Champaign October 12, 2016 Defining
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
We will show that the height of a RB tree on n vertices is approximately 2*log n. In class I presented a simple structural proof of this claim:
 We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
Complete Variable-Length "Fix-Free" Codes
 Designs, Codes and Cryptography, 5, 109-114 (1995) 9 1995 Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. Complete Variable-Length "Fix-Free" Codes DAVID GILLMAN* gillman @ es.toronto.edu
Designs, Codes and Cryptography, 5, 109-114 (1995) 9 1995 Kluwer Academic Publishers, Boston. Manufactured in The Netherlands. Complete Variable-Length "Fix-Free" Codes DAVID GILLMAN* gillman @ es.toronto.edu
Embedding Large Complete Binary Trees in Hypercubes with Load Balancing
 JOURNAL OF PARALLEL AND DISTRIBUTED COMPUTING 35, 104 109 (1996) ARTICLE NO. 0073 Embedding Large Complete Binary Trees in Hypercubes with Load Balancing KEMAL EFE Center for Advanced Computer Studies,
JOURNAL OF PARALLEL AND DISTRIBUTED COMPUTING 35, 104 109 (1996) ARTICLE NO. 0073 Embedding Large Complete Binary Trees in Hypercubes with Load Balancing KEMAL EFE Center for Advanced Computer Studies,
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
Parallel algorithms for generating combinatorial objects on linear processor arrays with reconfigurable bus systems*
 SOdhan& Vol. 22. Part 5, October 1997, pp. 62%636. Printed ill India. Parallel algorithms for generating combinatorial objects on linear processor arrays with reconfigurable bus systems* P THANGAVEL Department
SOdhan& Vol. 22. Part 5, October 1997, pp. 62%636. Printed ill India. Parallel algorithms for generating combinatorial objects on linear processor arrays with reconfigurable bus systems* P THANGAVEL Department
The PRAM model. A. V. Gerbessiotis CIS 485/Spring 1999 Handout 2 Week 2
 The PRAM model A. V. Gerbessiotis CIS 485/Spring 1999 Handout 2 Week 2 Introduction The Parallel Random Access Machine (PRAM) is one of the simplest ways to model a parallel computer. A PRAM consists of
The PRAM model A. V. Gerbessiotis CIS 485/Spring 1999 Handout 2 Week 2 Introduction The Parallel Random Access Machine (PRAM) is one of the simplest ways to model a parallel computer. A PRAM consists of
Derandomization by Exploiting Redundancy and Mutual Independence
 Derandomization by Exploiting Redundancy and Mutual Independence Yijie Han Yoshihide Igarashi Department of Computer Science University of Kentucky Lexington, KY 40506, USA Department of Computer Science
Derandomization by Exploiting Redundancy and Mutual Independence Yijie Han Yoshihide Igarashi Department of Computer Science University of Kentucky Lexington, KY 40506, USA Department of Computer Science
Real parallel computers
 CHAPTER 30 (in old edition) Parallel Algorithms The PRAM MODEL OF COMPUTATION Abbreviation for Parallel Random Access Machine Consists of p processors (PEs), P 0, P 1, P 2,, P p-1 connected to a shared
CHAPTER 30 (in old edition) Parallel Algorithms The PRAM MODEL OF COMPUTATION Abbreviation for Parallel Random Access Machine Consists of p processors (PEs), P 0, P 1, P 2,, P p-1 connected to a shared
THE EULER TOUR TECHNIQUE: EVALUATION OF TREE FUNCTIONS
 PARALLEL AND DISTRIBUTED ALGORITHMS BY DEBDEEP MUKHOPADHYAY AND ABHISHEK SOMANI http://cse.iitkgp.ac.in/~debdeep/courses_iitkgp/palgo/index.htm THE EULER TOUR TECHNIQUE: EVALUATION OF TREE FUNCTIONS 2
PARALLEL AND DISTRIBUTED ALGORITHMS BY DEBDEEP MUKHOPADHYAY AND ABHISHEK SOMANI http://cse.iitkgp.ac.in/~debdeep/courses_iitkgp/palgo/index.htm THE EULER TOUR TECHNIQUE: EVALUATION OF TREE FUNCTIONS 2
time using O( n log n ) processors on the EREW PRAM. Thus, our algorithm improves on the previous results, either in time complexity or in the model o
 Reconstructing a Binary Tree from its Traversals in Doubly-Logarithmic CREW Time Stephan Olariu Michael Overstreet Department of Computer Science, Old Dominion University, Norfolk, VA 23529 Zhaofang Wen
Reconstructing a Binary Tree from its Traversals in Doubly-Logarithmic CREW Time Stephan Olariu Michael Overstreet Department of Computer Science, Old Dominion University, Norfolk, VA 23529 Zhaofang Wen
: Parallel Algorithms Exercises, Batch 1. Exercise Day, Tuesday 18.11, 10:00. Hand-in before or at Exercise Day
 184.727: Parallel Algorithms Exercises, Batch 1. Exercise Day, Tuesday 18.11, 10:00. Hand-in before or at Exercise Day Jesper Larsson Träff, Francesco Versaci Parallel Computing Group TU Wien October 16,
184.727: Parallel Algorithms Exercises, Batch 1. Exercise Day, Tuesday 18.11, 10:00. Hand-in before or at Exercise Day Jesper Larsson Träff, Francesco Versaci Parallel Computing Group TU Wien October 16,
CSE 530A. B+ Trees. Washington University Fall 2013
 CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
CSE 530A B+ Trees Washington University Fall 2013 B Trees A B tree is an ordered (non-binary) tree where the internal nodes can have a varying number of child nodes (within some range) B Trees When a key
Algorithms & Data Structures 2
 Algorithms & Data Structures 2 PRAM Algorithms WS2017 B. Anzengruber-Tanase (Institute for Pervasive Computing, JKU Linz) (Institute for Pervasive Computing, JKU Linz) RAM MODELL (AHO/HOPCROFT/ULLMANN
Algorithms & Data Structures 2 PRAM Algorithms WS2017 B. Anzengruber-Tanase (Institute for Pervasive Computing, JKU Linz) (Institute for Pervasive Computing, JKU Linz) RAM MODELL (AHO/HOPCROFT/ULLMANN
would be included in is small: to be exact. Thus with probability1, the same partition n+1 n+1 would be produced regardless of whether p is in the inp
 1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
THE EULER TOUR TECHNIQUE: EVALUATION OF TREE FUNCTIONS
 PARALLEL AND DISTRIBUTED ALGORITHMS BY DEBDEEP MUKHOPADHYAY AND ABHISHEK SOMANI http://cse.iitkgp.ac.in/~debdeep/courses_iitkgp/palgo/index.htm THE EULER TOUR TECHNIQUE: EVALUATION OF TREE FUNCTIONS 2
PARALLEL AND DISTRIBUTED ALGORITHMS BY DEBDEEP MUKHOPADHYAY AND ABHISHEK SOMANI http://cse.iitkgp.ac.in/~debdeep/courses_iitkgp/palgo/index.htm THE EULER TOUR TECHNIQUE: EVALUATION OF TREE FUNCTIONS 2
CSE 4500 (228) Fall 2010 Selected Notes Set 2
 CSE 4500 (228) Fall 2010 Selected Notes Set 2 Alexander A. Shvartsman Computer Science and Engineering University of Connecticut Copyright c 2002-2010 by Alexander A. Shvartsman. All rights reserved. 2
CSE 4500 (228) Fall 2010 Selected Notes Set 2 Alexander A. Shvartsman Computer Science and Engineering University of Connecticut Copyright c 2002-2010 by Alexander A. Shvartsman. All rights reserved. 2
Notes on Binary Dumbbell Trees
 Notes on Binary Dumbbell Trees Michiel Smid March 23, 2012 Abstract Dumbbell trees were introduced in [1]. A detailed description of non-binary dumbbell trees appears in Chapter 11 of [3]. These notes
Notes on Binary Dumbbell Trees Michiel Smid March 23, 2012 Abstract Dumbbell trees were introduced in [1]. A detailed description of non-binary dumbbell trees appears in Chapter 11 of [3]. These notes
We assume uniform hashing (UH):
 We assume uniform hashing (UH): the probe sequence of each key is equally likely to be any of the! permutations of 0,1,, 1 UH generalizes the notion of SUH that produces not just a single number, but a
We assume uniform hashing (UH): the probe sequence of each key is equally likely to be any of the! permutations of 0,1,, 1 UH generalizes the notion of SUH that produces not just a single number, but a
Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms. Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms
 Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms Part 2 1 3 Maximum Selection Problem : Given n numbers, x 1, x 2,, x
Parallel Algorithms for (PRAM) Computers & Some Parallel Algorithms Reference : Horowitz, Sahni and Rajasekaran, Computer Algorithms Part 2 1 3 Maximum Selection Problem : Given n numbers, x 1, x 2,, x
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Parallel Random-Access Machines
 Parallel Random-Access Machines Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS3101 (Moreno Maza) Parallel Random-Access Machines CS3101 1 / 69 Plan 1 The PRAM Model 2 Performance
Parallel Random-Access Machines Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS3101 (Moreno Maza) Parallel Random-Access Machines CS3101 1 / 69 Plan 1 The PRAM Model 2 Performance
Yossi Shiioach. STAN-CS January COMPUTER SCIENCE DEPARTMENT School of Humanities and Sciences STANFORD UNIVERSITY
 UNION-MEMBER ALGORITHMS FOR NON-DISJOINT SETS by Yossi Shiioach STAN-CS-79-728 January 19 7 9 COMPUTER SCIENCE DEPARTMENT School of Humanities and Sciences STANFORD UNIVERSITY Union-Member Algorithms for
UNION-MEMBER ALGORITHMS FOR NON-DISJOINT SETS by Yossi Shiioach STAN-CS-79-728 January 19 7 9 COMPUTER SCIENCE DEPARTMENT School of Humanities and Sciences STANFORD UNIVERSITY Union-Member Algorithms for
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
Trapezoid and Chain Methods
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 05 Date: Febuary 17, 1993 Scribe: Peter C. McCluskey Trapezoid and Chain Methods 1 Trapezoid Method (continued) Continuing
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 05 Date: Febuary 17, 1993 Scribe: Peter C. McCluskey Trapezoid and Chain Methods 1 Trapezoid Method (continued) Continuing
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
(b) int count = 0; int i = 1; while (i<m) { for (int j=i; j<n; j++) { count = count + 1; i = i + 1; O(M + N 2 ) (c) int count = 0; int i,j,k; for (i=1
 CPS 100 Exam 2 Solutions Spring 199 Dr Rodger 1 (3 pts) A virtual function in C++ is bound dynamically or statically? dynamic 2 (3 pts) When does one use a class template in C++? Templates are used to
CPS 100 Exam 2 Solutions Spring 199 Dr Rodger 1 (3 pts) A virtual function in C++ is bound dynamically or statically? dynamic 2 (3 pts) When does one use a class template in C++? Templates are used to
CS 251, LE 2 Fall MIDTERM 2 Tuesday, November 1, 2016 Version 00 - KEY
 CS 251, LE 2 Fall 2016 MIDTERM 2 Tuesday, November 1, 2016 Version 00 - KEY W1.) (i) Show one possible valid 2-3 tree containing the nine elements: 1 3 4 5 6 8 9 10 12. (ii) Draw the final binary search
CS 251, LE 2 Fall 2016 MIDTERM 2 Tuesday, November 1, 2016 Version 00 - KEY W1.) (i) Show one possible valid 2-3 tree containing the nine elements: 1 3 4 5 6 8 9 10 12. (ii) Draw the final binary search
Heaps. 2/13/2006 Heaps 1
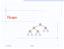 Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
Heaps /13/00 Heaps 1 Outline and Reading What is a heap ( 8.3.1) Height of a heap ( 8.3.) Insertion ( 8.3.3) Removal ( 8.3.3) Heap-sort ( 8.3.) Arraylist-based implementation ( 8.3.) Bottom-up construction
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
CREW PRAMS and Decision Trees. Noam Nisan 1
 CREW PRAMS and Decision Trees Noam Nisan 1 Laboratory of Computer Science M.I.T. Cambridge, MA 02139 ABSTRACT This paper gives a full characterization of the time needed to compute a boolean function on
CREW PRAMS and Decision Trees Noam Nisan 1 Laboratory of Computer Science M.I.T. Cambridge, MA 02139 ABSTRACT This paper gives a full characterization of the time needed to compute a boolean function on
Well, you need to capture the notions of atomicity, non-determinism, fairness etc. These concepts are not built into languages like JAVA, C++ etc!
 Hwajung Lee Why do we need these? Don t we already know a lot about programming? Well, you need to capture the notions of atomicity, non-determinism, fairness etc. These concepts are not built into languages
Hwajung Lee Why do we need these? Don t we already know a lot about programming? Well, you need to capture the notions of atomicity, non-determinism, fairness etc. These concepts are not built into languages
PRAM (Parallel Random Access Machine)
 PRAM (Parallel Random Access Machine) Lecture Overview Why do we need a model PRAM Some PRAM algorithms Analysis A Parallel Machine Model What is a machine model? Describes a machine Puts a value to the
PRAM (Parallel Random Access Machine) Lecture Overview Why do we need a model PRAM Some PRAM algorithms Analysis A Parallel Machine Model What is a machine model? Describes a machine Puts a value to the
Solutions. (a) Claim: A d-ary tree of height h has at most 1 + d +...
 Design and Analysis of Algorithms nd August, 016 Problem Sheet 1 Solutions Sushant Agarwal Solutions 1. A d-ary tree is a rooted tree in which each node has at most d children. Show that any d-ary tree
Design and Analysis of Algorithms nd August, 016 Problem Sheet 1 Solutions Sushant Agarwal Solutions 1. A d-ary tree is a rooted tree in which each node has at most d children. Show that any d-ary tree
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
Fast Parallel String Prex-Matching. Dany Breslauer. April 6, Abstract. n log m -processor CRCW-PRAM algorithm for the
 Fast Parallel String Prex-Matching Dany Breslauer April 6, 1995 Abstract An O(log logm) time n log m -processor CRCW-PRAM algorithm for the string prex-matching problem over general alphabets is presented.
Fast Parallel String Prex-Matching Dany Breslauer April 6, 1995 Abstract An O(log logm) time n log m -processor CRCW-PRAM algorithm for the string prex-matching problem over general alphabets is presented.
Expected Time in Linear Space
 Optimizing Integer Sorting in O(n log log n) Expected Time in Linear Space Ajit Singh M. E. (Computer Science and Engineering) Department of computer Science and Engineering, Thapar University, Patiala
Optimizing Integer Sorting in O(n log log n) Expected Time in Linear Space Ajit Singh M. E. (Computer Science and Engineering) Department of computer Science and Engineering, Thapar University, Patiala
How Hard Is It to Take a Snapshot?
 How Hard Is It to Take a Snapshot? Faith Ellen Fich University of Toronto Toronto, Canada fich@cs.utoronto.ca Abstract. The snapshot object is an important and well-studied primitive in distributed computing.
How Hard Is It to Take a Snapshot? Faith Ellen Fich University of Toronto Toronto, Canada fich@cs.utoronto.ca Abstract. The snapshot object is an important and well-studied primitive in distributed computing.
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Space vs Time, Cache vs Main Memory
 Space vs Time, Cache vs Main Memory Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS 4435 - CS 9624 (Moreno Maza) Space vs Time, Cache vs Main Memory CS 4435 - CS 9624 1 / 49
Space vs Time, Cache vs Main Memory Marc Moreno Maza University of Western Ontario, London, Ontario (Canada) CS 4435 - CS 9624 (Moreno Maza) Space vs Time, Cache vs Main Memory CS 4435 - CS 9624 1 / 49
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
CS Fall 2010 B-trees Carola Wenk
 CS 3343 -- Fall 2010 B-trees Carola Wenk 10/19/10 CS 3343 Analysis of Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CS 3343 -- Fall 2010 B-trees Carola Wenk 10/19/10 CS 3343 Analysis of Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
Provably Efficient Non-Preemptive Task Scheduling with Cilk
 Provably Efficient Non-Preemptive Task Scheduling with Cilk V. -Y. Vee and W.-J. Hsu School of Applied Science, Nanyang Technological University Nanyang Avenue, Singapore 639798. Abstract We consider the
Provably Efficient Non-Preemptive Task Scheduling with Cilk V. -Y. Vee and W.-J. Hsu School of Applied Science, Nanyang Technological University Nanyang Avenue, Singapore 639798. Abstract We consider the
Priority Queues. 1 Introduction. 2 Naïve Implementations. CSci 335 Software Design and Analysis III Chapter 6 Priority Queues. Prof.
 Priority Queues 1 Introduction Many applications require a special type of queuing in which items are pushed onto the queue by order of arrival, but removed from the queue based on some other priority
Priority Queues 1 Introduction Many applications require a special type of queuing in which items are pushed onto the queue by order of arrival, but removed from the queue based on some other priority
Recursion and Structural Induction
 Recursion and Structural Induction Mukulika Ghosh Fall 2018 Based on slides by Dr. Hyunyoung Lee Recursively Defined Functions Recursively Defined Functions Suppose we have a function with the set of non-negative
Recursion and Structural Induction Mukulika Ghosh Fall 2018 Based on slides by Dr. Hyunyoung Lee Recursively Defined Functions Recursively Defined Functions Suppose we have a function with the set of non-negative
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Union/Find Aka: Disjoint-set forest. Problem definition. Naïve attempts CS 445
 CS 5 Union/Find Aka: Disjoint-set forest Alon Efrat Problem definition Given: A set of atoms S={1, n E.g. each represents a commercial name of a drugs. This set consists of different disjoint subsets.
CS 5 Union/Find Aka: Disjoint-set forest Alon Efrat Problem definition Given: A set of atoms S={1, n E.g. each represents a commercial name of a drugs. This set consists of different disjoint subsets.
CH 8. HEAPS AND PRIORITY QUEUES
 CH 8. HEAPS AND PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CH 8. HEAPS AND PRIORITY QUEUES ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
An NC Algorithm for Sorting Real Numbers
 EPiC Series in Computing Volume 58, 2019, Pages 93 98 Proceedings of 34th International Conference on Computers and Their Applications An NC Algorithm for Sorting Real Numbers in O( nlogn loglogn ) Operations
EPiC Series in Computing Volume 58, 2019, Pages 93 98 Proceedings of 34th International Conference on Computers and Their Applications An NC Algorithm for Sorting Real Numbers in O( nlogn loglogn ) Operations
Figure 1: A complete binary tree.
 The Binary Heap A binary heap is a data structure that implements the abstract data type priority queue. That is, a binary heap stores a set of elements with a total order (that means that every two elements
The Binary Heap A binary heap is a data structure that implements the abstract data type priority queue. That is, a binary heap stores a set of elements with a total order (that means that every two elements
r (1,1) r (2,4) r (2,5) r(2,6) r (1,3) r (1,2)
 Routing on Trees via Matchings? Alan Roberts 1, Antonis Symvonis 1 and Louxin Zhang 2 1 Department of Computer Science, University of Sydney, N.S.W. 2006, Australia 2 Department of Computer Science, University
Routing on Trees via Matchings? Alan Roberts 1, Antonis Symvonis 1 and Louxin Zhang 2 1 Department of Computer Science, University of Sydney, N.S.W. 2006, Australia 2 Department of Computer Science, University
Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance
 Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI-33101 Tampere,
Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI-33101 Tampere,
Height of a Heap. Heaps. 1. Insertion into a Heap. Heaps and Priority Queues. The insertion algorithm consists of three steps
 Heaps A heap is a binary tree storing keys at its nodes and satisfying the folloing properties:! Heap-Order: " for every internal node v other than the root, key(v)! key(parent(v))! Complete Binary Tree:
Heaps A heap is a binary tree storing keys at its nodes and satisfying the folloing properties:! Heap-Order: " for every internal node v other than the root, key(v)! key(parent(v))! Complete Binary Tree:
(2,4) Trees Goodrich, Tamassia. (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 (2,4) Trees 1 Multi-Way Search Tree ( 9.4.1) A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 1 key-element items
(2,4) Trees 9 2 5 7 10 14 (2,4) Trees 1 Multi-Way Search Tree ( 9.4.1) A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d 1 key-element items
Planar Point Location
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
CH. 8 PRIORITY QUEUES AND HEAPS
 CH. 8 PRIORITY QUEUES AND HEAPS ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CH. 8 PRIORITY QUEUES AND HEAPS ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Greedy Algorithms. CLRS Chapters Introduction to greedy algorithms. Design of data-compression (Huffman) codes
 Greedy Algorithms CLRS Chapters 16.1 16.3 Introduction to greedy algorithms Activity-selection problem Design of data-compression (Huffman) codes (Minimum spanning tree problem) (Shortest-path problem)
Greedy Algorithms CLRS Chapters 16.1 16.3 Introduction to greedy algorithms Activity-selection problem Design of data-compression (Huffman) codes (Minimum spanning tree problem) (Shortest-path problem)
Euler Tours and Their Applications. Chris Moultrie CSc 8530
 Euler Tours and Their Applications Chris Moultrie CSc 8530 Topics Covered History Terminology Sequential Algorithm Parallel Algorithm BSP/CGM Algorithm History Started with the famous Konigsberg problem.
Euler Tours and Their Applications Chris Moultrie CSc 8530 Topics Covered History Terminology Sequential Algorithm Parallel Algorithm BSP/CGM Algorithm History Started with the famous Konigsberg problem.
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
where is a constant, 0 < <. In other words, the ratio between the shortest and longest paths from a node to a leaf is at least. An BB-tree allows ecie
 Maintaining -balanced Trees by Partial Rebuilding Arne Andersson Department of Computer Science Lund University Box 8 S-22 00 Lund Sweden Abstract The balance criterion dening the class of -balanced trees
Maintaining -balanced Trees by Partial Rebuilding Arne Andersson Department of Computer Science Lund University Box 8 S-22 00 Lund Sweden Abstract The balance criterion dening the class of -balanced trees
HEAPS ON HEAPS* Downloaded 02/04/13 to Redistribution subject to SIAM license or copyright; see
 SIAM J. COMPUT. Vol. 15, No. 4, November 1986 (C) 1986 Society for Industrial and Applied Mathematics OO6 HEAPS ON HEAPS* GASTON H. GONNET" AND J. IAN MUNRO," Abstract. As part of a study of the general
SIAM J. COMPUT. Vol. 15, No. 4, November 1986 (C) 1986 Society for Industrial and Applied Mathematics OO6 HEAPS ON HEAPS* GASTON H. GONNET" AND J. IAN MUNRO," Abstract. As part of a study of the general
CMPS 2200 Fall 2017 B-trees Carola Wenk
 CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
CMPS 2200 Fall 2017 B-trees Carola Wenk 9/18/17 CMPS 2200 Intro. to Algorithms 1 External memory dictionary Task: Given a large amount of data that does not fit into main memory, process it into a dictionary
Disk Accesses. CS 361, Lecture 25. B-Tree Properties. Outline
 Disk Accesses CS 361, Lecture 25 Jared Saia University of New Mexico Consider any search tree The number of disk accesses per search will dominate the run time Unless the entire tree is in memory, there
Disk Accesses CS 361, Lecture 25 Jared Saia University of New Mexico Consider any search tree The number of disk accesses per search will dominate the run time Unless the entire tree is in memory, there
COL351: Analysis and Design of Algorithms (CSE, IITD, Semester-I ) Name: Entry number:
 Name: Entry number: There are 6 questions for a total of 75 points. 1. Consider functions f(n) = 10n2 n + 3 n and g(n) = n3 n. Answer the following: (a) ( 1 / 2 point) State true or false: f(n) is O(g(n)).
Name: Entry number: There are 6 questions for a total of 75 points. 1. Consider functions f(n) = 10n2 n + 3 n and g(n) = n3 n. Answer the following: (a) ( 1 / 2 point) State true or false: f(n) is O(g(n)).
Lower Bound on Comparison-based Sorting
 Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Algorithms. Red-Black Trees
 Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Friday Four Square! 4:15PM, Outside Gates
 Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Binary Search Trees Friday Four Square! 4:15PM, Outside Gates Implementing Set On Monday and Wednesday, we saw how to implement the Map and Lexicon, respectively. Let's now turn our attention to the Set.
Binary Tree. Preview. Binary Tree. Binary Tree. Binary Search Tree 10/2/2017. Binary Tree
 0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
9. Heap : Priority Queue
 9. Heap : Priority Queue Where We Are? Array Linked list Stack Queue Tree Binary Tree Heap Binary Search Tree Priority Queue Queue Queue operation is based on the order of arrivals of elements FIFO(First-In
9. Heap : Priority Queue Where We Are? Array Linked list Stack Queue Tree Binary Tree Heap Binary Search Tree Priority Queue Queue Queue operation is based on the order of arrivals of elements FIFO(First-In
A New Algorithm for the Josephus Problem Using Binary Count Tree
 International Symposium on Communication Engineering & Computer Science (CECS 08) A New Algorithm for the Josephus Problem Using Binary Count Tree Jian Lia, Yanzhou Mab, Zesheng Gaoc and Xinyu Huc Luoyang
International Symposium on Communication Engineering & Computer Science (CECS 08) A New Algorithm for the Josephus Problem Using Binary Count Tree Jian Lia, Yanzhou Mab, Zesheng Gaoc and Xinyu Huc Luoyang
Multi-Way Search Tree
 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two and at most d children and stores d -1 data items (k i, D i ) Rule: Number of children = 1
Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two and at most d children and stores d -1 data items (k i, D i ) Rule: Number of children = 1
W4231: Analysis of Algorithms
 W4231: Analysis of Algorithms From Binomial Heaps to Fibonacci Heaps Fibonacci Heaps 10/7/1999 We first prove that in Binomial Heaps insert and find-min take amortized O(1) time, while still having insert,
W4231: Analysis of Algorithms From Binomial Heaps to Fibonacci Heaps Fibonacci Heaps 10/7/1999 We first prove that in Binomial Heaps insert and find-min take amortized O(1) time, while still having insert,
A Fast Algorithm for Optimal Alignment between Similar Ordered Trees
 Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
COMP Parallel Computing. PRAM (4) PRAM models and complexity
 COMP 633 - Parallel Computing Lecture 5 September 4, 2018 PRAM models and complexity Reading for Thursday Memory hierarchy and cache-based systems Topics Comparison of PRAM models relative performance
COMP 633 - Parallel Computing Lecture 5 September 4, 2018 PRAM models and complexity Reading for Thursday Memory hierarchy and cache-based systems Topics Comparison of PRAM models relative performance
AN O(LOGN) TIME COMMON CRCW PRAM ALGORITHM FOR MINIMUM SPANNING TREE
 October 1990 UILU-EN G-90-2250 ACT-114 Applied Computation Theory AN O(LOGN) TIME COMMON CRCW PRAM ALGORITHM FOR MINIMUM SPANNING TREE Michael M. Wu Coordinated Science Laboratory College o f Engineering
October 1990 UILU-EN G-90-2250 ACT-114 Applied Computation Theory AN O(LOGN) TIME COMMON CRCW PRAM ALGORITHM FOR MINIMUM SPANNING TREE Michael M. Wu Coordinated Science Laboratory College o f Engineering
Foundations of Computer Science Spring Mathematical Preliminaries
 Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A;
![How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A; How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A;](/thumbs/82/85312801.jpg) How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A; } if (n
How much space does this routine use in the worst case for a given n? public static void use_space(int n) { int b; int [] A; } if (n
CS24 Week 8 Lecture 1
 CS24 Week 8 Lecture 1 Kyle Dewey Overview Tree terminology Tree traversals Implementation (if time) Terminology Node The most basic component of a tree - the squares Edge The connections between nodes
CS24 Week 8 Lecture 1 Kyle Dewey Overview Tree terminology Tree traversals Implementation (if time) Terminology Node The most basic component of a tree - the squares Edge The connections between nodes
Algorithms for Memory Hierarchies Lecture 2
 Algorithms for emory Hierarchies Lecture Lecturer: odari Sitchianva Scribes: Robin Rehrmann, ichael Kirsten Last Time External memory (E) model Scan(): O( ) I/Os Stacks / queues: O( 1 ) I/Os / elt ergesort:
Algorithms for emory Hierarchies Lecture Lecturer: odari Sitchianva Scribes: Robin Rehrmann, ichael Kirsten Last Time External memory (E) model Scan(): O( ) I/Os Stacks / queues: O( 1 ) I/Os / elt ergesort:
Priority Queue ADT ( 7.1) Heaps and Priority Queues 2. Comparator ADT ( 7.1.4) Total Order Relation. Using Comparators in C++
 Heaps and Priority Queues Priority Queue ADT (.) A priority queue stores a collection of items An item is a pair (key, element) Main methods of the Priority Queue ADT insertitem(k, o) inserts an item ith
Heaps and Priority Queues Priority Queue ADT (.) A priority queue stores a collection of items An item is a pair (key, element) Main methods of the Priority Queue ADT insertitem(k, o) inserts an item ith
Abstract Relaxed balancing of search trees was introduced with the aim of speeding up the updates and allowing a high degree of concurrency. In a rela
 Chromatic Search Trees Revisited Institut fur Informatik Report 9 Sabine Hanke Institut fur Informatik, Universitat Freiburg Am Flughafen 7, 79 Freiburg, Germany Email: hanke@informatik.uni-freiburg.de.
Chromatic Search Trees Revisited Institut fur Informatik Report 9 Sabine Hanke Institut fur Informatik, Universitat Freiburg Am Flughafen 7, 79 Freiburg, Germany Email: hanke@informatik.uni-freiburg.de.
A New Graph Triconnectivity Algorithm and Its Parallelization*
 In COMBINATORICA, vol. 12, 1992, pp. 53-76. (Figures not yet included in this file.) A New Graph Triconnectivity Algorithm and Its Parallelization* Gary L. Miller University of Southern California, Los
In COMBINATORICA, vol. 12, 1992, pp. 53-76. (Figures not yet included in this file.) A New Graph Triconnectivity Algorithm and Its Parallelization* Gary L. Miller University of Southern California, Los
Seminar on. Edge Coloring Series Parallel Graphs. Mohammmad Tawhidul Islam. Masters of Computer Science Summer Semester 2002 Matrikel Nr.
 Seminar on Edge Coloring Series Parallel Graphs Mohammmad Tawhidul Islam Masters of Computer Science Summer Semester 2002 Matrikel Nr. 9003378 Fachhochschule Bonn-Rhein-Sieg Contents 1. Introduction. 2.
Seminar on Edge Coloring Series Parallel Graphs Mohammmad Tawhidul Islam Masters of Computer Science Summer Semester 2002 Matrikel Nr. 9003378 Fachhochschule Bonn-Rhein-Sieg Contents 1. Introduction. 2.
arxiv: v2 [cs.ds] 9 Apr 2009
![arxiv: v2 [cs.ds] 9 Apr 2009 arxiv: v2 [cs.ds] 9 Apr 2009](/thumbs/72/66843812.jpg) Pairing Heaps with Costless Meld arxiv:09034130v2 [csds] 9 Apr 2009 Amr Elmasry Max-Planck Institut für Informatik Saarbrücken, Germany elmasry@mpi-infmpgde Abstract Improving the structure and analysis
Pairing Heaps with Costless Meld arxiv:09034130v2 [csds] 9 Apr 2009 Amr Elmasry Max-Planck Institut für Informatik Saarbrücken, Germany elmasry@mpi-infmpgde Abstract Improving the structure and analysis
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Lecture 2 February 4, 2010
 6.897: Advanced Data Structures Spring 010 Prof. Erik Demaine Lecture February 4, 010 1 Overview In the last lecture we discussed Binary Search Trees(BST) and introduced them as a model of computation.
6.897: Advanced Data Structures Spring 010 Prof. Erik Demaine Lecture February 4, 010 1 Overview In the last lecture we discussed Binary Search Trees(BST) and introduced them as a model of computation.
Heap: A binary heap is a complete binary tree in which each, node other than root is smaller than its parent. Heap example: Fig 1. NPTEL IIT Guwahati
 Heap sort is an efficient sorting algorithm with average and worst case time complexities are in O(n log n). Heap sort does not use any extra array, like merge sort. This method is based on a data structure
Heap sort is an efficient sorting algorithm with average and worst case time complexities are in O(n log n). Heap sort does not use any extra array, like merge sort. This method is based on a data structure
ICS 691: Advanced Data Structures Spring Lecture 8
 ICS 691: Advanced Data Structures Spring 2016 Prof. odari Sitchinava Lecture 8 Scribe: Ben Karsin 1 Overview In the last lecture we continued looking at arborally satisfied sets and their equivalence to
ICS 691: Advanced Data Structures Spring 2016 Prof. odari Sitchinava Lecture 8 Scribe: Ben Karsin 1 Overview In the last lecture we continued looking at arborally satisfied sets and their equivalence to
Lecture Notes: External Interval Tree. 1 External Interval Tree The Static Version
 Lecture Notes: External Interval Tree Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk This lecture discusses the stabbing problem. Let I be
Lecture Notes: External Interval Tree Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk This lecture discusses the stabbing problem. Let I be
Paradigms for Parallel Algorithms
 S Parallel Algorithms Paradigms for Parallel Algorithms Reference : C. Xavier and S. S. Iyengar, Introduction to Parallel Algorithms Binary Tree Paradigm A binary tree with n nodes is of height log n Can
S Parallel Algorithms Paradigms for Parallel Algorithms Reference : C. Xavier and S. S. Iyengar, Introduction to Parallel Algorithms Binary Tree Paradigm A binary tree with n nodes is of height log n Can
Lecture 6: External Interval Tree (Part II) 3 Making the external interval tree dynamic. 3.1 Dynamizing an underflow structure
 Lecture 6: External Interval Tree (Part II) Yufei Tao Division of Web Science and Technology Korea Advanced Institute of Science and Technology taoyf@cse.cuhk.edu.hk 3 Making the external interval tree
Lecture 6: External Interval Tree (Part II) Yufei Tao Division of Web Science and Technology Korea Advanced Institute of Science and Technology taoyf@cse.cuhk.edu.hk 3 Making the external interval tree
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
