where is a constant, 0 < <. In other words, the ratio between the shortest and longest paths from a node to a leaf is at least. An BB-tree allows ecie
|
|
|
- Polly Bell
- 5 years ago
- Views:
Transcription
1 Maintaining -balanced Trees by Partial Rebuilding Arne Andersson Department of Computer Science Lund University Box 8 S Lund Sweden Abstract The balance criterion dening the class of -balanced trees states that the ratio between the shortest and longest paths from a node to a leaf be at least. We show that a straight-forward use of partial rebuilding p for maintenance of -balanced trees requires an amortized cost of ( n) per update. By slight modications of the maintenance algorithms the cost can be reduced to O(log n) for any value of, 0 < <. KEY WORDS -balanced trees, partial rebuilding, search trees. CR CATEGORIES: E., F.2, I..2. Introduction In his thesis Olivie [9] introduced a class of binary search trees, which he calls -balanced trees, or BB-trees. Let h(v) denote the length for the longest path from a node v to a leaf and let denote the length of the shortest path. We give a formal denition of -balanced trees below. Denition A binary tree is -balanced if the following is true for each node v in the tree: ; h(v) () h(v)? h(v)? ; h(v) < (2)? This work was partially supported by a grant from the National Swedish Board for Technical Development.
2 where is a constant, 0 < <. In other words, the ratio between the shortest and longest paths from a node to a leaf is at least. An BB-tree allows ecient element location, since its height is restricted to be h(t ) log n Olivie gave updating algorithms using local restructuring with good worst case behaviour for = =2 (half-balanced trees) [0]. He also gave a general insertion algorithm for the case 0 < =2 and a deletion algorithm for = =3. However, the question whether there are ecient algorithms for all possible values of was left open. According to Olivie, for =2 < < the design of ecient algorithms seems to be dicult. Later, Overmars [2] showed that by using weak deletions and global rebuilding an BB-tree may be maintained at an amortized cost of O(log n) per update for =2. Furthermore, a data structure consisting of two BB-trees may be maintained at O(log n) cost in the worst case. As pointed out by Olivie, there is an intersting many-to-one correspondence between -balanced trees ( = =2) and symmetric binary B-trees, or SBB-trees [3], such that each SBB-tree corresponds to one =2-balanced tree and each =2-balanced tree corresponds to a number of SBB-trees. In the same way the generalized symmetric binary B-trees, or SBB(k)-trees [2], satises the balance criterion of -balanced trees. Thus, using the algorithms for SBB(k)-trees ecient algorithms for =2 < can be formulated []. However, in this case the tree is actually not viewed as -balanced, and a tree which satises the -balance criterion may require restructuring in order to satisfy the SBB(k)-criterion. In this paper we analyze the behaviour of BB-trees when maintained by partial rebuilding. The method of partial rebuilding was introduced by Overmars and van Leeuwen [3] and it is a simple method to maintain balanced tree structures. The idea behind the method is brutal but powerful; each time a given balance criterion is violated at a node v the subtree rooted at v is rebuilt to achieve perfect balance. The simplicity of the method makes it useful in situations where local restructuring operations, such as rotations, does not work. Such a case occurs when maintaining k-d-trees [4]. A scheme for partial rebuilding of weight-balanced trees [8] with logarithmic amortized bounds was rst introduced by Overmars and van Leeuwen [2, 3]. They showed that the low amortized cost for maintaining such trees, O(log n) per 2 (3)
3 update, is due to the large number of updates required to make an initially well-balanced subtree become unbalanced. Other classes of trees maintained by partial rebuilding can be found in []. Making a careful analysis, we show that a straight-forward use of partial rebuilding for maintenance of -balanced trees requires an amortized cost of ( p n). Thus, the cost per update for this class of trees is not competitive to the cost for weight-balanced trees. However, the amortized cost when making only insertions is O(log n) for any value of. This fact may be used to apply the method of weak deletions on -balanced trees, resulting in an amortized cost of O(log n) per update. Thus, we have shown that there exist ecient algorithms for =2 < <, solving a problem left open by Olivie. 2 Terminology We assume that a binary search tree contains one element in each internal node and that the leaves are empty. The height of a tree T equals the number of edges on the longest path dow the tree and it is denoted h(t ). By the weight of T, denoted jt j, we mean the number of leaves in the tree. Observe that n elements are stored in a tree of weight n +. Since we do not distinguish between nodes and subtrees, the subtree v refers to the subtree rooted at the node v in T. The height and weight of v are denoted h(v) and jvj, respectively. The number of insertions and deletions made in the subtree v since the last time v was involved in a rebuilding are denoted in and del(v), respectively, and the total number of updates (deletions and insertions) is denoted upd(v). In order to measure changes in height, weight, and number of updates in a subtree, we denote the subtree v immediately after the latest time it was rebuilt as v o. The notation h(v o ), jv o j and so forth follows from above. In our analysis we assume that rebuilding of a subtree v takes linear time, examples of linear algorithms for balancing trees are found in [5, 6, 7, 4]. 3 Analysis of Partial Rebuilding The analysis of -balanced trees maintained by partial rebuilding is somewhat more complicated than the analysis of weight-balanced trees. Our analysis of the update cost is based on a computation of how many updates are required to make an initially well-balanced tree become out of balance. 3
4 In Lemmas we give a relation between the height and weight of a subtree. This relation is used in Lemma 2 to analyze the number of insertions required to increase the height of the tree by a certain amount. In a similar way the number of deletions required to decrease the length of the shortest path is given in Lemmas 3 and 4. Using these results we calculate the number of updates required to make a node unbalanced in Lemma 5. Finally, in Theorem we show that the maintenance cost for -balanced trees when maintained by partial rebuilding is (sqrtn) per update. Lemma For any possible value of h(v) there is a node v which satises the balance criterion of an -balanced tree such that Proof: by jvj 2(h(v)+)? From Denition () follows that the smallest value of is given (4) = dh(v)e (5) Let p denote the smallest child v may have. We have that If p has its smallest weight, then s(p) =? (6) jpj = 2 s(p) = 2? = 2 dh(v)?e (7) We get the minimal value of jvj by adding the weights of the smallest possible subtrees on a path down to a leaf. If we choose the longest path we get X h(v) jvj = + h(v) X i=0 i= 2 i 2 di?e = 2(h(v)+)? The constant is added since addition of the weights of subtrees along a path down a binary tree will leave one of the leaves uncounted. The proof follows from equation (8). 2 (8) 4
5 Lemma 2 Let T o be a perfectly balanced binary tree. Then the smallest number of insertions required to increase the height of T o by h is given by ins(t ) < 2 h+?? (9) Proof: In order to increase the height of T by h using a minimal number of insertions we add nodes to a subtree v to achieve h(v) = h(v o ) + h (0) We choose v as the smallest possible subtree in T with a height which may be increased by h without increasing the length of its shortest path. Without loss of generality we assume that v o is a complete binary tree, which implies that s(v o ) = h(v o ) = = dh(v)e () and Together with Lemma this gives that in = jvj? jv o j jv o j = 2 dh(v)e 2 h(v) (2) 2(h(v)+)?? 2 h(v) 2 (h(v)+)?? 2 (h(v)+) + 2 h(v) = = 2h(v)? Since the weight of v is at a minimum we have that (3) h(v)? h = = dh(v)e < h(v) + (4) which implies that From Eqs. (3) and (5) follows that h(v) < h +? in < 2 h+?? (5) (6) 5
6 which completes the proof. 2 The number of deletions required to decrease the height of a node is given in Lemmas 3-4 below. The computations are similar (but not identical) to the computations used in the proofs of Lemmas - 2 above. Lemma 3 Let v be a node in an -balanced tree. Then it is possible that X jvj > + i= 2 i=?2 = 4 2(+)=? 2 =? (7) Proof: From Denition () follows that the largest possible value of h(v) is given by h(v) = >? (8) Let p denote the largest child v may have. We have that If p is as large as possible then Together with Denition () this gives that h(p) = h(v)? (9) jpj = 2 h(p) = 2 h(v)? (20) jpj = 2 h(v)? > 2 b=c?2 (2) We get the maximal value of jvj by adding the weights of the largest possible subtrees on a path down to a leaf. If we choose the shortest path we get X jvj > + i= 2 i=?2 = 4 2(+)=? 2 =? (22) which completes the proof. 2 Lemma 4 Let T o be a perfectly balanced binary tree. Then the smallest number of deletions to decrease the shortest path of T o by s is given by del(t ) (3 < 2=? 4) 2 s+? (2 =? ) 4 + O() (23) 6
7 Proof: In order to decrease the shortest path of T by s using a minimal number of deletions we remove nodes from a subtree v to achieve = s(v o )? s (24) We choose v to be the smallest possible subtree in T in which the shortest path may be decreased by s without decreasing its height. Without loss of generality we assume that v is a complete binary tree, which implies that h(v o ) = s(v o ) = h(v) = (25) and This together with Lemma 3 gives that del(v) = jv o j? jvj jv o j = 2 b=c 2 = (26) 2 =? 4 2(+)=? 2 =?? 4 < 4 2(+)=? 4 2 =? 2 (+)= + (2 =? ) 4 = 3 2(+)=? 4 2 = (2 =? ) 4 = (3 2=? 4) 2 = (2 =? ) 4 Since v has maximal weight we have that + s = h(v) = =? 2 =? (27) >? (28) which implies that < s +? (29) From Eqs. (27) and (29) follows del(v) < (3 2=? 4) 2 = (2 =? ) =? (3 < 2=? 4) 2 s+? + (2 =? ) 4 2 =? (30) which completes the proof. 2 7
8 Lemma 5 In order to violate the balance criterion at a node v in an BBtree, O( p jvj) updates are sucient. Proof: Without loss of generality we may assume that v o is a complete binary tree. We make insertions to change the shape of v in a way that and deletions to achieve h(v) =? 2 h(v o) (3) =? h(v o ) + (32) 2 These updates cause a violation of the balance criterion at v since h(v) = h(v o)? h(v o ) + (h(v) = h(v o)?? 2 h(v o) h(v o ) +? 2 h(v o) = ( + )h(v o)? 2 ( + )h(v o ) < (33) The number of updates to achieve this violation is given by upd(v) = in + del(v) < 2 h(v)+??? = 2 2 h(vo)+?? = 2(h(vo)+)=2? + (3 2=? 4) 2 +? (2 =? ) 4 + O()? + (3 2 h(vo)++ 2=? 4) 2? (2 =? ) 4 + (3 2=? 4) 2 (h(vo)+2)=2 (2 =? ) 4 = O(2 h(vo)=2 ) + O(2 h(vo)=2 ) + O() = O( = O( q q jv o j) + O() + O() jvj) (34) which completes the proof. 2 8
9 Theorem Maintaining an -balanced tree by partial rebuilding results in an amortized cost of ( p n) per update. Proof: From Lemma 5 follows that we can force a rebuilding of the entire tree after every ( p n)th update. This gives an amortized cost of ( p n) per update, which completes the proof. 2 Thus, we conclude that a straight-forward implementation of partial rebuilding does not lead to ecient maintenance algorithms for -balanced trees. 4 Weak Deletions The result of Theorem does not allow us to maintain an -balanced tree eciently by partial rebuilding. Fortunately, a better complexity may be obtained by a modication of the maintenance algorithms. We can show that when only insertions are made the tree can be maintained by partial rebuilding at a logarithmic amortized cost. Together with a dierent strategy for deletion we can exploit this fact to obtain a logarithmic amortized bound for updates. Lemma 6 Let v be a node in an -balanced tree. Then jvj 2 2(h(v)+)? (35) Proof: The proof is similar to the proof of Lemma. The smallest possible weight of v is given by X h(v) jvj = + X i= h(v) 2 i? i=0 2 di?e = 2 2(h(v)+)? (36) which completes the proof. 2 9
10 Lemma 7 Let v be a node in an -balanced tree where no deletions are made. When v has become out of balance, the following is true: in > (2?? )jvj + O() (37) Proof: When v is out of balance h(v) < (38) Without loss of generality we may assume that v o tree. This implies that was a complete binary which implies that This together with Lemma 6 gives that This gives that in = jvj? jv o j h(v o ) = s(v o ) < < h(v) (39) jv o j < 2 h(v) (40) jv o j jv + 2? j < 2h(v) 2? = (? jv oj jvj )jvj = (? jv o j jvj + 2? > (? (2? 2? )) 2 2(h(v)+) = 2? 2? (4) )jvj + O() jvj + + O() = (2?? )jvj + O() (42) which completes the proof. 2 Lemma 8 An -balanced tree in which no deletions are made can be maintained by partial rebuilding at an amortized cost of O(log n) per insertion. 0
11 Proof: From Lemma 7 we know that (jvj) insertions are required to make a node v become unbalanced. Thus, the amortized cost per insertion below v is O(). Since each insertion is made below O(log n) nodes, the total amortized cost per update is O(log n). 2 Given the result of Lemma 8 we can use the method of global rebuilding and weak deletions [2] to maintain a set in an BB-tree during both insertion and deletion, for any value of, 0 < <. The idea is simple: Making deletions by marking the element as deleted instead of removing it, we can perform (n) deletions in the tree while the height of the tree is still logarithmic. After (n) deletions the entire tree is rebuilt and deleted elements are removed. The amortized cost of this global rebuilding is O() per update. Theorem 2 For 0 < < an ordered set may be maintained in an - balanced tree at an amortized cost of O(log n) per update. Proof: For each node in the tree we add a boolean variable, telling whether the stored element is present or deleted. We maintain the set by the following algorithm: Insertion: If the element is found in the tree we mark it as present. Otherwise we insert a new node. Whenever the balance criterion becomes violated at a node, we make a partial rebuilding there. Deletion: We mark the element as deleted. When n deletions have been 2 made, we remove all elements marked as deleted and rebuild the entire tree to perfect balance. Although the weight of the tree is larger than n +, it still have a height of O(log n), since the number of deleted elements is at most n 2. The logarithmic amortized cost for insertion follows from Lemma 8 and the logarithmic amortized cost for deletion follows from the fact that rebuilding is made only when (n) deletions have been made A Modied Shape To keep deleted elements left in the tree may seem like an unnecessary waste of space. This problem may be circumvented by introducing yet another strategy for deletion. Instead of marking an element as deleted, we remove it.
12 In order to avoid rebuildings generated by deletions we just omit updating the balance information (i.e. the value of ) during a deletion. The skewness caused by this method is taken care of by rebuilding the entire tree when (n) deletions have been made. This tree is simpler and more natural to implement than the one described in Theorem 2 above. However, due to the fact that the balance information is not updated during deletions, the tree may contain nodes which violate the balance criterion. Therefore, the tree is not strictly -balanced and we say that we have a modied version of -balanced trees. In spite of those violations the height of the tree remains logarithmic, although it might be slightly larger than the height of the original BB-tree. Theorem 3 A modied -balanced tree can be maintained at an amortized cost of O(log n) per update without keeping deleted elements in the tree. Proof: We modify the tree in the following way: The stored value of is only changed when the node v is involved in a rebuilding. The entire tree is rebuilt after every n 2 deletions. The logarithmic height is guaranteed by the periodic rebuilding and the fact that a deletion can not increase the height of the tree. From the fact that the stored values of are only changed during a rebuilding follows that the number of insertions between two rebuildings of a subtree is the same as if no deletions were made. Thus, from Lemma 8 we know that the cost per insertion is O(log n). The logarithmic amortized cost for deletion follows from the fact that rebuilding is made only when (n) deletions have been made. 2 5 Conclusions Contrary to the analysis of weight balanced trees [2, 3], the analysis of balanced trees maintained by partial rebuilding is nontrivial. The fact that the amortized cost is ( p n) is not intuitively clear. By improving the cost to O(log n) we have presented simple and ecient maintenance algorithms that can be used for an arbitrary value of 2
13 ; 0 < <. The fact that we use partial rebuilding implies that the - balance criterion may be used to maintain tree structures where local restructuring does not work, such as k-d-trees. References [] A. Andersson. Improving partial rebuilding by using simple balance criteria. In Proc. Workshop on Algorithms and Data Structures, Springer Verlag, pages 393{402, 989. [2] A. Andersson, Ch. Icking, R. Klein, and Th. Ottmann. Binary search trees of almost optimal height. Acta Informatica, 28:65{78, 990. [3] R. Bayer. Symmetric binary B-trees: Data structure and maintenance algorithms. Acta Informatica, (4):290{306, 972. [4] J. L. Bentley. Multidimensional binary search trees used for associative searching. Communications of the ACM, 8(9):509{57, 975. [5] H. Chang and S. S. Iynegar. Ecient algorithms to globally balance a binary search tree. Communications of the ACM, 27(7):695{702, 984. [6] A. C. Day. Balancing a binary tree. Computer Journal, 9(4):360{36, 976. [7] W. A. Martin and D. N. Ness. Optimizing binary trees grown with a sorting algorithm. Communications of the ACM, 5(2):88{93, 972. [8] J. Nievergelt and E. M. Reingold. Binary trees of bounded balance. SIAM Journal on Computing, 2():33{43, 973. [9] H. J. Olivie. A Study of Balanced Binary Trees and Balanced One- Two-Trees. Ph.D. Thesis, Dept of Mathematics, University of Antwerp, 980. [0] H. J. Olivie. A new class of balanced search trees: Half-balanced binary search trees. R. A. I. R. O. Informatique Theoretique, 6:5{7, 982. [] Th. Ottmann and D. Wood. Updating binary trees with constant linkage cost. In Proc. Scandinavian Workshop on Algorithm Theory,
14 [2] M. H. Overmars. The Design of Dynamic Data Structures, volume 56 of Lecture Notes in Computer Science. Springer Verlag, 983. ISBN X. [3] M. H. Overmars and J. van Leeuwen. Dynamic multi-dimensional data structures based on quad- and k-d trees. Acta Informatica, 7:267{285, 982. [4] Q. F. Stout and B. L. Warren. Tree rebalancing in optimal time and space. Communications of the ACM, 29(9):902{908,
Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of C
 Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of California, San Diego CA 92093{0114, USA Abstract. We
Optimum Alphabetic Binary Trees T. C. Hu and J. D. Morgenthaler Department of Computer Science and Engineering, School of Engineering, University of California, San Diego CA 92093{0114, USA Abstract. We
A Simple Balanced Search Tree. Rudolf Fleischer 2. ABSTRACT In this paper we showhowaslight modication of (a b)-trees allows us
 A Simple Balanced Search Tree With O(1) Worst-Case Update Time 1 by Rudolf Fleischer 2 ABSTRACT In this paper we showhowaslight modication of (a b)-trees allows us to perform member and neighbor queries
A Simple Balanced Search Tree With O(1) Worst-Case Update Time 1 by Rudolf Fleischer 2 ABSTRACT In this paper we showhowaslight modication of (a b)-trees allows us to perform member and neighbor queries
Abstract Relaxed balancing of search trees was introduced with the aim of speeding up the updates and allowing a high degree of concurrency. In a rela
 Chromatic Search Trees Revisited Institut fur Informatik Report 9 Sabine Hanke Institut fur Informatik, Universitat Freiburg Am Flughafen 7, 79 Freiburg, Germany Email: hanke@informatik.uni-freiburg.de.
Chromatic Search Trees Revisited Institut fur Informatik Report 9 Sabine Hanke Institut fur Informatik, Universitat Freiburg Am Flughafen 7, 79 Freiburg, Germany Email: hanke@informatik.uni-freiburg.de.
Deterministic Jumplists
 Nordic Journal of Computing Deterministic Jumplists Amr Elmasry Department of Computer Engineering and Systems Alexandria University, Egypt elmasry@alexeng.edu.eg Abstract. We give a deterministic version
Nordic Journal of Computing Deterministic Jumplists Amr Elmasry Department of Computer Engineering and Systems Alexandria University, Egypt elmasry@alexeng.edu.eg Abstract. We give a deterministic version
Finger Search Trees with Constant. Insertion Time. Gerth Stlting Brodal. Max-Planck-Institut fur Informatik. Im Stadtwald. D Saarbrucken
 Finger Search Trees with Constant Insertion Time Gerth Stlting Brodal Max-Planck-Institut fur Informatik Im Stadtwald D-66123 Saarbrucken Germany Email: brodal@mpi-sb.mpg.de September 26, 1997 Abstract
Finger Search Trees with Constant Insertion Time Gerth Stlting Brodal Max-Planck-Institut fur Informatik Im Stadtwald D-66123 Saarbrucken Germany Email: brodal@mpi-sb.mpg.de September 26, 1997 Abstract
Finger Search Trees with Constant Insertion Time. Gerth Stlting Brodal. Max-Planck-Institut fur Informatik. Im Stadtwald, D Saarbrucken, Germany
 Finger Search Trees with Constant Insertion Time Gerth Stlting Brodal Max-Planck-Institut fur Informatik Im Stadtwald, D-66123 Saarbrucken, Germany Abstract We consider the problem of implementing nger
Finger Search Trees with Constant Insertion Time Gerth Stlting Brodal Max-Planck-Institut fur Informatik Im Stadtwald, D-66123 Saarbrucken, Germany Abstract We consider the problem of implementing nger
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Binary Search Tree Balancing Methods: A Critical Study
 IJCSNS International Journal of Computer Science and Network Security, VOL.7 No.8, August 2007 237 Binary Search Tree Balancing Methods: A Critical Study Suri Pushpa 1, Prasad Vinod 2 1 Dept. of Computer
IJCSNS International Journal of Computer Science and Network Security, VOL.7 No.8, August 2007 237 Binary Search Tree Balancing Methods: A Critical Study Suri Pushpa 1, Prasad Vinod 2 1 Dept. of Computer
Part 2: Balanced Trees
 Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
A technique for adding range restrictions to. August 30, Abstract. In a generalized searching problem, a set S of n colored geometric objects
 A technique for adding range restrictions to generalized searching problems Prosenjit Gupta Ravi Janardan y Michiel Smid z August 30, 1996 Abstract In a generalized searching problem, a set S of n colored
A technique for adding range restrictions to generalized searching problems Prosenjit Gupta Ravi Janardan y Michiel Smid z August 30, 1996 Abstract In a generalized searching problem, a set S of n colored
Lecture Notes: External Interval Tree. 1 External Interval Tree The Static Version
 Lecture Notes: External Interval Tree Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk This lecture discusses the stabbing problem. Let I be
Lecture Notes: External Interval Tree Yufei Tao Department of Computer Science and Engineering Chinese University of Hong Kong taoyf@cse.cuhk.edu.hk This lecture discusses the stabbing problem. Let I be
Deletion Without Rebalancing in Multiway Search Trees
 Deletion Without Rebalancing in Multiway Search Trees Siddhartha Sen 1,3 and Robert E. Tarjan 1,2,3 1 Princeton University, {sssix,ret}@cs.princeton.edu 2 HP Laboratories, Palo Alto CA 94304 Abstract.
Deletion Without Rebalancing in Multiway Search Trees Siddhartha Sen 1,3 and Robert E. Tarjan 1,2,3 1 Princeton University, {sssix,ret}@cs.princeton.edu 2 HP Laboratories, Palo Alto CA 94304 Abstract.
On the other hand, the main disadvantage of the amortized approach is that it cannot be applied in real-time programs, where the worst-case bound on t
 Randomized Meldable Priority Queues Anna Gambin and Adam Malinowski Instytut Informatyki, Uniwersytet Warszawski, Banacha 2, Warszawa 02-097, Poland, faniag,amalg@mimuw.edu.pl Abstract. We present a practical
Randomized Meldable Priority Queues Anna Gambin and Adam Malinowski Instytut Informatyki, Uniwersytet Warszawski, Banacha 2, Warszawa 02-097, Poland, faniag,amalg@mimuw.edu.pl Abstract. We present a practical
Computing intersections in a set of line segments: the Bentley-Ottmann algorithm
 Computing intersections in a set of line segments: the Bentley-Ottmann algorithm Michiel Smid October 14, 2003 1 Introduction In these notes, we introduce a powerful technique for solving geometric problems.
Computing intersections in a set of line segments: the Bentley-Ottmann algorithm Michiel Smid October 14, 2003 1 Introduction In these notes, we introduce a powerful technique for solving geometric problems.
Fused Trees: Simple BST balancing method by partial & scheduled rebuilds
 Fused Trees: Simple BST balancing method by partial & scheduled rebuilds Tae Woo Kim Department of Computer Science Yonsei University, Korea travis829@yonsei.ac.r Abstract This paper proposes a simple
Fused Trees: Simple BST balancing method by partial & scheduled rebuilds Tae Woo Kim Department of Computer Science Yonsei University, Korea travis829@yonsei.ac.r Abstract This paper proposes a simple
l Heaps very popular abstract data structure, where each object has a key value (the priority), and the operations are:
 DDS-Heaps 1 Heaps - basics l Heaps very popular abstract data structure, where each object has a key value (the priority), and the operations are: l insert an object, find the object of minimum key (find
DDS-Heaps 1 Heaps - basics l Heaps very popular abstract data structure, where each object has a key value (the priority), and the operations are: l insert an object, find the object of minimum key (find
B-Trees with Relaxed Balance. Kim S. Larsen and Rolf Fagerberg. Department of Mathematics and Computer Science, Odense University
 B-Trees with Relaxed Balance Kim S. Larsen and Rolf Fagerberg Department of Mathematics and Computer Science, Odense University Campusvej 55, DK-53 Odense M, Denmark Abstract B-trees with relaxed balance
B-Trees with Relaxed Balance Kim S. Larsen and Rolf Fagerberg Department of Mathematics and Computer Science, Odense University Campusvej 55, DK-53 Odense M, Denmark Abstract B-trees with relaxed balance
Lecture 6: External Interval Tree (Part II) 3 Making the external interval tree dynamic. 3.1 Dynamizing an underflow structure
 Lecture 6: External Interval Tree (Part II) Yufei Tao Division of Web Science and Technology Korea Advanced Institute of Science and Technology taoyf@cse.cuhk.edu.hk 3 Making the external interval tree
Lecture 6: External Interval Tree (Part II) Yufei Tao Division of Web Science and Technology Korea Advanced Institute of Science and Technology taoyf@cse.cuhk.edu.hk 3 Making the external interval tree
3 Competitive Dynamic BSTs (January 31 and February 2)
 3 Competitive Dynamic BSTs (January 31 and February ) In their original paper on splay trees [3], Danny Sleator and Bob Tarjan conjectured that the cost of sequence of searches in a splay tree is within
3 Competitive Dynamic BSTs (January 31 and February ) In their original paper on splay trees [3], Danny Sleator and Bob Tarjan conjectured that the cost of sequence of searches in a splay tree is within
l So unlike the search trees, there are neither arbitrary find operations nor arbitrary delete operations possible.
 DDS-Heaps 1 Heaps - basics l Heaps an abstract structure where each object has a key value (the priority), and the operations are: insert an object, find the object of minimum key (find min), and delete
DDS-Heaps 1 Heaps - basics l Heaps an abstract structure where each object has a key value (the priority), and the operations are: insert an object, find the object of minimum key (find min), and delete
Red-black tree. Background and terminology. Uses and advantages
 Red-black tree A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically used to implement associative arrays. The original structure was invented
Red-black tree A red-black tree is a type of self-balancing binary search tree, a data structure used in computer science, typically used to implement associative arrays. The original structure was invented
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
On k-dimensional Balanced Binary Trees*
 journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
journal of computer and system sciences 52, 328348 (1996) article no. 0025 On k-dimensional Balanced Binary Trees* Vijay K. Vaishnavi Department of Computer Information Systems, Georgia State University,
A SIMPLE APPROXIMATION ALGORITHM FOR NONOVERLAPPING LOCAL ALIGNMENTS (WEIGHTED INDEPENDENT SETS OF AXIS PARALLEL RECTANGLES)
 Chapter 1 A SIMPLE APPROXIMATION ALGORITHM FOR NONOVERLAPPING LOCAL ALIGNMENTS (WEIGHTED INDEPENDENT SETS OF AXIS PARALLEL RECTANGLES) Piotr Berman Department of Computer Science & Engineering Pennsylvania
Chapter 1 A SIMPLE APPROXIMATION ALGORITHM FOR NONOVERLAPPING LOCAL ALIGNMENTS (WEIGHTED INDEPENDENT SETS OF AXIS PARALLEL RECTANGLES) Piotr Berman Department of Computer Science & Engineering Pennsylvania
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance
 Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI-33101 Tampere,
Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI-33101 Tampere,
AVL Trees. Version of September 6, AVL Trees Version of September 6, / 22
 VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
Data Structures Lesson 7
 Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
(mainly range and proximity queries), and simplicity. See recent surveys [2, 14, 27]. The proposed data structures can roughly be divided into two cla
![(mainly range and proximity queries), and simplicity. See recent surveys [2, 14, 27]. The proposed data structures can roughly be divided into two cla (mainly range and proximity queries), and simplicity. See recent surveys [2, 14, 27]. The proposed data structures can roughly be divided into two cla](/thumbs/72/67885950.jpg) A Framework for Index Bulk Loading and Dynamization Pankaj K. Agarwal?, Lars Arge??, Octavian Procopiuc???, and Jerey Scott Vitter y Center for Geometric Computing, Dept. of Computer Science, Duke University,
A Framework for Index Bulk Loading and Dynamization Pankaj K. Agarwal?, Lars Arge??, Octavian Procopiuc???, and Jerey Scott Vitter y Center for Geometric Computing, Dept. of Computer Science, Duke University,
r (1,1) r (2,4) r (2,5) r(2,6) r (1,3) r (1,2)
 Routing on Trees via Matchings? Alan Roberts 1, Antonis Symvonis 1 and Louxin Zhang 2 1 Department of Computer Science, University of Sydney, N.S.W. 2006, Australia 2 Department of Computer Science, University
Routing on Trees via Matchings? Alan Roberts 1, Antonis Symvonis 1 and Louxin Zhang 2 1 Department of Computer Science, University of Sydney, N.S.W. 2006, Australia 2 Department of Computer Science, University
Planar Point Location
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
CS350: Data Structures AVL Trees
 S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
DDS Dynamic Search Trees
 DDS Dynamic Search Trees 1 Data structures l A data structure models some abstract object. It implements a number of operations on this object, which usually can be classified into l creation and deletion
DDS Dynamic Search Trees 1 Data structures l A data structure models some abstract object. It implements a number of operations on this object, which usually can be classified into l creation and deletion
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Lecture 3 February 9, 2010
 6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
II (Sorting and) Order Statistics
 II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
II (Sorting and) Order Statistics Heapsort Quicksort Sorting in Linear Time Medians and Order Statistics 8 Sorting in Linear Time The sorting algorithms introduced thus far are comparison sorts Any comparison
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
A SIMPLE BALANCED SEARCH TREE WITH O(1) WORST-CASE UPDATE TIME
 International Journal of Foundations of Computer Science c World Scientific Publishing Company A SIMPLE BALANCED SEARCH TREE WITH O(1) WORST-CASE UPDATE TIME RUDOLF FLEISCHER Max-Planck-Institut für Informatik
International Journal of Foundations of Computer Science c World Scientific Publishing Company A SIMPLE BALANCED SEARCH TREE WITH O(1) WORST-CASE UPDATE TIME RUDOLF FLEISCHER Max-Planck-Institut für Informatik
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
T consists of finding an efficient implementation of access,
 968 IEEE TRANSACTIONS ON COMPUTERS, VOL. 38, NO. 7, JULY 1989 Multidimensional Balanced Binary Trees VIJAY K. VAISHNAVI A bstract-a new balanced multidimensional tree structure called a k-dimensional balanced
968 IEEE TRANSACTIONS ON COMPUTERS, VOL. 38, NO. 7, JULY 1989 Multidimensional Balanced Binary Trees VIJAY K. VAISHNAVI A bstract-a new balanced multidimensional tree structure called a k-dimensional balanced
1 Static-to-Dynamic Transformations
 You re older than you ve ever been and now you re even older And now you re even older And now you re even older You re older than you ve ever been and now you re even older And now you re older still
You re older than you ve ever been and now you re even older And now you re even older And now you re even older You re older than you ve ever been and now you re even older And now you re older still
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
time using O( n log n ) processors on the EREW PRAM. Thus, our algorithm improves on the previous results, either in time complexity or in the model o
 Reconstructing a Binary Tree from its Traversals in Doubly-Logarithmic CREW Time Stephan Olariu Michael Overstreet Department of Computer Science, Old Dominion University, Norfolk, VA 23529 Zhaofang Wen
Reconstructing a Binary Tree from its Traversals in Doubly-Logarithmic CREW Time Stephan Olariu Michael Overstreet Department of Computer Science, Old Dominion University, Norfolk, VA 23529 Zhaofang Wen
Fundamental Algorithms
 WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
The problem of minimizing the elimination tree height for general graphs is N P-hard. However, there exist classes of graphs for which the problem can
 A Simple Cubic Algorithm for Computing Minimum Height Elimination Trees for Interval Graphs Bengt Aspvall, Pinar Heggernes, Jan Arne Telle Department of Informatics, University of Bergen N{5020 Bergen,
A Simple Cubic Algorithm for Computing Minimum Height Elimination Trees for Interval Graphs Bengt Aspvall, Pinar Heggernes, Jan Arne Telle Department of Informatics, University of Bergen N{5020 Bergen,
Using the Holey Brick Tree for Spatial Data. in General Purpose DBMSs. Northeastern University
 Using the Holey Brick Tree for Spatial Data in General Purpose DBMSs Georgios Evangelidis Betty Salzberg College of Computer Science Northeastern University Boston, MA 02115-5096 1 Introduction There is
Using the Holey Brick Tree for Spatial Data in General Purpose DBMSs Georgios Evangelidis Betty Salzberg College of Computer Science Northeastern University Boston, MA 02115-5096 1 Introduction There is
ICS 691: Advanced Data Structures Spring Lecture 3
 ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
Lecture 21: Red-Black Trees
 15-150 Lecture 21: Red-Black Trees Lecture by Dan Licata April 3, 2012 Last time, we talked about the signature for dictionaries: signature ORDERED = sig type t val compare : t * t -> order signature DICT
15-150 Lecture 21: Red-Black Trees Lecture by Dan Licata April 3, 2012 Last time, we talked about the signature for dictionaries: signature ORDERED = sig type t val compare : t * t -> order signature DICT
Priority Queues. Meld(Q 1,Q 2 ) merge two sets
 Priority Queues MakeQueue Insert(Q,k,p) Delete(Q,k) DeleteMin(Q) Meld(Q 1,Q 2 ) Empty(Q) Size(Q) FindMin(Q) create new empty queue insert key k with priority p delete key k (given a pointer) delete key
Priority Queues MakeQueue Insert(Q,k,p) Delete(Q,k) DeleteMin(Q) Meld(Q 1,Q 2 ) Empty(Q) Size(Q) FindMin(Q) create new empty queue insert key k with priority p delete key k (given a pointer) delete key
A Fast Algorithm for Optimal Alignment between Similar Ordered Trees
 Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
Fundamenta Informaticae 56 (2003) 105 120 105 IOS Press A Fast Algorithm for Optimal Alignment between Similar Ordered Trees Jesper Jansson Department of Computer Science Lund University, Box 118 SE-221
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
arxiv: v2 [cs.ds] 9 Apr 2009
![arxiv: v2 [cs.ds] 9 Apr 2009 arxiv: v2 [cs.ds] 9 Apr 2009](/thumbs/72/66843812.jpg) Pairing Heaps with Costless Meld arxiv:09034130v2 [csds] 9 Apr 2009 Amr Elmasry Max-Planck Institut für Informatik Saarbrücken, Germany elmasry@mpi-infmpgde Abstract Improving the structure and analysis
Pairing Heaps with Costless Meld arxiv:09034130v2 [csds] 9 Apr 2009 Amr Elmasry Max-Planck Institut für Informatik Saarbrücken, Germany elmasry@mpi-infmpgde Abstract Improving the structure and analysis
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
Rank-Pairing Heaps. Bernard Haeupler Siddhartha Sen Robert E. Tarjan. SIAM JOURNAL ON COMPUTING Vol. 40, No. 6 (2011), pp.
 Rank-Pairing Heaps Bernard Haeupler Siddhartha Sen Robert E. Tarjan Presentation by Alexander Pokluda Cheriton School of Computer Science, University of Waterloo, Canada SIAM JOURNAL ON COMPUTING Vol.
Rank-Pairing Heaps Bernard Haeupler Siddhartha Sen Robert E. Tarjan Presentation by Alexander Pokluda Cheriton School of Computer Science, University of Waterloo, Canada SIAM JOURNAL ON COMPUTING Vol.
CSE100. Advanced Data Structures. Lecture 8. (Based on Paul Kube course materials)
 CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
6 Distributed data management I Hashing
 6 Distributed data management I Hashing There are two major approaches for the management of data in distributed systems: hashing and caching. The hashing approach tries to minimize the use of communication
6 Distributed data management I Hashing There are two major approaches for the management of data in distributed systems: hashing and caching. The hashing approach tries to minimize the use of communication
would be included in is small: to be exact. Thus with probability1, the same partition n+1 n+1 would be produced regardless of whether p is in the inp
 1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
Lecture 3 February 23, 2012
 6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 3 February 23, 2012 1 Overview In the last lecture we saw the concepts of persistence and retroactivity as well as several data structures
6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 3 February 23, 2012 1 Overview In the last lecture we saw the concepts of persistence and retroactivity as well as several data structures
ISA[k] Trees: a Class of Binary Search Trees with Minimal or Near Minimal Internal Path Length
![ISA[k] Trees: a Class of Binary Search Trees with Minimal or Near Minimal Internal Path Length ISA[k] Trees: a Class of Binary Search Trees with Minimal or Near Minimal Internal Path Length](/thumbs/80/82269246.jpg) SOFTWARE PRACTICE AND EXPERIENCE, VOL. 23(11), 1267 1283 (NOVEMBER 1993) ISA[k] Trees: a Class of Binary Search Trees with Minimal or Near Minimal Internal Path Length faris n. abuali and roger l. wainwright
SOFTWARE PRACTICE AND EXPERIENCE, VOL. 23(11), 1267 1283 (NOVEMBER 1993) ISA[k] Trees: a Class of Binary Search Trees with Minimal or Near Minimal Internal Path Length faris n. abuali and roger l. wainwright
ECE250: Algorithms and Data Structures AVL Trees (Part A)
 ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
Introduction to Machine Learning Lecture 4. Mehryar Mohri Courant Institute and Google Research
 Introduction to Machine Learning Lecture 4 Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Nearest-Neighbor Algorithms Nearest Neighbor Algorithms Definition: fix k 1, given a labeled
Introduction to Machine Learning Lecture 4 Mehryar Mohri Courant Institute and Google Research mohri@cims.nyu.edu Nearest-Neighbor Algorithms Nearest Neighbor Algorithms Definition: fix k 1, given a labeled
Heap-on-Top Priority Queues. March Abstract. We introduce the heap-on-top (hot) priority queue data structure that combines the
 Heap-on-Top Priority Queues Boris V. Cherkassky Central Economics and Mathematics Institute Krasikova St. 32 117418, Moscow, Russia cher@cemi.msk.su Andrew V. Goldberg NEC Research Institute 4 Independence
Heap-on-Top Priority Queues Boris V. Cherkassky Central Economics and Mathematics Institute Krasikova St. 32 117418, Moscow, Russia cher@cemi.msk.su Andrew V. Goldberg NEC Research Institute 4 Independence
Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1
 CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CME 305: Discrete Mathematics and Algorithms Instructor: Professor Aaron Sidford (sidford@stanford.edu) January 11, 2018 Lecture 2 - Graph Theory Fundamentals - Reachability and Exploration 1 In this lecture
CS350: Data Structures B-Trees
 B-Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Introduction All of the data structures that we ve looked at thus far have been memory-based
B-Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Introduction All of the data structures that we ve looked at thus far have been memory-based
A New Approach to the Dynamic Maintenance of Maximal Points in a Plane*
 Discrete Comput Geom 5:365-374 (1990) 1990 Springer-Verlag New York~Inc.~ A New Approach to the Dynamic Maintenance of Maximal Points in a Plane* Greg N. Frederickson and Susan Rodger Department of Computer
Discrete Comput Geom 5:365-374 (1990) 1990 Springer-Verlag New York~Inc.~ A New Approach to the Dynamic Maintenance of Maximal Points in a Plane* Greg N. Frederickson and Susan Rodger Department of Computer
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
ADAPTIVE SORTING WITH AVL TREES
 ADAPTIVE SORTING WITH AVL TREES Amr Elmasry Computer Science Department Alexandria University Alexandria, Egypt elmasry@alexeng.edu.eg Abstract A new adaptive sorting algorithm is introduced. The new implementation
ADAPTIVE SORTING WITH AVL TREES Amr Elmasry Computer Science Department Alexandria University Alexandria, Egypt elmasry@alexeng.edu.eg Abstract A new adaptive sorting algorithm is introduced. The new implementation
University of Alberta
 University of Alberta Asymmetry in Binary Search Tree Update Algorithms by Joseph Culberson and Patricia A. Evans Technical Report TR 9{09 May 199 DEPARTMENT OF COMPUTING SCIENCE The University of Alberta
University of Alberta Asymmetry in Binary Search Tree Update Algorithms by Joseph Culberson and Patricia A. Evans Technical Report TR 9{09 May 199 DEPARTMENT OF COMPUTING SCIENCE The University of Alberta
Search Trees (Ch. 9) > = Binary Search Trees 1
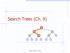 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Localization in Graphs. Richardson, TX Azriel Rosenfeld. Center for Automation Research. College Park, MD
 CAR-TR-728 CS-TR-3326 UMIACS-TR-94-92 Samir Khuller Department of Computer Science Institute for Advanced Computer Studies University of Maryland College Park, MD 20742-3255 Localization in Graphs Azriel
CAR-TR-728 CS-TR-3326 UMIACS-TR-94-92 Samir Khuller Department of Computer Science Institute for Advanced Computer Studies University of Maryland College Park, MD 20742-3255 Localization in Graphs Azriel
Balanced Binary Search Trees
 Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
The Number of Connected Components in Graphs and Its. Applications. Ryuhei Uehara. Natural Science Faculty, Komazawa University.
 The Number of Connected Components in Graphs and Its Applications Ryuhei Uehara uehara@komazawa-u.ac.jp Natural Science Faculty, Komazawa University Abstract For any given graph and an integer k, the number
The Number of Connected Components in Graphs and Its Applications Ryuhei Uehara uehara@komazawa-u.ac.jp Natural Science Faculty, Komazawa University Abstract For any given graph and an integer k, the number
An Optimal Algorithm for the Euclidean Bottleneck Full Steiner Tree Problem
 An Optimal Algorithm for the Euclidean Bottleneck Full Steiner Tree Problem Ahmad Biniaz Anil Maheshwari Michiel Smid September 30, 2013 Abstract Let P and S be two disjoint sets of n and m points in the
An Optimal Algorithm for the Euclidean Bottleneck Full Steiner Tree Problem Ahmad Biniaz Anil Maheshwari Michiel Smid September 30, 2013 Abstract Let P and S be two disjoint sets of n and m points in the
1 The range query problem
 CS268: Geometric Algorithms Handout #12 Design and Analysis Original Handout #12 Stanford University Thursday, 19 May 1994 Original Lecture #12: Thursday, May 19, 1994 Topics: Range Searching with Partition
CS268: Geometric Algorithms Handout #12 Design and Analysis Original Handout #12 Stanford University Thursday, 19 May 1994 Original Lecture #12: Thursday, May 19, 1994 Topics: Range Searching with Partition
Embedding Large Complete Binary Trees in Hypercubes with Load Balancing
 JOURNAL OF PARALLEL AND DISTRIBUTED COMPUTING 35, 104 109 (1996) ARTICLE NO. 0073 Embedding Large Complete Binary Trees in Hypercubes with Load Balancing KEMAL EFE Center for Advanced Computer Studies,
JOURNAL OF PARALLEL AND DISTRIBUTED COMPUTING 35, 104 109 (1996) ARTICLE NO. 0073 Embedding Large Complete Binary Trees in Hypercubes with Load Balancing KEMAL EFE Center for Advanced Computer Studies,
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
An intoductory tutorial on kd-trees. Andrew W. Moore. Carnegie Mellon University.
 An intoductory tutorial on kd-trees Andrew W. Moore Carnegie Mellon University awm@cs.cmu.edu Extract from Andrew Moore's PhD Thesis: Ecient Memory-based Learning for Robot Control PhD. Thesis; Technical
An intoductory tutorial on kd-trees Andrew W. Moore Carnegie Mellon University awm@cs.cmu.edu Extract from Andrew Moore's PhD Thesis: Ecient Memory-based Learning for Robot Control PhD. Thesis; Technical
8. Binary Search Tree
 8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
Revised version, February 1991, appeared in Information Processing Letters 38 (1991), 123{127 COMPUTING THE MINIMUM HAUSDORFF DISTANCE BETWEEN
 Revised version, February 1991, appeared in Information Processing Letters 38 (1991), 123{127 COMPUTING THE MINIMUM HAUSDORFF DISTANCE BETWEEN TWO POINT SETS ON A LINE UNDER TRANSLATION Gunter Rote Technische
Revised version, February 1991, appeared in Information Processing Letters 38 (1991), 123{127 COMPUTING THE MINIMUM HAUSDORFF DISTANCE BETWEEN TWO POINT SETS ON A LINE UNDER TRANSLATION Gunter Rote Technische
Lecture 13: AVL Trees and Binary Heaps
 Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Lecture 4 Feb 21, 2007
 6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 4 Feb 21, 2007 Scribe: Mashhood Ishaque 1 Overview In the last lecture we worked in a BST model. We discussed Wilber lower bounds
6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 4 Feb 21, 2007 Scribe: Mashhood Ishaque 1 Overview In the last lecture we worked in a BST model. We discussed Wilber lower bounds
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Analysis of Algorithms
 Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
CmpSci 187: Programming with Data Structures Spring 2015
 CmpSci 187: Programming with Data Structures Spring 2015 Lecture #17, Implementing Binary Search Trees John Ridgway April 2, 2015 1 Implementing Binary Search Trees Review: The BST Interface Binary search
CmpSci 187: Programming with Data Structures Spring 2015 Lecture #17, Implementing Binary Search Trees John Ridgway April 2, 2015 1 Implementing Binary Search Trees Review: The BST Interface Binary search
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
A Discrete and Dynamic Version of Klee s Measure Problem
 CCCG 2011, Toronto ON, August 10 12, 2011 A Discrete and Dynamic Version of Klee s Measure Problem Hakan Yıldız John Hershberger Subhash Suri Abstract Given a set of axis-aligned boxes B = {B 1, B 2,...,
CCCG 2011, Toronto ON, August 10 12, 2011 A Discrete and Dynamic Version of Klee s Measure Problem Hakan Yıldız John Hershberger Subhash Suri Abstract Given a set of axis-aligned boxes B = {B 1, B 2,...,
