Con$nuing CPS. COS 326 David Walker Princeton University
|
|
|
- Abigayle Garrison
- 5 years ago
- Views:
Transcription
1 Con$nuing CPS COS 326 David Walker Princeton University
2 Last Time We saw that code like this could take up a lot of stack space: let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0
3 Last Time We saw that code like this could take up a lot of stack space: let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0 work to do aeer the recursive call returns == not a tail- recursive func$on
4 Last Time We saw that code like this could take up a lot of stack space: let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0 Every recursive call requires we allocate a stack frame to store the return address + data used aeer the call return_address n = 99 return_address n = 100 return_address state fun s stack -> return (stack.n + s) fun s stack -> return (stack.n + s)
5 Last Time But we can capture the computa$on that happens aeer the call: let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0 fun result - > n + result a func$on that explains what to do next is called a con%nua%on
6 Last Time let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0 Conversion to CPS style: let rec sum_to_cont (n:int) (k:int -> int) : int = if n > 0 then sum_to_cont (n-1) (fun result -> k (n + result)) else 0
7 Many func$ons can be made tail- rec easily: let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0 ;; sum_to 100 let rec sum_to_opt (n:int) (acc:int) : int = if n > 0 then sum_to_opt (n-1) (acc + n) else acc ;; not only did we make the func$on tail- recursive, but we didn t add any stack or linked- list of closures! sum_to_opt 100
8 Many func$ons can be made tail- rec easily: let rec sum_to (n:int) : int = if n > 0 then n + sum_to (n-1) else 0 ;; sum_to 100 let rec sum_to_opt (n:int) (acc:int) : int = if n > 0 then sum_to_opt (n-1) (acc + n) else acc ;; not only did we make the func$on tail- recursive, but we didn t add any stack or linked- list of closures! sum_to_opt 100
9 Some are harder: let rec print_stack (n:int) : unit = if n > 0 then Printf.printf push %d\n n; print_stack (n-1); Printf.printf pop %d\n n else Printf.printf zero ;; print_stack 5 ;; output: push 4 push 3 push 2 push 1 zero pop 1 pop 2 pop 3 pop 4
10 Some are harder: let rec print_stack (n:int) : unit = if n > 0 then Printf.printf push %d\n n; print_stack (n-1); Printf.printf pop %d\n n else Printf.printf zero ;; print_stack 5 ;; output: push 4 push 3 push 2 push 1 zero pop 1 pop 2 pop 3 pop 4 let rec print_stack_cont (n:int) (k:unit -> unit) : unit = ;; print_stack_cont 5 (fun () -> ()) ;;
11 Some are harder: let rec print_stack (n:int) : unit = if n > 0 then Printf.printf push %d\n n; print_stack (n-1); Printf.printf pop %d\n n else Printf.printf zero ;; print_stack 5 ;; output: push 4 push 3 push 2 push 1 zero pop 1 pop 2 pop 3 pop 4 let rec print_stack_cont (n:int) (k:unit -> unit) : unit = if n > 0 then else Printf.printf_cont zero k ;; print_stack_cont 5 (fun () -> ()) ;;
12 Some are harder: let rec print_stack (n:int) : unit = if n > 0 then Printf.printf push %d\n n; print_stack (n-1); Printf.printf pop %d\n n else Printf.printf zero ;; print_stack 5 ;; output: push 4 push 3 push 2 push 1 zero pop 1 pop 2 pop 3 pop 4 let rec print_stack_cont (n:int) (k:unit -> unit) : unit = if n > 0 then Printf.printf_cont push %d\n n (fun () ->... ) else Printf.printf_cont zero k ;; print_stack_cont 5 (fun () -> ()) ;;
13 Some are harder: let rec print_stack (n:int) : unit = if n > 0 then Printf.printf push %d\n n; print_stack (n-1); Printf.printf pop %d\n n else Printf.printf zero ;; print_stack 5 ;; output: push 4 push 3 push 2 push 1 zero pop 1 pop 2 pop 3 pop 4 let rec print_stack_cont (n:int) (k:unit -> unit) : unit = if n > 0 then Printf.printf_cont push %d\n n (fun () -> print_stack (n-1) (fun () ->...)) else Printf.printf_cont zero k ;; print_stack_cont 5 (fun () -> ()) ;;
14 Some are harder: let rec print_stack (n:int) : unit = if n > 0 then Printf.printf push %d\n n; print_stack (n-1); Printf.printf pop %d\n n else Printf.printf zero ;; print_stack 5 ;; output: push 4 push 3 push 2 push 1 zero pop 1 pop 2 pop 3 pop 4 let rec print_stack_cont (n:int) (k:unit -> unit) : unit = if n > 0 then Printf.printf_cont push %d\n n (fun () -> print_stack (n-1) (fun () -> Printf.printf_cont pop %d\n n k)) else Printf.printf_cont zero k ;; print_stack_cont 5 (fun () -> ()) ;;
15 ANOTHER EXAMPLE
16 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> Node (i+j, incr left i, incr right i) ;; Hint: It is a livle easier to put the con$nua$ons in the order in which they are called.
17 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> Node (i+j, incr left i, incr right i) ;; type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) (k: tree -> tree) : tree = match t with Leaf -> Leaf Node (j,left,right) -> let t1 = incr left i in let t2 = incr right i in Node (i+j, t1, t2)
18 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> Node (i+j, incr left i, incr right i) ;; type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) (k: tree -> tree) : tree = match t with Leaf -> Leaf Node (j,left,right) -> let t1 = incr left i in let t2 = incr right i in Node (i+j, t1, t2) called A- Normal Form (no func$on calls as args to other func$on calls)
19 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> let t1 = incr left i in let t2 = incr right i in Node (i+j, t1, t2) type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) (k: tree -> tree) : tree = match t with Leaf -> k Leaf Node (j,left,right) -> let t1 = incr left i in let t2 = incr right i in Node (i+j, t1, t2))
20 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> let t1 = incr left i in let t2 = incr right i in Node (i+j, t1, t2) type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) (k: tree -> tree) : tree = match t with Leaf -> k Leaf Node (j,left,right) -> incr left i (fun result1 -> let t1 = result1 in let t2 = incr right i in Node (i+j, t1, t2))
21 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> incr left i (fun result1 -> let t1 = result1 in let t2 = incr right i in Node (i+j, t1, t2)) type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) (k: tree -> tree) : tree = match t with Leaf -> k Leaf Node (j,left,right) -> incr left i (fun result1 -> let t1 = result1 in incr right i (fun result2 -> let t2 = result2 in Node (i+j, t1, t2))
22 Challenge: CPS Convert the incr func$on type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) : tree = match t with Leaf -> Leaf Node (j,left,right) -> incr left i (fun result1 -> let t1 = result1 in incr right i (fun result2 -> let t2 = result2 in Node (i+j, t1, t2)) type tree = Leaf Node of int * tree * tree ;; let rec incr (t:tree) (i:int) (k: tree -> tree) : tree = match t with Leaf -> k Leaf Node (j,left,right) -> incr left i (fun result1 -> let t1 = result1 in incr right i (fun result2 -> let t2 = result2 in k (Node (i+j, t1, t2)))
23 In general let g input = f3 (f2 (f1 input)) Direct Style let g input = let x1 = f1 input in let x2 = f2 x1 in f3 x2 A- normal Form let g input k = f1 input (fun x1 -> f2 x1 (fun x2 -> f3 x2 k)) CPS converted
24 CORRECTNESS OF A CPS TRANSFORM
25 type cont = int -> int;; Are the two func$ons the same? let rec sum_cont (l:int list) (k:cont): int = match l with [] -> k 0 hd::tail -> sum_cont tail (fun s -> k (hd + s)) let sum2 (l:int list) : int = sum_cont l (fun s -> s) let rec sum (l:int list) : int = match l with [] -> 0 hd::tail -> hd + sum tail CPS is prevy tricky. Let's try to prove a theorem: for all l:int list, sum_cont l (fun x -> x) == sum l
26 AVemp$ng a Proof Theorem: For all l:int list, sum_cont l (fun s -> s) == sum l Proof: By induction on the structure of the list l. case l = []... case: hd::tail IH: sum_cont tail (fun s -> s) == sum tail
27 AVemp$ng a Proof Theorem: For all l:int list, sum_cont l (fun s -> s) == sum l Proof: By induction on the structure of the list l. case l = []... case: hd::tail IH: sum_cont tail (fun s -> s) == sum tail == sum_cont (hd::tail) (fun s -> s)
28 AVemp$ng a Proof Theorem: For all l:int list, sum_cont l (fun s -> s) == sum l Proof: By induction on the structure of the list l. case l = []... case: hd::tail IH: sum_cont tail (fun s -> s) == sum tail sum_cont (hd::tail) (fun s -> s) == sum_cont tail (fn s' -> (fn s -> s) (hd + s')) (eval)
29 AVemp$ng a Proof Theorem: For all l:int list, sum_cont l (fun s -> s) == sum l Proof: By induction on the structure of the list l. case l = []... case: hd::tail IH: sum_cont tail (fun s -> s) == sum tail sum_cont (hd::tail) (fun s -> s) == sum_cont tail (fn s' -> (fn s -> s) (hd + s')) (eval) == sum_cont tail (fn s' -> hd + s') (eval)
30 Need to Generalize the Theorem and IH Theorem: For all l:int list, sum_cont l (fun s -> s) == sum l Proof: By induction on the structure of the list l. case l = []... case: hd::tail IH: sum_cont tail (fun s -> s) == sum tail sum_cont (hd::tail) (fun s -> s) == sum_cont tail (fn s' -> (fn s -> s) (hd + s')) (eval) == sum_cont tail (fn s' -> hd + s') (eval) == darn! we'd like to use the IH, but we can't! we might like: not the iden$ty con$nua$on (fun s - > s) like the IH requires sum_cont tail (fn s' - > hd + s') == sum tail... but that's not even true
31 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l)
32 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] must prove: for all k:int->int, sum_cont [] k == k (sum [])
33 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] must prove: for all k:int->int, sum_cont [] k == k (sum []) pick an arbitrary k:
34 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] must prove: for all k:int->int, sum_cont [] k == k (sum []) pick an arbitrary k: sum_cont [] k
35 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] must prove: for all k:int->int, sum_cont [] k == k (sum []) pick an arbitrary k: sum_cont [] k == match [] with [] -> k 0 hd::tail ->... (eval) == k 0 (eval)
36 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] must prove: for all k:int->int, sum_cont [] k == k (sum []) pick an arbitrary k: sum_cont [] k == match [] with [] -> k 0 hd::tail ->... (eval) == k 0 (eval) == k (sum [])
37 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] must prove: for all k:int->int, sum_cont [] k == k (sum []) pick an arbitrary k: sum_cont [] k == match [] with [] -> k 0 hd::tail ->... (eval) == k 0 (eval) == k (0) (eval, reverse) == k (match [] with [] -> 0 hd::tail ->...) (eval, reverse) == k (sum []) case done!
38 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] ===> done! case l = hd::tail IH: for all k':int->int, sum_cont tail k' == k' (sum tail) MP: for all k:int->int, sum_cont (hd::tail) k == k (sum (hd::tail))
39 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] ===> done! case l = hd::tail IH: for all k':int->int, sum_cont tail k' == k' (sum tail) MP: for all k:int->int, sum_cont (hd::tail) k == k (sum (hd::tail)) Pick an arbitrary k, sum_cont (hd::tail) k
40 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] ===> done! case l = hd::tail IH: for all k':int->int, sum_cont tail k' == k' (sum tail) MP: for all k:int->int, sum_cont (hd::tail) k == k (sum (hd::tail)) Pick an arbitrary k, sum_cont (hd::tail) k == sum_cont tail (fun s -> k (hd + x)) (eval)
41 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] ===> done! case l = hd::tail IH: for all k':int->int, sum_cont tail k' == k' (sum tail) MP: for all k:int->int, sum_cont (hd::tail) k == k (sum (hd::tail)) Pick an arbitrary k, sum_cont (hd::tail) k == sum_cont tail (fun s -> k (hd + x)) (eval) == (fun s -> k (hd + s)) (sum tail) (IH with IH quantifier k' replacing (fun x -> k (hd+x))
42 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] ===> done! case l = hd::tail IH: for all k':int->int, sum_cont tail k' == k' (sum tail) MP: for all k:int->int, sum_cont (hd::tail) k == k (sum (hd::tail)) Pick an arbitrary k, sum_cont (hd::tail) k == sum_cont tail (fun s -> k (hd + x)) (eval) == (fun s -> k (hd + s)) (sum tail) (IH with IH quantifier k' replacing (fun x -> k (hd+x)) == k (hd + (sum tail)) (eval, since sum total and sum tail valuable)
43 Need to Generalize the Theorem and IH for all l:int list, for all k:int->int, sum_cont l k == k (sum l) Proof: By induction on the structure of the list l. case l = [] ===> done! case l = hd::tail IH: for all k':int->int, sum_cont tail k' == k' (sum tail) MP: for all k:int->int, sum_cont (hd::tail) k == k (sum (hd::tail)) Pick an arbitrary k, sum_cont (hd::tail) k == sum_cont tail (fun s -> k (hd + x)) (eval) == (fun s -> k (hd + s)) (sum tail) (IH) == k (hd + (sum tail)) (eval) == k (sum (hd:tail)) (eval sum, reverse) case done! QED!
44 Finishing Up Ok, now what we have is a proof of this theorem: for all l:int list, for all k:int->int, sum_cont l k == k (sum l) We can use that general theorem to get what we really want: for all l:int list, sum2 l == sum_cont l (fun s -> s) (by eval sum2) == (fun s -> s) (sum l) (by theorem, instantiating k with (fun s -> s) == sum l So, we've show that the func$on sum2, which is tail- recursive, is func$onally equivalent to the non- tail- recursive func$on sum.
45 SUMMARY
46 Summary of the CPS Proof We tried to prove the specific theorem we wanted: for all l:int list, sum_cont l (fun s -> s) == sum l But it didn't work because in the middle of the proof, the IH didn't apply - - inside our func$on we had the wrong kind of con$nua$on - - not (fun s - > s) like our IH required. So we had to prove a more general theorem about all con$nua$ons. for all l:int list, for all k:int->int, sum_cont l k == k (sum l) This is a common occurrence - - generalizing the induc%on hypothesis - - and it requires human ingenuity. It's why proving theorems is hard. It's also why wri$ng programs is hard - - you have to make the proofs and programs work more generally, around every itera$on of a loop.
A Functional Space Model. COS 326 David Walker Princeton University
 A Functional Space Model COS 326 David Walker Princeton University Data type representations: Last Time type tree = Leaf Node of int * tree * tree Leaf: Node(i, left, right): 0 Node 3 left right This Time
A Functional Space Model COS 326 David Walker Princeton University Data type representations: Last Time type tree = Leaf Node of int * tree * tree Leaf: Node(i, left, right): 0 Node 3 left right This Time
Fall Recursion and induction. Stephen Brookes. Lecture 4
 15-150 Fall 2018 Stephen Brookes Lecture 4 Recursion and induction Last time Specification format for a function F type assumption guarantee (REQUIRES) (ENSURES) For all (properly typed) x satisfying the
15-150 Fall 2018 Stephen Brookes Lecture 4 Recursion and induction Last time Specification format for a function F type assumption guarantee (REQUIRES) (ENSURES) For all (properly typed) x satisfying the
Modules and Representation Invariants
 Modules and Representation Invariants COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel In previous classes: Reasoning about individual OCaml expressions.
Modules and Representation Invariants COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel In previous classes: Reasoning about individual OCaml expressions.
Thinking Induc,vely. COS 326 David Walker Princeton University
 Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa,onal purposes Administra,on 2 Assignment
Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa,onal purposes Administra,on 2 Assignment
Thinking Induc,vely. COS 326 David Walker Princeton University
 Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel permission granted to reuse these slides for non-commercial educa,onal purposes
Thinking Induc,vely COS 326 David Walker Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel permission granted to reuse these slides for non-commercial educa,onal purposes
Induction in Coq. Nate Foster Spring 2018
 Induction in Coq Nate Foster Spring 2018 Review Previously in 3110: Functional programming in Coq Logic in Coq Curry-Howard correspondence (proofs are programs) Today: Induction in Coq REVIEW: INDUCTION
Induction in Coq Nate Foster Spring 2018 Review Previously in 3110: Functional programming in Coq Logic in Coq Curry-Howard correspondence (proofs are programs) Today: Induction in Coq REVIEW: INDUCTION
A Func'onal Space Model
 A Func'onal Space Model COS 26 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa'onal purposes 2 Because Halloween draws
A Func'onal Space Model COS 26 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educa'onal purposes 2 Because Halloween draws
Lecture 6: Sequential Sorting
 15-150 Lecture 6: Sequential Sorting Lecture by Dan Licata February 2, 2012 Today s lecture is about sorting. Along the way, we ll learn about divide and conquer algorithms, the tree method, and complete
15-150 Lecture 6: Sequential Sorting Lecture by Dan Licata February 2, 2012 Today s lecture is about sorting. Along the way, we ll learn about divide and conquer algorithms, the tree method, and complete
CS 4110 Programming Languages & Logics. Lecture 35 Typed Assembly Language
 CS 4110 Programming Languages & Logics Lecture 35 Typed Assembly Language 1 December 2014 Announcements 2 Foster Office Hours today 4-5pm Optional Homework 10 out Final practice problems out this week
CS 4110 Programming Languages & Logics Lecture 35 Typed Assembly Language 1 December 2014 Announcements 2 Foster Office Hours today 4-5pm Optional Homework 10 out Final practice problems out this week
Week 5 Tutorial Structural Induction
 Department of Computer Science, Australian National University COMP2600 / COMP6260 Formal Methods in Software Engineering Semester 2, 2016 Week 5 Tutorial Structural Induction You should hand in attempts
Department of Computer Science, Australian National University COMP2600 / COMP6260 Formal Methods in Software Engineering Semester 2, 2016 Week 5 Tutorial Structural Induction You should hand in attempts
A Func'onal Introduc'on. COS 326 David Walker Princeton University
 A Func'onal Introduc'on COS 326 David Walker Princeton University Thinking Func'onally In Java or C, you get (most) work done by changing something temp = pair.x; pair.x = pair.y; pair.y = temp; commands
A Func'onal Introduc'on COS 326 David Walker Princeton University Thinking Func'onally In Java or C, you get (most) work done by changing something temp = pair.x; pair.x = pair.y; pair.y = temp; commands
Fall Lecture 13 Thursday, October 11
 15-150 Fall 2018 Lecture 13 Thursday, October 11 n queens One s favorite ipod app n queens Queens attack on row, column, or diagonal Task: put n queens safely on an n-by-n board British Museum algorithm
15-150 Fall 2018 Lecture 13 Thursday, October 11 n queens One s favorite ipod app n queens Queens attack on row, column, or diagonal Task: put n queens safely on an n-by-n board British Museum algorithm
MPRI course 2-4 Functional programming languages Exercises
 MPRI course 2-4 Functional programming languages Exercises Xavier Leroy October 13, 2016 Part I: Interpreters and operational semantics Exercise I.1 (**) Prove theorem 2 (the unique decomposition theorem).
MPRI course 2-4 Functional programming languages Exercises Xavier Leroy October 13, 2016 Part I: Interpreters and operational semantics Exercise I.1 (**) Prove theorem 2 (the unique decomposition theorem).
Tail Calls. CMSC 330: Organization of Programming Languages. Tail Recursion. Tail Recursion (cont d) Names and Binding. Tail Recursion (cont d)
 CMSC 330: Organization of Programming Languages Tail Calls A tail call is a function call that is the last thing a function does before it returns let add x y = x + y let f z = add z z (* tail call *)
CMSC 330: Organization of Programming Languages Tail Calls A tail call is a function call that is the last thing a function does before it returns let add x y = x + y let f z = add z z (* tail call *)
Logic and Computation Lecture 20 CSU 290 Spring 2009 (Pucella) Thursday, Mar 12, 2009
 Logic and Computation Lecture 20 CSU 290 Spring 2009 (Pucella) Thursday, Mar 12, 2009 Note that I change the name of the functions slightly in these notes from what I used in class, to be consistent with
Logic and Computation Lecture 20 CSU 290 Spring 2009 (Pucella) Thursday, Mar 12, 2009 Note that I change the name of the functions slightly in these notes from what I used in class, to be consistent with
CSC236 Week 4. Larry Zhang
 CSC236 Week 4 Larry Zhang 1 Announcements PS2 is out Larry s office hours in the reading week: as usual Tuesday 12-2, Wednesday 2-4 2 NEW TOPIC Recursion To really understand the math of recursion, and
CSC236 Week 4 Larry Zhang 1 Announcements PS2 is out Larry s office hours in the reading week: as usual Tuesday 12-2, Wednesday 2-4 2 NEW TOPIC Recursion To really understand the math of recursion, and
Do you remember any iterative sorting methods? Can we produce a good sorting method by. We try to divide and conquer: break into subproblems
 MERGESORT 315 Sorting Recursively Do you remember any iterative sorting methods? How fast are they? Can we produce a good sorting method by thinking recursively? We try to divide and conquer: break into
MERGESORT 315 Sorting Recursively Do you remember any iterative sorting methods? How fast are they? Can we produce a good sorting method by thinking recursively? We try to divide and conquer: break into
Theorem Proving Principles, Techniques, Applications Recursion
 NICTA Advanced Course Theorem Proving Principles, Techniques, Applications Recursion 1 CONTENT Intro & motivation, getting started with Isabelle Foundations & Principles Lambda Calculus Higher Order Logic,
NICTA Advanced Course Theorem Proving Principles, Techniques, Applications Recursion 1 CONTENT Intro & motivation, getting started with Isabelle Foundations & Principles Lambda Calculus Higher Order Logic,
CS5371 Theory of Computation. Lecture 8: Automata Theory VI (PDA, PDA = CFG)
 CS5371 Theory of Computation Lecture 8: Automata Theory VI (PDA, PDA = CFG) Objectives Introduce Pushdown Automaton (PDA) Show that PDA = CFG In terms of descriptive power Pushdown Automaton (PDA) Roughly
CS5371 Theory of Computation Lecture 8: Automata Theory VI (PDA, PDA = CFG) Objectives Introduce Pushdown Automaton (PDA) Show that PDA = CFG In terms of descriptive power Pushdown Automaton (PDA) Roughly
Formal Methods of Software Design, Eric Hehner, segment 24 page 1 out of 5
 Formal Methods of Software Design, Eric Hehner, segment 24 page 1 out of 5 [talking head] This lecture we study theory design and implementation. Programmers have two roles to play here. In one role, they
Formal Methods of Software Design, Eric Hehner, segment 24 page 1 out of 5 [talking head] This lecture we study theory design and implementation. Programmers have two roles to play here. In one role, they
Foundations of Computation
 The Australian National University Semester 2, 2018 Research School of Computer Science Tutorial 5 Dirk Pattinson Foundations of Computation The tutorial contains a number of exercises designed for the
The Australian National University Semester 2, 2018 Research School of Computer Science Tutorial 5 Dirk Pattinson Foundations of Computation The tutorial contains a number of exercises designed for the
Overview. A mathema5cal proof technique Proves statements about natural numbers 0,1,2,... (or more generally, induc+vely defined objects) Merge Sort
 Goals for Today Induc+on Lecture 22 Spring 2011 Be able to state the principle of induc+on Iden+fy its rela+onship to recursion State how it is different from recursion Be able to understand induc+ve proofs
Goals for Today Induc+on Lecture 22 Spring 2011 Be able to state the principle of induc+on Iden+fy its rela+onship to recursion State how it is different from recursion Be able to understand induc+ve proofs
CS 310 Advanced Data Structures and Algorithms
 CS 310 Advanced Data Structures and Algorithms Recursion June 27, 2017 Tong Wang UMass Boston CS 310 June 27, 2017 1 / 20 Recursion Recursion means defining something, such as a function, in terms of itself
CS 310 Advanced Data Structures and Algorithms Recursion June 27, 2017 Tong Wang UMass Boston CS 310 June 27, 2017 1 / 20 Recursion Recursion means defining something, such as a function, in terms of itself
CS 4110 Programming Languages & Logics
 CS 4110 Programming Languages & Logics Lecture 38 Typed Assembly Language 30 November 2012 Schedule 2 Monday Typed Assembly Language Wednesday Polymorphism Stack Types Today Compilation Course Review Certi
CS 4110 Programming Languages & Logics Lecture 38 Typed Assembly Language 30 November 2012 Schedule 2 Monday Typed Assembly Language Wednesday Polymorphism Stack Types Today Compilation Course Review Certi
Behavioral Equivalence
 Behavioral Equivalence Prof. Clarkson Fall 2016 Today s music: Soul Bossa Nova by Quincy Jones Review Previously in 3110: Functional programming Modular programming & software engineering Interpreters
Behavioral Equivalence Prof. Clarkson Fall 2016 Today s music: Soul Bossa Nova by Quincy Jones Review Previously in 3110: Functional programming Modular programming & software engineering Interpreters
COSE212: Programming Languages. Lecture 4 Recursive and Higher-Order Programming
 COSE212: Programming Languages Lecture 4 Recursive and Higher-Order Programming Hakjoo Oh 2016 Fall Hakjoo Oh COSE212 2016 Fall, Lecture 4 September 27, 2016 1 / 21 Recursive and Higher-Order Programming
COSE212: Programming Languages Lecture 4 Recursive and Higher-Order Programming Hakjoo Oh 2016 Fall Hakjoo Oh COSE212 2016 Fall, Lecture 4 September 27, 2016 1 / 21 Recursive and Higher-Order Programming
Continuations and Continuation-Passing Style
 Continuations and Continuation-Passing Style Lecture 4 CS 390 1/16/08 Goal Weʼre interested in understanding how to represent the state of a co-routine Insight into what a thread really means How fundamental
Continuations and Continuation-Passing Style Lecture 4 CS 390 1/16/08 Goal Weʼre interested in understanding how to represent the state of a co-routine Insight into what a thread really means How fundamental
Parsing Scheme (+ (* 2 3) 1) * 1
 Parsing Scheme + (+ (* 2 3) 1) * 1 2 3 Compiling Scheme frame + frame halt * 1 3 2 3 2 refer 1 apply * refer apply + Compiling Scheme make-return START make-test make-close make-assign make- pair? yes
Parsing Scheme + (+ (* 2 3) 1) * 1 2 3 Compiling Scheme frame + frame halt * 1 3 2 3 2 refer 1 apply * refer apply + Compiling Scheme make-return START make-test make-close make-assign make- pair? yes
Induction for Data Types
 Induction for Data Types COMP1600 / COMP6260 Dirk Pattinson Australian National University Semester 2, 2017 Catch Up / Drop in Lab When Fridays, 15.00-17.00 Where N335, CSIT Building (bldg 108) Until the
Induction for Data Types COMP1600 / COMP6260 Dirk Pattinson Australian National University Semester 2, 2017 Catch Up / Drop in Lab When Fridays, 15.00-17.00 Where N335, CSIT Building (bldg 108) Until the
CMSC330 Fall 2013 Practice Problems 6 Solutions
 CMSC330 Fall 2013 Practice Problems 6 Solutions 1. Programming languages a. Describe how functional programming may be used to simulate OOP. An object may be simulated as a tuple, where each element of
CMSC330 Fall 2013 Practice Problems 6 Solutions 1. Programming languages a. Describe how functional programming may be used to simulate OOP. An object may be simulated as a tuple, where each element of
Tuples. CMSC 330: Organization of Programming Languages. Examples With Tuples. Another Example
 CMSC 330: Organization of Programming Languages OCaml 2 Higher Order Functions Tuples Constructed using (e1,..., en) Deconstructed using pattern matching Patterns involve parens and commas, e.g., (p1,p2,
CMSC 330: Organization of Programming Languages OCaml 2 Higher Order Functions Tuples Constructed using (e1,..., en) Deconstructed using pattern matching Patterns involve parens and commas, e.g., (p1,p2,
MoreIntro_annotated.v. MoreIntro_annotated.v. Printed by Zach Tatlock. Oct 04, 16 21:55 Page 1/10
 Oct 04, 16 21:55 Page 1/10 * Lecture 02 Infer some type arguments automatically. Set Implicit Arguments. Note that the type constructor for functions (arrow " >") associates to the right: A > B > C = A
Oct 04, 16 21:55 Page 1/10 * Lecture 02 Infer some type arguments automatically. Set Implicit Arguments. Note that the type constructor for functions (arrow " >") associates to the right: A > B > C = A
Announcements. CS243: Discrete Structures. Strong Induction and Recursively Defined Structures. Review. Example (review) Example (review), cont.
 Announcements CS43: Discrete Structures Strong Induction and Recursively Defined Structures Işıl Dillig Homework 4 is due today Homework 5 is out today Covers induction (last lecture, this lecture, and
Announcements CS43: Discrete Structures Strong Induction and Recursively Defined Structures Işıl Dillig Homework 4 is due today Homework 5 is out today Covers induction (last lecture, this lecture, and
Unit #2: Recursion, Induction, and Loop Invariants
 Unit #2: Recursion, Induction, and Loop Invariants CPSC 221: Algorithms and Data Structures Will Evans 2012W1 Unit Outline Thinking Recursively Recursion Examples Analyzing Recursion: Induction and Recurrences
Unit #2: Recursion, Induction, and Loop Invariants CPSC 221: Algorithms and Data Structures Will Evans 2012W1 Unit Outline Thinking Recursively Recursion Examples Analyzing Recursion: Induction and Recurrences
Begin at the beginning
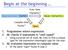 Begin at the beginning Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set of
Begin at the beginning Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set of
Homework 8: Matrices Due: 11:59 PM, Oct 30, 2018
 CS17 Integrated Introduction to Computer Science Klein Homework 8: Matrices Due: 11:59 PM, Oct 30, 2018 Contents 1 Reverse (Practice) 4 2 Main Diagonal (Practice) 5 3 Horizontal Flip 6 4 Vertical Flip
CS17 Integrated Introduction to Computer Science Klein Homework 8: Matrices Due: 11:59 PM, Oct 30, 2018 Contents 1 Reverse (Practice) 4 2 Main Diagonal (Practice) 5 3 Horizontal Flip 6 4 Vertical Flip
Introduction to dependent types in Coq
 October 24, 2008 basic use of the Coq system In Coq, you can play with simple values and functions. The basic command is called Check, to verify if an expression is well-formed and learn what is its type.
October 24, 2008 basic use of the Coq system In Coq, you can play with simple values and functions. The basic command is called Check, to verify if an expression is well-formed and learn what is its type.
6.046 Recitation 1: Proving Correctness Bill Thies, Fall 2004 Outline
 6.046 Recitation 1: Proving Correctness Bill Thies, Fall 2004 Outline Acknowledgement Much of these notes is adapted from David Liben Nowell s notes for the same subject (thanks David!) My contact information:
6.046 Recitation 1: Proving Correctness Bill Thies, Fall 2004 Outline Acknowledgement Much of these notes is adapted from David Liben Nowell s notes for the same subject (thanks David!) My contact information:
The Art of Recursion: Problem Set 10
 The Art of Recursion: Problem Set Due Tuesday, November Tail recursion A recursive function is tail recursive if every recursive call is in tail position that is, the result of the recursive call is immediately
The Art of Recursion: Problem Set Due Tuesday, November Tail recursion A recursive function is tail recursive if every recursive call is in tail position that is, the result of the recursive call is immediately
Complexity, Induction, and Recurrence Relations. CSE 373 Help Session 4/7/2016
 Complexity, Induction, and Recurrence Relations CSE 373 Help Session 4/7/2016 Big-O Definition Definition: g(n) is in O( f(n) ) if there exist positive constants c and n0 such that g(n) c f(n) for all
Complexity, Induction, and Recurrence Relations CSE 373 Help Session 4/7/2016 Big-O Definition Definition: g(n) is in O( f(n) ) if there exist positive constants c and n0 such that g(n) c f(n) for all
What does this print?
 public class Test_Static { int a; static int b; public Test_Static(int av, int bv) { a= av; b= bv; } public void print() { System.out.println ("a= " + a + " b= " + b); } public static void main (String
public class Test_Static { int a; static int b; public Test_Static(int av, int bv) { a= av; b= bv; } public void print() { System.out.println ("a= " + a + " b= " + b); } public static void main (String
Compositional Cutpoint Verification
 Compositional Cutpoint Verification Eric Smith (Stanford University) Collaborators: David Dill (Stanford University) David Hardin (Rockwell Collins) Contact ewsmith@stanford.edu Background Based on A Symbolic
Compositional Cutpoint Verification Eric Smith (Stanford University) Collaborators: David Dill (Stanford University) David Hardin (Rockwell Collins) Contact ewsmith@stanford.edu Background Based on A Symbolic
Parallelism; Parallel Collections
 Parallelism; Parallel Collections COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel let x = 1 + 2 in 3 + x Visualizing Computational Costs Visualizing
Parallelism; Parallel Collections COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel let x = 1 + 2 in 3 + x Visualizing Computational Costs Visualizing
Behavioral Equivalence
 Behavioral Equivalence Prof. Clarkson Fall 2015 Today s music: Soul Bossa Nova by Quincy Jones Review Previously in 3110: Functional programming Modular programming Interpreters Imperative and concurrent
Behavioral Equivalence Prof. Clarkson Fall 2015 Today s music: Soul Bossa Nova by Quincy Jones Review Previously in 3110: Functional programming Modular programming Interpreters Imperative and concurrent
Today. Types of graphs. Complete Graphs. Trees. Hypercubes.
 Today. Types of graphs. Complete Graphs. Trees. Hypercubes. Complete Graph. K n complete graph on n vertices. All edges are present. Everyone is my neighbor. Each vertex is adjacent to every other vertex.
Today. Types of graphs. Complete Graphs. Trees. Hypercubes. Complete Graph. K n complete graph on n vertices. All edges are present. Everyone is my neighbor. Each vertex is adjacent to every other vertex.
CMSC 132: Object-Oriented Programming II. Recursive Algorithms. Department of Computer Science University of Maryland, College Park
 CMSC 132: Object-Oriented Programming II Recursive Algorithms Department of Computer Science University of Maryland, College Park Recursion Recursion is a strategy for solving problems A procedure that
CMSC 132: Object-Oriented Programming II Recursive Algorithms Department of Computer Science University of Maryland, College Park Recursion Recursion is a strategy for solving problems A procedure that
Mutation. COS 326 David Walker Princeton University
 Mutation COS 326 David Walker Princeton University Mutation? 2 Thus far We have considered the (almost) purely functional subset of Ocaml. We ve had a few side effects: printing & raising exceptions. Two
Mutation COS 326 David Walker Princeton University Mutation? 2 Thus far We have considered the (almost) purely functional subset of Ocaml. We ve had a few side effects: printing & raising exceptions. Two
Mutation. COS 326 Andrew W. Appel Princeton University. slides copyright David Walker and Andrew W. Appel
 Mutation COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel Mutation? 2 Reasoning about Mutable State is Hard mutable set insert i s1; f x; member
Mutation COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel Mutation? 2 Reasoning about Mutable State is Hard mutable set insert i s1; f x; member
Type Inference. COS 326 David Walker Princeton University
 Type Inference COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educafonal purposes 2 Midterm Exam Wed Oct 25, 2017
Type Inference COS 326 David Walker Princeton University slides copyright 2017 David Walker permission granted to reuse these slides for non-commercial educafonal purposes 2 Midterm Exam Wed Oct 25, 2017
Proving Theorems with Athena
 Proving Theorems with Athena David R. Musser Aytekin Vargun August 28, 2003, revised January 26, 2005 Contents 1 Introduction 1 2 Proofs about order relations 2 3 Proofs about natural numbers 7 3.1 Term
Proving Theorems with Athena David R. Musser Aytekin Vargun August 28, 2003, revised January 26, 2005 Contents 1 Introduction 1 2 Proofs about order relations 2 3 Proofs about natural numbers 7 3.1 Term
C 101. Davide Vernizzi. April 29, 2011
 C 101 Davide Vernizzi April 9, 011 1 Input/Output Basic I/O. The basic I/O shown here can be used to get input from the user and to send output to the user. Note that usually input must be verified before
C 101 Davide Vernizzi April 9, 011 1 Input/Output Basic I/O. The basic I/O shown here can be used to get input from the user and to send output to the user. Note that usually input must be verified before
Calculating Correct Compilers
 university of copenhagen department of computer science Faculty of Science Calculating Correct Compilers Patrick Bahr1 Graham Hutton2 1 University of Copenhagen, Department of Computer Science paba@diku.dk
university of copenhagen department of computer science Faculty of Science Calculating Correct Compilers Patrick Bahr1 Graham Hutton2 1 University of Copenhagen, Department of Computer Science paba@diku.dk
Scope, Functions, and Storage Management
 Scope, Functions, and Storage Management Implementing Functions and Blocks cs3723 1 Simplified Machine Model (Compare To List Abstract Machine) Registers Code Data Program Counter (current instruction)
Scope, Functions, and Storage Management Implementing Functions and Blocks cs3723 1 Simplified Machine Model (Compare To List Abstract Machine) Registers Code Data Program Counter (current instruction)
Data Structures And Algorithms
 Data Structures And Algorithms Recursion Eng. Anis Nazer First Semester 2016-2017 Recursion Recursion: to define something in terms of itself Example: factorial n!={ 1 n=0 n (n 1)! n>0 Recursion Example:
Data Structures And Algorithms Recursion Eng. Anis Nazer First Semester 2016-2017 Recursion Recursion: to define something in terms of itself Example: factorial n!={ 1 n=0 n (n 1)! n>0 Recursion Example:
Solutions to In Class Problems Week 5, Wed.
 Massachusetts Institute of Technology 6.042J/18.062J, Fall 05: Mathematics for Computer Science October 5 Prof. Albert R. Meyer and Prof. Ronitt Rubinfeld revised October 5, 2005, 1119 minutes Solutions
Massachusetts Institute of Technology 6.042J/18.062J, Fall 05: Mathematics for Computer Science October 5 Prof. Albert R. Meyer and Prof. Ronitt Rubinfeld revised October 5, 2005, 1119 minutes Solutions
Unit #3: Recursion, Induction, and Loop Invariants
 Unit #3: Recursion, Induction, and Loop Invariants CPSC 221: Basic Algorithms and Data Structures Jan Manuch 2017S1: May June 2017 Unit Outline Thinking Recursively Recursion Examples Analyzing Recursion:
Unit #3: Recursion, Induction, and Loop Invariants CPSC 221: Basic Algorithms and Data Structures Jan Manuch 2017S1: May June 2017 Unit Outline Thinking Recursively Recursion Examples Analyzing Recursion:
Lecture Notes on Induction and Recursion
 Lecture Notes on Induction and Recursion 15-317: Constructive Logic Frank Pfenning Lecture 7 September 19, 2017 1 Introduction At this point in the course we have developed a good formal understanding
Lecture Notes on Induction and Recursion 15-317: Constructive Logic Frank Pfenning Lecture 7 September 19, 2017 1 Introduction At this point in the course we have developed a good formal understanding
Tail Recursion: Factorial. Begin at the beginning. How does it execute? Tail recursion. Tail recursive factorial. Tail recursive factorial
 Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Indicate the option which most accurately completes the sentence.
 Discrete Structures, CSCI 246, Fall 2015 Final, Dec. 10 Indicate the option which most accurately completes the sentence. 1. Say that Discrete(x) means that x is a discrete structures exam and Well(x)
Discrete Structures, CSCI 246, Fall 2015 Final, Dec. 10 Indicate the option which most accurately completes the sentence. 1. Say that Discrete(x) means that x is a discrete structures exam and Well(x)
CMPSCI 250: Introduction to Computation. Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013
 CMPSCI 250: Introduction to Computation Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013 Induction and Recursion Three Rules for Recursive Algorithms Proving
CMPSCI 250: Introduction to Computation Lecture #14: Induction and Recursion (Still More Induction) David Mix Barrington 14 March 2013 Induction and Recursion Three Rules for Recursive Algorithms Proving
Recursive Data and Recursive Functions
 Structural Recursion and Induction Of all the material in this course, this lesson is probably the hardest for students to grasp at first, but it s also one of the most fundamental. Once you understand
Structural Recursion and Induction Of all the material in this course, this lesson is probably the hardest for students to grasp at first, but it s also one of the most fundamental. Once you understand
Fall 2018 Lecture 7. Stephen Brookes
 15-150 Fall 2018 Lecture 7 Stephen Brookes last time Sorting a list of integers Specifications and proofs helper functions that really help principles Every function needs a spec Every spec needs a proof
15-150 Fall 2018 Lecture 7 Stephen Brookes last time Sorting a list of integers Specifications and proofs helper functions that really help principles Every function needs a spec Every spec needs a proof
CSE 143 Lecture 10. Recursion
 CSE 143 Lecture 10 Recursion slides created by Marty Stepp and Alyssa Harding http://www.cs.washington.edu/143/ Recursion Iteration: a programming technique in which you describe actions to be repeated
CSE 143 Lecture 10 Recursion slides created by Marty Stepp and Alyssa Harding http://www.cs.washington.edu/143/ Recursion Iteration: a programming technique in which you describe actions to be repeated
Basic Combinatorics. Math 40210, Section 01 Fall Homework 4 Solutions
 Basic Combinatorics Math 40210, Section 01 Fall 2012 Homework 4 Solutions 1.4.2 2: One possible implementation: Start with abcgfjiea From edge cd build, using previously unmarked edges: cdhlponminjkghc
Basic Combinatorics Math 40210, Section 01 Fall 2012 Homework 4 Solutions 1.4.2 2: One possible implementation: Start with abcgfjiea From edge cd build, using previously unmarked edges: cdhlponminjkghc
Side note: Tail Recursion. Begin at the beginning. Side note: Tail Recursion. Base Types. Base Type: int. Base Type: int
 Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
Begin at the beginning Epressions (Synta) Compile-time Static Eec-time Dynamic Types Values (Semantics) 1. Programmer enters epression 2. ML checks if epression is well-typed Using a precise set of rules,
The Worker/Wrapper Transformation
 The Worker/Wrapper Transformation Andy Gill 1 Graham Hutton 2 1 The University of Kansas 2 The University of Nottingham March 26th, 2009 Andy Gill, Graham Hutton The Worker/Wrapper Transformation March
The Worker/Wrapper Transformation Andy Gill 1 Graham Hutton 2 1 The University of Kansas 2 The University of Nottingham March 26th, 2009 Andy Gill, Graham Hutton The Worker/Wrapper Transformation March
CMSC351 - Fall 2014, Homework #2
 CMSC351 - Fall 2014, Homework #2 Due: October 8th at the start of class Name: Section: Grades depend on neatness and clarity. Write your answers with enough detail about your approach and concepts used,
CMSC351 - Fall 2014, Homework #2 Due: October 8th at the start of class Name: Section: Grades depend on neatness and clarity. Write your answers with enough detail about your approach and concepts used,
CS221: Algorithms and Data Structures Lecture #11 Recursion vs. Iteration Proofs about Recursion/Iteration
 CS221: Algorithms and Data Structures Lecture #11 Recursion vs. Iteration Proofs about Recursion/Iteration Alan J. Hu (Borrowing slides from Steve Wolfman) 1 Programming Project #1 First Milestone due
CS221: Algorithms and Data Structures Lecture #11 Recursion vs. Iteration Proofs about Recursion/Iteration Alan J. Hu (Borrowing slides from Steve Wolfman) 1 Programming Project #1 First Milestone due
Outline for Today. Why could we construct them in time O(n)? Analyzing data structures over the long term.
 Amortized Analysis Outline for Today Euler Tour Trees A quick bug fix from last time. Cartesian Trees Revisited Why could we construct them in time O(n)? Amortized Analysis Analyzing data structures over
Amortized Analysis Outline for Today Euler Tour Trees A quick bug fix from last time. Cartesian Trees Revisited Why could we construct them in time O(n)? Amortized Analysis Analyzing data structures over
Machine-checked proofs of program correctness
 Machine-checked proofs of program correctness COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel In this course, you saw how to prove that functional
Machine-checked proofs of program correctness COS 326 Andrew W. Appel Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel In this course, you saw how to prove that functional
Verification in Coq. Prof. Clarkson Fall Today s music: Check Yo Self by Ice Cube
 Verification in Coq Prof. Clarkson Fall 2017 Today s music: Check Yo Self by Ice Cube Review Previously in 3110: Functional programming in Coq Logic in Coq Curry-Howard correspondence (proofs are programs)
Verification in Coq Prof. Clarkson Fall 2017 Today s music: Check Yo Self by Ice Cube Review Previously in 3110: Functional programming in Coq Logic in Coq Curry-Howard correspondence (proofs are programs)
malloc(), calloc(), realloc(), and free()
 1 next CITS2002 CITS2002 schedule Dynamic data structures Initially, we focused on scalar and array variables, whose size is known at compile-time. More recently, we've focused on arrays of values, whose
1 next CITS2002 CITS2002 schedule Dynamic data structures Initially, we focused on scalar and array variables, whose size is known at compile-time. More recently, we've focused on arrays of values, whose
Implemen'ng OCaml in OCaml
 1 An OCaml defini'on of OCaml evalua'on, or, Implemen'ng OCaml in OCaml COS 326 David Walker Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel permission granted to reuse
1 An OCaml defini'on of OCaml evalua'on, or, Implemen'ng OCaml in OCaml COS 326 David Walker Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel permission granted to reuse
MIDTERM EXAMINATION Douglas Wilhelm Harder EIT 4018 x T09:30:00P1H20M Rooms: RCH-103 and RCH-302
 ECE 250 Algorithms and Data Structures MIDTERM EXAMINATION Douglas Wilhelm Harder dwharder@uwaterloo.ca EIT 4018 x37023 2013-10-23T09:30:00P1H20M Rooms: RCH-103 and RCH-302 Instructions: Read and initial
ECE 250 Algorithms and Data Structures MIDTERM EXAMINATION Douglas Wilhelm Harder dwharder@uwaterloo.ca EIT 4018 x37023 2013-10-23T09:30:00P1H20M Rooms: RCH-103 and RCH-302 Instructions: Read and initial
Recursion. What is Recursion? Simple Example. Repeatedly Reduce the Problem Into Smaller Problems to Solve the Big Problem
 Recursion Repeatedly Reduce the Problem Into Smaller Problems to Solve the Big Problem What is Recursion? A problem is decomposed into smaller sub-problems, one or more of which are simpler versions of
Recursion Repeatedly Reduce the Problem Into Smaller Problems to Solve the Big Problem What is Recursion? A problem is decomposed into smaller sub-problems, one or more of which are simpler versions of
Programming Languages and Techniques (CIS120)
 Programming Languages and Techniques (CIS120) Lecture 7 January 30 th, 2015 Binary Search Trees (Lecture notes Chapter 7) ! Homework #1 feedback dope assignment, got a 96.4 the first time, careless mistake,
Programming Languages and Techniques (CIS120) Lecture 7 January 30 th, 2015 Binary Search Trees (Lecture notes Chapter 7) ! Homework #1 feedback dope assignment, got a 96.4 the first time, careless mistake,
Programming Languages and Compilers (CS 421)
 Programming Languages and Compilers (CS 421) Elsa L Gunter 2112 SC, UIUC http://courses.engr.illinois.edu/cs421 Based in part on slides by Mattox Beckman, as updated by Vikram Adve and Gul Agha 9/18/17
Programming Languages and Compilers (CS 421) Elsa L Gunter 2112 SC, UIUC http://courses.engr.illinois.edu/cs421 Based in part on slides by Mattox Beckman, as updated by Vikram Adve and Gul Agha 9/18/17
COMP-202. Recursion. COMP Recursion, 2011 Jörg Kienzle and others
 COMP-202 Recursion Recursion Recursive Definitions Run-time Stacks Recursive Programming Recursion vs. Iteration Indirect Recursion Lecture Outline 2 Recursive Definitions (1) A recursive definition is
COMP-202 Recursion Recursion Recursive Definitions Run-time Stacks Recursive Programming Recursion vs. Iteration Indirect Recursion Lecture Outline 2 Recursive Definitions (1) A recursive definition is
Project Compiler. CS031 TA Help Session November 28, 2011
 Project Compiler CS031 TA Help Session November 28, 2011 Motivation Generally, it s easier to program in higher-level languages than in assembly. Our goal is to automate the conversion from a higher-level
Project Compiler CS031 TA Help Session November 28, 2011 Motivation Generally, it s easier to program in higher-level languages than in assembly. Our goal is to automate the conversion from a higher-level
Recursion. Tracing Method Calls via a Stack. Beyond this lecture...
 Recursion EECS2030 B: Advanced Object Oriented Programming Fall 2018 CHEN-WEI WANG Recursion: Principle Recursion is useful in expressing solutions to problems that can be recursively defined: Base Cases:
Recursion EECS2030 B: Advanced Object Oriented Programming Fall 2018 CHEN-WEI WANG Recursion: Principle Recursion is useful in expressing solutions to problems that can be recursively defined: Base Cases:
Binary Search Trees. Carlos Moreno uwaterloo.ca EIT https://ece.uwaterloo.ca/~cmoreno/ece250
 Carlos Moreno cmoreno @ uwaterloo.ca EIT-4103 https://ece.uwaterloo.ca/~cmoreno/ece250 Previously, on ECE-250... We discussed trees (the general type) and their implementations. We looked at traversals
Carlos Moreno cmoreno @ uwaterloo.ca EIT-4103 https://ece.uwaterloo.ca/~cmoreno/ece250 Previously, on ECE-250... We discussed trees (the general type) and their implementations. We looked at traversals
Recap: ML s Holy Trinity
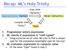 Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set
Recap: ML s Holy Trinity Expressions (Syntax) Exec-time Dynamic Values (Semantics) Compile-time Static Types 1. Programmer enters expression 2. ML checks if expression is well-typed Using a precise set
COMP 202 Recursion. CONTENTS: Recursion. COMP Recursion 1
 COMP 202 Recursion CONTENTS: Recursion COMP 202 - Recursion 1 Recursive Thinking A recursive definition is one which uses the word or concept being defined in the definition itself COMP 202 - Recursion
COMP 202 Recursion CONTENTS: Recursion COMP 202 - Recursion 1 Recursive Thinking A recursive definition is one which uses the word or concept being defined in the definition itself COMP 202 - Recursion
An experiment with variable binding, denotational semantics, and logical relations in Coq. Adam Chlipala University of California, Berkeley
 A Certified TypePreserving Compiler from Lambda Calculus to Assembly Language An experiment with variable binding, denotational semantics, and logical relations in Coq Adam Chlipala University of California,
A Certified TypePreserving Compiler from Lambda Calculus to Assembly Language An experiment with variable binding, denotational semantics, and logical relations in Coq Adam Chlipala University of California,
n What is its running time? 9/18/17 2 n poor_rev [1,2,3] = n (poor_rev [1] = n ((poor_rev [1] =
![n What is its running time? 9/18/17 2 n poor_rev [1,2,3] = n (poor_rev [1] = n ((poor_rev [1] = n What is its running time? 9/18/17 2 n poor_rev [1,2,3] = n (poor_rev [1] = n ((poor_rev [1] =](/thumbs/92/108912101.jpg) Recall Programming Languages and Compilers (CS 421) Elsa L Gunter 2112 SC, UIUC http://courses.engr.illinois.edu/cs421 Based in part on slides by Mattox Beckman, as updated by Vikram Adve and Gul Agha
Recall Programming Languages and Compilers (CS 421) Elsa L Gunter 2112 SC, UIUC http://courses.engr.illinois.edu/cs421 Based in part on slides by Mattox Beckman, as updated by Vikram Adve and Gul Agha
Recursion: Factorial (1) Recursion. Recursion: Principle. Recursion: Factorial (2) Recall the formal definition of calculating the n factorial:
 Recursion EECS2030: Advanced Object Oriented Programming Fall 2017 CHEN-WEI WANG Recursion: Factorial (1) Recall the formal definition of calculating the n factorial: 1 if n = 0 n! = n (n 1) (n 2) 3 2
Recursion EECS2030: Advanced Object Oriented Programming Fall 2017 CHEN-WEI WANG Recursion: Factorial (1) Recall the formal definition of calculating the n factorial: 1 if n = 0 n! = n (n 1) (n 2) 3 2
CSE 341 : Programming Languages Midterm, Spring 2015
 Name: CSE 341 : Programming Languages Midterm, Spring 2015 Please do not turn the page until 12:30. Rules: Closed book, closed note, except for one side of one 8.5x11in piece of paper. Please stop promptly
Name: CSE 341 : Programming Languages Midterm, Spring 2015 Please do not turn the page until 12:30. Rules: Closed book, closed note, except for one side of one 8.5x11in piece of paper. Please stop promptly
APCS-AB: Java. Recursion in Java December 12, week14 1
 APCS-AB: Java Recursion in Java December 12, 2005 week14 1 Check point Double Linked List - extra project grade Must turn in today MBCS - Chapter 1 Installation Exercises Analysis Questions week14 2 Scheme
APCS-AB: Java Recursion in Java December 12, 2005 week14 1 Check point Double Linked List - extra project grade Must turn in today MBCS - Chapter 1 Installation Exercises Analysis Questions week14 2 Scheme
SOME TYPICAL QUESTIONS, THEIR EXPECTED ANSWERS AND THINGS
 SOME TYPICAL QUESTIONS, THEIR EXPECTED ANSWERS AND THINGS TO WATCH OUT FOR ON THE TEST Nivedita Chopra 1: Contracts (The following question is Question 1 on Written Homework 2) Consider the following implementation
SOME TYPICAL QUESTIONS, THEIR EXPECTED ANSWERS AND THINGS TO WATCH OUT FOR ON THE TEST Nivedita Chopra 1: Contracts (The following question is Question 1 on Written Homework 2) Consider the following implementation
sum: tree -> int sum_leaf: tree -> int sum_leaf: tree -> int Representing Trees Next: Lets get cosy with Recursion Sum up the leaf values. E.g.
 Representing Trees Node Next: Lets get cosy with Recursion 1 2 3 1 Node 2 3 Node(Node( 1, 2), 3) sum: tree -> int Next: Lets get cosy with Recursion Sum up the leaf values. E.g. # let t0 = sum Node(Node(
Representing Trees Node Next: Lets get cosy with Recursion 1 2 3 1 Node 2 3 Node(Node( 1, 2), 3) sum: tree -> int Next: Lets get cosy with Recursion Sum up the leaf values. E.g. # let t0 = sum Node(Node(
Chapter 10 Recursion
 Chapter 10 Recursion Written by Dr. Mark Snyder [minor edits for this semester by Dr. Kinga Dobolyi] Recursion implies that something is defined in terms of itself. We will see in detail how code can be
Chapter 10 Recursion Written by Dr. Mark Snyder [minor edits for this semester by Dr. Kinga Dobolyi] Recursion implies that something is defined in terms of itself. We will see in detail how code can be
Variables and Bindings
 Net: Variables Variables and Bindings Q: How to use variables in ML? Q: How to assign to a variable? # let = 2+2;; val : int = 4 let = e;; Bind the value of epression e to the variable Variables and Bindings
Net: Variables Variables and Bindings Q: How to use variables in ML? Q: How to assign to a variable? # let = 2+2;; val : int = 4 let = e;; Bind the value of epression e to the variable Variables and Bindings
Recall our recursive multiply algorithm:
 Recall our recursive multiply algorithm: PRECONDITION: x and y are both binary bit arrays of length n, n a power of 2. POSTCONDITION: Returns a binary bit array equal to the product of x and y. REC MULTIPLY
Recall our recursive multiply algorithm: PRECONDITION: x and y are both binary bit arrays of length n, n a power of 2. POSTCONDITION: Returns a binary bit array equal to the product of x and y. REC MULTIPLY
Warmup January 9th, What is the value of the following C expression? 8*9 % 10/ 2
 Warmup January 9th, 2018 What is the value of the following C expression? 8*9 % 10/ 2 Warmup January 11th, 2018 What is the value of the following C expression? ( -42 3!= 3) && ( -3 < -2 < -1) Warmup January
Warmup January 9th, 2018 What is the value of the following C expression? 8*9 % 10/ 2 Warmup January 11th, 2018 What is the value of the following C expression? ( -42 3!= 3) && ( -3 < -2 < -1) Warmup January
Certified Programming with Dependent Types
 1/30 Certified Programming with Dependent Types Inductive Predicates Niels van der Weide March 7, 2017 2/30 Last Time We discussed inductive types Print nat. (* Inductive nat : Set := O : nat S : nat nat*)
1/30 Certified Programming with Dependent Types Inductive Predicates Niels van der Weide March 7, 2017 2/30 Last Time We discussed inductive types Print nat. (* Inductive nat : Set := O : nat S : nat nat*)
Notes for Recitation 8
 6.04/8.06J Mathematics for Computer Science October 5, 00 Tom Leighton and Marten van Dijk Notes for Recitation 8 Build-up error Recall a graph is connected iff there is a path between every pair of its
6.04/8.06J Mathematics for Computer Science October 5, 00 Tom Leighton and Marten van Dijk Notes for Recitation 8 Build-up error Recall a graph is connected iff there is a path between every pair of its
The Haskell HOP: Higher-order Programming
 The Haskell HOP: Higher-order Programming COS 441 Slides 6 Slide content credits: Ranjit Jhala, UCSD Agenda Haskell so far: First-order functions This time: Higher-order functions: Functions as data, arguments
The Haskell HOP: Higher-order Programming COS 441 Slides 6 Slide content credits: Ranjit Jhala, UCSD Agenda Haskell so far: First-order functions This time: Higher-order functions: Functions as data, arguments
Recursion. Chapter 7. Copyright 2012 by Pearson Education, Inc. All rights reserved
 Recursion Chapter 7 Contents What Is Recursion? Tracing a Recursive Method Recursive Methods That Return a Value Recursively Processing an Array Recursively Processing a Linked Chain The Time Efficiency
Recursion Chapter 7 Contents What Is Recursion? Tracing a Recursive Method Recursive Methods That Return a Value Recursively Processing an Array Recursively Processing a Linked Chain The Time Efficiency
Identify recursive algorithms Write simple recursive algorithms Understand recursive function calling
 Recursion Identify recursive algorithms Write simple recursive algorithms Understand recursive function calling With reference to the call stack Compute the result of simple recursive algorithms Understand
Recursion Identify recursive algorithms Write simple recursive algorithms Understand recursive function calling With reference to the call stack Compute the result of simple recursive algorithms Understand
COS 326 David Walker Princeton University
 Functional Abstractions over Imperative Infrastructure and Lazy Evaluation COS 326 David Walker Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel permission granted to reuse
Functional Abstractions over Imperative Infrastructure and Lazy Evaluation COS 326 David Walker Princeton University slides copyright 2013-2015 David Walker and Andrew W. Appel permission granted to reuse
