Graph algorithms based on infinite automata: logical descriptions and usable constructions
|
|
|
- Clarence Hutchinson
- 5 years ago
- Views:
Transcription
1 Graph algorithms based on infinite automata: logical descriptions and usable constructions Bruno Courcelle (joint work with Irène Durand) Bordeaux-1 University, LaBRI (CNRS laboratory) 1
2 Overview Algorithmic meta-theorems provide existence proofs of relatively efficient (FPT or XP) graph algorithms from logical descriptions of (difficult) problems. We give usable and tested constructions based on: - problem descriptions in extensions of MSO (Monadic Second-Order) logic, - hierarchical decompositions of graphs, - automata with infinitely many states. 2
3 Our graph parameter is clique-width, because : - it is easier to handle than (the very popular) tree-width for constructing automata, and more powerful : bounded tree-width implies bounded clique-width, - it is defined in terms of elementary graph operations, hence is easier than the equivalent notion of rank-width, - it works equally easily on directed graphs. The system AUTOGRAPH (by I.Durand) and the corresponding theory [B.C.&I.D.: Automata for the verification of monadic second-order graph properties, J. Applied Logic, 10 (2012) ] are based on clique-width. 3
4 Theorem : For each k, every MSO graph property P can be checked by a finite automaton that recognizes terms over the finite set of operations that generates the graphs of clique-width at most k. This automaton is computable (i.e., one can compute its set of states and its transition table) in theory but not in practice because it is much too large as soon as k > 3. To overcome this difficulty, we have introduced fly-automata (in French automates programmés ) whose states and transitions are described and not tabulated. Only the transitions necessary for an input term are computed, on the fly. 4
5 As states are not listed, a fly-automaton can use an infinite set of states and so, it can recognize sets of words, terms or graphs that are not monadic second-order definable : the language a n b n, the set of regular graphs (all vertices of same degree). It can also compute values: the number of p-colorings or of acyclic p-colorings of a graph. We construct fly-automata in uniform ways from logical descriptions of problems. We develop a theory of (some aspects of) dynamic programming. 5
6 Definition (skip?) : Monadic Second-Order Logic First-order logic extended with (quantified) variables denoting subsets of the domains. MSO (expressible) properties : transitive closure, properties of paths, connectedness, planarity (via Kuratowski), p-colorability. Examples of formulas for G = ( V G, edg G (.,.) ), undirected G is 3-colorable : X,Y ( X Y = u,v { edg(u,v) [(u X v X) (u Y v Y) (u X Y v X Y) ] } ) 6
7 G is not connected : Z ( x Z y Z ( u,v (u Z edg(u,v) v Z) ) Transitive and reflexive closure : TC(R, x, y) : Z { Z is R-closed x Z y Z } where Z is R-closed is defined by : u,v (u Z R(u,v) v Z) The relation R can be defined by a formula as in : x,y (x Y y Y TC( u Y v Y edg(u,v), x, y) expressing that G[Y ] is connected ( Y is free in R). 7
8 Application : Planarity is MSO-expressible (no minor K 5 or K 3,3 ). Non-MSO-expressible properties - G is isomorphic to K p,p for some p (p is not fixed; needs equipotence of two sets, hence quantification over binary relations to find if there is a bijection). - G has a nontrivial automorphism, or is regular (has all vertices of same degree). Reference : B.C. & J. Engelfriet : Graph structure and monadic secondorder logic, Cambridge University Press,
9 Definition (skip?) : Clique-width It is defined from graph operations. Graphs are simple, directed or not, and labelled by a, b, c,.... A vertex labelled by a is called an a-vertex. One binary operation: disjoint union : Unary operations: edge addition denoted by Add a,b Add a,b (G) is G augmented with undirected edges between every a-vertex and every b-vertex. The number of added edges depends on the argument graph. H = Add a,b (G) ; only 5 new edges added 9
10 Directed edges can be defined similarly. Vertex relabellings : Relab a b (G) is G with every a-vertex is made into a b-vertex Basic graphs : those with a single vertex a, labelled by a. Definition: A graph G has clique-width (denoted by cwd(g)) < k G=G(t) is defined by a term t using < k labels. Example : Cliques have clique-width 2. K n is defined by t n where t n+1 = Relab b a ( Add a,b (t n b) ) 10
11 The parsing problem: construction of terms, i.e. of decompositions. Automata take terms as inputs, not graphs : the parsing must be done before. (Graph automata do not exist in any satisfactory way). Deciding if cwd(g) < k (for input (G,k) ) is NP-complete (same for tree-width). There are FPT approximation algorithms, taking time f(k).n3, that output the following for given k and graph G with n vertices: (i) either the answer that cwd(g) > k, (ii) or a term witnessing that cwd(g) < g(k). Every FPT algorithm taking terms as inputs can be converted into an FPT algorithm taking graphs as inputs. (It parses and then checks). 11
12 However, graphs arising from concrete problems are not random. They usually have natural hierarchical decompositions from which terms of small tree-width or clique-width are not hard to construct. This situation arises in compilation (flow-graphs of structured programs), in linguistics and in chemistry. It is thus interesting to develop specific parsing algorithms for graph classes relevant to particular applications. 12
13 The MSO meta-theorem through finite automata: the basic scheme k ϕ (logical formula) Automaton Constructor Yes G Graph Analyzer t A(ϕ,k )) Error : cwd(g) > k k = g(k) Steps are done once for all, independently of G A(ϕ,k ): finite automaton, running on terms t cwd can be replaced by tree-width or rank-width. No 13
14 The MSO meta-theorem through fly-automata: a simpler scheme ϕ (MSO formula) 14 Fly-automaton Constructor Yes G Graph Analyzer t A(ϕ) No A(ϕ): infinite fly-automaton on the countable set of all graph operations that define clique-width. The time taken by A(ϕ) depends on t (the labels that occur in this term), not only on the size of G.
15 Automata that check graph properties We want to check a property P(G), for G = G(t), t T(F). For each labelled graph G, we define a piece of information q(g) that encodes properties of G and values attached to G, so that we have: (i) inductive behaviour of q : for f F and graphs G,H: q(f(g,h)) = f q (q(g), q(h)) for some computable function f q. (ii) P(G) can be decided from q(g). 15
16 Then q(g(t/u)) is computed bottom-up in a term t, for each node u. This information is relative to the graph G(t/u) (a subgraph of G ) defined by the subterm t/u of t issued from u. q(g(t/u)) is a state of a finite or infinite deterministic bottom-up automaton. These automata formalize some form of dynamic programming. Two possibilities: Direct construction for a well-understood graph property or automatic construction from an MSO formula. 16
17 Direct construction 1 : Connectedness. The state at node u is the set of types (sets of labels) of the connected components of the graph G(t/u). For k labels (k = bound on clique-width), the set of states has size < 2 ^ (2 ^ k). Proved lower bound : 2 ^ (2 ^ k/2). Impossible to compile the automaton (i.e., to list the transitions). Example of a state : q = { {a}, {a,b}, {b,c,d}, {b,d,f } }, (a,b,c,d,f : labels). Some transitions : Add a,c : q { {a,b,c,d}, {b,d,f } }, Relab a b: q { {b}, {b,c,d}, {b,d,f } } Transitions for : union of sets of types. Note : Also state (p,p) if G(t/u) has > 2 connected components, all of type p. 17
18 In a fly-automaton, states and transitions are computed and not tabulated. We can allow fly-automata with infinitely many states and, also, with outputs : numbers, finite sets of tuples of numbers, etc. Example continued : For computing the number of connected components, we use states such as : q = { ({a}, 4 ), ({a,b}, 2), ( {b,c,d},2), ( {b,d,f },3) }, where 4, 2, 2, 3 are the numbers of connected components of respective types {a}, {a,b}, {b,c,d}, {b,d,f }. 18
19 Direct construction 2 : Regularity (not MSO) A state is a tuple of counters that indicates, for each label a: the number of a-vertices and the common degree of all a-vertices. The state is Error if two a-vertices have different degrees: the edge addition operations will add the same numbers of edges to these vertices, hence the considered graph cannot be regular. 19
20 Definition : Fly-automaton (FA) A = < F, Q, δ, Out > F : finite or countable (effective) signature (set of operations), Q : finite or countable (effective) set of states (integers, pairs of integers, finite sets of integers: states can be encoded as finite words, integers in binary), Out : Q D (an effective domain, i.e., set of finite words), computable. δ : computable (bottom-up) transition function Nondeterministic case : δ is finitely multi-valued. 20
21 This automaton defines a computable function : T(F) D (or : T(F) P(D) if it is not deterministic) If D = { True, False }, it defines a decidable property, equivalently, a decidable subset of T(F). Deterministic computation of a nondeterministic FA : bottom-up computation of finite sets of states (classical simulation of the determinized automaton): these states are the useful ones of the determinized automaton; these sets are finite because the transition function is finitely multivalued. Fly-automata are implicitly determinized and they run deterministically 21
22 Computation time of a fly-automaton F : all graph operations, F k : those using labels 1,, k. On term t T(F k ) defining G(t) with n vertices, if a fly-automaton takes time bounded by : (k + n) c it is a P-FA (a polynomial-time FA), f(k).n c it is an FPT-FA, a.n g(k) it is an XP-FA. The associated algorithm is, respectively, polynomial-time, FPT or XP for clique-width as parameter. 22
23 Theorem [B.C & I.D.] : For each MSO property P, one can construct a single infinite FPT-FA over F that recognizes the terms t in T(F) such that P(G(t)) holds. For each k, its restriction to the finite signature F k is finite. Consequence : The same automaton (the same model-checking program) can be used for graphs of any clique-width. 23
24 Some experiments using FA (by Irène Durand) Number of 3-colorings of the 6 x 525 grid (of clique-width 8) in 10 minutes. 4-acyclic-colorability of the Petersen graph (clique-width 6) in 1.5 minutes. (3-colorable but not acyclically; red and green vertices induce a cycle). 24
25 The McGee graph is defined by a term with 10 labels (optimal?) of size 99 and depth 76. It is 3-acyclically colourable. Checked in 40 minutes. (Even in 2 seconds by enumerating the accepting runs, and stopping as soon as a success is found). 25
26 Constructions of automata (A) For Boolean and first-order constructions of properties and functions. P Q, P Q, P, g(α 1,, α p ) where g is poly-time computable (can be a relation such as a comparison of numbers), P[X Y] : property of subgraph induced on X Y (set term) First-order (FO) quantifications : x.p(x), x =tuple of FO var. Set of satisfying assignments : Sat x.p(x) (a query) Number of satisfying assignments : # x.p(x). Set of values α(x) such that P(x) is true. 26
27 Type of automata Finite P-FA FPT-FA XP-FA P Q,P Q, P, P[X Y] Finite P FPT XP g(α 1,, α p ), α(x Y) P FPT XP x.p(x), x.p(x) Finite P FPT XP Sat x.p(x), # x.p(x) P P FPT XP SetVal α(x) / P(x) ) P FPT XP Finite : Finite signature and sets of states. We have nice preservations of the types of automata. 27
28 Main proof ideas : (generalized) existential quantifications : x.p(x), # x.p(x), Sat x.p(x), where x is a p-tuple of first-order variables. Handling existential quantifications and sets of satisfying assignments needs to transform a deterministic automaton A for P(x) into a nondeterministic one B (that decides x.p(x)). But, its nondeterminism degree is < n p, hence polynomially bounded in the number n of vertices. We get a P-FA, an FPT-FA or an XP-FA if A is so. Same idea for Sat x.p(x). For # x.p(x), we transform B into a deterministic FA that counts the number of its accepting runs. 28
29 (B) Monadic second-order constructions The spectrum SpX.P(X) of a property P(X) is the set of tuples of cardinalities of the components of the tuples X that satisfy P(X). The multispectrum MSpX.P(X) is the corresponding multiset of tuples of SpX.P(X) hence, for X = X (one component): the set of pairs (m,i) such that i > 0 is the number of sets X of cardinality m that satisfy P(X). For a p-tuple X, a multispectrum is a function [ 0,n ] p [ 0,2 p.n ]; it can be encoded in size O(n p.log(2 p.n ) ) = O(n p+1 ). 29
30 Type of automaton A for P(X) Finite P-FA FPT-FA XP-FA X.P(X), X.P(X) Finite P FPT XP MSp X.P(X), Sp X.P(X), # X.P(X), P P FPT XP MaxCard X.P(X) P-FA means : A is P-FA and B (the associated nondeterministic FA) has a polynomially bounded nondeterminism degree. Similar for FPT and XP (with FPT- or XP-bounded nondeterminism degree). There are more contraints for the preservation of types of automata than for FO constructions. Note: the automata are constructed in the same way in all cases; the nondeterminism degree concerns only the computation time. 30
31 Some non-mso examples : (1) Equitable p-coloring : X 1,,X p (Partition(X 1,,X p ) Stable[X 1 ]... Stable[X p ] X 1 = = X i-1 > X i = = X p > X 1-1). It is FPT (for fixed p). (2) Partition into 2 regular graphs : X (Reg[X] Reg[X c ] ) Reg[X] means that the subgraph induced on X is regular; X c is the complement of X. It is XP. 31
32 (3) Counting p-colorings with particular properties, e.g., acyclic or equitable. (4) Minimizing the use of a particular color: this gives a distance to p-colorability for a graph that p+1-colorable but not p-colorable. In general, we can handle properties and functions of the forms X.P(X), MSp X.P(X), Sp X.P(X), # X.P(X) where P(X) is a Boolean combination of properties for which we have constructed fly-automata (Reg, NoCycle, Stable, etc ). 32
33 The system AUTOGRAPH (by I. Durand) Fly-automata for basic graph properties : Clique, Stable (no edge), Link(X,Y), NoCycle, Connectedness, Regularity, Partition(X, Y, Z), etc and functions : #Link(X,Y) (number of edges between X and Y), Maximum degree. 33
34 Procedures for combining fly-automata (combinations of descriptions) product : for P Q, P Q, g(α 1,, α p ) A A/X : for P P[X], (P in induced subgraph on X) and A A/(X Y) (Y Z) c for relativization to set terms. image automaton: A h(a) : in the transitions of A, each function symbol f is replaced by h(f) ; makes h(a) nondeterministic : for P(X) X.P(X) 34
35 Procedures to build automata that compute functions: #X.P(X) : the number of tuples X that satisfy P(X) in the input term (hence, in the associated graph). SpX.P(X) : the set of tuples of cardinalities of the components of the X that satisfy P(X). MSpX.P(X) : the corresponding multiset. SetValX.α(X)/P(X) : the set of values of α(x) for the tuples X that satisfy P(X). For each case, a procedure transforms FA for P(X) and α(x) into FA that compute the associated functions. (These transformations do not depend on P(X) and α(x).) 35
36 Conclusion In most cases, we get XP (or FPT ones) algorithms, that can be obtained independently. These algorithms are based on fly-automata, that can be quickly constructed from logical descriptions flexibility. These constructions are implemented. Tests have been made for colorability and connectedness problems. Thank you for suggesting interesting problems that could fit in this framework. 36
Infinite transducers on terms denoting graphs
 Infinite transducers on terms denoting graphs Irène Durand and Bruno Courcelle LaBRI, Université de Bordeaux June, 2013 European Lisp Symposium, ELS2013 2/30 Objectives What : Compute information about
Infinite transducers on terms denoting graphs Irène Durand and Bruno Courcelle LaBRI, Université de Bordeaux June, 2013 European Lisp Symposium, ELS2013 2/30 Objectives What : Compute information about
On Seese s Conjecture. Bruno Courcelle. Université Bordeaux 1, LaBRI
 On Seese s Conjecture Bruno Courcelle Université Bordeaux 1, LaBRI Summary 1. Graphs, Languages, Theories 2. MS-compatible structure transformations and MS-transductions 3. Seese s Conjecture 4. Tree-width
On Seese s Conjecture Bruno Courcelle Université Bordeaux 1, LaBRI Summary 1. Graphs, Languages, Theories 2. MS-compatible structure transformations and MS-transductions 3. Seese s Conjecture 4. Tree-width
Logic in Algorithmic Graph Structure Theory
 Logic in Algorithmic Graph Structure Theory Stephan Kreutzer Technical University Berlin Bruno s workshop June 18-20, 2012, LaBRI, Bordeaux STEPHAN KREUTZER LOGIC IN ALGORITHMIC GRAPH STRUCTURE THEORY
Logic in Algorithmic Graph Structure Theory Stephan Kreutzer Technical University Berlin Bruno s workshop June 18-20, 2012, LaBRI, Bordeaux STEPHAN KREUTZER LOGIC IN ALGORITHMIC GRAPH STRUCTURE THEORY
CONNECTIVITY CHECK IN 3-CONNECTED PLANAR GRAPHS WITH OBSTACLES
 CONNECTIVITY CHECK IN 3-CONNECTED PLANAR GRAPHS WITH OBSTACLES M. M. KANTÉ 1 B. COURCELLE 1 C. GAVOILLE 1 A. TWIGG 2 1 Université Bordeaux 1, LaBRI, CNRS. 2 Computer Laboratory, Cambridge University. Topological
CONNECTIVITY CHECK IN 3-CONNECTED PLANAR GRAPHS WITH OBSTACLES M. M. KANTÉ 1 B. COURCELLE 1 C. GAVOILLE 1 A. TWIGG 2 1 Université Bordeaux 1, LaBRI, CNRS. 2 Computer Laboratory, Cambridge University. Topological
FEDOR V. FOMIN. Lectures on treewidth. The Parameterized Complexity Summer School 1-3 September 2017 Vienna, Austria
 FEDOR V. FOMIN Lectures on treewidth The Parameterized Complexity Summer School 1-3 September 2017 Vienna, Austria Why treewidth? Very general idea in science: large structures can be understood by breaking
FEDOR V. FOMIN Lectures on treewidth The Parameterized Complexity Summer School 1-3 September 2017 Vienna, Austria Why treewidth? Very general idea in science: large structures can be understood by breaking
Fixed-Parameter Algorithms, IA166
 Fixed-Parameter Algorithms, IA166 Sebastian Ordyniak Faculty of Informatics Masaryk University Brno Spring Semester 2013 Introduction Outline 1 Introduction Algorithms on Locally Bounded Treewidth Layer
Fixed-Parameter Algorithms, IA166 Sebastian Ordyniak Faculty of Informatics Masaryk University Brno Spring Semester 2013 Introduction Outline 1 Introduction Algorithms on Locally Bounded Treewidth Layer
Introduction III. Graphs. Motivations I. Introduction IV
 Introduction I Graphs Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Graph theory was introduced in the 18th century by Leonhard Euler via the Königsberg
Introduction I Graphs Computer Science & Engineering 235: Discrete Mathematics Christopher M. Bourke cbourke@cse.unl.edu Graph theory was introduced in the 18th century by Leonhard Euler via the Königsberg
Tree Decompositions Why Matroids are Useful
 Petr Hliněný, W. Graph Decompositions, Vienna, 2004 Tree Decompositions Why Matroids are Useful Petr Hliněný Tree Decompositions Why Matroids are Useful Department of Computer Science FEI, VŠB Technical
Petr Hliněný, W. Graph Decompositions, Vienna, 2004 Tree Decompositions Why Matroids are Useful Petr Hliněný Tree Decompositions Why Matroids are Useful Department of Computer Science FEI, VŠB Technical
Graph Theory S 1 I 2 I 1 S 2 I 1 I 2
 Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
Graph Theory S I I S S I I S Graphs Definition A graph G is a pair consisting of a vertex set V (G), and an edge set E(G) ( ) V (G). x and y are the endpoints of edge e = {x, y}. They are called adjacent
CHAPTER 8. Copyright Cengage Learning. All rights reserved.
 CHAPTER 8 RELATIONS Copyright Cengage Learning. All rights reserved. SECTION 8.3 Equivalence Relations Copyright Cengage Learning. All rights reserved. The Relation Induced by a Partition 3 The Relation
CHAPTER 8 RELATIONS Copyright Cengage Learning. All rights reserved. SECTION 8.3 Equivalence Relations Copyright Cengage Learning. All rights reserved. The Relation Induced by a Partition 3 The Relation
W[1]-hardness. Dániel Marx. Recent Advances in Parameterized Complexity Tel Aviv, Israel, December 3, 2017
![W[1]-hardness. Dániel Marx. Recent Advances in Parameterized Complexity Tel Aviv, Israel, December 3, 2017 W[1]-hardness. Dániel Marx. Recent Advances in Parameterized Complexity Tel Aviv, Israel, December 3, 2017](/thumbs/92/108052593.jpg) 1 W[1]-hardness Dániel Marx Recent Advances in Parameterized Complexity Tel Aviv, Israel, December 3, 2017 2 Lower bounds So far we have seen positive results: basic algorithmic techniques for fixed-parameter
1 W[1]-hardness Dániel Marx Recent Advances in Parameterized Complexity Tel Aviv, Israel, December 3, 2017 2 Lower bounds So far we have seen positive results: basic algorithmic techniques for fixed-parameter
Recognizability Equals Definability for Graphs of Bounded Treewidth and Bounded Chordality
 Recognizability Equals Definability for Graphs of Bounded Treewidth and Bounded Chordality Hans L. Bodlaender, Utrecht University and Eindhoven University of Technology Pinar Heggernes, University of Bergen
Recognizability Equals Definability for Graphs of Bounded Treewidth and Bounded Chordality Hans L. Bodlaender, Utrecht University and Eindhoven University of Technology Pinar Heggernes, University of Bergen
Counting multiplicity over infinite alphabets
 Counting multiplicity over infinite alphabets Amal Dev Manuel and R. Ramanujam The Institute of Mathematical Sciences, Chennai, India {amal,jam}@imsc.res.in Summary Motivation for infinite data. We need
Counting multiplicity over infinite alphabets Amal Dev Manuel and R. Ramanujam The Institute of Mathematical Sciences, Chennai, India {amal,jam}@imsc.res.in Summary Motivation for infinite data. We need
PART 1 GRAPHICAL STRUCTURE
 PART 1 GRAPHICAL STRUCTURE in this web service in this web service 1 Treewidth and Hypertree Width Georg Gottlob, Gianluigi Greco, Francesco Scarcello This chapter covers methods for identifying islands
PART 1 GRAPHICAL STRUCTURE in this web service in this web service 1 Treewidth and Hypertree Width Georg Gottlob, Gianluigi Greco, Francesco Scarcello This chapter covers methods for identifying islands
NP-Completeness. Algorithms
 NP-Completeness Algorithms The NP-Completeness Theory Objective: Identify a class of problems that are hard to solve. Exponential time is hard. Polynomial time is easy. Why: Do not try to find efficient
NP-Completeness Algorithms The NP-Completeness Theory Objective: Identify a class of problems that are hard to solve. Exponential time is hard. Polynomial time is easy. Why: Do not try to find efficient
Slides for Faculty Oxford University Press All rights reserved.
 Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
Oxford University Press 2013 Slides for Faculty Assistance Preliminaries Author: Vivek Kulkarni vivek_kulkarni@yahoo.com Outline Following topics are covered in the slides: Basic concepts, namely, symbols,
A graph is finite if its vertex set and edge set are finite. We call a graph with just one vertex trivial and all other graphs nontrivial.
 2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
2301-670 Graph theory 1.1 What is a graph? 1 st semester 2550 1 1.1. What is a graph? 1.1.2. Definition. A graph G is a triple (V(G), E(G), ψ G ) consisting of V(G) of vertices, a set E(G), disjoint from
Interaction Between Input and Output-Sensitive
 Interaction Between Input and Output-Sensitive Really? Mamadou M. Kanté Université Blaise Pascal - LIMOS, CNRS Enumeration Algorithms Using Structure, Lorentz Institute, August 26 th, 2015 1 Introduction
Interaction Between Input and Output-Sensitive Really? Mamadou M. Kanté Université Blaise Pascal - LIMOS, CNRS Enumeration Algorithms Using Structure, Lorentz Institute, August 26 th, 2015 1 Introduction
Treewidth and graph minors
 Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
Treewidth and graph minors Lectures 9 and 10, December 29, 2011, January 5, 2012 We shall touch upon the theory of Graph Minors by Robertson and Seymour. This theory gives a very general condition under
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES
 DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
( A(x) B(x) C(x)) (A(x) A(y)) (C(x) C(y))
 1 Introduction Finite model theory studies the expressive power of logics on finite models. Classical model theory, on the other hand, concentrates on infinite structures: its origins are in mathematics,
1 Introduction Finite model theory studies the expressive power of logics on finite models. Classical model theory, on the other hand, concentrates on infinite structures: its origins are in mathematics,
Expressiveness and Complexity of a Graph Logic
 1 Expressiveness and Complexity of a Graph Logic (Cambridge) joint work with Philippa Gardner (Imperial College) and Giorgio Ghelli (Pisa) 2 A View of Process Algebras A term algebra T given by a functional
1 Expressiveness and Complexity of a Graph Logic (Cambridge) joint work with Philippa Gardner (Imperial College) and Giorgio Ghelli (Pisa) 2 A View of Process Algebras A term algebra T given by a functional
Computability Theory
 CS:4330 Theory of Computation Spring 2018 Computability Theory Other NP-Complete Problems Haniel Barbosa Readings for this lecture Chapter 7 of [Sipser 1996], 3rd edition. Sections 7.4 and 7.5. The 3SAT
CS:4330 Theory of Computation Spring 2018 Computability Theory Other NP-Complete Problems Haniel Barbosa Readings for this lecture Chapter 7 of [Sipser 1996], 3rd edition. Sections 7.4 and 7.5. The 3SAT
Foundations of Computer Science Spring Mathematical Preliminaries
 Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
Foundations of Computer Science Spring 2017 Equivalence Relation, Recursive Definition, and Mathematical Induction Mathematical Preliminaries Mohammad Ashiqur Rahman Department of Computer Science College
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES
 DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
DISTINGUISHING NUMBER AND ADJACENCY PROPERTIES ANTHONY BONATO AND DEJAN DELIĆ Dedicated to the memory of Roland Fraïssé. Abstract. The distinguishing number of countably infinite graphs and relational
Assignment 4 Solutions of graph problems
 Assignment 4 Solutions of graph problems 1. Let us assume that G is not a cycle. Consider the maximal path in the graph. Let the end points of the path be denoted as v 1, v k respectively. If either of
Assignment 4 Solutions of graph problems 1. Let us assume that G is not a cycle. Consider the maximal path in the graph. Let the end points of the path be denoted as v 1, v k respectively. If either of
Graph Theory: Introduction
 Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Graph Theory: Introduction Pallab Dasgupta, Professor, Dept. of Computer Sc. and Engineering, IIT Kharagpur pallab@cse.iitkgp.ernet.in Resources Copies of slides available at: http://www.facweb.iitkgp.ernet.in/~pallab
Math 776 Graph Theory Lecture Note 1 Basic concepts
 Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Math 776 Graph Theory Lecture Note 1 Basic concepts Lectured by Lincoln Lu Transcribed by Lincoln Lu Graph theory was founded by the great Swiss mathematician Leonhard Euler (1707-178) after he solved
Hardness of Subgraph and Supergraph Problems in c-tournaments
 Hardness of Subgraph and Supergraph Problems in c-tournaments Kanthi K Sarpatwar 1 and N.S. Narayanaswamy 1 Department of Computer Science and Engineering, IIT madras, Chennai 600036, India kanthik@gmail.com,swamy@cse.iitm.ac.in
Hardness of Subgraph and Supergraph Problems in c-tournaments Kanthi K Sarpatwar 1 and N.S. Narayanaswamy 1 Department of Computer Science and Engineering, IIT madras, Chennai 600036, India kanthik@gmail.com,swamy@cse.iitm.ac.in
On Structural Parameterizations of the Matching Cut Problem
 On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
On Structural Parameterizations of the Matching Cut Problem N. R. Aravind, Subrahmanyam Kalyanasundaram, and Anjeneya Swami Kare Department of Computer Science and Engineering, IIT Hyderabad, Hyderabad,
A Survey on Graph Automata and Tree-Width
 CHENNAI MATHEMATICAL INSTITUTE MASTERS THESIS A Survey on Graph Automata and Tree-Width Author: Adwitee Roy Supervisor: Aiswarya Cyriac A thesis submitted in partial fulfillment of the requirements for
CHENNAI MATHEMATICAL INSTITUTE MASTERS THESIS A Survey on Graph Automata and Tree-Width Author: Adwitee Roy Supervisor: Aiswarya Cyriac A thesis submitted in partial fulfillment of the requirements for
Reflection in the Chomsky Hierarchy
 Reflection in the Chomsky Hierarchy Henk Barendregt Venanzio Capretta Dexter Kozen 1 Introduction We investigate which classes of formal languages in the Chomsky hierarchy are reflexive, that is, contain
Reflection in the Chomsky Hierarchy Henk Barendregt Venanzio Capretta Dexter Kozen 1 Introduction We investigate which classes of formal languages in the Chomsky hierarchy are reflexive, that is, contain
DISCRETE MATHEMATICS
 DISCRETE MATHEMATICS WITH APPLICATIONS THIRD EDITION SUSANNA S. EPP DePaul University THOIVISON * BROOKS/COLE Australia Canada Mexico Singapore Spain United Kingdom United States CONTENTS Chapter 1 The
DISCRETE MATHEMATICS WITH APPLICATIONS THIRD EDITION SUSANNA S. EPP DePaul University THOIVISON * BROOKS/COLE Australia Canada Mexico Singapore Spain United Kingdom United States CONTENTS Chapter 1 The
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Acyclic Subgraphs of Planar Digraphs
 Acyclic Subgraphs of Planar Digraphs Noah Golowich Research Science Institute Department of Mathematics Massachusetts Institute of Technology Cambridge, Massachusetts, U.S.A. ngolowich@college.harvard.edu
Acyclic Subgraphs of Planar Digraphs Noah Golowich Research Science Institute Department of Mathematics Massachusetts Institute of Technology Cambridge, Massachusetts, U.S.A. ngolowich@college.harvard.edu
FIRST-ORDER QUERY EVALUATION ON STRUCTURES OF BOUNDED DEGREE
 Logical Methods in Computer Science Vol. 7 (2:20) 2011, pp. 1 8 www.lmcs-online.org Submitted Nov. 9, 2010 Published Jun. 29, 2011 FIRST-ORDER QUERY EVALUATION ON STRUCTURES OF BOUNDED DEGREE a INRIA and
Logical Methods in Computer Science Vol. 7 (2:20) 2011, pp. 1 8 www.lmcs-online.org Submitted Nov. 9, 2010 Published Jun. 29, 2011 FIRST-ORDER QUERY EVALUATION ON STRUCTURES OF BOUNDED DEGREE a INRIA and
Introduction to Graph Theory
 Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
9.1 Cook-Levin Theorem
 CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs { }
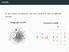 motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
motifs In the context of networks, the term motif may refer to di erent notions. Subgraph motifs Coloured motifs G M { } 2 subgraph motifs 3 motifs Find interesting patterns in a network. 4 motifs Find
Material from Recitation 1
 Material from Recitation 1 Darcey Riley Frank Ferraro January 18, 2011 1 Introduction In CSC 280 we will be formalizing computation, i.e. we will be creating precise mathematical models for describing
Material from Recitation 1 Darcey Riley Frank Ferraro January 18, 2011 1 Introduction In CSC 280 we will be formalizing computation, i.e. we will be creating precise mathematical models for describing
Clique-Width for Four-Vertex Forbidden Subgraphs
 Clique-Width for Four-Vertex Forbidden Subgraphs Andreas Brandstädt 1 Joost Engelfriet 2 Hoàng-Oanh Le 3 Vadim V. Lozin 4 March 15, 2005 1 Institut für Informatik, Universität Rostock, D-18051 Rostock,
Clique-Width for Four-Vertex Forbidden Subgraphs Andreas Brandstädt 1 Joost Engelfriet 2 Hoàng-Oanh Le 3 Vadim V. Lozin 4 March 15, 2005 1 Institut für Informatik, Universität Rostock, D-18051 Rostock,
More on Polynomial Time and Space
 CpSc 8390 Goddard Fall15 More on Polynomial Time and Space 20.1 The Original NP-Completeness Proof A configuration/snapshot of a machine is a representation of its current state (what info would be needed
CpSc 8390 Goddard Fall15 More on Polynomial Time and Space 20.1 The Original NP-Completeness Proof A configuration/snapshot of a machine is a representation of its current state (what info would be needed
Fixed Parameter Algorithms
 Fixed Parameter Algorithms Dániel Marx Tel Aviv University, Israel Open lectures for PhD students in computer science January 9, 2010, Warsaw, Poland Fixed Parameter Algorithms p.1/41 Parameterized complexity
Fixed Parameter Algorithms Dániel Marx Tel Aviv University, Israel Open lectures for PhD students in computer science January 9, 2010, Warsaw, Poland Fixed Parameter Algorithms p.1/41 Parameterized complexity
4. (a) Draw the Petersen graph. (b) Use Kuratowski s teorem to prove that the Petersen graph is non-planar.
 UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Graph Theory Frist, KandMa, IT 010 10 1 Problem sheet 4 Exam questions Solve a subset of, say, four questions to the problem session on friday.
UPPSALA UNIVERSITET Matematiska institutionen Anders Johansson Graph Theory Frist, KandMa, IT 010 10 1 Problem sheet 4 Exam questions Solve a subset of, say, four questions to the problem session on friday.
THREE LECTURES ON BASIC TOPOLOGY. 1. Basic notions.
 THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
THEORY OF COMPUTATION
 THEORY OF COMPUTATION UNIT-1 INTRODUCTION Overview This chapter begins with an overview of those areas in the theory of computation that are basic foundation of learning TOC. This unit covers the introduction
THEORY OF COMPUTATION UNIT-1 INTRODUCTION Overview This chapter begins with an overview of those areas in the theory of computation that are basic foundation of learning TOC. This unit covers the introduction
Rational subsets in HNN-extensions
 Rational subsets in HNN-extensions G. Sénizergues joint work with M. Lohrey ROUPE DE TRAVAIL-LGL-28/02/06 1 0- PLAN 0 INTRODUCTION 0.1 Problems 0.2 Motivations 0.3 Results 0.4 Tools 1- HNN EXTENSIONS 1.1
Rational subsets in HNN-extensions G. Sénizergues joint work with M. Lohrey ROUPE DE TRAVAIL-LGL-28/02/06 1 0- PLAN 0 INTRODUCTION 0.1 Problems 0.2 Motivations 0.3 Results 0.4 Tools 1- HNN EXTENSIONS 1.1
We ve studied the main models and concepts of the theory of computation:
 CMPSCI 601: Summary & Conclusions Lecture 27 We ve studied the main models and concepts of the theory of computation: Computability: what can be computed in principle Logic: how can we express our requirements
CMPSCI 601: Summary & Conclusions Lecture 27 We ve studied the main models and concepts of the theory of computation: Computability: what can be computed in principle Logic: how can we express our requirements
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS
 Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Point-Set Topology 1. TOPOLOGICAL SPACES AND CONTINUOUS FUNCTIONS Definition 1.1. Let X be a set and T a subset of the power set P(X) of X. Then T is a topology on X if and only if all of the following
Definability equals recognizability for graphs of bounded treewidth
 Definability equals recognizability for graphs of bounded treewidth Mikołaj Bojańczyk Michał Pilipczuk University of Warsaw {bojan,michal.pilipczuk}@mimuw.edu.pl Abstract We prove a conjecture of Courcelle,
Definability equals recognizability for graphs of bounded treewidth Mikołaj Bojańczyk Michał Pilipczuk University of Warsaw {bojan,michal.pilipczuk}@mimuw.edu.pl Abstract We prove a conjecture of Courcelle,
Matching Theory. Figure 1: Is this graph bipartite?
 Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Matching Theory 1 Introduction A matching M of a graph is a subset of E such that no two edges in M share a vertex; edges which have this property are called independent edges. A matching M is said to
Coloring edges and vertices of graphs without short or long cycles
 Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
Coloring edges and vertices of graphs without short or long cycles Marcin Kamiński and Vadim Lozin Abstract Vertex and edge colorability are two graph problems that are NPhard in general. We show that
Automata Theory for Reasoning about Actions
 Automata Theory for Reasoning about Actions Eugenia Ternovskaia Department of Computer Science, University of Toronto Toronto, ON, Canada, M5S 3G4 eugenia@cs.toronto.edu Abstract In this paper, we show
Automata Theory for Reasoning about Actions Eugenia Ternovskaia Department of Computer Science, University of Toronto Toronto, ON, Canada, M5S 3G4 eugenia@cs.toronto.edu Abstract In this paper, we show
Math 170- Graph Theory Notes
 1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
1 Math 170- Graph Theory Notes Michael Levet December 3, 2018 Notation: Let n be a positive integer. Denote [n] to be the set {1, 2,..., n}. So for example, [3] = {1, 2, 3}. To quote Bud Brown, Graph theory
Necessary edges in k-chordalizations of graphs
 Necessary edges in k-chordalizations of graphs Hans L. Bodlaender Abstract In this note, we look at which edges must always be added to a given graph G = (V, E), when we want to make it a chordal graph
Necessary edges in k-chordalizations of graphs Hans L. Bodlaender Abstract In this note, we look at which edges must always be added to a given graph G = (V, E), when we want to make it a chordal graph
Discrete Mathematics Lecture 4. Harper Langston New York University
 Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Discrete Mathematics Lecture 4 Harper Langston New York University Sequences Sequence is a set of (usually infinite number of) ordered elements: a 1, a 2,, a n, Each individual element a k is called a
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Algorithms For Inference Fall 2014
 Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Recitation-6: Hardness of Inference Contents 1 NP-Hardness Part-II
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Recitation-6: Hardness of Inference Contents 1 NP-Hardness Part-II
Controlling Cycles in Finite Hypergraphs
 Controlling Cycles in Finite Hypergraphs Martin Otto, Dpt of Mathematics, TU Darmstadt Martin Otto, Berlin 2011 Introduction Graphs Hypergraphs Results&Directions 1/28 acyclicity (of graphs & hypergraphs):
Controlling Cycles in Finite Hypergraphs Martin Otto, Dpt of Mathematics, TU Darmstadt Martin Otto, Berlin 2011 Introduction Graphs Hypergraphs Results&Directions 1/28 acyclicity (of graphs & hypergraphs):
COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES
 Volume 2, Number 1, Pages 61 66 ISSN 1715-0868 COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES MARCIN KAMIŃSKI AND VADIM LOZIN Abstract. Vertex and edge colorability are two graph problems
Volume 2, Number 1, Pages 61 66 ISSN 1715-0868 COLORING EDGES AND VERTICES OF GRAPHS WITHOUT SHORT OR LONG CYCLES MARCIN KAMIŃSKI AND VADIM LOZIN Abstract. Vertex and edge colorability are two graph problems
Binary Relations McGraw-Hill Education
 Binary Relations A binary relation R from a set A to a set B is a subset of A X B Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B. We can also represent
Binary Relations A binary relation R from a set A to a set B is a subset of A X B Example: Let A = {0,1,2} and B = {a,b} {(0, a), (0, b), (1,a), (2, b)} is a relation from A to B. We can also represent
XPath with transitive closure
 XPath with transitive closure Logic and Databases Feb 2006 1 XPath with transitive closure Logic and Databases Feb 2006 2 Navigating XML trees XPath with transitive closure Newton Institute: Logic and
XPath with transitive closure Logic and Databases Feb 2006 1 XPath with transitive closure Logic and Databases Feb 2006 2 Navigating XML trees XPath with transitive closure Newton Institute: Logic and
13 th Annual Johns Hopkins Math Tournament Saturday, February 19, 2011 Automata Theory EUR solutions
 13 th Annual Johns Hopkins Math Tournament Saturday, February 19, 011 Automata Theory EUR solutions Problem 1 (5 points). Prove that any surjective map between finite sets of the same cardinality is a
13 th Annual Johns Hopkins Math Tournament Saturday, February 19, 011 Automata Theory EUR solutions Problem 1 (5 points). Prove that any surjective map between finite sets of the same cardinality is a
Computer Science and Mathematics. Part I: Fundamental Mathematical Concepts Winfried Kurth
 Computer Science and Mathematics Part I: Fundamental Mathematical Concepts Winfried Kurth http://www.uni-forst.gwdg.de/~wkurth/csm17_home.htm 1. Mathematical Logic Propositions - can be either true or
Computer Science and Mathematics Part I: Fundamental Mathematical Concepts Winfried Kurth http://www.uni-forst.gwdg.de/~wkurth/csm17_home.htm 1. Mathematical Logic Propositions - can be either true or
LOGIC AND DISCRETE MATHEMATICS
 LOGIC AND DISCRETE MATHEMATICS A Computer Science Perspective WINFRIED KARL GRASSMANN Department of Computer Science University of Saskatchewan JEAN-PAUL TREMBLAY Department of Computer Science University
LOGIC AND DISCRETE MATHEMATICS A Computer Science Perspective WINFRIED KARL GRASSMANN Department of Computer Science University of Saskatchewan JEAN-PAUL TREMBLAY Department of Computer Science University
Decision Procedures for Recursive Data Structures with Integer Constraints
 Decision Procedures for Recursive Data Structures with Ting Zhang, Henny B Sipma, Zohar Manna Stanford University tingz,sipma,zm@csstanfordedu STeP Group, June 29, 2004 IJCAR 2004 - p 1/31 Outline Outline
Decision Procedures for Recursive Data Structures with Ting Zhang, Henny B Sipma, Zohar Manna Stanford University tingz,sipma,zm@csstanfordedu STeP Group, June 29, 2004 IJCAR 2004 - p 1/31 Outline Outline
Introduction to Parameterized Complexity
 Introduction to Parameterized Complexity M. Pouly Department of Informatics University of Fribourg, Switzerland Internal Seminar June 2006 Outline Introduction & Motivation The Misery of Dr. O The Perspective
Introduction to Parameterized Complexity M. Pouly Department of Informatics University of Fribourg, Switzerland Internal Seminar June 2006 Outline Introduction & Motivation The Misery of Dr. O The Perspective
CS6160 Theory of Computation Problem Set 2 Department of Computer Science, University of Virginia
 CS6160 Theory of Computation Problem Set 2 Department of Computer Science, University of Virginia Gabriel Robins Please start solving these problems immediately, and work in study groups. Please prove
CS6160 Theory of Computation Problem Set 2 Department of Computer Science, University of Virginia Gabriel Robins Please start solving these problems immediately, and work in study groups. Please prove
Endomorphisms and synchronization, 2: Graphs and transformation monoids
 Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras Given a relational structure R, there are several similar ways to produce
Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras Given a relational structure R, there are several similar ways to produce
CMSC Honors Discrete Mathematics
 CMSC 27130 Honors Discrete Mathematics Lectures by Alexander Razborov Notes by Justin Lubin The University of Chicago, Autumn 2017 1 Contents I Number Theory 4 1 The Euclidean Algorithm 4 2 Mathematical
CMSC 27130 Honors Discrete Mathematics Lectures by Alexander Razborov Notes by Justin Lubin The University of Chicago, Autumn 2017 1 Contents I Number Theory 4 1 The Euclidean Algorithm 4 2 Mathematical
arxiv: v1 [cs.lo] 28 Sep 2015
![arxiv: v1 [cs.lo] 28 Sep 2015 arxiv: v1 [cs.lo] 28 Sep 2015](/thumbs/80/81622249.jpg) Definability Equals Recognizability for k-outerplanar Graphs Lars Jaffke Hans L. Bodlaender arxiv:1509.08315v1 [cs.lo] 28 Sep 2015 Abstract One of the most famous algorithmic meta-theorems states that
Definability Equals Recognizability for k-outerplanar Graphs Lars Jaffke Hans L. Bodlaender arxiv:1509.08315v1 [cs.lo] 28 Sep 2015 Abstract One of the most famous algorithmic meta-theorems states that
REU Problems of the Czech Group
 REU Problems of the Czech Group Adam Juraszek, Tomáš Masařík, Jitka Novotná, Martin Töpfer, Tomáš Toufar, Jan Voborník, Peter Zeman Mentor: Dr. James Abello DIMACS REU 2015, Piscataway Dominating Sets
REU Problems of the Czech Group Adam Juraszek, Tomáš Masařík, Jitka Novotná, Martin Töpfer, Tomáš Toufar, Jan Voborník, Peter Zeman Mentor: Dr. James Abello DIMACS REU 2015, Piscataway Dominating Sets
P and NP (Millenium problem)
 CMPS 2200 Fall 2017 P and NP (Millenium problem) Carola Wenk Slides courtesy of Piotr Indyk with additions by Carola Wenk CMPS 2200 Introduction to Algorithms 1 We have seen so far Algorithms for various
CMPS 2200 Fall 2017 P and NP (Millenium problem) Carola Wenk Slides courtesy of Piotr Indyk with additions by Carola Wenk CMPS 2200 Introduction to Algorithms 1 We have seen so far Algorithms for various
Lecture 1: Examples, connectedness, paths and cycles
 Lecture 1: Examples, connectedness, paths and cycles Anders Johansson 2011-10-22 lör Outline The course plan Examples and applications of graphs Relations The definition of graphs as relations Connectedness,
Lecture 1: Examples, connectedness, paths and cycles Anders Johansson 2011-10-22 lör Outline The course plan Examples and applications of graphs Relations The definition of graphs as relations Connectedness,
Trees. 3. (Minimally Connected) G is connected and deleting any of its edges gives rise to a disconnected graph.
 Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Trees 1 Introduction Trees are very special kind of (undirected) graphs. Formally speaking, a tree is a connected graph that is acyclic. 1 This definition has some drawbacks: given a graph it is not trivial
Reference Sheet for CO142.2 Discrete Mathematics II
 Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
Reference Sheet for CO14. Discrete Mathematics II Spring 017 1 Graphs Defintions 1. Graph: set of N nodes and A arcs such that each a A is associated with an unordered pair of nodes.. Simple graph: no
1. [5 points each] True or False. If the question is currently open, write O or Open.
![1. [5 points each] True or False. If the question is currently open, write O or Open. 1. [5 points each] True or False. If the question is currently open, write O or Open.](/thumbs/89/98345819.jpg) University of Nevada, Las Vegas Computer Science 456/656 Spring 2018 Practice for the Final on May 9, 2018 The entire examination is 775 points. The real final will be much shorter. Name: No books, notes,
University of Nevada, Las Vegas Computer Science 456/656 Spring 2018 Practice for the Final on May 9, 2018 The entire examination is 775 points. The real final will be much shorter. Name: No books, notes,
W[1]-hardness. Dániel Marx 1. Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary
![W[1]-hardness. Dániel Marx 1. Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary W[1]-hardness. Dániel Marx 1. Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary](/thumbs/92/108052545.jpg) W[1]-hardness Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary School on Parameterized Algorithms and Complexity Będlewo, Poland
W[1]-hardness Dániel Marx 1 1 Institute for Computer Science and Control, Hungarian Academy of Sciences (MTA SZTAKI) Budapest, Hungary School on Parameterized Algorithms and Complexity Będlewo, Poland
CS 512, Spring 2017: Take-Home End-of-Term Examination
 CS 512, Spring 2017: Take-Home End-of-Term Examination Out: Tuesday, 9 May 2017, 12:00 noon Due: Wednesday, 10 May 2017, by 11:59 am Turn in your solutions electronically, as a single PDF file, by placing
CS 512, Spring 2017: Take-Home End-of-Term Examination Out: Tuesday, 9 May 2017, 12:00 noon Due: Wednesday, 10 May 2017, by 11:59 am Turn in your solutions electronically, as a single PDF file, by placing
Definition: A context-free grammar (CFG) is a 4- tuple. variables = nonterminals, terminals, rules = productions,,
 CMPSCI 601: Recall From Last Time Lecture 5 Definition: A context-free grammar (CFG) is a 4- tuple, variables = nonterminals, terminals, rules = productions,,, are all finite. 1 ( ) $ Pumping Lemma for
CMPSCI 601: Recall From Last Time Lecture 5 Definition: A context-free grammar (CFG) is a 4- tuple, variables = nonterminals, terminals, rules = productions,,, are all finite. 1 ( ) $ Pumping Lemma for
Computational problems. Lecture 2: Combinatorial search and optimisation problems. Computational problems. Examples. Example
 Lecture 2: Combinatorial search and optimisation problems Different types of computational problems Examples of computational problems Relationships between problems Computational properties of different
Lecture 2: Combinatorial search and optimisation problems Different types of computational problems Examples of computational problems Relationships between problems Computational properties of different
About the Tutorial. Audience. Prerequisites. Copyright & Disclaimer. Discrete Mathematics
 About the Tutorial Discrete Mathematics is a branch of mathematics involving discrete elements that uses algebra and arithmetic. It is increasingly being applied in the practical fields of mathematics
About the Tutorial Discrete Mathematics is a branch of mathematics involving discrete elements that uses algebra and arithmetic. It is increasingly being applied in the practical fields of mathematics
P = NP; P NP. Intuition of the reduction idea:
 1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
1 Polynomial Time Reducibility The question of whether P = NP is one of the greatest unsolved problems in the theoretical computer science. Two possibilities of relationship between P and N P P = NP; P
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Finite Automata. Dr. Nadeem Akhtar. Assistant Professor Department of Computer Science & IT The Islamia University of Bahawalpur
 Finite Automata Dr. Nadeem Akhtar Assistant Professor Department of Computer Science & IT The Islamia University of Bahawalpur PhD Laboratory IRISA-UBS University of South Brittany European University
Finite Automata Dr. Nadeem Akhtar Assistant Professor Department of Computer Science & IT The Islamia University of Bahawalpur PhD Laboratory IRISA-UBS University of South Brittany European University
arxiv:submit/ [math.co] 9 May 2011
![arxiv:submit/ [math.co] 9 May 2011 arxiv:submit/ [math.co] 9 May 2011](/thumbs/95/122578154.jpg) arxiv:submit/0243374 [math.co] 9 May 2011 Connectivity and tree structure in finite graphs J. Carmesin R. Diestel F. Hundertmark M. Stein 6 May, 2011 Abstract We prove that, for every integer k 0, every
arxiv:submit/0243374 [math.co] 9 May 2011 Connectivity and tree structure in finite graphs J. Carmesin R. Diestel F. Hundertmark M. Stein 6 May, 2011 Abstract We prove that, for every integer k 0, every
1. Draw the state graphs for the finite automata which accept sets of strings composed of zeros and ones which:
 P R O B L E M S Finite Autom ata. Draw the state graphs for the finite automata which accept sets of strings composed of zeros and ones which: a) Are a multiple of three in length. b) End with the string
P R O B L E M S Finite Autom ata. Draw the state graphs for the finite automata which accept sets of strings composed of zeros and ones which: a) Are a multiple of three in length. b) End with the string
Section 3.1: Nonseparable Graphs Cut vertex of a connected graph G: A vertex x G such that G x is not connected. Theorem 3.1, p. 57: Every connected
 Section 3.1: Nonseparable Graphs Cut vertex of a connected graph G: A vertex x G such that G x is not connected. Theorem 3.1, p. 57: Every connected graph G with at least 2 vertices contains at least 2
Section 3.1: Nonseparable Graphs Cut vertex of a connected graph G: A vertex x G such that G x is not connected. Theorem 3.1, p. 57: Every connected graph G with at least 2 vertices contains at least 2
CSE 20 DISCRETE MATH. Fall
 CSE 20 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Final exam The final exam is Saturday December 16 11:30am-2:30pm. Lecture A will take the exam in Lecture B will take the exam
CSE 20 DISCRETE MATH Fall 2017 http://cseweb.ucsd.edu/classes/fa17/cse20-ab/ Final exam The final exam is Saturday December 16 11:30am-2:30pm. Lecture A will take the exam in Lecture B will take the exam
Theory of Computation Dr. Weiss Extra Practice Exam Solutions
 Name: of 7 Theory of Computation Dr. Weiss Extra Practice Exam Solutions Directions: Answer the questions as well as you can. Partial credit will be given, so show your work where appropriate. Try to be
Name: of 7 Theory of Computation Dr. Weiss Extra Practice Exam Solutions Directions: Answer the questions as well as you can. Partial credit will be given, so show your work where appropriate. Try to be
Rigidity, connectivity and graph decompositions
 First Prev Next Last Rigidity, connectivity and graph decompositions Brigitte Servatius Herman Servatius Worcester Polytechnic Institute Page 1 of 100 First Prev Next Last Page 2 of 100 We say that a framework
First Prev Next Last Rigidity, connectivity and graph decompositions Brigitte Servatius Herman Servatius Worcester Polytechnic Institute Page 1 of 100 First Prev Next Last Page 2 of 100 We say that a framework
Topological Invariance under Line Graph Transformations
 Symmetry 2012, 4, 329-335; doi:103390/sym4020329 Article OPEN ACCESS symmetry ISSN 2073-8994 wwwmdpicom/journal/symmetry Topological Invariance under Line Graph Transformations Allen D Parks Electromagnetic
Symmetry 2012, 4, 329-335; doi:103390/sym4020329 Article OPEN ACCESS symmetry ISSN 2073-8994 wwwmdpicom/journal/symmetry Topological Invariance under Line Graph Transformations Allen D Parks Electromagnetic
 1 Introduction... 1 1.1 A Database Example... 1 1.2 An Example from Complexity Theory...................... 4 1.3 An Example from Formal Language Theory................. 6 1.4 An Overview of the Book.................................
1 Introduction... 1 1.1 A Database Example... 1 1.2 An Example from Complexity Theory...................... 4 1.3 An Example from Formal Language Theory................. 6 1.4 An Overview of the Book.................................
Key Graph Theory Theorems
 Key Graph Theory Theorems Rajesh Kumar MATH 239 Intro to Combinatorics August 19, 2008 3.3 Binary Trees 3.3.1 Problem (p.82) Determine the number, t n, of binary trees with n edges. The number of binary
Key Graph Theory Theorems Rajesh Kumar MATH 239 Intro to Combinatorics August 19, 2008 3.3 Binary Trees 3.3.1 Problem (p.82) Determine the number, t n, of binary trees with n edges. The number of binary
6 NFA and Regular Expressions
 Formal Language and Automata Theory: CS21004 6 NFA and Regular Expressions 6.1 Nondeterministic Finite Automata A nondeterministic finite automata (NFA) is a 5-tuple where 1. is a finite set of states
Formal Language and Automata Theory: CS21004 6 NFA and Regular Expressions 6.1 Nondeterministic Finite Automata A nondeterministic finite automata (NFA) is a 5-tuple where 1. is a finite set of states
Endomorphisms and synchronization, 2: Graphs and transformation monoids. Peter J. Cameron
 Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras From algebras to relations Given a relational structure R, there are
Endomorphisms and synchronization, 2: Graphs and transformation monoids Peter J. Cameron BIRS, November 2014 Relations and algebras From algebras to relations Given a relational structure R, there are
CSE 20 DISCRETE MATH. Winter
 CSE 20 DISCRETE MATH Winter 2017 http://cseweb.ucsd.edu/classes/wi17/cse20-ab/ Final exam The final exam is Saturday March 18 8am-11am. Lecture A will take the exam in GH 242 Lecture B will take the exam
CSE 20 DISCRETE MATH Winter 2017 http://cseweb.ucsd.edu/classes/wi17/cse20-ab/ Final exam The final exam is Saturday March 18 8am-11am. Lecture A will take the exam in GH 242 Lecture B will take the exam
9 About Intersection Graphs
 9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
9 About Intersection Graphs Since this lecture we focus on selected detailed topics in Graph theory that are close to your teacher s heart... The first selected topic is that of intersection graphs, i.e.
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2016
 Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2016 Lecture 15 Ana Bove May 23rd 2016 More on Turing machines; Summary of the course. Overview of today s lecture: Recap: PDA, TM Push-down
Finite Automata Theory and Formal Languages TMV027/DIT321 LP4 2016 Lecture 15 Ana Bove May 23rd 2016 More on Turing machines; Summary of the course. Overview of today s lecture: Recap: PDA, TM Push-down
A Parametrized Algorithm for Matroid Branch-Width
 A Parametrized Algorithm for Matroid Branch-Width Petr Hliněný Department of Computer Science FEI VŠB Technical University of Ostrava 17. listopadu 15, 708 33 Ostrava, Czech Republic E-mail: hlineny@member.ams.org
A Parametrized Algorithm for Matroid Branch-Width Petr Hliněný Department of Computer Science FEI VŠB Technical University of Ostrava 17. listopadu 15, 708 33 Ostrava, Czech Republic E-mail: hlineny@member.ams.org
