From Reference Frames to Reference Planes: Multi-View Parallax Geometry and Applications
|
|
|
- Ralph Maxwell
- 6 years ago
- Views:
Transcription
1 From Reference Frames to Reference Planes: Multi-View Parallax Geometry and Applications M. Irani 1, P. Anandan 2, and D. Weinshall 3 1 Dept. of Applied Math and CS, The Weizmann Inst. of Science, Rehovot, Israel, irani@wisdom.weizmann.ac.il 2 Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA, anandan@microsoft.com, 3 Institute of Computer Science Hebrew University Jerusalem, Israel daphna@cs.huji.ac.il Abstract. This paper presents a new framework for analyzing the geometry of multiple 3D scene points from multiple uncalibrated images, based on decomposing the projection of these points on the images into two stages: (i) the projection of the scene points onto a (real or virtual) physical reference planar surface in the scene; this creates a virtual image on the reference plane, and (ii) the re-projection of the virtual image onto the actual image plane of the camera. The positions of the virtual image points are directly related to the 3D locations of the scene points and the camera centers relative to the reference plane alone. All dependency on the internal camera calibration parameters and the orientation of the camera are folded into homographies relating each image plane to the reference plane. Bi-linear and tri-linear constraints involving multiple points and views are given a concrete physical interpretation in terms of geometric relations on the physical reference plane. In particular, the possible dualities in the relations between scene points and camera centers are shown to have simple and symmetric mathematical forms. In contrast to the plane+parallax (p+p) representation, which also uses a reference plane, the approach described here removes the dependency on a reference image plane and extends the analysis to multiple views. This leads to simpler geometric relations and complete symmetry in multi-point multiview duality. The simple and intuitive expressions derived in the reference-plane based formulation lead to useful applications in 3D scene analysis. In particular, simpler tri-focal constraints are derived that lead to simple methods for New View Synthesis. Moreover, the separation and compact packing of the unknown camera calibration and orientation into the 2D projection transformation (a homography) allows also partial reconstruction using partial calibration information. Keywords: Multi-point multi-view geometry, uncalibrated images, new view synthesis, duality of cameras and scene points, plane+parallax, trilinearity. M. Irani is supported in part by DARPA through ARL Contract DAAL01-97-K-0101
2 1 Introduction The analysis of 3D scenes from multiple perspective images has been a topic of considerable interest in the vision literature. Given two calibrated cameras, their relative orientations can be determined by applying the epipolar constraint to the observed image points, and the 3D structure of the scene can be recovered relative to the coordinate frame of a reference camera (referred to here as the reference frame e.g., see [13, 6]). This is done by using the epipolar constraint and recovering the Essential Matrix E which depends on the rotation R and translation T between the two cameras. Constraints directly involving the image positions of a point in three calibrated views of a point have also been derived [19]. If the calibration of the cameras is unavailable, then it is known that reconstruction is still possible from two views, but only up to a 3D projective transformation [4]. In this case the epipolar constraint still holds, but the Essential Matrix is replaced by the Fundamental Matrix, which also incorporates the unknown camera calibration information. The 3D scene points, the camera centers and their image positions are represented in 3D and 2D projective spaces (using homogeneous projective coordinates). In this case, the reference frame reconstruction may either be a reference camera coordinate frame [8], or as defined by a set of 5 basis points in the 3D world [14]. A complete set of constraints relating the image positions of multiple points in multiple views have been derived [5, 15]. Alternatively, given a projective coordinate system specified by 5 basis points, the set of constraints directly relating the projective coordinates of the camera centers to the image measurements (in 2D projective coordinates) and their dual constraints relating to the projective coordinates of the 3D scene points have also been derived [2, 20]. Alternatively, multiple uncalibrated images can be handled using the plane + parallax (P+P) approach, which analyzes the parallax displacements of a point between two views relative to a (real or virtual) physical planar surface Π in the scene [16, 12, 11]. The magnitude of the parallax displacement is called the relative-affine structure in [16]. [12] shows that this quantity depends both on the Height H of P from Π and its depth Z relative to the reference camera. Since the relative-affine-structure measure is relative to both the reference frame (through Z) and the reference plane (through H), we refer to the P+P framework also as the reference-frame + reference-plane formulation. The P+P has the practical advantage that it avoids the inherent ambiguities associated with estimating the relative orientation (rotation + translation) between the cameras; this is because it requires only estimating the homography induced by the reference plane between the two views, which folds together the rotation and translation. Also, when the scene is flat, the F matrix estimation is unstable, whereas the planar homography can be reliably recovered [18]. In this paper, we remove the dependency on the reference frame of the analysis of multi-point multi-view geometry. We break down the projection from 3D to 2D into 2 operations: the projection of the 3D world onto the 2D reference plane Π, followed by a 2D projective transformation (homography) which maps
3 the reference plane to the image plane. Given the virtual images formed by the projection onto the reference plane, we derive algebraic and geometric relations involving the image locations of multiple points in multiple views in these virtual images. The positions of virtual image points are directly related to the 3D locations of the scene points and the camera centers relative to the reference plane alone. All dependency on the internal camera calibration parameters and the orientation of the camera are folded into homographies relating each image plane to the reference plane. We obtain a structure measure that depends only on the heights of the scene points relative to the reference plane In this paper, we derive a complete set dual relationships involving 2 and 3 points in 2 and 3 views. On the reference plane the multi-point multi-view geometry is simple and intuitive. These relations are directly related to physical points on the reference plane such as the epipole and the dual-epipole[9]. We identify these points, and also two new entities called the tri-focal line and the dual trifocal-line which are analogous to the epipole and the dual-epipole when considering three-view and three-point geometries on the reference plane. Structures such as the fundamental matrix and the trilinear tensor have a rather simple form and depend only on the epipoles, and nothing else. The symmetry between points and cameras is complete, and they can be simply switched around to get from the epipolar geometry to the dual-epipolar geometry. The simple and intuitive expressions derived in the reference-plane based formulation in this paper lead to useful applications in 3D scene analysis. In particular, simpler tri-focal constraints are derived, and these lead to simple methods for New View Synthesis. Also, the separation and compact packing of the unknown camera calibration and orientation into the 2D projection transformation (a homography) that relates the image plane to the reference plane, leads to potentially powerful reconstruction and calibration algorithms. For instance, based on minimal partial domain information, partial calibration and partial reconstruction can be achieved. This is also briefly discussed in this paper. The remainder of this paper is organized as follows: Section 2 introduces our notations, and describes the two-view geometric and algebraic constraints (bilinearity and parallax) in the reference plane representation. Section 3 describes duality (between scene points and camera centers) on the reference plane. Section 4 examines the relations involving 3 views and the corresponding dual relations. Section 5 discusses applications of this representation and shows initial results for one particular application, namely new-view synthesis. 2 Two View Geometry on the Reference Plane Figure 1 illustrates the two stage decomposition of the image formation process. Figure 1a shows the projection of one scene point from two camera centers onto the reference plane Π. Figure 1b shows the re-projection from the plane to one of the camera image planes (the reference frame ). In this and in all subsequent figures in this paper, we adopt the following notations: P denotes scene points in 3D, C denotes camera centers; i, j, k are indices used for scene points (e.g.,
4 (a) C t H t P i H i Plane π C s H s p is p ts (b) p w C t p is e p P H Reference Image Plane C s Reference Plane π p ts Fig. 1. The reference plane representation: (a) the projection of the points onto the reference plane itself, removing the dependency on the reference image plane. p ts is the epipole, and the red line is the epipolar line. (b) the re-projection of the reference plane image onto a reference image frame (camera t ). P i ) and r, s, t are indices used for camera centers (e.g., C r ). Also, denotes the projection of the scene point P i through camera center C t. It is the intersection of the ray P i C t with the reference plane Π. Similarly p is is the intersection of P i C s with the reference plane. We define and p is as the virtual-images of P i on the reference plane from cameras C t and C s respectively. We define the intersection of C t C s with Π as the epipole on Π. We use p ts to denote the epipole. Note that the location of the epipole p ts on the reference plane Π is is independent of the orientations and the internal calibration parameters of the cameras s and t. To derive the algebraic constraints involving multiple points in multiple views, we define a coordinate system (x, y, Z) relative to the reference plane Π, where (x, y) are parallel to Π and Z is perpendicular to it. For points on the reference plane, we define Z = 1, for other points we define Z = H +1, where H denotes the height (i.e., the perpendicular distance) of the point from the plane Π. Thus, P i =(x i,y i,z i ), where Z i = H i + 1, denotes the 3D coordinates of the scene point P i. Similarly C t =(x t,y t,z t ) T, where Z t = H t + 1, and and C s =(x s,y s,z s ) T, where Z s = H s + 1. The points,p is and p ts on the reference plane are the intersections of the lines C t P i, C s P i, and C t C s with the reference plane Π: x it = y it 1 = H ix t H tx i H i H t H iy t H ty i p H is = i H t 1 x ts p ts = y ts 1 = x it y it 1 = H sx t H tx s H s H t H sy t H ty s H s H t 1 H ix s H sx i H i H s H iy s H sy i (1) H i H s 1 (2) Note that the expressions given above do not involve any of the camera internal calibration parameters or the orientations of the image planes. Also note that
5 there is only a single epipole, which is unlike the case of the reference-frame based formulation, which involves two epipoles, one on each image frame. The points,p is and p ts on the reference plane are related to their corresponding points on an image plane (e.g., a reference image) via a single 2D projective transformation, which is the homography between that image plane and the plane Π. Figure 1b shows the re-projection onto the reference image t the points p, p w, and e are the projections of the image points,p is, and the epipole p ts respectively. There are two basic results concerning two views of a point as observed on the reference plane Π. The first is the expression for the parallax on the reference plane, and the second is the bilinear constraint involving the two image locations of the scene point and the epipole. These are described below. Parallax on the Reference Plane: Given the expressions in Equations 1 and 2, it can be easily verified that p is = γ(p is p ts ), (3) where γ = Hi(Ht Hs) (H t H i)h s Note that this expression for parallax (Equation 3) involves only the heights of the scene point and of the camera centers relative to the reference plane Π. It does not include any quantities relative to any of the camera coordinate systems (e.g., the reference frame) such as Z or T Z as before. Also, the parallax magnitude γ does not depend on the x, y locations of either the camera centers or the scene point 1. The Bilinear Constraint: Equation 3 implies that,p is, and p ts are collinear. Similar to the definition of the epipolar line on the image plane, the line containing these three points on Π is the intersection of the epipolar plane containing P i,c t, and C s with Π. Thus, this is the epipolar line as observed on the referenceplane. The collinearity of these three points can be expressed as p T it Fp is =0 0 1 y ts where F = 1 0 x ts is the Fundamental Matrix. As opposed to the y ts x ts 0 reference frame based formulation, where the fundamental matrix depends on the camera rotations and the internal calibration parameters of the camera, here it depends only on the epipole. Moreover, the epipole is explicit in the F matrix here, whereas, it is implicit in the standard formulation. 1 The expression for γ = HT Z Zd π in the P+P case can be related to the current expression as follows: Consider a virtual camera centered at C t, whose image plane is the plane Π, and its optical axis coincides with the H direction. Then H = H i, Z = H t H i, T Z = H t H s and d π = H s.
6 What happens when the epipole goes to? In Equation 2, it can be seen that when H s = H t, the epipole p ts goes to. In this case, p ts = x ts y ts = x t x s y t y s, 0 0 H i (H t H i) p ts. and the expression for parallax can be rewritten as: (p is )= In other words, all the parallax vectors are parallel to each other (i.e., meet at ). The Fundamental Matrix F = 0 0 y ts 0 0 x ts. We can, of course, unify y ts x ts 0 the finite and the infinite case by using 2D projective notations. However, in this paper we choose to use 2D Euclidean coordinate representations, in order to emphasize the physical meaning of the various observed and derived quantities. Moreover, the parallax expression in Equation 3, which involves metric relations is meaningless in a projective coordinate representation. Also, when H t = H i or H s = H i, then or p is go to respectively. This occurs when, fortuitously, the plane Π is chosen to be parallel to the optic ray from the scene point to one of the cameras. In this case, the corresponding image point cannot be observed on the reference plane, and our analysis does not apply. 3 Duality on the Reference Plane In this section, we derive a set of dual relations on the reference-plane by switching the roles of camera centers and scene points as was previously done in [2, 20]. Consider two points P i and P j and one camera center C t. Consider the intersection of the rays P i P j, P i C t and P j C t with the reference plane Π (see Figure 2a). These occur respectively at p ij, and p jt. In a manner analogous to the epipolar plane (defined by 2 camera centers and a scene point), we define the plane containing P i,p j and C t (2 scene points and a camera center) as the dual epipolar plane. By the same analogy, we define its intersection with Π (i.e., the line connecting,p jt and p ij ) as the dual epipolar line, and p ij as the dual epipole. Note that the dual-epipole, the dual-epipolar lines, and the dual-epipolar planes relate to a pair of scene points over multiple views, in the same way the epipole, the epipolar lines, and the epipolar planes relate to multiple scene points over a pair of views. By applying the duality of scene points and camera centers, we can derive the dual of the bilinear constraint and the parallax expressions in algebraic form. They are: Dual Parallax: and Dual Bilinearity Constraint: p T it F d p jt =0, p jt = γ d ( p ij ), where γ d = Ht(Hj Hi) (H j H t)h i,
7 C t C t P j P j Ht P i H j Plane π p jt P i C s Plane π p jt H i p ts p ij p is pij (a) (b) p js Fig. 2. Duality on the reference plane: (a) the dual-epipolar geometry associated with two points in one view. p ij is the dual-epipole, and the blue line going through p ij is the dual-epipolar line. (b) both sets of epipolar lines (shown in red) and dual-epipolar lines (shown in blue) that arise when considering two points in two views. 0 1 y ij where F d = 1 0 x ij is (defined as) the Dual Fundamental Matrix. y ij x ij 0 The duality of the bilinear constraint has been previously explored - e.g., Carlsson[2] and Weinshall, et al.[20] derive dual bilinear and trilinear relations in terms of the projective coordinate representations of the scene points, camera centers, and image points. Here, however, we derive these relations in the context of the reference plane images, and provide physical meaning to the dual relations. Also, Irani and Anandan [9] pointed out the dual epipole in the context of the plane+parallax representation. In that case, since the projection on a camera image plane ( reference frame ) is included in the formulation, there exists an asymmetry in the various constraints and their dual constraints. Here, complete symmetry is achieved by projecting all the observed quantities onto the reference plane itself. Figure 2b completes the picture by considering two points (P i,p j )intwo views (C t,c s ). This configuration gives rise to one set of epipolar lines (corresponding to each scene point) going through the epipole p ts, and one set of dualepipolar lines (corresponding to each camera) going through the dual-epipole p ij. 4 Three View Geometry on the Reference Plane In this section we extend our treatment to three views. [5] shows that there are no additional independent constraints that can be derived in more than three views. In this section we present a geometric interpretation of the three-view constraints in terms of physical quantities on the reference plane Π. We derive the algebraic three-view constraints and show that they have a very simple mathematical form. We will also show that the tensor-representation of these constraints in
8 the reference-plane has a very simple mathematical form when compared to the tensors in the standard formulations[15, 7, 5]. 4.1 Geometric Observations Figure 3 shows three views p is,, and p ir of a point P i as projected onto the reference plane Π. The new camera center is labeled as C r, and the two new epipoles as p rt and p sr 2. C t C r C s Plane π P i p rt p is p ir p ts p sr Fig. 3. Geometry of three views on the reference plane a 3D view. The 3 red lines are the epipolar lines of pairs of views, and the turquoise line the trifocal-line. The 6 points on Π lie on 4 lines forming a complete quadrilateral. Taken pairwise at a time, the three views give rise to three epipolar constraints:,p is,p ts are collinear. p is,p ir,p sr are collinear. p ir,,p rt are collinear. There is, however, a fourth collinearity constraint, namely: The epipoles p ts,p sr,p rt are collinear. This line is simply the intersection of the plane containing the three camera centers C t,c s and C r with Π (see Figure 3). This plane is referred to as the tri-focal plane. Based on this definition we define the line connecting the three epipoles as the tri-focal line. The fact that the six points lie on four lines is fundamental to the projection of three views of a point onto a reference plane Π. Note that this figure on the 2 Note that geometrically this figure is identical to Figure 2b, but the labeling of the point is different. The scene point P j in Figure 2b has been replaced by a camera center C r. In fact, this is because of the complete symmetry between scene points and camera centers in our representation.
9 plane (Figure 4a) is known as the complete quadrilateral and plays a central role in plane projective geometry [3]. Given the three cameras, every point in the scene forms a triangle (e.g., with vertices,p is and p ir. Different points (e.g., indexed i, j, etc.) will form different triangles, all of which share the same tri-focal line (see Figure 4b). In other words, all these triangles are perspective from the tri-focal line The Trifocal Ratio Each pair of views from the three views provides an expression for parallax similar to Equation 3. For example, consider: p is = H i(h t H s ) (H t H i )H s (p is p ts ) p ir = H i(h t H r ) (H t H i )H r (p ir p rt ) (4) From these equations we can eliminate H i /(H t H i ) to obtain: p is p is p ts = λ p ir rst p ir p rt (5) where λ rst = (Ht Hs) H r H s (H t H r). The above equation is true upto a sign change. Note that λ rst does not depend on the point i. In other words, for every scene point, the locations of its image from the three views on the reference plane is related by the same Equation 5. This constraint is further explored in Section 4.3. Given two images of the point P i on Π, e.g., p is and p ir, and the corresponding epipoles, p rt and p ts, we can determine the location of the third image by intersecting the two epipolar lines p is p ts and p ir p rt (see Figure 4a). There are, however, two cases in which the three epipolar lines collapse into a single line (and hence, their intersection is not unique). These are the same situations noted in [5, 15], but here we examine it in the context of the referenceplane images. The first is the case when the three camera centers are collinear (see Figure 5) - in this case the three epipoles collapse into a single point (denoted as e in Figure 5). The three epipolar lines also collapse into a single line, and therefore cannot be determined by the intersection of the epipolar lines. However, given the common epipole e and λ rst, can be recovered from p is and p ir using Equation 5. In fact, in this case, λ rst is the cross ratio of these four points (the three image points and the epipole). 3 It is known in plane-projective geometry that if two triangles are perspective from a line they are also perspective from a point [3] this is the converse of the Desargues Theorem. Given the two triangles corresponding to i and j as in Figure 4b, then the point of perspectivity is in fact the dual-epipole p ij.
10 p rt p is p rt p is p ts p jt p js (a) p ir p sr p ts (b) p ir p sr p jr Fig. 4. Three view geometry on the reference plane: (a) the complete quadrilateral formed by the image of a single point in three views and the trifocalline (shown as a dashed line) containing the three epipoles. (b) different triangles due to different scene points share the same trifocal-line. Another interesting case is when the scene point P i lies on the tri-focal plane of the three cameras. In this case the three image points,p is and p ir all lie on the tri-focal line itself, i.e., once again the three epipolar lines collapse onto the tri-focal line. Hence we cannot use the intersection of epipolar lines to determine. In this case too, can be determined by Equation 5, using λ rst. The ratio λ rst has a special significance. If we consider the tri-focal line, we can show (by replacing P i with C r in Equation 3)that: p sr p rt = λ rst (p sr p ts ) (6) (Hence, the name trifocal-ratio.) In other words, in the general case: λ rst = p sr p rt p sr p ts = p is p ir p rt (7) p is p ts p ir Note that in the singular case, when the epipoles collapse, the ratio of the distances between the epipoles (the top equation) is undefined, but the bottom equation is still valid and can be used. 4.3 The Trifocal Tensor Returning to Equation 5, we can write down component equalities as follows: x is x it = y is y it x ir x it y ir y it = λ rst = λ rst (8) x is x ts y is y ts x ir x rt y ir y rt By taking two of these equalities at a time and cross-multiplying by the denominators we can get six linear constraints. Of these two are the same as the bilinear (epipolar) constraints involving only two views at a time. The other four, which involve all three views are: (x is x it )(x ir x rt )=λ rst (x ir x it )(x is x ts ) (x is x it )(y ir y rt )=λ rst (y ir y it )(x is x ts ) (y is y it )(x ir x rt )=λ rst (x ir x it )(y is y ts ) (y is y it )(y ir y rt )=λ rst (y ir y it )(y is y ts ) (9)
11 e = p ts = p sr = p rt p ir p is Fig. 5. The Epipolar Lines Collapse Note that these three view constraints are actually only bilinear in the image locations of the scene point (as opposed to the trilinear constraints in [15])). This is because by considering the projection of the points on the reference plane itself, we eliminate the homographies induced between the views (which appear in [16]). The trilinear forms given in Equation 9 can be unified into a single tensor equation in a manner analogous to [17]: where (s α )(r β p rt ) λ rst (r β )(s α p ts ) = 0 (10) [ ] [ ] 1 0 xis 1 0 xir s =, r = 0 1 y is 0 1 y ir and α, β =1, 2 indicate the row indices of s and r (e.g., s 1 =[ 1 0 x is ]) 4. Based on further algebraic manipulation, Equation 10 can be rewritten as: α, β =1, 2 0 = = a=1 b=1 c=1 a=1 b=1 c=1 ( ) a (r β ) b (s α ) c ((p rt ) b δ ac λ rst (p ts ) c δ ab ) ( ) a (r β ) b (s α ) c (T rst ) abc (11) where δ follows the standard definition: δ pq =1ifp = q and 0 otherwise. T rst is tensor (T rst ) abc =((p rt ) b δ ac λ rst (p ts ) c δ ab ) In the above equations, ( ) 1, ( ) 2, ( ) 3, etc. denote the first (i.e., x), the second (i.e., y), and the third (i.e, 1) components of, etc. Similarly (T rst ) abc denotes the entry indexed by a, b, c in the Tensor. 4 Note that as in [17], s 1 is the vertical line on Π passing through p is and s 2 is the horizontal line on Π passing through p is. Similarly r 1 and r 2 are the vertical and horizontal lines on Π passing through p ir. Also, as in [17] the relationships in Equation 10 are valid for any line passing through p is and any other line passing through p ir. In other words, Equation 10 captures the same point-line-line relationship described in [17] and [5].
12 Note that the elements of T rst depend on the two epipoles p rt and p ts and λ rst. This is in contrast to the general form of the trifocal tensor for example, the trilinear tensor in [15] also depends on the homographies due to the plane Π between the different cameras and the tensor described in [5] which depends on the camera projection matrices. As in the case of the Fundamental Matrix F in our formulation, the epipoles are explicit within the Tensor T, whereas in the general formulation, the tensor is implicitly related to the epipole. Given the Tensor T rst we can recover the two epipoles p rt and p ts and the trifocal-ration λ rst ; using Equation 6 we can recover the third epipole p sr. 4.4 Duals of the Three View Constraints 3 Scene Points + 1 Camera: As in the case of two-view analysis, the duality between scene points and camera centers also applies to three-view analysis. By switching the roles of scene points and camera centers in Figure 3 (i.e., P i C t,c t P i,c s P j,c r P k ) we can derive new constraints involving one camera center and three points. The resulting geometric configuration is also a complete quadrilateral, but with a different labeling of the points. Figure 6a indicates the labeling corresponding to one view of three points. In this case the dual-trifocal-line contains the dual-epipoles p ij,p jk, and p ki. The three-view constraint given in Equation 5 is replaced by p jt p jt p ij = λ p kt ijk p kt p ki (12) = (Hj Hi) H j H k where λ ijk (H k H,isthedual to the trifocal-ratio λ i) rst. Dual to the other forms of the three-view constraints, (e.g., Equation 9) can also be obtained by the same substitution of indices (i.e, i t, t i, s j, r k), leading to the dual-tensor form: and the corresponding constraint set: (T ijk ) abc =((p ki ) b δ ac λ ijk (p ij ) c δ ab )) α, β =1, 2 0 = a=1 b=1 c=1 ( ) a (k β ) b (j α ) c (T ijk ) abc (13) where the definitions of the 2 3 matrices k and s are analogous to the definitions of r and s given earlier. Note that the the three-view constraints and their dual, the three-point constraints are completely symmetric. The dual-tensor depends on the dual-epipoles and the dual to the trifocal-ratio, Other Combinations of 3+1 Points: The complete symmetry between scene points and camera centers implies that we can arbitrarily choose the label (either as a scene point or as a camera center) for each of the four 3D points in Figure 3. So far, we have considered two choices: 3 camera center + 1 scene point,
13 p kt p jt p jk p ij p ij p jt p js (a) p ki (b) p is p ts Fig. 6. Duals to the Three View Geometry: (a) the complete quadrilateral formed by 3 points + 1 camera center. (b) the quadrilateral formed by 2 points + 2 cameras. Note that the epipolar-lines (thin lines) intersect at an epipole, the dual-epipolar lines (thick lines) intersect at a dual-epipole, and an epipolar line intersects a dual-epipolar line at an image-point. and 3 scene points + 1 camera center. The basic structure is that four points are divided into a group of 3 and a single point. We can obtain other duals by choosing the four points to consist of 2 camera centers + 2 scene points and grouping them as 2 camera centers and a scene point + 1 scene point or as 2 scene points and a camera center + 1 camera center. In Figure 6b we show the resulting quadrilateral corresponding to the first of these groupings. Since the configuration shown in this figure is based on 2 camera centers and 2 scene points, the six points on the quadrilateral consist of four image points, one epipole, and one dual-epipole. Note that the two epipolar lines intersect at an epipole, the two dual-epipolar lines intersect at a dual-epipole, and each epipolar line intersects each dual-epipolar line at an image point. Unlike the 3D world, where there are two types of points, camera centers and scene points, on the reference-plane, there are three-types of points epipoles, dual-epipoles, and image points. Each of these form the center of a radial field of lines that go through that point, all three have completely dual-roles on Π. 5 Applications The simple and intuitive expressions derived in the reference-plane based formulation in this paper lead to useful applications in 3D scene analysis. In particular, the simpler (bilinear) tri-focal constraints with the identified tri-focal ratio lead to a simple method for New View Synthesis. Initial experimental results are shown in this section. Moreover, the separation and compact packing of the unknown camera calibration and orientation into the 2D projection transformation (a homography) that relates the image plane to the reference plane, leads to potentially powerful reconstruction and calibration algorithms. These are briefly discussed in this section. 5.1 New View Generation Using the Three-View Constraints In this section we show that the reference-plane based formulation provides a simple and intuitive way to generate new views from a given set of views. We first show some results, followed by an explanation how they were obtained.
14 Figure 7a and 7b display two images taken by a hand-held camera. The scene contained toys which were placed on a rug on the floor. The camera translated and rotated between the two views. The 3D parallax effects due to the camera translation are apparent in the change of the 2D distance (on the image) between the clown s hat and the upper-right corner of the rug. Figure 7c is a new synthesized view of the scene, as if obtained from a virtual camera positioned farther to the left of the scene relative to the two original views (and rotated, to compensate for the translation). Note the smaller distance between the clown s hat and the corner of the rug. For comparison and verification, Figure 7d shows an actual view obtained from the same viewing direction and orientation. Also, note the differences between the actual and synthesized view. There are image distortions where the flow was inaccurate (at depth discontinuities, e.g., on the rug around the clowns head, and near the ears of the smaller doll). Also, the synthesized view is missing the left part of the rug, as this portion of the rug was not viewed in any of the 2 input images. (a) (b) (d) (c) Fig. 7. New View Synthesis. (a) and (b) show two images taken by a hand-held camera. The camera translated and rotated between the two views. The 3D parallax effects due to the camera translation are apparent by the change in the 2D distance (on the image) between the clown s hat and the upper-right corner of the rug. (c) A new synthesized view of the scene, Note the smaller distance between the clown s hat and the corner of the rug. (d) an actual view obtained from the same viewing direction and orientation. Note the differences between the actual and synthesized view: There are image distortions where the flow was inaccurate (e.g., on the rug around the clowns head, and near the ears of the smaller doll). Also, the synthesized view is missing the left part of the rug, as this portion of the rug was not viewed in any of the 2 input images, (a and b).
15 Below is a brief description of how the synthesized view was generated. To work directly with quantities on the reference plane Π would require partial calibration information about the input views. But as explained below, new view synthesis is possible even without such information. Step I: One of the two input images (camera s ) is first warped towards the other input image (camera t ; the reference image) via a 2D projective transformation to align the images of the plane Π in the two input image s and t. (Π is the plane of the rug, in our case). The corresponding 2D projective transformation is computed automatically, without any prior or additional information, using a 2D registration technique described in [10]. This method locks onto a dominant 2D parametric transformation between a pair of images, even in the presence of moving objects or other outliers (such as the toys, in our case). For more details see [10]. Note that after such 2D warping, the two plane-stabilized images are in full alignment in all image regions which correspond to the rug, and are misaligned in all other (i.e., out-of-plane) image points (i.e., the toys). The farther a scene point is from the planar surface (rug), the larger its residual misalignment. We refer to these as planar-parallax displacements (see [11, 12, 9]). Note that the plane-stabilized sequence is in fact a 2D re-projection of the corresponding virtual images on the reference plane Π onto the reference image plane, t (See Figure 1.b). Therefore, a quadrilateral on Π will project to a quadrilateral on the image plane; different triangles on Π corresponding to different scene points and sharing a common tri-focal line will preserve this relation on the reference image plane t. It can be shown that for any quadrilateral, there exists some λ rst such that Equation (7) holds. In fact, it can be shown that λ rst = T Z ts H r tr H s T, (14) Z where T ts Z is the component of the translation between cameras t and s along the optical (Z) axis of the reference camera t. Similarly T tr Z for the third camera r. H s and H r are as before (i.e., heights relative to Π). Step II: Dense flow is estimated between the two plane-stabilized images (using the method described in [12]). Note that after plane stabilization, the flow field between the two images reduces to a radial epipolar field centered at the epipole (see Equation (3); see also [11, 12, 9]). The cancellation of the plane homography removes all effects of camera rotation and changes in calibration. This allows to compute the flow field between a plane-stabilized image pair more reliably than general flow, as it is constrained to satisfy a global epipolar constraint. Step III: We estimate the epipole (p ts ) from the radial flow field between the two input plane-stabilized images. We then specify: (i) the virtual epipole (e.g., p rt ) between the reference image and the virtual plane-stabilized image, (ii) a virtual tri-focal ratio λ rst in the
16 reference frame. Given the virtual tri-focal ratio λ rst, the virtual epipole p rt, the actual epipole p ts, and the dense flow field between the two plane-stabilized images (between s and corresponding p is s), we can estimate all image points in the virtual (plane-stabilized) image (namely, all p ir s) using Equation 8. The virtual tri-focal ratio λ rst and the virtual epipole p rt can either be specified directly (e.g., via Equation (14)), or else by specifying the location of two or more image points in the virtual (plane-stabilized) view, and estimate them accordingly. Step IV: Note that the synthesized plane-stabilized image is the same for any camera centered at C r. In other words, it is independent of the internal parameters and the orientation of that camera. By specifying a homography that relates the image plane of the virtual camera to the stabilized image from the reference view, we have the complete flexibility to generate an image obtained by any camera situated at C r. This is done by unwarping the synthesized plane-stabilized image via the corresponding 2D projective transformation D Reconstruction and Camera Calibration Given uncalibrated images, any approach for obtaining Euclidean (or Affine) reconstruction requires some type of calibration. One of the benefits of our approach is that this process is factored into two separate stages, each of which has a simple and intuitive solution. First, given the input images, the virtualimages on Π must be determined. This can be done by taking advantage of the P+P method[12] (i) determine the planar homography for Π between an arbitrarily chosen reference image and each other image, and (ii) determine the homography between the reference image and Π. Note that the parallax Equation 3 is valid even if the image locations on Π are known only upto a 2D affine transformation. This means that just by indicating two sets of parallel lines (that are in different orientations) Π, the 3D Heights relative to the reference plane can be recovered. From this information, the parallax magnitude γ (in Equation 3) can be determined. (Note that by specifying the 2D coordinates of four points on the reference plane, the homography can fully determined, leading to Euclidean reconstruction.) Given γ and the height of one 3D scene point relative to Π the Heights of all other points can be determined upto a global scale factor. Both these calibration steps are simple and intuitive and require minimal specification of information. The resulting reconstruction is with respect to the reference plane Π and does not involve the camera reference frames. The foregoing outline for a reconstruction method assumes that the correspondences of each point across the multiple-views can be estimated. This involves computing the parallax flow-field(s), and the epipole(s) these can be done in the same manner as described in [11, 12]. It is worth noting, however, the removal of the planar homography allows the parallax computation to be more robust and accurate [11, 12].
17 References 1. S. Avidan and A. Shashua. Novel view synthesis in tensor space. In IEEE Conference on Computer Vision and Pattern Recognition, pages , San-Juan, June S. Carlsson. Duality of reconstruction and positioning from projective views. In Workshop on Representations of Visual Scenes, H.S.M Coxeter, editor. Projective Geometry. Springer Verlag, O.D. Faugeras. What can be seen in three dimensions with an uncalibrated stereo rig? In European Conference on Computer Vision, pages , Santa Margarita Ligure, May O.D. Faugeras and B. Mourrain. On the geometry and algebra of the point and line correspondences between n images. In International Conference on Computer Vision, pages , Cambridge, MA, June Olivier Faugeras. Three-Dimensional Computer Vision A Geometric Viewpoint. MIT Press, Cambridge, MA, Richard Hartley. Lines and poins in three views a unified approach. In DARPA Image Understanding Workshop Proceedings, Richard Hartley. Euclidean Reconstruction from Uncalibrated Views. In Applications of Invariance in Computer Vision, J.L. Mundy, D. Forsyth, and A. Zisserman (Eds.), Springer-Verlag, M. Irani and P. Anandan. Parallax geometry of pairs of points for 3d scene analysis. In European Conference on Computer Vision, Cambridge, UK, April M. Irani, B. Rousso, and S. Peleg. Computing occluding and transparent motions. International Journal of Computer Vision, 12(1):5 16, January M. Irani, B. Rousso, and P. peleg. Recovery of ego-motion using region alignment. IEEE Trans. on Pattern Analysis and Machine Intelligence, 19(3): , March R. Kumar, P. Anandan, and K. Hanna. Direct recovery of shape from multiple views: a parallax based approach. In Proc 12th ICPR, H.C. Longuet-Higgins. A computer algorithm for reconstructing a scene from two projections. Nature, 293: , R. Mohr. Accurate Projective Reconstruction In Applications of Invariance in Computer Vision, J.L. Mundy, D. Forsyth, and A. Zisserman, (Eds.), Springer- Verlag, A. Shashua. Algebraic functions for recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 17: , A. Shashua and N. Navab. Relative affine structure: Theory and application to 3d reconstruction from perspective views. In IEEE Conference on Computer Vision and Pattern Recognition, pages , Seattle, Wa., June A. Shashua and P. Ananadan Trilinear Constraints revisited: generalized trilinear constraints and the tensor brightness constraint. IUW, Feb P.H.S. Torr. Motion Segmentation and Outlier Detection. PhD Thesis: Report No. OUEL 1987/93, Univ. of Oxford, UK, M. Spetsakis and J. Aloimonos. A unified theory of structure from motion. DARPA Image Understanding Workshop, pp , Pittsburgh, PA, D. Weinshall, M.Werman, and A. Shashua. Shape descriptors: Bilinear, trilinear and quadlinear relations for multi-point geometry, and linear projective reconstruction algorithms. In Workshop on Representations of Visual Scenes, 1995.
Multiple View Geometry in Computer Vision Second Edition
 Multiple View Geometry in Computer Vision Second Edition Richard Hartley Australian National University, Canberra, Australia Andrew Zisserman University of Oxford, UK CAMBRIDGE UNIVERSITY PRESS Contents
Multiple View Geometry in Computer Vision Second Edition Richard Hartley Australian National University, Canberra, Australia Andrew Zisserman University of Oxford, UK CAMBRIDGE UNIVERSITY PRESS Contents
Camera Calibration Using Line Correspondences
 Camera Calibration Using Line Correspondences Richard I. Hartley G.E. CRD, Schenectady, NY, 12301. Ph: (518)-387-7333 Fax: (518)-387-6845 Email : hartley@crd.ge.com Abstract In this paper, a method of
Camera Calibration Using Line Correspondences Richard I. Hartley G.E. CRD, Schenectady, NY, 12301. Ph: (518)-387-7333 Fax: (518)-387-6845 Email : hartley@crd.ge.com Abstract In this paper, a method of
calibrated coordinates Linear transformation pixel coordinates
 1 calibrated coordinates Linear transformation pixel coordinates 2 Calibration with a rig Uncalibrated epipolar geometry Ambiguities in image formation Stratified reconstruction Autocalibration with partial
1 calibrated coordinates Linear transformation pixel coordinates 2 Calibration with a rig Uncalibrated epipolar geometry Ambiguities in image formation Stratified reconstruction Autocalibration with partial
Object and Motion Recognition using Plane Plus Parallax Displacement of Conics
 Object and Motion Recognition using Plane Plus Parallax Displacement of Conics Douglas R. Heisterkamp University of South Alabama Mobile, AL 6688-0002, USA dheister@jaguar1.usouthal.edu Prabir Bhattacharya
Object and Motion Recognition using Plane Plus Parallax Displacement of Conics Douglas R. Heisterkamp University of South Alabama Mobile, AL 6688-0002, USA dheister@jaguar1.usouthal.edu Prabir Bhattacharya
CS 664 Slides #9 Multi-Camera Geometry. Prof. Dan Huttenlocher Fall 2003
 CS 664 Slides #9 Multi-Camera Geometry Prof. Dan Huttenlocher Fall 2003 Pinhole Camera Geometric model of camera projection Image plane I, which rays intersect Camera center C, through which all rays pass
CS 664 Slides #9 Multi-Camera Geometry Prof. Dan Huttenlocher Fall 2003 Pinhole Camera Geometric model of camera projection Image plane I, which rays intersect Camera center C, through which all rays pass
But First: Multi-View Projective Geometry
 View Morphing (Seitz & Dyer, SIGGRAPH 96) Virtual Camera Photograph Morphed View View interpolation (ala McMillan) but no depth no camera information Photograph But First: Multi-View Projective Geometry
View Morphing (Seitz & Dyer, SIGGRAPH 96) Virtual Camera Photograph Morphed View View interpolation (ala McMillan) but no depth no camera information Photograph But First: Multi-View Projective Geometry
Perception and Action using Multilinear Forms
 Perception and Action using Multilinear Forms Anders Heyden, Gunnar Sparr, Kalle Åström Dept of Mathematics, Lund University Box 118, S-221 00 Lund, Sweden email: {heyden,gunnar,kalle}@maths.lth.se Abstract
Perception and Action using Multilinear Forms Anders Heyden, Gunnar Sparr, Kalle Åström Dept of Mathematics, Lund University Box 118, S-221 00 Lund, Sweden email: {heyden,gunnar,kalle}@maths.lth.se Abstract
Multiple Views Geometry
 Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in January 2, 28 Epipolar geometry Fundamental geometric relationship between two perspective
Multiple Views Geometry Subhashis Banerjee Dept. Computer Science and Engineering IIT Delhi email: suban@cse.iitd.ac.in January 2, 28 Epipolar geometry Fundamental geometric relationship between two perspective
Computer Vision Lecture 17
 Announcements Computer Vision Lecture 17 Epipolar Geometry & Stereo Basics Seminar in the summer semester Current Topics in Computer Vision and Machine Learning Block seminar, presentations in 1 st week
Announcements Computer Vision Lecture 17 Epipolar Geometry & Stereo Basics Seminar in the summer semester Current Topics in Computer Vision and Machine Learning Block seminar, presentations in 1 st week
A General Expression of the Fundamental Matrix for Both Perspective and Affine Cameras
 A General Expression of the Fundamental Matrix for Both Perspective and Affine Cameras Zhengyou Zhang* ATR Human Information Processing Res. Lab. 2-2 Hikari-dai, Seika-cho, Soraku-gun Kyoto 619-02 Japan
A General Expression of the Fundamental Matrix for Both Perspective and Affine Cameras Zhengyou Zhang* ATR Human Information Processing Res. Lab. 2-2 Hikari-dai, Seika-cho, Soraku-gun Kyoto 619-02 Japan
Mathematics of a Multiple Omni-Directional System
 Mathematics of a Multiple Omni-Directional System A. Torii A. Sugimoto A. Imiya, School of Science and National Institute of Institute of Media and Technology, Informatics, Information Technology, Chiba
Mathematics of a Multiple Omni-Directional System A. Torii A. Sugimoto A. Imiya, School of Science and National Institute of Institute of Media and Technology, Informatics, Information Technology, Chiba
Computer Vision Lecture 17
 Computer Vision Lecture 17 Epipolar Geometry & Stereo Basics 13.01.2015 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Announcements Seminar in the summer semester
Computer Vision Lecture 17 Epipolar Geometry & Stereo Basics 13.01.2015 Bastian Leibe RWTH Aachen http://www.vision.rwth-aachen.de leibe@vision.rwth-aachen.de Announcements Seminar in the summer semester
METRIC PLANE RECTIFICATION USING SYMMETRIC VANISHING POINTS
 METRIC PLANE RECTIFICATION USING SYMMETRIC VANISHING POINTS M. Lefler, H. Hel-Or Dept. of CS, University of Haifa, Israel Y. Hel-Or School of CS, IDC, Herzliya, Israel ABSTRACT Video analysis often requires
METRIC PLANE RECTIFICATION USING SYMMETRIC VANISHING POINTS M. Lefler, H. Hel-Or Dept. of CS, University of Haifa, Israel Y. Hel-Or School of CS, IDC, Herzliya, Israel ABSTRACT Video analysis often requires
p w2 μ 2 Δp w p 2 epipole (FOE) p 1 μ 1 A p w1
 A Unied Approach to Moving Object Detection in 2D and 3D Scenes Michal Irani P. Anandan David Sarno Research Center CN5300, Princeton, NJ 08543-5300, U.S.A. Email: fmichal,anandang@sarno.com Abstract The
A Unied Approach to Moving Object Detection in 2D and 3D Scenes Michal Irani P. Anandan David Sarno Research Center CN5300, Princeton, NJ 08543-5300, U.S.A. Email: fmichal,anandang@sarno.com Abstract The
Model Refinement from Planar Parallax
 Model Refinement from Planar Parallax A. R. Dick R. Cipolla Department of Engineering, University of Cambridge, Cambridge, UK {ard28,cipolla}@eng.cam.ac.uk Abstract This paper presents a system for refining
Model Refinement from Planar Parallax A. R. Dick R. Cipolla Department of Engineering, University of Cambridge, Cambridge, UK {ard28,cipolla}@eng.cam.ac.uk Abstract This paper presents a system for refining
Epipolar Geometry Prof. D. Stricker. With slides from A. Zisserman, S. Lazebnik, Seitz
 Epipolar Geometry Prof. D. Stricker With slides from A. Zisserman, S. Lazebnik, Seitz 1 Outline 1. Short introduction: points and lines 2. Two views geometry: Epipolar geometry Relation point/line in two
Epipolar Geometry Prof. D. Stricker With slides from A. Zisserman, S. Lazebnik, Seitz 1 Outline 1. Short introduction: points and lines 2. Two views geometry: Epipolar geometry Relation point/line in two
Homography Tensors: On Algebraic Entities. Moving Planar Points. Amnon Shashua and Lior Wolf. The Hebrew University, Jerusalem 91904, Israel
 Homography Tensors: On Algebraic Entities That Represent Three Views of Static or Moving Planar Points Amnon Shashua and Lior Wolf School of Computer Science and Engineering, The Hebrew University, Jerusalem
Homography Tensors: On Algebraic Entities That Represent Three Views of Static or Moving Planar Points Amnon Shashua and Lior Wolf School of Computer Science and Engineering, The Hebrew University, Jerusalem
Unit 3 Multiple View Geometry
 Unit 3 Multiple View Geometry Relations between images of a scene Recovering the cameras Recovering the scene structure http://www.robots.ox.ac.uk/~vgg/hzbook/hzbook1.html 3D structure from images Recover
Unit 3 Multiple View Geometry Relations between images of a scene Recovering the cameras Recovering the scene structure http://www.robots.ox.ac.uk/~vgg/hzbook/hzbook1.html 3D structure from images Recover
Stereo Vision. MAN-522 Computer Vision
 Stereo Vision MAN-522 Computer Vision What is the goal of stereo vision? The recovery of the 3D structure of a scene using two or more images of the 3D scene, each acquired from a different viewpoint in
Stereo Vision MAN-522 Computer Vision What is the goal of stereo vision? The recovery of the 3D structure of a scene using two or more images of the 3D scene, each acquired from a different viewpoint in
Structure from Motion. Prof. Marco Marcon
 Structure from Motion Prof. Marco Marcon Summing-up 2 Stereo is the most powerful clue for determining the structure of a scene Another important clue is the relative motion between the scene and (mono)
Structure from Motion Prof. Marco Marcon Summing-up 2 Stereo is the most powerful clue for determining the structure of a scene Another important clue is the relative motion between the scene and (mono)
Robot Vision: Projective Geometry
 Robot Vision: Projective Geometry Ass.Prof. Friedrich Fraundorfer SS 2018 1 Learning goals Understand homogeneous coordinates Understand points, line, plane parameters and interpret them geometrically
Robot Vision: Projective Geometry Ass.Prof. Friedrich Fraundorfer SS 2018 1 Learning goals Understand homogeneous coordinates Understand points, line, plane parameters and interpret them geometrically
Today. Stereo (two view) reconstruction. Multiview geometry. Today. Multiview geometry. Computational Photography
 Computational Photography Matthias Zwicker University of Bern Fall 2009 Today From 2D to 3D using multiple views Introduction Geometry of two views Stereo matching Other applications Multiview geometry
Computational Photography Matthias Zwicker University of Bern Fall 2009 Today From 2D to 3D using multiple views Introduction Geometry of two views Stereo matching Other applications Multiview geometry
A Summary of Projective Geometry
 A Summary of Projective Geometry Copyright 22 Acuity Technologies Inc. In the last years a unified approach to creating D models from multiple images has been developed by Beardsley[],Hartley[4,5,9],Torr[,6]
A Summary of Projective Geometry Copyright 22 Acuity Technologies Inc. In the last years a unified approach to creating D models from multiple images has been developed by Beardsley[],Hartley[4,5,9],Torr[,6]
Recovering structure from a single view Pinhole perspective projection
 EPIPOLAR GEOMETRY The slides are from several sources through James Hays (Brown); Silvio Savarese (U. of Michigan); Svetlana Lazebnik (U. Illinois); Bill Freeman and Antonio Torralba (MIT), including their
EPIPOLAR GEOMETRY The slides are from several sources through James Hays (Brown); Silvio Savarese (U. of Michigan); Svetlana Lazebnik (U. Illinois); Bill Freeman and Antonio Torralba (MIT), including their
Visualization 2D-to-3D Photo Rendering for 3D Displays
 Visualization 2D-to-3D Photo Rendering for 3D Displays Sumit K Chauhan 1, Divyesh R Bajpai 2, Vatsal H Shah 3 1 Information Technology, Birla Vishvakarma mahavidhyalaya,sumitskc51@gmail.com 2 Information
Visualization 2D-to-3D Photo Rendering for 3D Displays Sumit K Chauhan 1, Divyesh R Bajpai 2, Vatsal H Shah 3 1 Information Technology, Birla Vishvakarma mahavidhyalaya,sumitskc51@gmail.com 2 Information
Rectification and Distortion Correction
 Rectification and Distortion Correction Hagen Spies March 12, 2003 Computer Vision Laboratory Department of Electrical Engineering Linköping University, Sweden Contents Distortion Correction Rectification
Rectification and Distortion Correction Hagen Spies March 12, 2003 Computer Vision Laboratory Department of Electrical Engineering Linköping University, Sweden Contents Distortion Correction Rectification
Multiple View Geometry of Projector-Camera Systems from Virtual Mutual Projection
 Multiple View Geometry of rojector-camera Systems from Virtual Mutual rojection Shuhei Kobayashi, Fumihiko Sakaue, and Jun Sato Department of Computer Science and Engineering Nagoya Institute of Technology
Multiple View Geometry of rojector-camera Systems from Virtual Mutual rojection Shuhei Kobayashi, Fumihiko Sakaue, and Jun Sato Department of Computer Science and Engineering Nagoya Institute of Technology
Feature Transfer and Matching in Disparate Stereo Views through the use of Plane Homographies
 Feature Transfer and Matching in Disparate Stereo Views through the use of Plane Homographies M. Lourakis, S. Tzurbakis, A. Argyros, S. Orphanoudakis Computer Vision and Robotics Lab (CVRL) Institute of
Feature Transfer and Matching in Disparate Stereo Views through the use of Plane Homographies M. Lourakis, S. Tzurbakis, A. Argyros, S. Orphanoudakis Computer Vision and Robotics Lab (CVRL) Institute of
Structure from Motion and Multi- view Geometry. Last lecture
 Structure from Motion and Multi- view Geometry Topics in Image-Based Modeling and Rendering CSE291 J00 Lecture 5 Last lecture S. J. Gortler, R. Grzeszczuk, R. Szeliski,M. F. Cohen The Lumigraph, SIGGRAPH,
Structure from Motion and Multi- view Geometry Topics in Image-Based Modeling and Rendering CSE291 J00 Lecture 5 Last lecture S. J. Gortler, R. Grzeszczuk, R. Szeliski,M. F. Cohen The Lumigraph, SIGGRAPH,
Stereo and Epipolar geometry
 Previously Image Primitives (feature points, lines, contours) Today: Stereo and Epipolar geometry How to match primitives between two (multiple) views) Goals: 3D reconstruction, recognition Jana Kosecka
Previously Image Primitives (feature points, lines, contours) Today: Stereo and Epipolar geometry How to match primitives between two (multiple) views) Goals: 3D reconstruction, recognition Jana Kosecka
The end of affine cameras
 The end of affine cameras Affine SFM revisited Epipolar geometry Two-view structure from motion Multi-view structure from motion Planches : http://www.di.ens.fr/~ponce/geomvis/lect3.pptx http://www.di.ens.fr/~ponce/geomvis/lect3.pdf
The end of affine cameras Affine SFM revisited Epipolar geometry Two-view structure from motion Multi-view structure from motion Planches : http://www.di.ens.fr/~ponce/geomvis/lect3.pptx http://www.di.ens.fr/~ponce/geomvis/lect3.pdf
Flexible Calibration of a Portable Structured Light System through Surface Plane
 Vol. 34, No. 11 ACTA AUTOMATICA SINICA November, 2008 Flexible Calibration of a Portable Structured Light System through Surface Plane GAO Wei 1 WANG Liang 1 HU Zhan-Yi 1 Abstract For a portable structured
Vol. 34, No. 11 ACTA AUTOMATICA SINICA November, 2008 Flexible Calibration of a Portable Structured Light System through Surface Plane GAO Wei 1 WANG Liang 1 HU Zhan-Yi 1 Abstract For a portable structured
Structure and motion in 3D and 2D from hybrid matching constraints
 Structure and motion in 3D and 2D from hybrid matching constraints Anders Heyden, Fredrik Nyberg and Ola Dahl Applied Mathematics Group Malmo University, Sweden {heyden,fredrik.nyberg,ola.dahl}@ts.mah.se
Structure and motion in 3D and 2D from hybrid matching constraints Anders Heyden, Fredrik Nyberg and Ola Dahl Applied Mathematics Group Malmo University, Sweden {heyden,fredrik.nyberg,ola.dahl}@ts.mah.se
Metric Rectification for Perspective Images of Planes
 789139-3 University of California Santa Barbara Department of Electrical and Computer Engineering CS290I Multiple View Geometry in Computer Vision and Computer Graphics Spring 2006 Metric Rectification
789139-3 University of California Santa Barbara Department of Electrical and Computer Engineering CS290I Multiple View Geometry in Computer Vision and Computer Graphics Spring 2006 Metric Rectification
P T p y T O Fig.. The coordinate system. The coordinate system ( ) is attached to the camera, and the corresponding image coordinates (x y) on the ima
 Recovery of Ego-Motion Using Region Alignment Michal Irani Benny Rousso Shmuel Peleg Abstract A method for computing the 3D camera motion (the egomotion) in a static scene is introduced, which is based
Recovery of Ego-Motion Using Region Alignment Michal Irani Benny Rousso Shmuel Peleg Abstract A method for computing the 3D camera motion (the egomotion) in a static scene is introduced, which is based
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Jayson Smith LECTURE 4 Planar Scenes and Homography 4.1. Points on Planes This lecture examines the special case of planar scenes. When talking
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Jayson Smith LECTURE 4 Planar Scenes and Homography 4.1. Points on Planes This lecture examines the special case of planar scenes. When talking
Vertical Parallax from Moving Shadows
 Vertical Parallax from Moving Shadows Yaron Caspi Faculty of Mathematics and Computer Science The Weizmann Institute of Science Rehovot, 76100, Israel Michael Werman School of Computer Science and Engineering
Vertical Parallax from Moving Shadows Yaron Caspi Faculty of Mathematics and Computer Science The Weizmann Institute of Science Rehovot, 76100, Israel Michael Werman School of Computer Science and Engineering
Integrating Local Affine into Global Projective Images in the Joint Image Space
 Integrating Local Affine into Global Projective Images in the Joint Image Space P. Anandan and Shai Avidan Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA, {anandan,avidan}@microsoft.com
Integrating Local Affine into Global Projective Images in the Joint Image Space P. Anandan and Shai Avidan Microsoft Research, One Microsoft Way, Redmond, WA 98052, USA, {anandan,avidan}@microsoft.com
Plane + Parallax, Tensors and Factorization
 Plane + Parallax, Tensors and Factorization Bill Triggs INRIA Rhône-Alpes, 655 avenue de l Europe, 38330 Montbonnot, France. Bill.Triggs@inrialpes.fr http://www.inrialpes.fr/movi/people/ Triggs Abstract
Plane + Parallax, Tensors and Factorization Bill Triggs INRIA Rhône-Alpes, 655 avenue de l Europe, 38330 Montbonnot, France. Bill.Triggs@inrialpes.fr http://www.inrialpes.fr/movi/people/ Triggs Abstract
A Canonical Framework for Sequences of Images
 A Canonical Framework for Sequences of Images Anders Heyden, Kalle Åström Dept of Mathematics, Lund University Box 118, S-221 00 Lund, Sweden email: andersp@maths.lth.se kalle@maths.lth.se Abstract This
A Canonical Framework for Sequences of Images Anders Heyden, Kalle Åström Dept of Mathematics, Lund University Box 118, S-221 00 Lund, Sweden email: andersp@maths.lth.se kalle@maths.lth.se Abstract This
Machine vision. Summary # 11: Stereo vision and epipolar geometry. u l = λx. v l = λy
 1 Machine vision Summary # 11: Stereo vision and epipolar geometry STEREO VISION The goal of stereo vision is to use two cameras to capture 3D scenes. There are two important problems in stereo vision:
1 Machine vision Summary # 11: Stereo vision and epipolar geometry STEREO VISION The goal of stereo vision is to use two cameras to capture 3D scenes. There are two important problems in stereo vision:
The Projective Vision Toolkit
 The Projective Vision Toolkit ANTHONY WHITEHEAD School of Computer Science Carleton University, Ottawa, Canada awhitehe@scs.carleton.ca Abstract: Projective vision research has recently received a lot
The Projective Vision Toolkit ANTHONY WHITEHEAD School of Computer Science Carleton University, Ottawa, Canada awhitehe@scs.carleton.ca Abstract: Projective vision research has recently received a lot
3D Reconstruction from Scene Knowledge
 Multiple-View Reconstruction from Scene Knowledge 3D Reconstruction from Scene Knowledge SYMMETRY & MULTIPLE-VIEW GEOMETRY Fundamental types of symmetry Equivalent views Symmetry based reconstruction MUTIPLE-VIEW
Multiple-View Reconstruction from Scene Knowledge 3D Reconstruction from Scene Knowledge SYMMETRY & MULTIPLE-VIEW GEOMETRY Fundamental types of symmetry Equivalent views Symmetry based reconstruction MUTIPLE-VIEW
A Comparison of Projective Reconstruction Methods for Pairs of Views
 A Comparison of Projective Reconstruction Methods for Pairs of Views Rothwell, C, Csurka, G and Faugeras, O INRIA, Sophia Antipolis, France email: [crothwel,csurka,faugeras]@sophiainriafr Abstract Recently,
A Comparison of Projective Reconstruction Methods for Pairs of Views Rothwell, C, Csurka, G and Faugeras, O INRIA, Sophia Antipolis, France email: [crothwel,csurka,faugeras]@sophiainriafr Abstract Recently,
Automatic Line Matching across Views
 Automatic Line Matching across Views Cordelia Schmid and Andrew Zisserman Department of Engineering Science, University of Oxford Parks Road, Oxford, UK OX1 3PJ Abstract This paper presents a new method
Automatic Line Matching across Views Cordelia Schmid and Andrew Zisserman Department of Engineering Science, University of Oxford Parks Road, Oxford, UK OX1 3PJ Abstract This paper presents a new method
COMPARATIVE STUDY OF DIFFERENT APPROACHES FOR EFFICIENT RECTIFICATION UNDER GENERAL MOTION
 COMPARATIVE STUDY OF DIFFERENT APPROACHES FOR EFFICIENT RECTIFICATION UNDER GENERAL MOTION Mr.V.SRINIVASA RAO 1 Prof.A.SATYA KALYAN 2 DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING PRASAD V POTLURI SIDDHARTHA
COMPARATIVE STUDY OF DIFFERENT APPROACHES FOR EFFICIENT RECTIFICATION UNDER GENERAL MOTION Mr.V.SRINIVASA RAO 1 Prof.A.SATYA KALYAN 2 DEPARTMENT OF COMPUTER SCIENCE AND ENGINEERING PRASAD V POTLURI SIDDHARTHA
Week 2: Two-View Geometry. Padua Summer 08 Frank Dellaert
 Week 2: Two-View Geometry Padua Summer 08 Frank Dellaert Mosaicking Outline 2D Transformation Hierarchy RANSAC Triangulation of 3D Points Cameras Triangulation via SVD Automatic Correspondence Essential
Week 2: Two-View Geometry Padua Summer 08 Frank Dellaert Mosaicking Outline 2D Transformation Hierarchy RANSAC Triangulation of 3D Points Cameras Triangulation via SVD Automatic Correspondence Essential
METR Robotics Tutorial 2 Week 2: Homogeneous Coordinates
 METR4202 -- Robotics Tutorial 2 Week 2: Homogeneous Coordinates The objective of this tutorial is to explore homogenous transformations. The MATLAB robotics toolbox developed by Peter Corke might be a
METR4202 -- Robotics Tutorial 2 Week 2: Homogeneous Coordinates The objective of this tutorial is to explore homogenous transformations. The MATLAB robotics toolbox developed by Peter Corke might be a
Automatic Estimation of Epipolar Geometry
 Robust line estimation Automatic Estimation of Epipolar Geometry Fit a line to 2D data containing outliers c b a d There are two problems: (i) a line fit to the data ;, (ii) a classification of the data
Robust line estimation Automatic Estimation of Epipolar Geometry Fit a line to 2D data containing outliers c b a d There are two problems: (i) a line fit to the data ;, (ii) a classification of the data
Two-View Geometry (Course 23, Lecture D)
 Two-View Geometry (Course 23, Lecture D) Jana Kosecka Department of Computer Science George Mason University http://www.cs.gmu.edu/~kosecka General Formulation Given two views of the scene recover the
Two-View Geometry (Course 23, Lecture D) Jana Kosecka Department of Computer Science George Mason University http://www.cs.gmu.edu/~kosecka General Formulation Given two views of the scene recover the
Computer Vision I - Algorithms and Applications: Multi-View 3D reconstruction
 Computer Vision I - Algorithms and Applications: Multi-View 3D reconstruction Carsten Rother 09/12/2013 Computer Vision I: Multi-View 3D reconstruction Roadmap this lecture Computer Vision I: Multi-View
Computer Vision I - Algorithms and Applications: Multi-View 3D reconstruction Carsten Rother 09/12/2013 Computer Vision I: Multi-View 3D reconstruction Roadmap this lecture Computer Vision I: Multi-View
N-Views (1) Homographies and Projection
 CS 4495 Computer Vision N-Views (1) Homographies and Projection Aaron Bobick School of Interactive Computing Administrivia PS 2: Get SDD and Normalized Correlation working for a given windows size say
CS 4495 Computer Vision N-Views (1) Homographies and Projection Aaron Bobick School of Interactive Computing Administrivia PS 2: Get SDD and Normalized Correlation working for a given windows size say
CSE 252B: Computer Vision II
 CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Sameer Agarwal LECTURE 1 Image Formation 1.1. The geometry of image formation We begin by considering the process of image formation when a
CSE 252B: Computer Vision II Lecturer: Serge Belongie Scribe: Sameer Agarwal LECTURE 1 Image Formation 1.1. The geometry of image formation We begin by considering the process of image formation when a
is used in many dierent applications. We give some examples from robotics. Firstly, a robot equipped with a camera, giving visual information about th
 Geometry and Algebra of Multiple Projective Transformations Anders Heyden Dept of Mathematics, Lund University Box 8, S-22 00 Lund, SWEDEN email: heyden@maths.lth.se Supervisor: Gunnar Sparr Abstract In
Geometry and Algebra of Multiple Projective Transformations Anders Heyden Dept of Mathematics, Lund University Box 8, S-22 00 Lund, SWEDEN email: heyden@maths.lth.se Supervisor: Gunnar Sparr Abstract In
Lecture 9: Epipolar Geometry
 Lecture 9: Epipolar Geometry Professor Fei Fei Li Stanford Vision Lab 1 What we will learn today? Why is stereo useful? Epipolar constraints Essential and fundamental matrix Estimating F (Problem Set 2
Lecture 9: Epipolar Geometry Professor Fei Fei Li Stanford Vision Lab 1 What we will learn today? Why is stereo useful? Epipolar constraints Essential and fundamental matrix Estimating F (Problem Set 2
Rectification and Disparity
 Rectification and Disparity Nassir Navab Slides prepared by Christian Unger What is Stereo Vision? Introduction A technique aimed at inferring dense depth measurements efficiently using two cameras. Wide
Rectification and Disparity Nassir Navab Slides prepared by Christian Unger What is Stereo Vision? Introduction A technique aimed at inferring dense depth measurements efficiently using two cameras. Wide
1D camera geometry and Its application to circular motion estimation. Creative Commons: Attribution 3.0 Hong Kong License
 Title D camera geometry and Its application to circular motion estimation Author(s Zhang, G; Zhang, H; Wong, KKY Citation The 7th British Machine Vision Conference (BMVC, Edinburgh, U.K., 4-7 September
Title D camera geometry and Its application to circular motion estimation Author(s Zhang, G; Zhang, H; Wong, KKY Citation The 7th British Machine Vision Conference (BMVC, Edinburgh, U.K., 4-7 September
Computer Vision Projective Geometry and Calibration. Pinhole cameras
 Computer Vision Projective Geometry and Calibration Professor Hager http://www.cs.jhu.edu/~hager Jason Corso http://www.cs.jhu.edu/~jcorso. Pinhole cameras Abstract camera model - box with a small hole
Computer Vision Projective Geometry and Calibration Professor Hager http://www.cs.jhu.edu/~hager Jason Corso http://www.cs.jhu.edu/~jcorso. Pinhole cameras Abstract camera model - box with a small hole
Linear Multi View Reconstruction and Camera Recovery Using a Reference Plane
 International Journal of Computer Vision 49(2/3), 117 141, 2002 c 2002 Kluwer Academic Publishers. Manufactured in The Netherlands. Linear Multi View Reconstruction and Camera Recovery Using a Reference
International Journal of Computer Vision 49(2/3), 117 141, 2002 c 2002 Kluwer Academic Publishers. Manufactured in The Netherlands. Linear Multi View Reconstruction and Camera Recovery Using a Reference
CS231A Course Notes 4: Stereo Systems and Structure from Motion
 CS231A Course Notes 4: Stereo Systems and Structure from Motion Kenji Hata and Silvio Savarese 1 Introduction In the previous notes, we covered how adding additional viewpoints of a scene can greatly enhance
CS231A Course Notes 4: Stereo Systems and Structure from Motion Kenji Hata and Silvio Savarese 1 Introduction In the previous notes, we covered how adding additional viewpoints of a scene can greatly enhance
Elements of Computer Vision: Multiple View Geometry. 1 Introduction. 2 Elements of Geometry. Andrea Fusiello
 Elements of Computer Vision: Multiple View Geometry. Andrea Fusiello http://www.sci.univr.it/~fusiello July 11, 2005 c Copyright by Andrea Fusiello. This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike
Elements of Computer Vision: Multiple View Geometry. Andrea Fusiello http://www.sci.univr.it/~fusiello July 11, 2005 c Copyright by Andrea Fusiello. This work is licensed under the Creative Commons Attribution-NonCommercial-ShareAlike
A linear algorithm for Camera Self-Calibration, Motion and Structure Recovery for Multi-Planar Scenes from Two Perspective Images
 A linear algorithm for Camera Self-Calibration, Motion and Structure Recovery for Multi-Planar Scenes from Two Perspective Images Gang Xu, Jun-ichi Terai and Heung-Yeung Shum Microsoft Research China 49
A linear algorithm for Camera Self-Calibration, Motion and Structure Recovery for Multi-Planar Scenes from Two Perspective Images Gang Xu, Jun-ichi Terai and Heung-Yeung Shum Microsoft Research China 49
3D reconstruction class 11
 3D reconstruction class 11 Multiple View Geometry Comp 290-089 Marc Pollefeys Multiple View Geometry course schedule (subject to change) Jan. 7, 9 Intro & motivation Projective 2D Geometry Jan. 14, 16
3D reconstruction class 11 Multiple View Geometry Comp 290-089 Marc Pollefeys Multiple View Geometry course schedule (subject to change) Jan. 7, 9 Intro & motivation Projective 2D Geometry Jan. 14, 16
Image Transfer Methods. Satya Prakash Mallick Jan 28 th, 2003
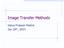 Image Transfer Methods Satya Prakash Mallick Jan 28 th, 2003 Objective Given two or more images of the same scene, the objective is to synthesize a novel view of the scene from a view point where there
Image Transfer Methods Satya Prakash Mallick Jan 28 th, 2003 Objective Given two or more images of the same scene, the objective is to synthesize a novel view of the scene from a view point where there
Midterm Exam Solutions
 Midterm Exam Solutions Computer Vision (J. Košecká) October 27, 2009 HONOR SYSTEM: This examination is strictly individual. You are not allowed to talk, discuss, exchange solutions, etc., with other fellow
Midterm Exam Solutions Computer Vision (J. Košecká) October 27, 2009 HONOR SYSTEM: This examination is strictly individual. You are not allowed to talk, discuss, exchange solutions, etc., with other fellow
Visual Recognition: Image Formation
 Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
Visual Recognition: Image Formation Raquel Urtasun TTI Chicago Jan 5, 2012 Raquel Urtasun (TTI-C) Visual Recognition Jan 5, 2012 1 / 61 Today s lecture... Fundamentals of image formation You should know
CS6670: Computer Vision
 CS6670: Computer Vision Noah Snavely Lecture 7: Image Alignment and Panoramas What s inside your fridge? http://www.cs.washington.edu/education/courses/cse590ss/01wi/ Projection matrix intrinsics projection
CS6670: Computer Vision Noah Snavely Lecture 7: Image Alignment and Panoramas What s inside your fridge? http://www.cs.washington.edu/education/courses/cse590ss/01wi/ Projection matrix intrinsics projection
University of Southern California, 1590 the Alameda #200 Los Angeles, CA San Jose, CA Abstract
 Mirror Symmetry 2-View Stereo Geometry Alexandre R.J. François +, Gérard G. Medioni + and Roman Waupotitsch * + Institute for Robotics and Intelligent Systems * Geometrix Inc. University of Southern California,
Mirror Symmetry 2-View Stereo Geometry Alexandre R.J. François +, Gérard G. Medioni + and Roman Waupotitsch * + Institute for Robotics and Intelligent Systems * Geometrix Inc. University of Southern California,
A Factorization Method for Structure from Planar Motion
 A Factorization Method for Structure from Planar Motion Jian Li and Rama Chellappa Center for Automation Research (CfAR) and Department of Electrical and Computer Engineering University of Maryland, College
A Factorization Method for Structure from Planar Motion Jian Li and Rama Chellappa Center for Automation Research (CfAR) and Department of Electrical and Computer Engineering University of Maryland, College
Computing Matched-epipolar Projections
 Computing Matched-epipolar Projections Richard I. Hartley G.E. CRD, Schenectady, NY, 12301. Ph: (518)-387-7333 Fax: (518)-387-6845 Email : hartley@crd.ge.com Abstract This paper gives a new method for
Computing Matched-epipolar Projections Richard I. Hartley G.E. CRD, Schenectady, NY, 12301. Ph: (518)-387-7333 Fax: (518)-387-6845 Email : hartley@crd.ge.com Abstract This paper gives a new method for
Invariance of l and the Conic Dual to Circular Points C
 Invariance of l and the Conic Dual to Circular Points C [ ] A t l = (0, 0, 1) is preserved under H = v iff H is an affinity: w [ ] l H l H A l l v 0 [ t 0 v! = = w w] 0 0 v = 0 1 1 C = diag(1, 1, 0) is
Invariance of l and the Conic Dual to Circular Points C [ ] A t l = (0, 0, 1) is preserved under H = v iff H is an affinity: w [ ] l H l H A l l v 0 [ t 0 v! = = w w] 0 0 v = 0 1 1 C = diag(1, 1, 0) is
Image Rectification (Stereo) (New book: 7.2.1, old book: 11.1)
 Image Rectification (Stereo) (New book: 7.2.1, old book: 11.1) Guido Gerig CS 6320 Spring 2013 Credits: Prof. Mubarak Shah, Course notes modified from: http://www.cs.ucf.edu/courses/cap6411/cap5415/, Lecture
Image Rectification (Stereo) (New book: 7.2.1, old book: 11.1) Guido Gerig CS 6320 Spring 2013 Credits: Prof. Mubarak Shah, Course notes modified from: http://www.cs.ucf.edu/courses/cap6411/cap5415/, Lecture
Structure from motion
 Structure from motion Structure from motion Given a set of corresponding points in two or more images, compute the camera parameters and the 3D point coordinates?? R 1,t 1 R 2,t R 2 3,t 3 Camera 1 Camera
Structure from motion Structure from motion Given a set of corresponding points in two or more images, compute the camera parameters and the 3D point coordinates?? R 1,t 1 R 2,t R 2 3,t 3 Camera 1 Camera
Structure from Motion. Introduction to Computer Vision CSE 152 Lecture 10
 Structure from Motion CSE 152 Lecture 10 Announcements Homework 3 is due May 9, 11:59 PM Reading: Chapter 8: Structure from Motion Optional: Multiple View Geometry in Computer Vision, 2nd edition, Hartley
Structure from Motion CSE 152 Lecture 10 Announcements Homework 3 is due May 9, 11:59 PM Reading: Chapter 8: Structure from Motion Optional: Multiple View Geometry in Computer Vision, 2nd edition, Hartley
Camera model and multiple view geometry
 Chapter Camera model and multiple view geometry Before discussing how D information can be obtained from images it is important to know how images are formed First the camera model is introduced and then
Chapter Camera model and multiple view geometry Before discussing how D information can be obtained from images it is important to know how images are formed First the camera model is introduced and then
Catadioptric camera model with conic mirror
 LÓPEZ-NICOLÁS, SAGÜÉS: CATADIOPTRIC CAMERA MODEL WITH CONIC MIRROR Catadioptric camera model with conic mirror G. López-Nicolás gonlopez@unizar.es C. Sagüés csagues@unizar.es Instituto de Investigación
LÓPEZ-NICOLÁS, SAGÜÉS: CATADIOPTRIC CAMERA MODEL WITH CONIC MIRROR Catadioptric camera model with conic mirror G. López-Nicolás gonlopez@unizar.es C. Sagüés csagues@unizar.es Instituto de Investigación
Compositing a bird's eye view mosaic
 Compositing a bird's eye view mosaic Robert Laganiere School of Information Technology and Engineering University of Ottawa Ottawa, Ont KN 6N Abstract This paper describes a method that allows the composition
Compositing a bird's eye view mosaic Robert Laganiere School of Information Technology and Engineering University of Ottawa Ottawa, Ont KN 6N Abstract This paper describes a method that allows the composition
The Geometry of Multiple Images The Laws That Govern the Formation of Multiple Images of a Scene and Some of Thcir Applications
 The Geometry of Multiple Images The Laws That Govern the Formation of Multiple Images of a Scene and Some of Thcir Applications Olivier Faugeras QUC1ng-Tuan Luong with contributions from Theo Papadopoulo
The Geometry of Multiple Images The Laws That Govern the Formation of Multiple Images of a Scene and Some of Thcir Applications Olivier Faugeras QUC1ng-Tuan Luong with contributions from Theo Papadopoulo
Partial Calibration and Mirror Shape Recovery for Non-Central Catadioptric Systems
 Partial Calibration and Mirror Shape Recovery for Non-Central Catadioptric Systems Abstract In this paper we present a method for mirror shape recovery and partial calibration for non-central catadioptric
Partial Calibration and Mirror Shape Recovery for Non-Central Catadioptric Systems Abstract In this paper we present a method for mirror shape recovery and partial calibration for non-central catadioptric
Fast Outlier Rejection by Using Parallax-Based Rigidity Constraint for Epipolar Geometry Estimation
 Fast Outlier Rejection by Using Parallax-Based Rigidity Constraint for Epipolar Geometry Estimation Engin Tola 1 and A. Aydın Alatan 2 1 Computer Vision Laboratory, Ecóle Polytechnique Fédéral de Lausanne
Fast Outlier Rejection by Using Parallax-Based Rigidity Constraint for Epipolar Geometry Estimation Engin Tola 1 and A. Aydın Alatan 2 1 Computer Vision Laboratory, Ecóle Polytechnique Fédéral de Lausanne
CS-9645 Introduction to Computer Vision Techniques Winter 2019
 Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Table of Contents Projective Geometry... 1 Definitions...1 Axioms of Projective Geometry... Ideal Points...3 Geometric Interpretation... 3 Fundamental Transformations of Projective Geometry... 4 The D
Multiple View Geometry
 Multiple View Geometry CS 6320, Spring 2013 Guest Lecture Marcel Prastawa adapted from Pollefeys, Shah, and Zisserman Single view computer vision Projective actions of cameras Camera callibration Photometric
Multiple View Geometry CS 6320, Spring 2013 Guest Lecture Marcel Prastawa adapted from Pollefeys, Shah, and Zisserman Single view computer vision Projective actions of cameras Camera callibration Photometric
Contents. 1 Introduction Background Organization Features... 7
 Contents 1 Introduction... 1 1.1 Background.... 1 1.2 Organization... 2 1.3 Features... 7 Part I Fundamental Algorithms for Computer Vision 2 Ellipse Fitting... 11 2.1 Representation of Ellipses.... 11
Contents 1 Introduction... 1 1.1 Background.... 1 1.2 Organization... 2 1.3 Features... 7 Part I Fundamental Algorithms for Computer Vision 2 Ellipse Fitting... 11 2.1 Representation of Ellipses.... 11
Camera Geometry II. COS 429 Princeton University
 Camera Geometry II COS 429 Princeton University Outline Projective geometry Vanishing points Application: camera calibration Application: single-view metrology Epipolar geometry Application: stereo correspondence
Camera Geometry II COS 429 Princeton University Outline Projective geometry Vanishing points Application: camera calibration Application: single-view metrology Epipolar geometry Application: stereo correspondence
Projective geometry for Computer Vision
 Department of Computer Science and Engineering IIT Delhi NIT, Rourkela March 27, 2010 Overview Pin-hole camera Why projective geometry? Reconstruction Computer vision geometry: main problems Correspondence
Department of Computer Science and Engineering IIT Delhi NIT, Rourkela March 27, 2010 Overview Pin-hole camera Why projective geometry? Reconstruction Computer vision geometry: main problems Correspondence
Stereo CSE 576. Ali Farhadi. Several slides from Larry Zitnick and Steve Seitz
 Stereo CSE 576 Ali Farhadi Several slides from Larry Zitnick and Steve Seitz Why do we perceive depth? What do humans use as depth cues? Motion Convergence When watching an object close to us, our eyes
Stereo CSE 576 Ali Farhadi Several slides from Larry Zitnick and Steve Seitz Why do we perceive depth? What do humans use as depth cues? Motion Convergence When watching an object close to us, our eyes
PROJECTIVE SPACE AND THE PINHOLE CAMERA
 PROJECTIVE SPACE AND THE PINHOLE CAMERA MOUSA REBOUH Abstract. Here we provide (linear algebra) proofs of the ancient theorem of Pappus and the contemporary theorem of Desargues on collineations. We also
PROJECTIVE SPACE AND THE PINHOLE CAMERA MOUSA REBOUH Abstract. Here we provide (linear algebra) proofs of the ancient theorem of Pappus and the contemporary theorem of Desargues on collineations. We also
Computer Vision. Coordinates. Prof. Flávio Cardeal DECOM / CEFET- MG.
 Computer Vision Coordinates Prof. Flávio Cardeal DECOM / CEFET- MG cardeal@decom.cefetmg.br Abstract This lecture discusses world coordinates and homogeneous coordinates, as well as provides an overview
Computer Vision Coordinates Prof. Flávio Cardeal DECOM / CEFET- MG cardeal@decom.cefetmg.br Abstract This lecture discusses world coordinates and homogeneous coordinates, as well as provides an overview
Textureless Layers CMU-RI-TR Qifa Ke, Simon Baker, and Takeo Kanade
 Textureless Layers CMU-RI-TR-04-17 Qifa Ke, Simon Baker, and Takeo Kanade The Robotics Institute Carnegie Mellon University 5000 Forbes Avenue Pittsburgh, PA 15213 Abstract Layers are one of the most well
Textureless Layers CMU-RI-TR-04-17 Qifa Ke, Simon Baker, and Takeo Kanade The Robotics Institute Carnegie Mellon University 5000 Forbes Avenue Pittsburgh, PA 15213 Abstract Layers are one of the most well
Recap: Features and filters. Recap: Grouping & fitting. Now: Multiple views 10/29/2008. Epipolar geometry & stereo vision. Why multiple views?
 Recap: Features and filters Epipolar geometry & stereo vision Tuesday, Oct 21 Kristen Grauman UT-Austin Transforming and describing images; textures, colors, edges Recap: Grouping & fitting Now: Multiple
Recap: Features and filters Epipolar geometry & stereo vision Tuesday, Oct 21 Kristen Grauman UT-Austin Transforming and describing images; textures, colors, edges Recap: Grouping & fitting Now: Multiple
Minimal Projective Reconstruction for Combinations of Points and Lines in Three Views
 Minimal Projective Reconstruction for Combinations of Points and Lines in Three Views Magnus Oskarsson, Andrew Zisserman and Kalle Åström Centre for Mathematical Sciences Lund University,SE 221 00 Lund,
Minimal Projective Reconstruction for Combinations of Points and Lines in Three Views Magnus Oskarsson, Andrew Zisserman and Kalle Åström Centre for Mathematical Sciences Lund University,SE 221 00 Lund,
Comments on Consistent Depth Maps Recovery from a Video Sequence
 Comments on Consistent Depth Maps Recovery from a Video Sequence N.P. van der Aa D.S. Grootendorst B.F. Böggemann R.T. Tan Technical Report UU-CS-2011-014 May 2011 Department of Information and Computing
Comments on Consistent Depth Maps Recovery from a Video Sequence N.P. van der Aa D.S. Grootendorst B.F. Böggemann R.T. Tan Technical Report UU-CS-2011-014 May 2011 Department of Information and Computing
Particle Tracking. For Bulk Material Handling Systems Using DEM Models. By: Jordan Pease
 Particle Tracking For Bulk Material Handling Systems Using DEM Models By: Jordan Pease Introduction Motivation for project Particle Tracking Application to DEM models Experimental Results Future Work References
Particle Tracking For Bulk Material Handling Systems Using DEM Models By: Jordan Pease Introduction Motivation for project Particle Tracking Application to DEM models Experimental Results Future Work References
55:148 Digital Image Processing Chapter 11 3D Vision, Geometry
 55:148 Digital Image Processing Chapter 11 3D Vision, Geometry Topics: Basics of projective geometry Points and hyperplanes in projective space Homography Estimating homography from point correspondence
55:148 Digital Image Processing Chapter 11 3D Vision, Geometry Topics: Basics of projective geometry Points and hyperplanes in projective space Homography Estimating homography from point correspondence
Structure from Motion
 Structure from Motion Outline Bundle Adjustment Ambguities in Reconstruction Affine Factorization Extensions Structure from motion Recover both 3D scene geoemetry and camera positions SLAM: Simultaneous
Structure from Motion Outline Bundle Adjustment Ambguities in Reconstruction Affine Factorization Extensions Structure from motion Recover both 3D scene geoemetry and camera positions SLAM: Simultaneous
arxiv: v1 [cs.cv] 28 Sep 2018
![arxiv: v1 [cs.cv] 28 Sep 2018 arxiv: v1 [cs.cv] 28 Sep 2018](/thumbs/93/113542646.jpg) Camera Pose Estimation from Sequence of Calibrated Images arxiv:1809.11066v1 [cs.cv] 28 Sep 2018 Jacek Komorowski 1 and Przemyslaw Rokita 2 1 Maria Curie-Sklodowska University, Institute of Computer Science,
Camera Pose Estimation from Sequence of Calibrated Images arxiv:1809.11066v1 [cs.cv] 28 Sep 2018 Jacek Komorowski 1 and Przemyslaw Rokita 2 1 Maria Curie-Sklodowska University, Institute of Computer Science,
55:148 Digital Image Processing Chapter 11 3D Vision, Geometry
 55:148 Digital Image Processing Chapter 11 3D Vision, Geometry Topics: Basics of projective geometry Points and hyperplanes in projective space Homography Estimating homography from point correspondence
55:148 Digital Image Processing Chapter 11 3D Vision, Geometry Topics: Basics of projective geometry Points and hyperplanes in projective space Homography Estimating homography from point correspondence
A 3D shape constraint on video
 1 A 3D shape constraint on video Hui Ji and Cornelia Fermüller Member, IEEE, Center for Automation Research University of Maryland College Park, MD 20742-3275, USA {jihui, fer}@cfar.umd.edu Abstract We
1 A 3D shape constraint on video Hui Ji and Cornelia Fermüller Member, IEEE, Center for Automation Research University of Maryland College Park, MD 20742-3275, USA {jihui, fer}@cfar.umd.edu Abstract We
Massachusetts Institute of Technology Department of Computer Science and Electrical Engineering 6.801/6.866 Machine Vision QUIZ II
 Massachusetts Institute of Technology Department of Computer Science and Electrical Engineering 6.801/6.866 Machine Vision QUIZ II Handed out: 001 Nov. 30th Due on: 001 Dec. 10th Problem 1: (a (b Interior
Massachusetts Institute of Technology Department of Computer Science and Electrical Engineering 6.801/6.866 Machine Vision QUIZ II Handed out: 001 Nov. 30th Due on: 001 Dec. 10th Problem 1: (a (b Interior
Geometry of Multiple views
 1 Geometry of Multiple views CS 554 Computer Vision Pinar Duygulu Bilkent University 2 Multiple views Despite the wealth of information contained in a a photograph, the depth of a scene point along the
1 Geometry of Multiple views CS 554 Computer Vision Pinar Duygulu Bilkent University 2 Multiple views Despite the wealth of information contained in a a photograph, the depth of a scene point along the
