Introduction to Algorithms Massachusetts Institute of Technology Professors Erik D. Demaine and Charles E. Leiserson.
|
|
|
- Jade Fox
- 6 years ago
- Views:
Transcription
1 Introduction to Algorithms Massachusetts Institute of Technolog Professors Erik D. Demaine and Charles E. Leiserson October 24, J/18.410J Handout 16 Problem Set 5 MIT students: This problem set is due in lecture on Monda, October 31, The homework lab for this problem set will be held 2 4 P.M. on Sunda, October 30, Reading: Chapter 14 and Skip List Handout. Both eercises and problems should be solved, but onl the problems should be turned in. Eercises are intended to help ou master the course material. Even though ou should not turn in the eercise solutions, ou are responsible for material covered in the eercises. Mark the top of each sheet with our name, the course number, the problem number, our recitation section, the date and the names of an students with whom ou collaborated. Please staple and turn in our solutions on 3-hole punched paper. You will often be called upon to give an algorithm to solve a certain problem. Your write-up should take the form of a short essa. A topic paragraph should summarize the problem ou are solving and what our results are. The bod of the essa should provide the following: 1. A description of the algorithm in English and, if helpful, pseudo-code. 2. At least one worked eample or diagram to show more precisel how our algorithm works. 3. A proof (or indication) of the correctness of the algorithm. 4. An analsis of the running time of the algorithm. Remember, our goal is to communicate. Full credit will be given onl to correct solutions which are described clearl. Convoluted and obtuse descriptions will receive low marks. Eercise 5-1. Do Eercise on page 307 of CLRS. Eercise 5-2. Do Eercise on page 310 of CLRS. Eercise 5-3. Do Eercise on page 317 of CLRS. Eercise 5-4. Do Problem 14.2 on page 318 of CLRS.
2 2 Handout 16: Problem Set 5 Problem 5-1. Skip Lists and B-trees Intuitivel, it is easier to find an element that is nearb an element ou ve alread seen. In a dnamic-set data structure, a finger search from to is the following quer: given the node in the data structure that stores the element, and given another element, find the node in the data structure that stores. Skip lists support fast finger searches in the following sense. (a) Give an algorithm for finger searching from to in a skip list. Your algorithm should run in O(lg(2+ rank() rank() )) time with high probabilit, where rank() denotes the current rank of element in the sorted order of the dnamic set. When we sa with high probabilit we mean high probabilit with respect to m = 2 + rank() rank(). That is, our algorithm should run in O(lg m) time with probabilit 1 1/m α, for an α 1. Assume that the finger-search operation is given the node in the bottommost list of the skip list that stores the element. To support fast finger searches in B-trees, we need two ideas: B + -trees and level linking. Throughout this problem, assume that B = O(1). A B + -tree is a B-tree in which all the kes are stored in the leaves, and internal nodes store copies of these kes. More precisel, an internal node p with k + 1 children c 1, c 2,..., c k+1 stores k kes: the maimum ke in c 1 s subtree, the maimum ke in c 2 s subtree,..., the maimum ke in c k s subtree. (b) Describe how to modif the B-tree SEARCH algorithm in order to find the leaf con taining a given ke in a B + -tree in O(lg n) time. (c) Describe how to modif the B-tree INSERT and DELETE algorithms to work for B + - trees in O(lg n) time. A level-linked B + -tree is a B + -tree in which each node has an additional pointer to the node immediatel to its left among nodes at the same depth, as well as an additional pointer to the node immediatel to its right among nodes at the same depth. (d) Describe how our B + -tree INSERT and DELETE algorithms from part (c) can be modified to maintain level links in O(log n) time per operation. (e) Give an algorithm for finger searching from to in a level-linked B + -tree. Your algorithm should run in O(lg(2 + rank() rank() )) time. These ideas suggest a connection between skip lists and level-linked trees. In fact, a skip list is essentiall a randomized version of level-linked B + -tree. (f) Describe how to implement a deterministic skip list. That is, our data structure should have the same general pointer structure as a skip list: a sequence of one or
3 Handout 16: Problem Set 5 3 ( 2, 3) m 1 = 3 (3, 3) ( 2, 3) m 6 = 3 m 1 = 3 (3, 3) m 6 = 3 (1, 1) m 4 = 4 (1, 1) m 4 = 4 ( 1, 1) (2, 1) m 2 = 2 m 8 = 2 ( 1, 1) m 2 = 2 (2, 1) m 8 = 2 min = 1 Figure 1: In this eample of eight points, if Figure 2: When min = 1, T (1) = f(p i ) = m i, then F (S) = 25. {p 3, p 4, p 5, p 6, p 7, p 8 } and F (T (1)) = 20. more linked lists with pointers between nodes in adjacent lists that store the same ke. The SEARCH algorithm should be identical to that of a skip list. You will need to modif the INSERT operation to avoid the use of randomization to determine whether a ke should be promoted. You ma ignore DELETE for this problem part. Problem 5-2. Fun with Points in the Plane It is 3 a.m. and ou are attempting to watch lectures on video, looking for hints for Problem Set 5. For some odd reason, possibl because ou are fading in and out of consciousness, ou start to notice a strange cloud of black dots on an otherwise white wall in our room. Thus, instead of watching the lecture, our subconscious mind starts tring to solve the following problem. Let S = {p 1, p 2,..., p n } be a set of n points in the plane. Each point p i has coordinates ( i, i ) and has a weight m i (a real number representing the size of the dot). Let f(p) = f(,, m) be an arbitrar function mapping a point p with coordinates (, ) and weight m to a real number, computable in O(1) time. For a subset T of S, define the function F (T ) to be the sum of f(p i ) over all points in T, i.e., F (T ) = f(p). p T For eample, if f(p i ) = m i, then F (S) is the sum of the weights of all n points. This case is depicted in Figure 1. Our goal is to compute the function F for certain subsets of the points. We call each subset a quer, and for each quer T, we want to calculate F (T ). Because there ma be a large number of queries, we want to design a data structure that will allow us to efficientl answer each quer.
4 4 Handout 16: Problem Set 5 First we consider queries that restrict the coordinate. In particular, consider the set of points whose coordinates are at least min. Formall, let T ( min ) be the set of points T ( min ) = {p i S i min }. We want to answer queries of the following form: given an value min as input, calculate the value F (T ( min )). Figure 2 is an eample of such a quer. In this case, min = 1, and the points of interest are those with coordinate at least 1. (a) Show how to modif a balanced binar search tree to support such a quer in O(lg n) time. More specificall, the computation of F (T ( min )) can be performed using onl a single walk down the tree. You do not need to support updates (insertions and deletions) for this problem part. (b) Consider the static problem, where all n points are known ahead of time. How long does it take to build our data structure from part (a)? (c) In total, given n points, how long does it take to build our data structure and answer k different queries? On the other hand, how long would it take to answer k different queries without using an data structure and using the naïve algorithm of computing F (T ( min )) from scratch for ever quer? For what values of k is it asmptoticall more efficient to use the data structure? (d) We can make this data structure dnamic b using a red-black tree. Argue that the augmentation for our solution in part (a) can be efficientl supported in a red-black tree, i.e., that points can be inserted or deleted in O(lg n) time. Net we consider queries that take an interval X = [ min, ma ] (with min ma ) as input instead of a single number min. Let T (X) be the set of points whose coordinates fall in that interval, i.e., T (X) = {p i i [ min, ma ]}. See Figure 3 for an eample of this sort of quer. We claim that we can use the same dnamic data structure from part (d) to compute F (T (X)). (e) Show how to modif our algorithm from part (a) to compute F (T (X)) in O(lg n) time. Hint: Find the shallowest node in the tree whose coordinate lies between min and ma. Finall, we generalize the static problem to two dimensions. Suppose that we are given two intervals, X = [ min, ma ] and Y = [ min, ma ]. Let T (X, Y ) be the set of all points in this rectangle, i.e., T (X, Y ) = {p i i X and i Y }. See Figure 4 for an eample of a two-dimensional quer.
5 Handout 16: Problem Set 5 5 ( 2, 3) m 1 = 3 (3, 3) m 6 = 3 ( 2, 3) m 1 = 3 ma = 2.5 (3, 3) m 6 = 3 (1, 1) m 4 = 4 (1, 1) m 4 = 4 ( 1, 1) (2, 1) m 2 = 2 m 8 = 2 ( 1, 1) m 2 = 2 (2, 1) m 8 = 2 ma = 3.5 min = 1 ma = 1 min = 1 min = 2 Figure 3: When X = [1, 3.5], T (X) = Figure 4: For X = [1, 3.5] and Y = {p 3, p 4, p 6, p 7, p 8 } and F (T (X)) = 14. [ 2, 2.5], T (X, Y ) = {p 3, p 4, p 8 } and F (T (X, Y )) = 8. (f) Describe a data structure that efficientl supports a quer to compute F (T (X, Y )) for arbitrar intervals X and Y. A quer should run in O(lg 2 n) time. Hint: Augment a range tree. (g) How long does it take to build our data structure? How much space does it use? Unfortunatel, there are problems with making this data structure dnamic. (h) Eplain whether our argument in part (d) can be generalized to the two-dimensional case. What is the worst-case time required to insert a new point into the data structure in part (f)? (i) Suppose that, once we construct the data structure with n initial points, we will per form at most O(lg n) updates. How can we modif the data structure to support both queries and updates efficientl in this case? Completel Optional Parts The remainder of this problem presents an eample of a function F that is useful in an actual application and that can be computed efficientl using the data structures ou described in the previous parts. Parts (j) through (l) outline the derivation of the corresponding function f(p i ). The remainder of this problem is completel optional. Please do not turn these parts in! As before, consider a set S = {p 1, p 2,..., p n } of n points in the plane, with each point p i having coordinates ( i, i ) and a weight m i. We want to compute the ais that minimizes the moment of
6 6 Handout 16: Problem Set 5 inertia of the points in the set. Formall, we want to compute a line L in the plane that minimizes the quantit n ( 2 m i d(l, p i ), i=1 where d(l, p i ) is the distance from point p i to the line L. If m i = 1 for all i, we can think of this ais as the orientation of the set. (j) One parameterization of a line in the plane is to describe it using a pair (ρ, θ), where ρ is the distance from the origin to the line and θ is the angle the line makes with the ais. It can be shown that the distance between a point (, ) and a line L parameterized b (ρ, θ) is sin θ cos θ + ρ. We defined the orientation of the set of points S as the line L = (ρ, θ) that minimizes the function n f (ρ, θ) = m i ( i sin θ i cos θ + ρ) 2. i=1 Show that setting αf = 0 gives us the constraint αρ where M 1 sin θ M 1 cos θ + M 0 ρ = 0, n n n M 0 = m i, M 1 = m i i, M 1 = m i i. i=1 i=1 i=1 (k) Show that setting αf = 0 and using the constraint from part (j) leads to the equation αθ where 2 (M 0 M M 1 M 1 ) tan 2θ = M0 (M 2 M 2 ) + M 2 M, n n n 2 2 M = m i i i, M 2 = m i i, M 2 = m i i i=1 i=1 i=1. (l) Give the function f (p i ) that makes the orientation problem a special case of the prob lem we just solved. Hint: The function f (p i ) is a vector-valued function.
Problem Set 5 Solutions
 Introduction to Algorithms November 4, 2005 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik D. Demaine and Charles E. Leiserson Handout 21 Problem Set 5 Solutions Problem 5-1. Skip
Introduction to Algorithms November 4, 2005 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik D. Demaine and Charles E. Leiserson Handout 21 Problem Set 5 Solutions Problem 5-1. Skip
Problem Set 5. MIT students: Each problem should be done on a separate sheet (or sheets) of three-hole punched paper.
 Introduction to Algorithms Day 17 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 19 Problem Set
Introduction to Algorithms Day 17 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 19 Problem Set
Problem Set 6 Solutions
 Introduction to Algorithms October 29, 2001 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 24
Introduction to Algorithms October 29, 2001 Massachusetts Institute of Technology 6.046J/18.410J Singapore-MIT Alliance SMA5503 Professors Erik Demaine, Lee Wee Sun, and Charles E. Leiserson Handout 24
Problem Set 9 Solutions
 Introduction to Algorithms December 8, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 34 Problem Set 9 Solutions Reading: Chapters 32.1
Introduction to Algorithms December 8, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Piotr Indyk and Charles E. Leiserson Handout 34 Problem Set 9 Solutions Reading: Chapters 32.1
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Binary Trees. Binary Search Trees
 Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent.
Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent.
Roberto s Notes on Differential Calculus Chapter 8: Graphical analysis Section 5. Graph sketching
 Roberto s Notes on Differential Calculus Chapter 8: Graphical analsis Section 5 Graph sketching What ou need to know alread: How to compute and interpret limits How to perform first and second derivative
Roberto s Notes on Differential Calculus Chapter 8: Graphical analsis Section 5 Graph sketching What ou need to know alread: How to compute and interpret limits How to perform first and second derivative
Essential Question What are the characteristics of the graph of the tangent function?
 8.5 Graphing Other Trigonometric Functions Essential Question What are the characteristics of the graph of the tangent function? Graphing the Tangent Function Work with a partner. a. Complete the table
8.5 Graphing Other Trigonometric Functions Essential Question What are the characteristics of the graph of the tangent function? Graphing the Tangent Function Work with a partner. a. Complete the table
Module 2, Section 2 Graphs of Trigonometric Functions
 Principles of Mathematics Section, Introduction 5 Module, Section Graphs of Trigonometric Functions Introduction You have studied trigonometric ratios since Grade 9 Mathematics. In this module ou will
Principles of Mathematics Section, Introduction 5 Module, Section Graphs of Trigonometric Functions Introduction You have studied trigonometric ratios since Grade 9 Mathematics. In this module ou will
CSC 263 Lecture 4. September 13, 2006
 S 263 Lecture 4 September 13, 2006 7 ugmenting Red-lack Trees 7.1 Introduction Suppose that ou are asked to implement an DT that is the same as a dictionar but has one additional operation: operation:
S 263 Lecture 4 September 13, 2006 7 ugmenting Red-lack Trees 7.1 Introduction Suppose that ou are asked to implement an DT that is the same as a dictionar but has one additional operation: operation:
Introduction to Algorithms 6.046J/18.401J/SMA5503
 Introduction to Algorithms 6.046J/18.401J/SMA5503 Lecture 1 Prof. Charles E. Leiserson Welcome to Introduction to Algorithms, Fall 01 Handouts 1. Course Information. Calendar 3. Registration (MIT students
Introduction to Algorithms 6.046J/18.401J/SMA5503 Lecture 1 Prof. Charles E. Leiserson Welcome to Introduction to Algorithms, Fall 01 Handouts 1. Course Information. Calendar 3. Registration (MIT students
The Quadratic function f(x) = x 2 2x 3. y y = x 2 2x 3. We will now begin to study the graphs of the trig functions, y = sinx, y = cosx and y = tanx.
 Chapter 7 Trigonometric Graphs Introduction We have alread looked at the graphs of various functions : The Linear function f() = The Quadratic function f() = The Hperbolic function f() = = = = We will
Chapter 7 Trigonometric Graphs Introduction We have alread looked at the graphs of various functions : The Linear function f() = The Quadratic function f() = The Hperbolic function f() = = = = We will
Splay Trees. Splay Trees 1
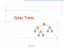 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Def.: a, b, and c are called the for the line L. x = y = z =
 Bob Brown, CCBC Dundalk Math 253 Calculus 3, Chapter Section 5 Completed Lines in Space Eercise : Consider the vector v = Sketch and describe the following set: t v ta, tb, tc : t a, b, c. Let P =,,. Sketch
Bob Brown, CCBC Dundalk Math 253 Calculus 3, Chapter Section 5 Completed Lines in Space Eercise : Consider the vector v = Sketch and describe the following set: t v ta, tb, tc : t a, b, c. Let P =,,. Sketch
Problem Set 4 Solutions
 Design and Analysis of Algorithms March 5, 205 Massachusetts Institute of Technology 6.046J/8.40J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 4 Solutions Problem Set 4 Solutions This
Design and Analysis of Algorithms March 5, 205 Massachusetts Institute of Technology 6.046J/8.40J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 4 Solutions Problem Set 4 Solutions This
Lecture 3 February 9, 2010
 6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
Introduction to Algorithms February 24, 2004 Massachusetts Institute of Technology Professors Erik Demaine and Shafi Goldwasser Handout 8
 Introduction to Algorithms February 24, 2004 Massachusetts Institute of Technology 6046J/18410J Professors Erik Demaine and Shafi Goldwasser Handout 8 Problem Set 2 This problem set is due in class on
Introduction to Algorithms February 24, 2004 Massachusetts Institute of Technology 6046J/18410J Professors Erik Demaine and Shafi Goldwasser Handout 8 Problem Set 2 This problem set is due in class on
Splay Trees Goodrich, Tamassia, Dickerson. Splay Trees 1
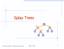 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
3.5 Rational Functions
 0 Chapter Polnomial and Rational Functions Rational Functions For a rational function, find the domain and graph the function, identifing all of the asmptotes Solve applied problems involving rational
0 Chapter Polnomial and Rational Functions Rational Functions For a rational function, find the domain and graph the function, identifing all of the asmptotes Solve applied problems involving rational
Student Instruction Sheet: Unit 4, Lesson 3. Primary Trigonometric Ratios
 Student Instruction Sheet: Unit 4, Lesson 3 Suggested Time: 75 minutes Primary Trigonometric Ratios What s important in this lesson: In this lesson, you will use trigonometry (sin, cos, tan) to measure
Student Instruction Sheet: Unit 4, Lesson 3 Suggested Time: 75 minutes Primary Trigonometric Ratios What s important in this lesson: In this lesson, you will use trigonometry (sin, cos, tan) to measure
Introduction to Homogeneous Transformations & Robot Kinematics
 Introduction to Homogeneous Transformations & Robot Kinematics Jennifer Ka Rowan Universit Computer Science Department. Drawing Dimensional Frames in 2 Dimensions We will be working in -D coordinates,
Introduction to Homogeneous Transformations & Robot Kinematics Jennifer Ka Rowan Universit Computer Science Department. Drawing Dimensional Frames in 2 Dimensions We will be working in -D coordinates,
Lecture 8 13 March, 2012
 6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 8 13 March, 2012 1 From Last Lectures... In the previous lecture, we discussed the External Memory and Cache Oblivious memory models.
6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 8 13 March, 2012 1 From Last Lectures... In the previous lecture, we discussed the External Memory and Cache Oblivious memory models.
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Balanced Trees Part Two
 Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
3.2 Polynomial Functions of Higher Degree
 71_00.qp 1/7/06 1: PM Page 6 Section. Polnomial Functions of Higher Degree 6. Polnomial Functions of Higher Degree What ou should learn Graphs of Polnomial Functions You should be able to sketch accurate
71_00.qp 1/7/06 1: PM Page 6 Section. Polnomial Functions of Higher Degree 6. Polnomial Functions of Higher Degree What ou should learn Graphs of Polnomial Functions You should be able to sketch accurate
Union-Find and Amortization
 Design and Analysis of Algorithms February 20, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas and Nancy Lynch Recitation 3 Union-Find and Amortization 1 Introduction
Design and Analysis of Algorithms February 20, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas and Nancy Lynch Recitation 3 Union-Find and Amortization 1 Introduction
1-1. Functions. Lesson 1-1. What You ll Learn. Active Vocabulary. Scan Lesson 1-1. Write two things that you already know about functions.
 1-1 Functions What You ll Learn Scan Lesson 1- Write two things that ou alread know about functions. Lesson 1-1 Active Vocabular New Vocabular Write the definition net to each term. domain dependent variable
1-1 Functions What You ll Learn Scan Lesson 1- Write two things that ou alread know about functions. Lesson 1-1 Active Vocabular New Vocabular Write the definition net to each term. domain dependent variable
Two Dimensional Viewing
 Two Dimensional Viewing Dr. S.M. Malaek Assistant: M. Younesi Two Dimensional Viewing Basic Interactive Programming Basic Interactive Programming User controls contents, structure, and appearance of objects
Two Dimensional Viewing Dr. S.M. Malaek Assistant: M. Younesi Two Dimensional Viewing Basic Interactive Programming Basic Interactive Programming User controls contents, structure, and appearance of objects
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Contents. How You May Use This Resource Guide
 Contents How You Ma Use This Resource Guide ii 0 Trigonometric Formulas, Identities, and Equations Worksheet 0.: Graphical Analsis of Trig Identities.............. Worksheet 0.: Verifing Trigonometric
Contents How You Ma Use This Resource Guide ii 0 Trigonometric Formulas, Identities, and Equations Worksheet 0.: Graphical Analsis of Trig Identities.............. Worksheet 0.: Verifing Trigonometric
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
Introduction to Algorithms May 14, 2003 Massachusetts Institute of Technology Professors Erik Demaine and Shafi Goldwasser.
 Introduction to Algorithms May 14, 2003 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik Demaine and Shafi Goldwasser Practice Final Practice Final Do not open this exam booklet until
Introduction to Algorithms May 14, 2003 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik Demaine and Shafi Goldwasser Practice Final Practice Final Do not open this exam booklet until
Transformations of Functions. 1. Shifting, reflecting, and stretching graphs Symmetry of functions and equations
 Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
y = f(x) x (x, f(x)) f(x) g(x) = f(x) + 2 (x, g(x)) 0 (0, 1) 1 3 (0, 3) 2 (2, 3) 3 5 (2, 5) 4 (4, 3) 3 5 (4, 5) 5 (5, 5) 5 7 (5, 7)
 0 Relations and Functions.7 Transformations In this section, we stud how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas. The transformations
0 Relations and Functions.7 Transformations In this section, we stud how the graphs of functions change, or transform, when certain specialized modifications are made to their formulas. The transformations
Data Structures and Algorithms CMPSC 465
 Data Structures and Algorithms CMPSC 465 LECTURE 24 Balanced Search Trees Red-Black Trees Adam Smith 4/18/12 A. Smith; based on slides by C. Leiserson and E. Demaine L1.1 Balanced search trees Balanced
Data Structures and Algorithms CMPSC 465 LECTURE 24 Balanced Search Trees Red-Black Trees Adam Smith 4/18/12 A. Smith; based on slides by C. Leiserson and E. Demaine L1.1 Balanced search trees Balanced
Essential Question How many turning points can the graph of a polynomial function have?
 .8 Analzing Graphs of Polnomial Functions Essential Question How man turning points can the graph of a polnomial function have? A turning point of the graph of a polnomial function is a point on the graph
.8 Analzing Graphs of Polnomial Functions Essential Question How man turning points can the graph of a polnomial function have? A turning point of the graph of a polnomial function is a point on the graph
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
Splay Trees 3/20/14. Splay Trees. Splay Trees are Binary Search Trees. note that two keys of equal value may be wellseparated (7,T) (1,Q) (1,C) (5,H)
 Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Week 10. Topic 1 Polynomial Functions
 Week 10 Topic 1 Polnomial Functions 1 Week 10 Topic 1 Polnomial Functions Reading Polnomial functions result from adding power functions 1 together. Their graphs can be ver complicated, so the come up
Week 10 Topic 1 Polnomial Functions 1 Week 10 Topic 1 Polnomial Functions Reading Polnomial functions result from adding power functions 1 together. Their graphs can be ver complicated, so the come up
2.2 Absolute Value Functions
 . Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
. Absolute Value Functions 7. Absolute Value Functions There are a few was to describe what is meant b the absolute value of a real number. You ma have been taught that is the distance from the real number
2. Find RS and the component form of RS. x. b) θ = 236, v = 35 y. b) 4i 3j c) 7( cos 200 i+ sin 200. a) 2u + v b) w 3v c) u 4v + 2w
 Pre Calculus Worksheet 6.1 For questions 1-3, let R = ( 5, 2) and S = (2, 8). 1. Sketch the vector RS and the standard position arrow for this vector. 2. Find RS and the component form of RS. 3. Show algebraicall
Pre Calculus Worksheet 6.1 For questions 1-3, let R = ( 5, 2) and S = (2, 8). 1. Sketch the vector RS and the standard position arrow for this vector. 2. Find RS and the component form of RS. 3. Show algebraicall
Section 2.2: Absolute Value Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a
 Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.: Absolute Value Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Cs445 Homework #1. Due 9/9/ :59 pm DRAFT
 Cs5 Homework #. Due 9/9/06 :59 pm DRAFT Instructions.. Solution may not be submitted by students in pairs.. You may submit a pdf of the homework, either printed or hand-written and scanned, as long as
Cs5 Homework #. Due 9/9/06 :59 pm DRAFT Instructions.. Solution may not be submitted by students in pairs.. You may submit a pdf of the homework, either printed or hand-written and scanned, as long as
Graphing Absolute Value Functions. Objectives To graph an absolute value function To translate the graph of an absolute value function
 5-8 CC-0 CC-6 Graphing Absolute Value Functions Content Standards F.BF.3 Identif the effect on the graph of replacing f () b f () k, kf (), f (k), and f ( k) for specific values of k (both positive and
5-8 CC-0 CC-6 Graphing Absolute Value Functions Content Standards F.BF.3 Identif the effect on the graph of replacing f () b f () k, kf (), f (k), and f ( k) for specific values of k (both positive and
Fractional Cascading
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 11 Scribe: Darren Erik Vengroff Date: March 15, 1993 Fractional Cascading 1 Introduction Fractional cascading is a data
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 11 Scribe: Darren Erik Vengroff Date: March 15, 1993 Fractional Cascading 1 Introduction Fractional cascading is a data
Computational Geometry
 Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
1. y = f(x) y = f(x + 3) 3. y = f(x) y = f(x 1) 5. y = 3f(x) 6. y = f(3x) 7. y = f(x) 8. y = f( x) 9. y = f(x 3) + 1
 .7 Transformations.7. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. Suppose (, ) is on the graph of = f(). In Eercises - 8, use Theorem.7 to find a point
.7 Transformations.7. Eercises To see all of the help resources associated with this section, click OSttS Chapter b. Suppose (, ) is on the graph of = f(). In Eercises - 8, use Theorem.7 to find a point
Introduction to Algorithms 6.046J/18.401J
 Introduction to Algorithms 6.046J/18.401J LECTURE 1 Analysis of Algorithms Insertion sort Merge sort Prof. Charles E. Leiserson Course information 1. Staff. Prerequisites 3. Lectures 4. Recitations 5.
Introduction to Algorithms 6.046J/18.401J LECTURE 1 Analysis of Algorithms Insertion sort Merge sort Prof. Charles E. Leiserson Course information 1. Staff. Prerequisites 3. Lectures 4. Recitations 5.
The Sine and Cosine Functions
 Lesson -5 Lesson -5 The Sine and Cosine Functions Vocabular BIG IDEA The values of cos and sin determine functions with equations = sin and = cos whose domain is the set of all real numbers. From the eact
Lesson -5 Lesson -5 The Sine and Cosine Functions Vocabular BIG IDEA The values of cos and sin determine functions with equations = sin and = cos whose domain is the set of all real numbers. From the eact
Matrix Representations
 CONDENSED LESSON 6. Matri Representations In this lesson, ou Represent closed sstems with transition diagrams and transition matrices Use matrices to organize information Sandra works at a da-care center.
CONDENSED LESSON 6. Matri Representations In this lesson, ou Represent closed sstems with transition diagrams and transition matrices Use matrices to organize information Sandra works at a da-care center.
1. A(-2, 2), B(4, -2) 3 EXAMPLE. Graph the line y = Move up 3 units. Quick Check See left.
 -. Plan Objectives To graph lines given their equations To write equations of lines Eamples Graphing Lines in Slope- Intercept Form Graphing Lines Using Intercepts Transforming to Slope- Intercept Form
-. Plan Objectives To graph lines given their equations To write equations of lines Eamples Graphing Lines in Slope- Intercept Form Graphing Lines Using Intercepts Transforming to Slope- Intercept Form
CS 157: Assignment 6
 CS 7: Assignment Douglas R. Lanman 8 Ma Problem : Evaluating Conve Polgons This write-up presents several simple algorithms for determining whether a given set of twodimensional points defines a conve
CS 7: Assignment Douglas R. Lanman 8 Ma Problem : Evaluating Conve Polgons This write-up presents several simple algorithms for determining whether a given set of twodimensional points defines a conve
Problem Set 5 Solutions
 Design and Analysis of Algorithms?? Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 5 Solutions Problem Set 5 Solutions This problem
Design and Analysis of Algorithms?? Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas, and Nancy Lynch Problem Set 5 Solutions Problem Set 5 Solutions This problem
4 B. 4 D. 4 F. 3. What are some common characteristics of the graphs of cubic and quartic polynomial functions?
 .1 Graphing Polnomial Functions COMMON CORE Learning Standards HSF-IF.B. HSF-IF.C.7c Essential Question What are some common characteristics of the graphs of cubic and quartic polnomial functions? A polnomial
.1 Graphing Polnomial Functions COMMON CORE Learning Standards HSF-IF.B. HSF-IF.C.7c Essential Question What are some common characteristics of the graphs of cubic and quartic polnomial functions? A polnomial
1.1. Parent Functions and Transformations Essential Question What are the characteristics of some of the basic parent functions?
 1.1 Parent Functions and Transformations Essential Question What are the characteristics of some of the basic parent functions? Identifing Basic Parent Functions JUSTIFYING CONCLUSIONS To be proficient
1.1 Parent Functions and Transformations Essential Question What are the characteristics of some of the basic parent functions? Identifing Basic Parent Functions JUSTIFYING CONCLUSIONS To be proficient
L3 Rigid Motion Transformations 3.1 Sequences of Transformations Per Date
 3.1 Sequences of Transformations Per Date Pre-Assessment Which of the following could represent a translation using the rule T (, ) = (, + 4), followed b a reflection over the given line? (The pre-image
3.1 Sequences of Transformations Per Date Pre-Assessment Which of the following could represent a translation using the rule T (, ) = (, + 4), followed b a reflection over the given line? (The pre-image
Tubes are Fun. By: Douglas A. Ruby Date: 6/9/2003 Class: Geometry or Trigonometry Grades: 9-12 INSTRUCTIONAL OBJECTIVES:
 Tubes are Fun B: Douglas A. Rub Date: 6/9/2003 Class: Geometr or Trigonometr Grades: 9-2 INSTRUCTIONAL OBJECTIVES: Using a view tube students will conduct an eperiment involving variation of the viewing
Tubes are Fun B: Douglas A. Rub Date: 6/9/2003 Class: Geometr or Trigonometr Grades: 9-2 INSTRUCTIONAL OBJECTIVES: Using a view tube students will conduct an eperiment involving variation of the viewing
6.856 Randomized Algorithms
 6.856 Randomized Algorithms David Karger Handout #4, September 21, 2002 Homework 1 Solutions Problem 1 MR 1.8. (a) The min-cut algorithm given in class works because at each step it is very unlikely (probability
6.856 Randomized Algorithms David Karger Handout #4, September 21, 2002 Homework 1 Solutions Problem 1 MR 1.8. (a) The min-cut algorithm given in class works because at each step it is very unlikely (probability
Computational Geometry
 Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Windowing queries Windowing Windowing queries Zoom in; re-center and zoom in; select by outlining Windowing Windowing queries Windowing Windowing queries Given a set of n axis-parallel line segments, preprocess
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1
 Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Quiz 1 Do not open this quiz booklet until directed to
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Quiz 1 Do not open this quiz booklet until directed to
Graphing f ( x) = ax 2 + c
 . Graphing f ( ) = a + c Essential Question How does the value of c affect the graph of f () = a + c? Graphing = a + c Work with a partner. Sketch the graphs of the functions in the same coordinate plane.
. Graphing f ( ) = a + c Essential Question How does the value of c affect the graph of f () = a + c? Graphing = a + c Work with a partner. Sketch the graphs of the functions in the same coordinate plane.
Introduction to Algorithms October 12, 2005 Massachusetts Institute of Technology Professors Erik D. Demaine and Charles E. Leiserson Quiz 1.
 Introduction to Algorithms October 12, 2005 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik D. Demaine and Charles E. Leiserson Quiz 1 Quiz 1 Do not open this quiz booklet until you
Introduction to Algorithms October 12, 2005 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik D. Demaine and Charles E. Leiserson Quiz 1 Quiz 1 Do not open this quiz booklet until you
CMSC 425: Lecture 10 Basics of Skeletal Animation and Kinematics
 : Lecture Basics of Skeletal Animation and Kinematics Reading: Chapt of Gregor, Game Engine Architecture. The material on kinematics is a simplification of similar concepts developed in the field of robotics,
: Lecture Basics of Skeletal Animation and Kinematics Reading: Chapt of Gregor, Game Engine Architecture. The material on kinematics is a simplification of similar concepts developed in the field of robotics,
HW1. Due: September 13, 2018
 CSCI 1010 Theory of Computation HW1 Due: September 13, 2018 Attach a fully filled-in cover sheet to the front of your printed homework. Your name should not appear anywhere; the cover sheet and each individual
CSCI 1010 Theory of Computation HW1 Due: September 13, 2018 Attach a fully filled-in cover sheet to the front of your printed homework. Your name should not appear anywhere; the cover sheet and each individual
Problem Set 5 Due: Friday, November 2
 CS231 Algorithms Handout # 19 Prof. Lyn Turbak October 26, 2001 Wellesley College Problem Set 5 Due: Friday, November 2 Important: On Friday, Nov. 2, you will receive a take-home midterm exam that is due
CS231 Algorithms Handout # 19 Prof. Lyn Turbak October 26, 2001 Wellesley College Problem Set 5 Due: Friday, November 2 Important: On Friday, Nov. 2, you will receive a take-home midterm exam that is due
Using a Table of Values to Sketch the Graph of a Polynomial Function
 A point where the graph changes from decreasing to increasing is called a local minimum point. The -value of this point is less than those of neighbouring points. An inspection of the graphs of polnomial
A point where the graph changes from decreasing to increasing is called a local minimum point. The -value of this point is less than those of neighbouring points. An inspection of the graphs of polnomial
SECTION 6-8 Graphing More General Tangent, Cotangent, Secant, and Cosecant Functions
 6-8 Graphing More General Tangent, Cotangent, Secant, and Cosecant Functions 9 duce a scatter plot in the viewing window. Choose 8 for the viewing window. (B) It appears that a sine curve of the form k
6-8 Graphing More General Tangent, Cotangent, Secant, and Cosecant Functions 9 duce a scatter plot in the viewing window. Choose 8 for the viewing window. (B) It appears that a sine curve of the form k
9. f(x) = x f(x) = x g(x) = 2x g(x) = 5 2x. 13. h(x) = 1 3x. 14. h(x) = 2x f(x) = x x. 16.
 Section 4.2 Absolute Value 367 4.2 Eercises For each of the functions in Eercises 1-8, as in Eamples 7 and 8 in the narrative, mark the critical value on a number line, then mark the sign of the epression
Section 4.2 Absolute Value 367 4.2 Eercises For each of the functions in Eercises 1-8, as in Eamples 7 and 8 in the narrative, mark the critical value on a number line, then mark the sign of the epression
(0, 2) y = x 1 2. y = x (2, 2) y = 2x + 2
 .5 Equations of Parallel and Perpendicular Lines COMMON CORE Learning Standards HSG-GPE.B.5 HSG-GPE.B. Essential Question How can ou write an equation of a line that is parallel or perpendicular to a given
.5 Equations of Parallel and Perpendicular Lines COMMON CORE Learning Standards HSG-GPE.B.5 HSG-GPE.B. Essential Question How can ou write an equation of a line that is parallel or perpendicular to a given
[ ] [ ] Orthogonal Transformation of Cartesian Coordinates in 2D & 3D. φ = cos 1 1/ φ = tan 1 [ 2 /1]
![[ ] [ ] Orthogonal Transformation of Cartesian Coordinates in 2D & 3D. φ = cos 1 1/ φ = tan 1 [ 2 /1] [ ] [ ] Orthogonal Transformation of Cartesian Coordinates in 2D & 3D. φ = cos 1 1/ φ = tan 1 [ 2 /1]](/thumbs/84/89383711.jpg) Orthogonal Transformation of Cartesian Coordinates in 2D & 3D A vector is specified b its coordinates, so it is defined relative to a reference frame. The same vector will have different coordinates in
Orthogonal Transformation of Cartesian Coordinates in 2D & 3D A vector is specified b its coordinates, so it is defined relative to a reference frame. The same vector will have different coordinates in
9.1 Exercises. Section 9.1 The Square Root Function 879. In Exercises 1-10, complete each of the following tasks.
 Section 9. The Square Root Function 879 9. Eercises In Eercises -, complete each of the following tasks. i. Set up a coordinate sstem on a sheet of graph paper. Label and scale each ais. ii. Complete the
Section 9. The Square Root Function 879 9. Eercises In Eercises -, complete each of the following tasks. i. Set up a coordinate sstem on a sheet of graph paper. Label and scale each ais. ii. Complete the
Week 3. Topic 5 Asymptotes
 Week 3 Topic 5 Asmptotes Week 3 Topic 5 Asmptotes Introduction One of the strangest features of a graph is an asmptote. The come in three flavors: vertical, horizontal, and slant (also called oblique).
Week 3 Topic 5 Asmptotes Week 3 Topic 5 Asmptotes Introduction One of the strangest features of a graph is an asmptote. The come in three flavors: vertical, horizontal, and slant (also called oblique).
5.2 Graphing Polynomial Functions
 Locker LESSON 5. Graphing Polnomial Functions Common Core Math Standards The student is epected to: F.IF.7c Graph polnomial functions, identifing zeros when suitable factorizations are available, and showing
Locker LESSON 5. Graphing Polnomial Functions Common Core Math Standards The student is epected to: F.IF.7c Graph polnomial functions, identifing zeros when suitable factorizations are available, and showing
Database Design 1DL400. Assignment 2:2
 Uppsala Universit Department of Information Technolog Kjell Orsborn Assignment : - Database Design II Database Design DL00 Assignment : A Scientific Database for Mesh-Based Data. Goals This eercise consists
Uppsala Universit Department of Information Technolog Kjell Orsborn Assignment : - Database Design II Database Design DL00 Assignment : A Scientific Database for Mesh-Based Data. Goals This eercise consists
Problem Set 6. Part A:
 Introduction to Algorithms: 6.006 Massachusetts Institute of Technology April 12, 2011 Professors Erik Demaine, Piotr Indyk, and Manolis Kellis Problem Set 6 Problem Set 6 This problem set is divided into
Introduction to Algorithms: 6.006 Massachusetts Institute of Technology April 12, 2011 Professors Erik Demaine, Piotr Indyk, and Manolis Kellis Problem Set 6 Problem Set 6 This problem set is divided into
Implicit differentiation
 Roberto s Notes on Differential Calculus Chapter 4: Basic differentiation rules Section 5 Implicit differentiation What ou need to know alread: Basic rules of differentiation, including the chain rule.
Roberto s Notes on Differential Calculus Chapter 4: Basic differentiation rules Section 5 Implicit differentiation What ou need to know alread: Basic rules of differentiation, including the chain rule.
Introduction to Algorithms
 Introduction to Algorithms 6.046J/18.401J LECTURE 19 Take-home exam Instructions Academic honesty Strategies for doing well Prof. Charles E. Leiserson Take-home quiz The take-home quiz contains 5 problems
Introduction to Algorithms 6.046J/18.401J LECTURE 19 Take-home exam Instructions Academic honesty Strategies for doing well Prof. Charles E. Leiserson Take-home quiz The take-home quiz contains 5 problems
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
ACTIVITY: Graphing a Linear Equation. 2 x x + 1?
 . Graphing Linear Equations How can ou draw its graph? How can ou recognize a linear equation? ACTIVITY: Graphing a Linear Equation Work with a partner. a. Use the equation = + to complete the table. (Choose
. Graphing Linear Equations How can ou draw its graph? How can ou recognize a linear equation? ACTIVITY: Graphing a Linear Equation Work with a partner. a. Use the equation = + to complete the table. (Choose
SECTION 3-4 Rational Functions
 20 3 Polnomial and Rational Functions 0. Shipping. A shipping bo is reinforced with steel bands in all three directions (see the figure). A total of 20. feet of steel tape is to be used, with 6 inches
20 3 Polnomial and Rational Functions 0. Shipping. A shipping bo is reinforced with steel bands in all three directions (see the figure). A total of 20. feet of steel tape is to be used, with 6 inches
Chapter 2: Introduction to Functions
 Chapter 2: Introduction to Functions Lesson 1: Introduction to Functions Lesson 2: Function Notation Lesson 3: Composition of Functions Lesson 4: Domain and Range Lesson 5: Restricted Domain Lesson 6:
Chapter 2: Introduction to Functions Lesson 1: Introduction to Functions Lesson 2: Function Notation Lesson 3: Composition of Functions Lesson 4: Domain and Range Lesson 5: Restricted Domain Lesson 6:
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CSci 231 Homework 7. Red Black Trees. CLRS Chapter 13 and 14
 CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 1. Problem 13-1 (persistent dynamic sets).. Problem 13-3 (AVL trees) 3. In this problem we consider a data structure for maintaining a multi-set
CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 1. Problem 13-1 (persistent dynamic sets).. Problem 13-3 (AVL trees) 3. In this problem we consider a data structure for maintaining a multi-set
Partial Fraction Decomposition
 Section 7. Partial Fractions 53 Partial Fraction Decomposition Algebraic techniques for determining the constants in the numerators of partial fractions are demonstrated in the eamples that follow. Note
Section 7. Partial Fractions 53 Partial Fraction Decomposition Algebraic techniques for determining the constants in the numerators of partial fractions are demonstrated in the eamples that follow. Note
MA123, Chapter 6: Extreme values, Mean Value Theorem, Curve sketching, and Concavity
 MA123, Chapter 6: Etreme values, Mean Value Theorem, Curve sketching, and Concavit Chapter Goals: Appl the Etreme Value Theorem to find the global etrema for continuous function on closed and bounded interval.
MA123, Chapter 6: Etreme values, Mean Value Theorem, Curve sketching, and Concavit Chapter Goals: Appl the Etreme Value Theorem to find the global etrema for continuous function on closed and bounded interval.
We will show that the height of a RB tree on n vertices is approximately 2*log n. In class I presented a simple structural proof of this claim:
 We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
Section 1.6: Graphs of Functions, from College Algebra: Corrected Edition by Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative
 Section.6: Graphs of Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Section.6: Graphs of Functions, from College Algebra: Corrected Edition b Carl Stitz, Ph.D. and Jeff Zeager, Ph.D. is available under a Creative Commons Attribution-NonCommercial-ShareAlike.0 license.
Unit 4 Trigonometry. Study Notes 1 Right Triangle Trigonometry (Section 8.1)
 Unit 4 Trigonometr Stud Notes 1 Right Triangle Trigonometr (Section 8.1) Objective: Evaluate trigonometric functions of acute angles. Use a calculator to evaluate trigonometric functions. Use trigonometric
Unit 4 Trigonometr Stud Notes 1 Right Triangle Trigonometr (Section 8.1) Objective: Evaluate trigonometric functions of acute angles. Use a calculator to evaluate trigonometric functions. Use trigonometric
Introduction to Algorithms April 21, 2004 Massachusetts Institute of Technology. Quiz 2 Solutions
 Introduction to Algorithms April 21, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik Demaine and Shafi Goldwasser Quiz 2 Solutions Quiz 2 Solutions Do not open this quiz booklet
Introduction to Algorithms April 21, 2004 Massachusetts Institute of Technology 6.046J/18.410J Professors Erik Demaine and Shafi Goldwasser Quiz 2 Solutions Quiz 2 Solutions Do not open this quiz booklet
12.4 The Ellipse. Standard Form of an Ellipse Centered at (0, 0) (0, b) (0, -b) center
 . The Ellipse The net one of our conic sections we would like to discuss is the ellipse. We will start b looking at the ellipse centered at the origin and then move it awa from the origin. Standard Form
. The Ellipse The net one of our conic sections we would like to discuss is the ellipse. We will start b looking at the ellipse centered at the origin and then move it awa from the origin. Standard Form
Introduction to Algorithms: Massachusetts Institute of Technology 7 October, 2011 Professors Erik Demaine and Srini Devadas Problem Set 4
 Introduction to Algorithms: 6.006 Massachusetts Institute of Technology 7 October, 2011 Professors Erik Demaine and Srini Devadas Problem Set 4 Problem Set 4 Both theory and programming questions are due
Introduction to Algorithms: 6.006 Massachusetts Institute of Technology 7 October, 2011 Professors Erik Demaine and Srini Devadas Problem Set 4 Problem Set 4 Both theory and programming questions are due
CSci 231 Homework 7. Red Black Trees. CLRS Chapter 13 and 14
 CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 Choose 4 problems from the list below. 1. (CLRS 13.1-6) What is the largest possible number of internal nodes in a red-black tree with black-height
CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 Choose 4 problems from the list below. 1. (CLRS 13.1-6) What is the largest possible number of internal nodes in a red-black tree with black-height
Exam January? 9:30 11:30
 UNIT STATISTICS Date Lesson TOPIC Homework Dec. 9 Dec. Dec. Jan. 9 Jan. 0 Jan....... Representing Data WS. Histograms WS. Measures of Central Tendenc Find the mean, median, and mode of the data sets on
UNIT STATISTICS Date Lesson TOPIC Homework Dec. 9 Dec. Dec. Jan. 9 Jan. 0 Jan....... Representing Data WS. Histograms WS. Measures of Central Tendenc Find the mean, median, and mode of the data sets on
Introduction to Algorithms
 Introduction to Algorithms 6.046J/18.401J LECTURE 16 Greedy Algorithms (and Graphs) Graph representation Minimum spanning trees Optimal substructure Greedy choice Prim s greedy MST algorithm Prof. Charles
Introduction to Algorithms 6.046J/18.401J LECTURE 16 Greedy Algorithms (and Graphs) Graph representation Minimum spanning trees Optimal substructure Greedy choice Prim s greedy MST algorithm Prof. Charles
CHECK Your Understanding
 CHECK Your Understanding. State the domain and range of each relation. Then determine whether the relation is a function, and justif our answer.. a) e) 5(, ), (, 9), (, 7), (, 5), (, ) 5 5 f) 55. State
CHECK Your Understanding. State the domain and range of each relation. Then determine whether the relation is a function, and justif our answer.. a) e) 5(, ), (, 9), (, 7), (, 5), (, ) 5 5 f) 55. State
Flux Integrals. Solution. We want to visualize the surface together with the vector field. Here s a picture of exactly that:
 Flu Integrals The pictures for problems # - #4 are on the last page.. Let s orient each of the three pictured surfaces so that the light side is considered to be the positie side. Decide whether each of
Flu Integrals The pictures for problems # - #4 are on the last page.. Let s orient each of the three pictured surfaces so that the light side is considered to be the positie side. Decide whether each of
would be included in is small: to be exact. Thus with probability1, the same partition n+1 n+1 would be produced regardless of whether p is in the inp
 1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
1 Introduction 1.1 Parallel Randomized Algorihtms Using Sampling A fundamental strategy used in designing ecient algorithms is divide-and-conquer, where that input data is partitioned into several subproblems
Online Homework Hints and Help Extra Practice
 Evaluate: Homework and Practice Use a graphing calculator to graph the polnomial function. Then use the graph to determine the function s domain, range, and end behavior. (Use interval notation for the
Evaluate: Homework and Practice Use a graphing calculator to graph the polnomial function. Then use the graph to determine the function s domain, range, and end behavior. (Use interval notation for the
Preparing for AS Level Further Mathematics
 Preparing for AS Level Further Mathematics Algebraic skills are incredibly important in the study of further mathematics at AS and A level. You should therefore make sure you are confident with all of
Preparing for AS Level Further Mathematics Algebraic skills are incredibly important in the study of further mathematics at AS and A level. You should therefore make sure you are confident with all of
6. 4 Transforming Linear Functions
 Name Class Date 6. Transforming Linear Functions Essential Question: What are the was in which ou can transform the graph of a linear function? Resource Locker Eplore 1 Building New Linear Functions b
Name Class Date 6. Transforming Linear Functions Essential Question: What are the was in which ou can transform the graph of a linear function? Resource Locker Eplore 1 Building New Linear Functions b
