Binary Trees. Binary Search Trees
|
|
|
- Wilfred Doyle
- 6 years ago
- Views:
Transcription
1 Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent. We alread met binar trees in the form of rank trees. A binar heap is also a binar tree (but we used an arra to implement this tree). We will now see how to use a binar tree to implement the set and map (dictionar) ADTs. Since we can think of a set as a special case of a map that maps elements of the set to True, in the following we will onl discuss the map ADT (called dict in Pthon). The two basic method of dict are contains and getitem. The method contains (k) determines if the ke k is present in the dictionar, the method getitem (k) returns the value stored with the ke k (and raises an eception if k is not present in the map). The setitem (k, v) method adds a new mapping for the given ke and value. The delitem (k) method removes the mapping for the ke k. We add methods firstke() and lastke() that return the smallest and largest ke present in the dict (this is not possible with standard Pthon dictionaries). Binar Search Trees A binar search tree is a binar tree where ever node stores one ke (and the value that corresponds to this ke), and that has the binar search tree propert: For an node v, all the kes in the left subtree of v are less than the ke of v, and all the kes in the right subtree of v are larger than the ke of v. As a result, an in-order traversal of a binar search tree returns the kes in sorted order. Here is the node class of our binar search tree: class _Node(): def init (self, ke, value, left=none, right=none): self.ke = ke self.value = value self.left = left self.right = right Finding kes. To implement contains (k) and getitem (k), we need to find the node containing a given ke k. We start at the root and compare k to the ke s of the root node. If k = s, then the node we are looking for is the root node itself. If k < s then b the search tree propert, we know that k can onl be in the left subtree of the root. If k > s, then k can onl be in the right subtree of the root. We proceed in this manner until we either find a node with ke k, or we reach an empt subtree: def _find(self, ke): if ke == self.ke: if ke < self.ke:.left._find(ke) if self.left else None.right._find(ke) if self.right else None Smallest and largest kes. To implement firstke(), we need to find the smallest ke in the search tree. For ever node, its left subtree contains all the kes smaller than the ke in the node itself, so the smallest ke in the tree can be found b alwas walking down to the left child until there is no more left child: def _find_first(self): p = self while p.left is not None: 1
2 p = p.left return p You ma recognie this from method findfirst() in our rank tree. Implementing lastke() works the same, walking down to the right child. Inserting a ke. To add a mapping (k, v), we first need to find the correct place for the ke k. Since we need to maintain the search tree propert, this needs to be done eactl as in _find(k). If we find a node n that alread contains the ke k, then we update the tree b changing the value at n to v. Otherwise, we reach an empt subtree, and we replace this empt subtree b a single node with ke k and value v. def _insert(self, ke, value): if ke == self.ke: self.value = value elif ke < self.ke: if self.left is None: self.left = _Node(ke, value) self.left._insert(ke, value) if self.right is None: self.right = _Node(ke, value) self.right._insert(ke, value) Removing a ke. Removing a mapping is the hardest part. Fortunatel, we alread learnt how to remove a node from a binar tree when we implemented rank trees, and we can use the eact same method here: We first find the node n containing the ke k to be deleted. If n is a leaf or has onl one child, we can remove the node n easil, b changing the link from n s parent. If n has two children, we do not remove the node n. Instead, we find the leftmost node u in the right subtree of n. The ke of u is the smallest ke in the tree that is larger than k. That means that we can move the ke and value information from u to n, and delete the node u. Since u has no left child, this is again eas. The _Node s internal method _remove(k) returns the root of a new subtree that is identical to the subtree rooted at n, ecept that the mapping for k has been removed: def _remove(self, ke): if ke < self.ke and self.left is not None: self.left = self.left._remove(ke) elif ke > self.ke and self.right is not None: self.right = self.right._remove(ke) elif ke == self.ke: if self.left is not None and self.right is not None: # Need to remove self, but has two children n = self.right._find_first() self.ke = n.ke self.value = n.value self.right = self.right._remove_first() # Need to remove self, which has ero or one child.left if self.left else self.right 2
3 _remove makes use of another internal method _remove_first(n), which again returns a new subtree, identical to the subtree at n ecept that the leftmost node has been removed: def _remove_first(self): if self.left is None:.right self.left = self.left._remove_first() Analsis Finding, inserting, and removing nodes from a binar search tree takes time O(h), where h is the current height of the tree. In a perfectl balanced binar tree we would have h = log n. Unfortunatel, it is quite eas to make ver unbalanced trees. For instance, this code import bst t = bst.dict() for i in range(n): t[i] = i+1 creates a tree of height n 1. Essentiall, this tree is a linked list: nodes have no left child, onl a right child. It can be shown that binar search trees offer O(log n) performance on insertions of randoml chosen or randoml ordered kes with high probabilit. As long as the trees remain reasonabl well-balanced, search operations will run in O(log n) time. In practice, ou ma need to resort to eperiments to determine whether our particular application uses binar search trees in a wa that tends to generate somewhat balanced trees or not. Unfortunatel, there are occasions where ou might fill a tree with entries that happen to be alread sorted. In this circumstance, a disastrousl imbalanced tree will be the result. Technicall, all operations on binar search trees have O(n) worst-case running time. For this reason, researchers have developed a variet of algorithms for keeping search trees balanced. Balanced means that the left and right subtree of ever node should have roughl equal sie. Man different kinds of balanced search trees have been developed we will discuss AVL-trees, trees, and red-black trees. AVL Trees AVL trees are height-balanced trees, and are the oldest balanced search trees (1962). The are named after their inventors, Georg Adelson-Velsk and Evgenii Landis. An AVL-tree is a binar search tree with an additional balance propert: For ever node of the tree, the height of the left subtree and the right subtree differ b at most one. Here, we count the height of the empt subtree as 1. Height of AVL-trees. We first show that AVL-trees have height O(log n). More precisel, we ask the opposite question: For a given height h, what is the smallest number of nodes N(h) that an AVL-tree with height h can have? A bit of drawing quickl shows that N(0) = 1, N(1) = 2, N(2) = 4, and N(3) = 7. For h 2, we have N(h) = N(h 1) + N(h 2) + 1. Indeed, consider an AVL-tree of height h. One of its subtrees, let s sa the left subtree, must be an AVL-tree of height h 1, and so it has at least N(h 1) nodes. The right subtree must have either height h 1 or height h 2, since otherwise the balance propert would be violated at the root. It follows that the right subtree has at least N(h 2) nodes, so the tree has at least N(h 1) + N(h 2) + 1 nodes. This shows that N(h) N(h 1) + N(h 2) + 1. We actuall have equalit in this recursive formula, because we can take a smallest possible AVL-tree of height h 1, a smallest possible AVL-tree of heigth h 2, and merge them into an AVL-tree of height h with N(h 1) + N(h 2) + 1 nodes. The trees constructed this wa are called Fibonacci-trees. 3
4 Since clearl N(h 1) N(h 2), we have N(h) 2N(h 2), and we immediatel get that N(h) 2 h/2. If we know that a tree has n nodes and height h, then this implies that n N(h) 2 h/2, and so log n h/2, and so h 2 log n. We can get a better bound b using the Fibonacci numbers. Remember that F 0 = 0, F 1 = 1, and F i = F i 1 + F i 2 for i 2. We now prove b induction that N(h) = F h+3 1. This is true for h = 0 and h = 1, so consider h 2. Then N(h) = N(h 1) + N(h 2) + 1 = F h F h = F h+3 1. Luckil for us, there is a formula for the Fibonacci numbers. We have F i = ϕ i / 5+(1 ϕ) i / 5, where ϕ is the golden ratio ϕ The second term is ver small, so we have N(h) = F h+3 1 ϕ h+3 / 5 1. It follows that for a tree with n nodes we have h + 3 log ϕ ( 5(n + 1)) and so h log(n + 1). Node objects. at v: To implement an AVL-tree, we store with each node v the height of the subtree rooted class _Node(): def init (self, ke, value, left=none, right=none, height=0): self.ke = ke self.value = value self.left = left self.right = right self.height = height def _left_height(self): return -1 if self.left is None else self.left.height def _right_height(self): return -1 if self.right is None else self.right.height def _recompute_height(self): left = self._left_height() right = self._right_height() self.height = ma(left, right) + 1 return abs(right - left) > 1 The methods _left_height() and _right_height() return the heights of the two subtrees, and correctl handle the case of an empt subtree, which we define to have height 1. The method _recompute_height() recomputes the height of a node from the heights of its two subtrees. It also returns True if the node is unbalanced, that is, if the height difference is larger than one. Finding kes, smallest and largest kes. An AVL-tree is a binar search tree: It fulfills the search tree propert. Therefore, all BST methods that do not modif the tree work unchanged on AVL trees: _find(k), _find_first(), and _find_last(). The big difference is: Since we have proven above that the height of an AVL-tree with n nodes is O(log n), we have a guarantee on the running time of these methods now. The take time O(log n) on an AVL tree that stores n elements. Maintaining balance. To add a mapping (k, v), we first follow the path through the tree as in _find(k). If we find a node n containing ke k, then we simpl update the tree b changing the value at n to v. Otherwise, we reach an empt subtree, and we replace this empt subtree b a single node w with ke k and value v. The height of all subtrees that include w ma change, and as a consequence the tree ma become unbalanced. 4
5 When we remove a mapping for k, we again first find the node as in _find(k). If the node is a leaf or has onl one child, we can delete it easil, otherwise we instead delete the leftmost node in its right subtree. Let w be the node that was deleted. Again, the height of all subtrees that include w ma change. In both cases, we observe first that the nodes whose subtree includes w are eactl the ancestors of w. These ancestors form a path from the root to w, and some of them ma have become unbalanced because of the insertion or deletion of w. Let be the lowest ancestor of w that is now unbalanced. Let be the child of with larger height (the two children cannot have equal height since is unbalanced). Let be the child of with larger height (if both children of have equal height, we chose to be the right child of if is the right child of, and chose to be the left child of if is the left child of ). We will now restructure the subtree with root. We distinguish four cases, depending on the ordering of the kes stored at,, and. Fig. 1 shows the four cases. If is the right child of, we are in the left T 0 T 1 T 0 T 1 T 0 T 1 T 0 T 1 Figure 1: Four cases for restructuring. column of Fig. 1. If the ke of lies inbetween the kes of and, we are in the bottom row, otherwise in the top row. Let T 0, T 1,, and be the four subtrees of,, and, as in Fig. 1. B our choice of, all four trees are balanced. Let h(t ) denote the height of a subtree T, and let h(v) denote the height of the subtree with root v (before restructuring). Recall that b our choice of, the nodes and are balanced, while is unbalanced (before restructuring). Left rotation. Let us first consider the case where is the right child of, and is the right child of (top left in Fig. 1). We restructure the subtree with root b making its new root, and moving into the left subtree of as in Fig. 2. This operation is called a left rotation about. We first argue that a left rotation maintains the search tree propert of the tree. Let us write T 0 to mean that all kes in T 0 are less than the ke of. Since the search tree propert held before the left rotation, we have T 0 T 1. 5
6 T 0 T 1 T 0 T 1 Figure 2: Left rotation about. This implies that the search tree propert holds after the left rotation. For instance, all kes in the subtree formed b T 0, T 1, and are less than the ke of. We now argue that after the left rotation the subtree (with new root ) is balanced. Without loss of generalit, let s assume that h( ) h( ). Since is balanced, that means h( ) h( ) h( ) 1. We have h() = h( ) + 1. Since is balanced, and we have chosen to be the child of with larger height, we have h( ) + 1 = h() h(t 1 ) h() 1 = h( ). The node, however, is unbalanced, and so h(t 0 ) = h() 2 = h( ). After the left rotation, node is still balanced, as its subtrees have not changed. Node is now balanced, since we have h(t 0 ) + 1 = h( ) + 1 h(t 1 ) h( ) = h(t 0.) Finall, node is balanced since h() = h(t 1 ) + 1 and h() = h( ) + 1, and so h() + 1 h() h(). In this wa, we have re-established the balance propert for this subtree. There ma still be ancestors of w (and therefore ancestors of the new node ) that are unbalanced, so we have to repeat the procedure there. Right rotation. The case where is the left child of and is the left child of is entirel smmetric. We perform a right rotation about. Fig. 3 shows an eample of an insertion that causes a right rotation. Double rotations. Let s now consider the case where is the right child of and is the left child of (bottom left in Fig. 1). In this case, we first perform a right rotation about, and then a left rotation about, see Fig. 4. We call this operation a (right-left) double rotation. Again, we first need to check that the resulting tree has the search tree propert. This is true because T 0 T 1. It remains to check the balance condition on the new subtree (with root ). Without loss of generalit, let s assume that h(t 1 ) h( ). Since is balanced, that means h(t 1 ) h( ) h(t 1 ) 1 and we have h() = h(t 1 ) + 1. Since is balanced, and we have chosen to be the child of with strictl larger height in this case, we have h( ) = h() 1 = h(t 1 ). Since, is unbalanced, we have h(t 0 ) = h() 2 = h(t 1 ). To summarie, we have h(t 0 ) = h(t 1 ) = h( ) h( ) h(t 1 ) 1. In the new tree, is balanced since h(t 0 ) = h(t 1 ). Similarl, is balanced since h( ) h( ) h( ) 1. The new root is balanced since h() = h(t 1 ) + 1 = h( ) + 1 = h(). Finall, the case where is the left child of and is the right child of completel smmetric, and we perform a left-right double rotation. 6
7 w Figure 3: Insertion of 1. Implementation. We start b two internal methods that implement left-rotations and right-rotations. _rotate_left(t) rotates about node t, and returns the new root of the subtree (which is the right child of t). The method alread recomputes the height of all nodes whose height has changed: def _rotate_left(self): root = self.right self.right = root.left self._recompute_height() root.left = self root._recompute_height() return root The method _rotate_right(t) is eactl smmetric: def _rotate_right(self): root = self.left self.left = root.right self._recompute_height() root.right = self root._recompute_height() return root The following internal method implements the restructuring operation. is the root of the subtree to be restructured. The method uses the heights of the children to determine which of the four cases we are in: def _restructure(self): if self._right_height() > self._left_height(): if self.right._left_height() > self.right._right_height(): 7
8 T 0 T 0 T 1 T 1 Figure 4: Double rotation self.right = self.right._rotate_right()._rotate_left() # left height > right height if self.left._right_height() > self.left._left_height(): self.left = self.left._rotate_left()._rotate_right() T 0 T 1 Now we have all the pieces to implement the insert function. t._insert(k, v) adds the mapping k v to the subtree rooted at t, and returns the new root of the subtree, guaranteed to be an AVL-tree again: def _insert(self, ke, value): if ke == self.ke: self.value = value if ke < self.ke: if self.left is None: self.left = _Node(ke, value) self.left = self.left._insert(ke, value) if self.right is None: self.right = _Node(ke, value) self.right = self.right._insert(ke, value) if self._recompute_height():._restructure() Remember that after inserting the node w we have to walk up again in the tree until we find the first node 8
9 that is now unbalanced. The method _insert implements the walking up using recursion: It inserts the mapping into the correct subtree, then updates the height of the current node t, and restructures if necessar. A more careful analsis of the restructuring cases shows that in insertions, this can actuall happen for one ancestor onl (that is, after one restructuring operation the entire tree is balanced). We do not discuss this refined analsis, as our code does not use this fact. It remains to discuss the remove function. The following internal function t._remove_first() removes the leftmost node (smallest ke) from the subtree with root t, and returns the root of the new subtree. The returned tree is alread balanced. def _remove_first(self): if self.left is None:.right self.left = self.left._remove_first() if self._recompute_height():._restructure() Finall, the following function removes the mapping for ke k from the subtree, and returns a new, balanced subtree: def _remove(self, ke): if ke < self.ke and self.left is not None: self.left = self.left._remove(ke) elif ke > self.ke and self.right is not None: self.right = self.right._remove(ke) elif ke == self.ke: if self.left is not None and self.right is not None: # Need to remove self, but has two children n = self.right._find_first() self.ke = n.ke self.value = n.value self.right = self.right._remove_first() # Need to remove self, which has ero or one child # No restructuring needed in this case.left if self.left else self.right if self._recompute_height():._restructure() Minimiing memor use. We use a integer field to store the height of each node. That wastes some memor since AVL-trees are balanced, the height cannot be more than, sa, 100, which would easil fit into one bte. In fact, it turns out that AVL-trees can be implemented using onl two bits per node: Instead of storing the height in each node, we store the difference of the heights of the two subtrees. B the balance condition, this difference is either 1, 0, or +1, and can be stored in two bits. We leave it as an eercise to make such an implementation trees A tree is a perfectl balanced tree, where all leaves are on the bottom level trees are thus named because ever node has 2, 3, or 4 children, ecept leaves. Each node stores 1, 2, or 3 kes (and the corresponding values), which determine how other entries are distributed among its children s subtrees. 9
10 Each internal (non-leaf) node has one more child than kes. For eample, a node with kes [20, 40, 50] has four children. Eack ke k in the subtree rooted at the first child satisfies k 20; at the second child, 20 k 40; at the third child, 40 k 50; and at the fourth child, k trees are a tpe of B-tree, which ou ma learn about someda in connection with fast disk access for database sstems. Finding a ke. Finding an entr is straightforward. Start at the root. At each node, check for the ke k; if it s not present, move down to the appropriate child chosen b comparing k against the kes. Continue until k is found, or k is not found at a leaf node. B the wa, ou can define an inorder traversal on trees analogous to that on binar trees, and it visits the kes in sorted order. Adding a mapping (bottom-up). To add the mapping k v, we first walk down the tree in search of the ke k. If we find a node with ke k, we update the mapping and are done. If k is not et in the tree, we find a leaf node v where k needs to be inserted. If v has at most 2 kes, we simpl insert k and are done. Otherwise, we sa that v overflows. In this case we split the node v into two nodes v 1 and v 2, with two kes each (including the new ke k). To be able to add both as children to v s parent p, we need to move one of the four kes up to p, increasing the number of kes in p. As a result, p ma overflow, and we have to repeat the process. The process ends when no overflow happens, or if we reach the root node. If the root node overflows, we simpl create a new root, and the height of the tree increases b one. Adding a mapping (top-down). The bottom-up method has the disadvantage that we need to walk down and up again in the tree. It is possible to avoid the second walk up, using top-down insertions. These can be implemented without recursion using a simple loop. As we walk down the tree, we sometimes modif nodes of the tree. Specificall, whenever we encounter a 3-ke node, the middle ke is ejected and is placed in the parent node instead. Since the parent was previousl treated the same wa, the parent has at most two kes, and alwas has room for a third. The other two kes in the 3-ke node are split into two separate 1-ke nodes, which are divided underneath the old middle ke. The reasons wh we split ever 3-ke node we encounter (and move its middle ke up one level) are (1) to make sure there s room for the new ke in the leaf node, and (2) to make sure that above the leaves, there s room for an ke that gets kicked upstairs. Sometimes, an insertion operation increases the height of the tree b one b creating a new root. Removing a ke (top-down). Removing a ke from a tree is similar to removing a ke in binar trees: ou find the entr ou want to remove (having ke k). If it s in a leaf, ou remove it. If it s in an internal node, ou replace it with the entr with the net higher ke. That entr is alwas in a leaf. In either case, ou remove an entr from a leaf in the end. Like insertions, deletions change nodes of the tree as we walk down. Whereas insertions eliminate 3-ke nodes (moving nodes up the tree) to make room for new kes, deletions eliminate 1-ke nodes (pulling kes down the tree) so that a ke can be removed from a leaf without leaving it empt. There are three was 1-ke nodes (ecept the root) are eliminated. Stealing. When we encounter a 1-ke node (ecept the root), we tr to steal a ke from an adjacent sibling. But we can t just steal the sibling s ke without violating the search tree invariant. We move a ke from the sibling to the parent, and we move a ke from the parent to the 1-ke node. We also move a subtree S from the sibling to the 1-ke node (now a 2-ke node). Note that we can t steal a ke from a non-adjacent sibling. 10
11 Fusion. If no adjacent sibling has more than one ke, we can t steal. In this case, the 1-ke node steals a ke from its parent. Since the parent was previousl treated the same wa (unless it s the root), it has at least two kes, and can spare one. The sibling is also absorbed, and the 1-ke node becomes a 3-ke node. If the parent is the root and contains onl one ke, then the current 1-ke node, its 1-ke sibling, and the 1-ke root are fused into one 3-ke node that serves as the new root. The height of the tree decreases b one. Eventuall we reach a leaf. After processing the leaf, it has at least two kes (if there are at least two kes in the tree), so we can delete the ke and still have one ke in the leaf. Analsis. A tree with height h has between 2 h and 4 h leaves. If n is the total number of nodes (including internal nodes), then n 2 h+1 1. B taking the logarithm of both sides, we find that h = O(log n). The time spent visiting a node is tpicall longer than in a binar search tree (because the nodes and the rotation and fusion operations are complicated), but the time per node is still in O(1). The number of nodes visited is proportional to the height of the tree. Hence, the running times of searching, insertions, and deletions are in O(h) and hence in O(log n), even in the worst case. Red-black trees The disadvantage of trees is that managing nodes becomes rather comple, and depends on the number of elements stored in the node. A red-black tree is an implementation of trees as a normal binar search tree, with the onl addition of one bit per node, used to mark a node as either black or red. To convert a tree to a red-black tree, we replace each node w of the tree b a small binar search tree T w. If w contains one element, then T w is simpl one black node. If w contains two elements, then T w consists of two nodes, a black root and a red child (note that there are two possible was of doing this). If w contains three elements, then T w consists of three nodes, a black root with two red children. We observe that the resulting tree has the following properties: The root is black. The parent of a red node is black. Ever path from the root to an empt subtree contains the same number of black nodes. The last propert follows from the fact that the number of black nodes on the path is the number of nodes that the path passes through, and all the leaves in a tree are on the same level. We can define a red-black-tree as a binar search tree where each node is either red or black and which satisfies the three conditions above. It is eas to see that ever such tree can be converted to an equivalent tree. It follows that the height of a red-black tree is at most 2 log n. Searching a red-black tree is eas, since it is a binar search tree. To implement insertions and deletions, we imitate the operations for trees. Bottom-up insertions. We first find the empt subtree where the new ke belongs, and replace it b a red node w. This corresponds to inserting the ke into a leaf of the tree. If w s parent is black, we are alread done (the node has enough space to store the new element). Otherwise, we first look at the uncle u of w. (The uncle is the sibling of w s parent.) If the uncle is black, then we can fi the problem b a rotation. (This is the case where the node had enough space for a new element, but we have to restructure its subtree to keep the correct representation.) If the uncle is red, this means that the node has overflowed, and we need to split it. We do this b changing the color of w s parent and w s uncle to black, and the color of w s grandparent v to red. In other words, the node v is kicked up into the parent node. Of course this could mean that this node now overflows, and so we have to repeat the process, with v taking the role of w. Note that if v is the root, then we immediatel change its color back to black, and we are done. 11
12 This algorithm can be eplained without mentioning trees at all. One can show its correctness simpl b arguing that it maintains the three properties of red-black-trees. Top-down insertions and deletions. Like for trees, insertions and deletions can be implemented b walking through the tree from the root to an empt subtree. When a black node v has two red children, we immediatel split it, b recoloring v red and its children black. If v s parent is red, its uncle must be black, and so we can use a rotation to fi the red-black-propert. If v is the root, we immediatel recolor it black. To implement deletions, we can again imitate the algorithm for trees. We leave this as an eercise for the reader. Acknowledgments These notes are based on the notes written b Jonathan Shewchuk for his course at UC Berkele. mistakes are mine, of course. All 12
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
AVL Trees. Reading: 9.2
 AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
Lecture 16 Notes AVL Trees
 Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Fall 2015) Frank Pfenning 1 Introduction Binar search trees are an ecellent data structure to implement associative arras, maps,
Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Fall 2015) Frank Pfenning 1 Introduction Binar search trees are an ecellent data structure to implement associative arras, maps,
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
Lecture Notes on AVL Trees
 Lecture Notes on AVL Trees 15-122: Principles of Imperative Computation Frank Pfenning Lecture 19 March 28, 2013 1 Introduction Binar search trees are an ecellent data structure to implement associative
Lecture Notes on AVL Trees 15-122: Principles of Imperative Computation Frank Pfenning Lecture 19 March 28, 2013 1 Introduction Binar search trees are an ecellent data structure to implement associative
Splay Trees Goodrich, Tamassia, Dickerson. Splay Trees 1
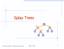 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
CSC 263 Lecture 4. September 13, 2006
 S 263 Lecture 4 September 13, 2006 7 ugmenting Red-lack Trees 7.1 Introduction Suppose that ou are asked to implement an DT that is the same as a dictionar but has one additional operation: operation:
S 263 Lecture 4 September 13, 2006 7 ugmenting Red-lack Trees 7.1 Introduction Suppose that ou are asked to implement an DT that is the same as a dictionar but has one additional operation: operation:
Binary search trees. We can define a node in a search tree using a Python class definition as follows: class SearchTree:
 Binary search trees An important use of binary trees is to store values that we may want to look up later. For instance, a binary search tree could be used to store a dictionary of words. A binary search
Binary search trees An important use of binary trees is to store values that we may want to look up later. For instance, a binary search tree could be used to store a dictionary of words. A binary search
CS 314H Algorithms and Data Structures Fall 2012 Programming Assignment #6 Treaps Due November 11/14/16, 2012
 CS H Algorithms and Data Structures Fall 202 Programming Assignment # Treaps Due November //, 202 In this assignment ou will work in pairs to implement a map (associative lookup) using a data structure
CS H Algorithms and Data Structures Fall 202 Programming Assignment # Treaps Due November //, 202 In this assignment ou will work in pairs to implement a map (associative lookup) using a data structure
CS 314H Honors Data Structures Fall 2017 Programming Assignment #6 Treaps Due November 12/15/17, 2017
 CS H Honors Data Structures Fall 207 Programming Assignment # Treaps Due November 2//7, 207 In this assignment ou will work individuall to implement a map (associative lookup) using a data structure called
CS H Honors Data Structures Fall 207 Programming Assignment # Treaps Due November 2//7, 207 In this assignment ou will work individuall to implement a map (associative lookup) using a data structure called
B + -trees. Kerttu Pollari-Malmi
 B + -trees Kerttu Pollari-Malmi This tet is based partl on the course tet book b Cormen and partl on the old lecture slides written b Matti Luukkainen and Matti Nkänen. 1 Introduction At first, read the
B + -trees Kerttu Pollari-Malmi This tet is based partl on the course tet book b Cormen and partl on the old lecture slides written b Matti Luukkainen and Matti Nkänen. 1 Introduction At first, read the
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Splay Trees. Splay Trees 1
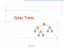 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Splay Trees 3/20/14. Splay Trees. Splay Trees are Binary Search Trees. note that two keys of equal value may be wellseparated (7,T) (1,Q) (1,C) (5,H)
 Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
2-3 Tree. Outline B-TREE. catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS
 Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Introduction to Algorithms Massachusetts Institute of Technology Professors Erik D. Demaine and Charles E. Leiserson.
 Introduction to Algorithms Massachusetts Institute of Technolog Professors Erik D. Demaine and Charles E. Leiserson October 24, 2005 6.046J/18.410J Handout 16 Problem Set 5 MIT students: This problem set
Introduction to Algorithms Massachusetts Institute of Technolog Professors Erik D. Demaine and Charles E. Leiserson October 24, 2005 6.046J/18.410J Handout 16 Problem Set 5 MIT students: This problem set
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Optional: Building a processor from scratch
 Optional: Building a processor from scratch In this assignment we are going build a computer processor from the ground up, starting with transistors, and ending with a small but powerful processor. The
Optional: Building a processor from scratch In this assignment we are going build a computer processor from the ground up, starting with transistors, and ending with a small but powerful processor. The
Transformations of Functions. 1. Shifting, reflecting, and stretching graphs Symmetry of functions and equations
 Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Chapter Transformations of Functions TOPICS.5.. Shifting, reflecting, and stretching graphs Smmetr of functions and equations TOPIC Horizontal Shifting/ Translation Horizontal Shifting/ Translation Shifting,
Balanced Binary Search Trees
 Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms
 Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
Department of Informatics, University of Zürich Vertiefungsarbeit Red-Black-Trees and Heaps in Timestamp-Adjusting Sweepline Based Algorithms Mirko Richter Matrikelnummer: 12-917-175 Email: mirko.richter@uzh.ch
n 1 i = n + i = n + f(n 1)
 2 Binary Search Trees Lab Objective: A tree is a linked list where each node in the list may refer to more than one other node. This structural flexibility makes trees more useful and efficient than regular
2 Binary Search Trees Lab Objective: A tree is a linked list where each node in the list may refer to more than one other node. This structural flexibility makes trees more useful and efficient than regular
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Balanced Binary Search Trees
 Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
CSI33 Data Structures
 Department of Mathematics and Computer Science Bronx Community College Section 13.3: Outline 1 Section 13.3: Section 13.3: Improving The Worst-Case Performance for BSTs The Worst Case Scenario In the worst
Department of Mathematics and Computer Science Bronx Community College Section 13.3: Outline 1 Section 13.3: Section 13.3: Improving The Worst-Case Performance for BSTs The Worst Case Scenario In the worst
Midterm solutions. n f 3 (n) = 3
 Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Multi-way Search Trees! M-Way Search! M-Way Search Trees Representation!
 Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline. An Application: A Binary Search Tree. 1 Chapter 7: Trees. favicon. CSI33 Data Structures
 Outline Chapter 7: Trees 1 Chapter 7: Trees Approaching BST Making a decision We discussed the trade-offs between linked and array-based implementations of sequences (back in Section 4.7). Linked lists
Outline Chapter 7: Trees 1 Chapter 7: Trees Approaching BST Making a decision We discussed the trade-offs between linked and array-based implementations of sequences (back in Section 4.7). Linked lists
Lecture 11: Multiway and (2,4) Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Implicit differentiation
 Roberto s Notes on Differential Calculus Chapter 4: Basic differentiation rules Section 5 Implicit differentiation What ou need to know alread: Basic rules of differentiation, including the chain rule.
Roberto s Notes on Differential Calculus Chapter 4: Basic differentiation rules Section 5 Implicit differentiation What ou need to know alread: Basic rules of differentiation, including the chain rule.
Lesson 21: AVL Trees. Rotation
 The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
 Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
CSE100. Advanced Data Structures. Lecture 8. (Based on Paul Kube course materials)
 CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
CSE100 Advanced Data Structures Lecture 8 (Based on Paul Kube course materials) CSE 100 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
12.4 The Ellipse. Standard Form of an Ellipse Centered at (0, 0) (0, b) (0, -b) center
 . The Ellipse The net one of our conic sections we would like to discuss is the ellipse. We will start b looking at the ellipse centered at the origin and then move it awa from the origin. Standard Form
. The Ellipse The net one of our conic sections we would like to discuss is the ellipse. We will start b looking at the ellipse centered at the origin and then move it awa from the origin. Standard Form
Lecture Overview. Readings. Recall: Binary Search Trees (BSTs) The importance of being balanced. AVL trees. Balance Insert. Other balanced trees
 alanced inar Search Trees Lecture Overview The importance of being balanced VL trees Definition alance Insert Other balanced trees Data structures in general Readings LRS hapter. and. (but different approach:
alanced inar Search Trees Lecture Overview The importance of being balanced VL trees Definition alance Insert Other balanced trees Data structures in general Readings LRS hapter. and. (but different approach:
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Do not turn this page until you have received the signal to start. In the meantime, please read the instructions below carefully.
 CSC 148 H1 / L0101 Term Test # 2 13 March 2013 Duration: Aids Allowed: 50 minutes None Student Number: Last (Family) Name(s): First (Given) Name(s): Do not turn this page until you have received the signal
CSC 148 H1 / L0101 Term Test # 2 13 March 2013 Duration: Aids Allowed: 50 minutes None Student Number: Last (Family) Name(s): First (Given) Name(s): Do not turn this page until you have received the signal
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
10.2 AVL Trees. Definition of an AVL Tree. 438 Chapter 10. Search Trees
 438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
An AVL tree with N nodes is an excellent data. The Big-Oh analysis shows that most operations finish within O(log N) time
 B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
Design and Analysis of Algorithms Lecture- 9: B- Trees
 Design and Analysis of Algorithms Lecture- 9: B- Trees Dr. Chung- Wen Albert Tsao atsao@svuca.edu www.408codingschool.com/cs502_algorithm 1/12/16 Slide Source: http://www.slideshare.net/anujmodi555/b-trees-in-data-structure
Design and Analysis of Algorithms Lecture- 9: B- Trees Dr. Chung- Wen Albert Tsao atsao@svuca.edu www.408codingschool.com/cs502_algorithm 1/12/16 Slide Source: http://www.slideshare.net/anujmodi555/b-trees-in-data-structure
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees (Ch. 9) > = Binary Search Trees 1
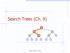 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Data Structure: Search Trees 2. Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering
 Data Structure: Search Trees 2 2017 Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered
Data Structure: Search Trees 2 2017 Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Advanced Tree Data Structures
 Advanced Tree Data Structures Fawzi Emad Chau-Wen Tseng Department of Computer Science University of Maryland, College Park Binary trees Traversal order Balance Rotation Multi-way trees Search Insert Overview
Advanced Tree Data Structures Fawzi Emad Chau-Wen Tseng Department of Computer Science University of Maryland, College Park Binary trees Traversal order Balance Rotation Multi-way trees Search Insert Overview
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
Solutions. Suppose we insert all elements of U into the table, and let n(b) be the number of elements of U that hash to bucket b. Then.
 Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
B-Trees. Disk Storage. What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree. Deletion in a B-tree
 B-Trees Disk Storage What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree Deletion in a B-tree Disk Storage Data is stored on disk (i.e., secondary memory) in blocks. A block is
B-Trees Disk Storage What is a multiway tree? What is a B-tree? Why B-trees? Insertion in a B-tree Deletion in a B-tree Disk Storage Data is stored on disk (i.e., secondary memory) in blocks. A block is
Module 4: Dictionaries and Balanced Search Trees
 Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
CS127: B-Trees. B-Trees
 CS127: B-Trees B-Trees 1 Data Layout on Disk Track: one ring Sector: one pie-shaped piece. Block: intersection of a track and a sector. Disk Based Dictionary Structures Use a disk-based method when the
CS127: B-Trees B-Trees 1 Data Layout on Disk Track: one ring Sector: one pie-shaped piece. Block: intersection of a track and a sector. Disk Based Dictionary Structures Use a disk-based method when the
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
CS Transform-and-Conquer
 CS483-11 Transform-and-Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-11 Transform-and-Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
DELETION WITHOUT REBALANCING IN BINARY SEARCH TREES
 DELETION WITHOUT RELNING IN INRY SERH TREES SIDDHRTH SEN, ROERT E. TRJN, ND DVID HONG KYUN KIM bstract. We address the veing issue of deletions in balanced trees. Rebalancing after a deletion is generall
DELETION WITHOUT RELNING IN INRY SERH TREES SIDDHRTH SEN, ROERT E. TRJN, ND DVID HONG KYUN KIM bstract. We address the veing issue of deletions in balanced trees. Rebalancing after a deletion is generall
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Binary Search Trees > = 2014 Goodrich, Tamassia, Goldwasser. Binary Search Trees 1
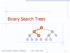 Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Purely Functional Data structures (3) Purely Functional Data structures (4) Numerical Representations (1)
 MGS 2011: FUN Lecture 2 Purel Functional Data Structures Henrik Nilsson Universit of Nottingham, UK Purel Functional Data structures (3) Linked list: After insert, if persistent: 1 2 3 1 7 Numerical Representations
MGS 2011: FUN Lecture 2 Purel Functional Data Structures Henrik Nilsson Universit of Nottingham, UK Purel Functional Data structures (3) Linked list: After insert, if persistent: 1 2 3 1 7 Numerical Representations
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Binary Search Tree. Revised based on textbook author s notes.
 Binary Search Tree Revised based on textbook author s notes. Search Trees The tree structure can be used for searching. Each node contains a search key as part of its data or payload. Nodes are organized
Binary Search Tree Revised based on textbook author s notes. Search Trees The tree structure can be used for searching. Each node contains a search key as part of its data or payload. Nodes are organized
AVL Trees. See Section 19.4of the text, p
 AVL Trees See Section 19.4of the text, p. 706-714. AVL trees are self-balancing Binary Search Trees. When you either insert or remove a node the tree adjusts its structure so that the remains a logarithm
AVL Trees See Section 19.4of the text, p. 706-714. AVL trees are self-balancing Binary Search Trees. When you either insert or remove a node the tree adjusts its structure so that the remains a logarithm
UNIT III BALANCED SEARCH TREES AND INDEXING
 UNIT III BALANCED SEARCH TREES AND INDEXING OBJECTIVE The implementation of hash tables is frequently called hashing. Hashing is a technique used for performing insertions, deletions and finds in constant
UNIT III BALANCED SEARCH TREES AND INDEXING OBJECTIVE The implementation of hash tables is frequently called hashing. Hashing is a technique used for performing insertions, deletions and finds in constant
B-Trees. Version of October 2, B-Trees Version of October 2, / 22
 B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
Lecture 13: AVL Trees and Binary Heaps
 Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
Data Structures Brett Bernstein Lecture 13: AVL Trees and Binary Heaps Review Exercises 1. ( ) Interview question: Given an array show how to shue it randomly so that any possible reordering is equally
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
Binary Tree. Preview. Binary Tree. Binary Tree. Binary Search Tree 10/2/2017. Binary Tree
 0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
Lecture 16 Notes AVL Trees
 Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Spring 2016) Frank Pfenning 1 Introduction Binary search trees are an excellent data structure to implement associative arrays,
Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Spring 2016) Frank Pfenning 1 Introduction Binary search trees are an excellent data structure to implement associative arrays,
Note that this is a rep invariant! The type system doesn t enforce this but you need it to be true. Should use repok to check in debug version.
 Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Trees. Tree Structure Binary Tree Tree Traversals
 Trees Tree Structure Binary Tree Tree Traversals The Tree Structure Consists of nodes and edges that organize data in a hierarchical fashion. nodes store the data elements. edges connect the nodes. The
Trees Tree Structure Binary Tree Tree Traversals The Tree Structure Consists of nodes and edges that organize data in a hierarchical fashion. nodes store the data elements. edges connect the nodes. The
Intermediate Algebra. Gregg Waterman Oregon Institute of Technology
 Intermediate Algebra Gregg Waterman Oregon Institute of Technolog c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license
Intermediate Algebra Gregg Waterman Oregon Institute of Technolog c 2017 Gregg Waterman This work is licensed under the Creative Commons Attribution 4.0 International license. The essence of the license
Operations on Heap Tree The major operations required to be performed on a heap tree are Insertion, Deletion, and Merging.
 Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
