Maximum Hitting Time
|
|
|
- Albert Noel Walsh
- 5 years ago
- Views:
Transcription
1 Maximum Hitting Time Longquan Qiao February 13, 013 Abstract For a specific connected, finite graph, there is always a maximum hitting time between any two different vertices in the graph. We call it the hitting time of G to avoid confusion, though it is the maximum hitting time in the graph. However, among various connected, finite graphs, we may be curious about the maximum value of hitting time for different graphs. This essay will give a thorough description and proof of the type of graph when the hitting time reaches its maximum value. The proof process will begin with a stronger induction and converge to the specific kind of graph eventually. The graph we need to find is called lollipop, formed by a clique and a path, with the maximum hitting time O[n 3 ], while the path only graph has a hitting time O[n ]. [1][] Finally, we will calculate to get the special 1-lollipop with the longest hitting time among all lollipops with different vertices distribution on clique and path. 1 Introduction The path graph is shown below. When starting at point i and finishing at point j, the expected time to consume is (j - i). This result can be obtained by adding 1, 3, 5 *(j i) 1, which are the expected walking times for each edge from j to i. Therefore, the hitting time of path graph is (n 0), which means the time complexity is O[n ]. Figure 1: path graph, length n+1 The lollipop graph is coming from the name lollipop intuitively. It contains two parts: a clique, which is a complete graph, and a path connected to the clique. The complete graph means there is an edge between any pair of vertices. For convenience, we will call a random point x in the clique, call the end of the path y and call the connected point z in both clique and path. In general, LL nn mm means a lollipop with n vertices and m of n vertices on the clique. In an extreme situation, all the vertices are in the clique, which is LL nn nn, we can use K n instead. [1][3] When walking on the lollipop graph, starting from clique and trying to reaching the end of the path, it will take a longer time than just a path which is easy to figure out based on the graph. However, the walk from x through z to y can be divided into
2 two parts: escaping from the clique and reaching Y before getting back to clique. The escaping probability is P(reaching z)*p(leaving clique). And the probability to reach y before back to z is 1/(n m). Therefore, the expected hitting time is (n 1) * n * (n m), whose complexity can be denoted as O[n 3 ]. Preliminaries Figure : various lollipop graphs Firstly, to represent the hitting time, we have the following definition: for distinct vertices x and y of a graph G, let s define T G (x, y) to be the expected hitting time of y for a random walk on G starting at x. [3] However, to prove the lollipop graph is the one we need seems impossible because there are no existing rules or models which are suitable for all kinds of graphs to compare them in the same situation. So it is very necessary to build a model to uniform all graphs to compare and calculate the maximum value. Based on this idea, and thanks to Professor Peter Winkler s help, the following function can provide a stronger introduction by ignoring the structure of graphs and only paying attention to the number of edges, vertices and the neighbor of y. Here is a sound and altered version of T G (x, y): for M 0, define T G M (x, y) T G (x, y) + M*e(G), where e(g) is the number of edges of graph G. Thus, if we find the lollipop graph can get the maximum value for T G M (x, y), then we will definitely get the result we want to prove (case M = 0). Before to prove, I need to set the T M (n) equal to the maximum of T G M (x, y)over all graphs G on n vertices. We may call the graph G (n, M)-extremal if T G M (x, y) = T M (n) for future convenience. [3] As mentioned above, we need connect this function to our final result lollipop graph. It is a useful notation to define a function f(n, M) as below.
3 ff(n, M) = T m Kn (x, y) (M n 1) ff(n, M) = T Ln m M (x, y) (M n 1) [3] 3 Full Proof For the full proof part, we need to consider the following two statements. If both of them hold, then we get the conclusion of lollipop above. 1. In every (n, M)-extremal graph G, the set of all neighbors of y, R(y), is a complete sub-graph of G.. Any graph which is not a lollipop graph cannot be (n, M)-extremal. Now let s begin to prove the first statement. Consider the following three graphs: G, A and B. Figure 3: Graph G, A and B. Suppose a and b are non-adjacent neighbors of y. In graph A, I remove edge a-y and add edge a-b. In graph B, I remove edge b-y and add edge a-b. We use this case to claim that the neighbors of vertex y must form a completer clique. Otherwise, either A or B will use a longer time to reach y than graph G. And because G, A and B have the same number of edges, G cannot be (n, M) extremal if y has two non-adjacent neighbors. Let S denote the set {a, b, y} in any of the three graphs. We have: T(x, S): expected time for a random walk from x to first hit S. p(x, a): probability of random walk, starting at x, hits a before b and y. T(a, S): expected time for a random walk from a, leaving S, to next hit S. p(a, a/b): probability of random walk, starting from a and leaving S, hits a/b before b and y/a and y. d(a): degree of a without considering y and b. If we can prove that in one of A and B, represented as C, T C (a, y) > T G (a, y) and T C (b, y) > T G (b, y) will sufficient for our statement one. T G (a, y) = 1 dd(aa)+1 + dd(aa) dd(aa)+1 TT(aa, SS) + pp(aa, aa)tt GG(aa, yy) + pp(aa, bb)tt GG (bb, yy) T G (b, y) = 1 dd(bb)+1 + dd(bb) dd(bb)+1 TT(bb, SS) + pp(bb, aa)tt GG(aa, yy) + pp(bb, bb)tt GG (bb, yy)
4 Let D(a) = 1 + d(a) d(a)p(a, a) and U(a) = 1 + d(a)t(a, S) and D(b), U(b) as the same. Without loss of generality, we assume that U(b)d(a)p(a, y) U(a)d(b)p(b, y). (*) T G (a, y) = DD(bb)UU(aa)+ dd(aa)pp(aa,bb)uu(bb) DD(aa)DD(bb) dd(aa)dd(bb)pp(aa,bb)pp(bb,aa), note as XX GGGG YY GGGG. T G (b, y) = DD(aa)UU(bb)+ dd(bb)pp(bb,aa)uu(aa) DD(aa)DD(bb) dd(aa)dd(bb)pp(aa,bb)pp(bb,aa), note as XX GGGG YY GGGG Now we repeat the calculation steps for graph A. We have: T A (a, y) = (DD(bb)+1)UU(aa)+(1+dd(aa)pp(aa,bb))(UU(bb)+1) DD(aa)(DD(bb)+1) (1+dd(aa)pp(aa,bb))(1+dd(bb)pp(bb,aa)), note as XX AAAA YY AAAA T A (b, y) = DD(aa)(UU(bb)+1)+(1+dd(bb)pp(bb,aa))UU(aa) DD(aa)(DD(bb)+1) (1+dd(aa)pp(aa,bb))(1+dd(bb)pp(bb,aa)). Now it s time to see the result: T A (a, y) T G (a, y) X Aa *Y Ga X Ga *Y Aa d(a)p(a, b)[u(a)d(b)(1 p(b, a) p(b, b))] U(b)d(a) p(a,b)[1 p(a, a) p(a, b)]. 0; It holds by using our assumption (*) above. T A (b, y) T G (b, y) X Ab *Y Gb X Gb *Y Ab > D(a)[U(a)d(b)(1 p(b, a) p(b, b)) U(b)d(a)(1 p(a, a) p(a, b))] 0. [3] Therefore, we successfully proved the statement one. Because there is always at least one graph having a longer hitting time to y than the graph G (a and b are two non-adjacent neighbors of y) with a specific n and M. We can put this into another way: Fix n and M, if (n, M) extremal value is obtained from graph G, the neighborhood R(y) of y is a clique. It means R(y) may consist only one vertex y or consist the whole graph except y. That s exactly what we want as a lollipop graph. Before proving the statement two, here is a useful lemma: Lemma 1: If a vertex y has a unique neighbor y, vertex x is not as same as Y, we have: (i) T M G (x, y) = T M+ G y (x, y ) + M + 1. (ii) And for M n 1, f(n, M) = f(n 1, M + ) + M + 1. It is not difficult to prove this lemma (i): because we have T G (x, y) = T G y (x, y ) + T G (y, y), and T G (y, y) = T G (y, y) 1 = *e(g) 1 = *e(g y) + 1. When we replace the graph G with the lollipop graph L n m, it is obvious that the lemma (ii) holds. [3]
5 Having this lemma, we can prove the second statement now: Assume we have a graph G is (n, M) extremal but not a lollipop graph. Case 1: R(y) =, by lemma (i), we know G y is (n 1, M + ) extremal if G is (n, M) extremal. Since G y is a lollipop graph, G is also a lollipop, contradicting the assumption. Case : R(y) = n, then G is complete graph K n, contradicting the assumption. Case 3: R(y) = n 1, in this case, y is connected to all vertices except x. We have: TT MM GG (xx, yy) = MM nn (nn ss ) MM(nn ss 1) + nn For M, it is less than (n nn MM nn ), which is TT KK nn MM (x, y). For M, it is less than (n 3 + (M +) nn 1 ), which is TT MM LLnn nn 1(x, y). Case 4: R(y) = r [3, n ], this is the last part we need to prove. We need another lemma to help work it out. Lemma : T G (x, y) T G/R (x, R) + 4*e(G)/r r + 1, where G/R means contracting all the neighbors of y to one point. It is obvious that T G (x, R) T G/R (x, R). So it is sufficient to prove max T G(w, y) 4*e(G)/r r + 1. Get the maximum one of T G (w, y) in R and suppose ωω RR the d(w) = r + k 1. The vertex w sends out k edges out of R and G is the graph formed by removing rr edges inside R from G. Because T G (w, R) + max uu RR T G(u, y) T G (w, w) + T G (w, y), we have: T G (w, y) u RR (TT rr+kk 1 GG(uu, yy) + 1) uu zz,yy + kk ee(gg) rr kk + TT GG (ww, yy) Because: (TT GG (uu, yy) + 1) u RR uu zz,yy = e(g) T G (w, y) 1, we can get the following: (r + k 1)T G (w, y) 1 + e(g) T G (w, y) 1 + e(g) r(r 1) + kt G (w, y) (4*e(G)/r r + 1)(r + k 1), which proves the lemma. By Lemma, we have: TT GG MM (xx, yy) T G/R (x, R) + (M + 4/r)e(G) r + 1 Therefore, T G/R (x, R) + (M + 4/r)[e(G/R) + rr + (n r)(r )] r + 1. TT MM GG (xx, yy) T M+4/r (n r + 1) + (M + 4/r)[ rr + (n r)(r )] r + 1 f(n r + 1, M + 4/r) + (M + 4/r)[ rr + (n r)(r )] r + 1. As coming to so far, we shall show that ΔΔ = f(n, M) f(n r + 1, M + 4/r) (M + 4/r) [ rr + (n r)(r )] + r 1 > 0 when M 0 and r [3, n ].
6 When M n 1, ΔΔ = (r 1) + (M + 4/r)(n r) n(n 1)/r (r 1) + (n 1 + 4/r)(n r) n(n 1)/r > 0. While n > r 3. When n 1 M n r 4/r, K n r + 1 is (n r + 1, M + 4/r)-extremal among lollipop graphs, it means we can prove as M n 1. When M n r 4/r, we can divide this into several smaller ranges to prove it one by one and get the final result is always greater than zero. [3] 4 Final Conclusion After finding out the lollipop graph, our task is now to calculate how to divide the n vertices to get the maximum hitting time among various lollipop graphs. Since T G (x, y) = T G (x, z) + T G (z, y) = m 1 + T G (z, y). tt Now I label the path as z(v 0 ), v 1, v v t-1, y(v t ). T G (z, y) = ii=1 TT GG (v i-1, v i ) tt = ii=1 (ee(gg {vv ii+1,, vv tt }) 1) = t mm + tt (i 1) ii=1 = t*m*(m 1) + t. T Ln m M (x, y) = t*m*(m 1) + t + m 1 + MM mm(mm 1) + M*t. Consider T M Ln m(x, y) T M Ln m+1(x, y) = (m 1)(3m n M + ) 0, we can get: m 1 (n + M ) 3 When M = 0, m = nn, the lollipop can get the maximum hitting time from x to 3 y. We may call this distribution 1-lollipop with 3 vertices on the clique and 1 3 on the path approximately. In a word, the lollipop is the graph having the maximum hitting time among all kinds of graphs. The 1-lollipop graph is the lollipop having the maximum hitting time among all lollipops with a fixed total vertex number n. Finally, for all lollipops, the complexity of hitting time is O[n 3 ] and for the special 1-lollipop, the hitting time is 4 7 n3 approximately. [1][][3] References [1] A.K. Chandra, P. Raghavan, W.L. Ruzzo, R. Smolensky and P. Tiwari, The electrical resistance of a graph captures its commute and cover times, Proceedings of the 1st Annual ACM Symposium on Theory of Computing, Seattle, Washington (May 1989), [] R. Aleliunas, R.M. Karp, R.J. Lipton, L. Lovasz, and C. Racko, Random walks, universal traversal sequences, and the complexity of maze problems, 0th Annual Symposium on Foundations of Computer Science, San Juan, Puerto Rico (October 1979), [3] Graham Brightwell, Peter Winkler, Maximum hitting time for random walks on graphs. (1990)
Random Walks and Universal Sequences
 Random Walks and Universal Sequences Xiaochen Qi February 28, 2013 Abstract A random walk is a chance process studied in probability, which plays an important role in probability theory and its applications.
Random Walks and Universal Sequences Xiaochen Qi February 28, 2013 Abstract A random walk is a chance process studied in probability, which plays an important role in probability theory and its applications.
Bounds for Edge-Cover by Random Walks
 Bounds for Edge-Cover by Random Walks Athina Panotopoulou February 24, 2013 Abstract Let G = (m, n) be an undirected graph with m edges and n vertices. For a random walk on G it is known that the time
Bounds for Edge-Cover by Random Walks Athina Panotopoulou February 24, 2013 Abstract Let G = (m, n) be an undirected graph with m edges and n vertices. For a random walk on G it is known that the time
DO NOT RE-DISTRIBUTE THIS SOLUTION FILE
 Professor Kindred Math 104, Graph Theory Homework 2 Solutions February 7, 2013 Introduction to Graph Theory, West Section 1.2: 26, 38, 42 Section 1.3: 14, 18 Section 2.1: 26, 29, 30 DO NOT RE-DISTRIBUTE
Professor Kindred Math 104, Graph Theory Homework 2 Solutions February 7, 2013 Introduction to Graph Theory, West Section 1.2: 26, 38, 42 Section 1.3: 14, 18 Section 2.1: 26, 29, 30 DO NOT RE-DISTRIBUTE
ASSIGNMENT 4 SOLUTIONS
 MATH 71 ASSIGNMENT SOLUTIONS 1. If F : X X is a function, define f (x) to be (f f)(x), and inductively define f k (x) (f f k 1 )(x) for each integer k. (So f (x) (f f )(x) f(f(f(x))) for instance.) We
MATH 71 ASSIGNMENT SOLUTIONS 1. If F : X X is a function, define f (x) to be (f f)(x), and inductively define f k (x) (f f k 1 )(x) for each integer k. (So f (x) (f f )(x) f(f(f(x))) for instance.) We
MATH20902: Discrete Maths, Solutions to Problem Set 1. These solutions, as well as the corresponding problems, are available at
 MATH20902: Discrete Maths, Solutions to Problem Set 1 These solutions, as well as the corresponding problems, are available at https://bit.ly/mancmathsdiscrete.. (1). The upper panel in the figure below
MATH20902: Discrete Maths, Solutions to Problem Set 1 These solutions, as well as the corresponding problems, are available at https://bit.ly/mancmathsdiscrete.. (1). The upper panel in the figure below
The NP-Completeness of Some Edge-Partition Problems
 The NP-Completeness of Some Edge-Partition Problems Ian Holyer y SIAM J. COMPUT, Vol. 10, No. 4, November 1981 (pp. 713-717) c1981 Society for Industrial and Applied Mathematics 0097-5397/81/1004-0006
The NP-Completeness of Some Edge-Partition Problems Ian Holyer y SIAM J. COMPUT, Vol. 10, No. 4, November 1981 (pp. 713-717) c1981 Society for Industrial and Applied Mathematics 0097-5397/81/1004-0006
On Strongly *-Graphs
 Proceedings of the Pakistan Academy of Sciences: A. Physical and Computational Sciences 54 (2): 179 195 (2017) Copyright Pakistan Academy of Sciences ISSN: 2518-4245 (print), 2518-4253 (online) Pakistan
Proceedings of the Pakistan Academy of Sciences: A. Physical and Computational Sciences 54 (2): 179 195 (2017) Copyright Pakistan Academy of Sciences ISSN: 2518-4245 (print), 2518-4253 (online) Pakistan
{ 1} Definitions. 10. Extremal graph theory. Problem definition Paths and cycles Complete subgraphs
 Problem definition Paths and cycles Complete subgraphs 10. Extremal graph theory 10.1. Definitions Let us examine the following forbidden subgraph problems: At most how many edges are in a graph of order
Problem definition Paths and cycles Complete subgraphs 10. Extremal graph theory 10.1. Definitions Let us examine the following forbidden subgraph problems: At most how many edges are in a graph of order
The vertex set is a finite nonempty set. The edge set may be empty, but otherwise its elements are two-element subsets of the vertex set.
 Math 3336 Section 10.2 Graph terminology and Special Types of Graphs Definition: A graph is an object consisting of two sets called its vertex set and its edge set. The vertex set is a finite nonempty
Math 3336 Section 10.2 Graph terminology and Special Types of Graphs Definition: A graph is an object consisting of two sets called its vertex set and its edge set. The vertex set is a finite nonempty
Solution of P versus NP problem
 Algorithms Research 2015, 4(1): 1-7 DOI: 105923/jalgorithms2015040101 Solution of P versus NP problem Mustapha Hamidi Meknes, Morocco Abstract This paper, taking Travelling Salesman Problem as our object,
Algorithms Research 2015, 4(1): 1-7 DOI: 105923/jalgorithms2015040101 Solution of P versus NP problem Mustapha Hamidi Meknes, Morocco Abstract This paper, taking Travelling Salesman Problem as our object,
Ramsey s Theorem on Graphs
 Ramsey s Theorem on Graphs 1 Introduction Exposition by William Gasarch Imagine that you have 6 people at a party. We assume that, for every pair of them, either THEY KNOW EACH OTHER or NEITHER OF THEM
Ramsey s Theorem on Graphs 1 Introduction Exposition by William Gasarch Imagine that you have 6 people at a party. We assume that, for every pair of them, either THEY KNOW EACH OTHER or NEITHER OF THEM
On the Convexity Number of Graphs
 On the Convexity Number of Graphs Mitre C. Dourado 1, Fábio Protti, Dieter Rautenbach 3, and Jayme L. Szwarcfiter 4 1 ICE, Universidade Federal Rural do Rio de Janeiro and NCE - UFRJ, Brazil, email: mitre@nce.ufrj.br
On the Convexity Number of Graphs Mitre C. Dourado 1, Fábio Protti, Dieter Rautenbach 3, and Jayme L. Szwarcfiter 4 1 ICE, Universidade Federal Rural do Rio de Janeiro and NCE - UFRJ, Brazil, email: mitre@nce.ufrj.br
Lesson 19: The Graph of a Linear Equation in Two Variables Is a Line
 The Graph of a Linear Equation in Two Variables Is a Line Classwork Exercises THEOREM: The graph of a linear equation yy = mmmm + bb is a non-vertical line with slope mm and passing through (0, bb), where
The Graph of a Linear Equation in Two Variables Is a Line Classwork Exercises THEOREM: The graph of a linear equation yy = mmmm + bb is a non-vertical line with slope mm and passing through (0, bb), where
Double Vertex Graphs and Complete Double Vertex Graphs. Jobby Jacob, Wayne Goddard and Renu Laskar Clemson University April, 2007
 Double Vertex Graphs and Complete Double Vertex Graphs Jobby Jacob, Wayne Goddard and Renu Laskar Clemson University April, 2007 Abstract Let G = (V, E) be a graph of order n 2. The double vertex graph,
Double Vertex Graphs and Complete Double Vertex Graphs Jobby Jacob, Wayne Goddard and Renu Laskar Clemson University April, 2007 Abstract Let G = (V, E) be a graph of order n 2. The double vertex graph,
Extremal Graph Theory: Turán s Theorem
 Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Bridgewater State University Virtual Commons - Bridgewater State University Honors Program Theses and Projects Undergraduate Honors Program 5-9-07 Extremal Graph Theory: Turán s Theorem Vincent Vascimini
Star Decompositions of the Complete Split Graph
 University of Dayton ecommons Honors Theses University Honors Program 4-016 Star Decompositions of the Complete Split Graph Adam C. Volk Follow this and additional works at: https://ecommons.udayton.edu/uhp_theses
University of Dayton ecommons Honors Theses University Honors Program 4-016 Star Decompositions of the Complete Split Graph Adam C. Volk Follow this and additional works at: https://ecommons.udayton.edu/uhp_theses
These notes present some properties of chordal graphs, a set of undirected graphs that are important for undirected graphical models.
 Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Undirected Graphical Models: Chordal Graphs, Decomposable Graphs, Junction Trees, and Factorizations Peter Bartlett. October 2003. These notes present some properties of chordal graphs, a set of undirected
Bipartite Roots of Graphs
 Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Bipartite Roots of Graphs Lap Chi Lau Department of Computer Science University of Toronto Graph H is a root of graph G if there exists a positive integer k such that x and y are adjacent in G if and only
Visit MathNation.com or search "Math Nation" in your phone or tablet's app store to watch the videos that go along with this workbook!
 Topic 1: Introduction to Angles - Part 1... 47 Topic 2: Introduction to Angles Part 2... 50 Topic 3: Angle Pairs Part 1... 53 Topic 4: Angle Pairs Part 2... 56 Topic 5: Special Types of Angle Pairs Formed
Topic 1: Introduction to Angles - Part 1... 47 Topic 2: Introduction to Angles Part 2... 50 Topic 3: Angle Pairs Part 1... 53 Topic 4: Angle Pairs Part 2... 56 Topic 5: Special Types of Angle Pairs Formed
K 4 C 5. Figure 4.5: Some well known family of graphs
 08 CHAPTER. TOPICS IN CLASSICAL GRAPH THEORY K, K K K, K K, K K, K C C C C 6 6 P P P P P. Graph Operations Figure.: Some well known family of graphs A graph Y = (V,E ) is said to be a subgraph of a graph
08 CHAPTER. TOPICS IN CLASSICAL GRAPH THEORY K, K K K, K K, K K, K C C C C 6 6 P P P P P. Graph Operations Figure.: Some well known family of graphs A graph Y = (V,E ) is said to be a subgraph of a graph
BRANDING AND STYLE GUIDELINES
 BRANDING AND STYLE GUIDELINES INTRODUCTION The Dodd family brand is designed for clarity of communication and consistency within departments. Bold colors and photographs are set on simple and clean backdrops
BRANDING AND STYLE GUIDELINES INTRODUCTION The Dodd family brand is designed for clarity of communication and consistency within departments. Bold colors and photographs are set on simple and clean backdrops
Decreasing the Diameter of Bounded Degree Graphs
 Decreasing the Diameter of Bounded Degree Graphs Noga Alon András Gyárfás Miklós Ruszinkó February, 00 To the memory of Paul Erdős Abstract Let f d (G) denote the minimum number of edges that have to be
Decreasing the Diameter of Bounded Degree Graphs Noga Alon András Gyárfás Miklós Ruszinkó February, 00 To the memory of Paul Erdős Abstract Let f d (G) denote the minimum number of edges that have to be
CUT VERTICES IN ZERO-DIVISOR GRAPHS OF FINITE COMMUTATIVE RINGS
 CUT VERTICES IN ZERO-DIVISOR GRAPHS OF FINITE COMMUTATIVE RINGS M. AXTELL, N. BAETH, AND J. STICKLES Abstract. A cut vertex of a connected graph is a vertex whose removal would result in a graph having
CUT VERTICES IN ZERO-DIVISOR GRAPHS OF FINITE COMMUTATIVE RINGS M. AXTELL, N. BAETH, AND J. STICKLES Abstract. A cut vertex of a connected graph is a vertex whose removal would result in a graph having
On Traversal and Exploration Sequences
 On Traversal and Exploration Sequences Michal Koucký Department of Computer Science Rutgers University, Piscataway NJ 8854, USA mkoucky@paul.rutgers.edu March 8, 3 Abstract Traversal sequences were defined
On Traversal and Exploration Sequences Michal Koucký Department of Computer Science Rutgers University, Piscataway NJ 8854, USA mkoucky@paul.rutgers.edu March 8, 3 Abstract Traversal sequences were defined
How can we lay cable at minimum cost to make every telephone reachable from every other? What is the fastest route between two given cities?
 1 Introduction Graph theory is one of the most in-demand (i.e. profitable) and heavily-studied areas of applied mathematics and theoretical computer science. May graph theory questions are applied in this
1 Introduction Graph theory is one of the most in-demand (i.e. profitable) and heavily-studied areas of applied mathematics and theoretical computer science. May graph theory questions are applied in this
The Structure of Bull-Free Perfect Graphs
 The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
The Structure of Bull-Free Perfect Graphs Maria Chudnovsky and Irena Penev Columbia University, New York, NY 10027 USA May 18, 2012 Abstract The bull is a graph consisting of a triangle and two vertex-disjoint
Acyclic Edge Colorings of Graphs
 Acyclic Edge Colorings of Graphs Noga Alon Ayal Zaks Abstract A proper coloring of the edges of a graph G is called acyclic if there is no 2-colored cycle in G. The acyclic edge chromatic number of G,
Acyclic Edge Colorings of Graphs Noga Alon Ayal Zaks Abstract A proper coloring of the edges of a graph G is called acyclic if there is no 2-colored cycle in G. The acyclic edge chromatic number of G,
Extremal functions for rooted minors
 Extremal functions for rooted minors Paul Wollan Abstract The graph G contains a graph H as a minor if there exist pair-wise disjoint sets {S i V (G) i = 1,..., V (H) } such that for every i, G[S i] is
Extremal functions for rooted minors Paul Wollan Abstract The graph G contains a graph H as a minor if there exist pair-wise disjoint sets {S i V (G) i = 1,..., V (H) } such that for every i, G[S i] is
Graph Algorithms. Chromatic Polynomials. Graph Algorithms
 Graph Algorithms Chromatic Polynomials Graph Algorithms Chromatic Polynomials Definition G a simple labelled graph with n vertices and m edges. k a positive integer. P G (k) number of different ways of
Graph Algorithms Chromatic Polynomials Graph Algorithms Chromatic Polynomials Definition G a simple labelled graph with n vertices and m edges. k a positive integer. P G (k) number of different ways of
Let G = (V, E) be a graph. If u, v V, then u is adjacent to v if {u, v} E. We also use the notation u v to denote that u is adjacent to v.
 Graph Adjacent Endpoint of an edge Incident Neighbors of a vertex Degree of a vertex Theorem Graph relation Order of a graph Size of a graph Maximum and minimum degree Let G = (V, E) be a graph. If u,
Graph Adjacent Endpoint of an edge Incident Neighbors of a vertex Degree of a vertex Theorem Graph relation Order of a graph Size of a graph Maximum and minimum degree Let G = (V, E) be a graph. If u,
1.2 Round-off Errors and Computer Arithmetic
 1.2 Round-off Errors and Computer Arithmetic 1 In a computer model, a memory storage unit word is used to store a number. A word has only a finite number of bits. These facts imply: 1. Only a small set
1.2 Round-off Errors and Computer Arithmetic 1 In a computer model, a memory storage unit word is used to store a number. A word has only a finite number of bits. These facts imply: 1. Only a small set
Adjacent: Two distinct vertices u, v are adjacent if there is an edge with ends u, v. In this case we let uv denote such an edge.
 1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
1 Graph Basics What is a graph? Graph: a graph G consists of a set of vertices, denoted V (G), a set of edges, denoted E(G), and a relation called incidence so that each edge is incident with either one
Problem Set 2 Solutions
 Problem Set 2 Solutions Graph Theory 2016 EPFL Frank de Zeeuw & Claudiu Valculescu 1. Prove that the following statements about a graph G are equivalent. - G is a tree; - G is minimally connected (it is
Problem Set 2 Solutions Graph Theory 2016 EPFL Frank de Zeeuw & Claudiu Valculescu 1. Prove that the following statements about a graph G are equivalent. - G is a tree; - G is minimally connected (it is
Sequence alignment is an essential concept for bioinformatics, as most of our data analysis and interpretation techniques make use of it.
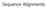 Sequence Alignments Overview Sequence alignment is an essential concept for bioinformatics, as most of our data analysis and interpretation techniques make use of it. Sequence alignment means arranging
Sequence Alignments Overview Sequence alignment is an essential concept for bioinformatics, as most of our data analysis and interpretation techniques make use of it. Sequence alignment means arranging
A TIGHT BOUND ON THE LENGTH OF ODD CYCLES IN THE INCOMPATIBILITY GRAPH OF A NON-C1P MATRIX
 A TIGHT BOUND ON THE LENGTH OF ODD CYCLES IN THE INCOMPATIBILITY GRAPH OF A NON-C1P MATRIX MEHRNOUSH MALEKESMAEILI, CEDRIC CHAUVE, AND TAMON STEPHEN Abstract. A binary matrix has the consecutive ones property
A TIGHT BOUND ON THE LENGTH OF ODD CYCLES IN THE INCOMPATIBILITY GRAPH OF A NON-C1P MATRIX MEHRNOUSH MALEKESMAEILI, CEDRIC CHAUVE, AND TAMON STEPHEN Abstract. A binary matrix has the consecutive ones property
Ma/CS 6b Class 26: Art Galleries and Politicians
 Ma/CS 6b Class 26: Art Galleries and Politicians By Adam Sheffer The Art Gallery Problem Problem. We wish to place security cameras at a gallery, such that they cover it completely. Every camera can cover
Ma/CS 6b Class 26: Art Galleries and Politicians By Adam Sheffer The Art Gallery Problem Problem. We wish to place security cameras at a gallery, such that they cover it completely. Every camera can cover
Wisconsin Retirement Testing Preparation
 Wisconsin Retirement Testing Preparation The Wisconsin Retirement System (WRS) is changing its reporting requirements from annual to every pay period starting January 1, 2018. With that, there are many
Wisconsin Retirement Testing Preparation The Wisconsin Retirement System (WRS) is changing its reporting requirements from annual to every pay period starting January 1, 2018. With that, there are many
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Subdivisions of Graphs: A Generalization of Paths and Cycles
 Subdivisions of Graphs: A Generalization of Paths and Cycles Ch. Sobhan Babu and Ajit A. Diwan Department of Computer Science and Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076,
Subdivisions of Graphs: A Generalization of Paths and Cycles Ch. Sobhan Babu and Ajit A. Diwan Department of Computer Science and Engineering, Indian Institute of Technology Bombay, Powai, Mumbai 400076,
Capture-time Extremal Cop-Win Graphs
 Capture-time Extremal Cop-Win Graphs arxiv:70.04427v2 [math.co] Feb 208 David Offner Department of Mathematics and Computer Science Westminster College New Wilmington, PA, U.S.A. offnerde@westminster.edu
Capture-time Extremal Cop-Win Graphs arxiv:70.04427v2 [math.co] Feb 208 David Offner Department of Mathematics and Computer Science Westminster College New Wilmington, PA, U.S.A. offnerde@westminster.edu
Discharging and reducible configurations
 Discharging and reducible configurations Zdeněk Dvořák March 24, 2018 Suppose we want to show that graphs from some hereditary class G are k- colorable. Clearly, we can restrict our attention to graphs
Discharging and reducible configurations Zdeněk Dvořák March 24, 2018 Suppose we want to show that graphs from some hereditary class G are k- colorable. Clearly, we can restrict our attention to graphs
time using O( n log n ) processors on the EREW PRAM. Thus, our algorithm improves on the previous results, either in time complexity or in the model o
 Reconstructing a Binary Tree from its Traversals in Doubly-Logarithmic CREW Time Stephan Olariu Michael Overstreet Department of Computer Science, Old Dominion University, Norfolk, VA 23529 Zhaofang Wen
Reconstructing a Binary Tree from its Traversals in Doubly-Logarithmic CREW Time Stephan Olariu Michael Overstreet Department of Computer Science, Old Dominion University, Norfolk, VA 23529 Zhaofang Wen
Math 575 Exam 3. (t). What is the chromatic number of G?
 Math 575 Exam 3 Name 1 (a) Draw the Grötsch graph See your notes (b) Suppose that G is a graph having 6 vertices and 9 edges and that the chromatic polynomial of G is given below Fill in the missing coefficients
Math 575 Exam 3 Name 1 (a) Draw the Grötsch graph See your notes (b) Suppose that G is a graph having 6 vertices and 9 edges and that the chromatic polynomial of G is given below Fill in the missing coefficients
Module 11. Directed Graphs. Contents
 Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
Module 11 Directed Graphs Contents 11.1 Basic concepts......................... 256 Underlying graph of a digraph................ 257 Out-degrees and in-degrees.................. 258 Isomorphism..........................
On vertex types of graphs
 On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
On vertex types of graphs arxiv:1705.09540v1 [math.co] 26 May 2017 Pu Qiao, Xingzhi Zhan Department of Mathematics, East China Normal University, Shanghai 200241, China Abstract The vertices of a graph
Lecture 19 Thursday, March 29. Examples of isomorphic, and non-isomorphic graphs will be given in class.
 CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 19 Thursday, March 29 GRAPH THEORY Graph isomorphism Definition 19.1 Two graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) are isomorphic, write G 1 G
CIS 160 - Spring 2018 (instructor Val Tannen) Lecture 19 Thursday, March 29 GRAPH THEORY Graph isomorphism Definition 19.1 Two graphs G 1 = (V 1, E 1 ) and G 2 = (V 2, E 2 ) are isomorphic, write G 1 G
Byzantine Consensus in Directed Graphs
 Byzantine Consensus in Directed Graphs Lewis Tseng 1,3, and Nitin Vaidya 2,3 1 Department of Computer Science, 2 Department of Electrical and Computer Engineering, and 3 Coordinated Science Laboratory
Byzantine Consensus in Directed Graphs Lewis Tseng 1,3, and Nitin Vaidya 2,3 1 Department of Computer Science, 2 Department of Electrical and Computer Engineering, and 3 Coordinated Science Laboratory
CSE 2331/5331. Topic 9: Basic Graph Alg. Representations Basic traversal algorithms Topological sort CSE 2331/5331
 Topic 9: Basic Graph Alg. Representations Basic traversal algorithms Topological sort What Is A Graph Graph G = (V, E) V: set of nodes E: set of edges a b c Example: d e f V ={ a, b, c, d, e, f } E ={(a,
Topic 9: Basic Graph Alg. Representations Basic traversal algorithms Topological sort What Is A Graph Graph G = (V, E) V: set of nodes E: set of edges a b c Example: d e f V ={ a, b, c, d, e, f } E ={(a,
Introduction to Graph Theory
 Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Introduction to Graph Theory Tandy Warnow January 20, 2017 Graphs Tandy Warnow Graphs A graph G = (V, E) is an object that contains a vertex set V and an edge set E. We also write V (G) to denote the vertex
Some Upper Bounds for Signed Star Domination Number of Graphs. S. Akbari, A. Norouzi-Fard, A. Rezaei, R. Rotabi, S. Sabour.
 Some Upper Bounds for Signed Star Domination Number of Graphs S. Akbari, A. Norouzi-Fard, A. Rezaei, R. Rotabi, S. Sabour Abstract Let G be a graph with the vertex set V (G) and edge set E(G). A function
Some Upper Bounds for Signed Star Domination Number of Graphs S. Akbari, A. Norouzi-Fard, A. Rezaei, R. Rotabi, S. Sabour Abstract Let G be a graph with the vertex set V (G) and edge set E(G). A function
EDGE MAXIMAL GRAPHS CONTAINING NO SPECIFIC WHEELS. Jordan Journal of Mathematics and Statistics (JJMS) 8(2), 2015, pp I.
 EDGE MAXIMAL GRAPHS CONTAINING NO SPECIFIC WHEELS M.S.A. BATAINEH (1), M.M.M. JARADAT (2) AND A.M.M. JARADAT (3) A. Let k 4 be a positive integer. Let G(n; W k ) denote the class of graphs on n vertices
EDGE MAXIMAL GRAPHS CONTAINING NO SPECIFIC WHEELS M.S.A. BATAINEH (1), M.M.M. JARADAT (2) AND A.M.M. JARADAT (3) A. Let k 4 be a positive integer. Let G(n; W k ) denote the class of graphs on n vertices
Topics in Combinatorial Optimization February 5, Lecture 2
 8.997 Topics in Combinatorial Optimization February 5, 2004 Lecture 2 Lecturer: Michel X. Goemans Scribe: Robert Kleinberg In this lecture, we will: Present Edmonds algorithm for computing a maximum matching
8.997 Topics in Combinatorial Optimization February 5, 2004 Lecture 2 Lecturer: Michel X. Goemans Scribe: Robert Kleinberg In this lecture, we will: Present Edmonds algorithm for computing a maximum matching
Faster parameterized algorithms for Minimum Fill-In
 Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
Faster parameterized algorithms for Minimum Fill-In Hans L. Bodlaender Pinar Heggernes Yngve Villanger Technical Report UU-CS-2008-042 December 2008 Department of Information and Computing Sciences Utrecht
6th Bay Area Mathematical Olympiad
 6th Bay Area Mathematical Olympiad February 4, 004 Problems and Solutions 1 A tiling of the plane with polygons consists of placing the polygons in the plane so that interiors of polygons do not overlap,
6th Bay Area Mathematical Olympiad February 4, 004 Problems and Solutions 1 A tiling of the plane with polygons consists of placing the polygons in the plane so that interiors of polygons do not overlap,
Power Set of a set and Relations
 Power Set of a set and Relations 1 Power Set (1) Definition: The power set of a set S, denoted P(S), is the set of all subsets of S. Examples Let A={a,b,c}, P(A)={,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}
Power Set of a set and Relations 1 Power Set (1) Definition: The power set of a set S, denoted P(S), is the set of all subsets of S. Examples Let A={a,b,c}, P(A)={,{a},{b},{c},{a,b},{b,c},{a,c},{a,b,c}}
Definition: A graph G = (V, E) is called a tree if G is connected and acyclic. The following theorem captures many important facts about trees.
 Tree 1. Trees and their Properties. Spanning trees 3. Minimum Spanning Trees 4. Applications of Minimum Spanning Trees 5. Minimum Spanning Tree Algorithms 1.1 Properties of Trees: Definition: A graph G
Tree 1. Trees and their Properties. Spanning trees 3. Minimum Spanning Trees 4. Applications of Minimum Spanning Trees 5. Minimum Spanning Tree Algorithms 1.1 Properties of Trees: Definition: A graph G
Discrete Mathematics Course Review 3
 21-228 Discrete Mathematics Course Review 3 This document contains a list of the important definitions and theorems that have been covered thus far in the course. It is not a complete listing of what has
21-228 Discrete Mathematics Course Review 3 This document contains a list of the important definitions and theorems that have been covered thus far in the course. It is not a complete listing of what has
Ambiguous Grammars and Compactification
 Ambiguous Grammars and Compactification Mridul Aanjaneya Stanford University July 17, 2012 Mridul Aanjaneya Automata Theory 1/ 44 Midterm Review Mathematical Induction and Pigeonhole Principle Finite Automata
Ambiguous Grammars and Compactification Mridul Aanjaneya Stanford University July 17, 2012 Mridul Aanjaneya Automata Theory 1/ 44 Midterm Review Mathematical Induction and Pigeonhole Principle Finite Automata
Complexity and approximation of satisfactory partition problems
 Complexity and approximation of satisfactory partition problems Cristina Bazgan, Zsolt Tuza, and Daniel Vanderpooten LAMSADE, Université Paris-Dauphine, France {bazgan,vdp}@lamsade.dauphine.fr Computer
Complexity and approximation of satisfactory partition problems Cristina Bazgan, Zsolt Tuza, and Daniel Vanderpooten LAMSADE, Université Paris-Dauphine, France {bazgan,vdp}@lamsade.dauphine.fr Computer
Discrete Mathematics and Probability Theory Fall 2013 Vazirani Note 7
 CS 70 Discrete Mathematics and Probability Theory Fall 2013 Vazirani Note 7 An Introduction to Graphs A few centuries ago, residents of the city of Königsberg, Prussia were interested in a certain problem.
CS 70 Discrete Mathematics and Probability Theory Fall 2013 Vazirani Note 7 An Introduction to Graphs A few centuries ago, residents of the city of Königsberg, Prussia were interested in a certain problem.
A New Game Chromatic Number
 Europ. J. Combinatorics (1997) 18, 1 9 A New Game Chromatic Number G. C HEN, R. H. S CHELP AND W. E. S HREVE Consider the following two-person game on a graph G. Players I and II move alternatively to
Europ. J. Combinatorics (1997) 18, 1 9 A New Game Chromatic Number G. C HEN, R. H. S CHELP AND W. E. S HREVE Consider the following two-person game on a graph G. Players I and II move alternatively to
Finding a -regular Supergraph of Minimum Order
 Finding a -regular Supergraph of Minimum Order Hans L. Bodlaender a, Richard B. Tan a,b and Jan van Leeuwen a a Department of Computer Science Utrecht University Padualaan 14, 3584 CH Utrecht The Netherlands
Finding a -regular Supergraph of Minimum Order Hans L. Bodlaender a, Richard B. Tan a,b and Jan van Leeuwen a a Department of Computer Science Utrecht University Padualaan 14, 3584 CH Utrecht The Netherlands
Graph Connectivity G G G
 Graph Connectivity 1 Introduction We have seen that trees are minimally connected graphs, i.e., deleting any edge of the tree gives us a disconnected graph. What makes trees so susceptible to edge deletions?
Graph Connectivity 1 Introduction We have seen that trees are minimally connected graphs, i.e., deleting any edge of the tree gives us a disconnected graph. What makes trees so susceptible to edge deletions?
K s,t -saturated bipartite graphs
 K s,t -saturated bipartite graphs Wenying Gan Dániel Korándi Benny Sudakov Abstract An n-by-n bipartite graph is H-saturated if the addition of any missing edge between its two parts creates a new copy
K s,t -saturated bipartite graphs Wenying Gan Dániel Korándi Benny Sudakov Abstract An n-by-n bipartite graph is H-saturated if the addition of any missing edge between its two parts creates a new copy
Chapter 2. Splitting Operation and n-connected Matroids. 2.1 Introduction
 Chapter 2 Splitting Operation and n-connected Matroids The splitting operation on an n-connected binary matroid may not yield an n-connected binary matroid. In this chapter, we provide a necessary and
Chapter 2 Splitting Operation and n-connected Matroids The splitting operation on an n-connected binary matroid may not yield an n-connected binary matroid. In this chapter, we provide a necessary and
COMPUTER GRAPHICS COURSE. LuxRender. Light Transport Foundations
 COMPUTER GRAPHICS COURSE LuxRender Light Transport Foundations Georgios Papaioannou - 2015 Light Transport Light is emitted at the light sources and scattered around a 3D environment in a practically infinite
COMPUTER GRAPHICS COURSE LuxRender Light Transport Foundations Georgios Papaioannou - 2015 Light Transport Light is emitted at the light sources and scattered around a 3D environment in a practically infinite
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS
 PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
PACKING DIGRAPHS WITH DIRECTED CLOSED TRAILS PAUL BALISTER Abstract It has been shown [Balister, 2001] that if n is odd and m 1,, m t are integers with m i 3 and t i=1 m i = E(K n) then K n can be decomposed
DO NOT RE-DISTRIBUTE THIS SOLUTION FILE
 Professor Kindred Math 104, Graph Theory Homework 3 Solutions February 14, 2013 Introduction to Graph Theory, West Section 2.1: 37, 62 Section 2.2: 6, 7, 15 Section 2.3: 7, 10, 14 DO NOT RE-DISTRIBUTE
Professor Kindred Math 104, Graph Theory Homework 3 Solutions February 14, 2013 Introduction to Graph Theory, West Section 2.1: 37, 62 Section 2.2: 6, 7, 15 Section 2.3: 7, 10, 14 DO NOT RE-DISTRIBUTE
Multi-view object segmentation in space and time. Abdelaziz Djelouah, Jean Sebastien Franco, Edmond Boyer
 Multi-view object segmentation in space and time Abdelaziz Djelouah, Jean Sebastien Franco, Edmond Boyer Outline Addressed problem Method Results and Conclusion Outline Addressed problem Method Results
Multi-view object segmentation in space and time Abdelaziz Djelouah, Jean Sebastien Franco, Edmond Boyer Outline Addressed problem Method Results and Conclusion Outline Addressed problem Method Results
Symmetric Product Graphs
 Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 5-20-2015 Symmetric Product Graphs Evan Witz Follow this and additional works at: http://scholarworks.rit.edu/theses
Rochester Institute of Technology RIT Scholar Works Theses Thesis/Dissertation Collections 5-20-2015 Symmetric Product Graphs Evan Witz Follow this and additional works at: http://scholarworks.rit.edu/theses
Discrete mathematics , Fall Instructor: prof. János Pach
 Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Discrete mathematics 2016-2017, Fall Instructor: prof. János Pach - covered material - Lecture 1. Counting problems To read: [Lov]: 1.2. Sets, 1.3. Number of subsets, 1.5. Sequences, 1.6. Permutations,
Section 6: Triangles Part 1
 Section 6: Triangles Part 1 Topic 1: Introduction to Triangles Part 1... 125 Topic 2: Introduction to Triangles Part 2... 127 Topic 3: rea and Perimeter in the Coordinate Plane Part 1... 130 Topic 4: rea
Section 6: Triangles Part 1 Topic 1: Introduction to Triangles Part 1... 125 Topic 2: Introduction to Triangles Part 2... 127 Topic 3: rea and Perimeter in the Coordinate Plane Part 1... 130 Topic 4: rea
(Received Judy 13, 1971) (devised Nov. 12, 1971)
 J. Math. Vol. 25, Soc. Japan No. 1, 1973 Minimal 2-regular digraphs with given girth By Mehdi BEHZAD (Received Judy 13, 1971) (devised Nov. 12, 1971) 1. Abstract. A digraph D is r-regular if degree v =
J. Math. Vol. 25, Soc. Japan No. 1, 1973 Minimal 2-regular digraphs with given girth By Mehdi BEHZAD (Received Judy 13, 1971) (devised Nov. 12, 1971) 1. Abstract. A digraph D is r-regular if degree v =
Fundamental Properties of Graphs
 Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Chapter three In many real-life situations we need to know how robust a graph that represents a certain network is, how edges or vertices can be removed without completely destroying the overall connectivity,
Superconcentrators of depth 2 and 3; odd levels help (rarely)
 Superconcentrators of depth 2 and 3; odd levels help (rarely) Noga Alon Bellcore, Morristown, NJ, 07960, USA and Department of Mathematics Raymond and Beverly Sackler Faculty of Exact Sciences Tel Aviv
Superconcentrators of depth 2 and 3; odd levels help (rarely) Noga Alon Bellcore, Morristown, NJ, 07960, USA and Department of Mathematics Raymond and Beverly Sackler Faculty of Exact Sciences Tel Aviv
recruitment Logo Typography Colourways Mechanism Usage Pip Recruitment Brand Toolkit
 Logo Typography Colourways Mechanism Usage Primary; Secondary; Silhouette; Favicon; Additional Notes; Where possible, use the logo with the striped mechanism behind. Only when it is required to be stripped
Logo Typography Colourways Mechanism Usage Primary; Secondary; Silhouette; Favicon; Additional Notes; Where possible, use the logo with the striped mechanism behind. Only when it is required to be stripped
Tranont Mission Statement. Tranont Vision Statement. Change the world s economy, one household at a time.
 STYLE GUIDE Tranont Mission Statement Change the world s economy, one household at a time. Tranont Vision Statement We offer individuals world class financial education and training, financial management
STYLE GUIDE Tranont Mission Statement Change the world s economy, one household at a time. Tranont Vision Statement We offer individuals world class financial education and training, financial management
Domination Cover Pebbling: Structural Results
 Domination Cover Pebbling: Structural Results arxiv:math.co/0509564 v 3 Sep 005 Nathaniel G. Watson Department of Mathematics Washington University at St. Louis Carl R. Yerger Department of Mathematics
Domination Cover Pebbling: Structural Results arxiv:math.co/0509564 v 3 Sep 005 Nathaniel G. Watson Department of Mathematics Washington University at St. Louis Carl R. Yerger Department of Mathematics
HW Graph Theory SOLUTIONS (hbovik) - Q
 1, Diestel 9.3: An arithmetic progression is an increasing sequence of numbers of the form a, a+d, a+ d, a + 3d.... Van der Waerden s theorem says that no matter how we partition the natural numbers into
1, Diestel 9.3: An arithmetic progression is an increasing sequence of numbers of the form a, a+d, a+ d, a + 3d.... Van der Waerden s theorem says that no matter how we partition the natural numbers into
MC 302 GRAPH THEORY 10/1/13 Solutions to HW #2 50 points + 6 XC points
 MC 0 GRAPH THEORY 0// Solutions to HW # 0 points + XC points ) [CH] p.,..7. This problem introduces an important class of graphs called the hypercubes or k-cubes, Q, Q, Q, etc. I suggest that before you
MC 0 GRAPH THEORY 0// Solutions to HW # 0 points + XC points ) [CH] p.,..7. This problem introduces an important class of graphs called the hypercubes or k-cubes, Q, Q, Q, etc. I suggest that before you
Pentagons vs. triangles
 Discrete Mathematics 308 (2008) 4332 4336 www.elsevier.com/locate/disc Pentagons vs. triangles Béla Bollobás a,b, Ervin Győri c,1 a Trinity College, Cambridge CB2 1TQ, UK b Department of Mathematical Sciences,
Discrete Mathematics 308 (2008) 4332 4336 www.elsevier.com/locate/disc Pentagons vs. triangles Béla Bollobás a,b, Ervin Győri c,1 a Trinity College, Cambridge CB2 1TQ, UK b Department of Mathematical Sciences,
Bounds on distances for spanning trees of graphs. Mr Mthobisi Luca Ntuli
 Bounds on distances for spanning trees of graphs Mr Mthobisi Luca Ntuli March 8, 2018 To Mphemba Legacy iii Acknowledgments I would like to thank my supervisors, Dr MJ Morgan and Prof S Mukwembi. It
Bounds on distances for spanning trees of graphs Mr Mthobisi Luca Ntuli March 8, 2018 To Mphemba Legacy iii Acknowledgments I would like to thank my supervisors, Dr MJ Morgan and Prof S Mukwembi. It
Basic Combinatorics. Math 40210, Section 01 Fall Homework 4 Solutions
 Basic Combinatorics Math 40210, Section 01 Fall 2012 Homework 4 Solutions 1.4.2 2: One possible implementation: Start with abcgfjiea From edge cd build, using previously unmarked edges: cdhlponminjkghc
Basic Combinatorics Math 40210, Section 01 Fall 2012 Homework 4 Solutions 1.4.2 2: One possible implementation: Start with abcgfjiea From edge cd build, using previously unmarked edges: cdhlponminjkghc
Math 485, Graph Theory: Homework #3
 Math 485, Graph Theory: Homework #3 Stephen G Simpson Due Monday, October 26, 2009 The assignment consists of Exercises 2129, 2135, 2137, 2218, 238, 2310, 2313, 2314, 2315 in the West textbook, plus the
Math 485, Graph Theory: Homework #3 Stephen G Simpson Due Monday, October 26, 2009 The assignment consists of Exercises 2129, 2135, 2137, 2218, 238, 2310, 2313, 2314, 2315 in the West textbook, plus the
Trees. Arash Rafiey. 20 October, 2015
 20 October, 2015 Definition Let G = (V, E) be a loop-free undirected graph. G is called a tree if G is connected and contains no cycle. Definition Let G = (V, E) be a loop-free undirected graph. G is called
20 October, 2015 Definition Let G = (V, E) be a loop-free undirected graph. G is called a tree if G is connected and contains no cycle. Definition Let G = (V, E) be a loop-free undirected graph. G is called
Sharp lower bound for the total number of matchings of graphs with given number of cut edges
 South Asian Journal of Mathematics 2014, Vol. 4 ( 2 ) : 107 118 www.sajm-online.com ISSN 2251-1512 RESEARCH ARTICLE Sharp lower bound for the total number of matchings of graphs with given number of cut
South Asian Journal of Mathematics 2014, Vol. 4 ( 2 ) : 107 118 www.sajm-online.com ISSN 2251-1512 RESEARCH ARTICLE Sharp lower bound for the total number of matchings of graphs with given number of cut
8 Colouring Planar Graphs
 8 Colouring Planar Graphs The Four Colour Theorem Lemma 8.1 If G is a simple planar graph, then (i) 12 v V (G)(6 deg(v)) with equality for triangulations. (ii) G has a vertex of degree 5. Proof: For (i),
8 Colouring Planar Graphs The Four Colour Theorem Lemma 8.1 If G is a simple planar graph, then (i) 12 v V (G)(6 deg(v)) with equality for triangulations. (ii) G has a vertex of degree 5. Proof: For (i),
EMBEDDING INTO l n. 1 Notation and Lemmas
 EMBEDDING INTO l n We are looking at trying to embed a metric space into l n, our goal is to try and embed an n point metric space into as low a dimension l m as possible. We will show that, in fact, every
EMBEDDING INTO l n We are looking at trying to embed a metric space into l n, our goal is to try and embed an n point metric space into as low a dimension l m as possible. We will show that, in fact, every
Graph Editing to a Given Degree Sequence,
 Graph Editing to a Given Degree Sequence, Petr A. Golovach a, George B. Mertzios b, a Department of Informatics, University of Bergen, N-5020 Bergen, Norway b School of Engineering and Computing Sciences,
Graph Editing to a Given Degree Sequence, Petr A. Golovach a, George B. Mertzios b, a Department of Informatics, University of Bergen, N-5020 Bergen, Norway b School of Engineering and Computing Sciences,
The Rainbow Connection of a Graph Is (at Most) Reciprocal to Its Minimum Degree
 The Rainbow Connection of a Graph Is (at Most) Reciprocal to Its Minimum Degree Michael Krivelevich 1 and Raphael Yuster 2 1 SCHOOL OF MATHEMATICS, TEL AVIV UNIVERSITY TEL AVIV, ISRAEL E-mail: krivelev@post.tau.ac.il
The Rainbow Connection of a Graph Is (at Most) Reciprocal to Its Minimum Degree Michael Krivelevich 1 and Raphael Yuster 2 1 SCHOOL OF MATHEMATICS, TEL AVIV UNIVERSITY TEL AVIV, ISRAEL E-mail: krivelev@post.tau.ac.il
Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science Algorithms For Inference Fall 2014
 Suggested Reading: Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Probabilistic Modelling and Reasoning: The Junction
Suggested Reading: Massachusetts Institute of Technology Department of Electrical Engineering and Computer Science 6.438 Algorithms For Inference Fall 2014 Probabilistic Modelling and Reasoning: The Junction
Math Introduction to Advanced Mathematics
 Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
Math 215 - Introduction to Advanced Mathematics Number Theory Fall 2017 The following introductory guide to number theory is borrowed from Drew Shulman and is used in a couple of other Math 215 classes.
Similar Polygons Date: Per:
 Math 2 Unit 6 Worksheet 1 Name: Similar Polygons Date: Per: [1-2] List the pairs of congruent angles and the extended proportion that relates the corresponding sides for the similar polygons. 1. AA BB
Math 2 Unit 6 Worksheet 1 Name: Similar Polygons Date: Per: [1-2] List the pairs of congruent angles and the extended proportion that relates the corresponding sides for the similar polygons. 1. AA BB
Visual Identity Guidelines. Abbreviated for Constituent Leagues
 Visual Identity Guidelines Abbreviated for Constituent Leagues 1 Constituent League Logo The logo is available in a horizontal and vertical format. Either can be used depending on the best fit for a particular
Visual Identity Guidelines Abbreviated for Constituent Leagues 1 Constituent League Logo The logo is available in a horizontal and vertical format. Either can be used depending on the best fit for a particular
Discrete Mathematics for CS Spring 2008 David Wagner Note 13. An Introduction to Graphs
 CS 70 Discrete Mathematics for CS Spring 2008 David Wagner Note 13 An Introduction to Graphs Formulating a simple, precise specification of a computational problem is often a prerequisite to writing a
CS 70 Discrete Mathematics for CS Spring 2008 David Wagner Note 13 An Introduction to Graphs Formulating a simple, precise specification of a computational problem is often a prerequisite to writing a
Graph Theory. Chapter 4.
 Graph Theory. Chapter 4. Wandering. Here is an algorithm, due to Tarry, that constructs a walk in a connected graph, starting at any vertex v 0, traversing each edge exactly once in each direction, and
Graph Theory. Chapter 4. Wandering. Here is an algorithm, due to Tarry, that constructs a walk in a connected graph, starting at any vertex v 0, traversing each edge exactly once in each direction, and
Vertex 3-colorability of claw-free graphs
 Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
Algorithmic Operations Research Vol.2 (27) 5 2 Vertex 3-colorability of claw-free graphs Marcin Kamiński a Vadim Lozin a a RUTCOR - Rutgers University Center for Operations Research, 64 Bartholomew Road,
BRAND STANDARD GUIDELINES 2014
 BRAND STANDARD GUIDELINES 2014 LOGO USAGE & TYPEFACES Logo Usage The Lackawanna College School of Petroleum & Natural Gas logo utilizes typography, two simple rule lines and the Lackawanna College graphic
BRAND STANDARD GUIDELINES 2014 LOGO USAGE & TYPEFACES Logo Usage The Lackawanna College School of Petroleum & Natural Gas logo utilizes typography, two simple rule lines and the Lackawanna College graphic
The Computational Complexity of Graph Contractions II: Two Tough Polynomially Solvable Cases
 The Computational Complexity of Graph Contractions II: Two Tough Polynomially Solvable Cases Asaf Levin Department of Statistics, The Hebrew University, Jerusalem 91905, Israel Daniel Paulusma Department
The Computational Complexity of Graph Contractions II: Two Tough Polynomially Solvable Cases Asaf Levin Department of Statistics, The Hebrew University, Jerusalem 91905, Israel Daniel Paulusma Department
The ABC s of Web Site Evaluation
 Aa Bb Cc Dd Ee Ff Gg Hh Ii Jj Kk Ll Mm Nn Oo Pp Qq Rr Ss Tt Uu Vv Ww Xx Yy Zz The ABC s of Web Site Evaluation by Kathy Schrock Digital Literacy by Paul Gilster Digital literacy is the ability to understand
Aa Bb Cc Dd Ee Ff Gg Hh Ii Jj Kk Ll Mm Nn Oo Pp Qq Rr Ss Tt Uu Vv Ww Xx Yy Zz The ABC s of Web Site Evaluation by Kathy Schrock Digital Literacy by Paul Gilster Digital literacy is the ability to understand
