Surfaces and Integral Curves
|
|
|
- Jeffery Singleton
- 5 years ago
- Views:
Transcription
1 MODULE 1: MATHEMATICAL PRELIMINARIES 16 Lecture 3 Surfaces and Integral Curves In Lecture 3, we recall some geometrical concepts that are essential for understanding the nature of solutions of partial differential equations to be discussed in the subsequent lectures. Surface: A surface is the locus of a point moving in space with two degrees of freedom. Generally, we use implicit and explicit representations for describing such a locus by mathematical formulas. In the implicit representation we describe a surface as a set S = {(x, y, z) F (x, y, z) = 0}, i.e., a set of points (x, y, z) satisfying an equation of the form F (x, y, z) = 0. Sometimes we can solve such an equation for one of the coordinates in terms of the other two, say for z in terms of x and y. When this is possible we obtain an explicit representation of the form z = f(x, y). EXAMPLE 1. A sphere of radius 1 and center at the origin has the implicit representation x 2 + y 2 + z 2 1 = 0. When this equation is solved for z it leads to two solutions: z = 1 x 2 y 2 and z = 1 x 2 y 2. The first equation gives an explicit representation of the upper hemisphere and the second of the lower hemisphere. We now describe here a class of surfaces more general than surfaces obtained as graphs of functions. For simplicity, we restrict the discussion to the case of three dimensions. Let Ω R 3 and let F (x, y, z) C 1 (Ω), where C 1 (Ω) := {F (x, y, x) C(Ω) : F x, F y, F z C(Ω)}. We know the gradient of F, denoted by F, is a vector valued function defined by F = ( F x, F y, F z ). One can visualize F as a field of vectors (vector fields), with one vector, F, emanating from each point (x, y, z) Ω. Assume that F (x, y, z) (0, 0, 0), x Ω. (1)
2 MODULE 1: MATHEMATICAL PRELIMINARIES 17 This means that the partial derivatives of F do not vanish simultaneously at any point of Ω. DEFINITION 2. (Level surface) The set S c = {(x, y, z) (x, y, z) Ω and F (x, y, z) = c}, for some appropriate value of the constant c, is a surface in Ω. This surface is called a level surface of F. Note: When Ω R 2, the set S c = {(x, y) (x, y) Ω and F (x, y) = c} is called a level curve in Ω. Let (x 0, y 0, z 0 ) Ω and set c = F (x 0, y 0, z 0 ). The equation F (x, y, z) = c (2) represents a surface in Ω passing through the point (x 0, y 0, z 0 ). For different values of c, (2) represents different surfaces in Ω. Each point of Ω lies on exactly one level surface of F. Any two points (x 0, y 0, z 0 ) and (x 1, y 1, z 1 ) of Ω lie on the same level surface if and only if F (x 0, y 0, z 0 ) = F (x 1, y 1, z 1 ). Thus, one may visualize Ω as being laminated by the level surfaces of F. The equation (2) represents one parameter family of surfaces in Ω. EXAMPLE 3. Take Ω = R 3 \(0, 0, 0) and let F (x, y, z) = x 2 + y 2 + z 2. Then F (x, y, z) = (2x, 2y, 2z). Note that the condition (1) is satisfied (x, y, z) Ω. The level surfaces of F are spheres with center at the origin. EXAMPLE 4. Take Ω = R 3. Then F (x, y, z) = (0, 0, 1). The condition (1) is satisfied at every point of Ω. The level surfaces are planes parallel to the (x, y)-plane. Consider the surface given by the equation (2) and let the point (x 0, y 0, z 0 ) lie on this surface. We now ask the following question: Is it possible to describe S c by an equation of the form z = f(x, y), (3) so that S c is the graph of f? This is equivalent to asking whether it is possible to solve (2) for z in terms of x and y. An answer to this question is contained in the following theorem.
3 MODULE 1: MATHEMATICAL PRELIMINARIES 18 THEOREM 5. (Implicit Function Theorem) If F is defined within a sphere containing the point (x 0, y 0, z 0 ), where F (x 0, y 0, z 0 ) = 0, F z (x 0, y 0, z 0 ) 0, and F x, F y and F z are continuous inside the sphere, then the equation F (x, y, z) = 0 defines z = f(x, y) near the point (x 0, y 0, z 0 ). EXAMPLE 6. Consider the unit sphere x 2 + y 2 + z 2 = 1. (4) Note that the point (0, 0, 1) lies on this surface and F z (0, 0, 1) = 2. By the implicit function function theorem, we can solve (4) for z near the point (0, 0, 1). In fact, we have z = + 1 x 2 y 2, x 2 + y 2 < 1. (5) In the upper half space z > 0, (4) and (5) describe the same surface. The point (0, 0, 1) is also an the surface (4) and F z (0, 0, 1) = 2. Near (0, 0, 1), we have z = 1 x 2 y 2, x 2 + y 2 < 1. (6) In the lower half space z < 0, (4) and (6) represents the same surface. On the other hand, at the point (1, 0, 0), we have F z (1, 0, 0) = 0. Clearly, it is not possible to solve (4) for z in terms of x and y near this point. Note that the set of points satisfying the equations F (x, y, z) = c 1, G(x, y, z) = c 2 (7) must lie on the intersection of these two surfaces. If F and G are not colinear at any point of the domain Ω, where both F and G are defined, i.e., F (x, y, z) G(x, y, z) 0, (x, y, z) Ω, (8) then the intersection of the two surfaces given by (7) is always a curve. Since where the Jacobian F G = ( (F, G) (y, z) (F, G) (y, z) = F G y z F G z y. ) (F, G) (F, G),,, (9) (z, x) (x, y) The condition (8) means that at every point of Ω at least one of the Jacobian on the right side of (9) is different from zero.
4 MODULE 1: MATHEMATICAL PRELIMINARIES 19 EXAMPLE 7. Let F (x, y, z) = x 2 + y 2 z, G(x, y, z) = z. Note that F = (2x, 2y, 1) and G = (0, 0, 1). It is easy to see that if Ω = R 3 with the z-axis removed, then the condition (8) is satisfied in Ω. The pair of equations x 2 + y 2 z = 0, z = 1 represents a circle which is the intersection of the paraboloidal surface represented by the first equation and the plane represented by the second equation. Systems of Surfaces: A one-parameter system of surfaces is represented by the equation of the form Consider the system of surfaces described by the equation corresponding to the slightly different value c + δc. f(x, y, z, c) = 0. (10) f(x, y, z, c + δc) = 0, (11) Note that these two surfaces will intersect in a curve whose equations are (10) and (11). This curve may be considered to be intersection of the equations f(x, y, z, c) = 0, The limiting curve described by the set of equations f(x, y, z, c) = 0, is called the characteristic curve (cf. [10]) of (10). f(x, y, z, c + δc) f(x, y, z, c) lim. δc 0 δc f(x, y, z, c) = 0. (12) c REMARK 8. Geometrically, it is the curve on the surface (10) approached by the intersection of (10) and (11) as δc 0. Note that as c varies, the characteristic curve (12) trace out a surface whose equation is of the form g(x, y, z) = 0. DEFINITION 9. (Envelope of one-parameter system) The surface determined by eliminating the parameter c between the equations f(x, y, z, c) = 0, f(x, y, z, c) = 0 c is called the envelope of the one-parameter system f(x, y, z, c) = 0.
5 MODULE 1: MATHEMATICAL PRELIMINARIES 20 EXAMPLE 10. Consider the equation x 2 + y 2 + (z c) 2 = 1. This equation represents the family of spheres of unit radius with centers on the z-axis. Set Then f c = z c. The set of equations f(x, y, z, c) = x 2 + y 2 + (z c) 2 1. x 2 + y 2 + (z c) 2 = 1, z = c describe the characteristic curve to the surface. Eliminating the parameter c, the envelope of this family is the cylinder x 2 + y 2 = 1. Now consider the two parameter system of surfaces defined by the equation where c and d are parameters. f(x, y, z, c, d) = 0, (13) In a similar way, the characteristics curve of the surface (13) passes through the point defined by the equations f(x, y, z, c, d) = 0, f(x, y, z, c, d) = 0, c f(x, y, z, c, d) = 0. d This point is called the characteristics point of the two-parameter system (13). As the parameters c and d vary, this point generates a surface which is called the envelope of the surfaces (13). DEFINITION 11. (Envelope of two-parameter system) The surface obtained by eliminating c and d from the equations f(x, y, z, c, d) = 0, f(x, y, z, c, d) = 0, c f(x, y, z, c, d) = 0 d is called the envelope of the two-parameter system f(x, y, z, c, d) = 0. EXAMPLE 12. Consider the equation where c and d are parameters. Observe that (x c) 2 + (y d) 2 + z 2 = 1, (x c) 2 + (y d) 2 + z 2 = 1, x c = 0, y d = 0. The characteristics points of the two-parameter system (13) are (c, d, ±1). Eliminating c and d, the envelope is the pair of parallel planes z = ±1.
6 MODULE 1: MATHEMATICAL PRELIMINARIES 21 Integral Curves of Vector Fields: Let V(x, y, z) = (P (x, y, z), Q(x, y, z), R(x, y, z)) be a vector field defined in some domain Ω R 3 satisfying the following two conditions: V 0 in Ω, i.e., the component functions P, Q and R of V do not vanish simultaneously at any point of Ω. P, Q, R C 1 (Ω). DEFINITION 13. A curve C in Ω is an integral curve of the vector field V if V is tangent to C at each of its points. EXAMPLE The integral curves of the constant vector fields V = (1, 0, 0) are lines parallel to the x-axis (see Fig. 1.1). 2. The integral curves of V = (y, x, 0) are circles parallel to the (x, y)-plane and centered on the z-axis (see Fig. 1.1). Figure 1.1: Integral curves of V = (1, 0, 0) and V = (y, x, 0) REMARK 15. In physics, if V is a force field, the integral curves of V are called lines of force. If V is the velocity of the fluid flow, the integral curves of V are called lines of flow. These are the paths of motion of the fluid particles. With V = (P, Q, R), associate the system of ODEs: dx dt = P (x, y, z), dy dt = Q(x, y, z), dz dt = R(x, y, z). (14) A solution (x(t), y(t), z(t)) of the system (14), defined for t in some interval I, may be regarded as a curve in Ω. We call this curve a solution curve of the system (14). Every solution curve of the system (14) is an integral curve of the vector field V. Conversely, if C is an integral curve of V, then there is a parametric representation x = x(t), y = y(t), z = z(t); t I,
7 MODULE 1: MATHEMATICAL PRELIMINARIES 22 of C such that (x(t), y(t), z(t)) is a solution of the system of equations (14). Thus, every integral curve of V, if parametrized appropriately, is a solution curve of the associated system of equations (14). It is customary to write the systems (14) in the form dx P = dy Q = dz R. (15) EXAMPLE 16. The systems associated with the vector fields V = (x, y, x) and V = (y, x, 0), respectively, are dx x = dy y = dz z, (16) dx y = dy x = dz 0. (17) Note that the zero which appears in the denominator of (17) should not be disturbing. It simply means that dz/dx = dz/dy = dz/dt = 0. Before we discuss the method of solutions of (15), let us introduce some basic definitions and facts (cf. [11]). DEFINITION 17. Two functions ϕ(x, y, z), ψ(x, y, z) C 1 (Ω) are functionally independent in Ω R 3 if ϕ(x, y, z) ψ(x, y, z) 0, (x, y, z) Ω. (18) Geometrically, condition (18) means that ϕ and ψ are not parallel at any point of Ω. DEFINITION 18. A function ϕ C 1 (Ω) is called a first integral of the vector field V = (P, Q, R) (or its associated system (15)) in Ω, if at each point of Ω, V is orthogonal to ϕ, i.e. V ϕ = 0 = P ϕ x + Qϕ y + Rϕ = 0 in Ω. z THEOREM 19. Let ϕ 1 and ϕ 2 be any two functionally independent first integrals of V in Ω. Then the equations describe the collection of all integrals of V in Ω. ϕ(x, y, z) = c 1, ϕ 2 (x, y, z) = c 2 (19)
8 MODULE 1: MATHEMATICAL PRELIMINARIES 23 If ϕ(x, y, z) is a first integral of V and f(ϕ) is a C 1 function of single variable ϕ then w(x, y, z) = f(ϕ(x, y, z)) is also a first integral of V. This follows from the fact that P w x + Qw y + Rw z = P f ϕ ϕ ϕ + Qf + Rf x y z ( = f P ϕ ) x + Qϕ y + Rϕ z = 0. Similarly, if f(u, v) is a C 1 function of two variables ϕ 1 and ϕ 2 and if ϕ 1 (x, y, z) and ϕ 2 (x, y, z) are any two first integrals of V then w(x, y, z) = f(ϕ 1 (x, y, z), ϕ 2 (x, y, z)) is also a first integral of V. EXAMPLE 20. Let V = (1, 0, 0) be a vector field and let Ω = R 3. A first integral of V is a solution of the equation ϕ x = 0. Any function of y and z only is a solution of this equation. For example, ϕ 1 = y, ϕ 2 = z are two solutions which are functionally independent. The integral curves of V are described by the equations y = c 1, z = c 2, and are straight lines parallel to the x-axis. EXAMPLE 21. Let V = (y, x, 0) be a vector field and let Ω = R 3 \ z-axis. A first integral of V is a solution of the equation yϕ x xϕ y = 0. It is easy to verify that ϕ 1 (x, y, z) = x 2 + y 2, ϕ 2 (x, y, z) = z (20) are two functionally independent first integrals of V. Therefore, the integrals curves of V in Ω are given by x 2 + y 2 = c 1, z = c 2. (21) The above equations describe circles parallel to the (x, y)-plane and centered on the z-axis (see the second figure of Fig 1.1).
9 MODULE 1: MATHEMATICAL PRELIMINARIES 24 Practice Problems 3 1. Find a vector V (x, y, z) normal to the surface z = x 2 + y 2 + (x 2 + y 2 ) 3/2. 2. If f(x, y, z) is always parallel to the vector (x, y, z), show that f must assume equal values at the points (0, 0, a) and (0, 0, a). 3. Find F, where F (x, y, z) = z 2 x 2 y 2. Find the largest set in which grad F does not vanish? 4. Find a vector normal to the surface z 2 x 2 y 2 = 0 at the point (1, 0, 1). 5. If possible, solve the equation z 2 x 2 y 2 = 0 in terms of x, y near the following points: (a) (1, 1, 2); ; (b) (1, 1, 2) ; (c) (0, 0, 0). 6. Find the integral curves of the following vector fields: (a) V = (x, 0, z), (b) V = (x 2, y 3, 0), (c) V = (2, 3y 2, 0). 7. Let u(x, y, z) be a first integral of V and let C be an integral curve of V given by x = x(t), y = y(t), z = z(t); t I. Show that C must lie on some level surface of u. [Hint: Compute d dt {u(x(t), y(t), z(t))}]. 8. If V be the vector field given by V = (x, y, z) and let Ω be the octant x > 0, y > 0, z > 0. Show that u 1 (x, y, z) = y x and u 2(x, y, z) = z x are functionally independent first integrals of V in Ω
REVIEW I MATH 254 Calculus IV. Exam I (Friday, April 29) will cover sections
 REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
Mathematically, the path or the trajectory of a particle moving in space in described by a function of time.
 Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Module 15 : Vector fields, Gradient, Divergence and Curl Lecture 45 : Curves in space [Section 45.1] Objectives In this section you will learn the following : Concept of curve in space. Parametrization
Chapter 15 Vector Calculus
 Chapter 15 Vector Calculus 151 Vector Fields 152 Line Integrals 153 Fundamental Theorem and Independence of Path 153 Conservative Fields and Potential Functions 154 Green s Theorem 155 urface Integrals
Chapter 15 Vector Calculus 151 Vector Fields 152 Line Integrals 153 Fundamental Theorem and Independence of Path 153 Conservative Fields and Potential Functions 154 Green s Theorem 155 urface Integrals
Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers. Lagrange Multipliers
 In this section we present Lagrange s method for maximizing or minimizing a general function f(x, y, z) subject to a constraint (or side condition) of the form g(x, y, z) = k. Figure 1 shows this curve
In this section we present Lagrange s method for maximizing or minimizing a general function f(x, y, z) subject to a constraint (or side condition) of the form g(x, y, z) = k. Figure 1 shows this curve
Equation of tangent plane: for implicitly defined surfaces section 12.9
 Equation of tangent plane: for implicitly defined surfaces section 12.9 Some surfaces are defined implicitly, such as the sphere x 2 + y 2 + z 2 = 1. In general an implicitly defined surface has the equation
Equation of tangent plane: for implicitly defined surfaces section 12.9 Some surfaces are defined implicitly, such as the sphere x 2 + y 2 + z 2 = 1. In general an implicitly defined surface has the equation
while its direction is given by the right hand rule: point fingers of the right hand in a 1 a 2 a 3 b 1 b 2 b 3 A B = det i j k
 I.f Tangent Planes and Normal Lines Again we begin by: Recall: (1) Given two vectors A = a 1 i + a 2 j + a 3 k, B = b 1 i + b 2 j + b 3 k then A B is a vector perpendicular to both A and B. Then length
I.f Tangent Planes and Normal Lines Again we begin by: Recall: (1) Given two vectors A = a 1 i + a 2 j + a 3 k, B = b 1 i + b 2 j + b 3 k then A B is a vector perpendicular to both A and B. Then length
Directional Derivatives and the Gradient Vector Part 2
 Directional Derivatives and the Gradient Vector Part 2 Lecture 25 February 28, 2007 Recall Fact Recall Fact If f is a dierentiable function of x and y, then f has a directional derivative in the direction
Directional Derivatives and the Gradient Vector Part 2 Lecture 25 February 28, 2007 Recall Fact Recall Fact If f is a dierentiable function of x and y, then f has a directional derivative in the direction
Parametric Surfaces. Substitution
 Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Quasilinear First-Order PDEs
 MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 16 Lecture 3 Quasilinear First-Order PDEs A first order quasilinear PDE is of the form a(x, y, z) + b(x, y, z) x y = c(x, y, z). (1) Such equations
MODULE 2: FIRST-ORDER PARTIAL DIFFERENTIAL EQUATIONS 16 Lecture 3 Quasilinear First-Order PDEs A first order quasilinear PDE is of the form a(x, y, z) + b(x, y, z) x y = c(x, y, z). (1) Such equations
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Grad operator, triple and line integrals. Notice: this material must not be used as a substitute for attending the lectures
 Grad operator, triple and line integrals Notice: this material must not be used as a substitute for attending the lectures 1 .1 The grad operator Let f(x 1, x,..., x n ) be a function of the n variables
Grad operator, triple and line integrals Notice: this material must not be used as a substitute for attending the lectures 1 .1 The grad operator Let f(x 1, x,..., x n ) be a function of the n variables
Chapter 6 Some Applications of the Integral
 Chapter 6 Some Applications of the Integral More on Area More on Area Integrating the vertical separation gives Riemann Sums of the form More on Area Example Find the area A of the set shaded in Figure
Chapter 6 Some Applications of the Integral More on Area More on Area Integrating the vertical separation gives Riemann Sums of the form More on Area Example Find the area A of the set shaded in Figure
MA 243 Calculus III Fall Assignment 1. Reading assignments are found in James Stewart s Calculus (Early Transcendentals)
 MA 43 Calculus III Fall 8 Dr. E. Jacobs Assignments Reading assignments are found in James Stewart s Calculus (Early Transcendentals) Assignment. Spheres and Other Surfaces Read. -. and.6 Section./Problems
MA 43 Calculus III Fall 8 Dr. E. Jacobs Assignments Reading assignments are found in James Stewart s Calculus (Early Transcendentals) Assignment. Spheres and Other Surfaces Read. -. and.6 Section./Problems
Math Exam III Review
 Math 213 - Exam III Review Peter A. Perry University of Kentucky April 10, 2019 Homework Exam III is tonight at 5 PM Exam III will cover 15.1 15.3, 15.6 15.9, 16.1 16.2, and identifying conservative vector
Math 213 - Exam III Review Peter A. Perry University of Kentucky April 10, 2019 Homework Exam III is tonight at 5 PM Exam III will cover 15.1 15.3, 15.6 15.9, 16.1 16.2, and identifying conservative vector
First we consider how to parameterize a surface (similar to a parameterized curve for line integrals). Surfaces will need two parameters.
 Math 55 - Vector Calculus II Notes 14.6 urface Integrals Let s develop some surface integrals. First we consider how to parameterize a surface (similar to a parameterized curve for line integrals). urfaces
Math 55 - Vector Calculus II Notes 14.6 urface Integrals Let s develop some surface integrals. First we consider how to parameterize a surface (similar to a parameterized curve for line integrals). urfaces
Calculus III. Math 233 Spring In-term exam April 11th. Suggested solutions
 Calculus III Math Spring 7 In-term exam April th. Suggested solutions This exam contains sixteen problems numbered through 6. Problems 5 are multiple choice problems, which each count 5% of your total
Calculus III Math Spring 7 In-term exam April th. Suggested solutions This exam contains sixteen problems numbered through 6. Problems 5 are multiple choice problems, which each count 5% of your total
d f(g(t), h(t)) = x dt + f ( y dt = 0. Notice that we can rewrite the relationship on the left hand side of the equality using the dot product: ( f
 Gradients and the Directional Derivative In 14.3, we discussed the partial derivatives f f and, which tell us the rate of change of the x y height of the surface defined by f in the x direction and the
Gradients and the Directional Derivative In 14.3, we discussed the partial derivatives f f and, which tell us the rate of change of the x y height of the surface defined by f in the x direction and the
Math 213 Calculus III Practice Exam 2 Solutions Fall 2002
 Math 13 Calculus III Practice Exam Solutions Fall 00 1. Let g(x, y, z) = e (x+y) + z (x + y). (a) What is the instantaneous rate of change of g at the point (,, 1) in the direction of the origin? We want
Math 13 Calculus III Practice Exam Solutions Fall 00 1. Let g(x, y, z) = e (x+y) + z (x + y). (a) What is the instantaneous rate of change of g at the point (,, 1) in the direction of the origin? We want
What you will learn today
 What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
f xx (x, y) = 6 + 6x f xy (x, y) = 0 f yy (x, y) = y In general, the quantity that we re interested in is
 1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
Chapter 6. Curves and Surfaces. 6.1 Graphs as Surfaces
 Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Directional Derivatives and the Gradient Vector Part 2
 Directional Derivatives and the Gradient Vector Part 2 Marius Ionescu October 26, 2012 Marius Ionescu () Directional Derivatives and the Gradient Vector Part October 2 26, 2012 1 / 12 Recall Fact Marius
Directional Derivatives and the Gradient Vector Part 2 Marius Ionescu October 26, 2012 Marius Ionescu () Directional Derivatives and the Gradient Vector Part October 2 26, 2012 1 / 12 Recall Fact Marius
Math 5BI: Problem Set 2 The Chain Rule
 Math 5BI: Problem Set 2 The Chain Rule April 5, 2010 A Functions of two variables Suppose that γ(t) = (x(t), y(t), z(t)) is a differentiable parametrized curve in R 3 which lies on the surface S defined
Math 5BI: Problem Set 2 The Chain Rule April 5, 2010 A Functions of two variables Suppose that γ(t) = (x(t), y(t), z(t)) is a differentiable parametrized curve in R 3 which lies on the surface S defined
University of California, Berkeley
 University of California, Berkeley FINAL EXAMINATION, Fall 2012 DURATION: 3 hours Department of Mathematics MATH 53 Multivariable Calculus Examiner: Sean Fitzpatrick Total: 100 points Family Name: Given
University of California, Berkeley FINAL EXAMINATION, Fall 2012 DURATION: 3 hours Department of Mathematics MATH 53 Multivariable Calculus Examiner: Sean Fitzpatrick Total: 100 points Family Name: Given
f (Pijk ) V. may form the Riemann sum: . Definition. The triple integral of f over the rectangular box B is defined to f (x, y, z) dv = lim
 Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Chapter 14 Multiple Integrals..1 Double Integrals, Iterated Integrals, Cross-sections.2 Double Integrals over more general regions, Definition, Evaluation of Double Integrals, Properties of Double Integrals.3
Solution of final examination
 of final examination Math 20, pring 201 December 9, 201 Problem 1 Let v(t) (2t e t ) i j + π cos(πt) k be the velocity of a particle with initial position r(0) ( 1, 0, 2). Find the accelaration at the
of final examination Math 20, pring 201 December 9, 201 Problem 1 Let v(t) (2t e t ) i j + π cos(πt) k be the velocity of a particle with initial position r(0) ( 1, 0, 2). Find the accelaration at the
Volumes of Solids of Revolution Lecture #6 a
 Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
1 Double Integral. 1.1 Double Integral over Rectangular Domain
 Double Integral. Double Integral over Rectangular Domain As the definite integral of a positive function of one variable represents the area of the region between the graph and the x-asis, the double integral
Double Integral. Double Integral over Rectangular Domain As the definite integral of a positive function of one variable represents the area of the region between the graph and the x-asis, the double integral
MATH 234. Excercises on Integration in Several Variables. I. Double Integrals
 MATH 234 Excercises on Integration in everal Variables I. Double Integrals Problem 1. D = {(x, y) : y x 1, 0 y 1}. Compute D ex3 da. Problem 2. Find the volume of the solid bounded above by the plane 3x
MATH 234 Excercises on Integration in everal Variables I. Double Integrals Problem 1. D = {(x, y) : y x 1, 0 y 1}. Compute D ex3 da. Problem 2. Find the volume of the solid bounded above by the plane 3x
Kevin James. MTHSC 206 Section 14.5 The Chain Rule
 MTHSC 206 Section 14.5 The Chain Rule Theorem (Chain Rule - Case 1) Suppose that z = f (x, y) is a differentiable function and that x(t) and y(t) are both differentiable functions as well. Then, dz dt
MTHSC 206 Section 14.5 The Chain Rule Theorem (Chain Rule - Case 1) Suppose that z = f (x, y) is a differentiable function and that x(t) and y(t) are both differentiable functions as well. Then, dz dt
Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane
 Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane Rafikul Alam Department of Mathematics IIT Guwahati Chain rule Theorem-A: Let x : R R n be differentiable at t 0 and f : R n R be differentiable
Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane Rafikul Alam Department of Mathematics IIT Guwahati Chain rule Theorem-A: Let x : R R n be differentiable at t 0 and f : R n R be differentiable
Math 209, Fall 2009 Homework 3
 Math 209, Fall 2009 Homework 3 () Find equations of the tangent plane and the normal line to the given surface at the specified point: x 2 + 2y 2 3z 2 = 3, P (2,, ). Solution Using implicit differentiation
Math 209, Fall 2009 Homework 3 () Find equations of the tangent plane and the normal line to the given surface at the specified point: x 2 + 2y 2 3z 2 = 3, P (2,, ). Solution Using implicit differentiation
MATH 261 FALL 2000 FINAL EXAM INSTRUCTIONS. 1. This test booklet has 14 pages including this one. There are 25 questions, each worth 8 points.
 MATH 261 FALL 2 FINAL EXAM STUDENT NAME - STUDENT ID - RECITATION HOUR - RECITATION INSTRUCTOR INSTRUCTOR - INSTRUCTIONS 1. This test booklet has 14 pages including this one. There are 25 questions, each
MATH 261 FALL 2 FINAL EXAM STUDENT NAME - STUDENT ID - RECITATION HOUR - RECITATION INSTRUCTOR INSTRUCTOR - INSTRUCTIONS 1. This test booklet has 14 pages including this one. There are 25 questions, each
Practice problems. 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b.
 Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Directional Derivatives. Directional Derivatives. Directional Derivatives. Directional Derivatives. Directional Derivatives. Directional Derivatives
 Recall that if z = f(x, y), then the partial derivatives f x and f y are defined as and represent the rates of change of z in the x- and y-directions, that is, in the directions of the unit vectors i and
Recall that if z = f(x, y), then the partial derivatives f x and f y are defined as and represent the rates of change of z in the x- and y-directions, that is, in the directions of the unit vectors i and
Functions of Several Variables
 Functions of Several Variables Directional Derivatives and the Gradient Vector Philippe B Laval KSU April 7, 2012 Philippe B Laval (KSU) Functions of Several Variables April 7, 2012 1 / 19 Introduction
Functions of Several Variables Directional Derivatives and the Gradient Vector Philippe B Laval KSU April 7, 2012 Philippe B Laval (KSU) Functions of Several Variables April 7, 2012 1 / 19 Introduction
The directional derivative of f x, y in the direction of at x, y u. f x sa y sb f x y (, ) (, ) 0 0 y 0 0
 Review: 0, lim D f u 0 0 0 0 u The directional derivative of f, in the direction of at, is denoted b D f, : u a, b must a unit vector u f sa sb f s 0 (, ) (, ) s f (, ) a f (, ) b 0 0 0 0 0 0 D f, f u
Review: 0, lim D f u 0 0 0 0 u The directional derivative of f, in the direction of at, is denoted b D f, : u a, b must a unit vector u f sa sb f s 0 (, ) (, ) s f (, ) a f (, ) b 0 0 0 0 0 0 D f, f u
PURE MATHEMATICS 212 Multivariable Calculus CONTENTS. Page. 1. Assignment Summary... i 2. Summary Assignments...2
 PURE MATHEMATICS 212 Multivariable Calculus CONTENTS Page 1. Assignment Summary... i 2. Summary...1 3. Assignments...2 i PMTH212, Multivariable Calculus Assignment Summary 2010 Assignment Date to be Posted
PURE MATHEMATICS 212 Multivariable Calculus CONTENTS Page 1. Assignment Summary... i 2. Summary...1 3. Assignments...2 i PMTH212, Multivariable Calculus Assignment Summary 2010 Assignment Date to be Posted
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES (SOLUTIONS ) CHAPTER 3: Partial derivatives and differentiation
 UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES SOLUTIONS ) 3-1. Find, for the following functions: a) fx, y) x cos x sin y. b) fx, y) e xy. c) fx, y) x + y ) lnx + y ). CHAPTER 3: Partial derivatives
UNIVERSIDAD CARLOS III DE MADRID MATHEMATICS II EXERCISES SOLUTIONS ) 3-1. Find, for the following functions: a) fx, y) x cos x sin y. b) fx, y) e xy. c) fx, y) x + y ) lnx + y ). CHAPTER 3: Partial derivatives
Chapter 5 Partial Differentiation
 Chapter 5 Partial Differentiation For functions of one variable, y = f (x), the rate of change of the dependent variable can dy be found unambiguously by differentiation: f x. In this chapter we explore
Chapter 5 Partial Differentiation For functions of one variable, y = f (x), the rate of change of the dependent variable can dy be found unambiguously by differentiation: f x. In this chapter we explore
Topic 5.1: Line Elements and Scalar Line Integrals. Textbook: Section 16.2
 Topic 5.1: Line Elements and Scalar Line Integrals Textbook: Section 16.2 Warm-Up: Derivatives of Vector Functions Suppose r(t) = x(t) î + y(t) ĵ + z(t) ˆk parameterizes a curve C. The vector: is: r (t)
Topic 5.1: Line Elements and Scalar Line Integrals Textbook: Section 16.2 Warm-Up: Derivatives of Vector Functions Suppose r(t) = x(t) î + y(t) ĵ + z(t) ˆk parameterizes a curve C. The vector: is: r (t)
Polar (BC Only) They are necessary to find the derivative of a polar curve in x- and y-coordinates. The derivative
 Polar (BC Only) Polar coordinates are another way of expressing points in a plane. Instead of being centered at an origin and moving horizontally or vertically, polar coordinates are centered at the pole
Polar (BC Only) Polar coordinates are another way of expressing points in a plane. Instead of being centered at an origin and moving horizontally or vertically, polar coordinates are centered at the pole
Coordinate Transformations in Advanced Calculus
 Coordinate Transformations in Advanced Calculus by Sacha Nandlall T.A. for MATH 264, McGill University Email: sacha.nandlall@mail.mcgill.ca Website: http://www.resanova.com/teaching/calculus/ Fall 2006,
Coordinate Transformations in Advanced Calculus by Sacha Nandlall T.A. for MATH 264, McGill University Email: sacha.nandlall@mail.mcgill.ca Website: http://www.resanova.com/teaching/calculus/ Fall 2006,
Curves, Tangent Planes, and Differentials ( ) Feb. 26, 2012 (Sun) Lecture 9. Partial Derivatives: Signs on Level Curves, Tangent
 Lecture 9. Partial Derivatives: Signs on Level Curves, Tangent Planes, and Differentials ( 11.3-11.4) Feb. 26, 2012 (Sun) Signs of Partial Derivatives on Level Curves Level curves are shown for a function
Lecture 9. Partial Derivatives: Signs on Level Curves, Tangent Planes, and Differentials ( 11.3-11.4) Feb. 26, 2012 (Sun) Signs of Partial Derivatives on Level Curves Level curves are shown for a function
MAC2313 Final A. a. The vector r u r v lies in the tangent plane of S at a given point. b. S f(x, y, z) ds = R f(r(u, v)) r u r v du dv.
 MAC2313 Final A (5 pts) 1. Let f(x, y, z) be a function continuous in R 3 and let S be a surface parameterized by r(u, v) with the domain of the parameterization given by R; how many of the following are
MAC2313 Final A (5 pts) 1. Let f(x, y, z) be a function continuous in R 3 and let S be a surface parameterized by r(u, v) with the domain of the parameterization given by R; how many of the following are
= w. w u. u ; u + w. x x. z z. y y. v + w. . Remark. The formula stated above is very important in the theory of. surface integral.
 1 Chain rules 2 Directional derivative 3 Gradient Vector Field 4 Most Rapid Increase 5 Implicit Function Theorem, Implicit Differentiation 6 Lagrange Multiplier 7 Second Derivative Test Theorem Suppose
1 Chain rules 2 Directional derivative 3 Gradient Vector Field 4 Most Rapid Increase 5 Implicit Function Theorem, Implicit Differentiation 6 Lagrange Multiplier 7 Second Derivative Test Theorem Suppose
Practice problems from old exams for math 233 William H. Meeks III December 21, 2009
 Practice problems from old exams for math 233 William H. Meeks III December 21, 2009 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III December 21, 2009 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
MAT175 Overview and Sample Problems
 MAT175 Overview and Sample Problems The course begins with a quick review/overview of one-variable integration including the Fundamental Theorem of Calculus, u-substitutions, integration by parts, and
MAT175 Overview and Sample Problems The course begins with a quick review/overview of one-variable integration including the Fundamental Theorem of Calculus, u-substitutions, integration by parts, and
Exam 2 Preparation Math 2080 (Spring 2011) Exam 2: Thursday, May 12.
 Multivariable Calculus Exam 2 Preparation Math 28 (Spring 2) Exam 2: Thursday, May 2. Friday May, is a day off! Instructions: () There are points on the exam and an extra credit problem worth an additional
Multivariable Calculus Exam 2 Preparation Math 28 (Spring 2) Exam 2: Thursday, May 2. Friday May, is a day off! Instructions: () There are points on the exam and an extra credit problem worth an additional
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Calculus III-Final review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the corresponding position vector. 1) Define the points P = (-,
Calculus III-Final review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the corresponding position vector. 1) Define the points P = (-,
MATH 2023 Multivariable Calculus
 MATH 2023 Multivariable Calculus Problem Sets Note: Problems with asterisks represent supplementary informations. You may want to read their solutions if you like, but you don t need to work on them. Set
MATH 2023 Multivariable Calculus Problem Sets Note: Problems with asterisks represent supplementary informations. You may want to read their solutions if you like, but you don t need to work on them. Set
Directional Derivatives as Vectors
 Directional Derivatives as Vectors John Ganci 1 Al Lehnen 2 1 Richland College Dallas, TX jganci@dcccd.edu 2 Madison Area Technical College Madison, WI alehnen@matcmadison.edu Statement of problem We are
Directional Derivatives as Vectors John Ganci 1 Al Lehnen 2 1 Richland College Dallas, TX jganci@dcccd.edu 2 Madison Area Technical College Madison, WI alehnen@matcmadison.edu Statement of problem We are
PURE MATHEMATICS 212 Multivariable Calculus CONTENTS. Page. 1. Assignment Summary... i 2. Introduction Timetable Assignments...
 PURE MATHEMATICS 212 Multivariable Calculus CONTENTS Page 1. Assignment Summary... i 2. Introduction...1 3. Timetable... 3 4. Assignments...5 i PMTH212, Multivariable Calculus Assignment Summary 2009
PURE MATHEMATICS 212 Multivariable Calculus CONTENTS Page 1. Assignment Summary... i 2. Introduction...1 3. Timetable... 3 4. Assignments...5 i PMTH212, Multivariable Calculus Assignment Summary 2009
Lecture 11 Differentiable Parametric Curves
 Lecture 11 Differentiable Parametric Curves 11.1 Definitions and Examples. 11.1.1 Definition. A differentiable parametric curve in R n of class C k (k 1) is a C k map t α(t) = (α 1 (t),..., α n (t)) of
Lecture 11 Differentiable Parametric Curves 11.1 Definitions and Examples. 11.1.1 Definition. A differentiable parametric curve in R n of class C k (k 1) is a C k map t α(t) = (α 1 (t),..., α n (t)) of
13.1. Functions of Several Variables. Introduction to Functions of Several Variables. Functions of Several Variables. Objectives. Example 1 Solution
 13 Functions of Several Variables 13.1 Introduction to Functions of Several Variables Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Objectives Understand
13 Functions of Several Variables 13.1 Introduction to Functions of Several Variables Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Objectives Understand
Multiple Integrals. max x i 0
 Multiple Integrals 1 Double Integrals Definite integrals appear when one solves Area problem. Find the area A of the region bounded above by the curve y = f(x), below by the x-axis, and on the sides by
Multiple Integrals 1 Double Integrals Definite integrals appear when one solves Area problem. Find the area A of the region bounded above by the curve y = f(x), below by the x-axis, and on the sides by
The Divergence Theorem
 The Divergence Theorem MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Summer 2011 Green s Theorem Revisited Green s Theorem: M(x, y) dx + N(x, y) dy = C R ( N x M ) da y y x Green
The Divergence Theorem MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Summer 2011 Green s Theorem Revisited Green s Theorem: M(x, y) dx + N(x, y) dy = C R ( N x M ) da y y x Green
Let and be a differentiable function. Let Then be the level surface given by
 Module 12 : Total differential, Tangent planes and normals Lecture 35 : Tangent plane and normal [Section 35.1] > Objectives In this section you will learn the following : The notion tangent plane to a
Module 12 : Total differential, Tangent planes and normals Lecture 35 : Tangent plane and normal [Section 35.1] > Objectives In this section you will learn the following : The notion tangent plane to a
16.6. Parametric Surfaces. Parametric Surfaces. Parametric Surfaces. Vector Calculus. Parametric Surfaces and Their Areas
 16 Vector Calculus 16.6 and Their Areas Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and Their Areas Here we use vector functions to describe more general
16 Vector Calculus 16.6 and Their Areas Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and Their Areas Here we use vector functions to describe more general
Review 1. Richard Koch. April 23, 2005
 Review Richard Koch April 3, 5 Curves From the chapter on curves, you should know. the formula for arc length in section.;. the definition of T (s), κ(s), N(s), B(s) in section.4. 3. the fact that κ =
Review Richard Koch April 3, 5 Curves From the chapter on curves, you should know. the formula for arc length in section.;. the definition of T (s), κ(s), N(s), B(s) in section.4. 3. the fact that κ =
1 Vector Functions and Space Curves
 ontents 1 Vector Functions and pace urves 2 1.1 Limits, Derivatives, and Integrals of Vector Functions...................... 2 1.2 Arc Length and urvature..................................... 2 1.3 Motion
ontents 1 Vector Functions and pace urves 2 1.1 Limits, Derivatives, and Integrals of Vector Functions...................... 2 1.2 Arc Length and urvature..................................... 2 1.3 Motion
27. Tangent Planes & Approximations
 27. Tangent Planes & Approximations If z = f(x, y) is a differentiable surface in R 3 and (x 0, y 0, z 0 ) is a point on this surface, then it is possible to construct a plane passing through this point,
27. Tangent Planes & Approximations If z = f(x, y) is a differentiable surface in R 3 and (x 0, y 0, z 0 ) is a point on this surface, then it is possible to construct a plane passing through this point,
18.02 Final Exam. y = 0
 No books, notes or calculators. 5 problems, 50 points. 8.0 Final Exam Useful formula: cos (θ) = ( + cos(θ)) Problem. (0 points) a) (5 pts.) Find the equation in the form Ax + By + z = D of the plane P
No books, notes or calculators. 5 problems, 50 points. 8.0 Final Exam Useful formula: cos (θ) = ( + cos(θ)) Problem. (0 points) a) (5 pts.) Find the equation in the form Ax + By + z = D of the plane P
First of all, we need to know what it means for a parameterize curve to be differentiable. FACT:
 CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
Lagrange multipliers October 2013
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
Definition 3.1 The partial derivatives of a function f(x, y) defined on an open domain containing (x, y) are denoted by f
 Chapter 3 Draft October 3, 009 3. Partial Derivatives Overview: Partial derivatives are defined by differentiation in one variable, viewing all others as constant (frozen at some value). The reduction
Chapter 3 Draft October 3, 009 3. Partial Derivatives Overview: Partial derivatives are defined by differentiation in one variable, viewing all others as constant (frozen at some value). The reduction
MAT203 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS
 MAT203 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT203 covers essentially the same material as MAT201, but is more in depth and theoretical. Exam problems are often more sophisticated in scope and difficulty
MAT203 OVERVIEW OF CONTENTS AND SAMPLE PROBLEMS MAT203 covers essentially the same material as MAT201, but is more in depth and theoretical. Exam problems are often more sophisticated in scope and difficulty
14.6 Directional Derivatives and the Gradient Vector
 14 Partial Derivatives 14.6 and the Gradient Vector Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and the Gradient Vector In this section we introduce
14 Partial Derivatives 14.6 and the Gradient Vector Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. and the Gradient Vector In this section we introduce
Topic 5-6: Parameterizing Surfaces and the Surface Elements ds and ds. Big Ideas. What We Are Doing Today... Notes. Notes. Notes
 Topic 5-6: Parameterizing Surfaces and the Surface Elements ds and ds. Textbook: Section 16.6 Big Ideas A surface in R 3 is a 2-dimensional object in 3-space. Surfaces can be described using two variables.
Topic 5-6: Parameterizing Surfaces and the Surface Elements ds and ds. Textbook: Section 16.6 Big Ideas A surface in R 3 is a 2-dimensional object in 3-space. Surfaces can be described using two variables.
Kevin James. MTHSC 206 Section 15.6 Directional Derivatives and the Gra
 MTHSC 206 Section 15.6 Directional Derivatives and the Gradient Vector Definition We define the directional derivative of the function f (x, y) at the point (x 0, y 0 ) in the direction of the unit vector
MTHSC 206 Section 15.6 Directional Derivatives and the Gradient Vector Definition We define the directional derivative of the function f (x, y) at the point (x 0, y 0 ) in the direction of the unit vector
Name: Class: Date: 1. Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint.
 . Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint. f (x, y) = x y, x + y = 8. Set up the triple integral of an arbitrary continuous function
. Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint. f (x, y) = x y, x + y = 8. Set up the triple integral of an arbitrary continuous function
Workbook. MAT 397: Calculus III
 Workbook MAT 397: Calculus III Instructor: Caleb McWhorter Name: Summer 2017 Contents Preface..................................................... 2 1 Spatial Geometry & Vectors 3 1.1 Basic n Euclidean
Workbook MAT 397: Calculus III Instructor: Caleb McWhorter Name: Summer 2017 Contents Preface..................................................... 2 1 Spatial Geometry & Vectors 3 1.1 Basic n Euclidean
Functions of Two variables.
 Functions of Two variables. Ferdinánd Filip filip.ferdinand@bgk.uni-obuda.hu siva.banki.hu/jegyzetek 27 February 217 Ferdinánd Filip 27 February 217 Functions of Two variables. 1 / 36 Table of contents
Functions of Two variables. Ferdinánd Filip filip.ferdinand@bgk.uni-obuda.hu siva.banki.hu/jegyzetek 27 February 217 Ferdinánd Filip 27 February 217 Functions of Two variables. 1 / 36 Table of contents
Appendix E Calculating Normal Vectors
 OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use
OpenGL Programming Guide (Addison-Wesley Publishing Company) Appendix E Calculating Normal Vectors This appendix describes how to calculate normal vectors for surfaces. You need to define normals to use
Let be a function. We say, is a plane curve given by the. Let a curve be given by function where is differentiable with continuous.
 Module 8 : Applications of Integration - II Lecture 22 : Arc Length of a Plane Curve [Section 221] Objectives In this section you will learn the following : How to find the length of a plane curve 221
Module 8 : Applications of Integration - II Lecture 22 : Arc Length of a Plane Curve [Section 221] Objectives In this section you will learn the following : How to find the length of a plane curve 221
Math 11 Fall 2016 Section 1 Monday, October 17, 2016
 Math 11 Fall 16 Section 1 Monday, October 17, 16 First, some important points from the last class: f(x, y, z) dv, the integral (with respect to volume) of f over the three-dimensional region, is a triple
Math 11 Fall 16 Section 1 Monday, October 17, 16 First, some important points from the last class: f(x, y, z) dv, the integral (with respect to volume) of f over the three-dimensional region, is a triple
Lagrange multipliers 14.8
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
This exam will be cumulative. Consult the review sheets for the midterms for reviews of Chapters
 Final exam review Math 265 Fall 2007 This exam will be cumulative. onsult the review sheets for the midterms for reviews of hapters 12 15. 16.1. Vector Fields. A vector field on R 2 is a function F from
Final exam review Math 265 Fall 2007 This exam will be cumulative. onsult the review sheets for the midterms for reviews of hapters 12 15. 16.1. Vector Fields. A vector field on R 2 is a function F from
Math 126 Final Examination Autumn CHECK that your exam contains 9 problems on 10 pages.
 Math 126 Final Examination Autumn 2016 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name CHECK that your exam contains 9 problems on 10 pages. This exam is closed book. You
Math 126 Final Examination Autumn 2016 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name CHECK that your exam contains 9 problems on 10 pages. This exam is closed book. You
6. Find the equation of the plane that passes through the point (-1,2,1) and contains the line x = y = z.
 Week 1 Worksheet Sections from Thomas 13 th edition: 12.4, 12.5, 12.6, 13.1 1. A plane is a set of points that satisfies an equation of the form c 1 x + c 2 y + c 3 z = c 4. (a) Find any three distinct
Week 1 Worksheet Sections from Thomas 13 th edition: 12.4, 12.5, 12.6, 13.1 1. A plane is a set of points that satisfies an equation of the form c 1 x + c 2 y + c 3 z = c 4. (a) Find any three distinct
A1:Orthogonal Coordinate Systems
 A1:Orthogonal Coordinate Systems A1.1 General Change of Variables Suppose that we express x and y as a function of two other variables u and by the equations We say that these equations are defining a
A1:Orthogonal Coordinate Systems A1.1 General Change of Variables Suppose that we express x and y as a function of two other variables u and by the equations We say that these equations are defining a
Continuity and Tangent Lines for functions of two variables
 Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
Multivariate Calculus Review Problems for Examination Two
 Multivariate Calculus Review Problems for Examination Two Note: Exam Two is on Thursday, February 28, class time. The coverage is multivariate differential calculus and double integration: sections 13.3,
Multivariate Calculus Review Problems for Examination Two Note: Exam Two is on Thursday, February 28, class time. The coverage is multivariate differential calculus and double integration: sections 13.3,
Tangent Planes and Linear Approximations
 February 21, 2007 Tangent Planes Tangent Planes Let S be a surface with equation z = f (x, y). Tangent Planes Let S be a surface with equation z = f (x, y). Let P(x 0, y 0, z 0 ) be a point on S. Tangent
February 21, 2007 Tangent Planes Tangent Planes Let S be a surface with equation z = f (x, y). Tangent Planes Let S be a surface with equation z = f (x, y). Let P(x 0, y 0, z 0 ) be a point on S. Tangent
True/False. MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY
 MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY True/False 10 points: points each) For the problems below, circle T if the answer is true and circle F is the answer is false. After you ve chosen
MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY True/False 10 points: points each) For the problems below, circle T if the answer is true and circle F is the answer is false. After you ve chosen
t dt ds Then, in the last class, we showed that F(s) = <2s/3, 1 2s/3, s/3> is arclength parametrization. Therefore,
 13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
MATH 2400: CALCULUS 3 MAY 9, 2007 FINAL EXAM
 MATH 4: CALCULUS 3 MAY 9, 7 FINAL EXAM I have neither given nor received aid on this exam. Name: 1 E. Kim................ (9am) E. Angel.............(1am) 3 I. Mishev............ (11am) 4 M. Daniel...........
MATH 4: CALCULUS 3 MAY 9, 7 FINAL EXAM I have neither given nor received aid on this exam. Name: 1 E. Kim................ (9am) E. Angel.............(1am) 3 I. Mishev............ (11am) 4 M. Daniel...........
Week 5: Geometry and Applications
 Week 5: Geometry and Applications Introduction Now that we have some tools from differentiation, we can study geometry, motion, and few other issues associated with functions of several variables. Much
Week 5: Geometry and Applications Introduction Now that we have some tools from differentiation, we can study geometry, motion, and few other issues associated with functions of several variables. Much
Direction Fields; Euler s Method
 Direction Fields; Euler s Method It frequently happens that we cannot solve first order systems dy (, ) dx = f xy or corresponding initial value problems in terms of formulas. Remarkably, however, this
Direction Fields; Euler s Method It frequently happens that we cannot solve first order systems dy (, ) dx = f xy or corresponding initial value problems in terms of formulas. Remarkably, however, this
Math 348 Differential Geometry of Curves and Surfaces
 Math 348 Differential Geometry of Curves and Surfaces Lecture 3 Curves in Calculus Xinwei Yu Sept. 12, 2017 CAB 527, xinwei2@ualberta.ca Department of Mathematical & Statistical Sciences University of
Math 348 Differential Geometry of Curves and Surfaces Lecture 3 Curves in Calculus Xinwei Yu Sept. 12, 2017 CAB 527, xinwei2@ualberta.ca Department of Mathematical & Statistical Sciences University of
Triple Integrals in Rectangular Coordinates
 Triple Integrals in Rectangular Coordinates P. Sam Johnson April 10, 2017 P. Sam Johnson (NIT Karnataka) Triple Integrals in Rectangular Coordinates April 10, 2017 1 / 28 Overview We use triple integrals
Triple Integrals in Rectangular Coordinates P. Sam Johnson April 10, 2017 P. Sam Johnson (NIT Karnataka) Triple Integrals in Rectangular Coordinates April 10, 2017 1 / 28 Overview We use triple integrals
INTRODUCTION TO LINE INTEGRALS
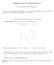 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
38. Triple Integration over Rectangular Regions
 8. Triple Integration over Rectangular Regions A rectangular solid region S in R can be defined by three compound inequalities, a 1 x a, b 1 y b, c 1 z c, where a 1, a, b 1, b, c 1 and c are constants.
8. Triple Integration over Rectangular Regions A rectangular solid region S in R can be defined by three compound inequalities, a 1 x a, b 1 y b, c 1 z c, where a 1, a, b 1, b, c 1 and c are constants.
1. Suppose that the equation F (x, y, z) = 0 implicitly defines each of the three variables x, y, and z as functions of the other two:
 Final Solutions. Suppose that the equation F (x, y, z) implicitly defines each of the three variables x, y, and z as functions of the other two: z f(x, y), y g(x, z), x h(y, z). If F is differentiable
Final Solutions. Suppose that the equation F (x, y, z) implicitly defines each of the three variables x, y, and z as functions of the other two: z f(x, y), y g(x, z), x h(y, z). If F is differentiable
MATH 116 REVIEW PROBLEMS for the FINAL EXAM
 MATH 116 REVIEW PROBLEMS for the FINAL EXAM The following questions are taken from old final exams of various calculus courses taught in Bilkent University 1. onsider the line integral (2xy 2 z + y)dx
MATH 116 REVIEW PROBLEMS for the FINAL EXAM The following questions are taken from old final exams of various calculus courses taught in Bilkent University 1. onsider the line integral (2xy 2 z + y)dx
Math 253, Section 102, Fall 2006 Practice Final Solutions
 Math 253, Section 102, Fall 2006 Practice Final Solutions 1 2 1. Determine whether the two lines L 1 and L 2 described below intersect. If yes, find the point of intersection. If not, say whether they
Math 253, Section 102, Fall 2006 Practice Final Solutions 1 2 1. Determine whether the two lines L 1 and L 2 described below intersect. If yes, find the point of intersection. If not, say whether they
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates
 COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
COMP30019 Graphics and Interaction Transformation geometry and homogeneous coordinates Department of Computer Science and Software Engineering The Lecture outline Introduction Vectors and matrices Translation
MA 174: Multivariable Calculus Final EXAM (practice) NO CALCULATORS, BOOKS, OR PAPERS ARE ALLOWED. Use the back of the test pages for scrap paper.
 MA 174: Multivariable alculus Final EXAM (practice) NAME lass Meeting Time: NO ALULATOR, BOOK, OR PAPER ARE ALLOWED. Use the back of the test pages for scrap paper. Points awarded 1. (5 pts). (5 pts).
MA 174: Multivariable alculus Final EXAM (practice) NAME lass Meeting Time: NO ALULATOR, BOOK, OR PAPER ARE ALLOWED. Use the back of the test pages for scrap paper. Points awarded 1. (5 pts). (5 pts).
Dr. Allen Back. Nov. 21, 2014
 Dr. Allen Back of Nov. 21, 2014 The most important thing you should know (e.g. for exams and homework) is how to setup (and perhaps compute if not too hard) surface integrals, triple integrals, etc. But
Dr. Allen Back of Nov. 21, 2014 The most important thing you should know (e.g. for exams and homework) is how to setup (and perhaps compute if not too hard) surface integrals, triple integrals, etc. But
