THE PLATONIC SOLIDS BOOK DAN RADIN
|
|
|
- Ezra Taylor
- 6 years ago
- Views:
Transcription
1 THE PLATONIC SOLIDS BOOK DAN RADIN
2 Copyright 2008 by Daniel R. Radin All rights reserved. Published by CreateSpace Publishing 3-D renderings were created on a thirteen-year-old Macintosh computer using Infini-D software.
3 for my daughter Chelsea
4
5 TABLE OF CONTENTS Introduction... 1 Chapter 1 How to Make a Platonic Solid... 3 Chapter 2 Dual Pairs Chapter 3 Paper Polyhedra Chapter 4 Origami Chapter 5 Proof?! Appendix Lesson Plans... 83
6
7 1 INTRODUCTION The Platonic solids are the five most symmetric examples of polyhedra. The word, polyhedra is the plural form of the word, polyhedron. I once read that the direct translation of the Greek word, polyhedron, is many seats. Apparently, hedron means seat and a cathedral is a place where people sit. Today, mathematicians generally translate it as a solid having many flat faces. But I can see how seats could work too. Maybe you can sit on them in many ways, or they contain many surfaces upon which they can sit. By most symmetric, I mean that there are many ways that you can turn them around and have them still appear the same from different angles. I also mean that they look the same if you view them in a mirror. The Platonic solids get their name from the Greek philosopher, Plato, who wrote about them. They were, in fact, known long before Plato by many different cultures. Plato wrote about them in his book Timaeus. This work was a mixture of philosophy, science, mathematics, and theology, which is not surprising since, at that time, the four fields were all considered part of the same whole. In Timaeus, Plato came up with an early version of atomic chemistry where all of matter was made up of combinations of these five shapes at a microscopic scale, and where it was these shapes that gave matter its properties. It is not surprising that Plato believed that the gods had chosen these five most perfect forms from which to make all others. I know that I find them somehow intrinsically attractive, fascinating, and magical. I hope that you too will appreciate them as you read through this book and look at all of the beautiful images.
8 2
9 3 CHAPTER 1 HOW TO MAKE A PLATONIC SOLID All five Platonic solids are made from three different regular polygons: the equilateral triangle, the square, and the regular pentagon. To be a Platonic solid, all of the polygon faces must be identical and the same number of faces must meet together at each vertex. Vertex is the word mathematicians use for the corners or points. The plural of vertex is vertices. The remainder of this chapter is devoted to instructions for making each of the five Platonic solids. After you finish reading it, you may want to skip to chapter three and start building your own models. Or, you may decide to just read on and enjoy the pretty pictures. The Tetrahedron The most basic Platonic solid is called the tetrahedron. The word tetra is Greek for four. The tetrahedron has four triangular faces. To make a tetrahedron, place three equilateral triangles point-to-point on a flat plane.
10 4 HOW TO MAKE A PLATONIC SOLID With the center points still on the plane, swing the triangles up out of the plane.
11 HOW TO MAKE A PLATONIC SOLID 5 Place a fourth equilateral triangle on the top. In a certain way, the tetrahedron is the most symmetric of the Platonic solids. Notice that each of its faces has three sides and that three faces meet at each vertex. The tetrahedron is the only Platonic solid with this dual nature between the number of
12 6 HOW TO MAKE A PLATONIC SOLID sides on each face and the number of faces meeting at each vertex. You will see, in chapter two, that this feature of the tetrahedron has a very special consequence. The Octahedron The next triangle-based Platonic solid is called the octahedron. The word octa is Greek for eight. The octahedron consists of eight equilateral triangle faces. To make an octahedron, place four equilateral triangles point-to-point on a flat plane. With the center points still on the plane, swing the triangles up out of the plane.
13 HOW TO MAKE A PLATONIC SOLID 7 Start the whole process over again with four more triangles on the plane point-topoint. Swing the new triangles up out of the plane. Place the second set of four triangles on top of the first set.
14 8 HOW TO MAKE A PLATONIC SOLID This is the octahedron, the second triangle-based Platonic solid. The Icosahedron The last triangle-based Platonic solid is called the icosahedron. The word icosa is Greek for twenty. The icosahedron consists of twenty equilateral triangle faces. To make an icosahedron, place five equilateral triangles point-to-point on a flat plane.
15 HOW TO MAKE A PLATONIC SOLID 9 With the center points still on the plane, swing the triangles up out of the plane.
16 10 HOW TO MAKE A PLATONIC SOLID Now place five more triangles around the rim. Now start the whole process over again with five more triangles on the plane pointto-point. Swing the new triangles up out of the plane, and place five more triangles around the rim.
17 HOW TO MAKE A PLATONIC SOLID 11 Place the second set of ten triangles on top of the first set. This is the icosahedron, the last of the triangle-based Platonic solids. This shape is the basis for most geodesic domes. The reason why there are no other triangle-based Platonic solids is that, when you place six equilateral triangles together on the plane point-to-point, they are already touching, and so you can t swing them up out of the plane.
18 12 HOW TO MAKE A PLATONIC SOLID So the only ways that equilateral triangles can meet at the vertices of a platonic solid are in sets of three (the tetrahedron), four (the octahedron), or five (the icosahedron). The Cube I am sure you are familiar with the Platonic solid that is made from squares. It is the familiar cube. It is also known as the hexahedron since hexa is Greek for six, and the cube has six faces. To make a cube, place three squares point-to-point on a flat plane.
19 HOW TO MAKE A PLATONIC SOLID 13 With the center points still on the plane, swing the squares up out of the plane.
20 14 HOW TO MAKE A PLATONIC SOLID Start the whole process over again with three more squares on the plane point-topoint. Swing the new squares up out of the plane. Place the second set of three squares on top of the first set.
21 HOW TO MAKE A PLATONIC SOLID 15 This is the cube or hexahedron, the only square-based Platonic solid. Perhaps you do not think the cube fits in with the other Platonic solids. It may seem too ordinary and perhaps not crystalline. Actually, there are several cube-shaped crystals. You will learn in the chapter on dual pairs that the cube fits in perfectly with the other Platonic solids. The reason why there are no other square-based Platonic solids is that, when you place four squares together on the plane point-to-point, they are already touching, and so you can t swing them up out of the plane.
22 16 HOW TO MAKE A PLATONIC SOLID So the only way that squares can meet at the vertices of a platonic solid is in sets of three. The Dodecahedron The fifth and last Platonic solid is the dodecahedron. The word dodeca is Greek for twelve. The dodecahedron has twelve pentagon faces. To make a dodecahedron, place three pentagons point-to-point on a flat plane.
23 HOW TO MAKE A PLATONIC SOLID 17 With the center points still on the plane, swing the pentagons up out of the plane.
24 18 HOW TO MAKE A PLATONIC SOLID Place three more pentagons around the rim. Start the whole process over again with three more pentagons on the plane point-topoint. Swing the new pentagons up out of the plane and place three more pentagons around the rim.
25 HOW TO MAKE A PLATONIC SOLID 19 Place the second set of six pentagons on top of the first set. The dodecahedron is the basis of the pattern used for most soccer balls and volley balls. The reason why there are no other pentagon-based Platonic solids is that you can t place more than three pentagons together on the plane point-to-point. They won t fit together.
26 20 HOW TO MAKE A PLATONIC SOLID So the only way that pentagons can meet at the vertices of a Platonic solid is in sets of three. Three hexagons fit together on the plane point-to-point with no room left to swing up.
27 HOW TO MAKE A PLATONIC SOLID 21 Three heptagons (seven-sided polygons) won t fit together on the plane point-topoint. So the dodecahedron is the last of the Platonic solids. For some strange (some might say magical) reason, there are exactly five solids consisting of regular polygons, all of the same type, all fitting together in the same way. These are Plato s five sacred solids. Questions to Ponder How could the preceding constructions be taught starting each solid with one regular polygon on the plane surrounded by other polygons placed together edge-to-edge? Why is it that, no matter what type and number of identical regular polygons you start with, if they can swing up out of the plane, they always fit together perfectly to complete a closed polyhedron? Why do crystals naturally form in the shapes of Platonic solids?
28 22 HOW TO MAKE A PLATONIC SOLID Why are people attracted to these forms even when they do not know about the mathematics behind them? How is it that our convention of there being 360 degrees in a full circle results in the fact that the first several regular polygons have integer degree measures in their angles, and how do these angles relate to the fact that there are exactly five Platonic solids? Given the number and type of polygons originally placed point-to-point on the plane, is there a way to calculate the total number of faces that will be in the completed Platonic solid? Is there a way to calculate the dihedral angle (the angle between two faces of the completed Platonic solid)? If one or more of the restrictions on Platonic solids is selectively removed or changed, what other classes of solids result?
29 23 CHAPTER 2 DUAL PAIRS The Cube-Octa Pair While the cube may not, at first, seem like a Platonic solid, it turns out that there is an octahedron hidden inside of every cube. If you connect the centers of the six faces of a cube, you will discover that they correspond to the six vertices of an octahedron in the interior of the cube. This relationship has to do with the numbers three, four, six, eight, and twelve. The cube has three faces meeting at each vertex, four sides to each face, six faces in all, and eight vertices in all. The octahedron has three sides to each face, four faces meeting at each vertex, six vertices in all, and eight faces in all. In this way, the faces of the cube are analogous to the vertices of the octahedron. Notice also, that they
30 24 LESSON PLANS both have exactly twelve edges. The cube and the octahedron are a numerically bound pair. cube octahedron 3 faces meet at each vertex 4 faces meet at each vertex 4 sides on each face 3 sides on each face 6 faces in all 8 faces in all 8 vertices in all 6 vertices in all 12 edges in all 12 edges in all If you connect the centers of the eight faces of an octahedron, you will discover that they correspond to the eight vertices of a cube in the interior of the octahedron. If you superimpose a cube with an octahedron of the same size, you get a beautiful compound solid.
31 LESSON PLANS 25 Notice that each square face has a square-based pyramid protruding from it, and that each triangle face has a triangle-based pyramid protruding from it. You can use the patterns in chapter three to build your own paper models of this and other compound solids. The Dodeca-Icosa Pair If you connect the centers of the twelve faces of a dodecahedron, you will discover that they correspond to the twelve vertices of an icosahedron in the interior of the dodecahedron. To keep reading, purchase your own copy of The Platonic Solids Book at
REGULAR TILINGS. Hints: There are only three regular tilings.
 REGULAR TILINGS Description: A regular tiling is a tiling of the plane consisting of multiple copies of a single regular polygon, meeting edge to edge. How many can you construct? Comments: While these
REGULAR TILINGS Description: A regular tiling is a tiling of the plane consisting of multiple copies of a single regular polygon, meeting edge to edge. How many can you construct? Comments: While these
A Physical Proof for Five and Only Five Regular Solids
 A Physical Proof for Five and Only Five Regular Solids Robert McDermott Center for High Performance Computing University of Utah Salt Lake City, Utah, 84112, USA E-mail: mcdermott@chpc.utah.edu Abstract
A Physical Proof for Five and Only Five Regular Solids Robert McDermott Center for High Performance Computing University of Utah Salt Lake City, Utah, 84112, USA E-mail: mcdermott@chpc.utah.edu Abstract
Mathematics As A Liberal Art
 Math 105 Fall 2015 BY: 2015 Ron Buckmire Mathematics As A Liberal Art Class 26: Friday November 13 Fowler 302 MWF 10:40am- 11:35am http://sites.oxy.edu/ron/math/105/15/ Euclid, Geometry and the Platonic
Math 105 Fall 2015 BY: 2015 Ron Buckmire Mathematics As A Liberal Art Class 26: Friday November 13 Fowler 302 MWF 10:40am- 11:35am http://sites.oxy.edu/ron/math/105/15/ Euclid, Geometry and the Platonic
3.D. The Platonic solids
 3.D. The Platonic solids The purpose of this addendum to the course notes is to provide more information about regular solid figures, which played an important role in Greek mathematics and philosophy.
3.D. The Platonic solids The purpose of this addendum to the course notes is to provide more information about regular solid figures, which played an important role in Greek mathematics and philosophy.
Polyhedra. Kavitha d/o Krishnan
 Polyhedra Kavitha d/o Krishnan Supervisor: Associate Professor Helmer Aslaksen Department of Mathematics National University of Singapore Semester I 2001/2002 Abstract Introduction The report focuses on
Polyhedra Kavitha d/o Krishnan Supervisor: Associate Professor Helmer Aslaksen Department of Mathematics National University of Singapore Semester I 2001/2002 Abstract Introduction The report focuses on
Lesson/Unit Plan Name: Platonic Solids Using geometric nets to explore Platonic solids and discovering Euler s formula.
 Grade Level/Course: Grade 6 Lesson/Unit Plan Name: Platonic Solids Using geometric nets to explore Platonic solids and discovering Euler s formula. Rationale/Lesson Abstract: An activity where the students
Grade Level/Course: Grade 6 Lesson/Unit Plan Name: Platonic Solids Using geometric nets to explore Platonic solids and discovering Euler s formula. Rationale/Lesson Abstract: An activity where the students
Platonic Polyhedra and How to Construct Them
 Platonic Polyhedra and How to Construct Them Tarun Biswas June 17, 2016 The platonic polyhedra (or platonic solids) are convex regular polyhedra that have identical regular polygons as faces They are characterized
Platonic Polyhedra and How to Construct Them Tarun Biswas June 17, 2016 The platonic polyhedra (or platonic solids) are convex regular polyhedra that have identical regular polygons as faces They are characterized
SHAPE AND STRUCTURE. Shape and Structure. An explanation of Mathematical terminology
 Shape and Structure An explanation of Mathematical terminology 2005 1 POINT A dot Dots join to make lines LINE A line is 1 dimensional (length) A line is a series of points touching each other and extending
Shape and Structure An explanation of Mathematical terminology 2005 1 POINT A dot Dots join to make lines LINE A line is 1 dimensional (length) A line is a series of points touching each other and extending
Answer Key: Three-Dimensional Cross Sections
 Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
Geometry A Unit Answer Key: Three-Dimensional Cross Sections Name Date Objectives In this lesson, you will: visualize three-dimensional objects from different perspectives be able to create a projection
1 The Platonic Solids
 1 The We take the celebration of Dodecahedron Day as an opportunity embark on a discussion of perhaps the best-known and most celebrated of all polyhedra the Platonic solids. Before doing so, however,
1 The We take the celebration of Dodecahedron Day as an opportunity embark on a discussion of perhaps the best-known and most celebrated of all polyhedra the Platonic solids. Before doing so, however,
Key Concept Euler s Formula
 11-1 Space Figures and Cross Sections Objectives To recognize polyhedrons and their parts To visualize cross sections of space figures Common Core State Standards G-GMD.B.4 Identify the shapes of two-dimensional
11-1 Space Figures and Cross Sections Objectives To recognize polyhedrons and their parts To visualize cross sections of space figures Common Core State Standards G-GMD.B.4 Identify the shapes of two-dimensional
Date: Wednesday, 18 January :00AM. Location: Barnard's Inn Hall
 Wallpaper Patterns and Buckyballs Transcript Date: Wednesday, 18 January 2006-12:00AM Location: Barnard's Inn Hall WALLPAPER PATTERNS AND BUCKYBALLS Professor Robin Wilson My lectures this term will be
Wallpaper Patterns and Buckyballs Transcript Date: Wednesday, 18 January 2006-12:00AM Location: Barnard's Inn Hall WALLPAPER PATTERNS AND BUCKYBALLS Professor Robin Wilson My lectures this term will be
Math 311. Polyhedra Name: A Candel CSUN Math
 1. A polygon may be described as a finite region of the plane enclosed by a finite number of segments, arranged in such a way that (a) exactly two segments meets at every vertex, and (b) it is possible
1. A polygon may be described as a finite region of the plane enclosed by a finite number of segments, arranged in such a way that (a) exactly two segments meets at every vertex, and (b) it is possible
Explore Solids
 1212.1 Explore Solids Surface Area and Volume of Solids 12.2 Surface Area of Prisms and Cylinders 12.3 Surface Area of Pyramids and Cones 12.4 Volume of Prisms and Cylinders 12.5 Volume of Pyramids and
1212.1 Explore Solids Surface Area and Volume of Solids 12.2 Surface Area of Prisms and Cylinders 12.3 Surface Area of Pyramids and Cones 12.4 Volume of Prisms and Cylinders 12.5 Volume of Pyramids and
11.4 Three-Dimensional Figures
 11. Three-Dimensional Figures Essential Question What is the relationship between the numbers of vertices V, edges E, and faces F of a polyhedron? A polyhedron is a solid that is bounded by polygons, called
11. Three-Dimensional Figures Essential Question What is the relationship between the numbers of vertices V, edges E, and faces F of a polyhedron? A polyhedron is a solid that is bounded by polygons, called
Math 366 Lecture Notes Section 11.4 Geometry in Three Dimensions
 Math 366 Lecture Notes Section 11.4 Geometry in Three Dimensions Simple Closed Surfaces A simple closed surface has exactly one interior, no holes, and is hollow. A sphere is the set of all points at a
Math 366 Lecture Notes Section 11.4 Geometry in Three Dimensions Simple Closed Surfaces A simple closed surface has exactly one interior, no holes, and is hollow. A sphere is the set of all points at a
of Nebraska - Lincoln
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-2008 Archimedean Solids Anna Anderson University of
Rectangular prism. The two bases of a prism. bases
 Page 1 of 8 9.1 Solid Figures Goal Identify and name solid figures. Key Words solid polyhedron base face edge The three-dimensional shapes on this page are examples of solid figures, or solids. When a
Page 1 of 8 9.1 Solid Figures Goal Identify and name solid figures. Key Words solid polyhedron base face edge The three-dimensional shapes on this page are examples of solid figures, or solids. When a
Five Platonic Solids: Three Proofs
 Five Platonic Solids: Three Proofs Vincent J. Matsko IMSA, Dodecahedron Day Workshop 18 November 2011 Convex Polygons convex polygons nonconvex polygons Euler s Formula If V denotes the number of vertices
Five Platonic Solids: Three Proofs Vincent J. Matsko IMSA, Dodecahedron Day Workshop 18 November 2011 Convex Polygons convex polygons nonconvex polygons Euler s Formula If V denotes the number of vertices
Researches on polyhedra, Part I A.-L. Cauchy
 Researches on polyhedra, Part I A.-L. Cauchy Translated into English by Guy Inchbald, 2006 from the original: A.-L. Cauchy, Recherches sur les polyèdres. Première partie, Journal de l École Polytechnique,
Researches on polyhedra, Part I A.-L. Cauchy Translated into English by Guy Inchbald, 2006 from the original: A.-L. Cauchy, Recherches sur les polyèdres. Première partie, Journal de l École Polytechnique,
We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance.
 Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
Solid geometry We have set up our axioms to deal with the geometry of space but have not yet developed these ideas much. Let s redress that imbalance. First, note that everything we have proven for the
1 Appendix to notes 2, on Hyperbolic geometry:
 1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
1230, notes 3 1 Appendix to notes 2, on Hyperbolic geometry: The axioms of hyperbolic geometry are axioms 1-4 of Euclid, plus an alternative to axiom 5: Axiom 5-h: Given a line l and a point p not on l,
Platonic Solids and the Euler Characteristic
 Platonic Solids and the Euler Characteristic Keith Jones Sanford Society, SUNY Oneonta September 2013 What is a Platonic Solid? A Platonic Solid is a 3-dimensional object with flat faces and straight edges
Platonic Solids and the Euler Characteristic Keith Jones Sanford Society, SUNY Oneonta September 2013 What is a Platonic Solid? A Platonic Solid is a 3-dimensional object with flat faces and straight edges
Question. Why is the third shape not convex?
 1. CONVEX POLYGONS Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D. Convex 6 gon Another convex 6 gon Not convex Question. Why is the third
1. CONVEX POLYGONS Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D. Convex 6 gon Another convex 6 gon Not convex Question. Why is the third
Classifying 3D Shapes
 Classifying 3D Shapes Middle School Texas Essential Knowledge and Skills (TEKS) Math 5.4B Algebraic reasoning The student applies mathematical process standards to develop concepts of expressions and equations.
Classifying 3D Shapes Middle School Texas Essential Knowledge and Skills (TEKS) Math 5.4B Algebraic reasoning The student applies mathematical process standards to develop concepts of expressions and equations.
MATHEMATICS. Y4 Understanding shape Visualise, describe and classify 3-D and 2-D shapes. Equipment
 MATHEMATICS Y4 Understanding shape 4501 Visualise, describe and classify 3-D and 2-D shapes Paper, pencil, ruler Equipment Maths Go Go Go 4501 Visualise, describe and classify 3-D and 2-D shapes. Page
MATHEMATICS Y4 Understanding shape 4501 Visualise, describe and classify 3-D and 2-D shapes Paper, pencil, ruler Equipment Maths Go Go Go 4501 Visualise, describe and classify 3-D and 2-D shapes. Page
State if each pair of triangles is similar. If so, state how you know they are similar (AA, SAS, SSS) and complete the similarity statement.
 Geometry 1-2 est #7 Review Name Date Period State if each pair of triangles is similar. If so, state how you know they are similar (AA, SAS, SSS) and complete the similarity statement. 1) Q R 2) V F H
Geometry 1-2 est #7 Review Name Date Period State if each pair of triangles is similar. If so, state how you know they are similar (AA, SAS, SSS) and complete the similarity statement. 1) Q R 2) V F H
Week 7 Convex Hulls in 3D
 1 Week 7 Convex Hulls in 3D 2 Polyhedra A polyhedron is the natural generalization of a 2D polygon to 3D 3 Closed Polyhedral Surface A closed polyhedral surface is a finite set of interior disjoint polygons
1 Week 7 Convex Hulls in 3D 2 Polyhedra A polyhedron is the natural generalization of a 2D polygon to 3D 3 Closed Polyhedral Surface A closed polyhedral surface is a finite set of interior disjoint polygons
Planar Graphs, Solids, and Surfaces. Planar Graphs 1/28
 Planar Graphs, Solids, and Surfaces Planar Graphs 1/28 Last time we discussed the Four Color Theorem, which says that any map can be colored with at most 4 colors and not have two regions that share a
Planar Graphs, Solids, and Surfaces Planar Graphs 1/28 Last time we discussed the Four Color Theorem, which says that any map can be colored with at most 4 colors and not have two regions that share a
Platonic Solids. Jennie Sköld. January 21, Karlstad University. Symmetries: Groups Algebras and Tensor Calculus FYAD08
 Platonic Solids Jennie Sköld January 21, 2015 Symmetries: Groups Algebras and Tensor Calculus FYAD08 Karlstad University 1 Contents 1 What are Platonic Solids? 3 2 Symmetries in 3-Space 5 2.1 Isometries
Platonic Solids Jennie Sköld January 21, 2015 Symmetries: Groups Algebras and Tensor Calculus FYAD08 Karlstad University 1 Contents 1 What are Platonic Solids? 3 2 Symmetries in 3-Space 5 2.1 Isometries
Leonardo s Elevated Polyhedra - Models
 Leonardo s Elevated Polyhedra - Models Rinus Roelofs Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl www.rinusroelofs.nl Information Rinus Roelofs was born in 1954. After studying
Leonardo s Elevated Polyhedra - Models Rinus Roelofs Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl www.rinusroelofs.nl Information Rinus Roelofs was born in 1954. After studying
Polygons and Convexity
 Geometry Week 4 Sec 2.5 to ch. 2 test Polygons and Convexity section 2.5 convex set has the property that any two of its points determine a segment contained in the set concave set a set that is not convex
Geometry Week 4 Sec 2.5 to ch. 2 test Polygons and Convexity section 2.5 convex set has the property that any two of its points determine a segment contained in the set concave set a set that is not convex
Today we will be exploring three-dimensional objects, those that possess length, width, and depth.
 Lesson 22 Lesson 22, page 1 of 13 Glencoe Geometry Chapter 11.1 3-D figures & Polyhedra Today we will be exploring three-dimensional objects, those that possess length, width, and depth. In Euclidean,
Lesson 22 Lesson 22, page 1 of 13 Glencoe Geometry Chapter 11.1 3-D figures & Polyhedra Today we will be exploring three-dimensional objects, those that possess length, width, and depth. In Euclidean,
CARDSTOCK MODELING Math Manipulative Kit. Student Activity Book
 CARDSTOCK MODELING Math Manipulative Kit Student Activity Book TABLE OF CONTENTS Activity Sheet for L.E. #1 - Getting Started...3-4 Activity Sheet for L.E. #2 - Squares and Cubes (Hexahedrons)...5-8 Activity
CARDSTOCK MODELING Math Manipulative Kit Student Activity Book TABLE OF CONTENTS Activity Sheet for L.E. #1 - Getting Started...3-4 Activity Sheet for L.E. #2 - Squares and Cubes (Hexahedrons)...5-8 Activity
Non-flat tilings with flat tiles
 Non-flat tilings with flat tiles Rinus Roelofs Sculptor Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl www.rinusroelofs.nl Abstract In general a tiling is considered to be a
Non-flat tilings with flat tiles Rinus Roelofs Sculptor Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl www.rinusroelofs.nl Abstract In general a tiling is considered to be a
Elevations and Stellations
 Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture Elevations and Stellations Rinus Roelofs Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl www.rinusroelofs.nl
Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture Elevations and Stellations Rinus Roelofs Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl www.rinusroelofs.nl
Principles and Standards for School Mathematics. Content Standards. Process Standards. Emphasis across the Grades. Principles
 1 Navigating through Geometry Grades 3-5 Principles and Standards for School Mathematics Presented by Dr. Karol L. Yeatts Navigations Writer Navigating through Algebra Grades 3-5 Navigating through Number
1 Navigating through Geometry Grades 3-5 Principles and Standards for School Mathematics Presented by Dr. Karol L. Yeatts Navigations Writer Navigating through Algebra Grades 3-5 Navigating through Number
Triangles and Squares David Eppstein, ICS Theory Group, April 20, 2001
 Triangles and Squares David Eppstein, ICS Theory Group, April 20, 2001 Which unit-side-length convex polygons can be formed by packing together unit squares and unit equilateral triangles? For instance
Triangles and Squares David Eppstein, ICS Theory Group, April 20, 2001 Which unit-side-length convex polygons can be formed by packing together unit squares and unit equilateral triangles? For instance
Example: The following is an example of a polyhedron. Fill the blanks with the appropriate answer. Vertices:
 11.1: Space Figures and Cross Sections Polyhedron: solid that is bounded by polygons Faces: polygons that enclose a polyhedron Edge: line segment that faces meet and form Vertex: point or corner where
11.1: Space Figures and Cross Sections Polyhedron: solid that is bounded by polygons Faces: polygons that enclose a polyhedron Edge: line segment that faces meet and form Vertex: point or corner where
The radius for a regular polygon is the same as the radius of the circumscribed circle.
 Perimeter and Area The perimeter and area of geometric shapes are basic properties that we need to know. The more complex a shape is, the more complex the process can be in finding its perimeter and area.
Perimeter and Area The perimeter and area of geometric shapes are basic properties that we need to know. The more complex a shape is, the more complex the process can be in finding its perimeter and area.
Geometro: Developing Concepts for Math, Science and O&M with Students who are Visually Impaired October 5, 2012
 Texas School for the Blind and Visually Impaired Outreach Programs www.tsbvi.edu 512-454-8631 1100 W. 45 th St. Austin, Texas 78756 Geometro: Developing Concepts for Math, Science and O&M with Students
Texas School for the Blind and Visually Impaired Outreach Programs www.tsbvi.edu 512-454-8631 1100 W. 45 th St. Austin, Texas 78756 Geometro: Developing Concepts for Math, Science and O&M with Students
1. CONVEX POLYGONS. Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D.
 1. CONVEX POLYGONS Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D. Convex 6 gon Another convex 6 gon Not convex Question. Why is the third
1. CONVEX POLYGONS Definition. A shape D in the plane is convex if every line drawn between two points in D is entirely inside D. Convex 6 gon Another convex 6 gon Not convex Question. Why is the third
Ma/CS 6b Class 9: Euler s Formula
 Ma/CS 6b Class 9: Euler s Formula By Adam Sheffer Recall: Plane Graphs A plane graph is a drawing of a graph in the plane such that the edges are noncrossing curves. 1 Recall: Planar Graphs The drawing
Ma/CS 6b Class 9: Euler s Formula By Adam Sheffer Recall: Plane Graphs A plane graph is a drawing of a graph in the plane such that the edges are noncrossing curves. 1 Recall: Planar Graphs The drawing
7th Bay Area Mathematical Olympiad
 7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
Junior Math Circles March 3, D Geometry I
 1 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Junior Math Circles March 3, 2010 3D Geometry I Opening Problem Max received a gumball machine for his
1 University of Waterloo Faculty of Mathematics Centre for Education in Mathematics and Computing Junior Math Circles March 3, 2010 3D Geometry I Opening Problem Max received a gumball machine for his
The Volume of a Platonic Solid
 University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-007 The Volume of a Platonic Solid Cindy Steinkruger
University of Nebraska - Lincoln DigitalCommons@University of Nebraska - Lincoln MAT Exam Expository Papers Math in the Middle Institute Partnership 7-007 The Volume of a Platonic Solid Cindy Steinkruger
Geometry AP Book 8, Part 2: Unit 7
 Geometry P ook 8, Part 2: Unit 7 P ook G8-7 page 168 1. base # s V F 6 9 5 4 8 12 6 C 5 10 15 7 6 12 18 8 8 16 24 10 n n-agon n 2n n n + 2 2. 4; 5; 8; 5; No. a) 4 6 6 4 = 24 8 e) ii) top, and faces iii)
Geometry P ook 8, Part 2: Unit 7 P ook G8-7 page 168 1. base # s V F 6 9 5 4 8 12 6 C 5 10 15 7 6 12 18 8 8 16 24 10 n n-agon n 2n n n + 2 2. 4; 5; 8; 5; No. a) 4 6 6 4 = 24 8 e) ii) top, and faces iii)
LESSON. Bigger and Bigger. Years 5 to 9. Enlarging Figures to Construct Polyhedra Nets
 LESSON 4 Bigger and Bigger Years 5 to 9 Enlarging Figures to Construct Polyhedra Nets This lesson involves students using their MATHOMAT to enlarge regular polygons to produce nets of selected polyhedra,
LESSON 4 Bigger and Bigger Years 5 to 9 Enlarging Figures to Construct Polyhedra Nets This lesson involves students using their MATHOMAT to enlarge regular polygons to produce nets of selected polyhedra,
Week 9: Planar and non-planar graphs. 7 and 9 November, 2018
 (1/27) MA284 : Discrete Mathematics Week 9: Planar and non-planar graphs http://www.maths.nuigalway.ie/ niall/ma284/ 7 and 9 November, 2018 1 Planar graphs and Euler s formula 2 Non-planar graphs K 5 K
(1/27) MA284 : Discrete Mathematics Week 9: Planar and non-planar graphs http://www.maths.nuigalway.ie/ niall/ma284/ 7 and 9 November, 2018 1 Planar graphs and Euler s formula 2 Non-planar graphs K 5 K
CARDSTOCK MODELING Math Manipulative Kit. Revised July 25, 2006
 CARDSTOCK MODELING Math Manipulative Kit Revised July 25, 2006 TABLE OF CONTENTS Unit Overview...3 Format & Background Information...3-5 Learning Experience #1 - Getting Started...6-7 Learning Experience
CARDSTOCK MODELING Math Manipulative Kit Revised July 25, 2006 TABLE OF CONTENTS Unit Overview...3 Format & Background Information...3-5 Learning Experience #1 - Getting Started...6-7 Learning Experience
Computer Graphics using OpenGL, 3 rd Edition F. S. Hill, Jr. and S. Kelley
 Computer Graphics using OpenGL, 3 rd Edition F. S. Hill, Jr. and S. Kelley Chapter 6.1-3 Modeling Shapes with Polygonal Meshes S. M. Lea University of North Carolina at Greensboro 2007, Prentice Hall 3D
Computer Graphics using OpenGL, 3 rd Edition F. S. Hill, Jr. and S. Kelley Chapter 6.1-3 Modeling Shapes with Polygonal Meshes S. M. Lea University of North Carolina at Greensboro 2007, Prentice Hall 3D
MATHEMATICS. Y4 Understanding shape Visualise 3-D objects and make nets of common solids. Equipment
 MATHEMATICS Y4 Understanding shape 4502 Visualise 3-D objects and make nets of common solids Equipment Paper, pencil, boxes, range of 3-D shapes, straws and pipe cleaners or 3-D model construction kits.
MATHEMATICS Y4 Understanding shape 4502 Visualise 3-D objects and make nets of common solids Equipment Paper, pencil, boxes, range of 3-D shapes, straws and pipe cleaners or 3-D model construction kits.
Mathematics Concepts 2 Exam 1 Version 4 21 September 2018
 Mathematics Concepts 2 Exam 1 Version 4 21 September 2018 Name: Permissible Aides: The small ruler distributed by the proctor Prohibited: Class Notes Class Handouts Study Guides and Materials The Book
Mathematics Concepts 2 Exam 1 Version 4 21 September 2018 Name: Permissible Aides: The small ruler distributed by the proctor Prohibited: Class Notes Class Handouts Study Guides and Materials The Book
The Game of Criss-Cross
 Chapter 5 The Game of Criss-Cross Euler Characteristic ( ) Overview. The regions on a map and the faces of a cube both illustrate a very natural sort of situation: they are each examples of regions that
Chapter 5 The Game of Criss-Cross Euler Characteristic ( ) Overview. The regions on a map and the faces of a cube both illustrate a very natural sort of situation: they are each examples of regions that
Lesson Polygons
 Lesson 4.1 - Polygons Obj.: classify polygons by their sides. classify quadrilaterals by their attributes. find the sum of the angle measures in a polygon. Decagon - A polygon with ten sides. Dodecagon
Lesson 4.1 - Polygons Obj.: classify polygons by their sides. classify quadrilaterals by their attributes. find the sum of the angle measures in a polygon. Decagon - A polygon with ten sides. Dodecagon
Unit I: Euler's Formula (and applications).
 Unit I: Euler's Formula (and applications). We define a roadmap to be a nonempty finite collection of possibly curvedlil1e segments in a piane, each with exactly two endpoints, such that if any pair of
Unit I: Euler's Formula (and applications). We define a roadmap to be a nonempty finite collection of possibly curvedlil1e segments in a piane, each with exactly two endpoints, such that if any pair of
Intermediate Math Circles Fall 2018 Patterns & Counting
 Intermediate Math Circles Fall 2018 Patterns & Counting Michael Miniou The Centre for Education in Mathematics and Computing Faculty of Mathematics University of Waterloo December 5, 2018 Michael Miniou
Intermediate Math Circles Fall 2018 Patterns & Counting Michael Miniou The Centre for Education in Mathematics and Computing Faculty of Mathematics University of Waterloo December 5, 2018 Michael Miniou
About Finish Line Mathematics 5
 Table of COntents About Finish Line Mathematics 5 Unit 1: Big Ideas from Grade 1 7 Lesson 1 1.NBT.2.a c Understanding Tens and Ones [connects to 2.NBT.1.a, b] 8 Lesson 2 1.OA.6 Strategies to Add and Subtract
Table of COntents About Finish Line Mathematics 5 Unit 1: Big Ideas from Grade 1 7 Lesson 1 1.NBT.2.a c Understanding Tens and Ones [connects to 2.NBT.1.a, b] 8 Lesson 2 1.OA.6 Strategies to Add and Subtract
Math 462: Review questions
 Math 462: Review questions Paul Hacking 4/22/10 (1) What is the angle between two interior diagonals of a cube joining opposite vertices? [Hint: It is probably quickest to use a description of the cube
Math 462: Review questions Paul Hacking 4/22/10 (1) What is the angle between two interior diagonals of a cube joining opposite vertices? [Hint: It is probably quickest to use a description of the cube
MATERIAL FOR A MASTERCLASS ON HYPERBOLIC GEOMETRY. Timeline. 10 minutes Exercise session: Introducing curved spaces
 MATERIAL FOR A MASTERCLASS ON HYPERBOLIC GEOMETRY Timeline 10 minutes Introduction and History 10 minutes Exercise session: Introducing curved spaces 5 minutes Talk: spherical lines and polygons 15 minutes
MATERIAL FOR A MASTERCLASS ON HYPERBOLIC GEOMETRY Timeline 10 minutes Introduction and History 10 minutes Exercise session: Introducing curved spaces 5 minutes Talk: spherical lines and polygons 15 minutes
3D shapes introduction
 3D shapes introduction 2D shapes have 2 dimensions width and height. They re flat. height 3D shapes have 3 dimensions height, width and depth. Sometimes we call them solids. When we draw them, we often
3D shapes introduction 2D shapes have 2 dimensions width and height. They re flat. height 3D shapes have 3 dimensions height, width and depth. Sometimes we call them solids. When we draw them, we often
Glossary of dictionary terms in the AP geometry units
 Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
Glossary of dictionary terms in the AP geometry units affine linear equation: an equation in which both sides are sums of terms that are either a number times y or a number times x or just a number [SlL2-D5]
One simple example is that of a cube. Each face is a square (=regular quadrilateral) and each vertex is connected to exactly three squares.
 Berkeley Math Circle Intermediate I, 1/23, 1/20, 2/6 Presenter: Elysée Wilson-Egolf Topic: Polygons, Polyhedra, Polytope Series Part 1 Polygon Angle Formula Let s start simple. How do we find the sum of
Berkeley Math Circle Intermediate I, 1/23, 1/20, 2/6 Presenter: Elysée Wilson-Egolf Topic: Polygons, Polyhedra, Polytope Series Part 1 Polygon Angle Formula Let s start simple. How do we find the sum of
TOURNAMENT OF THE TOWNS, Glossary
 TOURNAMENT OF THE TOWNS, 2003 2004 Glossary Absolute value The size of a number with its + or sign removed. The absolute value of 3.2 is 3.2, the absolute value of +4.6 is 4.6. We write this: 3.2 = 3.2
TOURNAMENT OF THE TOWNS, 2003 2004 Glossary Absolute value The size of a number with its + or sign removed. The absolute value of 3.2 is 3.2, the absolute value of +4.6 is 4.6. We write this: 3.2 = 3.2
Tessellations: Wallpapers, Escher & Soccer Balls. Robert Campbell
 Tessellations: Wallpapers, Escher & Soccer Balls Robert Campbell Tessellation Examples What Is What is a Tessellation? A Tessellation (or tiling) is a pattern made by copies of one or
Tessellations: Wallpapers, Escher & Soccer Balls Robert Campbell Tessellation Examples What Is What is a Tessellation? A Tessellation (or tiling) is a pattern made by copies of one or
Grade VIII. Mathematics Geometry Notes. #GrowWithGreen
 Grade VIII Mathematics Geometry Notes #GrowWithGreen Polygons can be classified according to their number of sides (or vertices). The sum of all the interior angles of an n -sided polygon is given by,
Grade VIII Mathematics Geometry Notes #GrowWithGreen Polygons can be classified according to their number of sides (or vertices). The sum of all the interior angles of an n -sided polygon is given by,
Chapter 11 Part 2. Measurement of Figures and Solids
 Chapter 11 Part 2 Measurement of Figures and Solids 11.5 Explore Solids Objective: Identify Solids Essential Question: When is a solid a polyhedron? Using properties of polyhedra A is a solid that is bounded
Chapter 11 Part 2 Measurement of Figures and Solids 11.5 Explore Solids Objective: Identify Solids Essential Question: When is a solid a polyhedron? Using properties of polyhedra A is a solid that is bounded
Ready To Go On? Skills Intervention 10-1 Solid Geometry
 10A Find these vocabulary words in Lesson 10-1 and the Multilingual Glossary. Vocabulary Ready To Go On? Skills Intervention 10-1 Solid Geometry face edge vertex prism cylinder pyramid cone cube net cross
10A Find these vocabulary words in Lesson 10-1 and the Multilingual Glossary. Vocabulary Ready To Go On? Skills Intervention 10-1 Solid Geometry face edge vertex prism cylinder pyramid cone cube net cross
Keeping it Platonic. Anna Romanova. February 2, infinity, five, six, three, three, three, three,...
 MFA UTAH TEACHERS MATH CIRCLE Keeping it Platonic Anna Romanova February 2, 2016 1 THE PUZZLE IN THE ABSTRACT What is the pattern in this sequence? infinity, five, six, three, three, three, three,... Our
MFA UTAH TEACHERS MATH CIRCLE Keeping it Platonic Anna Romanova February 2, 2016 1 THE PUZZLE IN THE ABSTRACT What is the pattern in this sequence? infinity, five, six, three, three, three, three,... Our
Euler s Formula. Math 123. March 2006
 Euler s Formula Math 123 March 2006 1 Purpose Although Euler s Formula is relatively simple to memorize, it is actually a manifestation of a very deep mathematical phenomenon. In this activity, we will
Euler s Formula Math 123 March 2006 1 Purpose Although Euler s Formula is relatively simple to memorize, it is actually a manifestation of a very deep mathematical phenomenon. In this activity, we will
Closed Loops with Antiprisms
 Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture Closed Loops with Antiprisms Melle Stoel Dacostastraat 18 1053 zc Amsterdam E-mail: mellestoel@gmail.com mellestoel.wordpress.com
Proceedings of Bridges 2014: Mathematics, Music, Art, Architecture, Culture Closed Loops with Antiprisms Melle Stoel Dacostastraat 18 1053 zc Amsterdam E-mail: mellestoel@gmail.com mellestoel.wordpress.com
Euler's formula and Platonic solids
 University of Washington Euler's formula and Platonic solids Name: David Clark, Kelsey Kyllo, Kurt Maugerle, Yue Yuan Zhang Course Number: Math 445 Professor: Julia Pevtsova Date: 2013/06/03 Table of Contents:
University of Washington Euler's formula and Platonic solids Name: David Clark, Kelsey Kyllo, Kurt Maugerle, Yue Yuan Zhang Course Number: Math 445 Professor: Julia Pevtsova Date: 2013/06/03 Table of Contents:
Map-colouring with Polydron
 Map-colouring with Polydron The 4 Colour Map Theorem says that you never need more than 4 colours to colour a map so that regions with the same colour don t touch. You have to count the region round the
Map-colouring with Polydron The 4 Colour Map Theorem says that you never need more than 4 colours to colour a map so that regions with the same colour don t touch. You have to count the region round the
Draw and Classify 3-Dimensional Figures
 Introduction to Three-Dimensional Figures Draw and Classify 3-Dimensional Figures Identify various three-dimensional figures. Course 2 Introduction to Three-Dimensional Figures Insert Lesson Title Here
Introduction to Three-Dimensional Figures Draw and Classify 3-Dimensional Figures Identify various three-dimensional figures. Course 2 Introduction to Three-Dimensional Figures Insert Lesson Title Here
Week 9: Planar and non-planar graphs. 1st and 3rd of November, 2017
 (1/26) MA284 : Discrete Mathematics Week 9: Planar and non-planar graphs http://www.maths.nuigalway.ie/~niall/ma284/ 1st and 3rd of November, 2017 1 Recall... planar graphs and Euler s formula 2 Non-planar
(1/26) MA284 : Discrete Mathematics Week 9: Planar and non-planar graphs http://www.maths.nuigalway.ie/~niall/ma284/ 1st and 3rd of November, 2017 1 Recall... planar graphs and Euler s formula 2 Non-planar
Planar Graphs and Surfaces. Graphs 2 1/58
 Planar Graphs and Surfaces Graphs 2 1/58 Last time we discussed the Four Color Theorem, which says that any map can be colored with at most 4 colors and not have two regions that share a border having
Planar Graphs and Surfaces Graphs 2 1/58 Last time we discussed the Four Color Theorem, which says that any map can be colored with at most 4 colors and not have two regions that share a border having
The Concept of Elevation applied to Flat Tiling Patterns
 Proceedings of Bridges 2015: Mathematics, Music, Art, Architecture, Culture The Concept of Elevation applied to Flat Tiling Patterns Rinus Roelofs Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl
Proceedings of Bridges 2015: Mathematics, Music, Art, Architecture, Culture The Concept of Elevation applied to Flat Tiling Patterns Rinus Roelofs Lansinkweg 28 7553AL Hengelo The Netherlands E-mail: rinus@rinusroelofs.nl
From a Subdivided Tetrahedron to the Dodecahedron: Exploring Regular Colorings
 From a Subdivided Tetrahedron to the Dodecahedron: Exploring Regular Colorings Eva Knoll School of Education, University of Exeter, England evaknoll@netscape.net Abstract The following paper recounts the
From a Subdivided Tetrahedron to the Dodecahedron: Exploring Regular Colorings Eva Knoll School of Education, University of Exeter, England evaknoll@netscape.net Abstract The following paper recounts the
Patterned Polyhedra: Tiling the Platonic Solids
 Patterned Polyhedra: Tiling the Platonic Solids B.G. Thomas* and M.A. Hann School of Design, University of Leeds Leeds, LS2 9JT, UK b.g.thomas@leeds.ac.uk Abstract This paper examines a range of geometric
Patterned Polyhedra: Tiling the Platonic Solids B.G. Thomas* and M.A. Hann School of Design, University of Leeds Leeds, LS2 9JT, UK b.g.thomas@leeds.ac.uk Abstract This paper examines a range of geometric
tetrahedron octahedron icosahedron cube dodecahedron (Fire) (Air) (Water) (Earth) (Universe)
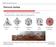 Platonic Solids A regular polyhedron is one whose faces are identical regular polygons. The solids as drawn in Kepler s Mysterium Cosmographicum: tetrahedron octahedron icosahedron cube dodecahedron (Fire)
Platonic Solids A regular polyhedron is one whose faces are identical regular polygons. The solids as drawn in Kepler s Mysterium Cosmographicum: tetrahedron octahedron icosahedron cube dodecahedron (Fire)
Section 9.4. Volume and Surface Area. Copyright 2013, 2010, 2007, Pearson, Education, Inc.
 Section 9.4 Volume and Surface Area What You Will Learn Volume Surface Area 9.4-2 Volume Volume is the measure of the capacity of a three-dimensional figure. It is the amount of material you can put inside
Section 9.4 Volume and Surface Area What You Will Learn Volume Surface Area 9.4-2 Volume Volume is the measure of the capacity of a three-dimensional figure. It is the amount of material you can put inside
Geometry Vocabulary. acute angle-an angle measuring less than 90 degrees
 Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
Geometry Vocabulary acute angle-an angle measuring less than 90 degrees angle-the turn or bend between two intersecting lines, line segments, rays, or planes angle bisector-an angle bisector is a ray that
INTRODUCTION TO GRAPH THEORY. 1. Definitions
 INTRODUCTION TO GRAPH THEORY D. JAKOBSON 1. Definitions A graph G consists of vertices {v 1, v 2,..., v n } and edges {e 1, e 2,..., e m } connecting pairs of vertices. An edge e = (uv) is incident with
INTRODUCTION TO GRAPH THEORY D. JAKOBSON 1. Definitions A graph G consists of vertices {v 1, v 2,..., v n } and edges {e 1, e 2,..., e m } connecting pairs of vertices. An edge e = (uv) is incident with
Mathematics Concepts 2 Exam 1 Version 2 22 September 2017
 Mathematics Concepts 2 Exam 1 Version 2 22 September 2017 Name: Permissible Aides: The small ruler distributed by the proctor Prohibited: Class Notes Class Handouts Study Guides and Materials The Book
Mathematics Concepts 2 Exam 1 Version 2 22 September 2017 Name: Permissible Aides: The small ruler distributed by the proctor Prohibited: Class Notes Class Handouts Study Guides and Materials The Book
The Construction of Uniform Polyhedron with the aid of GeoGebra
 The Construction of Uniform Polyhedron with the aid of GeoGebra JiangPing QiuFaWen 71692686@qq.com 3009827@qq.com gifted Department High-school northeast yucai school northeast yucai school 110179 110179
The Construction of Uniform Polyhedron with the aid of GeoGebra JiangPing QiuFaWen 71692686@qq.com 3009827@qq.com gifted Department High-school northeast yucai school northeast yucai school 110179 110179
Regular Polygons. by construction and paper folding. Paul Yiu Department of Mathematics Florida Atlantic University.
 Regular Polygons by construction and paper folding Paul Yiu Department of Mathematics Florida tlantic University January 22, 2009 1 Regular polygons (a) Triangle (b) Square (c) Pentagon (d) Hexagon (e)
Regular Polygons by construction and paper folding Paul Yiu Department of Mathematics Florida tlantic University January 22, 2009 1 Regular polygons (a) Triangle (b) Square (c) Pentagon (d) Hexagon (e)
Lecture 19: Introduction To Topology
 Chris Tralie, Duke University 3/24/2016 Announcements Group Assignment 2 Due Wednesday 3/30 First project milestone Friday 4/8/2016 Welcome to unit 3! Table of Contents The Euler Characteristic Spherical
Chris Tralie, Duke University 3/24/2016 Announcements Group Assignment 2 Due Wednesday 3/30 First project milestone Friday 4/8/2016 Welcome to unit 3! Table of Contents The Euler Characteristic Spherical
Regular polygons and tessellations Criterion D: Reflection
 Regular polygons and tessellations Criterion D: Reflection Aika Kim 12/13/2012 Math 9+ Assignment task: Our task in this project is to identify what a tessellation is, and what shapes do and don t. But
Regular polygons and tessellations Criterion D: Reflection Aika Kim 12/13/2012 Math 9+ Assignment task: Our task in this project is to identify what a tessellation is, and what shapes do and don t. But
Zipper Unfoldings of Polyhedral Complexes
 Zipper Unfoldings of Polyhedral Complexes Erik D. Demaine Martin L. Demaine Anna Lubiw Arlo Shallit Jonah L. Shallit Abstract We explore which polyhedra and polyhedral complexes can be formed by folding
Zipper Unfoldings of Polyhedral Complexes Erik D. Demaine Martin L. Demaine Anna Lubiw Arlo Shallit Jonah L. Shallit Abstract We explore which polyhedra and polyhedral complexes can be formed by folding
PLC Papers Created For:
 PLC Papers Created For: Year 10 Topic Practice Papers: Polygons Polygons 1 Grade 4 Look at the shapes below A B C Shape A, B and C are polygons Write down the mathematical name for each of the polygons
PLC Papers Created For: Year 10 Topic Practice Papers: Polygons Polygons 1 Grade 4 Look at the shapes below A B C Shape A, B and C are polygons Write down the mathematical name for each of the polygons
Unit 4 Reasoning about shape. Year 4. Five daily lessons. Autumn term. Unit Objectives. Link Objectives
 Unit 4 Reasoning about shape Five daily lessons Year 4 Autumn term (Key objectives in bold) Unit Objectives Year 4 Describe and visualise 3-D and 2-D shapes, Page 102 including the tetrahedron and heptagon.
Unit 4 Reasoning about shape Five daily lessons Year 4 Autumn term (Key objectives in bold) Unit Objectives Year 4 Describe and visualise 3-D and 2-D shapes, Page 102 including the tetrahedron and heptagon.
25. How would you make the octahedral die shown below?
 304450_ch_08_enqxd 12/6/06 1:39 PM Page 577 Chapter Summary 577 draw others you will not necessarily need all of them. Describe your method, other than random trial and error. How confident are you that
304450_ch_08_enqxd 12/6/06 1:39 PM Page 577 Chapter Summary 577 draw others you will not necessarily need all of them. Describe your method, other than random trial and error. How confident are you that
REVIEWS Edited by Underwood Dudley
 REVIEWS Edited by Underwood Dudley Mathematics Department, Pauw University, Greencastle, IN 46135 "Invertible" Polyhedron Models. Distributed by Snyder Engineering, 7552 Dumas Drive, Cupertino, California
REVIEWS Edited by Underwood Dudley Mathematics Department, Pauw University, Greencastle, IN 46135 "Invertible" Polyhedron Models. Distributed by Snyder Engineering, 7552 Dumas Drive, Cupertino, California
TESSELLATION. For me it remains an open question whether [this work] pertains to the realm of mathematics or to that of art. M.C.
![TESSELLATION. For me it remains an open question whether [this work] pertains to the realm of mathematics or to that of art. M.C. TESSELLATION. For me it remains an open question whether [this work] pertains to the realm of mathematics or to that of art. M.C.](/thumbs/78/77863811.jpg) TESSELLATION For me it remains an open question whether [this work] pertains to the realm of mathematics or to that of art. M.C. Escher Activity 1: Guessing the lesson Doc. 1 Word Cloud 1) What do you
TESSELLATION For me it remains an open question whether [this work] pertains to the realm of mathematics or to that of art. M.C. Escher Activity 1: Guessing the lesson Doc. 1 Word Cloud 1) What do you
Part Two Development of Single Solids - The Five Plutonic Solids
 1 Part Two Development of Single Solids - The Five Plutonic Solids We will now proceed to learn different topics of descriptive geometry using AutoCAD 2D tools and settings. Throughout this and subsequent
1 Part Two Development of Single Solids - The Five Plutonic Solids We will now proceed to learn different topics of descriptive geometry using AutoCAD 2D tools and settings. Throughout this and subsequent
Euler Characteristic
 Euler Characteristic Face Classification set_view(gl_render); set_scene(gl_render); glgetdoublev(gl_modelview_matrix, modelview_matrix1); glgetdoublev(gl_projection_matrix, projection_matrix1); glgetintegerv(gl_viewport,
Euler Characteristic Face Classification set_view(gl_render); set_scene(gl_render); glgetdoublev(gl_modelview_matrix, modelview_matrix1); glgetdoublev(gl_projection_matrix, projection_matrix1); glgetintegerv(gl_viewport,
Curvature Berkeley Math Circle January 08, 2013
 Curvature Berkeley Math Circle January 08, 2013 Linda Green linda@marinmathcircle.org Parts of this handout are taken from Geometry and the Imagination by John Conway, Peter Doyle, Jane Gilman, and Bill
Curvature Berkeley Math Circle January 08, 2013 Linda Green linda@marinmathcircle.org Parts of this handout are taken from Geometry and the Imagination by John Conway, Peter Doyle, Jane Gilman, and Bill
Key Question. Focus. What are the geometric properties of a regular tetrahedron, and how do these compare to a bird tetrahedron?
 Key Question What are the geometric properties of a regular tetrahedron, and how do these compare to a bird tetrahedron? Math Properties of polyhedra faces edges vertices Surface area Integrated Processes
Key Question What are the geometric properties of a regular tetrahedron, and how do these compare to a bird tetrahedron? Math Properties of polyhedra faces edges vertices Surface area Integrated Processes
acute angle An angle with a measure less than that of a right angle. Houghton Mifflin Co. 2 Grade 5 Unit 6
 acute angle An angle with a measure less than that of a right angle. Houghton Mifflin Co. 2 Grade 5 Unit 6 angle An angle is formed by two rays with a common end point. Houghton Mifflin Co. 3 Grade 5 Unit
acute angle An angle with a measure less than that of a right angle. Houghton Mifflin Co. 2 Grade 5 Unit 6 angle An angle is formed by two rays with a common end point. Houghton Mifflin Co. 3 Grade 5 Unit
Angles, Polygons, Circles
 Page 1 of 5 Part One Last week we learned about the angle properties of circles and used them to solve a simple puzzle. This week brings a new puzzle that will make us use our algebra a bit more. But first,
Page 1 of 5 Part One Last week we learned about the angle properties of circles and used them to solve a simple puzzle. This week brings a new puzzle that will make us use our algebra a bit more. But first,
