Probabilistic systems a place where categories meet probability
|
|
|
- William Henry
- 5 years ago
- Views:
Transcription
1 Probabilistic systems a place where categories meet probability Ana Sokolova SOS group, Radboud University Nijmegen University Dortmund, CS Kolloquium, p.1/32
2 Outline Introduction - probabilistic systems and coalgebras University Dortmund, CS Kolloquium, p.2/32
3 Outline Introduction - probabilistic systems and coalgebras Bisimilarity - the strong end of the spectrum University Dortmund, CS Kolloquium, p.2/32
4 Outline Introduction - probabilistic systems and coalgebras Bisimilarity - the strong end of the spectrum Application - expressiveness hierarchy (older result) University Dortmund, CS Kolloquium, p.2/32
5 Outline Introduction - probabilistic systems and coalgebras Bisimilarity - the strong end of the spectrum Application - expressiveness hierarchy (older result) Trace semantics - the weak end of the spectrum (newer result) University Dortmund, CS Kolloquium, p.2/32
6 Systems are formal objects, transition systems (e.g. LTS), that serve as models of real (software, hardware,...) systems University Dortmund, CS Kolloquium, p.3/32
7 Systems are formal objects, transition systems (e.g. LTS), that serve as models of real (software, hardware,...) systems University Dortmund, CS Kolloquium, p.3/32
8 Systems are formal objects, transition systems (e.g. LTS), that serve as models of real (software, hardware,...) systems a b c c a University Dortmund, CS Kolloquium, p.3/32
9 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: University Dortmund, CS Kolloquium, p.4/32
10 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: University Dortmund, CS Kolloquium, p.4/32
11 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: a[1] a[ 1 3 ] b[ 2 3 ] University Dortmund, CS Kolloquium, p.4/32
12 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: a University Dortmund, CS Kolloquium, p.4/32
13 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: 1 a b University Dortmund, CS Kolloquium, p.4/32
14 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: 1 a 1 b a University Dortmund, CS Kolloquium, p.4/32
15 Probabilistic systems arise by enriching transition systems with (discrete) probabilities as labels on the transitions. Examples: a 1 3 b University Dortmund, CS Kolloquium, p.4/32
16 Coalgebras are an elegant generalization of transition systems with states + transitions University Dortmund, CS Kolloquium, p.5/32
17 Coalgebras are an elegant generalization of transition systems with states + transitions as pairs S, α : S FS, for F a functor University Dortmund, CS Kolloquium, p.5/32
18 Coalgebras are an elegant generalization of transition systems with states + transitions as pairs S, α : S FS, for F a functor based on category theory provide a uniform way of treating transition systems provide general notions and results e.g. a generic notion of bisimulation University Dortmund, CS Kolloquium, p.5/32
19 Examples A TS is a pair S, α : S PS!! coalgebra of the powerset functor P University Dortmund, CS Kolloquium, p.6/32
20 Examples A TS is a pair S, α : S PS!! coalgebra of the powerset functor P An LTS is a pair S, α : S PS A!!! coalgebra of the functor P A Note: P A = P(A ) University Dortmund, CS Kolloquium, p.6/32
21 More examples Thanks to the probability distribution functor D DS = {µ : S [0, 1], µ[s] = 1}, µ[x] = s X µ(x) Df : DS DT, Df(µ)(t) = µ[f 1 ({t})] the probabilistic systems are also coalgebras University Dortmund, CS Kolloquium, p.7/32
22 More examples Thanks to the probability distribution functor D DS = {µ : S [0, 1], µ[s] = 1}, µ[x] = s X µ(x) Df : DS DT, Df(µ)(t) = µ[f 1 ({t})] the probabilistic systems are also coalgebras... of functors built by the following syntax F ::= A P D G + H G H G A G H University Dortmund, CS Kolloquium, p.7/32
23 reactive, generative evolve from LTS - functor P (A ) = P A University Dortmund, CS Kolloquium, p.8/32
24 reactive, generative evolve from LTS - functor P (A ) = P A reactive systems: functor (D + 1) A University Dortmund, CS Kolloquium, p.8/32
25 reactive, generative evolve from LTS - functor P (A ) = P A reactive systems: functor (D + 1) A generative systems: functor (D + 1)(A ) = D(A ) + 1 University Dortmund, CS Kolloquium, p.8/32
26 reactive, generative evolve from LTS - functor P (A ) = P A reactive systems: functor (D + 1) A generative systems: functor (D + 1)(A ) = D(A ) + 1 note: in the probabilistic case (D + 1) A = D(A ) + 1 University Dortmund, CS Kolloquium, p.8/32
27 Probabilistic system types MC D DLTS ( + 1) A LTS P(A ) = P A React (D + 1) A Gen D(A ) + 1 Str D + (A ) + 1 Alt D + P(A ) Var D(A ) + P(A ) SSeg P(A D) Seg PD(A ) University Dortmund, CS Kolloquium, p.9/32
28 Probabilistic system types MC D DLTS ( + 1) A LTS P(A ) = P A React (D + 1) A Gen D(A ) + 1 Str D + (A ) + 1 Alt D + P(A ) Var D(A ) + P(A ) SSeg P(A D) Seg PD(A ) b[1] a[ 1 3 ] a[ 2 3 ] b[1] a[1] University Dortmund, CS Kolloquium, p.9/32
29 Probabilistic system types MC D DLTS ( + 1) A LTS P(A ) = P A React (D + 1) A Gen D(A ) + 1 Str D + (A ) + 1 Alt D + P(A ) Var D(A ) + P(A ) SSeg P(A D) Seg PD(A ) a[ 1 2 ] a[ 1 4 ] c[1] b[ 1 4 ] c[1] University Dortmund, CS Kolloquium, p.9/32
30 Probabilistic system types MC D DLTS ( + 1) A LTS P(A ) = P A React (D + 1) A Gen D(A ) + 1 Str D + (A ) + 1 Alt D + P(A ) Var D(A ) + P(A ) SSeg P(A D) Seg PD(A ) a b University Dortmund, CS Kolloquium, p.9/32
31 Probabilistic system types MC D DLTS ( + 1) A LTS P(A ) = P A React (D + 1) A Gen D(A ) + 1 Str D + (A ) + 1 Alt D + P(A ) Var D(A ) + P(A ) SSeg P(A D) Seg PD(A ) a a b University Dortmund, CS Kolloquium, p.9/32
32 Probabilistic system types MC D DLTS ( + 1) A LTS P(A ) = P A React (D + 1) A Gen D(A ) + 1 Str D + (A ) + 1 Alt D + P(A ) Var D(A ) + P(A ) SSeg P(A D) Seg PD(A ) b[ 3 4 ] a[ 1 3 ] a[ 1 4 ] a[ 2 3 ] University Dortmund, CS Kolloquium, p.9/32
33 Bisimulation - LTS Consider the LTS a s0 t0 a t2 a b b s1 t1 t3 b University Dortmund, CS Kolloquium, p.10/32
34 Bisimulation - LTS Consider the LTS a s0 t0 a t2 a b b s1 t1 t3 b The states s 0 and t 0 are bisimilar since there is a bisimulation R relating them... University Dortmund, CS Kolloquium, p.10/32
35 Bisimulation - LTS Consider the LTS a s0 t0 a t2 a b b s1 t1 t3 Transfer condition: s, t R = s a s ( t ) t a t, s, t R, t a t ( s ) s a s, s, t R b University Dortmund, CS Kolloquium, p.10/32
36 Bisimulation - generative Consider the generative systems a[ 1 2 ] s0 b[ 1 2 ] t0 b[ 1 2 ] a[ 1 2 ] a[ 1 3 ] a[ 1 6 ] t2 s1 t1 t3 b[ 1 2 ] University Dortmund, CS Kolloquium, p.11/32
37 Bisimulation - generative Consider the generative systems a[ 1 2 ] s0 b[ 1 2 ] t0 b[ 1 2 ] a[ 1 2 ] a[ 1 3 ] a[ 1 6 ] t2 s1 t1 t3 b[ 1 2 ] The states s 0 and t 0 are bisimilar, and so are s 0 and t 2, since there is a bisimulation R relating them... University Dortmund, CS Kolloquium, p.11/32
38 Bisimulation - generative Consider the generative systems a[ 1 2 ] s0 b[ 1 2 ] t0 b[ 1 2 ] a[ 1 2 ] a[ 1 3 ] a[ 1 6 ] t2 s1 t1 t3 b[ 1 2 ] Transfer condition: s, t R = s µ ( µ ) t µ, µ R,A µ University Dortmund, CS Kolloquium, p.11/32
39 Bisimulation - simple Segala Consider the simple Segala systems a s0 t a 3 t2 a b b s1 t1 t3 b University Dortmund, CS Kolloquium, p.12/32
40 Bisimulation - simple Segala Consider the simple Segala systems a s0 t a 3 t2 a b b s1 t1 t3 b The states s 0 and t 0 are bisimilar, since there is a bisimulation R relating them... University Dortmund, CS Kolloquium, p.12/32
41 Bisimulation - simple Segala Consider the simple Segala systems a s0 t a 3 t2 a b b s1 t1 t3 b Transfer condition: s, t R = s a µ ( µ ) t a µ, µ R µ University Dortmund, CS Kolloquium, p.12/32
42 Coalgebraic bisimulation A bisimulation between S, α : S FS and T, β : S FS is R S T such that γ: University Dortmund, CS Kolloquium, p.13/32
43 Coalgebraic bisimulation A bisimulation between S, α : S FS and T, β : S FS is R S T such that γ: S π 1 R π 2 T α FS Fπ 1 γ FR Fπ 2 β FT University Dortmund, CS Kolloquium, p.13/32
44 Coalgebraic bisimulation A bisimulation between S, α : S FS and T, β : S FS is R S T such that γ: S π 1 R π 2 T α FS Fπ 1 γ FR Fπ 2 β FT Transfer condition: s, t R = α(s), β(t) Rel(F)(R) University Dortmund, CS Kolloquium, p.13/32
45 Coalgebraic bisimulation A bisimulation between S, α : S FS and T, β : S FS is R S T such that γ: S π 1 R π 2 T α FS Fπ 1 γ FR Fπ 2 β FT Theorem: Coalgebraic and concrete bisimilarity coincide! University Dortmund, CS Kolloquium, p.13/32
46 Expressiveness simple Segala system Segala system a p 1 p 2 p n... University Dortmund, CS Kolloquium, p.14/32
47 Expressiveness simple Segala system Segala system a p 1 p 2 p n... a[p 1 ] a[p n ] a[p 2 ]... University Dortmund, CS Kolloquium, p.14/32
48 Expressiveness simple Segala system Segala system a p 1 p 2 p n... a[p 1 ] a[p n ] a[p 2 ]... When do we consider one type of systems more expressive than another? University Dortmund, CS Kolloquium, p.14/32
49 Comparison criterion Coalg F Coalg G if there is a mapping S, α : S FS T S, α : S GS that preserves and reflects bisimilarity University Dortmund, CS Kolloquium, p.15/32
50 Comparison criterion Coalg F Coalg G if there is a mapping S, α : S FS T S, α : S GS that preserves and reflects bisimilarity s S,α t T,β s T S,α t T T,β University Dortmund, CS Kolloquium, p.15/32
51 Comparison criterion Coalg F Coalg G if there is a mapping S, α : S FS T S, α : S GS that preserves and reflects bisimilarity Theorem: An injective natural transformation F G is sufficient for Coalg F Coalg G University Dortmund, CS Kolloquium, p.15/32
52 Comparison criterion Coalg F Coalg G if there is a mapping S, α : S FS T S, α : S GS that preserves and reflects bisimilarity Theorem: An injective natural transformation F G is sufficient for Coalg F Coalg G proof via cocongruences - behavioral equivalence University Dortmund, CS Kolloquium, p.15/32
53 Example Indeed SSeg Seg since P(A D) Pτ PD(A injective for ) is University Dortmund, CS Kolloquium, p.16/32
54 Example Indeed SSeg Seg since P(A D) Pτ PD(A injective for ) is given by (A D) τ D(A ) University Dortmund, CS Kolloquium, p.16/32
55 Example Indeed SSeg Seg since P(A D) Pτ PD(A injective for ) is (A D) τ D(A ) given by τ X ( a, µ ) = δ a µ, where University Dortmund, CS Kolloquium, p.16/32
56 Example Indeed SSeg Seg since P(A D) Pτ PD(A injective for ) is (A D) τ D(A ) given by τ X ( a, µ ) = δ a µ, where µ µ ( x, x ) = µ(x) µ (x ) University Dortmund, CS Kolloquium, p.16/32
57 Example Indeed SSeg Seg since P(A D) Pτ PD(A injective for ) is (A D) τ D(A ) given by τ X ( a, µ ) = δ a µ, where µ µ ( x, x ) = µ(x) µ (x ) and δ a is Dirac distribution for a University Dortmund, CS Kolloquium, p.16/32
58 The hierarchy... MG PZ Seg Bun SSeg Var Alt React LTS Gen Str DLTS MC University Dortmund, CS Kolloquium, p.17/32
59 The hierarchy... MG PZ Seg Bun SSeg Var Alt React LTS Gen Str DLTS MC * Falk Bartels, AS, Erik de Vink University Dortmund, CS Kolloquium, p.17/32
60 LT/BT spectrum Bisimilarity is not the only semantics... University Dortmund, CS Kolloquium, p.18/32
61 LT/BT spectrum Are these non-deterministic systems equal? x a b c a b y a c University Dortmund, CS Kolloquium, p.18/32
62 LT/BT spectrum Are these non-deterministic systems equal? x a b c a b y a x and y are: different wrt. bisimilarity c University Dortmund, CS Kolloquium, p.18/32
63 LT/BT spectrum Are these non-deterministic systems equal? x a b c a b y a x and y are: different wrt. bisimilarity, but equivalent wrt. trace semantics tr(x) = tr(y) = {ab, ac} c University Dortmund, CS Kolloquium, p.18/32
64 Traces - LTS For LTS with explicit termination (NA) the set of all possible trace = linear behaviors University Dortmund, CS Kolloquium, p.19/32
65 Traces - LTS For LTS with explicit termination (NA) the set of all possible trace = linear behaviors Example: a a y x b tr(y) = b, tr(x) = a + tr(y) = a + b University Dortmund, CS Kolloquium, p.19/32
66 Traces - generative For generative probabilistic systems with ex. termination sub-probability distribution over trace = possible linear behaviors University Dortmund, CS Kolloquium, p.20/32
67 Traces - generative For generative probabilistic systems with ex. termination sub-probability distribution over trace = possible linear behaviors Example: x b[ 1 3 ] z a[1] a[ 1 3 ] 1 3 a[ 1 2 ] y 1 2 tr(x) : 1 3 a a University Dortmund, CS Kolloquium, p.20/32
68 Trace of a coalgebra? University Dortmund, CS Kolloquium, p.21/32
69 Trace of a coalgebra? Power&Turi 99 Jacobs 04 Hasuo& Jacobs 05 Ichiro Hasuo, Bart Jacobs, AS: Generic Trace Theory, CMCS 06 University Dortmund, CS Kolloquium, p.21/32
70 Trace of a coalgebra? Power&Turi 99 Jacobs 04 Hasuo& Jacobs 05 Ichiro Hasuo, Bart Jacobs, AS: Generic Trace Theory, CMCS 06 main idea: coinduction in a Kleisli category University Dortmund, CS Kolloquium, p.21/32
71 Coinduction FX F(beh) FZ α = X system beh Z final coalgebra University Dortmund, CS Kolloquium, p.22/32
72 Coinduction FX F(beh) FZ α = X system beh Z final coalgebra finality =!(morphism for any F- coalgebra) beh gives the behavior of the system this yields final coalgebra semantics University Dortmund, CS Kolloquium, p.22/32
73 Coinduction FX F(beh) FZ α = X system beh Z final coalgebra f.c.s. in Sets = bisimilarity f.c.s. in a Kleisli category = trace semantics University Dortmund, CS Kolloquium, p.22/32
74 Types of systems For trace semantics systems are suitably modelled as coalgebras in Sets X c T F X University Dortmund, CS Kolloquium, p.23/32
75 Types of systems For trace semantics systems are suitably modelled as coalgebras in Sets X c T F X monad - branching type University Dortmund, CS Kolloquium, p.23/32
76 Types of systems For trace semantics systems are suitably modelled as coalgebras in Sets X c T F X monad - branching type functor - linear i/o type University Dortmund, CS Kolloquium, p.23/32
77 Types of systems For trace semantics systems are suitably modelled as coalgebras in Sets X c T F X monad - branching type functor - linear i/o type needed: distributive law FT T F University Dortmund, CS Kolloquium, p.23/32
78 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) University Dortmund, CS Kolloquium, p.24/32
79 Distributive law is needed since branching is irrelevant: a LTS with - PF = P(1 + A ) x a a b b University Dortmund, CS Kolloquium, p.24/32
80 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab University Dortmund, CS Kolloquium, p.24/32
81 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX University Dortmund, CS Kolloquium, p.24/32
82 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX University Dortmund, CS Kolloquium, p.24/32
83 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX PFc PFPFX University Dortmund, CS Kolloquium, p.24/32
84 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX PFc PFPFX University Dortmund, CS Kolloquium, p.24/32
85 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX PFc PFPFX d.l. PPFFX University Dortmund, CS Kolloquium, p.24/32
86 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX PFc PFPFX d.l. PPFFX University Dortmund, CS Kolloquium, p.24/32
87 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX PFc PFPFX d.l. PPFFX m.m. PFFX University Dortmund, CS Kolloquium, p.24/32
88 Distributive law is needed since branching is irrelevant: LTS with - PF = P(1 + A ) a x a a b b aa x ab X c PFX PFc PFPFX d.l. PPFFX m.m. PFFX University Dortmund, CS Kolloquium, p.24/32
89 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. University Dortmund, CS Kolloquium, p.25/32
90 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. objects - sets arrows - X f Y are functions f : X T Y University Dortmund, CS Kolloquium, p.25/32
91 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. FT T F : F lifts to F Kl(T ) on Kl(T ). University Dortmund, CS Kolloquium, p.25/32
92 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. FT T F : F lifts to F Kl(T ) on Kl(T ). Hence: coalgebra X c F Kl(T ) X in Kl(T )!!! University Dortmund, CS Kolloquium, p.25/32
93 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. FT T F : F lifts to F Kl(T ) on Kl(T ). Hence: coalgebra X c F Kl(T ) X in Kl(T )!!! in Kl(T ) : X c F Kl(T ) X University Dortmund, CS Kolloquium, p.25/32
94 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. FT T F : F lifts to F Kl(T ) on Kl(T ). Hence: coalgebra X c F Kl(T ) X in Kl(T )!!! in Kl(T ) : X c F Kl(T ) X University Dortmund, CS Kolloquium, p.25/32
95 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. FT T F : F lifts to F Kl(T ) on Kl(T ). Hence: coalgebra X c F Kl(T ) X in Kl(T )!!! in Kl(T ) : X c F Kl(T ) X F Kl(T )c F Kl(T ) F Kl(T ) X University Dortmund, CS Kolloquium, p.25/32
96 Distributive law is needed for X c T FX to be a coalgebra in the Kleisli category Kl(T ).. FT T F : F lifts to F Kl(T ) on Kl(T ). Hence: coalgebra X c F Kl(T ) X in Kl(T )!!! in Kl(T ) : X c F Kl(T ) X F Kl(T )c F Kl(T ) F Kl(T ) X University Dortmund, CS Kolloquium, p.25/32
97 Main theorem - traces If, then F Kl(T ) I F Kl(T ) I η I α = η FI α 1 = I I is initial is final in Kl(T ) University Dortmund, CS Kolloquium, p.26/32
98 Main theorem - traces If, then F Kl(T ) I F Kl(T ) I η I α = η FI α 1 = I I is initial is final in Kl(T ) [α : FI = I denotes the initial F-algebra in Sets] University Dortmund, CS Kolloquium, p.26/32
99 Main theorem - traces If, then F Kl(T ) I F Kl(T ) I η I α = η FI α 1 = I I is initial is final in Kl(T ) [α : FI = I denotes the initial F-algebra in Sets] proof: via limit-colimit coincidence Smyth&Plotkin 82 University Dortmund, CS Kolloquium, p.26/32
100 The assumptions : A monad T s.t. Kl(T ) is DCpo -enriched left-strict composition University Dortmund, CS Kolloquium, p.27/32
101 The assumptions : A monad T s.t. Kl(T ) is DCpo -enriched left-strict composition A functor F that preserves ω-colimits University Dortmund, CS Kolloquium, p.27/32
102 The assumptions : A monad T s.t. Kl(T ) is DCpo -enriched left-strict composition A functor F that preserves ω-colimits A distributive law FT T F: lifting F Kl(T ) University Dortmund, CS Kolloquium, p.27/32
103 The assumptions : A monad T s.t. Kl(T ) is DCpo -enriched left-strict composition A functor F that preserves ω-colimits A distributive law FT T F: lifting F Kl(T ) F Kl(T ) should be locally monotone University Dortmund, CS Kolloquium, p.27/32
104 Corollary ( ) For X c F Kl(T ) X in Kl(T ) University Dortmund, CS Kolloquium, p.28/32
105 Corollary ( ) For X c F Kl(T ) X in Kl(T )... X c T FX in Sets University Dortmund, CS Kolloquium, p.28/32
106 Corollary ( ) For X c F Kl(T ) X in Kl(T )... X c T FX in Sets! finite trace map tr c : X T I in Sets: University Dortmund, CS Kolloquium, p.28/32
107 Corollary ( ) For X c F Kl(T ) X in Kl(T )... X c T FX in Sets! finite trace map tr c : X T I in Sets: in Kl(T ) F Kl(T ) X F Kl(T )(tr c ) c F Kl(T ) I = X tr c I University Dortmund, CS Kolloquium, p.28/32
108 It works for... lift, powerset, sub-distribution monad University Dortmund, CS Kolloquium, p.29/32
109 It works for... lift, powerset, sub-distribution monad shapely functors - almost all polynomial University Dortmund, CS Kolloquium, p.29/32
110 It works for... lift, powerset, sub-distribution monad shapely functors - almost all polynomial Hence: University Dortmund, CS Kolloquium, p.29/32
111 It works for... lift, powerset, sub-distribution monad shapely functors - almost all polynomial Hence: * for LTS with explicit termination P(1 + A ) University Dortmund, CS Kolloquium, p.29/32
112 It works for... lift, powerset, sub-distribution monad shapely functors - almost all polynomial Hence: * for LTS with explicit termination P(1 + A ) * for generative systems with explicit termination D(1 + A ) University Dortmund, CS Kolloquium, p.29/32
113 It works for... lift, powerset, sub-distribution monad shapely functors - almost all polynomial Hence: * for LTS with explicit termination P(1 + A ) * for generative systems with explicit termination D(1 + A ) Note: Initial 1 + A - algebra is A [nil,cons] = 1 + A A University Dortmund, CS Kolloquium, p.29/32
114 Finite traces - LTS with the finality diagram in Kl(P) F Kl(P) X F Kl(P)(tr c ) c F Kl(P) A = X tr c A University Dortmund, CS Kolloquium, p.30/32
115 Finite traces - LTS with the finality diagram in Kl(P) 1 + A X (1+A ) Kl(P)(tr c ) c 1 + A A = X tr c A University Dortmund, CS Kolloquium, p.30/32
116 Finite traces - LTS with the finality diagram in Kl(P) 1 + A X (1+A ) Kl(P)(tr c ) c 1 + A A = X amounts to tr c A tr c (x) c(x) a w tr c (x) ( x ) a, x c(x), w tr c (x ) University Dortmund, CS Kolloquium, p.30/32
117 Finite traces - generative the finality diagram in Kl(D) F Kl(D) X F Kl(D)(tr c ) F Kl(D) A c = X tr c A University Dortmund, CS Kolloquium, p.31/32
118 Finite traces - generative the finality diagram in Kl(D) 1 + A X (1+A ) Kl(D)(tr c ) c 1 + A A = X tr c A University Dortmund, CS Kolloquium, p.31/32
119 Finite traces - generative the finality diagram in Kl(D) 1 + A X (1+A ) Kl(D)(tr c ) c 1 + A A = X amounts to tr c (x) : tr c A c(x)( ) a w y X c(x)(a, y) c(y)(w) University Dortmund, CS Kolloquium, p.31/32
120 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS University Dortmund, CS Kolloquium, p.32/32
121 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS Coinduction gives us semantic relations: University Dortmund, CS Kolloquium, p.32/32
122 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS Coinduction gives us semantic relations: * bisimilarity for F-systems in Sets University Dortmund, CS Kolloquium, p.32/32
123 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS Coinduction gives us semantic relations: * bisimilarity for F-systems in Sets * trace semantics for T F-systems in Kl(T ) University Dortmund, CS Kolloquium, p.32/32
124 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS Coinduction gives us semantic relations: * bisimilarity for F-systems in Sets * trace semantics for T F-systems in Kl(T ) Other monads e.g. PD?... suitable monad/order structure yet to be found (Varacca&Winskel) University Dortmund, CS Kolloquium, p.32/32
125 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS Coinduction gives us semantic relations: * bisimilarity for F-systems in Sets * trace semantics for T F-systems in Kl(T ) Other monads e.g. PD?... suitable monad/order structure yet to be found (Varacca&Winskel) Other semantics?.. between bisimilarity and trace in the spectrum University Dortmund, CS Kolloquium, p.32/32
126 Conclusions & future work Coalgebras allow for a unified treatment and expressiveness study of (P)TS Coinduction gives us semantic relations: * bisimilarity for F-systems in Sets * trace semantics for T F-systems in Kl(T ) Other monads e.g. PD?... suitable monad/order structure yet to be found (Varacca&Winskel) Other semantics?.. between bisimilarity and trace in the spectrum University Dortmund, CS Kolloquium, p.32/32
A Coalgebraic Foundation for Coinductive Union Types
 A Coalgebraic Foundation for Coinductive Union Types M. Bonsangue 1,2, J. Rot 1,2,, D. Ancona 3, F. de Boer 2,1, and J. Rutten 2,4 1 LIACS Leiden University 2 Formal Methods Centrum Wiskunde en Informatica
A Coalgebraic Foundation for Coinductive Union Types M. Bonsangue 1,2, J. Rot 1,2,, D. Ancona 3, F. de Boer 2,1, and J. Rutten 2,4 1 LIACS Leiden University 2 Formal Methods Centrum Wiskunde en Informatica
Resource-bound process algebras for Schedulability and Performance Analysis of Real-Time and Embedded Systems
 Resource-bound process algebras for Schedulability and Performance Analysis of Real-Time and Embedded Systems Insup Lee 1, Oleg Sokolsky 1, Anna Philippou 2 1 RTG (Real-Time Systems Group) Department of
Resource-bound process algebras for Schedulability and Performance Analysis of Real-Time and Embedded Systems Insup Lee 1, Oleg Sokolsky 1, Anna Philippou 2 1 RTG (Real-Time Systems Group) Department of
Lecture 17: Continuous Functions
 Lecture 17: Continuous Functions 1 Continuous Functions Let (X, T X ) and (Y, T Y ) be topological spaces. Definition 1.1 (Continuous Function). A function f : X Y is said to be continuous if the inverse
Lecture 17: Continuous Functions 1 Continuous Functions Let (X, T X ) and (Y, T Y ) be topological spaces. Definition 1.1 (Continuous Function). A function f : X Y is said to be continuous if the inverse
Monads T T T T T. Dually (by inverting the arrows in the given definition) one can define the notion of a comonad. T T
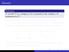 Monads Definition A monad T is a category C is a monoid in the category of endofunctors C C. More explicitly, a monad in C is a triple T, η, µ, where T : C C is a functor and η : I C T, µ : T T T are natural
Monads Definition A monad T is a category C is a monoid in the category of endofunctors C C. More explicitly, a monad in C is a triple T, η, µ, where T : C C is a functor and η : I C T, µ : T T T are natural
Monads and More: Part 3
 Monads and More: Part 3 Tarmo Uustalu, Tallinn Nottingham, 14 18 May 2007 Arrows (Hughes) Arrows are a generalization of strong monads on symmetric monoidal categories (in their Kleisli triple form). An
Monads and More: Part 3 Tarmo Uustalu, Tallinn Nottingham, 14 18 May 2007 Arrows (Hughes) Arrows are a generalization of strong monads on symmetric monoidal categories (in their Kleisli triple form). An
On the duality of topological Boolean algebras
 On the duality of topological Boolean algebras Matthew de Brecht 1 Graduate School of Human and Environmental Studies, Kyoto University Workshop on Mathematical Logic and its Applications 2016 1 This work
On the duality of topological Boolean algebras Matthew de Brecht 1 Graduate School of Human and Environmental Studies, Kyoto University Workshop on Mathematical Logic and its Applications 2016 1 This work
Contents Introduction and Technical Preliminaries Composition of Schema Mappings: Syntax and Semantics
 1 Introduction and Technical Preliminaries... 1 1.1 Historical Background... 1 1.2 Introduction to Lattices, Algebras and Intuitionistic Logics... 5 1.3 Introduction to First-Order Logic (FOL)... 12 1.3.1
1 Introduction and Technical Preliminaries... 1 1.1 Historical Background... 1 1.2 Introduction to Lattices, Algebras and Intuitionistic Logics... 5 1.3 Introduction to First-Order Logic (FOL)... 12 1.3.1
A more elegant specification for FRP
 A more elegant specification for FRP Conal Elliott LambdaJam 2015 Conal Elliott A more elegant specification for FRP LambdaJam 2015 1 / 20 The story so far Conal Elliott A more elegant specification for
A more elegant specification for FRP Conal Elliott LambdaJam 2015 Conal Elliott A more elegant specification for FRP LambdaJam 2015 1 / 20 The story so far Conal Elliott A more elegant specification for
Duality for first order logic
 Duality for first order logic Dion Coumans Radboud University Nijmegen MLNL, May 2010 Outline 1 Duality in logic 2 Algebraic semantics for classical first order logic: Boolean hyperdoctrines 3 Dual notion
Duality for first order logic Dion Coumans Radboud University Nijmegen MLNL, May 2010 Outline 1 Duality in logic 2 Algebraic semantics for classical first order logic: Boolean hyperdoctrines 3 Dual notion
Substitution in Structural Operational Semantics and value-passing process calculi
 Substitution in Structural Operational Semantics and value-passing process calculi Sam Staton Computer Laboratory University of Cambridge Abstract Consider a process calculus that allows agents to communicate
Substitution in Structural Operational Semantics and value-passing process calculi Sam Staton Computer Laboratory University of Cambridge Abstract Consider a process calculus that allows agents to communicate
A MODEL CATEGORY STRUCTURE ON THE CATEGORY OF SIMPLICIAL CATEGORIES
 A MODEL CATEGORY STRUCTURE ON THE CATEGORY OF SIMPLICIAL CATEGORIES JULIA E. BERGNER Abstract. In this paper we put a cofibrantly generated model category structure on the category of small simplicial
A MODEL CATEGORY STRUCTURE ON THE CATEGORY OF SIMPLICIAL CATEGORIES JULIA E. BERGNER Abstract. In this paper we put a cofibrantly generated model category structure on the category of small simplicial
The essence of dataflow programming
 The essence of dataflow programming Tarmo Uustalu 1 2 1 Institute of Cybernetics Tallinn University of Technology 2 Department of Computer Science University of Tartu WG2.8 workshop, Kalvi, 1-4 September
The essence of dataflow programming Tarmo Uustalu 1 2 1 Institute of Cybernetics Tallinn University of Technology 2 Department of Computer Science University of Tartu WG2.8 workshop, Kalvi, 1-4 September
Homotopy theory of higher categorical structures
 University of California, Riverside August 8, 2013 Higher categories In a category, we have morphisms, or functions, between objects. But what if you have functions between functions? This gives the idea
University of California, Riverside August 8, 2013 Higher categories In a category, we have morphisms, or functions, between objects. But what if you have functions between functions? This gives the idea
A NOTE ON MORPHISMS DETERMINED BY OBJECTS
 A NOTE ON MORPHISMS DETERMINED BY OBJECTS XIAO-WU CHEN, JUE LE Abstract. We prove that a Hom-finite additive category having determined morphisms on both sides is a dualizing variety. This complements
A NOTE ON MORPHISMS DETERMINED BY OBJECTS XIAO-WU CHEN, JUE LE Abstract. We prove that a Hom-finite additive category having determined morphisms on both sides is a dualizing variety. This complements
Recursively defined cpo algebras
 Recursively defined cpo algebras Ohad Kammar and Paul Blain Levy July 13, 2018 Ohad Kammar and Paul Blain Levy Recursively defined cpo algebras July 13, 2018 1 / 16 Outline 1 Bilimit compact categories
Recursively defined cpo algebras Ohad Kammar and Paul Blain Levy July 13, 2018 Ohad Kammar and Paul Blain Levy Recursively defined cpo algebras July 13, 2018 1 / 16 Outline 1 Bilimit compact categories
Functions. How is this definition written in symbolic logic notation?
 functions 1 Functions Def. Let A and B be sets. A function f from A to B is an assignment of exactly one element of B to each element of A. We write f(a) = b if b is the unique element of B assigned by
functions 1 Functions Def. Let A and B be sets. A function f from A to B is an assignment of exactly one element of B to each element of A. We write f(a) = b if b is the unique element of B assigned by
Recursive Types. Chapter 7
 Chapter 7 Recursive Types By adding special rules for natural numbers to λ, we obtained system T. We may now want to have separate rules for other data structures: lists, binary trees, streams. We can
Chapter 7 Recursive Types By adding special rules for natural numbers to λ, we obtained system T. We may now want to have separate rules for other data structures: lists, binary trees, streams. We can
Lecture Note: Types. 1 Introduction 2. 2 Simple Types 3. 3 Type Soundness 6. 4 Recursive Types Subtyping 17
 Jens Palsberg Sep 24, 1999 Contents Lecture Note: Types 1 Introduction 2 2 Simple Types 3 3 Type Soundness 6 4 Recursive Types 12 5 Subtyping 17 6 Decision Procedure for Subtyping 19 7 First-Order Unification
Jens Palsberg Sep 24, 1999 Contents Lecture Note: Types 1 Introduction 2 2 Simple Types 3 3 Type Soundness 6 4 Recursive Types 12 5 Subtyping 17 6 Decision Procedure for Subtyping 19 7 First-Order Unification
Topos Theory. Lectures 3-4: Categorical preliminaries II. Olivia Caramello. Topos Theory. Olivia Caramello. Basic categorical constructions
 Lectures 3-4: Categorical preliminaries II 2 / 17 Functor categories Definition Let C and D be two categories. The functor category [C,D] is the category having as objects the functors C D and as arrows
Lectures 3-4: Categorical preliminaries II 2 / 17 Functor categories Definition Let C and D be two categories. The functor category [C,D] is the category having as objects the functors C D and as arrows
From Types to Sets in Isabelle/HOL
 From Types to Sets in Isabelle/HOL Extented Abstract Ondřej Kunčar 1 and Andrei Popescu 1,2 1 Fakultät für Informatik, Technische Universität München, Germany 2 Institute of Mathematics Simion Stoilow
From Types to Sets in Isabelle/HOL Extented Abstract Ondřej Kunčar 1 and Andrei Popescu 1,2 1 Fakultät für Informatik, Technische Universität München, Germany 2 Institute of Mathematics Simion Stoilow
Petri Nets ee249 Fall 2000
 Petri Nets ee249 Fall 2000 Marco Sgroi Most slides borrowed from Luciano Lavagno s lecture ee249 (1998) 1 Models Of Computation for reactive systems Main MOCs: Communicating Finite State Machines Dataflow
Petri Nets ee249 Fall 2000 Marco Sgroi Most slides borrowed from Luciano Lavagno s lecture ee249 (1998) 1 Models Of Computation for reactive systems Main MOCs: Communicating Finite State Machines Dataflow
in simplicial sets, or equivalently a functor
 Contents 21 Bisimplicial sets 1 22 Homotopy colimits and limits (revisited) 10 23 Applications, Quillen s Theorem B 23 21 Bisimplicial sets A bisimplicial set X is a simplicial object X : op sset in simplicial
Contents 21 Bisimplicial sets 1 22 Homotopy colimits and limits (revisited) 10 23 Applications, Quillen s Theorem B 23 21 Bisimplicial sets A bisimplicial set X is a simplicial object X : op sset in simplicial
Modelling environments in call-by-value programming languages
 Modelling environments in call-by-value programming languages Paul Blain Levy University of Birmingham, Birmingham B15 2TT, UK pbl@cs.bham.ac.uk and John Power 1 University of Edinburgh, Edinburgh EH9
Modelling environments in call-by-value programming languages Paul Blain Levy University of Birmingham, Birmingham B15 2TT, UK pbl@cs.bham.ac.uk and John Power 1 University of Edinburgh, Edinburgh EH9
Initial Algebra Semantics for Cyclic Sharing Structures. Makoto Hamana
 Initial Algebra Semantics for Cyclic Sharing Structures Makoto Hamana Department of Computer Science, Gunma University, Japan July, 2009, TLCA 09 http://www.cs.gunma-u.ac.jp/ hamana/ This Work How to inductively
Initial Algebra Semantics for Cyclic Sharing Structures Makoto Hamana Department of Computer Science, Gunma University, Japan July, 2009, TLCA 09 http://www.cs.gunma-u.ac.jp/ hamana/ This Work How to inductively
COALGEBRAIC MODELS FOR COMBINATORIAL MODEL CATEGORIES
 COALGEBRAIC MODELS FOR COMBINATORIAL MODEL CATEGORIES MICHAEL CHING AND EMILY RIEHL Abstract. We show that the category of algebraically cofibrant objects in a combinatorial and simplicial model category
COALGEBRAIC MODELS FOR COMBINATORIAL MODEL CATEGORIES MICHAEL CHING AND EMILY RIEHL Abstract. We show that the category of algebraically cofibrant objects in a combinatorial and simplicial model category
Lecture 008 (November 13, 2009)
 Lecture 008 (November 13, 2009) 17 The Dold-Kan correspondence Suppose that A : op R Mod is a simplicial R-module. Examples to keep in mind are the free simplicial objects R(X) associated to simplicial
Lecture 008 (November 13, 2009) 17 The Dold-Kan correspondence Suppose that A : op R Mod is a simplicial R-module. Examples to keep in mind are the free simplicial objects R(X) associated to simplicial
Inductive Types for Free
 Inductive Types for Free Representing Nested Inductive Types using W-types Michael Abbott (U. Leicester) Thorsten Altenkirch (U. Nottingham) Neil Ghani (U. Leicester) Inductive Types for Free p.1/22 Ideology
Inductive Types for Free Representing Nested Inductive Types using W-types Michael Abbott (U. Leicester) Thorsten Altenkirch (U. Nottingham) Neil Ghani (U. Leicester) Inductive Types for Free p.1/22 Ideology
The formal theory of homotopy coherent monads
 The formal theory of homotopy coherent monads Emily Riehl Harvard University http://www.math.harvard.edu/~eriehl 23 July, 2013 Samuel Eilenberg Centenary Conference Warsaw, Poland Joint with Dominic Verity.
The formal theory of homotopy coherent monads Emily Riehl Harvard University http://www.math.harvard.edu/~eriehl 23 July, 2013 Samuel Eilenberg Centenary Conference Warsaw, Poland Joint with Dominic Verity.
Point-Set Topology II
 Point-Set Topology II Charles Staats September 14, 2010 1 More on Quotients Universal Property of Quotients. Let X be a topological space with equivalence relation. Suppose that f : X Y is continuous and
Point-Set Topology II Charles Staats September 14, 2010 1 More on Quotients Universal Property of Quotients. Let X be a topological space with equivalence relation. Suppose that f : X Y is continuous and
Behavioural Equivalences and Abstraction Techniques. Natalia Sidorova
 Behavioural Equivalences and Abstraction Techniques Natalia Sidorova Part 1: Behavioural Equivalences p. p. The elevator example once more How to compare this elevator model with some other? The cabin
Behavioural Equivalences and Abstraction Techniques Natalia Sidorova Part 1: Behavioural Equivalences p. p. The elevator example once more How to compare this elevator model with some other? The cabin
Sheaves and Stacks. November 5, Sheaves and Stacks
 November 5, 2014 Grothendieck topologies Grothendieck topologies are an extra datum on a category. They allow us to make sense of something being locally defined. Give a formal framework for glueing problems
November 5, 2014 Grothendieck topologies Grothendieck topologies are an extra datum on a category. They allow us to make sense of something being locally defined. Give a formal framework for glueing problems
Lecture 18: Groupoids and spaces
 Lecture 18: Groupoids and spaces The simplest algebraic invariant of a topological space T is the set π 0 T of path components. The next simplest invariant, which encodes more of the topology, is the fundamental
Lecture 18: Groupoids and spaces The simplest algebraic invariant of a topological space T is the set π 0 T of path components. The next simplest invariant, which encodes more of the topology, is the fundamental
THE DOLD-KAN CORRESPONDENCE
 THE DOLD-KAN CORRESPONDENCE 1. Simplicial sets We shall now introduce the notion of a simplicial set, which will be a presheaf on a suitable category. It turns out that simplicial sets provide a (purely
THE DOLD-KAN CORRESPONDENCE 1. Simplicial sets We shall now introduce the notion of a simplicial set, which will be a presheaf on a suitable category. It turns out that simplicial sets provide a (purely
Inductive datatypes in HOL. lessons learned in Formal-Logic Engineering
 Inductive datatypes in HOL lessons learned in Formal-Logic Engineering Stefan Berghofer and Markus Wenzel Institut für Informatik TU München = Isabelle λ β HOL α 1 Introduction Applications of inductive
Inductive datatypes in HOL lessons learned in Formal-Logic Engineering Stefan Berghofer and Markus Wenzel Institut für Informatik TU München = Isabelle λ β HOL α 1 Introduction Applications of inductive
Towards a Coalgebraic Semantics of UML: Class Diagrams and Use Cases
 UNU/IIST International Institute for Software Technology Towards a Coalgebraic Semantics of UML: Class Diagrams and Use Cases Sun Meng and Bernhard K. Aichernig January, 2003 UNU/IIST Report No. 272 R
UNU/IIST International Institute for Software Technology Towards a Coalgebraic Semantics of UML: Class Diagrams and Use Cases Sun Meng and Bernhard K. Aichernig January, 2003 UNU/IIST Report No. 272 R
Cubical sets as a classifying topos
 Chalmers CMU Now: Aarhus University Homotopy Type Theory The homotopical interpretation of type theory: types as spaces upto homotopy dependent types as fibrations (continuous families of spaces) identity
Chalmers CMU Now: Aarhus University Homotopy Type Theory The homotopical interpretation of type theory: types as spaces upto homotopy dependent types as fibrations (continuous families of spaces) identity
The essence of dataflow programming. Teooriapäevad Kokel 2,
 The essence of dataflow programming Tarmo UUSTALU Varmo VENE Teooriapäevad Kokel 2, 4.-6.2.2005 Motivation Following Moggi and Wadler, it is standard in programming and semantics to analyze various notions
The essence of dataflow programming Tarmo UUSTALU Varmo VENE Teooriapäevad Kokel 2, 4.-6.2.2005 Motivation Following Moggi and Wadler, it is standard in programming and semantics to analyze various notions
Part 2.2 Continuous functions and their properties v1 2018
 Part 2.2 Continuous functions and their properties v 208 Intermediate Values Recall R is complete. This means that ever non-empt subset of R which is bounded above has a least upper bound. That is: (A
Part 2.2 Continuous functions and their properties v 208 Intermediate Values Recall R is complete. This means that ever non-empt subset of R which is bounded above has a least upper bound. That is: (A
Simplicial Objects and Homotopy Groups
 Simplicial Objects and Homotopy Groups Jie Wu Department of Mathematics National University of Singapore July 8, 2007 Simplicial Objects and Homotopy Groups -Objects and Homology Simplicial Sets and Homotopy
Simplicial Objects and Homotopy Groups Jie Wu Department of Mathematics National University of Singapore July 8, 2007 Simplicial Objects and Homotopy Groups -Objects and Homology Simplicial Sets and Homotopy
Metrics on diagrams and persistent homology
 Background Categorical ph Relative ph More structure Department of Mathematics Cleveland State University p.bubenik@csuohio.edu http://academic.csuohio.edu/bubenik_p/ July 18, 2013 joint work with Vin
Background Categorical ph Relative ph More structure Department of Mathematics Cleveland State University p.bubenik@csuohio.edu http://academic.csuohio.edu/bubenik_p/ July 18, 2013 joint work with Vin
Labelled Transition Systems For a Game Graph
 Labelled Transition Systems For a Game Graph Soren Lassen 1 Paul Blain Levy 2 1 Google, Inc. 2 University of Birmingham March 29, 2009 Soren Lassen, Paul Blain Levy ( Google, Inc., UniversityLTSs of Birmingham)
Labelled Transition Systems For a Game Graph Soren Lassen 1 Paul Blain Levy 2 1 Google, Inc. 2 University of Birmingham March 29, 2009 Soren Lassen, Paul Blain Levy ( Google, Inc., UniversityLTSs of Birmingham)
On the Expressiveness of Polyadicity in Higher-Order Process Calculi
 On the Expressiveness of Polyadicity in Higher-Order Process Calculi Ivan Lanese, Jorge A. Pérez, Davide Sangiorgi (Univ. di Bologna) Alan Schmitt (INRIA Grenoble - Rhône Alpes) ICTCS 09 Cremona, September
On the Expressiveness of Polyadicity in Higher-Order Process Calculi Ivan Lanese, Jorge A. Pérez, Davide Sangiorgi (Univ. di Bologna) Alan Schmitt (INRIA Grenoble - Rhône Alpes) ICTCS 09 Cremona, September
Homology cycle bases from acyclic matchings
 Homology cycle bases from acyclic matchings Dmitry Feichtner-Kozlov University of Bremen Kyoto Workshop, January 019 What is... Applied Topology? studying global features of shapes applications in other
Homology cycle bases from acyclic matchings Dmitry Feichtner-Kozlov University of Bremen Kyoto Workshop, January 019 What is... Applied Topology? studying global features of shapes applications in other
Schema-Guided Query Induction
 Schema-Guided Query Induction Jérôme Champavère Ph.D. Defense September 10, 2010 Supervisors: Joachim Niehren and Rémi Gilleron Advisor: Aurélien Lemay Introduction Big Picture XML: Standard language for
Schema-Guided Query Induction Jérôme Champavère Ph.D. Defense September 10, 2010 Supervisors: Joachim Niehren and Rémi Gilleron Advisor: Aurélien Lemay Introduction Big Picture XML: Standard language for
On partial order semantics for SAT/SMT-based symbolic encodings of weak memory concurrency
 On partial order semantics for SAT/SMT-based symbolic encodings of weak memory concurrency Alex Horn and Daniel Kroening University of Oxford April 30, 2015 Outline What s Our Problem? Motivation and Example
On partial order semantics for SAT/SMT-based symbolic encodings of weak memory concurrency Alex Horn and Daniel Kroening University of Oxford April 30, 2015 Outline What s Our Problem? Motivation and Example
Topoi: Theory and Applications
 : Theory and Applications 1 1 Computer Science, Swansea University, UK http://cs.swan.ac.uk/~csoliver Categorical logic seminar Swansea, March 19+23, 2012 Meaning I treat topos theory as a theory, whose
: Theory and Applications 1 1 Computer Science, Swansea University, UK http://cs.swan.ac.uk/~csoliver Categorical logic seminar Swansea, March 19+23, 2012 Meaning I treat topos theory as a theory, whose
EECS 144/244: Fundamental Algorithms for System Modeling, Analysis, and Optimization
 EECS 144/244: Fundamental Algorithms for System Modeling, Analysis, and Optimization Dataflow Lecture: SDF, Kahn Process Networks Stavros Tripakis University of California, Berkeley Stavros Tripakis: EECS
EECS 144/244: Fundamental Algorithms for System Modeling, Analysis, and Optimization Dataflow Lecture: SDF, Kahn Process Networks Stavros Tripakis University of California, Berkeley Stavros Tripakis: EECS
Using context and model categories to define directed homotopies
 Using context and model categories to define directed homotopies p. 1/57 Using context and model categories to define directed homotopies Peter Bubenik Ecole Polytechnique Fédérale de Lausanne (EPFL) peter.bubenik@epfl.ch
Using context and model categories to define directed homotopies p. 1/57 Using context and model categories to define directed homotopies Peter Bubenik Ecole Polytechnique Fédérale de Lausanne (EPFL) peter.bubenik@epfl.ch
Measurable Preorders and Complexity
 Measurable Preorders and Complexity Thomas Seiller 1 Proofs, Programs, Systems Paris 7 University seiller@ihes.fr TACL 2015 June 26th, 2015 1 Partially supported by ANR-12-JS02-006-01 COQUAS. T. Seiller
Measurable Preorders and Complexity Thomas Seiller 1 Proofs, Programs, Systems Paris 7 University seiller@ihes.fr TACL 2015 June 26th, 2015 1 Partially supported by ANR-12-JS02-006-01 COQUAS. T. Seiller
Combinatorics I (Lecture 36)
 Combinatorics I (Lecture 36) February 18, 2015 Our goal in this lecture (and the next) is to carry out the combinatorial steps in the proof of the main theorem of Part III. We begin by recalling some notation
Combinatorics I (Lecture 36) February 18, 2015 Our goal in this lecture (and the next) is to carry out the combinatorial steps in the proof of the main theorem of Part III. We begin by recalling some notation
CATEGORIES AND COMPUTATION BRIEF MONAD EXAMPLE. Andrew R. Plummer. Department of Linguistics The Ohio State University.
 BRIEF MONAD EXAMPLE Andrew R. Plummer Department of Linguistics The Ohio State University 28 Oct, 2009 OUTLINE 1 CATEGORIES AND COMPUTATION IO PROBLEM AS MOTIVATION Suppose we have a relation R between
BRIEF MONAD EXAMPLE Andrew R. Plummer Department of Linguistics The Ohio State University 28 Oct, 2009 OUTLINE 1 CATEGORIES AND COMPUTATION IO PROBLEM AS MOTIVATION Suppose we have a relation R between
Tutorial: Computable Model Theory and Differential Algebra
 Tutorial: Computable Model Theory and Differential Algebra Russell Miller, Queens College & Graduate Center C.U.N.Y. April 12, 2007 Workshop in Differential Algebra and Related Topics Rutgers University,
Tutorial: Computable Model Theory and Differential Algebra Russell Miller, Queens College & Graduate Center C.U.N.Y. April 12, 2007 Workshop in Differential Algebra and Related Topics Rutgers University,
Topological Rewriting & Patch Transformations
 Topological Rewriting & Patch Transformations Antoine Spicher www.spatial-computing.org/mgs SUPMECA June 2015 Outline MGS: a Formal Introduction Patch Transformations Differential Operators An Integrative
Topological Rewriting & Patch Transformations Antoine Spicher www.spatial-computing.org/mgs SUPMECA June 2015 Outline MGS: a Formal Introduction Patch Transformations Differential Operators An Integrative
On the Component Number of Links from Plane Graphs
 On the Component Number of Links from Plane Graphs Daniel S. Silver Susan G. Williams January 20, 2015 Abstract A short, elementary proof is given of the result that the number of components of a link
On the Component Number of Links from Plane Graphs Daniel S. Silver Susan G. Williams January 20, 2015 Abstract A short, elementary proof is given of the result that the number of components of a link
ACLT: Algebra, Categories, Logic in Topology - Grothendieck's generalized topological spaces (toposes)
 ACLT: Algebra, Categories, Logic in Topology - Grothendieck's generalized topological spaces (toposes) Steve Vickers CS Theory Group Birmingham 4. Toposes and geometric reasoning How to "do generalized
ACLT: Algebra, Categories, Logic in Topology - Grothendieck's generalized topological spaces (toposes) Steve Vickers CS Theory Group Birmingham 4. Toposes and geometric reasoning How to "do generalized
The universal triangle-free graph has finite big Ramsey degrees
 The universal triangle-free graph has finite big Ramsey degrees Natasha Dobrinen University of Denver ASL, March 22, 2017 Dobrinen big Ramsey degrees University of Denver 1 / 59 Ramsey s Theorem Ramsey
The universal triangle-free graph has finite big Ramsey degrees Natasha Dobrinen University of Denver ASL, March 22, 2017 Dobrinen big Ramsey degrees University of Denver 1 / 59 Ramsey s Theorem Ramsey
Inductive Definitions, continued
 1 / 27 Inductive Definitions, continued Assia Mahboubi Jan 7th, 2016 2 / 27 Last lecture Introduction to Coq s inductive types: Introduction, elimination and computation rules; Twofold implementation :
1 / 27 Inductive Definitions, continued Assia Mahboubi Jan 7th, 2016 2 / 27 Last lecture Introduction to Coq s inductive types: Introduction, elimination and computation rules; Twofold implementation :
PS Geometric Modeling Homework Assignment Sheet I (Due 20-Oct-2017)
 Homework Assignment Sheet I (Due 20-Oct-2017) Assignment 1 Let n N and A be a finite set of cardinality n = A. By definition, a permutation of A is a bijective function from A to A. Prove that there exist
Homework Assignment Sheet I (Due 20-Oct-2017) Assignment 1 Let n N and A be a finite set of cardinality n = A. By definition, a permutation of A is a bijective function from A to A. Prove that there exist
An introduction to Category Theory for Software Engineers*
 An introduction to Category Theory for Software Engineers* Dr Steve Easterbrook Associate Professor, Dept of Computer Science, University of Toronto sme@cs.toronto.edu *slides available at http://www.cs.toronto.edu/~sme/presentations/cat101.pdf
An introduction to Category Theory for Software Engineers* Dr Steve Easterbrook Associate Professor, Dept of Computer Science, University of Toronto sme@cs.toronto.edu *slides available at http://www.cs.toronto.edu/~sme/presentations/cat101.pdf
Lecture 009 (November 25, 2009) Suppose that I is a small category, and let s(r Mod) I be the category of I-diagrams in simplicial modules.
 Lecture 009 (November 25, 2009) 20 Homotopy colimits Suppose that I is a small category, and let s(r Mod) I be the category of I-diagrams in simplicial modules. The objects of this category are the functors
Lecture 009 (November 25, 2009) 20 Homotopy colimits Suppose that I is a small category, and let s(r Mod) I be the category of I-diagrams in simplicial modules. The objects of this category are the functors
Towards a Logical Reconstruction of Relational Database Theory
 Towards a Logical Reconstruction of Relational Database Theory On Conceptual Modelling, Lecture Notes in Computer Science. 1984 Raymond Reiter Summary by C. Rey November 27, 2008-1 / 63 Foreword DB: 2
Towards a Logical Reconstruction of Relational Database Theory On Conceptual Modelling, Lecture Notes in Computer Science. 1984 Raymond Reiter Summary by C. Rey November 27, 2008-1 / 63 Foreword DB: 2
Crash Course in Monads. Vlad Patryshev
 Crash Course in Monads Vlad Patryshev Introduction Monads in programming seem to be the most mysterious notion of the century. I find two reasons for this: lack of familiarity with category theory; many
Crash Course in Monads Vlad Patryshev Introduction Monads in programming seem to be the most mysterious notion of the century. I find two reasons for this: lack of familiarity with category theory; many
On the Recognizability of Arrow and Graph Languages
 On the Recognizability of Arrow and Graph Languages Christoph Blume Sander Bruggink Barbara König Universität Duisburg-Essen, Germany Background Applications of finite automata and regular (word) languages
On the Recognizability of Arrow and Graph Languages Christoph Blume Sander Bruggink Barbara König Universität Duisburg-Essen, Germany Background Applications of finite automata and regular (word) languages
4. Definition: topological space, open set, topology, trivial topology, discrete topology.
 Topology Summary Note to the reader. If a statement is marked with [Not proved in the lecture], then the statement was stated but not proved in the lecture. Of course, you don t need to know the proof.
Topology Summary Note to the reader. If a statement is marked with [Not proved in the lecture], then the statement was stated but not proved in the lecture. Of course, you don t need to know the proof.
XPath with transitive closure
 XPath with transitive closure Logic and Databases Feb 2006 1 XPath with transitive closure Logic and Databases Feb 2006 2 Navigating XML trees XPath with transitive closure Newton Institute: Logic and
XPath with transitive closure Logic and Databases Feb 2006 1 XPath with transitive closure Logic and Databases Feb 2006 2 Navigating XML trees XPath with transitive closure Newton Institute: Logic and
Partial semigroups: Categories and Constellations
 Partial semigroups: Categories and Constellations CSA 2016 In honour of Jorge Almeida and Gracinda Gomes Lisbon, 21st June 2016 Victoria Gould University of York Gracinda Gracinda Jorge Jorge Partial semigroups
Partial semigroups: Categories and Constellations CSA 2016 In honour of Jorge Almeida and Gracinda Gomes Lisbon, 21st June 2016 Victoria Gould University of York Gracinda Gracinda Jorge Jorge Partial semigroups
Generic Programming with Adjunctions
 Generic Programming with Adjunctions 0.0 Generic Programming with Adjunctions Ralf Hinze Computing Laboratory, University of Oxford Wolfson Building, Parks Road, Oxford, OX1 3QD, England ralf.hinze@comlab.ox.ac.uk
Generic Programming with Adjunctions 0.0 Generic Programming with Adjunctions Ralf Hinze Computing Laboratory, University of Oxford Wolfson Building, Parks Road, Oxford, OX1 3QD, England ralf.hinze@comlab.ox.ac.uk
On the Boolean Algebra of Shape Analysis Constraints
 On the Boolean Algebra of Shape Analysis Constraints Viktor Kuncak and Martin Rinard Computer Science and Artificial Intelligence Laboratory Massachusetts Institute of Technology Cambridge, MA 02139, USA
On the Boolean Algebra of Shape Analysis Constraints Viktor Kuncak and Martin Rinard Computer Science and Artificial Intelligence Laboratory Massachusetts Institute of Technology Cambridge, MA 02139, USA
Notes on categories, the subspace topology and the product topology
 Notes on categories, the subspace topology and the product topology John Terilla Fall 2014 Contents 1 Introduction 1 2 A little category theory 1 3 The subspace topology 3 3.1 First characterization of
Notes on categories, the subspace topology and the product topology John Terilla Fall 2014 Contents 1 Introduction 1 2 A little category theory 1 3 The subspace topology 3 3.1 First characterization of
Higher Gauge Theory: 2-Connections
 Higher Gauge Theory: 2-Connections John C. Baez joint work with: Toby Bartels, Alissa Crans, Aaron Lauda, Urs Schreiber, Danny Stevenson. Union College Mathematics Conference December 4, 2005 g jl g il
Higher Gauge Theory: 2-Connections John C. Baez joint work with: Toby Bartels, Alissa Crans, Aaron Lauda, Urs Schreiber, Danny Stevenson. Union College Mathematics Conference December 4, 2005 g jl g il
The Set-Open topology
 Volume 37, 2011 Pages 205 217 http://topology.auburn.edu/tp/ The Set-Open topology by A. V. Osipov Electronically published on August 26, 2010 Topology Proceedings Web: http://topology.auburn.edu/tp/ Mail:
Volume 37, 2011 Pages 205 217 http://topology.auburn.edu/tp/ The Set-Open topology by A. V. Osipov Electronically published on August 26, 2010 Topology Proceedings Web: http://topology.auburn.edu/tp/ Mail:
Shape Modeling. Differential Geometry Primer Smooth Definitions Discrete Theory in a Nutshell. CS 523: Computer Graphics, Spring 2011
 CS 523: Computer Graphics, Spring 2011 Shape Modeling Differential Geometry Primer Smooth Definitions Discrete Theory in a Nutshell 2/15/2011 1 Motivation Geometry processing: understand geometric characteristics,
CS 523: Computer Graphics, Spring 2011 Shape Modeling Differential Geometry Primer Smooth Definitions Discrete Theory in a Nutshell 2/15/2011 1 Motivation Geometry processing: understand geometric characteristics,
Chapter 6. Curves and Surfaces. 6.1 Graphs as Surfaces
 Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
Chapter 6 Curves and Surfaces In Chapter 2 a plane is defined as the zero set of a linear function in R 3. It is expected a surface is the zero set of a differentiable function in R n. To motivate, graphs
THREE LECTURES ON BASIC TOPOLOGY. 1. Basic notions.
 THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
THREE LECTURES ON BASIC TOPOLOGY PHILIP FOTH 1. Basic notions. Let X be a set. To make a topological space out of X, one must specify a collection T of subsets of X, which are said to be open subsets of
Reducing Clocks in Timed Automata while Preserving Bisimulation
 Reducing Clocks in Timed Automata while Preserving Bisimulation Shibashis Guha Chinmay Narayan S. Arun-Kumar Indian Institute of Technology Delhi {shibashis, chinmay, sak}@cse.iitd.ac.in arxiv:1404.6613v2
Reducing Clocks in Timed Automata while Preserving Bisimulation Shibashis Guha Chinmay Narayan S. Arun-Kumar Indian Institute of Technology Delhi {shibashis, chinmay, sak}@cse.iitd.ac.in arxiv:1404.6613v2
Programming with Dependent Types Interactive programs and Coalgebras
 Programming with Dependent Types Interactive programs and Coalgebras Anton Setzer Swansea University, Swansea, UK 14 August 2012 1/ 50 A Brief Introduction into ML Type Theory Interactive Programs in Dependent
Programming with Dependent Types Interactive programs and Coalgebras Anton Setzer Swansea University, Swansea, UK 14 August 2012 1/ 50 A Brief Introduction into ML Type Theory Interactive Programs in Dependent
Part VI. Imperative Functional Programming
 Part VI Imperative Functional Programming Chapter 14 Mutable Storage MinML is said to be a pure language because the execution model consists entirely of evaluating an expression for its value. ML is
Part VI Imperative Functional Programming Chapter 14 Mutable Storage MinML is said to be a pure language because the execution model consists entirely of evaluating an expression for its value. ML is
The Typed λ Calculus and Type Inferencing in ML
 Notes on Types S. Arun-Kumar Department of Computer Science and Engineering Indian Institute of Technology New Delhi, 110016 email: sak@cse.iitd.ernet.in April 14, 2002 2 Chapter 1 The Typed λ Calculus
Notes on Types S. Arun-Kumar Department of Computer Science and Engineering Indian Institute of Technology New Delhi, 110016 email: sak@cse.iitd.ernet.in April 14, 2002 2 Chapter 1 The Typed λ Calculus
Compiler Construction
 Compiler Construction Thomas Noll Software Modeling and Verification Group RWTH Aachen University https://moves.rwth-aachen.de/teaching/ss-16/cc/ Conceptual Structure of a Compiler Source code x1 := y2
Compiler Construction Thomas Noll Software Modeling and Verification Group RWTH Aachen University https://moves.rwth-aachen.de/teaching/ss-16/cc/ Conceptual Structure of a Compiler Source code x1 := y2
From natural numbers to the lambda calculus
 From natural numbers to the lambda calculus Benedikt Ahrens joint work with Ralph Matthes and Anders Mörtberg Outline 1 About UniMath 2 Signatures and associated syntax Outline 1 About UniMath 2 Signatures
From natural numbers to the lambda calculus Benedikt Ahrens joint work with Ralph Matthes and Anders Mörtberg Outline 1 About UniMath 2 Signatures and associated syntax Outline 1 About UniMath 2 Signatures
Categorical models of type theory
 1 / 59 Categorical models of type theory Michael Shulman February 28, 2012 2 / 59 Outline 1 Type theory and category theory 2 Categorical type constructors 3 Dependent types and display maps 4 Fibrations
1 / 59 Categorical models of type theory Michael Shulman February 28, 2012 2 / 59 Outline 1 Type theory and category theory 2 Categorical type constructors 3 Dependent types and display maps 4 Fibrations
Types and Programming Languages. Lecture 8. Recursive type
 Types and Programming Languages Lecture 8. Recursive type Xiaojuan Cai cxj@sjtu.edu.cn BASICS Lab, Shanghai Jiao Tong University Fall, 2016 List[T] List[T] is a type constructor whose elements are lists
Types and Programming Languages Lecture 8. Recursive type Xiaojuan Cai cxj@sjtu.edu.cn BASICS Lab, Shanghai Jiao Tong University Fall, 2016 List[T] List[T] is a type constructor whose elements are lists
Quasi-categories vs Simplicial categories
 Quasi-categories vs Simplicial categories André Joyal January 07 2007 Abstract We show that the coherent nerve functor from simplicial categories to simplicial sets is the right adjoint in a Quillen equivalence
Quasi-categories vs Simplicial categories André Joyal January 07 2007 Abstract We show that the coherent nerve functor from simplicial categories to simplicial sets is the right adjoint in a Quillen equivalence
Outline. Petri nets. Introduction Examples Properties Analysis techniques. 1 EE249Fall04
 Outline Petri nets Introduction Examples Properties Analysis techniques 1 Petri Nets (PNs) Model introduced by C.A. Petri in 1962 Ph.D. Thesis: Communication with Automata Applications: distributed computing,
Outline Petri nets Introduction Examples Properties Analysis techniques 1 Petri Nets (PNs) Model introduced by C.A. Petri in 1962 Ph.D. Thesis: Communication with Automata Applications: distributed computing,
Principles of Program Analysis: A Sampler of Approaches
 Principles of Program Analysis: A Sampler of Approaches Transparencies based on Chapter 1 of the book: Flemming Nielson, Hanne Riis Nielson and Chris Hankin: Principles of Program Analysis Springer Verlag
Principles of Program Analysis: A Sampler of Approaches Transparencies based on Chapter 1 of the book: Flemming Nielson, Hanne Riis Nielson and Chris Hankin: Principles of Program Analysis Springer Verlag
Cheng Soon Ong & Christian Walder. Canberra February June 2018
 Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
Cheng Soon Ong & Christian Walder Research Group and College of Engineering and Computer Science Canberra February June 2018 Outlines Overview Introduction Linear Algebra Probability Linear Regression
DUALITY, TRACE, AND TRANSFER
 DUALITY, TRACE, AND TRANSFER RUNE HAUGSENG ABSTRACT. For any fibration of spaces whose fibres are finite complexes there exists a stable map going the wrong way, called a transfer map. A nice way to construct
DUALITY, TRACE, AND TRANSFER RUNE HAUGSENG ABSTRACT. For any fibration of spaces whose fibres are finite complexes there exists a stable map going the wrong way, called a transfer map. A nice way to construct
Program Calculus Calculational Programming
 Program Calculus Calculational Programming National Institute of Informatics June 21 / June 28 / July 5, 2010 Program Calculus Calculational Programming What we will learn? Discussing the mathematical
Program Calculus Calculational Programming National Institute of Informatics June 21 / June 28 / July 5, 2010 Program Calculus Calculational Programming What we will learn? Discussing the mathematical
Parameterization of triangular meshes
 Parameterization of triangular meshes Michael S. Floater November 10, 2009 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to
Parameterization of triangular meshes Michael S. Floater November 10, 2009 Triangular meshes are often used to represent surfaces, at least initially, one reason being that meshes are relatively easy to
Provable Anonymity. Epistemic Logic for Anonymizing Protocols. Ichiro Hasuo. Radboud University Nijmegen The Netherlands
 Provable Anonymity Epistemic Logic for Anonymizing Protocols Ichiro Hasuo Radboud University Nijmegen The Netherlands Internatinal Summer School Marktoberdorf Provable Anonymity Ichiro Hasuo, Nijmegen,
Provable Anonymity Epistemic Logic for Anonymizing Protocols Ichiro Hasuo Radboud University Nijmegen The Netherlands Internatinal Summer School Marktoberdorf Provable Anonymity Ichiro Hasuo, Nijmegen,
MODELS OF CUBIC THEORIES
 Bulletin of the Section of Logic Volume 43:1/2 (2014), pp. 19 34 Sergey Sudoplatov MODELS OF CUBIC THEORIES Abstract Cubic structures and cubic theories are defined on a base of multidimensional cubes.
Bulletin of the Section of Logic Volume 43:1/2 (2014), pp. 19 34 Sergey Sudoplatov MODELS OF CUBIC THEORIES Abstract Cubic structures and cubic theories are defined on a base of multidimensional cubes.
Model-Checking and Simulation for Stochastic Timed Systems
 Model-Checking and Simulation for Stochastic Timed Systems QUASIMODO FMCO 2010, Graz Universität des Saarlandes Outline 1. Stochastic Timed Automata STA Submodels Modest 2. Model-Checking mcpta PTA Case
Model-Checking and Simulation for Stochastic Timed Systems QUASIMODO FMCO 2010, Graz Universität des Saarlandes Outline 1. Stochastic Timed Automata STA Submodels Modest 2. Model-Checking mcpta PTA Case
Categories, posets, Alexandrov spaces, simplicial complexes, with emphasis on finite spaces. J.P. May
 Categories, posets, Alexandrov spaces, simplicial complexes, with emphasis on finite spaces J.P. May November 10, 2008 K(,1) Groups i Cats π 1 N Spaces S Simp. Sets Sd Reg. Simp. Sets Sd 2 τ Sd 1 i Simp.
Categories, posets, Alexandrov spaces, simplicial complexes, with emphasis on finite spaces J.P. May November 10, 2008 K(,1) Groups i Cats π 1 N Spaces S Simp. Sets Sd Reg. Simp. Sets Sd 2 τ Sd 1 i Simp.
Diagrams encoding group actions
 University of California, Riverside July 27, 2012 Segal monoids Definition A Segal monoid is a functor X : op ssets such that X 0 = [0] and the Segal maps X n (X 1 ) n are weak equivalences for n 2. There
University of California, Riverside July 27, 2012 Segal monoids Definition A Segal monoid is a functor X : op ssets such that X 0 = [0] and the Segal maps X n (X 1 ) n are weak equivalences for n 2. There
Product constructions for transitive decompositions of graphs
 116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
116 Product constructions for transitive decompositions of graphs Geoffrey Pearce Abstract A decomposition of a graph is a partition of the edge set, giving a set of subgraphs. A transitive decomposition
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3.
 TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
TOPOLOGY, DR. BLOCK, FALL 2015, NOTES, PART 3. 301. Definition. Let m be a positive integer, and let X be a set. An m-tuple of elements of X is a function x : {1,..., m} X. We sometimes use x i instead
SIMPLICIAL STRUCTURES ON MODEL CATEGORIES AND FUNCTORS
 SIMPLICIAL STRUCTURES ON MODEL CATEGORIES AND FUNCTORS CHARLES REZK, STEFAN SCHWEDE, AND BROOKE SHIPLEY Abstract. We produce a highly structured way of associating a simplicial category to a model category
SIMPLICIAL STRUCTURES ON MODEL CATEGORIES AND FUNCTORS CHARLES REZK, STEFAN SCHWEDE, AND BROOKE SHIPLEY Abstract. We produce a highly structured way of associating a simplicial category to a model category
Chapter 1. Introduction
 Chapter 1 Introduction A Monte Carlo method is a compuational method that uses random numbers to compute (estimate) some quantity of interest. Very often the quantity we want to compute is the mean of
Chapter 1 Introduction A Monte Carlo method is a compuational method that uses random numbers to compute (estimate) some quantity of interest. Very often the quantity we want to compute is the mean of
Definability and full abstraction in lambda-calculi
 Definability and full abstraction in lambda-calculi Antonio Bucciarelli Laboratoire Preuves, Programmes et Systèmes Université Paris Diderot Outline 1 Introduction 2 The full abstraction problem for PCF
Definability and full abstraction in lambda-calculi Antonio Bucciarelli Laboratoire Preuves, Programmes et Systèmes Université Paris Diderot Outline 1 Introduction 2 The full abstraction problem for PCF
Interpolation by Spline Functions
 Interpolation by Spline Functions Com S 477/577 Sep 0 007 High-degree polynomials tend to have large oscillations which are not the characteristics of the original data. To yield smooth interpolating curves
Interpolation by Spline Functions Com S 477/577 Sep 0 007 High-degree polynomials tend to have large oscillations which are not the characteristics of the original data. To yield smooth interpolating curves
