ICS 691: Advanced Data Structures Spring Lecture 3
|
|
|
- Tyrone Townsend
- 5 years ago
- Views:
Transcription
1 ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front querying of un-sorted lists, as introduced in [ST85a]. Using amortized analysis, we proved that using move-to-front is 4-competitive with the optimal solution. In this lecture we focus the discussion on splay trees, as detailed in [ST85b]. In Section 2, we discuss Binary Search Trees in the context of optimal layout for performing m queries. In Section 3 we introduce the splay tree and illustrate the 3 operations: zig, zig-zag, and zig-zig. We perform amortized analysis on these 3 operations in Section 3.3 and show that it is c-competitive with the optimal solution. 2 Binary Search Trees Balanced binary search trees (BST) implement dictionary APIs in O(log N) time for insert/delete/search. If access frequencies, f(x i ) are known for all m queries (i.e., item x i is accessed f(x i ) times, we can consider the optimal BST. The method of constructing this optimal off-line BST in O(n 3 ) is given in chapter 15 of [CLRS09]. The work to create this optimal BST can be further reduced to O(n 2 ), as discussed in exercise 15-3 of [CLRS09]. If we define = f(x) m, we can consider the cost of m queries, C m as: m C m = f(x) log 1 m = m log 1 n = m log 1 = m H n Where H n = n 1 log is the entropy of the query set. Hence, if all queries are equally likely, H n = log n and the total cost is m log(n). 1
2 Figure 1: A case where the zig operation is used to move target node x to the root. This is only used when the target node is the direct child of the root node. 3 Self-adjusting BSTs: Splay Trees Splay trees, detailed in [ST85b] are self-adjusting BSTs that: implement dictionary APIs, like the move-to-front list, are simply structured with limited overhead, are c-competitive with best offline BST, i.e., when all queries are known in advance, are conjectured to be c-competitive with the best online BST, i.e., when future queries are not know in advance 3.1 Splay Tree Operations Simply, Splay trees are BSTs that move search targets to the root of the tree. This is accomplished by 3 simple rotate rules that are applied repeatedly until the search target reaches root. The 3 rotate rules are zig, zig-zag, and zig-zig, and are detailed below: Zig The zig operation is applied if the element being moved, x, is the child of the root, as seen in Figure 1. When this is the case, the element, x, is simply rotated with the root node, making it the new root Zig-zag The zig-zag operation is applied when the target element being moved, x, needs to be moved up in alternate directions, as illustrated in Figure 2. When a node being moved up the tree falls on the opposite direction of its parent as its parent falls from its grandparent, we employ the zig-zag 2
3 Figure 2: A case where the zig-zag operation is employed to move target node x up the tree. The zig-zag operation would also be used in the symmetric case (i.e., where x is the right child of y and y is the left child of z). operation. The zig-zag operation involves rotating x with its parent (y), and then rotating again with its new parent (z) Zig-zig The final operation, zig-zig, is used when both the node being moved up falls on the same side of its parent as its parent does (from its grandparent). When this occurs, we first perform Rotate on the targets parent node, followed by Rotate on the target node itself. Figure 3 illustrates how the zig-zig operation is performed on an example tree. 3.2 Splay Tree Example We consider the worst-case initial BST and look at how the splay tree and its operations would perform. Clearly, our worst-case BST would be a tree where each node has only 1 child, and the other is null. In this case, searching the leaf node would result in an O(n) time search. However, using a splay tree, each search would result in the splay operation moving the searched (leaf) node to the root, thereby moving lots of other elements. Figure 4 illustrates how a splay tree would perform when repeatedly searching such a target. We see in Figure 4 that, after just 3 searches on a worst-case tree, we have a tree that has optimal height. All subsequent searches will be O(log n), and would further adjust the tree as needed. This example shows how splay trees quickly self-balance and achieve optimal or near-optimal performance quickly. Amortized over a large number of queries, the cost of searching (and splaying a node to the root) is O(log n). 3.3 Amortized Analysis We use the potential method of amortized analysis and first define several variables: 3
4 Figure 3: An example of how the zig-zig operation is performed by a splay tree. First, y is rotated upwards, then x is rotated up to the root. This is only employed when both the target (x) and its parent y fall on the same side of their respective parent nodes. Figure 4: An example worst-case tree and result of repeatedly searching (and using the splay operation) it. We see that, after searching just 3 times, we have a tree of optimal height for the input size. 4
5 Definition 1. Let w(x) be the weight associated with node x. Definition 2. Let s i (x) be the size of node x after performing the ith query, defined formally as: Definition 3. Let r i (x) be the rank of x: s i (x) = w(v) v subtree rooted at x r i (x) = log (s i (x)) Note that if we set w(x) = 1 for all x, then s i (x) is just the number of nodes in the subtree and r i (x) is the minimum levels in the subtree rooted at x. Using these definitions, we define our potential function to perform the amortized analysis as: Φ(T i ) = x T i r ( x), where T i is the entire splay tree structure after the ith query. To perform amortized analysis, we look at the 3 individual splay tree operations defined in Section 3.1. Recall that the amortized cost using the potential method is defined as: ĉ i = c i + Φ i Consider the zig-zig operation defined in Section 3.1 and the 2 rotations it involves. The cost of performing a rotation is 1, therefore: ĉ i = 2 + Φ i = 2 + (Φ(T i ) Φ(T i 1 )) Where T i 1 and T i are the potential function values before and after performing the zig-zig operation, respectively. We see in Figure 3 that the potential of subtrees A,B,C, and D don t change, so they cancel out in Φ i and we only need to consider the 3 nodes involved in the rotations: the target node (x), its parent (y), and its grandparent (z). Therefore, we expand the above formula to the changes in potential for each of the nodes x, y, and z: ĉ i (x) = 2 + r i (x) + r i (y) + r i (z) r i 1 (x) r i 1 (y) r i 1 (z) We note, that, as seen in Figure 3: 5
6 r i 1 (z) = r i (x) r i (y) r i (x) r i 1 (y) r i 1 (x) Therefore, our amortized cost is: ĉ i (x) 2 + r i (x) + r i (z) r i 1 (x) r i 1 (x) We can further simplify this using the fact that log a+log b 2 log a+b 2 and that s i (z)+s i 1 (x) s i (x): r i (z) = log s i (z) r i 1 (x) = log s i 1 (x) log s i (z) + log s i 1 (x) 2 log s i(z) + s i 1 (x) 2 2(log s i (x) 1) = 2(r i (x) 1) Using this simplification, our amortized cost becomes: ĉ i (x) 2 + r i (x) + (2r i (x) 2 r i 1 (x)) r i 1 (x) r i 1 (x) = 3(r i (x) r i 1 (x)) We can use a similar analysis to show that the zig-zag operation has amortized cost ĉ i (x) 3(r i (x) r i 1 (x)). The amortized cost of the zig operation, described in Section 3.1: ĉ i (x) = 1 + Φ i = 1 + r i (x) + r i (y) r i 1 (x) r i 1 (y) Where x is our target node being moved up and y is its parent (and the root node of the tree). We note from Figure 1 that: r i (y) r i (x) r i 1 (y) = r i (x) Therefore, we can simplify our amortized cost to: 6
7 ĉ i (x) 1 + r i (x) + r i (x) r i 1 (x) r i (x) = 1 + r i (x) r i 1 (x) And because r i (x) r i 1 (x), it follows that ĉ i (x) 1 + 3(r i (x) r i 1 (x)) With these amortized cost values for each rotation operation, we compute the total cost to splay a node x from its position to the root as: ĉ splay = k ĉ i (x) k 1 ĉ k (x) + ĉ i (x) Since we perform either zig-zag or zig-zig operations for all steps from i = 1 to k 1 and at most one final zig operation to move x to the root, our amortized cost becomes: k 1 ĉ splay 1 + 3(r k (x) r k 1 (x)) + 3(r i (x) r i 1 (x)) 1 + k 3(r i (x) r i 1 (x)) 1 + 3(r k (x) r 0 (x)) 1 + 3(log s root log s 0 (x)) = log s root s 0 (x) ( = O log s ) root s 0 (x) Theorem 4. The amortized cost of searching a splay tree is O(log n) Proof. Setting w(x) = 1, we get s root = n, s 0 1, so the amortized cost of a splay operation is bounded by: ĉ(x) O(log n ) = O(log n) 1 Using other values for node weights, we can prove other theorems about splay trees: Theorem 5. (Static optimality) Given a sequence S of queries with known access frequences f(x i ), splay trees are O(1)-competitive with the best offline BST for S. 7
8 Proof. Let w(x) = = f(x) m, therefore our amortized cost is: ĉ = x S ĉ(x) = x S O(log s root s(x) ) Where S is the sequence of queries being performed. Note that, since s root is the sum of weights on all nodes: s root = w(x) = = x T x T x T = 1 f(x) m Furthermore, since s(x) includes the weight of x, s(x) = w(x). Using these, our amortized cost can be written as: m 1 ĉ log p(x i ) = f(x) log 1 x S = O(m log 1 ) = O(m H n ) Where H n is the entropy of the sequence of queries, S on n keys. Recall from Section 2 that the cost of m queries on the optimal static BST is C m = m H n. References [CLRS09] T. Cormen, C. Lieserson, R. Rivest, and C. Stein. Introduction to Algorithms. MIT Press, third edition, [ST85a] [ST85b] D.D. Sleator and R. E. Tarjan. Amortized efficiency of list update and paging rules. Communications of the ACM, 28(2): , D.D. Sleator and R. E. Tarjan. Self-adjusting binary search trees. Journal of the ACM, 32(3): ,
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Splay Trees. (Splay Trees) Data Structures and Programming Spring / 27
 Splay Trees (Splay Trees) Data Structures and Programming Spring 2017 1 / 27 Basic Idea Invented by Sleator and Tarjan (1985) Blind rebalancing no height info kept! Worst-case time per operation is O(n)
Splay Trees (Splay Trees) Data Structures and Programming Spring 2017 1 / 27 Basic Idea Invented by Sleator and Tarjan (1985) Blind rebalancing no height info kept! Worst-case time per operation is O(n)
Self Adjusting Data Structures
 Self Adjusting Data Structures Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Self Adjusting Data Structures 2014/2015 1 / 31 What are self adjusting data structures? Data structures that can
Self Adjusting Data Structures Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Self Adjusting Data Structures 2014/2015 1 / 31 What are self adjusting data structures? Data structures that can
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Randomized Splay Trees Final Project
 Randomized Splay Trees 6.856 Final Project Robi Bhattacharjee robibhat@mit.edu Ben Eysenbach bce@mit.edu May 17, 2016 Abstract We propose a randomization scheme for splay trees with the same time complexity
Randomized Splay Trees 6.856 Final Project Robi Bhattacharjee robibhat@mit.edu Ben Eysenbach bce@mit.edu May 17, 2016 Abstract We propose a randomization scheme for splay trees with the same time complexity
ICS 691: Advanced Data Structures Spring Lecture 8
 ICS 691: Advanced Data Structures Spring 2016 Prof. odari Sitchinava Lecture 8 Scribe: Ben Karsin 1 Overview In the last lecture we continued looking at arborally satisfied sets and their equivalence to
ICS 691: Advanced Data Structures Spring 2016 Prof. odari Sitchinava Lecture 8 Scribe: Ben Karsin 1 Overview In the last lecture we continued looking at arborally satisfied sets and their equivalence to
Red-Black, Splay and Huffman Trees
 Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Recall from Last Time: AVL Trees
 CSE 326 Lecture 8: Getting to now AVL Trees Today s Topics: Balanced Search Trees AVL Trees and Rotations Splay trees Covered in Chapter 4 of the text Recall from Last Time: AVL Trees AVL trees are height-balanced
CSE 326 Lecture 8: Getting to now AVL Trees Today s Topics: Balanced Search Trees AVL Trees and Rotations Splay trees Covered in Chapter 4 of the text Recall from Last Time: AVL Trees AVL trees are height-balanced
1 Figure 1: Zig operation on x Figure 2: Zig-zig operation on x
 www.alepho.com 1 1 Splay tree Motivation for this data structure is to have binary tree which performs rotations when nodes is accessed. Operations of interest are finding, inserting and deleting key,
www.alepho.com 1 1 Splay tree Motivation for this data structure is to have binary tree which performs rotations when nodes is accessed. Operations of interest are finding, inserting and deleting key,
Balanced Binary Search Trees. Victor Gao
 Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Red-Black Trees. Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood
 Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Lecture 4 Feb 21, 2007
 6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 4 Feb 21, 2007 Scribe: Mashhood Ishaque 1 Overview In the last lecture we worked in a BST model. We discussed Wilber lower bounds
6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 4 Feb 21, 2007 Scribe: Mashhood Ishaque 1 Overview In the last lecture we worked in a BST model. We discussed Wilber lower bounds
6.854J / J Advanced Algorithms Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
MIT OpenCourseWare http://ocw.mit.edu 6.854J / 18.415J Advanced Algorithms Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms. 18.415/6.854 Advanced
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Upper Bounds for Maximally Greedy Binary Search Trees
 Upper Bounds for Maximally Greedy Binary Search Trees Kyle Fox -- University of Illinois at Urbana-Champaign Balanced Binary Search Trees Want data structures for dictionary, predecessor search, etc. Red-black
Upper Bounds for Maximally Greedy Binary Search Trees Kyle Fox -- University of Illinois at Urbana-Champaign Balanced Binary Search Trees Want data structures for dictionary, predecessor search, etc. Red-black
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
8.1. Optimal Binary Search Trees:
 DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
OPPA European Social Fund Prague & EU: We invest in your future.
 OPPA European Social Fund Prague & EU: We invest in your future. ECE 250 Algorithms and Data Structures Splay Trees Douglas Wilhelm Harder, M.Math. LEL Department of Electrical and Computer Engineering
OPPA European Social Fund Prague & EU: We invest in your future. ECE 250 Algorithms and Data Structures Splay Trees Douglas Wilhelm Harder, M.Math. LEL Department of Electrical and Computer Engineering
CSE 326: Data Structures Splay Trees. James Fogarty Autumn 2007 Lecture 10
 CSE 32: Data Structures Splay Trees James Fogarty Autumn 2007 Lecture 10 AVL Trees Revisited Balance condition: Left and right subtrees of every node have heights differing by at most 1 Strong enough :
CSE 32: Data Structures Splay Trees James Fogarty Autumn 2007 Lecture 10 AVL Trees Revisited Balance condition: Left and right subtrees of every node have heights differing by at most 1 Strong enough :
Chapter 22 Splay Trees
 Chapter 22 Splay Trees Introduction Splay trees support all the operations of binary trees. But they do not guarantee Ο(log N) worst-case performance. Instead, its bounds are amortized, meaning that although
Chapter 22 Splay Trees Introduction Splay trees support all the operations of binary trees. But they do not guarantee Ο(log N) worst-case performance. Instead, its bounds are amortized, meaning that although
Lower Bound on Comparison-based Sorting
 Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Lower Bound on Comparison-based Sorting Different sorting algorithms may have different time complexity, how to know whether the running time of an algorithm is best possible? We know of several sorting
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
Dynamic Optimality Almost
 Dynamic Optimality Almost Erik D. Demaine Dion Harmon John Iacono Mihai Pǎtraşcu Abstract We present an O(lg lg n)-competitive online binary search tree, improving upon the best previous (trivial) competitive
Dynamic Optimality Almost Erik D. Demaine Dion Harmon John Iacono Mihai Pǎtraşcu Abstract We present an O(lg lg n)-competitive online binary search tree, improving upon the best previous (trivial) competitive
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Data Structures and Algorithms(12)
 Ming Zhang "Data s and Algorithms" Data s and Algorithms(12) Instructor: Ming Zhang Textbook Authors: Ming Zhang, Tengjiao Wang and Haiyan Zhao Higher Education Press, 28.6 (the "Eleventh Five-Year" national
Ming Zhang "Data s and Algorithms" Data s and Algorithms(12) Instructor: Ming Zhang Textbook Authors: Ming Zhang, Tengjiao Wang and Haiyan Zhao Higher Education Press, 28.6 (the "Eleventh Five-Year" national
ECE 242 Data Structures and Algorithms. Trees IV. Lecture 21. Prof.
 ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/27/17
 01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
Recall: Properties of B-Trees
 CSE 326 Lecture 10: B-Trees and Heaps It s lunch time what s cookin? B-Trees Insert/Delete Examples and Run Time Analysis Summary of Search Trees Introduction to Heaps and Priority Queues Covered in Chapters
CSE 326 Lecture 10: B-Trees and Heaps It s lunch time what s cookin? B-Trees Insert/Delete Examples and Run Time Analysis Summary of Search Trees Introduction to Heaps and Priority Queues Covered in Chapters
3 Competitive Dynamic BSTs (January 31 and February 2)
 3 Competitive Dynamic BSTs (January 31 and February ) In their original paper on splay trees [3], Danny Sleator and Bob Tarjan conjectured that the cost of sequence of searches in a splay tree is within
3 Competitive Dynamic BSTs (January 31 and February ) In their original paper on splay trees [3], Danny Sleator and Bob Tarjan conjectured that the cost of sequence of searches in a splay tree is within
Splay Trees. Splay Trees 1
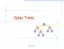 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Lecture 3 February 9, 2010
 6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
6.851: Advanced Data Structures Spring 2010 Dr. André Schulz Lecture 3 February 9, 2010 Scribe: Jacob Steinhardt and Greg Brockman 1 Overview In the last lecture we continued to study binary search trees
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Are Fibonacci Heaps Optimal? Diab Abuaiadh and Jeffrey H. Kingston ABSTRACT
 Are Fibonacci Heaps Optimal? Diab Abuaiadh and Jeffrey H. Kingston ABSTRACT In this paper we investigate the inherent complexity of the priority queue abstract data type. We show that, under reasonable
Are Fibonacci Heaps Optimal? Diab Abuaiadh and Jeffrey H. Kingston ABSTRACT In this paper we investigate the inherent complexity of the priority queue abstract data type. We show that, under reasonable
Dynamic Optimality Almost
 ynamic Optimality Almost Erik. emaine ion Harmon John Iacono Mihai Pǎtraşcu Abstract We present an O(lg lg n)-competitive online binary search tree, improving upon the best previous (trivial) competitive
ynamic Optimality Almost Erik. emaine ion Harmon John Iacono Mihai Pǎtraşcu Abstract We present an O(lg lg n)-competitive online binary search tree, improving upon the best previous (trivial) competitive
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Splay tree, tree Marko Berezovský Radek Mařík PAL 2012
 Splay tree, --4 tree Marko erezovský Radek Mařík PL 0 p < Hi!?/ x+y x--y To read [] Weiss M.., Data Structures and lgorithm nalysis in ++, rd Ed., ddison Wesley, 4.5, pp.49-58. [] Daniel D. Sleator and
Splay tree, --4 tree Marko erezovský Radek Mařík PL 0 p < Hi!?/ x+y x--y To read [] Weiss M.., Data Structures and lgorithm nalysis in ++, rd Ed., ddison Wesley, 4.5, pp.49-58. [] Daniel D. Sleator and
Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance
 Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI-33101 Tampere,
Poketree: A Dynamically Competitive Data Structure with Good Worst-Case Performance Jussi Kujala and Tapio Elomaa Institute of Software Systems Tampere University of Technology P.O. Box 553, FI-33101 Tampere,
SFU CMPT Lecture: Week 9
 SFU CMPT-307 2008-2 1 Lecture: Week 9 SFU CMPT-307 2008-2 Lecture: Week 9 Ján Maňuch E-mail: jmanuch@sfu.ca Lecture on July 8, 2008, 5.30pm-8.20pm SFU CMPT-307 2008-2 2 Lecture: Week 9 Binary search trees
SFU CMPT-307 2008-2 1 Lecture: Week 9 SFU CMPT-307 2008-2 Lecture: Week 9 Ján Maňuch E-mail: jmanuch@sfu.ca Lecture on July 8, 2008, 5.30pm-8.20pm SFU CMPT-307 2008-2 2 Lecture: Week 9 Binary search trees
Lecture 3 February 20, 2007
 6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 3 February 20, 2007 Scribe: Hui Tang 1 Overview In the last lecture we discussed Binary Search Trees and the many bounds which achieve
6.897: Advanced Data Structures Spring 2007 Prof. Erik Demaine Lecture 3 February 20, 2007 Scribe: Hui Tang 1 Overview In the last lecture we discussed Binary Search Trees and the many bounds which achieve
CS 310: Tree Rotations and AVL Trees
 CS 310: Tree Rotations and AVL Trees Chris Kauffman Week 12-2 Practice/Demo Sites jgrasp is so-so for seeing tree operations Play with Blanced Binary Search Trees online using the following applets (titles
CS 310: Tree Rotations and AVL Trees Chris Kauffman Week 12-2 Practice/Demo Sites jgrasp is so-so for seeing tree operations Play with Blanced Binary Search Trees online using the following applets (titles
Balanced Trees Part Two
 Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
Balanced Trees Part Two Outline for Today Recap from Last Time Review of B-trees, 2-3-4 trees, and red/black trees. Order Statistic Trees BSTs with indexing. Augmented Binary Search Trees Building new
Dynamic Optimality and Multi-Splay Trees 1
 Dynamic Optimality and Multi-Splay Trees 1 Daniel Dominic Sleator and Chengwen Chris Wang November 5, 2004 CMU-CS-04-171 School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Abstract
Dynamic Optimality and Multi-Splay Trees 1 Daniel Dominic Sleator and Chengwen Chris Wang November 5, 2004 CMU-CS-04-171 School of Computer Science Carnegie Mellon University Pittsburgh, PA 15213 Abstract
Balanced search trees. DS 2017/2018
 Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
Balanced search trees. DS 2017/2018 Red-black trees Symmetric binary B-tree, Rudolf Bayer, 1972. The balancing is maintained by using a coloring of the nodes. The red-black trees are binary search trees
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Advanced Algorithms. Class Notes for Thursday, September 18, 2014 Bernard Moret
 Advanced Algorithms Class Notes for Thursday, September 18, 2014 Bernard Moret 1 Amortized Analysis (cont d) 1.1 Side note: regarding meldable heaps When we saw how to meld two leftist trees, we did not
Advanced Algorithms Class Notes for Thursday, September 18, 2014 Bernard Moret 1 Amortized Analysis (cont d) 1.1 Side note: regarding meldable heaps When we saw how to meld two leftist trees, we did not
AVL Trees. Version of September 6, AVL Trees Version of September 6, / 22
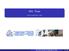 VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
VL Trees Version of September 6, 6 VL Trees Version of September 6, 6 / inary Search Trees x 8 4 4 < x > x 7 9 3 inary-search-tree property For every node x ll eys in its left subtree are smaller than
Balanced search trees
 Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
8. Binary Search Tree
 8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES
 HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
Treaps. 1 Binary Search Trees (BSTs) CSE341T/CSE549T 11/05/2014. Lecture 19
 CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
CSE34T/CSE549T /05/04 Lecture 9 Treaps Binary Search Trees (BSTs) Search trees are tree-based data structures that can be used to store and search for items that satisfy a total order. There are many types
Search Trees (Ch. 9) > = Binary Search Trees 1
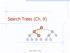 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
CSCI 136 Data Structures & Advanced Programming. Lecture 25 Fall 2018 Instructor: B 2
 CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Union-Find and Amortization
 Design and Analysis of Algorithms February 20, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas and Nancy Lynch Recitation 3 Union-Find and Amortization 1 Introduction
Design and Analysis of Algorithms February 20, 2015 Massachusetts Institute of Technology 6.046J/18.410J Profs. Erik Demaine, Srini Devadas and Nancy Lynch Recitation 3 Union-Find and Amortization 1 Introduction
Splay tree, tree Marko Berezovský Radek Mařík PAL 2012
 Splay tree, --4 tree Marko erezovský Radek Mařík PL 0 p < Hi!?/ x+y To read x--y [] Weiss M.., Data Structures and lgorithm nalysis in ++, rd Ed., ddison Wesley, 4.5, pp.49-58. [] Daniel D. Sleator and
Splay tree, --4 tree Marko erezovský Radek Mařík PL 0 p < Hi!?/ x+y To read x--y [] Weiss M.., Data Structures and lgorithm nalysis in ++, rd Ed., ddison Wesley, 4.5, pp.49-58. [] Daniel D. Sleator and
Binary Trees. BSTs. For example: Jargon: Data Structures & Algorithms. root node. level: internal node. edge.
 Binary Trees 1 A binary tree is either empty, or it consists of a node called the root together with two binary trees called the left subtree and the right subtree of the root, which are disjoint from
Binary Trees 1 A binary tree is either empty, or it consists of a node called the root together with two binary trees called the left subtree and the right subtree of the root, which are disjoint from
DYNAMIC OPTIMALITY ALMOST
 DYNAMIC OPTIMALITY ALMOST ERIK D. DEMAINE, DION HARMON, JOHN IACONO, AND MIHAI PǍTRAŞCU Abstract. We present an O(lg lg n)-competitive online binary search tree, improving upon the best previous (trivial)
DYNAMIC OPTIMALITY ALMOST ERIK D. DEMAINE, DION HARMON, JOHN IACONO, AND MIHAI PǍTRAŞCU Abstract. We present an O(lg lg n)-competitive online binary search tree, improving upon the best previous (trivial)
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
13.4 Deletion in red-black trees
 The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
The operation of Deletion in a red-black tree is similar to the operation of Insertion on the tree. That is, apply the deletion algorithm for binary search trees to delete a node z; apply node color changes
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Splay Trees Goodrich, Tamassia, Dickerson. Splay Trees 1
 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Comparison Based Sorting Algorithms. Algorithms and Data Structures: Lower Bounds for Sorting. Comparison Based Sorting Algorithms
 Comparison Based Sorting Algorithms Algorithms and Data Structures: Lower Bounds for Sorting Definition 1 A sorting algorithm is comparison based if comparisons A[i] < A[j], A[i] A[j], A[i] = A[j], A[i]
Comparison Based Sorting Algorithms Algorithms and Data Structures: Lower Bounds for Sorting Definition 1 A sorting algorithm is comparison based if comparisons A[i] < A[j], A[i] A[j], A[i] = A[j], A[i]
Planar Point Location
 C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
C.S. 252 Prof. Roberto Tamassia Computational Geometry Sem. II, 1992 1993 Lecture 04 Date: February 15, 1993 Scribe: John Bazik Planar Point Location 1 Introduction In range searching, a set of values,
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Rank-Pairing Heaps. Bernard Haeupler Siddhartha Sen Robert E. Tarjan. SIAM JOURNAL ON COMPUTING Vol. 40, No. 6 (2011), pp.
 Rank-Pairing Heaps Bernard Haeupler Siddhartha Sen Robert E. Tarjan Presentation by Alexander Pokluda Cheriton School of Computer Science, University of Waterloo, Canada SIAM JOURNAL ON COMPUTING Vol.
Rank-Pairing Heaps Bernard Haeupler Siddhartha Sen Robert E. Tarjan Presentation by Alexander Pokluda Cheriton School of Computer Science, University of Waterloo, Canada SIAM JOURNAL ON COMPUTING Vol.
Analysis of Algorithms
 Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
Sorted Arrays. Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min
 Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
Search Trees. Chapter 11
 Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Search Trees Chapter 6 4 8 9 Outline Binar Search Trees AVL Trees Spla Trees Outline Binar Search Trees AVL Trees Spla Trees Binar Search Trees A binar search tree is a proper binar tree storing ke-value
Algorithms and Data Structures: Lower Bounds for Sorting. ADS: lect 7 slide 1
 Algorithms and Data Structures: Lower Bounds for Sorting ADS: lect 7 slide 1 ADS: lect 7 slide 2 Comparison Based Sorting Algorithms Definition 1 A sorting algorithm is comparison based if comparisons
Algorithms and Data Structures: Lower Bounds for Sorting ADS: lect 7 slide 1 ADS: lect 7 slide 2 Comparison Based Sorting Algorithms Definition 1 A sorting algorithm is comparison based if comparisons
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
Data Structures Week #6. Special Trees
 Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees October 5, 2015 Borahan Tümer, Ph.D. 2 AVL Trees October 5, 2015 Borahan Tümer, Ph.D. 3 Motivation for
Data Structures Week #6 Special Trees Outline Adelson-Velskii-Landis (AVL) Trees Splay Trees B-Trees October 5, 2015 Borahan Tümer, Ph.D. 2 AVL Trees October 5, 2015 Borahan Tümer, Ph.D. 3 Motivation for
The Geometry of Binary Search Trees
 The Geometry of Binary Search Trees Erik Demaine MIT John Iacono Poly Inst. of NYU Dion Harmon NECSI Daniel Kane Harvard Mihai Pătraşcu IBM Almaden ASS Point set in the plane ASS = any nontrivial rectangle
The Geometry of Binary Search Trees Erik Demaine MIT John Iacono Poly Inst. of NYU Dion Harmon NECSI Daniel Kane Harvard Mihai Pătraşcu IBM Almaden ASS Point set in the plane ASS = any nontrivial rectangle
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Programming II (CS300)
 1 Programming II (CS300) Chapter 11: Binary Search Trees MOUNA KACEM mouna@cs.wisc.edu Fall 2018 General Overview of Data Structures 2 Introduction to trees 3 Tree: Important non-linear data structure
1 Programming II (CS300) Chapter 11: Binary Search Trees MOUNA KACEM mouna@cs.wisc.edu Fall 2018 General Overview of Data Structures 2 Introduction to trees 3 Tree: Important non-linear data structure
Midterm solutions. n f 3 (n) = 3
 Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Lecture 8 13 March, 2012
 6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 8 13 March, 2012 1 From Last Lectures... In the previous lecture, we discussed the External Memory and Cache Oblivious memory models.
6.851: Advanced Data Structures Spring 2012 Prof. Erik Demaine Lecture 8 13 March, 2012 1 From Last Lectures... In the previous lecture, we discussed the External Memory and Cache Oblivious memory models.
CMPS 2200 Fall 2017 Red-black trees Carola Wenk
 CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
Algorithm 23 works. Instead of a spanning tree, one can use routing.
 Chapter 5 Shared Objects 5.1 Introduction Assume that there is a common resource (e.g. a common variable or data structure), which different nodes in a network need to access from time to time. If the
Chapter 5 Shared Objects 5.1 Introduction Assume that there is a common resource (e.g. a common variable or data structure), which different nodes in a network need to access from time to time. If the
lecture17: AVL Trees
 lecture17: Largely based on slides by Cinda Heeren CS 225 UIUC 9th July, 2013 Announcements mt2 tonight! mp5.1 extra credit due Friday (7/12) An interesting tree Can you make a BST that looks like a zig
lecture17: Largely based on slides by Cinda Heeren CS 225 UIUC 9th July, 2013 Announcements mt2 tonight! mp5.1 extra credit due Friday (7/12) An interesting tree Can you make a BST that looks like a zig
Algorithms for Memory Hierarchies Lecture 2
 Algorithms for emory Hierarchies Lecture Lecturer: odari Sitchianva Scribes: Robin Rehrmann, ichael Kirsten Last Time External memory (E) model Scan(): O( ) I/Os Stacks / queues: O( 1 ) I/Os / elt ergesort:
Algorithms for emory Hierarchies Lecture Lecturer: odari Sitchianva Scribes: Robin Rehrmann, ichael Kirsten Last Time External memory (E) model Scan(): O( ) I/Os Stacks / queues: O( 1 ) I/Os / elt ergesort:
CS 61B Data Structures and Programming Methodology. Aug 11, 2008 David Sun
 CS 61B Data Structures and Programming Methodology Aug 11, 2008 David Sun Announcements Final is to be held this Thursday from 11:00 2:00 pm in 306 and 310 Soda. Open book format. If you have conflicts
CS 61B Data Structures and Programming Methodology Aug 11, 2008 David Sun Announcements Final is to be held this Thursday from 11:00 2:00 pm in 306 and 310 Soda. Open book format. If you have conflicts
Dynamic trees (Steator and Tarjan 83)
 Dynamic trees (Steator and Tarjan 83) 1 Operations that we do on the trees maketree(v) w = findroot(v) (w,c) = mincost(v) (can do maxcost(v) instead) addcost(v,c) link(v,w,c(v,w)) cut(v) evert(v) 2 Applications
Dynamic trees (Steator and Tarjan 83) 1 Operations that we do on the trees maketree(v) w = findroot(v) (w,c) = mincost(v) (can do maxcost(v) instead) addcost(v,c) link(v,w,c(v,w)) cut(v) evert(v) 2 Applications
Data Structures in Java
 Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Chapter 5 Data Structures Algorithm Theory WS 2016/17 Fabian Kuhn
 Chapter 5 Data Structures Algorithm Theory WS 06/ Fabian Kuhn Examples Dictionary: Operations: insert(key,value), delete(key), find(key) Implementations: Linked list: all operations take O(n) time (n:
Chapter 5 Data Structures Algorithm Theory WS 06/ Fabian Kuhn Examples Dictionary: Operations: insert(key,value), delete(key), find(key) Implementations: Linked list: all operations take O(n) time (n:
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
