Search Trees. Chapter 11
|
|
|
- Aubrey Potter
- 6 years ago
- Views:
Transcription
1 Search Trees Chapter
2 Outline Binar Search Trees AVL Trees Spla Trees
3 Outline Binar Search Trees AVL Trees Spla Trees
4 Binar Search Trees A binar search tree is a proper binar tree storing ke-value entries at its internal nodes and satisfing the following propert: Let u, v, and w be three nodes such that u is in the left subtree of v and w is in the right subtree of v. We have ke(u) ke(v) ke(w) We will assume that eternal nodes are placeholders : the do not store entries (makes algorithms a little simpler) An inorder traversal of a binar search trees visits the kes in increasing order Binar search trees are ideal for maps or dictionaries with ordered kes
5 Binar Search Tree All nodes in left subtree An node All nodes in right subtree
6 Maintain a sub-tree. Search: Loop Invariant If the ke is contained in the original tree, then the ke is contained in the sub-tree. ke
7 Search: Define Step Cut sub-tree in half. Determine which half the ke would be in. Keep that half. ke If ke < root, then ke is in left half. If ke = root, then ke is found If ke > root, then ke is in right half.
8 Search: Algorithm To search for a ke k, we trace a downward path starting at the root The net node visited depends on the outcome of the comparison of k with the ke of the current node If we reach a leaf, the ke is not found and return of an eternal node signals this. Eample: find(4): Call TreeSearch(4,root) Algorithm TreeSearch(k, v) if T.isEternal (v) return v if k ke(v) return TreeSearch(k, T.left(v)) else if k ke(v) return v else { k ke(v) } return TreeSearch(k, T.right(v))
9 Insertion To perform operation insert(k, o), we search for ke k (using TreeSearch) Suppose k is not alread in the tree, and let w be the leaf reached b the search We insert k at node w and epand w into an internal node Eample: insert 5 w w w 5 9
10 Insertion Suppose k is alread in the tree, at node v. We continue the downward search through v, and let w be the leaf reached b the search Note that it would be correct to go either left or right at v. We go left b convention. We insert k at node w and epand w into an internal node Eample: insert w 6 9 w 4 8 w 6 6 9
11 Deletion To perform operation remove(k), we search for ke k Suppose ke k is in the tree, and let v be the node storing k If node v has an eternal leaf child w, we remove v and w from the tree with operation removeeternal(w), which removes w and its parent Eample: remove v 8 w w
12 Deletion (cont.) Now consider the case where the ke k to be removed is stored at a node v whose children are both internal we find the internal node w that follows v in an inorder traversal we cop the entr stored at w into node v we remove node w and its left child (which must be a leaf) b means of operation removeeternal() Eample: remove 3 3 v 5 v 8 8 w
13 Performance Consider a dictionar with n items implemented b means of a linked binar search tree of height h the space used is O(n) methods find, insert and remove take O(h) time The height h is O(n) in the worst case and O(log n) in the best case It is thus worthwhile to balance the tree (net topic)!
14 Outline Binar Search Trees AVL Trees Spla Trees
15 AVL Trees The AVL tree is the first balanced binar search tree ever invented. It is named after its two inventors, G.M. Adelson-Velskii and E.M. Landis, who published it in their 96 paper "An algorithm for the organiation of information.
16 AVL Trees AVL trees are balanced. An AVL Tree is a binar search tree in which the heights of siblings can differ b at most height
17 Height of an AVL Tree Claim: The height of an AVL tree storing n kes is O(log n).
18 Height of an AVL Tree Proof: We compute a lower bound n(h) on the number of internal nodes of an AVL tree of height h. Observe that n() = and n() = For h >, a minimal AVL tree contains the root node, one minimal AVL subtree of height h - and another of height h -. That is, n(h) = + n(h - ) + n(h - ) Knowing n(h - ) > n(h - ), we get n(h) > n(h - ). So n(h) > n(h - ), n(h) > 4n(h - 4), n(h) > 8n(n - 6), > i n(h - i) If h is even, we let i = h/-, so that n(h) > h/- n() = h/ If h is odd, we let i = h/-/, so that n(h) > h/-/ n() = h/-/ In either case, n(h) > h/- Taking logarithms: h < log(n(h)) + Thus the height of an AVL tree is O(log n) n() 3 4 n()
19 Insertion height = 7 height = Insert() 4 Problem!
20 Insertion Imbalance ma occur at an ancestor of the inserted node. height = 3 7 height = Insert() 3 4 Problem!
21 Insertion: Rebalancing Strateg Step : Search Starting at the inserted node, traverse toward the root until an imbalance is discovered. height = Problem! 8 3 5
22 Insertion: Rebalancing Strateg Step : Repair The repair strateg is called trinode restructuring. 3 nodes, and are distinguished: = the parent of the high sibling = the high sibling = the high child of the high sibling We can now think of the subtree 3 rooted at as consisting of these 3 nodes plus their 4 subtrees 3 height = Problem! 8 5
23 Step : Repair Insertion: Rebalancing Strateg The idea is to rearrange these 3 nodes so that the middle value becomes the root and the other two becomes its children. Thus the grandparent parent child structure becomes a triangular parent two children structure. Note that must be either bigger than both and or smaller than both and. Thus either or is made the root of this subtree. height = h h- T Then the subtrees T are attached at the appropriate places. Since the heights of subtrees T differ b at most, the resulting tree is balanced. T T one is & one is h-4
24 Insertion: Trinode Restructuring Eample Note that is the middle value. height = h h- Restructure h- T T T T T T one is & one is h-4 one is & one is h-4
25 Insertion: Trinode Restructuring - 4 Cases There are 4 different possible relationships between the three nodes, and before restructuring: height = h height = h height = h height = h h- h- T h- h- T T T T T T T T T T T one is & one is h- 4 one is & one is h- 4 one is & one is h- 4 one is & one is h- 4
26 Insertion: Trinode Restructuring - 4 Cases This leads to 4 different solutions, all based on the same principle. height = h height = h height = h height = h h- h- T h- h- T T T T T T T T T T T one is & one is h- 4 one is & one is h- 4 one is & one is h- 4 one is & one is h- 4
27 Insertion: Trinode Restructuring - Case Note that is the middle value. height = h h- Restructure h- T T T T T T one is & one is h-4 one is & one is h-4
28 Insertion: Trinode Restructuring - Case height = h h- h- T Restructure T T T T T one is & one is h-4 one is & one is h-4
29 Insertion: Trinode Restructuring - Case 3 height = h h- h- Restructure T T T T T T one is & one is h-4 one is & one is h-4
30 Insertion: Trinode Restructuring - Case 4 height = h h- T h- Restructure T 3 T T T T T one is & one is h-4 one is & one is h-4
31 Insertion: Trinode Restructuring - The Whole Tree Do we have to repeat this process further up the tree? No! The tree was balanced before the insertion. Insertion raised the height of the subtree b. Rebalancing lowered the height of the subtree b. Thus the whole tree is still balanced. height = h h- Restructure h- T 3 T T T T T 3 T T one is & one is h-4 one is & one is h-4
32 Removal Imbalance ma occur at an ancestor of the removed node. height = 3 7 height = Remove(8) 4 Problem!
33 Removal: Rebalancing Strateg Step : Search Let w be the node actuall removed (i.e., the node matching the ke if it has a leaf child, otherwise the node following in an in-order traversal. Starting at w, traverse toward the root until an imbalance is discovered. height = Problem! 3 5
34 Removal: Rebalancing Strateg Step : Repair We again use trinode restructuring. 3 nodes, and are distinguished: height = 3 7 = the parent of the high sibling = the high sibling = the high child of the high sibling (if children are equall high, keep chain linear) 3 4 Problem! 5
35 Removal: Rebalancing Strateg Step : Repair The idea is to rearrange these 3 nodes so that the middle value becomes the root and the other two becomes its children. Thus the grandparent parent child structure becomes a triangular parent two children structure. Note that must be either bigger than both and or smaller than both and. Thus either or is made the root of this subtree, and is lowered b. Then the subtrees T are attached at the appropriate places. Although the subtrees T can differ in height b up to, after restructuring, sibling subtrees will differ b at most. T T or & h- 4 height = h h- or T
36 Removal: Trinode Restructuring - 4 Cases There are 4 different possible relationships between the three nodes, and before restructuring: height = h height = h height = h height = h h- h- T h- h- T or h- 3 T T or h- 3 T T T T T T T T or & h-4 or & h-4 or & h-4 or & h-4
37 Removal: Trinode Restructuring - Case Note that is the middle value. height = h h- Restructure h or h- h- or T T or T T T T or & h- 4 or or & h- 4
38 Removal: Trinode Restructuring - Case height = h h- T T or Restructure h- or h or h- T T T T or or & h- 4 or & h-4
39 Removal: Trinode Restructuring - Case 3 height = h h- h- Restructure T T T T T T or & h- 4 or & h-4
40 Removal: Trinode Restructuring - Case 4 height = h h- T h- Restructure T 3 T T T T T or & h- 4 or & h-4
41 Step : Repair Removal: Rebalancing Strateg Unfortunatel, trinode restructuring ma reduce the height of the subtree, causing another imbalance further up the tree. Thus this search and repair process must in the worst case be repeated until we reach the root.
42 Java Implementation of AVL Trees Please see tet
43 Running Times for AVL Trees a single restructure is O() using a linked-structure binar tree find is O(log n) height of tree is O(log n), no restructures needed insert is O(log n) initial find is O(log n) Restructuring is O() remove is O(log n) initial find is O(log n) Restructuring up the tree, maintaining heights is O(log n)
44 AVLTree Eample
45 Outline Binar Search Trees AVL Trees Spla Trees
46 Self-balancing BST Spla Trees Invented b Daniel Sleator and Bob Tarjan Allows quick access to recentl accessed elements D. Sleator Bad: worst-case O(n) Good: average (amortied) case O(log n) Often perform better than other BSTs in practice R. Tarjan
47 Splaing Splaing is an operation performed on a node that iterativel moves the node to the root of the tree. In spla trees, each BST operation (find, insert, remove) is augmented with a spla operation. In this wa, recentl searched and inserted elements are near the top of the tree, for quick access.
48 3 Tpes of Spla Steps Each spla operation on a node consists of a sequence of spla steps. Each spla step moves the node up toward the root b or levels. There are tpes of step: Zig-Zig Zig-Zag Zig These steps are iterated until the node is moved to the root.
49 Zig-Zig Performed when the node forms a linear chain with its parent and grandparent. i.e., right-right or left-left T 4 ig-ig T T T T T 4
50 Zig-Zag Performed when the node forms a non-linear chain with its parent and grandparent i.e., right-left or left-right ig-ag T T 4 T T T 4 T
51 Zig Performed when the node has no grandparent i.e., its parent is the root ig T 4 w w T T T 4 T T
52 Spla Trees & Ordered Dictionaries which nodes are splaed after each operation? method find(k) insert(k,v) spla node if ke found, use that node if ke not found, use parent of eternal node where search terminated use the new node containing the entr inserted remove(k) use the parent of the internal node w that was actuall removed from the tree (the parent of the node that the removed item was swapped with)
53 Recall BST Deletion Now consider the case where the ke k to be removed is stored at a node v whose children are both internal we find the internal node w that follows v in an inorder traversal we cop ke(w) into node v we remove node w and its left child (which must be a leaf) b means of operation removeeternal() Eample: remove 3 which node will be splaed? 3 v 5 v 8 8 w
54 Note on Deletion The tet (Goodrich, p. 463) uses a different convention for BST deletion in their splaing eample Instead of deleting the leftmost internal node of the right subtree, the delete the rightmost internal node of the left subtree. We will stick with the convention of deleting the leftmost internal node of the right subtree (the node immediatel following the element to be removed in an inorder traversal).
55 Spla Tree Eample
56 Worst-case is O(n) Eample: Performance Find all elements in sorted order This will make the tree a left linear chain of height n, with the smallest element at the bottom Subsequent search for the smallest element will be O(n)
57 Average-case is O(log n) Performance Proof uses amortied analsis We will not cover this Operations on more frequentl-accessed entries are faster. Given a sequence of m operations, the running time to access entr i is: O log m / f (i) where f(i) is the number of times entr i is accessed.
58 (, 4) Trees Other Forms of Search Trees These are multi-wa search trees (not binar trees) in which internal nodes have between and 4 children Have the propert that all eternal nodes have eactl the same depth. Worst-case O(log n) operations Somewhat complicated to implement Red-Black Trees Binar search trees Worst-case O(log n) operations Somewhat easier to implement Requires onl O() structural changes per update
59 Summar Binar Search Trees AVL Trees Spla Trees
Splay Trees Goodrich, Tamassia, Dickerson. Splay Trees 1
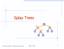 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: entries stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored
AVL Trees. Reading: 9.2
 AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
AVL Trees Reading: 9.2 Balance Factor of a Node The difference in height of its two subtrees (h R -h L ) Balanced Node if -1 BF 1 Unbalanced Node if BF 1 h L h R Balance Factor of a Binar Tree Corresponds
Splay Trees 3/20/14. Splay Trees. Splay Trees are Binary Search Trees. note that two keys of equal value may be wellseparated (7,T) (1,Q) (1,C) (5,H)
 Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Spla Trees 3/20/14 Presentation for use with the tetbook Data Structures and Algorithms in Java, 6 th edition, b M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wile, 2014 Spla Trees v 6 3 8 4 2013
Splay Trees. Splay Trees 1
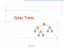 Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Spla Trees v 6 3 8 4 Spla Trees 1 Spla Trees are Binar Search Trees BST Rules: items stored onl at internal nodes kes stored at nodes in the left subtree of v are less than or equal to the ke stored at
Final Exam. EECS 2011 Prof. J. Elder - 1 -
 Final Exam Ø Wed Apr 11 2pm 5pm Aviva Tennis Centre Ø Closed Book Ø Format similar to midterm Ø Will cover whole course, with emphasis on material after midterm (maps and hash tables, binary search, loop
Final Exam Ø Wed Apr 11 2pm 5pm Aviva Tennis Centre Ø Closed Book Ø Format similar to midterm Ø Will cover whole course, with emphasis on material after midterm (maps and hash tables, binary search, loop
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
Search Trees - 2. Venkatanatha Sarma Y. Lecture delivered by: Assistant Professor MSRSAS-Bangalore. M.S Ramaiah School of Advanced Studies - Bangalore
 Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 2 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
B Tree. Also, every non leaf node must have at least two successors and all leaf nodes must be at the same level.
 B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
B Tree If there is just one item in the node, then the B Tree is organised as a binar search tree: all items in the left sub tree must be less than the item in the node, and all items in the right sub
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Binary Search Trees > = 2014 Goodrich, Tamassia, Goldwasser. Binary Search Trees 1
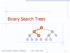 Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Binary Search Trees < > = Binary Search Trees 1 Ordered Dictionary (Map) ADT get (k): record with key k put (k,data): add record (k,data) remove (k): delete record with key k smallest(): record with smallest
Search Trees (Ch. 9) > = Binary Search Trees 1
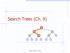 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Binary Trees. Binary Search Trees
 Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent.
Binar Trees A binar tree is a rooted tree where ever node has at most two children. When a node has onl one child, we still distinguish whether this is the left child or the right child of the parent.
Splay Trees. (Splay Trees) Data Structures and Programming Spring / 27
 Splay Trees (Splay Trees) Data Structures and Programming Spring 2017 1 / 27 Basic Idea Invented by Sleator and Tarjan (1985) Blind rebalancing no height info kept! Worst-case time per operation is O(n)
Splay Trees (Splay Trees) Data Structures and Programming Spring 2017 1 / 27 Basic Idea Invented by Sleator and Tarjan (1985) Blind rebalancing no height info kept! Worst-case time per operation is O(n)
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Algorithms and Data Structures
 Ordered Dictionaries and Binary Search Trees Page 1 BFH-TI: Softwareschule Schweiz Ordered Dictionaries and Binary Search Trees Dr. CAS SD01 Ordered Dictionaries and Binary Search Trees Page Outline Ordered
Ordered Dictionaries and Binary Search Trees Page 1 BFH-TI: Softwareschule Schweiz Ordered Dictionaries and Binary Search Trees Dr. CAS SD01 Ordered Dictionaries and Binary Search Trees Page Outline Ordered
Binary Search Trees (10.1) Dictionary ADT (9.5.1)
 Binary Search Trees (10.1) CSE 011 Winter 011 4 March 011 1 Dictionary ADT (..1) The dictionary ADT models a searchable collection of keyelement items The main operations of a dictionary are searching,
Binary Search Trees (10.1) CSE 011 Winter 011 4 March 011 1 Dictionary ADT (..1) The dictionary ADT models a searchable collection of keyelement items The main operations of a dictionary are searching,
Suggested Study Strategy
 Final Exam Thursday, 7 August 2014,19:00 22:00 Closed Book Will cover whole course, with emphasis on material after midterm (hash tables, binary search trees, sorting, graphs) Suggested Study Strategy
Final Exam Thursday, 7 August 2014,19:00 22:00 Closed Book Will cover whole course, with emphasis on material after midterm (hash tables, binary search trees, sorting, graphs) Suggested Study Strategy
CS2210 Data Structures and Algorithms. Lecture 9: AVL TREES definition, properties, insertion
 CS2210 Data Structures and Algorithms Lecture 9: AVL TREES definition, roerties, insertion v 6 3 8 4 BST Performance BST ith n nodes and of height h methods find, insert and remove take O(h) time h is
CS2210 Data Structures and Algorithms Lecture 9: AVL TREES definition, roerties, insertion v 6 3 8 4 BST Performance BST ith n nodes and of height h methods find, insert and remove take O(h) time h is
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Chapter 2: Basic Data Structures
 Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
Chapter 2: Basic Data Structures Basic Data Structures Stacks Queues Vectors, Linked Lists Trees (Including Balanced Trees) Priority Queues and Heaps Dictionaries and Hash Tables Spring 2014 CS 315 2 Two
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Dictionaries. 2/17/2006 Dictionaries 1
 Dictionaries < 6 > 1 4 = 8 9 /17/006 Dictionaries 1 Outline and Reading Dictionary ADT ( 9.3) Log file ( 9.3.1) Binary search ( 9.3.3) Lookup table ( 9.3.3) Binary search tree ( 10.1) Search ( 10.1.1)
Dictionaries < 6 > 1 4 = 8 9 /17/006 Dictionaries 1 Outline and Reading Dictionary ADT ( 9.3) Log file ( 9.3.1) Binary search ( 9.3.3) Lookup table ( 9.3.3) Binary search tree ( 10.1) Search ( 10.1.1)
Lecture 11: Multiway and (2,4) Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
Lecture 11: Multiway and (2,4) Trees 9 2 5 7 10 14 Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline Multiway Seach Tree: a new type of search trees: for ordered d dictionary
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
CSI33 Data Structures
 Outline Department of Mathematics and Computer Science Bronx Community College November 21, 2018 Outline Outline 1 C++ Supplement 1.3: Balanced Binary Search Trees Balanced Binary Search Trees Outline
Outline Department of Mathematics and Computer Science Bronx Community College November 21, 2018 Outline Outline 1 C++ Supplement 1.3: Balanced Binary Search Trees Balanced Binary Search Trees Outline
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
(2,4) Trees. 2/22/2006 (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
(2,4) Trees 9 2 5 7 10 14 2/22/2006 (2,4) Trees 1 Outline and Reading Multi-way search tree ( 10.4.1) Definition Search (2,4) tree ( 10.4.2) Definition Search Insertion Deletion Comparison of dictionary
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 2015
 Presentation for use ith the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Ch.03 Binary Search Trees Binary Search Binary search can perform nearest neighbor queries
Presentation for use ith the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 0 Ch.03 Binary Search Trees Binary Search Binary search can perform nearest neighbor queries
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Final Exam. CSE 2011 Prof. J. Elder Last Updated: :41 PM
 Final Exam Ø Tue, 17 Apr 2012 19:00 22:00 LAS B Ø Closed Book Ø Format similar to midterm Ø Will cover whole course, with emphasis on material after midterm (maps, hashing, binary search trees, sorting,
Final Exam Ø Tue, 17 Apr 2012 19:00 22:00 LAS B Ø Closed Book Ø Format similar to midterm Ø Will cover whole course, with emphasis on material after midterm (maps, hashing, binary search trees, sorting,
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
Computational Optimization ISE 407. Lecture 16. Dr. Ted Ralphs
 Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Computational Optimization ISE 407 Lecture 16 Dr. Ted Ralphs ISE 407 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms in
Advanced Tree Data Structures
 Advanced Tree Data Structures Fawzi Emad Chau-Wen Tseng Department of Computer Science University of Maryland, College Park Binary trees Traversal order Balance Rotation Multi-way trees Search Insert Overview
Advanced Tree Data Structures Fawzi Emad Chau-Wen Tseng Department of Computer Science University of Maryland, College Park Binary trees Traversal order Balance Rotation Multi-way trees Search Insert Overview
Balanced Binary Search Trees. Victor Gao
 Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Data Structure: Search Trees 2. Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering
 Data Structure: Search Trees 2 2017 Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered
Data Structure: Search Trees 2 2017 Instructor: Prof. Young-guk Ha Dept. of Computer Science & Engineering Search Trees Tree data structures that can be used to implement a dictionary, especially an ordered
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Trees. Courtesy to Goodrich, Tamassia and Olga Veksler
 Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Lecture 12: BT Trees Courtesy to Goodrich, Tamassia and Olga Veksler Instructor: Yuzhen Xie Outline B-tree Special case of multiway search trees used when data must be stored on the disk, i.e. too large
Balanced Binary Search Trees
 Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
Balanced Binary Search Trees Pedro Ribeiro DCC/FCUP 2017/2018 Pedro Ribeiro (DCC/FCUP) Balanced Binary Search Trees 2017/2018 1 / 48 Motivation Let S be a set of comparable objects/items: Let a and b be
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
(2,4) Trees Goodrich, Tamassia (2,4) Trees 1
 (2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
(2,4) Trees 9 2 5 7 10 14 2004 Goodrich, Tamassia (2,4) Trees 1 Multi-Way Search Tree A multi-way search tree is an ordered tree such that Each internal node has at least two children and stores d -1 key-element
10.2 AVL Trees. Definition of an AVL Tree. 438 Chapter 10. Search Trees
 438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
438 Chapter 10. Search Trees 10. AVL Trees In theprevioussection,wediscussedwhatshouldbeanefficientmapdatastructure, but the worst-case performance it achieves for the various operations is linear time,
Chapter. Binary Search Trees. Contents
 Chapter 4 Balanced Binary Search Trees U.S. Navy Blue Angels, performing their delta formation during the Blues on the Bay Air Show at Marine Corps Base Hawaii in 2007. U.S. government photo by Petty Officer
Chapter 4 Balanced Binary Search Trees U.S. Navy Blue Angels, performing their delta formation during the Blues on the Bay Air Show at Marine Corps Base Hawaii in 2007. U.S. government photo by Petty Officer
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Search Trees. COMPSCI 355 Fall 2016
 Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Search Trees COMPSCI 355 Fall 2016 2-4 Trees Search Trees AVL trees Red-Black trees Splay trees Multiway Search Trees (2, 4) Trees External Search Trees (optimized for reading and writing large blocks)
Introduction. for large input, even access time may be prohibitive we need data structures that exhibit times closer to O(log N) binary search tree
 Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Chapter 4 Trees 2 Introduction for large input, even access time may be prohibitive we need data structures that exhibit running times closer to O(log N) binary search tree 3 Terminology recursive definition
Red-Black Trees. 2/24/2006 Red-Black Trees 1
 Red-Black Trees 3 8 //00 Red-Black Trees 1 Outline and Reading From (,) trees to red-black trees ( 10.5) Red-black tree ( 10.5.1) Definition Height Insertion restructuring recoloring Deletion restructuring
Red-Black Trees 3 8 //00 Red-Black Trees 1 Outline and Reading From (,) trees to red-black trees ( 10.5) Red-black tree ( 10.5.1) Definition Height Insertion restructuring recoloring Deletion restructuring
Solutions. Suppose we insert all elements of U into the table, and let n(b) be the number of elements of U that hash to bucket b. Then.
 Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Red-black trees (19.5), B-trees (19.8), trees
 Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-Black Trees. Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood
 Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
 Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Multi-Way Search Trees
 Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
Multi-Way Search Trees Manolis Koubarakis 1 Multi-Way Search Trees Multi-way trees are trees such that each internal node can have many children. Let us assume that the entries we store in a search tree
8.1. Optimal Binary Search Trees:
 DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
DATA STRUCTERS WITH C 10CS35 UNIT 8 : EFFICIENT BINARY SEARCH TREES 8.1. Optimal Binary Search Trees: An optimal binary search tree is a binary search tree for which the nodes are arranged on levels such
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
Outline. Definition. 2 Height-Balance. 3 Searches. 4 Rotations. 5 Insertion. 6 Deletions. 7 Reference. 1 Every node is either red or black.
 Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Outline 1 Definition Computer Science 331 Red-Black rees Mike Jacobson Department of Computer Science University of Calgary Lectures #20-22 2 Height-Balance 3 Searches 4 Rotations 5 s: Main Case 6 Partial
Binary search trees (chapters )
 Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Maps and Dictionaries
 Map and ictionary Ts Maps and ictionaries The dictionary T models a searchable collection of key-element items The main operations of a dictionary are searching, inserting, and deleting items MP: Multiple
Map and ictionary Ts Maps and ictionaries The dictionary T models a searchable collection of key-element items The main operations of a dictionary are searching, inserting, and deleting items MP: Multiple
CS Transform-and-Conquer
 CS483-11 Transform-and-Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
CS483-11 Transform-and-Conquer Instructor: Fei Li Room 443 ST II Office hours: Tue. & Thur. 1:30pm - 2:30pm or by appointments lifei@cs.gmu.edu with subject: CS483 http://www.cs.gmu.edu/ lifei/teaching/cs483_fall07/
Multiway Search Trees. Multiway-Search Trees (cont d)
 Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
Multiway Search Trees Each internal node v of a multi-way search tree T has at least two children contains d-1 items, where d is the number of children of v an item is of the form (k i,x i ) for 1 i d-1,
An AVL tree with N nodes is an excellent data. The Big-Oh analysis shows that most operations finish within O(log N) time
 B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
B + -TREES MOTIVATION An AVL tree with N nodes is an excellent data structure for searching, indexing, etc. The Big-Oh analysis shows that most operations finish within O(log N) time The theoretical conclusion
Data Structures and Algorithms
 Data Structures and Algorithms Spring 2009-2010 Outline BST Trees (contd.) 1 BST Trees (contd.) Outline BST Trees (contd.) 1 BST Trees (contd.) The bad news about BSTs... Problem with BSTs is that there
Data Structures and Algorithms Spring 2009-2010 Outline BST Trees (contd.) 1 BST Trees (contd.) Outline BST Trees (contd.) 1 BST Trees (contd.) The bad news about BSTs... Problem with BSTs is that there
Lecture 16 Notes AVL Trees
 Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Fall 2015) Frank Pfenning 1 Introduction Binar search trees are an ecellent data structure to implement associative arras, maps,
Lecture 16 Notes AVL Trees 15-122: Principles of Imperative Computation (Fall 2015) Frank Pfenning 1 Introduction Binar search trees are an ecellent data structure to implement associative arras, maps,
Red-Black, Splay and Huffman Trees
 Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
Multi-way Search Trees. (Multi-way Search Trees) Data Structures and Programming Spring / 25
 Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
Multi-way Search Trees (Multi-way Search Trees) Data Structures and Programming Spring 2017 1 / 25 Multi-way Search Trees Each internal node of a multi-way search tree T: has at least two children contains
CSCI2100B Data Structures Trees
 CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
CSCI2100B Data Structures Trees Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction General Tree
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
CSCI 136 Data Structures & Advanced Programming. Lecture 25 Fall 2018 Instructor: B 2
 CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
CSCI 136 Data Structures & Advanced Programming Lecture 25 Fall 2018 Instructor: B 2 Last Time Binary search trees (Ch 14) The locate method Further Implementation 2 Today s Outline Binary search trees
COSC160: Data Structures Balanced Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
Lecture Overview. Readings. Recall: Binary Search Trees (BSTs) The importance of being balanced. AVL trees. Balance Insert. Other balanced trees
 alanced inar Search Trees Lecture Overview The importance of being balanced VL trees Definition alance Insert Other balanced trees Data structures in general Readings LRS hapter. and. (but different approach:
alanced inar Search Trees Lecture Overview The importance of being balanced VL trees Definition alance Insert Other balanced trees Data structures in general Readings LRS hapter. and. (but different approach:
B + -trees. Kerttu Pollari-Malmi
 B + -trees Kerttu Pollari-Malmi This tet is based partl on the course tet book b Cormen and partl on the old lecture slides written b Matti Luukkainen and Matti Nkänen. 1 Introduction At first, read the
B + -trees Kerttu Pollari-Malmi This tet is based partl on the course tet book b Cormen and partl on the old lecture slides written b Matti Luukkainen and Matti Nkänen. 1 Introduction At first, read the
Binary search trees (chapters )
 Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Binary search trees (chapters 18.1 18.3) Binary search trees In a binary search tree (BST), every node is greater than all its left descendants, and less than all its right descendants (recall that this
Fundamental Algorithms
 WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
WS 2007/2008 Fundamental Algorithms Dmytro Chibisov, Jens Ernst Fakultät für Informatik TU München http://www14.in.tum.de/lehre/2007ws/fa-cse/ Fall Semester 2007 1. AVL Trees As we saw in the previous
CSE 326: Data Structures Splay Trees. James Fogarty Autumn 2007 Lecture 10
 CSE 32: Data Structures Splay Trees James Fogarty Autumn 2007 Lecture 10 AVL Trees Revisited Balance condition: Left and right subtrees of every node have heights differing by at most 1 Strong enough :
CSE 32: Data Structures Splay Trees James Fogarty Autumn 2007 Lecture 10 AVL Trees Revisited Balance condition: Left and right subtrees of every node have heights differing by at most 1 Strong enough :
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Balanced Search Trees
 Balanced Search Trees Michael P. Fourman February 2, 2010 To investigate the efficiency of binary search trees, we need to establish formulae that predict the time required for these dictionary or set
Balanced Search Trees Michael P. Fourman February 2, 2010 To investigate the efficiency of binary search trees, we need to establish formulae that predict the time required for these dictionary or set
Balanced Binary Search Trees
 Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
Balanced Binary Search Trees In the previous section we looked at building a binary search tree. As we learned, the performance of the binary search tree can degrade to O(n) for operations like getand
CS350: Data Structures AVL Trees
 S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
S35: Data Structures VL Trees James Moscola Department of Engineering & omputer Science York ollege of Pennsylvania S35: Data Structures James Moscola Balanced Search Trees Binary search trees are not
CMPE 160: Introduction to Object Oriented Programming
 CMPE 6: Introduction to Object Oriented Programming General Tree Concepts Binary Trees Trees Definitions Representation Binary trees Traversals Expression trees These are the slides of the textbook by
CMPE 6: Introduction to Object Oriented Programming General Tree Concepts Binary Trees Trees Definitions Representation Binary trees Traversals Expression trees These are the slides of the textbook by
Augmenting Data Structures
 Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Augmenting Data Structures [Not in G &T Text. In CLRS chapter 14.] An AVL tree by itself is not very useful. To support more useful queries we need more structure. General Definition: An augmented data
Self Adjusting Data Structures
 Self Adjusting Data Structures Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Self Adjusting Data Structures 2014/2015 1 / 31 What are self adjusting data structures? Data structures that can
Self Adjusting Data Structures Pedro Ribeiro DCC/FCUP 2014/2015 Pedro Ribeiro (DCC/FCUP) Self Adjusting Data Structures 2014/2015 1 / 31 What are self adjusting data structures? Data structures that can
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
CS 314H Honors Data Structures Fall 2017 Programming Assignment #6 Treaps Due November 12/15/17, 2017
 CS H Honors Data Structures Fall 207 Programming Assignment # Treaps Due November 2//7, 207 In this assignment ou will work individuall to implement a map (associative lookup) using a data structure called
CS H Honors Data Structures Fall 207 Programming Assignment # Treaps Due November 2//7, 207 In this assignment ou will work individuall to implement a map (associative lookup) using a data structure called
Data Structures Lesson 7
 Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
Data Structures Lesson 7 BSc in Computer Science University of New York, Tirana Assoc. Prof. Dr. Marenglen Biba 1-1 Binary Search Trees For large amounts of input, the linear access time of linked lists
ECE250: Algorithms and Data Structures AVL Trees (Part A)
 ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
ECE250: Algorithms and Data Structures AVL Trees (Part A) Ladan Tahvildari, PEng, SMIEEE Associate Professor Software Technologies Applied Research (STAR) Group Dept. of Elect. & Comp. Eng. University
Dictionaries. Priority Queues
 Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
Red-Black-Trees.1 Dictionaries Sets and Multisets; Opers: (Ins., Del., Mem.) Sequential sorted or unsorted lists. Linked sorted or unsorted lists. Tries and Hash Tables. Binary Search Trees. Priority Queues
CSE Data Structures and Introduction to Algorithms... In Java! Instructor: Fei Wang. Binary Search Trees. CSE2100 DS & Algorithms 1
 CSE 2100 Data Structures and Introduction to Algorithms...! In Java!! Instructor: Fei Wang! Binary Search Trees 1 R-10.6, 10.7!!! Draw the 11-entry hash table that results from using the hash function
CSE 2100 Data Structures and Introduction to Algorithms...! In Java!! Instructor: Fei Wang! Binary Search Trees 1 R-10.6, 10.7!!! Draw the 11-entry hash table that results from using the hash function
Lesson 21: AVL Trees. Rotation
 The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
The time required to perform operations on a binary search tree is proportional to the length of the path from root to leaf. This isn t bad in a well-balanced tree. But nothing prevents a tree from becoming
Red-Black Trees Goodrich, Tamassia. Red-Black Trees 1
 Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES
 HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
HEAPS: IMPLEMENTING EFFICIENT PRIORITY QUEUES 2 5 6 9 7 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H., Wiley, 2014
