Drawing curves automatically: procedures as arguments
|
|
|
- Rosaline Copeland
- 5 years ago
- Views:
Transcription
1 CHAPTER 7 Drawing curves automatically: procedures as arguments moveto lineto stroke fill clip The process of drawing curves by programming each one specially is too complicated to be done easily. In this chapter we shall see how to construct procedures to help out enormously. We proceed in stages, starting with a reasonably simple example. 1. Drawing an hyperbola The curves we have drawn so far are really too simple to give you an idea of how useful Bézier curves are. This is because the Bézier curve is guaranteed to match exactly the graph of any polynomial of degree 3 or less, so no approximation is involved. In this section we will develop a procedure hyperbola with three arguments x 0, x 1, N that constructs the graph of the upper branch of an hyperbola by using N Bézier segments in between x 0 and x 1. y 2 x 2 = 1, y = 1 + x 2. As is usually the best idea, the procedure builds the path without drawing it. Thus the sequence newpath hyperbola stroke will draw the curve y = 1 + x 2 from x = 2 to x = 2 in 4 Bézier segments. Paths drawn by hyperbola (pink) and hyperbola (red). What goes into the procedurehyperbola? We can immediately write down the skeleton /hyperbola { 16 dict begin /x1 exch def /x0 exch def
2 Chapter 7. Drawing curves automatically: procedures as arguments 2... and we must now fill in the real computation. First we set a step size h = (x 1 x 0 )/N so that in N steps we cross from x 0 to x 1 : /h x1 x0 sub N div def Then we introduce variables x and y which are going to change as the procedure runs, and move to the first point on the graph. It will also help to keep a variable s to hold the current value of the slope. Note that if y = f(x) = 1 + x 2 = (1 + x 2 ) 1/2 then s = f (x) = (1/2)(2x)(1 + x 2 ) 1/2 = x 1 + x 2 = x y. Recall that the control points are (x 0, y 0 ) (x 0 + h/3, y 0 + y (x 0 )/3 (x 1 h/3, y 1 y (x 1 )/3 (x 1, y 1 ). where x 1 = x + h, y 1 = y(x 1 ). The code begins: /x x0 def /y 1 x x mul add sqrt def /s x y div def x y moveto Now we must build N Bézier segments, using arepeat loop. N { % repeat x h 3 div add y h 3 div s mul add /x x h add def /y 1 x x mul add sqrt def /s x y div def x h 3 div sub y h 3 div s mul sub x y and that s it. We could make this program somewhat more readable and more flexible if we add to it a couple of procedures that calculate f(x) and f (x), instead of doing it in line. Each of the procedures should have a single argument x. They are short enough that we do not need to use a variable inside them. Explicitly: % sqrt(1 + x^2) /f { dup mul 1 add sqrt } def % x/sqrt(1 + x^2) /f { dup dup mul 1 add sqrt div
3 Chapter 7. Drawing curves automatically: procedures as arguments 3 } def Recall thatdup just duplicates the item on the top of the stack. The new loop would be N { % repeat x h 3 div add y h 3 div s mul add /x x h add def /y x f def /s x f def x h 3 div sub y h 3 div s mul sub x y It would be better to have a single procedure that calculates f(x) and f (x) all in one package. For one thing, it would be more efficient since we wouldn t have to calculate square roots more often than necessary. For another, I prefer to have things that go together... well, go together. The calculation of f(x) and f (x) are related, and if you modify one to draw some different graph, then you will have to modify the other. For this reason they should be dealt with in one visible and indivisible unit. We can do this by using a single procedure with one argument x and as output an array of two numbers [y s]. But now a variable to hold the value of x is useful. It might be a good idea here to exhibit all procedures we are using: % x -> [sqrt(1 + x^2), x/sqrt(1 + x^2)] /f { 2 dict begin /x exch def /y 1 x x mul add sqrt def [ y x y div ] % x0 x1 N /hyperbola { 16 dict begin /x1 exch def /x0 exch def % h = (x1 - x0)/n /h x1 x0 sub N div def /x x0 def /F x f def /y F 0 get def /s F 1 get def x y moveto N { % repeat x h 3 div add y h 3 div s mul add /x x h add def /F x f def /y F 0 get def /s F 1 get def
4 Chapter 7. Drawing curves automatically: procedures as arguments 4 x h 3 div sub y h 3 div s mul sub x y It is true that using a dictionary and an array has made the program somewhat less efficient than it was at the start. On the good side, the program is now perhaps a bit more readable or perhaps not, depending probably on your own taste. It has one great virtue, however it is a great deal more flexible. If we want to draw some other graph, we need only to rewrite the single proceduref, making sure that it, too, has a single argument x and returns an array of two values [y s]. Exercise 1. Modify the procedure f so you can use essentially the same stuff to graph the function y = x 3 x between 1 and 1. Exercise 2. Modify the procedure f so you can use essentially the same stuff to graph the function y = sin x between 1 and 1. Be careful about degrees and radians it is only when x is expressed in radians that sin x = cosx. Use it to draw the graph of sin x between x = 0 and x = π with 1, 2, 4 segments, all on one plot. Make them successively lighter so you can distinguish them. 2. Parametrized curves We now have a good idea of how to draw smooth function graphs. However, not all curves in the plane are the graphs of functions. What is true is that almost any curve we can imagine is the union of a number of smooth segments, where each segment is a parametrized path (x(t), y(t)) in the plane. I recall that to draw by Bézier curves a segment between t = t 0 and t 1 I use control points P 0 = (x 0, y 0 ) = (x(t 0 ), y(t 0 )) P 1 = (x 1, y 1 ) = (x(t 1 ), y(t 1 )) [ ] x1/3 P 1/3 = y 1/3 [ ] x0 = + t [ ] x 0 y 0 3 y 0 [ ] x2/3 P 2/3 = y 2/3 [ ] x1 = t [ ] x 1 y 1 3 y 1. Let s look again at the problem posed at the beginning of this section, and see how we would draw a parametrized path by using Bézier curves. We must first divide it up into a certain number of segments. Calculate the position and velocity at the endpoints of each of the segments. Move to the first point and add one Bézier curve for each segment. (The command moveto is not necessary in the intermediate curves, because drawing a Bézier curve in PostScript advances the current point to the end point.) Then stroke it or fill it or clip it (if in the latter cases it is closed).
5 Chapter 7. Drawing curves automatically: procedures as arguments 5 3. Drawing graphs automatically In the next section I ll explain a technique for drawing parametrized curves which will become a standard trick in your bag of tools. There are several new ingredients in it, and it may help if I explain one of them by improving the procedure for drawing hyperbolas along the same lines. We have already made that procedure reasonably flexible by isolating how the actual function f(x) is used to draw the graph. What I will do now is show how you can change functions by using the graphing function itself as an argument to a general procedure for making graphs. The only part of the procedure hyperbola which must be changed is the very first part. Since the procedure no longer draws only hyperbolas, its name must be changed. And it has an extra argument, the name of the function f, which must be a procedure into which you put x and out of which you get an array [f(x) f (x)]. We must read this fourth argument and convert that name into a procedure so we can call it. The few lines of this procedure where it differs from the older one are here: /mkgraph { load 16 dict begin /f exch def /x1 exch def /x0 exch def Not quite as simple as might be expected. A slight technical difficulty is caused by the fact that the name of the parametrization procedure being used here might be redefined inside the procedure it might, for example, be /f so it must be retrieved from its dictionary with load before a new dictionary is introduced. Here is a complete program which uses this to draw the graph of y = x 4. % x0 x1 N /f /mkgraph { load /f exch def 1 dict begin /x1 exch def /x0 exch def % h = (x1 - x0)/n /h x1 x0 sub N div def /x x0 def /F x f def /y F 0 get def /s F 1 get def x y moveto N { x h 3 div add y h 3 div s mul add /x x h add def /F x f def /y F 0 get def /s F 1 get def x h 3 div sub y h 3 div s mul sub x y
6 Chapter 7. Drawing curves automatically: procedures as arguments 6 % [x^4 4x^3] /quartic { 2 dict begin /x exch def [ x x mul x mul x mul x x mul x mul 4 mul ] % scale translate 1 72 div setlinewidth newpath /quartic mkgraph stroke In the next section we ll see a procedure which is rather similar to this one, but differs in these aspects: (1) It deals with parametrized curves instead of graphs; (2) it allows you to use a single procedure to draw any one of a large family of curves, for example all of the graphs y = cx 4 where c is a constant you can specify when you draw the curve; (3) it adds the new path to the path that already exists, if there is one. Like the commandarc. Exercise 3. Write a PostScript procedure with the same arguments as mkgraph but which simply draws a polygon among the successive points. (This can be used to debug your calculus.) Exercise 4. Write a PostScript procedure that will graph a polynomial betweenx 0 and x 1 withn Bézier segments. There are a number of things you have to think about: (1) For evaluating a polynomial in a program it is easiest to use an expression like 5x 3 + 2x + 3x + 4 = ((5x + 2)x + 3)x + 4. (2) You will have to add an argument to this procedure to pass the polynomial coefficients as an array. Recall that length returns the size of an array. (See Appendix 6 for more about polynomial evaluation.) 4. Drawing parametrized paths automatically If you are given a parametrized path and you want to draw it by using Bézier curves, you must calculate position and velocity at several points of the path. This is tedious and prone to error, and you will quickly ask if there is some way to get PostScript to do the work. This is certainly possible, if you can write a PostScript routine which calculates position and velocity for the parametrization. One tricky point is that we don t want to rewrite the drawing routine for every path we draw, but would like instead to put in the parametrization itself as an argument passed to the routine. The parametrization should be a procedure which has a single argument, namely a value of t, and returns data giving position and velocity for that value of t. We shall in fact do this, and make the name of the routine which calculates position and velocity one of the arguments. How PostScript handles this is somewhat technical, but you won t have to understand underlying details to understand the routine. Another tricky point is that we would like to make a routine for drawing a family of curves we don t want to have to make separate routines for y = x 2, y = 2x 2, etc. We would like to be able at least to write one routine that can draw y = cx 2 for any specified constant c. This will be accomplished by passing to the routine an array of parameters to pick a specific curve from a family. The terminology is a bit clumsy we have the parameters determining which path from a family is to be drawn and the variable t which parametrizes the curve. The last, to avoid confusion, I shall call the parametrizing variable. I will first simply lay out the main routine we shall use from now on for drawing parametrized paths. It is a bit complicated. In the next two sections I shall explain how to use it and how it works.
7 Chapter 7. Drawing curves automatically: procedures as arguments 7 % stack: t0 t1 N [parameters] /f /mkpath { load 1 dict begin /f exch def /pars exch def /t1 exch def /t0 exch def % h = (t1-t0)/n /h t1 t0 sub N div def % h3 = h/3 /h3 h 3 div def % set current location = [f(t0) f (t0)] /currentloc pars t0 f def pars t0 f 0 get aload pop % calculate the first point thereisacurrentpoint % if a path already under construction... { lineto } { moveto } ifelse N { % x y = currentpoint currentloc 0 get 0 get % x0 dx0 currentloc 1 get 0 get h3 mul add % x1 currentloc 0 get 1 get currentloc 1 get 1 get h3 mul add % y1 /t0 t0 h add def % move ahead one step /currentloc pars t0 f def currentloc 0 get 0 get currentloc 1 get 0 get h3 mul sub currentloc 0 get 1 get currentloc 1 get 1 get h3 mul sub % x2 y2 currentloc 0 get 0 get currentloc 0 get 1 get % x3 y3 The procedure thereisacurrentpoint returns true or false, depending on whether a path has been started. We have already seen it in Chapter 6.
8 Chapter 7. Drawing curves automatically: procedures as arguments 8 5. How to use it The input to the procedure consists of five items on the stack. The first is the initial value of t for the path. The second is the final value of t. third is the number N of Bézier segments to be drawn. Fourth comes an array[... ] of parameters, which I shall say something more about in a moment. It can be just the empty array[], but it must be there. Last follows the name of a routine specifying the parametrization in PostScript. A name in PostScript starts with the symbol /. As I have already said, this routine has two arguments. The first is an array of things which the routine can use to do its calculation. The second is the variable t. Its output (left on the stack) will be a 2 2 matrix written according to my conventions as an array of two 2D arrays. The most important, and complicated, item here is the parametrization routine. For example, suppose we want to draw circles of varying radii, centred at the origin. The parametrization of such a circle is t P(t) = (R cost, R sin t) and the velocity vector of this parametrization is t P (t) = ( R sint, R cost) if t is in radians. The variable t is the parameter which traverse the path, while R is a parameter specifying which of several possible circles are to be drawn. Thus the input to the circle drawing routine will be a pair[r] t and output will be[[xt yt][dxt dyt]]. Here is a more explicit block of PostScript code (assuming pi defined elsewhere to be π). Note that PostScript uses degrees instead of radians, but that the formula for the velocity vector assumes radians. /circle { 4 dict begin /t exch def /pars exch def /R pars 0 get def /t t 180 mul //pi div def [ [ t cos R mul t sin R mul ] [ t sin neg R mul t cos R mul ] ] (mkpath.inc) run newpath [2] /circle 0 2 //pi mul 8 mkpath closepath stroke You might not have seen anything like//pi before using// before a variable name means the interpreter puts its current value in place immediately, rather than wait until the procedure is run to look uppi and evaluate it. The array of parameters passed to one of these routines can be of any size you want. It can even be empty if in fact you just want to draw one of a kind. But you will probably find that most paths you want to draw are just part of a larger family.
9 Chapter 7. Drawing curves automatically: procedures as arguments 9 There is one other point. It is very common to get the routine for the velocity vector wrong, since after all you must first calculate a derivative. When this happens, the curve will hit the points representing position, but will wander wildly in between. One way to see if in fact you have computed the derivative correctly is to use a routine that might be called mkpolypath which simply draws a polygonal path instead of one made up of Bézier segments. It has exactly the same usage asmkpath, but ignores the velocity vector in building the path, and can hence be used to see if the rest of your routine is working. Exercise 5. Write a procedure mkpolypath which has the same arguments as mkpath but draws a polygon instead. Exercise 6. Write down a parametrization of the ellipse x 2 a 2 + y2 b 2 = 1. Write a procedure which will draw it. For example you would write3 4 drawellipse. Exercise 7. Draw the image of the grid centred at (0, 0), under the map (x, y) (x 2 y 2, 2xy). The spacing between grid lines is to be 0.25 cm. 6. How it works The basic idea is simply to automate the procedure you used earlier to draw the graph of y = x 4. The point is that if we are given a parametrization of a path we can draw an approximation by Bézier curves using the velocity vectors associated to the parametrization in order to construct control points. The routine is fairly straightforward, except that it calls a procedure thereisacurrentpoint to tell whether the path being drawn is the beginning of a new path or the continuation of an old one. You don t have to know the details of the procedure called it operates in a very simple manner at a somewhat low level of PostScript. This routine all by itself is very useful, and is capable of making interesting pictures. But the ideas behind it are applicable in a wide range of circumstances. thales pythagoras eudoxus euclid archimedes 7. Code The filemkpath.inc contains a proceduremkpath as well asmkgraph a few related ones.
Drawing polygons: loops and arrays
 CHAPTER 5 Drawing polygons: loops and arrays repeat:1 We begin by learning how to draw regular polygons, and then look at arbitrary polygons. Both will use loops, and the second will require learning about
CHAPTER 5 Drawing polygons: loops and arrays repeat:1 We begin by learning how to draw regular polygons, and then look at arbitrary polygons. Both will use loops, and the second will require learning about
Mathematics 308 Geometry. Chapter 9. Drawing three dimensional objects
 Mathematics 308 Geometry Chapter 9. Drawing three dimensional objects In this chapter we will see how to draw three dimensional objects with PostScript. The task will be made easier by a package of routines
Mathematics 308 Geometry Chapter 9. Drawing three dimensional objects In this chapter we will see how to draw three dimensional objects with PostScript. The task will be made easier by a package of routines
Drawing polygons: loops and arrays
 CHAPTER 5 Drawing polygons: loops and arrays Webeginbylearninghowtodrawregularpolygons,andthenlookatarbitrarypolygons.Bothwilluseloops, and the second will require learning about arrays. There are several
CHAPTER 5 Drawing polygons: loops and arrays Webeginbylearninghowtodrawregularpolygons,andthenlookatarbitrarypolygons.Bothwilluseloops, and the second will require learning about arrays. There are several
Updated: August 24, 2016 Calculus III Section Math 232. Calculus III. Brian Veitch Fall 2015 Northern Illinois University
 Updated: August 24, 216 Calculus III Section 1.2 Math 232 Calculus III Brian Veitch Fall 215 Northern Illinois University 1.2 Calculus with Parametric Curves Definition 1: First Derivative of a Parametric
Updated: August 24, 216 Calculus III Section 1.2 Math 232 Calculus III Brian Veitch Fall 215 Northern Illinois University 1.2 Calculus with Parametric Curves Definition 1: First Derivative of a Parametric
To sketch the graph we need to evaluate the parameter t within the given interval to create our x and y values.
 Module 10 lesson 6 Parametric Equations. When modeling the path of an object, it is useful to use equations called Parametric equations. Instead of using one equation with two variables, we will use two
Module 10 lesson 6 Parametric Equations. When modeling the path of an object, it is useful to use equations called Parametric equations. Instead of using one equation with two variables, we will use two
Package epsdice a scalable dice font
 Package epsdice a scalable dice font 2007/02/15 Version 2.1 Thomas Heim (thomas.heim@unibas.ch) 1 Introduction Dice fonts are already available in metafont format. (I should know, I wrote one myself: dice3d.mf.)
Package epsdice a scalable dice font 2007/02/15 Version 2.1 Thomas Heim (thomas.heim@unibas.ch) 1 Introduction Dice fonts are already available in metafont format. (I should know, I wrote one myself: dice3d.mf.)
Postscript Intro. References. What is Postscript? Hello World! in Ghostscript. CSE 413, Autumn 2005 Programming Languages. Page description language
 References Postscript Intro CSE 413, Autumn 2005 Programming Languages http://www.cs.washington.edu/education/courses/413/05au/ Postscript Language Reference, Adobe Postscript Language Tutorial and Cookbook,
References Postscript Intro CSE 413, Autumn 2005 Programming Languages http://www.cs.washington.edu/education/courses/413/05au/ Postscript Language Reference, Adobe Postscript Language Tutorial and Cookbook,
An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s.
 Using Monte Carlo to Estimate π using Buffon s Needle Problem An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s. Here s the problem (in a simplified form). Suppose
Using Monte Carlo to Estimate π using Buffon s Needle Problem An interesting related problem is Buffon s Needle which was first proposed in the mid-1700 s. Here s the problem (in a simplified form). Suppose
Informatique Graphique. Traitement de l'information et automatisation. Traitement de l'information et automatisation
 Un programme mystérieux Informatique Graphique Professeur: Victor Ostromoukhov Page 1 Page 2 Un programme mystérieux Traitement de l'information et automatisation Page 3 Page 4 Traitement de l'information
Un programme mystérieux Informatique Graphique Professeur: Victor Ostromoukhov Page 1 Page 2 Un programme mystérieux Traitement de l'information et automatisation Page 3 Page 4 Traitement de l'information
8 Project # 2: Bézier curves
 8 Project # 2: Bézier curves Let s say that we are given two points, for example the points (1, 1) and (5, 4) shown in Figure 1. The objective of linear interpolation is to define a linear function that
8 Project # 2: Bézier curves Let s say that we are given two points, for example the points (1, 1) and (5, 4) shown in Figure 1. The objective of linear interpolation is to define a linear function that
Basics of Computational Geometry
 Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Basics of Computational Geometry Nadeem Mohsin October 12, 2013 1 Contents This handout covers the basic concepts of computational geometry. Rather than exhaustively covering all the algorithms, it deals
Lab copy. Do not remove! Mathematics 152 Spring 1999 Notes on the course calculator. 1. The calculator VC. The web page
 Mathematics 152 Spring 1999 Notes on the course calculator 1. The calculator VC The web page http://gamba.math.ubc.ca/coursedoc/math152/docs/ca.html contains a generic version of the calculator VC and
Mathematics 152 Spring 1999 Notes on the course calculator 1. The calculator VC The web page http://gamba.math.ubc.ca/coursedoc/math152/docs/ca.html contains a generic version of the calculator VC and
Partial Derivatives (Online)
 7in x 10in Felder c04_online.tex V3 - January 21, 2015 9:44 A.M. Page 1 CHAPTER 4 Partial Derivatives (Online) 4.7 Tangent Plane Approximations and Power Series It is often helpful to use a linear approximation
7in x 10in Felder c04_online.tex V3 - January 21, 2015 9:44 A.M. Page 1 CHAPTER 4 Partial Derivatives (Online) 4.7 Tangent Plane Approximations and Power Series It is often helpful to use a linear approximation
4 Visualization and. Approximation
 4 Visualization and Approximation b A slope field for the differential equation y tan(x + y) tan(x) tan(y). It is not always possible to write down an explicit formula for the solution to a differential
4 Visualization and Approximation b A slope field for the differential equation y tan(x + y) tan(x) tan(y). It is not always possible to write down an explicit formula for the solution to a differential
Euler s Method for Approximating Solution Curves
 Euler s Method for Approximating Solution Curves As you may have begun to suspect at this point, time constraints will allow us to learn only a few of the many known methods for solving differential equations.
Euler s Method for Approximating Solution Curves As you may have begun to suspect at this point, time constraints will allow us to learn only a few of the many known methods for solving differential equations.
OpenGL Graphics System. 2D Graphics Primitives. Drawing 2D Graphics Primitives. 2D Graphics Primitives. Mathematical 2D Primitives.
 D Graphics Primitives Eye sees Displays - CRT/LCD Frame buffer - Addressable pixel array (D) Graphics processor s main function is to map application model (D) by projection on to D primitives: points,
D Graphics Primitives Eye sees Displays - CRT/LCD Frame buffer - Addressable pixel array (D) Graphics processor s main function is to map application model (D) by projection on to D primitives: points,
Coordinates and conditionals
 CHAPTER 4 Coordinates and conditionals We ll take up here a number of drawing problems which require some elementary mathematics and a few new PostScript techniques. These will require that we can interpret
CHAPTER 4 Coordinates and conditionals We ll take up here a number of drawing problems which require some elementary mathematics and a few new PostScript techniques. These will require that we can interpret
FUNCTIONS AND MODELS
 1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS In this section, we assume that you have access to a graphing calculator or a computer with graphing software. FUNCTIONS AND MODELS 1.4 Graphing Calculators
1 FUNCTIONS AND MODELS FUNCTIONS AND MODELS In this section, we assume that you have access to a graphing calculator or a computer with graphing software. FUNCTIONS AND MODELS 1.4 Graphing Calculators
Animations involving numbers
 136 Chapter 8 Animations involving numbers 8.1 Model and view The examples of Chapter 6 all compute the next picture in the animation from the previous picture. This turns out to be a rather restrictive
136 Chapter 8 Animations involving numbers 8.1 Model and view The examples of Chapter 6 all compute the next picture in the animation from the previous picture. This turns out to be a rather restrictive
Exercise: Graphing and Least Squares Fitting in Quattro Pro
 Chapter 5 Exercise: Graphing and Least Squares Fitting in Quattro Pro 5.1 Purpose The purpose of this experiment is to become familiar with using Quattro Pro to produce graphs and analyze graphical data.
Chapter 5 Exercise: Graphing and Least Squares Fitting in Quattro Pro 5.1 Purpose The purpose of this experiment is to become familiar with using Quattro Pro to produce graphs and analyze graphical data.
To graph the point (r, θ), simply go out r units along the initial ray, then rotate through the angle θ. The point (1, 5π 6. ) is graphed below:
 Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
For each question, indicate whether the statement is true or false by circling T or F, respectively.
 True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
True/False For each question, indicate whether the statement is true or false by circling T or F, respectively. 1. (T/F) Rasterization occurs before vertex transformation in the graphics pipeline. 2. (T/F)
y= sin( x) y= cos( x)
 . The graphs of sin(x) and cos(x). Now I am going to define the two basic trig functions: sin(x) and cos(x). Study the diagram at the right. The circle has radius. The arm OP starts at the positive horizontal
. The graphs of sin(x) and cos(x). Now I am going to define the two basic trig functions: sin(x) and cos(x). Study the diagram at the right. The circle has radius. The arm OP starts at the positive horizontal
Catalan Numbers. Table 1: Balanced Parentheses
 Catalan Numbers Tom Davis tomrdavis@earthlink.net http://www.geometer.org/mathcircles November, 00 We begin with a set of problems that will be shown to be completely equivalent. The solution to each problem
Catalan Numbers Tom Davis tomrdavis@earthlink.net http://www.geometer.org/mathcircles November, 00 We begin with a set of problems that will be shown to be completely equivalent. The solution to each problem
Inverse and Implicit functions
 CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
CHAPTER 3 Inverse and Implicit functions. Inverse Functions and Coordinate Changes Let U R d be a domain. Theorem. (Inverse function theorem). If ϕ : U R d is differentiable at a and Dϕ a is invertible,
Lecture 15. Lecturer: Prof. Sergei Fedotov Calculus and Vectors. Length of a Curve and Parametric Equations
 Lecture 15 Lecturer: Prof. Sergei Fedotov 10131 - Calculus and Vectors Length of a Curve and Parametric Equations Sergei Fedotov (University of Manchester) MATH10131 2011 1 / 5 Lecture 15 1 Length of a
Lecture 15 Lecturer: Prof. Sergei Fedotov 10131 - Calculus and Vectors Length of a Curve and Parametric Equations Sergei Fedotov (University of Manchester) MATH10131 2011 1 / 5 Lecture 15 1 Length of a
Not for reproduction
 x=a GRAPHING CALCULATORS AND COMPUTERS (a, d ) y=d (b, d ) (a, c ) y=c (b, c) (a) _, by _, 4 x=b FIGURE 1 The viewing rectangle a, b by c, d _4 4 In this section we assume that you have access to a graphing
x=a GRAPHING CALCULATORS AND COMPUTERS (a, d ) y=d (b, d ) (a, c ) y=c (b, c) (a) _, by _, 4 x=b FIGURE 1 The viewing rectangle a, b by c, d _4 4 In this section we assume that you have access to a graphing
CCNY Math Review Chapter 2: Functions
 CCN Math Review Chapter : Functions Section.1: Functions.1.1: How functions are used.1.: Methods for defining functions.1.3: The graph of a function.1.: Domain and range.1.5: Relations, functions, and
CCN Math Review Chapter : Functions Section.1: Functions.1.1: How functions are used.1.: Methods for defining functions.1.3: The graph of a function.1.: Domain and range.1.5: Relations, functions, and
MTH 122 Calculus II Essex County College Division of Mathematics and Physics 1 Lecture Notes #11 Sakai Web Project Material
 MTH Calculus II Essex County College Division of Mathematics and Physics Lecture Notes # Sakai Web Project Material Introduction - - 0 - Figure : Graph of y sin ( x y ) = x cos (x + y) with red tangent
MTH Calculus II Essex County College Division of Mathematics and Physics Lecture Notes # Sakai Web Project Material Introduction - - 0 - Figure : Graph of y sin ( x y ) = x cos (x + y) with red tangent
4.7 Approximate Integration
 4.7 Approximate Integration Some anti-derivatives are difficult to impossible to find. For example, 1 0 e x2 dx or 1 1 1 + x3 dx We came across this situation back in calculus I when we introduced the
4.7 Approximate Integration Some anti-derivatives are difficult to impossible to find. For example, 1 0 e x2 dx or 1 1 1 + x3 dx We came across this situation back in calculus I when we introduced the
1
 Zeros&asymptotes Example 1 In an early version of this activity I began with a sequence of simple examples (parabolas and cubics) working gradually up to the main idea. But now I think the best strategy
Zeros&asymptotes Example 1 In an early version of this activity I began with a sequence of simple examples (parabolas and cubics) working gradually up to the main idea. But now I think the best strategy
Graded Assignment 2 Maple plots
 Graded Assignment 2 Maple plots The Maple part of the assignment is to plot the graphs corresponding to the following problems. I ll note some syntax here to get you started see tutorials for more. Problem
Graded Assignment 2 Maple plots The Maple part of the assignment is to plot the graphs corresponding to the following problems. I ll note some syntax here to get you started see tutorials for more. Problem
Here are some of the more basic curves that we ll need to know how to do as well as limits on the parameter if they are required.
 1 of 10 23/07/2016 05:15 Paul's Online Math Notes Calculus III (Notes) / Line Integrals / Line Integrals - Part I Problems] [Notes] [Practice Problems] [Assignment Calculus III - Notes Line Integrals Part
1 of 10 23/07/2016 05:15 Paul's Online Math Notes Calculus III (Notes) / Line Integrals / Line Integrals - Part I Problems] [Notes] [Practice Problems] [Assignment Calculus III - Notes Line Integrals Part
Use Parametric notation. Interpret the effect that T has on the graph as motion.
 Learning Objectives Parametric Functions Lesson 3: Go Speed Racer! Level: Algebra 2 Time required: 90 minutes One of the main ideas of the previous lesson is that the control variable t does not appear
Learning Objectives Parametric Functions Lesson 3: Go Speed Racer! Level: Algebra 2 Time required: 90 minutes One of the main ideas of the previous lesson is that the control variable t does not appear
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer
 Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
Midterm Exam Fundamentals of Computer Graphics (COMP 557) Thurs. Feb. 19, 2015 Professor Michael Langer The exam consists of 10 questions. There are 2 points per question for a total of 20 points. You
ORTHOGONAL FAMILIES OF CURVES
 8 ORTHOGONAL CURVES Spring her winning the car is the probability of her initially choosing a door with a goat behind it, that is 66%! There is a very nice, complete discussion of this topic, and the controversy
8 ORTHOGONAL CURVES Spring her winning the car is the probability of her initially choosing a door with a goat behind it, that is 66%! There is a very nice, complete discussion of this topic, and the controversy
15. PARAMETRIZED CURVES AND GEOMETRY
 15. PARAMETRIZED CURVES AND GEOMETRY Parametric or parametrized curves are based on introducing a parameter which increases as we imagine travelling along the curve. Any graph can be recast as a parametrized
15. PARAMETRIZED CURVES AND GEOMETRY Parametric or parametrized curves are based on introducing a parameter which increases as we imagine travelling along the curve. Any graph can be recast as a parametrized
SOFTWARE ENGINEERING DESIGN I
 2 SOFTWARE ENGINEERING DESIGN I 3. Schemas and Theories The aim of this course is to learn how to write formal specifications of computer systems, using classical logic. The key descriptional technique
2 SOFTWARE ENGINEERING DESIGN I 3. Schemas and Theories The aim of this course is to learn how to write formal specifications of computer systems, using classical logic. The key descriptional technique
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
3.7. Vertex and tangent
 3.7. Vertex and tangent Example 1. At the right we have drawn the graph of the cubic polynomial f(x) = x 2 (3 x). Notice how the structure of the graph matches the form of the algebraic expression. The
3.7. Vertex and tangent Example 1. At the right we have drawn the graph of the cubic polynomial f(x) = x 2 (3 x). Notice how the structure of the graph matches the form of the algebraic expression. The
Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves
 Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Calculus I Review Handout 1.3 Introduction to Calculus - Limits. by Kevin M. Chevalier
 Calculus I Review Handout 1.3 Introduction to Calculus - Limits by Kevin M. Chevalier We are now going to dive into Calculus I as we take a look at the it process. While precalculus covered more static
Calculus I Review Handout 1.3 Introduction to Calculus - Limits by Kevin M. Chevalier We are now going to dive into Calculus I as we take a look at the it process. While precalculus covered more static
10 Polar Coordinates, Parametric Equations
 Polar Coordinates, Parametric Equations ½¼º½ ÈÓÐ Ö ÓÓÖ Ò Ø Coordinate systems are tools that let us use algebraic methods to understand geometry While the rectangular (also called Cartesian) coordinates
Polar Coordinates, Parametric Equations ½¼º½ ÈÓÐ Ö ÓÓÖ Ò Ø Coordinate systems are tools that let us use algebraic methods to understand geometry While the rectangular (also called Cartesian) coordinates
12 Polar Coordinates, Parametric Equations
 54 Chapter Polar Coordinates, Parametric Equations Polar Coordinates, Parametric Equations Just as we describe curves in the plane using equations involving x and y, so can we describe curves using equations
54 Chapter Polar Coordinates, Parametric Equations Polar Coordinates, Parametric Equations Just as we describe curves in the plane using equations involving x and y, so can we describe curves using equations
Roadmap for tonight. What are Bezier curves (mathematically)? Programming Bezier curves (very high level view).
 Roadmap for tonight Some background. What are Bezier curves (mathematically)? Characteristics of Bezier curves. Demo. Programming Bezier curves (very high level view). Why Bezier curves? Bezier curves
Roadmap for tonight Some background. What are Bezier curves (mathematically)? Characteristics of Bezier curves. Demo. Programming Bezier curves (very high level view). Why Bezier curves? Bezier curves
Continuity and Tangent Lines for functions of two variables
 Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
To graph the point (r, θ), simply go out r units along the initial ray, then rotate through the angle θ. The point (1, 5π 6
 Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Polar Coordinates Any point in the plane can be described by the Cartesian coordinates (x, y), where x and y are measured along the corresponding axes. However, this is not the only way to represent points
Math 213 Calculus III Practice Exam 2 Solutions Fall 2002
 Math 13 Calculus III Practice Exam Solutions Fall 00 1. Let g(x, y, z) = e (x+y) + z (x + y). (a) What is the instantaneous rate of change of g at the point (,, 1) in the direction of the origin? We want
Math 13 Calculus III Practice Exam Solutions Fall 00 1. Let g(x, y, z) = e (x+y) + z (x + y). (a) What is the instantaneous rate of change of g at the point (,, 1) in the direction of the origin? We want
An introduction to interpolation and splines
 An introduction to interpolation and splines Kenneth H. Carpenter, EECE KSU November 22, 1999 revised November 20, 2001, April 24, 2002, April 14, 2004 1 Introduction Suppose one wishes to draw a curve
An introduction to interpolation and splines Kenneth H. Carpenter, EECE KSU November 22, 1999 revised November 20, 2001, April 24, 2002, April 14, 2004 1 Introduction Suppose one wishes to draw a curve
Math 21a Homework 22 Solutions Spring, 2014
 Math 1a Homework Solutions Spring, 014 1. Based on Stewart 11.8 #6 ) Consider the function fx, y) = e xy, and the constraint x 3 + y 3 = 16. a) Use Lagrange multipliers to find the coordinates x, y) of
Math 1a Homework Solutions Spring, 014 1. Based on Stewart 11.8 #6 ) Consider the function fx, y) = e xy, and the constraint x 3 + y 3 = 16. a) Use Lagrange multipliers to find the coordinates x, y) of
CS3621 Midterm Solution (Fall 2005) 150 points
 CS362 Midterm Solution Fall 25. Geometric Transformation CS362 Midterm Solution (Fall 25) 5 points (a) [5 points] Find the 2D transformation matrix for the reflection about the y-axis transformation (i.e.,
CS362 Midterm Solution Fall 25. Geometric Transformation CS362 Midterm Solution (Fall 25) 5 points (a) [5 points] Find the 2D transformation matrix for the reflection about the y-axis transformation (i.e.,
n! = 1 * 2 * 3 * 4 * * (n-1) * n
 The Beauty and Joy of Computing 1 Lab Exercise 9: Problem self-similarity and recursion Objectives By completing this lab exercise, you should learn to Recognize simple self-similar problems which are
The Beauty and Joy of Computing 1 Lab Exercise 9: Problem self-similarity and recursion Objectives By completing this lab exercise, you should learn to Recognize simple self-similar problems which are
CALCULUS II. Parametric Equations and Polar Coordinates. Paul Dawkins
 CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
INTRODUCTION TO LINE INTEGRALS
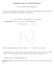 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
Graphing with a Graphing Calculator
 APPENDIX C Graphing with a Graphing Calculator A graphing calculator is a powerful tool for graphing equations and functions. In this appendix we give general guidelines to follow and common pitfalls to
APPENDIX C Graphing with a Graphing Calculator A graphing calculator is a powerful tool for graphing equations and functions. In this appendix we give general guidelines to follow and common pitfalls to
0 Graphical Analysis Use of Excel
 Lab 0 Graphical Analysis Use of Excel What You Need To Know: This lab is to familiarize you with the graphing ability of excels. You will be plotting data set, curve fitting and using error bars on the
Lab 0 Graphical Analysis Use of Excel What You Need To Know: This lab is to familiarize you with the graphing ability of excels. You will be plotting data set, curve fitting and using error bars on the
6 Appendix B: Quick Guide to MATLAB R
 6 Appendix B: Quick Guide to MATLAB R 6.1 Introduction In this course we will be using the software package MATLAB R. Version 17.12.0, Release R2011a has been installed in Foster 100, the labs on the third
6 Appendix B: Quick Guide to MATLAB R 6.1 Introduction In this course we will be using the software package MATLAB R. Version 17.12.0, Release R2011a has been installed in Foster 100, the labs on the third
Lab 2B Parametrizing Surfaces Math 2374 University of Minnesota Questions to:
 Lab_B.nb Lab B Parametrizing Surfaces Math 37 University of Minnesota http://www.math.umn.edu/math37 Questions to: rogness@math.umn.edu Introduction As in last week s lab, there is no calculus in this
Lab_B.nb Lab B Parametrizing Surfaces Math 37 University of Minnesota http://www.math.umn.edu/math37 Questions to: rogness@math.umn.edu Introduction As in last week s lab, there is no calculus in this
Lab 4. Recall, from last lab the commands Table[], ListPlot[], DiscretePlot[], and Limit[]. Go ahead and review them now you'll be using them soon.
![Lab 4. Recall, from last lab the commands Table[], ListPlot[], DiscretePlot[], and Limit[]. Go ahead and review them now you'll be using them soon. Lab 4. Recall, from last lab the commands Table[], ListPlot[], DiscretePlot[], and Limit[]. Go ahead and review them now you'll be using them soon.](/thumbs/95/122797207.jpg) Calc II Page 1 Lab 4 Wednesday, February 19, 2014 5:01 PM Recall, from last lab the commands Table[], ListPlot[], DiscretePlot[], and Limit[]. Go ahead and review them now you'll be using them soon. Use
Calc II Page 1 Lab 4 Wednesday, February 19, 2014 5:01 PM Recall, from last lab the commands Table[], ListPlot[], DiscretePlot[], and Limit[]. Go ahead and review them now you'll be using them soon. Use
Math 21a Tangent Lines and Planes Fall, What do we know about the gradient f? Tangent Lines to Curves in the Plane.
 Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14
 Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
Computer Graphics Prof. Sukhendu Das Dept. of Computer Science and Engineering Indian Institute of Technology, Madras Lecture - 14 Scan Converting Lines, Circles and Ellipses Hello everybody, welcome again
More Ways to Solve & Graph Quadratics The Square Root Property If x 2 = a and a R, then x = ± a
 More Ways to Solve & Graph Quadratics The Square Root Property If x 2 = a and a R, then x = ± a Example: Solve using the square root property. a) x 2 144 = 0 b) x 2 + 144 = 0 c) (x + 1) 2 = 12 Completing
More Ways to Solve & Graph Quadratics The Square Root Property If x 2 = a and a R, then x = ± a Example: Solve using the square root property. a) x 2 144 = 0 b) x 2 + 144 = 0 c) (x + 1) 2 = 12 Completing
Computer Science 210 Data Structures Siena College Fall Topic Notes: Trees
 Computer Science 0 Data Structures Siena College Fall 08 Topic Notes: Trees We ve spent a lot of time looking at a variety of structures where there is a natural linear ordering of the elements in arrays,
Computer Science 0 Data Structures Siena College Fall 08 Topic Notes: Trees We ve spent a lot of time looking at a variety of structures where there is a natural linear ordering of the elements in arrays,
Dr. Allen Back. Nov. 21, 2014
 Dr. Allen Back of Nov. 21, 2014 The most important thing you should know (e.g. for exams and homework) is how to setup (and perhaps compute if not too hard) surface integrals, triple integrals, etc. But
Dr. Allen Back of Nov. 21, 2014 The most important thing you should know (e.g. for exams and homework) is how to setup (and perhaps compute if not too hard) surface integrals, triple integrals, etc. But
: Intro Programming for Scientists and Engineers Assignment 1: Turtle Graphics
 Assignment 1: Turtle Graphics Page 1 600.112: Intro Programming for Scientists and Engineers Assignment 1: Turtle Graphics Peter H. Fröhlich phf@cs.jhu.edu Joanne Selinski joanne@cs.jhu.edu Due Date: Wednesdays
Assignment 1: Turtle Graphics Page 1 600.112: Intro Programming for Scientists and Engineers Assignment 1: Turtle Graphics Peter H. Fröhlich phf@cs.jhu.edu Joanne Selinski joanne@cs.jhu.edu Due Date: Wednesdays
MATH 162 Calculus II Computer Laboratory Topic: Introduction to Mathematica & Parametrizations
 MATH 162 Calculus II Computer Laboratory Topic: Introduction to Mathematica & Goals of the lab: To learn some basic operations in Mathematica, such as how to define a function, and how to produce various
MATH 162 Calculus II Computer Laboratory Topic: Introduction to Mathematica & Goals of the lab: To learn some basic operations in Mathematica, such as how to define a function, and how to produce various
, etc. Let s work with the last one. We can graph a few points determined by this equation.
 1. Lines By a line, we simply mean a straight curve. We will always think of lines relative to the cartesian plane. Consider the equation 2x 3y 4 = 0. We can rewrite it in many different ways : 2x 3y =
1. Lines By a line, we simply mean a straight curve. We will always think of lines relative to the cartesian plane. Consider the equation 2x 3y 4 = 0. We can rewrite it in many different ways : 2x 3y =
6.001 Notes: Section 15.1
 6.001 Notes: Section 15.1 Slide 15.1.1 Our goal over the next few lectures is to build an interpreter, which in a very basic sense is the ultimate in programming, since doing so will allow us to define
6.001 Notes: Section 15.1 Slide 15.1.1 Our goal over the next few lectures is to build an interpreter, which in a very basic sense is the ultimate in programming, since doing so will allow us to define
Green Globs And Graphing Equations
 Green Globs And Graphing Equations Green Globs and Graphing Equations has four parts to it which serve as a tool, a review or testing device, and two games. The menu choices are: Equation Plotter which
Green Globs And Graphing Equations Green Globs and Graphing Equations has four parts to it which serve as a tool, a review or testing device, and two games. The menu choices are: Equation Plotter which
1.7 Limit of a Function
 1.7 Limit of a Function We will discuss the following in this section: 1. Limit Notation 2. Finding a it numerically 3. Right and Left Hand Limits 4. Infinite Limits Consider the following graph Notation:
1.7 Limit of a Function We will discuss the following in this section: 1. Limit Notation 2. Finding a it numerically 3. Right and Left Hand Limits 4. Infinite Limits Consider the following graph Notation:
Repetition Through Recursion
 Fundamentals of Computer Science I (CS151.02 2007S) Repetition Through Recursion Summary: In many algorithms, you want to do things again and again and again. For example, you might want to do something
Fundamentals of Computer Science I (CS151.02 2007S) Repetition Through Recursion Summary: In many algorithms, you want to do things again and again and again. For example, you might want to do something
f xx (x, y) = 6 + 6x f xy (x, y) = 0 f yy (x, y) = y In general, the quantity that we re interested in is
 1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
Math 32, August 20: Review & Parametric Equations
 Math 3, August 0: Review & Parametric Equations Section 1: Review This course will continue the development of the Calculus tools started in Math 30 and Math 31. The primary difference between this course
Math 3, August 0: Review & Parametric Equations Section 1: Review This course will continue the development of the Calculus tools started in Math 30 and Math 31. The primary difference between this course
An Introduction to Using Maple in Math 23
 An Introduction to Using Maple in Math 3 R. C. Daileda The purpose of this document is to help you become familiar with some of the tools the Maple software package offers for visualizing solutions to
An Introduction to Using Maple in Math 3 R. C. Daileda The purpose of this document is to help you become familiar with some of the tools the Maple software package offers for visualizing solutions to
Calculus III. 1 Getting started - the basics
 Calculus III Spring 2011 Introduction to Maple The purpose of this document is to help you become familiar with some of the tools the Maple software package offers for visualizing curves and surfaces in
Calculus III Spring 2011 Introduction to Maple The purpose of this document is to help you become familiar with some of the tools the Maple software package offers for visualizing curves and surfaces in
Generating Functions
 6.04/8.06J Mathematics for Computer Science Srini Devadas and Eric Lehman April 7, 005 Lecture Notes Generating Functions Generating functions are one of the most surprising, useful, and clever inventions
6.04/8.06J Mathematics for Computer Science Srini Devadas and Eric Lehman April 7, 005 Lecture Notes Generating Functions Generating functions are one of the most surprising, useful, and clever inventions
Polar Coordinates. 2, π and ( )
 Polar Coordinates Up to this point we ve dealt exclusively with the Cartesian (or Rectangular, or x-y) coordinate system. However, as we will see, this is not always the easiest coordinate system to work
Polar Coordinates Up to this point we ve dealt exclusively with the Cartesian (or Rectangular, or x-y) coordinate system. However, as we will see, this is not always the easiest coordinate system to work
10.2 Calculus with Parametric Curves
 CHAPTER 1. PARAMETRIC AND POLAR 91 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t + sin() y t + cos() (a) Find the Cartesian
CHAPTER 1. PARAMETRIC AND POLAR 91 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t + sin() y t + cos() (a) Find the Cartesian
t dt ds Then, in the last class, we showed that F(s) = <2s/3, 1 2s/3, s/3> is arclength parametrization. Therefore,
 13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
Math 231E, Lecture 34. Polar Coordinates and Polar Parametric Equations
 Math 231E, Lecture 34. Polar Coordinates and Polar Parametric Equations 1 Definition of polar coordinates Let us first recall the definition of Cartesian coordinates: to each point in the plane we can
Math 231E, Lecture 34. Polar Coordinates and Polar Parametric Equations 1 Definition of polar coordinates Let us first recall the definition of Cartesian coordinates: to each point in the plane we can
MAT 003 Brian Killough s Instructor Notes Saint Leo University
 MAT 003 Brian Killough s Instructor Notes Saint Leo University Success in online courses requires self-motivation and discipline. It is anticipated that students will read the textbook and complete sample
MAT 003 Brian Killough s Instructor Notes Saint Leo University Success in online courses requires self-motivation and discipline. It is anticipated that students will read the textbook and complete sample
EXAMINATIONS 2016 TRIMESTER 2
 EXAMINATIONS 2016 TRIMESTER 2 CGRA 151 INTRODUCTION TO COMPUTER GRAPHICS Time Allowed: TWO HOURS CLOSED BOOK Permitted materials: Silent non-programmable calculators or silent programmable calculators
EXAMINATIONS 2016 TRIMESTER 2 CGRA 151 INTRODUCTION TO COMPUTER GRAPHICS Time Allowed: TWO HOURS CLOSED BOOK Permitted materials: Silent non-programmable calculators or silent programmable calculators
Chapter 10 Homework: Parametric Equations and Polar Coordinates
 Chapter 1 Homework: Parametric Equations and Polar Coordinates Name Homework 1.2 1. Consider the parametric equations x = t and y = 3 t. a. Construct a table of values for t =, 1, 2, 3, and 4 b. Plot the
Chapter 1 Homework: Parametric Equations and Polar Coordinates Name Homework 1.2 1. Consider the parametric equations x = t and y = 3 t. a. Construct a table of values for t =, 1, 2, 3, and 4 b. Plot the
Evaluation of postfix
 Postfix Infix notation: Operator appears between operands: 2 + 3 5 3 + 6 9 Implied precedence: 2 + 3 * 4 2 + (3 * 4 ), not (2 + 3 ) * 4 Prefix notation: Operator precedes operands: + 2 3 5 + 2 * 3 5 (+
Postfix Infix notation: Operator appears between operands: 2 + 3 5 3 + 6 9 Implied precedence: 2 + 3 * 4 2 + (3 * 4 ), not (2 + 3 ) * 4 Prefix notation: Operator precedes operands: + 2 3 5 + 2 * 3 5 (+
Introduction to Geogebra
 Aims Introduction to Geogebra Using Geogebra in the A-Level/Higher GCSE Classroom To provide examples of the effective use of Geogebra in the teaching and learning of mathematics at A-Level/Higher GCSE.
Aims Introduction to Geogebra Using Geogebra in the A-Level/Higher GCSE Classroom To provide examples of the effective use of Geogebra in the teaching and learning of mathematics at A-Level/Higher GCSE.
Kuratowski Notes , Fall 2005, Prof. Peter Shor Revised Fall 2007
 Kuratowski Notes 8.30, Fall 005, Prof. Peter Shor Revised Fall 007 Unfortunately, the OCW notes on Kuratowski s theorem seem to have several things substantially wrong with the proof, and the notes from
Kuratowski Notes 8.30, Fall 005, Prof. Peter Shor Revised Fall 007 Unfortunately, the OCW notes on Kuratowski s theorem seem to have several things substantially wrong with the proof, and the notes from
Table of Laplace Transforms
 Table of Laplace Transforms 1 1 2 3 4, p > -1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Heaviside Function 27 28. Dirac Delta Function 29 30. 31 32. 1 33 34. 35 36. 37 Laplace Transforms
Table of Laplace Transforms 1 1 2 3 4, p > -1 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 Heaviside Function 27 28. Dirac Delta Function 29 30. 31 32. 1 33 34. 35 36. 37 Laplace Transforms
Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ x + 5y + 7z 9x + 3y + 11z
 Basic Linear Algebra Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ 1 5 ] 7 9 3 11 Often matrices are used to describe in a simpler way a series of linear equations.
Basic Linear Algebra Linear algebra deals with matrixes: two-dimensional arrays of values. Here s a matrix: [ 1 5 ] 7 9 3 11 Often matrices are used to describe in a simpler way a series of linear equations.
CPSC / Scan Conversion
 CPSC 599.64 / 601.64 Computer Screens: Raster Displays pixel rasters (usually) square pixels in rectangular raster evenly cover the image problem no such things such as lines, circles, etc. scan conversion
CPSC 599.64 / 601.64 Computer Screens: Raster Displays pixel rasters (usually) square pixels in rectangular raster evenly cover the image problem no such things such as lines, circles, etc. scan conversion
First of all, we need to know what it means for a parameterize curve to be differentiable. FACT:
 CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
MATH11007 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC.
 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
Hot X: Algebra Exposed
 Hot X: Algebra Exposed Solution Guide for Chapter 10 Here are the solutions for the Doing the Math exercises in Hot X: Algebra Exposed! DTM from p.137-138 2. To see if the point is on the line, let s plug
Hot X: Algebra Exposed Solution Guide for Chapter 10 Here are the solutions for the Doing the Math exercises in Hot X: Algebra Exposed! DTM from p.137-138 2. To see if the point is on the line, let s plug
Hello world. 2. Stack-based Programming. Oscar Nierstrasz
 2. Stack-based Programming Oscar Nierstrasz /Times-Roman findfont % look up Times Roman font 18 scalefont % scale it to 18 points setfont % set this to be the current font 100 500 moveto % go to coordinate
2. Stack-based Programming Oscar Nierstrasz /Times-Roman findfont % look up Times Roman font 18 scalefont % scale it to 18 points setfont % set this to be the current font 100 500 moveto % go to coordinate
6.001 Notes: Section 6.1
 6.001 Notes: Section 6.1 Slide 6.1.1 When we first starting talking about Scheme expressions, you may recall we said that (almost) every Scheme expression had three components, a syntax (legal ways of
6.001 Notes: Section 6.1 Slide 6.1.1 When we first starting talking about Scheme expressions, you may recall we said that (almost) every Scheme expression had three components, a syntax (legal ways of
Postscript Control Flow
 Postscript Control Flow CSE 413, Autumn 2005 Programming Languages http://www.cs.washington.edu/education/courses/413/05au/ Variables Postscript uses dictionaries to associate a name with an object value»
Postscript Control Flow CSE 413, Autumn 2005 Programming Languages http://www.cs.washington.edu/education/courses/413/05au/ Variables Postscript uses dictionaries to associate a name with an object value»
Lecture 34: Curves defined by Parametric equations
 Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Intro. Scheme Basics. scm> 5 5. scm>
 Intro Let s take some time to talk about LISP. It stands for LISt Processing a way of coding using only lists! It sounds pretty radical, and it is. There are lots of cool things to know about LISP; if
Intro Let s take some time to talk about LISP. It stands for LISt Processing a way of coding using only lists! It sounds pretty radical, and it is. There are lots of cool things to know about LISP; if
2D/3D Geometric Transformations and Scene Graphs
 2D/3D Geometric Transformations and Scene Graphs Week 4 Acknowledgement: The course slides are adapted from the slides prepared by Steve Marschner of Cornell University 1 A little quick math background
2D/3D Geometric Transformations and Scene Graphs Week 4 Acknowledgement: The course slides are adapted from the slides prepared by Steve Marschner of Cornell University 1 A little quick math background
Equations of planes in
 Roberto s Notes on Linear Algebra Chapter 6: Lines, planes and other straight objects Section Equations of planes in What you need to know already: What vectors and vector operations are. What linear systems
Roberto s Notes on Linear Algebra Chapter 6: Lines, planes and other straight objects Section Equations of planes in What you need to know already: What vectors and vector operations are. What linear systems
PreCalculus Chapter 9 Practice Test Name:
 This ellipse has foci 0,, and therefore has a vertical major axis. The standard form for an ellipse with a vertical major axis is: 1 Note: graphs of conic sections for problems 1 to 1 were made with the
This ellipse has foci 0,, and therefore has a vertical major axis. The standard form for an ellipse with a vertical major axis is: 1 Note: graphs of conic sections for problems 1 to 1 were made with the
