MATH11007 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC.
|
|
|
- Tracey O’Neal’
- 5 years ago
- Views:
Transcription
1 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For instance, take x(t) = (x(t), y(t), z(t)). x(t) = cost, y(t) = sin t, z(t) = for t >. We might think of the parameter t as time. As t varies, the particle s position changes, and the curve described by the above equation is the trajectory of the particle. In this particular example, it is obvious that the trajectory is circular; indeed x 2 (t) + y 2 (t) = 1 for every t >. We say that (cost,sint,), t < 2π, is a parametric representation of the circle of equation x 2 + y 2 = 1 in R 3. Example Some examples and a bit of MAPLE (x(t),y(t)) = (t 2, t/(t 2)), t R, is a parametric representation of a hyberbola. To see this, we eliminate the parameter t: t = x + 2. Hence y = (x + 2)/x = 1 + 2/x. Example 2.2. The curve represented parametrically by (x(t), y(t)) = (t + sin t, 1 cost), t R, is not so familiar. We can use MAPLE to plot it. MAPLE is a mathematical software for which the university has a license, and which is installed on the undergraduate computers in the laboratory. Look for it amongst the applications, double-click. When it comes up, select the Start with a blank worksheet option. At the prompt, type?plot[parametric]. This explains how to plot parametric curves, and provides some examples. To plot our curve, we use > plot([t+sin(t),1-cos(t),t=-2*pi..2*pi]); c University of Bristol 212. This material is copyright of the University unless explicitly stated otherwise. It is provided exclusively for educational purposes at the University and is to be downloaded or copied for your private stu only. 1
2 2 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. The result is shown in Figure 1 (a). The curve is called the cycloid; it is the curve that describes the trajectory of a point fixed on the rim of a bicycle wheel, as the wheel goes forward. Example 2.3. Consider the curve defined parametrically by (x(t), y(t)) = ( 3t/(1 + t 3 ),3t 2 /(1 + t 3 ) ), t R. The MAPLE command > plot([3*t/(1+t^3),3*t^2/(1+t^3),t=-1/2..16*pi]); produces the plot shown in Figure 1 (b). You can easily verify that x 3 + y 3 = 3xy. The curve is called the folium of Descartes. (a) (b) Figure 1. Two famous curves: (a) the cycloid; (b) the folium of Descartes. 3. The tangent line of a curve (in two dimensions) at a point We have alrea discussed the problem of determining the line tangent to a curve at a point when the curve can be expressed in the form y = f(x). But now we consider the case where the curve is expressed in parametric form, i.e. (x(t), y(t)), t [a, b]. To find the equation of the line tangent to the curve at, say t [a, b], we need to compute dx at (x(t ), y(t )).
3 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 3 We have, by the chain rule, d y(x(t)) = dt dx (x(t))dx dt (t). So we find dx (x(t dt )) = (t ) dx dt (t ). This result is more neatly expressed if we use the prime symbol to indicate differentiation with respect to x, and the dot symbol to indicate differentiation with respect to t. Then y (x(t )) = ẏ(t ) ẋ(t ). So the equation for the tangent line is x x(t ) = ẏ(t ) ẋ(t ). The equation of the normal line is easily deduced: Example 3.1. For the circle the equation of the tangent line at t is The equation of the normal line at t is Consider a curve of equation x x(t ) = ẋ(t ) ẏ(t ). x(t) = cost and y(t) = sin t, x x(t ) = cott. x x(t ) = tant. 4. Arclength y = f(x). The length of the infinitesimal arc between the points of horizontal coordinates x and x + dx is ds = dx See Figure 2. If the curve is expressed in the parametric form then (x(t), y(t)), a t b, ds = ẋ 2 + ẏ 2 dt. We deduce that the length of the curve between t = a and t = b is b a ẋ2 + ẏ 2 dt.
4 4 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. Example 4.1. The perimeter of the circle of equation is x(t) = a cost, y(t) = a sin t, a 2 sin 2 t + a 2 cos 2 t dt = Example 4.2. The curve defined parametrically by is an ellipse. Its perimeter is x(t) = a cost, y(t) = b sint, a 2 sin 2 t + b 2 cos 2 t dt. a dt = 2π a. It is not straightforward to compute the value of this integral. It may be expressed in terms of the so-called elliptic functions. 5. Curvature For a curve of equation y = f(x) this is defined as y (x) (5.1) κ(x) := {. 1 + [y (x)] 2}3 2 See Sheet 3, Q 9. Let us work out the curvature when the curve is expressed in the parametric form (x(t), y(t)). We have shown earlier that y = ẏ ẋ. Hence, by the chain rule, d dt y = y ẋ, and so d dt y d ẏ = dt ẋ y ÿẋ ẏẍ = = ẋ ẋ ẋ 3. Hence the parametric form of the curvature (5.1) is ÿẋ ẏẍ κ(t) =. [ẋ 2 + ẏ 2 ] 3 2 Example 5.1. For the ellipse of equation we find κ(t) = x(t) = a cost ab sin 2 t + ab cos 2 t [ a2 sin 2 t + b 2 cos 2 t ]3 2 and y(t) = b sint = ab [ a2 sin 2 t + b 2 cos 2 t ] 3 2 In particular, for the circle, a = b and we obtain the expected result κ(t) = 1 a..
5 MATH117 NOTES 15: PARAMETRIC CURVES, ARCLENGTH ETC. 5 y = f(x) ds Figure 2. The length of an infinitesimal arc of the curve y = f(x) is ds = dx dx References 1. Frank Ayres, Jr. and Elliott Mendelson, Schaum s Outline of Calculus, Fourth Edition, Mc- Graw Hill, E. Hairer and G. Wanner, Analysis by its History, Springer-Verlag, New-York, 1996.
MATH11007 NOTES 12: PARAMETRIC CURVES, ARCLENGTH ETC.
 MATH117 NOTES 12: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
MATH117 NOTES 12: PARAMETRIC CURVES, ARCLENGTH ETC. 1. Parametric representation of curves The position of a particle moving in three-dimensional space is often specified by an equation of the form For
Lecture 15. Lecturer: Prof. Sergei Fedotov Calculus and Vectors. Length of a Curve and Parametric Equations
 Lecture 15 Lecturer: Prof. Sergei Fedotov 10131 - Calculus and Vectors Length of a Curve and Parametric Equations Sergei Fedotov (University of Manchester) MATH10131 2011 1 / 5 Lecture 15 1 Length of a
Lecture 15 Lecturer: Prof. Sergei Fedotov 10131 - Calculus and Vectors Length of a Curve and Parametric Equations Sergei Fedotov (University of Manchester) MATH10131 2011 1 / 5 Lecture 15 1 Length of a
Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves
 Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Block #1: Vector-Valued Functions Goals: Course Unit: Describing Moving Objects Different Ways of Representing Functions Vector-valued Functions, or Parametric Curves 1 The Calculus of Moving Objects Problem.
Updated: August 24, 2016 Calculus III Section Math 232. Calculus III. Brian Veitch Fall 2015 Northern Illinois University
 Updated: August 24, 216 Calculus III Section 1.2 Math 232 Calculus III Brian Veitch Fall 215 Northern Illinois University 1.2 Calculus with Parametric Curves Definition 1: First Derivative of a Parametric
Updated: August 24, 216 Calculus III Section 1.2 Math 232 Calculus III Brian Veitch Fall 215 Northern Illinois University 1.2 Calculus with Parametric Curves Definition 1: First Derivative of a Parametric
Chapter 10 Homework: Parametric Equations and Polar Coordinates
 Chapter 1 Homework: Parametric Equations and Polar Coordinates Name Homework 1.2 1. Consider the parametric equations x = t and y = 3 t. a. Construct a table of values for t =, 1, 2, 3, and 4 b. Plot the
Chapter 1 Homework: Parametric Equations and Polar Coordinates Name Homework 1.2 1. Consider the parametric equations x = t and y = 3 t. a. Construct a table of values for t =, 1, 2, 3, and 4 b. Plot the
Math 348 Differential Geometry of Curves and Surfaces
 Math 348 Differential Geometry of Curves and Surfaces Lecture 3 Curves in Calculus Xinwei Yu Sept. 12, 2017 CAB 527, xinwei2@ualberta.ca Department of Mathematical & Statistical Sciences University of
Math 348 Differential Geometry of Curves and Surfaces Lecture 3 Curves in Calculus Xinwei Yu Sept. 12, 2017 CAB 527, xinwei2@ualberta.ca Department of Mathematical & Statistical Sciences University of
10.2 Calculus with Parametric Curves
 CHAPTER 1. PARAMETRIC AND POLAR 1 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t +sin() y t + cos() (a) Find the cartesian
CHAPTER 1. PARAMETRIC AND POLAR 1 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t +sin() y t + cos() (a) Find the cartesian
t dt ds Then, in the last class, we showed that F(s) = <2s/3, 1 2s/3, s/3> is arclength parametrization. Therefore,
 13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
13.4. Curvature Curvature Let F(t) be a vector values function. We say it is regular if F (t)=0 Let F(t) be a vector valued function which is arclength parametrized, which means F t 1 for all t. Then,
1. no trace exists correct. 2. hyperbola : z 2 y 2 = ellipse : y z2 = ellipse : 5. circle : y 2 +z 2 = 2
 grandi (rg38778) Homework 5 grandi () This print-out should have 3 questions. Multiple-choice questions may continue on the next column or page find all choices before answering.. points Classify the quadric
grandi (rg38778) Homework 5 grandi () This print-out should have 3 questions. Multiple-choice questions may continue on the next column or page find all choices before answering.. points Classify the quadric
Background for Surface Integration
 Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Background for urface Integration 1 urface Integrals We have seen in previous work how to define and compute line integrals in R 2. You should remember the basic surface integrals that we will need to
Practice problems. 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b.
 Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
Practice problems 1. Given a = 3i 2j and b = 2i + j. Write c = i + j in terms of a and b. 1, 1 = c 1 3, 2 + c 2 2, 1. Solve c 1, c 2. 2. Suppose a is a vector in the plane. If the component of the a in
ENGI Parametric & Polar Curves Page 2-01
 ENGI 3425 2. Parametric & Polar Curves Page 2-01 2. Parametric and Polar Curves Contents: 2.1 Parametric Vector Functions 2.2 Parametric Curve Sketching 2.3 Polar Coordinates r f 2.4 Polar Curve Sketching
ENGI 3425 2. Parametric & Polar Curves Page 2-01 2. Parametric and Polar Curves Contents: 2.1 Parametric Vector Functions 2.2 Parametric Curve Sketching 2.3 Polar Coordinates r f 2.4 Polar Curve Sketching
MAT1B01: Curves defined by parametric equations
 MAT1B01: Curves defined by parametric equations Dr Craig 24 October 2016 My details: acraig@uj.ac.za Consulting hours: Thursday 11h20 12h55 Friday 11h30 13h00 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
MAT1B01: Curves defined by parametric equations Dr Craig 24 October 2016 My details: acraig@uj.ac.za Consulting hours: Thursday 11h20 12h55 Friday 11h30 13h00 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane
 Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane Rafikul Alam Department of Mathematics IIT Guwahati Chain rule Theorem-A: Let x : R R n be differentiable at t 0 and f : R n R be differentiable
Lecture 6: Chain rule, Mean Value Theorem, Tangent Plane Rafikul Alam Department of Mathematics IIT Guwahati Chain rule Theorem-A: Let x : R R n be differentiable at t 0 and f : R n R be differentiable
What you will learn today
 What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
What you will learn today Tangent Planes and Linear Approximation and the Gradient Vector Vector Functions 1/21 Recall in one-variable calculus, as we zoom in toward a point on a curve, the graph becomes
10.2 Calculus with Parametric Curves
 CHAPTER 1. PARAMETRIC AND POLAR 91 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t + sin() y t + cos() (a) Find the Cartesian
CHAPTER 1. PARAMETRIC AND POLAR 91 1.2 Calculus with Parametric Curves Example 1. Return to the parametric equations in Example 2 from the previous section: x t + sin() y t + cos() (a) Find the Cartesian
Tangent & normal vectors The arc-length parameterization of a 2D curve The curvature of a 2D curve
 Local Analysis of 2D Curve Patches Topic 4.2: Local analysis of 2D curve patches Representing 2D image curves Estimating differential properties of 2D curves Tangent & normal vectors The arc-length parameterization
Local Analysis of 2D Curve Patches Topic 4.2: Local analysis of 2D curve patches Representing 2D image curves Estimating differential properties of 2D curves Tangent & normal vectors The arc-length parameterization
Math 136 Exam 1 Practice Problems
 Math Exam Practice Problems. Find the surface area of the surface of revolution generated by revolving the curve given by around the x-axis? To solve this we use the equation: In this case this translates
Math Exam Practice Problems. Find the surface area of the surface of revolution generated by revolving the curve given by around the x-axis? To solve this we use the equation: In this case this translates
University of California, Berkeley
 University of California, Berkeley FINAL EXAMINATION, Fall 2012 DURATION: 3 hours Department of Mathematics MATH 53 Multivariable Calculus Examiner: Sean Fitzpatrick Total: 100 points Family Name: Given
University of California, Berkeley FINAL EXAMINATION, Fall 2012 DURATION: 3 hours Department of Mathematics MATH 53 Multivariable Calculus Examiner: Sean Fitzpatrick Total: 100 points Family Name: Given
INTRODUCTION TO LINE INTEGRALS
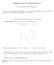 INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
INTRODUTION TO LINE INTEGRALS PROF. MIHAEL VANVALKENBURGH Last week we discussed triple integrals. This week we will study a new topic of great importance in mathematics and physics: line integrals. 1.
Name: Date: 1. Match the equation with its graph. Page 1
 Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
Name: Date: 1. Match the equation with its graph. y 6x A) C) Page 1 D) E) Page . Match the equation with its graph. ( x3) ( y3) A) C) Page 3 D) E) Page 4 3. Match the equation with its graph. ( x ) y 1
Topic 5.1: Line Elements and Scalar Line Integrals. Textbook: Section 16.2
 Topic 5.1: Line Elements and Scalar Line Integrals Textbook: Section 16.2 Warm-Up: Derivatives of Vector Functions Suppose r(t) = x(t) î + y(t) ĵ + z(t) ˆk parameterizes a curve C. The vector: is: r (t)
Topic 5.1: Line Elements and Scalar Line Integrals Textbook: Section 16.2 Warm-Up: Derivatives of Vector Functions Suppose r(t) = x(t) î + y(t) ĵ + z(t) ˆk parameterizes a curve C. The vector: is: r (t)
Continuity and Tangent Lines for functions of two variables
 Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
Continuity and Tangent Lines for functions of two variables James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University April 4, 2014 Outline 1 Continuity
Directional Derivatives as Vectors
 Directional Derivatives as Vectors John Ganci 1 Al Lehnen 2 1 Richland College Dallas, TX jganci@dcccd.edu 2 Madison Area Technical College Madison, WI alehnen@matcmadison.edu Statement of problem We are
Directional Derivatives as Vectors John Ganci 1 Al Lehnen 2 1 Richland College Dallas, TX jganci@dcccd.edu 2 Madison Area Technical College Madison, WI alehnen@matcmadison.edu Statement of problem We are
f xx (x, y) = 6 + 6x f xy (x, y) = 0 f yy (x, y) = y In general, the quantity that we re interested in is
 1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
1. Let f(x, y) = 5 + 3x 2 + 3y 2 + 2y 3 + x 3. (a) Final all critical points of f. (b) Use the second derivatives test to classify the critical points you found in (a) as a local maximum, local minimum,
9.1 Parametric Curves
 Math 172 Chapter 9A notes Page 1 of 20 9.1 Parametric Curves So far we have discussed equations in the form. Sometimes and are given as functions of a parameter. Example. Projectile Motion Sketch and axes,
Math 172 Chapter 9A notes Page 1 of 20 9.1 Parametric Curves So far we have discussed equations in the form. Sometimes and are given as functions of a parameter. Example. Projectile Motion Sketch and axes,
MATH 1020 WORKSHEET 10.1 Parametric Equations
 MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
MATH WORKSHEET. Parametric Equations If f and g are continuous functions on an interval I, then the equations x ft) and y gt) are called parametric equations. The parametric equations along with the graph
3. The three points (2, 4, 1), (1, 2, 2) and (5, 2, 2) determine a plane. Which of the following points is in that plane?
 Math 4 Practice Problems for Midterm. A unit vector that is perpendicular to both V =, 3, and W = 4,, is (a) V W (b) V W (c) 5 6 V W (d) 3 6 V W (e) 7 6 V W. In three dimensions, the graph of the equation
Math 4 Practice Problems for Midterm. A unit vector that is perpendicular to both V =, 3, and W = 4,, is (a) V W (b) V W (c) 5 6 V W (d) 3 6 V W (e) 7 6 V W. In three dimensions, the graph of the equation
Volumes of Solids of Revolution Lecture #6 a
 Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Volumes of Solids of Revolution Lecture #6 a Sphereoid Parabaloid Hyperboloid Whateveroid Volumes Calculating 3-D Space an Object Occupies Take a cross-sectional slice. Compute the area of the slice. Multiply
Without fully opening the exam, check that you have pages 1 through 11.
 Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 11. Show all your work on the standard
Name: Section: Recitation Instructor: INSTRUCTIONS Fill in your name, etc. on this first page. Without fully opening the exam, check that you have pages 1 through 11. Show all your work on the standard
Parametric Surfaces. Substitution
 Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Calculus Lia Vas Parametric Surfaces. Substitution Recall that a curve in space is given by parametric equations as a function of single parameter t x = x(t) y = y(t) z = z(t). A curve is a one-dimensional
Equation of tangent plane: for implicitly defined surfaces section 12.9
 Equation of tangent plane: for implicitly defined surfaces section 12.9 Some surfaces are defined implicitly, such as the sphere x 2 + y 2 + z 2 = 1. In general an implicitly defined surface has the equation
Equation of tangent plane: for implicitly defined surfaces section 12.9 Some surfaces are defined implicitly, such as the sphere x 2 + y 2 + z 2 = 1. In general an implicitly defined surface has the equation
Solution 2. ((3)(1) (2)(1), (4 3), (4)(2) (3)(3)) = (1, 1, 1) D u (f) = (6x + 2yz, 2y + 2xz, 2xy) (0,1,1) = = 4 14
 Vector and Multivariable Calculus L Marizza A Bailey Practice Trimester Final Exam Name: Problem 1. To prepare for true/false and multiple choice: Compute the following (a) (4, 3) ( 3, 2) Solution 1. (4)(
Vector and Multivariable Calculus L Marizza A Bailey Practice Trimester Final Exam Name: Problem 1. To prepare for true/false and multiple choice: Compute the following (a) (4, 3) ( 3, 2) Solution 1. (4)(
Lab 2B Parametrizing Surfaces Math 2374 University of Minnesota Questions to:
 Lab_B.nb Lab B Parametrizing Surfaces Math 37 University of Minnesota http://www.math.umn.edu/math37 Questions to: rogness@math.umn.edu Introduction As in last week s lab, there is no calculus in this
Lab_B.nb Lab B Parametrizing Surfaces Math 37 University of Minnesota http://www.math.umn.edu/math37 Questions to: rogness@math.umn.edu Introduction As in last week s lab, there is no calculus in this
Math 213 Calculus III Practice Exam 2 Solutions Fall 2002
 Math 13 Calculus III Practice Exam Solutions Fall 00 1. Let g(x, y, z) = e (x+y) + z (x + y). (a) What is the instantaneous rate of change of g at the point (,, 1) in the direction of the origin? We want
Math 13 Calculus III Practice Exam Solutions Fall 00 1. Let g(x, y, z) = e (x+y) + z (x + y). (a) What is the instantaneous rate of change of g at the point (,, 1) in the direction of the origin? We want
Math 259 Winter Unit Test 1 Review Problems Set B
 Math 259 Winter 2009 Unit Test 1 Review Problems Set B We have chosen these problems because we think that they are representative of many of the mathematical concepts that we have studied. There is no
Math 259 Winter 2009 Unit Test 1 Review Problems Set B We have chosen these problems because we think that they are representative of many of the mathematical concepts that we have studied. There is no
MA 114 Worksheet #17: Average value of a function
 Spring 2019 MA 114 Worksheet 17 Thursday, 7 March 2019 MA 114 Worksheet #17: Average value of a function 1. Write down the equation for the average value of an integrable function f(x) on [a, b]. 2. Find
Spring 2019 MA 114 Worksheet 17 Thursday, 7 March 2019 MA 114 Worksheet #17: Average value of a function 1. Write down the equation for the average value of an integrable function f(x) on [a, b]. 2. Find
Math 126C: Week 3 Review
 Math 126C: Week 3 Review Note: These are in no way meant to be comprehensive reviews; they re meant to highlight the main topics and formulas for the week. Doing homework and extra problems is always the
Math 126C: Week 3 Review Note: These are in no way meant to be comprehensive reviews; they re meant to highlight the main topics and formulas for the week. Doing homework and extra problems is always the
MAT01B1: Curves defined by parametric equations
 MAT01B1: Curves defined by parametric equations Dr Craig 10 October 2018 My details: acraig@uj.ac.za Consulting hours: Monday 14h40 15h25 Thursday 11h20 12h55 Friday 11h20 12h55 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
MAT01B1: Curves defined by parametric equations Dr Craig 10 October 2018 My details: acraig@uj.ac.za Consulting hours: Monday 14h40 15h25 Thursday 11h20 12h55 Friday 11h20 12h55 Office C-Ring 508 https://andrewcraigmaths.wordpress.com/
10.1 Curves Defined by Parametric Equations
 10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? There are 2 ways to describe it: x 2 + y 2 = 1 and x = cos θ y = sin θ When
10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? There are 2 ways to describe it: x 2 + y 2 = 1 and x = cos θ y = sin θ When
Multivariate Calculus Review Problems for Examination Two
 Multivariate Calculus Review Problems for Examination Two Note: Exam Two is on Thursday, February 28, class time. The coverage is multivariate differential calculus and double integration: sections 13.3,
Multivariate Calculus Review Problems for Examination Two Note: Exam Two is on Thursday, February 28, class time. The coverage is multivariate differential calculus and double integration: sections 13.3,
Curvature. Corners. curvature of a straight segment is zero more bending = larger curvature
 Curvature curvature of a straight segment is zero more bending = larger curvature Corners corner defined by large curvature value (e.g., a local maxima) borders (i.e., edges in gray-level pictures) can
Curvature curvature of a straight segment is zero more bending = larger curvature Corners corner defined by large curvature value (e.g., a local maxima) borders (i.e., edges in gray-level pictures) can
MATH 162 Calculus II Computer Laboratory Topic: Introduction to Mathematica & Parametrizations
 MATH 162 Calculus II Computer Laboratory Topic: Introduction to Mathematica & Goals of the lab: To learn some basic operations in Mathematica, such as how to define a function, and how to produce various
MATH 162 Calculus II Computer Laboratory Topic: Introduction to Mathematica & Goals of the lab: To learn some basic operations in Mathematica, such as how to define a function, and how to produce various
Math 113 Calculus III Final Exam Practice Problems Spring 2003
 Math 113 Calculus III Final Exam Practice Problems Spring 23 1. Let g(x, y, z) = 2x 2 + y 2 + 4z 2. (a) Describe the shapes of the level surfaces of g. (b) In three different graphs, sketch the three cross
Math 113 Calculus III Final Exam Practice Problems Spring 23 1. Let g(x, y, z) = 2x 2 + y 2 + 4z 2. (a) Describe the shapes of the level surfaces of g. (b) In three different graphs, sketch the three cross
: = Curves Defined by Parametric Equations. Ex: Consider the unit circle from Trigonometry. What is the equation of that circle?
 10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-12=1 There are 2 ways to describe it: x 2 + y 2 = 1 x = cos!
10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-12=1 There are 2 ways to describe it: x 2 + y 2 = 1 x = cos!
Math 32, August 20: Review & Parametric Equations
 Math 3, August 0: Review & Parametric Equations Section 1: Review This course will continue the development of the Calculus tools started in Math 30 and Math 31. The primary difference between this course
Math 3, August 0: Review & Parametric Equations Section 1: Review This course will continue the development of the Calculus tools started in Math 30 and Math 31. The primary difference between this course
9/30/2014 FIRST HOURLY PRACTICE VIII Math 21a, Fall Name:
 9/30/2014 FIRST HOURLY PRACTICE VIII Math 21a, Fall 2014 Name: MWF 9 Oliver Knill MWF 9 Chao Li MWF 10 Gijs Heuts MWF 10 Yu-Wen Hsu MWF 10 Yong-Suk Moon MWF 11 Rosalie Belanger-Rioux MWF 11 Gijs Heuts
9/30/2014 FIRST HOURLY PRACTICE VIII Math 21a, Fall 2014 Name: MWF 9 Oliver Knill MWF 9 Chao Li MWF 10 Gijs Heuts MWF 10 Yu-Wen Hsu MWF 10 Yong-Suk Moon MWF 11 Rosalie Belanger-Rioux MWF 11 Gijs Heuts
: = Curves Defined by Parametric Equations. Ex: Consider the unit circle from Trigonometry. What is the equation of that circle?
 10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-121 There are 2 ways to describe it: x 2 + y 2 1 x cos! : 9
10.1 Curves Defined by Parametric Equations Ex: Consider the unit circle from Trigonometry. What is the equation of that circle? of 8* * # 2+-121 There are 2 ways to describe it: x 2 + y 2 1 x cos! : 9
REPRESENTATION OF CURVES IN PARAMETRIC FORM
 - Representation of curves in parametric form 1 REPRESENTATION OF CURVES IN PARAMETRIC FORM.1. Parametrization of curves in the plane Given a curve in parametric form, its graphical representation in a
- Representation of curves in parametric form 1 REPRESENTATION OF CURVES IN PARAMETRIC FORM.1. Parametrization of curves in the plane Given a curve in parametric form, its graphical representation in a
Math 265 Exam 3 Solutions
 C Roettger, Fall 16 Math 265 Exam 3 Solutions Problem 1 Let D be the region inside the circle r 5 sin θ but outside the cardioid r 2 + sin θ. Find the area of D. Note that r and θ denote polar coordinates.
C Roettger, Fall 16 Math 265 Exam 3 Solutions Problem 1 Let D be the region inside the circle r 5 sin θ but outside the cardioid r 2 + sin θ. Find the area of D. Note that r and θ denote polar coordinates.
Math 5BI: Problem Set 2 The Chain Rule
 Math 5BI: Problem Set 2 The Chain Rule April 5, 2010 A Functions of two variables Suppose that γ(t) = (x(t), y(t), z(t)) is a differentiable parametrized curve in R 3 which lies on the surface S defined
Math 5BI: Problem Set 2 The Chain Rule April 5, 2010 A Functions of two variables Suppose that γ(t) = (x(t), y(t), z(t)) is a differentiable parametrized curve in R 3 which lies on the surface S defined
Polar (BC Only) They are necessary to find the derivative of a polar curve in x- and y-coordinates. The derivative
 Polar (BC Only) Polar coordinates are another way of expressing points in a plane. Instead of being centered at an origin and moving horizontally or vertically, polar coordinates are centered at the pole
Polar (BC Only) Polar coordinates are another way of expressing points in a plane. Instead of being centered at an origin and moving horizontally or vertically, polar coordinates are centered at the pole
Surfaces and Partial Derivatives
 Surfaces and Partial Derivatives James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 9, 2016 Outline Partial Derivatives Tangent Planes
Surfaces and Partial Derivatives James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 9, 2016 Outline Partial Derivatives Tangent Planes
MTH 122 Calculus II Essex County College Division of Mathematics and Physics 1 Lecture Notes #11 Sakai Web Project Material
 MTH Calculus II Essex County College Division of Mathematics and Physics Lecture Notes # Sakai Web Project Material Introduction - - 0 - Figure : Graph of y sin ( x y ) = x cos (x + y) with red tangent
MTH Calculus II Essex County College Division of Mathematics and Physics Lecture Notes # Sakai Web Project Material Introduction - - 0 - Figure : Graph of y sin ( x y ) = x cos (x + y) with red tangent
True/False. MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY
 MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY True/False 10 points: points each) For the problems below, circle T if the answer is true and circle F is the answer is false. After you ve chosen
MATH 1C: SAMPLE EXAM 1 c Jeffrey A. Anderson ANSWER KEY True/False 10 points: points each) For the problems below, circle T if the answer is true and circle F is the answer is false. After you ve chosen
MATH 261 FALL 2000 FINAL EXAM INSTRUCTIONS. 1. This test booklet has 14 pages including this one. There are 25 questions, each worth 8 points.
 MATH 261 FALL 2 FINAL EXAM STUDENT NAME - STUDENT ID - RECITATION HOUR - RECITATION INSTRUCTOR INSTRUCTOR - INSTRUCTIONS 1. This test booklet has 14 pages including this one. There are 25 questions, each
MATH 261 FALL 2 FINAL EXAM STUDENT NAME - STUDENT ID - RECITATION HOUR - RECITATION INSTRUCTOR INSTRUCTOR - INSTRUCTIONS 1. This test booklet has 14 pages including this one. There are 25 questions, each
Surfaces and Partial Derivatives
 Surfaces and James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 15, 2017 Outline 1 2 Tangent Planes Let s go back to our simple surface
Surfaces and James K. Peterson Department of Biological Sciences and Department of Mathematical Sciences Clemson University November 15, 2017 Outline 1 2 Tangent Planes Let s go back to our simple surface
The diagram above shows a sketch of the curve C with parametric equations
 1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
1. The diagram above shows a sketch of the curve C with parametric equations x = 5t 4, y = t(9 t ) The curve C cuts the x-axis at the points A and B. (a) Find the x-coordinate at the point A and the x-coordinate
Measuring Lengths The First Fundamental Form
 Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Differential Geometry Lia Vas Measuring Lengths The First Fundamental Form Patching up the Coordinate Patches. Recall that a proper coordinate patch of a surface is given by parametric equations x = (x(u,
Midterm Review II Math , Fall 2018
 Midterm Review II Math 2433-3, Fall 218 The test will cover section 12.5 of chapter 12 and section 13.1-13.3 of chapter 13. Examples in class, quizzes and homework problems are the best practice for the
Midterm Review II Math 2433-3, Fall 218 The test will cover section 12.5 of chapter 12 and section 13.1-13.3 of chapter 13. Examples in class, quizzes and homework problems are the best practice for the
ds dt ds 1 dt 1 dt v v v dt ds and the normal vector is given by N
 Normal Vectors and Curvature In the last section, we stated that reparameterization by arc length would help us analyze the twisting and turning of a curve. In this section, we ll see precisely how to
Normal Vectors and Curvature In the last section, we stated that reparameterization by arc length would help us analyze the twisting and turning of a curve. In this section, we ll see precisely how to
Direction Fields; Euler s Method
 Direction Fields; Euler s Method It frequently happens that we cannot solve first order systems dy (, ) dx = f xy or corresponding initial value problems in terms of formulas. Remarkably, however, this
Direction Fields; Euler s Method It frequently happens that we cannot solve first order systems dy (, ) dx = f xy or corresponding initial value problems in terms of formulas. Remarkably, however, this
Daily WeBWorK, #1. This means the two planes normal vectors must be multiples of each other.
 Daily WeBWorK, #1 Consider the ellipsoid x 2 + 3y 2 + z 2 = 11. Find all the points where the tangent plane to this ellipsoid is parallel to the plane 2x + 3y + 2z = 0. In order for the plane tangent to
Daily WeBWorK, #1 Consider the ellipsoid x 2 + 3y 2 + z 2 = 11. Find all the points where the tangent plane to this ellipsoid is parallel to the plane 2x + 3y + 2z = 0. In order for the plane tangent to
Math 126 Final Examination Autumn CHECK that your exam contains 9 problems on 10 pages.
 Math 126 Final Examination Autumn 2016 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name CHECK that your exam contains 9 problems on 10 pages. This exam is closed book. You
Math 126 Final Examination Autumn 2016 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name CHECK that your exam contains 9 problems on 10 pages. This exam is closed book. You
Lesson 4: Gradient Vectors, Level Curves, Maximums/Minimums/Saddle Points
 Lesson 4: Gradient Vectors, Level Curves, Maximums/Minimums/Saddle Points Example 1: The Gradient Vector 2 df Let f(x) x. Then 2x. This can be thought of as a vector that dx tells you the direction of
Lesson 4: Gradient Vectors, Level Curves, Maximums/Minimums/Saddle Points Example 1: The Gradient Vector 2 df Let f(x) x. Then 2x. This can be thought of as a vector that dx tells you the direction of
f sin the slope of the tangent line is given by f sin f cos cos sin , but it s also given by 2. So solve the DE with initial condition: sin cos
 Math 414 Activity 1 (Due by end of class August 1) 1 Four bugs are placed at the four corners of a square with side length a The bugs crawl counterclockwise at the same speed and each bug crawls directly
Math 414 Activity 1 (Due by end of class August 1) 1 Four bugs are placed at the four corners of a square with side length a The bugs crawl counterclockwise at the same speed and each bug crawls directly
Curvature Adjusted Parameterization of Curves
 Purdue University Purdue e-pubs Department of Computer Science Technical Reports Department of Computer Science 1989 Curvature Adjusted Parameterization of Curves Richard R. Patterson Chanderjit Bajaj
Purdue University Purdue e-pubs Department of Computer Science Technical Reports Department of Computer Science 1989 Curvature Adjusted Parameterization of Curves Richard R. Patterson Chanderjit Bajaj
Multivariate Calculus: Review Problems for Examination Two
 Multivariate Calculus: Review Problems for Examination Two Note: Exam Two is on Tuesday, August 16. The coverage is multivariate differential calculus and double integration. You should review the double
Multivariate Calculus: Review Problems for Examination Two Note: Exam Two is on Tuesday, August 16. The coverage is multivariate differential calculus and double integration. You should review the double
WW Prob Lib1 Math course-section, semester year
 WW Prob Lib Math course-section, semester year WeBWorK assignment due /25/06 at :00 PM..( pt) Consider the parametric equation x = 7(cosθ + θsinθ) y = 7(sinθ θcosθ) What is the length of the curve for
WW Prob Lib Math course-section, semester year WeBWorK assignment due /25/06 at :00 PM..( pt) Consider the parametric equation x = 7(cosθ + θsinθ) y = 7(sinθ θcosθ) What is the length of the curve for
The Divergence Theorem
 The Divergence Theorem MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Summer 2011 Green s Theorem Revisited Green s Theorem: M(x, y) dx + N(x, y) dy = C R ( N x M ) da y y x Green
The Divergence Theorem MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Summer 2011 Green s Theorem Revisited Green s Theorem: M(x, y) dx + N(x, y) dy = C R ( N x M ) da y y x Green
PURE MATHEMATICS 212 Multivariable Calculus CONTENTS. Page. 1. Assignment Summary... i 2. Summary Assignments...2
 PURE MATHEMATICS 212 Multivariable Calculus CONTENTS Page 1. Assignment Summary... i 2. Summary...1 3. Assignments...2 i PMTH212, Multivariable Calculus Assignment Summary 2010 Assignment Date to be Posted
PURE MATHEMATICS 212 Multivariable Calculus CONTENTS Page 1. Assignment Summary... i 2. Summary...1 3. Assignments...2 i PMTH212, Multivariable Calculus Assignment Summary 2010 Assignment Date to be Posted
. Tutorial Class V 3-10/10/2012 First Order Partial Derivatives;...
 Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; Tutorial Class V 3-10/10/2012 1 First Order Partial Derivatives; 2 Application of Gradient; Tutorial Class V 3-10/10/2012 1 First Order
Math 131. Implicit Differentiation Larson Section 2.5
 Math 131. Implicit Differentiation Larson Section.5 So far we have ealt with ifferentiating explicitly efine functions, that is, we are given the expression efining the function, such as f(x) = 5 x. However,
Math 131. Implicit Differentiation Larson Section.5 So far we have ealt with ifferentiating explicitly efine functions, that is, we are given the expression efining the function, such as f(x) = 5 x. However,
Math 21a Tangent Lines and Planes Fall, What do we know about the gradient f? Tangent Lines to Curves in the Plane.
 Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Polar Coordinates. Chapter 10: Parametric Equations and Polar coordinates, Section 10.3: Polar coordinates 28 / 46
 Polar Coordinates Polar Coordinates: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ)
Polar Coordinates Polar Coordinates: Given any point P = (x, y) on the plane r stands for the distance from the origin (0, 0). θ stands for the angle from positive x-axis to OP. Polar coordinate: (r, θ)
Name: Class: Date: 1. Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint.
 . Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint. f (x, y) = x y, x + y = 8. Set up the triple integral of an arbitrary continuous function
. Use Lagrange multipliers to find the maximum and minimum values of the function subject to the given constraint. f (x, y) = x y, x + y = 8. Set up the triple integral of an arbitrary continuous function
Arc Length, Curvature and The TNB Frame
 Arc Length, Curvature and The TNB Frame Introduction and Goals: The main goal of this lab will help you visualize the tools we use to describe the geometry of vector-valued functions. Moreover, we want
Arc Length, Curvature and The TNB Frame Introduction and Goals: The main goal of this lab will help you visualize the tools we use to describe the geometry of vector-valued functions. Moreover, we want
CALCULUS II. Parametric Equations and Polar Coordinates. Paul Dawkins
 CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
CALCULUS II Parametric Equations and Polar Coordinates Paul Dawkins Table of Contents Preface... ii Parametric Equations and Polar Coordinates... 3 Introduction... 3 Parametric Equations and Curves...
First of all, we need to know what it means for a parameterize curve to be differentiable. FACT:
 CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
CALCULUS WITH PARAMETERIZED CURVES In calculus I we learned how to differentiate and integrate functions. In the chapter covering the applications of the integral, we learned how to find the length of
Lecture 34: Curves defined by Parametric equations
 Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Curves defined by Parametric equations When the path of a particle moving in the plane is not the graph of a function, we cannot describe it using a formula that express y directly in terms of x, or x
Line_Integrals.mth: Solving problems of Line Integrals with Derive 6
 Dresden International Symposium on Technology and its Integration into Mathematics Education 2006 DES-TIME 2006 DRESDEN 20th-23th July 2006 Line_Integrals.mth: Solving problems of Line Integrals with Derive
Dresden International Symposium on Technology and its Integration into Mathematics Education 2006 DES-TIME 2006 DRESDEN 20th-23th July 2006 Line_Integrals.mth: Solving problems of Line Integrals with Derive
10 Polar Coordinates, Parametric Equations
 Polar Coordinates, Parametric Equations ½¼º½ ÈÓÐ Ö ÓÓÖ Ò Ø Coordinate systems are tools that let us use algebraic methods to understand geometry While the rectangular (also called Cartesian) coordinates
Polar Coordinates, Parametric Equations ½¼º½ ÈÓÐ Ö ÓÓÖ Ò Ø Coordinate systems are tools that let us use algebraic methods to understand geometry While the rectangular (also called Cartesian) coordinates
12 Polar Coordinates, Parametric Equations
 54 Chapter Polar Coordinates, Parametric Equations Polar Coordinates, Parametric Equations Just as we describe curves in the plane using equations involving x and y, so can we describe curves using equations
54 Chapter Polar Coordinates, Parametric Equations Polar Coordinates, Parametric Equations Just as we describe curves in the plane using equations involving x and y, so can we describe curves using equations
Solution of final examination
 of final examination Math 20, pring 201 December 9, 201 Problem 1 Let v(t) (2t e t ) i j + π cos(πt) k be the velocity of a particle with initial position r(0) ( 1, 0, 2). Find the accelaration at the
of final examination Math 20, pring 201 December 9, 201 Problem 1 Let v(t) (2t e t ) i j + π cos(πt) k be the velocity of a particle with initial position r(0) ( 1, 0, 2). Find the accelaration at the
MAT 275 Laboratory 1 Introduction to MATLAB
 MATLAB sessions: Laboratory 1 1 MAT 275 Laboratory 1 Introduction to MATLAB MATLAB is a computer software commonly used in both education and industry to solve a wide range of problems. This Laboratory
MATLAB sessions: Laboratory 1 1 MAT 275 Laboratory 1 Introduction to MATLAB MATLAB is a computer software commonly used in both education and industry to solve a wide range of problems. This Laboratory
Week 5: Geometry and Applications
 Week 5: Geometry and Applications Introduction Now that we have some tools from differentiation, we can study geometry, motion, and few other issues associated with functions of several variables. Much
Week 5: Geometry and Applications Introduction Now that we have some tools from differentiation, we can study geometry, motion, and few other issues associated with functions of several variables. Much
Parametric Surfaces and Surface Area
 Parametric Surfaces and Surface Area What to know: 1. Be able to parametrize standard surfaces, like the ones in the handout.. Be able to understand what a parametrized surface looks like (for this class,
Parametric Surfaces and Surface Area What to know: 1. Be able to parametrize standard surfaces, like the ones in the handout.. Be able to understand what a parametrized surface looks like (for this class,
9/30/2014 FIRST HOURLY PRACTICE VII Math 21a, Fall Name:
 9/30/2014 FIRST HOURLY PRACTICE VII Math 21a, Fall 2014 Name: MWF 9 Oliver Knill MWF 9 Chao Li MWF 10 Gijs Heuts MWF 10 Yu-Wen Hsu MWF 10 Yong-Suk Moon MWF 11 Rosalie Belanger-Rioux MWF 11 Gijs Heuts MWF
9/30/2014 FIRST HOURLY PRACTICE VII Math 21a, Fall 2014 Name: MWF 9 Oliver Knill MWF 9 Chao Li MWF 10 Gijs Heuts MWF 10 Yu-Wen Hsu MWF 10 Yong-Suk Moon MWF 11 Rosalie Belanger-Rioux MWF 11 Gijs Heuts MWF
Kevin James. MTHSC 206 Section 15.6 Directional Derivatives and the Gra
 MTHSC 206 Section 15.6 Directional Derivatives and the Gradient Vector Definition We define the directional derivative of the function f (x, y) at the point (x 0, y 0 ) in the direction of the unit vector
MTHSC 206 Section 15.6 Directional Derivatives and the Gradient Vector Definition We define the directional derivative of the function f (x, y) at the point (x 0, y 0 ) in the direction of the unit vector
This exam will be cumulative. Consult the review sheets for the midterms for reviews of Chapters
 Final exam review Math 265 Fall 2007 This exam will be cumulative. onsult the review sheets for the midterms for reviews of hapters 12 15. 16.1. Vector Fields. A vector field on R 2 is a function F from
Final exam review Math 265 Fall 2007 This exam will be cumulative. onsult the review sheets for the midterms for reviews of hapters 12 15. 16.1. Vector Fields. A vector field on R 2 is a function F from
REVIEW I MATH 254 Calculus IV. Exam I (Friday, April 29) will cover sections
 REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
REVIEW I MATH 254 Calculus IV Exam I (Friday, April 29 will cover sections 14.1-8. 1. Functions of multivariables The definition of multivariable functions is similar to that of functions of one variable.
Calculators ARE NOT Permitted On This Portion Of The Exam 28 Questions - 55 Minutes
 1 of 11 1) Give f(g(1)), given that Calculators ARE NOT Permitted On This Portion Of The Exam 28 Questions - 55 Minutes 2) Find the slope of the tangent line to the graph of f at x = 4, given that 3) Determine
1 of 11 1) Give f(g(1)), given that Calculators ARE NOT Permitted On This Portion Of The Exam 28 Questions - 55 Minutes 2) Find the slope of the tangent line to the graph of f at x = 4, given that 3) Determine
PARAMETERIZATIONS OF PLANE CURVES
 PARAMETERIZATIONS OF PLANE CURVES Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the
PARAMETERIZATIONS OF PLANE CURVES Suppose we want to plot the path of a particle moving in a plane. This path looks like a curve, but we cannot plot it like we would plot any other type of curve in the
Review 1. Richard Koch. April 23, 2005
 Review Richard Koch April 3, 5 Curves From the chapter on curves, you should know. the formula for arc length in section.;. the definition of T (s), κ(s), N(s), B(s) in section.4. 3. the fact that κ =
Review Richard Koch April 3, 5 Curves From the chapter on curves, you should know. the formula for arc length in section.;. the definition of T (s), κ(s), N(s), B(s) in section.4. 3. the fact that κ =
Math 206 First Midterm October 5, 2012
 Math 206 First Midterm October 5, 2012 Name: EXAM SOLUTIONS Instructor: Section: 1. Do not open this exam until you are told to do so. 2. This exam has 8 pages including this cover AND IS DOUBLE SIDED.
Math 206 First Midterm October 5, 2012 Name: EXAM SOLUTIONS Instructor: Section: 1. Do not open this exam until you are told to do so. 2. This exam has 8 pages including this cover AND IS DOUBLE SIDED.
48. Logistic Growth (BC) Classwork
 48. Logistic Growth (BC) Classwork Using the exponential growth model, the growth of a population is proportion to its current size. The differential equation for exponential growth is dp = kp leading
48. Logistic Growth (BC) Classwork Using the exponential growth model, the growth of a population is proportion to its current size. The differential equation for exponential growth is dp = kp leading
HOW CAN I USE MAPLE TO HELP MY STUDENTS LEARN MULTIVARIATE CALCULUS?
 HOW CAN I USE MAPLE TO HELP MY STUDENTS LEARN MULTIVARIATE CALCULUS? Thomas G. Wangler Benedictine University 5700 College Road, Lisle, IL 6053-0900 twangler@ben.edu Introduction Maple is a powerful software
HOW CAN I USE MAPLE TO HELP MY STUDENTS LEARN MULTIVARIATE CALCULUS? Thomas G. Wangler Benedictine University 5700 College Road, Lisle, IL 6053-0900 twangler@ben.edu Introduction Maple is a powerful software
Constrained Optimization and Lagrange Multipliers
 Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
Constrained Optimization and Lagrange Multipliers MATH 311, Calculus III J. Robert Buchanan Department of Mathematics Fall 2011 Constrained Optimization In the previous section we found the local or absolute
Coordinate Transformations in Advanced Calculus
 Coordinate Transformations in Advanced Calculus by Sacha Nandlall T.A. for MATH 264, McGill University Email: sacha.nandlall@mail.mcgill.ca Website: http://www.resanova.com/teaching/calculus/ Fall 2006,
Coordinate Transformations in Advanced Calculus by Sacha Nandlall T.A. for MATH 264, McGill University Email: sacha.nandlall@mail.mcgill.ca Website: http://www.resanova.com/teaching/calculus/ Fall 2006,
Parametric and Polar Curves
 Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
Chapter 2 Parametric and Polar Curves 2.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves Parametric Equations So far we ve described a curve by giving an equation that the coordinates
