Non-convex Representations of Graphs
|
|
|
- Moses Ford
- 5 years ago
- Views:
Transcription
1 Non-conex Representations of Graphs Giseppe Di Battista, Fabrizio Frati, and Marizio Patrignani Dip. di Informatica e Atomazione Roma Tre Uniersity Abstract. We sho that eery plane graph admits a planar straight-line draing in hich all faces ith more than three ertices are non-conex polygons. 1 Introdction In a straight-line planar draing of a graph each edge is dran as a segment and no to segments intersect. A conex draing is a straight-line planar draing in hich each face is a conex polygon. While eery plane graph admits a planar straight-line draing [6], not eery plane graph admits a conex draing. Ttte shoed that eery triconnected plane graph admits sch a draing ith its oter face dran as an arbitrary conex polygon [12]. Thomassen [11] characterized the graphs admitting a conex draing and Chiba et al. [3] presented a linear-time algorithm for prodcing sch draings. Conex draings can be efficiently constrcted in small area [4,2]. Hong and Nagamochi proed that for eery triconnected plane graph hose bondary is a star-shaped polygon a draing in hich eery internal face is a conex polygon can be obtained in linear time [8]. The same athors also inestigated draings here the oter face is a conex polygon and the internal faces are star-shaped [9,10]. As opposed to traditional conex graph draing, some research orks explored the properties of draings ith non-conexity reqirements [7,1]. A pointed draing is sch that each ertex is incident to an angle larger than π. In [7] it is shon that a planar graph admits a straight-line pointed draing iff it is minimally rigid or a sbgraph of a minimally rigid graph. Since there exist planar graphs that do not admit straight-line pointed draings, algorithms that constrct pointed draings ith tangent-continos biarcs, circlar arcs, or parabolic arcs are stdied in [1]. In this paper e address the problem of prodcing non-conex draings, i.e., draings here all faces ith more than three ertices are non-conex. This can be considered as the opposite of the classic problem of constrcting conex draings. Also, it can be seen as the dal of the problem of constrcting pointed draings, since faces, and not ertices, are constrained to hae an angle greater than π. We proe the folloing: Theorem 1. Eery plane graph admits a non-conex draing. In Sect. 3 e proe the preios theorem for biconnected graphs by means of a constrctie algorithm hose indctie approach is reminescent of Fary s constrction [6], althogh it applies to non-trianglated graphs and relies on a more complex case stdy. De to space restrictions, some proofs are omitted and can be fond in [5]. In Sect. 4 e discss ho to extend the reslt to general plane graphs. Work partially spported by MUR nder Project MAINSTREAM: Algoritmi per strttre informatie di grandi dimensioni e data streams. I.G. Tollis and M. Patrignani (Eds.): GD 2008, LNCS 5417, pp , c Springer-Verlag Berlin Heidelberg 2009
2 Non-conex Representations of Graphs Preliminaries AgraphG is simple if it has no mltiple edges and no self-loops. A planar draing of G determines a circlar ordering of the edges incident to each ertex. To draings of G are eqialent if they determine the same circlar ordering arond each ertex. A planar embedding is an eqialence class of planar draings. A planar draing partitions the plane into faces. The nbonded face is the oter face and is denoted by f(g).achord of f(g) is an edge connecting to non-adjacent ertices of f(g). A graph ith a planar embedding and an oter face is called a plane graph.anon-conex draing of a plane graph G is a planar straight-line draing of G in hich each internal (external) face ith more thanthree ertices has an angle greaterthan π (smaller than π). Consider a face f of G and to non-adjacent ertices and incident to f. The contraction of and inside f leads to a graph G in hich and are replaced by asingleertex, connected to all ertices and are connected to in G. If and are connected to the same ertex y, theng contains to edges (, y) (hence G is not simple), nless (, y) and (y, ) are incident to f (in this case there is only one edge (, y)). A contraction can also be performed on to adjacent ertices and, by remoing edge (, ) and contracting and inside the face created by the remoal. 3 Proof of Theorem 1 In this section e assme that graph G is biconnected. The folloing lemmata hold. Lemma 1. Sppose that G has a face f ith at least for incident ertices. Then there exist to ertices and incident to f, sch that edge (, ) can be added to G inside f, so that the reslting plane graph G is simple. Lemma 2. Let G be a plane graph ith a face f haing more than for incident ertices. Let G be the plane graph obtained by inserting inside f an edge e beteen to non-adjacent ertices of f. Sppose that a non-conex draing Γ of G exists. Then the draing Γ obtained by remoing e from Γ is a non-conex draing of G. In order to proe Theorem 1 for biconnected plane graphs, e proe the folloing: Theorem 2. Let G be a biconnected plane graph sch that all the faces of G hae three or for incident ertices. Let f(g) be the oter face of G. Iff(G) has three ertices, then, for eery triangle T in the plane, G admits a non-conex draing in hich f(g) is represented by T.Iff(G) has for ertices and no chord, then, for eery non-conex qadrilateral Q in the plane, G admits a non-conex draing in hich f(g) is represented by Q. The mapping of the ertices of f(g) to the ertices of T or Q is arbitrary, proided that the circlar ordering of the ertices of f(g) is respected. Theorem 2, together ith Lemmata 1 and 2, implies Theorem 1. Namely, let G be any biconnected plane graph. While G has any face f ith at least fie ertices, add, by Lemma 1, a dmmy edge inside f so that the agmented graph is still plane and simple. The obtained graph G has (at least) one face ith for incident ertices for each face of G ith more than three incident ertices. In order to apply Theorem 2, consider
3 392 G. Di Battista, F. Frati, and M. Patrignani 2 4 l3,5 l 1, l 5 1,2 l4, (a) (b) Fig. 1. (a) G 6. (b) Constrction of a non-conex draing of G 6. f(g ) and, if f(g ) has for incident ertices and has a chord, insert a dmmy edge inside f(g ) beteen the to ertices not incident to the chord, trning f(g ) into a trianglar face. Constrct a non-conex draing of G, as in the proof of Theorem 2. By Lemma 2, remoing the dmmy edges inserted leaes the draing non-conex. Before proing Theorem 2, e gie to more lemmata. Let G 5 be the plane graph haing a 4-cycle (, 2, 3, 4 ) as oter face and one internal ertex 5 connected to, 2, 3,and 4.LetG 6 be the plane graph haing a 4-cycle (, 2, 3, 4 ) as oter face and to connected internal ertices 5 and 6 ith 5 connected to and 2,and 6 connected to 3 and 4 (see Fig. 1.a). Lemma 3. For any non-conex qadrilateral Q in the plane, there exists a non-conex draing of G 5 sch that f(g 5 ) is represented by Q. Lemma 4. For any non-conex qadrilateral Q in the plane, there exists a non-conex draing of G 6 sch that f(g 6) is represented by Q (see Fig. 1.b). Proof of Theorem 2. Let G be a biconnected plane graph haing all faces of size three or for and sch that, if f(g) has size for, then it has no chord. The proof is by indction on the nmber of internal ertices of G. In the base case, either G has no internal ertex and the statement is triially tre, or G = G 5,orG = G 6. In the latter cases the statement follos by Lemmata 3 and 4, respectiely. Indctiely assme that the statement holds for any biconnected plane graph ith less than n internal ertices. Sppose that G has n internal ertices. Three are the cases. G has a separating 3-cycle C. Denote by G 1 the graph obtained by remoing from G all ertices internal to C. Denote by G 2 the sbgraph of G indced by the ertices internal to and on the border of C. Iff(G 1 ) has three (for) ertices, then consider any triangle T (resp. any non-conex qadrilateral Q) and constrct a non-conex draing Γ 1 of G 1 haing T (resp. Q) as oter face. Consider the triangle T representing C in Γ 1. Constrct a non-conex draing Γ 2 of G 2 haing T as oter face and insert Γ 2 inside Γ 1 by gling the to draings along the common face C represented by T in both draings. The reslting draing Γ is a non-conexdraingof G. G has no separating 3-cycle and G has a separating 4-cycle C. Denote by G 1 the graph obtained by remoing from G all ertices internal to C. Denote by G 2 the sbgraph of G indced by the ertices internal to and on the border of C. Notice that f(g 2 ) has no chords, otherise G 2 (and then G) old hae a separating triangle. If
4 Non-conex Representations of Graphs z (a) (b) (c) Fig. 2. (a) Both and 2 are incident to f(g).(b)both and 2 are internal ertices of G.(c) Vertex is incident to f(g) and ertex 2 is not. f(g 1 ) has three (for) ertices, then consider any triangle T (resp. any non-conex qadrilateral Q) and constrct a non-conex draing Γ 1 of G 1 haing T (resp. Q) as oter face. Consider the non-conex qadrilateral Q representing C in Γ 1. Constrct a non-conex draing Γ 2 of G 2 haing Q as oter face and insert Γ 2 inside Γ 1 by gling the to draings along the common face C represented by Q in both draings. The reslting draing Γ is a non-conexdraingof G. G has no separating 3-cycle and no separating 4-cycle. We are going to contract to ertices of G to obtain a graph ith n 1 ertices in order to apply indction. Consider any internal ertex of G. First, e sho that at least one of the folloing statements holds: (i) there exist to trianglar faces incident to and sharing an edge (, ), sch that contracting edge (, ) does not create chords of f(g); (ii) there exists a qadrilateral face f =(,,, 2 ), sch that either contracting and or contracting and 2 does not create chords of f(g); (iii) G is G 5 ;(i)g is G 6. First, sppose that to trianglar faces (,, ) and (,, 2 ) exist. If also is internal to G, then contracting (, ) does not create chords of f(g) and statement (i) holds. Otherise, assme that is incident to f(g). Then, statement (i) does not hold only if both the folloing are tre: (a) f(g) is a 4-cycle and (b) there exists an edge connecting and the ertex of f(g) not adjacent to. In fact, if (a) does not hold, then f(g) is a 3-cycle and no chord can be generated by contracting any to ertices. Also, if (b) does not hold, then contracting to does not create chords of f(g). Then, sppose that f(g) is a 4-cycle (, 1,, 2 ) and that edge (, ) exists. If at least one of and 2 is internal to G, then either (,,, 1 ) or (,,, 2 ) is a separating 4-cycle, contradicting the hypotheses. Hence, assme that both and 2 are incident to f(g). The for 3-cycles (,, ), (,, 2 ), (,, ),and(,, 2 ) do not hae internal ertices by hypothesis. Hence, G contains no internal ertex other than, G = G 5, and statement (iii) holds. If to trianglar faces incident to and sharing an edge do no exist, then there exists a face f =(,,, 2 ). Edge (, ) does not belong to G, otherise either (,, ) or (,, 2 ) old be a separating 3-cycle. Analogosly, edge (, 2 ) does not belong to G. If is internal to G, then contracting and in f does not create chords of f(g) and statement (ii) holds. Otherise, ith similar argments as aboe, statement (ii) does not hold for and only if both the folloing are tre: (a) f(g) is a 4-cycle and (b) there exists an edge connecting and the ertex of f(g) not adjacent to.
5 394 G. Di Battista, F. Frati, and M. Patrignani l l 2 l l 2 l l 2 (a) (b) (c) Fig. 3. (a) and (b): Indctie constrction of Γ, hen statement (i) holds. The light shaded region represents disk D. (a) and (c): Indctie constrction of Γ, hen statement (ii) holds. The dark shaded region represents face (,,, 2) in Γ. Then, sppose that f(g) is a 4-cycle and that edge (, ) exists. We distingish three cases: (1) If both and 2 are incident to f(g) (see Fig. 2.a), then G contains 3-cycles (,,) and ( 2,,). SinceG has no separating triangle, sch cycles are faces of G, contradicting the hypothesis that to trianglar faces incident to and sharing an edge do no exist. (2) If both and 2 are internal ertices of G (see Fig. 2.b), then contracting and 2 does not create chords of f(g) and statement (ii) holds. (3) If one ot of and 2,say,isincidenttof(G) and the other, say 2, is not (see Fig. 2.c), consider the forth ertex z of f(g). If edge ( 2,z) does not exist, ertices and 2 can be contracted ithot creating chords of f(g) and statement (ii) holds. If edge ( 2,z) exists, there exist 3-cycles (,,) and (, 2,z), and4-cycles (,,, 2 ) and (,, z, 2 ). Sch cycles contain no ertices in their interior, since G has no separating 3-cycle or 4-cycle. Hence, G = G 6 and statement (i) holds. We proe that hicheer of the statements holds, a non-conex draing of G can be constrcted. Sppose that statement (i) holds, ith G haing faces (,, 1 ) and (,, 2 ). Contract edge (, ) to a ertex. The reslting graph G is simple. If not, then there old exist a ertex 3 adjacent to both and in G, ith 3 1, 2. This old imply that (,, 3 ) is a separating triangle, contradicting the hypotheses. Indctiely constrct a non-conex draing Γ of G (see Fig. 3.a). No consider the point p here ertex is dran in Γ. There exists a small disk D (see Fig. 3.b) centered at p sch that moing p to any point inside D leaes Γ a non-conex draing. Consider the line l throgh p and orthogonal to the line l connecting and 2. Remoe and its incident edges. Insert ertices and on l, so that both are inside D. Connect and to their neighbors. It is easy to see that all faces that had an angle greater than π in Γ still hae an angle greater than π in Γ and that the draing is still planar. No, sppose that statement (ii) holds. More precisely, sppose that contracting and insideafacef =(,,, 2 ) does not create chords of f(g). Contract and inside f to a ertex. The reslting graph G is simple. If not, then there old exist a ertex 3 adjacent to both and in G, ith 3, 2. This old imply that either (,,, 3 ) or (,, 2, 3 ) is a separating 4-cycle, contradicting the hypotheses. Indctiely constrct a non-conex draing Γ of G (see Fig. 3.a). Pertrb the ertices so that they are in general position and that Γ is still a non-conex draing. Consider the point p here is dran in Γ and consider the line l throgh p and orthogonal to the line l connecting and 2. There exists a small disk D (see Fig. 3.c) centered at p sch that D does not intersect l and sch that moing p to any point inside
6 Non-conex Representations of Graphs 395 D leaes Γ non-conex. Remoe and its incident edges. Insert ertices and on l, so that both are inside D. Connect and to their neighbors. It is easy to see that all faces that had an angle greater than π in Γ still hae an angle greater than π in Γ and that the draing is still planar. Frther, face (,,, 2 ) is non-conex, as ell, since the angle incident to the one of and farther from l is greater than π. Finally, sppose that statement (iii) or (i) holds. We are in one of the base cases and the claim directly follos from Lemmata 3 or 4, respectiely. 4 Conclsions We hae proed that eery biconnected plane graph admits a draing in hich each face ith more than three ertices has an angle greater than π. This reslt can be extended to general plane graphs as follos. Any simply-connected graph G can be sitably agmented to a biconnected graph G by adding dmmy edges in sch a ay that for each face of G ith more than three ertices there exists a corresponding face of G ith more than three ertices. Remoing dmmy edges from a non-conex draing of G yields a non-conex draing of G. We beliee it is of interest to determine hether non-conex draings can be realized on a polynomial-size grid. References 1. Aichholzer, O., Rote, G., Schlz, A., Vogtenhber, B.: Pointed draings of planar graphs. In: Bose, P. (ed.) CCCG 2007, pp (2007) 2. Bárány, I., Rote, G.: Strictly conex draings of planar graphs. Doc. Math. 11, (2006) 3. Chiba, N., Yamanochi, T., Nishizeki, T.: Linear algorithms for conex draings of planar graphs. In: Bondy, J.A., Mrty, U.S.R. (eds.) Progress in Graph Theory, pp Academic Press, Ne York (1984) 4. Chrobak, M., Goodrich, M.T., Tamassia, R.: Conex draings of graphs in to and three dimensions. In: Symposim on Comptational Geometry, pp (1996) 5. Di Battista, G., Frati, F., Patrignani, M.: Non-conex representations of graphs. Tech. Report RT-DIA , Dip. Informatica e Atomazione, Uni. Roma Tre (2008) 6. Fary, I.: On straight line representations of planar graphs. Acta. Sci. Math. 11, (1948) 7. Haas, R., Orden, D., Rote, G., Santos, F., Seratis, B., Seratis, H., Soaine, D., Strein, I., Whiteley, W.: Planar minimally rigid graphs and psedo-trianglations. Compt. Geometry Theory Appl. 31, (2005) 8. Hong, S., Nagamochi, H.: Conex draings of graphs ith non-conex bondary. In: Fomin, F.V. (ed.) WG LNCS, ol. 4271, pp Springer, Heidelberg (2006) 9. Hong, S., Nagamochi, H.: Star-shaped draings of planar graphs. In: Brankoich, L., Lin, Y., Smyth, W.F. (eds.) IWOCA College Pblications (2007) 10. Hong, S., Nagamochi, H.: Star-shaped draing of planar graphs ith fixed embedding and concae corner constraints. In: H, X., Wang, J. (eds.) COCOON LNCS, ol. 5092, pp Springer, Heidelberg (2008) 11. Thomassen, C.: Plane representations of graphs. In: Progress in Graph Theory, pp Academic Press, London (1984) 12. Ttte, W.T.: Conex representations of graphs. Proc. London Math. Soc. 10, (1960)
Università degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, Roma, Italy
 R O M A TRE DIA Università degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 00146 Roma, Italy Non-Convex Representations of Graphs Giuseppe Di Battista, Fabrizio
R O M A TRE DIA Università degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 00146 Roma, Italy Non-Convex Representations of Graphs Giuseppe Di Battista, Fabrizio
On Plane Constrained Bounded-Degree Spanners
 On Plane Constrained Bonded-Degree Spanners Prosenjit Bose 1, Rolf Fagerberg 2, André an Renssen 1, Sander Verdonschot 1 1 School of Compter Science, Carleton Uniersity, Ottaa, Canada. Email: jit@scs.carleton.ca,
On Plane Constrained Bonded-Degree Spanners Prosenjit Bose 1, Rolf Fagerberg 2, André an Renssen 1, Sander Verdonschot 1 1 School of Compter Science, Carleton Uniersity, Ottaa, Canada. Email: jit@scs.carleton.ca,
On Plane Constrained Bounded-Degree Spanners
 Algorithmica manscript No. (ill be inserted by the editor) 1 On Plane Constrained Bonded-Degree Spanners 2 3 Prosenjit Bose Rolf Fagerberg André an Renssen Sander Verdonschot 4 5 Receied: date / Accepted:
Algorithmica manscript No. (ill be inserted by the editor) 1 On Plane Constrained Bonded-Degree Spanners 2 3 Prosenjit Bose Rolf Fagerberg André an Renssen Sander Verdonschot 4 5 Receied: date / Accepted:
Combinatorial and Geometric Properties of Planar Laman Graphs
 Combinatorial and Geometric Properties of Planar Laman Graphs Stephen Koboro 1, Torsten Ueckerdt 2, and Kein Verbeek 3 1 Department of Compter Science, Uniersity of Arizona 2 Department of Applied Mathematics,
Combinatorial and Geometric Properties of Planar Laman Graphs Stephen Koboro 1, Torsten Ueckerdt 2, and Kein Verbeek 3 1 Department of Compter Science, Uniersity of Arizona 2 Department of Applied Mathematics,
Drawing Outer-Planar Graphs in O(n log n) Area
 Draing Oter-Planar Graphs in O(n log n) Area Therese Biedl School of Compter Science, Uniersity of Waterloo, Waterloo, ON N2L 3G1, Canada, biedl@aterloo.ca Abstract. In this paper, e stdy draings of oter-planar
Draing Oter-Planar Graphs in O(n log n) Area Therese Biedl School of Compter Science, Uniersity of Waterloo, Waterloo, ON N2L 3G1, Canada, biedl@aterloo.ca Abstract. In this paper, e stdy draings of oter-planar
Rectangle-of-influence triangulations
 CCCG 2016, Vancoer, British Colmbia, Ag 3 5, 2016 Rectangle-of-inflence trianglations Therese Biedl Anna Lbi Saeed Mehrabi Sander Verdonschot 1 Backgrond The concept of rectangle-of-inflence (RI) draings
CCCG 2016, Vancoer, British Colmbia, Ag 3 5, 2016 Rectangle-of-inflence trianglations Therese Biedl Anna Lbi Saeed Mehrabi Sander Verdonschot 1 Backgrond The concept of rectangle-of-inflence (RI) draings
[1] Hopcroft, J., D. Joseph and S. Whitesides, Movement problems for twodimensional
![[1] Hopcroft, J., D. Joseph and S. Whitesides, Movement problems for twodimensional [1] Hopcroft, J., D. Joseph and S. Whitesides, Movement problems for twodimensional](/thumbs/93/112680156.jpg) Acknoledgement. The athors thank Bill Lenhart for interesting discssions on the recongration of rlers. References [1] Hopcroft, J., D. Joseph and S. Whitesides, Moement problems for todimensional linkages,
Acknoledgement. The athors thank Bill Lenhart for interesting discssions on the recongration of rlers. References [1] Hopcroft, J., D. Joseph and S. Whitesides, Moement problems for todimensional linkages,
Henneberg Steps for Triangle Representations
 Henneberg Steps or Triangle Representations Nieke Aerts and Stean Felsner {aerts,elsner}@math.t-berlin.de Technische Uniersität Berlin Institt ür Mathematik Strasse des 17. Jni 136 10623 Berlin, Germany
Henneberg Steps or Triangle Representations Nieke Aerts and Stean Felsner {aerts,elsner}@math.t-berlin.de Technische Uniersität Berlin Institt ür Mathematik Strasse des 17. Jni 136 10623 Berlin, Germany
Triangle-Free Planar Graphs as Segments Intersection Graphs
 Triangle-ree Planar Graphs as Segments Intersection Graphs N. de Castro 1,.J.Cobos 1, J.C. Dana 1,A.Márqez 1, and M. Noy 2 1 Departamento de Matemática Aplicada I Universidad de Sevilla, Spain {natalia,cobos,dana,almar}@cica.es
Triangle-ree Planar Graphs as Segments Intersection Graphs N. de Castro 1,.J.Cobos 1, J.C. Dana 1,A.Márqez 1, and M. Noy 2 1 Departamento de Matemática Aplicada I Universidad de Sevilla, Spain {natalia,cobos,dana,almar}@cica.es
Planarity-Preserving Clustering and Embedding for Large Planar Graphs
 Planarity-Presering Clstering and Embedding for Large Planar Graphs Christian A. Dncan, Michael T. Goodrich, and Stephen G. Koboro Center for Geometric Compting The Johns Hopkins Uniersity Baltimore, MD
Planarity-Presering Clstering and Embedding for Large Planar Graphs Christian A. Dncan, Michael T. Goodrich, and Stephen G. Koboro Center for Geometric Compting The Johns Hopkins Uniersity Baltimore, MD
arxiv: v1 [cs.cg] 31 Aug 2017
![arxiv: v1 [cs.cg] 31 Aug 2017 arxiv: v1 [cs.cg] 31 Aug 2017](/thumbs/88/115848123.jpg) Lombardi Drawings of Knots and Links Philipp Kindermann 1, Stephen Koboro 2, Maarten Löffler 3, Martin Nöllenbrg 4, André Schlz 1, and Birgit Vogtenhber 5 arxi:1708.098191 [cs.cg] 31 Ag 2017 1 FernUniersität
Lombardi Drawings of Knots and Links Philipp Kindermann 1, Stephen Koboro 2, Maarten Löffler 3, Martin Nöllenbrg 4, André Schlz 1, and Birgit Vogtenhber 5 arxi:1708.098191 [cs.cg] 31 Ag 2017 1 FernUniersität
Lemma 1 Let the components of, Suppose. Trees. A tree is a graph which is. (a) Connected and. (b) has no cycles (acyclic). (b)
 Trees Lemma Let the components of ppose "! be (a) $&%('*)+ - )+ / A tree is a graph which is (b) 0 %(')+ - 3)+ / 6 (a) (a) Connected and (b) has no cycles (acyclic) (b) roof Eery path 8 in which is not
Trees Lemma Let the components of ppose "! be (a) $&%('*)+ - )+ / A tree is a graph which is (b) 0 %(')+ - 3)+ / 6 (a) (a) Connected and (b) has no cycles (acyclic) (b) roof Eery path 8 in which is not
COMPOSITION OF STABLE SET POLYHEDRA
 COMPOSITION OF STABLE SET POLYHEDRA Benjamin McClosky and Illya V. Hicks Department of Comptational and Applied Mathematics Rice University November 30, 2007 Abstract Barahona and Mahjob fond a defining
COMPOSITION OF STABLE SET POLYHEDRA Benjamin McClosky and Illya V. Hicks Department of Comptational and Applied Mathematics Rice University November 30, 2007 Abstract Barahona and Mahjob fond a defining
Convex Drawings of Graphs with Non-convex Boundary Constraints
 Convex Draings of Graphs ith Non-convex Boundary Constraints Seok-Hee Hong School of Information Technologies University of Sydney NICTA (National ICT Australia) shhong@it.usyd.edu.au Hiroshi Nagamochi
Convex Draings of Graphs ith Non-convex Boundary Constraints Seok-Hee Hong School of Information Technologies University of Sydney NICTA (National ICT Australia) shhong@it.usyd.edu.au Hiroshi Nagamochi
Reconstructing Generalized Staircase Polygons with Uniform Step Length
 Jornal of Graph Algorithms and Applications http://jgaa.info/ ol. 22, no. 3, pp. 431 459 (2018) DOI: 10.7155/jgaa.00466 Reconstrcting Generalized Staircase Polygons with Uniform Step Length Nodari Sitchinaa
Jornal of Graph Algorithms and Applications http://jgaa.info/ ol. 22, no. 3, pp. 431 459 (2018) DOI: 10.7155/jgaa.00466 Reconstrcting Generalized Staircase Polygons with Uniform Step Length Nodari Sitchinaa
Triangle Contact Representations
 Triangle Contact Representations Stean Felsner elsner@math.t-berlin.de Technische Uniersität Berlin, Institt ür Mathematik Strasse des 7. Jni 36, 0623 Berlin, Germany Abstract. It is conjectred that eery
Triangle Contact Representations Stean Felsner elsner@math.t-berlin.de Technische Uniersität Berlin, Institt ür Mathematik Strasse des 7. Jni 36, 0623 Berlin, Germany Abstract. It is conjectred that eery
Chapter 5. Plane Graphs and the DCEL
 Chapter 5 Plane Graphs and the DCEL So far we hae been talking abot geometric strctres sch as trianglations of polygons and arrangements of line segments withot paying mch attention to how to represent
Chapter 5 Plane Graphs and the DCEL So far we hae been talking abot geometric strctres sch as trianglations of polygons and arrangements of line segments withot paying mch attention to how to represent
UPWARD PLANAR DRAWING OF SINGLE SOURCE ACYCLIC DIGRAPHS. MICHAEL D. HUTTON y AND ANNA LUBIW z
 UPWARD PLANAR DRAWING OF SINGLE SOURCE ACYCLIC DIGRAPHS MICHAEL D. HUTTON y AND ANNA LUBIW z Abstract. An pward plane drawing of a directed acyclic graph is a plane drawing of the digraph in which each
UPWARD PLANAR DRAWING OF SINGLE SOURCE ACYCLIC DIGRAPHS MICHAEL D. HUTTON y AND ANNA LUBIW z Abstract. An pward plane drawing of a directed acyclic graph is a plane drawing of the digraph in which each
Coloring Eulerian triangulations of the Klein bottle
 Coloring Eulerian triangulations of the Klein bottle Daniel Král Bojan Mohar Atsuhiro Nakamoto Ondřej Pangrác Yusuke Suzuki Abstract We sho that an Eulerian triangulation of the Klein bottle has chromatic
Coloring Eulerian triangulations of the Klein bottle Daniel Král Bojan Mohar Atsuhiro Nakamoto Ondřej Pangrác Yusuke Suzuki Abstract We sho that an Eulerian triangulation of the Klein bottle has chromatic
arxiv: v1 [cs.cg] 27 Nov 2015
![arxiv: v1 [cs.cg] 27 Nov 2015 arxiv: v1 [cs.cg] 27 Nov 2015](/thumbs/89/100184774.jpg) On Visibility Representations of Non-planar Graphs Therese Biedl 1, Giseppe Liotta 2, Fabrizio Montecchiani 2 David R. Cheriton School of Compter Science, University of Waterloo, Canada biedl@waterloo.ca
On Visibility Representations of Non-planar Graphs Therese Biedl 1, Giseppe Liotta 2, Fabrizio Montecchiani 2 David R. Cheriton School of Compter Science, University of Waterloo, Canada biedl@waterloo.ca
Towards Tight Bounds on Theta-Graphs
 Toards Tight Bonds on Theta-Graphs arxiv:10.633v1 [cs.cg] Apr 01 Prosenjit Bose Jean-Lo De Carfel Pat Morin André van Renssen Sander Verdonschot Abstract We present improved pper and loer bonds on the
Toards Tight Bonds on Theta-Graphs arxiv:10.633v1 [cs.cg] Apr 01 Prosenjit Bose Jean-Lo De Carfel Pat Morin André van Renssen Sander Verdonschot Abstract We present improved pper and loer bonds on the
Fixed-Parameter Algorithms for Cluster Vertex Deletion
 Fixed-Parameter Algorithms for Clster Vertex Deletion Falk Hüffner Christian Komsieicz Hannes Moser Rolf Niedermeier Institt für Informatik, Friedrich-Schiller-Uniersität Jena, Ernst-Abbe-Platz 2, D-07743
Fixed-Parameter Algorithms for Clster Vertex Deletion Falk Hüffner Christian Komsieicz Hannes Moser Rolf Niedermeier Institt für Informatik, Friedrich-Schiller-Uniersität Jena, Ernst-Abbe-Platz 2, D-07743
arxiv: v1 [cs.cg] 1 Feb 2016
![arxiv: v1 [cs.cg] 1 Feb 2016 arxiv: v1 [cs.cg] 1 Feb 2016](/thumbs/87/97196435.jpg) The Price of Order Prosenjit Bose Pat Morin André van Renssen, arxiv:160.00399v1 [cs.cg] 1 Feb 016 Abstract We present tight bonds on the spanning ratio of a large family of ordered θ-graphs. A θ-graph
The Price of Order Prosenjit Bose Pat Morin André van Renssen, arxiv:160.00399v1 [cs.cg] 1 Feb 016 Abstract We present tight bonds on the spanning ratio of a large family of ordered θ-graphs. A θ-graph
Motivation: Art gallery problem. Polygon decomposition. Art gallery problem: upper bound. Art gallery problem: lower bound
 CG Lecture 3 Polygon decomposition 1. Polygon triangulation Triangulation theory Monotone polygon triangulation 2. Polygon decomposition into monotone pieces 3. Trapezoidal decomposition 4. Conex decomposition
CG Lecture 3 Polygon decomposition 1. Polygon triangulation Triangulation theory Monotone polygon triangulation 2. Polygon decomposition into monotone pieces 3. Trapezoidal decomposition 4. Conex decomposition
An Extended Fault-Tolerant Link-State Routing Protocol in the Internet
 An Extended Falt-Tolerant Link-State Roting Protocol in the Internet Jie W, Xiaola Lin, Jiannong Cao z, and Weijia Jia x Department of Compter Science and Engineering Florida Atlantic Uniersit Boca Raton,
An Extended Falt-Tolerant Link-State Roting Protocol in the Internet Jie W, Xiaola Lin, Jiannong Cao z, and Weijia Jia x Department of Compter Science and Engineering Florida Atlantic Uniersit Boca Raton,
Morphing Planar Graph Drawings
 Morphing Planar Graph Drawings Giuseppe Di Battista Università degli Studi Roma Tre The 12th International Conference and Workshops on Algorithms and Computation WALCOM 2018 Basic definitions Graph drawing
Morphing Planar Graph Drawings Giuseppe Di Battista Università degli Studi Roma Tre The 12th International Conference and Workshops on Algorithms and Computation WALCOM 2018 Basic definitions Graph drawing
Università degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, Roma, Italy
 R O M A TRE DIA Università degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 046 Roma, Italy Topological Morphing of Planar Graphs P. Angelini, P.F. Cortese,
R O M A TRE DIA Università degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 046 Roma, Italy Topological Morphing of Planar Graphs P. Angelini, P.F. Cortese,
Drawing Simultaneously Embedded Graphs with Few Bends
 Drawing Simultaneously Embedded Graphs with Few Bends Luca Grilli 1, Seok-Hee Hong 2, Jan Kratochvíl 3, and Ignaz Rutter 3,4 1 Dipartimento di Ingegneria, Università degli Studi di Perugia luca.grilli@unipg.it
Drawing Simultaneously Embedded Graphs with Few Bends Luca Grilli 1, Seok-Hee Hong 2, Jan Kratochvíl 3, and Ignaz Rutter 3,4 1 Dipartimento di Ingegneria, Università degli Studi di Perugia luca.grilli@unipg.it
arxiv: v1 [cs.cg] 12 Dec 2013
![arxiv: v1 [cs.cg] 12 Dec 2013 arxiv: v1 [cs.cg] 12 Dec 2013](/thumbs/89/100997823.jpg) Smooth Orthogonal Drawings of Planar Graphs Md. Jawaherl Alam, Michael A. Bekos, Michael Kafmann, Philipp Kindermann, Stephen G. Koboro, and Alexander Wolff arxi:.58 [cs.cg] Dec 0 Department of Compter
Smooth Orthogonal Drawings of Planar Graphs Md. Jawaherl Alam, Michael A. Bekos, Michael Kafmann, Philipp Kindermann, Stephen G. Koboro, and Alexander Wolff arxi:.58 [cs.cg] Dec 0 Department of Compter
Cutting Cycles of Rods in Space: Hardness and Approximation
 Ctting Cycles of Rods in Space: Hardness and pproximation oris rono ark de erg Chris Gray Elena mford bstract We stdy the problem of ctting a set of rods (line segments in R 3 ) into fragments, sing a
Ctting Cycles of Rods in Space: Hardness and pproximation oris rono ark de erg Chris Gray Elena mford bstract We stdy the problem of ctting a set of rods (line segments in R 3 ) into fragments, sing a
Augmenting the edge connectivity of planar straight line graphs to three
 Agmenting the edge connectivity of planar straight line graphs to three Marwan Al-Jbeh Mashhood Ishaqe Kristóf Rédei Diane L. Sovaine Csaba D. Tóth Pavel Valtr Abstract We characterize the planar straight
Agmenting the edge connectivity of planar straight line graphs to three Marwan Al-Jbeh Mashhood Ishaqe Kristóf Rédei Diane L. Sovaine Csaba D. Tóth Pavel Valtr Abstract We characterize the planar straight
UNIVERSITÀ DEGLI STUDI DI ROMA TRE Dipartimento di Informatica e Automazione. Constrained Simultaneous and Near-Simultaneous Embeddings
 R O M A TRE DIA UNIVERSITÀ DEGLI STUDI DI ROMA TRE Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 00146 Roma, Italy Constrained Simultaneous and Near-Simultaneous Embeddings FABRIZIO
R O M A TRE DIA UNIVERSITÀ DEGLI STUDI DI ROMA TRE Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 00146 Roma, Italy Constrained Simultaneous and Near-Simultaneous Embeddings FABRIZIO
h-vectors of PS ear-decomposable graphs
 h-vectors of PS ear-decomposable graphs Nima Imani 2, Lee Johnson 1, Mckenzie Keeling-Garcia 1, Steven Klee 1 and Casey Pinckney 1 1 Seattle University Department of Mathematics, 901 12th Avene, Seattle,
h-vectors of PS ear-decomposable graphs Nima Imani 2, Lee Johnson 1, Mckenzie Keeling-Garcia 1, Steven Klee 1 and Casey Pinckney 1 1 Seattle University Department of Mathematics, 901 12th Avene, Seattle,
Straight-Line Drawings of 2-Outerplanar Graphs on Two Curves
 Straight-Line Drawings of 2-Outerplanar Graphs on Two Curves (Extended Abstract) Emilio Di Giacomo and Walter Didimo Università di Perugia ({digiacomo,didimo}@diei.unipg.it). Abstract. We study how to
Straight-Line Drawings of 2-Outerplanar Graphs on Two Curves (Extended Abstract) Emilio Di Giacomo and Walter Didimo Università di Perugia ({digiacomo,didimo}@diei.unipg.it). Abstract. We study how to
Constrained Routing Between Non-Visible Vertices
 Constrained Roting Between Non-Visible Vertices Prosenjit Bose 1, Matias Korman 2, André van Renssen 3,4, and Sander Verdonschot 1 1 School of Compter Science, Carleton University, Ottawa, Canada. jit@scs.carleton.ca,
Constrained Roting Between Non-Visible Vertices Prosenjit Bose 1, Matias Korman 2, André van Renssen 3,4, and Sander Verdonschot 1 1 School of Compter Science, Carleton University, Ottawa, Canada. jit@scs.carleton.ca,
Fixed-Parameter Tractability Results for Full-Degree Spanning Tree and Its Dual
 Fixed-Parameter Tractability Results for Full-Degree Spanning Tree and Its Dual Jiong Guo, Rolf Niedermeier, and Sebastian Wernicke Institut für Informatik, Friedrich-Schiller-Uniersität Jena Ernst-Abbe-Platz
Fixed-Parameter Tractability Results for Full-Degree Spanning Tree and Its Dual Jiong Guo, Rolf Niedermeier, and Sebastian Wernicke Institut für Informatik, Friedrich-Schiller-Uniersität Jena Ernst-Abbe-Platz
Chapter 7 TOPOLOGY CONTROL
 Chapter TOPOLOGY CONTROL Oeriew Topology Control Gabriel Graph et al. XTC Interference SINR & Schedling Complexity Distribted Compting Grop Mobile Compting Winter 00 / 00 Distribted Compting Grop MOBILE
Chapter TOPOLOGY CONTROL Oeriew Topology Control Gabriel Graph et al. XTC Interference SINR & Schedling Complexity Distribted Compting Grop Mobile Compting Winter 00 / 00 Distribted Compting Grop MOBILE
Vertex Guarding in Weak Visibility Polygons
 Vertex Garding in Weak Visibility Polygons Pritam Bhattacharya, Sbir Kmar Ghosh*, Bodhayan Roy School of Technology and Compter Science Tata Institte of Fndamental Research Mmbai 400005, India arxi:1409.46212
Vertex Garding in Weak Visibility Polygons Pritam Bhattacharya, Sbir Kmar Ghosh*, Bodhayan Roy School of Technology and Compter Science Tata Institte of Fndamental Research Mmbai 400005, India arxi:1409.46212
Pushing squares around
 Pshing sqares arond Adrian Dmitresc János Pach Ý Abstract We stdy dynamic self-reconfigration of modlar metamorphic systems. We garantee the feasibility of motion planning in a rectanglar model consisting
Pshing sqares arond Adrian Dmitresc János Pach Ý Abstract We stdy dynamic self-reconfigration of modlar metamorphic systems. We garantee the feasibility of motion planning in a rectanglar model consisting
Windrose Planarity: Embedding Graphs with Direction-Constrained Edges
 Windrose Planarity: Embedding Graphs with Direction-Constrained Edges Patrizio Angelini Giordano Da Lozzo Giuseppe Di Battista Valentino Di Donato Philipp Kindermann Günter Rote Ignaz Rutter Abstract Gien
Windrose Planarity: Embedding Graphs with Direction-Constrained Edges Patrizio Angelini Giordano Da Lozzo Giuseppe Di Battista Valentino Di Donato Philipp Kindermann Günter Rote Ignaz Rutter Abstract Gien
Henneberg construction
 Henneberg construction Seminar über Algorithmen FU-Berlin, WS 2007/08 Andrei Haralevich Abstract: In this work will be explained two different types of steps of Henneberg construction. And how Henneberg
Henneberg construction Seminar über Algorithmen FU-Berlin, WS 2007/08 Andrei Haralevich Abstract: In this work will be explained two different types of steps of Henneberg construction. And how Henneberg
On Bichromatic Triangle Game
 On Bichromatic Triangle Game Gordana Manić Daniel M. Martin Miloš Stojakoić Agst 16, 2012 Abstract We stdy a combinatorial game called Bichromatic Triangle Game, defined as follows. Two players R and B
On Bichromatic Triangle Game Gordana Manić Daniel M. Martin Miloš Stojakoić Agst 16, 2012 Abstract We stdy a combinatorial game called Bichromatic Triangle Game, defined as follows. Two players R and B
Patrizio Angelini, Giordano Da Lozzo, Giuseppe Di Battista, Fabrizio Frati, Maurizio Patrignani, Vincenzo Roselli
 Patrizio Angelini, Giordano Da Lozzo, Giuseppe Di Battista, Fabrizio Frati, Maurizio Patrignani, Vincenzo Roselli Graph G = (V,E) Vertices are points Edges are straight-line segments Planar: edges
Patrizio Angelini, Giordano Da Lozzo, Giuseppe Di Battista, Fabrizio Frati, Maurizio Patrignani, Vincenzo Roselli Graph G = (V,E) Vertices are points Edges are straight-line segments Planar: edges
Straight-line Drawings of 1-planar Graphs
 Straight-line Drawings of 1-planar Graphs Peter Eades 1, Seok-Hee Hong 1, Giuseppe Liotta 2, and Sheung-Hung Poon 3 1 University of Sydney, Australia {peter,shhong}@it.usyd.edu.au 2 Università di Perugia,
Straight-line Drawings of 1-planar Graphs Peter Eades 1, Seok-Hee Hong 1, Giuseppe Liotta 2, and Sheung-Hung Poon 3 1 University of Sydney, Australia {peter,shhong}@it.usyd.edu.au 2 Università di Perugia,
Multiple Source Shortest Paths in a Genus g Graph
 Mltiple Sorce Shortest Paths in a Gens g Graph Sergio Cabello Erin W. Chambers Abstract We gie an O(g n log n) algorithm to represent the shortest path tree from all the ertices on a single specified face
Mltiple Sorce Shortest Paths in a Gens g Graph Sergio Cabello Erin W. Chambers Abstract We gie an O(g n log n) algorithm to represent the shortest path tree from all the ertices on a single specified face
Authors. Tamilnadu, India 2.
 International Jornal of Emerging Trends in Science and Technology Impact Factor: 2.838 DOI: http://dx.doi.org/10.18535/ijetst/3i03.04 Irredndant Complete Domination Nmber of Graphs Athors A.Nellai Mrgan
International Jornal of Emerging Trends in Science and Technology Impact Factor: 2.838 DOI: http://dx.doi.org/10.18535/ijetst/3i03.04 Irredndant Complete Domination Nmber of Graphs Athors A.Nellai Mrgan
Improving Network Connectivity Using Trusted Nodes and Edges
 Improing Network Connectiity Using Trsted Nodes and Edges Waseem Abbas, Aron Laszka, Yegeniy Vorobeychik, and Xenofon Kotsokos Abstract Network connectiity is a primary attribte and a characteristic phenomenon
Improing Network Connectiity Using Trsted Nodes and Edges Waseem Abbas, Aron Laszka, Yegeniy Vorobeychik, and Xenofon Kotsokos Abstract Network connectiity is a primary attribte and a characteristic phenomenon
Math 365 Wednesday 4/10/ & 10.2 Graphs
 Math 365 Wednesda 4/10/19 10.1 & 10.2 Graphs Eercise 44. (Relations and digraphs) For each the relations in Eercise 43(a), dra the corresponding directed graph here V = {0, 1, 2, 3} and a! b if a b. What
Math 365 Wednesda 4/10/19 10.1 & 10.2 Graphs Eercise 44. (Relations and digraphs) For each the relations in Eercise 43(a), dra the corresponding directed graph here V = {0, 1, 2, 3} and a! b if a b. What
On the Characterization of Plane Bus Graphs
 On the Characterization of Plane Bus Graphs Till Bruckdorfer 1, Stefan Felsner 2, and Michael Kaufmann 1 1 Wilhelm-Schickard-Institut für Informatik, Universität Tübingen, Germany, {bruckdor,mk}@informatik.uni-tuebingen.de
On the Characterization of Plane Bus Graphs Till Bruckdorfer 1, Stefan Felsner 2, and Michael Kaufmann 1 1 Wilhelm-Schickard-Institut für Informatik, Universität Tübingen, Germany, {bruckdor,mk}@informatik.uni-tuebingen.de
Nonempty Intersection of Longest Paths in Series-Parallel Graphs
 Nonempty Intersection of Longest aths in Series-arallel Graphs Jlia Ehrenmüller 1,, Cristina G. Fernandes 2,, and Carl Georg Heise 1,, 1 Institt für Mathematik, Technische Uniersität Hambrg-Harbrg, Germany,
Nonempty Intersection of Longest aths in Series-arallel Graphs Jlia Ehrenmüller 1,, Cristina G. Fernandes 2,, and Carl Georg Heise 1,, 1 Institt für Mathematik, Technische Uniersität Hambrg-Harbrg, Germany,
Friend of My Friend: Network Formation with Two-Hop Benefit
 Friend of My Friend: Network Formation with Two-Hop Benefit Elliot Ansheleich, Onkar Bhardwaj, and Michael Usher Rensselaer Polytechnic Institte, Troy NY, USA Abstract. How and why people form ties is
Friend of My Friend: Network Formation with Two-Hop Benefit Elliot Ansheleich, Onkar Bhardwaj, and Michael Usher Rensselaer Polytechnic Institte, Troy NY, USA Abstract. How and why people form ties is
On shortest-path all-optical networks without wavelength conversion requirements
 Research Collection Working Paper On shortest-path all-optical networks withot waelength conersion reqirements Athor(s): Erlebach, Thomas; Stefanakos, Stamatis Pblication Date: 2002 Permanent Link: https://doi.org/10.3929/ethz-a-004446054
Research Collection Working Paper On shortest-path all-optical networks withot waelength conersion reqirements Athor(s): Erlebach, Thomas; Stefanakos, Stamatis Pblication Date: 2002 Permanent Link: https://doi.org/10.3929/ethz-a-004446054
Computing NodeTrix Representations of Clustered Graphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 22, no. 2, pp. 139 176 (2018) DOI: 10.7155/jgaa.00461 Computing NodeTrix Representations of Clustered Graphs Giordano Da Lozzo Giuseppe
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 22, no. 2, pp. 139 176 (2018) DOI: 10.7155/jgaa.00461 Computing NodeTrix Representations of Clustered Graphs Giordano Da Lozzo Giuseppe
Maximal Cliques in Unit Disk Graphs: Polynomial Approximation
 Maximal Cliqes in Unit Disk Graphs: Polynomial Approximation Rajarshi Gpta, Jean Walrand, Oliier Goldschmidt 2 Department of Electrical Engineering and Compter Science Uniersity of California, Berkeley,
Maximal Cliqes in Unit Disk Graphs: Polynomial Approximation Rajarshi Gpta, Jean Walrand, Oliier Goldschmidt 2 Department of Electrical Engineering and Compter Science Uniersity of California, Berkeley,
arxiv: v3 [math.co] 7 Sep 2018
![arxiv: v3 [math.co] 7 Sep 2018 arxiv: v3 [math.co] 7 Sep 2018](/thumbs/87/97242203.jpg) Cts in matchings of 3-connected cbic graphs Kolja Knaer Petr Valicov arxiv:1712.06143v3 [math.co] 7 Sep 2018 September 10, 2018 Abstract We discss conjectres on Hamiltonicity in cbic graphs (Tait, Barnette,
Cts in matchings of 3-connected cbic graphs Kolja Knaer Petr Valicov arxiv:1712.06143v3 [math.co] 7 Sep 2018 September 10, 2018 Abstract We discss conjectres on Hamiltonicity in cbic graphs (Tait, Barnette,
Mobility Control and Its Applications in Mobile Ad Hoc Networks
 Mobility Control and Its Applications in Mobile Ad Hoc Netorks Jie W and Fei Dai Department of Compter Science and Engineering Florida Atlantic Uniersity Boca Raton, FL 3331 Abstract Most existing localized
Mobility Control and Its Applications in Mobile Ad Hoc Netorks Jie W and Fei Dai Department of Compter Science and Engineering Florida Atlantic Uniersity Boca Raton, FL 3331 Abstract Most existing localized
Introduction to Computational Manifolds and Applications
 IMPA - Institto de Matemática Pra e Aplicada, Rio de Janeiro, RJ, Brazil Introdction to Comptational Manifolds and Applications Part 1 - Constrctions Prof. Marcelo Ferreira Siqeira mfsiqeira@dimap.frn.br
IMPA - Institto de Matemática Pra e Aplicada, Rio de Janeiro, RJ, Brazil Introdction to Comptational Manifolds and Applications Part 1 - Constrctions Prof. Marcelo Ferreira Siqeira mfsiqeira@dimap.frn.br
Upward Straight-Line Embeddings of Directed Graphs into Point Sets
 Upward Straight-Line Embeddings of Directed Graphs into Point Sets Alejandro Estrella-Balderrama, Fabrizio Frati 2, and Stephen G. Kobourov Department of Computer Science University of Arizona, U.S.A.
Upward Straight-Line Embeddings of Directed Graphs into Point Sets Alejandro Estrella-Balderrama, Fabrizio Frati 2, and Stephen G. Kobourov Department of Computer Science University of Arizona, U.S.A.
Tri-Edge-Connectivity Augmentation for Planar Straight Line Graphs
 Tri-Edge-Connectivity Agmentation for Planar Straight Line Graphs Marwan Al-Jbeh 1, Mashhood Ishaqe 1, Kristóf Rédei 1, Diane L. Sovaine 1, and Csaba D. Tóth 1,2 1 Department of Compter Science, Tfts University,
Tri-Edge-Connectivity Agmentation for Planar Straight Line Graphs Marwan Al-Jbeh 1, Mashhood Ishaqe 1, Kristóf Rédei 1, Diane L. Sovaine 1, and Csaba D. Tóth 1,2 1 Department of Compter Science, Tfts University,
Bar k-visibility Graphs: Bounds on the Number of Edges, Chromatic Number, and Thickness
 Bar k-visibility Graphs: Bounds on the Number of Edges, Chromatic Number, and Thickness Alice M. Dean, William Evans, Ellen Gethner 3,JoshuaD.Laison, Mohammad Ali Safari 5, and William T. Trotter 6 Department
Bar k-visibility Graphs: Bounds on the Number of Edges, Chromatic Number, and Thickness Alice M. Dean, William Evans, Ellen Gethner 3,JoshuaD.Laison, Mohammad Ali Safari 5, and William T. Trotter 6 Department
arxiv: v2 [cs.cg] 5 Aug 2014
![arxiv: v2 [cs.cg] 5 Aug 2014 arxiv: v2 [cs.cg] 5 Aug 2014](/thumbs/94/118540623.jpg) The θ 5 -graph is a spanner Prosenjit Bose Pat Morin André van Renssen Sander Verdonschot November 5, 2018 arxiv:12120570v2 [cscg] 5 Ag 2014 Abstract Given a set of points in the plane, e sho that the
The θ 5 -graph is a spanner Prosenjit Bose Pat Morin André van Renssen Sander Verdonschot November 5, 2018 arxiv:12120570v2 [cscg] 5 Ag 2014 Abstract Given a set of points in the plane, e sho that the
Localized Delaunay Triangulation with Application in Ad Hoc Wireless Networks
 1 Localized Delanay Trianglation with Application in Ad Hoc Wireless Networks Xiang-Yang Li Gria Călinesc Peng-Jn Wan Y Wang Department of Compter Science, Illinois Institte of Technology, Chicago, IL
1 Localized Delanay Trianglation with Application in Ad Hoc Wireless Networks Xiang-Yang Li Gria Călinesc Peng-Jn Wan Y Wang Department of Compter Science, Illinois Institte of Technology, Chicago, IL
Multi-Way Search Tree ( ) (2,4) Trees. Multi-Way Inorder Traversal. Multi-Way Search Tree ( ) Multi-Way Searching. Multi-Way Searching
 Mlti-Way Search Tree ( 0..) (,) Trees 9 5 7 0 (,) Trees (,) Trees Mlti-Way Search Tree ( 0..) A mlti-ay search tree is an ordered tree sch that Each internal node has at least to children and stores d
Mlti-Way Search Tree ( 0..) (,) Trees 9 5 7 0 (,) Trees (,) Trees Mlti-Way Search Tree ( 0..) A mlti-ay search tree is an ordered tree sch that Each internal node has at least to children and stores d
Straight-line Drawability of Embedded Graphs
 Straight-line Drawability of Embedded Graphs Hiroshi Nagamochi Department of Applied Mathematics and Physics, Kyoto University, Yoshida Honmachi, Sakyo, Kyoto 606-8501, Japan. nag@amp.i.kyoto-u.ac.jp Abstract:
Straight-line Drawability of Embedded Graphs Hiroshi Nagamochi Department of Applied Mathematics and Physics, Kyoto University, Yoshida Honmachi, Sakyo, Kyoto 606-8501, Japan. nag@amp.i.kyoto-u.ac.jp Abstract:
Bar k-visibility Graphs
 Bar k-visibility Graphs Alice M. Dean Department of Mathematics Skidmore College adean@skidmore.edu William Evans Department of Computer Science University of British Columbia will@cs.ubc.ca Ellen Gethner
Bar k-visibility Graphs Alice M. Dean Department of Mathematics Skidmore College adean@skidmore.edu William Evans Department of Computer Science University of British Columbia will@cs.ubc.ca Ellen Gethner
Universal Line-Sets for Drawing Planar 3-Trees
 Universal Line-Sets for Drawing Planar -Trees Md. Iqbal Hossain, Debajyoti Mondal, Md. Saidur Rahman, and Sammi Abida Salma Graph Drawing and Information Visualization Laboratory, Department of Computer
Universal Line-Sets for Drawing Planar -Trees Md. Iqbal Hossain, Debajyoti Mondal, Md. Saidur Rahman, and Sammi Abida Salma Graph Drawing and Information Visualization Laboratory, Department of Computer
Select-and-Protest-based Beaconless Georouting with Guaranteed Delivery in Wireless Sensor Networks
 Select-and-Protest-based Beaconless Georoting ith Garanteed Deliery in Wireless Sensor Netorks Hanna Kalosha, Amiya Nayak, Stefan Rührp, Ian Stojmenoić School of Information Technology and Engineering
Select-and-Protest-based Beaconless Georoting ith Garanteed Deliery in Wireless Sensor Netorks Hanna Kalosha, Amiya Nayak, Stefan Rührp, Ian Stojmenoić School of Information Technology and Engineering
arxiv:math/ v2 [math.co] 26 Apr 2006
![arxiv:math/ v2 [math.co] 26 Apr 2006 arxiv:math/ v2 [math.co] 26 Apr 2006](/thumbs/87/95262623.jpg) arxi:math/05094782 [math.co] 26 Apr 2006 Simultaneous Diagonal Flips in Plane Triangulations Prosenjit Bose Jurek Czyzoicz Zhicheng Gao Pat Morin Daid R. Wood March 13, 2018 Abstract Simultaneous diagonal
arxi:math/05094782 [math.co] 26 Apr 2006 Simultaneous Diagonal Flips in Plane Triangulations Prosenjit Bose Jurek Czyzoicz Zhicheng Gao Pat Morin Daid R. Wood March 13, 2018 Abstract Simultaneous diagonal
v e v 1 C 2 b) Completely assigned T v a) Partially assigned Tv e T v 2 p k
 Approximation Algorithms for a Capacitated Network Design Problem R. Hassin 1? and R. Rai 2?? and F. S. Salman 3??? 1 Department of Statistics and Operations Research, Tel-Ai Uniersity, Tel Ai 69978, Israel.
Approximation Algorithms for a Capacitated Network Design Problem R. Hassin 1? and R. Rai 2?? and F. S. Salman 3??? 1 Department of Statistics and Operations Research, Tel-Ai Uniersity, Tel Ai 69978, Israel.
Intersection-Link Representations of Graphs
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 21, no. 4, pp. 731 755 (2017) DOI: 10.7155/jgaa.00437 Intersection-Link Representations of Graphs Patrizio Angelini 1 Giordano Da Lozzo
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 21, no. 4, pp. 731 755 (2017) DOI: 10.7155/jgaa.00437 Intersection-Link Representations of Graphs Patrizio Angelini 1 Giordano Da Lozzo
Queries. Inf 2B: Ranking Queries on the WWW. Suppose we have an Inverted Index for a set of webpages. Disclaimer. Kyriakos Kalorkoti
 Qeries Inf B: Ranking Qeries on the WWW Kyriakos Kalorkoti School of Informatics Uniersity of Edinbrgh Sppose e hae an Inerted Index for a set of ebpages. Disclaimer I Not really the scenario of Lectre.
Qeries Inf B: Ranking Qeries on the WWW Kyriakos Kalorkoti School of Informatics Uniersity of Edinbrgh Sppose e hae an Inerted Index for a set of ebpages. Disclaimer I Not really the scenario of Lectre.
FINITE ELEMENT APPROXIMATION OF CONVECTION DIFFUSION PROBLEMS USING GRADED MESHES
 FINITE ELEMENT APPROXIMATION OF CONVECTION DIFFUSION PROBLEMS USING GRADED MESHES RICARDO G. DURÁN AND ARIEL L. LOMBARDI Abstract. We consider the nmerical approximation of a model convection-diffsion
FINITE ELEMENT APPROXIMATION OF CONVECTION DIFFUSION PROBLEMS USING GRADED MESHES RICARDO G. DURÁN AND ARIEL L. LOMBARDI Abstract. We consider the nmerical approximation of a model convection-diffsion
Red-Black Trees Goodrich, Tamassia. Red-Black Trees 1
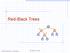 Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Red-Black Trees 3 8 00 Goodrich, Tamassia Red-Black Trees 1 From (,) to Red-Black Trees A red-black tree is a representation of a (,) tree by means of a binary tree hose nodes are colored red or black
Partitioning Orthogonal Polygons by Extension of All Edges Incident to Reflex Vertices: lower and upper bounds on the number of pieces
 Partitioning Orthogonal Polygons by Extension of All Edges Incident to Reflex Vertices: lower and upper bounds on the number of pieces António Leslie Bajuelos 1, Ana Paula Tomás and Fábio Marques 3 1 Dept.
Partitioning Orthogonal Polygons by Extension of All Edges Incident to Reflex Vertices: lower and upper bounds on the number of pieces António Leslie Bajuelos 1, Ana Paula Tomás and Fábio Marques 3 1 Dept.
Practical Level Planarity Testing and Layout with Embedding Constraints
 Practical Level Planarity Testing and Layout with Embedding Constraints Martin Harrigan and Patrick Healy Department of Computer Science and Information Systems, University of Limerick, Ireland {martin.harrigan,
Practical Level Planarity Testing and Layout with Embedding Constraints Martin Harrigan and Patrick Healy Department of Computer Science and Information Systems, University of Limerick, Ireland {martin.harrigan,
arxiv: v1 [cs.cg] 14 Apr 2014
![arxiv: v1 [cs.cg] 14 Apr 2014 arxiv: v1 [cs.cg] 14 Apr 2014](/thumbs/90/102648787.jpg) Complexity of Higher-Degree Orthogonal Graph Embedding in the Kandinsky Model arxi:1405.23001 [cs.cg] 14 Apr 2014 Thomas Bläsius Guido Brückner Ignaz Rutter Abstract We show that finding orthogonal grid-embeddings
Complexity of Higher-Degree Orthogonal Graph Embedding in the Kandinsky Model arxi:1405.23001 [cs.cg] 14 Apr 2014 Thomas Bläsius Guido Brückner Ignaz Rutter Abstract We show that finding orthogonal grid-embeddings
Topological Drawings of Complete Bipartite Graphs
 Topological Drawings of Complete Bipartite Graphs Jean Cardinal Stefan Felsner y Febrary 017 Abstract Topological drawings are natral representations of graphs in the plane, where vertices are represented
Topological Drawings of Complete Bipartite Graphs Jean Cardinal Stefan Felsner y Febrary 017 Abstract Topological drawings are natral representations of graphs in the plane, where vertices are represented
Planar Open Rectangle-of-Influence Drawings with Non-aligned Frames
 Planar Open Rectangle-of-Influence Drawings with Non-aligned Frames Soroush Alamdari and Therese Biedl David R. Cheriton School of Computer Science, University of Waterloo {s6hosse,biedl}@uwaterloo.ca
Planar Open Rectangle-of-Influence Drawings with Non-aligned Frames Soroush Alamdari and Therese Biedl David R. Cheriton School of Computer Science, University of Waterloo {s6hosse,biedl}@uwaterloo.ca
Assigning AS Relationships to Satisfy the Gao-Rexford Conditions
 Assigning AS Relationships to Satisfy the Gao-Rexford Conditions Lca Cittadini, Giseppe Di Battista, Thomas Erlebach, Marizio Patrignani, and Massimo Rimondini Dept. of Compter Science and Atomation, Roma
Assigning AS Relationships to Satisfy the Gao-Rexford Conditions Lca Cittadini, Giseppe Di Battista, Thomas Erlebach, Marizio Patrignani, and Massimo Rimondini Dept. of Compter Science and Atomation, Roma
ABSTRACT Finding a cut or nding a matching in a graph are so simple problems that hardly are considered problems at all. Finding a cut whose split edg
 R O M A TRE DIA Universita degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 { 00146 Roma, Italy The Complexity of the Matching-Cut Problem Maurizio Patrignani
R O M A TRE DIA Universita degli Studi di Roma Tre Dipartimento di Informatica e Automazione Via della Vasca Navale, 79 { 00146 Roma, Italy The Complexity of the Matching-Cut Problem Maurizio Patrignani
Tutte Embeddings of Planar Graphs
 Spectral Graph Theory and its Applications Lectre 21 Ttte Embeddings o Planar Graphs Lectrer: Daniel A. Spielman November 30, 2004 21.1 Ttte s Theorem We sally think o graphs as being speciied by vertices
Spectral Graph Theory and its Applications Lectre 21 Ttte Embeddings o Planar Graphs Lectrer: Daniel A. Spielman November 30, 2004 21.1 Ttte s Theorem We sally think o graphs as being speciied by vertices
5-colouring graphs with 4 crossings
 5-colouring graphs with 4 crossings Rok Erman a, Frédéric Haet b, Bernard Lidický c, and Ondřej Pangrác c August 6, 2010 a Department of Mathematics, Uniersity of Ljubljana, Jadranska 21, 1000 Ljubljana,
5-colouring graphs with 4 crossings Rok Erman a, Frédéric Haet b, Bernard Lidický c, and Ondřej Pangrác c August 6, 2010 a Department of Mathematics, Uniersity of Ljubljana, Jadranska 21, 1000 Ljubljana,
[8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra
![[8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra [8] that this cannot happen on the projective plane (cf. also [2]) and the results of Robertson, Seymour, and Thomas [5] on linkless embeddings of gra](/thumbs/85/93035794.jpg) Apex graphs with embeddings of face-width three Bojan Mohar Department of Mathematics University of Ljubljana Jadranska 19, 61111 Ljubljana Slovenia bojan.mohar@uni-lj.si Abstract Aa apex graph is a graph
Apex graphs with embeddings of face-width three Bojan Mohar Department of Mathematics University of Ljubljana Jadranska 19, 61111 Ljubljana Slovenia bojan.mohar@uni-lj.si Abstract Aa apex graph is a graph
On the complexity of Submap Isomorphism
 On the compleit of Sbmap Isomorphism Christine Solnon 1,2, Gillame Damiand 1,2, Colin de la Higera 3, and Jean-Christophe Janodet 4 1 INSA de Lon, LIRIS, UMR 5205 CNRS, 69621 Villerbanne, France 2 Université
On the compleit of Sbmap Isomorphism Christine Solnon 1,2, Gillame Damiand 1,2, Colin de la Higera 3, and Jean-Christophe Janodet 4 1 INSA de Lon, LIRIS, UMR 5205 CNRS, 69621 Villerbanne, France 2 Université
The Domination and Competition Graphs of a Tournament. University of Colorado at Denver, Denver, CO K. Brooks Reid 3
 The omination and Competition Graphs of a Tornament avid C. Fisher, J. Richard Lndgren 1, Sarah K. Merz University of Colorado at enver, enver, CO 817 K. rooks Reid California State University, San Marcos,
The omination and Competition Graphs of a Tornament avid C. Fisher, J. Richard Lndgren 1, Sarah K. Merz University of Colorado at enver, enver, CO 817 K. rooks Reid California State University, San Marcos,
Incremental Convex Planarity Testing 1
 Information and Computation 169, 94 126 (2001) doi:10.1006/inco.2001.3031, available online at http://www.idealibrary.com on Incremental Convex Planarity Testing 1 Giuseppe Di Battista 2 Dipartimento di
Information and Computation 169, 94 126 (2001) doi:10.1006/inco.2001.3031, available online at http://www.idealibrary.com on Incremental Convex Planarity Testing 1 Giuseppe Di Battista 2 Dipartimento di
From (2,4) to Red-Black Trees
 Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Red-Black Trees 3/0/1 Presentation for use ith the textbook Data Structures and Algorithms in Jaa, th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldasser, Wiley, 01 Red-Black Trees 3 8 01 Goodrich,
Point Location. The Slab Method. Optimal Schemes. The Slab Method. Preprocess a planar, polygonal subdivision for point location queries.
 Point Location The Slab Method Prerocess a lanar, olygonal sbdiision for oint location qeries. = (18, 11) raw a ertical line throgh each ertex. This decomoses the lane into slabs. In each slab, the ertical
Point Location The Slab Method Prerocess a lanar, olygonal sbdiision for oint location qeries. = (18, 11) raw a ertical line throgh each ertex. This decomoses the lane into slabs. In each slab, the ertical
Straight-Line Rectangular Drawings of Clustered Graphs
 Discrete Comput Geom (2011) 45: 88 140 DOI 10.1007/s00454-010-9302-z Straight-Line Rectangular Drawings of Clustered Graphs Patrizio Angelini Fabrizio Frati Michael Kaufmann Received: 15 August 2009 /
Discrete Comput Geom (2011) 45: 88 140 DOI 10.1007/s00454-010-9302-z Straight-Line Rectangular Drawings of Clustered Graphs Patrizio Angelini Fabrizio Frati Michael Kaufmann Received: 15 August 2009 /
Fast Ray Tetrahedron Intersection using Plücker Coordinates
 Fast Ray Tetrahedron Intersection sing Plücker Coordinates Nikos Platis and Theoharis Theoharis Department of Informatics & Telecommnications University of Athens Panepistemiopolis, GR 157 84 Ilissia,
Fast Ray Tetrahedron Intersection sing Plücker Coordinates Nikos Platis and Theoharis Theoharis Department of Informatics & Telecommnications University of Athens Panepistemiopolis, GR 157 84 Ilissia,
Monotone crossing number
 Monotone crossing number János Pach and Géza Tóth Rényi Institute, Budapest Abstract The monotone crossing number of G is defined as the smallest number of crossing points in a drawing of G in the plane,
Monotone crossing number János Pach and Géza Tóth Rényi Institute, Budapest Abstract The monotone crossing number of G is defined as the smallest number of crossing points in a drawing of G in the plane,
A Note on Rectilinearity and Angular Resolution
 Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 8, no. 1, pp. 89 94 (2004) A Note on Rectilinearity and Angular Resolution Hans L. Bodlaender Gerard Tel Institute of Information and
Journal of Graph Algorithms and Applications http://jgaa.info/ vol. 8, no. 1, pp. 89 94 (2004) A Note on Rectilinearity and Angular Resolution Hans L. Bodlaender Gerard Tel Institute of Information and
Ma/CS 6b Class 11: Kuratowski and Coloring
 Ma/CS 6b Class 11: Kuratowski and Coloring By Adam Sheffer Kuratowski's Theorem Theorem. A graph is planar if and only if it does not have K 5 and K 3,3 as topological minors. We know that if a graph contains
Ma/CS 6b Class 11: Kuratowski and Coloring By Adam Sheffer Kuratowski's Theorem Theorem. A graph is planar if and only if it does not have K 5 and K 3,3 as topological minors. We know that if a graph contains
On Minimum Weight Pseudo-Triangulations
 On Minimum Weight Pseudo-Triangulations Oswin Aichholzer Franz Aurenhammer Thomas Hackl Bettina Speckmann Abstract In this note we discuss some structural properties of minimum weight pseudo-triangulations.
On Minimum Weight Pseudo-Triangulations Oswin Aichholzer Franz Aurenhammer Thomas Hackl Bettina Speckmann Abstract In this note we discuss some structural properties of minimum weight pseudo-triangulations.
Math 777 Graph Theory, Spring, 2006 Lecture Note 1 Planar graphs Week 1 Weak 2
 Math 777 Graph Theory, Spring, 006 Lecture Note 1 Planar graphs Week 1 Weak 1 Planar graphs Lectured by Lincoln Lu Definition 1 A drawing of a graph G is a function f defined on V (G) E(G) that assigns
Math 777 Graph Theory, Spring, 006 Lecture Note 1 Planar graphs Week 1 Weak 1 Planar graphs Lectured by Lincoln Lu Definition 1 A drawing of a graph G is a function f defined on V (G) E(G) that assigns
Quadrilateral Meshes with Provable Angle Bounds
 Quadrilateral Meshes with Proable Angle Bounds F. Betul Atalay Suneeta Ramaswami Dianna Xu March 3, 2011 Abstract In this paper, we present an algorithm that utilizes a quadtree data structure to construct
Quadrilateral Meshes with Proable Angle Bounds F. Betul Atalay Suneeta Ramaswami Dianna Xu March 3, 2011 Abstract In this paper, we present an algorithm that utilizes a quadtree data structure to construct
Reachability on a region bounded by two attached squares
 Reachability on a region bounded by two attached squares Ali Mohades mohades@cic.aku.ac.ir AmirKabir University of Tech., Math. and Computer Sc. Dept. Mohammadreza Razzazi razzazi@ce.aku.ac.ir AmirKabir
Reachability on a region bounded by two attached squares Ali Mohades mohades@cic.aku.ac.ir AmirKabir University of Tech., Math. and Computer Sc. Dept. Mohammadreza Razzazi razzazi@ce.aku.ac.ir AmirKabir
Mobility Control and Its Applications in Mobile Ad Hoc Networks
 Mobility Control and Its Applications in Mobile Ad Hoc Netorks Jie W and Fei Dai, Florida Atlantic Uniersity Abstract Most eisting localized protocols in mobile ad hoc netorks, sch as data commnication
Mobility Control and Its Applications in Mobile Ad Hoc Netorks Jie W and Fei Dai, Florida Atlantic Uniersity Abstract Most eisting localized protocols in mobile ad hoc netorks, sch as data commnication
Representing a Cubic Graph as the Intersection Graph of Axis-parallel Boxes in Three Dimensions
 Representing a Cbic Graph as the Intersection Graph of Axis-parallel Boxes in Three Dimensions ABSTRACT Abhijin Adiga Network Dynamics and Simlation Science Laboratory Virginia Bioinformatics Institte,
Representing a Cbic Graph as the Intersection Graph of Axis-parallel Boxes in Three Dimensions ABSTRACT Abhijin Adiga Network Dynamics and Simlation Science Laboratory Virginia Bioinformatics Institte,
Today. B-splines. B-splines. B-splines. Computergrafik. Curves NURBS Surfaces. Bilinear patch Bicubic Bézier patch Advanced surface modeling
 Comptergrafik Matthias Zwicker Uniersität Bern Herbst 29 Cres Srfaces Parametric srfaces Bicbic Bézier patch Adanced srface modeling Piecewise Bézier cres Each segment spans for control points Each segment
Comptergrafik Matthias Zwicker Uniersität Bern Herbst 29 Cres Srfaces Parametric srfaces Bicbic Bézier patch Adanced srface modeling Piecewise Bézier cres Each segment spans for control points Each segment
