Lesson 6 MA Nick Egbert

Transcription

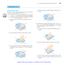
1 Overview From kindergarten we all know ow to find te slope of a line: rise over run, or cange in over cange in. We want to be able to determine slopes of functions wic are not lines. To do tis we use te idea of te derivative, wic is te instantaneous rate of cange at a single point. Lesson Secant and tangent lines Before we figure out ow to formall define te derivative we first need te notion of a secant line and a tangent line. Consider te grap of f() below. f() a b Te red line wic passes troug te points (a, f(a)) and (b, f(b)) is called a secant line. In general an line wic intersects te curve at two points we call a secant line. Te green line above is called a tangent line at a. In oter words, a tangent line touces (but does not cross) te curve locall. Te word locall ere just means tat it s possible for te line to intersect te curve at multiple points. If tis appens we just restrict our attention to a smaller interval. For eample, if we etended te green line to te left, we would eventuall cross te curve at some negative -value. We are eventuall after te slope of te tangent line at a, wic is wat we will call te derivative of f at a. Tis is no eas task, so we start wit an easier problem: finding te slope of te secant line between a and b. As we mentioned before, we alread know ow to do tis from kindergarten. Te slope of te secant line between te points (a, f(a)) and (b, f(b)) is given b slope f(b) f(a). b a So ow are we going to find te slope of te tangent line at a? Using te notion of limits from te previous few lessons of course! If we imagine moving b closer and closer to a, ten eventuall our secant line will move into te tangent line. To visualize tis, we ll sow a progression of a few graps tat demonstrate tis idea. 1

2 f() f() f() f() Te difference quotient Now tat we know were we re eaded, let us again consider te original grap wit te secant line. f() a b We will denote b a; tat is, is te distance along te -ais from a to b. Some people will also denote tis. Tis means tat we can rewrite b a +, and ten we can write te slope of te secant line as slope f(a + ) f(a) (a + ) a Notice tat we can simplif te denominator b canceling out te a and a. We call tis te difference quotient, wic we often denote f(a + ) f(a) 2

3 Te important takeawa from te difference quotient is tat it is just te slope of te secant line between a and b a +. Recall tat we wanted to move te point (b, f(b)) closer and closer to te point (a, f(a)). Matematicall tis means we want to take te limit at goes to 0. Since te derivative is also a function of (meaning tat te point a tat we picked wasn t special), we ll replace a wit, and we ave te following definition. Te derivative of f() at, denoted f () is f f( + ) f() () lim. 0 Remark. Te definition in te bo above is often referred to as te formal definition of te derivative. Alternativel, finding te derivative in tis manner is referred to as using te limit process to find te slope of te tangent line. Important. In subsequent lessons we will learn more efficient metods for computing te derivative. However, trougout tis lesson and wenever specified, ou must compute te derivative in tis manner. Eamples Eample 1. Use te limit process to find te slope of te tangent line to te grap of at. f() 8 3 Solution. Step one in tese problems is alwas to find te difference quotient, DQ. Here, So Ten b definition, f( + ) 8 3( + ) f( + ) f() (8 3) f () lim Tis souldn t be surprising since f() is a line wose slope is 3. 3

4 Note. Recall tat f( + ) means tat we want to plug in ( + ) for ever instance of tat we see. Tat is, we are evaluating f at +. Eample 2. Use te limit process to find te slope of te tangent line to te grap of at. Solution. In tis case, Now, Finall, f() f( + ) 6( + ) ( ) f( + ) f() ( ) (12 + 6) f () lim 0 (12 + 6) 12. Remark. Simplifing te difference quotient completel is generall te ke to being able to take te limit as 0. Notice tat as we tried just evaluating at 0 from te beginning, we would ave gotten 0 0. Eample 3. Find te equation of te tangent line to te grap of at 1. f() Remark. In order to find te equation of a line, we need to pieces of information: te slope and a point. From tere we will be able to use point-slope form to determine te equation of te line: m( 1 ) + 1 were m denotes te slope of te line and ( 1, 1 ) is a point on tat line. 4

5 Solution to Eample 3. B te above remark we need te slope and a point. Te onl point we know for sure tat will be on te tangent line is at 1. To find te -value, we simpl plug 1 into f(). Doing so, we get f(1) 7 6. So (1, 7/6) is a point on te tangent line. Now we need to find te slope. As ou ll recall f (1) is te slope of te tangent line at 1. So we need to find te derivative evaluated at 1. We start b computing te difference quotient. Observe first tat f( + ) 7 6( + ) 2 so tat f( + ) f() 7 6(+) (+) 2 7(+)2 6 2 (+) (+) (+) ( + ) ( + ) ( ) 6 2 ( + ) ( + ) ( + ) 2 ( 14 7) 6 2 ( + ) 2 ( 14 7) 6 2 ( + ) 2. And finall we are read to take te limit as 0. f ( 14 () lim 0 7) ( + ) But unfortunatel we re still not finised. We need to find te equation of te tangent line 5

6 at 1. As mentioned above, te slope of tis line is simpl f (1). Well, f (1) 7 3(1) Now all tat s left to do is to plug tis into point-slope form: 7 3 ( 1) Remark. Te given answer is a fine and complete final answer. Point-slope form is an equation of a line. If ou prefer slope-intercept form or if ou are asked to give an answer in slope-intercept form, we could also write tis as 7 3 ( 1) In particular, on Loncapa ou ma leave our answer in point-slope form. 6