Assignment 3 Solutions, COMP 251B
|
|
|
- Teresa Barnett
- 5 years ago
- Views:
Transcription
1 Assignment 3 Solutions, COMP 251B Dipinder S. Rekhi March 24, Exercise Binary search tree can be thought of as a sorted structure that is created using comparisons only. This weakly implies that the lower-bound for creating such a tree in the worst-case is Ω(nlog n), because if it was asymptotically lower than that then it would mean that we ll have a comparison-based sorting algorithm with a lower-bound for the worst case asympotically smaller than nlog n. However, it is not the case, as proved in the book. For a more rigorous proof, we would use decision trees. Consider a decision tree for a comparisonbased algorithm that creates a binary search tree from a given sequence on n numbers. The inner-nodes of this tree refer to the comparisons, and the edges emanating from those nodes refer to different paths the algorithm takes based on the comparison made. The leaf nodes refer to the BSTs formed after following one particular path in the tree. Since there are n! ways of arranging n input numbers, it means that there are n! possible BSTs (assuming that no two numbers are the same). In other words, the decision tree would have n! nodes. The decision tree would be a binary tree because a comparison of two non-identical numbers at each inner-node will result in either the first one being greater than the other or vice-versa. Let the length of the longest path from root to the leaf be h. h would also be the height of the decision tree. Any binary tree of height h would have at the most 2 h leaves. So, n! 2 h log n! h h =Ω(nlog n) Hence, in the worst case constructing a BST would take Ω(nlog n) time. 1
2 2 Join Operation on Red Black Trees a) To update bh[t] in O(log n) time within RB-INSERT and RB-DELETE functions, we make use of the property that number of black nodes from root to any leaf is the same. After RB-INSERT and RB-DELETE do their usual work, we travel from root to one of the leafs by following the left most path (we can follow any path). Along the way we count the number of black nodes encountered. The root is not counted. The number of black nodes encountered becomes the new value of bh[t]. Since the height of RB-tree is O(log n), therefore this operation takes O(log n) time. Hence, it dosent increase the asymptotic running time of RB-INSERT or RB-DELETE. Calculating the black height of the nodes while descending down the tree is simple. Given the black height of the parent, the childs black height depends on its color. If it is black then the black height is one less than its parents, whereas, if it is red then its black height is the same as its parents. Therefore, it takes O(1) to do this. b) Given bh[t 1 ] bh[t 2 ]. Consider the right most path is the tree T 1.Right most path means that when descending down the tree starting from the root, we always visit the right child. When we go down any path in a RB-Tree, the black height of the nodes decrease (see part a to convince yourself). It decreases from bh[t 1 ] down to zero, such that all the values in this range belong to atleast one particular node in the descending path. The point of following the right most path is that we ll encounter the largest values. So while descending the right most path, when we encounter a black-node of black height h, it means that it is the largest black node in the tree with a black height h. Using the above reasoning, we descend down the right most path of tree T 1, until we encounter the black node of height bh[t 2 ]. Since the height of RB-tree is O(log n), therefore this operation takes O(log n)time. c and d) These parts follow part (b) of the question and fit in the whole scheme of performing a join operation. Consequently, we can safely assume that y is a black node and tree subrooted at y has the same black height as tree T 2. Put node x in y s position. Make node y the left child and root of T 2 the right child of x. Color node x red so that properties 1,3 and 5 are maintained. To enforce properties 2 and 4 assign z = x, T = T 1 and execute RB-INSERT-FIXUP(T,z). To get a better understanding of how this works, 2
3 please refer to the book. This operation runs in O(log n) time. e and f) Part e is obvious. When bh[t 1 ] <bh[t 2 ], the method is exactly the same except that we follow the left most path in tree T 2 to find the smallest black node that has the same black height as tree T 1. After that a similar procedure follows as in the above parts. Join operation is actually a sequence of the above steps. Since these steps are performed in time O(log n), therefore Join operation can be performed in time O(log n). 3 AVL Trees a) Let n(h) be the number of nodes in the AVL tree of height h. n(0) 0and n(1) 1 are easy to imagine. Now consider a AVL tree of height h>1. The root will have two subtrees where 1) either both the subtrees have a height h-1 or 2) one has a height h-1 and the other has the height h-2. If both the subtrees are of height h-2 then the given tree cannot be of the height h. The above reasoning follows the AVL tree property. So the number of nodes in the above tree would be at least n(h 1) + n(h 2). Or n(h) n(h 1) + n(h 2) The above recurrence is a fibonacci recurrence (see problem 4-5, page 87 of the book). n(h 1) + n(h 2) is the h th fibonacci number F h,where F h = ( 1+ 5 ) h 2 5 or n(h) ( 1+ 5 ) h 2 5 Taking log on both the sides (let n(h) =n) or h = O(log n) log n h log( 1+ 5 ) log( 5) 2 b) Given, a subtree rooted at x whose right and left subtrees are height 3
4 balanced, but x itself is not height balanced. Lets consider the case where left subtree is of the height h and right subtree is of the height h+2. Similar method should be followed for the opposite case with orientations changed from left to right and vice-versa. Let L be the left child and R be the right child of x. Let α and β be left and right children of R. If height(α) height(β) thenlef T ROTATE(T,x) elseifheight(α) > height(β) then first RIGHT ROTATE(T,R)andthenLEF T ROTATE(T,x)where T is the tree immediately after the insertion. Set the heights accordingly. c) Following is the INSERT code INSERT(x, z) - if(x = NULL) (Root) - root = Z - return - if(key[z] key[x]) - if(right [x] =NULL) - RIGHT [x] =z - h[x] =newheightof x - return - else - INSERT(RIGHT [x],z) - else - if(lef T [x] =NULL) - LEF T [x] =z - h[x] =newheightof x - return - else - INSERT(LEF T [x],z) - h[x] =max(left[x],right[x]) if(not BALANCED(x)) - BALANCE(x) d) Consider the function INSERT (see above) running on an AVL tree. Since we go down from root to find a node whose child the new node z would become, it takes O(log n) time. This is because height of the AVL tree is O(log n). Now consider the path from root to the newly inserted node z. Let the first node (going up the path from z) that is imbalanced be x. If there 4
5 are other nodes up the path that are imba;anced then it would be because subtree at x is imbalanced (as a node got added to it). So if we fix this imbalance at x then we would not need to perform any more rotations. The new height of x after the insertion is h+1 where h was the height before insertion was done (we are considering the case where addition of a new node icreases the height of some nodes. otherwise we would not have to worry about imbalances). Now, after we perform a rotation at x, the height of the node that will be in x s position would go back to h. Hence, the balance is achieved. If you look carefully at how balance works you would see that the height of the node in x s position would not stay the same, but decrease by one. This is because by just adding a single node we dont get into the situation where α and β have the same height. 4 Planning a Company Party Let C T be the total cost of the tree rooted at T. In this tree, if T is invited to the party then none of its children is invited. However, if T is not invited then some of its children may and some may not be invited. Let C Ti be the cost of the tree rooted at T when T is invited. Let C Tn be the cost of the tree rooted at T when T is not invited. It is obvious that C T = max(c Tn,C Ti ) In turn, C Ti = C xn x Childrenof T Also, C Tn = C x x Childrenof T For the node x, of the final optimal tree, that is a leaf, C xi = C(x) where C(x) is the conviviality rating of x and C xn = 0. Using this and the above equations we can build an optimal tree in a bottom-up fashion. 5
6 5 Moving on a Checker Board Let your current position on the board be x. If x belongs to the topmost row then the game is over and print the total. Otherwise, let Y be the set of positions that you can go from x. Let C x be the maximum number of dollars that one can earn following a certain optimal path from x. Then following recusion holds, C x = max z Y (p(x, z)+c z ) Calculating C x this way and finding the optimal path can be time consuming due to redundancy in recusion. Many problems have the same subproblems that are recalculated. To avoid this we start from the next to top most row. Calculate the C x values for all the nodes x in this row. C x values for all the nodes in the topmost row is zero. Go down one row and do similar calculations. Carry on like this until you get to the bottom most row. If the board is of the dimensions NxN, then these calculations can all be done in time O(N 2 ). 6
Algorithms. AVL Tree
 Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
Algorithms AVL Tree Balanced binary tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time needed to perform insertion and deletion and many other
AVL Tree Definition. An example of an AVL tree where the heights are shown next to the nodes. Adelson-Velsky and Landis
 Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
Presentation for use with the textbook Data Structures and Algorithms in Java, 6 th edition, by M. T. Goodrich, R. Tamassia, and M. H. Goldwasser, Wiley, 0 AVL Trees v 6 3 8 z 0 Goodrich, Tamassia, Goldwasser
AVL Trees Goodrich, Tamassia, Goldwasser AVL Trees 1
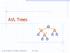 AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
AVL Trees v 6 3 8 z 20 Goodrich, Tamassia, Goldwasser AVL Trees AVL Tree Definition Adelson-Velsky and Landis binary search tree balanced each internal node v the heights of the children of v can 2 3 7
CHAPTER 10 AVL TREES. 3 8 z 4
 CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
CHAPTER 10 AVL TREES v 6 3 8 z 4 ACKNOWLEDGEMENT: THESE SLIDES ARE ADAPTED FROM SLIDES PROVIDED WITH DATA STRUCTURES AND ALGORITHMS IN C++, GOODRICH, TAMASSIA AND MOUNT (WILEY 2004) AND SLIDES FROM NANCY
Lecture 6: Analysis of Algorithms (CS )
 Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
Lecture 6: Analysis of Algorithms (CS583-002) Amarda Shehu October 08, 2014 1 Outline of Today s Class 2 Traversals Querying Insertion and Deletion Sorting with BSTs 3 Red-black Trees Height of a Red-black
CS350: Data Structures Red-Black Trees
 Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Red-Black Trees James Moscola Department of Engineering & Computer Science York College of Pennsylvania James Moscola Red-Black Tree An alternative to AVL trees Insertion can be done in a bottom-up or
Search Trees (Ch. 9) > = Binary Search Trees 1
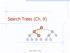 Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Search Trees (Ch. 9) < 6 > = 1 4 8 9 Binary Search Trees 1 Ordered Dictionaries Keys are assumed to come from a total order. New operations: closestbefore(k) closestafter(k) Binary Search Trees Binary
Analysis of Algorithms
 Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
Analysis of Algorithms Trees-I Prof. Muhammad Saeed Tree Representation.. Analysis Of Algorithms 2 .. Tree Representation Analysis Of Algorithms 3 Nomenclature Nodes (13) Size (13) Degree of a node Depth
COSC160: Data Structures Balanced Trees. Jeremy Bolton, PhD Assistant Teaching Professor
 COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
COSC160: Data Structures Balanced Trees Jeremy Bolton, PhD Assistant Teaching Professor Outline I. Balanced Trees I. AVL Trees I. Balance Constraint II. Examples III. Searching IV. Insertions V. Removals
Analysis of Algorithms
 Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
Analysis of Algorithms Concept Exam Code: 16 All questions are weighted equally. Assume worst case behavior and sufficiently large input sizes unless otherwise specified. Strong induction Consider this
Self-Balancing Search Trees. Chapter 11
 Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
Self-Balancing Search Trees Chapter 11 Chapter Objectives To understand the impact that balance has on the performance of binary search trees To learn about the AVL tree for storing and maintaining a binary
CISC 235: Topic 4. Balanced Binary Search Trees
 CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
CISC 235: Topic 4 Balanced Binary Search Trees Outline Rationale and definitions Rotations AVL Trees, Red-Black, and AA-Trees Algorithms for searching, insertion, and deletion Analysis of complexity CISC
Chapter 10: Search Trees
 < 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
< 6 > 1 4 = 8 9 Chapter 10: Search Trees Nancy Amato Parasol Lab, Dept. CSE, Texas A&M University Acknowledgement: These slides are adapted from slides provided with Data Structures and Algorithms in C++,
Module 4: Index Structures Lecture 13: Index structure. The Lecture Contains: Index structure. Binary search tree (BST) B-tree. B+-tree.
 The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
The Lecture Contains: Index structure Binary search tree (BST) B-tree B+-tree Order file:///c /Documents%20and%20Settings/iitkrana1/My%20Documents/Google%20Talk%20Received%20Files/ist_data/lecture13/13_1.htm[6/14/2012
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Midterm solutions. n f 3 (n) = 3
 Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
Introduction to Computer Science 1, SE361 DGIST April 20, 2016 Professors Min-Soo Kim and Taesup Moon Midterm solutions Midterm solutions The midterm is a 1.5 hour exam (4:30pm 6:00pm). This is a closed
CIS265/ Trees Red-Black Trees. Some of the following material is from:
 CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
CIS265/506 2-3-4 Trees Red-Black Trees Some of the following material is from: Data Structures for Java William H. Ford William R. Topp ISBN 0-13-047724-9 Chapter 27 Balanced Search Trees Bret Ford 2005,
Lecture: Analysis of Algorithms (CS )
 Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Lecture: Analysis of Algorithms (CS583-002) Amarda Shehu Fall 2017 1 Binary Search Trees Traversals, Querying, Insertion, and Deletion Sorting with BSTs 2 Example: Red-black Trees Height of a Red-black
Linked Structures Songs, Games, Movies Part III. Fall 2013 Carola Wenk
 Linked Structures Songs, Games, Movies Part III Fall 2013 Carola Wenk Biological Structures Nature has evolved vascular and nervous systems in a hierarchical manner so that nutrients and signals can quickly
Linked Structures Songs, Games, Movies Part III Fall 2013 Carola Wenk Biological Structures Nature has evolved vascular and nervous systems in a hierarchical manner so that nutrients and signals can quickly
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Lecture 9 - Jan. 22, 2018 CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba 1 / 12 Binary Search Trees (review) Structure
Balanced Binary Search Trees. Victor Gao
 Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
Balanced Binary Search Trees Victor Gao OUTLINE Binary Heap Revisited BST Revisited Balanced Binary Search Trees Rotation Treap Splay Tree BINARY HEAP: REVIEW A binary heap is a complete binary tree such
COMP171. AVL-Trees (Part 1)
 COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
COMP11 AVL-Trees (Part 1) AVL Trees / Slide 2 Data, a set of elements Data structure, a structured set of elements, linear, tree, graph, Linear: a sequence of elements, array, linked lists Tree: nested
Part 2: Balanced Trees
 Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Part 2: Balanced Trees 1 AVL Trees We could dene a perfectly balanced binary search tree with N nodes to be a complete binary search tree, one in which every level except the last is completely full. A
Operations on Heap Tree The major operations required to be performed on a heap tree are Insertion, Deletion, and Merging.
 Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Priority Queue, Heap and Heap Sort In this time, we will study Priority queue, heap and heap sort. Heap is a data structure, which permits one to insert elements into a set and also to find the largest
Transform & Conquer. Presorting
 Transform & Conquer Definition Transform & Conquer is a general algorithm design technique which works in two stages. STAGE : (Transformation stage): The problem s instance is modified, more amenable to
Transform & Conquer Definition Transform & Conquer is a general algorithm design technique which works in two stages. STAGE : (Transformation stage): The problem s instance is modified, more amenable to
A red-black tree is a balanced binary search tree with the following properties:
 Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
Binary search trees work best when they are balanced or the path length from root to any leaf is within some bounds. The red-black tree algorithm is a method for balancing trees. The name derives from
AVL Trees (10.2) AVL Trees
 AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
AVL Trees (0.) CSE 0 Winter 0 8 February 0 AVL Trees AVL trees are balanced. An AVL Tree is a binary search tree such that for every internal node v of T, the heights of the children of v can differ by
Binary heaps (chapters ) Leftist heaps
 Binary heaps (chapters 20.3 20.5) Leftist heaps Binary heaps are arrays! A binary heap is really implemented using an array! 8 18 29 20 28 39 66 Possible because of completeness property 37 26 76 32 74
Binary heaps (chapters 20.3 20.5) Leftist heaps Binary heaps are arrays! A binary heap is really implemented using an array! 8 18 29 20 28 39 66 Possible because of completeness property 37 26 76 32 74
CSci 231 Homework 7. Red Black Trees. CLRS Chapter 13 and 14
 CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 1. Problem 13-1 (persistent dynamic sets).. Problem 13-3 (AVL trees) 3. In this problem we consider a data structure for maintaining a multi-set
CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 1. Problem 13-1 (persistent dynamic sets).. Problem 13-3 (AVL trees) 3. In this problem we consider a data structure for maintaining a multi-set
Trees. Eric McCreath
 Trees Eric McCreath 2 Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 3 Trees Trees are recursive data structures. They are useful for:
Trees Eric McCreath 2 Overview In this lecture we will explore: general trees, binary trees, binary search trees, and AVL and B-Trees. 3 Trees Trees are recursive data structures. They are useful for:
Sorted Arrays. Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min
 Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees FRIDAY ALGORITHMS Sorted Arrays Operation Access Search Selection Predecessor Successor Output (print) Insert Delete Extract-Min 6 10 11 17 2 0 6 Running Time O(1) O(lg n) O(1) O(1)
Binary Search Trees, etc.
 Chapter 12 Binary Search Trees, etc. Binary Search trees are data structures that support a variety of dynamic set operations, e.g., Search, Minimum, Maximum, Predecessors, Successors, Insert, and Delete.
Chapter 12 Binary Search Trees, etc. Binary Search trees are data structures that support a variety of dynamic set operations, e.g., Search, Minimum, Maximum, Predecessors, Successors, Insert, and Delete.
Search Trees - 1 Venkatanatha Sarma Y
 Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Search Trees - 1 Lecture delivered by: Venkatanatha Sarma Y Assistant Professor MSRSAS-Bangalore 11 Objectives To introduce, discuss and analyse the different ways to realise balanced Binary Search Trees
Algorithms. Red-Black Trees
 Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Algorithms Red-Black Trees Red-Black Trees Balanced binary search trees guarantee an O(log n) running time Red-black-tree Binary search tree with an additional attribute for its nodes: color which can
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Properties of red-black trees
 Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-Black Trees Introduction We have seen that a binary search tree is a useful tool. I.e., if its height is h, then we can implement any basic operation on it in O(h) units of time. The problem: given
Red-black trees (19.5), B-trees (19.8), trees
 Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
Red-black trees (19.5), B-trees (19.8), 2-3-4 trees Red-black trees A red-black tree is a balanced BST It has a more complicated invariant than an AVL tree: Each node is coloured red or black A red node
CS 206 Introduction to Computer Science II
 CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
CS 206 Introduction to Computer Science II 04 / 26 / 2017 Instructor: Michael Eckmann Today s Topics Questions? Comments? Balanced Binary Search trees AVL trees Michael Eckmann - Skidmore College - CS
COMP Analysis of Algorithms & Data Structures
 COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
COMP 3170 - Analysis of Algorithms & Data Structures Shahin Kamali Binary Search Trees CLRS 12.2, 12.3, 13.2, read problem 13-3 University of Manitoba COMP 3170 - Analysis of Algorithms & Data Structures
Graduate Algorithms CS F-07 Red/Black Trees
 Graduate Algorithms CS673-2016F-07 Red/lack Trees David Galles Department of Computer Science University of San Francisco 07-0: inary Search Trees inary Trees For each node n, (value stored at node n)
Graduate Algorithms CS673-2016F-07 Red/lack Trees David Galles Department of Computer Science University of San Francisco 07-0: inary Search Trees inary Trees For each node n, (value stored at node n)
COMP251: Red-black trees
 COMP251: Red-black trees Jérôme Waldispühl School of Computer Science McGill University Based on (Cormen et al., 2002) Based on slides from D. Plaisted (UNC) The running Rme of inserrons in BST trees with
COMP251: Red-black trees Jérôme Waldispühl School of Computer Science McGill University Based on (Cormen et al., 2002) Based on slides from D. Plaisted (UNC) The running Rme of inserrons in BST trees with
Red-Black, Splay and Huffman Trees
 Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Red-Black, Splay and Huffman Trees Kuan-Yu Chen ( 陳冠宇 ) 2018/10/22 @ TR-212, NTUST AVL Trees Review Self-balancing binary search tree Balance Factor Every node has a balance factor of 1, 0, or 1 2 Red-Black
Uses for Trees About Trees Binary Trees. Trees. Seth Long. January 31, 2010
 Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
Uses for About Binary January 31, 2010 Uses for About Binary Uses for Uses for About Basic Idea Implementing Binary Example: Expression Binary Search Uses for Uses for About Binary Uses for Storage Binary
CS102 Binary Search Trees
 CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
CS102 Binary Search Trees Prof Tejada 1 To speed up insertion, removal and search, modify the idea of a Binary Tree to create a Binary Search Tree (BST) Binary Search Trees Binary Search Trees have one
We will show that the height of a RB tree on n vertices is approximately 2*log n. In class I presented a simple structural proof of this claim:
 We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
We have seen that the insert operation on a RB takes an amount of time proportional to the number of the levels of the tree (since the additional operations required to do any rebalancing require constant
Advanced Set Representation Methods
 Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Advanced Set Representation Methods AVL trees. 2-3(-4) Trees. Union-Find Set ADT DSA - lecture 4 - T.U.Cluj-Napoca - M. Joldos 1 Advanced Set Representation. AVL Trees Problem with BSTs: worst case operation
Binary Heaps in Dynamic Arrays
 Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Yufei Tao ITEE University of Queensland We have already learned that the binary heap serves as an efficient implementation of a priority queue. Our previous discussion was based on pointers (for getting
Note that this is a rep invariant! The type system doesn t enforce this but you need it to be true. Should use repok to check in debug version.
 Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Announcements: Prelim tonight! 7:30-9:00 in Thurston 203/205 o Handed back in section tomorrow o If you have a conflict you can take the exam at 5:45 but can t leave early. Please email me so we have a
Balanced Search Trees. CS 3110 Fall 2010
 Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Balanced Search Trees CS 3110 Fall 2010 Some Search Structures Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Ch04 Balanced Search Trees
 Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
Presentation for use with the textbook Algorithm Design and Applications, by M. T. Goodrich and R. Tamassia, Wiley, 05 Ch0 Balanced Search Trees v 3 8 z Why care about advanced implementations? Same entries,
BINARY SEARCH TREES cs2420 Introduction to Algorithms and Data Structures Spring 2015
 BINARY SEARCH TREES cs2420 Introduction to Algorithms and Data Structures Spring 2015 1 administrivia 2 -assignment 7 due tonight at midnight -asking for regrades through assignment 5 and midterm must
BINARY SEARCH TREES cs2420 Introduction to Algorithms and Data Structures Spring 2015 1 administrivia 2 -assignment 7 due tonight at midnight -asking for regrades through assignment 5 and midterm must
TREES. Trees - Introduction
 TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
TREES Chapter 6 Trees - Introduction All previous data organizations we've studied are linear each element can have only one predecessor and successor Accessing all elements in a linear sequence is O(n)
Data Structures in Java
 Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Data Structures in Java Lecture 10: AVL Trees. 10/1/015 Daniel Bauer Balanced BSTs Balance condition: Guarantee that the BST is always close to a complete binary tree (every node has exactly two or zero
Chapter 13. Michelle Bodnar, Andrew Lohr. April 12, 2016
 Chapter 13 Michelle Bodnar, Andrew Lohr April 1, 016 Exercise 13.1-1 8 4 1 6 10 14 1 3 5 7 9 11 13 15 We shorten IL to so that it can be more easily displayed in the document. The following has black height.
Chapter 13 Michelle Bodnar, Andrew Lohr April 1, 016 Exercise 13.1-1 8 4 1 6 10 14 1 3 5 7 9 11 13 15 We shorten IL to so that it can be more easily displayed in the document. The following has black height.
Balanced search trees
 Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Balanced search trees Ordinary binary search trees have expected height Θ(log n) if items are inserted and deleted in random order, but for other orders the height can be Θ(n). This is undesirable, since
Search Trees. Undirected graph Directed graph Tree Binary search tree
 Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Search Trees Undirected graph Directed graph Tree Binary search tree 1 Binary Search Tree Binary search key property: Let x be a node in a binary search tree. If y is a node in the left subtree of x, then
Section 4 SOLUTION: AVL Trees & B-Trees
 Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Section 4 SOLUTION: AVL Trees & B-Trees 1. What 3 properties must an AVL tree have? a. Be a binary tree b. Have Binary Search Tree ordering property (left children < parent, right children > parent) c.
Quiz 1 Solutions. (a) f(n) = n g(n) = log n Circle all that apply: f = O(g) f = Θ(g) f = Ω(g)
 Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Solutions Problem 1. Quiz 1 Solutions Asymptotic orders
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Solutions Problem 1. Quiz 1 Solutions Asymptotic orders
Search Trees: BSTs and B-Trees
 3//13 Search Trees: BSTs and B-Trees Administrative David Kauchak cs302 Spring 13 Proof by contradiction Number guessing game I m thinking of a number between 1 and n You are trying to guess the answer
3//13 Search Trees: BSTs and B-Trees Administrative David Kauchak cs302 Spring 13 Proof by contradiction Number guessing game I m thinking of a number between 1 and n You are trying to guess the answer
CS 380 ALGORITHM DESIGN AND ANALYSIS
 CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
CS 380 ALGORITHM DESIGN AND ANALYSIS Lecture 12: Red-Black Trees Text Reference: Chapters 12, 13 Binary Search Trees (BST): Review Each node in tree T is a object x Contains attributes: Data Pointers to
CSci 231 Homework 7. Red Black Trees. CLRS Chapter 13 and 14
 CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 Choose 4 problems from the list below. 1. (CLRS 13.1-6) What is the largest possible number of internal nodes in a red-black tree with black-height
CSci 31 Homework 7 Red Black Trees CLRS Chapter 13 and 14 Choose 4 problems from the list below. 1. (CLRS 13.1-6) What is the largest possible number of internal nodes in a red-black tree with black-height
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Binary Search Tree - Best Time All BST operations are O(d), where d is tree depth minimum d is d = ëlog for a binary tree
Trees. (Trees) Data Structures and Programming Spring / 28
 Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
Trees (Trees) Data Structures and Programming Spring 2018 1 / 28 Trees A tree is a collection of nodes, which can be empty (recursive definition) If not empty, a tree consists of a distinguished node r
CS60020: Foundations of Algorithm Design and Machine Learning. Sourangshu Bhattacharya
 CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CS62: Foundations of Algorithm Design and Machine Learning Sourangshu Bhattacharya Balanced search trees Balanced search tree: A search-tree data structure for which a height of O(lg n) is guaranteed when
CMPS 2200 Fall 2017 Red-black trees Carola Wenk
 CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
CMPS 2200 Fall 2017 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with changes by Carola Wenk 9/13/17 CMPS 2200 Intro. to Algorithms 1 Dynamic Set A dynamic set, or dictionary, is a
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1
 Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Quiz 1 Do not open this quiz booklet until directed to
Introduction to Algorithms March 11, 2009 Massachusetts Institute of Technology 6.006 Spring 2009 Professors Sivan Toledo and Alan Edelman Quiz 1 Quiz 1 Do not open this quiz booklet until directed to
8. Binary Search Tree
 8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
8 Binary Search Tree Searching Basic Search Sequential Search : Unordered Lists Binary Search : Ordered Lists Tree Search Binary Search Tree Balanced Search Trees (Skipped) Sequential Search int Seq-Search
10/23/2013. AVL Trees. Height of an AVL Tree. Height of an AVL Tree. AVL Trees
 // AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
// AVL Trees AVL Trees An AVL tree is a binary search tree with a balance condition. AVL is named for its inventors: Adel son-vel skii and Landis AVL tree approximates the ideal tree (completely balanced
Binary Tree. Preview. Binary Tree. Binary Tree. Binary Search Tree 10/2/2017. Binary Tree
 0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
0/2/ Preview Binary Tree Tree Binary Tree Property functions In-order walk Pre-order walk Post-order walk Search Tree Insert an element to the Tree Delete an element form the Tree A binary tree is a tree
Trees. Reading: Weiss, Chapter 4. Cpt S 223, Fall 2007 Copyright: Washington State University
 Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Trees Reading: Weiss, Chapter 4 1 Generic Rooted Trees 2 Terms Node, Edge Internal node Root Leaf Child Sibling Descendant Ancestor 3 Tree Representations n-ary trees Each internal node can have at most
Binary Search Trees. Analysis of Algorithms
 Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
Binary Search Trees Analysis of Algorithms Binary Search Trees A BST is a binary tree in symmetric order 31 Each node has a key and every node s key is: 19 23 25 35 38 40 larger than all keys in its left
2-3 Tree. Outline B-TREE. catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } ADD SLIDES ON DISJOINT SETS
 Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
Outline catch(...){ printf( "Assignment::SolveProblem() AAAA!"); } Balanced Search Trees 2-3 Trees 2-3-4 Trees Slide 4 Why care about advanced implementations? Same entries, different insertion sequence:
1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1
![1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1](/thumbs/80/82301067.jpg) Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. O(logn) 2. O(n) 3. O(nlogn) 4. O(n 2 ) 5. O(2 n ) 2. [1 pt] What is the solution
Asymptotics, Recurrence and Basic Algorithms 1. [1 pt] What is the solution to the recurrence T(n) = 2T(n-1) + 1, T(1) = 1 1. O(logn) 2. O(n) 3. O(nlogn) 4. O(n 2 ) 5. O(2 n ) 2. [1 pt] What is the solution
Multi-way Search Trees! M-Way Search! M-Way Search Trees Representation!
 Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Lecture 10: Multi-way Search Trees: intro to B-trees 2-3 trees 2-3-4 trees Multi-way Search Trees A node on an M-way search tree with M 1 distinct and ordered keys: k 1 < k 2 < k 3
Binary Trees, Binary Search Trees
 Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Binary Trees, Binary Search Trees Trees Linear access time of linked lists is prohibitive Does there exist any simple data structure for which the running time of most operations (search, insert, delete)
Solutions. Suppose we insert all elements of U into the table, and let n(b) be the number of elements of U that hash to bucket b. Then.
 Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Assignment 3 1. Exercise [11.2-3 on p. 229] Modify hashing by chaining (i.e., bucketvector with BucketType = List) so that BucketType = OrderedList. How is the runtime of search, insert, and remove affected?
Data Structures and Algorithms
 Data Structures and Algorithms Searching Red-Black and Other Dynamically BalancedTrees PLSD210 Searching - Re-visited Binary tree O(log n) if it stays balanced Simple binary tree good for static collections
Data Structures and Algorithms Searching Red-Black and Other Dynamically BalancedTrees PLSD210 Searching - Re-visited Binary tree O(log n) if it stays balanced Simple binary tree good for static collections
CS 3343 Fall 2007 Red-black trees Carola Wenk
 CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
CS 3343 Fall 2007 Red-black trees Carola Wenk Slides courtesy of Charles Leiserson with small changes by Carola Wenk CS 334 Analysis of Algorithms 1 Search Trees A binary search tree is a binary tree.
Dynamic Access Binary Search Trees
 Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
Dynamic Access Binary Search Trees 1 * are self-adjusting binary search trees in which the shape of the tree is changed based upon the accesses performed upon the elements. When an element of a splay tree
AVL Trees. (AVL Trees) Data Structures and Programming Spring / 17
 AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees (AVL Trees) Data Structures and Programming Spring 2017 1 / 17 Balanced Binary Tree The disadvantage of a binary search tree is that its height can be as large as N-1 This means that the time
AVL Trees / Slide 2. AVL Trees / Slide 4. Let N h be the minimum number of nodes in an AVL tree of height h. AVL Trees / Slide 6
 COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
COMP11 Spring 008 AVL Trees / Slide Balanced Binary Search Tree AVL-Trees Worst case height of binary search tree: N-1 Insertion, deletion can be O(N) in the worst case We want a binary search tree with
Balanced BST. Balanced BSTs guarantee O(logN) performance at all times
 Balanced BST Balanced BSTs guarantee O(logN) performance at all times the height or left and right sub-trees are about the same simple BST are O(N) in the worst case Categories of BSTs AVL, SPLAY trees:
Balanced BST Balanced BSTs guarantee O(logN) performance at all times the height or left and right sub-trees are about the same simple BST are O(N) in the worst case Categories of BSTs AVL, SPLAY trees:
Some Search Structures. Balanced Search Trees. Binary Search Trees. A Binary Search Tree. Review Binary Search Trees
 Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Some Search Structures Balanced Search Trees Lecture 8 CS Fall Sorted Arrays Advantages Search in O(log n) time (binary search) Disadvantages Need to know size in advance Insertion, deletion O(n) need
Module 4: Dictionaries and Balanced Search Trees
 Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
Module 4: Dictionaries and Balanced Search Trees CS 24 - Data Structures and Data Management Jason Hinek and Arne Storjohann Based on lecture notes by R. Dorrigiv and D. Roche David R. Cheriton School
ECE 242 Data Structures and Algorithms. Trees IV. Lecture 21. Prof.
 ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
ECE 22 Data Structures and Algorithms http://www.ecs.umass.edu/~polizzi/teaching/ece22/ Trees IV Lecture 2 Prof. Eric Polizzi Summary previous lectures Implementations BST 5 5 7 null 8 null null 7 null
Data Structures and Algorithms for Engineers
 04-630 Data Structures and Algorithms for Engineers David Vernon Carnegie Mellon University Africa vernon@cmu.edu www.vernon.eu Data Structures and Algorithms for Engineers 1 Carnegie Mellon University
04-630 Data Structures and Algorithms for Engineers David Vernon Carnegie Mellon University Africa vernon@cmu.edu www.vernon.eu Data Structures and Algorithms for Engineers 1 Carnegie Mellon University
CSE 332, Spring 2010, Midterm Examination 30 April 2010
 CSE 332, Spring 2010, Midterm Examination 30 April 2010 Please do not turn the page until the bell rings. Rules: The exam is closed-book, closed-note. You may use a calculator for basic arithmetic only.
CSE 332, Spring 2010, Midterm Examination 30 April 2010 Please do not turn the page until the bell rings. Rules: The exam is closed-book, closed-note. You may use a calculator for basic arithmetic only.
13.4 Deletion in red-black trees
 Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Deletion in a red-black tree is similar to insertion. Apply the deletion algorithm for binary search trees. Apply node color changes and left/right rotations to fix the violations of RBT tree properties.
Lecture 5. Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs
 Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
Lecture 5 Treaps Find, insert, delete, split, and join in treaps Randomized search trees Randomized search tree time costs Reading: Randomized Search Trees by Aragon & Seidel, Algorithmica 1996, http://sims.berkeley.edu/~aragon/pubs/rst96.pdf;
ICS 691: Advanced Data Structures Spring Lecture 3
 ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
ICS 691: Advanced Data Structures Spring 2016 Prof. Nodari Sitchinava Lecture 3 Scribe: Ben Karsin 1 Overview In the last lecture we started looking at self-adjusting data structures, specifically, move-to-front
DATA STRUCTURES AND ALGORITHMS. Hierarchical data structures: AVL tree, Bayer tree, Heap
 DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
DATA STRUCTURES AND ALGORITHMS Hierarchical data structures: AVL tree, Bayer tree, Heap Summary of the previous lecture TREE is hierarchical (non linear) data structure Binary trees Definitions Full tree,
Data Structures and Algorithms
 Data Structures and Algorithms CS245-2008S-19 B-Trees David Galles Department of Computer Science University of San Francisco 19-0: Indexing Operations: Add an element Remove an element Find an element,
Data Structures and Algorithms CS245-2008S-19 B-Trees David Galles Department of Computer Science University of San Francisco 19-0: Indexing Operations: Add an element Remove an element Find an element,
Binary Search Tree: Balanced. Data Structures and Algorithms Emory University Jinho D. Choi
 Binary Search Tree: Balanced Data Structures and Algorithms Emory University Jinho D. Choi Binary Search Tree Worst-case Complexity Search Insert Delete Unbalanced O(n) O(n) O(n) + α Balanced O(log n)
Binary Search Tree: Balanced Data Structures and Algorithms Emory University Jinho D. Choi Binary Search Tree Worst-case Complexity Search Insert Delete Unbalanced O(n) O(n) O(n) + α Balanced O(log n)
Algorithms. Deleting from Red-Black Trees B-Trees
 Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Algorithms Deleting from Red-Black Trees B-Trees Recall the rules for BST deletion 1. If vertex to be deleted is a leaf, just delete it. 2. If vertex to be deleted has just one child, replace it with that
Red-Black Trees. Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood
 Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
Red-Black Trees Based on materials by Dennis Frey, Yun Peng, Jian Chen, and Daniel Hood Quick Review of Binary Search Trees n Given a node n... q All elements of n s left subtree are less than n.data q
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/27/17
 01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
01.433/33 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Priority Queues / Heaps Date: 9/2/1.1 Introduction In this lecture we ll talk about a useful abstraction, priority queues, which are
B-Trees. Version of October 2, B-Trees Version of October 2, / 22
 B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
B-Trees Version of October 2, 2014 B-Trees Version of October 2, 2014 1 / 22 Motivation An AVL tree can be an excellent data structure for implementing dictionary search, insertion and deletion Each operation
CSCI2100B Data Structures Heaps
 CSCI2100B Data Structures Heaps Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction In some applications,
CSCI2100B Data Structures Heaps Irwin King king@cse.cuhk.edu.hk http://www.cse.cuhk.edu.hk/~king Department of Computer Science & Engineering The Chinese University of Hong Kong Introduction In some applications,
9/29/2016. Chapter 4 Trees. Introduction. Terminology. Terminology. Terminology. Terminology
 Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Introduction Chapter 4 Trees for large input, even linear access time may be prohibitive we need data structures that exhibit average running times closer to O(log N) binary search tree 2 Terminology recursive
Algorithms in Systems Engineering ISE 172. Lecture 16. Dr. Ted Ralphs
 Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
Algorithms in Systems Engineering ISE 172 Lecture 16 Dr. Ted Ralphs ISE 172 Lecture 16 1 References for Today s Lecture Required reading Sections 6.5-6.7 References CLRS Chapter 22 R. Sedgewick, Algorithms
