Stochastic Submodular Maximization: The Case of Coverage Functions
|
|
|
- Meghan Burns
- 5 years ago
- Views:
Transcription
1 Stochastic Submodular Maximization: The Case of Coverage Functions Mohammad Reza Karimi Department of Computer Science ETH Zurich Mario Lucic Department of Computer Science ETH Zurich Hamed Hassani Department of Electrical and Systems Engineering University of Pennsylvania Andreas Krause Department of Computer Science ETH Zurich Abstract Stochastic optimization of continuous objectives is at the heart of modern machine learning. However, many important problems are of discrete nature and often involve submodular objectives. We seek to unleash the power of stochastic continuous optimization, namely stochastic gradient descent and its variants, to such discrete problems. We first introduce the problem of stochastic submodular optimization, where one needs to optimize a submodular objective which is given as an expectation. Our model captures situations where the discrete objective arises as an empirical risk (e.g., in the case of exemplar-based clustering), or is given as an explicit stochastic model (e.g., in the case of influence maximization in social networks). By exploiting that common extensions act linearly on the class of submodular functions, we employ projected stochastic gradient ascent and its variants in the continuous domain, and perform rounding to obtain discrete solutions. We focus on the rich and widely used family of weighted coverage functions. We show that our approach yields solutions that are guaranteed to match the optimal approximation guarantees, while reducing the computational cost by several orders of magnitude, as we demonstrate empirically. 1 Introduction Submodular functions are discrete analogs of convex functions. They arise naturally in many areas, such as the study of graphs, matroids, covering problems, and facility location problems. These functions are extensively studied in operations research and combinatorial optimization [22]. Recently, submodular functions have proven to be key concepts in other areas such as machine learning, algorithmic game theory, and social sciences. As such, they have been applied to a host of important problems such as modeling valuation functions in combinatorial auctions, feature and variable selection [23], data summarization [27], and influence maximization [20]. Classical results in submodular optimization consider the oracle model whereby the access to the optimization objective is provided through a black box an oracle. However, in many applications, the objective has to be estimated from data and is subject to stochastic fluctuations. In other cases the value of the objective may only be obtained through simulation. As such, the exact computation might not be feasible due to statistical or computational constraints. As a concrete example, consider the problem of influence maximization in social networks [20]. The objective function is defined as the expectation of a stochastic process, quantifying the size of the (random) subset of nodes 31st Conference on Neural Information Processing Systems (NIPS 2017), Long Beach, CA, USA.
2 influenced from a selected seed set. This expectation cannot be computed efficiently, and is typically approximated via random sampling, which introduces an error in the estimate of the value of a seed set. Another practical example is the exemplar-based clustering problem, which is an instance of the facility location problem. Here, the objective is the sum of similarities of all the points inside a (large) collection of data points to a selected set of centers. Given a distribution over point locations, the true objective is defined as the expected value w.r.t. this distribution, and can only be approximated as a sample average. Moreover, evaluating the function on a sample involves computation of many pairwise similarities, which is computationally prohibitive in the context of massive data sets. In this work, we provide a formalization of such stochastic submodular maximization tasks. More precisely, we consider set functions f :2 V! R +, defined as f(s) =E [f (S)] for S V, where is an arbitrary distribution and for each realization, the set function f :2 V! R + is monotone and submodular (hence f is monotone submodular). The goal is to maximize f subject to some constraints (e.g. the k-cardinality constraint) having access only to i.i.d. samples f ( ). Methods for submodular maximization fall into two major categories: (i) The classic approach is to directly optimize the objective using discrete optimization methods (e.g. the GREEDY algorithm and its accelerated variants), which are state-of-the-art algorithms (both in practice and theory), at least in the case of simple constraints, and are most widely considered in the literature; (ii) The alternative is to lift the problem into a continuous domain and exploit continuous optimization techniques available therein [7]. While the continuous approaches may lead to provably good results, even for more complex constraints, their high computational complexity inhibits their practicality. In this paper we demonstrate how modern stochastic optimization techniques (such as SGD, ADA- GRAD [8] and ADAM [21]), can be used to solve an important class of discrete optimization problems which can be modeled using weighted coverage functions. In particular, we show how to efficiently maximize them under matroid constraints by (i) lifting the problem into the continuous domain using the multilinear extension [37], (ii) efficiently computing a concave relaxation of the multilinear extension [32], (iii) efficiently computing an unbiased estimate of the gradient for the concave relaxation thus enabling (projected) stochastic gradient ascent-style algorithms to maximize the concave relaxation, and (iv) rounding the resulting fractional solution without loss of approximation quality [7]. In addition to providing convergence and approximation guarantees, we demonstrate that our algorithms enjoy strong empirical performance, often achieving an order of magnitude speedup with less than 1% error with respect to GREEDY. As a result, the presented approach unleashes the powerful toolkit of stochastic gradient based approaches to discrete optimization problems. Our contributions. In this paper we (i) introduce a framework for stochastic submodular optimization, (ii) provide a general methodology for constrained maximization of stochastic submodular objectives, (iii) prove that the proposed approach guarantees a (1 1/e) approximation in expectation for the class of weighted coverage functions, which is the best approximation guarantee achievable in polynomial time unless P = NP, (iv) highlight the practical benefit and efficiency of using continuous-based stochastic optimization techniques for submodular maximization, (v) demonstrate the practical utility of the proposed framework in an extensive experimental evaluation. We show for the first time that continuous optimization is a highly practical, scalable avenue for maximizing submodular set functions. 2 Background and problem formulation Let V be a ground set of n elements. A set function f :2 V! R + is submodular if for every A, B V, it holds f(a)+f(b) f(a \ B)+f(A [ B). Function f is said to be monotone if f(a) apple f(b) for all A B V. We focus on maximizing f subject to some constraints on S V. The prototypical example is maximization under the cardinality constraint, i.e., for a given integer k, find S V, S applek, which maximizes f. Finding an exact solution for monotone submodular functions is NP-hard [10], but a (1 1/e)-approximation can be efficiently determined [30]. Going beyond the (1 1/e)-approximation is NP-hard for many classes of submodular functions [30, 24]. More generally, one may consider matroid constraints, whereby (V,I) is a matroid with the family of independent sets I, and maximize f such that S 2I. The GREEDY algorithm achieves a 1/2- approximation [13], but CONTINUOUS GREEDY introduced by Vondrák [37], Calinescu et al. [6] can achieve a (1 1/e)-optimal solution in expectation. Their approach is based on the multilinear 2
3 extension of f, F :[0, 1] V! R +, defined as F (x) = X S V f(s) Y i2s Y x i (1 x j ), (1) for all x = (x 1,,x n ) 2 [0, 1] V. In other words, F (x) is the expected value of of f over sets wherein each element i is included with probability x i independently. Then, instead of optimizing f(s) over I, we can optimize F over the matroid base polytope corresponding to (V,I): P = {x 2 R n + x(s) apple r(s), 8S V,x(V ) = r(v )}, where r( ) is the matroid s rank function. The CONTINUOUS GREEDY algorithm then finds a solution x 2Pwhich provides a (1 1/e) approximation. Finally, the continuous solution x is then efficiently rounded to a feasible discrete solution without loss in objective value, using PIPAGE ROUNDING [1, 6]. The idea of converting a discrete optimization problem into a continuous one was first exploited by Lovász [28] in the context of submodular minimization and this approach was recently applied to a variety of problems [36, 19, 3]. Problem formulation. The aforementioned results are based on the oracle model, whereby the exact value of f(s) for any S V is given by an oracle. In absence of such an oracle, we face the additional challenges of evaluating f, both statistical and computational. In particular, consider set functions that are defined as expectations, i.e. for S V we have j/2s f(s) =E [f (S)], (2) where is an arbitrary distribution and for each realization, the set function f :2 V! R is submodular. The goal is to efficiently maximize f subject to constraints such as the k-cardinality constraint, or more generally, a matroid constraint. As a motivating example, consider the problem of propagation of contagions through a network. The objective is to identify the most influential seed set of a given size. A propagation instance (concrete realization of a contagion) is specified by a graph G =(V,E). The influence f G (S) of a set of nodes S in instance G is the fraction of nodes reachable from S using the edges E. To handle uncertainties in the concrete realization, it is natural to introduce a probabilistic model such as the Independent Cascade [20] model which defines a distribution G over instances G Gthat share a set V of nodes. The influence of a seed set S is then the expectation f(s) =E G G [f G (S)], which is a monotone submodular function. Hence, estimating the expected influence is computationally demanding, as it requires summing over exponentially many functions f G. Assuming f as in (2), one can easily obtain an unbiased estimate of f for a fixed set S by random sampling according to. The critical question is, given that the underlying function is an expectation, can we optimize it more efficiently? Our approach is based on continuous extensions that are linear operators on the class of set functions, namely, linear continuous extensions. As a specific example, considering the multilinear extension, we can write F (x) =E [F (x)], where F denotes the extension of f. As a consequence, the value of F (x), when, is an unbiased estimator for F (x) and unbiased estimates of the (sub)gradients may be obtained analogously. We explore this avenue to develop efficient algorithms for maximizing an important subclass of submodular functions that can be expressed as weighted coverage functions. Our approach harnesses a concave relaxation detailed in Section 3. Further related work. The emergence of new applications, combined with a massive increase in the amount of data has created a demand for fast algorithms for submodular optimization. A variety of approximation algorithms have been presented, ranging from submodular maximization subject to a cardinality constraint [29, 39, 4], submodular maximization subject to a matroid constraint [6], non-monotone submodular maximization [11], approximately submodular functions [17], and algorithms for submodular maximization subject to a wide variety of constraints [25, 12, 38, 18, 9]. A closely related setting to ours is online submodular maximization [35], where functions come one at a time and the goal is to provide time-dependent solutions (sets) such that a cumulative regret is minimized. In contrast, our goal is to find a single (time-independent) set that maximizes the objective (2). Another relevant setting is noisy submodular maximization, where the evaluations returned by the oracle are noisy [16, 34]. Specifically, [34] assumes a noisy but unbiased oracle (with an independent sub-gaussian noise) which allows one to sufficiently estimate the marginal gains of items by averaging. In the context of cardinality constraints, some of these ideas can be carried to our setting by introducing additional assumptions on how the values f (S) vary w.r.t. to their expectation f(s). However, we provide a different approach that does not rely on uniform convergence and compare sample and running time complexity comparison with variants of GREEDY in Section 3. 3
4 3 Stochastic Submodular Optimization We follow the general framework of [37] whereby the problem is lifted into the continuous domain, a continuous optimization algorithm is designed to maximize the transferred objective, and the resulting solution is rounded. Maximizing f subject to a matroid constraint can then be done by first maximizing its multilinear extension F over the matroid base polytope and then rounding the solution. Methods such as the projected stochastic gradient ascent can be used to maximize F over this polytope. Critically, we have to assure that the computed local optima are good in expectation. Unfortunately, the multilinear extension F lacks concavity and therefore may have bad local optima. Hence, we consider concave continuous extensions of F that are efficiently computable, and at most a constant factor away from F to ensure solution quality. As a result, such a concave extension F could then be efficiently maximized over a polytope using projected stochastic gradient ascent which would enable the application of modern continuous optimization techniques. One class of important functions for which such an extension can be efficiently computed is the class of weighted coverage functions. The class of weighted coverage functions (WCF). Let U be a set and let g be a nonnegative modular function on U, i.e. g(s) = P u2s w(u), S U. Let V = {B 1,...,B n } be a collection of subsets of U. The weighted coverage function f :2 V! R + defined as 8S V : f(s) =g S B i2s B i is monotone submodular. For all u 2 U, let us denote by P u := {B i 2 V u 2 B i } and by I( ) the indicator function. The multilinear extension of f can be expressed in a more compact way: X F (x) =E S [f(s)] = E S I(u 2 B i for some B i 2 S) w(u) = X u2u u2u w(u) P(u 2 B i for some B i 2 S) = X w(u) 1 u2u where we used the fact that each element B i 2 V was chosen with probability x i. Q B i2p u (1 x i ) Concave upper bound for weighted coverage functions. To efficiently compute a concave upper bound on the multilinear extension we use the framework of Seeman and Singer [32]. Given that all the weights w(u), u 2 U in (3) are non-negative, we can construct a concave upper bound for the multilinear extension F (x) using the following Lemma. Proofs can be found in the Appendix A. Q` Lemma 1. For x 2 [0, 1]` n define (x) :=1 i=1 (1 x i). Then the Fenchel concave biconjugate of ( ) is (x) :=min 1, P` o i=1 x i. Also (1 1/e) (x) apple (x) apple (x) 8x 2 [0, 1]`. Furthermore, is an extension of, i.e. 8x 2{0, 1}`: (x) = (x). Consequently, given a weighted coverage function f with F (x) represented as in (3), we can define F (x) := X X w(u)min 1, x v (4) u2u B v2p u and conclude using Lemma 1 that (1 1/e) F (x) apple F (x) apple F (x), as desired. Furthermore, F has three interesting properties: (1) It is a concave function over [0, 1] V, (2) it is equal to f on vertices of the hypercube, i.e. for x 2{0, 1} n one has F (x) =f({i : x i =1}), and (3) it can be computed efficiently and deterministically given access to the sets P u, u 2 U. In other words, we can compute the value of F (x) using at most O( U V ) operations. Note that F is not the tightest concave upper bound of F, even though we use the tightest concave upper bounds for each term of F. Optimizing the concave upper bound by stochastic gradient ascent. Instead of maximizing F over a polytope P, one can now attempt to maximize F over P. Critically, this task can be done efficiently, as F is concave, by using projected stochastic gradient ascent. In particular, one can (3) 4
5 Algorithm 1 Stochastic Submodular Maximization via concave relaxation Require: matroid M with base polytope P, t (step size), T (maximum # of iterations) 1: x (0) starting point in P 2: for t 0 to T 1 do 3: Choose g t at random from a distribution such that E[g t x (0),...,x (t) ] F (x (t) ) 4: x (t+1/2) x (t) + t g t 5: x (t+1) Project P (x (t+1/2) ) 6: end for P 1 T 7: x T T t=1 x(t) 8: S RANDOMIZED-PIPAGE-ROUND( x T ) 9: return S such that S 2M, E[f(S)] (1 1/e)f(OP T) "(T ). control the convergence speed by choosing from the toolbox of modern continuous optimization algorithms, such as SGD, ADAGRAD and ADAM. Let us denote a maximizer of F over P by x, and also a maximizer of F over P by x. We can thus write F ( x ) (1 1/e) F ( x ) (1 1/e) F (x ) (1 1/e)F (x ), which is the exact guarantee that previous methods give, and in general is the best near-optimality ratio that one can give in poly-time. Finally, to round the continuous solution we may apply RANDOMIZED- PIPAGE-ROUNDING [7] as the quality of the approximation is preserved in expectation. Matroid constraints. Constrained optimization can be efficiently performed by projected gradient ascent whereby after each step of the stochastic ascent, we need to project the solution back onto the feasible set. For the case of matroid constraints, it is sufficient to consider projection onto the matroid base polytope. This problem of projecting on the base polytope has been widely studied and fast algorithms exist in many cases [2, 5, 31]. While these projection algorithms were used as a key subprocedure in constrained submodular minimization, here we consider them for submodular maximization. Details of a fast projection algorithm for the problems considered in this work are presented the Appendix D. Algorithm 1 summarizes all steps required to maximize f subject to matroid constraints. Convergence rate. Since we are maximizing a concave function F ( ) over a matroid base polytope P, convergence rate (and hence running time) depends on B := max x2p x, as well as maximum gradient norm (i.e. g t apple with probability 1). 1 In the case of the base polytope for a matroid of rank r, B is p r, since each vertex of the polytope has exactly r ones. Also, from (4), one can build a rough upper bound for the norm of the gradient: g apple P u2u w(u)1 P u apple max P u 1/2 X w(u), u2u u2u which depends on the weights w(u) as well as P u and is hence problem-dependent. We will provide tighter upper bounds for gradient norm in our specific examples in the later sections. With t = B/ p t, and classic results for SGD [33], we have that F (x ) E[ F ( x T )] apple B / p T, where T is the total number of SGD iterations and x T is the final outcome of SGD (see Algorithm 1). Therefore, for a given ">0, after T B 2 2 /" 2 iterations, we have F (x ) E[ F ( x T )] apple ". Summing up, we will have the following theorem: Theorem 2. Let f be a weighted coverage function, P be the base polytope of a matroid M, and and B be as above. Then for each >0, Algorithm 1 after T = B 2 2 /" 2 iterations, produces a set S 2Msuch that E[f(S )] (1 1/e) max S2M f(s) ". 1 Note that the function F is neither smooth nor strongly concave as functions such as min{1,x} are not smooth or strongly concave. 5
6 Remark. Indeed this approximation ratio is the best ratio one can achieve, unless P=NP [10]. A key point to make here is that our approach also works for more general constraints (in particular is efficient for simple matroids such as partition matroids). In the latter case, GREEDY only gives 1 2-approximation and fast discrete methods like STOCHASTIC-GREEDY [29] do not apply, whereas our method still yields an (1 1/e)-optimal solution. Time Complexity. One can compute an upper bound for the running time of Algorithm 1 by estimating the time required to perform gradient computations, projection on P, and rounding. For the case of uniform matroids, projection and rounding take O(n log n) and O(n) time, respectively (see Appendix D). Furthermore, for the applications considered in this work, namely expected influence maximization and exemplar-based clustering, we provide linear time algorithms to compute the gradients. Also when our matroid is the k-uniform matroid (i.e. k-cardinality constraint), we have B = p k. By Theorem 2, the total computational complexity of our algorithm is O( 2 kn(log n)/" 2 ). Comparison to GREEDY. Let us relate our results to the classical approach. When running the GREEDY algorithm in the stochastic setting, one estimates ˆf(S) := 1 P s s i=1 f (S) where i 1,..., s are i.i.d. samples from. The following proposition bounds the sample and computational complexity of GREEDY. The proof is detailed in the Appendix B. Proposition 3. Let f be a submodular function defined as (2). Suppose 0 apple f (S) apple H for all S V and all. Assume S denotes the optimal solution for f subject to k-cardinality constraint and S k denotes the solution computed by the greedy algorithm on ˆf after k steps. Then, in order to guarantee P[f(S k ) (1 1/e)f(S ) "] 1, it is enough to have s 2 H 2 (k log n + log(1/ ))/" 2, i.i.d. samples from. The running time of GREEDY is then bounded by O H 2 nk(k log n + log(1/ ))/" 2, where is an upper bound on the computation time for a single evaluation of f (S). As an example, let us compare the worst-case complexity bound obtained for SGD (i.e. O( 2 kn(log n)/" 2 )) with that of GREEDY for the influence maximization problem. Each single function evaluation for GREEDY amounts to computing the total influence of a set in a sample graph, which makes = O(n) (here we assume our sample graphs satisfy E = O( V )). Also, a crude upper bound for the size of the gradient for each sample function is H p n (see Appendix E.1). Hence, we can deduce that SGD can have a factor k speedup w.r.t. to GREEDY. 4 Applications We will now show how to instantiate the stochastic submodular maximization framework using several prototypical discrete optimization problems. Influence maximization. As discussed in Section 2, the Independent Cascade [20] model defines a distribution G over instances G Gthat share a set V of nodes. The influence f G (S) of a set of nodes S in instance G is the fraction of nodes reachable from S using the edges E(G). The following Lemma shows that the influence belongs to the class of WCF. Lemma 4. The influence function f G ( ) is a WCF. Moreover, F G (x) =E S [f G (S)] = 1 X Q (1 u2p V v (1 x u )) (5) F G (x) = 1 V v2v X min{1, P u2p v x u }, (6) v2v where P v is the set of all nodes having a (directed) path to v. 6
7 We return to the problem of maximizing f G (S) =E G G [f G (S)] given a distribution over graphs G sharing nodes V. Since f G is a weighted sum of submodular functions, it is submodular. Moreover, F (x) =E S [f G (S)] = E S [E G [f G (S)]] = E G [E S [f G (S)]] = E G [F G (x)] " # 1 X Q = E G (1 u2p V v (1 x u )). v2v Let U be the uniform distribution over vertices. Then, apple apple 1 F (x) =E G Pv2V (1 Q u2p v (1 x u )) = E G E v U [1 V Q u2p v (1 x u )], (7) and the corresponding upper bound would be F (x) =E G apple E v U min{1, Pu2P v x u }. (8) This formulation proves to be helpful in efficient calculation of subgradients, as one can obtain a random subgradient in linear time. For more details see Appendix E.1. We also provide a more efficient, biased estimator of the expectation in the Appendix. Facility location. Let G =(X [Y,E) be a complete weighted bipartite graph with parts X and Y and nonnegative weights w x,y. The weights can be considered as utilities or some similarity metric. We select a subset S X and each y 2 Y selects s 2 S with the highest weight w s,y. Our goal is to maximize the average weight of these selected edges, i.e. to maximize f(s) = 1 X max Y w s,y (9) s2s y2y given some constraints on S. This problem is indeed the Facility Location problem, if one takes X to be the set of facilities and Y to be the set of customers and w x,y to be the utility of facility x for customer y. Another interesting instance is the Exemplar-based Clustering problem, in which X = Y is a set of objects and w x,y is the similarity (or inverted distance) between objects x and y, and one tries to find a subset S of exemplars (i.e. centroids) for these objects. The stochastic nature of this problem is revealed when one writes (9) as the expectation f(s) = E y [f y (S)], where is the uniform distribution over Y and f y (S) := max s2s w s,y. One can also consider this more general case, where y s are drawn from an unknown distribution, and one tries to maximize the aforementioned expectation. First, we claim that f y ( ) for each y 2 Y is again a weighted coverage function. For simplicity, let.. X = {1,...,n} and set m i = wi,y, with m 1 m n and m n+1 =0. Lemma 5. The utility function f y ( ) is a WCF. Moreover, F y (x) = P n i=1 (m Q i i m i+1 )(1 j=1 (1 x j)), (10) F y (x) = P n i=1 (m i m i+1 )min{1, P i j=1 x j}. (11) We remark that the gradient of both F y and F y can be computed in linear time using a recursive procedure. We refer to Appendix E.2 for more details. 5 Experimental Results We demonstrate the practical utility of the proposed framework and compare it to standard baselines. We compare the performance of the algorithms in terms of their wall-clock running time and the obtained utility. We consider the following problems: Influence Maximization for the Epinions network 2. The network consists of nodes and directed edges. We consider the subgraph induced by the top nodes with the largest out-degree and use the independent cascade model [20]. The diffusion model is specified by a fixed probability for each node to influence its neighbors in the underlying graph. We set this probability p to be 0.02, and chose the number of seeds k =
8 Blogs 14 CIFAR-10 e = e = e = 0.01 T = 100K T = 8K e = 0.3 e = 0.1 Utility Utility e = e = e = 0.3 e = 0.5 T = 8K 2.16 SSM/AdaGrad L AZY-G REEDY L AZY-S TOCH -G REEDY R ANDOM -S ELECT 4 e = 0.9 SSM/AdaGrad L AZY-G REEDY L AZY-S TOCH -G REEDY R ANDOM -S ELECT Cost (seconds) Cost (seconds) Epinions Epinions (Partition Matroid) 16.5 T = e = 0.01 e = Utility Utility 16.0 e = e = SSM/AdaGrad L AZY-G REEDY L AZY-S TOCH -G REEDY R ANDOM -S ELECT SSM/AdaGrad L AZY-G REEDY k (# of seeds) Cost (seconds) Figure 1: In the case of Facility location for Blog selection as well as on influence maximization on Epinions, the proposed approach reaches the same utility significantly faster. On the exemplarbased clustering of CIFAR, the proposed approach is outperformed by S TOCHASTIC -G REEDY, but nevertheless reaches 98.4% of the G REEDY utility in a few seconds (after less than 1000 iterations). On Influence Maximization over partition matroids, the proposed approach significantly outperforms G REEDY. Facility Location for Blog Selection. We use the data set used in [14], consisting of blogs, and cascades. The goal is to detect information cascades/stories spreading over the blogosphere. This dataset is heavy-tailed, hence a small random sample of the events has high variance in terms of the cascade sizes. We set k = 100. Exemplar-based Clustering on CIFAR-10. The data set contains color images with resolution We use a single batch of images and compare our algorithms to variants of G REEDY over the full data set. We use the Euclidean norm as the distance function and set k = 50. Further details about preprocessing of the data as well as formulation of the submodular function can be found in Appendix E.3. Baselines. In the case of cardinality constraints, we compare our stochastic continuous optimization approach against the most efficient discrete approaches (L AZY-)G REEDY and (L AZY-)S TOCHASTIC G REEDY, which both provide optimal approximation guarantees. For S TOCHASTIC -G REEDY, we vary the parameter " in order to explore the running time/utility tradeoff. We also report the performance of randomly selected sets. For the two facility location problems, when applying the greedy variants we can evaluate the exact objective (true expectation). In the Influence Maximization application, computing the exact expectation is intractable. Hence, we use an empirical average of s samples (cascades) from the model. We note that the number of samples suggested by Proposition 3 is overly conservative, and instead we make a practical choice of s = 103 samples. 8
9 Results. The results are summarized in Figure 1. On the blog selection and influence maximization applications, the proposed continuous optimization approach outperforms STOCHASTIC-GREEDY in terms of the running time/utility tradeoff. In particular, for blog selection we can compute a solution with the same utility 26 faster than STOCHASTIC-GREEDY with " =0.5. Similarly, for influence maximization on Epinions we the solution 88 faster than STOCHASTIC-GREEDY with " =0.1. On the exemplar-based clustering application STOCHASTIC-GREEDY outperforms the proposed approach. We note that the proposed approach is still competitive as it recovers 98.4% of the value after less than thousand iterations. We also include an experiment on Influence Maximization over partition matroids for the Epinions network. In this case, GREEDY only provides a 1/2 approximation guarantee and STOCHASTIC- GREEDY does not apply. To create the partition, we first sorted all the vertices by their out-degree. Using this order on the vertices, we divided the vertices into two partitions, one containing vertices with even positions, other containing the rest. Figure 1 clearly demonstrates that the proposed approach outperforms GREEDY in terms of utility (as well as running time). Acknowledgments The research was partially supported by ERC StG We would like to thank Yaron Singer for helpful comments and suggestions. References [1] Alexander A Ageev and Maxim I Sviridenko. Pipage rounding: A new method of constructing algorithms with proven performance guarantee. Journal of Combinatorial Optimization, 8(3): , [2] Francis Bach et al. Learning with submodular functions: A convex optimization perspective. Foundations and Trends R in Machine Learning, 6(2-3): , [3] Francis R. Bach. Convex analysis and optimization with submodular functions: a tutorial. CoRR, abs/ , [4] Ashwinkumar Badanidiyuru and Jan Vondrák. Fast algorithms for maximizing submodular functions. In Proceedings of the Twenty-Fifth Annual ACM-SIAM Symposium on Discrete Algorithms, pages SIAM, [5] P. Brucker. An o(n) algorithm for quadratic knapsack problems. Operations Research Letters, 3 (3): , [6] Gruia Calinescu, Chandra Chekuri, Martin Pál, and Jan Vondrák. Maximizing a submodular set function subject to a matroid constraint. In International Conference on Integer Programming and Combinatorial Optimization, pages Springer, [7] Gruia Calinescu, Chandra Chekuri, Martin Pál, and Jan Vondrák. Maximizing a monotone submodular function subject to a matroid constraint. SIAM Journal on Computing, 40(6): , [8] John Duchi, Elad Hazan, and Yoram Singer. Adaptive subgradient methods for online learning and stochastic optimization. Journal of Machine Learning Research, [9] Alina Ene and Huy L. Nguyen. Constrained submodular maximization: Beyond 1/e. pages , [10] Uriel Feige. A threshold of ln n for approximating set cover. Journal of the ACM, 45(4):634? 652, [11] Uriel Feige, Vahab S Mirrokni, and Jan Vondrak. Maximizing non-monotone submodular functions. SIAM Journal on Computing, 40(4): , [12] Moran Feldman, Joseph Naor, and Roy Schwartz. A unified continuous greedy algorithm for submodular maximization. In Foundations of Computer Science (FOCS), 2011 IEEE 52nd Annual Symposium on, pages IEEE,
10 [13] Marshall L Fisher, George L Nemhauser, and Laurence A Wolsey. An analysis of approximations for maximizing submodular set functions. In Polyhedral combinatorics, pages Springer, [14] Natalie Glance, Matthew Hurst, Kamal Nigam, Matthew Siegler, Robert Stockton, and Takashi Tomokiyo. Deriving marketing intelligence from online discussion. In Proceedings of the eleventh ACM SIGKDD international conference on Knowledge discovery in data mining, pages , [15] Ryan Gomez and Andreas Krause. Budgeted nonparametric learning from data streams. Proceedings of the 27 th International Conference on Machine Learning, [16] Avinatan Hassidim and Yaron Singer. Submodular optimization under noise. CoRR, abs/ , [17] Thibaut Horel and Yaron Singer. Maximizing approximately submodular functions. NIPS, [18] Rishabh K Iyer and Jeff A Bilmes. Submodular optimization with submodular cover and submodular knapsack constraints. In Advances in Neural Information Processing Systems, pages , [19] Rishabh K. Iyer and Jeff A. Bilmes. Polyhedral aspects of submodularity, convexity and concavity. Arxiv, CoRR, abs/ , [20] David Kempe, Jon Kleinberg, and Eva. Tardos. Maximizing the spread of influence through a social network. 9 th ACM SIGKDD Conference on Knowledge Discovery and Data Mining, pages , [21] Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. ICLR, [22] Andreas Krause and Daniel Golovin. Submodular function maximization. Tractability: Practical Approaches to Hard Problems, 3(19):8, [23] Andreas Krause and Carlos Guestrin. Near-optimal nonmyopic value of information in graphical models. In Conference on Uncertainty in Artificial Intelligence (UAI), July [24] Andreas Krause and Carlos Guestrin. Near-optimal nonmyopic value of information in graphical models. In Proceedings of the Twenty-First Conference on Uncertainty in Artificial Intelligence, pages AUAI Press, [25] Ariel Kulik, Hadas Shachnai, and Tami Tamir. Maximizing submodular set functions subject to multiple linear constraints. In Proceedings of the twentieth Annual ACM-SIAM Symposium on Discrete Algorithms, pages Society for Industrial and Applied Mathematics, [26] K. S. Sesh Kumar and Francis Bach. Active-set methods for submodular minimization problems. hal v3, [27] Hui Lin and Jeff Bilmes. A class of submodular functions for document summarization. In Proceedings of the 49th Annual Meeting of the Association for Computational Linguistics: Human Language Technologies-Volume 1, pages Association for Computational Linguistics, [28] László Lovász. Submodular functions and convexity. In Mathematical Programming The State of the Art, pages Springer, [29] Baharan Mirzasoleiman, Ashwinkumar Badanidiyuru, Amin Karbasi, Jan Vondrak, and Andreas Krause. Lazier than lazy greedy. Association for the Advancement of Artificial Intelligence, [30] George L. Nemhauser, Laurence A. Wolsey, and Marshall L. Fisher. An analysis of approximations for maximizing submodular set functions - i. Mathematical Programming, 14(1): ,
11 [31] P. M. Pardalos and N. Kovoor. An algorithm for a singly constrained class of quadratic programs subject to upper and lower bounds. Mathematical Programming, 46(1): , [32] Lior Seeman and Yaron Singer. Adaptive seeding in social networks. pages , [33] Shai Shalev-Shwartz and Shai Ben-David. Understanding Machine Learning : From Theory to Algorithms. Cambridge University Press, [34] Adish Singla, Sebastian Tschiatschek, and Andreas Krause. Noisy submodular maximization via adaptive sampling with applications to crowdsourced image collection summarization. In Proc. Conference on Artificial Intelligence (AAAI), February [35] Matthew Streeter and Daniel Golovin. An online algorithm for maximizing submodular functions. NIPS, [36] Jan Vondrák. Submodularity in combinatorial optimization. Charles University, Prague, [37] Jan Vondrák. Optimal approximation for the submodular welfare problem in the value oracle model. In Proceedings of the fortieth annual ACM symposium on Theory of computing, pages ACM, [38] Jan Vondrák. Symmetry and approximability of submodular maximization problems. SIAM Journal on Computing, 42(1): , [39] Kai Wei, Rishabh Iyer, and Jeff Bilmes. Fast multi-stage submodular maximization. In International Conference on Machine Learning (ICML), Beijing, China,
A survey of submodular functions maximization. Yao Zhang 03/19/2015
 A survey of submodular functions maximization Yao Zhang 03/19/2015 Example Deploy sensors in the water distribution network to detect contamination F(S): the performance of the detection when a set S of
A survey of submodular functions maximization Yao Zhang 03/19/2015 Example Deploy sensors in the water distribution network to detect contamination F(S): the performance of the detection when a set S of
Learning Sparse Combinatorial Representations via Two-stage Submodular Maximization
 Learning Sparse Combinatorial Representations via Two-stage Submodular Maximization Eric Balkanski Harvard University Andreas Krause ETH Zurich Baharan Mirzasoleiman ETH Zurich Yaron Singer Harvard University
Learning Sparse Combinatorial Representations via Two-stage Submodular Maximization Eric Balkanski Harvard University Andreas Krause ETH Zurich Baharan Mirzasoleiman ETH Zurich Yaron Singer Harvard University
On Distributed Submodular Maximization with Limited Information
 On Distributed Submodular Maximization with Limited Information Bahman Gharesifard Stephen L. Smith Abstract This paper considers a class of distributed submodular maximization problems in which each agent
On Distributed Submodular Maximization with Limited Information Bahman Gharesifard Stephen L. Smith Abstract This paper considers a class of distributed submodular maximization problems in which each agent
CS 598CSC: Approximation Algorithms Lecture date: March 2, 2011 Instructor: Chandra Chekuri
 CS 598CSC: Approximation Algorithms Lecture date: March, 011 Instructor: Chandra Chekuri Scribe: CC Local search is a powerful and widely used heuristic method (with various extensions). In this lecture
CS 598CSC: Approximation Algorithms Lecture date: March, 011 Instructor: Chandra Chekuri Scribe: CC Local search is a powerful and widely used heuristic method (with various extensions). In this lecture
Viral Marketing and Outbreak Detection. Fang Jin Yao Zhang
 Viral Marketing and Outbreak Detection Fang Jin Yao Zhang Paper 1: Maximizing the Spread of Influence through a Social Network Authors: David Kempe, Jon Kleinberg, Éva Tardos KDD 2003 Outline Problem Statement
Viral Marketing and Outbreak Detection Fang Jin Yao Zhang Paper 1: Maximizing the Spread of Influence through a Social Network Authors: David Kempe, Jon Kleinberg, Éva Tardos KDD 2003 Outline Problem Statement
Lecture 9: Pipage Rounding Method
 Recent Advances in Approximation Algorithms Spring 2015 Lecture 9: Pipage Rounding Method Lecturer: Shayan Oveis Gharan April 27th Disclaimer: These notes have not been subjected to the usual scrutiny
Recent Advances in Approximation Algorithms Spring 2015 Lecture 9: Pipage Rounding Method Lecturer: Shayan Oveis Gharan April 27th Disclaimer: These notes have not been subjected to the usual scrutiny
Noisy Submodular Maximization via Adaptive Sampling with Applications to Crowdsourced Image Collection Summarization
 Noisy Submodular Maximization via Adaptive Sampling with Applications to Crowdsourced Image Collection Summarization Adish Singla ETH Zurich adish.singla@inf.ethz.ch Sebastian Tschiatschek ETH Zurich sebastian.tschiatschek@inf.ethz.ch
Noisy Submodular Maximization via Adaptive Sampling with Applications to Crowdsourced Image Collection Summarization Adish Singla ETH Zurich adish.singla@inf.ethz.ch Sebastian Tschiatschek ETH Zurich sebastian.tschiatschek@inf.ethz.ch
Influence Maximization in the Independent Cascade Model
 Influence Maximization in the Independent Cascade Model Gianlorenzo D Angelo, Lorenzo Severini, and Yllka Velaj Gran Sasso Science Institute (GSSI), Viale F. Crispi, 7, 67100, L Aquila, Italy. {gianlorenzo.dangelo,lorenzo.severini,yllka.velaj}@gssi.infn.it
Influence Maximization in the Independent Cascade Model Gianlorenzo D Angelo, Lorenzo Severini, and Yllka Velaj Gran Sasso Science Institute (GSSI), Viale F. Crispi, 7, 67100, L Aquila, Italy. {gianlorenzo.dangelo,lorenzo.severini,yllka.velaj}@gssi.infn.it
Maximizing the Spread of Influence through a Social Network. David Kempe, Jon Kleinberg and Eva Tardos
 Maximizing the Spread of Influence through a Social Network David Kempe, Jon Kleinberg and Eva Tardos Group 9 Lauren Thomas, Ryan Lieblein, Joshua Hammock and Mary Hanvey Introduction In a social network,
Maximizing the Spread of Influence through a Social Network David Kempe, Jon Kleinberg and Eva Tardos Group 9 Lauren Thomas, Ryan Lieblein, Joshua Hammock and Mary Hanvey Introduction In a social network,
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email: mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Approximation Algorithms
 Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A new 4 credit unit course Part of Theoretical Computer Science courses at the Department of Mathematics There will be 4 hours
Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A new 4 credit unit course Part of Theoretical Computer Science courses at the Department of Mathematics There will be 4 hours
Distributed Submodular Maximization in Massive Datasets. Alina Ene. Joint work with Rafael Barbosa, Huy L. Nguyen, Justin Ward
 Distributed Submodular Maximization in Massive Datasets Alina Ene Joint work with Rafael Barbosa, Huy L. Nguyen, Justin Ward Combinatorial Optimization Given A set of objects V A function f on subsets
Distributed Submodular Maximization in Massive Datasets Alina Ene Joint work with Rafael Barbosa, Huy L. Nguyen, Justin Ward Combinatorial Optimization Given A set of objects V A function f on subsets
Submodular Optimization
 Submodular Optimization Nathaniel Grammel N. Grammel Submodular Optimization 1 / 28 Submodularity Captures the notion of Diminishing Returns Definition Suppose U is a set. A set function f :2 U! R is submodular
Submodular Optimization Nathaniel Grammel N. Grammel Submodular Optimization 1 / 28 Submodularity Captures the notion of Diminishing Returns Definition Suppose U is a set. A set function f :2 U! R is submodular
Clustering. SC4/SM4 Data Mining and Machine Learning, Hilary Term 2017 Dino Sejdinovic
 Clustering SC4/SM4 Data Mining and Machine Learning, Hilary Term 2017 Dino Sejdinovic Clustering is one of the fundamental and ubiquitous tasks in exploratory data analysis a first intuition about the
Clustering SC4/SM4 Data Mining and Machine Learning, Hilary Term 2017 Dino Sejdinovic Clustering is one of the fundamental and ubiquitous tasks in exploratory data analysis a first intuition about the
Approximation Algorithms
 Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A 4 credit unit course Part of Theoretical Computer Science courses at the Laboratory of Mathematics There will be 4 hours
Approximation Algorithms Prof. Tapio Elomaa tapio.elomaa@tut.fi Course Basics A 4 credit unit course Part of Theoretical Computer Science courses at the Laboratory of Mathematics There will be 4 hours
arxiv: v2 [cs.ai] 1 Dec 2015
![arxiv: v2 [cs.ai] 1 Dec 2015 arxiv: v2 [cs.ai] 1 Dec 2015](/thumbs/84/90648547.jpg) Noisy Submodular Maximization via Adaptive Sampling with Applications to Crowdsourced Image Collection Summarization Adish Singla ETH Zurich adish.singla@inf.ethz.ch Sebastian Tschiatschek ETH Zurich sebastian.tschiatschek@inf.ethz.ch
Noisy Submodular Maximization via Adaptive Sampling with Applications to Crowdsourced Image Collection Summarization Adish Singla ETH Zurich adish.singla@inf.ethz.ch Sebastian Tschiatschek ETH Zurich sebastian.tschiatschek@inf.ethz.ch
Graphs and Network Flows IE411. Lecture 21. Dr. Ted Ralphs
 Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Graphs and Network Flows IE411 Lecture 21 Dr. Ted Ralphs IE411 Lecture 21 1 Combinatorial Optimization and Network Flows In general, most combinatorial optimization and integer programming problems are
Theorem 2.9: nearest addition algorithm
 There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
There are severe limits on our ability to compute near-optimal tours It is NP-complete to decide whether a given undirected =(,)has a Hamiltonian cycle An approximation algorithm for the TSP can be used
An Efficient Approximation for the Generalized Assignment Problem
 An Efficient Approximation for the Generalized Assignment Problem Reuven Cohen Liran Katzir Danny Raz Department of Computer Science Technion Haifa 32000, Israel Abstract We present a simple family of
An Efficient Approximation for the Generalized Assignment Problem Reuven Cohen Liran Katzir Danny Raz Department of Computer Science Technion Haifa 32000, Israel Abstract We present a simple family of
Clustering. (Part 2)
 Clustering (Part 2) 1 k-means clustering 2 General Observations on k-means clustering In essence, k-means clustering aims at minimizing cluster variance. It is typically used in Euclidean spaces and works
Clustering (Part 2) 1 k-means clustering 2 General Observations on k-means clustering In essence, k-means clustering aims at minimizing cluster variance. It is typically used in Euclidean spaces and works
Optimality certificates for convex minimization and Helly numbers
 Optimality certificates for convex minimization and Helly numbers Amitabh Basu Michele Conforti Gérard Cornuéjols Robert Weismantel Stefan Weltge October 20, 2016 Abstract We consider the problem of minimizing
Optimality certificates for convex minimization and Helly numbers Amitabh Basu Michele Conforti Gérard Cornuéjols Robert Weismantel Stefan Weltge October 20, 2016 Abstract We consider the problem of minimizing
6. Lecture notes on matroid intersection
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans May 2, 2017 6. Lecture notes on matroid intersection One nice feature about matroids is that a simple greedy algorithm
Towards more efficient infection and fire fighting
 Towards more efficient infection and fire fighting Peter Floderus Andrzej Lingas Mia Persson The Centre for Mathematical Sciences, Lund University, 00 Lund, Sweden. Email: pflo@maths.lth.se Department
Towards more efficient infection and fire fighting Peter Floderus Andrzej Lingas Mia Persson The Centre for Mathematical Sciences, Lund University, 00 Lund, Sweden. Email: pflo@maths.lth.se Department
A Class of Submodular Functions for Document Summarization
 A Class of Submodular Functions for Document Summarization Hui Lin, Jeff Bilmes University of Washington, Seattle Dept. of Electrical Engineering June 20, 2011 Lin and Bilmes Submodular Summarization June
A Class of Submodular Functions for Document Summarization Hui Lin, Jeff Bilmes University of Washington, Seattle Dept. of Electrical Engineering June 20, 2011 Lin and Bilmes Submodular Summarization June
2386 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 6, JUNE 2006
 2386 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 6, JUNE 2006 The Encoding Complexity of Network Coding Michael Langberg, Member, IEEE, Alexander Sprintson, Member, IEEE, and Jehoshua Bruck,
2386 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 52, NO. 6, JUNE 2006 The Encoding Complexity of Network Coding Michael Langberg, Member, IEEE, Alexander Sprintson, Member, IEEE, and Jehoshua Bruck,
Online Coloring Known Graphs
 Online Coloring Known Graphs Magnús M. Halldórsson Science Institute University of Iceland IS-107 Reykjavik, Iceland mmh@hi.is, www.hi.is/ mmh. Submitted: September 13, 1999; Accepted: February 24, 2000.
Online Coloring Known Graphs Magnús M. Halldórsson Science Institute University of Iceland IS-107 Reykjavik, Iceland mmh@hi.is, www.hi.is/ mmh. Submitted: September 13, 1999; Accepted: February 24, 2000.
PTAS for Matroid Matching
 PTAS for Matroid Matching Jon Lee 1 Maxim Sviridenko 1 Jan Vondrák 2 1 IBM Watson Research Center Yorktown Heights, NY 2 IBM Almaden Research Center San Jose, CA May 6, 2010 Jan Vondrák (IBM Almaden) PTAS
PTAS for Matroid Matching Jon Lee 1 Maxim Sviridenko 1 Jan Vondrák 2 1 IBM Watson Research Center Yorktown Heights, NY 2 IBM Almaden Research Center San Jose, CA May 6, 2010 Jan Vondrák (IBM Almaden) PTAS
Expected Approximation Guarantees for the Demand Matching Problem
 Expected Approximation Guarantees for the Demand Matching Problem C. Boucher D. Loker September 2006 Abstract The objective of the demand matching problem is to obtain the subset M of edges which is feasible
Expected Approximation Guarantees for the Demand Matching Problem C. Boucher D. Loker September 2006 Abstract The objective of the demand matching problem is to obtain the subset M of edges which is feasible
Optimization of submodular functions
 Optimization of submodular functions Law Of Diminishing Returns According to the Law of Diminishing Returns (also known as Diminishing Returns Phenomenon), the value or enjoyment we get from something
Optimization of submodular functions Law Of Diminishing Returns According to the Law of Diminishing Returns (also known as Diminishing Returns Phenomenon), the value or enjoyment we get from something
6 Randomized rounding of semidefinite programs
 6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
Online Learning of Assignments
 Online Learning of Assignments Matthew Streeter Google, Inc. Pittsburgh, PA 15213 mstreeter@google.com Daniel Golovin Carnegie Mellon University Pittsburgh, PA 15213 dgolovin@cs.cmu.edu Andreas Krause
Online Learning of Assignments Matthew Streeter Google, Inc. Pittsburgh, PA 15213 mstreeter@google.com Daniel Golovin Carnegie Mellon University Pittsburgh, PA 15213 dgolovin@cs.cmu.edu Andreas Krause
Case Study 1: Estimating Click Probabilities
 Case Study 1: Estimating Click Probabilities SGD cont d AdaGrad Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade March 31, 2015 1 Support/Resources Office Hours Yao Lu:
Case Study 1: Estimating Click Probabilities SGD cont d AdaGrad Machine Learning for Big Data CSE547/STAT548, University of Washington Sham Kakade March 31, 2015 1 Support/Resources Office Hours Yao Lu:
1. Lecture notes on bipartite matching
 Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Massachusetts Institute of Technology 18.453: Combinatorial Optimization Michel X. Goemans February 5, 2017 1. Lecture notes on bipartite matching Matching problems are among the fundamental problems in
Secretary Problems and Incentives via Linear Programming
 Secretary Problems and Incentives via Linear Programming Niv Buchbinder Microsoft Research, New England and Kamal Jain Microsoft Research, Redmond and Mohit Singh Microsoft Research, New England In the
Secretary Problems and Incentives via Linear Programming Niv Buchbinder Microsoft Research, New England and Kamal Jain Microsoft Research, Redmond and Mohit Singh Microsoft Research, New England In the
Monotone Paths in Geometric Triangulations
 Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Monotone Paths in Geometric Triangulations Adrian Dumitrescu Ritankar Mandal Csaba D. Tóth November 19, 2017 Abstract (I) We prove that the (maximum) number of monotone paths in a geometric triangulation
Optimality certificates for convex minimization and Helly numbers
 Optimality certificates for convex minimization and Helly numbers Amitabh Basu Michele Conforti Gérard Cornuéjols Robert Weismantel Stefan Weltge May 10, 2017 Abstract We consider the problem of minimizing
Optimality certificates for convex minimization and Helly numbers Amitabh Basu Michele Conforti Gérard Cornuéjols Robert Weismantel Stefan Weltge May 10, 2017 Abstract We consider the problem of minimizing
Online Stochastic Matching CMSC 858F: Algorithmic Game Theory Fall 2010
 Online Stochastic Matching CMSC 858F: Algorithmic Game Theory Fall 2010 Barna Saha, Vahid Liaghat Abstract This summary is mostly based on the work of Saberi et al. [1] on online stochastic matching problem
Online Stochastic Matching CMSC 858F: Algorithmic Game Theory Fall 2010 Barna Saha, Vahid Liaghat Abstract This summary is mostly based on the work of Saberi et al. [1] on online stochastic matching problem
Part I Part II Part III Part IV Part V. Influence Maximization
 Part I Part II Part III Part IV Part V Influence Maximization 1 Word-of-mouth (WoM) effect in social networks xphone is good xphone is good xphone is good xphone is good xphone is good xphone is good xphone
Part I Part II Part III Part IV Part V Influence Maximization 1 Word-of-mouth (WoM) effect in social networks xphone is good xphone is good xphone is good xphone is good xphone is good xphone is good xphone
The Maximum Facility Location Problem
 The Maximum Facility Location Problem MITCHELL JONES Supervisor: Dr. Julián Mestre This thesis is submitted in partial fulfillment of the requirements for the degree of Bachelor of Computer Science and
The Maximum Facility Location Problem MITCHELL JONES Supervisor: Dr. Julián Mestre This thesis is submitted in partial fulfillment of the requirements for the degree of Bachelor of Computer Science and
1. Lecture notes on bipartite matching February 4th,
 1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
1. Lecture notes on bipartite matching February 4th, 2015 6 1.1.1 Hall s Theorem Hall s theorem gives a necessary and sufficient condition for a bipartite graph to have a matching which saturates (or matches)
On the Complexity of the Policy Improvement Algorithm. for Markov Decision Processes
 On the Complexity of the Policy Improvement Algorithm for Markov Decision Processes Mary Melekopoglou Anne Condon Computer Sciences Department University of Wisconsin - Madison 0 West Dayton Street Madison,
On the Complexity of the Policy Improvement Algorithm for Markov Decision Processes Mary Melekopoglou Anne Condon Computer Sciences Department University of Wisconsin - Madison 0 West Dayton Street Madison,
Integer Programming Theory
 Integer Programming Theory Laura Galli October 24, 2016 In the following we assume all functions are linear, hence we often drop the term linear. In discrete optimization, we seek to find a solution x
Integer Programming Theory Laura Galli October 24, 2016 In the following we assume all functions are linear, hence we often drop the term linear. In discrete optimization, we seek to find a solution x
Mathematical and Algorithmic Foundations Linear Programming and Matchings
 Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Adavnced Algorithms Lectures Mathematical and Algorithmic Foundations Linear Programming and Matchings Paul G. Spirakis Department of Computer Science University of Patras and Liverpool Paul G. Spirakis
Projection onto the probability simplex: An efficient algorithm with a simple proof, and an application
 Proection onto the probability simplex: An efficient algorithm with a simple proof, and an application Weiran Wang Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science, University of
Proection onto the probability simplex: An efficient algorithm with a simple proof, and an application Weiran Wang Miguel Á. Carreira-Perpiñán Electrical Engineering and Computer Science, University of
The complement of PATH is in NL
 340 The complement of PATH is in NL Let c be the number of nodes in graph G that are reachable from s We assume that c is provided as an input to M Given G, s, t, and c the machine M operates as follows:
340 The complement of PATH is in NL Let c be the number of nodes in graph G that are reachable from s We assume that c is provided as an input to M Given G, s, t, and c the machine M operates as follows:
On Covering a Graph Optimally with Induced Subgraphs
 On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
On Covering a Graph Optimally with Induced Subgraphs Shripad Thite April 1, 006 Abstract We consider the problem of covering a graph with a given number of induced subgraphs so that the maximum number
Online algorithms for clustering problems
 University of Szeged Department of Computer Algorithms and Artificial Intelligence Online algorithms for clustering problems Summary of the Ph.D. thesis by Gabriella Divéki Supervisor Dr. Csanád Imreh
University of Szeged Department of Computer Algorithms and Artificial Intelligence Online algorithms for clustering problems Summary of the Ph.D. thesis by Gabriella Divéki Supervisor Dr. Csanád Imreh
1 Overview. 2 Applications of submodular maximization. AM 221: Advanced Optimization Spring 2016
 AM : Advanced Optimization Spring 06 Prof. Yaron Singer Lecture 0 April th Overview Last time we saw the problem of Combinatorial Auctions and framed it as a submodular maximization problem under a partition
AM : Advanced Optimization Spring 06 Prof. Yaron Singer Lecture 0 April th Overview Last time we saw the problem of Combinatorial Auctions and framed it as a submodular maximization problem under a partition
arxiv: v1 [cs.ds] 19 Nov 2018
![arxiv: v1 [cs.ds] 19 Nov 2018 arxiv: v1 [cs.ds] 19 Nov 2018](/thumbs/90/104114958.jpg) Towards Nearly-linear Time Algorithms for Submodular Maximization with a Matroid Constraint Alina Ene Huy L. Nguy ên arxiv:1811.07464v1 [cs.ds] 19 Nov 2018 Abstract We consider fast algorithms for monotone
Towards Nearly-linear Time Algorithms for Submodular Maximization with a Matroid Constraint Alina Ene Huy L. Nguy ên arxiv:1811.07464v1 [cs.ds] 19 Nov 2018 Abstract We consider fast algorithms for monotone
Alina Ene. From Minimum Cut to Submodular Minimization Leveraging the Decomposable Structure. Boston University
 From Minimum Cut to Submodular Minimization Leveraging the Decomposable Structure Alina Ene Boston University Joint work with Huy Nguyen (Northeastern University) Laszlo Vegh (London School of Economics)
From Minimum Cut to Submodular Minimization Leveraging the Decomposable Structure Alina Ene Boston University Joint work with Huy Nguyen (Northeastern University) Laszlo Vegh (London School of Economics)
The strong chromatic number of a graph
 The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
The strong chromatic number of a graph Noga Alon Abstract It is shown that there is an absolute constant c with the following property: For any two graphs G 1 = (V, E 1 ) and G 2 = (V, E 2 ) on the same
Notes on Minimum Cuts and Modular Functions
 Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
Notes on Minimum Cuts and Modular Functions 1 Introduction The following are my notes on Cunningham s paper [1]. Given a submodular function f and a set S, submodular minimisation is the problem of finding
5. Lecture notes on matroid intersection
 Massachusetts Institute of Technology Handout 14 18.433: Combinatorial Optimization April 1st, 2009 Michel X. Goemans 5. Lecture notes on matroid intersection One nice feature about matroids is that a
Massachusetts Institute of Technology Handout 14 18.433: Combinatorial Optimization April 1st, 2009 Michel X. Goemans 5. Lecture notes on matroid intersection One nice feature about matroids is that a
CS229 Final Project: k-means Algorithm
 CS229 Final Project: k-means Algorithm Colin Wei and Alfred Xue SUNet ID: colinwei axue December 11, 2014 1 Notes This project was done in conjuction with a similar project that explored k-means in CS
CS229 Final Project: k-means Algorithm Colin Wei and Alfred Xue SUNet ID: colinwei axue December 11, 2014 1 Notes This project was done in conjuction with a similar project that explored k-means in CS
Topic: Local Search: Max-Cut, Facility Location Date: 2/13/2007
 CS880: Approximations Algorithms Scribe: Chi Man Liu Lecturer: Shuchi Chawla Topic: Local Search: Max-Cut, Facility Location Date: 2/3/2007 In previous lectures we saw how dynamic programming could be
CS880: Approximations Algorithms Scribe: Chi Man Liu Lecturer: Shuchi Chawla Topic: Local Search: Max-Cut, Facility Location Date: 2/3/2007 In previous lectures we saw how dynamic programming could be
Randomized Composable Core-sets for Distributed Optimization Vahab Mirrokni
 Randomized Composable Core-sets for Distributed Optimization Vahab Mirrokni Mainly based on joint work with: Algorithms Research Group, Google Research, New York Hossein Bateni, Aditya Bhaskara, Hossein
Randomized Composable Core-sets for Distributed Optimization Vahab Mirrokni Mainly based on joint work with: Algorithms Research Group, Google Research, New York Hossein Bateni, Aditya Bhaskara, Hossein
General properties of staircase and convex dual feasible functions
 General properties of staircase and convex dual feasible functions JÜRGEN RIETZ, CLÁUDIO ALVES, J. M. VALÉRIO de CARVALHO Centro de Investigação Algoritmi da Universidade do Minho, Escola de Engenharia
General properties of staircase and convex dual feasible functions JÜRGEN RIETZ, CLÁUDIO ALVES, J. M. VALÉRIO de CARVALHO Centro de Investigação Algoritmi da Universidade do Minho, Escola de Engenharia
Online Facility Location
 Online Facility Location Adam Meyerson Abstract We consider the online variant of facility location, in which demand points arrive one at a time and we must maintain a set of facilities to service these
Online Facility Location Adam Meyerson Abstract We consider the online variant of facility location, in which demand points arrive one at a time and we must maintain a set of facilities to service these
Probabilistic Graphical Models
 School of Computer Science Probabilistic Graphical Models Theory of Variational Inference: Inner and Outer Approximation Eric Xing Lecture 14, February 29, 2016 Reading: W & J Book Chapters Eric Xing @
School of Computer Science Probabilistic Graphical Models Theory of Variational Inference: Inner and Outer Approximation Eric Xing Lecture 14, February 29, 2016 Reading: W & J Book Chapters Eric Xing @
/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/27/18
 601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/27/18 22.1 Introduction We spent the last two lectures proving that for certain problems, we can
601.433/633 Introduction to Algorithms Lecturer: Michael Dinitz Topic: Approximation algorithms Date: 11/27/18 22.1 Introduction We spent the last two lectures proving that for certain problems, we can
Fast Approximate Energy Minimization via Graph Cuts
 IEEE Transactions on PAMI, vol. 23, no. 11, pp. 1222-1239 p.1 Fast Approximate Energy Minimization via Graph Cuts Yuri Boykov, Olga Veksler and Ramin Zabih Abstract Many tasks in computer vision involve
IEEE Transactions on PAMI, vol. 23, no. 11, pp. 1222-1239 p.1 Fast Approximate Energy Minimization via Graph Cuts Yuri Boykov, Olga Veksler and Ramin Zabih Abstract Many tasks in computer vision involve
FUTURE communication networks are expected to support
 1146 IEEE/ACM TRANSACTIONS ON NETWORKING, VOL 13, NO 5, OCTOBER 2005 A Scalable Approach to the Partition of QoS Requirements in Unicast and Multicast Ariel Orda, Senior Member, IEEE, and Alexander Sprintson,
1146 IEEE/ACM TRANSACTIONS ON NETWORKING, VOL 13, NO 5, OCTOBER 2005 A Scalable Approach to the Partition of QoS Requirements in Unicast and Multicast Ariel Orda, Senior Member, IEEE, and Alexander Sprintson,
CS599: Convex and Combinatorial Optimization Fall 2013 Lecture 14: Combinatorial Problems as Linear Programs I. Instructor: Shaddin Dughmi
 CS599: Convex and Combinatorial Optimization Fall 2013 Lecture 14: Combinatorial Problems as Linear Programs I Instructor: Shaddin Dughmi Announcements Posted solutions to HW1 Today: Combinatorial problems
CS599: Convex and Combinatorial Optimization Fall 2013 Lecture 14: Combinatorial Problems as Linear Programs I Instructor: Shaddin Dughmi Announcements Posted solutions to HW1 Today: Combinatorial problems
Solutions for the Exam 6 January 2014
 Mastermath and LNMB Course: Discrete Optimization Solutions for the Exam 6 January 2014 Utrecht University, Educatorium, 13:30 16:30 The examination lasts 3 hours. Grading will be done before January 20,
Mastermath and LNMB Course: Discrete Optimization Solutions for the Exam 6 January 2014 Utrecht University, Educatorium, 13:30 16:30 The examination lasts 3 hours. Grading will be done before January 20,
Random Walk Distributed Dual Averaging Method For Decentralized Consensus Optimization
 Random Walk Distributed Dual Averaging Method For Decentralized Consensus Optimization Cun Mu, Asim Kadav, Erik Kruus, Donald Goldfarb, Martin Renqiang Min Machine Learning Group, NEC Laboratories America
Random Walk Distributed Dual Averaging Method For Decentralized Consensus Optimization Cun Mu, Asim Kadav, Erik Kruus, Donald Goldfarb, Martin Renqiang Min Machine Learning Group, NEC Laboratories America
The Encoding Complexity of Network Coding
 The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email mikel,spalex,bruck @caltech.edu Abstract In the multicast network
The Encoding Complexity of Network Coding Michael Langberg Alexander Sprintson Jehoshua Bruck California Institute of Technology Email mikel,spalex,bruck @caltech.edu Abstract In the multicast network
Algorithms for Storage Allocation Based on Client Preferences
 Algorithms for Storage Allocation Based on Client Preferences Tami Tamir Benny Vaksendiser Abstract We consider a packing problem arising in storage management of Video on Demand (VoD) systems. The system
Algorithms for Storage Allocation Based on Client Preferences Tami Tamir Benny Vaksendiser Abstract We consider a packing problem arising in storage management of Video on Demand (VoD) systems. The system
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching
 Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Reducing Directed Max Flow to Undirected Max Flow and Bipartite Matching Henry Lin Division of Computer Science University of California, Berkeley Berkeley, CA 94720 Email: henrylin@eecs.berkeley.edu Abstract
Lecture 7: Asymmetric K-Center
 Advanced Approximation Algorithms (CMU 18-854B, Spring 008) Lecture 7: Asymmetric K-Center February 5, 007 Lecturer: Anupam Gupta Scribe: Jeremiah Blocki In this lecture, we will consider the K-center
Advanced Approximation Algorithms (CMU 18-854B, Spring 008) Lecture 7: Asymmetric K-Center February 5, 007 Lecturer: Anupam Gupta Scribe: Jeremiah Blocki In this lecture, we will consider the K-center
Ranking Clustered Data with Pairwise Comparisons
 Ranking Clustered Data with Pairwise Comparisons Alisa Maas ajmaas@cs.wisc.edu 1. INTRODUCTION 1.1 Background Machine learning often relies heavily on being able to rank the relative fitness of instances
Ranking Clustered Data with Pairwise Comparisons Alisa Maas ajmaas@cs.wisc.edu 1. INTRODUCTION 1.1 Background Machine learning often relies heavily on being able to rank the relative fitness of instances
Communication Complexity of Combinatorial Auctions with Submodular Valuations
 Communication Complexity of Combinatorial Auctions with Submodular Valuations Shahar Dobzinski Weizmann Institute of Science Jan Vondrák IBM Almaden Research ACM-SIAM SODA 2013, New Orleans Dobzinski-Vondrák
Communication Complexity of Combinatorial Auctions with Submodular Valuations Shahar Dobzinski Weizmann Institute of Science Jan Vondrák IBM Almaden Research ACM-SIAM SODA 2013, New Orleans Dobzinski-Vondrák
CS 435, 2018 Lecture 2, Date: 1 March 2018 Instructor: Nisheeth Vishnoi. Convex Programming and Efficiency
 CS 435, 2018 Lecture 2, Date: 1 March 2018 Instructor: Nisheeth Vishnoi Convex Programming and Efficiency In this lecture, we formalize convex programming problem, discuss what it means to solve it efficiently
CS 435, 2018 Lecture 2, Date: 1 March 2018 Instructor: Nisheeth Vishnoi Convex Programming and Efficiency In this lecture, we formalize convex programming problem, discuss what it means to solve it efficiently
On the Max Coloring Problem
 On the Max Coloring Problem Leah Epstein Asaf Levin May 22, 2010 Abstract We consider max coloring on hereditary graph classes. The problem is defined as follows. Given a graph G = (V, E) and positive
On the Max Coloring Problem Leah Epstein Asaf Levin May 22, 2010 Abstract We consider max coloring on hereditary graph classes. The problem is defined as follows. Given a graph G = (V, E) and positive
3 No-Wait Job Shops with Variable Processing Times
 3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
3 No-Wait Job Shops with Variable Processing Times In this chapter we assume that, on top of the classical no-wait job shop setting, we are given a set of processing times for each operation. We may select
Chordal deletion is fixed-parameter tractable
 Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
Chordal deletion is fixed-parameter tractable Dániel Marx Institut für Informatik, Humboldt-Universität zu Berlin, Unter den Linden 6, 10099 Berlin, Germany. dmarx@informatik.hu-berlin.de Abstract. It
The Index Coding Problem: A Game-Theoretical Perspective
 The Index Coding Problem: A Game-Theoretical Perspective Yu-Pin Hsu, I-Hong Hou, and Alex Sprintson Department of Electrical and Computer Engineering Texas A&M University {yupinhsu, ihou, spalex}@tamu.edu
The Index Coding Problem: A Game-Theoretical Perspective Yu-Pin Hsu, I-Hong Hou, and Alex Sprintson Department of Electrical and Computer Engineering Texas A&M University {yupinhsu, ihou, spalex}@tamu.edu
Learning to Match. Jun Xu, Zhengdong Lu, Tianqi Chen, Hang Li
 Learning to Match Jun Xu, Zhengdong Lu, Tianqi Chen, Hang Li 1. Introduction The main tasks in many applications can be formalized as matching between heterogeneous objects, including search, recommendation,
Learning to Match Jun Xu, Zhengdong Lu, Tianqi Chen, Hang Li 1. Introduction The main tasks in many applications can be formalized as matching between heterogeneous objects, including search, recommendation,
arxiv:cs/ v1 [cs.cc] 28 Apr 2003
![arxiv:cs/ v1 [cs.cc] 28 Apr 2003 arxiv:cs/ v1 [cs.cc] 28 Apr 2003](/thumbs/72/66900170.jpg) ICM 2002 Vol. III 1 3 arxiv:cs/0304039v1 [cs.cc] 28 Apr 2003 Approximation Thresholds for Combinatorial Optimization Problems Uriel Feige Abstract An NP-hard combinatorial optimization problem Π is said
ICM 2002 Vol. III 1 3 arxiv:cs/0304039v1 [cs.cc] 28 Apr 2003 Approximation Thresholds for Combinatorial Optimization Problems Uriel Feige Abstract An NP-hard combinatorial optimization problem Π is said
Word Alignment via Submodular Maximization over Matroids
 Word Alignment via Submodular Maximization over Matroids Hui Lin Dept. of Electrical Engineering University of Washington Seattle, WA 98195, USA hlin@ee.washington.edu Jeff Bilmes Dept. of Electrical Engineering
Word Alignment via Submodular Maximization over Matroids Hui Lin Dept. of Electrical Engineering University of Washington Seattle, WA 98195, USA hlin@ee.washington.edu Jeff Bilmes Dept. of Electrical Engineering
1. Introduction. Abstract. Geometric Rounding: A Dependent Rounding Scheme for Allocation Problems
 Geometric Rounding: A Dependent Rounding Scheme for Allocation Problems Dongdong Ge, Simai He, Zizhuo Wang, Yinyu Ye, Shuzhong Zhang April 11, 2008 Abstract This paper presents a general technique to develop
Geometric Rounding: A Dependent Rounding Scheme for Allocation Problems Dongdong Ge, Simai He, Zizhuo Wang, Yinyu Ye, Shuzhong Zhang April 11, 2008 Abstract This paper presents a general technique to develop
In this lecture, we ll look at applications of duality to three problems:
 Lecture 7 Duality Applications (Part II) In this lecture, we ll look at applications of duality to three problems: 1. Finding maximum spanning trees (MST). We know that Kruskal s algorithm finds this,
Lecture 7 Duality Applications (Part II) In this lecture, we ll look at applications of duality to three problems: 1. Finding maximum spanning trees (MST). We know that Kruskal s algorithm finds this,
Small Survey on Perfect Graphs
 Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Small Survey on Perfect Graphs Michele Alberti ENS Lyon December 8, 2010 Abstract This is a small survey on the exciting world of Perfect Graphs. We will see when a graph is perfect and which are families
Approximability Results for the p-center Problem
 Approximability Results for the p-center Problem Stefan Buettcher Course Project Algorithm Design and Analysis Prof. Timothy Chan University of Waterloo, Spring 2004 The p-center
Approximability Results for the p-center Problem Stefan Buettcher Course Project Algorithm Design and Analysis Prof. Timothy Chan University of Waterloo, Spring 2004 The p-center
ITERATIVE decoders have gained widespread attention
 IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 11, NOVEMBER 2007 4013 Pseudocodewords of Tanner Graphs Christine A. Kelley, Member, IEEE, and Deepak Sridhara, Member, IEEE Abstract This paper presents
IEEE TRANSACTIONS ON INFORMATION THEORY, VOL. 53, NO. 11, NOVEMBER 2007 4013 Pseudocodewords of Tanner Graphs Christine A. Kelley, Member, IEEE, and Deepak Sridhara, Member, IEEE Abstract This paper presents
Influence Maximization in Location-Based Social Networks Ivan Suarez, Sudarshan Seshadri, Patrick Cho CS224W Final Project Report
 Influence Maximization in Location-Based Social Networks Ivan Suarez, Sudarshan Seshadri, Patrick Cho CS224W Final Project Report Abstract The goal of influence maximization has led to research into different
Influence Maximization in Location-Based Social Networks Ivan Suarez, Sudarshan Seshadri, Patrick Cho CS224W Final Project Report Abstract The goal of influence maximization has led to research into different
Unlabeled equivalence for matroids representable over finite fields
 Unlabeled equivalence for matroids representable over finite fields November 16, 2012 S. R. Kingan Department of Mathematics Brooklyn College, City University of New York 2900 Bedford Avenue Brooklyn,
Unlabeled equivalence for matroids representable over finite fields November 16, 2012 S. R. Kingan Department of Mathematics Brooklyn College, City University of New York 2900 Bedford Avenue Brooklyn,
NP-Hardness. We start by defining types of problem, and then move on to defining the polynomial-time reductions.
 CS 787: Advanced Algorithms NP-Hardness Instructor: Dieter van Melkebeek We review the concept of polynomial-time reductions, define various classes of problems including NP-complete, and show that 3-SAT
CS 787: Advanced Algorithms NP-Hardness Instructor: Dieter van Melkebeek We review the concept of polynomial-time reductions, define various classes of problems including NP-complete, and show that 3-SAT
ON WEIGHTED RECTANGLE PACKING WITH LARGE RESOURCES*
 ON WEIGHTED RECTANGLE PACKING WITH LARGE RESOURCES* Aleksei V. Fishkin, 1 Olga Gerber, 1 Klaus Jansen 1 1 University of Kiel Olshausenstr. 40, 24118 Kiel, Germany {avf,oge,kj}@informatik.uni-kiel.de Abstract
ON WEIGHTED RECTANGLE PACKING WITH LARGE RESOURCES* Aleksei V. Fishkin, 1 Olga Gerber, 1 Klaus Jansen 1 1 University of Kiel Olshausenstr. 40, 24118 Kiel, Germany {avf,oge,kj}@informatik.uni-kiel.de Abstract
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME
 PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
PLANAR GRAPH BIPARTIZATION IN LINEAR TIME SAMUEL FIORINI, NADIA HARDY, BRUCE REED, AND ADRIAN VETTA Abstract. For each constant k, we present a linear time algorithm that, given a planar graph G, either
Submodular Optimization in Computational Sustainability. Andreas Krause
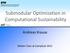 Submodular Optimization in Computational Sustainability Andreas Krause Master Class at CompSust 2012 Combinatorial optimization in computational sustainability Many applications in computational sustainability
Submodular Optimization in Computational Sustainability Andreas Krause Master Class at CompSust 2012 Combinatorial optimization in computational sustainability Many applications in computational sustainability
Formal Model. Figure 1: The target concept T is a subset of the concept S = [0, 1]. The search agent needs to search S for a point in T.
![Formal Model. Figure 1: The target concept T is a subset of the concept S = [0, 1]. The search agent needs to search S for a point in T. Formal Model. Figure 1: The target concept T is a subset of the concept S = [0, 1]. The search agent needs to search S for a point in T.](/thumbs/72/66819767.jpg) Although this paper analyzes shaping with respect to its benefits on search problems, the reader should recognize that shaping is often intimately related to reinforcement learning. The objective in reinforcement
Although this paper analyzes shaping with respect to its benefits on search problems, the reader should recognize that shaping is often intimately related to reinforcement learning. The objective in reinforcement
Parameterized graph separation problems
 Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
Parameterized graph separation problems Dániel Marx Department of Computer Science and Information Theory, Budapest University of Technology and Economics Budapest, H-1521, Hungary, dmarx@cs.bme.hu Abstract.
A Hybrid Recursive Multi-Way Number Partitioning Algorithm
 Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence A Hybrid Recursive Multi-Way Number Partitioning Algorithm Richard E. Korf Computer Science Department University
Proceedings of the Twenty-Second International Joint Conference on Artificial Intelligence A Hybrid Recursive Multi-Way Number Partitioning Algorithm Richard E. Korf Computer Science Department University
Submodularity on Hypergraphs: From Sets to Sequences
 Marko Mitrovic Moran Feldman Andreas Krause Amin Karbasi Yale University Open University of Israel ETH Zurich Yale University Abstract In a nutshell, submodular functions encode an intuitive notion of
Marko Mitrovic Moran Feldman Andreas Krause Amin Karbasi Yale University Open University of Israel ETH Zurich Yale University Abstract In a nutshell, submodular functions encode an intuitive notion of
12.1 Formulation of General Perfect Matching
 CSC5160: Combinatorial Optimization and Approximation Algorithms Topic: Perfect Matching Polytope Date: 22/02/2008 Lecturer: Lap Chi Lau Scribe: Yuk Hei Chan, Ling Ding and Xiaobing Wu In this lecture,
CSC5160: Combinatorial Optimization and Approximation Algorithms Topic: Perfect Matching Polytope Date: 22/02/2008 Lecturer: Lap Chi Lau Scribe: Yuk Hei Chan, Ling Ding and Xiaobing Wu In this lecture,
Feedback Arc Set in Bipartite Tournaments is NP-Complete
 Feedback Arc Set in Bipartite Tournaments is NP-Complete Jiong Guo 1 Falk Hüffner 1 Hannes Moser 2 Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany
Feedback Arc Set in Bipartite Tournaments is NP-Complete Jiong Guo 1 Falk Hüffner 1 Hannes Moser 2 Institut für Informatik, Friedrich-Schiller-Universität Jena, Ernst-Abbe-Platz 2, D-07743 Jena, Germany
Algorithmic Aspects of Acyclic Edge Colorings
 Algorithmic Aspects of Acyclic Edge Colorings Noga Alon Ayal Zaks Abstract A proper coloring of the edges of a graph G is called acyclic if there is no -colored cycle in G. The acyclic edge chromatic number
Algorithmic Aspects of Acyclic Edge Colorings Noga Alon Ayal Zaks Abstract A proper coloring of the edges of a graph G is called acyclic if there is no -colored cycle in G. The acyclic edge chromatic number
9.1 Cook-Levin Theorem
 CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
CS787: Advanced Algorithms Scribe: Shijin Kong and David Malec Lecturer: Shuchi Chawla Topic: NP-Completeness, Approximation Algorithms Date: 10/1/2007 As we ve already seen in the preceding lecture, two
1. Introduction. performance of numerical methods. complexity bounds. structural convex optimization. course goals and topics
 1. Introduction EE 546, Univ of Washington, Spring 2016 performance of numerical methods complexity bounds structural convex optimization course goals and topics 1 1 Some course info Welcome to EE 546!
1. Introduction EE 546, Univ of Washington, Spring 2016 performance of numerical methods complexity bounds structural convex optimization course goals and topics 1 1 Some course info Welcome to EE 546!
Monotone Closure of Relaxed Constraints in Submodular Optimization: Connections Between Minimization and Maximization: Extended Version
 Monotone Closure of Relaxed Constraints in Submodular Optimization: Connections Between Minimization and Maximization: Extended Version Rishabh Iyer Dept. of Electrical Engineering University of Washington
Monotone Closure of Relaxed Constraints in Submodular Optimization: Connections Between Minimization and Maximization: Extended Version Rishabh Iyer Dept. of Electrical Engineering University of Washington
