CORNEA: Drawing large co-expression networks for genes
|
|
|
- Esther Simpson
- 5 years ago
- Views:
Transcription
1 CORNEA: Drawing large co-expression networks for genes Asger Bachmann, Master s Thesis, Computer Science January 2017 Advisor: Christian N. S. Pedersen AARHUS AU UNIVERSITY DEPARTMENT OF COMPUTER SCIENCE
2 Abstract Gene co-expression is of great importance to scientists studying biology and molecular biology. To make sense of expression datasets, we present a tool, CORNEA, to create and visualize large co-expression networks. These networks allows end users to explore gene co-expression relationsships for large datasets with many genes. CORNEA is implemented as a web service at Lotus Base and the tool is described in detail in this thesis. We are limited by three requirements: Ease of maintenance, performance and limited resources. We create a system with high performance by deriving efficient ways to evaluate levels of co-expression as well as calculate co-expression network layouts. Through several experiments on real-world datasets, we evaluate the performance of co-expression measures, and the performance and quality of network layout algorithms. In conclusion, we establish the most suitable algorithm for generating co-expression networks and provide a tool for generating and visualizing large co-expression networks. ii
3 Contents 1 Introduction Problem statement Background Calculating co-expression values Drawing networks Force-based layout Spectral layout High-dimensional embedding Evaluating graph drawings Drawing networks with multiple subgraphs Alternatives to rectangle tessellation Evaluating subgraph layouts Displaying the network to the end user Methods Calculating gene co-expression levels Pearson s r Spearman s ρ Biweight midcorrelation Laying out graphs Fruchterman-Reingold (force-directed) Multilevel force-directed approach Spectral graph layout High-Dimensional Embedding Laying out subgraphs (tessellation) Squarified Treemap Counting the number of edge crossings in a graph Implementation details Difference with CORNEA at Lotus Base Experiments Datasets Lotus japonicus gene expression atlas Medicago truncatula gene expression atlas Breast cancer Calculating co-expression values Performance gain from matrix operations iii
4 5.2.2 Correlation values for real-world datasets Memory consumption: 32 bit or 64 bit floats Memory consumption: Calculating in batches Drawing large graphs Fruchterman-Reingold in batches Evaluating all graph layout algorithms Combining everything Conclusion Correlation measures Layout algorithms Fulfilling the requirements Bibliography 49 Appendix A Survey of correlation measures 53 iv
5 Chapter 1 Introduction In biology, a gene g is said to be expressed when information from g is used to form a gene product such as a protein. By measuring g s level of expression in a number of experiments, or under a number of conditions such as drought, we obtain an expression profile for g. If we consider two genes g 1 and g 2 and their expression profiles, we can calculate the level of co-expression between g 1 and g 2 by comparing their expression profiles. Pairs of genes with similar patterns of expression across a number of experiments, have a high level of co-expression. Gene co-expression is a concept of great interest, as co-expression between genes may indicate functional relationships between the genes, and help uncover regulatory mechanisms in organisms (Aoki et al. 2007). It is therefore beneficial to provide tools for scientists such as biologists and molecular biologists to explore and study gene co-expression. A gene co-expression network is a graph G(V, E) with nodes V and edges E. We will use the terms network and graph interchangeably. Nodes represent genes, and two nodes u, v V are connected with an edge (u, v) E, if the genes which are represented by u and v show a significant level of co-expression. The threshold for significance is arbitrary and based on the measure of coexpression. An edge (u, v) E may have a weight associated corresponding to the level of co-expression between the genes represented by u and v. G is undirected if the measure of co-expression is symmetric and directed otherwise. Typically, some measure of correlation is used as a measure of co-expression, meaning that gene co-expression networks are just correlation networks. We use both term interchangeably here. In short, this thesis explores ways to generate and lay out high quality co-expression networks in an efficient way. We will explore the two primary steps involved in generating the networks: 1) Calculating co-expression values. 2) Drawing networks based on the co-expression values. Based on the results of this analysis, we present a tool, Co-expression Network Analysis (CORNEA), for integrating co-expression networks on any webpage using any kind of expression data. In particular, this tool is implemented at Lotus Base by the thesis author as described by Mun et al. (2016). CORNEA was originally implemented in an ad-hoc fashion without proper prior research, and this thesis is an attempt at performing this proper research. CORNEA can be seen as a practical implementation of the ideas in this thesis, and CORNEA is the main contribution in this thesis. The other important contribution is the evaluation of different 1
6 graph layout algorithms for laying out large correlation networks. The thesis structure is as follows: The remainder of this chapter, Chapter 1, gives a brief introduction to the problem we attempt to solve in this thesis. Background theory and related work is presented in Chapter 2. Chapter 3 describes the methods used in this thesis in detail. We present formulas for efficiently calculating co-expression measures, and algorithms for efficiently drawing or laying out large networks. A brief overview of the implementation details of the experiments and the CORNEA tool that is the product of this thesis is presented in Chapter 4. The experiments that form the basis of the conclusion is presented in Chapter 5. In short, we explore the methods presented in Chapter 3. Chapter 6 contains the thesis primary conclusions based on the experiments in Chapter 5. A report for a 5 ECTS Project in Bioinformatics is included in Appendix A. This report includes details about the co-expression measures used in this thesis. The report can be skipped entirely, but we refer to it in Chapter Problem statement This thesis builds on the thesis author s contributions to Lotus Base (https: //lotus.au.dk/ and Mun et al. 2016), specifically the CORNEA tool for exploring co-expressed genes in networks. CORNEA can be accessed at https: //lotus.au.dk/tools/cornea. The Lotus Base authors wanted to allow their users to visualize and explore co-expression networks based on Lotus japonicus genes expression profiles. Three requirements were posed for the tool: 1) The system should be maintainable by other Lotus Base authors if necessary. In particular, the other Lotus Base authors had relatively limited programming experience, and the Python programming language ( was chosen as the implementation language due to its relative simplicity. 2) The system should have low turnaround or high performance in the sense that it should respond quickly to a user s request. 3) For monetary reasons, the requirement for server resources per user should be as low as possible. Choosing Python as the programming language creates a conflict with requirement 2 as well as requirement 3, because Python has arguably poor performance due to its interpreted nature. Similarly, requirement 3 conflicts with requirement 2. In the end, we are left with a trade-off between ease of maintenance, performance, and budget constraints. 2
7 Chapter 2 Background With the increasing availability of large gene expression datasets, more and more people are interested in gene co-expression networks (for example Stuart et al and Oldham et al. 2006). Consequently, a number of software packages for computing and drawing co-expression networks are available. WGCNA by Zhang, Horvath, et al. (2005) is an example of a very popular software package for analysing correlation networks and in particular gene co-expression networks. The primary focus of WGCNA is not exploratory analysis of networks but on statistical analysis performed directly on the gene expression data. None of these software packages are designed with a non-technical end-user in mind, often requiring knowledge of a programming or scripting language such as R ( for WGCNA. As mentioned in the introduction, this thesis builds on the CORNEA tool at Lotus Base ( and Mun et al. 2016) as implemented by the thesis author. Lotus Base is a genomics resource for the plant Lotus japonicus, and is described in detail by Mun et al. CORNEA, however, is only described superficially in that paper. The tool was implemented in an ad-hoc manner, and we seek here to remedy that by re-creating the tool based on thorough analysis of the algorithms and ideas used. CORNEA allows the user to create networks with different parameters on-the-fly. For example, the user can select the threshold for which genes to include in the final network, and which experiments to include in the co-expression analysis. Several genomics resources for other species than Lotus japonicus support visualizing gene co-expression networks in one way or another. However, these networks are pre-generated and the end-user must depend on the network creators choices of, for example, experiments to include in the network. To our knowledge Lotus Base is the only genomics resource which supports on-the-fly creation of gene co-expression networks as dictated by the end-user (see Table 7 by Mun et al.). This puts extra requirements on the performance of the involved tools, as Lotus Base can not simply pre-generate networks, and must support continually generating networks as users request them. It should be noted, that several pre-generated networks are also available at Lotus Base to excessive resource consumption by particularly popular network configurations. 3
8 2.1 Calculating co-expression values Finding V and E for a gene co-expression network G(V, E) requires calculating all pairwise co-expression levels. In itself this may be an expensive computation if either the number of genes or experiments is very large. Any correlation measure can be used, however, Pearson product-moment correlation coefficient (Pearson s r) is the most widely used correlation measure. Song et al. (2012) compares a number of different measures of co-expression, and concludes that biweight midcorrelation is the best measure to use. The WGCNA package defaults to Pearson s r. Any function returning values between -1 and 1 can be specified, however, and Spearman s rank correlation coefficient (Spearman s ρ) as well as biweight midcorrelation and other measures are also built-in to WGCNA. The thesis author has also explored different correlation measures. This analysis is included in Appendix A and will be referred to when necessary. Consider a dataset with n genes and k experiments. Define M to be a matrix of size n k, with each row in M being a vector of expression levels for a particular gene. Now, define P to be the n n matrix of correlations with entry (i, j) in P being the correlation between rows i and j from M. To calculate P, we have to consider n 2 pairs of genes and for each gene pair perform a calculation involving the k measures of expression from each gene. If n or k is very large, a naive implementation of calculating the correlation for each n 2 pair of genes one at a time, may be very expensive in terms of CPU time. Many measures of co-expression such as Pearson s r can be defined in terms of matrix and vector multiplications, meaning that we can exploit extremely efficient linear algebra libraries and calculate all n 2 correlations using a single call to such a library. This does of course not change the theoretical complexity of the problem, however, in practice it will speed up the calculations significantly. This approach, on the other hand, may require large amounts of memory, because we have to keep all n 2 pairs of correlations, as well as intermediate matrices used for calculation, in memory at the same time. We are left with a trade-off of CPU time usage and memory usage. 2.2 Drawing networks Having obtained the correlation matrix P of pairwise correlations, we can now select from P those pairwise correlations that are larger than some threshold δ r. This filtering gives us V and E for our graph G(V, E). A lot of research focuses on graph drawing algorithms. Some algorithms work with specific types of graphs, for example trees, planar graphs and directed graphs, while other algorithms work for general graphs. Tamassia (2013) present a very nice overview of different approaches to graph drawing. In this thesis, we will focus on general graphs for the following reasons. 1) Gene co-expression networks cannot be represented by trees or any other kind of hierarchical structure. 2) Because of the high connectivity (connections per node), gene co-expression networks are very seldom planar and many edges will overlap each other. 3) The correlation measures used in this thesis are symmetric, meaning that the resulting graphs are undirected. A complete co-expression graph for a dataset of n gene profiles is of course a graph with n nodes and n(n 1) 2 edges. Gene expression datasets may contain 4
9 several thousands or hundreds of thousands of gene expression profiles. The selected threshold for including an edge in the graph will limit the number of edges as well as the number of nodes, because we can simply not draw nodes that doesn t have any edges. We can still end up with very large graphs, however. Together with the demand for on-the-fly generation of networks, we must keep the runtime complexity in mind when selecting graph drawing algorithms. In the following subsections, we present the most widely studied approaches to laying out a general graph s nodes Force-based layout The Fruchterman-Reingold algorithm (Fruchterman and Reingold 1991) is a representative algorithm for the so-called force-directed layout method. The idea behind force-directed algorithms is to model a graph s vertices and edges according to some physical system with forces. Fruchterman-Reingold considers two forces: A repulsion force pushing vertices away from each other, and an attraction force pulling connected vertices towards each other. In each iteration of the algorithm, unconnected vertices are moved away from each other, while connected vertices are moved towards each other. The system has a so-called temperature which is the maximum amount a vertex can be displaced in each iteration. After each iteration, the system cools down, and eventually the graph becomes stable as the temperature ensures that no displacement can take place. Although force-directed layout methods typically produce high-quality layouts, the running time for a naive implementation is high. Fruchterman- Reingold, for example, has a runtime complexity of O( E + V 2 ) per iteration and the number of iterations needed to produce a good layout can be very high. Several ideas have been proposed to improve the runtime complexity. Fruchterman and Reingold themselves suggested a grid approach in which nodes that are distant to each other do not exhibit repulsion force on each other. Depending on the distribution of nodes, this can improve the runtime complexity to O( E + V log( V ). This grid approach is similar to the approach taken by Quigley and Eades (2000) in their FADE algorithm. They find the vertices to include in the repulsion forces using a range query on a quadtree. The main difference between the two algorithms is that FADE lets distant vertices act on a vertex by combining the distance vertices into a single so-called pseudo-node. The time complexity of the two algorithms is the same (at least in theory), and the Fruchterman-Reingold algorithm can also be extended to include pseudonodes if needed. Therefore, we will not pursue the FADE algorithm further in this thesis. Finally, for force-directed approaches, several so-called multilevel algorithms have been proposed (Walshaw 2003 and Hu 2005, for example). In general, multilevel refers to creating an initial coarse graph layout, and then optimizing the layout of the graph afterwards. As an example, Walshaw creates several coarse graph layouts, creating layers of coarser and coarser graphs, each one with fewer nodes than the previous. He then optimize the layout of each layer using a force-directed algorithm such as Fruchterman-Reingold. The optimized layout of a coarser layer is used as the starting point for the layout of a finer layer. According to Walshaw, the approach produces better graphs faster than traditional force-directed algorithms. 5
10 2.2.2 Spectral layout Spectral layout methods are all based on the idea of eigenvalue and eigenvector decomposition. Koren (2005) presents a nice overview of spectral layout methods in general. He shows how the eigenvalues of matrices related to the graph are solutions to minimization problems which attempts to minimize a specific error function. The error function might, for example, punish unconnected nodes that are in near vicinity of each other as well as attempt to minimize the total edge length of the connected nodes which is similar to many force-directed approaches goals. The related matrices are usually the graph s adjacency matrix A, the graph s Laplacian matrix L or the graph s normalized Laplacian L norm. The idea behind spectral graph layout methods is similar to the idea behind principal component analysis, in which we find eigenvalues and eigenvectors of a covariance matrix. No matter which related matrix L you use, we find the eigenvalues and the associated eigenvectors of L and use a subset of the eigenvectors as the coordinates used in the graph layout. As any textbook covering linear algebra will tell you, the eigenvectors of L are the vectors v satisfying Lv = λv λ is the eigenvalue associated with v. Koren (2005) has many more details on spectral graph layouts, and relates them to force-directed layout methods by showing that finding eigenvalues and eigenvectors is equivalent to minimizing a certain energy function. See the description by Koren for more conceptual details, and Section for computational considerations High-dimensional embedding The idea behind high-dimensional embedding algorithms is to generate a layout of a graph in a very high dimension and then projecting it down to 2 (or 3) dimensions. It is easier to lay out a graph in a high dimension without making neither nodes or edges intersect. Harel and Koren (2004) presents one such approach. Their approach claims to be linear in the size of the number of nodes, O( V ). Their algorithm involves breadth-first searches on the graph, so the actual complexity is O( E + V ). For fully connected graphs, E = V 2, making the algorithm quadratic in the number of nodes. Furthermore, for weighted correlation networks, Dijkstra s algorithm (Dijkstra 1959) is suggested, which itself has a complexity of O( V 2 ) (or O( E + V log( V )) when implemented using a heap with specific properties as per Fredman and Tarjan (1987)). Harel and Koren uses eigenvalue decomposition on the covariance matrix of the nodes high-dimensional positions (principal component analysis) to project the layout to fewer dimensions. This makes their algorithm and other highdimensional embedding algorithms using eigenvalue decomposition very similar to spectral layouts. Harel and Koren s algorithm can be seen as a spectral layout algorithm in which the related matrix is the covariance matrix of the high-dimensional coordinates. 6
11 2.3 Evaluating graph drawings Several measures have been proposed for evaluating the aesthetics of graph drawings (Bennett et al. 2007). One commonly used measure is the number of edge crossings in a graph. Purchase (1997) showed that, out of the measures she tested, the number of edge crossings was the measure which influenced the readability of a graph the most. Care should be taken to transfer this result to our scenario, as Purchase evaluated relatively small graphs with tens of nodes and edges, whereas co-expression networks may contain several thousand nodes and significantly more edges. In any case, it seems reasonable to minimize the number of crossing edges, if we wish to make a co-expression network more readable. The sharpest angle formed by two edges of a node is called that node s angular resolution. From a viewer s perspective, it is difficult to separate the paths formed by the edges of a node with low angular resolution. Therefore, it is also a reasonable measure for evaluating a graph drawing. Both the edge crossings measure, and the angular resolution measure are commonly used (Bennett et al and Purchase 2002). The problem of minimizing the number of edge crossings has been shown to be NP-complete (Garey and Johnson 1983), and the problem of maximizing the angular resolution has been shown to be NP-hard (Formann et al. 1993). An algorithm which draws a graph with a minimal number of edge crossings or the maximum angular resolution is therefore not feasible. We can still, of course, evaluate graph drawings using the measures. Finally, Bennett et al. (2007) discusses minimizing the total edge length without referring to any studies evaluating this measure. Intuition tells us that a graph with smaller total edge length is easier to comprehend because nodes will be closer together. This measure cannot stand alone, however, because a graph with many vertices and edges and a very small total edge length might be completely incomprehensible. One reason for this can be that unconnected nodes are positioned too close together. Therefore, we will include a measure of average distance between unconnected nodes, and all four measures should be considered when evaluating a graph. It turns out that a subjective evaluation of the graphs aesthetics can be needed as well because the measures does not tell the full story. 2.4 Drawing networks with multiple subgraphs For a correlation network G(V, E), we might see several non-overlapping sets of nodes and edges. Graphically, this results in multiple clusters sharing no edges. Formally, we have V = m i=1 V i and E = m i=1 E i such that G(V i, E i ) are all correlation networks, and m i=1 V i = m i=1 E i =. In this thesis, we take the following approach to minimize the runtime of the graph drawing algorithm and to optimize the use of screen space. Call each G(V i, E i ) a subgraph (you can also view it as a diconnected component in the larger graph). Draw each of the subgraphs independently of the others using a graph drawing algorithm. Depending on the size of each of the subgraphs, this may reduce the overall graph drawing time significantly. To optimize the use of screen space, a tessellation algorithm is applied to the 7
12 Figure 2.1: An example graph layout from Lotus Base with 16 subgraphs (disconnected components) laid out using Fruchterman-Reingold and tesselated by Squarified Treemap. subgraph s graphs. Tessellation is the process of covering a plane using geometric shapes. In this case, the plane is the 2-dimensional plane corresponding to the user s screen, and the geometric shapes are the subgraphs layout. The relative size of the graphs can be determined, for example, by their node or edge count, and the tessellation algorithm s objective is then to cover the available screen area with the graphs while preserving their relative size. One option for converting a graph to a geometric shape is to use the graph s bounding rectangle. This allows us to use a tessellation algorithm such as Squarified Treemap by Bruls et al. (2000). Although developed for producing hierarchies of nested rectangles called treemaps, we can use the algorithm s tessellation procedure to achieve our goal. Let s i be the size (for example, node or edge count) for subgraph i. We then use Squarified Treemap to lay out m rectangles with rectangle i s areas corresponding to s i. The resulting rectangles are treated as the subgraph s bounding rectangles, and we can scale the subgraphs layout to fit within these bounding rectangles. Figure 2.1 shows an example of a layout produced by this approach. In fact, this kind of subgraph drawing is necessary for the high-dimensional embedding algorithm (Section 2.2.3) to work. When constructing the highdimensional layout, breadth-first search or Dijkstras algorithm will not find nodes in other subgraphs than the one we start in. Therefore, we might end up with some subgraphs without a high-dimensional layout, ultimately defeating the purpose of the algorithm. Several other tessellation algorithms exist, however, as shown by Bruls et al., they tend to create rectangles with very high aspect ratios. On the other hand, Squarified Treemap focuses on creating rectangles with an aspect ratio as close to 1 as possible. Intuitively, a low aspect ratio close to 1 is better than a very high aspect ratio, as the layout algorithm can spread out nodes evenly in both dimensions. Therefore, we will not pursue alternative tessellation algorithms in this thesis except to discuss them briefly them below. 8
13 2.4.1 Alternatives to rectangle tessellation Two problems exist with the tessellation approach described above. 1) Bounding rectangles may waste a lot of space in case the subgraph s overall shape is not close to rectangular. 2) The rescaling of the subgraphs using the calculated bounding rectangles may produce poor quality layouts. Problem 1 can be partly mitigated by using the subgraph s convex hull and a packing algorithm for packing the convex hulls in a rectangle (the user s screen). This problem, like almost all non-trivial packing problems, is NP-complete, but Bennell and Oliveira (2009) presents a nice overview of approximation algorithms related to the problem. In particular, the algorithm by Burke et al. (2007) appears to produce very good results. Problem 1 is not a problem in practice, though, except purely for aesthetic reasons, because the libraries we use to display the graph to the user allows zooming in and out. Therefore, as long as we can show the subgraphs without zooming so far out that we cannot differentiate the subgraphs from each other, we can just let the user zoom in on the individual subgraphs and the wasted space will be a non-issue. On the other hand, having some space between the subgraphs can be a good thing, as it helps separate the subgraphs from each other. Problem 2 can be partly mitigated by still using bounding rectangles but switching to a packing algorithm instead of a tessellation algorithm. This may introduce even more unused space between the bounding rectangles but will ensure that the subgraphs bounding rectangles will keep their aspect ratio. Again, this packing problem is NP-complete but you can find approximate solutions. In this thesis, we will not pursue these alternatives to tessellations and only note that they exist Evaluating subgraph layouts To evaluate the layout of several subgraphs, we average the individual subgraphs evaluation measures (angular resolution, edge crossings and total edge length as described in Section 2.3). Furthermore, as always, runtime is an important evaluation measure, and runtime should be reduced when using this tessellation approach. 2.5 Displaying the network to the end user Eventually, we would like to display the correlation network to an end user. Although extremely important for a final product, this part will play a minor role in this thesis. We will focus on displaying the correlation networks on a website in a browser. Several JavaScript frameworks exists which allow the user to explore a graph, such as a correlation network, when it has been drawn. Two such examples are SigmaJS ( and D3 (https: //d3js.org/). Both libraries support force-directed layouts calculated on the client side in the browser. For very large graphs, this becomes infeasible due to the performance limitations on client-side calculations requiring the user to have a lot of processing power available. Therefore, we will only use a library to display the graph and allow the user to interact with the graph such as zooming in and out. In short, the layout itself is calculated server-side and displayed client-side. Furthermore, to take advantage of the information stored 9
14 in the networks, the networks should be integrated with the website they are implemented on. For example, on Lotus Base, CORNEA is integrated with the Expression Atlas tool on the site, allowing the user to quickly look up co-expressed genes expression profiles. 10
15 Chapter 3 Methods In this chapter, we will present all methods and algorithms used for the experiments presented in Chapter 5. We focus on three parts: 1) Calculating the co-expression levels using correlation measures. 2) Drawing or laying out a graph such as a correlation network. 3) Drawing or laying out several subgraphs which arise from treating separate clusters in a graph as individual graphs. 3.1 Calculating gene co-expression levels This section builds on the report included in Appendix A. The report describes a survey of correlation measures for use in gene co-expression analysis. Apart from the conclusions in the report, we make use of the description the correlation measures as well as two real-world datasets. We will strive to include all relevant information directly in this section, but you can refer to Appendix A if necessary. We define the gene co-expression level between two gene profiles g i and g j to be the correlation between g i and g j for some measure of correlation. Here we represent the three measures of correlation that we will focus on in this thesis. In Appendix A, we conclude that the extra power to detect arbitrary relationships provided by mutual information is not needed. In particular, Song et al. (2012) conclude that gene expression relationships are linear or monotonic, and our conclusion support that. As we also describe in Appendix A, for the sake of generalization, we will present the measures in terms of random variables instead of gene profiles. We will use X and Y to denote two random variables, and we treat a random variable as a row vector of k values. Each value represent an observation of the random variable, for example an expression value for a particular experiment for a particular gene. For a vector X, X i is the ith value of X. For a matrix A, A ij is the entry of A at row i and column j. X Y is the dot product of X and Y, and X is X transposed Pearson s r The Pearson product-moment correlation coefficient (Pearson s r) is probably the most well-known correlation measure, and also the most commonly used measure for co-expression networks. Pearson s r captures only linear correlation. 11
16 From Appendix A we know that for a sample, Pearson s r, denoted by r X,Y is given by r X,Y = cov (X, Y ) σ X σ Y = k i k i ( Xi X ) ( Y i Y ) ( Xi X ) 2 k i ( Yi Y ) 2 (3.1) for random variables X and Y. By treating X and Y as vectors, we can rewrite r X,Y using dot products: r X,Y = X Y X X Y Y Here, X = X X, that is X normalized to have mean 0. Let X (1),..., X (n) denote n random variables of k values. They might for example represent n gene profiles over k experiments. Let M be the n k matrix where row i of M is X (i). Define the matrix M = M M to be M with each row having mean 0. Let A = M M. A is a n n matrix, and A ij = X (i) X (j) Similarly, define the column vector B = diag(a) of length n. The square root is applied element-wise, and diag(a) is the diagonal of A. B is a column vector of length n, and B i = X (i) X (i). Define C = B B to be the outer product of B and B itself transposed as a row vector, such that C ij = B i B j = X (i) X (i) X (j) X (j) Now, we can calculate Pearson s r for all n 2 pairs of gene profiles: P = A C (3.2) Here we used to represent element-wise division. P has been constructed such that P ij = r X (i),x (j). This rather cumbersome derivation of P has the advantage that P can be expressed entirely by linear algebra operations on vectors and matrices. Instead of naively calculating Equation 3.1 for each pair of gene profiles, we can take advantage of highly optimized linear algebra libraries such as the Python library NumPy by Van Der Walt et al. (2011) to calculate Equation 3.2. As in Appendix A, we are only interested in the strength of the correlation, not whether or not P ij > 0 or P ij < 0. Unlike in the appendix, we will consider the normalization P 2 instead of P, simply because that was decided by the designers of Lotus Base. Using P 2 has the advantage that we are more confident in high correlation values as the effect of P 2 is more pronounced for smaller values of P ij. Furthermore, many scientists are used to working with Pearson s r values as r 2 values, for example, when considering the variance explained in a linear regression. For Spearman s ρ and bicor, both described below, we also take the square value of the raw correlation values as the final correlation value. 12
17 Memory consumption and calculating in batches For very large values of n, it might be too memory intensive to calculate Equation 3.2 entirely in memory, as P is of size n 2. Instead, one can calculate P in batches, keeping only a subset of correlation values from each batch. This means calculating Pearson s r between a subset of rows (the batch) and all other rows. For a batch from row i to row j, let A i:j = M i:j M be an (j i) n matrix, where M i:j is row i to row j in M. Using batches, we cannot express calculating B using only matrix and vector operations as above. Instead, we must compute B by iterating through each X (i) : [ B = X (1) X (1),..., X (n) X ] (n) Although this cannot be expressed as a singe matrix operation, it can be calculated efficiently using functions built into the NumPy library. Furthermore, we only have to calculate B once before iterating through the batches. For each batch, C i:j = B i:j B. The resulting correlation values is given by the (j i) n matrix P i:j = A i:j C i:j (3.3) The batch size can vary from 1 to n depending on the amount of memory available. As the batch size approaches n, the time needed to calculate all batches approaches the time needed to calculate Equation 3.2 without batches. Not using batches should always be faster, though, because we can more quickly calculate B by reusing A s diagonal when not using batches. The memory saved is the difference between storing all n 2 correlation values in memory at once and storing (j i)n correlation values in memory at once where j i is the batch size. Additional memory is required to store the correlation values we keep from each batch, but assuming we only keep a small subset of all possible correlation values, the memory savings can be very large. It is worth mentioning that using the batch approach, we can also store batches in non-ram storage such as a disk as they are calculated. This is useful is we do not want to throw away any correlation values from each batch as it is assumed in the discussion above. This solution will be limited by the storage s performance, and non-ram storage tend to be very slow. Exploiting multiple cores If multiple cores (or threads) are available and memory consumption is not an issue, we can use the batch method described above to speed-up the computation. In theory this should result in a speed-up factor that is almost linear in the number of cores available. We write in theory and almost because the computation of B is done before spawning jobs on multiple cores, and because overhead might be associated with running multiple threads on the operating system. We will not pursue this idea further as we are very focused on limiting server resources per user or network generation. 13
18 3.1.2 Spearman s ρ Spearman s rank correlation coefficient (Spearman s ρ) is a measure of rank correlation and builds on Pearson s r. It is less sensitive to outliers because the smallest and largest values are always assigned rank 1 and k, respectively. Spearman s ρ captures monotonic relationships, whereas Pearson s r is only a measure of linear correlation. For two random variables X and Y, Spearman s ρ (denoted by r s ) is defined as Pearson s r on the ranked versions of X and Y : r (s) X,Y = cov (rank(x), rank(y )) σ rank(x) σ rank(y ) rank(x) assigns fractional ranks to the values of X. We can calculate r (s) X,Y using Equation 3.1, but for multiple random variables X (1),..., X (n), we can use the fast matrix version in Equation 3.2 or the batch version in Equation Biweight midcorrelation Although biweight midcorrelation (bicor) also only captures linear relationships, bicor is less sensitive to outliers than Pearson s r. Song et al. (2012) suggests using bicor for co-expression networks. It is based on median values instead of means, which imply that it has a breakdown point of around 0.5 (Wilcox 2012). As such, it is not affected by changing up to 50% of the values, as the median is not affected by that change. In Appendix A, we define the biweight midcovariance between random variables X and Y cov (b) X,Y = 1 k and the biweight midvariance k a i (X i med(x))b i (Y i med(y )) i σ (b) 2 1 X = k k (a i (X i med(x))) 2 i for weights a i and b i as also defined in Appendix A. bicor is then given by X,Y = cov (b) r (b) σ (b) X X,Y 2 σ (b) 2 Y (3.4) Just like for Pearson s r, we can define derive bicor using matrix notation which is useful for calculating bicor between all pairs of random variables X (1),..., X (n). As for Pearson s r, let M be the n k matrix where row i of M is X (i). Define the matrix M = M med(m) to be M with each row having median 0. Define the median absolute deviation (mad) in terms of M : mad(m ) = med(abs(m )) 14
19 Here med is assumed to return a column vector with each row s median. Create the matrix Z = mad(m ) [1,..., 1] Again, is the outer product. Row i in Z is now the vector Z i = [mad(m ) i,..., mad(m ) i ] that is X (i) s median absolute deviation repeated k times. Now, define each row s auxiliary weights in an n k matrix U: U = M (9Z) Here is still element-wise division, and 9 is a constant chosen by Wilcox (2012) as discussed in Appendix A. The final weights for each entry in M is then given by W = (abs(u) 1) ( 1 U 2) 2 assuming the operator returns either 0 or 1. is the Hadamard product (element-wise product), and the powers are Hadamard powers (element-wise power) as well. Now, W is defined such that W ij is X (i) j s weight. Weight each row in M using W : M W = W M Finally, let A = M W M W. Using this A in the derivation of Equation 3.2, we can calculate Equation 3.4 for each pair of X (1),..., X (n) using Equation 3.2 or (a slightly modified) Equation 3.3 if memory consumption is an issue or multiple cores are available. 3.2 Laying out graphs In this section we present the layout algorithms used in this thesis. Each algorithm is described in detail in their own subsection, and example layouts of the four algorithms can be seen in Figure Fruchterman-Reingold (force-directed) Fruchterman and Reingold (1991) presents pseudo-code for the Fruchterman- Reingold algorithm. Here, we derive a version of the algorithm using matrix notation and operations for the same reason as we did it for the correlation measures in Section 3.1: Performance. For simplicity, we assume the area defined in the pseudo-code is 1 and we can re-scale the layout s area afterwards if necessary. For a graph G(V, E), let X and Y be vectors of length V containing the x and y coordinate, respectively, of each vertex. We initialize X and Y to contain random values drawn from the normal distribution N(0, 1). In Section 5.3 we will also experiment with using a Spectral layout (Section 3.2.3) as the initial layout for Fruchterman-Reingold. Let δx be the V V matrix containing the difference between each vertex and every other vertex x coordinates (the subtraction equivalent of an outer product). That is, δx ij = X i X j. Let δy be the equivalent matrix for 15
20 the vertices y coordinates. Now, calculate the Euclidean distance between any two vertices: D = ( δx 2 + δy 2) 1 2 The repulsion force is defined as and the attraction force as f r = k2 D f a = A D2 k The forces both depend on the pairwise distance between the vertices and k. k is the optimal distance between vertices, assuming uniform distribution of vertices, and k = V 1 2. A is the graph s adjacency matrix. If two vertices i and j are not connected, A ij = 0 and the vertices pairwise attraction force, fij a, will be 0 as well. If we wish to weight the edges of the graph, we can replace A with the correlation matrix containing actual correlation values instead of 0s and 1s. A large correlation value between vertices i and j results in a large attraction force, which eventually results in i and j being closer to each other in the final graph. We can now calculate the vertices displacement in their x and y coordinates: ( ) δx X = [1,..., 1] D (f r f a ) ( ) δy Y = [1,..., 1] D (f r f a ) Although slightly convoluted, the formulas are conceptually simple. We multiply each pairwise vertex coordinate difference (normalized to have magnitude 1) by the combined force affecting the vertex pair. This gives us a V V matrix of pairwise displacements due to forces. To get the combined forces affecting each individual vertex, we perform a sum over each row by calculating the dot product with a column vector of V 1s. X and Y is now a column vector of size V as well. Finally, to prevent the displacements from getting too large and the vertices moving all over the graph, we limit the displacement s magnitude to be at most the temperature t of the system before updating the position vectors: X = X + X D min (D, t) Y = Y + Y D min (D, t) Throughout this thesis, we will use a starting temperature of 0.1, and use a linear cooling scheme to decrease the temperature every iteration until it is 0. At the end of each iteration, we scale the coordinates to [0, 1] to prevent the vertices from spreading too far apart: X = X min (X) max (X) min (X) 16
21 Figure 3.1: Example layouts with our scaling method (left) and Fruchterman and Reingold s original method on the same graph. Notice how the nodes clump together near the corners and edges in the original method. Y = Y min (Y ) max (Y ) min (Y ) This scaling is different from Fruchterman and Reingold s original method in which they simply move a coordinate in-bounds. This results in many nodes directly at the border of the [0, 1] domain which are then clumped together. As shown in Figure 3.1, our solution mitigates this somewhat compared to Fruchterman and Reingold s original algorithm. The runtime complexity of the algorithm is O(m( E + V 2 )) for m iterations. In Section we show how to improve this runtime in practice. Memory consumption and calculating in batches The space requirements for this matrix version are O ( V 2) because of the size of all the intermediate matrices. Similarly to the correlation measures (see Equation 3.3), we can calculate the coordinate displacements in batches. This reduces the space requirement to O( V ) for all intermediate matrices. The changes to the calculations are straight-forward. For example, using notation similar to Equation 3.3, the distance matrix D becomes D i:j = ( δxi:j 2 + δyi:j 2 ) 1 2 for a batch from row i to j. D i:j is a (j i) V matrix containing the Euclidean distance between the batch vertices and all other vertices. Although the adjacency matrix A takes O ( V 2) space to store, we can either use the batch approach to reduce the required memory usage by storing unused parts of A on secondary storage such as disk. This can affect performance quite significantly, as we have to read A in batches from the secondary storage. An alternative solution (or a complementary solution) is to store A as a sparse matrix. As we will see, the graphs we are working on, are typically only sparsely connected. Building on NumPy, SciPy (Jones et al. 2001) implements sparse matrices for Python. Although the worst-case storage requirements for the sparse matrix is still O ( V 2), storing A as a sparse matrix can significantly reduce the memory consumption in practice. Using a sparse matrix is equivalent to storing the graph s edges using adjacency lists, however an implementation of Fruchterman-Reingold using 17
22 Figure 3.2: The grid approach visualized. The task is to find the nodes that are within distance 2k of node A as indicated by the blue circle. We immediately discard D and E as they are outside the neighbouring (highlighted) grid cells. We calculate the distance to C and B, and discard C when calculating the repulsive force. adjacency lists, would not be directly compatible with the matrix notation introduced above. Speeding up calculations by using a grid Although they are not very clear on the details, Fruchterman and Reingold suggests speeding up the calculation of their algorithm by placing vertices in a grid and only consider points within a certain radius when calculating the repulsion forces. They argue that a vertex should not be affected by other vertices that are more than 2k away. One way to interpret this, which also conforms to the idea of using batches, is to assign each vertex to a cell in a grid square cells with sides of length 2k. For each cell c, consider the surrounding 8 cells. They must contain the possible vertices that are within distance 2k of the vertices in cell c. When calculating the repulsion force affecting the vertices in cell c, only include the vertices in the 8 adjacent cells. Some of those vertices may be more than 2k away from some of the vertices in cell c, so we should remember to exclude them after calculating the distance between the vertices. By considering all vertices in cell c and all their possible neighbours at once, we can use matrix calculations as described above. The attraction forces are calculated as usual and possibly in batches. Figure 3.2 shows a visualization of this approach. The area containing the grid is 1, the width and height of the grid cells is 18
23 2k, and k = V 1 2. This gives us 1 4k 2 = 1 V 1 = 4 V 4 grid cells. If the nodes are uniformly distributed across the grid cells, we expect only 4 nodes per cell, meaning that the repulsion force calculation can be reduced to an O( V ) operation instead of O( V 2 ), resulting in a total runtime complexity of O(m( E + V )) for m iterations. Of course, in the worst-case this approach does not improve the runtime complexity compared to the standard algorithm, as all nodes may be contained in few grid cells Multilevel force-directed approach Here we present the multilevel force-directed approach as proposed by Walshaw (2003). The idea behind a multilevel algorithm is to create an initial coarse layout of the graph and subsequently refining the layout. In this particular example, we start be defining coarser and coarser layers of the graph with fewer and fewer nodes before refining the layout one layer at a time. Assume we have a graph G i (V i, E i ). The graph G i+1 (V i+1, E i+1 ) of the next layer is constructed by collapsing nodes and edges in G i. We randomly traverse the nodes v of G i, find a neighbour u (that is, (v, u) E i ) and collapse v and u to a single node w V i+1. Edges (v, a) E i and (u, a) E i, become (w, a) E i+1 (or rather, a is replaced by whatever node a is collapsed into). v and u are removed from our list of neighbours so we don t collapse them again in this layer. We do this for as many nodes as possible. Any remaining nodes are simply added to V i+1 without being collapsed. The intuition is that we create a very coarse clustering of the graph s nodes where each cluster consists of at most 2 nodes from the previous layer. We start with our original graph G 1 (V 1, E 1 ) and repeat the above process until we end up with a graph G j (V j, E j ) with V j = t where t is a parameter which must be chosen. Experimentally, we found that t = 0.25 V 1 works well in terms of performance, that is we collapse nodes until we have less than 25% of the number of nodes in the full graph. These two nodes in G j are laid out randomly. The Fruchterman-Reingold layout algorithm is applied to G j which results in a refined layout. This refined layout is used as the initial layout for G j 1 in which the nodes of G j are expanded to their original nodes which share the initial position from the refined layout. We can then repeat the layout refinement using Fruchterman-Reingold to and up with an initial layout for G j 2. We repeat this procedure until we have a refined layout for our original graph G 1. The idea behind this layered Fruchterman-Reingold approach is that we end up with an initial layout for G 1 which is better than random. Therefore, the final refined layout should become stable after fewer iterations compared to simply running Fruchterman-Reingold using a random initial layout. For densely connected graphs, we end up with O(log( V )) layers because we can halve the number of nodes in each layer. With sparsely connected graphs, we risk ending up with O( V ) layers because we can only collapse 2 nodes in every layer. Assuming the best case of O(log( V )) layers, we end up with a runtime complexity of O(log( V )m( E + V 2 )) which will be an improvement over the 19
24 standard Fruchterman-Reingold algorithm if log( V )m is less than the number of iterations required in the standard algorithm. This is not the whole story, of course, as we can expect to use fewer iterations and less time per iteration on the coarsest layers of the graph as they have fewer nodes and edges. Here, we chose to increase the number of iterations per layer in a linear fashion. That is, if we use 50 iterations at the last layer, and we have 5 layers, we increase the number of iterations by 10 per layer Spectral graph layout Koren (2005) writes that the spectral approach for graph visualization computes the layout of a graph using certain eigenvectors of related matrices. The related matrices is usually the graph s adjacency matrix A, the graph s Laplacian matrix L which is defined as L = D A D is the degree matrix which is a diagonal matrix with D ii being the degree of vertex i. The degree of vertex i can be found by summing over row i of A. Instead of L, we can use the so-called normalized Laplacian L norm defined by L norm = I D 1 2 AD 1 2 D is the degree matrix from before and I is the identity matrix. The powers are computed element-wise in D. A, L and L norm are all symmetric, and we can use specialized algorithms for finding the eigenvectors and eigenvalues. Examples of such algorithms are Lanczos algorithm (Lanczos 1950), and Cuppen s divide-and-conquer approach (Rutter 1994). SciPy uses Lanczos algorithm for sparse matrices (utilizing the ARPACK library). A variant of the divide-and-conquer approach is used by NumPy (through the use of the LAPACK library) for dense matrices. When using A, we should use the eigenvectors corresponding to the two largest eigenvalues. When using L or L norm, we should use the eigenvectors corresponding to the second-smallest and third-smallest eigenvalues. Because the rows of L are linearly dependent, there will always be a zero eigenvalue which we skip. The same applies for L norm. For either A, L or L norm we use the two relevant eigenvectors, v 1 and v 2, as the nodes x and y coordinates respectively High-Dimensional Embedding As a representative algorithm for the high-dimensional embedding approach, we present the algorithm by Harel and Koren (2004). The algorithm has 2 parts: 1) We find a very coarse high-dimensional layout of the graph s nodes. 2) We project the high-dimensional layout to 2 dimensions. Harel and Koren proposes using principal component analysis (PCA) for the second step. Assume we want to use m dimensions in the high-dimensional layout. Harel and Koren suggests m = 50. The intuition behind the algorithm is to associate each dimension i [1; m] with a pivot p i. The pivots should be approximately uniformly distributed on the resulting high-dimensional layout. As seen in Figure 1 in Harel and Koren s paper, we select pivot p 1 randomly from V. Then for each dimension i, we find all nodes shortest path to p i. The lengths of the 20
25 shortest paths are used as the nodes coordinate in dimension i. We then choose pivot p i+1 as the node with the longest shortest path to any of the previous i pivots p 1,..., p i in order to maximize the spread of the pivots. As noted in Section 2.4, high-dimensional embedding requires that G only has a single connected component, that is, all nodes are connected to each other directly or indirectly through other nodes. If not, some nodes may not recieve a high-dimensional position, simply because the chosen pivots are in other connected components. One could imagine changing this algorithm to ensure that all connected components are represented by a pivot, however, this is almost the same as simply running the original algorithm for each connected component, which is the approach we take in this thesis. Projecting coordinates to 2 dimensions As mentioned in Section 2.2.3, we can view this algorithm as a spectral layout algorithm for which the related matrix is the covariance matrix of the highdimensional coordinates. Let M be the n m matrix where each row corresponds to the n nodes coordinate in dimension m. Normalize the M to have mean 0 in each dimension, M = M M. Construct the covariance matrix, cov(m ) = M M Now, apply an eigenvalue decomposition algorithm on cov(m ) and select the eigenvectors with the largest corresponding eigenvalues, v 1 and v 2. Unlike for the spectral algorithms where we simply use the eigenvectors as coordinates, we reduce the high-dimensional coordinates to 2 dimensions using the eigenvectors: X = M v 1 Y = M v 2 X and Y are now our final 2 dimensional coordinates. Runtime complexity If we have a graph without weights, we can find the shortest path using breadth-first search for a total runtime complexity of O(m( E + V )). If we want to weight the edges, we can use Dijkstra s algorithm (Dijkstra 1959) for a total runtime complexity of O(m( V 2 )). Using a Fibonacci heap in the implementation, we can improve the total runtime complexity to O(m( E + V log( V ))) (Fredman and Tarjan 1987). The runtime complexity of finding the 2 relevant eigenvalues depends on V and m, however, the total runtime of this step is very small compared to finding the coarse, high dimensional positions. 3.3 Laying out subgraphs (tessellation) As described in Section 2.4, a correlation network may consist of several separate subgraphs. This section describes the Squarified Treemap algorithm which we use to determine the positions of these individual subgraphs in a final layout displayed to the user. We use the subgraphs bounding rectangles relative sizes 21
26 Figure 3.3: Example layouts using the 4 overall algorithms: Fruchterman- Reingold without grid (top left), multilevel force-directed (top right), spectral based on non-normalized-laplacian (bottom left), and high-dimensional embedding (bottom right). For this particular data, the spectral layout is not very good with lots of overlapping edges and nodes. You can clearly see the breadth-first search s influence on the high-dimensional embedding algorithm. 22
27 (a) Input areas unsorted. (b) Input areas sorted by size (ascending). Figure 3.4: An example of a tessellation produced by Squarified Treemap. The rectangles are coloured, and the numbers are the rectangles areas and aspect ratios. In both cases, the input is 4, 7, 1, 2, 10, 2, 5, however, for (b), the input is sorted in ascending order. The average aspect ratio is 1.7 for both (a) and (b), but the input order clearly matters to the final layout. as input to make sure the larger subgraphs take up more space than the smaller subgraphs. Two simple measures for a subgraph s size are its node count and edge count. In this thesis, we will use node count. Subgraphs can be found as disconnected components using breadth-first search in the adjacency matrix of the overall graph Squarified Treemap Bruls et al. (2000) present the Squarified Treemap algorithm used to create treemaps which are hierarchies of nested rectangles used to visualize information. We make use of the squarify method from the paper, which produces a single layer of the treemap, that is a tessellation of rectangles within a larger rectangle. Figure 3.4 shows examples of running the algorithm on a small data set. From the figure, it is clear that the input order matters to the final tessellation. Based on subjective evaluation of layouts such as those in Figure 3.4, we choose to always sort input in ascending order. The number of subgraphs, that is, the size of the input to Squarified Treemap, is very limited compared to, for example, the number of nodes or edges, and sorting does not influence the overall runtime. When laying out a rectangle, squarify considers two alternatives: 1) The rectangle is added to the current row, or 2) a new row is started and the rectangle is added to this row. Which alternative is chosen depends on whether adding the rectangle will improve the layout of the current row or not. Bruls et al. define the worst value of a row r as ( w 2 r + s 2 ) r max, w 2 r s 2 r w is the width of the containing rectangle (that is, the shortest of the two dimensions which may change whenever new rectangles are added to the con- 23
28 tainer). s r is the sum of all the areas in the current row, r, and r + and r are the maximum and minimum area in r, respectively. The idea is then that if the value of the worst function increases when adding a new rectangle, we should add the rectangle to a new row instead. Bruls et al. present pseudo-code for a recursive implementation of squarify which we won t repeat here. In practice, as we shall see, the number of areas input to this algorithm (that is, the number of subgraphs in a graph) is quite limited. However, in any case, the runtime complexity of the algorithm is linear in the number of areas. Specifically, for each area, we either add the area to the current row, or start a new row to which we can immediately add the area. Therefore, we only consider each area once. 3.4 Counting the number of edge crossings in a graph Although not of primary interest to the thesis, we include here a brief description of the approach taken to count the number of edge crossings in a graph. Instead of naively checking all O( E 2 ) pairs of edges for intersections, we construct bounding rectangles for each edge and insert it into an R-tree. The R-tree allows checking bounding rectangle intersections efficiently. For each edge e i, we only have to check for intersections between e i and another edge e j if e i and e j s bounding rectangles intersect. In the worst case, this can of course result in just as many intersection checks as the naive solution, however, in practice the number of intersection checks are reduced significantly. We performed a simple experiment on a network generated from a random subset of the LjGEA dataset. The network had V = and E = and was laid out using 50 iterations of the Fruchterman-Reingold algorithm. A naive implementation would check all pairs of edges for intersections, whereas the R-tree version only performed such checks, that is roughly 1/30 of the checks. Because finding rectangle intersections in the R-tree is relatively inexpensive and is only performed E = times, the total runtime for the evaluation measure is significantly reduced. Several variations of the so-called line-sweep type of algorithms exists for calculating the intersection between a set of line segments such as edges. See for an overview. The optimal worst-case complexity of those algorithms are O( E log( E ) + c) where c is the number of edge crossings, that is, the runtime complexity is output sensitive. For our small experiment, c = and the number of intersection checks would be for such an algorithm - when disregarding any low-order terms hidden by the O-notation. This is an improvement of a little more than 2, however an informal experiment (not included here) showed that one such line-sweep algorithm did not improve the actual runtime compared to the R-tree approach. 24
29 Chapter 4 Implementation details Code used in the thesis is available at This includes both the implementation of the algorithms used as well as the experiments performed in the next chapter. Everything is implemented in Python 3 ( The implementation of the correlation measures and layout algorithms are implemented from scratch and are almost self-contained. They only rely on the NumPy and SciPy libraries for matrix and vector operations as well as eigenvalue decomposition algorithms. The edge crossings evaluation measure optionally depends on the Rtree package ( for performance reasons as explained in Section 3.4. Furthermore, MatPlotLib ( and NetworkX ( are used for the figures in the thesis. Although the edge crossings measure is implemented in Python 3, we also ported the code to Rust ( using the Spatial crate ( for R-trees. The purpose was to test the implementation s performance as the Python implementation took a long time to evaluate graphs with many edges. An informal test showed that the Rust implementation was 51.5 times faster than the Python implementation (3.01 seconds and seconds, respectively). This test was on a relatively small graph with edges (MtGEA dataset, correlation threshold 0.85). The largest graph we work with has 1.5 million edges (see Section 5.3). The Rust implementation took 12 hours and 12 minutes to evaluate that graph. As we did not want to wait around 25 days for the evaluation to complete, we ended up using the Rust implementation in the rest of this thesis. To support as many simultaneous users as possible with as few CPU cores as possible, we require that all experiments are performed using only a single thread or core. Specifically, NumPy and SciPy supports multi-threading using the underlying BLAS (Basic Linear Algebra Subprograms), and we limit the BLAS implementation to only use a single thread. To preserve memory, we attempt reuse as much memory as possible instead of allocating new memory. For example, we do in-place division of A and C when calculating P in Equation 3.2 and store the result back in A instead of actually allocating new memory for P. Furthermore, we use 32 bit floating points numbers (floats) instead of 64 bit floats to cut the memory usage in half when possible. Section shows an experiment which confirms that this does not affect the calculated values too much. 25
30 4.1 Difference with CORNEA at Lotus Base The system as implemented at Lotus Base under the name CORNEA includes a queuing system for requests for network creations. That is, when a user submits a request to create a co-expression network, it is added to a queue which is continually emptied as resources becomes available. This queuing system is not a part of the code available at Similarly, Sigma.js, the library used to display the network in the user s browser, is enhanced to include support for z-ordering the nodes and edges. This allows us to show highlighted nodes and edges in front of non-highlighted nodes and edges making them easier to see. This code is also only a part of CORNEA. The changes to Sigma.js and the queuing system is available at Lotus Base s GitHub repository: This repository also contains the remaining code which constitutes the entire CORNEA tool and its integration with Lotus Base. At the time of writing this, the CORNEA only supports Fruchterman-Reingold (non-grid) in conjunction with Squarified Treemaps for laying out graphs, and Pearson s r as the correlation measure. In order to implement the remaining layout methods and correlation measures, use the code available at this thesis repository. 26
31 Chapter 5 Experiments This chapter presents the experiments performed using the methods described in the previous chapters. The datasets used are also described. All experiments are performed on the GenomeDK HPC cluster ( on nodes with 2.67 GHz CPUs with 8 cores and 64 GB memory, however, as described in Chapter 4, only a single core is used per experiment. 5.1 Datasets Lotus japonicus gene expression atlas As described by Mun et al. (2016), Lotus Base uses the Lotus japonicus gene expression atlas (LjGEA) by Verdier et al. (2013) for gene expression data on Lotus japonicus. LjGEA probe data is available from v2/ and contains probes over 81 experiments. To map from probes to genes, we follow the same approach as Mun et al.: We have mapped probe identifiers from the LjGEA dataset against the annotated proteins of L. japonicus genome v3.0 by performing BLAST alignments of LjGEA probe set against the predicted transcripts from L. japonicus genome v3.0 and selecting for hits with the lowest E-value(s). This mapping results in data for n = genes over k = 81 experiments Medicago truncatula gene expression atlas Although LjGEA is the dataset of primary interest because it is the dataset used at Lotus Base, we want to ensure the conclusions in this thesis are more general. The Medicago truncatula gene expression atlas (MtGEA) is similar in nature to LjGEA, except that is of course contains expression data for a different plant. This dataset is described in Section 4.2 in Appendix A, and contains n = genes over k = 274 experiments Breast cancer The 3rd dataset is from an experiment involving detecting early stage breast cancer in humans with microrna (Kojima et al. 2015), downloaded from This dataset helps ensure our conclusions hold for non-plant datasets as well. Furthermore, it 27
32 is also an example of a dataset with very large k compared to LjGEA and MtGEA. The dataset contains n = patients and k = microrna expression levels. Some of the expression levels are non-existing (indicated by null in the data files). We replace those levels by the mean of the microrna s other expression levels (that is, the column mean). There are only of such values out the total values. Furthermore, several of the micrornas have very low variance in their expression levels. In short, this results in all patients being highly correlated with all other patients, in fact 84% of all patient pairs have a correlation level higher than 0.85 (using Pearson s r). To remedy this, we chose to remove all micrornas with expression level variance less than 1. This brings the aforementioned percent of patient pairs with Pearson s r correlation levels higher than 0.85 down to 3% which is comparable to the LjGEA and MtGEA datasets. We remove 637 low-variance columns from the dataset, resulting in a dataset with n = and k = which we refer to as cancer. 5.2 Calculating co-expression values Performance gain from matrix operations In the following experiment, we seek to confirm that the matrix version of the correlation measures is faster than a naive, one-at-a-time implementation. The naive implementations of Pearson s r, Spearman s ρ and bicor are described in Appendix A and are implemented in pure Python as described in Section 4.1 in Appendix A. The naive version of bicor uses quickselect to select median values which was the fastest of the naive bicor implementations. We generate n random vectors of length k = 100 by sampling nk times from the normal distribution N(0, 1). We then calculate all pairs of correlation values using the three naive and three matrix versions of the correlation measures. For the naive versions, we only calculate n(n+1) 2 pairs that are unique due to symmetry. We let n vary from 100 to in steps of 100, and for each n we report the best of 5 runs on the same random matrix. In total, this gives us 10 data points for each algorithm. The results are shown in Figure 5.1. The matrix implementations are faster by a huge margin even for such small ns as we see here. We can clearly discard the naive implementations in favour of the matrix operations, and we will do that for the rest of the thesis. To show how the matrix implementations scale relative to each other, we re-do the experiment without the naive implementations and for values of n between and in steps of The results are shown in Figure 5.2. Here, we can see that the sorting required by Spearman s ρ has a price. Whether or not it matters in the larger context is not clear yet. Somewhat surprisingly, bicor is almost as fast as Pearson s r even though a lot more work is involved in calculating bicor including finding median values. The result of a similar experiment with k = can be seen in Figure 5.3. We can see that the time spend on ranking the vectors goes down in Spearman s ρ. That is, the time we spend ranking vectors is outgrown by the time we spend calculating the correlations between the ranked vectors. We can also see that the absolute runtime increases by a factor of 5 for an increase in k of a factor of
33 Pearson's r (matrix) Spearman's rho (matrix) Bicor (matrix) Pearson's r Spearman's rho Bicor Bicor n Figure 5.1: Comparing naive pure-python implementations of correlation measures to matrix implementations using NumPy. Pearson s r (matrix) and Bicor (matrix) are completely overlapping. The time grow as n 2 because we work on all pairs of n vectors Pearson's r Spearman's rho Bicor Bicor n Figure 5.2: Comparing matrix implementations of correlation measures with n 100 matrices. The time grow as n 2 because we work on all pairs of n vectors. 29
34 8 7 6 Pearson's r Spearman's rho Bicor 5 Bicor n Figure 5.3: Comparing matrix implementations of correlation measures with n matrices. The time grow as n 2 because we work on all pairs of n vectors Correlation values for real-world datasets To test the performance of the correlation measure implementation on real-world data, we ran the three correlation measures on all pairs of genes in our three real-world datasets, LjGEA, MtGEA and cancer. To simulate support for the requirement of selecting arbitrary subsets of the experiments in each dataset, the x axis is k, that is, the number of experiments included. Generally, there is k! subsets, however, the subsets can only have k different sizes. Therefore, we select the first k experiments as our subset for each value of k. To reduce the runtime of the experiment, we increase k in different step sizes depending on the dataset. We always include the full dataset, though. The results are shown in Figure 5.4, Figure 5.5, and Figure 5.6, respectively. The best of 5 runs are reported for each measure. As expected, the datasets with largest n takes the longest time to calculate. Also, to no ones surprise, increasing k increases the runtime. However, even for low values of k the runtime is several seconds for LjGEA and MtGEA. As we also saw in Section 5.2.1, the relative difference between Spearman s ρ and the other measures is smaller when n is larger. For large k as in Figure 5.6, the difference between Pearson s r and bicor becomes more apparent. We can also see that the runtime difference between the measures is small enough that it does not matter which correlation measure we use in terms of runtime. This is also in-line with the experiments reported in Appendix A where Pearson s r, Spearman s ρ and bicor have approximately the same runtime. We can see that calculating the correlation values takes a significant amount 30
35 Pearson's r Spearman's rho Bicor Bicor k Figure 5.4: Calculating all pairwise correlation values in LjGEA using the first k columns. n = and k up to 81 with step size 20. of time for LjGEA even with these matrix version of the correlation measures. Hence, to be in line with the requirements for Lotus Base, it is important to make this part of the overall process as fast as possible. On the other hand, the total runtime quickly drops when n is lower. For example, for the cancer dataset, even with correlation values, the total runtime is only a few seconds for all k even though k is relatively large for this dataset. For comparison, humans have roughly protein-coding genes (Pertea and Salzberg 2010), while rice have up to protein-coding genes (Goff et al. 2002), resulting in up to gene pairs for rice. The total runtime on such datasets will of course also depend on the number of experiments included in the dataset Memory consumption: 32 bit or 64 bit floats First, we show that the choice of using 32 bit floats instead of 64 bit floats (see Chapter 4) does not make a significant difference. Using all three correlation measures, we compute the correlation matrices P 32 and P 64 using 32 bit and 64 bit floats, respectively. We then look at the maximum absolute deviation between the values in P 32 and P 64. That is, max ( P 32 P 64 ) where is element-wise subtraction, and the absolute values are taken elementwise as well. This gives a number showing how similar P 32 and P 64 are. Although it does not convey statistical significance, it does show whether or not the loss of precision from using 32 bit floats has a large effect or not. 31
36 8 7 Pearson's r Spearman's rho Bicor 6 Bicor k Figure 5.5: Calculating all pairwise correlation values in MtGEA using the first k columns. n = and k up to 274 with step size Pearson's r Spearman's rho Bicor 2.0 Bicor k Figure 5.6: Calculating all pairwise correlation values in cancer using the first k columns. n = and k up to with step size
37 Dataset Pearson s r Spearman s ρ Bicor LjGEA MtGEA cancer Table 5.1: Calculating the maximum absolute deviation resulting from using 32 bit floats instead of 64 bit floats. Table 5.1 shows the result of calculating the maximum absolute deviation between P 32 and P 64 for the three real-world datasets. The effect of using 32 bit floats only shows in the 5th or later fractional digit. From experience on Lotus Base, we know that users rarely care about anything but the first 2 fractional digits, and we conclude that 32 bit floats are good enough for our use case. Although this is not hard statistical evidence, we treat it as such, and we can cut the memory usage of our implementation in half using 32 bit floats instead of 64 bit floats. We can see that the more involved formulas means that the loss of precision in 32 bit floats in bicor compared to Pearson s r and Spearman s ρ. Intuitively, the error due to reduced precision can accumulate in bicor simply because there are more calculations involved. On the other hand, Spearman s ρ turns out to be less affected by the loss of precision in this experiment which can of course be attributed only to the ranking involved Memory consumption: Calculating in batches Figure show the memory consumption and total runtime of Pearson s r on the three real world datasets for different batch sizes. We ignore Spearman s ρ and bicor because the extra memory usage and runtime imposed by those measures are negligible. The memory usage is the maximum memory used during the calculations and include storing the dataset in memory. The batch sizes are chosen uniformly from 100 to n for all three datasets. It is clear, that we have a trade-off between memory consumption and runtime. However, it is also clear that we can limit memory consumption drastically without increasing the runtime. For example, for LjGEA in Figure 5.7, the runtime is almost the same for batch sizes and onwards, while the memory usage drastically increases. A batch size between and seems to be the most reasonable compromise in terms of limiting server resources. For MtGEA in Figure 5.8, the results are not nearly as clear, and the total memory consumption, even without batches, is quite limited. Even then, a batch size of around seems like a reasonable compromise between runtime and memory consumption. Finally, for cancer in Figure 5.9, because the dataset is so small, we do not really save any memory in absolute terms, and batching does not really make sense for this dataset. The first couple of batch sizes in Figure 5.8 and Figure 5.9 show constant memory usage of around 300 MB. A likely explanation for this is that Python preallocates around 300 MB of memory when it starts. A deeper investigation of Python s memory model is needed to find the actual explanation. 33
38 Memory (MB) Time (s) Memory (MB) Batch size Time (s) Figure 5.7: Memory consumption and total runtime for different batch sizes using Pearson s r on the LjGEA dataset. For the runtime, the best of 5 runs is reported for each batch size. The batch sizes are chosen uniformly in the range [log 10 (100), log 10 (n)] Memory (MB) Time (s) Memory (MB) Time (s) Batch size 0 Figure 5.8: Memory consumption and total runtime for different batch sizes using Pearson s r on the MtGEA dataset. For the runtime, the best of 5 runs is reported for each batch size. The batch sizes are chosen uniformly in the range [log 10 (100), log 10 (n)]. 34
39 Memory (MB) Time (s) 7 Memory (MB) Time (s) Batch size 0 Figure 5.9: Memory consumption and total runtime for different batch sizes using Pearson s r on the cancer dataset. For the runtime, the best of 5 runs is reported for each batch size. The batch sizes are chosen uniformly in the range [log 10 (100), log 10 (n)]. 5.3 Drawing large graphs Fruchterman-Reingold in batches The non-batch version of Fruchterman-Reingold may use a lot of memory to store the intermediate calculations such as the n 2 pairwise distances between all nodes. Therefore, like for the correlation measure in Section 5.2.4, it is interesting to investigate the compromise of memory consumption and CPU usage for various batch sizes. We create a dataset from each of the real-world datasets by calculating all pairwise correlation values using Pearson s r and arbitrarily setting a correlation value threshold of 0.7 and The memory usage is the maximum memory use monitored during the layout process. We do not consider the non-grid version of the algorithm as any potential savings in the calculation of the repulsive forces are negated by the requirement to calculate the distance between all pairs of nodes when considering the attractive forces. The times are chosen as the best of 5 runs for a particular batch size. The batch sizes are chosen uniformly from to n for all three datasets. We remove any small subgraphs (less than size 15) but perform the layout on the combination of all subgraphs. This will overestimate the memory usage and runtime compared to a real-world scenario where we lay out the subgraphs individually, however, it serves to show how the memory and runtime scales with different batch sizes. Figure 5.10 and Figure 5.11 shows the results of this experiment for the LjGEA dataset. We do not include the figures for MtGEA and cancer as you can draw the same 35
40 Memory (MB) Time (s) Memory (MB) Time (s) Batch size 0 Figure 5.10: Memory usage and runtime for different batch sizes for the Fruchterman-Reingold layout algorithm on the LjGEA dataset. The correlation threshold is 0.7. V = and E = conclusions from them as from the LjGEA figures. Surprisingly, the results are very different from the results in Section We can save a lot of memory by using a small batch size, however this doesn t come at a cost in terms of runtime. In fact, in Figure 5.10, it is quicker to use a small batch size rather than a large one. Initially, we saw the same results in Section for the correlation measures, however, this turned out to be due to multiple threads being used by the underlying BLAS library used by NumPy on our system, OpenBLAS. OpenBLAS is apparently better at parallelizing smaller matrices, that is, smaller batch sizes. After forcing OpenBLAS to use a single thread, this effect was removed, and we saw the results we expected as indicated in Section This, however, was not the case with this experiment. Benchmarking the Fruchterman-Reingold algorithm line-by-line showed that the single most expensive part of the algorithm is calculating the distances between all pairs of nodes (40% of the time or more depending on the number of nodes). For some reason, this particular step is significantly slower for larger matrices than for multiple iterations of smaller matrices. Therefore, any reduction from using larger matrices in the other steps of the algorithm is negated by this step. We have tried using NumPy s built-in functions for calculating norms as well as calculating the distance in separate, explicit steps and the results are the same. At this point, we are unable to explain this effect. Although a batch size of is best both in terms of memory usage and runtime, we decide to use a batch size of The reason is that this artifact of large batch sizes being slower might be due to an issue in our benchmarking system, and a batch size of still limits the RAM usage greatly without increasing the runtime. From Section a batch size of made the best compromise of memory usage and runtime for the correlation measures, and 36
41 Memory (MB) Time (s) Memory (MB) Time (s) Batch size 0 Figure 5.11: Memory usage and runtime for different batch sizes for the Fruchterman-Reingold layout algorithm on the LjGEA dataset. The correlation threshold is V = and E = we would expect this experiment to follow the same pattern as the correlation measure experiment in the absence of the observed artifact. This reasoning also applies to the multilevel force-directed approach (Section 3.2.2) in which we use Fruchterman-Reingold on each layer. The multilevel approach will in total use more memory because we have to store adjacency matrices for each layer, however, laying out each layer can be cheaper in terms of memory usage. The other approaches to graph drawing, spectral layouts (Section 3.2.3) and high-dimensional embedding (Section 3.2.4), does not use significantly more memory than storing the graph itself does. Therefore, they do not benefit from any kind of batching of calculations Evaluating all graph layout algorithms Here we attempt to evaluate all our graph layout algorithms using the quality measures established in Section 2.3. We perform the experiment using correlation threshold 0.7 and 0.85 and all three datasets, although, we only present and interpret the results from LjGEA as the other datasets give rise to the same conclusions. For each of the following algorithms we follow the same procedure: After finding all subgraphs G i (V i, E i ) from the correlation values using a minimum subgraph size of 15, we run the layout algorithm on the subgraphs one at a time. The layout algorithm is profiled for total runtime (best of 5 runs) and maximum memory usage. We scale the nodes positions according to a tessellation using Squarified Treemap and evaluate the nodes global positions, that is the full graph G(V, E), according to the quality measures. We run the following layout algorithms: 37
42 Fruchterman-Reingold (FR) using a batch size of 5 000, a random initial layout, and 50 iterations. FR in the grid version using a batch size of 5 000, a random initial layout, and 50 iterations. Spectral using the Laplacian. Spectral using the normalized Laplacian. Spectral using the adjacency matrix. FR using a batch size of 5 000, initial positions from the Spectral (Laplacian) algorithm, and 30 iterations. FR in the grid version using a batch size of 5 000, initial positions from the Spectral (Laplacian) algorithm, and 30 iterations. Multilevel force-directed approach where we create layers until 25% of the original number of nodes are left. FR (batch size 5 000) is used at each level with 30 iterations in the final layer and a linear increase in iterations at each layer. Multilevel force-directed approach as above but with the grid version of FR. High-dimensional embedding with min( V i, 50), that is up to 50, pivots. We run each algorithm with both weighted and unweighted edges, however, the weighting only makes a difference to the high-dimensional embedding algorithm, so we don t show the weighted results for the other layout algorithms. The results are shown in Table 5.2 and Table 5.3. First, the reason why the weighing means to much to the high-dimensional embedding algorithm is because we use an entirely different shortest-path algorithm when using weights. Namely, we use BFS for unweighted graphs and Dijkstra s algorithm for weighted graphs. This is especially evident in the runtime, however, the number of edge crossings are also significantly higher for the weighted version. On the other hand, the angular resolution, the edge length and the unconnected nodes distance measure are all better for the weighted version. Disregarding this layout algorithm, whether or not you use weighted or unweighted edges are largely a matter of preference and does not affect the quality measures. The spectral approaches are by far the fastest as well as the best in terms of memory usage (including unweighted high-dimensional embedding). This comes at a price in terms of edge lengths and unconnected node distances (Laplacian and normalized Laplacian versions), and edge crossings (adjacency matrix version and all three versions for threshold 0.85). These statistics does not tell the full picture, though. The bottom left graph of Figure 3.3 is very representative of layouts produced by the spectral methods. It appears that nodes with high connectivity are clumped together closely, and nodes with lower connectivity are dispersed extremely far from the other nodes. As our graphs are very imbalanced in terms of connectivity (that is, some nodes have very high connectivity and some nodes have very low connectivity), this heavily 38
43 impacts the spectral layouts. In many presentations of spectral algorithms, for example by Koren (2005), they use so-called mesh graphs in which almost all nodes are connected to, for example, 3 or 4 other nodes depending on the mesh structure. Similarly to the spectral approaches, although the unweighted high dimensional embedding approach do very well, it tends to produce graphs looking like trees such as the one in the bottom right of Figure 3.3. This gives the impression that the underlying data is hierarchical which correlation data is not. Therefore, this may not be the best choice of algorithm for laying out correlation networks and presenting them to end user without prior education. The reason for the extreme number of edge crossings in Table 5.2 (threshold 0.7) is because we end up with only 2 subgraphs with a total of edges shared among them. On average, each of the nodes are connected to 75 other nodes, and the resulting graph is extremely non-planer with a lot of overlapping edges. The number of edge crossings are much smaller in Table 5.3 (threshold 0.85), which is a result, of course, of a much smaller number of nodes and edges ( V = and E = ), but also a result of the graph consisting of 17 subgraphs which share the edges among them. Each node is still, on average, connected to 34 other nodes, resulting in many edge crossings even for threshold Another thing to note is that the multilevel approaches does not bring any improvements over the traditional Fruchterman-Reingold algorithm (grid and non-grid) in terms of the quality measures. In fact they take longer to compute. The multilevel approaches runtime can be reduced by limiting the number of layers to create or by limiting the number of iterations of Fruchterman-Reingold, however, this will most likely affect the quality measures. Furthermore, the multilevel approaches are at a disadvantage because the layer creation code is written in pure Python and the Fruchterman-Reingold implementation relies heavily on NumPy which is written in C. By implementing the multilevel approaches (and also the high-dimensional embedding approach) in a language more focused on performance, such as C or Rust ( org/), the runtime will presumably be brought down significantly. This is also the case for the grid version of Fruchterman-Reingold in which the repulsive forces are calculated mostly in pure Python (with some helper functions in NumPy). However, as seen in the tables, the grid version is faster than the non-grid version. For threshold 0.85 (Table 5.3), the Spectral approach using the Laplacian matrix failed because the eigenvector decomposition did not converge. The Laplacian is a symmetric positive-semidefinite matrix, and its eigenvalues should in theory always be computable (Koren 2005), however, when using sparse matrices in SciPy, the algorithm does not always converge. This is of course a major shortcoming of the approach. Although it could be fixed by using non-sparse matrices at the price of increased memory usage and runtime, we decided to leave it as-is to highlight the approach s shortcoming. All-in-all, also considering the MtGEA and cancer datasets, which we do not show here, the grid version of Frucherman-Reingold appears to provide a stable and compromise in terms of runtime and quality measures. The only major drawback to the approach is the memory usage, which could be further reduced by using a smaller batch size as seen in Section
44 Algorithm Runtime Memory usage Edge crossings Angular resolution Edge length Node distance FR FR grid Spectral, Laplacian Spectral, norm. Laplacian Spectral, adj. matrix FR, init. spectral FR grid, init. spectral Multilevel Multilevel grid High dim. embedding High dim. embedding (weighted) Table 5.2: Benchmarking layout algorithms on the LjGEA dataset. Correlation threshold 0.7. V = , E = in 2 subgraphs. Edge length is the total edge length. Node distance is the average distance between unconnected nodes. Only high dimensional embedding is included in a weighted version as the other algorithms perform almost exactly the same when using weighted edges.
45 Algorithm Runtime Memory usage Edge crossings Angular resolution Edge length Node distance FR FR grid Spectral, Laplacian Spectral, norm. Laplacian Spectral, adj. matrix FR, init. spectral FR grid, init. spectral Multilevel Multilevel grid High dim. embedding High dim. embedding (weighted) Table 5.3: Benchmarking layout algorithms on the LjGEA dataset. Correlation threshold V = 8 002, E = in 17 subgraphs. Edge length is the total edge length. Node distance is the average distance between unconnected nodes. Only high dimensional embedding is included in a weighted version as the other algorithms perform almost exactly the same when using weighted edges. Spectral using the Laplacian failed because the eigenvector decomposition did not converge.
46 5.4 Combining everything In this section we look at the backend of CORNEA in entirety from loading data to scaling node positions according to the tessellation. In particular, we attempt to mimic a real-world usage scenario by timing the runtime of the following steps: Read data: Reading the data from the disk and storing it in memory in a suitable format. Correlation: Calculating the correlation values between all rows of the dataset. This step also includes saving the highly correlated row pairs. The result is a graph G(V, E) (with no positions associated to v V yet). Subgraphs: Finding the disconnected components or subgraphs G i (V i, E i ) of G. Adj. matrices: Converting the subgraphs G i from adjacency lists to a sparse adjacency matrix to allow the layout algorithms to use matrix operations. Layout: Calculate the positions of v V i for all subgraphs G i one at a time. Tessellation: Find a tessellation and scale the subgraphs nodes positions according to this tessellation. In Section we saw that the choice of correlation measure at most changes the runtime by a few seconds, so we fix the correlation measure to be Pearson s r in this experiment. Based on Section we use a batch size of for the correlation measure. For the layout algorithm, we use Fruchterman-Reingold in a grid variant as this algorithm produced the best results in Section For Frucherman- Reingold we decided on a batch size of 5 000, although the results in Section were less clear-cut compared to the equivalent results for the correlation measures. We run this experiment on all three real-world datasets using correlation value thresholds of 0.70 and The results are shown in Table 5.5 and Table 5.4. The MtGEA and cancer data is stored in plain text files, whereas LjGEA is stored as a NumPy binary file. This explains the observed values in the Read data columns, as the binary file is much faster to read. The effect on the total runtime is of course negligible. Clearly, in general, laying out the networks are the most expensive part of the process. For a high threshold value (0.85) and a small dataset (MtGEA and cancer), the correlation calculation is more expensive than the layout, but the overall process takes very little time in these cases, making this difference negligible. As such, reducing the runtime of the layout process is the most important to reduce the total runtime of CORNEA. For large correlation thresholds such as 0.85, and even for the large LjGEA dataset, we can create high quality networks in less than 3 minutes. For a threshold of 0.7, we observe a runtime of around 20 minutes. Whether or not that is fast enough is of course dependent on the individual application. 42
47 Dataset Read data Correlation Subgraphs Adj. matrices Layout Tessellation Total LjGEA MtGEA cancer Absolute (s) Relative (%) Absolute (s) Relative (%) Absolute (s) Relative (%) Table 5.4: Timing all the steps involved in CORNEA with correlation threshold Pearson s r is used as the correlation measure, Fruchterman-Reingold (grid-version) is used for layout. Both Pearson s r and Fruchterman-Reingold uses batches of size Dataset Read data Correlation Subgraphs Adj. matrices Layout Tessellation Total LjGEA MtGEA cancer Absolute (s) Relative (%) Absolute (s) Relative (%) Absolute (s) Relative (%) Table 5.5: Timing all the steps involved in CORNEA with correlation threshold 0.7. Pearson s r is used as the correlation measure, Fruchterman-Reingold (grid version) is used for layout. Both Pearson s r and Fruchterman-Reingold uses batches of size
48
49 Chapter 6 Conclusion 6.1 Correlation measures First, we evaluated three correlation measures. We derived matrix operation versions of the correlation measures and contrasted them with implementations using naive loops instead of the matrix operations. The performance gains from using matrix operations in specialized and optimized libraries (here NumPy and SciPy) are huge, especially for a arguably slow language as Python. Comparing the correlation measures against each other, we see that they have similar runtime. For smaller values of k (the number of experiments or conditions in the gene expression dataset), Spearman s ρ is decidedly slower than Pearson s r and bicor due to the preprocessing involved. For example, for the LjGEA dataset, Spearman s ρ is roughly 25% slower. However, we also show that the time spent calculating correlation values is insignificant compared to the time spent laying out the correlation networks. As such, the choice of correlation measure should not be based on runtime. In the report included in Appendix A, we conclude - in line with Song et al that any of the three measures are reasonable choices, and in the end it boils down to what assumptions you have about your data. Regarding the correlation measures, we also show that we can reduce memory usage by half by using 32 bit floats instead of 64 bit floats. We show, for our three real-world datasets, the choice of 32 bit floats at most changes the correlation values by around This is important when considering our initial requirement of reducing server requirements as much as possible, in order to support many concurrent users with as little memory usage as possible. Finally, we show that we can reduce memory usage even further by calculating the correlation values in batches. In short, using a batch size of, for example, while using 32 bit floats results in a memory usage of around 2 GB for the LjGEA dataset. Not using batches would put the memory usage at around 9 GB (and 18 GB for 64 bit floats). This reduction comes at a price in terms of runtime, however, the choice of a batch size of leads to a very reasonable compromise between memory usage and runtime. 45
50 6.2 Layout algorithms The idea of batches mentioned above is also examined for the Fruchterman- Reingold force-directed layout algorithm. The algorithm is very memory intensive, and for large correlation networks we see memory usage of up to 37 GB. Supporting multiple users would of course require a multiple of these 37 GB of memory, making it infeasible to support multiple simultaneous layout processes to run. By using batches we can significantly reduce the memory usage. A batch size of, for example, results in a memory usage of around 10 GB on the same network. Unlike for the batched versions of the correlation measures, this does not result in a larger runtime. Why this is the case is not clear at this point and requires further examination. As such, we could use even smaller batch sizes for an even larger reduction in memory usage. We did not investigate whether we could use 32 bit floats instead of 64 bit floats for the layout process, although we suspect that we could. That would of course cut down memory usage by half as well, making it possible to support even more users or reduce server costs further. One of the main contributions in this thesis is the evaluation of 10 variants of four different layout algorithms on real-world gene expression datasets. We evaluate them in terms of their runtime and memory usage as well as the quality of the layouts they produce. We have chosen four reasonable quality measures, however, it turns out that these measures do not tell the full story. For example, a visual evaluation of layouts produced by the variants of the spectral algorithms and the high-dimensional embedding algorithm is required to show that these algorithms are not satisfactory. We conclude that Fruchterman-Reingold s force-directed approach in a grid variant is the most reasonable choice of layout algorithm for this type of data. In our final experiment, we show that the layout process is the most time consuming part of CORNEA s workflow when dealing with large datasets and using Fruchterman-Reingold s algorithm. Any work on optimizing CORNEA s runtime should thus be focused on the layout algorithm and not the correlation measure, for example. 6.3 Fulfilling the requirements Coming back to the three requirements for CORNEA put forward in Chapter 1, we note that we have focused very much on reducing both the runtime and the memory usage of the network generation process. A lot of work have focused on making the used methods as fast as possible by utilizing, for example, matrix operations. In that regard, choosing Python as the implementation language seems like a bad choice. For example, in an informal experiment in Chapter 4, we showed that code written in Rust was 50 times faster than the equivalent code written in Python. As such, choosing an implementation language which focuses more on performance could potentially have saved a lot of time and effort. As with many other things in this thesis, this is of course a compromise, specifically a compromise between ease of maintenance and performance. However, as the remaining Lotus Base team s programming experience is limited, Python was the most reasonable choice when considering ease of maintenance. Finally, we note that whether or not the other requirements (requirement 2 46
51 and 3) have been fulfilled can of course not be answered completely objectively. We could have reduced server requirements further (requirement 3), but that reduction would come at a price in terms of performance (requirement 2). The correct compromise between these two requirements is of course a subjective choice that depends on the specific situation. 47
52
53 Bibliography Aoki, Koh, Yoshiyuki Ogata, and Daisuke Shibata Approaches for extracting practical information from gene co-expression networks in plant biology. Plant and cell physiology 48 (3): Bennell, Julia A, and José F Oliveira A tutorial in irregular shape packing problems. Journal of the Operational Research Society 60 (1): S93 S105. Bennett, Chris, Jody Ryall, Leo Spalteholz, and Amy Gooch The aesthetics of graph visualization. In Proceedings of the Third Eurographics conference on Computational Aesthetics in Graphics, Visualization and Imaging, Eurographics Association. Bruls, Mark, Kees Huizing, and Jarke J Van Wijk Squarified treemaps. In Data Visualization 2000, Springer. Burke, Edmund K, Robert SR Hellier, Graham Kendall, and Glenn Whitwell Complete and robust no-fit polygon generation for the irregular stock cutting problem. European Journal of Operational Research 179 (1): Dijkstra, Edsger W A note on two problems in connexion with graphs. Numerische mathematik 1 (1): Formann, Michael, Torben Hagerup, James Haralambides, Michael Kaufmann, Frank Thomson Leighton, Antonios Symvonis, Emo Welzl, and G Woeginger Drawing graphs in the plane with high resolution. SIAM Journal on Computing 22 (5): Fredman, Michael L, and Robert Endre Tarjan Fibonacci heaps and their uses in improved network optimization algorithms. Journal of the ACM (JACM) 34 (3): Fruchterman, Thomas MJ, and Edward M Reingold Graph drawing by force-directed placement. Software: Practice and experience 21 (11): Garey, Michael R, and David S Johnson Crossing number is NPcomplete. SIAM Journal on Algebraic Discrete Methods 4 (3): Goff, Stephen A, Darrell Ricke, Tien-Hung Lan, Gernot Presting, Ronglin Wang, Molly Dunn, Jane Glazebrook, Allen Sessions, Paul Oeller, Hemant Varma, et al A draft sequence of the rice genome (Oryza sativa L. ssp. japonica). Science 296 (5565):
54 Harel, David, and Yehuda Koren Graph drawing by high-dimensional embedding. J. Graph Algorithms Appl. 8 (2): Hu, Yifan Efficient, high-quality force-directed graph drawing. Mathematica Journal 10 (1): Jones, Eric, Travis Oliphant, Pearu Peterson, et al SciPy: Open source scientific tools for Python. accessed on Kojima, Motohiro, Hiroko Sudo, Junpei Kawauchi, Satoko Takizawa, Satoshi Kondou, Hitoshi Nobumasa, and Atsushi Ochiai MicroRNA markers for the diagnosis of pancreatic and biliary-tract cancers. PLoS One 10 (2): e Koren, Yehuda Drawing graphs by eigenvectors: theory and practice. Computers & Mathematics with Applications 49 (11): Lanczos, Cornelius An iteration method for the solution of the eigenvalue problem of linear differential and integral operators. Journal of Research of the National Bureau of Standards 45 (4): Mun, Terry, Asger Bachmann, Vikas Gupta, Jens Stougaard, and Stig U Andersen Lotus Base: An integrated information portal for the model legume Lotus japonicus. Scientific Reports 6: Oldham, Michael C, Steve Horvath, and Daniel H Geschwind Conservation and evolution of gene coexpression networks in human and chimpanzee brains. Proceedings of the National Academy of Sciences 103 (47): Pertea, Mihaela, and Steven L Salzberg Between a chicken and a grape: estimating the number of human genes. Genome biology 11 (5): 1. Purchase, Helen Which aesthetic has the greatest effect on human understanding? In International Symposium on Graph Drawing, Springer. Purchase, Helen Metrics for graph drawing aesthetics. Journal of Visual Languages & Computing 13 (5): Quigley, Aaron, and Peter Eades FADE: Graph drawing, clustering, and visual abstraction. In International Symposium on Graph Drawing, Springer. Rutter, Jeffery D A serial implementation of Cuppen s divide and conquer algorithm for the symmetric eigenvalue problem. Song, Lin, Peter Langfelder, and Steve Horvath Comparison of coexpression measures: mutual information, correlation, and model based indices. BMC bioinformatics 13 (1): 328. Stuart, Joshua M, Eran Segal, Daphne Koller, and Stuart K Kim A genecoexpression network for global discovery of conserved genetic modules. science 302 (5643):
55 Tamassia, Roberto Handbook of graph drawing and visualization. Draft available from accessed on CRC press. Van Der Walt, Stefan, S Chris Colbert, and Gael Varoquaux The NumPy array: a structure for efficient numerical computation. Computing in Science & Engineering 13 (2): Verdier, Jerome, Ivone Torres-Jerez, Mingyi Wang, Andry Andriankaja, Stacy N Allen, Ji He, Yuhong Tang, Jeremy D Murray, and Michael K Udvardi Establishment of the Lotus japonicus Gene Expression Atlas (LjGEA) and its use to explore legume seed maturation. The Plant Journal 74 (2): Walshaw, Chris A multilevel algorithm for force-directed graph-drawing. J. Graph Algorithms Appl. 7 (3): Wilcox, Rand R Introduction to robust estimation and hypothesis testing. Academic Press. Zhang, Bin, Steve Horvath, et al A general framework for weighted gene co-expression network analysis. Statistical applications in genetics and molecular biology 4 (1):
56
57 Appendix A Survey of correlation measures The following pages are a report for a project the author did as part of a 5 ECTS project at Bioinformatics Research Centre, Aarhus University. The project was supervised by the thesis supervisor, Christian N. S. Pedersen, as well. As the conclusions from the project are used in the thesis, the project report is included here in full for completeness. 53
58 A survey of correlation measures for gene co-expression analysis Asger Bachmann ( ) Project in Bioinformatics, October 2016 Abstract This survey considers different measures of correlation used to estimate levels of gene co-expression. We look at their statistical and algorithmic properties and use simulated datasets as well as real-world gene expression datasets. We consider the correlation measures assumptions about the input data, and consider their theoretical as well as practical runtime. Finally, we look at the agreement between the correlation measures in terms of finding highly correlated pairs of genes. We show that Pearson s r, Spearman s ρ and biweight midcorrelation behave similarly when considering their algorithmic properties but are very different when it comes to determining which gene pairs are highly correlated. Further, we conclude that mutual information can be replaced by other correlation measures.
59 Contents Contents 2 1 Introduction 3 2 Background 4 3 Methods Pearson s r Spearman s ρ Biweight midcorrelation Time complexity of bicor Mutual information Estimating probabilities Experiments Implementation details Datasets Testing the underlying assumptions Runtime experiments Approaches to calculating the median in bicor and quartiles in IQR Runtime experiments for the correlation algorithms Comparing co-expression values Conclusion 24 Bibliography 25 2
60 Chapter 1 Introduction This report presents a survey of different correlation measures used for finding relationships between random variables in general. Correlation between random variables is used for a variety of things in many different contexts. In particular we are interested in the context of biology, namely using correlation measures for constructing gene co-expression networks by using gene expression correlation as a proxy for gene co-expression. This is, unsurprisingly, Chapter 1. Chapter 2 presents a background overview of the methodologies used in this survey. We focus on what correlation measures are used for, how to obtain data used in gene co-expression networks, and present previous work on the subject of this report. Chapter 3, presents the particular methods we are surveying in this report. We show how to calculate them and look at the different correlation measures properties and runtime complexity from an algorithmic point of view. Chapter 4 show the experiments which forms the basis of the conclusions presented in Chapter 5. 3
61 Chapter 2 Background When a gene is used to form a gene product, such as a protein, the gene is expressed. By subjecting an organism to various experiments such as drought, it is possible to create a gene expression profile by measuring the organism s genes expression levels throughout the experiments. Such high-throughput gene expression profiling can be done using DNA microarrays or using real-time polymerase chain reaction. Both methods function by counting the number of copies of a gene s RNA transcripts in a cell. The RNA transcript is part of the gene expression process and results when the gene s DNA is transcribed into RNA. The more expressed the gene is, the more RNA transcript copies, you will find. DNA microarrays contain many probes which bind to targets, which are the DNA fragments we are interested in quantifying. One gene may be targeted by several probes, and a probe may overlap several genes. The datasets used in this survey are microarray datasets as described in Section 4.2. Several books cover the topic of quantifying and analysing gene expression (for example Alberts et al. (2002, Chapter 8)). In this survey we focus on gene co-expression which is the study of how similar genes expression profiles are. Typically, a correlation measure applied to gene expression profiles is used for quantifying co-expression. A popular tool for analysing gene co-expression is WGCNA Zhang et al. (2005), and WGCNA calculates pairwise correlation values for all pairs of input genes as a proxy for gene co-expression. WGCNA offers several possible measures of correlation, however, it offers no insight into which correlation measure to use. Song et al. (2012) evaluates different correlation measures and finds that the correlation measure mutual information can be replaced by simpler measures of correlation. Although similar in aim to this survey, the work by Song et al. (2012) does not cover algorithmic properties at all. The most well-known measure of correlation is the Pearson product-moment correlation coefficient, otherwise known as Pearson s r. Several variations on the idea behind Pearson s r exist, for example, Spearman s rank correlation coefficient (Spearman s ρ). Spearman s ρ is Pearson s r applied to ranked data. Similarly, biweight midcorrelation (bicor) is a more robust measure of correlation based on the so-called biweight midcovariance and biweight midvariance instead of the normal covariance and variance which Pearson s r uses. Mutual information is different in nature and is not a variation on Pearson s r. Unlike the other measures, as we will see, mutual information does 4
62 not make any assumptions on the distribution of the input data. Although the word correlation is often used to refer to Pearson s r, we use the word in a broad sense, and it is interchangeable with dependence. We will present all four measures of correlation in Chapter 3. Further, Pearson s r and Spearman s ρ is covered in detail by most introductory statistics text books, Wilcox (2012) covers bicor, and Paninski (2003) covers mutual information. Several other correlation measures exist, and if time would have allowed it, they would have been included in this survey as well. 5
63 Chapter 3 Methods In this chapter we present the measures of correlation examined in this project. Apart from presenting formulas, we focus on similarities between the measures and on their runtime complexity. For the sake of generalization, we will present the measures in terms of random variables instead of gene profiles. We will use X and Y to denote two random variables, and we treat a random variable as a row vector of k values. Each value represent an observation of the random variable, for example an expression value for a particular experiment for a particular gene. For a vector X, X i is the ith value of X 3.1 Pearson s r The Pearson product-moment correlation coefficient (Pearson s r) is probably the most commonly used measure of correlation. Pearson s r assumes linearity of the random variables and thus captures only linear correlation. For a population, Pearson s r is typically denoted by ρ, and for two random variables, X and Y, ρ X,Y is defined as ρ X,Y = cov(x, Y ) σ X σ Y where cov(x, Y ) is the covariance of X and Y and σ X is the standard deviation of X. For a sample, cov(x, Y ) is cov(x, Y ) = E [(X E[X]) (Y E[Y ])] = 1 k ( Xi X ) ( Y i Y ) k i where X is the mean of the observed values of X. For a sample, σ X is denoted by s X and is given by s X = E [(X E [X]) 2] = 1 k ( Xi X ) 2 k i 6
64 3.2. SPEARMAN S ρ 7 As a result, the sample correlation coefficient, denoted by r X,Y, is r X,Y = cov(x, Y ) s X s Y ( Xi X ) ( Y i Y ) = = = 1 k k i 1 k k 1 k k i ( Xi X ) k k i k i k i i k k i ( Yi Y ) 2 ( Xi X ) ( Y i Y ) ( Xi X ) 2 1 k k ( Xi X ) ( Y i Y ) ( Xi X ) 2 k i i ( Yi Y ) 2 ( Yi Y ) 2 (3.1) When manipulating the square roots, we made use of the fact that k > 0 and x R : x 2 0. The range of r X,Y is [ 1, 1]. This evident from Cauchy s Inequality (Weisstein, 2016) which states ( k ( k ) ( k ) i a i b i ) 2 for any a i and b i. Substituting a i for X i X and b i for Y i Y and taking the principal square root on both sides of the inequality, we get k (X i X)(Y i Y ) k (X i X) 2 k (Y i Y ) 2 and more specifically i i i a 2 i cov(x, Y ) s X s Y This gives us a bound on r X,Y, namely r X,Y 1 or 1 r X,Y 1. r X,Y > 0 means that X and Y are positively correlated, while r X,Y < 0 means that they are negatively correlated. We usually don t care if the correlation is positive or negative, and a correlation of r has the same strength as a correlation of r. Therefore, we define a normalized version of Pearson s r, namely i b 2 i ˆr X,Y = abs(r X,Y ) (3.2) where abs(x) is the absolute value of x. The range of ˆr X,Y is [0, 1], and this allows us to compare Pearson s r with other measures of correlation which are always positive, such as mutual information. Each sum in Equation 3.1 is linear in the length of X and Y. As a result, the time complexity of computing ˆr X,Y is O(k) where k is the length of X and Y. 3.2 Spearman s ρ Spearman s rank correlation coefficient (Spearman s ρ) is a measure of rank correlation and builds on Pearson s r. Because it is based on rank, Spearman s i
65 8 CHAPTER 3. METHODS ρ is less sensitive to outliers. It captures correlation of any two monotonic functions, while Pearson s r only captures linear correlations. For two random variables X and Y, Spearman s ρ (denoted by r (s) X,Y ) is defined as Pearson s r on the ranked versions of X and Y : r (s) X,Y r (s) X,Y = cov (rank(x), rank(y )) σ rank(x) σ rank(y ) can of course be calculated using Equation 3.1. rank(x) is a function that takes as input a vector of observed values from a random variable X and returns a vector of ranks for those values. When assigning ranks to values, ties are resolved by assigning them the average of the ranks they would have under an ordinal ranking. In the case of continuous random variables, the probability of observing the same value more than once is zero, meaning that fractional ranks are somewhat unnecessary. However, compared to a normal ordinal ranking scheme, fractional ranking does not add computational complexity. For sorted data, both schemes can be implemented in linear time in the length of the random variable we are ranking. Any reasonable ranking scheme, however, requires the data to be sorted in one way or another, meaning that the rank function (and therefore Spearman s ρ in general) has time complexity O(k log(k)). Just as for Pearson s r, we normalize Spearman s ρ to obtain a domain of [0, 1]. As in Equation 3.2, we define as the final value for Spearman s ρ. ( ) ˆr (s) X,Y = abs r (s) X,Y 3.3 Biweight midcorrelation Biweight midcorrelation (bicor) is less sensitive to outliers than Pearson s r and Spearman s ρ because bicor is based on median values, whereas the other measures are based on mean values. Song et al. (2012) suggests using bicor over other correlation measures for gene co-expression networks. bicor is described by Wilcox (2012), and we start by defining u i = X i med(x) 9 mad(x) v i = Y i med(y ) 9 mad(y ) for i {1,..., k}, that is a u and v value for each observation in X and Y. The number 9 is a coefficient chosen by Wilcox as it has the highest so-called triefficiency, roughly meaning that it has low variance across different sampling methods and is thus robust to sampling methods. med(x) is the median of X, and mad(x) is the median absolute deviation which is the median of the absolute deviations of X from the median of X: mad(x) = med({abs(x i med(x)) i {1,..., k}})
66 3.3. BIWEIGHT MIDCORRELATION 9 Now, define the following weights {( ) 1 u 2 2 a i = i if 1 u i 1 0 otherwise b i = {( 1 v 2 i ) 2 if 1 v i 1 0 otherwise Roughly speaking, with these weights, each value in X and Y are given a weight according to how close to the median absolute deviation they are. Values that deviate too far from the median absolute deviation (this is what the factor of 9 described above is used for) are given a weight of 0. bicor, denoted by r (b) X,Y, is then given by r (b) X,Y = k i a i(x i med(x))b i (Y i med(y )) k i (a i(x i med(x)) 2 k i (b i(y i med(y ))) 2 If we define the sample biweight midcovariance as cov (b) X,Y = 1 k k a i (X i med(x))b i (Y i med(y )) i and the sample biweight midvariance as s (b) 2 1 X = k k (a i (X i med(x)) 2 i the connection between Pearson s r and bicor is obvious, as bicor is simply X,Y = cov (b) r (b) s (b) X X,Y 2 s (b) 2 Y Just like Pearson s r, bicor can be bounded above and below by Cauchy s Inequality, and 1 r (b) X,Y 1 Here, we also define the absolute value of bicor as our final correlation measure, ( ) ˆr (b) X,Y = abs r (b) X,Y According to Wilcox, bicor has a so-called breakdown point of around 0.5, meaning that our data can contain roughly 50% outliers (really large or really small values) before bicor is affected by the outliers. On the other hand, Pearson s r and other mean-based approaches has a breakdown point around 0 because the mean is affected by a single outlier.
67 10 CHAPTER 3. METHODS Time complexity of bicor bicor s time complexity of O(k) is obvious for all operations except finding the median. A simple approach to finding the median of a sequence involves sorting the sequence and selecting the middle element (rounding down) from the sorted sequence. This approach is O(k log(k)), however. Blum et al. (1973) describes an O(k) algorithm (the so-called median of medians algorithm) for finding the ith lowest element (and therefore also the median) of a sequence. Blum et al. s algorithm works similarly to Quicksort (Hoare, 1962) in that it partitions the input around a pivot. The choice of pivot makes Blum et al. s algorithm O(k), however calculating the pivot is relatively expensive, making the algorithm slow in practice except for very large values of k. The Quickselect algorithm, also by Hoare, chooses a pivot at random. Although the worst-case runtime of Quickselect is O(k 2 ), the chance of observing this runtime is extremely small, and the expected runtime is O(k) (see for example the analysis by Schwarz (2013)). 3.4 Mutual information A strong point for mutual information (MI ) as a measure of correlation is that MI can measure arbitrary relationships, and not only linear or monotonic relationships. In general, MI is a measure of how much you learn about one random variable by observing another random variable. MI was introduced by Shannon (1948) as a quantity of information. For two random variables X and Y, MI is defined as I(X; Y ) = H(X) + H(Y ) H(X, Y ) where H(X) and H(X, Y ) is the marginal entropy and joint entropy, respectively, which are defined as H(X) = E X [ log(p(x))] H(X, Y ) = E [ log(p(x, Y ))] X,Y Entropy is a measure of uncertainty about a random variable (or multiple random variables in the case of the joint entropy). For example, a random variable describing outcomes of rolling a fair die has maximum entropy because we do not learn anything about outcome i by looking at outcome i 1. We say that roll i contains as much new information as possible and the event s self-information is as high as possible. For continuous random variables such as gene profiles, H(X) and H(X, Y ) becomes H(X) = p(x) log(p(x)) dx H(X, Y ) = x X x X y Y p(x, y) log(p(x, y)) dx dy Unless the probability distributions of the random variables are known and their ranges are finite, it is unfeasible to calculate entropy and MI in the continuous case. To calculate entropy and MI we can regularize the problem by discretizing
68 3.4. MUTUAL INFORMATION 11 or binning the continuous random variables to make them discrete. Entropy for discrete random variables is defined as H(X) = x X p(x) log(p(x)) H(X, Y ) = x X p(x, y) log(p(x, y)) y Y Binning is equivalent to the so-called direct method described by Paninski (2003), and make use of the data processing inequality for MI: I(X; Y ) I(S(X), T (Y )) S and T are maps over the range of X and Y respectively, and in this case maps values to bins. It is clear then, that we can calculate a lower bound on I(X; Y ) using binning. This sort of discretization is often called histogram estimation, and choosing a bin size here is equivalent to choosing a bin size when creating any sort of histogram. An obvious choice for a binning procedure is to distribute bins of equal size in the range of the random variables. Freedman and Diaconis (1981) proposed the aptly-called Freedman-Diaconis rule for choosing a bin size. For a random variable X of length k, they suggest a bin size of s Freedman-Diaconis = 2 IQR(X) 3 k IQR(X) is X s interquartile range define as the difference between X s 3rd and 1st quartile. Whereas X s range (measured by the difference between the maximum and minimum values) has a breakdown point of 0, IQR has a breakdown point of 0.25, making IQR a robust estimate of X s range. The quartiles can be found using the exact same approaches to finding the median described in Section 3.3. The start values for the bins is then equal to b Freedman-Diaconis = [min(x) + i s Freedman-Diaconis i 1,..., b] A value X i can be assigned to a bin b Xi by a simple linear transformation: Xi min(x) b Xi = s Freedman-Diaconis In general, choosing an appropriate number of bins is important. Too many bins (or equivalently, too small a bin size) leads to estimation errors for the joint distribution p(x, y) as many bins will be empty. Similarly, too few bins (too large a bin size) will lead to problems with capturing the actual relationship between the variables as more and more data is lumped together. Estimating probabilities The problem is now reduced to estimating the probabilities p(x), p(y) and p(x, y) in H(X), H(Y ) and H(X, Y ). One approach is to use maximum likelihood (ML) estimation, and replace the probabilities by the observed frequencies of
69 12 CHAPTER 3. METHODS the bins. This estimate is negatively biased, and Miller (1955) proposed the correction Ĥ Miller (X) = ĤML(X) + m 1 2k (3.3) and equivalently for H(X, Y ). Ĥ ML (X) is the maximum likelihood estimate for H(X), k is the number of observations (the number of experiments in the case of co-expression networks), and m is the number of bins with non-zero probability. I(X; Y ) s range is [0, min(h(x), H(Y ))]. To facilitate comparing values of correlation across the different measures, several normalization techniques for I(X; Y ) have been proposed. Kvalseth (1987) argues that I(X; Y ) normalized = 2I(X; Y ) H(X) + H(Y ) is the best choice of normalization, and we will use that in this project. The time complexity for calculating H(X) and H(Y ) is O(k). Even though H(X, Y ) involves a nested sum, making the complexity of a naive implementation O(k 2 ), we can calculate it in O(k) as well. When doing maximum likelihood estimation, p(x, y) = 0 for any x X, y Y which we do not observe together, and we can simply skip those pairs of x and y. By interleaving the observed values of X and Y, we can find the only possible x and y pairs for which p(x, y) > 0 which is at most k pairs. As discussed in Section 3.3, calculating the IQR in Freedman-Diaconis rule can be done in O(k) time. In the end, calculating I(X, Y ) is O(k).
70 Chapter 4 Experiments 4.1 Implementation details All algorithms are implemented in Python 3 ( To make the experiments as fair as possible, every built-in Python function such as sorted (returning the sorted version of a sequence) and sum (returning the sum of a sequence) are re-written in pure Python. The built-in equivalents are written in C, making them much faster than their pure-python counterparts. The goal is to achieve a fair comparison with unbiased relative speeds of the algorithms. All experiments are performed on an Intel Core i7-5600u CPU operating at 2.60GHz. Although the CPU has multiple cores, this is not exploited in these experiments. All code is available at Datasets Cancer in mice The first dataset, d mouse, involves appetite regulators in mice (Mus musculus) with cancer-induced cachexia (roughly defined as unintended and uncontrollable weight loss). The data is available at EBI s ArrayExpress database as experiment E-GEOD ( EOD-44082/). The raw data contains gene expression data for probes. To map from probes to genes, the following approach was taken. A file with mappings from probes to genes is also available at the Array- Express database. The mapping file contains both one-to-zero, one-to-one, one-to-many and many-to-one relationships between probes and genes. 1) When a probe does not map to any gene, discard the probe. 2) When there is a one-to-one correspondence between genes and probes, the probe is simply replaced by the gene. 3) When a single gene maps to multiple probes, the gene s expression is taken as the average of the probes expression data across all experiments/columns. 4) When multiple genes map to a single probe, the probe s data is discarded. The original data contains 35,556 probes over 14 experiments. After the mapping procedure, d mouse contains 3853 genes over 14 experiments. Viewed as a matrix, d mouse has 3853 rows and 14 columns. 13
71 14 CHAPTER 4. EXPERIMENTS Description X Y Figure Linear U(0, 1) 2X 4.1(a) Linear with noise U(0, 1) 2X + ε 4.1(b) Semi-linear U(0, 1) cos(sin(x)) 4.2(a) Semi-linear with noise U(0, 1) cos(sin(x)) + ε 4.2(b) Non-linear U( 4, 4) cos(sin(x)) 4.3(a) Non-linear with noise U( 4, 4) cos(sin(x)) + ε 4.3(b) No relationship U(0, 1) U(0, 1) 4.4 Table 4.1: Random variables for showing the effect of assumptions. U(x, y) means that the random variable is sampled from the uniform probability distribution from x to y. ε is sampled from N(0, 0.1). In all cases, 10,000 samples are drawn. Medicago truncatula The second dataset, d medicago, is an expression dataset for Medicago truncatula available at Specifically, the dataset consists of all means across all experiments for Medicago truncatula available at the MtGEA site. The raw data contains gene expression data for probes from a DNA microarray setup. To convert this to gene expression data, the following approach were taken. A file containing mappings between probes and genes are also available at the dataset s site. This mapping file contains both one-to-one, one-to-many and many-to-one relationships between genes and probes. The cases are the same as case 2, 3 and 4 in the mouse dataset. The original data contains 50,900 probes over 274 experiments. After the mapping procedure, d medicago contains 15,807 genes over 274 experiments. Viewed as a matrix, d medicago has 15,807 rows and 274 columns. Randomly generated datasets Apart from the read-world datasets described above, we ll also use randomly generated datasets. These are described in detail wherever they are used. 4.3 Testing the underlying assumptions Pearson s r and bicor assume linearity between random variables. Spearman s ρ assume monotonicity between random variables. Mutual information make no assumption about the random variables, although it is unclear if the estimation method does. To show the effect of these assumptions, we create different pairs of random variables X and Y as shown in Table 4.1. Table 4.2 show the corresponding correlation values for the four correlation measures. All measures handle the perfect linear relationship well with correlation values equal to 1. Similarly, when there is no relationship, the correlation values are almost 0 for all four measures. As expected, the semi-linear relationship is
72 4.3. TESTING THE UNDERLYING ASSUMPTIONS 15 Description Pearson s r Spearman s ρ bicor MI Linear Linear with noise Semi-linear Semi-linear with noise Non-linear Non-linear with noise No relationship Table 4.2: Calculated correlation values for the four measures with the random variables from Table 4.1. (a) Perfect relationship without noise. (b) Imperfect relationship with noise. Figure 4.1: Linear relationship between X and Y. See Table 4.1. (a) Perfect relationship without noise. (b) Imperfect relationship with noise. Figure 4.2: Semi-linear relationship between X and Y. See Table 4.1.
73 16 CHAPTER 4. EXPERIMENTS (a) Perfect relationship without noise. (b) Imperfect relationship with noise. Figure 4.3: Non-linear relationship between X and Y. See Table 4.1. Figure 4.4: No relationship between X and Y. See Table 4.1. handled relatively well by the linear measures. As the semi-linear relationship is monotonic decreasing, Spearman s ρ captures the relationship completely. For the semi-linear relationship, mutual information sees a large drop in correlation value compared to the linear relationship. Only mutual information captures some dependence in the non-linear relationship. Compared to the other measures, mutual information is extremely sensitive to noise. For example, in the semi-linear relationship, mutual information almost completely misses the relationship when noise is added. Spearman s ρ captures the semi-linear relationship completely as the relationship is monotonically decreasing. Although bicor is less robust to the deviations from linearity than Pearson s r and Spearman s ρ, there is slight evidence that it is more robust to the noise in the semi-linear example relative to the noise-free example. Why does mutual information fail to capture the noiseless semi-linear and non-linear relationships completely? The estimate of mutual information is just that, an estimate. Furthermore, the method used for estimating mutual information might impose some assumptions on the data. We will not pursue this thought further, except noting that, in the form we present it here, mutual information cannot capture noiseless non-linear relationships completely. To mutual information s defence, the other measures completely miss the non-linear relationship.
TELCOM2125: Network Science and Analysis
 School of Information Sciences University of Pittsburgh TELCOM2125: Network Science and Analysis Konstantinos Pelechrinis Spring 2015 2 Part 4: Dividing Networks into Clusters The problem l Graph partitioning
School of Information Sciences University of Pittsburgh TELCOM2125: Network Science and Analysis Konstantinos Pelechrinis Spring 2015 2 Part 4: Dividing Networks into Clusters The problem l Graph partitioning
Chapter 2 Basic Structure of High-Dimensional Spaces
 Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Chapter 2 Basic Structure of High-Dimensional Spaces Data is naturally represented geometrically by associating each record with a point in the space spanned by the attributes. This idea, although simple,
Coarse-to-fine image registration
 Today we will look at a few important topics in scale space in computer vision, in particular, coarseto-fine approaches, and the SIFT feature descriptor. I will present only the main ideas here to give
Today we will look at a few important topics in scale space in computer vision, in particular, coarseto-fine approaches, and the SIFT feature descriptor. I will present only the main ideas here to give
Week 7 Picturing Network. Vahe and Bethany
 Week 7 Picturing Network Vahe and Bethany Freeman (2005) - Graphic Techniques for Exploring Social Network Data The two main goals of analyzing social network data are identification of cohesive groups
Week 7 Picturing Network Vahe and Bethany Freeman (2005) - Graphic Techniques for Exploring Social Network Data The two main goals of analyzing social network data are identification of cohesive groups
1 Graph Visualization
 A Linear Algebraic Algorithm for Graph Drawing Eric Reckwerdt This paper will give a brief overview of the realm of graph drawing, followed by a linear algebraic approach, ending with an example of our
A Linear Algebraic Algorithm for Graph Drawing Eric Reckwerdt This paper will give a brief overview of the realm of graph drawing, followed by a linear algebraic approach, ending with an example of our
Lofting 3D Shapes. Abstract
 Lofting 3D Shapes Robby Prescott Department of Computer Science University of Wisconsin Eau Claire Eau Claire, Wisconsin 54701 robprescott715@gmail.com Chris Johnson Department of Computer Science University
Lofting 3D Shapes Robby Prescott Department of Computer Science University of Wisconsin Eau Claire Eau Claire, Wisconsin 54701 robprescott715@gmail.com Chris Johnson Department of Computer Science University
Cluster Analysis. Mu-Chun Su. Department of Computer Science and Information Engineering National Central University 2003/3/11 1
 Cluster Analysis Mu-Chun Su Department of Computer Science and Information Engineering National Central University 2003/3/11 1 Introduction Cluster analysis is the formal study of algorithms and methods
Cluster Analysis Mu-Chun Su Department of Computer Science and Information Engineering National Central University 2003/3/11 1 Introduction Cluster analysis is the formal study of algorithms and methods
( ) =cov X Y = W PRINCIPAL COMPONENT ANALYSIS. Eigenvectors of the covariance matrix are the principal components
 Review Lecture 14 ! PRINCIPAL COMPONENT ANALYSIS Eigenvectors of the covariance matrix are the principal components 1. =cov X Top K principal components are the eigenvectors with K largest eigenvalues
Review Lecture 14 ! PRINCIPAL COMPONENT ANALYSIS Eigenvectors of the covariance matrix are the principal components 1. =cov X Top K principal components are the eigenvectors with K largest eigenvalues
Clustering analysis of gene expression data
 Clustering analysis of gene expression data Chapter 11 in Jonathan Pevsner, Bioinformatics and Functional Genomics, 3 rd edition (Chapter 9 in 2 nd edition) Human T cell expression data The matrix contains
Clustering analysis of gene expression data Chapter 11 in Jonathan Pevsner, Bioinformatics and Functional Genomics, 3 rd edition (Chapter 9 in 2 nd edition) Human T cell expression data The matrix contains
SUPPLEMENTARY FILE S1: 3D AIRWAY TUBE RECONSTRUCTION AND CELL-BASED MECHANICAL MODEL. RELATED TO FIGURE 1, FIGURE 7, AND STAR METHODS.
 SUPPLEMENTARY FILE S1: 3D AIRWAY TUBE RECONSTRUCTION AND CELL-BASED MECHANICAL MODEL. RELATED TO FIGURE 1, FIGURE 7, AND STAR METHODS. 1. 3D AIRWAY TUBE RECONSTRUCTION. RELATED TO FIGURE 1 AND STAR METHODS
SUPPLEMENTARY FILE S1: 3D AIRWAY TUBE RECONSTRUCTION AND CELL-BASED MECHANICAL MODEL. RELATED TO FIGURE 1, FIGURE 7, AND STAR METHODS. 1. 3D AIRWAY TUBE RECONSTRUCTION. RELATED TO FIGURE 1 AND STAR METHODS
CSE 547: Machine Learning for Big Data Spring Problem Set 2. Please read the homework submission policies.
 CSE 547: Machine Learning for Big Data Spring 2019 Problem Set 2 Please read the homework submission policies. 1 Principal Component Analysis and Reconstruction (25 points) Let s do PCA and reconstruct
CSE 547: Machine Learning for Big Data Spring 2019 Problem Set 2 Please read the homework submission policies. 1 Principal Component Analysis and Reconstruction (25 points) Let s do PCA and reconstruct
Space Filling Curves and Hierarchical Basis. Klaus Speer
 Space Filling Curves and Hierarchical Basis Klaus Speer Abstract Real world phenomena can be best described using differential equations. After linearisation we have to deal with huge linear systems of
Space Filling Curves and Hierarchical Basis Klaus Speer Abstract Real world phenomena can be best described using differential equations. After linearisation we have to deal with huge linear systems of
CS 140: Sparse Matrix-Vector Multiplication and Graph Partitioning
 CS 140: Sparse Matrix-Vector Multiplication and Graph Partitioning Parallel sparse matrix-vector product Lay out matrix and vectors by rows y(i) = sum(a(i,j)*x(j)) Only compute terms with A(i,j) 0 P0 P1
CS 140: Sparse Matrix-Vector Multiplication and Graph Partitioning Parallel sparse matrix-vector product Lay out matrix and vectors by rows y(i) = sum(a(i,j)*x(j)) Only compute terms with A(i,j) 0 P0 P1
Matrices. Chapter Matrix A Mathematical Definition Matrix Dimensions and Notation
 Chapter 7 Introduction to Matrices This chapter introduces the theory and application of matrices. It is divided into two main sections. Section 7.1 discusses some of the basic properties and operations
Chapter 7 Introduction to Matrices This chapter introduces the theory and application of matrices. It is divided into two main sections. Section 7.1 discusses some of the basic properties and operations
A Course in Machine Learning
 A Course in Machine Learning Hal Daumé III 13 UNSUPERVISED LEARNING If you have access to labeled training data, you know what to do. This is the supervised setting, in which you have a teacher telling
A Course in Machine Learning Hal Daumé III 13 UNSUPERVISED LEARNING If you have access to labeled training data, you know what to do. This is the supervised setting, in which you have a teacher telling
Statistical Physics of Community Detection
 Statistical Physics of Community Detection Keegan Go (keegango), Kenji Hata (khata) December 8, 2015 1 Introduction Community detection is a key problem in network science. Identifying communities, defined
Statistical Physics of Community Detection Keegan Go (keegango), Kenji Hata (khata) December 8, 2015 1 Introduction Community detection is a key problem in network science. Identifying communities, defined
Shadows for Many Lights sounds like it might mean something, but In fact it can mean very different things, that require very different solutions.
 1 2 Shadows for Many Lights sounds like it might mean something, but In fact it can mean very different things, that require very different solutions. 3 We aim for something like the numbers of lights
1 2 Shadows for Many Lights sounds like it might mean something, but In fact it can mean very different things, that require very different solutions. 3 We aim for something like the numbers of lights
Centrality Book. cohesion.
 Cohesion The graph-theoretic terms discussed in the previous chapter have very specific and concrete meanings which are highly shared across the field of graph theory and other fields like social network
Cohesion The graph-theoretic terms discussed in the previous chapter have very specific and concrete meanings which are highly shared across the field of graph theory and other fields like social network
Correlation. January 12, 2019
 Correlation January 12, 2019 Contents Correlations The Scattterplot The Pearson correlation The computational raw-score formula Survey data Fun facts about r Sensitivity to outliers Spearman rank-order
Correlation January 12, 2019 Contents Correlations The Scattterplot The Pearson correlation The computational raw-score formula Survey data Fun facts about r Sensitivity to outliers Spearman rank-order
Clustering and Visualisation of Data
 Clustering and Visualisation of Data Hiroshi Shimodaira January-March 28 Cluster analysis aims to partition a data set into meaningful or useful groups, based on distances between data points. In some
Clustering and Visualisation of Data Hiroshi Shimodaira January-March 28 Cluster analysis aims to partition a data set into meaningful or useful groups, based on distances between data points. In some
Interactive Math Glossary Terms and Definitions
 Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Terms and Definitions Absolute Value the magnitude of a number, or the distance from 0 on a real number line Addend any number or quantity being added addend + addend = sum Additive Property of Area the
Feature Selection for fmri Classification
 Feature Selection for fmri Classification Chuang Wu Program of Computational Biology Carnegie Mellon University Pittsburgh, PA 15213 chuangw@andrew.cmu.edu Abstract The functional Magnetic Resonance Imaging
Feature Selection for fmri Classification Chuang Wu Program of Computational Biology Carnegie Mellon University Pittsburgh, PA 15213 chuangw@andrew.cmu.edu Abstract The functional Magnetic Resonance Imaging
Dynamic Parameter Spring Model for Automatic Graph Layout. Xuejun Liu. (Doctoral Program in Computer Science) Advised by Jiro Tanaka
 Dynamic Parameter Spring Model for Automatic Graph Layout Xuejun Liu (Doctoral Program in Computer Science) Advised by Jiro Tanaka Submitted to the Graduate School of Systems and Information Engineering
Dynamic Parameter Spring Model for Automatic Graph Layout Xuejun Liu (Doctoral Program in Computer Science) Advised by Jiro Tanaka Submitted to the Graduate School of Systems and Information Engineering
Glossary Common Core Curriculum Maps Math/Grade 6 Grade 8
 Glossary Common Core Curriculum Maps Math/Grade 6 Grade 8 Grade 6 Grade 8 absolute value Distance of a number (x) from zero on a number line. Because absolute value represents distance, the absolute value
Glossary Common Core Curriculum Maps Math/Grade 6 Grade 8 Grade 6 Grade 8 absolute value Distance of a number (x) from zero on a number line. Because absolute value represents distance, the absolute value
GraphBLAS Mathematics - Provisional Release 1.0 -
 GraphBLAS Mathematics - Provisional Release 1.0 - Jeremy Kepner Generated on April 26, 2017 Contents 1 Introduction: Graphs as Matrices........................... 1 1.1 Adjacency Matrix: Undirected Graphs,
GraphBLAS Mathematics - Provisional Release 1.0 - Jeremy Kepner Generated on April 26, 2017 Contents 1 Introduction: Graphs as Matrices........................... 1 1.1 Adjacency Matrix: Undirected Graphs,
Exploratory data analysis for microarrays
 Exploratory data analysis for microarrays Jörg Rahnenführer Computational Biology and Applied Algorithmics Max Planck Institute for Informatics D-66123 Saarbrücken Germany NGFN - Courses in Practical DNA
Exploratory data analysis for microarrays Jörg Rahnenführer Computational Biology and Applied Algorithmics Max Planck Institute for Informatics D-66123 Saarbrücken Germany NGFN - Courses in Practical DNA
V4 Matrix algorithms and graph partitioning
 V4 Matrix algorithms and graph partitioning - Community detection - Simple modularity maximization - Spectral modularity maximization - Division into more than two groups - Other algorithms for community
V4 Matrix algorithms and graph partitioning - Community detection - Simple modularity maximization - Spectral modularity maximization - Division into more than two groups - Other algorithms for community
X Std. Topic Content Expected Learning Outcomes Mode of Transaction
 X Std COMMON SYLLABUS 2009 - MATHEMATICS I. Theory of Sets ii. Properties of operations on sets iii. De Morgan s lawsverification using example Venn diagram iv. Formula for n( AÈBÈ C) v. Functions To revise
X Std COMMON SYLLABUS 2009 - MATHEMATICS I. Theory of Sets ii. Properties of operations on sets iii. De Morgan s lawsverification using example Venn diagram iv. Formula for n( AÈBÈ C) v. Functions To revise
2.3 Algorithms Using Map-Reduce
 28 CHAPTER 2. MAP-REDUCE AND THE NEW SOFTWARE STACK one becomes available. The Master must also inform each Reduce task that the location of its input from that Map task has changed. Dealing with a failure
28 CHAPTER 2. MAP-REDUCE AND THE NEW SOFTWARE STACK one becomes available. The Master must also inform each Reduce task that the location of its input from that Map task has changed. Dealing with a failure
1 More configuration model
 1 More configuration model In the last lecture, we explored the definition of the configuration model, a simple method for drawing networks from the ensemble, and derived some of its mathematical properties.
1 More configuration model In the last lecture, we explored the definition of the configuration model, a simple method for drawing networks from the ensemble, and derived some of its mathematical properties.
Renderer Implementation: Basics and Clipping. Overview. Preliminaries. David Carr Virtual Environments, Fundamentals Spring 2005
 INSTITUTIONEN FÖR SYSTEMTEKNIK LULEÅ TEKNISKA UNIVERSITET Renderer Implementation: Basics and Clipping David Carr Virtual Environments, Fundamentals Spring 2005 Feb-28-05 SMM009, Basics and Clipping 1
INSTITUTIONEN FÖR SYSTEMTEKNIK LULEÅ TEKNISKA UNIVERSITET Renderer Implementation: Basics and Clipping David Carr Virtual Environments, Fundamentals Spring 2005 Feb-28-05 SMM009, Basics and Clipping 1
Visual Representations for Machine Learning
 Visual Representations for Machine Learning Spectral Clustering and Channel Representations Lecture 1 Spectral Clustering: introduction and confusion Michael Felsberg Klas Nordberg The Spectral Clustering
Visual Representations for Machine Learning Spectral Clustering and Channel Representations Lecture 1 Spectral Clustering: introduction and confusion Michael Felsberg Klas Nordberg The Spectral Clustering
8. Visual Analytics. Prof. Tulasi Prasad Sariki SCSE, VIT, Chennai
 8. Visual Analytics Prof. Tulasi Prasad Sariki SCSE, VIT, Chennai www.learnersdesk.weebly.com Graphs & Trees Graph Vertex/node with one or more edges connecting it to another node. Cyclic or acyclic Edge
8. Visual Analytics Prof. Tulasi Prasad Sariki SCSE, VIT, Chennai www.learnersdesk.weebly.com Graphs & Trees Graph Vertex/node with one or more edges connecting it to another node. Cyclic or acyclic Edge
Curvilinear Graph Drawing Using The Force-Directed Method. by Benjamin Finkel Sc. B., Brown University, 2003
 Curvilinear Graph Drawing Using The Force-Directed Method by Benjamin Finkel Sc. B., Brown University, 2003 A Thesis submitted in partial fulfillment of the requirements for Honors in the Department of
Curvilinear Graph Drawing Using The Force-Directed Method by Benjamin Finkel Sc. B., Brown University, 2003 A Thesis submitted in partial fulfillment of the requirements for Honors in the Department of
THE preceding chapters were all devoted to the analysis of images and signals which
 Chapter 5 Segmentation of Color, Texture, and Orientation Images THE preceding chapters were all devoted to the analysis of images and signals which take values in IR. It is often necessary, however, to
Chapter 5 Segmentation of Color, Texture, and Orientation Images THE preceding chapters were all devoted to the analysis of images and signals which take values in IR. It is often necessary, however, to
General Instructions. Questions
 CS246: Mining Massive Data Sets Winter 2018 Problem Set 2 Due 11:59pm February 8, 2018 Only one late period is allowed for this homework (11:59pm 2/13). General Instructions Submission instructions: These
CS246: Mining Massive Data Sets Winter 2018 Problem Set 2 Due 11:59pm February 8, 2018 Only one late period is allowed for this homework (11:59pm 2/13). General Instructions Submission instructions: These
Lesson 2 7 Graph Partitioning
 Lesson 2 7 Graph Partitioning The Graph Partitioning Problem Look at the problem from a different angle: Let s multiply a sparse matrix A by a vector X. Recall the duality between matrices and graphs:
Lesson 2 7 Graph Partitioning The Graph Partitioning Problem Look at the problem from a different angle: Let s multiply a sparse matrix A by a vector X. Recall the duality between matrices and graphs:
Mining Social Network Graphs
 Mining Social Network Graphs Analysis of Large Graphs: Community Detection Rafael Ferreira da Silva rafsilva@isi.edu http://rafaelsilva.com Note to other teachers and users of these slides: We would be
Mining Social Network Graphs Analysis of Large Graphs: Community Detection Rafael Ferreira da Silva rafsilva@isi.edu http://rafaelsilva.com Note to other teachers and users of these slides: We would be
EECS730: Introduction to Bioinformatics
 EECS730: Introduction to Bioinformatics Lecture 15: Microarray clustering http://compbio.pbworks.com/f/wood2.gif Some slides were adapted from Dr. Shaojie Zhang (University of Central Florida) Microarray
EECS730: Introduction to Bioinformatics Lecture 15: Microarray clustering http://compbio.pbworks.com/f/wood2.gif Some slides were adapted from Dr. Shaojie Zhang (University of Central Florida) Microarray
9/29/13. Outline Data mining tasks. Clustering algorithms. Applications of clustering in biology
 9/9/ I9 Introduction to Bioinformatics, Clustering algorithms Yuzhen Ye (yye@indiana.edu) School of Informatics & Computing, IUB Outline Data mining tasks Predictive tasks vs descriptive tasks Example
9/9/ I9 Introduction to Bioinformatics, Clustering algorithms Yuzhen Ye (yye@indiana.edu) School of Informatics & Computing, IUB Outline Data mining tasks Predictive tasks vs descriptive tasks Example
Monte Carlo Integration
 Lab 18 Monte Carlo Integration Lab Objective: Implement Monte Carlo integration to estimate integrals. Use Monte Carlo Integration to calculate the integral of the joint normal distribution. Some multivariable
Lab 18 Monte Carlo Integration Lab Objective: Implement Monte Carlo integration to estimate integrals. Use Monte Carlo Integration to calculate the integral of the joint normal distribution. Some multivariable
Fast Hierarchical Clustering via Dynamic Closest Pairs
 Fast Hierarchical Clustering via Dynamic Closest Pairs David Eppstein Dept. Information and Computer Science Univ. of California, Irvine http://www.ics.uci.edu/ eppstein/ 1 My Interest In Clustering What
Fast Hierarchical Clustering via Dynamic Closest Pairs David Eppstein Dept. Information and Computer Science Univ. of California, Irvine http://www.ics.uci.edu/ eppstein/ 1 My Interest In Clustering What
Linear Methods for Regression and Shrinkage Methods
 Linear Methods for Regression and Shrinkage Methods Reference: The Elements of Statistical Learning, by T. Hastie, R. Tibshirani, J. Friedman, Springer 1 Linear Regression Models Least Squares Input vectors
Linear Methods for Regression and Shrinkage Methods Reference: The Elements of Statistical Learning, by T. Hastie, R. Tibshirani, J. Friedman, Springer 1 Linear Regression Models Least Squares Input vectors
Text Modeling with the Trace Norm
 Text Modeling with the Trace Norm Jason D. M. Rennie jrennie@gmail.com April 14, 2006 1 Introduction We have two goals: (1) to find a low-dimensional representation of text that allows generalization to
Text Modeling with the Trace Norm Jason D. M. Rennie jrennie@gmail.com April 14, 2006 1 Introduction We have two goals: (1) to find a low-dimensional representation of text that allows generalization to
Parallel Computation of Spherical Parameterizations for Mesh Analysis. Th. Athanasiadis and I. Fudos University of Ioannina, Greece
 Parallel Computation of Spherical Parameterizations for Mesh Analysis Th. Athanasiadis and I. Fudos, Greece Introduction Mesh parameterization is a powerful geometry processing tool Applications Remeshing
Parallel Computation of Spherical Parameterizations for Mesh Analysis Th. Athanasiadis and I. Fudos, Greece Introduction Mesh parameterization is a powerful geometry processing tool Applications Remeshing
10-701/15-781, Fall 2006, Final
 -7/-78, Fall 6, Final Dec, :pm-8:pm There are 9 questions in this exam ( pages including this cover sheet). If you need more room to work out your answer to a question, use the back of the page and clearly
-7/-78, Fall 6, Final Dec, :pm-8:pm There are 9 questions in this exam ( pages including this cover sheet). If you need more room to work out your answer to a question, use the back of the page and clearly
Depth First Search A B C D E F G A B C 5 D E F 3 2 G 2 3
 Depth First Search A B C D E F G A 4 3 2 B 4 5 4 3 C 5 D 3 4 2 E 2 2 3 F 3 2 G 2 3 Minimum (Weight) Spanning Trees Let G be a graph with weights on the edges. We define the weight of any subgraph of G
Depth First Search A B C D E F G A 4 3 2 B 4 5 4 3 C 5 D 3 4 2 E 2 2 3 F 3 2 G 2 3 Minimum (Weight) Spanning Trees Let G be a graph with weights on the edges. We define the weight of any subgraph of G
Clustering. Robert M. Haralick. Computer Science, Graduate Center City University of New York
 Clustering Robert M. Haralick Computer Science, Graduate Center City University of New York Outline K-means 1 K-means 2 3 4 5 Clustering K-means The purpose of clustering is to determine the similarity
Clustering Robert M. Haralick Computer Science, Graduate Center City University of New York Outline K-means 1 K-means 2 3 4 5 Clustering K-means The purpose of clustering is to determine the similarity
Joint Entity Resolution
 Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Joint Entity Resolution Steven Euijong Whang, Hector Garcia-Molina Computer Science Department, Stanford University 353 Serra Mall, Stanford, CA 94305, USA {swhang, hector}@cs.stanford.edu No Institute
Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong)
 Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong) References: [1] http://homepages.inf.ed.ac.uk/rbf/hipr2/index.htm [2] http://www.cs.wisc.edu/~dyer/cs540/notes/vision.html
Biometrics Technology: Image Processing & Pattern Recognition (by Dr. Dickson Tong) References: [1] http://homepages.inf.ed.ac.uk/rbf/hipr2/index.htm [2] http://www.cs.wisc.edu/~dyer/cs540/notes/vision.html
E-Companion: On Styles in Product Design: An Analysis of US. Design Patents
 E-Companion: On Styles in Product Design: An Analysis of US Design Patents 1 PART A: FORMALIZING THE DEFINITION OF STYLES A.1 Styles as categories of designs of similar form Our task involves categorizing
E-Companion: On Styles in Product Design: An Analysis of US Design Patents 1 PART A: FORMALIZING THE DEFINITION OF STYLES A.1 Styles as categories of designs of similar form Our task involves categorizing
Math 7 Glossary Terms
 Math 7 Glossary Terms Absolute Value Absolute value is the distance, or number of units, a number is from zero. Distance is always a positive value; therefore, absolute value is always a positive value.
Math 7 Glossary Terms Absolute Value Absolute value is the distance, or number of units, a number is from zero. Distance is always a positive value; therefore, absolute value is always a positive value.
Lab # 2 - ACS I Part I - DATA COMPRESSION in IMAGE PROCESSING using SVD
 Lab # 2 - ACS I Part I - DATA COMPRESSION in IMAGE PROCESSING using SVD Goals. The goal of the first part of this lab is to demonstrate how the SVD can be used to remove redundancies in data; in this example
Lab # 2 - ACS I Part I - DATA COMPRESSION in IMAGE PROCESSING using SVD Goals. The goal of the first part of this lab is to demonstrate how the SVD can be used to remove redundancies in data; in this example
Decimals should be spoken digit by digit eg 0.34 is Zero (or nought) point three four (NOT thirty four).
 Numeracy Essentials Section 1 Number Skills Reading and writing numbers All numbers should be written correctly. Most pupils are able to read, write and say numbers up to a thousand, but often have difficulty
Numeracy Essentials Section 1 Number Skills Reading and writing numbers All numbers should be written correctly. Most pupils are able to read, write and say numbers up to a thousand, but often have difficulty
Downloaded from
 UNIT 2 WHAT IS STATISTICS? Researchers deal with a large amount of data and have to draw dependable conclusions on the basis of data collected for the purpose. Statistics help the researchers in making
UNIT 2 WHAT IS STATISTICS? Researchers deal with a large amount of data and have to draw dependable conclusions on the basis of data collected for the purpose. Statistics help the researchers in making
Geometric Computations for Simulation
 1 Geometric Computations for Simulation David E. Johnson I. INTRODUCTION A static virtual world would be boring and unlikely to draw in a user enough to create a sense of immersion. Simulation allows things
1 Geometric Computations for Simulation David E. Johnson I. INTRODUCTION A static virtual world would be boring and unlikely to draw in a user enough to create a sense of immersion. Simulation allows things
Catalan Numbers. Table 1: Balanced Parentheses
 Catalan Numbers Tom Davis tomrdavis@earthlink.net http://www.geometer.org/mathcircles November, 00 We begin with a set of problems that will be shown to be completely equivalent. The solution to each problem
Catalan Numbers Tom Davis tomrdavis@earthlink.net http://www.geometer.org/mathcircles November, 00 We begin with a set of problems that will be shown to be completely equivalent. The solution to each problem
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into
 2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
2D rendering takes a photo of the 2D scene with a virtual camera that selects an axis aligned rectangle from the scene. The photograph is placed into the viewport of the current application window. A pixel
MSA220 - Statistical Learning for Big Data
 MSA220 - Statistical Learning for Big Data Lecture 13 Rebecka Jörnsten Mathematical Sciences University of Gothenburg and Chalmers University of Technology Clustering Explorative analysis - finding groups
MSA220 - Statistical Learning for Big Data Lecture 13 Rebecka Jörnsten Mathematical Sciences University of Gothenburg and Chalmers University of Technology Clustering Explorative analysis - finding groups
Clustering. CE-717: Machine Learning Sharif University of Technology Spring Soleymani
 Clustering CE-717: Machine Learning Sharif University of Technology Spring 2016 Soleymani Outline Clustering Definition Clustering main approaches Partitional (flat) Hierarchical Clustering validation
Clustering CE-717: Machine Learning Sharif University of Technology Spring 2016 Soleymani Outline Clustering Definition Clustering main approaches Partitional (flat) Hierarchical Clustering validation
Random projection for non-gaussian mixture models
 Random projection for non-gaussian mixture models Győző Gidófalvi Department of Computer Science and Engineering University of California, San Diego La Jolla, CA 92037 gyozo@cs.ucsd.edu Abstract Recently,
Random projection for non-gaussian mixture models Győző Gidófalvi Department of Computer Science and Engineering University of California, San Diego La Jolla, CA 92037 gyozo@cs.ucsd.edu Abstract Recently,
3. Multidimensional Information Visualization II Concepts for visualizing univariate to hypervariate data
 3. Multidimensional Information Visualization II Concepts for visualizing univariate to hypervariate data Vorlesung Informationsvisualisierung Prof. Dr. Andreas Butz, WS 2009/10 Konzept und Basis für n:
3. Multidimensional Information Visualization II Concepts for visualizing univariate to hypervariate data Vorlesung Informationsvisualisierung Prof. Dr. Andreas Butz, WS 2009/10 Konzept und Basis für n:
Alaska Mathematics Standards Vocabulary Word List Grade 7
 1 estimate proportion proportional relationship rate ratio rational coefficient rational number scale Ratios and Proportional Relationships To find a number close to an exact amount; an estimate tells
1 estimate proportion proportional relationship rate ratio rational coefficient rational number scale Ratios and Proportional Relationships To find a number close to an exact amount; an estimate tells
ENV Laboratory 2: Graphing
 Name: Date: Introduction It is often said that a picture is worth 1,000 words, or for scientists we might rephrase it to say that a graph is worth 1,000 words. Graphs are most often used to express data
Name: Date: Introduction It is often said that a picture is worth 1,000 words, or for scientists we might rephrase it to say that a graph is worth 1,000 words. Graphs are most often used to express data
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings
 On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
On the Relationships between Zero Forcing Numbers and Certain Graph Coverings Fatemeh Alinaghipour Taklimi, Shaun Fallat 1,, Karen Meagher 2 Department of Mathematics and Statistics, University of Regina,
Digital Image Processing Chapter 11: Image Description and Representation
 Digital Image Processing Chapter 11: Image Description and Representation Image Representation and Description? Objective: To represent and describe information embedded in an image in other forms that
Digital Image Processing Chapter 11: Image Description and Representation Image Representation and Description? Objective: To represent and describe information embedded in an image in other forms that
Supplementary text S6 Comparison studies on simulated data
 Supplementary text S Comparison studies on simulated data Peter Langfelder, Rui Luo, Michael C. Oldham, and Steve Horvath Corresponding author: shorvath@mednet.ucla.edu Overview In this document we illustrate
Supplementary text S Comparison studies on simulated data Peter Langfelder, Rui Luo, Michael C. Oldham, and Steve Horvath Corresponding author: shorvath@mednet.ucla.edu Overview In this document we illustrate
Algorithms: Lecture 7. Chalmers University of Technology
 Algorithms: Lecture 7 Chalmers University of Technology Today s Lecture Divide & Conquer Counting Inversions Closest Pair of Points Multiplication of large integers Intro to the forthcoming problems Graphs:
Algorithms: Lecture 7 Chalmers University of Technology Today s Lecture Divide & Conquer Counting Inversions Closest Pair of Points Multiplication of large integers Intro to the forthcoming problems Graphs:
Preliminaries: Size Measures and Shape Coordinates
 2 Preliminaries: Size Measures and Shape Coordinates 2.1 Configuration Space Definition 2.1 The configuration is the set of landmarks on a particular object. The configuration matrix X is the k m matrix
2 Preliminaries: Size Measures and Shape Coordinates 2.1 Configuration Space Definition 2.1 The configuration is the set of landmarks on a particular object. The configuration matrix X is the k m matrix
6.871 Expert System: WDS Web Design Assistant System
 6.871 Expert System: WDS Web Design Assistant System Timur Tokmouline May 11, 2005 1 Introduction Today, despite the emergence of WYSIWYG software, web design is a difficult and a necessary component of
6.871 Expert System: WDS Web Design Assistant System Timur Tokmouline May 11, 2005 1 Introduction Today, despite the emergence of WYSIWYG software, web design is a difficult and a necessary component of
Simplicial Global Optimization
 Simplicial Global Optimization Julius Žilinskas Vilnius University, Lithuania September, 7 http://web.vu.lt/mii/j.zilinskas Global optimization Find f = min x A f (x) and x A, f (x ) = f, where A R n.
Simplicial Global Optimization Julius Žilinskas Vilnius University, Lithuania September, 7 http://web.vu.lt/mii/j.zilinskas Global optimization Find f = min x A f (x) and x A, f (x ) = f, where A R n.
Spectral Graph Sparsification: overview of theory and practical methods. Yiannis Koutis. University of Puerto Rico - Rio Piedras
 Spectral Graph Sparsification: overview of theory and practical methods Yiannis Koutis University of Puerto Rico - Rio Piedras Graph Sparsification or Sketching Compute a smaller graph that preserves some
Spectral Graph Sparsification: overview of theory and practical methods Yiannis Koutis University of Puerto Rico - Rio Piedras Graph Sparsification or Sketching Compute a smaller graph that preserves some
Data analysis using Microsoft Excel
 Introduction to Statistics Statistics may be defined as the science of collection, organization presentation analysis and interpretation of numerical data from the logical analysis. 1.Collection of Data
Introduction to Statistics Statistics may be defined as the science of collection, organization presentation analysis and interpretation of numerical data from the logical analysis. 1.Collection of Data
Clustering. Informal goal. General types of clustering. Applications: Clustering in information search and analysis. Example applications in search
 Informal goal Clustering Given set of objects and measure of similarity between them, group similar objects together What mean by similar? What is good grouping? Computation time / quality tradeoff 1 2
Informal goal Clustering Given set of objects and measure of similarity between them, group similar objects together What mean by similar? What is good grouping? Computation time / quality tradeoff 1 2
Chapter 14 Global Search Algorithms
 Chapter 14 Global Search Algorithms An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Introduction We discuss various search methods that attempts to search throughout the entire feasible set.
Chapter 14 Global Search Algorithms An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Introduction We discuss various search methods that attempts to search throughout the entire feasible set.
Averages and Variation
 Averages and Variation 3 Copyright Cengage Learning. All rights reserved. 3.1-1 Section 3.1 Measures of Central Tendency: Mode, Median, and Mean Copyright Cengage Learning. All rights reserved. 3.1-2 Focus
Averages and Variation 3 Copyright Cengage Learning. All rights reserved. 3.1-1 Section 3.1 Measures of Central Tendency: Mode, Median, and Mean Copyright Cengage Learning. All rights reserved. 3.1-2 Focus
Approximation Algorithms for Geometric Intersection Graphs
 Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Approximation Algorithms for Geometric Intersection Graphs Subhas C. Nandy (nandysc@isical.ac.in) Advanced Computing and Microelectronics Unit Indian Statistical Institute Kolkata 700108, India. Outline
Drawing Problem. Possible properties Minimum number of edge crossings Small area Straight or short edges Good representation of graph structure...
 Graph Drawing Embedding Embedding For a given graph G = (V, E), an embedding (into R 2 ) assigns each vertex a coordinate and each edge a (not necessarily straight) line connecting the corresponding coordinates.
Graph Drawing Embedding Embedding For a given graph G = (V, E), an embedding (into R 2 ) assigns each vertex a coordinate and each edge a (not necessarily straight) line connecting the corresponding coordinates.
(Refer Slide Time: 00:02:24 min)
 CAD / CAM Prof. Dr. P. V. Madhusudhan Rao Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture No. # 9 Parametric Surfaces II So these days, we are discussing the subject
CAD / CAM Prof. Dr. P. V. Madhusudhan Rao Department of Mechanical Engineering Indian Institute of Technology, Delhi Lecture No. # 9 Parametric Surfaces II So these days, we are discussing the subject
Estimating the Free Region of a Sensor Node
 Estimating the Free Region of a Sensor Node Laxmi Gewali, Navin Rongratana, Jan B. Pedersen School of Computer Science, University of Nevada 4505 Maryland Parkway Las Vegas, NV, 89154, USA Abstract We
Estimating the Free Region of a Sensor Node Laxmi Gewali, Navin Rongratana, Jan B. Pedersen School of Computer Science, University of Nevada 4505 Maryland Parkway Las Vegas, NV, 89154, USA Abstract We
Rank Measures for Ordering
 Rank Measures for Ordering Jin Huang and Charles X. Ling Department of Computer Science The University of Western Ontario London, Ontario, Canada N6A 5B7 email: fjhuang33, clingg@csd.uwo.ca Abstract. Many
Rank Measures for Ordering Jin Huang and Charles X. Ling Department of Computer Science The University of Western Ontario London, Ontario, Canada N6A 5B7 email: fjhuang33, clingg@csd.uwo.ca Abstract. Many
D-Optimal Designs. Chapter 888. Introduction. D-Optimal Design Overview
 Chapter 888 Introduction This procedure generates D-optimal designs for multi-factor experiments with both quantitative and qualitative factors. The factors can have a mixed number of levels. For example,
Chapter 888 Introduction This procedure generates D-optimal designs for multi-factor experiments with both quantitative and qualitative factors. The factors can have a mixed number of levels. For example,
(Lec 14) Placement & Partitioning: Part III
 Page (Lec ) Placement & Partitioning: Part III What you know That there are big placement styles: iterative, recursive, direct Placement via iterative improvement using simulated annealing Recursive-style
Page (Lec ) Placement & Partitioning: Part III What you know That there are big placement styles: iterative, recursive, direct Placement via iterative improvement using simulated annealing Recursive-style
SEEK User Manual. Introduction
 SEEK User Manual Introduction SEEK is a computational gene co-expression search engine. It utilizes a vast human gene expression compendium to deliver fast, integrative, cross-platform co-expression analyses.
SEEK User Manual Introduction SEEK is a computational gene co-expression search engine. It utilizes a vast human gene expression compendium to deliver fast, integrative, cross-platform co-expression analyses.
Lesson 3. Prof. Enza Messina
 Lesson 3 Prof. Enza Messina Clustering techniques are generally classified into these classes: PARTITIONING ALGORITHMS Directly divides data points into some prespecified number of clusters without a hierarchical
Lesson 3 Prof. Enza Messina Clustering techniques are generally classified into these classes: PARTITIONING ALGORITHMS Directly divides data points into some prespecified number of clusters without a hierarchical
Robust Kernel Methods in Clustering and Dimensionality Reduction Problems
 Robust Kernel Methods in Clustering and Dimensionality Reduction Problems Jian Guo, Debadyuti Roy, Jing Wang University of Michigan, Department of Statistics Introduction In this report we propose robust
Robust Kernel Methods in Clustering and Dimensionality Reduction Problems Jian Guo, Debadyuti Roy, Jing Wang University of Michigan, Department of Statistics Introduction In this report we propose robust
Computer Vision I - Filtering and Feature detection
 Computer Vision I - Filtering and Feature detection Carsten Rother 30/10/2015 Computer Vision I: Basics of Image Processing Roadmap: Basics of Digital Image Processing Computer Vision I: Basics of Image
Computer Vision I - Filtering and Feature detection Carsten Rother 30/10/2015 Computer Vision I: Basics of Image Processing Roadmap: Basics of Digital Image Processing Computer Vision I: Basics of Image
6 Randomized rounding of semidefinite programs
 6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
6 Randomized rounding of semidefinite programs We now turn to a new tool which gives substantially improved performance guarantees for some problems We now show how nonlinear programming relaxations can
Graphs. The ultimate data structure. graphs 1
 Graphs The ultimate data structure graphs 1 Definition of graph Non-linear data structure consisting of nodes & links between them (like trees in this sense) Unlike trees, graph nodes may be completely
Graphs The ultimate data structure graphs 1 Definition of graph Non-linear data structure consisting of nodes & links between them (like trees in this sense) Unlike trees, graph nodes may be completely
Prime Time (Factors and Multiples)
 CONFIDENCE LEVEL: Prime Time Knowledge Map for 6 th Grade Math Prime Time (Factors and Multiples). A factor is a whole numbers that is multiplied by another whole number to get a product. (Ex: x 5 = ;
CONFIDENCE LEVEL: Prime Time Knowledge Map for 6 th Grade Math Prime Time (Factors and Multiples). A factor is a whole numbers that is multiplied by another whole number to get a product. (Ex: x 5 = ;
CLUSTERING IN BIOINFORMATICS
 CLUSTERING IN BIOINFORMATICS CSE/BIMM/BENG 8 MAY 4, 0 OVERVIEW Define the clustering problem Motivation: gene expression and microarrays Types of clustering Clustering algorithms Other applications of
CLUSTERING IN BIOINFORMATICS CSE/BIMM/BENG 8 MAY 4, 0 OVERVIEW Define the clustering problem Motivation: gene expression and microarrays Types of clustering Clustering algorithms Other applications of
Chapter 15 Introduction to Linear Programming
 Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Chapter 15 Introduction to Linear Programming An Introduction to Optimization Spring, 2015 Wei-Ta Chu 1 Brief History of Linear Programming The goal of linear programming is to determine the values of
Universiteit Leiden Computer Science
 Universiteit Leiden Computer Science Optimizing octree updates for visibility determination on dynamic scenes Name: Hans Wortel Student-no: 0607940 Date: 28/07/2011 1st supervisor: Dr. Michael Lew 2nd
Universiteit Leiden Computer Science Optimizing octree updates for visibility determination on dynamic scenes Name: Hans Wortel Student-no: 0607940 Date: 28/07/2011 1st supervisor: Dr. Michael Lew 2nd
Graph Drawing by High-Dimensional Embedding
 Graph Drawing by High-Dimensional Embedding David Harel and Yehuda Koren Dept. of Computer Science and Applied Mathematics The Weizmann Institute of Science, Rehovot, Israel {harel,yehuda}@wisdom.weizmann.ac.il
Graph Drawing by High-Dimensional Embedding David Harel and Yehuda Koren Dept. of Computer Science and Applied Mathematics The Weizmann Institute of Science, Rehovot, Israel {harel,yehuda}@wisdom.weizmann.ac.il
Edge Equalized Treemaps
 Edge Equalized Treemaps Aimi Kobayashi Department of Computer Science University of Tsukuba Ibaraki, Japan kobayashi@iplab.cs.tsukuba.ac.jp Kazuo Misue Faculty of Engineering, Information and Systems University
Edge Equalized Treemaps Aimi Kobayashi Department of Computer Science University of Tsukuba Ibaraki, Japan kobayashi@iplab.cs.tsukuba.ac.jp Kazuo Misue Faculty of Engineering, Information and Systems University
T. Biedl and B. Genc. 1 Introduction
 Complexity of Octagonal and Rectangular Cartograms T. Biedl and B. Genc 1 Introduction A cartogram is a type of map used to visualize data. In a map regions are displayed in their true shapes and with
Complexity of Octagonal and Rectangular Cartograms T. Biedl and B. Genc 1 Introduction A cartogram is a type of map used to visualize data. In a map regions are displayed in their true shapes and with
Understanding Geospatial Data Models
 Understanding Geospatial Data Models 1 A geospatial data model is a formal means of representing spatially referenced information. It is a simplified view of physical entities and a conceptualization of
Understanding Geospatial Data Models 1 A geospatial data model is a formal means of representing spatially referenced information. It is a simplified view of physical entities and a conceptualization of
Gene expression & Clustering (Chapter 10)
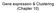 Gene expression & Clustering (Chapter 10) Determining gene function Sequence comparison tells us if a gene is similar to another gene, e.g., in a new species Dynamic programming Approximate pattern matching
Gene expression & Clustering (Chapter 10) Determining gene function Sequence comparison tells us if a gene is similar to another gene, e.g., in a new species Dynamic programming Approximate pattern matching
Cluster Analysis for Microarray Data
 Cluster Analysis for Microarray Data Seventh International Long Oligonucleotide Microarray Workshop Tucson, Arizona January 7-12, 2007 Dan Nettleton IOWA STATE UNIVERSITY 1 Clustering Group objects that
Cluster Analysis for Microarray Data Seventh International Long Oligonucleotide Microarray Workshop Tucson, Arizona January 7-12, 2007 Dan Nettleton IOWA STATE UNIVERSITY 1 Clustering Group objects that
Clustering Using Graph Connectivity
 Clustering Using Graph Connectivity Patrick Williams June 3, 010 1 Introduction It is often desirable to group elements of a set into disjoint subsets, based on the similarity between the elements in the
Clustering Using Graph Connectivity Patrick Williams June 3, 010 1 Introduction It is often desirable to group elements of a set into disjoint subsets, based on the similarity between the elements in the
