University of South Florida Department of Physics 4202 E Fowler Ave.Tampa,FL 33620
|
|
|
- Cuthbert Park
- 6 years ago
- Views:
Transcription
1 Malfatti-Steiner Problem I.A.Sakmar University of South Florida Department of Physics 4202 E Fowler Ave.Tampa,FL Abstract Based on Julius Petersen s work we give detailed proofs of his statements on the proof of Steiner s conjecture. M.S.C.2000: 51A99 Key words: Malfatti circles, Steiner s line, inversion. Malfatti problem was posed by the Italian mathematician Giovanni Francesco Malfatti ( ) in The problem has two aspects. One is to maximize the area of three circles within a triangle. Malfatti thought that the answer was three mutually touching circles which are also tangent to the sides of the triangle.this was later shown to be incorrect (Lob and Richmond 1929). The other is to give a Euclidean construction of these three circles. Malfatti gave only an analytic solution, by calculating the radii of the circles. The key to the solution was found by Jacob Steiner ( ). Steiner did not prove his discovery. It is an amazing and very unlikely discovery. One might think that he perhaps guessed it by a construction. But it is such an intriguing relation that even after one knows it, it is not easy to see it, even with a large and exact construction. Steiner also indicated the way by which his conjecture could be proved. The proof was given according to some sources by Hart in 1856 and others (Julius Petersen) by Schroeter in No matter who gave the proof first, the long time interval (30, or 48 years) between the conjecture and the proof is a testimony to the complexity of the problem. Here I would like to look at the solution of Julius Petersen ( ). This Danish geometer is best known for his small problem book with about 400 problems, many of which are challenging.at the end of his book he outlines in a few lines his simpler solution. There is not even a single figure in the French translation I used. This paper is based on his work. I tried to fill in all the needed proofs to clarify the construction in my mind. Most of them are based on inversion. They may or may not be what Peterson had in mind. I start with a simple figure and every time an element of the proof is introduced I give a new figure. This way when the figure finally gets very complex the reader hopefully will be familiar with all the elements of the last figure. I also give separate figures for the proofs by inversion. -1-
2 Fig.1 Take the triangle ABC.Consider the problem solved. Call the circles S a, S b, and S c. Let their mutual contact points be a, ß, and?. Let the points where they touch the sides AB and CA be C 1, C 2 and ß 1, ß 2 Fig.2 Draw the circle which is tangent to the circles S a, and S b at their contact point ß and goes through the point C 2. Call this circle S M, and its center M. -2-
3 Call the intersection of S M with the side CA D. Draw two tangent lines to the circle SM at points C 2 and D. Call the intersection point of these tangent lines F. We claim that the circle S M intersects the circle S b and the side CA under equal angles. That is, the angle AC 2 F is complementary to the angle FDA. Fig.3 Proof: Theorem: Given two circles S 1, and S 2 which intersect each other at points A, and B. Any circle C which goes through A and B intersects all circles like C a, and C ß which are tangent to S 1, and S 2 under equal angles. (Complementary angles if the circles are on opposite sides.) -3-
4 Fig.4 We invert the system with respect to the inversion center A. With this inversion S 1 becomes a line l 1 S 2 becomes a line l 2 C becomes a line l The point A, being the inversion center goes to infinity. The point B becomes B. The linesl 1, l 2, and l go through the point B, because the circles S 1, S 2, and C go through the point B. The circles C a and C ß become again circles C a, and C ß since they don t go through the inversion center A. The circles C a, and C ß are tangent to the lines l 1,and l 2 because the circles C a, and C ß were tangent to the circles S 1, and S 2 before the inversion. From the inverted drawing it is seen that the line l intersects the circles C a, and C ß under equal angles. Since the inversion does not change angles, the uninverted circle C intersects the uninverted circles C a, and C ß under equal angles. (If C a, and C ß are on opposite sides, the angles are complementary.) -4-
5 In our case the circles S 1, and S 2 are S a, and S c. The points A and B coincide at the point ß, since in our case S a, and S c are tangent. The tangent circles C a, and C ß are in our case S b, and the line CA (degenerate circle with its center at infinity). The circle C is in our case S M. Thus we showed that the circle S M intersects S b, and CA under complementary angles. That is FC 2 A + FDA = 180 o Fig.5 Consider the quadrilaterals MC 2 FD and MC 2 FD. -5-
6 We just proved that the opposed angles at C 2 and D in the quadrilateral AC 2 FD add up to 180 o. Now in the quadrilateral MC 2 FD the tangent C 2 F is to the radius MC 2. Thus the angle MC 2 F = 90 o. Similarly FD MD. Thus the angle FDM = 90 o. Hence the sum of these two opposite angles is 180 o. Also, the two quadrilaterals have the angle C 2 FD common. Thus C 2 MD = C 2 AD. Now connect A to F. We will prove that AF is the bisector of the angle C 2 MD= A. Let D be the point on AB with FC 2 = FD. The triangles AD F = ADF. Because: 1) AF = AF is common to both triangles. 2) FD = FD.Because FD=FC 2 are tangents to the circle S M and we took FD = FC 2. 3) AD F = ADF. Because the triangle C 2 FD being isosceles ADF is complementary to AC 2 F. But we also showed that FDA is complementary to AC 2 F. Hence AD F = ADF Fig.5 We now claim that the points a, ß, C 1, and C 2 lie on a circle. We shall call this circle S t and prove the claim below. -6-
7 Fig.6 Theorem: Given two mutually tangent circles S a, and S b which touch at?. Consider the circles S c, and S d which touch S a, and S b ats the points a, ß, d, and e. The points a, ß, d, and e lie on a circle. The proof is again by inversion. Take? as the center of inversion. S a, and S b become under inversion two lines l a, and l b. the point? goes to infinity. Since S a, and S b do not have a second intersection point (they are tangent) they become parallel lines under inversion. S c, and S d are tangent to both S a, and S b. therefore their images must be tangent to the inverted images of S a, and S b. Fig.7 Obviously the points a, ß, d, and e lie on a circle. Because they lie at the corners of a rectangle. Hence the inverted image of this circle goes through the points a, ß, d, and e. In our case S d is degenerate ( it is the line C 1 C 2 tangent to the circles Sa, and S b ). Thus we established that the points a, ß, C 1, and C 2 lie on a circle, we called S t. -7-
8 Fig.8 Draw the circle through ß, D, and ß 2. Call this circle S u. S u intersects S t at E. Connect C 1 to E, also ß 2 to E. Connect C 2 to ß, also E to ß. We will prove that E lies on the circle with the center A, which goes through C 1, and ß 2. From the circle S t C 1 Eß = 180 o C 1 C 2 ß From the circle S u ß 2 Eß = 180 o ß 2 Dß Adding C 1 Eß + ß 2 Eß = 360 o ( C 1 C 2 ß + ß 2 Dß) But C 1 Eß + ß 2 Eß = 360 o C 1 Eß 2 Hence C 1 Eß 2 = C 1 C 2 ß + ß 2 Dß But C 1 C 2 ß + ß 2 Dß = 360 o A C 2 ßD C 2 ßD is an angle in the circle S M and C 2 ßD = 180 o A Finally C 1 Eß 2 = 360 o - A o A = 180 o A -8-
9 This shows that E is on the circle with the center A and which goes through C 1 and ß 2. Fig.9 Consider the circle S t. C 1 C 2 = EL Because AC 1 = AE We prove now that C 2 K = C 1 C 2 To show that these two segments of the circle S t are equal, we will prove that the angles they make with the tangent to S t at C 2 are equal. That is? =? -9-
10 Fig.10 We invert the system with respect to the inversion center?. The circle S a becomes a line l a. The circle S b becomes a line l b. These two lines are parallel because the only common point? of the two circles S a and S b goes to infinity. The line C 1 C 2 becomes a circle. Thus S b and C 1 C 2 exchange roles under inversion. Before the inversion the line C 1 C 2 is tangent to the circle S b. After the inversion the circle C 1 C 2 is tangent to the line l b. Also, the line C 1 C 2 was tangent to the circles S a, and S b before the inversion.. After the inversion the circle C 1 C 2 becomes tangent to the parallel lines l a, and l b. The circle S M through the points C 2 and ß becomes a circle S M through the points C 2, an ß. The circle S t through the points C 1,C 2 and ß becomes a circle S t through the points C 1, C 2, and ß. -10-
11 The circle S C which was tangent to the circles S a, and S b before the inversion becomes a circle S C tangent to the parallel lines l a, and l b after the inversion. Consider now the inverted drawing. Because l a is tangent to S M at ß, a perpendicular line to this tangent goes through the center M of S M. Take the tangent line (4) to S M at C 2 and draw a perpendicular line (3) to this tangent. This perpendicular line goes through the center M of S M. Note also that C 2 ß is a diameter of S t. In the uninverted drawing? is the angle between C 2 F (tangent to S M at C 2 ) and the tangent to S t at C 2. When this is inverted? is the angle between the line (4) (tangent to S M at C 2 ) and the line (2) (tangent to S t at C 2 ). The line (1) C 2 ß is to the line (2), because a radius of S t is to the tangent of S t. Also the line (3) C 2 M is to the line (4), because a radius of S M is to the tangent of S M. Hence? =? 1 Next in the uninverted drawing,? is the angle between the tangent to S t at C 2 and C 1 C 2 which is the tangent line to the circle S b. When this is inverted, the tangent to S t at C 2 becomes the tangent to S t at C 2 which is the line (2). C 1 C 2, which was the tangent line to the circle S b becomes the circle C 1 C 2 tangent to the line l b. Thus? is the angle between the lines (2) and l b. Now M ß l b Line (1) Line (2)? 1 =? 1 But we already found that? =? 1. Thus? =? 1 =? 1 =?? =? since the inversion does not change angles at intersections of curves, we find that also in the uninverted drawing? =?. this proves that C 2 K = C 2 C 1 Because these segments are the corresponding segments to the tangent line to S t at C 2 with equal angles. We now observe that the circles S t and S u play similar roles with respect to circle S M and the point F. We proved that C 2 C 1 =C 2 K where C 2 K is on the tangent from F to CM. Exactly the same proof can be given to show that Dß 2 =DV where DV is on the tangent from F to C M. consequently EU=DV. -11-
12 Fig.11. There remains one more point to be proven. Namely, the line AE goes through F. This we prove now: Suppose AE does not go through F. Let us call the intersection points of AE with the tangent line C 2 F G and with the tangent line FD H. It then follows: (1) FC 2 = FD (Tangents to the same circle S M ) (2) GC 2 = GE (Because of the equality of the segments C 2 K = EL ) (3) HD = HE (Because of the equality of the segments EU = DV ) Subtracting (1)-(2) GC 2 FC 2 = FG = FD-GE = FH+HD-(GH+HE) FG = FH-GH+HD-HE FG+GH = FH This tells us that the sum of the two sides of a triangle equals its third side. Hence F, G and H are one and the -12-
13 This means that E is on the bisector AF. Fig.12. Now we show that the segment XY of the bisector of the angle B is also equal to the segments we discussed. Namely: XY = C 2 C 1 = C 2 K = EL The reason for this is as follows: The segment C 2 C 1 plays similar roles with respect to the two sides of our triangle (of A and B). We focused on the circles S a and S u on the A side. We thus found that AC 1 = AE and C 2 C 1 = EL. Had we constructed the analogue of the circle S u on the B corner side, we would have found the counterpart of C 2 C 1 = EL which is C 2 C 1 = XY. Next, construct the tangent line to S a and S c at ß. This gives us the segment ßZ, and ßZ = C 1 C 2. The reason for this is as follows: Consider the circles S t and S a. they intersect at C 1 and ß. If we construct at C 1 and ß tangents to S a they are symmetric with respect to the line connecting the centers of S t, and S a. Therefore ßZ = C 1 C
14 Thus we have the following segments of S t which are all equal. C 1 C 2 = EL = C 2 K = XY = ßZ Consequently we can draw a circle which is tangent to all those segments. Let us call this circle S v. Obviously S v has the same center as the circle S t. this circle is also seen to be the in-circle of the triangle ABO where O is the intersection point of the bisectors of the triangle ABC. Moreover the tangent to the circles S a, and S c at ß is also tangent to this circle S v. Finally this very tangent is also tangent to the in-circle of the triangle OBC, which we will call S w. The reason for this is that the roles of S v and S w with respect to the circles S a, and S c are similar. Had we focused on S w instead of on S v we would find that the tangent line to S a and S c at ß is also tangent to the circle S w. This finally proves Steiner s conjecture. Fig.13 Steiner s Conjecture: Suppose the problem of finding three Malfatti circles is solved. Then the tangent line to two of these three circles, say S a and S c at their contact point ß is tangent to both of the circles S v, and S w inscribed into the triangles ABO and OBC where O is the intersection point of the bisectors of the angles of the given triangle ABC. -14-
15 Fig.14 Since Steiner s line is so difficult to recognize in an actual triangle,we give here an exaggerated picture of it. Here S a and S c are two of the Malfatti-Steiner circles. The other circles are two of the circles inscribed into the triangles formed by one side of the triangle and two of the bisectors. Fig.15 Construction: Constructing the three bisectors AO, BO, and CO of the triangle ABC, three triangles are found. Construct the in-circle S v of the triangle ABO. Construct the in-circle S w of the triangle OBC. -15-
16 Construct one of the common inner tangents of the circles S v and S w. Call this line the Steiner line. Steiner line is also tangent to one of the three Malfatti circles. Thus the problem is to construct the circle which touches two sides, say AB and CA of the triangle ABC and the Steiner line. To construct the common inner tangent of two given circles with centers C 1, and C 2 and radii R 1, and R 2 we draw around the circle C 1 a circle with radius R 1 + R 2. We next draw a tangent from the point C 2 to this circle. Finally we draw a parallel line to this tangent at a distance R 2 on the circle s side. This gives the common inner tangent of the given circle. -16-
17 A C K N O W L E D G M E N T S I dedicate this paper to my late friend Umit Camat, who gave me Julius Petersen s book as a present. Without him I would not have the motivation for working on this problem. I am grateful to Dr.Denver Jones for proof-reading the manuscript I am grateful to Drs.Pritish Mukherjee and Dr.Robert Chang for their support. I would like to acknowledge and express my thanks to Dr.M.Elhamdadi and Dr.S.Suen for making it possible for me to give a talk in the Mathematics Depatments colloquium. I would also like to thank Jason Bevans for generating the very complicated geometric drawings with the computer. -17-
18 References Julius Petersen, Methodes et theories pour la resolution des problemes de constructions geometriques, (Translated from Danish.) Editions Jacques Gabay. Hart, Quarterly J.Math.1 (1856) 219 Schellbach, Crelle Journal fuer reine und angewandte Mathematik. Vol.45 See for instance in 100 Great Problems of Elementary Mathematics. Their History and Solution, Heinrich Doerry. Translation published by Dover Books. -18-
19
A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY
 i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
i MATH 119 A HISTORICAL INTRODUCTION TO ELEMENTARY GEOMETRY Geometry is an word derived from ancient Greek meaning earth measure ( ge = earth or land ) + ( metria = measure ). Euclid wrote the Elements
CONSTRUCTIONS Introduction Division of a Line Segment
 216 MATHEMATICS CONSTRUCTIONS 11 111 Introduction In Class IX, you have done certain constructions using a straight edge (ruler) and a compass, eg, bisecting an angle, drawing the perpendicular bisector
216 MATHEMATICS CONSTRUCTIONS 11 111 Introduction In Class IX, you have done certain constructions using a straight edge (ruler) and a compass, eg, bisecting an angle, drawing the perpendicular bisector
Topics in geometry Exam 1 Solutions 7/8/4
 Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
Topics in geometry Exam 1 Solutions 7/8/4 Question 1 Consider the following axioms for a geometry: There are exactly five points. There are exactly five lines. Each point lies on exactly three lines. Each
5 The Pythagorean theorem revisited
 230 Chapter 5. AREAS 5 The Pythagorean theorem revisited 259. Theorem. The areas of squares constructed on the legs of a right triangle add up to the area of the square constructed on its hypotenuse. This
230 Chapter 5. AREAS 5 The Pythagorean theorem revisited 259. Theorem. The areas of squares constructed on the legs of a right triangle add up to the area of the square constructed on its hypotenuse. This
11 The Regular Pentagon
 11 The Regular Pentagon 11.1 The Euclidean construction with the Golden Ratio The figure on page 561 shows an easy Euclidean construction of a regular pentagon. The justification of the construction begins
11 The Regular Pentagon 11.1 The Euclidean construction with the Golden Ratio The figure on page 561 shows an easy Euclidean construction of a regular pentagon. The justification of the construction begins
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 8 Table of Contents Title Author Regular Triangles Cameron Hertzler Regular Pentagon Cameron Hertzler Hemispheres and Right Angles Cameron Hertzler
Transactions in Euclidean Geometry Volume 207F Issue # 8 Table of Contents Title Author Regular Triangles Cameron Hertzler Regular Pentagon Cameron Hertzler Hemispheres and Right Angles Cameron Hertzler
And Now From a New Angle Special Angles and Postulates LEARNING GOALS
 And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
And Now From a New Angle Special Angles and Postulates LEARNING GOALS KEY TERMS. In this lesson, you will: Calculate the complement and supplement of an angle. Classify adjacent angles, linear pairs, and
no triangle can have more than one right angle or obtuse angle.
 Congruence Theorems in Action Isosceles Triangle Theorems.3 Learning Goals In this lesson, you will: Prove the Isosceles Triangle Base Theorem. Prove the Isosceles Triangle Vertex Angle Theorem. Prove
Congruence Theorems in Action Isosceles Triangle Theorems.3 Learning Goals In this lesson, you will: Prove the Isosceles Triangle Base Theorem. Prove the Isosceles Triangle Vertex Angle Theorem. Prove
Geometry: Traditional Pathway
 GEOMETRY: CONGRUENCE G.CO Prove geometric theorems. Focus on validity of underlying reasoning while using variety of ways of writing proofs. G.CO.11 Prove theorems about parallelograms. Theorems include:
GEOMETRY: CONGRUENCE G.CO Prove geometric theorems. Focus on validity of underlying reasoning while using variety of ways of writing proofs. G.CO.11 Prove theorems about parallelograms. Theorems include:
Acute Triangulations of Polygons
 Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
Europ. J. Combinatorics (2002) 23, 45 55 doi:10.1006/eujc.2001.0531 Available online at http://www.idealibrary.com on Acute Triangulations of Polygons H. MAEHARA We prove that every n-gon can be triangulated
CIRCLE. Circle is a collection of all points in a plane which are equidistant from a fixed point.
 CIRCLE Circle is a collection of all points in a plane which are equidistant from a fixed point. The fixed point is called as the centre and the constant distance is called as the radius. Parts of a Circle
CIRCLE Circle is a collection of all points in a plane which are equidistant from a fixed point. The fixed point is called as the centre and the constant distance is called as the radius. Parts of a Circle
UNM - PNM STATEWIDE MATHEMATICS CONTEST XLI. February 7, 2009 Second Round Three Hours
 UNM - PNM STATEWIDE MATHEMATICS CONTEST XLI February 7, 009 Second Round Three Hours (1) An equilateral triangle is inscribed in a circle which is circumscribed by a square. This square is inscribed in
UNM - PNM STATEWIDE MATHEMATICS CONTEST XLI February 7, 009 Second Round Three Hours (1) An equilateral triangle is inscribed in a circle which is circumscribed by a square. This square is inscribed in
Lesson 3.6 Overlapping Triangles
 Lesson 3.6 Overlapping Triangles Getting Ready: Each division in the given triangle is 1 unit long. Hence, the side of the largest triangle is 4- unit long. Figure 3.6.1. Something to think about How many
Lesson 3.6 Overlapping Triangles Getting Ready: Each division in the given triangle is 1 unit long. Hence, the side of the largest triangle is 4- unit long. Figure 3.6.1. Something to think about How many
Jim Sauerberg and Alan Tarr
 Integre Technical Publishing Co., Inc. College Mathematics Journal 33:1 September 28, 2001 11:30 a.m. sauerberg.tex Centering Jim Sauerberg and Alan Tarr Jim Sauerberg (jsauerb@stmarys-ca.edu) is an associate
Integre Technical Publishing Co., Inc. College Mathematics Journal 33:1 September 28, 2001 11:30 a.m. sauerberg.tex Centering Jim Sauerberg and Alan Tarr Jim Sauerberg (jsauerb@stmarys-ca.edu) is an associate
Math 308, Section 101 Solutions to Study Questions for Final Exam (Thursday, December 16, 2004)
 NEUTRAL GEOMETRY Math 308, Section 0 Solutions to Study Questions for Final Exam (Thursday, December 6, 00) I. Given a triangle AEF, let M be the midpoint of the segment EF. Choose a point D on the ray
NEUTRAL GEOMETRY Math 308, Section 0 Solutions to Study Questions for Final Exam (Thursday, December 6, 00) I. Given a triangle AEF, let M be the midpoint of the segment EF. Choose a point D on the ray
Pi at School. Arindama Singh Department of Mathematics Indian Institute of Technology Madras Chennai , India
 Pi at School rindama Singh epartment of Mathematics Indian Institute of Technology Madras Chennai-600036, India Email: asingh@iitm.ac.in bstract: In this paper, an attempt has been made to define π by
Pi at School rindama Singh epartment of Mathematics Indian Institute of Technology Madras Chennai-600036, India Email: asingh@iitm.ac.in bstract: In this paper, an attempt has been made to define π by
Study Guide - Geometry
 Study Guide - Geometry (NOTE: This does not include every topic on the outline. Take other steps to review those.) Page 1: Rigid Motions Page 3: Constructions Page 12: Angle relationships Page 14: Angle
Study Guide - Geometry (NOTE: This does not include every topic on the outline. Take other steps to review those.) Page 1: Rigid Motions Page 3: Constructions Page 12: Angle relationships Page 14: Angle
7th Bay Area Mathematical Olympiad
 7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
7th Bay Area Mathematical Olympiad February 22, 2005 Problems and Solutions 1 An integer is called formidable if it can be written as a sum of distinct powers of 4, and successful if it can be written
MATH 113 Section 8.2: Two-Dimensional Figures
 MATH 113 Section 8.2: Two-Dimensional Figures Prof. Jonathan Duncan Walla Walla University Winter Quarter, 2008 Outline 1 Classifying Two-Dimensional Shapes 2 Polygons Triangles Quadrilaterals 3 Other
MATH 113 Section 8.2: Two-Dimensional Figures Prof. Jonathan Duncan Walla Walla University Winter Quarter, 2008 Outline 1 Classifying Two-Dimensional Shapes 2 Polygons Triangles Quadrilaterals 3 Other
Elementary Planar Geometry
 Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Elementary Planar Geometry What is a geometric solid? It is the part of space occupied by a physical object. A geometric solid is separated from the surrounding space by a surface. A part of the surface
Angles. An angle is: the union of two rays having a common vertex.
 Angles An angle is: the union of two rays having a common vertex. Angles can be measured in both degrees and radians. A circle of 360 in radian measure is equal to 2π radians. If you draw a circle with
Angles An angle is: the union of two rays having a common vertex. Angles can be measured in both degrees and radians. A circle of 360 in radian measure is equal to 2π radians. If you draw a circle with
ME 111: Engineering Drawing. Geometric Constructions
 ME 111: Engineering Drawing Lecture 2 01-08-2011 Geometric Constructions Indian Institute of Technology Guwahati Guwahati 781039 Geometric Construction Construction of primitive geometric forms (points,
ME 111: Engineering Drawing Lecture 2 01-08-2011 Geometric Constructions Indian Institute of Technology Guwahati Guwahati 781039 Geometric Construction Construction of primitive geometric forms (points,
11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will
 11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will be necessary. This firstly pertains to the basic concepts
11 1. Introductory part In order to follow the contents of this book with full understanding, certain prerequisites from high school mathematics will be necessary. This firstly pertains to the basic concepts
Transactions in Euclidean Geometry
 Transactions in Euclidean Geometry Volume 207F Issue # 6 Table of Contents Title Author Not All Kites are Parallelograms Steven Flesch Constructing a Kite Micah Otterbein Exterior Angles of Pentagons Kaelyn
Transactions in Euclidean Geometry Volume 207F Issue # 6 Table of Contents Title Author Not All Kites are Parallelograms Steven Flesch Constructing a Kite Micah Otterbein Exterior Angles of Pentagons Kaelyn
Unit 2: Triangles and Polygons
 Unit 2: Triangles and Polygons Background for Standard G.CO.9: Prove theorems about lines and angles. Objective: By the end of class, I should Using the diagram below, answer the following questions. Line
Unit 2: Triangles and Polygons Background for Standard G.CO.9: Prove theorems about lines and angles. Objective: By the end of class, I should Using the diagram below, answer the following questions. Line
Preliminary: First you must understand the relationship between inscribed and circumscribed, for example:
 10.7 Inscribed and Circumscribed Polygons Lesson Objective: After studying this section, you will be able to: Recognize inscribed and circumscribed polygons Apply the relationship between opposite angles
10.7 Inscribed and Circumscribed Polygons Lesson Objective: After studying this section, you will be able to: Recognize inscribed and circumscribed polygons Apply the relationship between opposite angles
Geometry: general information, symbols, and theorems
 Foundations of Mathematics 11 Chapter 2 Geometry seems like it s full of rules. They do need to be in your head, but not really by memorizing them. It s more a case of understanding them. In this section,
Foundations of Mathematics 11 Chapter 2 Geometry seems like it s full of rules. They do need to be in your head, but not really by memorizing them. It s more a case of understanding them. In this section,
Answers. (1) Parallelogram. Remember: A four-sided flat shape where the opposite sides are parallel is called a parallelogram. Here, AB DC and BC AD.
 Answers (1) Parallelogram Remember: A four-sided flat shape where the opposite sides are parallel is called a parallelogram. Here, AB DC and BC AD. (2) straight angle The angle whose measure is 180 will
Answers (1) Parallelogram Remember: A four-sided flat shape where the opposite sides are parallel is called a parallelogram. Here, AB DC and BC AD. (2) straight angle The angle whose measure is 180 will
EUCLID S GEOMETRY. Raymond Hoobler. January 27, 2008
 EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
EUCLID S GEOMETRY Raymond Hoobler January 27, 2008 Euclid rst codi ed the procedures and results of geometry, and he did such a good job that even today it is hard to improve on his presentation. He lived
Select the best answer. Bubble the corresponding choice on your scantron. Team 13. Geometry
 Team Geometry . What is the sum of the interior angles of an equilateral triangle? a. 60 b. 90 c. 80 d. 60. The sine of angle A is. What is the cosine of angle A? 6 4 6 a. b. c.. A parallelogram has all
Team Geometry . What is the sum of the interior angles of an equilateral triangle? a. 60 b. 90 c. 80 d. 60. The sine of angle A is. What is the cosine of angle A? 6 4 6 a. b. c.. A parallelogram has all
Midpoint and Distance Formulas
 CP1 Math Unit 5: Coordinate Geometry: Day Name Midpoint Formula: Midpoint and Distance Formulas The midpoint of the line segment between any two points (x!, y! ) to (x!, y! ) is given by: In your groups,
CP1 Math Unit 5: Coordinate Geometry: Day Name Midpoint Formula: Midpoint and Distance Formulas The midpoint of the line segment between any two points (x!, y! ) to (x!, y! ) is given by: In your groups,
Modeling with Geometry
 Modeling with Geometry 6.3 Parallelograms https://mathbitsnotebook.com/geometry/quadrilaterals/qdparallelograms.html Properties of Parallelograms Sides A parallelogram is a quadrilateral with both pairs
Modeling with Geometry 6.3 Parallelograms https://mathbitsnotebook.com/geometry/quadrilaterals/qdparallelograms.html Properties of Parallelograms Sides A parallelogram is a quadrilateral with both pairs
Problem 2.1. Complete the following proof of Euclid III.20, referring to the figure on page 1.
 Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
Math 3181 Dr. Franz Rothe October 30, 2015 All3181\3181_fall15t2.tex 2 Solution of Test Name: Figure 1: Central and circumference angle of a circular arc, both obtained as differences Problem 2.1. Complete
added to equal quantities, their sum is equal. Same holds for congruence.
 Mr. Cheung s Geometry Cheat Sheet Theorem List Version 6.0 Updated 3/14/14 (The following is to be used as a guideline. The rest you need to look up on your own, but hopefully this will help. The original
Mr. Cheung s Geometry Cheat Sheet Theorem List Version 6.0 Updated 3/14/14 (The following is to be used as a guideline. The rest you need to look up on your own, but hopefully this will help. The original
Geometry Definitions, Postulates, and Theorems. Chapter 3: Parallel and Perpendicular Lines. Section 3.1: Identify Pairs of Lines and Angles.
 Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Geometry Definitions, Postulates, and Theorems Chapter : Parallel and Perpendicular Lines Section.1: Identify Pairs of Lines and Angles Standards: Prepare for 7.0 Students prove and use theorems involving
Find the locus of the center of a bicycle wheel touching the floor and two corner walls.
 WFNMC conference - Riga - July 00 Maurice Starck - mstarck@canl.nc Three problems My choice of three problems, ordered in increasing difficulty. The first is elementary, but the last is a very difficult
WFNMC conference - Riga - July 00 Maurice Starck - mstarck@canl.nc Three problems My choice of three problems, ordered in increasing difficulty. The first is elementary, but the last is a very difficult
September 23,
 1. In many ruler and compass constructions it is important to know that the perpendicular bisector of a secant to a circle is a diameter of that circle. In particular, as a limiting case, this obtains
1. In many ruler and compass constructions it is important to know that the perpendicular bisector of a secant to a circle is a diameter of that circle. In particular, as a limiting case, this obtains
5. THE ISOPERIMETRIC PROBLEM
 Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Math 501 - Differential Geometry Herman Gluck March 1, 2012 5. THE ISOPERIMETRIC PROBLEM Theorem. Let C be a simple closed curve in the plane with length L and bounding a region of area A. Then L 2 4 A,
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1
 Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Plane Geometry: Reflection Across a Line Does It! at the Marin Math Circle 1 by Zvezdelina Stankova Berkeley Math Circle Director September 29 and October 13, 2010 Note: We shall work on the problems below
Understand and Apply Theorems About Circles
 Teaching Circles in High School Geometry According to the Common Core Standards For 9 th and 10 th grade using Basic Geometry by Ray Jurgensen and Richard G. brown V. Martinez January 27, 2014 Understand
Teaching Circles in High School Geometry According to the Common Core Standards For 9 th and 10 th grade using Basic Geometry by Ray Jurgensen and Richard G. brown V. Martinez January 27, 2014 Understand
Geometry. Parallel Lines.
 1 Geometry Parallel Lines 2015 10 21 www.njctl.org 2 Table of Contents Lines: Intersecting, Parallel & Skew Lines & Transversals Parallel Lines & Proofs Properties of Parallel Lines Constructing Parallel
1 Geometry Parallel Lines 2015 10 21 www.njctl.org 2 Table of Contents Lines: Intersecting, Parallel & Skew Lines & Transversals Parallel Lines & Proofs Properties of Parallel Lines Constructing Parallel
Exploring. After my honors geometry students. Familiar sets of points defined by distances appear as unexpected shapes in larger-distance geometry.
 Exploring Familiar sets of points defined by distances appear as unexpected shapes in larger-distance geometry. New Ge Wayne Nirode After my honors geometry students have studied Euclidean plane geometry,
Exploring Familiar sets of points defined by distances appear as unexpected shapes in larger-distance geometry. New Ge Wayne Nirode After my honors geometry students have studied Euclidean plane geometry,
Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points.
 Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Math 3181 Dr. Franz Rothe Name: All3181\3181_spr13t1.tex 1 Solution of Test I Definition 1 (Hand-shake model). A hand shake model is an incidence geometry for which every line has exactly two points. Definition
Steiner's Porism: An Activity Using the TI-92 Paul Beem Indiana University South Bend, IN
 Steiner's Porism: An Activity Using the TI-9 Paul Beem Indiana University South Bend, IN pbeem@iusb.edu Suppose you are given two circles, one inside the other. Suppose you start drawing circles whose
Steiner's Porism: An Activity Using the TI-9 Paul Beem Indiana University South Bend, IN pbeem@iusb.edu Suppose you are given two circles, one inside the other. Suppose you start drawing circles whose
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions
 Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
Proving Triangles and Quadrilaterals Satisfy Transformational Definitions 1. Definition of Isosceles Triangle: A triangle with one line of symmetry. a. If a triangle has two equal sides, it is isosceles.
Inversive Plane Geometry
 Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
Inversive Plane Geometry An inversive plane is a geometry with three undefined notions: points, circles, and an incidence relation between points and circles, satisfying the following three axioms: (I.1)
8. T(3, 4) and W(2, 7) 9. C(5, 10) and D(6, -1)
 Name: Period: Chapter 1: Essentials of Geometry In exercises 6-7, find the midpoint between the two points. 6. T(3, 9) and W(15, 5) 7. C(1, 4) and D(3, 2) In exercises 8-9, find the distance between the
Name: Period: Chapter 1: Essentials of Geometry In exercises 6-7, find the midpoint between the two points. 6. T(3, 9) and W(15, 5) 7. C(1, 4) and D(3, 2) In exercises 8-9, find the distance between the
Bicentric Quadrilaterals through Inversion
 Forum Geometricorum Volume 13 (013) 11 15. FOUM GEOM ISSN 1534-1178 Bicentric Quadrilaterals through Inversion Albrecht Hess Abstract. We show that inversion is a delightful tool for making some recent
Forum Geometricorum Volume 13 (013) 11 15. FOUM GEOM ISSN 1534-1178 Bicentric Quadrilaterals through Inversion Albrecht Hess Abstract. We show that inversion is a delightful tool for making some recent
SOL Chapter Due Date
 Name: Block: Date: Geometry SOL Review SOL Chapter Due Date G.1 2.2-2.4 G.2 3.1-3.5 G.3 1.3, 4.8, 6.7, 9 G.4 N/A G.5 5.5 G.6 4.1-4.7 G.7 6.1-6.6 G.8 7.1-7.7 G.9 8.2-8.6 G.10 1.6, 8.1 G.11 10.1-10.6, 11.5,
Name: Block: Date: Geometry SOL Review SOL Chapter Due Date G.1 2.2-2.4 G.2 3.1-3.5 G.3 1.3, 4.8, 6.7, 9 G.4 N/A G.5 5.5 G.6 4.1-4.7 G.7 6.1-6.6 G.8 7.1-7.7 G.9 8.2-8.6 G.10 1.6, 8.1 G.11 10.1-10.6, 11.5,
Standards-Based Curriculum Support!
 Coach is the leader in standards-based, state-customized instruction for grades K 12 in English language arts, mathematics, science, and social studies. Our student texts deliver everything you need to
Coach is the leader in standards-based, state-customized instruction for grades K 12 in English language arts, mathematics, science, and social studies. Our student texts deliver everything you need to
Math 311. Trees Name: A Candel CSUN Math
 1. A simple path in a graph is a path with no repeated edges. A simple circuit is a circuit without repeated edges. 2. Trees are special kinds of graphs. A tree is a connected graph with no simple circuits.
1. A simple path in a graph is a path with no repeated edges. A simple circuit is a circuit without repeated edges. 2. Trees are special kinds of graphs. A tree is a connected graph with no simple circuits.
2.1 Angles, Lines and Parallels & 2.2 Congruent Triangles and Pasch s Axiom
 2 Euclidean Geometry In the previous section we gave a sketch overview of the early parts of Euclid s Elements. While the Elements set the standard for the modern axiomatic approach to mathematics, it
2 Euclidean Geometry In the previous section we gave a sketch overview of the early parts of Euclid s Elements. While the Elements set the standard for the modern axiomatic approach to mathematics, it
DEFINITIONS. Perpendicular Two lines are called perpendicular if they form a right angle.
 DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
DEFINITIONS Degree A degree is the 1 th part of a straight angle. 180 Right Angle A 90 angle is called a right angle. Perpendicular Two lines are called perpendicular if they form a right angle. Congruent
Mathematics Scope & Sequence Geometry
 Mathematics Scope & Sequence Geometry Readiness Standard(s) First Six Weeks (29 ) Coordinate Geometry G.7.B use slopes and equations of lines to investigate geometric relationships, including parallel
Mathematics Scope & Sequence Geometry Readiness Standard(s) First Six Weeks (29 ) Coordinate Geometry G.7.B use slopes and equations of lines to investigate geometric relationships, including parallel
Geometry Mathematics Content Standards
 85 The geometry skills and concepts developed in this discipline are useful to all students. Aside from learning these skills and concepts, students will develop their ability to construct formal, logical
85 The geometry skills and concepts developed in this discipline are useful to all students. Aside from learning these skills and concepts, students will develop their ability to construct formal, logical
Squaring the Circle in Elliptic Geometry
 Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 2 Article 1 Squaring the Circle in Elliptic Geometry Noah Davis Aquinas College Kyle Jansens Aquinas College, kyle.jansens@aquinas.edu Follow
Rose-Hulman Undergraduate Mathematics Journal Volume 18 Issue 2 Article 1 Squaring the Circle in Elliptic Geometry Noah Davis Aquinas College Kyle Jansens Aquinas College, kyle.jansens@aquinas.edu Follow
Another Proof of the Steiner Result for Three Equidistant Points in Euclidean Space and an Analogous Proof in Hyperbolic Space
 Rose-Hulman Undergraduate Mathematics Journal Volume 5 Issue 2 Article 1 Another Proof of the Steiner Result for Three Equidistant Points in Euclidean Space and an Analogous Proof in Hyperbolic Space Diana
Rose-Hulman Undergraduate Mathematics Journal Volume 5 Issue 2 Article 1 Another Proof of the Steiner Result for Three Equidistant Points in Euclidean Space and an Analogous Proof in Hyperbolic Space Diana
Geometry (H) Worksheet: 1st Semester Review:True/False, Always/Sometimes/Never
 1stSemesterReviewTrueFalse.nb 1 Geometry (H) Worksheet: 1st Semester Review:True/False, Always/Sometimes/Never Classify each statement as TRUE or FALSE. 1. Three given points are always coplanar. 2. A
1stSemesterReviewTrueFalse.nb 1 Geometry (H) Worksheet: 1st Semester Review:True/False, Always/Sometimes/Never Classify each statement as TRUE or FALSE. 1. Three given points are always coplanar. 2. A
MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined
 MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined terms used to create definitions. Definitions are used
MTH 362 Study Guide Exam 1 System of Euclidean Geometry 1. Describe the building blocks of Euclidean geometry. a. Point, line, and plane - undefined terms used to create definitions. Definitions are used
Math 6, Unit 8 Notes: Geometric Relationships
 Math 6, Unit 8 Notes: Geometric Relationships Points, Lines and Planes; Line Segments and Rays As we begin any new topic, we have to familiarize ourselves with the language and notation to be successful.
Math 6, Unit 8 Notes: Geometric Relationships Points, Lines and Planes; Line Segments and Rays As we begin any new topic, we have to familiarize ourselves with the language and notation to be successful.
Geometry Where everything is made up and the points matter
 Geometry Where everything is made up and the points matter Based on LAMC handouts by Po-Shen Loh and Alin Galatan Math Circle April 15th, 2018 Today we will be returning to the roots of mathematics. Euclidean
Geometry Where everything is made up and the points matter Based on LAMC handouts by Po-Shen Loh and Alin Galatan Math Circle April 15th, 2018 Today we will be returning to the roots of mathematics. Euclidean
Basic Euclidean Geometry
 hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
hapter 1 asic Euclidean Geometry This chapter is not intended to be a complete survey of basic Euclidean Geometry, but rather a review for those who have previously taken a geometry course For a definitive
8 Standard Euclidean Triangle Geometry
 8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
8 Standard Euclidean Triangle Geometry 8.1 The circum-center Figure 8.1: In hyperbolic geometry, the perpendicular bisectors can be parallel as shown but this figure is impossible in Euclidean geometry.
Spherical Geometry MATH430
 Spherical Geometry MATH430 Fall 014 In these notes we summarize some results about the geometry of the sphere that complement should the textbook. Most notions we had on the plane (points, lines, angles,
Spherical Geometry MATH430 Fall 014 In these notes we summarize some results about the geometry of the sphere that complement should the textbook. Most notions we had on the plane (points, lines, angles,
Instructional Unit CPM Geometry Unit Content Objective Performance Indicator Performance Task State Standards Code:
 306 Instructional Unit Area 1. Areas of Squares and The students will be -Find the amount of carpet 2.4.11 E Rectangles able to determine the needed to cover various plane 2. Areas of Parallelograms and
306 Instructional Unit Area 1. Areas of Squares and The students will be -Find the amount of carpet 2.4.11 E Rectangles able to determine the needed to cover various plane 2. Areas of Parallelograms and
Suggested problems - solutions
 Suggested problems - solutions Quadrilaterals Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section 3.7, pp 190-193.
Suggested problems - solutions Quadrilaterals Material for this section references College Geometry: A Discovery Approach, 2/e, David C. Kay, Addison Wesley, 2001. In particular, see section 3.7, pp 190-193.
Explorations of Rigid Motions and Congruence
 Explorations of Rigid Motions and Congruence James King University of Washington Department of Mathematics king@uw.edu http://www.math.washington.edu/~king The Plan In this session, we will explore exploring.
Explorations of Rigid Motions and Congruence James King University of Washington Department of Mathematics king@uw.edu http://www.math.washington.edu/~king The Plan In this session, we will explore exploring.
Understanding Quadrilaterals
 Understanding Quadrilaterals Parallelogram: A quadrilateral with each pair of opposite sides parallel. Properties: (1) Opposite sides are equal. (2) Opposite angles are equal. (3) Diagonals bisect one
Understanding Quadrilaterals Parallelogram: A quadrilateral with each pair of opposite sides parallel. Properties: (1) Opposite sides are equal. (2) Opposite angles are equal. (3) Diagonals bisect one
Math Circle Beginners Group May 8, 2016 Geometry
 Math Circle Beginners Group May 8, 2016 Geometry Warm-up Problem: Grandfather and Grandson 1. In 1932, I was as old as the last two digits of my birth year. When I mentioned this interesting coincidence
Math Circle Beginners Group May 8, 2016 Geometry Warm-up Problem: Grandfather and Grandson 1. In 1932, I was as old as the last two digits of my birth year. When I mentioned this interesting coincidence
Lines Plane A flat surface that has no thickness and extends forever.
 Lines Plane A flat surface that has no thickness and extends forever. Point an exact location Line a straight path that has no thickness and extends forever in opposite directions Ray Part of a line that
Lines Plane A flat surface that has no thickness and extends forever. Point an exact location Line a straight path that has no thickness and extends forever in opposite directions Ray Part of a line that
Mathematics For Class IX Lines and Angles
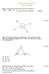 Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
Mathematics For Class IX Lines and Angles (Q.1) In Fig, lines PQ and RS intersect each other at point O. If, find angle POR and angle ROQ (1 Marks) (Q.2) An exterior angle of a triangle is 110 and one
SOME IMPORTANT PROPERTIES/CONCEPTS OF GEOMETRY (Compiled by Ronnie Bansal)
 1 SOME IMPORTANT PROPERTIES/CONCEPTS OF GEOMETRY (Compiled by Ronnie Bansal) 1. Basic Terms and Definitions: a) Line-segment: A part of a line with two end points is called a line-segment. b) Ray: A part
1 SOME IMPORTANT PROPERTIES/CONCEPTS OF GEOMETRY (Compiled by Ronnie Bansal) 1. Basic Terms and Definitions: a) Line-segment: A part of a line with two end points is called a line-segment. b) Ray: A part
Gergonne and Nagel Points for Simplices in the n-dimensional Space
 Journal for Geometry and Graphics Volume 4 (2000), No. 2, 119 127. Gergonne and Nagel Points for Simplices in the n-dimensional Space Edwin Koźniewsi 1, Renata A. Górsa 2 1 Institute of Civil Engineering,
Journal for Geometry and Graphics Volume 4 (2000), No. 2, 119 127. Gergonne and Nagel Points for Simplices in the n-dimensional Space Edwin Koźniewsi 1, Renata A. Górsa 2 1 Institute of Civil Engineering,
Commutative property. Associative property. Distributive property
 Math 4. Class work 4. Algebra Addition Multiplication a+b=b+a Commutative a b=b a a+(b+c)=(a+b)+c Associative a (b c)=(a b) c Distributive a (b+c)=a b + a c a (b c)=a b a c Commutative and associative
Math 4. Class work 4. Algebra Addition Multiplication a+b=b+a Commutative a b=b a a+(b+c)=(a+b)+c Associative a (b c)=(a b) c Distributive a (b+c)=a b + a c a (b c)=a b a c Commutative and associative
edunepal_info
 facebook.com/edunepal.info @ edunepal_info Tangent Constructions Session 1 Drawing and designing logos Many symbols are constructed using geometric shapes. The following section explains common geometrical
facebook.com/edunepal.info @ edunepal_info Tangent Constructions Session 1 Drawing and designing logos Many symbols are constructed using geometric shapes. The following section explains common geometrical
Math 3315: Geometry Vocabulary Review Human Dictionary: WORD BANK
 Math 3315: Geometry Vocabulary Review Human Dictionary: WORD BANK [acute angle] [acute triangle] [adjacent interior angle] [alternate exterior angles] [alternate interior angles] [altitude] [angle] [angle_addition_postulate]
Math 3315: Geometry Vocabulary Review Human Dictionary: WORD BANK [acute angle] [acute triangle] [adjacent interior angle] [alternate exterior angles] [alternate interior angles] [altitude] [angle] [angle_addition_postulate]
UNIT 5 GEOMETRY TEMPLATE CREATED BY REGION 1 ESA UNIT 5
 UNIT 5 GEOMETRY TEMPLATE CREATED BY REGION 1 ESA UNIT 5 Geometry Unit 5 Overview: Circles With and Without Coordinates In this unit, students prove basic theorems about circles, with particular attention
UNIT 5 GEOMETRY TEMPLATE CREATED BY REGION 1 ESA UNIT 5 Geometry Unit 5 Overview: Circles With and Without Coordinates In this unit, students prove basic theorems about circles, with particular attention
Constructions with Compass and Straightedge - Part 2
 Name: Constructions with Compass and Straightedge - Part 2 Original Text By Dr. Bradley Material Supplemented by Mrs.de Nobrega 4.8 Points of Concurrency in a Triangle Our last four constructions are our
Name: Constructions with Compass and Straightedge - Part 2 Original Text By Dr. Bradley Material Supplemented by Mrs.de Nobrega 4.8 Points of Concurrency in a Triangle Our last four constructions are our
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Name Honors Geometry Final Exam Review
 2014-2015 Name Honors Geometry Final Eam Review Chapter 5 Use the picture at the right to answer the following questions. 1. AC= 2. m BFD = 3. m CAE = A 29 C B 71⁰ 19 D 16 F 65⁰ E 4. Find the equation
2014-2015 Name Honors Geometry Final Eam Review Chapter 5 Use the picture at the right to answer the following questions. 1. AC= 2. m BFD = 3. m CAE = A 29 C B 71⁰ 19 D 16 F 65⁰ E 4. Find the equation
Geometry GEOMETRY. Congruence
 Geometry Geometry builds on Algebra I concepts and increases students knowledge of shapes and their properties through geometry-based applications, many of which are observable in aspects of everyday life.
Geometry Geometry builds on Algebra I concepts and increases students knowledge of shapes and their properties through geometry-based applications, many of which are observable in aspects of everyday life.
Videos, Constructions, Definitions, Postulates, Theorems, and Properties
 Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
Videos, Constructions, Definitions, Postulates, Theorems, and Properties Videos Proof Overview: http://tinyurl.com/riehlproof Modules 9 and 10: http://tinyurl.com/riehlproof2 Module 9 Review: http://tinyurl.com/module9livelesson-recording
9 Circles CHAPTER. Chapter Outline. Chapter 9. Circles
 www.ck12.org Chapter 9. Circles CHAPTER 9 Circles Chapter Outline 9.1 PARTS OF CIRCLES & TANGENT LINES 9.2 PROPERTIES OF ARCS 9.3 PROPERTIES OF CHORDS 9.4 INSCRIBED ANGLES 9.5 ANGLES OF CHORDS, SECANTS,
www.ck12.org Chapter 9. Circles CHAPTER 9 Circles Chapter Outline 9.1 PARTS OF CIRCLES & TANGENT LINES 9.2 PROPERTIES OF ARCS 9.3 PROPERTIES OF CHORDS 9.4 INSCRIBED ANGLES 9.5 ANGLES OF CHORDS, SECANTS,
Geometric Constructions
 HISTORY OF MATHEMATICS Spring 2005 Geometric Constructions Notes, activities, assignment; #3 in a series. Note: I m not giving a specific due date for this somewhat vague assignment. The idea is that it
HISTORY OF MATHEMATICS Spring 2005 Geometric Constructions Notes, activities, assignment; #3 in a series. Note: I m not giving a specific due date for this somewhat vague assignment. The idea is that it
MATHia Unit MATHia Workspace Overview TEKS
 1 Tools of Geometry Lines, Rays, Segments, and Angles Distances on the Coordinate Plane Parallel and Perpendicular Lines Angle Properties Naming Lines, Rays, Segments, and Angles Working with Measures
1 Tools of Geometry Lines, Rays, Segments, and Angles Distances on the Coordinate Plane Parallel and Perpendicular Lines Angle Properties Naming Lines, Rays, Segments, and Angles Working with Measures
ANGLES See the Math Notes boxes in Lessons and for more information about angle relationships.
 CC1 Basic Definitions Defense Practice ANGLES 2.1.1 2.1.5 Applications of geometr in everda settings often involve the measures of angles. In this chapter we begin our stud of angle measurement. After
CC1 Basic Definitions Defense Practice ANGLES 2.1.1 2.1.5 Applications of geometr in everda settings often involve the measures of angles. In this chapter we begin our stud of angle measurement. After
Term Definition Figure
 Notes LT 1.1 - Distinguish and apply basic terms of geometry (coplanar, collinear, bisectors, congruency, parallel, perpendicular, etc.) Term Definition Figure collinear on the same line (note: you do
Notes LT 1.1 - Distinguish and apply basic terms of geometry (coplanar, collinear, bisectors, congruency, parallel, perpendicular, etc.) Term Definition Figure collinear on the same line (note: you do
If three points A (h, 0), P (a, b) and B (0, k) lie on a line, show that: a b 1.
 ASSIGNMENT ON STRAIGHT LINES LEVEL 1 (CBSE/NCERT/STATE BOARDS) 1 Find the angle between the lines joining the points (0, 0), (2, 3) and the points (2, 2), (3, 5). 2 What is the value of y so that the line
ASSIGNMENT ON STRAIGHT LINES LEVEL 1 (CBSE/NCERT/STATE BOARDS) 1 Find the angle between the lines joining the points (0, 0), (2, 3) and the points (2, 2), (3, 5). 2 What is the value of y so that the line
The Four-Gon Family Tree
 Classification of Quadrilaterals The Four-Gon Family Tree A Diagonal Connect in the classroom Classification is traditionally defined as the precinct of biologists. But classification has great pedagogical
Classification of Quadrilaterals The Four-Gon Family Tree A Diagonal Connect in the classroom Classification is traditionally defined as the precinct of biologists. But classification has great pedagogical
Thomas Jefferson High School for Science and Technology Program of Studies TJ Math 1
 Course Description: This course is designed for students who have successfully completed the standards for Honors Algebra I. Students will study geometric topics in depth, with a focus on building critical
Course Description: This course is designed for students who have successfully completed the standards for Honors Algebra I. Students will study geometric topics in depth, with a focus on building critical
EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS
 EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS Steps to Find the Median of a Triangle: -Find the midpoint of a segment using the midpoint formula. -Use the vertex and midpoint to find the
EQUATIONS OF ALTITUDES, MEDIANS, and PERPENDICULAR BISECTORS Steps to Find the Median of a Triangle: -Find the midpoint of a segment using the midpoint formula. -Use the vertex and midpoint to find the
Example G1: Triangles with circumcenter on a median. Prove that if the circumcenter of a triangle lies on a median, the triangle either is isosceles
 1 Example G1: Triangles with circumcenter on a median. Prove that if the circumcenter of a triangle lies on a median, the triangle either is isosceles or contains a right angle. D D 2 Solution to Example
1 Example G1: Triangles with circumcenter on a median. Prove that if the circumcenter of a triangle lies on a median, the triangle either is isosceles or contains a right angle. D D 2 Solution to Example
GEOMETRY. Changes to the original 2010 COS is in red. If it is red and crossed out, it has been moved to another course.
 The Geometry course builds on Algebra I concepts and increases students knowledge of shapes and their properties through geometry-based applications, many of which are observable in aspects of everyday
The Geometry course builds on Algebra I concepts and increases students knowledge of shapes and their properties through geometry-based applications, many of which are observable in aspects of everyday
Laguerre Planes: A Basic Introduction
 Laguerre Planes: A Basic Introduction Tam Knox Spring 2009 1 1 Introduction Like a projective plane, a Laguerre plane is a type of incidence structure, defined in terms of sets of elements and an incidence
Laguerre Planes: A Basic Introduction Tam Knox Spring 2009 1 1 Introduction Like a projective plane, a Laguerre plane is a type of incidence structure, defined in terms of sets of elements and an incidence
3 Geometric inequalities in convex quadrilaterals Geometric inequalities of Erdős-Mordell type in the convex quadrilateral
 Contents 1 The quadrilateral 9 1.1 General notions........................... 9 1. Determining conditions...................... 10 1.3 Euler s Theorem and Leibniz-type relations........... 14 1.4 Ptolemy
Contents 1 The quadrilateral 9 1.1 General notions........................... 9 1. Determining conditions...................... 10 1.3 Euler s Theorem and Leibniz-type relations........... 14 1.4 Ptolemy
Department: Course: Chapter 1
 Department: Course: 2016-2017 Term, Phrase, or Expression Simple Definition Chapter 1 Comprehension Support Point Line plane collinear coplanar A location in space. It does not have a size or shape The
Department: Course: 2016-2017 Term, Phrase, or Expression Simple Definition Chapter 1 Comprehension Support Point Line plane collinear coplanar A location in space. It does not have a size or shape The
Trig Functions, Equations & Identities May a. [2 marks] Let. For what values of x does Markscheme (M1)
![Trig Functions, Equations & Identities May a. [2 marks] Let. For what values of x does Markscheme (M1) Trig Functions, Equations & Identities May a. [2 marks] Let. For what values of x does Markscheme (M1)](/thumbs/82/86594449.jpg) Trig Functions, Equations & Identities May 2008-2014 1a. Let. For what values of x does () 1b. [5 marks] not exist? Simplify the expression. EITHER OR [5 marks] 2a. 1 In the triangle ABC,, AB = BC + 1.
Trig Functions, Equations & Identities May 2008-2014 1a. Let. For what values of x does () 1b. [5 marks] not exist? Simplify the expression. EITHER OR [5 marks] 2a. 1 In the triangle ABC,, AB = BC + 1.
Geometry Definitions and Theorems. Chapter 9. Definitions and Important Terms & Facts
 Geometry Definitions and Theorems Chapter 9 Definitions and Important Terms & Facts A circle is the set of points in a plane at a given distance from a given point in that plane. The given point is the
Geometry Definitions and Theorems Chapter 9 Definitions and Important Terms & Facts A circle is the set of points in a plane at a given distance from a given point in that plane. The given point is the
Geometry Curriculum Guide Lunenburg County Public Schools June 2014
 Marking Period: 1 Days: 4 Reporting Category/Strand: Reasoning, Lines, and Transformations SOL G.1 The student will construct and judge the validity of a logical argument consisting of a set of premises
Marking Period: 1 Days: 4 Reporting Category/Strand: Reasoning, Lines, and Transformations SOL G.1 The student will construct and judge the validity of a logical argument consisting of a set of premises
Grade 6 Math Circles October 16 & Non-Euclidean Geometry and the Globe
 Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles October 16 & 17 2018 Non-Euclidean Geometry and the Globe (Euclidean) Geometry Review:
