Two-Parameter Selection Techniques for Projection-based Regularization Methods: Application to Partial-Fourier pmri
|
|
|
- Norma Sanders
- 6 years ago
- Views:
Transcription
1 Two-Parameter Selection Techniques for Projection-based Regularization Methods: Application to Partial-Fourier pmri Misha E. Kilmer 1 Scott Hoge 1 Dept. of Mathematics, Tufts University Medford, MA Dept. of Radiology, Brigham and Women s Hospital and Harvard Medical School, Boston, MA Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 1/9
2 Overview Hybrid Methods for single parameter Tihonov regularization Generalization to specialized, two parameter case Parallel MRI bacground Numerical results Conclusions and future wor Two-Parameter Selection Techniques for Projection-based Regularization Methods p. /9
3 Motivation Forward model is a (real) linear system where A is Ax η = b ex, m n, (e.g. n 100, 000,m n) not available explicitly (fast matvecs) ill-conditioned Only b = b ex + η measured (nown) η white (or close) Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 3/9
4 Regularized Problem min x Ax b + λ L 1 x + µ L x where λ,µ are not nown a priori. Our Motivation: Image reconstruction in partial Fourier, parallel (i.e. multiple coil) MRI. Assumption : L 1,L,n/ n, [ L1 L invertible. Issue: Choosing appropriate (λ, µ) without naive solution over a grid of possible choices. *can be relaxed Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 4/9
5 Single Parameter Case First consider min x Ax b + λ Lx, where L is (cheaply) invertible. A change of variables y = Lx gives min y [ AL 1 λi y [ b 0 Naive Approach: for fixed set of λ s, repeatedly solve and use a heuristic (e.g. L-curve, methods from previous tal) to approximate the best one.. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 5/9
6 Single Parameter Case, cont Since cheap to compute Av and L 1 v, use LSQR to solve. Solve instead min y K [ AL 1 λi [ b 0 where, with C = AL 1, K = span{c T b, (C T C)C T b, (C T C) C T b,...,(c T C) 1 C T b} Soln. cost times sum of matvec cost with A and cost of L 1 v. If we wanted to solve this accurately for each specific λ, could change and be large. Too expensive! Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 6/9
7 Projected Problem In LSQR we have the relations AL 1 V = U +1 B, u 1 = U +1 e 1 = βb where V is n, U is m each with orthogonal columns and B is + 1 bidiagonal. min y K [ AL 1 λi y [ b 0 becomes, with x = V y : min z [ B λi z βe 1 Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 7/9
8 Regularized, Projected Problem min z [ B λi z βe 1 This is a size (small), Tihonov-regularized, projected problem. KEY: Choose λ optimally for this problem. Then, the regularized solution to the original equation is set as y (λ ) = V z (λ ). Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 8/9
9 Benefits min z [ B λi z βe 1 Can compute y (λ) = L 1 x (λ) with short-term recurrences for multiple λ simultaneously. Try to choose optimal λ for projected problem using appropriate heuristic [K. and O Leary, 01 Lx (λ) = y(λ) = z(λ) virtually free b = AL 1 y (λ) virtually free Ax (λ) b = B +1 z (λ) βe 1 If not too large, other options possible (e.g. WGCV, [Chung, Nagy, O Leary 08) Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 9/9
10 Two Parameter Case min x Ax b + λ L 1 x + µ L x Recall the assumption L 1,L,n/ n, min x Ax b + λ Fix c = µ/λ, define L c = [ L1 cl [ L1 µ λ L [ L1 L x invertible. and y (λ,µ) = L c x (λ,µ) : min y [ AL 1 c λi y [ b 0 Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 10/9
11 Two Parameter Case min z [ B,c λi z,c βe 1 For a fixed value of c, a different projected problem, regularized using Tihonov. Question: Which values of λ need to be tested for fixed c? Question: What information about the projected problems do we retain to mae a decision about both λ and µ? Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 11/9
12 Grid Typically, choose a set of l 1 values for λ equally spaced in log space. Liewise, l log-equispaced points for µ. Then search over the l 1 l possible pairs in the grid. Thus, in logspace, each pair (λ,µ) lies on one of the l 1 + l 1 lines of slope 1 in this grid. Using µ = cλ, each line corresponds to one value of c. For each fixed c, we need only tae the λ values on this line. For each projected problem, at most min(l 1,l ) λ values are tested, at best, 1. Wor could be done in parallel. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 1/9
13 Summary Original: y (λ,µ) = arg min y [ AL 1 c λi y [ b 0, x (λ,µ) = L 1 c y (λ,µ), µ = cλ. Apply steps of LSQR to approximately it, equivalent to: z (λ),c = arg min [ B,c λi z βe 1 Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 13/9
14 Summary, Cont We are able to compute the following with short-term recurrences, for all appropriate values of c, λ 1 by considering multiple projected problems: Solutions y (λ,µ) y (λ,µ) = z (λ),c r (λ,µ) = Ax (λ,µ) = L c x (λ,µ) b = B +1,c z (λ),c βe 1 * Not needed to obtain items and 3. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 14/9
15 Goal Compute near optimal values of λ,µ. Would lie to do this using only information that was cheaply computed for each projected problem. Following single-parameter case logic, nowing an optimal value of λ for each fixed-c line might be useful. Added difficulty: each projected problem depends on a fixed choice of c, but need whole picture. In particular, L c x (λ,µ) is what is returned, not L 1 x (λ,µ), L x (λ,µ). Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 15/9
16 Regularization Parameter Selection Scheme somewhat problem specific, main idea but may be useful in other applications as well. For each c, select regularization parameter λ for the corresponding projected problem. Using µ = cλ, gives us l 1 + l 1 possible choices. Next use other (problem dependent) a priori information to select from among these. For our application, enough to monitor sharp transitions in residual norms (cheap, available). Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 16/9
17 Bacground: pmri (D) MRI uses magnetic field gradients and RF signals to encode field-of-view F Encoding typically corresponds to DFT, both sides data is acquired in space domain space is sampled in line-by-line fashion. Reduce number of lines Reduce acquisition time Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 17/9
18 D pmri Sub-sampling -space produces aliasing in spatial domain. F Use multiple receiver coils and each coil subsamples in parallel. 4 coils, each subsampling by 4 16 min. scan now taes 4 min. W 1 W W W 3 Reconstruct image one column at a time (regularized soln. to Wρ = s). Similarly, 3D, reconstruct volume one D image slice at a time. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 18/9
19 Fast imaging using partial-fourier encoding Strategy: Acquire one half of -space (top 1/) Use conjugate-symmetry assumption to reconstruct the other half Issues: Conjugate-symmetry implies a real-valued image Field inhomogeneity and gradient field errors prevent exact conjugate-symmetry in -space encoding. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 19/9
20 Partial-Fourier Problem Formulation Want to constrain solution to be nearly real. We use a two-parameter minimization, to constrain real and imaginary components separately. { min Wρ s ρ + λ re R{ρ} + λ im I{ρ} } which is equivalent to solving min x Ax b + λ L 1 x + µ L x with A = [ R{W } I{W } I{W } R{W },x = [ R{ρ} I{ρ},L 1 = [I n, 0,L = [0,I n Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 0/9
21 Parameter Selection STEP 1: For each c (line) do: Compute the residual norms, as function of λ 1, for the projected problem (cheap!). Note these are the same as residual norms corresponding to the large problem. Compute relative difference between neighboring terms on that line. Record λ value corresponding the sharpest transition. STEP : If haven t already, compute the x λ,µ s for these pairs. Throw out any non-physical solutions (e.g. ratio of imaginary part to real part too large). Choose the remaining term with smallest residual norm. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 1/9
22 Numerical Results High resolution phantom, 8 coil GE Scanner at BWH, single 56x56 slice of 3D data set Sampled (partial Fourier) in y-space 73 lines (at or above 18); Sampled in x-space 114 lines, nonuniformly. Acceleration factor 8 A is 133,15 x 131,07 λ 1 = logspace(-5,,10); λ = logspace(-3,4,10) fixed at 30 Simple thresholding on aliased image to throw out non-physical solutions. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. /9
23 Full Data Reconstruction Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 3/9
24 Plot of Residual Norms (log) Residual norm as function of parameters λ re λ im Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 4/9
25 Plot of Relative Error (log) error norm as function of parameters λ re λ im 1 Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 5/9
26 Reconstruction λ 1 (6) = 7.7e, λ (5) = Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 6/9
27 Reconstruction, zoom Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 7/9
28 Phantom results Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 8/9
29 Conclusions and Future Wor Projection approaches can be very computationally efficient choose the regularization parameter for the smaller, projected problem (cheaper). For D, we select first for individual projected problems, then over the whole. Best selection methods may be problem dependent. Basic idea valid when L 1,L not this special: Transform to standard form or use hybrid approach of [K., Hansen, Espanol, 07. Issue of choosing [Chung, Nagy, O Leary 08. Not a factor for our application. Two-Parameter Selection Techniques for Projection-based Regularization Methods p. 9/9
Sparse sampling in MRI: From basic theory to clinical application. R. Marc Lebel, PhD Department of Electrical Engineering Department of Radiology
 Sparse sampling in MRI: From basic theory to clinical application R. Marc Lebel, PhD Department of Electrical Engineering Department of Radiology Objective Provide an intuitive overview of compressed sensing
Sparse sampling in MRI: From basic theory to clinical application R. Marc Lebel, PhD Department of Electrical Engineering Department of Radiology Objective Provide an intuitive overview of compressed sensing
Improved Spatial Localization in 3D MRSI with a Sequence Combining PSF-Choice, EPSI and a Resolution Enhancement Algorithm
 Improved Spatial Localization in 3D MRSI with a Sequence Combining PSF-Choice, EPSI and a Resolution Enhancement Algorithm L.P. Panych 1,3, B. Madore 1,3, W.S. Hoge 1,3, R.V. Mulkern 2,3 1 Brigham and
Improved Spatial Localization in 3D MRSI with a Sequence Combining PSF-Choice, EPSI and a Resolution Enhancement Algorithm L.P. Panych 1,3, B. Madore 1,3, W.S. Hoge 1,3, R.V. Mulkern 2,3 1 Brigham and
1. Techniques for ill-posed least squares problems. We write throughout this lecture = 2. Consider the following least squares problems:
 ILL-POSED LEAST SQUARES PROBLEMS. Techniques for ill-posed least squares problems. We write throughout this lecture = 2. Consider the following least squares problems: where A = min b Ax, min b A ε x,
ILL-POSED LEAST SQUARES PROBLEMS. Techniques for ill-posed least squares problems. We write throughout this lecture = 2. Consider the following least squares problems: where A = min b Ax, min b A ε x,
Constrained Reconstruction of Sparse Cardiac MR DTI Data
 Constrained Reconstruction of Sparse Cardiac MR DTI Data Ganesh Adluru 1,3, Edward Hsu, and Edward V.R. DiBella,3 1 Electrical and Computer Engineering department, 50 S. Central Campus Dr., MEB, University
Constrained Reconstruction of Sparse Cardiac MR DTI Data Ganesh Adluru 1,3, Edward Hsu, and Edward V.R. DiBella,3 1 Electrical and Computer Engineering department, 50 S. Central Campus Dr., MEB, University
ADVANCED RECONSTRUCTION TECHNIQUES IN MRI - 2
 ADVANCED RECONSTRUCTION TECHNIQUES IN MRI - 2 Presented by Rahil Kothari PARTIAL FOURIER RECONSTRUCTION WHAT IS PARTIAL FOURIER RECONSTRUCTION? In Partial Fourier Reconstruction data is not collected symmetrically
ADVANCED RECONSTRUCTION TECHNIQUES IN MRI - 2 Presented by Rahil Kothari PARTIAL FOURIER RECONSTRUCTION WHAT IS PARTIAL FOURIER RECONSTRUCTION? In Partial Fourier Reconstruction data is not collected symmetrically
Partial Derivatives. Partial Derivatives. Partial Derivatives. Partial Derivatives. Partial Derivatives. Partial Derivatives
 In general, if f is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant. By the definition of a derivative, we have Then we are really
In general, if f is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant. By the definition of a derivative, we have Then we are really
Imaging Notes, Part IV
 BME 483 MRI Notes 34 page 1 Imaging Notes, Part IV Slice Selective Excitation The most common approach for dealing with the 3 rd (z) dimension is to use slice selective excitation. This is done by applying
BME 483 MRI Notes 34 page 1 Imaging Notes, Part IV Slice Selective Excitation The most common approach for dealing with the 3 rd (z) dimension is to use slice selective excitation. This is done by applying
Blind Compressed Sensing Using Sparsifying Transforms
 Blind Compressed Sensing Using Sparsifying Transforms Saiprasad Ravishankar and Yoram Bresler Department of Electrical and Computer Engineering and Coordinated Science Laboratory University of Illinois
Blind Compressed Sensing Using Sparsifying Transforms Saiprasad Ravishankar and Yoram Bresler Department of Electrical and Computer Engineering and Coordinated Science Laboratory University of Illinois
NIH Public Access Author Manuscript Proc Soc Photo Opt Instrum Eng. Author manuscript; available in PMC 2014 October 07.
 NIH Public Access Author Manuscript Published in final edited form as: Proc Soc Photo Opt Instrum Eng. 2014 March 21; 9034: 903442. doi:10.1117/12.2042915. MRI Brain Tumor Segmentation and Necrosis Detection
NIH Public Access Author Manuscript Published in final edited form as: Proc Soc Photo Opt Instrum Eng. 2014 March 21; 9034: 903442. doi:10.1117/12.2042915. MRI Brain Tumor Segmentation and Necrosis Detection
Nuts & Bolts of Advanced Imaging. Image Reconstruction Parallel Imaging
 Nuts & Bolts of Advanced Imaging Image Reconstruction Parallel Imaging Michael S. Hansen, PhD Magnetic Resonance Technology Program National Institutes of Health, NHLBI Declaration of Financial Interests
Nuts & Bolts of Advanced Imaging Image Reconstruction Parallel Imaging Michael S. Hansen, PhD Magnetic Resonance Technology Program National Institutes of Health, NHLBI Declaration of Financial Interests
Collaborative Sparsity and Compressive MRI
 Modeling and Computation Seminar February 14, 2013 Table of Contents 1 T2 Estimation 2 Undersampling in MRI 3 Compressed Sensing 4 Model-Based Approach 5 From L1 to L0 6 Spatially Adaptive Sparsity MRI
Modeling and Computation Seminar February 14, 2013 Table of Contents 1 T2 Estimation 2 Undersampling in MRI 3 Compressed Sensing 4 Model-Based Approach 5 From L1 to L0 6 Spatially Adaptive Sparsity MRI
Sparse Reconstruction / Compressive Sensing
 Sparse Reconstruction / Compressive Sensing Namrata Vaswani Department of Electrical and Computer Engineering Iowa State University Namrata Vaswani Sparse Reconstruction / Compressive Sensing 1/ 20 The
Sparse Reconstruction / Compressive Sensing Namrata Vaswani Department of Electrical and Computer Engineering Iowa State University Namrata Vaswani Sparse Reconstruction / Compressive Sensing 1/ 20 The
Slide 1. Technical Aspects of Quality Control in Magnetic Resonance Imaging. Slide 2. Annual Compliance Testing. of MRI Systems.
 Slide 1 Technical Aspects of Quality Control in Magnetic Resonance Imaging Slide 2 Compliance Testing of MRI Systems, Ph.D. Department of Radiology Henry Ford Hospital, Detroit, MI Slide 3 Compliance Testing
Slide 1 Technical Aspects of Quality Control in Magnetic Resonance Imaging Slide 2 Compliance Testing of MRI Systems, Ph.D. Department of Radiology Henry Ford Hospital, Detroit, MI Slide 3 Compliance Testing
CoE4TN3 Medical Image Processing
 CoE4TN3 Medical Image Processing Image Restoration Noise Image sensor might produce noise because of environmental conditions or quality of sensing elements. Interference in the image transmission channel.
CoE4TN3 Medical Image Processing Image Restoration Noise Image sensor might produce noise because of environmental conditions or quality of sensing elements. Interference in the image transmission channel.
Super-resolution Reconstruction of Fetal Brain MRI
 Super-resolution Reconstruction of Fetal Brain MRI Ali Gholipour and Simon K. Warfield Computational Radiology Laboratory Children s Hospital Boston, Harvard Medical School Worshop on Image Analysis for
Super-resolution Reconstruction of Fetal Brain MRI Ali Gholipour and Simon K. Warfield Computational Radiology Laboratory Children s Hospital Boston, Harvard Medical School Worshop on Image Analysis for
Role of Parallel Imaging in High Field Functional MRI
 Role of Parallel Imaging in High Field Functional MRI Douglas C. Noll & Bradley P. Sutton Department of Biomedical Engineering, University of Michigan Supported by NIH Grant DA15410 & The Whitaker Foundation
Role of Parallel Imaging in High Field Functional MRI Douglas C. Noll & Bradley P. Sutton Department of Biomedical Engineering, University of Michigan Supported by NIH Grant DA15410 & The Whitaker Foundation
Multi-slice CT Image Reconstruction Jiang Hsieh, Ph.D.
 Multi-slice CT Image Reconstruction Jiang Hsieh, Ph.D. Applied Science Laboratory, GE Healthcare Technologies 1 Image Generation Reconstruction of images from projections. textbook reconstruction advanced
Multi-slice CT Image Reconstruction Jiang Hsieh, Ph.D. Applied Science Laboratory, GE Healthcare Technologies 1 Image Generation Reconstruction of images from projections. textbook reconstruction advanced
ComputerLab: compressive sensing and application to MRI
 Compressive Sensing, 207-8 ComputerLab: compressive sensing and application to MRI Aline Roumy This computer lab addresses the implementation and analysis of reconstruction algorithms for compressive sensing.
Compressive Sensing, 207-8 ComputerLab: compressive sensing and application to MRI Aline Roumy This computer lab addresses the implementation and analysis of reconstruction algorithms for compressive sensing.
A Lagrange method based L-curve for image restoration
 Journal of Physics: Conference Series OPEN ACCESS A Lagrange method based L-curve for image restoration To cite this article: G Landi 2013 J. Phys.: Conf. Ser. 464 012011 View the article online for updates
Journal of Physics: Conference Series OPEN ACCESS A Lagrange method based L-curve for image restoration To cite this article: G Landi 2013 J. Phys.: Conf. Ser. 464 012011 View the article online for updates
Algebraic Iterative Methods for Computed Tomography
 Algebraic Iterative Methods for Computed Tomography Per Christian Hansen DTU Compute Department of Applied Mathematics and Computer Science Technical University of Denmark Per Christian Hansen Algebraic
Algebraic Iterative Methods for Computed Tomography Per Christian Hansen DTU Compute Department of Applied Mathematics and Computer Science Technical University of Denmark Per Christian Hansen Algebraic
Calculating the Distance Map for Binary Sampled Data
 MITSUBISHI ELECTRIC RESEARCH LABORATORIES http://www.merl.com Calculating the Distance Map for Binary Sampled Data Sarah F. Frisken Gibson TR99-6 December 999 Abstract High quality rendering and physics-based
MITSUBISHI ELECTRIC RESEARCH LABORATORIES http://www.merl.com Calculating the Distance Map for Binary Sampled Data Sarah F. Frisken Gibson TR99-6 December 999 Abstract High quality rendering and physics-based
Parallel Imaging. Marcin.
 Parallel Imaging Marcin m.jankiewicz@gmail.com Parallel Imaging initial thoughts Over the last 15 years, great progress in the development of pmri methods has taken place, thereby producing a multitude
Parallel Imaging Marcin m.jankiewicz@gmail.com Parallel Imaging initial thoughts Over the last 15 years, great progress in the development of pmri methods has taken place, thereby producing a multitude
G Practical Magnetic Resonance Imaging II Sackler Institute of Biomedical Sciences New York University School of Medicine. Compressed Sensing
 G16.4428 Practical Magnetic Resonance Imaging II Sackler Institute of Biomedical Sciences New York University School of Medicine Compressed Sensing Ricardo Otazo, PhD ricardo.otazo@nyumc.org Compressed
G16.4428 Practical Magnetic Resonance Imaging II Sackler Institute of Biomedical Sciences New York University School of Medicine Compressed Sensing Ricardo Otazo, PhD ricardo.otazo@nyumc.org Compressed
Redundancy Encoding for Fast Dynamic MR Imaging using Structured Sparsity
 Redundancy Encoding for Fast Dynamic MR Imaging using Structured Sparsity Vimal Singh and Ahmed H. Tewfik Electrical and Computer Engineering Dept., The University of Texas at Austin, USA Abstract. For
Redundancy Encoding for Fast Dynamic MR Imaging using Structured Sparsity Vimal Singh and Ahmed H. Tewfik Electrical and Computer Engineering Dept., The University of Texas at Austin, USA Abstract. For
Classification of Subject Motion for Improved Reconstruction of Dynamic Magnetic Resonance Imaging
 1 CS 9 Final Project Classification of Subject Motion for Improved Reconstruction of Dynamic Magnetic Resonance Imaging Feiyu Chen Department of Electrical Engineering ABSTRACT Subject motion is a significant
1 CS 9 Final Project Classification of Subject Motion for Improved Reconstruction of Dynamic Magnetic Resonance Imaging Feiyu Chen Department of Electrical Engineering ABSTRACT Subject motion is a significant
Phase Difference Reconstruction. Outline
 Advanced MRI Phase Difference Reconstruction Faik Can MERAL Outline Introduction Quantitative Description Arctangent operation ATAN2 Phased-Array Multiple Coil Data Correction of Predictable Phase Errors
Advanced MRI Phase Difference Reconstruction Faik Can MERAL Outline Introduction Quantitative Description Arctangent operation ATAN2 Phased-Array Multiple Coil Data Correction of Predictable Phase Errors
Algebraic Iterative Methods for Computed Tomography
 Algebraic Iterative Methods for Computed Tomography Per Christian Hansen DTU Compute Department of Applied Mathematics and Computer Science Technical University of Denmark Per Christian Hansen Algebraic
Algebraic Iterative Methods for Computed Tomography Per Christian Hansen DTU Compute Department of Applied Mathematics and Computer Science Technical University of Denmark Per Christian Hansen Algebraic
Partial k-space Reconstruction
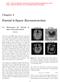 Chapter 2 Partial k-space Reconstruction 2.1 Motivation for Partial k- Space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position, and hence
Chapter 2 Partial k-space Reconstruction 2.1 Motivation for Partial k- Space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position, and hence
Improved 3D image plane parallel magnetic resonance imaging (pmri) method
 B. Wu, R. P. Millane, R. Watts, P. J. Bones, Improved 3D Image Plane Parallel Magnetic Resonance Imaging (pmri) Method, Proceedings of Image and Vision Computing New Zealand 2007, pp. 311 316, Hamilton,
B. Wu, R. P. Millane, R. Watts, P. J. Bones, Improved 3D Image Plane Parallel Magnetic Resonance Imaging (pmri) Method, Proceedings of Image and Vision Computing New Zealand 2007, pp. 311 316, Hamilton,
Partial k-space Recconstruction
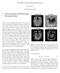 Partial k-space Recconstruction John Pauly September 29, 2005 1 Motivation for Partial k-space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position,
Partial k-space Recconstruction John Pauly September 29, 2005 1 Motivation for Partial k-space Reconstruction a) Magnitude b) Phase In theory, most MRI images depict the spin density as a function of position,
MRI image formation 8/3/2016. Disclosure. Outlines. Chen Lin, PhD DABR 3. Indiana University School of Medicine and Indiana University Health
 MRI image formation Indiana University School of Medicine and Indiana University Health Disclosure No conflict of interest for this presentation 2 Outlines Data acquisition Spatial (Slice/Slab) selection
MRI image formation Indiana University School of Medicine and Indiana University Health Disclosure No conflict of interest for this presentation 2 Outlines Data acquisition Spatial (Slice/Slab) selection
03 - Reconstruction. Acknowledgements: Olga Sorkine-Hornung. CSCI-GA Geometric Modeling - Spring 17 - Daniele Panozzo
 3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
3 - Reconstruction Acknowledgements: Olga Sorkine-Hornung Geometry Acquisition Pipeline Scanning: results in range images Registration: bring all range images to one coordinate system Stitching/ reconstruction:
XI Signal-to-Noise (SNR)
 XI Signal-to-Noise (SNR) Lecture notes by Assaf Tal n(t) t. Noise. Characterizing Noise Noise is a random signal that gets added to all of our measurements. In D it looks like this: while in D
XI Signal-to-Noise (SNR) Lecture notes by Assaf Tal n(t) t. Noise. Characterizing Noise Noise is a random signal that gets added to all of our measurements. In D it looks like this: while in D
2 Michael E. Leventon and Sarah F. F. Gibson a b c d Fig. 1. (a, b) Two MR scans of a person's knee. Both images have high resolution in-plane, but ha
 Model Generation from Multiple Volumes using Constrained Elastic SurfaceNets Michael E. Leventon and Sarah F. F. Gibson 1 MIT Artificial Intelligence Laboratory, Cambridge, MA 02139, USA leventon@ai.mit.edu
Model Generation from Multiple Volumes using Constrained Elastic SurfaceNets Michael E. Leventon and Sarah F. F. Gibson 1 MIT Artificial Intelligence Laboratory, Cambridge, MA 02139, USA leventon@ai.mit.edu
Recovery of Piecewise Smooth Images from Few Fourier Samples
 Recovery of Piecewise Smooth Images from Few Fourier Samples Greg Ongie*, Mathews Jacob Computational Biomedical Imaging Group (CBIG) University of Iowa SampTA 2015 Washington, D.C. 1. Introduction 2.
Recovery of Piecewise Smooth Images from Few Fourier Samples Greg Ongie*, Mathews Jacob Computational Biomedical Imaging Group (CBIG) University of Iowa SampTA 2015 Washington, D.C. 1. Introduction 2.
Introduction to Topics in Machine Learning
 Introduction to Topics in Machine Learning Namrata Vaswani Department of Electrical and Computer Engineering Iowa State University Namrata Vaswani 1/ 27 Compressed Sensing / Sparse Recovery: Given y :=
Introduction to Topics in Machine Learning Namrata Vaswani Department of Electrical and Computer Engineering Iowa State University Namrata Vaswani 1/ 27 Compressed Sensing / Sparse Recovery: Given y :=
3 Interior Point Method
 3 Interior Point Method Linear programming (LP) is one of the most useful mathematical techniques. Recent advances in computer technology and algorithms have improved computational speed by several orders
3 Interior Point Method Linear programming (LP) is one of the most useful mathematical techniques. Recent advances in computer technology and algorithms have improved computational speed by several orders
THE STEP BY STEP INTERACTIVE GUIDE
 COMSATS Institute of Information Technology, Islamabad PAKISTAN A MATLAB BASED INTERACTIVE GRAPHICAL USER INTERFACE FOR ADVANCE IMAGE RECONSTRUCTION ALGORITHMS IN MRI Medical Image Processing Research
COMSATS Institute of Information Technology, Islamabad PAKISTAN A MATLAB BASED INTERACTIVE GRAPHICAL USER INTERFACE FOR ADVANCE IMAGE RECONSTRUCTION ALGORITHMS IN MRI Medical Image Processing Research
Investigating Mixed-Integer Hulls using a MIP-Solver
 Investigating Mixed-Integer Hulls using a MIP-Solver Matthias Walter Otto-von-Guericke Universität Magdeburg Joint work with Volker Kaibel (OvGU) Aussois Combinatorial Optimization Workshop 2015 Outline
Investigating Mixed-Integer Hulls using a MIP-Solver Matthias Walter Otto-von-Guericke Universität Magdeburg Joint work with Volker Kaibel (OvGU) Aussois Combinatorial Optimization Workshop 2015 Outline
Signal and Noise in Complex-Valued SENSE MR Image Reconstruction
 Signal and Noise in omplex-valued SENSE M mage econstruction Daniel B. owe, Ph.D. (Joint with ain P. Bruce) Associate Professor omputational Sciences Program Department of Mathematics, Statistics, and
Signal and Noise in omplex-valued SENSE M mage econstruction Daniel B. owe, Ph.D. (Joint with ain P. Bruce) Associate Professor omputational Sciences Program Department of Mathematics, Statistics, and
1. Show that the rectangle of maximum area that has a given perimeter p is a square.
 Constrained Optimization - Examples - 1 Unit #23 : Goals: Lagrange Multipliers To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
Constrained Optimization - Examples - 1 Unit #23 : Goals: Lagrange Multipliers To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
Weighted-CS for reconstruction of highly under-sampled dynamic MRI sequences
 Weighted- for reconstruction of highly under-sampled dynamic MRI sequences Dornoosh Zonoobi and Ashraf A. Kassim Dept. Electrical and Computer Engineering National University of Singapore, Singapore E-mail:
Weighted- for reconstruction of highly under-sampled dynamic MRI sequences Dornoosh Zonoobi and Ashraf A. Kassim Dept. Electrical and Computer Engineering National University of Singapore, Singapore E-mail:
Compressed Sensing Algorithm for Real-Time Doppler Ultrasound Image Reconstruction
 Mathematical Modelling and Applications 2017; 2(6): 75-80 http://www.sciencepublishinggroup.com/j/mma doi: 10.11648/j.mma.20170206.14 ISSN: 2575-1786 (Print); ISSN: 2575-1794 (Online) Compressed Sensing
Mathematical Modelling and Applications 2017; 2(6): 75-80 http://www.sciencepublishinggroup.com/j/mma doi: 10.11648/j.mma.20170206.14 ISSN: 2575-1786 (Print); ISSN: 2575-1794 (Online) Compressed Sensing
An Iterative Approach for Reconstruction of Arbitrary Sparsely Sampled Magnetic Resonance Images
 An Iterative Approach for Reconstruction of Arbitrary Sparsely Sampled Magnetic Resonance Images Hamed Pirsiavash¹, Mohammad Soleymani², Gholam-Ali Hossein-Zadeh³ ¹Department of electrical engineering,
An Iterative Approach for Reconstruction of Arbitrary Sparsely Sampled Magnetic Resonance Images Hamed Pirsiavash¹, Mohammad Soleymani², Gholam-Ali Hossein-Zadeh³ ¹Department of electrical engineering,
arxiv: v2 [physics.med-ph] 22 Jul 2014
![arxiv: v2 [physics.med-ph] 22 Jul 2014 arxiv: v2 [physics.med-ph] 22 Jul 2014](/thumbs/83/87658058.jpg) Multichannel Compressive Sensing MRI Using Noiselet Encoding arxiv:1407.5536v2 [physics.med-ph] 22 Jul 2014 Kamlesh Pawar 1,2,3, Gary Egan 4, and Jingxin Zhang 1,5,* 1 Department of Electrical and Computer
Multichannel Compressive Sensing MRI Using Noiselet Encoding arxiv:1407.5536v2 [physics.med-ph] 22 Jul 2014 Kamlesh Pawar 1,2,3, Gary Egan 4, and Jingxin Zhang 1,5,* 1 Department of Electrical and Computer
Blind Image Deblurring Using Dark Channel Prior
 Blind Image Deblurring Using Dark Channel Prior Jinshan Pan 1,2,3, Deqing Sun 2,4, Hanspeter Pfister 2, and Ming-Hsuan Yang 3 1 Dalian University of Technology 2 Harvard University 3 UC Merced 4 NVIDIA
Blind Image Deblurring Using Dark Channel Prior Jinshan Pan 1,2,3, Deqing Sun 2,4, Hanspeter Pfister 2, and Ming-Hsuan Yang 3 1 Dalian University of Technology 2 Harvard University 3 UC Merced 4 NVIDIA
Steen Moeller Center for Magnetic Resonance research University of Minnesota
 Steen Moeller Center for Magnetic Resonance research University of Minnesota moeller@cmrr.umn.edu Lot of material is from a talk by Douglas C. Noll Department of Biomedical Engineering Functional MRI Laboratory
Steen Moeller Center for Magnetic Resonance research University of Minnesota moeller@cmrr.umn.edu Lot of material is from a talk by Douglas C. Noll Department of Biomedical Engineering Functional MRI Laboratory
MODEL-based recovery of images from noisy and sparse. MoDL: Model Based Deep Learning Architecture for Inverse Problems
 1 MoDL: Model Based Deep Learning Architecture for Inverse Problems Hemant K. Aggarwal, Member, IEEE, Merry P. Mani, and Mathews Jacob, Senior Member, IEEE arxiv:1712.02862v3 [cs.cv] 10 Aug 2018 Abstract
1 MoDL: Model Based Deep Learning Architecture for Inverse Problems Hemant K. Aggarwal, Member, IEEE, Merry P. Mani, and Mathews Jacob, Senior Member, IEEE arxiv:1712.02862v3 [cs.cv] 10 Aug 2018 Abstract
arxiv: v3 [math.na] 14 Jun 2018
![arxiv: v3 [math.na] 14 Jun 2018 arxiv: v3 [math.na] 14 Jun 2018](/thumbs/92/110495339.jpg) LAP: A LINEARIZE AND PROJECT METHOD FOR SOLVING INVERSE PROBLEMS WITH COUPLED VARIABLES JAMES L. HERRING, JAMES G. NAGY, AND LARS RUTHOTTO arxiv:1705.09992v3 [math.na] 14 Jun 2018 Abstract. Many inverse
LAP: A LINEARIZE AND PROJECT METHOD FOR SOLVING INVERSE PROBLEMS WITH COUPLED VARIABLES JAMES L. HERRING, JAMES G. NAGY, AND LARS RUTHOTTO arxiv:1705.09992v3 [math.na] 14 Jun 2018 Abstract. Many inverse
Computer Vision 2. SS 18 Dr. Benjamin Guthier Professur für Bildverarbeitung. Computer Vision 2 Dr. Benjamin Guthier
 Computer Vision 2 SS 18 Dr. Benjamin Guthier Professur für Bildverarbeitung Computer Vision 2 Dr. Benjamin Guthier 1. IMAGE PROCESSING Computer Vision 2 Dr. Benjamin Guthier Content of this Chapter Non-linear
Computer Vision 2 SS 18 Dr. Benjamin Guthier Professur für Bildverarbeitung Computer Vision 2 Dr. Benjamin Guthier 1. IMAGE PROCESSING Computer Vision 2 Dr. Benjamin Guthier Content of this Chapter Non-linear
Bindel, Spring 2015 Numerical Analysis (CS 4220) Figure 1: A blurred mystery photo taken at the Ithaca SPCA. Proj 2: Where Are My Glasses?
 Figure 1: A blurred mystery photo taken at the Ithaca SPCA. Proj 2: Where Are My Glasses? 1 Introduction The image in Figure 1 is a blurred version of a picture that I took at the local SPCA. Your mission
Figure 1: A blurred mystery photo taken at the Ithaca SPCA. Proj 2: Where Are My Glasses? 1 Introduction The image in Figure 1 is a blurred version of a picture that I took at the local SPCA. Your mission
Lucy Phantom MR Grid Evaluation
 Lucy Phantom MR Grid Evaluation Anil Sethi, PhD Loyola University Medical Center, Maywood, IL 60153 November 2015 I. Introduction: The MR distortion grid, used as an insert with Lucy 3D QA phantom, is
Lucy Phantom MR Grid Evaluation Anil Sethi, PhD Loyola University Medical Center, Maywood, IL 60153 November 2015 I. Introduction: The MR distortion grid, used as an insert with Lucy 3D QA phantom, is
Parallel Magnetic Resonance Imaging (pmri): How Does it Work, and What is it Good For?
 Parallel Magnetic Resonance Imaging (pmri): How Does it Work, and What is it Good For? Nathan Yanasak, Ph.D. Chair, AAPM TG118 Department of Radiology Georgia Regents University Overview Phased-array coils
Parallel Magnetic Resonance Imaging (pmri): How Does it Work, and What is it Good For? Nathan Yanasak, Ph.D. Chair, AAPM TG118 Department of Radiology Georgia Regents University Overview Phased-array coils
P-LORAKS: Low-Rank Modeling of Local k-space Neighborhoods with Parallel Imaging Data
 P-LORAKS: Low-Rank Modeling of Local k-space Neighborhoods with Parallel Imaging Data Justin P. Haldar 1, Jingwei Zhuo 2 1 Electrical Engineering, University of Southern California, Los Angeles, CA, USA
P-LORAKS: Low-Rank Modeling of Local k-space Neighborhoods with Parallel Imaging Data Justin P. Haldar 1, Jingwei Zhuo 2 1 Electrical Engineering, University of Southern California, Los Angeles, CA, USA
Compressed Sensing Reconstructions for Dynamic Contrast Enhanced MRI
 1 Compressed Sensing Reconstructions for Dynamic Contrast Enhanced MRI Kevin T. Looby klooby@stanford.edu ABSTRACT The temporal resolution necessary for dynamic contrast enhanced (DCE) magnetic resonance
1 Compressed Sensing Reconstructions for Dynamic Contrast Enhanced MRI Kevin T. Looby klooby@stanford.edu ABSTRACT The temporal resolution necessary for dynamic contrast enhanced (DCE) magnetic resonance
Iterative Algorithms I: Elementary Iterative Methods and the Conjugate Gradient Algorithms
 Iterative Algorithms I: Elementary Iterative Methods and the Conjugate Gradient Algorithms By:- Nitin Kamra Indian Institute of Technology, Delhi Advisor:- Prof. Ulrich Reude 1. Introduction to Linear
Iterative Algorithms I: Elementary Iterative Methods and the Conjugate Gradient Algorithms By:- Nitin Kamra Indian Institute of Technology, Delhi Advisor:- Prof. Ulrich Reude 1. Introduction to Linear
Characterizing Improving Directions Unconstrained Optimization
 Final Review IE417 In the Beginning... In the beginning, Weierstrass's theorem said that a continuous function achieves a minimum on a compact set. Using this, we showed that for a convex set S and y not
Final Review IE417 In the Beginning... In the beginning, Weierstrass's theorem said that a continuous function achieves a minimum on a compact set. Using this, we showed that for a convex set S and y not
6 credits. BMSC-GA Practical Magnetic Resonance Imaging II
 BMSC-GA 4428 - Practical Magnetic Resonance Imaging II 6 credits Course director: Ricardo Otazo, PhD Course description: This course is a practical introduction to image reconstruction, image analysis
BMSC-GA 4428 - Practical Magnetic Resonance Imaging II 6 credits Course director: Ricardo Otazo, PhD Course description: This course is a practical introduction to image reconstruction, image analysis
Accelerated MRI Techniques: Basics of Parallel Imaging and Compressed Sensing
 Accelerated MRI Techniques: Basics of Parallel Imaging and Compressed Sensing Peng Hu, Ph.D. Associate Professor Department of Radiological Sciences PengHu@mednet.ucla.edu 310-267-6838 MRI... MRI has low
Accelerated MRI Techniques: Basics of Parallel Imaging and Compressed Sensing Peng Hu, Ph.D. Associate Professor Department of Radiological Sciences PengHu@mednet.ucla.edu 310-267-6838 MRI... MRI has low
Computer Graphics : Bresenham Line Drawing Algorithm, Circle Drawing & Polygon Filling
 Computer Graphics : Bresenham Line Drawing Algorithm, Circle Drawing & Polygon Filling Downloaded from :www.comp.dit.ie/bmacnamee/materials/graphics/006- Contents In today s lecture we ll have a loo at:
Computer Graphics : Bresenham Line Drawing Algorithm, Circle Drawing & Polygon Filling Downloaded from :www.comp.dit.ie/bmacnamee/materials/graphics/006- Contents In today s lecture we ll have a loo at:
Lagrange multipliers October 2013
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 1 1 3/2 Example: Optimization
MRI Physics II: Gradients, Imaging
 MRI Physics II: Gradients, Imaging Douglas C., Ph.D. Dept. of Biomedical Engineering University of Michigan, Ann Arbor Magnetic Fields in MRI B 0 The main magnetic field. Always on (0.5-7 T) Magnetizes
MRI Physics II: Gradients, Imaging Douglas C., Ph.D. Dept. of Biomedical Engineering University of Michigan, Ann Arbor Magnetic Fields in MRI B 0 The main magnetic field. Always on (0.5-7 T) Magnetizes
HST.583 Functional Magnetic Resonance Imaging: Data Acquisition and Analysis Fall 2008
 MIT OpenCourseWare http://ocw.mit.edu HST.583 Functional Magnetic Resonance Imaging: Data Acquisition and Analysis Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
MIT OpenCourseWare http://ocw.mit.edu HST.583 Functional Magnetic Resonance Imaging: Data Acquisition and Analysis Fall 2008 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.
Geometric Representations. Stelian Coros
 Geometric Representations Stelian Coros Geometric Representations Languages for describing shape Boundary representations Polygonal meshes Subdivision surfaces Implicit surfaces Volumetric models Parametric
Geometric Representations Stelian Coros Geometric Representations Languages for describing shape Boundary representations Polygonal meshes Subdivision surfaces Implicit surfaces Volumetric models Parametric
In SigmaPlot, a restricted but useful version of the global fit problem can be solved using the Global Fit Wizard.
 Global Fitting Problem description Global fitting (related to Multi-response onlinear Regression) is a process for fitting one or more fit models to one or more data sets simultaneously. It is a generalization
Global Fitting Problem description Global fitting (related to Multi-response onlinear Regression) is a process for fitting one or more fit models to one or more data sets simultaneously. It is a generalization
Five Dimensional Interpolation:exploring different Fourier operators
 Five Dimensional Interpolation:exploring different Fourier operators Daniel Trad CREWES-University of Calgary Summary Five-Dimensional interpolation has become a very popular method to pre-condition data
Five Dimensional Interpolation:exploring different Fourier operators Daniel Trad CREWES-University of Calgary Summary Five-Dimensional interpolation has become a very popular method to pre-condition data
Lagrange multipliers 14.8
 Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
Lagrange multipliers 14.8 14 October 2013 Example: Optimization with constraint. Example: Find the extreme values of f (x, y) = x + 2y on the ellipse 3x 2 + 4y 2 = 3. 3/2 Maximum? 1 1 Minimum? 3/2 Idea:
NIH Public Access Author Manuscript Magn Reson Med. Author manuscript; available in PMC 2014 June 23.
 NIH Public Access Author Manuscript Published in final edited form as: Magn Reson Med. 2008 September ; 60(3): 650 660. doi:10.1002/mrm.21679. Comparison of Parallel MRI Reconstruction Methods for Accelerated
NIH Public Access Author Manuscript Published in final edited form as: Magn Reson Med. 2008 September ; 60(3): 650 660. doi:10.1002/mrm.21679. Comparison of Parallel MRI Reconstruction Methods for Accelerated
Sparse wavelet expansions for seismic tomography: Methods and algorithms
 Sparse wavelet expansions for seismic tomography: Methods and algorithms Ignace Loris Université Libre de Bruxelles International symposium on geophysical imaging with localized waves 24 28 July 2011 (Joint
Sparse wavelet expansions for seismic tomography: Methods and algorithms Ignace Loris Université Libre de Bruxelles International symposium on geophysical imaging with localized waves 24 28 July 2011 (Joint
WHAT YOU SHOULD LEARN
 GRAPHS OF EQUATIONS WHAT YOU SHOULD LEARN Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs of equations. Find equations of and sketch graphs of
GRAPHS OF EQUATIONS WHAT YOU SHOULD LEARN Sketch graphs of equations. Find x- and y-intercepts of graphs of equations. Use symmetry to sketch graphs of equations. Find equations of and sketch graphs of
Module 4. K-Space Symmetry. Review. K-Space Review. K-Space Symmetry. Partial or Fractional Echo. Half or Partial Fourier HASTE
 MRES 7005 - Fast Imaging Techniques Module 4 K-Space Symmetry Review K-Space Review K-Space Symmetry Partial or Fractional Echo Half or Partial Fourier HASTE Conditions for successful reconstruction Interpolation
MRES 7005 - Fast Imaging Techniques Module 4 K-Space Symmetry Review K-Space Review K-Space Symmetry Partial or Fractional Echo Half or Partial Fourier HASTE Conditions for successful reconstruction Interpolation
A Model-Independent, Multi-Image Approach to MR Inhomogeneity Correction
 Tina Memo No. 2007-003 Published in Proc. MIUA 2007 A Model-Independent, Multi-Image Approach to MR Inhomogeneity Correction P. A. Bromiley and N.A. Thacker Last updated 13 / 4 / 2007 Imaging Science and
Tina Memo No. 2007-003 Published in Proc. MIUA 2007 A Model-Independent, Multi-Image Approach to MR Inhomogeneity Correction P. A. Bromiley and N.A. Thacker Last updated 13 / 4 / 2007 Imaging Science and
Crash-Starting the Simplex Method
 Crash-Starting the Simplex Method Ivet Galabova Julian Hall School of Mathematics, University of Edinburgh Optimization Methods and Software December 2017 Ivet Galabova, Julian Hall Crash-Starting Simplex
Crash-Starting the Simplex Method Ivet Galabova Julian Hall School of Mathematics, University of Edinburgh Optimization Methods and Software December 2017 Ivet Galabova, Julian Hall Crash-Starting Simplex
Efficient Use of Iterative Solvers in Nested Topology Optimization
 Efficient Use of Iterative Solvers in Nested Topology Optimization Oded Amir, Mathias Stolpe and Ole Sigmund Technical University of Denmark Department of Mathematics Department of Mechanical Engineering
Efficient Use of Iterative Solvers in Nested Topology Optimization Oded Amir, Mathias Stolpe and Ole Sigmund Technical University of Denmark Department of Mathematics Department of Mechanical Engineering
Compressed Sensing for Electron Tomography
 University of Maryland, College Park Department of Mathematics February 10, 2015 1/33 Outline I Introduction 1 Introduction 2 3 4 2/33 1 Introduction 2 3 4 3/33 Tomography Introduction Tomography - Producing
University of Maryland, College Park Department of Mathematics February 10, 2015 1/33 Outline I Introduction 1 Introduction 2 3 4 2/33 1 Introduction 2 3 4 3/33 Tomography Introduction Tomography - Producing
X-ray tomography. X-ray tomography. Applications in Science. X-Rays. Notes. Notes. Notes. Notes
 X-ray tomography Important application of the Fast Fourier transform: X-ray tomography. Also referred to as CAT scan (Computerized Axial Tomography) X-ray tomography This has revolutionized medical diagnosis.
X-ray tomography Important application of the Fast Fourier transform: X-ray tomography. Also referred to as CAT scan (Computerized Axial Tomography) X-ray tomography This has revolutionized medical diagnosis.
Iterative CT Reconstruction Using Curvelet-Based Regularization
 Iterative CT Reconstruction Using Curvelet-Based Regularization Haibo Wu 1,2, Andreas Maier 1, Joachim Hornegger 1,2 1 Pattern Recognition Lab (LME), Department of Computer Science, 2 Graduate School in
Iterative CT Reconstruction Using Curvelet-Based Regularization Haibo Wu 1,2, Andreas Maier 1, Joachim Hornegger 1,2 1 Pattern Recognition Lab (LME), Department of Computer Science, 2 Graduate School in
B023 Seismic Data Interpolation by Orthogonal Matching Pursuit
 B023 Seismic Data Interpolation by Orthogonal Matching Pursuit Y. Hollander* (Paradigm Geophysical), D. Kosloff (Paradigm Geophysical), Z. Koren (Paradigm Geophysical) & A. Bartana (Paradigm Geophysical)
B023 Seismic Data Interpolation by Orthogonal Matching Pursuit Y. Hollander* (Paradigm Geophysical), D. Kosloff (Paradigm Geophysical), Z. Koren (Paradigm Geophysical) & A. Bartana (Paradigm Geophysical)
Efficient Iterative Semi-supervised Classification on Manifold
 . Efficient Iterative Semi-supervised Classification on Manifold... M. Farajtabar, H. R. Rabiee, A. Shaban, A. Soltani-Farani Sharif University of Technology, Tehran, Iran. Presented by Pooria Joulani
. Efficient Iterative Semi-supervised Classification on Manifold... M. Farajtabar, H. R. Rabiee, A. Shaban, A. Soltani-Farani Sharif University of Technology, Tehran, Iran. Presented by Pooria Joulani
M R I Physics Course
 M R I Physics Course Multichannel Technology & Parallel Imaging Nathan Yanasak, Ph.D. Jerry Allison Ph.D. Tom Lavin, B.S. Department of Radiology Medical College of Georgia References: 1) The Physics of
M R I Physics Course Multichannel Technology & Parallel Imaging Nathan Yanasak, Ph.D. Jerry Allison Ph.D. Tom Lavin, B.S. Department of Radiology Medical College of Georgia References: 1) The Physics of
Machine Learning: Think Big and Parallel
 Day 1 Inderjit S. Dhillon Dept of Computer Science UT Austin CS395T: Topics in Multicore Programming Oct 1, 2013 Outline Scikit-learn: Machine Learning in Python Supervised Learning day1 Regression: Least
Day 1 Inderjit S. Dhillon Dept of Computer Science UT Austin CS395T: Topics in Multicore Programming Oct 1, 2013 Outline Scikit-learn: Machine Learning in Python Supervised Learning day1 Regression: Least
An Approximate Singular Value Decomposition of Large Matrices in Julia
 An Approximate Singular Value Decomposition of Large Matrices in Julia Alexander J. Turner 1, 1 Harvard University, School of Engineering and Applied Sciences, Cambridge, MA, USA. In this project, I implement
An Approximate Singular Value Decomposition of Large Matrices in Julia Alexander J. Turner 1, 1 Harvard University, School of Engineering and Applied Sciences, Cambridge, MA, USA. In this project, I implement
Super-resolution Reconstruction of Fetal Brain MRI
 Super-resolution Reconstruction of Fetal Brain MRI Ali Gholipour, Simon K. Warfield Children s Hospital Boston, Harvard Medical School 300 Longwood Ave. Boston MA 0115 USA ali.gholipour@childrens.harvard.edu,
Super-resolution Reconstruction of Fetal Brain MRI Ali Gholipour, Simon K. Warfield Children s Hospital Boston, Harvard Medical School 300 Longwood Ave. Boston MA 0115 USA ali.gholipour@childrens.harvard.edu,
Lecture Notes on Wave Optics (04/23/14) 2.71/2.710 Introduction to Optics Nick Fang
 .7/.70 Introduction to Optics Nic Fang Outline: Fresnel Diffraction The Depth of Focus and Depth of Field(DOF) Fresnel Zones and Zone Plates Holography A. Fresnel Diffraction For the general diffraction
.7/.70 Introduction to Optics Nic Fang Outline: Fresnel Diffraction The Depth of Focus and Depth of Field(DOF) Fresnel Zones and Zone Plates Holography A. Fresnel Diffraction For the general diffraction
Regional Phase Correction of Inversion-Recovery MR Images
 MAGNETIC RESONANCE IN MEDICINE 14,56-67 ( 1990) Regional Phase Correction of Inversion-Recovery MR Images JOSEPH A. BORRELLO, THOMAS L. CHENEVERT, AND ALEX M. AISEN Department of Radiology, University
MAGNETIC RESONANCE IN MEDICINE 14,56-67 ( 1990) Regional Phase Correction of Inversion-Recovery MR Images JOSEPH A. BORRELLO, THOMAS L. CHENEVERT, AND ALEX M. AISEN Department of Radiology, University
Lecture 4. Digital Image Enhancement. 1. Principle of image enhancement 2. Spatial domain transformation. Histogram processing
 Lecture 4 Digital Image Enhancement 1. Principle of image enhancement 2. Spatial domain transformation Basic intensity it tranfomation ti Histogram processing Principle Objective of Enhancement Image enhancement
Lecture 4 Digital Image Enhancement 1. Principle of image enhancement 2. Spatial domain transformation Basic intensity it tranfomation ti Histogram processing Principle Objective of Enhancement Image enhancement
IEEE TRANSACTIONS ON MEDICAL IMAGING 1. Robust Super-resolution Volume Reconstruction from Slice Acquisitions: Application to Fetal Brain MRI
 IEEE TRANSACTIONS ON MEDICAL IMAGING 1 Robust Super-resolution Volume Reconstruction from Slice Acquisitions: Application to Fetal Brain MRI Ali Gholipour, Judy A. Estroff, and Simon K. Warfield, Senior
IEEE TRANSACTIONS ON MEDICAL IMAGING 1 Robust Super-resolution Volume Reconstruction from Slice Acquisitions: Application to Fetal Brain MRI Ali Gholipour, Judy A. Estroff, and Simon K. Warfield, Senior
REDUCED ORDER MODELING IN MULTISPECTRAL PHOTOACOUSTIC TOMOGRAPHY
 REDUCED ORDER MODELING IN MULTISPECTRAL PHOTOACOUSTIC TOMOGRAPHY Arvind Saibaba Sarah Vallélian Statistical and Applied Mathematical Sciences Institute & North Carolina State University May 26, 2016 OUTLINE
REDUCED ORDER MODELING IN MULTISPECTRAL PHOTOACOUSTIC TOMOGRAPHY Arvind Saibaba Sarah Vallélian Statistical and Applied Mathematical Sciences Institute & North Carolina State University May 26, 2016 OUTLINE
Computer Vision I. Announcements. Fourier Tansform. Efficient Implementation. Edge and Corner Detection. CSE252A Lecture 13.
 Announcements Edge and Corner Detection HW3 assigned CSE252A Lecture 13 Efficient Implementation Both, the Box filter and the Gaussian filter are separable: First convolve each row of input image I with
Announcements Edge and Corner Detection HW3 assigned CSE252A Lecture 13 Efficient Implementation Both, the Box filter and the Gaussian filter are separable: First convolve each row of input image I with
Evaluation of Spectrum Mismatching using Spectrum Binning Approach for Statistical Polychromatic Reconstruction in CT
 Evaluation of Spectrum Mismatching using Spectrum Binning Approach for Statistical Polychromatic Reconstruction in CT Qiao Yang 1,4, Meng Wu 2, Andreas Maier 1,3,4, Joachim Hornegger 1,3,4, Rebecca Fahrig
Evaluation of Spectrum Mismatching using Spectrum Binning Approach for Statistical Polychromatic Reconstruction in CT Qiao Yang 1,4, Meng Wu 2, Andreas Maier 1,3,4, Joachim Hornegger 1,3,4, Rebecca Fahrig
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3
 A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
A TESSELLATION FOR ALGEBRAIC SURFACES IN CP 3 ANDREW J. HANSON AND JI-PING SHA In this paper we present a systematic and explicit algorithm for tessellating the algebraic surfaces (real 4-manifolds) F
Math 21a Tangent Lines and Planes Fall, What do we know about the gradient f? Tangent Lines to Curves in the Plane.
 Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Math 21a Tangent Lines and Planes Fall, 2016 What do we know about the gradient f? Tangent Lines to Curves in the Plane. 1. For each of the following curves, find the tangent line to the curve at the point
Student Exploration: Quadratics in Polynomial Form
 Name: Date: Student Exploration: Quadratics in Polynomial Form Vocabulary: axis of symmetry, parabola, quadratic function, vertex of a parabola Prior Knowledge Questions (Do these BEFORE using the Gizmo.)
Name: Date: Student Exploration: Quadratics in Polynomial Form Vocabulary: axis of symmetry, parabola, quadratic function, vertex of a parabola Prior Knowledge Questions (Do these BEFORE using the Gizmo.)
coding of various parts showing different features, the possibility of rotation or of hiding covering parts of the object's surface to gain an insight
 Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Three-Dimensional Object Reconstruction from Layered Spatial Data Michael Dangl and Robert Sablatnig Vienna University of Technology, Institute of Computer Aided Automation, Pattern Recognition and Image
Reconstruction in CT and relation to other imaging modalities
 Reconstruction in CT and relation to other imaging modalities Jørgen Arendt Jensen November 1, 2017 Center for Fast Ultrasound Imaging, Build 349 Department of Electrical Engineering Center for Fast Ultrasound
Reconstruction in CT and relation to other imaging modalities Jørgen Arendt Jensen November 1, 2017 Center for Fast Ultrasound Imaging, Build 349 Department of Electrical Engineering Center for Fast Ultrasound
Convex Optimization / Homework 2, due Oct 3
 Convex Optimization 0-725/36-725 Homework 2, due Oct 3 Instructions: You must complete Problems 3 and either Problem 4 or Problem 5 (your choice between the two) When you submit the homework, upload a
Convex Optimization 0-725/36-725 Homework 2, due Oct 3 Instructions: You must complete Problems 3 and either Problem 4 or Problem 5 (your choice between the two) When you submit the homework, upload a
WEIGHTED L1 AND L2 NORMS FOR IMAGE RECONSTRUCTION: FIRST CLINICAL RESULTS OF EIT LUNG VENTILATION DATA
 WEIGHTED L1 AND L2 NORMS FOR IMAGE RECONSTRUCTION: FIRST CLINICAL RESULTS OF EIT LUNG VENTILATION DATA PRESENTER: PEYMAN RAHMATI, PHD CANDIDATE, Biomedical Eng., Dept. of Systems and Computer Eng., Carleton
WEIGHTED L1 AND L2 NORMS FOR IMAGE RECONSTRUCTION: FIRST CLINICAL RESULTS OF EIT LUNG VENTILATION DATA PRESENTER: PEYMAN RAHMATI, PHD CANDIDATE, Biomedical Eng., Dept. of Systems and Computer Eng., Carleton
Outline Introduction Problem Formulation Proposed Solution Applications Conclusion. Compressed Sensing. David L Donoho Presented by: Nitesh Shroff
 Compressed Sensing David L Donoho Presented by: Nitesh Shroff University of Maryland Outline 1 Introduction Compressed Sensing 2 Problem Formulation Sparse Signal Problem Statement 3 Proposed Solution
Compressed Sensing David L Donoho Presented by: Nitesh Shroff University of Maryland Outline 1 Introduction Compressed Sensing 2 Problem Formulation Sparse Signal Problem Statement 3 Proposed Solution
Optimal Sampling Geometries for TV-Norm Reconstruction of fmri Data
 Optimal Sampling Geometries for TV-Norm Reconstruction of fmri Data Oliver M. Jeromin, Student Member, IEEE, Vince D. Calhoun, Senior Member, IEEE, and Marios S. Pattichis, Senior Member, IEEE Abstract
Optimal Sampling Geometries for TV-Norm Reconstruction of fmri Data Oliver M. Jeromin, Student Member, IEEE, Vince D. Calhoun, Senior Member, IEEE, and Marios S. Pattichis, Senior Member, IEEE Abstract
A Study of Nonlinear Approaches to Parallel Magnetic Resonance Imaging
 University of Wisconsin Milwaukee UWM Digital Commons Theses and Dissertations December 2012 A Study of Nonlinear Approaches to Parallel Magnetic Resonance Imaging Yuchou Chang University of Wisconsin-Milwaukee
University of Wisconsin Milwaukee UWM Digital Commons Theses and Dissertations December 2012 A Study of Nonlinear Approaches to Parallel Magnetic Resonance Imaging Yuchou Chang University of Wisconsin-Milwaukee
